1 Introduction
The fundamental principle of a directed line’s motion in connection with a solid body is referred to as the concept in spatial kinematics. This notion holds great importance in conventional differential geometry and has been the subject of extensive research by numerous scholars, as demonstrated by [1–7]. From a geometric perspective, the properties of and their offset surfaces have been analyzed in both Euclidean and non-Euclidean spaces. Bertrand curves were examined in the field of line-geometry by Ravani and Ku, revealing that can possess an infinite number of , similar to how a plane curve can possess an infinite number of mates [8]. Küçük and Gürsoy provided certain characterizations of related to the trajectory of by studying the relationships between the projection areas for the spherical curves of and their integral invariants [9]. Kasap and Kuruoğlu conducted an analysis of the integral invariants of the couple of in the Euclidean 3-space , as documented in [10]. By considering the orthonormal frame along striction curve of a ruled surface, Önder has defined slant ruled surfaces in the Euclidean 3-space [11]. Moreover, Kaya and Önder have studied the position vectors and some differential equation characterizations for slant ruled surfaces in the Euclidean 3-space [12–14]. They have also defined a new type of slant ruled surface as the Darboux slant ruled surface and characterized for this type of slant surfaces [15]. In [16], Önder introduced some characterizations for a non-null ruled surface to be a slant ruled surface in Minkowski 3-space . In their study, Kasap and Kuruoğlu investigated of in Minkowski 3-space , as documented in [17]. [18] demonstrated the involute–evolute offsets of . Orbay et al. began studying the Mannheim offsets of in [19]. Önder and Uğurlu conducted a study on the relationships between invariants of Mannheim offsets of . They also formulated many considerations for the development of these surface offsets [20, 21]. In view of the involute–evolute offsets of the ruled surface in [7], Şentürk and Yüce described the integral invariants of the involute–evolute offsets of s using the geodesic Frenet frame [22].
In recent times, Yoon has investigated the evolute offsets of in with a stationary Gaussian curvature and mean curvature [23]. A plethora of comprehensive treatises has been published on this subject, as demonstrated by the numerous written works, such as [24–27]. However, to the best of our knowledge, no prior work has focused on constructing of slant , utilizing the geometric attributes of the striction curve . Here, we intend to fill the gap in the existing literature.
In this paper, with the identification of slant curves, we treat the structure issue of the of a slant family in Minkowski 3-space . Therefore, we extend the parametrization of for any slant non-developable . Furthermore, we inquire into the ownerships of these surfaces and grant their distribution. Meanwhile, we extend some interpretative paradigms to display surfaces with their along mutual geodesic, line of curvature, and asymptotic curve. Our ramifications in this paper may be beneficial in any area that demands documentation around surfaces due to the descriptions supplying insights into surfaces theory.
2 Basic concepts
Let indicate the Minkowski 3-space [28, 29]. For vectors and in
is named the Lorentzian inner product. We also explain a vector
Since is an indefinite metric, recall that a vector can have one of three causal natures; it can be if or , timelike if , and null or lightlike if and . The norm of is explained by ; then, the hyperbolic and Lorentzian (de Sitter space) unit spheres are
and
2.1 Ruled surface
is a surface produced by a line mobile on a curve . The several locations of the line coined the producers or rulings of the surface. Such a surface, thus, has the ruled form [1–6]
such that ; . In this circumstance, the curve is the striction curve and is the arc length of the spherical non-null curve . If is not stationary or not null or null, then the Blaschke Frame for will be registered as
where are named the ruling, the central normal, and the central tangent, respectively. The Blaschke formula is from Equation 4
where is the spherical curvature of . In view of with signs , , and , is
, , and are titled the curvature parameters of . The geometrical view of these parameters is proved as follows: is the spherical curvature of the spherical image curve ; depicts the angle through the tangent of and the ruling of ; and is the distribution parameter of , from Equation 3 at the ruling .
In this study, we will meditate a non-developable nominated by . Then,
where is the Darboux vector from Equation 6, and
Therefore, a non-developable can be perceived as follows:
The unit normal vector is
Note that is identical with , which is the central normal at the striction point. The curvature axis of is from Equations 1, 2
Let be the radii of curvature through and . Then, from Equation 11
Definition 1. [16] In , a surface can be determined by the induced metric on it. Hence, a surface is called
surface iff the metric is Lorentzian metric.
surface iff the metric is a positive definite Riemannian metric.
Null surface iff the metric is null.
Corollary 1. The curvature , the torsion , and the geodesic curvature of fulfill that
Corollary 2. If is a specified, then is a Lorentzian circle.
Proof. Through Equation 13, we can see that , which is stationary, yields , and is stationary, which reveals is a Lorentzian circle (If ) or a Lorentzian great circle (when ).
Let’s state the Darboux frame ; let be the tangent unit to , is the surface unit normal along , and be the tangent unit to . Therefore, we can write
and
Let be the arc length of , that is, . Then, from Equations 14, 15 the Darboux formula is expressed as
where
, , and are the geodesic curvature, the normal curvature, and the geodesic torsion of , respectively. Therefore, using Equations 16, 17
1) is a geodesic curve iff ;
2) is a asymptotic curve iff ;
3) is a curvature line iff .
(a) if , then is a tangential developable, and
(b) if , then is a binormal surface, and
(c) if , then is a cone, and
Definition 2. [14] A ruled surface is named a slant ruled surface if all its rulings have a stationary angle with a definite line.
3 Bertrand offsets for slant surfaces
In this section, we contemplate and analyze the for slant . Then, a theory hassling to the theory of the Bertrand curves can be broadened for such surfaces.
In comparable with [30], a point will be heading an curvature axis of the curve; for all such that , but . Here, signalizes the tth derivative of with regard to . For the first curvature axis of, we find , and . So, is at least an curvature axis of . We now sign a height function , by . We set the notation for any specified point .
Proposition 1. Under the overhead presumptions, we capture the following:
i) will be specified in the first evaluation iff , that is,
for real numbers , and .
ii) will be specified in the second evaluation iff is the curvature axis of , that is,
iii) will be specified in the third evaluation iff is the curvature axis of , that is,
iv) will be specified in the fourth evaluation iff is the curvature axis of , that is,
Proof. For , we determine
So, we realize
for real numbers , , and , the consequence is evident.2- Derivation of Equation 18 displays that
By Equations 18–20, we determine
3- Differentiation of Equation 20 displays that
Thus, we gain
4- By corresponding debates, we can also determine
The proof is finished.
In view of Proposition 1, we determine
(a) The osculating circle of is displayed by
which are pointed via the situation that the osculating circle must have touch of at least third order at iff .
(b) The curve and the osculating circle have touched at least fourth order at iff and .
Through this method, by catching into meditation the curvature axes of , we can attain a concatenation of curvature axes , ,…, . The ownerships and the joint links via these curvature axes are much pleasant troubles. For example, it is facile to catch that if and , located at is specified relative to . At this position, the curvature axis is fixed up to second order and is a slant .
Theorem 1. A non-developable is a slant iff its geodesic curvature is fixed.
Definition 3. Let and be two non-developable ruled surfaces in . is entitled a of if there exists a bijection via their rulings such that and possess a reciprocal central normal at the conformable striction points.
Let be a of and is the of , as shown in Equations 7–9. Then, the surface can be allocated by
where
Here, is the distance through the proportional striction points of and . Through the differentiation of Equation 21 via and considering Equation 22, we assign
Since at the congruent striction points of and , we gain is fixed. Furthermore, given that is the angle among the rulings of and , that is,
By differentiation of Equation 23, we gain
Since , then we realize is fixed. Moreover, at the congruent striction points of and , we observe that . Then, by Equation 24
If (resp. ), then and are parallel (resp. oriented) offsets.
Theorem 2. The couple is fixed at the corresponding striction points of and .
It is apparent from Theorem 2 that a non-developable , frequently, has a binary infinity of . Every can be displayed by a fixed linear offset and a fixed-angle offset . Therefore, if is a of , then is also a of .
Let be the unit normal of . Then, as shown in Equation 10, we locate
where is the distribution parameter of .
The dissimilarity between the normal to a and its is apparent from Equations 10, 26. This demonstrates that the of a is often not a parallel offset. Therefore, the parallel circumstances through in view of can be exhibited by the following:
Theorem 3. and are parallel offsets iff , with , their Blaschke frames, being conformable.
Proof. Let , that is, and are parallel offsets. Then, by Equations 10, 26, we acquire
which is assumed true for any value , that is, , and .
Let the two events hold true, that is, and . Then, substituting them into using Equation 27, we acquire
which indicates that and are parallel offsets since the previous is a zero vector.
Using the same approach, but with a developable surface , we encounter the following:
Corollary 3. A developable and its developable are parallel offsets iff their Blaschke frames are identical.
Corollary 4. A developable and its non-developable cannot be parallel offsets.
Furthermore, we also detect
where
By takeoff , we locate using Equations 28, 29
This presents a new perspective of of surfaces, specifically focusing on their geodesic curvatures.
Theorem 4. and are surfaces iff Equation 30 is fulfilled.
Corollary 5. and are parallel offsets iff .
Corollary 6. and are oriented offsets iff .
For being fixed, from Equations 7, 12, we have the ODE, . In accordance with several algebraic manipulations, the solution is
where is fixed and . Then,
Therefore, from Equations 8, 30, 31, is expressed as
Hence, from Equations 9, 30–33, the slant is expressed as
Furthermore, by Equations 20, 25, 33, is expressed as
where and can control the shape of ; here, we will set , , , and .
3.1 Classifications of the slant and its
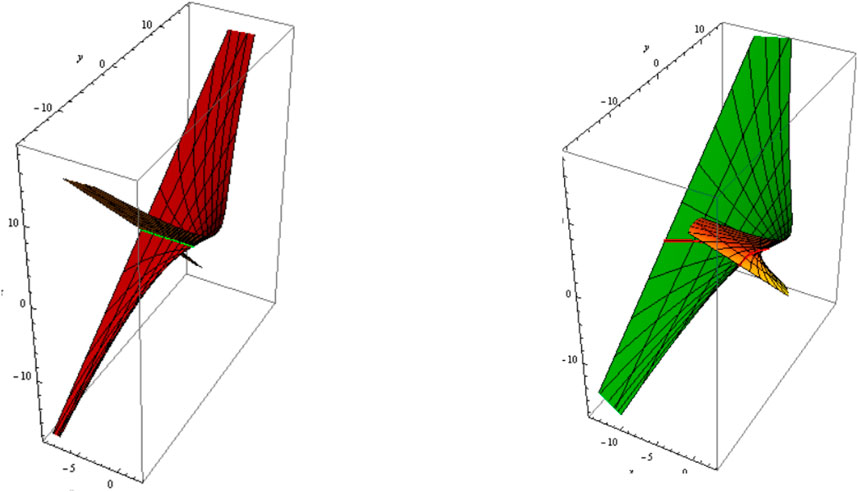
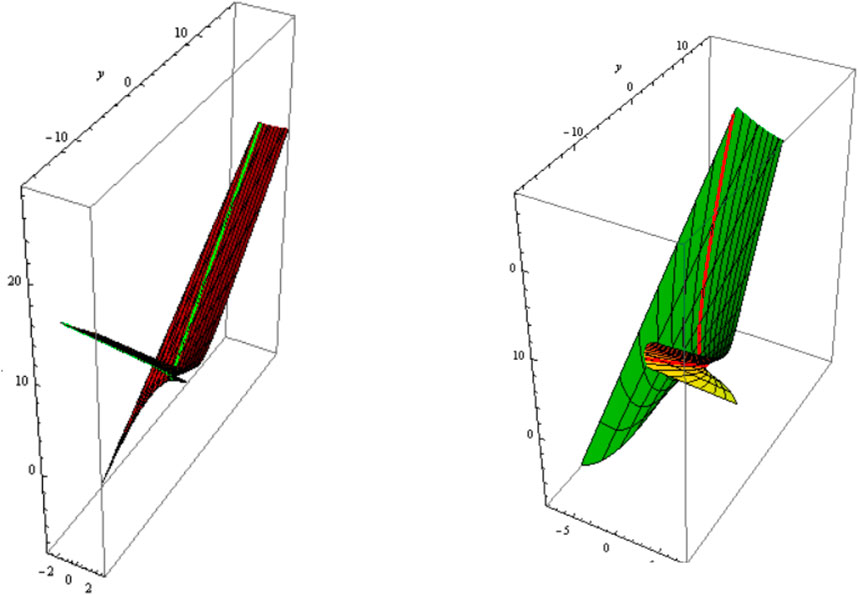
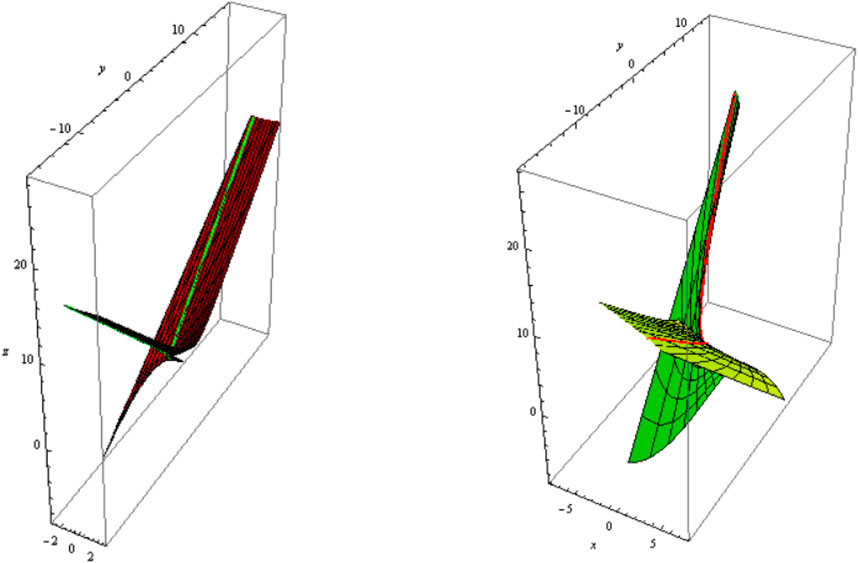
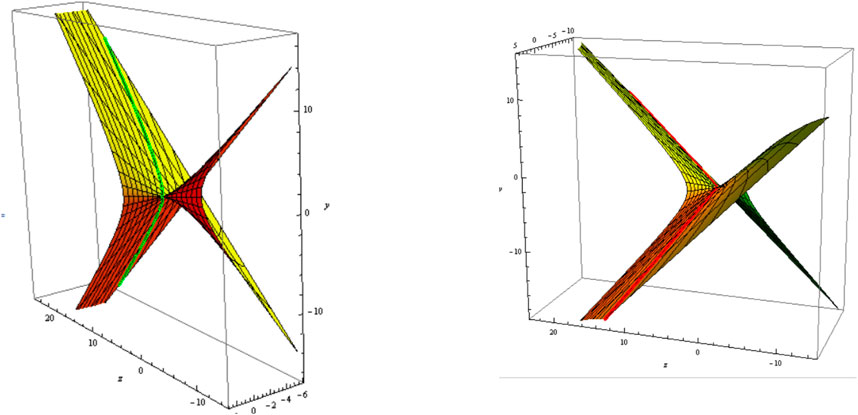
From Equations 34, 35, the slant and its can be distributed as follows:1) Let be a asymptotic curve, i.e., . The slant and its parallel (oriented) are shown in Figure 1 ;Figure 2; .
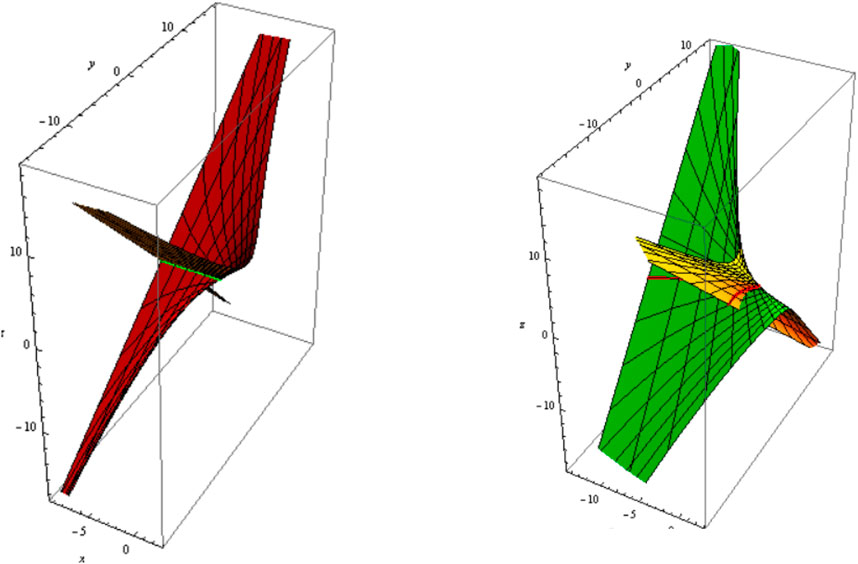
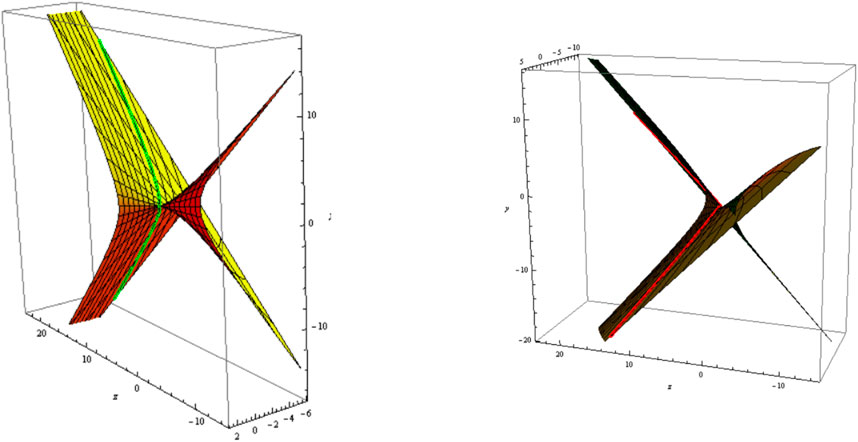
2) Let be a geodesic curve, i.e.,
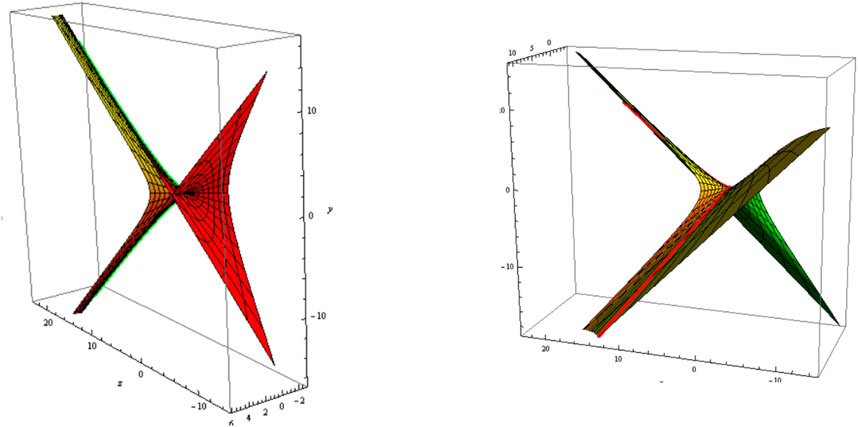
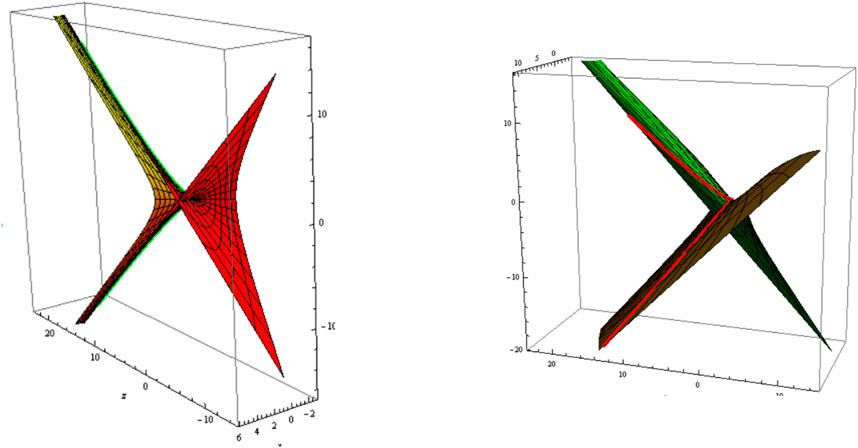
where is a real constant. The slant and its parallel (oriented) are shown in Figure 3 (Figure 4); and .
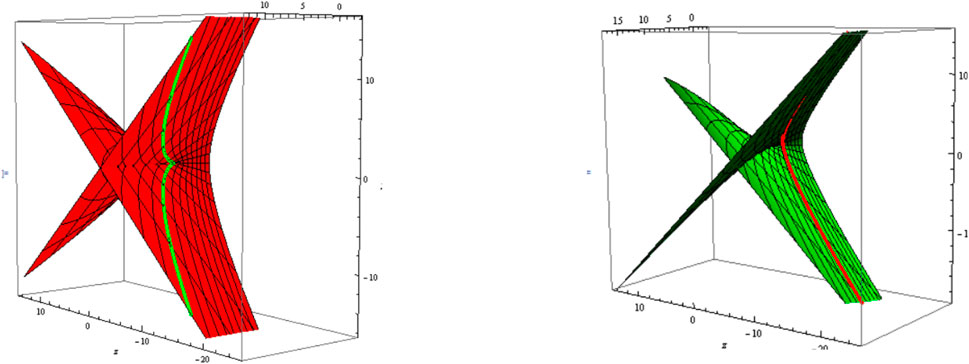
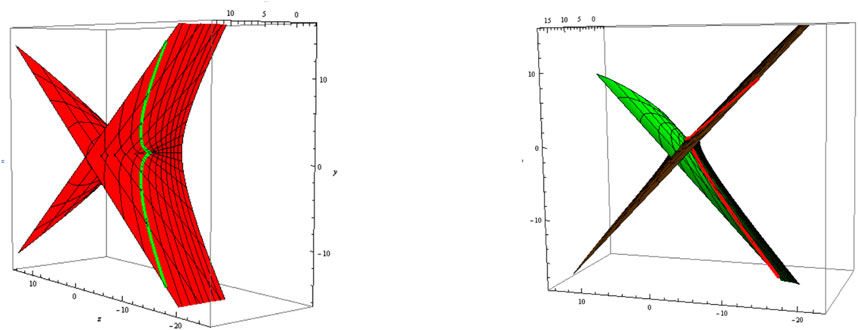
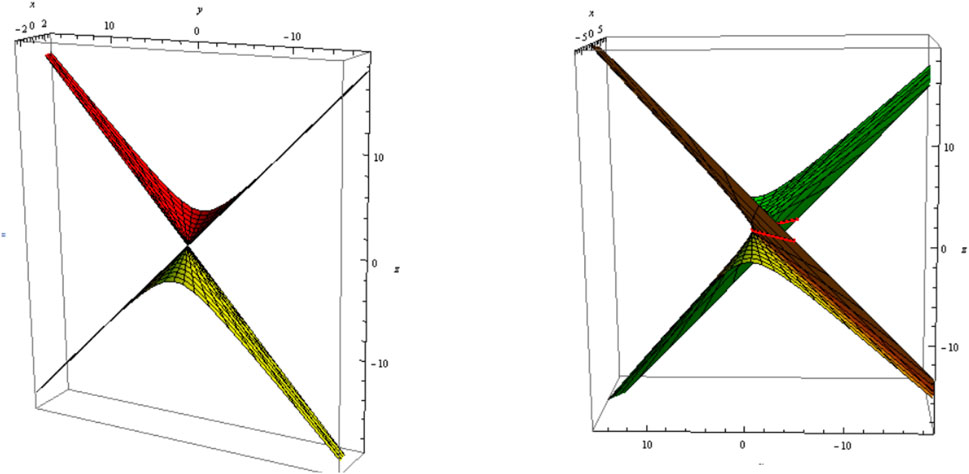
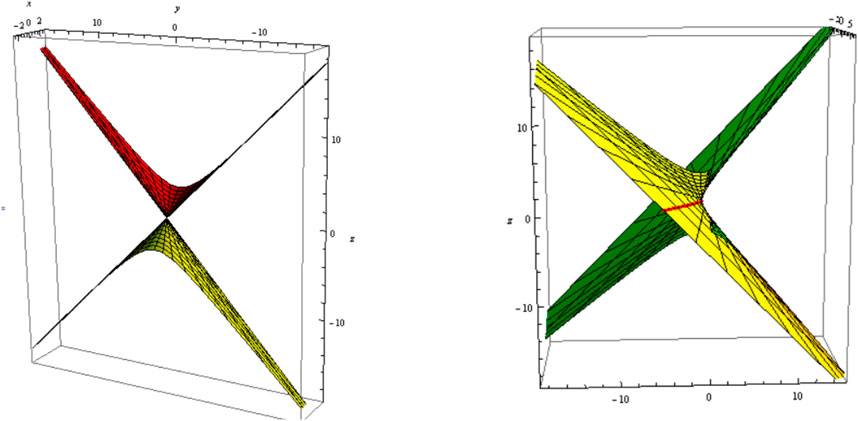
3) Let be a curvature line, i.e., . The slant and its parallel (oriented) are shown in Figure 5 (Figure 6); .
4) Let , i.e., be a tangential developable. The slant and its parallel (oriented) are shown in Figure 7 (Figure 8); .
5) Let , that is, be a binormal. The slant binormal and its parallel (oriented) are shown in Figure 9 (Figure 10); .
6) Let , that is, be a cone. The slant cone and its parallel (oriented) are shown in Figure 11 (Figure 12); .
4 Conclusion
This work explores the features of slant curves and develops and classifies slant surfaces and their in Minkowski 3-space using the Blaschke domain. Next, we construct contemporary surfaces in Lorentzian line space and determine their . In addition, we also obtain various groupings by a slant and its striction curve. These advancements are expected to enhance the usefulness of model-based manufacturing in mechanical outputs and geometric patterning. The authors intend to correlate this study across several domains and examine the classification of singularities, as identified in [31, 32].
Data availability statement
The original contributions presented in the study are included in the article/supplementary material; further inquiries can be directed to the corresponding author.
Author contributions
AA: conceptualization, data curation, formal analysis, funding acquisition, methodology, resources, writing–original draft, and writing–review and editing. RA-B: conceptualization, data curation, formal analysis, investigation, methodology, resources, supervision, validation, visualization, and writing–original draft.
Funding
The author(s) declare that financial support was received for the research, authorship, and/or publication of this article: Princess Nourah Bint Abdulrahman University Researchers Supporting Project number (PNURSP2024R337).
Conflict of interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Publisher’s note
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors, and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
References
1. Gugenheimer HW. Differential geometry. New York: Graw-Hill (1956). 162–9.
Google Scholar
2. Bottema O, Roth B. Theoretical kinematics. New York: North-Holland Press (1979).
Google Scholar
3. Karger A, Novak J. Space kinematics and lie groups. New York: Gordon and Breach Science Publishers (1985).
Google Scholar
4. Papaionnou SG, Kiritsis D. An application of Bertrand curves and surfaces to CAD/CAM. Computer Aided Des (1985) 17(8):348–52. doi:10.1016/0010-4485(85)90025-9
CrossRef Full Text | Google Scholar
5. Schaaf JA, Ravani B. Geometric continuity of ruled surfaces. Computer Aided Geometric Des (1998) 15:289–310. doi:10.1016/s0167-8396(97)00032-0
CrossRef Full Text | Google Scholar
6. Peternell M, Pottmann H, Ravani B. On the computational geometry of ruled surfaces. Comput.-Aided Des (1999) 31:17–32. doi:10.1016/s0010-4485(98)00077-3
CrossRef Full Text | Google Scholar
7. Pottman H, Wallner J. Computational line geometry. Berlin, Heidelberg: Springer-Verlag (2001).
Google Scholar
8. Ravani B, Ku TS. Bertrand offsets of ruled and developable surfaces. Computer Aided Des (1991) 23(2):145–52. doi:10.1016/0010-4485(91)90005-h
CrossRef Full Text | Google Scholar
10. Kasap E, Kuruoglu N. Integral invariants of the pairs of the Bertrand ruled surface. Bull Pure Appl Sci Sect E Math (2002) 21:37–44.
Google Scholar
11. Önder M. Slant ruled surfaces. Transnational J Pure Appl Mathematics (2018) 1(1):63–82.
Google Scholar
12. Kaya O, Önder M. Position vector of a developable h-slant ruled surfaces. TWMS J App Eng Math (2017) 7(2):322–31.
Google Scholar
13. Kaya O, Önder M. Position vector of a developable q-slant ruled surfaces. Korean J Math (2018) 26(4):545–59. doi:10.11568/kjm.2018.26.4.545
CrossRef Full Text | Google Scholar
14. Önder M. Onur Kaya, characterizations of slant ruled surfaces in the euclidean 3-space. Caspian J Math Sci (2017) 6(1):82–9. doi:10.22080/cjms.2017.1637
CrossRef Full Text | Google Scholar
15. Önder M. Onur Kaya, Darboux slant ruled surfaces. Azerbaijan J Mathematics (2015) 5(1):64–72.
Google Scholar
17. Kasap E, Kuruoglu N. The Bertrand offsets of ruled surfaces in R13. Acta Math Vietnam (2006) 31:39–48.
Google Scholar
18. Kasap E, Yuce S, Kuruoglu N. The involute-evolute offsets of ruled surfaces. Iranian J Sci Tech Transaction A (2009) 33:195–201.
Google Scholar
20. Önder M, Uğurlu HH. Frenet frames and invariants of timelike ruled surfaces. Ain Shams Eng J (2013) 4:507–13. doi:10.1016/j.asej.2012.10.003
CrossRef Full Text | Google Scholar
21. Önder M, Uğurlu HH. Spacelike regle yüzeylerin Frenet çatıları ve Frenet i̇nvaryantları. Dokuz Eylul University-Faculty Eng J Sci Eng (2017) 19(57):712–22. doi:10.21205/deufmd.2017195764
CrossRef Full Text | Google Scholar
22. Şentürk GY, Yüce S. Properties of integral invariants of the involute-evolute offsets of ruled surfaces. Int J Pure Appl Math (2015) 102:757–68. doi:10.12732/ijpam.v102i4.13
CrossRef Full Text | Google Scholar
23. Yoon DW. On the evolute offsets of ruled surfaces in Minkowski 3-space. Turk J Math (2016) 40(40):594–604. doi:10.3906/mat-1502-11
CrossRef Full Text | Google Scholar
24. Yıldırım H. Slant ruled surfaces and slant developable surfaces of spacelike curves in Lorentz-Minkowski 3-space. Filomat (2018) 32(14):4875–95. doi:10.2298/fil1814875y
CrossRef Full Text | Google Scholar
25. Alluhaibi N, Abdel-Baky RA, Naghi M. On the Bertrand offsets of timelike ruled surfaces in Minkowski 3-space. Symmetry (2022) 14(4):673. doi:10.3390/sym14040673
CrossRef Full Text | Google Scholar
26. Nazra S, Abdel-Baky RA. Bertrand offsets of ruled surfaces with Blaschke frame in Euclidean 3-space. Axioms (2023) 12:649. doi:10.3390/axioms12070649
CrossRef Full Text | Google Scholar
27. Mofarreh F, Abdel-Baky RA. Surface pencil pair interpolating Bertrand pair as common asymptotic curves in Euclidean 3-space. Mathematics (2023) 11(16):3495. doi:10.3390/math11163495
CrossRef Full Text | Google Scholar
28. Walrave J, Leuven KU. Curves and surfaces in Minkowski space. Leuven, Belgium: Faculty of Science (1995). Ph.D. Thesis.
Google Scholar
29. O’Neil B. Semi-riemannian geometry geometry, with applications to relativity. New York, NY, USA: Academic Press (1983).
Google Scholar
30. W Bruce J, Giblin PJ. Curves and singularities. 2nd ed. Cambridge: Cambridge University Press (1992).
Google Scholar
31. Almoneef A, Abdel-Baky RA. Singularity properties of spacelike circular surfaces. Symmetry (2023) 15:842. doi:10.3390/sym15040842
CrossRef Full Text | Google Scholar
32. Nazra S, Abdel-Baky RA. Singularities of non-lightlike developable surfaces in Minkowski 3-space. Mediterr J Math (2023) 20:45. doi:10.1007/s00009-022-02252-7
CrossRef Full Text | Google Scholar
 Areej A. Almoneef
Areej A. Almoneef Rashad A. Abdel-Baky
Rashad A. Abdel-Baky