- 1School of Computer Science and Technology, Anhui University, Hefei, Anhui, China
- 2College of Information and Network Engineering, Anhui Science and Technology University, Bengbu, Anhui, China
- 3College of Electronic and Optical Engineering and College of Flexible Electronics (Future Technology), Nanjing University of Posts and Telecommunications, Nanjing, Jiangsu, China
- 4Mechanical and Electrical Engineering College, Hainan University, Haikou, Hainan, China
The internal kink mode is one of the crucial factors affecting the stability of magnetically confined fusion devices. This paper explores the key features influencing the growth rate of internal kink modes using machine learning techniques such as Random Forest, Extreme Gradient Boosting (XGboost), Permutation, and SHapley Additive exPlanations (SHAP). We conduct an in-depth analysis of the significant physical mechanisms by which these key features impact the growth rate of internal kink modes. Numerical simulation data were used to train high-precision machine learning models, namely Random Forest and XGBoost, which achieved coefficients of determination values of 95.07% and 94.57%, respectively, demonstrating their capability to accurately predict the growth rate of internal kink modes. Based on these models, key feature analysis was systematically performed with Permutation and SHAP methods. The results indicate that resistance, pressure at the magnetic axis, viscosity, and plasma rotation are the primary features influencing the growth rate of internal kink modes. Specifically, resistance affects the evolution of internal kink modes by altering current distribution and magnetic field structure; pressure at the magnetic axis impacts the driving force of internal kink modes through the pressure gradient directly related to plasma stability; viscosity modifies the dynamic behavior of internal kink modes by regulating plasma flow; and plasma rotation introduces additional shear forces, affecting the stability and growth rate of internal kink modes. This paper describes the mechanisms by which these four key features influence the growth rate of internal kink modes, providing essential theoretical insights into the behavior of internal kink modes in magnetically confined fusion devices.
1 Introduction
In controlled nuclear fusion research, the stability of plasma is one of the core challenges for achieving long-term stable fusion discharges [1, 2]. The internal kink mode is a typical magnetohydrodynamic (MHD) instability that profoundly impacts the performance and safety of fusion devices [3, 4]. To achieve a more efficient and stable fusion reaction, it is crucial to deeply understand and control the growth of internal kink modes [5, 6]. This understanding not only helps to enhance the energy output efficiency of the fusion reaction but also prevents safety issues such as plasma disruptions caused by instabilities [7–13]. Therefore, identifying the key features influencing the growth of internal kink modes and elucidating their physical mechanisms has become a focal point of current fusion research [14, 15].
Existing research methods on internal kink modes mainly focus on the construction of theoretical models and numerical simulations [16, 17]. Theoretical models provide a fundamental explanation of plasma behavior, while numerical simulation methods offer distinct advantages in handling complex systems, exploring extreme conditions, and obtaining detailed internal information of the system [18, 19]. While these methods can simulate the dynamic behavior of internal kink modes, they often face issues of low accuracy or high computational complexity in determining the specific impact of various physical parameters on mode growth [20, 21]. Moreover, traditional methods frequently struggle to comprehensively consider the interactions among various factors and their combined effects on the growth of internal kink modes [22].
To better understand which physical parameters significantly affect the growth of internal kink modes, thereby optimizing reaction conditions and improving fusion efficiency, this paper employs machine learning-based methods for in-depth analysis. As a powerful data analysis tool, machine learning excels in handling complex multivariate relationships within intricate systems [23]. For instance, Shakil Ahmed et al. combined Random Forest and SHAP values to analyze feature importance in road traffic accident prediction models and identified two critical influencing factors [24]. Jaemin Seo et al. used deep reinforcement learning technology and multimodal data to achieve active control of tearing mode instabilities in the DIII-D fusion device, thus avoiding the occurrence of tearing modes [25]. Yu-Xing Li et al. employed Permutation to extract key features influencing ship radiated noise [26]. K.J. Montes et al. utilized semi-supervised learning algorithms to detect anomalous events in fusion discharges using datasets requiring minimal labeled data [27]. Yong-Geon Lee et al. proposed a method for calculating SHAP values incorporating the coefficient of determination and performed feature importance analysis for the Korean power system load forecasting model [28]. By training models to learn the underlying patterns in the data, machine learning techniques can accurately identify features that significantly impact the growth rate of internal kink modes [5, 29]. In this study, two commonly used machine learning models, Random Forest and XGBoost, were selected, and feature importance analysis was conducted using Permutation and SHAP methods. Ensemble learning methods like Random Forest and XGBoost can evaluate feature importance by constructing multiple decision trees, while methods such as Permutation and SHAP provide specific numerical values and interpretability of feature impacts [30].
This paper first employs numerical simulation data to train Random Forest and XGBoost models, achieving high-precision predictions of the growth rate of internal kink modes. Subsequently, feature importance analysis is conducted using Permutation and SHAP methods. The results indicate that resistance, pressure at the magnetic axis, viscosity, and rotation are the most significant features influencing the growth rate of internal kink modes. Resistance regulates the growth of internal kink modes by affecting current distribution and magnetic field structure; pressure at the magnetic axis creates a pressure gradient directly related to the degree of magnetic field twist; viscosity determines plasma fluidity, thereby impacting the stability of internal kink modes; and rotation influences the interaction between the flow field and the magnetic field by generating additional shear forces. These findings not only deepen the understanding of the growth mechanisms of internal kink modes but also provide robust data support for optimizing fusion reaction conditions.
The paper is organized as follows: Section 2 describes the fundamental principles of Random Forest, XGBoost, Permutation, and SHAP, providing theoretical support for subsequent feature analysis. Section 3 details the sources of training data, training methods, and evaluation criteria for the Random Forest and XGBoost models. Section 4 presents the performance of the Random Forest and XGBoost models, identifies the most significant features influencing the growth rate of internal kink modes, and discusses the underlying physical mechanisms in depth.
2 Feature importance analysis theory
In machine learning, feature importance analysis is a critical step for understanding models and enhancing predictive performance. Common methods for feature importance analysis include tree-based feature importance evaluation, permutation tests, Shapley value-based interpretation, model weight-based feature importance analysis, statistical test-based feature selection, and mutual information methods [31]. This study employs Random Forest and XGBoost, both of which are tree-based models that can naturally evaluate the importance of features by quantifying the change in impurity at split nodes. This method is intuitive and effective. Permutation tests assess feature importance by shuffling the values of features and observing changes in model performance, providing a straightforward reflection of the impact of features on model predictions. SHAP, based on Shapley values from cooperative game theory, considers feature interactions and offers a more detailed analysis of feature contributions, enhancing the interpretability of the model [32].
2.1 Random Forest
Random Forest is an ensemble learning method based on decision trees that conducts classification or regression through building multiple decision trees and combining their outputs [33]. In a Random Forest, each decision tree is independently trained on a randomly sampled subset of the training data and a randomly selected subset of features. This randomness helps reduce the model’s variance, thereby enhancing predictive accuracy and generalization capability. For classification tasks, Random Forest aggregates the classification results from all decision trees, selecting the most frequent class as the last prediction. In regression works, it typically averages the predictions from all decision trees. Due to its exceptional performance and ease of implementation, Random Forest has been widely applied to various machine learning tasks, including data classification, regression, and feature selection [34]. Additionally, Random Forest can offer variable importance assessment, aiding in the understanding of how data features impact prediction outcomes. Overall, Random Forest is a powerful and flexible machine learning algorithm [35].
The pseudocode for the Random Forest algorithm is as follows:
1. Input: Training data
2. Parameters: Number of trees (T), number of features (m) to consider for each split
3. Output: An ensemble of decision trees
4. For (t = 1) to (T):
i. Draw a bootstrap sample (D_t) from (D)
ii. Train a decision tree (h_t) on (D_t):
a. For each node in the tree:
a. Randomly select (m) features from the total (p) features
b. Select the best feature and split point among the (m) features based on a certain criterion (e.g., Gini impurity for classification or mean squared error for regression)
c. Split the node into two child nodes
b. Repeat until the stopping criterion is met (e.g., maximum depth or minimum number of samples in a node)
5. End For
6. For classification:
i. Output: Majority vote of the predictions from all decision trees
7. For regression:
i. Output: Average of the predictions from all decision trees
2.2 Extreme gradient boosting
XGBoost (Extreme Gradient Boosting) is an efficient gradient boosting machine learning method widely used for classification and regression tasks. It represents an optimized and enhanced version of the conventional Gradient Boosting Decision Tree (GBDT) algorithm. XGBoost iteratively adds new decision trees to correct the residuals of the previous models, thereby continuously improving model performance [36]. The core of XGBoost lies in its optimized objective function, which includes both the training loss and a regularization term. The objective function for the model at the (t)th iteration can be expressed as Equation 1:
XGBoost incorporates numerous optimizations, such as using approximate algorithms for selecting split points, supporting distributed computing, and memory optimization, allowing it to maintain high training efficiency even when handling large-scale datasets [37]. Additionally, XGBoost offers a flexible parameter tuning space, enabling users to achieve better model performance by modifying parameters such as learning rate, tree depth, and subsampling ratio. Overall, XGBoost has become an indispensable tool in the fields of machine learning and data science due to its exceptional performance and flexibility. It has demonstrated strong application potential and broad prospects both in industry and academia [38].
2.3 Permutation
Permutation is a powerful feature analysis method that quantifies the function of each feature to the model’s predictive performance. The fundamental principle of Permutation is to randomly shuffle the values of a special feature and observe the change in the model’s performance. If a feature is significant for the model’s predictions, shuffling its values will significantly degrade the model’s performance [39]. This approach allows for ranking the importance of each feature, thereby providing a better understanding of the model’s decision-making process. The importance of each feature can be quantified using the following formula 4:
where
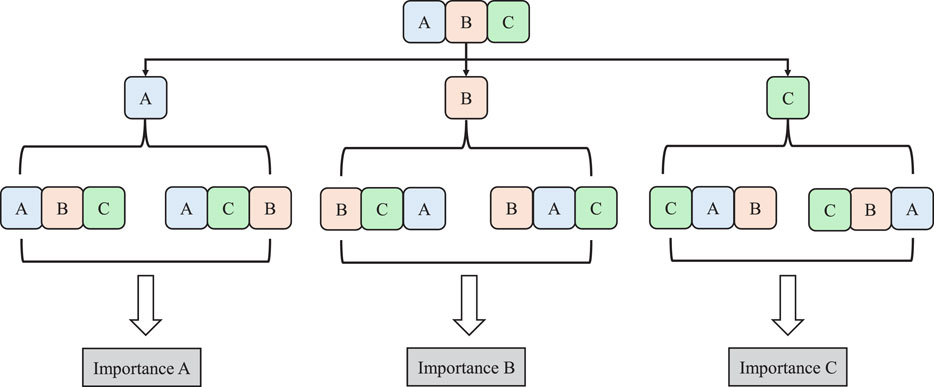
As illustrated in Figure 1, the principle of Permutation is depicted schematically. Specifically, the implementation steps of Permutation are as follows: First, a model is trained with the original dataset, and its capability metrics are recorded. Then, a specific feature is selected, and its values are randomly shuffled while maintaining other features unchanged. Next, the model’s efficiency is re-evaluated using the dataset with the shuffled feature. By comparing the performance metrics before and after shuffling, the influence of that feature on the model’s performance can be calculated. This operation is repeated for each feature in the dataset, resulting in a ranking of feature importance. The advantage of Permutation lies in its intuitiveness and generality. It can be applied to various machine learning models and is capable of handling different types of features, such as continuous and discrete features. Furthermore, the results of Permutation are easy to interpret, aiding in the understanding of the model’s decision boundaries and the interactions between features [40, 41].
2.4 SHapley additive exPlanations
SHAP is a feature analysis tool applied to interpret the forecast results of machine learning algorithms. SHAP is based on the Shapley value obtained from cooperative game theory, assigning a specific value to each feature to represent its contribution to the model’s prediction. The unique aspect of this method is that it considers interactions between features and provides a fair distribution of the prediction contribution [42]. The core idea of SHAP is to determine the Shapley value of each feature by calculating its contribution to the model’s prediction across all possible combinations of feature subsets. Although this process is computationally intensive, the SHAP library employs efficient algorithms to obtain results quickly in practical applications. Each feature’s Shapley value reflects its marginal contribution to the model’s prediction while accounting for the influence of all other features [43].
Using SHAP, one can determine the specific impact of each feature on individual predictions, aiding in understanding why the model makes certain predictions [44]. Additionally, SHAP offers global feature importance analysis by aggregating Shapley values from multiple predictions, which reveals each feature’s impact on the model’s performance across the entire dataset. The merit of SHAP comes from its ability to provide detailed feature analysis, considering both individual feature impacts and interactions between features. This makes SHAP a powerful tool that helps researchers, data scientists, and machine learning engineers better understand and explain the prediction outcome of complex machine learning algorithms [45].
The calculation formula for SHAP values is as Equation 5:
where
The steps for computing SHAP values are as follows:
(1) Initialization: For each feature, initialize the SHAP value to zero.
(2) Iterate Combinations: Traverse all possible feature combinations.
(3) Compute Marginal Contribution: For each feature combination, calculate the change in the model’s prediction after adding the new feature.
(4) Assign Shapley Value: Distribute the marginal contribution equally among the features in the combination based on the Shapley value formula.
(5) Accumulate SHAP Values: Accumulate the computed SHAP values to the total SHAP value for each feature.
3 Materials and methods
To determine the key features influencing the growth rate of internal kink modes based on machine learning, it is necessary first to identify the range of features to be studied. Subsequently, a dataset comprising various features and the corresponding growth rates of internal kink modes is constructed, followed by training the relevant machine learning models. This section introduces the dataset utilized for training the machine learning models, the training process, and the evaluation methods.
3.1 Data source
The internal kink mode is the result of the combined effects of different driving features, with the growth rate serving as a numerical indicator of its rate of change. For convenience, this paper collectively refers to the various features influencing the growth rate of the internal kink mode as input features, and the growth rate of the internal kink mode as the output feature.
3.1.1 Input features
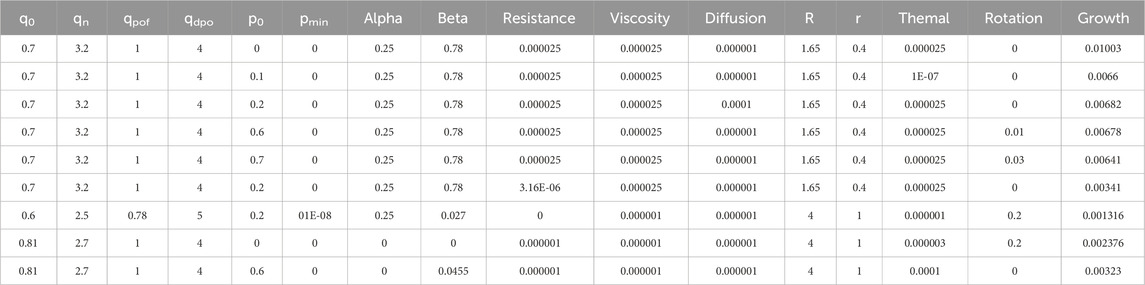
During our simulation studies on internal kink modes based on the magnetohydrodynamic code CLT (Ci-Liu-Ti), we identified 15 features that need to be predefined in the code [46]. These 15 features are used as input features in our analysis. The 15 input features are as follows:
1) Central safety factor q0, dimensionless parameter, unitless, range: 0.6–0.81.
2) Boundary safety factor qn, dimensionless parameter, unitless, range: 2.5–3.2.
3) Derivative of the central safety factor with respect to the magnetic flux qpof,
4) Derivative of the boundary safety factor with respect to the magnetic flux qdpo,
5) Central pressure p0, unit: pascals, range: 0–0.99.
6) Boundary pressure pmin, unit: pascals, range: 0–e−8, tend to zero in the research.
7) Pressure profile parameter alpha,
8) Another pressure profile parameter beta,
9) Resistivity resistance, unitless, range: 0–e−4.
10) Viscosity coefficient viscosity, unitless, range: e−7–e−4.
11) Diffusion coefficient diffusion, unitless, range: e−7–e−4.
12) Major radius R, unit:meter, range: 1.65–4.
13) Minor radius r, unit:meter, range: 0.4–1.
14) Perpendicular thermal conductivity coefficient thermal, unitless, range: e−7 – e−4.
15) Rotation rotation,
In above formulas,
These 15 input features constitute the subjects of this study, and various methods are employed to comprehensively assess which features significantly impact the growth rate of internal kink modes. A number of papers on the numerical simulation of internal torsion modes have been published in the public domain, including several papers using the CLT as a simulation tool. Aggregation of these existing data and appropriate modifications to some of the variables form the values of all the input parameters [47, 48]. Due to the substantial computational resources and time needed for a single numerical simulation of an internal kink mode instance, we have so far accumulated data on 196 instances of input features [49]. A subset of these feature data is shown in Table 1.
3.1.2 Output feature
Different combinations of input features ultimately yield varying growth rates of internal kink modes [50]. In this study, the output feature is the growth rate of the internal kink mode. The growth rate of the internal kink mode refers to the development rate of the internal magnetic deformation process within a tokamak device [51]. Table 1 presents data on the growth rates of internal kink modes under the influence of different input features. To more effectively control the nuclear fusion reaction, it is crucial to identify which features have a critical impact on the growth rate of internal kink modes [52, 53]. By recognizing these key influencing factors, reaction parameters such as plasma resistance, safety factors, and pressure gradients can be adjusted to optimize reaction conditions and improve fusion efficiency [54].
All the input features and output feature data are from the CLT program [55, 56]. The numerical simulation programme CLT is based on a one-fluid model and ignores mass differences between electrons and ions as well as multi-fluid effects. It ignores plasma displacement currents in solving the MHD system of equations and calculates only perturbations rather than complete physical quantities. In addition, we assume that the pressure tends to zero at the edge of the tokamak device.
3.2 Model training
This paper employs Random Forest and XGBoost models to analyze the importance of input features for internal kink modes. To ensure accurate feature importance analysis, these models must first be trained to achieve high performance. During the machine learning model training process, appropriate model hyperparameters must be selected, and suitable methods must be utilized to evaluate model performance. The input and output feature data summarized in the Section 3.1 are used to train the Random Forest and XGBoost models. Random Forest and XGBoost models were both trained and tested with the Scikit-learn function library using Python programming language.
3.2.1 Data preprocess
The dataset is preprocessed to ensure there are no missing values in either the input or output features. Ensuring the completeness of model inputs can be achieved by imputing or removing missing data, while detecting and handling outliers prevents the model from overfitting to a few extreme data points. Different features may have varying units or ranges, which can affect the model’s convergence speed or lead to certain features disproportionately influencing the results. Normalization or standardization can place all features within the same scale, thereby enhancing the efficiency and effectiveness of model training. Since Random Forest and XGBoost are tree-based models and are insensitive to the distances between data points, normalization is not required.
Eighty percent of the data is employed to train the model, while the rest of twenty percent is applied to evaluate model performance. The training set (80%) is used during the learning process of the model, where the model iteratively updates its parameters to identify patterns within the data. However, strong performance on the training set alone does not guarantee the model will perform well on unseen data. This phenomenon is known as overfitting, where the model excels on the training set but performs poorly on validation or real-world applications. Therefore, it is crucial to assess the model’s generalization capability by testing it on previously unseen data. The testing set (20%) is employed after the training process to evaluate the model’s performance, allowing for monitoring of how well the model handles new data and guiding further optimization. Such a division helps prevent overfitting and ensures the model’s ability to handle data beyond the training set.
3.2.2 Hyperparameters tuning
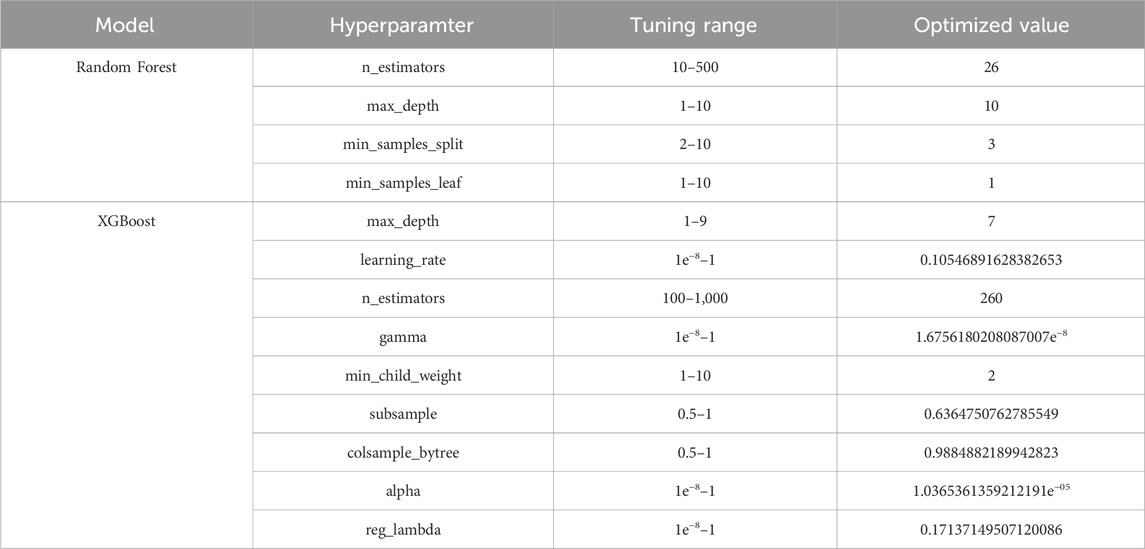
Suitable hyperparameters are chosen. Determining hyperparameters during the training of machine learning models is crucial, as they largely affect the model’s performance and convergence speed. Unlike model parameters, hyperparameters are values set before training and cannot be directly learned from the data. Hyperparameters determine the model’s complexity, learning ability, and generalization capacity. General hyperparameter optimization ways include grid search, random search, and Bayesian optimization. A proper choice of hyperparameters can significantly improve model performance, making their optimization a key step in enhancing the effectiveness of machine learning models. This study selects Random Forest and XGBoost methods as the algorithms for feature importance evaluation, and hyperparameters are adjusted to ensure model performance. For instance, for the Random Forest model, parameters such as the amount of trees and their depth are adjusted, while for the XGBoost model, hyperparameters including learning rate, number of trees, and their depth are optimized. During hyperparameter selection, the Optuna hyperparameter tuning tool is used to determine the best parameter combination. Hyperparameters of Random Forest and XGBoost are optimized with the automated tool Optuna, which are showed in Table 2. Optuna combines different hyperparameter configurations and uses the training set to train the model, subsequently calculating the prediction error. The hyperparameters used by the model with the smallest prediction error are considered the optimal result, and the corresponding model performance is deemed the best.
3.2.3 Model performance evaluation
Specific metrics are required for model performance evaluation; this study uses the coefficient of determination (R2) and the root mean square error (RMSE) to assess model performance. The formulas for these metrics are as Equations 6, 7:
Where
4 Results and discussions
This paper conducts a feature importance analysis of factors influencing the growth rate of internal kink modes using Random Forest, XGBoost, Permutation, and SHAP methods. This section presents the performance of the Random Forest and XGBoost algorithms in predicting the growth rate of internal kink modes, identifies the features that significantly impact the growth rate, and discusses their underlying physical mechanisms.
4.1 Model performance
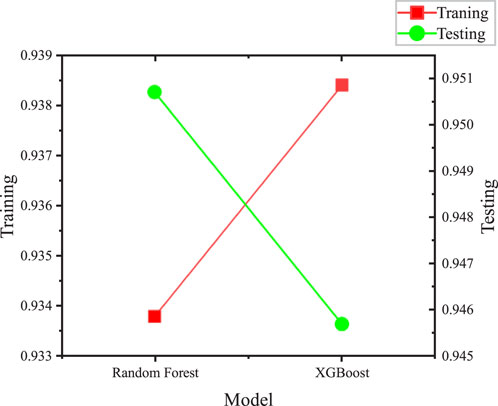
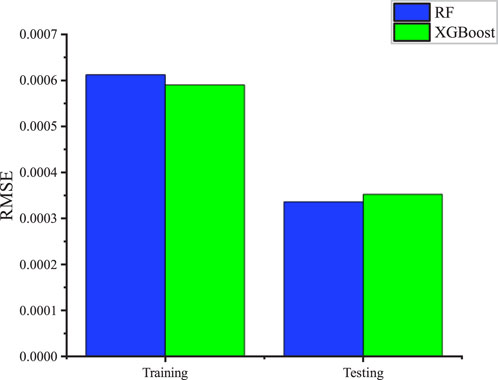
The conclusions drawn from the analysis of features influencing the growth rate of internal kink modes are only reliable when using highly performant Random Forest and XGBoost models. The dataset compiled from simulation data was used to train both models, which demonstrated excellent performance. The Random Forest model achieved a R2 of 0.9338 and a RMSE of 0.000611 on the training set; on the test set, it achieved a R2 of 0.9507 and a RMSE of 0.000336. The XGBoost model obtained a R2 of 0.9384 and a RMSE of 0.000589 on the training set, and a R2 of 0.9457 and a RMSE of 0.000352 on the test set.
Figure 2 illustrates the R2 values for the Random Forest and XGBoost models on both the training and test sets, showing that both models achieved very high accuracy. During the training phase, XGBoost performed slightly better, whereas, in the testing phase, the Random Forest model excelled. Figure 3 shows the RMSE distribution for both models, indicating that XGBoost had a smaller RMSE during training, while Random Forest performed better during testing. The performance differences between the two models were minimal. Overall, both models achieved very high R2 values and very low RMSE values, indicating that they are well-suited for feature importance analysis.
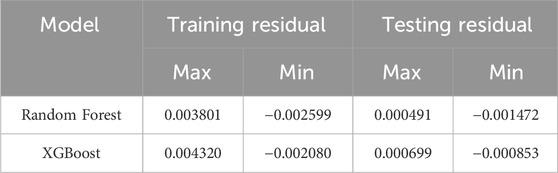
In Figure 4, the residual analysis during the training and testing phases indicates that the residual values are largely close to zero, demonstrating an ideal fit of the model. This suggests that both models exhibit high accuracy in predicting the growth rate of intrinsic kink modes, achieving an almost perfect fit to the data. Furthermore, the near-zero residual values imply that the models are capable of capturing the relationship between features and growth rates well during the training phase, while maintaining similar performance in the testing phase, reflecting strong generalization ability. In Table 3, the analysis of the maximum and minimum residuals in both the training and testing phases reveals a narrow range of residual fluctuations, further confirming the model’s robustness against outliers and noise. This is particularly critical for predicting the growth rate of intrinsic kink modes, as this physical phenomenon is subject to complex interactions among multiple factors, which can introduce data noise. The residual analysis of both the Random Forest and XGBoost models validates their effectiveness in handling data variability, providing a solid foundation for subsequent feature importance analysis.

Figure 4. (A) Random Forest model residuals during training; (B) Random Forest model residuals during testing; (C) XGBoost model residuals during training; (D) XGBoost model residuals during testing.
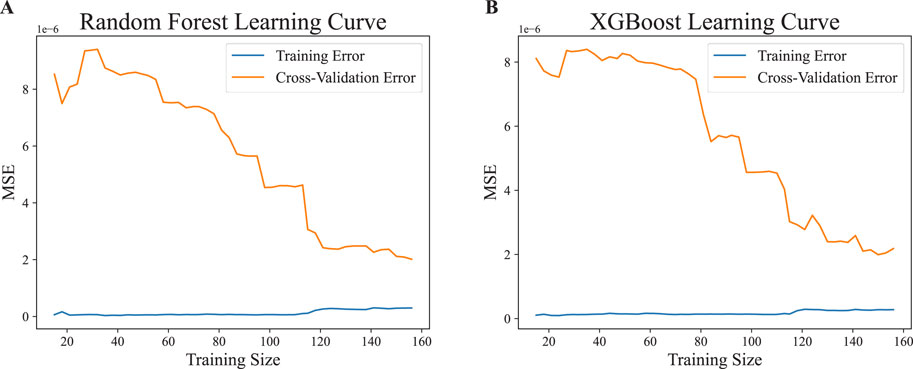
Figure 5 presents the learning curves of both models during the training phase. It can be observed that the residuals remained at a low level throughout the training, indicating that the models were well-fitted to the training data and effectively captured the features influencing the growth rate of the internal kink mode. Furthermore, the cross-validation results demonstrated that as the dataset size increased, the model errors gradually decreased and eventually converged to a relatively stable state. This suggests that the models’ learning capabilities improved with the expansion of the training dataset, enhancing their generalization performance. During cross-validation, both Random Forest and XGBoost exhibited a consistent trend of error reduction, further validating the robustness and reliability of these models in addressing this type of problem. Based on these results, it can be confirmed that the selected model architecture and feature processing methods were appropriate, laying the foundation for subsequent feature importance analysis using methods such as Permutation and SHAP, and providing strong support for identifying key features influencing the growth rate of the internal kink mode.
4.2 Key feature determination
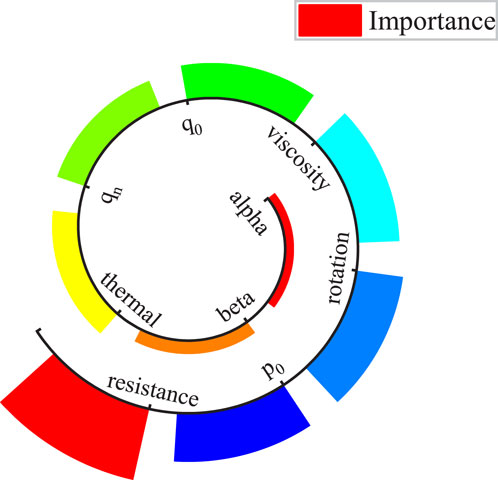
Once the Random Forest and XGBoost models are trained, they can be used to analyze the features that influence the growth rate of internal kink modes. Both Random Forest and XGBoost have built-in feature importance analysis tools, which can directly output results once the model training is complete. During the study, it was found that the influence of the least significant five of the 15 input features on the growth rate of internal kink modes was negligible. Therefore, only the top 10 most important features are presented, excluding the five features with the least impact. Figure 6 shows the feature importance analysis results from the Random Forest model, while Figure 7 shows the results from the XGBoost model. The results reveal significant discrepancies in the ranking of feature importance between the two models. According to the Random Forest algorithm, the 5 features with the greatest impact on the growth rate of internal kink modes are resistance, pressure at the magnetic axis, viscosity, rotation, and perpendicular thermal conductivity. In contrast, XGBoost identifies resistance, pressure at the magnetic axis, rotation, viscosity, and the central safety factor as the most influential. For features with a smaller impact on the growth rate of internal kink modes, the ranking provided by the two models also differs. The datasets for both models were split in the same way during training and tested using the same data, indicating that the differences in feature importance results arise from the models themselves rather than the data. While both Random Forest and XGBoost are tree-based models, their construction and optimization objectives differ. Random Forest improves accuracy and controls overfitting by averaging results from multiple decision trees, whereas XGBoost uses a gradient boosting framework to optimize the loss function, focusing more on the model’s generalization ability. The inherent randomness in the models, such as tree construction and feature selection in Random Forest, can also contribute to the inconsistency in results.
Next, Permutation and SHAP methods are employed to analyze the features influencing the growth rate of internal kink modes. Since both methods need to be combined with trained machine learning models, they are used in conjunction with the Random Forest and XGBoost models, respectively. The results are shown in Figures 8, 9. Figure 8A presents the feature importance obtained from the Permutation method combined with the Random Forest model. It indicates that resistance, viscosity, rotation, and pressure at the magnetic axis significantly impact the growth rate of internal kink modes, while the influence of other features is minimal. Figure 8B shows the results of the Permutation method combined with the XGBoost model, which are consistent with the results in Figure 8A. Furthermore, regardless of the machine learning model used, the final feature ranking and the scores for each feature provided by the Permutation method remain the same. This indicates that the Permutation method is a model-agnostic tool for feature analysis.

Figure 8. (A) Feature importance results from Permutation and Random Forest; (B) Feature importance results from Permutation and XGBoost.
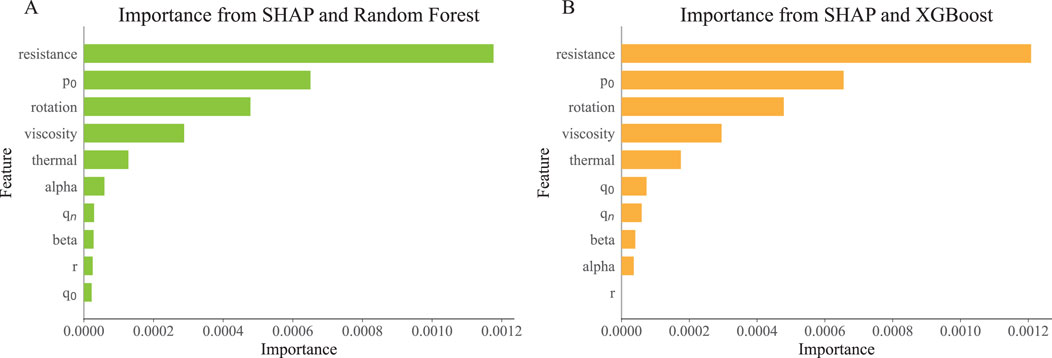
Figure 9. (A) Feature importance results from SHAP and Random Forest; (B) Feature importance results from SHAP and XGBoost.
Figure 9 presents the feature importance results obtained from the SHAP study. Figure 9A shows the results from the SHAP investigation combined with the Random Forest model, indicating that resistance, rotation, pressure at the magnetic axis, and viscosity have a crucial impact on the growth rate of internal kink modes. In Figure 9B, the top four features influencing the growth rate of internal kink modes are consistent with those in Figure 9A; however, the results for the remaining less influential features differ. This suggests that the output of the SHAP analysis is not model-agnostic and is strongly influenced by the specific machine learning model used.
Based on the above analysis, it can be summarized that the four features with the greatest impact on the growth rate of internal kink modes are resistance, pressure at the magnetic axis, viscosity, and rotation. Among these, resistance has the most significant effect, while the relative importance of the other three features requires further investigation. The remaining 11 features have a relatively smaller influence on the growth rate of internal kink modes, and their rankings are not consistent.
The feature importance displayed in Figures 7–9 represents a comprehensive evaluation of each feature’s contribution to predicting the growth rate of internal kink modes. Subsequently, we analyze the impact of the four key features—resistance, pressure at the magnetic axis, viscosity, and rotation—on the growth rate of internal kink modes from the perspective of individual data points in the dataset. The results are shown in Figure 10. For this analysis, SHAP values are calculated for each feature across all data points in the dataset. With 196 data points in total, each feature has 196 corresponding SHAP values, represented as points in the figure. A red point indicates that the SHAP value was generated from a greater feature value, while a blue point represents a smaller feature value. Points on the right side of the y-axis indicate a positive contribution, suggesting that higher feature values are associated with an increased growth rate of internal kink modes. Conversely, points on the left side indicate a negative contribution, suggesting that lower feature values are associated with a decreased growth rate. The results show that the impact of each feature on the growth rate of internal kink modes is complex, and it is challenging to assert that a higher or lower value of a particular feature definitively correlates with a faster or slower growth rate. However, the significant influence of resistance, pressure at the magnetic axis, viscosity, and rotation on the growth rate of internal kink modes is clearly confirmed in the analysis.
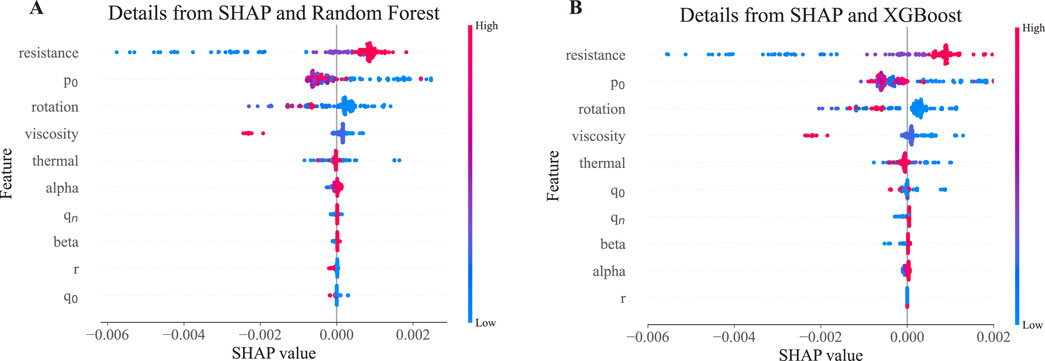
Figure 10. (A) Shapely value of 10 most influential features from Random Forest; (B) Shapely value of 10 most influential features from XGBoost.
4.3 Key feature description
The above experiments indicate that among all the features influencing the growth rate of internal kink modes, resistance, pressure at the magnetic axis, viscosity, and rotation have the greatest impact on the final growth rate. The subsequent analysis will focus on the reasons why these four features prominently affect the growth rate of internal kink modes.
4.3.1 Influence of resistance to internal kink mode
In the dataset, the relevant feature is resistivity, which fundamentally affects the plasma’s electrical resistance. In tokamak devices, plasma carries the current, while resistance hinders the flow of this current. The growth rate of internal kink modes is closely related to the plasma’s resistance. When resistance is present in the plasma, it impedes the current flow, resulting in energy dissipation. This dissipation impacts the plasma’s dynamic behavior, subsequently altering the growth rate of internal kink modes. During the occurrence of internal kink modes, the twisting motion of the plasma increases the path length of the current, thereby enhancing the resistive dissipation effect. Resistance also influences the distribution of the electromagnetic field within the plasma. In tokamak devices, the magnetic field is a critical factor in confining the plasma. The presence of resistance alters the current distribution, which in turn affects the distribution and intensity of the magnetic field. These changes in the electromagnetic field directly impact the stability of internal kink modes, as the growth rate of these modes is closely tied to magnetic field strength. The existence of resistance causes variations in the plasma’s electric and flow fields, influencing the dynamic behaviour of internal kink modes. Specifically, higher resistance in the plasma can lead to slower or unstable plasma flow, thereby changing the growth rate of internal kink modes. Plasma resistance not only affects current flow but is also closely related to the plasma’s flow state. During the development of internal kink modes, the presence of resistance causes the current to preferentially flow toward regions with larger perturbations, altering the growth of the internal kink modes.
4.3.2 Influence of pressure to internal kink mode
The pressure at the magnetic axis directly reflects the energy density in the central area of the plasma. Higher pressure at the magnetic axis usually indicates higher plasma temperature and density, thus enhancing the overall stability of the plasma. According to the MHD theory, plasma stability is closely related to its pressure distribution. Higher central pressure helps maintain a higher plasma pressure gradient, thereby increasing MHD stability and influencing the formation and growth of internal kink modes. The driving force of internal kink modes primarily originates from the pressure gradient and current gradient within the plasma. Higher pressure at the magnetic axis can strengthen the plasma pressure gradient, thus altering the distribution of the driving force for internal kink modes. Specifically, under high-pressure conditions, the plasma pressure gradient is larger, increasing the intrinsic energy reserve of the plasma and enhancing its ability to resist external perturbations, thereby affecting the growth rate of internal kink modes. Higher pressure at the magnetic axis leads to a more concentrated plasma current in the central region, reducing the current density at the edge region and weakening the driving source of internal kink modes in the edge area. The pressure at the magnetic axis also affects the plasma’s transport properties; higher pressure at the magnetic axis enhances plasma thermal conduction and particle diffusion, thereby reducing energy deposition from internal kink modes within the plasma.
4.3.3 Influence of viscosity to internal kink modes
The viscosity coefficient, or viscosity, is a physical quantity that describes the internal resistance of a fluid. It reflects the fluid’s ability to resist shear deformation when subjected to shear forces. In tokamak devices, the viscosity of the plasma affects its internal dynamic behaviour and stability. The greater the viscosity, the larger the internal frictional forces generated during shear, which imposes a damping effect on the internal kink modes. The internal kink mode is an instable pattern within the plasma, characterized by internal twisting deformations. Increased viscosity enhances the frictional forces between fluid layers, making it more difficult for the fluid to undergo shear and twist. High viscosity strengthens the shear viscosity of the fluid, stabilizing the shear flows within the plasma. Viscosity also affects the overall flow characteristics and dynamic behaviour of the plasma. In a tokamak, the flow and stability of the plasma are closely linked. Changes in viscosity can alter the plasma’s velocity distribution and dynamic properties such as vortex formation, thereby impacting the development of internal kink modes. The influence of viscosity on internal kink modes can be understood from the MHD equations. In the MHD equations, viscous force is a crucial component of the momentum conservation equation and is proportional to the velocity gradient of the plasma. As viscosity increases, the internal viscous force within the plasma also increases, leading to slower plasma flows and consequently affecting the development of internal kink modes.
4.3.4 Influence of rotation to internal kink mode
In tokamak plasmas, the Coriolis force generated by rotation exerts a stabilizing effect on the plasma. When the plasma rotates at a certain velocity, the Coriolis force can suppress instabilities perpendicular to the rotation axis, including internal kink modes. This suppression effect increases with the rotation speed, thereby altering the growth rate of internal kink modes. Plasma rotation introduces shear flow, which can significantly affect plasma stability. Shear flow disrupts perturbations within the plasma, effectively influencing the growth of internal kink modes. Physically, the shear can increase the twist of perturbations, making it difficult for them to maintain structural integrity, thus reducing the growth of unstable modes. This effect is particularly important in tokamak devices because shear flow can dynamically interact to suppress instabilities caused by the plasma’s own current. The radial gradient of the rotation speed is also a critical factor influencing the growth rate of internal kink modes. A velocity gradient can introduce additional hydrodynamic shear, which is especially effective in suppressing internal kink mode instabilities. In tokamak plasmas, if the rotation speed gradient is sufficiently large, it can hinder the radial transport of energy and momentum, thus preventing the spread of unstable modes. Plasma rotation also introduces an inertial stabilization mechanism. The momentum of rotating plasma has the ability to suppress perturbations, similar to the gyroscopic effect, making it more difficult for disturbances to develop rapidly. Particularly under high-speed rotation, the plasma inertia induced by rotation can effectively impact the internal kink modes.
4.4 Key feature discussion
Through machine learning analysis of the factors affecting the growth rate of the internal kink mode, electrical resistivity was identified as having the most significant impact. Its influence was observed to be far more pronounced compared to other features. Additionally, pressure at the magnetic axis, the viscosity coefficient, and plasma rotation were found to have a notable but less pronounced effect on the growth rate. These features, while significant, exhibited a much lower level of influence compared to resistivity. Further investigation is required regarding the viscosity coefficient and plasma rotation, as the current machine learning models, though able to identify their importance, could not provide a precise quantification of their specific impact on the growth rate. Although the models consistently ranked these features as impactful, their relative contribution to the growth rate remains less clearly defined. Current findings suggest that viscosity and plasma rotation have an observable effect on the internal kink mode, but more detailed research is necessary to fully ascertain their influence. The results highlight the distinct and dominant role of resistivity, with other factors playing a secondary but still relevant role. The uncertainty surrounding the precise impact of viscosity and plasma rotation emphasizes the need for additional analysis to further refine these findings and develop a clearer understanding of their roles in the growth rate of the internal kink mode.
Machine learning approaches, particularly ensemble methods like Random Forest and XGBoost, offer several advantages over traditional methods. Firstly, these methods excel in handling high-dimensional data efficiently, enabling the simultaneous analysis of multiple features and their complex interactions, which can be challenging to capture through experimental measurements or numerical simulations alone. The use of Permutation and SHAP further enhances the interpretability of these models, providing clear insights into feature importance. Secondly, machine learning models can identify non-linear relationships between features and the target variable, which may not be evident from linear analysis or simple statistical tests often used in experimental and numerical studies. This capability is crucial in understanding the nuanced effects of various parameters on the internal kink mode growth rate, as demonstrated by the disproportionate influence of resistance identified in this study. Moreover, machine learning algorithms can process large datasets rapidly, significantly reducing the time required for analysis compared to detailed numerical simulations or extensive experimental campaigns. This efficiency allows for a more comprehensive exploration of parameter space and the identification of trends that might be obscured by the limitations of traditional methods.
Despite their advantages, machine learning approaches also have limitations when applied to the study of internal kink mode features. One significant drawback is the reliance on high-quality, well-labeled datasets. In practice, obtaining such datasets can be challenging, particularly in experimental settings where measurements may be noisy or incomplete. This can lead to biased models or reduced accuracy in predicting the growth rate. Another limitation is the interpretability of machine learning models, especially deep learning algorithms, which can act as “black boxes,” making it difficult to understand the underlying physical mechanisms driving the predictions. While methods like SHAP and Permutation improve interpretability, they may not fully capture the intricate physics governing the internal kink mode, which could be better elucidated through detailed numerical simulations or experimental observations. Furthermore, machine learning models are sensitive to the choice of hyperparameters and the specific training data used, which can affect the generalizability of the results. Careful cross-validation and model tuning are necessary to ensure robustness and reliability, but even then, the models may not perform consistently across all scenarios, particularly in regimes not well-represented in the training data. In contrast, traditional experimental and numerical simulation methods provide a more direct connection to the underlying physics, allowing for a deeper understanding of the mechanisms at play. Experiments can directly observe phenomena and validate theoretical predictions, while numerical simulations can model complex systems with high fidelity, capturing intricate details that may be overlooked by machine learning algorithms.
Given that machine learning is inherently data-driven, the methodology used in this study to investigate internal kink modes can indeed be extended to other fusion devices, such as stellarators and spherical tokamaks [57, 58]. While the current study focuses on specific data from a particular tokamak configuration, the same approach can be applied to any fusion device as long as sufficient and relevant data is available. However, it is important to note that machine learning models are sensitive to variations in the input data. Therefore, changes in device design or operating parameters, such as magnetic field configurations, plasma pressure profiles, or current distributions, could significantly affect the identified key features and their relative impacts on the internal kink modes. The generalizability of our findings to different types of fusion reactors, such as stellarators and spherical tokamaks, would depend heavily on the availability of diverse datasets encompassing a broad range of operational scenarios. Consequently, collecting as much data as possible from various configurations and operating conditions would improve the robustness and reliability of the results. In future work, expanding the dataset to include information from different devices could provide more insights into how device-specific factors influence key features, further enhancing the applicability of machine learning models in plasma physics research across different fusion reactor designs.
5 Conclusion
This study conducts a comprehensive feature importance analysis affecting the growth rate of internal kink modes by integrating Random Forest, XGBoost, Permutation, and SHAP methods. By training on numerical simulation data, high-precision Random Forest and XGBoost models were successfully constructed, with R2 reaching 95.07% and 94.57%, respectively, demonstrating robust predictive capabilities for the growth rate of internal kink modes. In the feature analysis phase, multiple methods were employed for cross-validation, ensuring the robustness of the results. The findings indicate that resistance, pressure at the magnetic axis, viscosity, and rotation are the most significant features influencing the growth rate of internal kink modes. This discovery provides critical insights into the physical mechanisms underlying internal kink modes. Furthermore, the study elucidates the physical mechanisms by which these key features affect the growth rate of internal kink modes. Variations in resistance directly influence the current distribution and magnetic field structure, thereby regulating the stability of internal kink modes. Pressure at the magnetic axis affects the development of internal kink modes by influencing the pressure gradient within the plasma. Viscosity exerts a damping effect on internal kink modes by altering the plasma’s fluidity. Rotation impacts the growth rate of internal kink modes through the generation of shear flows. In summary, this study not only identifies the key features influencing the growth rate of internal kink modes but also delves into the physical mechanisms underlying these features. While four critical features affecting the growth rate of internal kink modes have been identified, the specific ranking of their importance has yet to be determined. Future research could focus on quantifying the numerical relationships between each feature and the growth rate of internal kink modes, which would have greater theoretical and practical significance for studying internal kink mode instabilities.
Data availability statement
The raw data supporting the conclusions of this article will be made available by the authors, without undue reservation.
Author contributions
HN: Data curation, Formal Analysis, Funding acquisition, Methodology, Software, Visualization, Writing–original draft. SL: Formal Analysis, Investigation, Validation, Writing–original draft. JW: Conceptualization, Project administration, Supervision, Writing–review and editing. TZ: Conceptualization, Funding acquisition, Methodology, Resources, Writing–review and editing.
Funding
The author(s) declare that financial support was received for the research, authorship, and/or publication of this article. This work was funded by the National Natural Science Foundation of China (No. 52075138) and Hainan Province Science and Technology Special Fund (No. ZDYF2022SHFZ301), the Natural Science Foundation for the Higher Education Institutions of Anhui Province (Grant No. 2022AH051631), the key Discipline Construction Project of Anhui Science and Technology University (XK-XJGY002).
Acknowledgments
We are very grateful to the CLT project development team led by Professor Ma Zhiwei of Zhejiang University.
Conflict of interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Publisher’s note
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
References
1. Mirnov SV. Tokamak evolution and view to future. Nucl Fusion (2018) 59(1):015001. doi:10.1088/1741-4326/aaee92
2. Yushmanov PN, Takizuka T, Riedel KS, Kardaun OJWF, Cordey JG, Kaye SM, et al. Scalings for tokamak energy confinement. Nucl Fusion (1990) 30(10):1999–2006. doi:10.1088/0029-5515/30/10/001
3. Zhou T, He X, Zhao J, Shi L, Wen L. Electrokinetic transport of nanoparticles in functional group modified nanopores. Chin Chem Lett (2023) 34(6):107667. doi:10.1016/j.cclet.2022.07.010
4. Lazarus EA. An investigation of coupling of the internal kink mode to error field correction coils in tokamaks. Nucl Fusion (2013) 53(12):123020. doi:10.1088/0029-5515/53/12/123020
5. Chapman IT, Graves JP, Wahlberg C, Team M. The effect of plasma profile variation on the stability of the N= 1 internal kink mode in rotating tokamak plasmas. Nucl Fusion (2010) 50(2):025018. doi:10.1088/0029-5515/50/2/025018
6. Gates DA, Delgado-Aparicio L. Origin of tokamak density limit scalings. Phys Rev Lett (2012) 108(16):165004. doi:10.1103/PhysRevLett.108.165004
7. Xu L, Hu L, Chen K, Li E, Wang F, Zhong G, et al. Observation of 1/1 impurity-related ideal internal kink mode locking in the east tokamak. Plasma Phys Controlled Fusion (2013) 55(3):032001. doi:10.1088/0741-3335/55/3/032001
8. Jian-Gang LI. The status and progress of tokamak research. Physics (2015) 45(2):88–97. doi:10.7693/wl20160203
9. Bonofiglo PJ, Kiptily VG, Rivero-Rodriguez J, Nocente M, Podestà M, Štancar Ž, et al. Alpha particle loss measurements and analysis in jet dt plasmas. Nucl Fusion (2024) 64(9):096038. doi:10.1088/1741-4326/ad69a1
10. Brochard G, Bao J, Liu C, Gorelenkov N, Choi G, Dong G, et al. Verification and validation of linear gyrokinetic and kinetic-mhd simulations for internal kink instability in diii-D tokamak. Nucl Fusion (2022) 62(3):036021. doi:10.1088/1741-4326/ac48a6
11. Lee SJ, Hu D, Lehnen M, Nardon E, Kim J, Bonfiglio D, et al. Nonlinear mhd modeling of neon doped shattered pellet injection with jorek and its comparison to experiments in kstar. Nucl Fusion (2024) 64(10):106042. doi:10.1088/1741-4326/ad6ea1
12. Vega J, Hernández F, Dormido-Canto S, Isayama A, Joffrin E, Matsunaga G, et al. Assessment of linear disruption predictors using jt-60u data. Fusion Eng Des (2019) 146:1291–4. doi:10.1016/j.fusengdes.2019.02.061
13. Zhang YP, Tong RH, Yang ZY, Chen ZY, Hu D, Dong YB, et al. Recent progress on the control and mitigation of runaway electrons and disruption prediction in the hl-2a and J-text tokamaks. Rev Mod Plasma Phys (2023) 7(1):12. doi:10.1007/s41614-022-00110-3
14. Wahlberg C, Bondeson A. Stabilization of the internal kink mode in a tokamak by toroidal plasma rotation. Phys Plasmas (2000) 7(3):923–30. doi:10.1063/1.873889
15. Martynov A, Graves JP, Sauter O. The stability of the ideal internal kink mode in realistic tokamak geometry. Plasma Phys controlled fusion (2005) 47(10):1743–62. doi:10.1088/0741-3335/47/10/009
16. Meneghini O, Smith SP, Lao LL, Izacard O, Ren Q, Park JM, et al. Integrated modeling applications for tokamak experiments with omfit. Nucl Fusion (2015) 55(8):083008. doi:10.1088/0029-5515/55/8/083008
17. Zhang N, Liu YQ, Yu DL, Wang S, Xia GL, Dong GQ, et al. Modeling of toroidal torques exerted by internal kink instability in a tokamak plasma. Phys Plasmas (2017) 24(8):082507. doi:10.1063/1.4995271
18. Walayat K, Haeri S, Iqbal I, Zhang Y. Hybrid Pd-dem approach for modeling surface erosion by particles impact. Comput Part Mech (2023) 10(6):1895–911. doi:10.1007/s40571-023-00596-9
19. Walayat K, Haeri S, Iqbal I, Zhang Y. Pd–Dem hybrid modeling of leading edge erosion in wind turbine blades under controlled impact scenarios. Comput Part Mech (2024) 11(5):1903–21. doi:10.1007/s40571-024-00717-y
20. Zakharov LE. The theory of the kink mode during the vertical plasma disruption events in tokamaks. Phys Plasmas (2008) 15(6):062507. doi:10.1063/1.2926630
21. Zhuang G, Pan Y, Hu XW, Wang ZJ, Ding YH, Zhang M, et al. The reconstruction and research progress of the text-U tokamak in China. Nucl Fusion (2011) 51(9):094020. doi:10.1088/0029-5515/51/9/094020
22. Halpern FD, Leblond D, Lütjens H, Luciani JF. Oscillation regimes of the internal kink mode in tokamak plasmas. Plasma Phys Controlled Fusion (2010) 53(1):015011. doi:10.1088/0741-3335/53/1/015011
23. Ning H, Li R, Zhou T. Machine learning for microalgae detection and utilization. Front Mar Sci (2022) 9:947394. doi:10.3389/fmars.2022.947394
24. Ahmed S, Hossain MA, Ray SK, Bhuiyan MMI, Sabuj SR. A study on road accident prediction and contributing factors using explainable machine learning models: analysis and performance. Transportation Res Interdiscip Perspect (2023) 19:100814. doi:10.1016/j.trip.2023.100814
25. Seo J, Kim S, Jalalvand A, Conlin R, Rothstein A, Abbate J, et al. Avoiding fusion plasma tearing instability with deep reinforcement learning. Nature (2024) 626(8000):746–51. doi:10.1038/s41586-024-07024-9
26. Li Y-X, Li Y-A, Chen Z, Chen X. Feature extraction of ship-radiated noise based on permutation entropy of the intrinsic mode function with the highest energy. Entropy (2016) 18(11):393. doi:10.3390/e18110393
27. Montes KJ, Rea C, Tinguely RA, Sweeney R, Zhu J, Granetz RS. A semi-supervised machine learning detector for physics events in tokamak discharges. Nucl Fusion (2021) 61(2):026022. doi:10.1088/1741-4326/abcdb9
28. Lee Y-G, Oh J-Y, Kim D, Kim G. Shap value-based feature importance analysis for short-term load forecasting. J Electr Eng and Technol (2023) 18(1):579–88. doi:10.1007/s42835-022-01161-9
29. Pustovitov VD, Rubinacci G, Villone F. Sideways force due to coupled rotating kink modes in tokamaks. Nucl Fusion (2021) 61(3):036018. doi:10.1088/1741-4326/abce3e
30. Meng Y, Yang N, Qian Z, Zhang G. What makes an online review more helpful: an interpretation framework using xgboost and shap values. J Theor Appl Electron Commerce Res (2020) 16(3):466–90. doi:10.3390/jtaer16030029
31. Panda C, Mishra AK, Dash AK, Nawab H. Predicting and explaining severity of road accident using artificial intelligence techniques, shap and feature analysis. Int J crashworthiness (2023) 28(2):186–201. doi:10.1080/13588265.2022.2074643
32. Liu Y, Liu Z, Luo X, Zhao H. Diagnosis of Parkinson's disease based on shap value feature selection. Biocybernetics Biomed Eng (2022) 42(3):856–69. doi:10.1016/j.bbe.2022.06.007
34. Paul A, Mukherjee DP, Das P, Gangopadhyay A, Chintha AR, Kundu S. Improved random forest for classification. IEEE Trans Image Process (2018) 27(8):4012–24. doi:10.1109/TIP.2018.2834830
35. Speiser JL, Miller ME, Tooze J, Ip E. A comparison of random forest variable selection methods for classification prediction modeling. Expert Syst Appl (2019) 134:93–101. doi:10.1016/j.eswa.2019.05.028
36. Asselman A, Khaldi M, Aammou S. Enhancing the prediction of student performance based on the machine learning xgboost algorithm. Interactive Learn Environments (2023) 31(6):3360–79. doi:10.1080/10494820.2021.1928235
37. Ogunleye A, Wang Q-G. Xgboost model for chronic kidney disease diagnosis. IEEE/ACM Trans Comput Biol Bioinformatics (2019) 17(6):2131–40. doi:10.1109/TCBB.2019.2911071
38. Amjad M, Ahmad I, Ahmad M, Wróblewski P, Kamiński P, Amjad U. Prediction of pile bearing capacity using xgboost algorithm: modeling and performance evaluation. Appl Sci (2022) 12(4):2126. doi:10.3390/app12042126
39. Altmann A, Toloşi L, Sander O, Lengauer T. Permutation importance: a corrected feature importance measure. Bioinformatics (2010) 26(10):1340–7. doi:10.1093/bioinformatics/btq134
40. Huang N, Lu G, Xu D. A permutation importance-based feature selection method for short-term electricity load forecasting using random forest. Energies (2016) 9(10):767. doi:10.3390/en9100767
41. Mi X, Zou B, Zou F, Hu J. Permutation-based identification of important biomarkers for complex diseases via machine learning models. Nat Commun (2021) 12(1):3008. doi:10.1038/s41467-021-22756-2
42. Parsa AB, Movahedi A, Taghipour H, Derrible S, Mohammadian AK. Toward safer highways, application of xgboost and shap for real-time accident detection and feature analysis. Accid Anal and Prev (2020) 136:105405. doi:10.1016/j.aap.2019.105405
43. Raihan MJ, Khan MA-M, Kee S-H, Nahid A-A. Detection of the chronic kidney disease using xgboost classifier and explaining the influence of the attributes on the model using shap. Scientific Rep (2023) 13(1):6263. doi:10.1038/s41598-023-33525-0
44. Jabeur SB, Mefteh-Wali S, Viviani J-L. Forecasting gold price with the xgboost algorithm and shap interaction values. Ann Operations Res (2024) 334(1):679–99. doi:10.1007/s10479-021-04187-w
45. Nohara Y, Matsumoto K, Soejima H, Nakashima N. Explanation of machine learning models using Shapley additive explanation and application for real data in hospital. Comput Methods Programs Biomed (2022) 214:106584. doi:10.1016/j.cmpb.2021.106584
46. Zhang HW, Ma ZW, Zhang W, Sun YW, Yang X. Penetration properties of resonant magnetic perturbation in east tokamak. Phys Plasmas (2019) 26(11):112502. doi:10.1063/1.5116669
47. McClenaghan J, Lin Z, Holod I, Deng W, Wang Z. Verification of gyrokinetic particle simulation of current-driven instability in fusion plasmas. I. Internal kink mode. Phys Plasmas (2014) 21(12):122519. doi:10.1063/1.4905073
48. Zhang W, Ma ZW, Zhang HW, Zhu J. Dynamic evolution of resistive kink mode with electron diamagnetic drift in tokamaks. Phys Plasmas (2019) 26(4):042514. doi:10.1063/1.5090226
49. Ning H, Qian S, Zhou T. Applications of level set method in computational fluid dynamics: a review. Int J Hydromechatronics (2023) 6(1):1–33. doi:10.1504/IJHM.2023.129126
50. Hu B, Betti R, Manickam J. Kinetic stability of the internal kink mode in iter. Phys Plasmas (2006) 13(11):112505. doi:10.1063/1.2364147
51. Wong KL, Chu MS, Luce TC, Petty CC, Politzer PA, Prater R, et al. Internal kink instability during off-Axis electron cyclotron current drive in the diii-D tokamak. Phys Rev Lett (2000) 85(5):996–9. doi:10.1103/PhysRevLett.85.996
52. Hastie RJ, Hender TC. Toroidal internal kink stability in tokamaks with ultra flat Q profiles. Nucl fusion (1988) 28(4):585–94. doi:10.1088/0029-5515/28/4/005
53. Xu L, Hu L, Chen K, Li E, Wang F, Xu M, et al. Observations of pressure gradient driven M= 1 internal kink mode in east tokamak. Phys Plasmas (2012) 19(12):122504. doi:10.1063/1.4773032
54. Zhang W, Ma ZW, Zhang HW, Chen WJ, Wang X. Influence of aspect ratio, plasma viscosity, and radial position of the resonant surfaces on the plasmoid formation in the low resistivity plasma in tokamak. Nucl Fusion (2022) 62(3):036007. doi:10.1088/1741-4326/ac46f8
55. Wang S, Ma ZW. Influence of toroidal rotation on resistive tearing modes in tokamaks. Phys Plasmas (2015) 22(12):122504. doi:10.1063/1.4936977
56. Zhang W, Wang S, Ma ZW. Influence of helical external driven current on nonlinear resistive tearing mode evolution and saturation in tokamaks. Phys Plasmas (2017) 24(6):062510. doi:10.1063/1.4986113
57. Szűcs M, Szepesi T, Biedermann C, Cseh G, Jakubowski M, Kocsis G, et al. Detecting plasma detachment in the wendelstein 7-X stellarator using machine learning. Appl Sci (2022) 12(1):269. doi:10.3390/app12010269
58. Tkachenko EE, Kurskiev GS, Zhiltsov NS, Voronin AV, Goryainov VY, Mukhin EE, et al. Application of machine learning to determine electron temperature in globus-M2 tokamak using the soft X-ray emission data and the thomson scattering diagnostics data. Phys At Nuclei (2022) 85(7):1214–22. doi:10.1134/S1063778822070122
Keywords: feature importance, internal kink mode, Random Forest, XGboost, permutation, SHAP
Citation: Ning H, Lou S, Wu J and Zhou T (2024) Key feature identification of internal kink mode using machine learning. Front. Phys. 12:1476618. doi: 10.3389/fphy.2024.1476618
Received: 06 August 2024; Accepted: 16 October 2024;
Published: 29 October 2024.
Edited by:
Peter Manz, University of Greifswald, GermanyReviewed by:
Shishir Purohit, Institute for Plasma Research (IPR), IndiaImran Iqbal, New York University, United States
Copyright © 2024 Ning, Lou, Wu and Zhou. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Teng Zhou, emhvdXRlbmdAaGFpbmFudS5lZHUuY24=
 Hongwei Ning
Hongwei Ning Shuyong Lou
Shuyong Lou Jianguo Wu
Jianguo Wu Teng Zhou
Teng Zhou