Differential rotation in neutron stars at finite temperatures

Introduction: This paper investigates the impact of differential rotation on the bulk properties and onset of rotational instabilities in neutron stars at finite temperatures up to 50 MeV.

Methods: Utilizing the relativistic Brueckner-Hartree-Fock (RBHF) formalism in full Dirac space, the study constructs equation of state (EOS) models for hot neutron star matter, including conditions relevant for high temperatures. These finite-temperature EOS models are applied to compute the bulk properties of differentially rotating neutron stars with varying structural deformations.

Results: The findings demonstrate that the stability of these stars against bar-mode deformation, a key rotational instability, is only weakly dependent on temperature. Differential rotation significantly affects the maximum mass and radius of neutron stars, and the threshold for the onset of bar-mode instability shows minimal sensitivity to temperature changes within the examined range.

Discussion: These findings are crucial for interpreting observational data from neutron star mergers and other high-energy astrophysical events. The research underscores the necessity of incorporating differential rotation and finite temperature effects in neutron star models to predict their properties and stability accurately.

1 Introduction

Neutron stars provide a unique, naturally occurring laboratory for studying matter at extreme pressures and densities not reproducible by experiments in terrestrial laboratories (see, for instance, [1–3]). The cold, highly isospin asymmetric matter within the core of a massive neutron star can reach densities up to an order of magnitude higher than nuclear saturation density. During a binary neutron star merger event, the resulting matter may promptly collapse into a black hole or form a remnant neutron star. If formed, the remnant star is characterized by a high mass, extreme temperatures on the order of 50–100 MeV, and rapid differential rotation [4–7]. These massive, differentially rotating remnant stars may also deviate from spherical or axial symmetry by exhibiting extreme triaxial deformations. The structural deformation, thermal pressure, and differential rotation allow the remnant to remain stable on short, dynamical timescales, for masses that would be otherwise unstable in the static and uniform-rotation cases.

Differential rotation in neutron stars has been explored in the literature through numerical simulations [8–11], with more recent studies incorporating finite temperature equation of state (EOS) models [12, 13]. The inclusion of temperature when modeling the EOS of neutron star matter, however, is a formidable task. Theoretical modeling of neutron star matter as a dense, many-body system can be done in a phenomenological or ab initio framework [3, 14–16, 16–18, 20]. Phenomenological models employ density functional theories with effective nucleon-nucleon (NN) interactions to reproduce the empirical saturation properties of symmetric nuclear matter while adhering to constraints extracted from nuclear physics and astrophysics [19, 21–23]. In contrast, ab initio methods use realistic NN interactions determined by nucleon-nucleon scattering data and the properties of the deuteron. Relativistic ab initio methods, such as the relativistic Brueckner-Hartree-Fock (RBHF) approximation, closely reproduce the saturation properties of empirical data [24–29]. The RBHF approximation couples the propagation of baryons to the many-body background and encapsulates dynamical correlations between baryons, computed using a relativistic scattering $(\mathbf{T})$ matrix. Importantly, the RBHF method does not involve adjustable parameters, distinguishing it from many phenomenological models.

While most studies using the RBHF approximation are conducted at zero temperature, our previous work [30] extended the approximation to model nuclear matter at finite temperatures, where EOS models were derived in different temperature regimes. The nuclear EOS models incorporate finite temperatures in a self-consistent manner, unlike previous studies that added thermal effects to models of cold nuclear matter [31–33]. This framework ensures a more comprehensive and accurate representation of the thermodynamic properties of dense nuclear matter. In previous work, these EOS models were used to determine bulk properties of non-rotating, uniformly rotating, and differentially rotating neutron stars.

In this paper, we expand on previous work by exploring more deformed stars and dynamical rotation instabilities. This paper is organized as follows: Section 2 describes the theoretical framework for deriving EOS models at finite temperatures using the RBHF approximation and for constructing equilibrium models of differentially rotating stars. Section 3 presents the calculated results, where Section 3.1 shows stellar sequences over ranges of structural deformation, Section 3.2 discusses the stability of calculated models to dynamical bar mode excitation, Section 3.3 presents density and frequency profiles for stars with high degrees of differential rotation and structural deformation, and Section 3.4 discusses how various approximations introduced in the numerical calculations may influence the presented results. Section 4 gives a summary of the work presented.

2 Theoretical framework

This section discusses the theoretical framework for constructing equation of state (EOS) models for neutron star matter at finite temperatures using the relativistic Brueckner-Hartree-Fock (RBHF) theory. The EOS models are used as input to construct equilibrium models of differentially rotating objects, for which the theory is described below.

2.1 Relativistic Brueckner-Hartree-Fock theory at finite temperatures

The essential structure of modeling nuclear matter using RBHF theory is outlined in this section. A more detailed explanation of the approach can be found in Poschenrieder and Weigel [24]; Weber [14], with finite temperature extensions given in our previous work [30, 34]. Nuclear matter at supranuclear densities can be described as a complex, many-body system whose dynamics are governed by the Lagrangian density:

$\mathcal{L}={\mathcal{L}}_N+{\displaystyle \sum _M}\left({\mathcal{L}}_M+{\mathcal{L}}_{MN}\right),$

where ${\mathcal{L}}_N$ denotes the Lagrangian of non-interacting nucleons, ${\mathcal{L}}_M$ is the Lagrangian density of different free meson fields, and ${\mathcal{L}}_{MN}$ describes the interaction between nucleons and mesons. In the relativistic framework, nucleons are treated as effective Dirac particles, which are described by the relativistic Dirac equation. The equations of motion for the various particle fields within the many-body system are derived from the Euler-Lagrange equation and solved using the Martin-Schwinger hierarchy of coupled Green’s functions [35].

The formal structure of the RBHF approach is to solve a system of highly nonlinear, coupled equations, which include the Dyson equation for the two-body Green’s function $G_1$, a Bethe-Salpeter type integral equation for the scattering matrix $\mathbf{T}$, and the equation for the self-energy $\mathrm{\Sigma }$. In this formalism, the Dyson equation is used to determine the two-body Green’s function $G_1$ for all nucleons as:

$\left[\cancel{p}-m-\mathrm{\Sigma }\left(p\right)\right]G_1\left(p\right)=1,$

where $\cancel{p}={\gamma }^{\mu }{p}_{\mu }={\gamma }^{\mu }{g}_{\mu \nu }{p}^{\nu }={\gamma }^0{p}^0-{\sum }_{i=1}^3{\gamma }^i{p}^i$ and ${\gamma }^0$ and ${\gamma }^i$ are the Dirac matrices. Following the determination of the $G_1$, the in-medium scattering matrix $\mathbf{T}$ is determined with Bethe-Salpeter type integral equation:

$\mathbf{T}\left(P;p,p^{\prime }\right)=V\left(p-p^{\prime }\right)+\int \frac{d^4{p}^{\prime \prime }}{{\left(2\pi \right)}^4}V\left(p-p^{\prime \prime }\right)\mathrm{\Lambda }\left(\frac{P}{2}+p^{\prime \prime },\frac{P}{2}-k^{\prime \prime }\right)\mathbf{T}\left(P;p^{\prime \prime },p^{\prime }\right),(1)$

where $\mathrm{\Lambda }$ is the intermediate nucleon-nucleon propagator and $V$ represents the repeated sums of two-particle interactions given by a one-boson-exchange (OBE) potential, which describes the interaction among two nucleons in terms of the exchange of scalar, pseudo-scalar, and vector mesons. In this work, we use the so-called Bonn B potential [36] to describe the OBE interaction, which employs a pseudoscalar type of pion-nucleon coupling. This potential is widely used in high-density nuclear matter studies due to its reliability and numerical stability, particularly in RBHF theory. While newer relativistic OBE potentials have been proposed (e.g., in [37]), the Bonn-B potential has been extensively tested in dense nuclear environments, making it a robust and reliable choice for modeling the equation of state under extreme conditions.

The final coupled equation in the formal scheme is for the self-energy $\mathrm{\Sigma }$, written in momentum space as:

$\mathrm{\Sigma }\left(p\right)=\frac{i}{{\left(2\pi \right)}^4}\int d^4{p}^{\prime }\left[⟨\left.\frac{p-p^{\prime }}{2}\right|\mathbf{T}\left(p+p^{\prime }\right)\left|\frac{p-p^{\prime }}{2}\right.⟩-⟨\left.\frac{p-p^{\prime }}{2}\right|\mathbf{T}\left(p+p^{\prime }\right)\left|\frac{p^{\prime }-p}{2}\right.⟩\right]G_1\left(p^{\prime }\right).$

The self-consistent calculations are carried out using a complete basis of particles $({\mathrm{\Phi }}_{\lambda })$ and antiparticles $({\theta }_{\lambda })$ to decouple the integral equations and make the two-body propagator $\mathrm{\Lambda }$ diagonal, where $\lambda =\pm 1/2$ are the helicity eigenvalues.

The particle propagator $\mathrm{\Lambda }$ in Equation 1 takes the form of the Brueckner propagator, which is defined as the following at finite temperatures:

$\mathrm{\Lambda }\left(\vec{p},{\vec{p}}^{\prime };P^0\right)=2\pi \frac{f\left(|\vec{p}|\right)f\left(|{\vec{p}}^{\prime }|\right)}{P^0-{\omega }_1\left(|\vec{p}|\right)-{\omega }_1\left(|{\vec{p}}^{\prime }|\right)},$

where $f$ signifies the Fermi-Dirac distribution functions, given by:

$f_1\left(\vec{p}\right)=\frac{1}{e^{\beta \left({\omega }_1\left(\vec{p}\right)-\mu \right)}+1},$

$f_2\left(\vec{p}\right)=\frac{1}{e^{\beta \left(-{\omega }_2\left(\vec{p}\right)+\mu \right)}+1},$

where “1” indicates the positive energy states and “2” indicates the thermally-excited negative energy states. We recall here that at finite temperatures, the behavior of nuclear matter undergoes important modification, attributed to thermal baryonic excitations surpassing the Fermi surface. As $T\to 0$, the Fermi-Dirac distribution for positive energy states becomes:

$f_1\left(\vec{p}\right)\to \mathrm{\Theta }\left(\mu -{\omega }_1\left(\vec{p}\right)\right),$

and for negative energy states, $f_2\to 0$.

An elegant technique used to make the many-body equations numerically tractable and to calculate the key quantities of many-body systems is to utilize the spectral representation of the $G_1$ function [24]. $G_1$ can then be defined in Fourier space at finite temperatures as [14, 38]:

$G_1\left(p^0,\vec{p}\right)=\int d\omega \frac{\mathrm{\Xi }\left(\omega ,\vec{p}\right)}{\omega -\left(p^0-\mu \right)\left(1+i\eta \right)}-2i\pi \text{sign}\left(p^0-\mu \right)\frac{\mathrm{\Xi }\left(p^0-\mu ,\vec{p}\right)}{e^{\beta |p^0-\mu |}+1}$

where $\mathrm{\Xi }$ represents the spectral function which is dependent on the single-particle energy $\omega$, $\mu$ is the nucleon chemical potential, and $\eta$ is used to circumvent a singularity occurring as integrals are carried out in the complex plane. The temperature inclusion arises through $\beta =1/k_{B}T$, where $k_B$ is the Stefan-Boltzmann constant and $T$ is the temperature.

Once a self-consistent solution to the coupled system of equations is found, the self-energy $\mathrm{\Sigma }$ and spectral function $A$ are used to determine the EOS. The number density $\rho$ of the system follows from:

$\rho =\frac{4}{{\left(2\pi \right)}^3}\int d^{3}p{\mathrm{\Xi }}_0\left(\omega ,\vec{p}\right)f\left(p\right),$

where ${\mathrm{\Xi }}_0$ is the time-like component of the spectral function and $f$ denotes the Fermi-Dirac distributions. The pressure of the system at finite temperatures is determined from the free energy per nucleon, denoted as $F$, which is defined as:

$F\left(\rho ,T\right)=U\left(\rho ,T\right)-TS\left(\rho ,T\right),$

where $U$ is the internal energy, $T$ is the temperature, and $S$ is the entropy ter Haar and Malfliet [39]. In this approach, $T$ is held constant and $S$ is determined by:

$S\left(\rho ,T\right)=\frac{-1}{{\left(2\pi \right)}^3\rho }\int d^{3}p\left[\left(1-f\right)\ln \left(1-f\right)+f\ln \left(f\right)\right].(2)$

Both particles and antiparticles contribute to $S$, but the antiparticle contribution is very small $(f_2\ll f_1)$. Therefore, Equation 2 can be approximated with only the particle contribution, $f=f_1$. Once the entropy $S$, and subsequently the free energy $F$, are calculated, the pressure is derived as:

$P\left(\rho ,T\right)={\rho }^2\frac{\partial F\left(\rho ,T\right)}{\partial \rho }.$

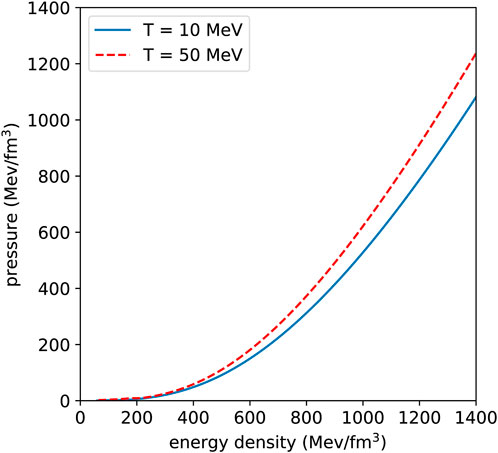
Using the outlined theory, two models for the EOS of neutron star matter are constructed at temperatures T = 10 and 50 MeV, shown visually in Figure 1. As shown in previous work Farrell and Weber [30], the maximum mass of each EOS for non-rotating and uniformly rotating stellar sequences at their mass-shedding limit is over 2 ${\mathrm{M}}_{\odot }$, as required by observational constraints. These models will be used as input to determine equilibrium models for differentially rotating objects, of which the formalism is discussed below.

Figure 1

Figure 1. Pressure as a function energy density for the two EOS models at $T=10$ and 50 MeV.

2.2 Differential rotation

The theoretical framework for modeling differential rotation in neutron stars described in this work follows from the framework laid out by Komatsu et al. [40], which was then modified in Cook et al. [8] (referred to as CST throughout the text). The equations shown in this section directly follow the modifications introduced in CST.

To model differentially rotating neutron stars, we begin with the definition of the line element [8]:

$d{s}^2=-e^{\gamma -\rho }d{t}^2+e^{2\alpha }\left(d{r}^2+r^{2}d\theta \right)+e^{\gamma -\rho }{r}^2{\sin }^2\theta {\left(d\varphi -\omega dt\right)}^2,(3)$

where the metric potentials $\rho$, $\gamma$, $\alpha$, and $\omega$ are dependent on both the radial $r$ and polar $\theta$ coordinates. For both uniform and differential rotation, Equation 3 models neutron stars as stationary, axisymmetric configurations of a (self-gravitating) perfect fluid [8]. Under the assumption of neutron star matter as a perfect fluid, sources of non-isotropic stresses such as magnetic fields or heat transport are ignored [41]. This assumption also allows neutron star matter to be described by the energy-momentum (or stress-energy) tensor given by:

$T^{\kappa \sigma }=\left(ϵ+P\right)u^{\kappa }{u}^{\sigma }+g^{\kappa \sigma }P,$

where $u$ is the fluid’s 4-velocity, $\kappa$ and $\sigma$ are indices ranging from 0 to 3, and $ϵ$ and $P$ are given by the underlying EOS. Equilibrium models for neutron stars must obey the equation of hydrostatic equilibrium as Einstein’s field equation, given as:

$R^{\kappa \sigma }-\frac{1}{2}R{g}^{\kappa \sigma }=8\pi T^{\kappa \sigma },$

where $R^{\kappa \sigma }$ is the Ricci tensor, $R$ is the curvature scalar, and $g^{\kappa \sigma }$ is the metric tensor.

Equilibrium models for neutron stars must obey the equation of hydrostatic equilibrium, which has the form:

$h\left(P\right)-h_p={\int }_{P_p}^P\frac{dP}{ϵ+P}=\ln u^t-\ln u_p^t-{\int }_{{\mathrm{\Omega }}_c}^{\mathrm{\Omega }}F\left(\mathrm{\Omega }\right)d\mathrm{\Omega },$

where $h(P)$ is enthalpy as a function of the pressure, $u^t$ is the time-like component of the 4-velocity $u^{\mu }$, and the subscripts $p$ and $c$ denote the variable’s value at the pole or center, respectively. The integrand of the final integral term, $F(\mathrm{\Omega })$, is the function that defines the rotation law of the matter in the case of differential rotation. Following CST, we define $F(\mathrm{\Omega })$ as a linear rotation law:

$F\left(\bar{\mathrm{\Omega }}\right)=A^2\left({\bar{\mathrm{\Omega }}}_c-\bar{\mathrm{\Omega }}\right),(4)$

where $A$ is a parameter that dictates the degree of differential rotation within the star. In the case of uniform rotation, Equation 4 disappears as the value for the frequency at the center of the star is constant throughout (i.e., ${\mathrm{\Omega }}_c=\mathrm{\Omega }$). It is important to note that the choice of rotation law directly impacts the maximum mass for a given EOS. While many implementations of CST use the linear rotation law in Equation 4 (see, for example, [42, 43]), other studies of differential rotation have explored the impact of using either modified versions of the linear law or non-linear rotation laws, as shown in Galeazzi et al. [10]; Hanauske et al. [11]; Zhou et al. [44].

Using the linear rotation law in Equation 4, the equation of hydrostatic equilibrium can be integrated to give:

$h\left(P\right)-h_p=\frac{1}{2}\left[{\gamma }_p+{\rho }_p-\gamma -\rho -\ln \left(1-v^2\right)+{\widehat{A}}^2{\left(\widehat{\mathrm{\Omega }}-{\widehat{\mathrm{\Omega }}}_c\right)}^2\right],(5)$

where $\widehat{A}$ is the rotation parameter scaled as $\widehat{A}=A/{\bar{r}}_e$. The matrix of angular frequency $\widehat{\mathrm{\Omega }}$ can be derived using the following equation:

$\left({\widehat{\mathrm{\Omega }}}_c-\widehat{\mathrm{\Omega }}\right)=\frac{1}{{\widehat{A}}^2}\left[\frac{\left(\widehat{\mathrm{\Omega }}-\widehat{\omega }\right)s^2\left(1-{\mu }^2\right)e^{-2\rho }}{{\left(1-s\right)}^2-{\left(\widehat{\mathrm{\Omega }}-\widehat{\omega }\right)}^2{s}^2\left(1-{\mu }^2\right)e^{-2\rho }}\right].$

As the rotation parameter $A$ appears throughout the numerical scheme scaled and inverted, we follow the lead of previous work which parameterized calculated sequences of differentially rotating stars by values of ${\widehat{A}}^{-1}$ = 0.3, 0.5, 0.7, and 1.0 [8, 10]. Uniform rotation is obtained in the limit ${\widehat{A}}^{-1}\to 0$, and an upper bound of the scaled rotation parameter in this study is ${\widehat{A}}^{-1}=1.0$.

In the numerical scheme, the metric potentials ($\rho$, $\gamma$, $\widehat{\omega }$, and $\alpha$) are used to determine a value for the radius at the equator, $r_e$ of the star:

${\bar{r}}_e^2=\frac{2\left[h\left(\bar{P}\left({\overline{ϵ}}_c\right)\right)-h_p\right]}{\widehat{\gamma }+p+{\widehat{\rho }}_p-{\widehat{\gamma }}_m-{\widehat{\rho }}_m},(6)$

which is equivalent to Equation 5 evaluated at the location of the maximum (denoted by subscript $m$) density of the star. In CST, this location is assumed to be at the star’s center. The equation for updating $r_e$ changes when the maximum density within the star is not in the center, which is the case in very deformed configurations. We modify the original CST algorithm by instead fixing the maximum interior density, thus redefining Equation 6 as:

$r_e^2=\frac{2\left(h\left(P_m\right)-h_p\right)+\ln \left(1-v_m^2\right)-{\widehat{A}}^2{\left({\widehat{\mathrm{\Omega }}}_m-{\widehat{\mathrm{\Omega }}}_c\right)}^2}{\left[{\widehat{\gamma }}_p+{\widehat{\rho }}_p-{\widehat{\gamma }}_m-{\widehat{\rho }}_m\right]},$

where the subscript $m$ denotes the quantity’s value at the coordinates of the maximum density.

3 Results

Equilibrium models of differentially rotating stars at finite temperatures are computed using the theoretical formalism described in the sections above. For the two EOS models at $T=10$ and 50 MeV, both stellar sequences and individual stellar models are constructed to explore the impact varying degrees of differential rotation has on bulk properties and structural deformation. Computed models are tested for stability against the dynamical bar-mode instability. It is important to note that while the core is treated at finite temperatures, the crust of the neutron star is nevertheless treated at zero temperature, which may impact the properties of neutron stars at the high-temperature end of this study.Additionally, approximations are introduced both in the determination of the finite temperature EOS models using RBHF theory and when numerically modeling differential rotation in neutron stars. These approximations, which may introduce some level of uncertainty in the results presented in this section, are discussed in detail below in Section 3.4.

3.1 Stellar sequences: Varying the ratio of polar to equatorial radius

In this section, stellar sequences are constructed over a range of constant central densities for the two EOS models at temperatures of 10 and 50 MeV. These sequences are calculated with a fixed value for the rotation parameter set the degree of differential rotation; as mentioned in Section 2.2, sequences are parameterized by fixing ${\widehat{A}}^{-1}$ to be 0.3, 0.5, 0.7, or 1.0. When assuming the maximum density of the star is no longer in the center, more extreme configurations with lower values of $r_{ratio}$ can be calculated. Sequences presented in this section are also calculated over a range of $r_{ratio}$ values to demonstrate the parameter’s impact on the maximum mass for a given EOS.

For each EOS, sequences over a range of constant central densities are computed for varying values of $r_{ratio}$. These sequences are shown for the EOS model with temperature $T=10$ MeV in Figure 2 and for $T=50$ MeV in Figure 3. In both figures, a sequence of stars rotating uniformly at their mass-shedding limit is plotted for comparison. As echoed in previous work, more extreme differential rotation $({\widehat{A}}^{-1}\to 1.0)$ paired with more extreme structural deformation $(r_{ratio}\to 0.0)$ results in higher masses at lower central densities, which then taper off to the Kepler limit at higher central densities. This trend is also encountered in Morrison et al. [43], who make similar modifications to the CST algorithm.

Figure 2

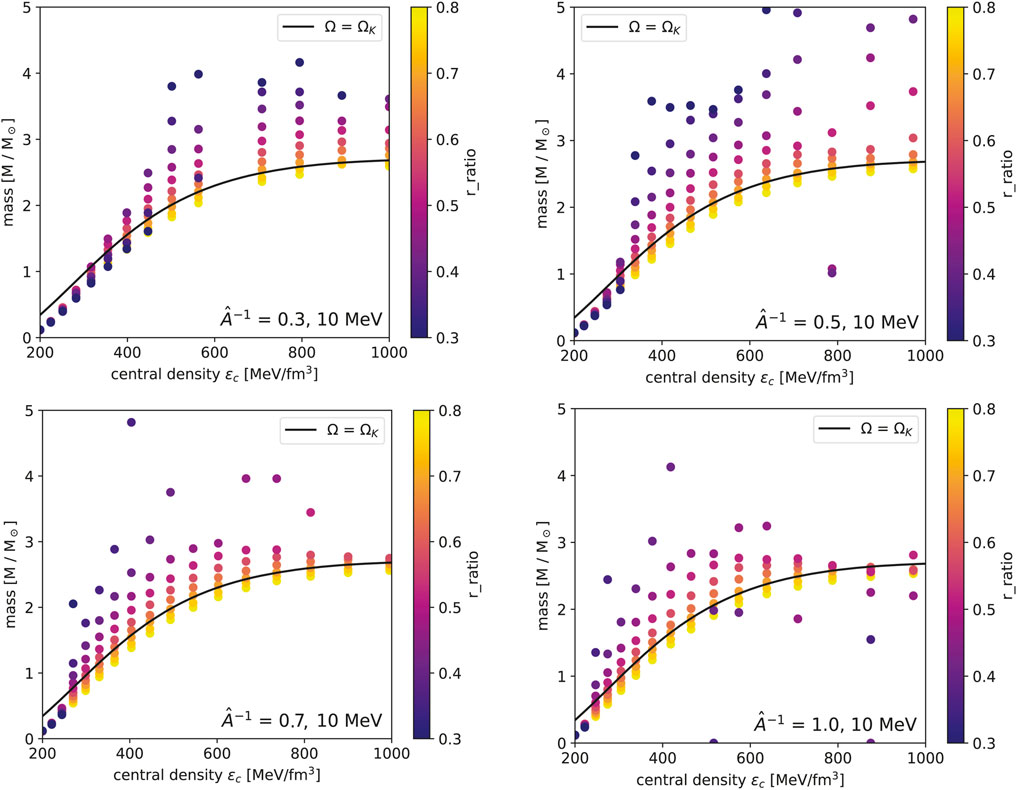
Figure 2. Mass vs. central density of sequences of differentially rotating neutron stars constructed using the EOS model at $T=10$ MeV. The four panes show values for four instances of the rotation parameter ${\widehat{A}}^{-1}$ over a range of central densities and $r_{ratio}$ values compared to a sequence of uniformly rotating stars at the respective Kepler limit (see text for more details).

Figure 3

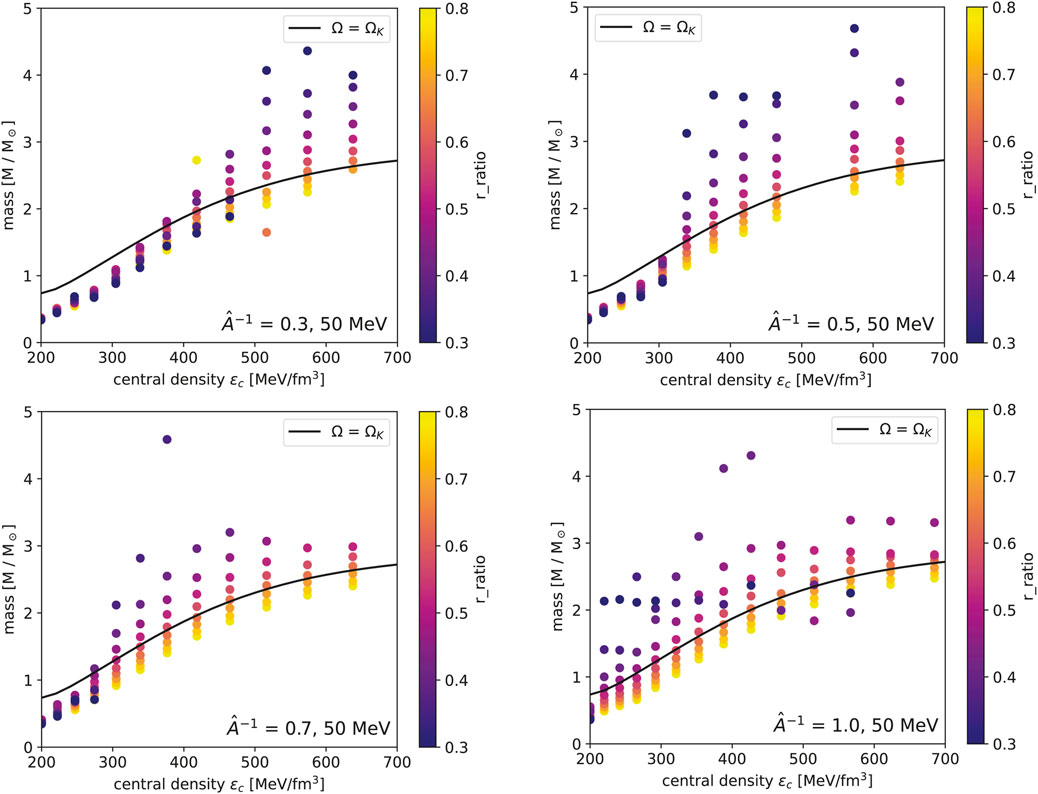
Figure 3. Mass vs. central density of differentially rotating neutron stars constructed using the EOS model at $T=50$ MeV. The four panes show values for four instances of the rotation parameter ${\widehat{A}}^{-1}$ over a range of central densities and $r_{ratio}$ values compared to a sequence of uniformly rotating stars at the respective Kepler limit (see text for more details).

3.2 Dynamical bar-mode instability

Rotating neutron stars formed from a core-collapse suprenova (CCSN) or binary stellar mergers may experience nonaxisymmetric instabilities that directly impact their rotation rates and overall stability. Previous studies (see [45, 46]) in Newtonian gravity have shown rotational instabilities arise from non-radial toroidal modes, i.e., $e^{im\varphi }$ $(m=\pm \mathrm{1,2},\dots )$, which result in the stability parameter, or the ratio of rotational $(T)$ to gravitational $(W)$ energy $\beta =T/|W|$, exceeding some critical value ${\beta }_c$. These rotational instabilities are likely to impact a star’s gravitational radiation signal, making the study of such instabilities an important topic in the wake of new gravitational wave detectors. In this section, we will focus on determining if calculated stellar models are subject to the so-called bar-mode instability, where $m=\pm 2$, which is expected to be the fastest-growing mode and the subject of many instability studies for both uniformly and differentially rotating neutron stars.

Two mechanisms cause rotating stars to be unstable to bar-mode deformation: secular and dynamical instabilities. In Newtonian theory, uniformly rotating incompressible neutron stars become secularly unstable to bar-mode deformation at a critical value of ${\beta }_c\ge 0.14$ with similar findings in studies of post-Newtonian theories [47]. In general, the secular instability grows only in the presence of a small dissipative mechanism like viscosity or gravitational radiation at lower rotation rates [48]. The secular instability usually has a longer growth time when compared to the dynamic timescale of the system. A similar critical value of ${\beta }_c$ has been observed in numerical studies of relativistic stars but is also dependent on the compaction (M/R) of the star and the dissipative mechanism. For example, viscosity-driven secular instability has been shown to occur at ${\beta }_c>0.14$ in more compact configurations with higher rotation rates, but gravitational radiation-driven instabilities occur at ${\beta }_c<0.14$ at lower rotation rates. A more in-depth review of this topic is given by Paschalidis and Stergioulas [49].

The dynamical bar-mode instability occurs independent of any dissipative mechanism and with a growth rate determined by the dynamical timescale of the system, which is generally faster than the timescale of growth for secular instabilities. Therefore, numerical simulations of hydrodynamical equations are necessary to determine the onset threshold of the dynamical bar-mode instability. Many simulations have been carried out in Newtonian theory, the consensus of which gives the critical value ${\beta }_c\ge 0.27$ [4]. Simulations of the dynamical bar-mode instability in general relativity are less common, as solving the nonlinear hydrodynamical equations in full relativity is more complex. However, there have been reliable studies carried out by Shibata and Uryu (2000); Saijo et al. [50] for uniformly rotating stars and by Bodenheimer and Ostriker [51]; Shibata et al. [52, 53]; Camarda et al. [54]; Di Giovanni et al. [55] for differentially rotating stars.

The relativistic simulation of differentially rotating stars carried out by Shibata et al. [52] finds that the critical value of the stability parameter for the dynamic bar-mode instability is ${\beta }_c\approx 0.24-0.25$, slightly lower than the Newtonian limit. These simulations were carried out using the same linear rotation law as in this chapter (and the proceeding one) for similar values of $r_{ratio}$. Therefore, we adhere to their specified threshold of $\beta$ to determine whether differentially rotating stars are stable or unstable to the dynamical bar-mode deformation. Specifically, we use the upper limit for the critical threshold, so stars deemed unstable in this section will have a stability parameter ${\beta }_c\ge 0.25$.

A visual representation of stable and unstable models using this criterion at $T=50$ MeV for two degrees of differential rotation is shown in Figure 4. The two panels in each row show the same information, mass vs. central density for a range of $r_{ratio}$ values, where the figures in the right column categorize each stellar model as stable with a blue square or unstable with a red dot based on the calculated stability parameter for each stellar model. The top row presents a lesser degree of differential rotation $({\widehat{A}}^{-1}=0.3)$, where 81.6% of calculated stellar models are considered stable against dynamical bar-mode deformation. In contrast, the bottom row has the highest degree of differential rotation $({\widehat{A}}^{-1}=1.0)$, and the increase in differential rotation decreases the percentage of stable models to 67.2%. For both cases of differential rotation, the majority of the unstable configurations have small values for $r_{ratio}$, a trend that will be echoed in the next section.

Figure 4

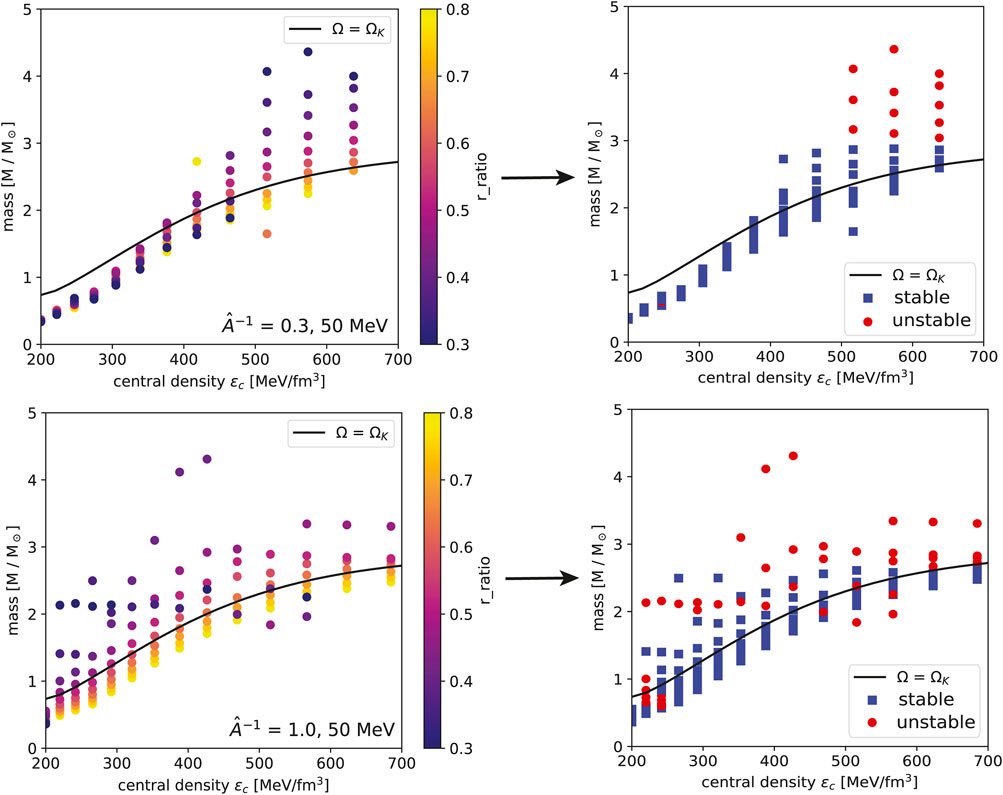
Figure 4. Mass vs. central density of differentially rotating stellar sequences using the EOS at $T=50$ MeV. The top row shows a lesser degree of differential rotation, characterized by the rotation parameter ${\widehat{A}}^{-1}=0.3$, and the bottom row shows a higher degree of differential rotation, characterized by ${\widehat{A}}^{-1}=1.0$. The left plots show mass vs. central density for various values of $r_{ratio}$ as shown in Figure 3, while the right plots show the same values color-coded based on the value of the star’s stability parameter $\beta =T/|W|$. Stars are deemed “unstable” if $\beta \ge 0.25$ (see text for more details).

Table 1 gives the percentage of unstable models and the average $r_{ratio}$ of those unstable models for four degrees of differential rotation for both temperatures of 10 and 50 MeV. The general trend shows the percentage of unstable models decreases as temperature increases. For both temperatures, ${\bar{r}}_{ratio}$ generally tends to fall between 0.4 and 0.5. Stars with $r_{ratio}\le 0.5$ are extremely deformed and thus likely vulnerable to dynamical instabilities. These findings imply temperature plays less of a role when compared to the star’s deformation on its stability against dynamical bar-mode excitation.

Table 1

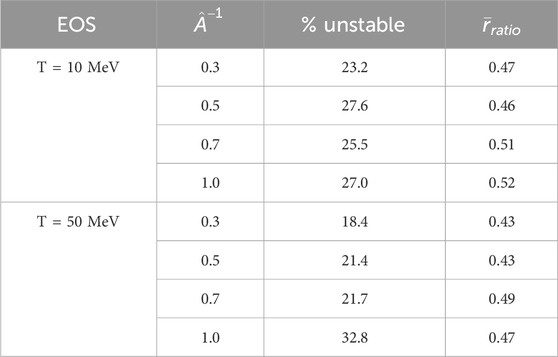
Table 1. The percentage of unstable models and the average $r_{ratio}$, ${\bar{r}}_{ratio}$, of unstable models for four degrees of differential rotation EOS models at 10 and 50 MeV.

3.3 Structural deformation

In this section, we examine density and frequency maps of individual stellar models. For each temperature, two models are computed: the first with a lesser degree of differential rotation (${\widehat{A}}^{-1}$ = 0.3) and the second with a larger degree of differential rotation (${\widehat{A}}^{-1}$ = 1.0). All four models are computed with an $r_{ratio}$ = 0.4, a significant degree of structural deformation. Information on the stars’ masses, radii, and stability parameters are given in Table 2.

Table 2

Table 2. Bulk properties of highly deformed neutron stars, all with $r_{ratio}$ = 0.4, at two temperatures: 10 MeV and 50 MeV. For both temperatures, results are presented for a small degree of differential rotation $({\widehat{A}}^{-1}=0.3)$ and a large degree of differential rotation $({\widehat{A}}^{-1}=1.0)$. Calculated properties include the gravitational mass ${\mathrm{M}}_G$, baryonic mass ${\mathrm{M}}_B$, equatorial radius ${\mathrm{r}}_e$, polar radius ${\mathrm{r}}_p$, the ratio of central to equatorial frequency ${\mathrm{\Omega }}_c/{\mathrm{\Omega }}_e$, and stability parameter $T/|W|$. The $T=10$ MeV entries correspond to Figure 5 and the $T=50$ MeV entries correspond to Figure 6; see text for more details.

The density and frequency maps for $T=10$ MeV are shown in Figure 5, where the top row shows results for ${\widehat{A}}^{-1}$ = 0.3 and the bottom for ${\widehat{A}}^{-1}=1.0$. The lesser degree of differential rotation is shown very clearly in the frequency map, where the difference of frequency values in the star only spans 320 Hz. In contrast, the star with a higher degree of differential rotation sees a span of 5,600 Hz from the highest to lowest frequency values. The density maps show an interesting depiction of the overall structural deformation. For ${\widehat{A}}^{-1}=0.3$, the star takes an ellipsoid-like shape, but for ${\widehat{A}}^{-1}=1.0$, the star instead takes a quasi-toroidal shape. While each star was initialized with the same central density of 400 MeV/fm³, the star with ${\widehat{A}}^{-1}=1.0$ experiences much higher densities outside of the center of the star. A similar story is seen for $T=50$ MeV in Figure 6 but with even higher densities observed at the higher temperature.

Figure 5

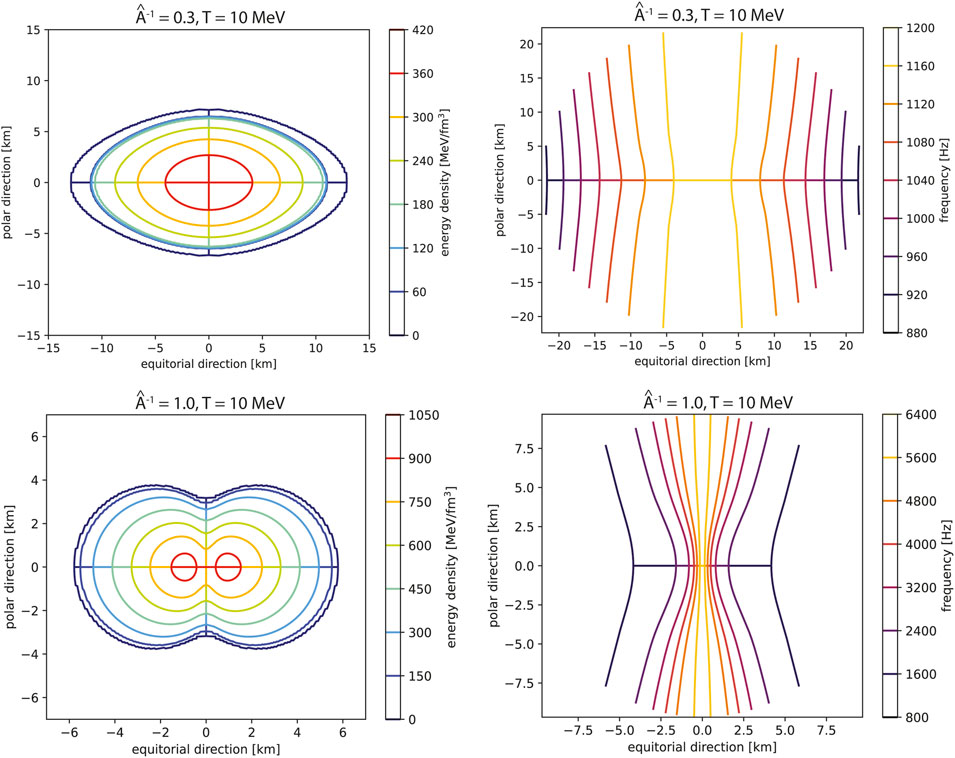
Figure 5. Energy density (left) and frequency (right) contours for individual stellar models at two degrees of differential rotation, constructed using the EOS model at $T=10$ MeV. The top row has a lower degree of differential rotation $({\widehat{A}}^{-1}=0.3)$ and the bottom has a higher degree $({\widehat{A}}^{-1}=1.0)$.

Figure 6

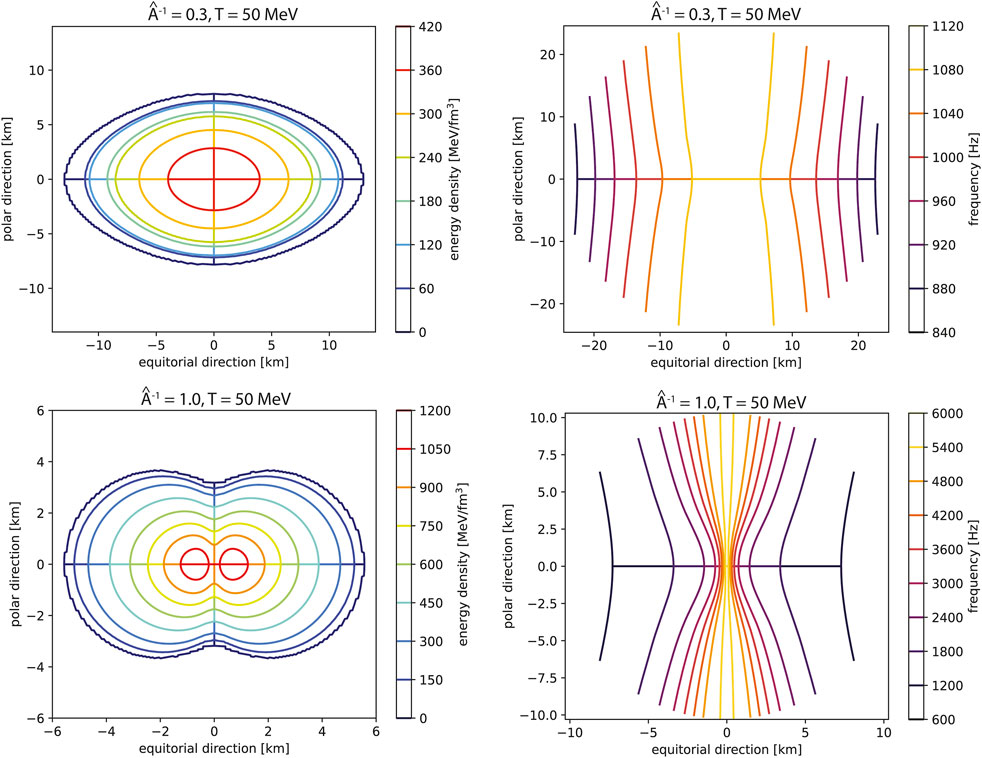
Figure 6. Energy density (left) and frequency (right) contours for individual stellar models at two degrees of differential rotation, constructed using the EOS model at $T=50$ MeV. The top row has a lower degree of differential rotation $({\widehat{A}}^{-1}=0.3)$ and the bottom has a higher degree $({\widehat{A}}^{-1}=1.0)$.

As shown in Section 3.2, the stability of the star depends not only on the deformation characterized by $r_{ratio}$ but also on the degree of differential rotation. In Table 2, all four models have the same value of $r_{ratio}$. For both temperatures, the stars computed with ${\widehat{A}}^{-1}=0.3$ have stability parameters $T/|W|$ well below the critical limit of 0.25. However, the stars with ${\widehat{A}}^{-1}=1.0$ are well above the critical limit for $\beta$, where the stability parameter is 0.64 for $T=10$ MeV and 0.75 for $T=50$ MeV. These stars are well beyond the threshold for the dynamical bar-mode instability and thus likely unphysical.

The timescale over which the dynamical bar-mode instability develops, also known as the dynamical timescale, is proportional to $\frac{{\text{R}}^{3/2}}{{\text{M}}^{1/2}}$. While this is not a definite indication of the growth time of the instability, which would instead require a full simulation in both time and space (see Ref. [52] for a good example), for extremely unstable configurations the dynamical timescale can provide some idea of how long these stars may exist with the bar-mode instability excited before collapse. For the unstable configuration at $T=10$ MeV, the dynamical timescale is $\propto$ 35.8 s, and for the unstable configuration at $T=50$ MeV, the dynamical timescale is $\propto$ 34.9 s.

3.4 Key approximations

The preceding sections present results dependent on the the underlying theoretical frameworks discussed in Section 2, which employ important approximations, discussed below.

The finite temperature EOS models at $T=10$ and 50 MeV are derived from calculations utilizing the RBHF approximation, described in Section 2.1. While this method offers significant improvements over other approaches to modeling relativistic numerical matter, it still involves key approximations [36]. For instance, nucleon-nucleon interactions are modeled using OBE potentials, with the Bonn-B potential selected in this paper for stability at high densities. Although RBHF theory does not require adjustable parameters, which is an advantage, it omits higher-order quantum corrections [56, 57]. One of the most important higher-order effects missing in RBHF is the inclusion of three-nucleon forces, which are known to significantly influence high-density matter [58]. Other potentially influential effects excluded in the RBHF approximation include higher-order relativistic many-body corrections, ring diagrams, vertex corrections, self-energy insertions, and medium polarization effects; a more complete discussion of these effects can be found in [14, 59, 60].

Variations in the choice of OBE potential and omission of quantum corrections, such as three-body forces, can introduce errors in the RBHF EOS of up to 10%, as demonstrated in Brockmann and Machleidt [36]. Using chiral effective field theory, Hebeler and Schwenk [61] and Tews et al. [62] concluded that including three-body forces affects neutron star radius and mass predictions by 5%–10%.

In addition, the EOS models include finite temperatures (10 MeV and 50 MeV), which are essential for modeling neutron stars formed in extreme events like supernovae or binary neutron star mergers Steiner et al. [63]. However, as mentioned before, the neutron star crust is assumed to be at zero temperature, while the core is modeled at finite temperatures. This approximation may introduce inconsistencies in the determination of properties like neutron star mass and radius, especially in higher temperature regimes. In particular, the radius increases due to thermal pressure in the crust, potentially making the star slightly larger.

When modeling differential rotation in neutron stars, the rotation profile, given in Equation 4, is parameterized by ${\widehat{A}}^{-1}$, representing the degree of differential rotation. This profile, while consistent with the original CST algorithm discussed in Section 2.2, is chosen for mathematical convenience rather than based on astrophysical observations, potentially limiting its accuracy for real neutron stars. Uncertainties in the choice of the rotation profile may cause errors of 5%–15% in star mass and radius predictions; for more on uncertainties related to differential rotation profiles and their impact on neutron star stability and mass limits, see Baumgarte and Shapiro [64]. Additionally, the assumption of axial symmetry is a simplification. In reality, neutron stars may exhibit more complex geometries, especially under differential rotation and dynamical instabilities.

For a comprehensive review discussing EOS uncertainties, neutron star mass-radius relationships, and the challenges of matching theoretical models with astrophysical data, see Lattimer and Prakash [65].

4 Discussion and conclusion

In this paper, we present a comprehensive investigation into the properties of differentially rotating neutron stars at finite temperatures up to 50 MeV. In Section 2.1, we detailed the process of constructing models for the equation of state of neutron star matter at two temperatures, 10 and 50 MeV, using the relativistic Brueckner-Hartree-Fock (RBHF) formalism modified to include thermal effects, utilizing the Bonn-B potential for the one-boson exchange (OBE) interaction. The inclusion of temperature is essential for the realistic modeling of extreme astrophysical events, such as binary neutron star (BNS) mergers or core-collapse supernovae, where differential rotation is prevalent.

The RBHF approach goes well beyond standard relativistic mean-field (RMF) calculations and relativistic Hartree-Fock (RHF) methods. The RBHF formalism includes the relativistic scattering $(\mathbf{T})$ matrix, which accounts for dynamical correlations among nucleons that are ignored in RMF and RHF. Furthermore, in sharp contrast to RMF and RHF, there are no adjustable parameters in the RBHF approach, making it a more fundamental and predictive theory compared to RMF and RHF models.

The two EOS models were used as input to the numerical scheme to determine the bulk properties of differentially rotating compact objects, focusing on heavily deformed objects characterized by the ratio of their polar to equatorial radii, $r_{ratio}$. In Section 3.1, we constructed stellar sequences with varying $r_{ratio}$ values (0.8–0.3) over a range of central densities for all four finite temperature EOS models. Our results are consistent with previous literature at zero temperature, demonstrating that a higher degree of differential rotation $({\widehat{A}}^{-1}\to 1.0)$ results in higher mass stars at lower central densities compared to lower values of ${\widehat{A}}^{-1}$, especially as $r_{ratio}$ decreases.

In Section 3.2, we explored the stability of the calculated stellar models against rotational instabilities, specifically the dynamical bar-mode instability. At a temperature of 10 MeV, the average $r_{ratio}$ value for stars unstable against dynamical bar-mode excitement is 0.49. For the higher temperature of 50 MeV, the average $r_{ratio}$ for unstable stars is 0.455. These results highlight that deformation, characterized by $r_{ratio}$, has a more significant impact on the star’s stability against dynamical instabilities compared to temperature.

In Section 3.3, we presented individual stellar maps of density and frequency distributions for two degrees of differential rotation for each EOS model. As expected, the frequency range for higher degrees of differential rotation (and higher values of ${\widehat{A}}^{-1}$ was much wider. Higher values of ${\widehat{A}}^{-1}$ also resulted in more pronounced structural deformations, indicating a strong dependence of the rotational profile on the degree of differential rotation.Finally, in Section 3.4, key approximations and their influence on calculated results are discussed. Variations in the choice of OBE potential and omission of quantum corrections like three-body forces can introduce errors in the RBHF EOS of up to 10%, which can, in turn, affect neutron star radius and mass predictions by 5%–10%. Additional uncertainty may be introduced by the choice of a linear rotational profile described in Section 2.2, on the order of 5%–15% in star mass and radius predictions.In conclusion, our study underscores the necessity of incorporating differential rotation and finite temperature effects in neutron star models to predict their properties and stability accurately. The stability of differentially rotating neutron stars against bar-mode deformation, a key rotational instability, is only weakly dependent on temperature. Differential rotation significantly affects the maximum mass and radius of neutron stars, and the threshold for the onset of bar-mode instability shows minimal sensitivity to temperature changes within the examined range. These findings are crucial for interpreting observational data from neutron star mergers and other high-energy astrophysical events (see, for instance, [66–74]).

The insights gained from this research are particularly relevant in the context of observations from current and future gravitational wave detectors such as LIGO [75], Virgo [76], KAGRA [77], and the upcoming Einstein Telescope [78]. Moreover, X-ray and radio telescopes, including the Chandra X-ray Observatory [79], XMM-Newton [80], the Very Large Array (VLA) [81], the Square Kilometre Array (SKA) [82], and the Five-hundred-meter Aperture Spherical Radio Telescope (FAST) [83] provide crucial observational data that can further constrain the models presented here.

Future work should extend these models to include additional physical effects, such as magnetic fields and more sophisticated treatments of thermal transport processes, to provide an even more comprehensive understanding of neutron star dynamics and stability under extreme conditions.

Data availability statement

The raw data supporting the conclusions of this article will be made available by the authors, without undue reservation.

Author contributions

DF: Conceptualization, Data curation, Formal Analysis, Investigation, Methodology, Software, Validation, Visualization, Writing–original draft, Writing–review and editing. FW: Conceptualization, Data curation, Formal Analysis, Funding acquisition, Investigation, Methodology, Project administration, Software, Supervision, Validation, Writing–original draft, Writing–review and editing. RN: Conceptualization, Funding acquisition, Methodology, Software, Validation, Writing–original draft, Writing–review and editing.

Funding

The author(s) declare that financial support was received for the research, authorship, and/or publication of this article. DF and FW are supported by the National Science Foundation (USA) under Grant No. PHY-2012152.

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

1. Becker W. Neutron stars and pulsars. Astrophysics and space science library. Berlin Heidelberg: Springer (2009).

Google Scholar

2. Reddy S. Neutron stars as astrophysical laboratories. Rev Mod Phys (2012) 84:85–120. doi:10.1103/RevModPhys.84.85

CrossRef Full Text | Google Scholar

3. Burgio G, Schulze H-J, Vidaña I, Wei J-B. Neutron stars and the nuclear equation of state. Prog Part Nucl Phys (2021) 120:103879. doi:10.1016/j.ppnp.2021.103879

CrossRef Full Text | Google Scholar

4. Shibata M, Uryu K. Simulation of merging binary neutron stars in full general relativity: γ= 2 case. Phys Rev D (2000) 61:064001. doi:10.1103/physrevd.61.064001

CrossRef Full Text | Google Scholar

5. Shibata M, Kiuchi K. Gravitational waves from remnant massive neutron stars of binary neutron star merger: viscous hydrodynamics effects. Phys Rev D (2017) 95:123003. doi:10.1103/physrevd.95.123003

CrossRef Full Text | Google Scholar

6. Fujibayashi S, Kiuchi K, Nishimura N, Sekiguchi Y, Shibata M. Mass ejection from the remnant of a binary neutron star merger: viscous-radiation hydrodynamics study. Astrophysical J (2018) 860:64. doi:10.3847/1538-4357/aabafd

CrossRef Full Text | Google Scholar

7. Perego A, Bernuzzi S, Radice D. Thermodynamics conditions of matter in neutron star mergers. The Eur Phys J A (2019) 55:124. doi:10.1140/epja/i2019-12810-7

CrossRef Full Text | Google Scholar

8. Cook GB, Shapiro SL, Teukolsky SA. Rapidly rotating neutron stars in general relativity: realistic equations of state. Astrophysical J (1994) 424:823–45. doi:10.1086/173934

CrossRef Full Text | Google Scholar

9. Schaab C, Weigel MK. Differential rotation in neutron stars. Phys Lett B (1999) 450:187–94. doi:10.1016/S0370-2693(99)00195-3

CrossRef Full Text | Google Scholar

10. Galeazzi F, Yoshida S, Eriguchi Y. Differentially-rotating neutron star models with a parametrized rotation profile. Astron & Astrophysics (2012) 541:A156. doi:10.1051/0004-6361/201016316

CrossRef Full Text | Google Scholar

11. Hanauske M, Takami K, Bovard L, Rezzolla L, Font JA, Galeazzi F, et al. Rotational properties of hypermassive neutron stars from binary mergers. Phys Rev D (2017) 96:043004. doi:10.1103/physrevd.96.043004

CrossRef Full Text | Google Scholar

12. Marques M, Oertel M, Hempel M, Novak J. New temperature dependent hyperonic equation of state: application to rotating neutron star models and i-q relations. Phys Rev C (2017) 96:045806. doi:10.1103/physrevc.96.045806

CrossRef Full Text | Google Scholar

13. Camelio G, Dietrich T, Marques M, Rosswog S. Rotating neutron stars with nonbarotropic thermal profile. Phys Rev D (2019) 100:123001. doi:10.1103/physrevd.100.123001

CrossRef Full Text | Google Scholar

14. Weber F. Pulsars as astrophysical laboratories for nuclear and particle physics series in high energy physics, cosmology and gravitation. FL, USA: CRC Press (1999). doi:10.1201/9780203741719

CrossRef Full Text | Google Scholar

15. Glendenning N. Compact stars: nuclear physics particle physics and general relativity. Astronomy and astrophysics library (2012).

Google Scholar

16. Spinella WM, Weber F. Dense baryonic matter in the cores of neutron stars. In: Topics on strong gravity: a modern view on theories and experiments (world scientific) (2020). p. 85–152.

CrossRef Full Text | Google Scholar

17. Weber F, Farrell D, Spinella WM, Malfatti G, Orsaria MG, Contrera GA, et al. Phases of hadron-quark matter in (proto) neutron stars. Universe (2019) 5:169. doi:10.3390/universe5070169

CrossRef Full Text | Google Scholar

18. Malfatti G, Orsaria MG, Contrera GA, Weber F, Ranea-Sandoval IF. Hot quark matter and (proto-) neutron stars. Phys Rev C (2019) 100:015803. doi:10.1103/PhysRevC.100.015803

CrossRef Full Text | Google Scholar

19. Malfatti G, Orsaria MG, Ranea-Sandoval IF, Contrera GA, Weber F. Delta baryons and diquark formation in the cores of neutron stars. Phys Rev D (2020) 102:063008. doi:10.1103/PhysRevD.102.063008

CrossRef Full Text | Google Scholar

20. Sedrakian A, Li JJ, Weber F. Heavy baryons in compact stars. Prog Part Nucl Phys (2023) 475:104041. doi:10.1016/j.ppnp.2023.104041

CrossRef Full Text | Google Scholar

21. Lattimer JM, Steiner AW. Constraints on the symmetry energy using the mass-radius relation of neutron stars. Eur Phys J A (2014) 50:40–24. doi:10.1140/epja/i2014-14040-y

CrossRef Full Text | Google Scholar

22. Lattimer JM. Neutron star mass and radius measurements. Universe (2019) 5:159. doi:10.3390/universe5070159

CrossRef Full Text | Google Scholar

23. Stone JR. Nuclear physics and astrophysics constraints on the high density matter equation of state. Universe (2021) 7:257. doi:10.3390/universe7080257

CrossRef Full Text | Google Scholar

24. Poschenrieder P, Weigel M. Nuclear matter problem in the relativistic green’s function approach. Phys Rev C (1988) 38:471–86. doi:10.1103/physrevc.38.471

PubMed Abstract | CrossRef Full Text | Google Scholar

25. Horowitz C, Serot BD. The relativistic two-nucleon problem in nuclear matter. Nucl Phys A (1987) 464:613–99. doi:10.1016/0375-9474(87)90370-8

CrossRef Full Text | Google Scholar

26. Zuo W, Bombaci I, Lombardo U. Asymmetric nuclear matter from an extended brueckner-Hartree-Fock approach. Phys Rev C (1999) 60:024605. doi:10.1103/PhysRevC.60.024605

CrossRef Full Text | Google Scholar

27. Wang S, Zhao Q, Ring P, Meng J. Nuclear matter in relativistic brueckner-Hartree-Fock theory with bonn potential in the full Dirac space. Phys Rev C (2021) 103:054319. doi:10.1103/physrevc.103.054319

CrossRef Full Text | Google Scholar

28. Lovato A, Bombaci I, Logoteta D, Piarulli M, Wiringa RB. Benchmark calculations of infinite neutron matter with realistic two- and three-nucleon potentials. Phys Rev C (2022) 105:055808. doi:10.1103/PhysRevC.105.055808

CrossRef Full Text | Google Scholar

29. Tong H, Wang C, Wang S. Nuclear matter and neutron stars from relativistic brueckner–Hartree–Fock theory. Astrophysical J (2022) 930:137. doi:10.3847/1538-4357/ac65fc

CrossRef Full Text | Google Scholar

30. Farrell D, Weber F. Relativistic brueckner–Hartree–Fock calculations for cold and hot neutron stars. Astrophysical J (2024) 969:49. doi:10.3847/1538-4357/ad47b8

CrossRef Full Text | Google Scholar

31. Faber JA, Rasio FA. Binary neutron star mergers. Living Rev Relativity (2012) 15:8–83. doi:10.12942/lrr-2012-8

CrossRef Full Text | Google Scholar

32. Baiotti L, Rezzolla L. Binary neutron star mergers: a review of einstein’s richest laboratory. Rep Prog Phys (2017) 80:096901. doi:10.1088/1361-6633/aa67bb

PubMed Abstract | CrossRef Full Text | Google Scholar

33. Raithel CA, Özel F, Psaltis D. Finite-temperature extension for cold neutron star equations of state. Astrophysical J (2019) 875:12. doi:10.3847/1538-4357/ab08ea

CrossRef Full Text | Google Scholar

34. Farrell D, Alp A, Weber F, Spinella W, Malfatti G, Orsaria MG, et al. Hot neutron star matter and proto-neutron stars. World Scientific (2023) 199–259. doi:10.1142/9789811220913_0005

CrossRef Full Text | Google Scholar

35. Martin PC, Schwinger J. Theory of many-particle systems. i. Phys Rev (1959) 115:1342–73. doi:10.1103/physrev.115.1342

CrossRef Full Text | Google Scholar

36. Brockmann R, Machleidt R. Relativistic nuclear structure. i. nuclear matter. Phys Rev C (1990) 42:1965–80. doi:10.1103/physrevc.42.1965

PubMed Abstract | CrossRef Full Text | Google Scholar

37. Wang C, Wang S, Tong H, Hu J, Yao J. Low-momentum relativistic nucleon-nucleon potentials: nuclear matter. Phys Rev C (2024) 109:034002. doi:10.1103/physrevc.109.034002

CrossRef Full Text | Google Scholar

38. Dolan L, Jackiw R. Symmetry behavior at finite temperature. Phys Rev D (1974) 9:3320–41. doi:10.1103/PhysRevD.9.3320

CrossRef Full Text | Google Scholar

39. ter Haar B, Malfliet R. Equation of state of nuclear matter in the relativistic Dirac-brueckner approach. Phys Rev Lett (1986) 56:1237–40. doi:10.1103/physrevlett.56.1237

PubMed Abstract | CrossRef Full Text | Google Scholar

40. Komatsu H, Eriguchi Y, Hachisu I. Rapidly rotating general relativistic stars–i. numerical method and its application to uniformly rotating polytropes. Monthly Notices R Astronomical Soc (1989) 237:355–79. doi:10.1093/mnras/237.2.355

CrossRef Full Text | Google Scholar

41. Stergioulas N. Rotating stars in relativity. Living Rev Relativity (2003) 6:3–109. doi:10.12942/lrr-2003-3

CrossRef Full Text | Google Scholar

42. Shapiro SL. Differential rotation in neutron stars: magnetic braking and viscous damping. Astrophysical J (2000) 544:397–408. doi:10.1086/317209

CrossRef Full Text | Google Scholar

43. Morrison IA, Baumgarte TW, Shapiro SL. Effect of differential rotation on the maximum mass of neutron stars: realistic nuclear equations of state. Astrophysical J (2004) 610:941–7. doi:10.1086/421897

CrossRef Full Text | Google Scholar

44. Zhou E, Tsokaros A, Uryu K, Xu R, Shibata M. Differentially rotating strange star in general relativity. Phys Rev D (2019) 100:043015. doi:10.1103/physrevd.100.043015

CrossRef Full Text | Google Scholar

45. Chandrasekhar S. Ellipsoidal figures of equilibrium. New York: Dover (1987).

Google Scholar

46. Shapiro SL, Teukolsky SA. Black holes, white dwarfs, and neutron stars: the physics of compact objects. John Wiley & Sons (2008).

Google Scholar

47. Cutler C, Lindblom L. Post-Newtonian frequencies for the pulsations of rapidly rotating neutron stars. Astrophysical J (1992) 385:630–41. doi:10.1086/170968

CrossRef Full Text | Google Scholar

48. Hunter C. On secular stability, secular instability, and points of bifurcation of rotating gaseous masses. Astrophysical J (1977) 213:497–517. doi:10.1086/155181

CrossRef Full Text | Google Scholar

49. Paschalidis V, Stergioulas N. Rotating stars in relativity. Living Rev Relativity (2017) 20:7–169. doi:10.1007/s41114-017-0008-x

PubMed Abstract | CrossRef Full Text | Google Scholar

50. Saijo M, Shibata M, Baumgarte TW, Shapiro SL. Dynamical bar instability in rotating stars: effect of general relativity. Astrophysical J (2001) 548:919–31. doi:10.1086/319016

CrossRef Full Text | Google Scholar

51. Bodenheimer P, Ostriker JP. Rapidly rotating stars. viii. zero-viscosity polytropic sequences. Astrophysical J (1973) 180:159–70. doi:10.1086/151951

CrossRef Full Text | Google Scholar

52. Shibata M, Baumgarte TW, Shapiro SL. The bar-mode instability in differentially rotating neutron stars: simulations in full general relativity. Astrophysical J (2000) 542:453–63. doi:10.1086/309525

CrossRef Full Text | Google Scholar

53. Shibata M, Karino S, Eriguchi Y. Dynamical instability of differentially rotating stars. Monthly Notices R Astronomical Soc (2002) 334:L27–L31. doi:10.1046/j.1365-8711.2002.05724.x

CrossRef Full Text | Google Scholar

54. Camarda KD, Anninos P, Fragile PC, Font JA. Dynamical bar-mode instability in differentially rotating magnetized neutron stars. Astrophysical J (2009) 707:1610–22. doi:10.1088/0004-637x/707/2/1610

CrossRef Full Text | Google Scholar

55. Di Giovanni F, Sanchis-Gual N, Cerdá-Durán P, Zilhao M, Herdeiro C, Font JA, et al. Dynamical bar-mode instability in spinning bosonic stars. Phys Rev D (2020) 102:124009. doi:10.1103/physrevd.102.124009

CrossRef Full Text | Google Scholar

56. Ring P. Relativistic mean field theory in finite nuclei. Prog Part Nucl Phys (1996) 37:193–263. doi:10.1016/0146-6410(96)00054-3

CrossRef Full Text | Google Scholar

57. Akmal A, Pandharipande V, Ravenhall D. Equation of state of nucleon matter and neutron star structure. Phys Rev C (1998) 58:1804–28. doi:10.1103/physrevc.58.1804

CrossRef Full Text | Google Scholar

58. Epelbaum E, Hammer H-W, Meissner U-G. Modern theory of nuclear forces. Rev Mod Phys (2009) 81:1773–825. doi:10.1103/RevModPhys.81.1773

CrossRef Full Text | Google Scholar

59. Sammarruca F, Chen B, Coraggio L, Itaco N, Machleidt R. Dirac-brueckner-Hartree-Fock versus chiral effective field theory. Phys Rev C—Nuclear Phys (2012) 86:054317. doi:10.1103/physrevc.86.054317

CrossRef Full Text | Google Scholar

60. Shen S, Liang H, Meng J, Ring P, Zhang S. Fully self-consistent relativistic brueckner-Hartree-Fock theory for finite nuclei. Phys Rev C (2017) 96:014316. doi:10.1103/physrevc.96.014316

CrossRef Full Text | Google Scholar

61. Hebeler K, Schwenk A. Chiral three-nucleon forces and neutron matter. Phys Rev C (2010) 82:014314. doi:10.1103/physrevc.82.014314

CrossRef Full Text | Google Scholar

62. Tews I, Krüger T, Hebeler K, Schwenk A. Neutron matter at next-to-next-to-next-to-leading order in chiral effective field theory. Phys Rev Lett (2013) 110:032504. doi:10.1103/physrevlett.110.032504

PubMed Abstract | CrossRef Full Text | Google Scholar

63. Steiner A, Hempel M, Fischer T. Core-collapse supernova equations of state. Astrophysical J (2013) 774:17. doi:10.1088/0004-637x/774/1/17

CrossRef Full Text | Google Scholar

64. Baumgarte T, Shapiro S. On the maximum mass of differentially rotating neutron stars. Astrophysical J (2003) 585:921–8. doi:10.1086/312425

CrossRef Full Text | Google Scholar

65. Lattimer J, Prakash M. Neutron star structure and the equation of state. Astrophysical J (2001) 550:426–42. doi:10.1086/319702

CrossRef Full Text | Google Scholar

66. Lattimer JM, Prakash M. Neutron star observations: progress and problems. Phys Rep (2007) 442:109–65. doi:10.1016/j.physrep.2007.02.003

CrossRef Full Text | Google Scholar

67. Chirenti CL, Rezzolla L. The merger of two neutron stars: gravitational waves and electromagnetic signals. Astrophysical J (2012) 760:150. doi:10.1088/0004-637X/760/2/150

CrossRef Full Text | Google Scholar

68. Metzger BD, Berger E. Kilonovae. Annu Rev Astron Astrophysics (2012) 50:503–46. doi:10.1146/annurev-astro-081811-125339

CrossRef Full Text | Google Scholar

69. Zhang B. The origin of long-duration gamma-ray bursts. Nat Phys (2016) 12:737–41. doi:10.1038/nphys3805

CrossRef Full Text | Google Scholar

70. Abbott BP, Abbott R, Abbott T, Acernese F, Ackley K, Adams C, et al. Gw170817: observation of gravitational waves from a binary neutron star inspiral. Phys Rev Lett (2017) 119:161101. doi:10.1103/PhysRevLett.119.161101

PubMed Abstract | CrossRef Full Text | Google Scholar

71. Kasen D, Metzger B, Barnes J, Quataert E, Ramirez-Ruiz E Kilonova from the ejecta of a neutron star merger. Nature (2017) 551:80–84. doi:10.1038/nature24063

PubMed Abstract | CrossRef Full Text | Google Scholar

72. Margalit B, Metzger BD. Constraining the maximum mass of neutron stars from multi-messenger observations of GW170817. Astrophysical J Lett (2017) 850:L19. doi:10.3847/2041-8213/aa991c

CrossRef Full Text | Google Scholar

73. Piro AL. The role of neutron star merger kinematics in explaining the diversity of short gamma-ray bursts. Astrophysical J (2019) 885:10. doi:10.3847/1538-4357/ab3f99

CrossRef Full Text | Google Scholar

74. Orsaria MG, Malfatti G, Mariani M, Ranea-Sandoval IF, García F, Spinella WM, et al. Phase transitions in neutron stars and their links to gravitational waves. J Phys G: Nucl Part Phys (2019) 46:073002. doi:10.1088/1361-6471/ab1d81

CrossRef Full Text | Google Scholar

75. Aasi J, Abbott B, Abbott R, Abernathy MR, Ackley K, Adams C, et al. Advanced ligo. Class Quan Gravity (2015) 32, 074001, doi:10.1088/0264-9381/32/7/074001

CrossRef Full Text | Google Scholar

76. Acernese F, Agathos M, Agatsuma K, Aisa D, Allemandou N, Allocca A, et al. Advanced virgo: a second-generation interferometric gravitational wave detector. Classical Quan Gravity (2015) 32:024001. doi:10.1088/0264-9381/32/2/024001

CrossRef Full Text | Google Scholar

77. Aso Y, Michimura Y, Somiya K, Ando M, Mio N, Sekiguchi T, et al. Kagra: 2.5 generation interferometric gravitational wave detector. Phys Rev D (2020) 88:043007. doi:10.1103/physrevd.88.043007

CrossRef Full Text | Google Scholar

78. Punturo M, Abernathy M, Acernese F, Allen B, Andersson N, Arun K, et al. The einstein telescope: a third-generation gravitational wave observatory. Classical Quan Gravity (2010) 27:194002. doi:10.1088/0264-9381/27/19/194002

CrossRef Full Text | Google Scholar

79. Weisskopf M, Tananbaum H, Van Speybroeck L, O’Dell S The chandra x-ray observatory: exploring the high-energy universe, 112. WA, USA: Publications of the Astronomical Society of the Pacific (2000). 586.

Google Scholar

80. Jansen F, Lumb D, Altieri B, Clavel J, Ehle M, Erd C, et al. The xmm-Newton observatory. Astron & Astrophysics (2001) 365. doi:10.1051/0004-6361:20000036

CrossRef Full Text | Google Scholar

81. Perley R, Chandler C, Butler B, Wrobel J. The expanded very large array: a new telescope for new science. Astrophysical J Lett (2011) 739:L1. doi:10.1088/2041-8205/739/1/l1

CrossRef Full Text | Google Scholar

82. Braun R, Bourke T, Green JA, Keane E, Wagg J The square kilometre array. Proc Sci AASKA14 (2015) 174.

CrossRef Full Text | Google Scholar

83. Nan R, Li D, Jin C, Wang Q, Zhu Y, Zhu W, et al. The five-hundred-meter aperture spherical radio telescope (fast) project. Int J Mod Phys D (2011) 20:989–1024. doi:10.1142/s0218271811019335

CrossRef Full Text | Google Scholar