Pattern phase transition of spin particle lattice system

To better understand the pattern phase transition of both physical and biological systems, we investigate a two-dimensional spin particle lattice system using statistical mechanics methods together with XY model governed by Hamiltonian equations of motion. By tweaking the coupling strength and the intensity of the generalization field, we observe phase transitions among four patterns of spin particles, i.e., vortex, ferromagnet, worm and anti-ferromagnet. In addition, we analyze the effect of space boundaries on the formations of vortex and worm. Considering the inherent dynamics of individual particles, we revealed the forming mechanism of such phase transitions, which provides a new perspective for understanding the emergence of phase transition of spin particles systems.

1 Introduction

Various types of phase transition are appealing features of both physical and biological particle systems, which have been extensively studied during recent decades. In general, pattern phase transition means a system composed of a large number of interacting particles undergoes a transition from one pattern phase to another responding to the change of one or more external parameters. There are abundant pattern phase transitions in natural, biological, chemical and physical systems, such as bird flocks [1–4], insects [5–7], bacterial colonies [8–10], fish schools and shoals [11–13], groups of mammals and crowds [14–16], crystals and superfluids [17, 18], etc. Researchers in the fields of physics, control engineering, system science, artificial intelligence and computer science recently have become more and more interested in the appealing pattern phase transition for such abundant particle systems.

Revealing the mechanism of phase transition is fairly helpful to understand complex physical and biological collective behaviors. The various pattern phase inspired by self-propelled particle systems are highly dependent on the interaction between particles, but the interaction mechanism of the phase transition is unknown, and one of the difficulties is the lack of the ability to predict the final equilibrium state and its stability only through the interaction between self-driven particles. In biological, physical and engineering multi-agent systems, researchers have discovered a large number of phase transitions between different modes. Among these investigations, Carrillo et al [19] researched the formation conditions of single and double rotating mills. Single-vortex configurations can be observed under generally random initial conditions, however, double-vortex configurations (i.e., half of the particles rotating clockwise and the other half counterclockwise) are only possible under carefully chosen initial conditions. Birnir [20] found the circling and flocking solutions of ordinary differential equations derived from the Vicsek model. Building on the work of Gautrais et al. [21], Calovi et al. [22] showed a switched phase diagram between the circular (milling) patterns and migratory patterns of fish schools by varying the weights of two control terms in the model. Cheng et al. [23] discovered pattern transitions among gaseous, liquid, and crystalline flocks by slightly varying the zero crossing slope of the inter-particle interaction function.

Analogous to kinetic systems, study of structure and phase transitions like lattices has drawn increasing attentions in recent years. The well-known statistical-mechanical models of particles like XY model and Ising model have intrinsic phase transitions for regular and irregular lattices [24]. From the perspective of statistical physics, the XY model with Hamiltonian equations of motion is probably one of the most concise models which have continuous degrees of freedom. In the field of condensed matter physics, it is a model which realized the phase transition of superfluid $H{e}^4$, High-$T_c$ cuprate and Josephson junction arrays [25, 26]. The system undergoes the well-known Berezinsky-Kosterlitz-Thouless transition in two-dimensional spaces [27], whereas experiencing a second-order phase transition in three-dimensional spaces [28]. Nowadays, the study of physical particle systems has shed some lights onto both physical and biological collective motion investigation [29]. Interestingly, in recent years, researchers have found that the phase transitions that exist in natural biological or physical systems have similarities, and it is possible to learn from each other in the theoretical study of phase transition mechanisms. For instance, by slightly varying the vision range in a group of freely moving particles, Cheng et al. [30] discovered various pattern phase transitions between crystalline, liquid, gaseous, and mill-liquid coexistence states. Referring to a lattice-gas model for superfluid helium, Attanasi et al. [4] established a new model nourished by conservation-law and spontaneous symmetry breaking principle that nicely explains the universal fast synchronization behaviors in starling flocks.

With the pioneer efforts devoted to the collective motions on XY model, quite a few fascinating collective motion patterns are observed with the XY model, like flocking and torus. In this letter, we seek to refine the kinetic description of XY model which helps reveal the phase transition principles of XY model with Hamiltonian equations of motion. Following the dynamics of the XY model, we have meticulously described the role of model parameters in governing the state of the system so as to figure out the actual physical meaning of the parameters. By tweaking model parameters, a series of phase transitions emerge among vortex, ferromagnet, worm and anti-ferromagnet patterns.

2 Methods and results

The XY model has been widely applied to a large volume of physical systems like superfluids, nematic liquid crystals, electron nematics, planar magnets, and among others [25–28]. In this letter, we study an XY model considering an external field effects with Hamiltonian equations of motion and focus on the statistical properties from the perspective of particles dynamics. In the presence of a $p$-fold generalization field [31], we consider the $2D$ XY model with spin in the direction ${\theta }_i\in [\mathrm{0,2}\pi )$ on a square lattice with $M\times M$ particles.

$H_{XY}=-h\sum (\text{cos}\left(p{\theta }_i-\psi \right)-J{\displaystyle \sum _{⟨i,j⟩}}\text{cos}\left({\theta }_i-{\theta }_j\right),(1)$

where $h$ is the intensity of a $p$-fold generalization field and $J$ denotes the coupling strength within nearest neighbor. When $p=1$ and $p>1$, the first term denotes a uniaxial and $p$-fold generalization field, respectively [31]. $\psi$ is a fixed constant representing the direction of the $p$-fold generalization field. The $i$ and $j$ label the lattice sites on a 2D square lattice, $⟨i,j⟩$ denotes a nearest-neighbor set of the particle $i$, which is one unit away from particle $i$.

Consider the $i$-th particle’s spin, i.e., ${\theta }_i(t)$, the spin becomes rotator, and hence the XY model turns into a system of coupled rotators [32, 33]. By virtue of the process of taking the negative gradient for the Hamiltonian system in [34], the first derivative for the $i$-th object is obtained by taking negative gradient for system (1). Considering the effects of external noises, the spin particles obey the stochastic ordinary equation below,

$d{\theta }_i=\left[\mu \sin \left(\psi -p{\theta }_i\right)+J{\displaystyle \sum _{⟨i,j⟩}}\sin \left({\theta }_j-{\theta }_i\right)\right]dt+\sigma dW,(2)$

where $i=\mathrm{1,2},\dots ,M\times M$, $\mu =ph$, $\sigma dW$ is the external Gaussian white noise, and $\sigma$ is the corresponding magnitude.

Let $S_i=[\text{cos}({\theta }_i),\sin ({\theta }_i)]$, the phases of spin are quantified by three order parameters, i.e., the consensus state order of spin direction

$V_c=\frac{1}{M\times M}‖{\displaystyle \sum _{i=1}^{M\times M}}{S}_i‖,(3)$

the parallel state order quantifying the parallel tendency

$V_p=1-\frac{1}{M\times M-1}{\displaystyle \sum _{i=1}^{M\times M-1}}‖S_i\times S_{i+1}‖,(4)$

and the vortex state order quantifying the vortex tendency

$V_v=\left\{\begin{array}{cc}1-\frac{1}{n}{\displaystyle \sum _{l\in \mathcal{N}}}‖{\displaystyle \sum _{k\in K}}{S}_{l+k}‖,\hfill & \text{if}n>0\hfill \\ 0,\hfill & \text{if}n=0\hfill \end{array}\right.,(5)$

where $\mathcal{N}=\{l|\parallel {\sum }_{k\in K}{S}_{l+k}\parallel <1,S_l\times S_{l+1}\ne 0,l=\mathrm{1,2},\dots ,M\times (M-1),\text{mod}(l,M)\ne 0\}$is the set of positions with vortices, $K=\{\mathrm{0,1},M,M+1\}$, “$\times$” denotes cross product, and $n=|\mathcal{N}|$is the number of a set $\mathcal{N}$.

Apparently, $V_c$ is obtained by taking the norm of the sum of all particle directions and then averaging it, which is crucial for quantifying the consistency of spin directions and obtaining the alignment degree of the entire system. That is, $V_c=1$indicates that the spin particles reach direction consensus state. $V_p$is calculated by averaging the magnitudes of the outer products of the directions of any two adjacent particles, which is essential for representing the parallel state of adjacent particles and obtaining the parallel trend of the entire system. That is, $V_p=1$indicates that the spin particles reach direction parallel state. Moreover, $n>0$means that vortex state occurs, $V_v$is derived by summing the directions of four adjacent particles and then averaging them, which is crucial for judging the vortex state of these four particles. Therefore, $V_v$is vital for measuring the vortex state sequence and reflecting vortex formation by quantifying local rotational arrangements. That is, $V_v=1$means that spin particles reach standard vortex state. Therefore, these parameters are chosen because they provide a straightforward method to differentiate between the various patterns emerging from our system. In order to show the order parameter characteristics of the four phases more clearly, the schematic diagram Figure 1 is exhibited. $V_v=1$ and $V_c=1$ mean the standard vortex (Figure 1A) and ferromagnet phase (Figure 1B), respectively. It is worth noting that we define a parallel state order parameter $V_p$ to distinguish worm and anti-ferromagnetic phases by combining the consensus and vortex state order parameters together. More precisely, $V_p<1$ and $V_v=0$ implies the worm phase (Figure 1C), whereas $V_p=1$ and $V_c<1$ represent the anti-ferromagnet phase (Figure 1D).

Figure 1

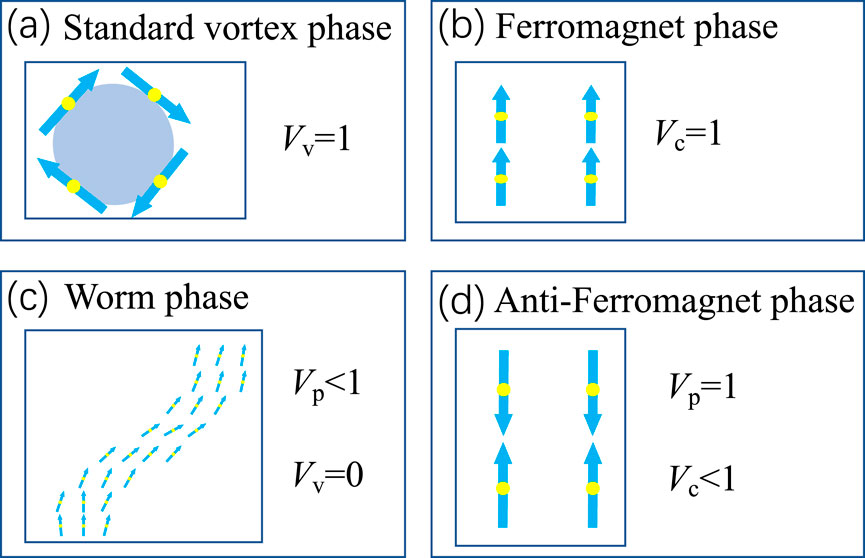
Figure 1. The order parameter characteristics of the four phases, i.e., vortex (A), ferromagnet (B), worm (C), and anti-ferromagnet (D), respectively.

In the numerical simulations, $M\times M$ particles are randomly initialized as ${\theta }_i(0)\in [\mathrm{0,2}\pi )$. The parameters are picked as: $\psi =\pi$, $p=2$, $M=50$ and $\sigma =0$. In order to highlight the phase transition, we demonstrate the spin motional phases in the space spanned by the two parameters $\widehat{\mu }={\text{log}}_{10}\mu$ and $\widehat{J}={\text{log}}_{10}J$.The parameters are presented on a logarithmic scale to encompass a wide range of values, this approach allows us to explore the behavior of the system across multiple orders of magnitude. This is important for understanding the fundamental properties and scalability of the system. With different combinations of $\widehat{\mu }$ and $\widehat{J}$, three phase transitions emerge from vortex (Figures 2D–H) to ferromagnet (Figure 2A), to worm (Figure 2B), and then to anti-ferromagnet (Figure 2C). More precisely, in the ferromagnet phase, the spin particles form parallel arrays and direction consensus, whereas in the anti-ferromagnet phase, the spin particles form anti-parallel pattern. In the worm phase, spin particles form a curved line arrangement configuration pattern like a worm. By contrast, in the vortex pattern, there are four adjacent spin particles that form an ordered rotation, crossover, relative arrangement, etc. In the vortex pattern, multiple vortex modes occur simultaneously.

Figure 2

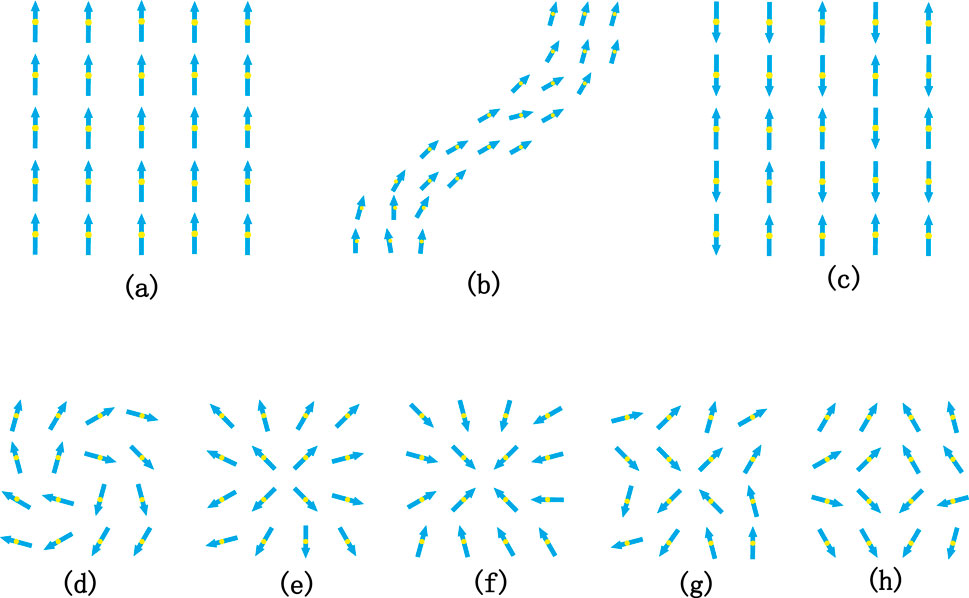
Figure 2. Ferromagnet (A), worm (B), anti-ferromagnet (C), and vortex in different forms (D–H). Dots represent the locations of the particles whereas arrows the spin directions. The particles are arranged with equal distances similar to crystals. Patterns (D–H) are rotational vortex, positive vortex, cross vortex, relative vortex and anti-vortex, respectively. Similar patterns [35] universally exist in superfluid, planar magnets, superconductors and electron nematics, etc. The XY dynamics system of spin particles undergoes phase transition among patterns (A–H) simply by tweaking a few model parameters.

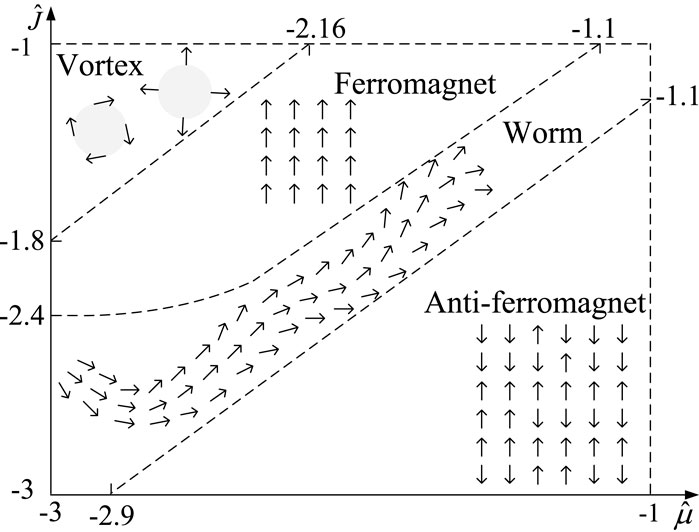
Figure 3 demonstrates the phase transitions among vortex, ferromagnet, worm and anti-ferromagnet patterns. At the top-left corner of the $\widehat{\mu }$-$\widehat{J}$ space, vortex pattern emerges by four adjacent spin particles, where the parameter $n>0$, implying the appearance of vortices. Appealingly, five distinct vortex modes have been observed in this phase, namely, rotational vortex, positive vortex, cross vortex, relative vortex and anti-vortex, as illustrated in Figures 2D–H. With increasing parameter $\widehat{\mu }$, that is, the upper middle of Figure 3, spin particles finally reach direction synchronization, which naturally forms a ferromagnet phase, i.e., $V_c=1$. In the middle diagonal stripe of Figure 3, group direction no longer reaches synchronization (i.e., $V_c<1$), the parameter $V_p<1$ and $V_v=0$ implying the emergence of worm phase. By keeping increasing the parameter $\widehat{\mu }$, that is, the bottom-right corner of Figure 3, anti-ferromagnet phase (i.e., $V_c<1$ and $V_p=1$) is yielded. In order to show the above four phase transition processes more vividly, we provide numerical simulation videos in the supplementary material and the link http://imds.aia.hust.edu.cn/info/1247/2403.htm.

Figure 3

Figure 3. Spin pattern phase diagram in the space spanned by parameters $\widehat{J}$and $\widehat{\mu }$.

In order to investigate more deeply into the principles governing the pattern phase transitions, we present three heat maps of $V_c$, $V_p$ and $V_v$ in Figures 4–6 along increasing parameters $\widehat{\mu }$ and $\widehat{J}$, respectively. Each point is an average over 50 independent runs, with each run lasting $1\times 10^5$ running steps guaranteeing the attainment of steady states.Note that the choice of $10^5$ stepsis a conservative estimate to ensure that steady states are attained uniformly across the entire parameter range.

Figure 4

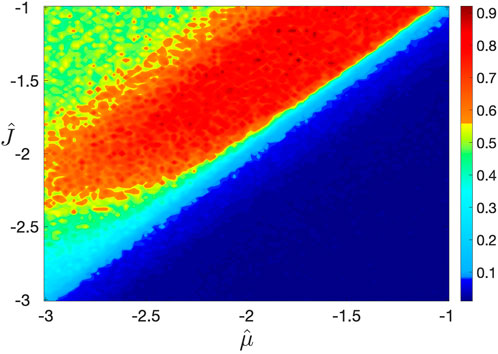
Figure 4. Heat map of the consensus state order parameter $V_c$. Here, $\widehat{J}$and $\widehat{\mu }$are sampled within the range of [−3, −1] with an interval of 0.02, resulting in a total of 10,201 data points, and each point is an average over 50 independent runs, with each run lasting $1\times 10^5$ running steps, guaranteeing the attainment of steady states. Parameter: $M=50$.

Figure 5

Figure 5. Heat map of the parallel state order parameter $V_p$. Here, $\widehat{J}$and $\widehat{\mu }$are sampled within the range of [−3, −1] with an interval of 0.02, resulting in a total of 10,201 data points, and each point is an average over 50 independent runs, with each run lasting $1\times 10^5$ running steps, guaranteeing the attainment of steady states. Parameter: $M=50$.

Figure 6

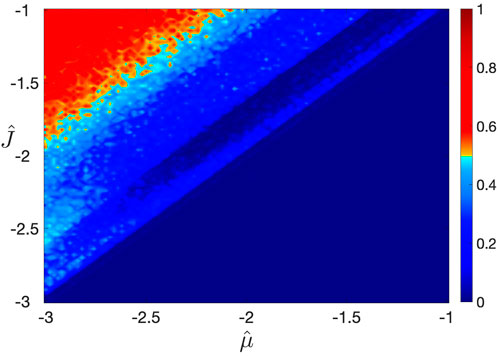
Figure 6. Heat map of the vortex state order parameter $V_v$. Here, $\widehat{J}$and $\widehat{\mu }$are sampled within the range of [−3, −1] with an interval of 0.02, resulting in a total of 10,201 data points, and each point is an average over 50 independent runs, with each run lasting $1\times 10^5$ running steps, guaranteeing the attainment of steady states. Parameter: $M=50$.

Significantly, the order parameter $V_c=1$implies ferromagnet. It is observed from Figure 4 that the red region corresponds to the ferromagnetic phase $(V_c=1)$. It is noteworthy that the value presented here is an average over 50 independent runs, thus there is a very small probability that there will be a non-ferromagnetic phase (i.e., $V_c\ne 1$). Consequently, the red region does not exactly equal 1, especially near the boundaries of pattern phase transition where the probability of a non-ferromagnetic phase increases, leading to the average value less than 1. Therefore, the pattern phase discussed here is a ferromagnetic phase in a probabilistic sense. The order parameter $V_p=1$means that the spin particles reach parallel state, from Figure 5, the parallel state in the blue region can be observed, which serves as an important basis for identifying the worm phase $(V_p<1,V_v=0)$ and the anti-ferromagnet phase $(V_p=1,V_c<1)$. Notably, in the bottom-right corners of Figure 5, the spin motion of particles in the system is governed by the 2-fold generalization field term, i.e., $\sin (\psi -2{\theta }_i)$. However, there are two stable equilibria, namely, $\psi /2$and $\psi /2+\pi$, so an anti-ferromagnet effect will be formed. The order parameter $V_v=1$implies vortex phase. It is observed from Figure 6 that the red region corresponds to the vortex phase. Meanwhile, in the middle-upper diagonal striped region of Figure 6, the system undergoes a phase transition from a vortex $(V_v=1)$to a ferromagnet $(V_c=1)$. In conclusion, by combining Figures 4–6, a sequential phase transition process can be observed, including the vortex phase $(V_v=1)$, the ferromagnetic phase $(V_c=1)$, the worm phase $(V_p<1,V_v=0)$, and finally the anti-ferromagnetic phase $(V_p=1,V_c<1)$.

To investigate more deeply into the phase transition mechanism, we conduct the effects of the side length parameter $M$ on vortex-worm phase transitions. Along ascending $M$ from 5 to 20, as shown in Figure 7A, the vortex phase begins to appear. Upon reaching $M=25$, the occurrence frequency of vortex phase exceeds that of ferromagnet phase, where occurrence frequency refers to the number of times a specific phase (e.g., vortex or worm) is observed across multiple simulations (same below). Until $M\ge 80$, only the vortex phase exists, whose number increases rapidly with rising $M$ (see Figures 7B, C), where vortex number quantifies the number of vortices formed in the system during a single simulation, and the error bars representing the standard deviation across 200 independent runs (same below). Analogously, in Figure 8A, when $M\ge 10$, the occurrence frequency of the worm phase exceeds that of the parallel patterns (i.e., ferromagnet and anti-ferromagnet phases). Upon reaching $M=25$ only the worm phase exists. Figure 8B shows the evolution of the parallel order parameter $V_p$ value along increasing $M$, which can quantitatively identifies the worm phase. A plausible explanation is given below. From the spin dynamics XY model (2), it can be observed that the model has many stable equilibria, including spin particles aligned in a parallel or vertical direction, relative to each other. However, according to the characteristics of the dynamic model (2), spin particles on the four corners and four sides of a square lattice have only two and three neighbors, respectively, which forms a boundary effect. Specifically, in the scenario of random initial values, the spin particles on the boundary and their neighbors will be prone to reach the consensus of heading directions, which drives the inner side spin particles to reach the same direction. However, with increasing number of the spin particles, the proportion of spin particles on the boundary decreases, and hence the influence of the boundary effect on the inner side particles will be weakened. In such a situation, vortex and worm patterns can be formed.

Figure 7

Figure 7. Evolution of the occurrence frequencies of the ferromagnet and vortex phases (A), the vortex state order parameter $V_v$ (B) and the vortex number (C) with increasing $M$. Here, each point is an average over 200 independent runs, with each run lasting $1\times 10^5$ running steps, guaranteeing the attainment of steady states. Parameters: $\widehat{\mu }=-3$ and $\widehat{J}=-1$.

Figure 8

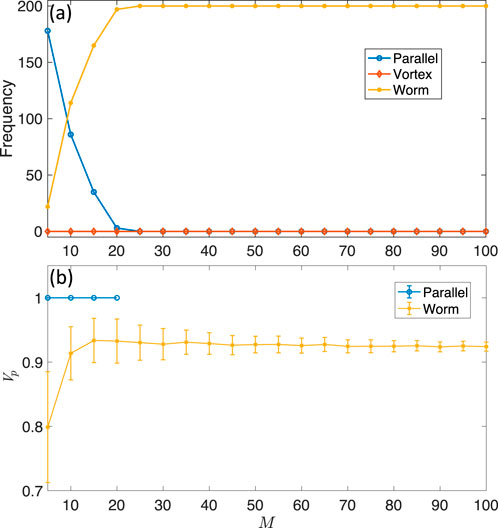
Figure 8. Evolution of the occurrence frequencies of the two parallel patterns (i.e., ferromagnet and anti-ferromagnet phases), vortex and worm phases (A), the parallel state order parameter $V_p$ (B) with increasing system size $M$. Here, each point is an average over 200 independent runs, with each run lasting $1\times 10^5$ running steps, guaranteeing the attainment of steady states.Parameters: $\widehat{\mu }=-1$ and $\widehat{J}=-1$.

So far, the phases and their transitions discussed above are noise-free, i.e., $\sigma =0$. Next, we conduct an investigation on the effect of $\sigma$ on the formation of vortex and worm phase in model (2). As shown in Figure 9A, with the increase of $\sigma$, the number of vortices gradually decreases until the vortex phase is totally ruined by noise. It is observed that vortex phase can be maintained for $\sigma \le 0.07$. In the blue curves of Figure 9B, it is shown that with moderate increase of external noise, a new phase appeared, that is, when $\sigma \in [0.05,0.1]$, $V_c$ would approach 1, but could not exactly reach 1 due to the influence of the external noise, i.e., $V_c\in [0.98,1)$, which is called quasi ferromagnet phase. As shown in Figure 9B, when $\sigma \ge 0.05$, the quasi ferromagnet phase appears, and the variance of $V_c$ in the worm phase grows larger.

Figure 9

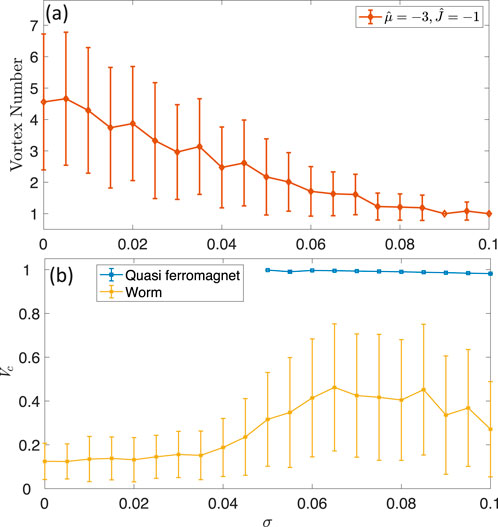
Figure 9. Evolution of the vortex number (A) and the consensus state order parameter $V_c$ (B) with increasing $\sigma$. Here, each point is an average over 200 independent runs, with each run lasting $1\times 10^5$ running steps, guaranteeing the attainment of steady states. Parameters in (B): $\widehat{\mu }=-1$ and $\widehat{J}=-1$.

3 Conclusion

This letter investigates the pattern phase transition mechanism for a class of the XY model with Hamiltonian equations of motion. Three phase transitions among four patterns, i.e., vortex, ferromagnet, worm and anti-ferromagnet, are revealed simply by tweaking two parameters $J$ and $\mu$. Specifically, the occurrence frequency of vortex phase exceeds that of ferromagnet phase for a sufficiently large space. This study is expected to provide an insight for understanding the emergence of single vortex and tight vortices pairs in pattern phase transition of spin particle groups. The observed phase transition may shed some lights onto the self-assembly dynamics analysis of magnets, electron nematics, and quantum gases.

Data availability statement

Publicly available datasets were analyzed in this study. This data can be found here: http://imds.aia.hust.edu.cn/info/1247/2403.htm.

Author contributions

YW: Writing–original draft, Writing–review and editing. JY: Writing–original draft. BX: Writing–review and editing. YZ: Writing–review and editing. DC: Writing–review and editing.

Funding

The author(s) declare that financial support was received for the research, authorship, and/or publication of this article. This work was supported by the National Natural Science Foundation of China under Grant. 62273053, Fundamental Research Funds for the Central Universities of China (BLX202128), China Postdoctoral Science Foundation under Grant No. 2024M754222, and the Natural Science Foundation of Shanxi Province under Grant No. 2024JC-YBQN-0663.

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

1. Flack A, Nagy M, Fiedler W, Couzin ID, Wikelski M. From local collective behavior to global migratory patterns in white storks. Science (2018) 360:911–4. doi:10.1126/science.aap7781

PubMed Abstract | CrossRef Full Text | Google Scholar

2. Chen D, Vicsek T, Liu X, Zhou T, Zhang H-T. Switching hierarchical leadership mechanism in homing flight of pigeon flocks. Europhysics Lett (2016) 114:60008. doi:10.1209/0295-5075/114/60008

CrossRef Full Text | Google Scholar

3. Lukeman R, Li Y-X, Edelstein-Keshet L. Inferring individual rules from collective behavior. Proc Natl Acad Sci (2010) 107:12576–80. doi:10.1073/pnas.1001763107

PubMed Abstract | CrossRef Full Text | Google Scholar

4. Attanasi A, Cavagna A, Castello LD, Giardina I, Grigera TS, Jelić A, et al. Information transfer and behavioural inertia in starling flocks. Nat Phys (2014) 10:691–6. doi:10.1038/nphys3035

PubMed Abstract | CrossRef Full Text | Google Scholar

5. Buhl J, Sumpter D, Couzin I, Hale JJ, Despland E, Miller ER, et al. From disorder to order in marching locusts. Science (2006) 312:1402–6. doi:10.1126/science.1125142

PubMed Abstract | CrossRef Full Text | Google Scholar

6. Franks NR, Pratt SC, Mallon EB, Britton NF, Sumpter DJT. Information flow, opinion polling and collective intelligence in house–hunting social insects. Philosophical Trans R Soc Lond Ser B: Biol Sci (2002) 357:1567–83. doi:10.1098/rstb.2002.1066

PubMed Abstract | CrossRef Full Text | Google Scholar

7. Bazazi S, Buhl J, Hale JJ, Anstey ML, Sword GA, Simpson SJ, et al. Collective motion and cannibalism in locust migratory bands. Curr Biol (2008) 18:735–9. doi:10.1016/j.cub.2008.04.035

PubMed Abstract | CrossRef Full Text | Google Scholar

8. Curatolo A, Zhou N, Zhao Y, Liu C, Daerr A, Tailleur J, et al. Cooperative pattern formation in multi-component bacterial systems through reciprocal motility regulation. Nat Phys (2020) 16:1152–7. doi:10.1038/s41567-020-0964-z

CrossRef Full Text | Google Scholar

9. Szabo B, Szollosi GJ, Gönci B, Jurányi Z, Selmeczi D, Vicsek T. Phase transition in the collective migration of tissue cells: experiment and model. Phys Rev E—Statistical, Nonlinear, Soft Matter Phys (2006) 74:061908. doi:10.1103/PhysRevE.74.061908

PubMed Abstract | CrossRef Full Text | Google Scholar

10. Deisboeck TS, Couzin ID. Collective behavior in cancer cell populations. Bioessays (2009) 31:190–7. doi:10.1002/bies.200800084

PubMed Abstract | CrossRef Full Text | Google Scholar

11. Ward AJW, Sumpter DJT, Couzin ID, Hart PJB, Krause J. Quorum decision-making facilitates information transfer in fish shoals. Proc Natl Acad Sci (2008) 105:6948–53. doi:10.1073/pnas.0710344105

PubMed Abstract | CrossRef Full Text | Google Scholar

12. Hein AM, Gil MA, Twomey CR, Couzin ID, Levin SA. Conserved behavioral circuits govern high-speed decision-making in wild fish shoals. Proc Natl Acad Sci (2018) 115:12224–8. doi:10.1073/pnas.1809140115

PubMed Abstract | CrossRef Full Text | Google Scholar

13. Hoare D, Couzin ID, Godin J-GJ, Krause J. Context-dependent group size choice in fish. Anim Behav (2004) 67:155–64. doi:10.1016/j.anbehav.2003.04.004

CrossRef Full Text | Google Scholar

14. Helbing D, Farkas I, Vicsek T. Simulating dynamical features of escape panic. Nature (2000) 407:487–90. doi:10.1038/35035023

PubMed Abstract | CrossRef Full Text | Google Scholar

15. Fischhoff I, Sundaresan SR, Cordingley J, Larkin HM, Sellier MJ, Rubenstein DI. Social relationships and reproductive state influence leadership roles in movements of plains zebra, equus burchellii. Anim Behav (2007) 73:825–31. doi:10.1016/j.anbehav.2006.10.012

CrossRef Full Text | Google Scholar

16. Sarova R, Spinka M, Panamá J, Simecek P (2010). Graded leadership by dominant animals in a herd of female beef cattle on pasture. Anim Behav 79, 1037–45. doi:10.1016/j.anbehav.2010.01.019

CrossRef Full Text | Google Scholar

17. Liu H, Lv J, Chen Q. Ising-like phase transition in the fully frustrated xyz model with weak disorder. Europhysics Lett (2008) 84:66004. doi:10.1209/0295-5075/84/66004

CrossRef Full Text | Google Scholar

18. Jesariew D, Ilczyszyn MM, Pietraszko A. The crystal structure and the phase transitions of pyridinium trifluoromethanesulfonate. Mater Res Express (2014) 1:015705. doi:10.1088/2053-1591/1/1/015705

CrossRef Full Text | Google Scholar

19. Carrillo JA, D’Orsogna M, Panferov V. Double milling in self-propelled swarms from kinetic theory. Kinetic Relat Models (2009) 2:363–78. doi:10.3934/krm.2009.2.363

CrossRef Full Text | Google Scholar

20. Birnir B. An ode model of the motion of pelagic fish. J Stat Phys (2007) 128:535–68. doi:10.1007/s10955-007-9292-2

CrossRef Full Text | Google Scholar

21. Gautrais J, Ginelli F, Fournier R, Blanco S, Soria M, Chaté H, et al. Deciphering interactions in moving animal groups. PLoS Comput Biol (2012) 8:e1002678. doi:10.1371/journal.pcbi.1002678

PubMed Abstract | CrossRef Full Text | Google Scholar

22. Calovi DS, Lopez U, Ngo S, Sire C, Chaté H, Theraulaz G. Swarming, schooling, milling: phase diagram of a data-driven fish school model. New J Phys (2014) 16:015026. doi:10.1088/1367-2630/16/1/015026

CrossRef Full Text | Google Scholar

23. Cheng Z-X, Sun B, Wang S-J, Gao Y, Zhang YM, Zhou HX, et al. Nuclear factor-κb–dependent epithelial to mesenchymal transition induced by HIF-1α activation in pancreatic cancer cells under hypoxic Conditionsα activation in pancreatic cancer cells under hypoxic conditions. PLoS One (2011) 6:e23752. doi:10.1371/journal.pone.0023752

PubMed Abstract | CrossRef Full Text | Google Scholar

24. Baek SK, Minnhagen P, Kim BJ. Phase transition of xyz model in heptagonal lattice. Europhysics Lett (2007) 79:26002. doi:10.1209/0295-5075/79/26002

CrossRef Full Text | Google Scholar

25. de Souza LC, de Souza AJF, Lyra ML. Hamiltonian short-time critical dynamics of the three-dimensional xyz model. Phys Rev E (2019) 99:052104. doi:10.1103/PhysRevE.99.052104

PubMed Abstract | CrossRef Full Text | Google Scholar

26. Mon K, Teitel S. Phase coherence and nonequilibrium behavior in josephs junction arrays. Phys Rev Lett (1989) 62:673–6. doi:10.1103/PhysRevLett.62.673

PubMed Abstract | CrossRef Full Text | Google Scholar

27. Kosterlitz JM. The critical properties of the two-dimensional xyz model. J Phys C: Solid State Phys (1974) 7:1046–60. doi:10.1088/0022-3719/7/6/005

CrossRef Full Text | Google Scholar

28. Li Y-H, Teitel S. Finite-size scaling study of the three-dimensional classical xyz model. Phys Rev B (1989) 40:9122–5. doi:10.1103/PhysRevB.40.9122

PubMed Abstract | CrossRef Full Text | Google Scholar

29. Vicsek T, Zafeiris A. Collective motion. Phys Rep (2012) 517:71–140. doi:10.1016/j.physrep.2012.03.004

CrossRef Full Text | Google Scholar

30. Cheng Z, Chen Z, Vicsek T, Chen D, Zhang HT. Pattern phase transitions of self-propelled particles: gases, crystals, liquids, and mills. New J Phys (2016) 18:103005. doi:10.1088/1367-2630/18/10/103005

CrossRef Full Text | Google Scholar

31. Minchau BJ, Pelcovits RA. Two-dimensional xyz model in a random uniaxial field. Phys Rev B (1985) 32:3081–7. doi:10.1103/PhysRevB.32.3081

PubMed Abstract | CrossRef Full Text | Google Scholar

32. Asad A, Zheng B. Non-equilibrium critical dynamics of the two-dimensional xyz model with Hamiltonian equations of motion. J Phys A: Math Theor (2007) 40:9957–68. doi:10.1088/1751-8113/40/33/001

CrossRef Full Text | Google Scholar

33. Leoncini X, Verga AD, Ruffo S. Hamiltonian dynamics and the phase transition of the xyz model. Phys Rev E (1998) 57:6377–89. doi:10.1103/PhysRevE.57.6377

CrossRef Full Text | Google Scholar

34. Matteo P, Marconi UMB, Maggi C. Effective equilibrium picture in the xyz model with exponentially correlated noise. Phys Rev E (2018) 97:022605. doi:10.1103/PhysRevE.97.022605

PubMed Abstract | CrossRef Full Text | Google Scholar

35. Basak S, Dahmen K, Carlson E. Period multiplication cascade at the order-by-disorder transition in uniaxial random field xyz magnets. Nat Commun (2020) 11:4665. doi:10.1038/s41467-020-18270-6

PubMed Abstract | CrossRef Full Text | Google Scholar