FSE-RBFNN-based LPF-AILC of finite time complete tracking for a class of time-varying NPNL systems with initial state errors

The paper proposes a low-pass filter adaptive iterative learning control (LPF-AILC) strategy for unmatched, uncertain, time-varying, non-parameterized nonlinear systems (NPNL systems). To address the difficulty of nonlinear parameterization terms in system models, a new function approximator (FSE-RBFNN), which combines the radial basis function neural network (RBFNN) and Fourier series expansion (FSE), is introduced to model each time-varying nonlinear parameterized function. The adaptive backstepping method is used to design control laws and parameter adaptive laws. In the process of controller design, we may encounter the problem of too many derivatives, which can cause parameter explosions after derivatives. Therefore, we introduce a first-order low-pass filter to solve this problem and simplify the structure of the controller. As the number of iterations increases, the maximum tracking error gradually decreases until it converges to the nearby region, approaching zero within the entire given interval $[0,T]$, according to the Lyapunov-like synthesis. To mitigate the impact of initial state errors, a dynamically changing boundary layer is introduced, along with a series to deal with the unknown error upper bounds. Finally, two simulation examples prove the correctness of the proposed control method.

1 Introduction

Adaptive iterative learning control (AILC) is a useful control strategy for solving repetitive tracking control task problems for uncertain nonlinear systems. It continuously adjusts its control algorithm through iterative learning to gradually approach the ideal trajectory of the unknown system. AILC has extensive application value and promising development prospects for practical applications. Repeat systems include uncertain robotic manipulators and uncertain hard disk drivers. The task requirements specify that it can quickly achieve exact tracking as the number of iterations increases [1–4].

A non-parameterized nonlinear (NPNL) system refers to a dynamic characteristic that exhibits a complex nonlinear relationship and unknown parameters, making it difficult to design effective control strategies. It is particularly challenging to achieve high-precision tracking and control within a limited time frame. Traditional control methods often require the establishment of a mathematical model for the system, but for the NPNL system, this step is usually very difficult or even impossible to complete. AILC technology has become an important method for solving these problems [5, 6].

There are many challenging problems in the research of AILC. This paper considers three difficult problems of AILC. The first problem is the processing problem of uncertain nonlinear parameterization terms with time-varying parameters. In the field of control, the control problem of nonlinear systems with uncertain time-varying parameters is very challenging. Adaptive control and robust control are common methods to deal with uncertain problems [7, 8]. Through learning, adaptive control can mitigate the impact of uncertainties. In order to handle uncertain nonlinear terms, adaptive control is often combined with some approximation methods, such as neural networks (NNs) and Fuzzy Logic Systems (FLSs). However, these adaptive controls only solve the uncertain linearly parameterized disturbances and ensure the stability of the system [7–20]. For the uncertain system, a fuzzy AILC was presented [21]. The composite energy function–adaptive iterative learning control (CEF–AILC) is an effective scheme for systems with time-varying disturbances [21–23]. Few AILC research results focus on uncertain, non-parameterized nonlinear systems [24–26]. Specifically, for systems with non-separable time-varying parameters, the tracking control problem on finite time intervals is still an open problem.

The second problem of AILC is ensuring complete tracking over a finite time interval when the initial state has errors. In these studies [27–31], the stability analysis section requires that initial state errors be strictly zero. Although the research on this problem is well done in traditional D-type or P-type ILC [32–41], it has not been well solved based on Lyapunov analysis for AILC. Specifically, in the presence of an initial state error, ensuring the system’s completion of accurate tracking tasks within a specified time frame presents a complex challenge. [39] solved the tracking control problem of the unmatched uncertain NPNL systems. [41] solved the tracking problem of a class of high-order nonlinear systems with random initial state shifts, which relaxes the requirement of initial positioning in ILC. So far, no relevant research results have been found for AILC applied to NPNL systems with uncertain time-varying parameters and initial state errors.

The last problem is parameter explosions after the derivative of the virtual controller. When designing a controller, we may encounter the problem of too many derivatives, which can cause parameter explosions after derivatives. Addressing this issue and streamlining the controller’s structure to ensure the effective tracking of the non-parametric, nonlinear, time-varying system is a challenging and crucial problem. [42–44] employed a first-order low-pass filter to address the challenge of parameter explosions and achieve satisfactory performance. Therefore, we introduce a first-order low-pass filter to solve this problem and simplify the structure of the controller.

Motivated by the above discussion, we will use a low-pass filter AILC (LPF-AILC) method for uncertain time-varying NPNL systems. The AILC is given by the adaptive backstepping technique and Lyapunov-like theorem. In response to the difficult issues discussed above, the main contributions of this article are as follows:

1) An LPF-AILC strategy is proposed for a class of strongly time-varying, non-parameterized, nonlinear systems combined with a new approximation method.

2) The processing problem of uncertain time-varying nonlinear parameterization terms was solved. This is a very important and difficult problem. Specifically, in the field of AILC, no relevant research results have been found.

3) The difficulty problem of AILC is ensuring complete tracking on a given interval when the initial state has errors.

4) The problem of parameter explosions was solved by applying a derivative to the virtual controller and simplifying its structure.

In this paper, a combination of Fourier series expansion and radial basis function neural network (RBFNN) (FSE-RBFNNs) is used to model the uncertain, time-varying nonlinear dynamics by using their uniform approximation [24, 38]. An updating time-varying boundary layer is used to design the error function to deal with the initial state error. A common convergence series sequence is employed to mitigate the impact of approximation errors on the control performance of the system. A low-pass filter was introduced to solve the problem of parameter explosions resulting from the derivative of the virtual controller and simplify the structure of the controller. Theoretical analysis can demonstrate the bounded nature of all signals within the closed-loop system. The maximum value of errors will gradually converge to a narrow range close to zero as the boundary layer width satisfies the convergence condition with the number of iterations. Finally, two simulation examples are given to prove the effectiveness and correctness of the control method.

2 Problem description and mathematical foundations

2.1 Problem description

Uncertain time-varying NPNL systems are considered:

$\begin{array}{ccc}\hfill {\dot{x}}_{1,k}& =\hfill & x_{2,k}+f_1\left({\bar{x}}_{1,k},{\theta }_1\left(t\right)\right)+g_1\left({\bar{x}}_{1,k}\right)\hfill \\ \hfill {\dot{x}}_{i,k}& =\hfill & x_{i+1,k}+f_i\left({\bar{x}}_{i,k},{\theta }_i\left(t\right)\right)+g_i\left({\bar{x}}_{i,k}\right)\hfill \\ \hfill {\dot{x}}_{n,k}& =\hfill & u_k+f_n\left({\bar{x}}_{m,k},{\theta }_n\left(t\right)\right)+g_n\left({\bar{x}}_{n,k}\right)\hfill \\ \hfill y_k& =\hfill & x_{1,k},\hfill \end{array}(1)$

where ${\bar{x}}_{i,k}={[x_{1,k},\dots ,x_{i,k}]}^T\in R^i$ and $x={\bar{x}}_n$ represents measurable state vectors. $u_k\in R$ is the control input. $y_k\in R$ is the system output. $f_i({\bar{x}}_{i,k},{\theta }_i(t))$, $g_i({\bar{x}}_{i,k})$, and $i=\mathrm{1,2},\dots ,n$ are uncertain time-varying functions, and ${\theta }_i(t)$ represents unknown time-varying parameters. $k$ denotes the iteration time.

The design objective of this article is to find $u_k(t)$ for system (1) to ensure that $y_k(t)$ follows the ideal trajectory $y_{d1}(t)$ on $[0,T]$.

2.2 Mathematical foundations

The mathematical knowledge used in this article is provided with relevant references, and the specific definitions and principles will not be elaborated. Here, we only provide the conclusions that need to be used in this article.

In system (1), the processing of unknown time-varying, nonlinear, parameterized function terms $f({\chi }_k,\theta (t))$ is a challenge. Since the function $\theta (t)$ is not known, $\theta (t)$ is expanded using Fourier series as $\theta (t)=M^T\mathrm{\Phi }(t)+{\delta }_{\theta }(t),\Vert {\delta }_{\theta }(t)\Vert \le {\bar{\delta }}_{\theta }$; based on this, uncertain time-varying nonlinear functions $f({\chi }_k,\theta (t))$ can be approximated as

$f\left({\chi }_k,{\theta }_k\left(t\right)\right)=W_k^{T}S\left({\chi }_k,M_k^T\mathrm{\Phi }\left(t\right)+{\delta }_{\theta ,k}\right)+{\delta }_{f,k}.(2)$

A new FSE-RBFNN approximator is built:

$G\left({\chi }_k,t\right)=W_k^{T}S\left({\chi }_k,M_k^T\mathrm{\Phi }\left(t\right)\right),(3)$

representing $f({\chi }_k,{\theta }_k(t))$ as

$f\left({\chi }_k,{\theta }_k\left(t\right)\right)=W_k^{T}S\left({\chi }_k,M_k^T\mathrm{\Phi }\left(t\right)\right)+{\delta }_k\left({\chi }_k,t\right),(4)$

where

${\delta }_k\left({\chi }_k,t\right)={\delta }_{f,k}+W_k^{T}S\left({\chi }_k,M_k^T\mathrm{\Phi }\left(t\right)+{\delta }_{\theta ,k}\right)-W_k^{T}S\left({\chi }_k,M_k^T\mathrm{\Phi }\left(t\right)\right).(5)$

$\mathbf{\text{Assumption}}1$: In the compact domain ${\mathrm{\Omega }}_k$, the weights $W_k$ and $M_k$ are constrained, and $\Vert W_k\Vert \le w_{m,k}$ and $\Vert M_k\Vert \le m_{a,k}$ with $w_{m,k},m_{a,k}$ being unknown positive numbers.

Lemma 1^[38]: For $({\chi }_k,{\theta }_k(t))\in {\mathrm{\Omega }}_k$, ${\delta }_k({\chi }_k,t)$ in (5) is bound, and

$|{\delta }_k\left({\chi }_k,t\right)|\le \overline{{\delta }_k},(6)$

where $\overline{{\delta }_k}$ represents the supremum of ${\delta }_k({\chi }_k,t)$.

Because $W_k$ and $M_k$ are unknown, we estimate them with ${\widehat{W}}_k$ and ${\widehat{M}}_k$, respectively. ${\tilde{W}}_k={\widehat{W}}_k-W_k$ and ${\tilde{M}}_k={\widehat{M}}_k-M_k$ are estimation errors.

Lemma 2^[38]: In the surrogate model (4), the following conclusion holds:

$\begin{array}{ccc}\hfill W_k^{T}S\left({\chi }_k,M_k^T\mathrm{\Phi }\left(t\right)\right)-{\widehat{W}}_k^{T}S\left({\chi }_k,{\widehat{M}}_k^T\mathrm{\Phi }\left(t\right)\right)& \hfill & \hfill \\ \hfill & \hfill & ={\tilde{W}}_k^T\left(S\left({\chi }_k,{\widehat{M}}_k^T\mathrm{\Phi }\left(t\right)\right)-{\widehat{S}}_k^{\prime }{\widehat{M}}_k^T\mathrm{\Phi }\left(t\right)\right)\hfill \\ \hfill & \hfill & +{\widehat{W}}_k^T{\widehat{S}}_k^{\prime }{\tilde{M}}_k^T\mathrm{\Phi }\left(t\right)+d,\hfill \end{array}(7)$

where ${\widehat{S}}_k^{\prime }=[{\widehat{s}}_{1,k}^{\prime },{\widehat{s}}_{2,k}^{\prime },\dots ,{\widehat{s}}_{p,k}^{\prime }]\in {\mathfrak{R}}^{m\times p}$ with ${\widehat{s}}_{i,k}^{\prime }=(\partial s_i({\chi }_k,{\omega }_k))/\partial {\omega }_k{|}_{{\omega }_k={\widehat{M}}_k\mathrm{\Phi }(t)}$ and $i=1,\dots ,p$, and the remainder $d_k$ is bounded by

$|d_k|\le \Vert M_k{\Vert }_F\Vert \mathrm{\Phi }\left(t\right){\widehat{W}}_k^T{\widehat{S}}_k^{\prime }{\Vert }_F+\Vert W_k\Vert \Vert {\widehat{S}}_k^{\prime }{\widehat{M}}_k^T\mathrm{\Phi }\left(t\right)\Vert +|W_k{|}_1.(8)$

For the processing of the supremum of each error term, this article introduces the following typical series sequence:

Lemma 2^[39] For a sequence ${\mathrm{\Delta }}_k=\{\frac{1}{k^l}\}$, where $k=\mathrm{1,2},\cdots$ and $l\ge 2$, the following result exists:

$li{m}_{k\to \infty }{\mathrm{\Sigma }}_{i=1}^k\frac{1}{i^l}\le 2.(9)$

Assumption 2: The initial error value at the beginning of each iteration should meet $|z_{i,k}(0)|={ϵ}_{i,k}$ with ${ϵ}_{i,k}$ being a convergence series sequence, where $i=1,\dots ,n$.

Considering the initial errors, a new function $z_{\varphi ,k}^{[34]}$is accepted:

$\begin{array}{ccc}\hfill z_{\varphi ,k}& =\hfill & z_k-{\varphi }_k\left(t\right)sat\left(\frac{z_k}{{\varphi }_k\left(t\right)}\right)\hfill \\ \hfill {\varphi }_k\left(t\right)& =\hfill & {ϵ}_k{e}^{-\eta t},\hfill \end{array}(10)$

where $sat$ is the saturation function given as

$sat\left(\frac{z_k}{{\varphi }_k\left(t\right)}\right)=\left\{\begin{array}{cc}1\hfill & \text{if}{z}_k>{\varphi }_k\left(t\right)\hfill \\ \frac{z_k}{{\varphi }_k\left(t\right)}\hfill & \text{if}{z}_k\le {\varphi }_k\left(t\right)\hfill \\ -1\hfill & \text{if}{z}_k<-{\varphi }_k\left(t\right)\hfill \end{array}\right.,$

with ${\varphi }_k(t)$ being an updating time-varying boundary layer. When $li{m}_{k\to \infty }{z}_{\varphi ,k}=0$ and considering assumption 2 again, we have $li{m}_{k\to \infty }|z_k|=0$.

In order to prevent the problem of gradient explosion, we introduce the first-order low-pass filter ${\beta }_k$, which is given as follows:

${\dot{\beta }}_k=-{\xi }_k\left({\beta }_k-{\alpha }_k\right),(11)$

where ${\beta }_k$ results from filtering an instruction with ${\alpha }_k$ as its input, with ${\alpha }_k$ being the virtual controller, ${\xi }_k>0$, and ${\beta }_k(0)={\alpha }_k(0)$. Because part of ${\alpha }_k{\beta }_k-{\alpha }_k$ cannot pass through the filter, an error compensation mechanism ${\zeta }_k$ is introduced to overcome the influence of the instruction filter. Therefore, a new function $Z_k$ is introduced as follows:

$Z_k=z_{\varphi ,k}-{\zeta }_k.(12)$

3 AILC design

Based on the above mathematical foundations, we present the specific controller design process.

3.1 Designing the AILC controller

Step 1: Denote $N_1={\omega }_{M1}^2$, which will be defined later. $z_{1,k}=x_{1,k}-y_{d1}$ and $z_{2,k}=x_{2,k}-{\alpha }_{1,k}$, where ${\alpha }_{1,k}$ is the virtual controller. Because the initial state values of the system have errors and gradient explosion, the new error functions $Z_{1,k}$ and $Z_{2,k}$ are given as

$\begin{array}{ccc}\hfill Z_{1,k}& =\hfill & z_{1\varphi ,k}-{\zeta }_{1,k}\hfill \\ \hfill z_{1\varphi ,k}& =\hfill & z_{1,k}-{\varphi }_{1,k}\left(t\right)sat\left(\frac{z_{1,k}}{{\varphi }_{1,k}\left(t\right)}\right)\hfill \\ \hfill z_{1,k}& =\hfill & x_{1,k}-y_{d1}\hfill \\ \hfill {\varphi }_{1,k}\left(t\right)& =\hfill & {ϵ}_{1,k}{e}^{-{\eta }_{1}t},\hfill \end{array}(13)$

$\begin{array}{ccc}\hfill Z_{2,k}& =\hfill & z_{2\varphi ,k}-{\zeta }_{2,k}\hfill \\ \hfill z_{2\varphi ,k}& =\hfill & z_{2,k}-{\varphi }_{2,k}\left(t\right)sat\left(\frac{z_{2,k}}{{\varphi }_{2,k}\left(t\right)}\right)\hfill \\ \hfill z_{2,k}& =\hfill & x_{2,k}-{\beta }_{1,k}\hfill \\ \hfill {\varphi }_{2,k}\left(t\right)& =\hfill & {ϵ}_{2,k}{e}^{-{\eta }_{2}t}.\hfill \end{array}(14)$

We recall that

${\dot{x}}_{1,k}=x_{2,k}+f_1\left({\bar{x}}_{1,k},{\theta }_1\left(t\right)\right)+g_1\left({\bar{x}}_{1,k}\right).(15)$

Given the derivative of $z_{1\varphi ,k}$,

$\begin{array}{ccc}\hfill {\dot{z}}_{1\varphi ,k}& =\hfill & \left\{\begin{array}{cc}{\dot{z}}_{1,k}-{\dot{\varphi }}_{1,k}\hfill & \text{if}{z}_{1,k}>{\varphi }_{1,k}\left(t\right)\hfill \\ 0\hfill & \text{if}{z}_{1,k}\le {\varphi }_{1,k}\left(t\right)\hfill \\ {\dot{z}}_{1,k}+{\dot{\varphi }}_{1,k}\hfill & \text{if}{z}_{1,k}<-{\varphi }_{1,k}\left(t\right)\hfill \end{array}\right.\hfill \\ \hfill & =\hfill & {\dot{z}}_{1,k}-sgn\left(z_{1\varphi ,k}\left(t\right)\right){\dot{\varphi }}_{1,k}\hfill \\ \hfill & =\hfill & z_{2,k}+{\beta }_{1,k}+f_1\left({\bar{x}}_{1,k},{\theta }_1\left(t\right)\right)+g_1\left({\bar{x}}_{1,k}\right)\hfill \\ \hfill & \hfill & -{\dot{y}}_{d1}-sgn\left(z_{1\varphi ,k}\right){\dot{\varphi }}_{1,k}.\hfill \end{array}(16)$

Therefore, the derivative of $Z_{1,k}$ with respect to time is as follows:

$\begin{array}{ccc}\hfill {\dot{Z}}_{1,k}& =\hfill & z_{2,k}+{\beta }_{1,k}+f_1\left({\bar{x}}_{1,k},{\theta }_1\left(t\right)\right)+g_1\left({\bar{x}}_{1,k}\right)\hfill \\ \hfill & \hfill & -{\dot{y}}_{d1}-sgn\left(z_{1\varphi ,k}\right){\dot{\varphi }}_{1,k}-{\dot{\zeta }}_{1,k}.\hfill \end{array}(17)$

The error compensation mechanism is considered as follows:

${\dot{\zeta }}_{1,k}={\beta }_{1,k}+{\zeta }_{2,k}-{\eta }_1{\zeta }_{1,k}-{\alpha }_{1,k}.(18)$

Using Equation 18, we can find the time derivative of the error function as follows:

$\begin{array}{ccc}\hfill {\dot{Z}}_{1,k}& =\hfill & z_{2,k}-{\zeta }_{2,k}+{\eta }_{1,k}{\zeta }_{1,k}+{\alpha }_{1,k}-{\dot{y}}_{d1}\hfill \\ \hfill & \hfill & +f_1\left({\bar{x}}_{1,k},{\theta }_1\left(t\right)\right)+g_1\left({\bar{x}}_{1,k}\right)-sgn\left(z_{1\varphi ,k}\right){\dot{\varphi }}_{1,k}.\hfill \end{array}(19)$

The unknown time-varying, nonlinear functions $f_1({\bar{x}}_{1,k},{\theta }_1(t))$ and $g_1({\bar{x}}_{1,k})$ may be approximated by FSE-RBFNN and RBFNN, respectively.

$\begin{array}{ccc}\hfill f_1\left({\bar{x}}_{1,k},{\theta }_1\left(t\right)\right)& =\hfill & W_{f1}^T{S}_{f1}\left({\bar{x}}_{1,k},M_1^T{\varphi }_1\left(t\right)\right)+{\delta }_{f1}\hfill \\ \hfill g_1\left({\bar{x}}_{1,k}\right)& =\hfill & W_{g1}^T{S}_{g1}\left({\bar{x}}_{1,k}\right)+{\delta }_{g1},\hfill \end{array}(20)$

where ${\delta }_{f1}$ and ${\delta }_{g1}$ are the truncation errors after approximation and $W_{f1}$ and $W_{g1}$ are weight vectors.

Consider ${\mathrm{\Delta }}_k=\frac{a}{k^l}$, $a>0$, and $l\ge 2$. The virtual control law is designed as

$\begin{array}{ccc}\hfill {\alpha }_{1,k}& =\hfill & -{\widehat{W}}_{f1,k}^T{S}_{f1}\left({\bar{x}}_{1,k},{\widehat{M}}_{1,k}^T{\mathrm{\Phi }}_1\left(t\right)\right)-{\widehat{W}}_{g1,k}^T{S}_{g1}\left({\bar{x}}_{1,k}\right)\hfill \\ \hfill & \hfill & -{\widehat{N}}_{1,k}\frac{1}{{\mathrm{\Delta }}_k}{Z}_{1,k}+{\dot{y}}_{d1}-{\eta }_1{z}_{1,k}.\hfill \end{array}(21)$

By substituting Equations 20, 21 into Equation 19, we obtain

$\begin{array}{ccc}\hfill {\dot{Z}}_{1,k}& =\hfill & z_{2,k}-{\widehat{N}}_{1,k}\frac{1}{{\mathrm{\Delta }}_k}{Z}_{1,k}-{\zeta }_{2,k}+{\eta }_{1,k}{\zeta }_{1,k}\hfill \\ \hfill & \hfill & +W_{f1}^T{S}_{f1}\left({\bar{x}}_{1,k},M_1^T{\mathrm{\Phi }}_1\left(t\right)\right)+{\delta }_{f1}-{\widehat{W}}_{f1,k}^T{S}_{f1}\left({\bar{x}}_{1,k},{\widehat{M}}_{1,k}^T{\mathrm{\Phi }}_1\left(t\right)\right)\hfill \\ \hfill & \hfill & +W_{g1}^T{S}_{g1}\left({\bar{x}}_{1,k}\right)+{\delta }_{g1}-{\widehat{W}}_{g1,k}^T{S}_{g1}\left({\bar{x}}_{1,k}\right)\hfill \\ \hfill & \hfill & -{\eta }_1{z}_{1,k}-sgn\left(z_{1\varphi ,k}\right){\dot{\varphi }}_{1,k}\left(t\right)\hfill \\ \hfill & =\hfill & Z_{2,k}-{\widehat{N}}_{1,k}\frac{1}{{\mathrm{\Delta }}_k}{Z}_{1,k}-{\zeta }_{2,k}+{\eta }_{1,k}{\zeta }_{1,k}\hfill \\ \hfill & \hfill & +W_{f1}^T{S}_{f1}\left({\bar{x}}_{1,k},M_1^T{\mathrm{\Phi }}_1\left(t\right)\right)-{\widehat{W}}_{f1,k}^T{S}_{f1}\left({\bar{x}}_{1,k},{\widehat{M}}_{1,k}^T{\mathrm{\Phi }}_1\left(t\right)\right)\hfill \\ \hfill & \hfill & +W_{g1}^T{S}_{g1}\left({\bar{x}}_{1,k}\right)-{\widehat{W}}_{g1,k}^T{S}_{g1}\left({\bar{x}}_{1,k}\right)+{\delta }_{f1}+{\delta }_{g1}\hfill \\ \hfill & \hfill & +{\varphi }_{2,k}\left(t\right)sat\left(\frac{z_{2,k}}{{\varphi }_{2,k}\left(t\right)}\right)+{\zeta }_{2,k}\hfill \\ \hfill & \hfill & -{\eta }_1{z}_{1,k}-sgn\left(z_{1\varphi ,k}\right){\dot{\varphi }}_{1,k}\left(t\right)\hfill \\ \hfill & =\hfill & Z_{2,k}-{\widehat{N}}_{1,k}\frac{1}{{\mathrm{\Delta }}_k}{Z}_{1,k}+{\varphi }_{2,k}\left(t\right)sat\left(\frac{z_{2,k}}{{\varphi }_{2,k}\left(t\right)}\right)\hfill \\ \hfill & \hfill & +W_{f1}^T{S}_{f1}\left({\bar{x}}_{1,k},M_1^T{\mathrm{\Phi }}_1\left(t\right)\right)-{\widehat{W}}_{f1,k}^T{S}_{f1}\left({\bar{x}}_{1,k},{\widehat{M}}_{1,k}^T{\mathrm{\Phi }}_1\left(t\right)\right)\hfill \\ \hfill & \hfill & +W_{g1}^T{S}_{g1}\left({\bar{x}}_{1,k}\right)-{\widehat{W}}_{g1,k}^T{S}_{g1}\left({\bar{x}}_{1,k}\right)+{\delta }_{f1}+{\delta }_{g1}\hfill \\ \hfill & \hfill & -{\eta }_1{z}_{1,k}-sgn\left(z_{1\varphi ,k}\right){\dot{\varphi }}_{1,k}\left(t\right)+{\eta }_{1,k}{\zeta }_{1,k},\hfill \end{array}(22)$

where ${\widehat{W}}_{f1,k}$, ${\widehat{W}}_{g1,k}$, ${\widehat{M}}_{1,k}$, and ${\widehat{N}}_{1,k}$ are estimations of $W_{f1}$, $W_{g1}$, $M_1$, and $N_1$, respectively. ${\tilde{W}}_{f1,k}={\widehat{W}}_{f1,k}-W_{f1}$, ${\tilde{W}}_{g1,k}={\widehat{W}}_{g1,k}-W_{g1}$, ${\tilde{M}}_{1,k}={\widehat{M}}_{1,k}-M_1$, and ${\tilde{N}}_{1,k}={\widehat{N}}_{1,k}-N_1$ are the estimation errors. It can be proved that the following result is correct.

$\begin{array}{ccc}\hfill -{\eta }_1{z}_{1,k}-sgn\left(z_{1\varphi ,k}\right){\dot{\varphi }}_{1,k}\left(t\right)+{\eta }_1{\zeta }_{1,k}& =\hfill & -{\eta }_1{z}_{1\varphi ,k}-{\eta }_1{\varphi }_{1,k}\left(t\right)sat\left(\frac{z_{1,k}}{{\varphi }_{1,k}\left(t\right)}\right)\hfill \\ \hfill & \hfill & -sgn\left(z_{1\varphi ,k}\right){\dot{\varphi }}_{1,k}\left(t\right)+{\eta }_1{\zeta }_{1,k}\hfill \\ \hfill & =\hfill & -{\eta }_1{z}_{1\varphi ,k}+{\eta }_1{\zeta }_{1,k}\hfill \\ \hfill & \hfill & -sgn\left(z_{1\varphi ,k}\right)\left({\dot{\varphi }}_{1,k}\left(t\right)+{\eta }_1{\varphi }_{1,k}\left(t\right)\right)\hfill \\ \hfill & =\hfill & -{\eta }_1\left(z_{1\varphi ,k}-{\zeta }_{1,k}\right)\hfill \\ \hfill & =\hfill & -{\eta }_1{Z}_{1,k}.\hfill \end{array}(23)$

Using Equations 7, 23, Equation 22 can be rewritten as

$\begin{array}{ccc}\hfill {\dot{Z}}_{1,k}& =\hfill & Z_{2,k}-{\widehat{N}}_{1,k}\frac{1}{{\mathrm{\Delta }}_k}{Z}_{1,k}-{\eta }_1{Z}_{1,k}\hfill \\ \hfill & \hfill & +{\tilde{W}}_{f1}^T\left(S_{f1}\left({\bar{x}}_{1,k},{\widehat{M}}_{1,k}^T{\mathrm{\Phi }}_1\left(t\right)\right)-{\widehat{S}}_{f1,k}^{\prime }{\widehat{M}}_{1,k}^T{\mathrm{\Phi }}_1\left(t\right)\right)\hfill \\ \hfill & \hfill & +{\widehat{W}}_{f1,k}^T{\widehat{S}}_{f1,k}^{\prime }{\tilde{M}}_{1,k}^T{\mathrm{\Phi }}_1\left(t\right)-{\tilde{W}}_{g1}^T{S}_{g1}\left({\bar{x}}_{1,k}\right)\hfill \\ \hfill & \hfill & +d_1+{\delta }_{f1}+{\delta }_{g1}+{\varphi }_{2,k}\left(t\right)sat\left(\frac{z_{2,k}}{{\varphi }_{2,k}\left(t\right)}\right).\hfill \end{array}(24)$

Let ${\omega }_1=d_1+{\delta }_{f1}+{\delta }_{g1}+{\varphi }_{2,k}(t)sat(\frac{z_{2,k}(t)}{{\varphi }_{2,k}(t)})$, where $d_1$ is the remaining term of the estimation error after FSE-RBFNN expansion, and $d_i$ is also the same; then, Equation 24 becomes

$\begin{array}{ccc}\hfill {\dot{Z}}_{1,k}& =\hfill & Z_{2,k}-{\widehat{N}}_{1,k}\frac{1}{{\mathrm{\Delta }}_k}{Z}_{1,k}-{\eta }_1{Z}_{1,k}+{\omega }_1\hfill \\ \hfill & \hfill & +{\tilde{W}}_{f1}^T\left(S_{f1}\left({\bar{x}}_{1,k},{\widehat{M}}_{1,k}^T{\mathrm{\Phi }}_1\left(t\right)\right)-{\widehat{S}}_{f1,k}^{\prime }{\widehat{M}}_{1,k}^T{\mathrm{\Phi }}_1\left(t\right)\right)\hfill \\ \hfill & \hfill & +{\widehat{W}}_{f1,k}^T{\widehat{S}}_{f1,k}^{\prime }{\tilde{M}}_{1,k}^T{\mathrm{\Phi }}_1\left(t\right)-{\tilde{W}}_{g1}^T{S}_{g1}\left({\bar{x}}_{1,k}\right).\hfill \end{array}(25)$

$\mathrm{Assumption}3$ The remainder ${\omega }_i=d_i+{\delta }_{fi}+{\delta }_{gi}+{\varphi }_{i+1,k}(t)sat(\frac{z_{i+1,k}(t)}{{\varphi }_{i+1,k}(t)})(i=\mathrm{1,2},\dots ,n-1)$ is bounded with $|{\omega }_i|\le {\omega }_{Mi}$ and ${\omega }_{Mi}>0$.

Remark 1: This assumption is easily satisfied because 1) $d_i$, ${\delta }_{fi}$, and ${\delta }_{gi}$ are bounded and 2) when ${\eta }_i$ is large enough, ${\varphi }_{i,k}(t)sat(\frac{z_{i,k}(t)}{{\varphi }_{i,k}(t)})$ is sufficiently small.

The Lyapunov-like function is chosen as follows:

$\begin{array}{ccc}\hfill V_{1,k}& =\hfill & \frac{1}{2}{Z}_{1,k}^2+\frac{1}{2}{\tilde{W}}_{f1,k}^T{\mathrm{\Gamma }}_{\mathit{f11}}^{-1}{\tilde{W}}_{f1,k}+\frac{1}{2}{\tilde{W}}_{g1,k}^T{\mathrm{\Gamma }}_{\mathit{g11}}^{-1}{\tilde{W}}_{g1,k}\hfill \\ \hfill & \hfill & +\frac{1}{2}{\tilde{M}}_{1,k}^T{\mathrm{\Gamma }}_{\mathit{m11}}^{-1}{\tilde{M}}_{1,k}+\frac{1}{2}{\mathrm{\Gamma }}_{\mathit{n11}}^{-1}{\tilde{N}}_{1,k}^2,\hfill \end{array}(26)$

where ${\mathrm{\Gamma }}_{\mathit{f11}}$, ${\mathrm{\Gamma }}_{\mathit{g11}}$, ${\mathrm{\Gamma }}_{\mathit{m11}}$, and ${\mathrm{\Gamma }}_{\mathit{n11}}$ are adjustable matrices, each being positive, definite, and symmetric. Consider the derivative of $V_{1,k}$ by system (25), we obtain

$\begin{array}{ccc}\hfill {\dot{V}}_{1,k}& =\hfill & Z_{1,k}{Z}_{2,k}-{\eta }_1{Z}_{1,k}^2\hfill \\ \hfill & \hfill & +{\tilde{W}}_{f1,k}^T{\mathrm{\Gamma }}_{\mathit{f11}}^{-1}\left({\mathrm{\Gamma }}_{\mathit{f11}}\left(S_{f1}\left({\bar{x}}_{1,k},{\widehat{M}}_{1,k}^T{\mathrm{\Phi }}_1\left(t\right)\right)-{\widehat{S}}_{f1,k}^{\prime }{\widehat{M}}_{1,k}^T{\mathrm{\Phi }}_1\left(t\right)\right)Z_{1,k}\right.\hfill \\ \hfill & \hfill & \left.+{\dot{\widehat{W}}}_{f1,k}\right)-{\tilde{W}}_{g1,k}^T{\mathrm{\Gamma }}_{\mathit{g11}}^{-1}\left({\mathrm{\Gamma }}_{\mathit{g11}}{S}_{g1}\left({\bar{x}}_{1,k}\right)Z_{1,k}-{\dot{\widehat{W}}}_{g1,k}\right)\hfill \\ \hfill & \hfill & +{\tilde{M}}_{1,k}^T{\mathrm{\Gamma }}_{\mathit{m11}}^{-1}\left({\mathrm{\Gamma }}_{\mathit{m11}}{\mathrm{\Phi }}_1\left(t\right){\widehat{W}}_{f1,k}^T{\widehat{S}}_{f1,k}^{\prime }{Z}_{1,k}+{\dot{\widehat{M}}}_{1,k}\right)\hfill \\ \hfill & \hfill & -{\widehat{N}}_{1,k}\frac{1}{{\mathrm{\Delta }}_k}{Z}_{1,k}^2+{\omega }_{1,k}{Z}_{1,k}+{\mathrm{\Gamma }}_{\mathit{n11}}^{-1}{\tilde{N}}_{1,k}{\dot{\widehat{N}}}_{1,k}\hfill \\ \hfill & \hfill & \le Z_{1,k}{Z}_{2,k}-{\eta }_1{Z}_{1,k}^2\hfill \\ \hfill & \hfill & +{\tilde{W}}_{f1,k}^T{\mathrm{\Gamma }}_{\mathit{f11}}^{-1}\left({\mathrm{\Gamma }}_{\mathit{f11}}\left(S_{f1}\left({\bar{x}}_{1,k},{\widehat{M}}_{1,k}^T{\mathrm{\Phi }}_1\left(t\right)\right)-{\widehat{S}}_{f1,k}^{\prime }{\widehat{M}}_{1,k}^T{\mathrm{\Phi }}_1\left(t\right)\right)Z_{1,k}\right.\hfill \\ \hfill & \hfill & \left.+{\dot{\widehat{W}}}_{f1,k}\right)-{\tilde{W}}_{g1,k}^T{\mathrm{\Gamma }}_{\mathit{g11}}^{-1}\left({\mathrm{\Gamma }}_{\mathit{g11}}{S}_{g1}\left({\bar{x}}_{1,k}\right)Z_{1,k}-{\dot{\widehat{W}}}_{g1,k}\right)\hfill \\ \hfill & \hfill & +{\tilde{M}}_{1,k}^T{\mathrm{\Gamma }}_{\mathit{m11}}^{-1}\left({\mathrm{\Gamma }}_{\mathit{m11}}{\mathrm{\Phi }}_1\left(t\right){\widehat{W}}_{f1,k}^T{\widehat{S}}_{f1,k}^{\prime }{Z}_{1,k}+{\dot{\widehat{M}}}_{1,k}\right)\hfill \\ \hfill & \hfill & -{\widehat{N}}_{1,k}\frac{1}{{\mathrm{\Delta }}_k}{Z}_{1,k}^2+\frac{1}{{\mathrm{\Delta }}_k}{\omega }_{M1}^2{Z}_{1,k}^2+\frac{1}{4}{\mathrm{\Delta }}_k+{\mathrm{\Gamma }}_{\mathit{n11}}^{-1}{\tilde{N}}_{1,k}{\dot{\widehat{N}}}_{1,k}\hfill \\ \hfill & =\hfill & Z_{1,k}{Z}_{2,k}-{\eta }_1{Z}_{1,k}^2\hfill \\ \hfill & \hfill & +{\tilde{W}}_{f1,k}^T{\mathrm{\Gamma }}_{\mathit{f11}}^{-1}\left({\mathrm{\Gamma }}_{\mathit{f11}}\left(S_{f1}\left({\bar{x}}_{1,k},{\widehat{M}}_{1,k}^T{\mathrm{\Phi }}_1\left(t\right)\right)-{\widehat{S}}_{f1,k}^{\prime }{\widehat{M}}_{1,k}^T{\mathrm{\Phi }}_1\left(t\right)\right)Z_{1,k}\right.\hfill \\ \hfill & \hfill & \left.+{\dot{\widehat{W}}}_{f1,k}\right)-{\tilde{W}}_{g1,k}^T{\mathrm{\Gamma }}_{\mathit{g11}}^{-1}\left({\mathrm{\Gamma }}_{\mathit{g11}}{S}_{g1}\left({\bar{x}}_{1,k}\right)Z_{1,k}-{\dot{\widehat{W}}}_{g1,k}\right)\hfill \\ \hfill & \hfill & +{\tilde{M}}_{1,k}^T{\mathrm{\Gamma }}_{\mathit{m11}}^{-1}\left({\mathrm{\Gamma }}_{\mathit{m11}}{\mathrm{\Phi }}_1\left(t\right){\widehat{W}}_{f1,k}^T{\widehat{S}}_{f1,k}^{\prime }{Z}_{1,k}+{\dot{\widehat{M}}}_{1,k}\right)\hfill \\ \hfill & \hfill & -{\widehat{N}}_{1,k}\frac{1}{{\mathrm{\Delta }}_k}{Z}_{1,k}^2+\frac{1}{{\mathrm{\Delta }}_k}{N}_{1,k}{Z}_{1,k}^2+\frac{1}{4}{\mathrm{\Delta }}_k+{\mathrm{\Gamma }}_{\mathit{n11}}^{-1}{\tilde{N}}_{1,k}{\dot{\widehat{N}}}_{1,k}\hfill \\ \hfill & =\hfill & Z_{1,k}{Z}_{2,k}-{\eta }_1{Z}_{1,k}^2\hfill \\ \hfill & \hfill & +{\tilde{W}}_{f1,k}^T{\mathrm{\Gamma }}_{\mathit{f11}}^{-1}\left({\mathrm{\Gamma }}_{\mathit{f11}}\left(S_{f1}\left({\bar{x}}_{1,k},{\widehat{M}}_{1,k}^T{\mathrm{\Phi }}_1\left(t\right)\right)-{\widehat{S}}_{f1,k}^{\prime }{\widehat{M}}_{1,k}^T{\mathrm{\Phi }}_1\left(t\right)\right)Z_{1,k}\right.\hfill \\ \hfill & \hfill & \left.+{\dot{\widehat{W}}}_{f1,k}\right)-{\tilde{W}}_{g1,k}^T{\mathrm{\Gamma }}_{\mathit{g11}}^{-1}\left({\mathrm{\Gamma }}_{\mathit{g11}}{S}_{g1}\left({\bar{x}}_{1,k}\right)Z_{1,k}-{\dot{\widehat{W}}}_{g1,k}\right)\hfill \\ \hfill & \hfill & +{\tilde{M}}_{1,k}^T{\mathrm{\Gamma }}_{\mathit{m11}}^{-1}\left({\mathrm{\Gamma }}_{\mathit{m11}}{\mathrm{\Phi }}_1\left(t\right){\widehat{W}}_{f1,k}^T{\widehat{S}}_{f1,k}^{\prime }{Z}_{1,k}+{\dot{\widehat{M}}}_{1,k}\right)\hfill \\ \hfill & \hfill & -{\tilde{N}}_{1,k}{\mathrm{\Gamma }}_{\mathit{n11}}^{-1}\left({\mathrm{\Gamma }}_{\mathit{n11}}\frac{1}{{\mathrm{\Delta }}_k}{Z}_{1,k}^2-{\dot{\widehat{N}}}_{1,k}\right)+\frac{1}{4}{\mathrm{\Delta }}_k,\hfill \end{array}(27)$

where for any $r>0$ and $mn\le \frac{1}{r}{m}^2+\frac{1}{4}{n}^{2}r$, $r={\mathrm{\Delta }}_k$.

We choose

$\begin{array}{ccc}\hfill {\dot{\widehat{W}}}_{f1,k}& =\hfill & -{\mathrm{\Gamma }}_{\mathit{f11}}\left(S_{f1}\left({\bar{x}}_{1,k},{\widehat{M}}_{1,k}^T{\mathrm{\Phi }}_1\left(t\right)\right)-{\widehat{S}}_{f1,k}^{\prime }{\widehat{M}}_{1,k}^T{\mathrm{\Phi }}_1\left(t\right)\right)Z_{1,k}\hfill \\ \hfill {\dot{\widehat{W}}}_{g1,k}& =\hfill & {\mathrm{\Gamma }}_{\mathit{g11}}{S}_{g1}\left({\bar{x}}_{1,k}\right)Z_{1,k}\hfill \\ \hfill {\dot{\widehat{M}}}_{1,k}& =\hfill & -{\mathrm{\Gamma }}_{\mathit{m11}}{\mathrm{\Phi }}_1\left(t\right){\widehat{W}}_{f1,k}^T{\widehat{S}}_{f1,k}^{\prime }{Z}_{1,k}\hfill \\ \hfill {\dot{\widehat{N}}}_{1,k}& =\hfill & {\mathrm{\Gamma }}_{\mathit{n11}}\frac{1}{{\mathrm{\Delta }}_k}{Z}_{1,k}^2,\hfill \end{array}(28)$

so Equation 27 becomes

${\dot{V}}_{1,k}\le Z_{1,k}{Z}_{2,k}-{\eta }_1{Z}_{1,k}^2+\frac{1}{4}{\mathrm{\Delta }}_k.(29)$

Step 2: Denote $N_2={\omega }_{M2}^2$, which will be defined later. Due to initial state errors and gradient explosion, we introduce the following error function $Z_{3,k}$ as

$\begin{array}{ccc}\hfill Z_{3,k}& =\hfill & z_{3\varphi ,k}-{\zeta }_{3,k}\hfill \\ \hfill z_{3\varphi ,k}& =\hfill & z_{3,k}-{\varphi }_{3,k}\left(t\right)sat\left(\frac{z_{3,k}}{{\varphi }_{3,k}\left(t\right)}\right)\hfill \\ \hfill z_{3,k}& =\hfill & x_{3,k}-{\beta }_{2,k}\hfill \\ \hfill {\varphi }_{3,k}\left(t\right)& =\hfill & {ϵ}_{3,k}{e}^{-{\eta }_{3}t}.\hfill \end{array}(30)$

The derivative of $Z_{2,k}$ is shown as follows:

$\begin{array}{ccc}\hfill {\dot{Z}}_{2,k}& =\hfill & {\dot{z}}_{2,k}-sgn\left(z_{2\varphi ,k}\left(t\right)\right){\dot{\varphi }}_{2,k}-{\dot{\zeta }}_{2,k}\hfill \\ \hfill & =\hfill & z_{3,k}+{\beta }_{2,k}+f_2\left({\bar{x}}_{2,k},{\theta }_2\left(t\right)\right)+g_2\left({\bar{x}}_{2,k}\right)\hfill \\ \hfill & \hfill & -{\dot{\beta }}_{1,k}-sgn\left(z_{2\varphi ,k}\right){\dot{\varphi }}_{2,k}-{\dot{\zeta }}_{2,k}.\hfill \end{array}(31)$

Let the error compensation mechanism be defined as follows:

${\dot{\zeta }}_{2,k}={\beta }_{2,k}+{\zeta }_{3,k}-{\eta }_2{\zeta }_{2,k}-{\zeta }_{1,k}-{\alpha }_{2,k}.(32)$

Using Equation 32, we can find the time derivative of error function as

$\begin{array}{ccc}\hfill {\dot{Z}}_{2,k}& =\hfill & z_{3,k}-{\zeta }_{3,k}+{\eta }_{2,k}{\zeta }_{2,k}+{\zeta }_{1,k}+{\alpha }_{2,k}-{\dot{\beta }}_{1,k}\hfill \\ \hfill & \hfill & +f_2\left({\bar{x}}_{2,k},{\theta }_2\left(t\right)\right)+g_2\left({\bar{x}}_{2,k}\right)-sgn\left(z_{2\varphi ,k}\right){\dot{\varphi }}_{2,k}.\hfill \end{array}(33)$

The uncertain time-varying, nonlinear functions $f_2({\bar{x}}_{2,k},{\theta }_2(t))$ and $G_2({\bar{x}}_{2,k})$ are approximated by FSE-RBFNN and RBFNN, respectively.

$\begin{array}{ccc}\hfill f_2\left({\bar{x}}_{2,k},{\theta }_2\left(t\right)\right)& =\hfill & W_{f2}^T{S}_{f2}\left({\bar{x}}_{2,k},M_2^T{\mathrm{\Phi }}_2\left(t\right)\right)+{\delta }_{f2}\hfill \\ \hfill G_2\left({\bar{x}}_{2,k}\right)& =\hfill & W_{g2}^T{S}_{g2}\left({\bar{x}}_{2,k}\right)+{\delta }_{g2},\hfill \end{array}(34)$

where ${\delta }_{f2}$ and ${\delta }_{g2}$ are reconstructed errors and $W_{f2}$ and $W_{g2}$ are optimal weight vectors.

Let the virtual control be defined as follows:

$\begin{array}{ccc}\hfill {\alpha }_{2,k}& =\hfill & -{\widehat{W}}_{f2,k}^T{S}_{f2}\left({\bar{x}}_{2,k},{\widehat{M}}_{2,k}^T{\mathrm{\Phi }}_2\left(t\right)\right)-{\widehat{W}}_{g2,k}^T{S}_{g2}\left({\bar{x}}_{2,k}\right)\hfill \\ \hfill & \hfill & -{\widehat{N}}_{2,k}\frac{1}{{\mathrm{\Delta }}_k}{Z}_{2,k}+{\dot{\beta }}_{1,k}-{\eta }_2{z}_{2,k}-z_{1\varphi ,k}.\hfill \end{array}(35)$

Substituting Equations 34, 35 into Equation 33, we obtain

$\begin{array}{ccc}\hfill {\dot{Z}}_{2,k}& =\hfill & -z_{1\varphi ,k}+{\zeta }_{1,k}+z_{3,k}-{\varphi }_{3,k}\left(t\right)sat\left(\frac{z_{3,k}}{{\varphi }_{3,k}\left(t\right)}\right)-{\zeta }_{3,k}\hfill \\ \hfill & \hfill & +W_{f2}^T{S}_{f2}\left({\bar{x}}_{2,k},M_2^T{\mathrm{\Phi }}_2\left(t\right)\right)+{\delta }_{f2}-{\widehat{W}}_{f2,k}^T{S}_{f2}\left({\bar{x}}_{2,k},{\widehat{M}}_{2,k}^T{\mathrm{\Phi }}_2\left(t\right)\right)\hfill \\ \hfill & \hfill & +W_{g2}^T{S}_{g2}\left({\bar{x}}_{2,k}\right)+{\delta }_{g2}-{\widehat{W}}_{g2,k}^T{S}_{g2}\left({\bar{x}}_{2,k}\right)\hfill \\ \hfill & \hfill & -{\widehat{N}}_{2,k}\frac{1}{{\mathrm{\Delta }}_k}{z}_{2\varphi ,k}+{\varphi }_{3,k}\left(t\right)sat\left(\frac{z_{3,k}}{{\varphi }_{3,k}\left(t\right)}\right)\hfill \\ \hfill & \hfill & -{\eta }_2{z}_{2,k}+{\eta }_2{\zeta }_{2,k}-sgn\left(z_{2\varphi ,k}\right){\dot{\varphi }}_{2,k}\hfill \\ \hfill & =\hfill & -Z_{1,k}+Z_{3,k}-{\widehat{N}}_{2,k}\frac{1}{{\mathrm{\Delta }}_k}{z}_{2\varphi ,k}+{\varphi }_{3,k}\left(t\right)sat\left(\frac{z_{3,k}}{{\varphi }_{3,k}\left(t\right)}\right)\hfill \\ \hfill & \hfill & +W_{f2}^T{S}_{f2}\left({\bar{x}}_{2,k},M_2^T{\mathrm{\Phi }}_2\left(t\right)\right)+{\delta }_{f2}-{\widehat{W}}_{f2,k}^T{S}_{f2}\left({\bar{x}}_{2,k},{\widehat{M}}_{2,k}^T{\mathrm{\Phi }}_2\left(t\right)\right)\hfill \\ \hfill & \hfill & +W_{g2}^T{S}_{g2}\left({\bar{x}}_{2,k}\right)+{\delta }_{g2}-{\widehat{W}}_{g2,k}^T{S}_{g2}\left({\bar{x}}_{2,k}\right)\hfill \\ \hfill & \hfill & -{\eta }_2{z}_{2,k}+{\eta }_2{\zeta }_{2,k}-sgn\left(z_{2\varphi ,k}\right){\dot{\varphi }}_{2,k},\hfill \end{array}(36)$

where ${\widehat{W}}_{f2,k}$, ${\widehat{W}}_{g2,k}$, ${\widehat{M}}_{2,k}$, and ${\widehat{N}}_{2,k}$ are the estimators of $W_{f2}$, $W_{g2}$, $M_2$, and $N_2$, respectively. ${\tilde{W}}_{f2,k}={\widehat{W}}_{f2,k}-W_{f2}$, ${\tilde{W}}_{g2,k}={\widehat{W}}_{g2,k}-W_{g2}$, ${\tilde{M}}_{2,k}={\widehat{M}}_{2,k}-M_2$, and ${\tilde{N}}_{2,k}={\widehat{N}}_{2,k}-N_2$ are estimation errors. It can be proved that the following results are correct.

$\begin{array}{ccc}\hfill -{\eta }_2{z}_{2,k}-sgn\left(z_{2\varphi ,k}\right){\dot{\varphi }}_{2,k}\left(t\right)+{\eta }_2{\zeta }_{2,k}& =\hfill & -{\eta }_2{z}_{2\varphi ,k}-{\eta }_2{\varphi }_{2,k}\left(t\right)sat\left(\frac{z_{2,k}}{{\varphi }_{2,k}\left(t\right)}\right)\hfill \\ \hfill & \hfill & -sgn\left(z_{2\varphi ,k}\right){\dot{\varphi }}_{2,k}\left(t\right)+{\eta }_2{\zeta }_{2,k}\hfill \\ \hfill & =\hfill & -{\eta }_2{z}_{2\varphi ,k}+{\eta }_2{\zeta }_{2,k}\hfill \\ \hfill & \hfill & -sgn\left(z_{2\varphi ,k}\right)\left({\dot{\varphi }}_{2,k}\left(t\right)+{\eta }_2{\varphi }_{2,k}\left(t\right)\right)\hfill \\ \hfill & =\hfill & -{\eta }_2{z}_{2\varphi ,k}+{\eta }_2{\zeta }_{2,k}\hfill \\ \hfill & =\hfill & -{\eta }_2\left(z_{2\varphi ,k}-{\zeta }_{2,k}\right)\hfill \\ \hfill & =\hfill & -{\eta }_2{Z}_{2,k}.\hfill \end{array}(37)$

Using Equations 7, 37, Equation 36 can be written as

$\begin{array}{ccc}\hfill {\dot{Z}}_{2,k}& =\hfill & -Z_{1,k}+Z_{3,k}-{\widehat{N}}_{2,k}\frac{1}{{\mathrm{\Delta }}_k}{z}_{2\varphi ,k}-{\eta }_2{Z}_{2,k}\hfill \\ \hfill & \hfill & +{\tilde{W}}_{f2}^T\left(S_{f2}\left({\bar{x}}_{2,k},{\widehat{M}}_{2,k}^T{\mathrm{\Phi }}_2\left(t\right)\right)-{\widehat{S}}_{f2,k}^{\prime }{\widehat{M}}_{2,k}^T{\mathrm{\Phi }}_2\left(t\right)\right)\hfill \\ \hfill & \hfill & +{\widehat{W}}_{f2,k}^T{\widehat{S}}_{f2,k}^{\prime }{\tilde{M}}_{2,k}^T{\mathrm{\Phi }}_2\left(t\right)-{\tilde{W}}_{g2}^T{S}_{g2}\left({\bar{x}}_{2,k}\right)\hfill \\ \hfill & \hfill & +d_2+{\delta }_{f2}+{\delta }_{g2}+{\varphi }_{3,k}\left(t\right)sat\left(\frac{z_{3,k}}{{\varphi }_{3,k}\left(t\right)}\right).\hfill \end{array}(38)$

Let ${\omega }_2=d_2+{\delta }_{f2}+{\delta }_{g2}+{\varphi }_{3,k}(t)sat(\frac{z_{3,k}(t)}{{\varphi }_{3,k}(t)})$, then Equation 38 becomes

$\begin{array}{ccc}\hfill {\dot{Z}}_{2,k}& =\hfill & -Z_{1,k}+Z_{3,k}-{\widehat{N}}_{2,k}\frac{1}{{\mathrm{\Delta }}_k}{Z}_{2,k}-{\eta }_2{Z}_{2,k}+{\omega }_2\hfill \\ \hfill & \hfill & +{\tilde{W}}_{f2,k}^T\left(S_{f2}\left({\bar{x}}_{2,k},{\widehat{M}}_{2,k}^T{\mathrm{\Phi }}_2\left(t\right)\right)-{\widehat{S}}_{f2,k}^{\prime }{\widehat{M}}_{2,k}^T{\mathrm{\Phi }}_2\left(t\right)\right)\hfill \\ \hfill & \hfill & +{\widehat{W}}_{f2,k}^T{\widehat{S}}_{f2,k}^{\prime }{\tilde{M}}_{2,k}^T{\mathrm{\Phi }}_2\left(t\right)-{\tilde{W}}_{g2}^T{S}_{g2}\left({\bar{x}}_{2,k}\right).\hfill \end{array}(39)$

The Lyapunov-like function was chosen as follows:

$\begin{array}{ccc}\hfill V_{2,k}& =\hfill & V_{1,k}+\frac{1}{2}{Z}_{2,k}^2+\frac{1}{2}{\tilde{W}}_{f2,k}^T{\mathrm{\Gamma }}_{\mathit{f21}}^{-1}{\tilde{W}}_{f2,k}+\frac{1}{2}{\tilde{W}}_{g2,k}^T{\mathrm{\Gamma }}_{\mathit{g21}}^{-1}{\tilde{W}}_{g2,k}\hfill \\ \hfill & \hfill & +\frac{1}{2}{\tilde{M}}_{2,k}^T{\mathrm{\Gamma }}_{\mathit{m21}}^{-1}{\tilde{M}}_{2,k}+\frac{1}{2}{\mathrm{\Gamma }}_{\mathit{n21}}^{-1}{\tilde{N}}_{2,k}^2,\hfill \end{array}(40)$

where ${\mathrm{\Gamma }}_{\mathit{f21}}$, ${\mathrm{\Gamma }}_{\mathit{g21}}$, ${\mathrm{\Gamma }}_{\mathit{m21}}$, and ${\mathrm{\Gamma }}_{\mathit{n21}}$ are adjustable, positive, definite, and symmetric matrices. According to Equation 39, Assumption 3, and Remark 1, $V_{2,k}$ can be expressed as

$\begin{array}{ccc}\hfill {\dot{V}}_{2,k}& =\hfill & {\dot{V}}_{1,k}+Z_{2,k}{\dot{Z}}_{2,k}+{\tilde{W}}_{f2,k}^T{\mathrm{\Gamma }}_{\mathit{f21}}^{-1}{\dot{\widehat{W}}}_{f2,k}\hfill \\ \hfill & \hfill & +{\tilde{W}}_{g2,k}^T{\mathrm{\Gamma }}_{\mathit{g21}}^{-1}{\dot{\widehat{W}}}_{g2,k}+{\tilde{M}}_{2,k}^T{\mathrm{\Gamma }}_{\mathit{m21}}^{-1}{\dot{\widehat{M}}}_{2,k}+{\mathrm{\Gamma }}_{\mathit{n21}}^{-1}{\tilde{N}}_{2,k}{\dot{\widehat{N}}}_{2,k}\hfill \\ \hfill & \hfill & \le Z_{1,k}{Z}_{2,k}-{\eta }_1{Z}_{1,k}^2+\frac{1}{4}{\mathrm{\Delta }}_k-Z_{1,k}{Z}_{2,k}+Z_{2,k}{Z}_{3,k}-{\eta }_2{Z}_{2,k}^2\hfill \\ \hfill & \hfill & +{\tilde{W}}_{f2,k}^T{\mathrm{\Gamma }}_{\mathit{f21}}^{-1}\left({\mathrm{\Gamma }}_{\mathit{f21}}\left(S_{f2}\left({\bar{x}}_{2,k},{\widehat{M}}_{2,k}^T{\mathrm{\Phi }}_2\left(t\right)\right)-{\widehat{S}}_{f2,k}^{\prime }{\widehat{M}}_{2,k}^T{\mathrm{\Phi }}_2\left(t\right)\right)Z_{2,k}\right.\hfill \\ \hfill & \hfill & \left.+{\dot{\widehat{W}}}_{f2,k}\right)-{\tilde{W}}_{g2,k}^T{\mathrm{\Gamma }}_{\mathit{g21}}^{-1}\left({\mathrm{\Gamma }}_{\mathit{g21}}{S}_{g2}\left({\bar{x}}_{2,k}\right)Z_{2,k}-{\dot{\widehat{W}}}_{g2,k}\right)\hfill \\ \hfill & \hfill & +{\tilde{M}}_{2,k}^T{\mathrm{\Gamma }}_{\mathit{m21}}^{-1}\left({\mathrm{\Gamma }}_{\mathit{m21}}{\mathrm{\Phi }}_2\left(t\right){\widehat{W}}_{f2,k}^T{\widehat{S}}_{f2,k}^{\prime }{Z}_{2,k}+{\dot{\widehat{M}}}_{2,k}\right)\hfill \\ \hfill & \hfill & -{\widehat{N}}_{2,k}\frac{1}{{\mathrm{\Delta }}_k}{Z}_{2,k}^2+{\omega }_2{Z}_{2,k}+{\mathrm{\Gamma }}_{\mathit{n21}}^{-1}{\tilde{N}}_{2,k}{\dot{\widehat{N}}}_{2,k}\hfill \\ \hfill & \hfill & \le -{\eta }_1{Z}_{1,k}^2+\frac{1}{4}{\mathrm{\Delta }}_k+Z_{2,k}{Z}_{3,k}-{\eta }_2{Z}_{2,k}^2\hfill \\ \hfill & \hfill & +{\tilde{W}}_{f2,k}^T{\mathrm{\Gamma }}_{\mathit{f21}}^{-1}\left({\mathrm{\Gamma }}_{\mathit{f21}}\left(S_{f2}\left({\bar{x}}_{2,k},{\widehat{M}}_{2,k}^T{\mathrm{\Phi }}_2\left(t\right)\right)-{\widehat{S}}_{f2,k}^{\prime }{\widehat{M}}_{2,k}^T{\mathrm{\Phi }}_2\left(t\right)\right)Z_{2,k}\right.\hfill \\ \hfill & \hfill & \left.+{\dot{\widehat{W}}}_{f2,k}\right)-{\tilde{W}}_{g2,k}^T{\mathrm{\Gamma }}_{\mathit{g21}}^{-1}\left({\mathrm{\Gamma }}_{\mathit{g21}}{S}_{g2}\left({\bar{x}}_{2,k}\right)Z_{2,k}-{\dot{\widehat{W}}}_{g2,k}\right)\hfill \\ \hfill & \hfill & +{\tilde{M}}_{2,k}^T{\mathrm{\Gamma }}_{\mathit{m21}}^{-1}\left({\mathrm{\Gamma }}_{\mathit{m21}}{\mathrm{\Phi }}_2\left(t\right){\widehat{W}}_{f2,k}^T{\widehat{S}}_{f2,k}^{\prime }{Z}_{2,k}+{\dot{\widehat{M}}}_{2,k}\right)\hfill \\ \hfill & \hfill & -{\widehat{N}}_{2,k}\frac{1}{{\mathrm{\Delta }}_k}{Z}_{2,k}^2+\frac{1}{{\mathrm{\Delta }}_k}{\omega }_{M2}^2{Z}_{2,k}^2+\frac{1}{4}{\mathrm{\Delta }}_k+{\mathrm{\Gamma }}_{\mathit{n21}}^{-1}{\tilde{N}}_{2,k}{\dot{\widehat{N}}}_{2,k}\hfill \\ \hfill & =\hfill & Z_{2,k}{Z}_{3,k}-{\displaystyle \sum _{i=1}^2}{\eta }_i{Z}_{i,k}^2+\frac{1}{4}{\mathrm{\Delta }}_k\hfill \\ \hfill & \hfill & +{\tilde{W}}_{f2,k}^T{\mathrm{\Gamma }}_{\mathit{f21}}^{-1}\left({\mathrm{\Gamma }}_{\mathit{f21}}\left(S_{f2}\left({\bar{x}}_{2,k},{\widehat{M}}_{2,k}^T{\mathrm{\Phi }}_2\left(t\right)\right)-{\widehat{S}}_{f2,k}^{\prime }{\widehat{M}}_{2,k}^T{\mathrm{\Phi }}_2\left(t\right)\right)Z_{2,k}\right.\hfill \\ \hfill & \hfill & \left.+{\dot{\widehat{W}}}_{f2,k}\right)-{\tilde{W}}_{g2,k}^T{\mathrm{\Gamma }}_{\mathit{g21}}^{-1}\left({\mathrm{\Gamma }}_{\mathit{g21}}{S}_{g2}\left({\bar{x}}_{2,k}\right)Z_{2,k}-{\dot{\widehat{W}}}_{g2,k}\right)\hfill \\ \hfill & \hfill & +{\tilde{M}}_{2,k}^T{\mathrm{\Gamma }}_{\mathit{m21}}^{-1}\left({\mathrm{\Gamma }}_{\mathit{m21}}{\mathrm{\Phi }}_2\left(t\right){\widehat{W}}_{f2,k}^T{\widehat{S}}_{f2,k}^{\prime }{Z}_{2,k}+{\dot{\widehat{M}}}_{2,k}\right)\hfill \\ \hfill & \hfill & -{\widehat{N}}_{2,k}\frac{1}{{\mathrm{\Delta }}_k}{Z}_{2,k}^2+\frac{1}{{\mathrm{\Delta }}_k}{N}_{2,k}{Z}_{2,k}^2+\frac{1}{4}{\mathrm{\Delta }}_k+{\mathrm{\Gamma }}_{\mathit{n21}}^{-1}{\tilde{N}}_{2,k}{\dot{\widehat{N}}}_{2,k}\hfill \\ \hfill & =\hfill & Z_{2,k}{Z}_{3,k}-{\displaystyle \sum _{i=1}^2}{\eta }_i{Z}_{i,k}^2+\frac{2}{4}{\mathrm{\Delta }}_k\hfill \\ \hfill & \hfill & +{\tilde{W}}_{f2,k}^T{\mathrm{\Gamma }}_{\mathit{f21}}^{-1}\left({\mathrm{\Gamma }}_{\mathit{f21}}\left(S_{f2}\left({\bar{x}}_{2,k},{\widehat{M}}_{2,k}^T{\mathrm{\Phi }}_2\left(t\right)\right)-{\widehat{S}}_{f2,k}^{\prime }{\widehat{M}}_{2,k}^T{\mathrm{\Phi }}_2\left(t\right)\right)Z_{2,k}\right.\hfill \\ \hfill & \hfill & \left.+{\dot{\widehat{W}}}_{f2,k}\right)-{\tilde{W}}_{g2,k}^T{\mathrm{\Gamma }}_{\mathit{g21}}^{-1}\left({\mathrm{\Gamma }}_{\mathit{g21}}{S}_{g2}\left({\bar{x}}_{2,k}\right)Z_{2,k}-{\dot{\widehat{W}}}_{g2,k}\right)\hfill \\ \hfill & \hfill & +{\tilde{M}}_{2,k}^T{\mathrm{\Gamma }}_{\mathit{m21}}^{-1}\left({\mathrm{\Gamma }}_{\mathit{m21}}{\mathrm{\Phi }}_2\left(t\right){\widehat{W}}_{f2,k}^T{\widehat{S}}_{f2,k}^{\prime }{Z}_{2,k}+{\dot{\widehat{M}}}_{2,k}\right)\hfill \\ \hfill & \hfill & -{\tilde{N}}_{2,k}{\mathrm{\Gamma }}_{\mathit{n21}}^{-1}\left({\mathrm{\Gamma }}_{\mathit{n21}}\frac{1}{{\mathrm{\Delta }}_k}{Z}_{2,k}^2-{\dot{\widehat{N}}}_{2,k}\right).\hfill \end{array}(41)$

We choose

$\begin{array}{ccc}\hfill {\dot{\widehat{W}}}_{f2,k}& =\hfill & -{\mathrm{\Gamma }}_{\mathit{f21}}\left(S_{f2}\left({\bar{x}}_{2,k},{\widehat{M}}_{2,k}^T{\mathrm{\Phi }}_2\left(t\right)\right)-{\widehat{S}}_{f2,k}^{\prime }{\widehat{M}}_{2,k}^T{\mathrm{\Phi }}_2\left(t\right)\right)Z_{2,k}\hfill \\ \hfill {\dot{\widehat{W}}}_{g2,k}& =\hfill & {\mathrm{\Gamma }}_{\mathit{g21}}{S}_{g2}\left({\bar{x}}_{2,k}\right)Z_{2,k}\hfill \\ \hfill {\dot{\widehat{M}}}_{2,k}& =\hfill & -{\mathrm{\Gamma }}_{\mathit{m21}}{\mathrm{\Phi }}_2\left(t\right){\widehat{W}}_{f2,k}^T{\widehat{S}}_{f2,k}^{\prime }{Z}_{2,k}\hfill \\ \hfill {\dot{\widehat{N}}}_{2,k}& =\hfill & {\mathrm{\Gamma }}_{\mathit{n21}}\frac{1}{{\mathrm{\Delta }}_k}{Z}_{2,k}^2.\hfill \end{array}(42)$

Then, Equation 41 can be changed as

${\dot{V}}_{2,k}\le Z_{2,k}{Z}_{3,k}-{\displaystyle \sum _{i=1}^2}{\eta }_i{Z}_{i,k}^2+\frac{2}{4}{\mathrm{\Delta }}_k.(43)$

Step i: $(3\le i\le n-1)$. Denote $N_i={\omega }_{Mi}^2$, which will be defined later. Because there exist initial state errors and gradient explosion, the error functions $Z_{i,k}$ and $Z_{i+1,k}$ are defined as

$\begin{array}{ccc}\hfill Z_{i,k}& =\hfill & z_{i\varphi ,k}-{\zeta }_{i,k}\hfill \\ \hfill z_{i\varphi ,k}& =\hfill & z_{i,k}-{\varphi }_{i,k}\left(t\right)sat\left(\frac{z_{i,k}}{{\varphi }_{i,k}\left(t\right)}\right)\hfill \\ \hfill z_{i,k}& =\hfill & x_{i,k}-{\beta }_{i-1,k}\hfill \\ \hfill {\varphi }_{i,k}\left(t\right)& =\hfill & {ϵ}_{i,k}{e}^{-{\eta }_{i}t},\hfill \end{array}(44)$

$\begin{array}{ccc}\hfill Z_{i+1,k}& =\hfill & z_{i+1\varphi ,k}-{\zeta }_{i+1,k}\hfill \\ \hfill z_{i+1\varphi ,k}& =\hfill & z_{i+1,k}-{\varphi }_{i+1,k}\left(t\right)sat\left(\frac{z_{i+1,k}}{{\varphi }_{i+1,k}\left(t\right)}\right)\hfill \\ \hfill z_{i+1,k}& =\hfill & x_{i+1,k}-{\beta }_{i,k}\hfill \\ \hfill {\varphi }_{i+1,k}\left(t\right)& =\hfill & {ϵ}_{i+1,k}{e}^{-{\eta }_{i+1}t}.\hfill \end{array}(45)$

Therefore, ${\dot{Z}}_{i,k}$ can be deduced as follows:

$\begin{array}{ccc}\hfill {\dot{Z}}_{i,k}& =\hfill & {\dot{z}}_{i,k}-sgn\left(z_{i\varphi ,k}\left(t\right)\right){\dot{\varphi }}_{i,k}-{\dot{\zeta }}_{i,k}\hfill \\ \hfill & =\hfill & z_{i+1,k}+{\beta }_{i,k}+f_i\left({\bar{x}}_{i,k},{\theta }_i\left(t\right)\right)+g_i\left({\bar{x}}_{i,k}\right)\hfill \\ \hfill & \hfill & -{\dot{\beta }}_{i-1,k}-sgn\left(z_{i\varphi ,k}\right){\dot{\varphi }}_{i,k}-{\dot{\zeta }}_{i,k}.\hfill \end{array}(46)$

Let the error compensation mechanism be defined as

${\dot{\zeta }}_{i,k}={\beta }_{i,k}+{\zeta }_{i+1,k}-{\eta }_i{\zeta }_{i,k}-{\zeta }_{i-1,k}-{\alpha }_{i,k}.(47)$

Using Equation 47, we can find the time derivative of the error function as

$\begin{array}{ccc}\hfill {\dot{Z}}_{i,k}& =\hfill & z_{i+1,k}-{\zeta }_{i+1,k}+{\eta }_{i,k}{\zeta }_{i,k}+{\zeta }_{i-1,k}+{\alpha }_{i,k}-{\dot{\beta }}_{i-1,k}\hfill \\ \hfill & \hfill & +f_i\left({\bar{x}}_{i,k},{\theta }_i\left(t\right)\right)+g_i\left({\bar{x}}_{i,k}\right)-sgn\left(z_{i\varphi ,k}\right){\dot{\varphi }}_{i,k}.\hfill \end{array}(48)$

The uncertain time-varying, nonlinear functions $f_i({\bar{x}}_{i,k},{\theta }_i(t))$ and $G_i({\bar{x}}_{i,k})$ are approximated by FSE-RBFNN and RBFNN, respectively, and reconstruction errors ${\delta }_{fi}$ and ${\delta }_{gi}$ are as given follows:

$\begin{array}{ccc}\hfill f_i\left({\bar{x}}_{i,k},{\theta }_i\left(t\right)\right)& =\hfill & W_{fi}^T{S}_{fi}\left({\bar{x}}_{i,k},M_i^T{\mathrm{\Phi }}_i\left(t\right)\right)+{\delta }_{fi}\hfill \\ \hfill G_i\left({\bar{x}}_{i,k}\right)& =\hfill & W_{gi}^T{S}_{gi}\left({\bar{x}}_{i,k}\right)+{\delta }_{gi},\hfill \end{array}(49)$

where ${\delta }_{fi}$ and ${\delta }_{gi}$ are the approximation errors and $W_{fi}$ and $W_{gi}$ are ideal weight vectors.

Define ${\mathrm{\Delta }}_k=\frac{a}{k^l}$, where $a$ is any arbitrary number with $a>0$; meanwhile, $l\ge 2$. Let the virtual control be defined as

$\begin{array}{ccc}\hfill {\alpha }_{i,k}& =\hfill & -{\widehat{W}}_{fi,k}^T{S}_{fi}\left({\bar{x}}_{i,k},{\widehat{M}}_{i,k}^T{\mathrm{\Phi }}_i\left(t\right)\right)-{\widehat{W}}_{gi,k}^T{S}_{gi}\left({\bar{x}}_{i,k}\right)\hfill \\ \hfill & \hfill & -{\widehat{N}}_{i,k}\frac{1}{{\mathrm{\Delta }}_k}{Z}_{i,k}+{\dot{\beta }}_{i-1,k}-{\eta }_i{z}_{i,k}-z_{i-1\varphi ,k}.\hfill \end{array}(50)$

By substituting Equations 49, 50 into Equation 48, we obtain

$\begin{array}{ccc}\hfill {\dot{Z}}_{i,k}& =\hfill & -z_{i-1\varphi ,k}+{\zeta }_{i-1,k}+z_{i+1,k}-{\varphi }_{i+1,k}\left(t\right)sat\left(\frac{z_{i+1,k}}{{\varphi }_{i+1,k}\left(t\right)}\right)-{\zeta }_{i+1,k}\hfill \\ \hfill & \hfill & +W_{fi}^T{S}_{fi}\left({\bar{x}}_{i,k},M_i^T{\mathrm{\Phi }}_i\left(t\right)\right)+{\delta }_{fi}-{\widehat{W}}_{fi,k}^T{S}_{fi}\left({\bar{x}}_{i,k},{\widehat{M}}_{i,k}^T{\mathrm{\Phi }}_i\left(t\right)\right)\hfill \\ \hfill & \hfill & +W_{gi}^T{S}_{gi}\left({\bar{x}}_{i,k}\right)+{\delta }_{gi}-{\widehat{W}}_{gi,k}^T{S}_{gi}\left({\bar{x}}_{i,k}\right)\hfill \\ \hfill & \hfill & -{\widehat{N}}_{i,k}\frac{1}{{\mathrm{\Delta }}_k}{z}_{i\varphi ,k}+{\varphi }_{i+1,k}\left(t\right)sat\left(\frac{z_{i+1,k}}{{\varphi }_{i+1,k}\left(t\right)}\right)\hfill \\ \hfill & \hfill & -{\eta }_i{z}_{i,k}+{\eta }_i{\zeta }_{i,k}-sgn\left(z_{i\varphi ,k}\right){\dot{\varphi }}_{i,k}\hfill \\ \hfill & =\hfill & -Z_{i-1,k}+Z_{i+1,k}-{\widehat{N}}_{i,k}\frac{1}{{\mathrm{\Delta }}_k}{z}_{i\varphi ,k}+{\varphi }_{i+1,k}\left(t\right)sat\left(\frac{z_{i+1,k}}{{\varphi }_{i+1,k}\left(t\right)}\right)\hfill \\ \hfill & \hfill & +W_{fi}^T{S}_{fi}\left({\bar{x}}_{i,k},M_i^T{\mathrm{\Phi }}_i\left(t\right)\right)+{\delta }_{fi}-{\widehat{W}}_{fi,k}^T{S}_{fi}\left({\bar{x}}_{i,k},{\widehat{M}}_{i,k}^T{\mathrm{\Phi }}_i\left(t\right)\right)\hfill \\ \hfill & \hfill & +W_{gi}^T{S}_{gi}\left({\bar{x}}_{i,k}\right)+{\delta }_{gi}-{\widehat{W}}_{gi,k}^T{S}_{gi}\left({\bar{x}}_{i,k}\right)\hfill \\ \hfill & \hfill & -{\eta }_i{z}_{i,k}+{\eta }_i{\zeta }_{i,k}-sgn\left(z_{i\varphi ,k}\right){\dot{\varphi }}_{i,k},\hfill \end{array}(51)$

where ${\widehat{W}}_{fi,k}$, ${\widehat{W}}_{gi,k}$, ${\widehat{M}}_{i,k}$, and ${\widehat{N}}_{i,k}$ are the estimations of $W_{fi}$, $W_{gi}$, $M_i$, and $N_i$, respectively. ${\tilde{W}}_{fi,k}={\widehat{W}}_{fi,k}-W_{fi}$, ${\tilde{W}}_{gi,k}={\widehat{W}}_{gi,k}-W_{gi}$, ${\tilde{M}}_{i,k}={\widehat{M}}_{i,k}-M_i$, and ${\tilde{N}}_{i,k}={\widehat{N}}_{i,k}-N_i$ are estimation errors. We can rephrase the final three components on the right side of Equation 51 as

$\begin{array}{ccc}\hfill -{\eta }_i{z}_{i,k}-sgn\left(z_{i\varphi ,k}\right){\dot{\varphi }}_{i,k}\left(t\right)+{\eta }_i{\zeta }_{i,k}& =\hfill & -{\eta }_i{z}_{i\varphi ,k}-{\eta }_i{\varphi }_{i,k}\left(t\right)sat\left(\frac{z_{i,k}}{{\varphi }_{i,k}\left(t\right)}\right)\hfill \\ \hfill & \hfill & -sgn\left(z_{i\varphi ,k}\right){\dot{\varphi }}_{i,k}\left(t\right)+{\eta }_i{\zeta }_{i,k}\hfill \\ \hfill & =\hfill & -{\eta }_i{z}_{i\varphi ,k}+{\eta }_i{\zeta }_{i,k}\hfill \\ \hfill & \hfill & -sgn\left(z_{i\varphi ,k}\right)\left({\dot{\varphi }}_{i,k}\left(t\right)+{\eta }_i{\varphi }_{i,k}\left(t\right)\right)\hfill \\ \hfill & =\hfill & -{\eta }_i{z}_{i\varphi ,k}+{\eta }_i{\zeta }_{i,k}\hfill \\ \hfill & =\hfill & -{\eta }_i\left(z_{i\varphi ,k}-{\zeta }_{i,k}\right)\hfill \\ \hfill & =\hfill & -{\eta }_i{Z}_{i,k},\hfill \end{array}(52)$

Using Equations 7, 52, Equation 51 can be reformulated as

$\begin{array}{ccc}\hfill {\dot{Z}}_{i,k}& =\hfill & -Z_{i-1,k}+Z_{i+1,k}-{\widehat{N}}_{i,k}\frac{1}{{\mathrm{\Delta }}_k}{z}_{i\varphi ,k}-{\eta }_i{Z}_{i,k}\hfill \\ \hfill & \hfill & +{\tilde{W}}_{fi}^T\left(S_{fi}\left({\bar{x}}_{i,k},{\widehat{M}}_{i,k}^T{\mathrm{\Phi }}_i\left(t\right)\right)-{\widehat{S}}_{fi,k}^{\prime }{\widehat{M}}_{i,k}^T{\mathrm{\Phi }}_i\left(t\right)\right)\hfill \\ \hfill & \hfill & +{\widehat{W}}_{fi,k}^T{\widehat{S}}_{fi,k}^{\prime }{\tilde{M}}_{i,k}^T{\mathrm{\Phi }}_i\left(t\right)-{\tilde{W}}_{gi}^T{S}_{gi}\left({\bar{x}}_{i,k}\right)\hfill \\ \hfill & \hfill & +d_i+{\delta }_{fi}+{\delta }_{gi}+{\varphi }_{i+1,k}\left(t\right)sat\left(\frac{z_{i+1,k}}{{\varphi }_{i+1,k}\left(t\right)}\right).\hfill \end{array}(53)$

Let ${\omega }_i=d_i+{\delta }_{fi}+{\delta }_{gi}+{\varphi }_{i+1,k}(t)sat(\frac{z_{i+1,k}(t)}{{\varphi }_{i+1,k}(t)})$, then Equation 53 becomes

$\begin{array}{ccc}\hfill {\dot{Z}}_{i,k}& =\hfill & -Z_{i-1,k}+Z_{i+1,k}-{\widehat{N}}_{i,k}\frac{1}{{\mathrm{\Delta }}_k}{Z}_{i,k}-{\eta }_i{Z}_{i,k}+{\omega }_i\hfill \\ \hfill & \hfill & +{\tilde{W}}_{fi,k}^T\left(S_{fi}\left({\bar{x}}_{i,k},{\widehat{M}}_{i,k}^T{\mathrm{\Phi }}_i\left(t\right)\right)-{\widehat{S}}_{fi,k}^{\prime }{\widehat{M}}_{i,k}^T{\mathrm{\Phi }}_i\left(t\right)\right)\hfill \\ \hfill & \hfill & +{\widehat{W}}_{fi,k}^T{\widehat{S}}_{fi,k}^{\prime }{\tilde{M}}_{i,k}^T{\mathrm{\Phi }}_i\left(t\right)-{\tilde{W}}_{gi}^T{S}_{gi}\left({\bar{x}}_{i,k}\right).\hfill \end{array}(54)$

Consider the following nonnegative function:

$\begin{array}{ccc}\hfill V_{i,k}& =\hfill & V_{i-1,k}+\frac{1}{2}{Z}_{i,k}^2+\frac{1}{2}{\tilde{W}}_{fi,k}^T{\mathrm{\Gamma }}_{\mathit{fi1}}^{-1}{\tilde{W}}_{fi,k}+\frac{1}{2}{\tilde{W}}_{gi,k}^T{\mathrm{\Gamma }}_{\mathit{gi1}}^{-1}{\tilde{W}}_{gi,k}\hfill \\ \hfill & \hfill & +\frac{1}{2}{\tilde{M}}_{i,k}^T{\mathrm{\Gamma }}_{\mathit{mi1}}^{-1}{\tilde{M}}_{i,k}+\frac{1}{2}{\mathrm{\Gamma }}_{\mathit{ni1}}^{-1}{\tilde{N}}_{i,k}^2,\hfill \end{array}(55)$

where ${\mathrm{\Gamma }}_{\mathit{fi1}}$, ${\mathrm{\Gamma }}_{\mathit{gi1}}$, ${\mathrm{\Gamma }}_{\mathit{mi1}}$, and ${\mathrm{\Gamma }}_{\mathit{ni1}}$ are adjustable, positive, definite, and symmetric matrices. According to Equation 54, Assumption 3, and Remark 1, $V_{i,k}$ can be expressed as

$\begin{array}{ccc}\hfill {\dot{V}}_{i,k}& =\hfill & {\dot{V}}_{i-1,k}+Z_{i,k}{\dot{Z}}_{i,k}+{\tilde{W}}_{fi,k}^T{\mathrm{\Gamma }}_{\mathit{fi1}}^{-1}{\dot{\widehat{W}}}_{fi,k}\hfill \\ \hfill & \hfill & +{\tilde{W}}_{gi,k}^T{\mathrm{\Gamma }}_{\mathit{gi1}}^{-1}{\dot{\widehat{W}}}_{gi,k}+{\tilde{M}}_{i,k}^T{\mathrm{\Gamma }}_{\mathit{mi1}}^{-1}{\dot{\widehat{M}}}_{i,k}+{\mathrm{\Gamma }}_{\mathit{ni1}}^{-1}{\tilde{N}}_{i,k}{\dot{\widehat{N}}}_{i,k}\hfill \\ \hfill & \le \hfill & Z_{i-1,k}{Z}_{i,k}-{\displaystyle \sum _{j=1}^{i-1}}{\eta }_j{Z}_{j,k}^2+\frac{i-1}{4}{\mathrm{\Delta }}_k-Z_{i-1,k}{Z}_{i,k}+Z_{i,k}{Z}_{i+1,k}-{\eta }_i{Z}_{i,k}^2\hfill \\ \hfill & \hfill & +{\tilde{W}}_{fi,k}^T{\mathrm{\Gamma }}_{\mathit{fi1}}^{-1}\left({\mathrm{\Gamma }}_{\mathit{fi1}}\left(S_{fi}\left({\bar{x}}_{i,k},{\widehat{M}}_{i,k}^T{\mathrm{\Phi }}_i\left(t\right)\right)-{\widehat{S}}_{fi,k}^{\prime }{\widehat{M}}_{i,k}^T{\mathrm{\Phi }}_i\left(t\right)\right)Z_{i,k}+{\dot{\widehat{W}}}_{fi,k}\right)\hfill \\ \hfill & \hfill & -{\tilde{W}}_{gi,k}^T{\mathrm{\Gamma }}_{\mathit{gi1}}^{-1}\left({\mathrm{\Gamma }}_{\mathit{gi1}}{S}_{gi}\left({\bar{x}}_{i,k}\right)Z_{i,k}-{\dot{\widehat{W}}}_{gi,k}\right)\hfill \\ \hfill & \hfill & +{\tilde{M}}_{i,k}^T{\mathrm{\Gamma }}_{\mathit{mi1}}^{-1}\left({\mathrm{\Gamma }}_{\mathit{mi1}}{\mathrm{\Phi }}_i\left(t\right){\widehat{W}}_{fi,k}^T{\widehat{S}}_{fi,k}^{\prime }{Z}_{i,k}+{\dot{\widehat{M}}}_{i,k}\right)\hfill \\ \hfill & \hfill & -{\widehat{N}}_{i,k}\frac{1}{{\mathrm{\Delta }}_k}{Z}_{i,k}^2+{\omega }_i{Z}_{i,k}+{\mathrm{\Gamma }}_{\mathit{ni1}}^{-1}{\tilde{N}}_{i,k}{\dot{\widehat{N}}}_{i,k}\hfill \\ \hfill & \le \hfill & -{\displaystyle \sum _{j=1}^{i-1}}{\eta }_j{Z}_{j,k}^2+\frac{i-1}{4}{\mathrm{\Delta }}_k+Z_{i,k}{Z}_{i+1,k}-{\eta }_i{Z}_{i,k}^2\hfill \\ \hfill & \hfill & +{\tilde{W}}_{fi,k}^T{\mathrm{\Gamma }}_{\mathit{fi1}}^{-1}\left({\mathrm{\Gamma }}_{\mathit{fi1}}\left(S_{fi}\left({\bar{x}}_{i,k},{\widehat{M}}_{i,k}^T{\mathrm{\Phi }}_i\left(t\right)\right)-{\widehat{S}}_{fi,k}^{\prime }{\widehat{M}}_{i,k}^T{\mathrm{\Phi }}_i\left(t\right)\right)Z_{i,k}+{\dot{\widehat{W}}}_{fi,k}\right)\hfill \\ \hfill & \hfill & -{\tilde{W}}_{gi,k}^T{\mathrm{\Gamma }}_{\mathit{gi1}}^{-1}\left({\mathrm{\Gamma }}_{\mathit{gi1}}{S}_{gi}\left({\bar{x}}_{i,k}\right)Z_{i,k}-{\dot{\widehat{W}}}_{gi,k}\right)\hfill \\ \hfill & \hfill & +{\tilde{M}}_{i,k}^T{\mathrm{\Gamma }}_{\mathit{mi1}}^{-1}\left({\mathrm{\Gamma }}_{\mathit{mi1}}{\mathrm{\Phi }}_i\left(t\right){\widehat{W}}_{fi,k}^T{\widehat{S}}_{fi,k}^{\prime }{Z}_{i,k}+{\dot{\widehat{M}}}_{i,k}\right)\hfill \\ \hfill & \hfill & -{\widehat{N}}_{i,k}\frac{1}{{\mathrm{\Delta }}_k}{Z}_{i,k}^2+\frac{1}{{\mathrm{\Delta }}_k}{\omega }_{Mi}^2{Z}_{i,k}^2+\frac{1}{4}{\mathrm{\Delta }}_k+{\mathrm{\Gamma }}_{\mathit{ni1}}^{-1}{\tilde{N}}_{i,k}{\dot{\widehat{N}}}_{i,k}\hfill \\ \hfill & =\hfill & -{\displaystyle \sum _{j=1}^i}{\eta }_j{Z}_{j,k}^2+\frac{i-1}{4}{\mathrm{\Delta }}_k+Z_{i,k}{Z}_{i+1,k}\hfill \\ \hfill & \hfill & +{\tilde{W}}_{fi,k}^T{\mathrm{\Gamma }}_{\mathit{fi1}}^{-1}\left({\mathrm{\Gamma }}_{\mathit{fi1}}\left(S_{fi}\left({\bar{x}}_{i,k},{\widehat{M}}_{i,k}^T{\mathrm{\Phi }}_i\left(t\right)\right)-{\widehat{S}}_{fi,k}^{\prime }{\widehat{M}}_{i,k}^T{\mathrm{\Phi }}_i\left(t\right)\right)Z_{i,k}+{\dot{\widehat{W}}}_{fi,k}\right)\hfill \\ \hfill & \hfill & -{\tilde{W}}_{gi,k}^T{\mathrm{\Gamma }}_{\mathit{gi1}}^{-1}\left({\mathrm{\Gamma }}_{\mathit{gi1}}{S}_{gi}\left({\bar{x}}_{i,k}\right)Z_{i,k}-{\dot{\widehat{W}}}_{gi,k}\right)\hfill \\ \hfill & \hfill & +{\tilde{M}}_{i,k}^T{\mathrm{\Gamma }}_{\mathit{mi1}}^{-1}\left({\mathrm{\Gamma }}_{\mathit{mi1}}{\mathrm{\Phi }}_i\left(t\right){\widehat{W}}_{fi,k}^T{\widehat{S}}_{fi,k}^{\prime }{Z}_{i,k}+{\dot{\widehat{M}}}_{i,k}\right)-{\widehat{N}}_{i,k}\frac{1}{{\mathrm{\Delta }}_k}{Z}_{i,k}^2+\frac{1}{{\mathrm{\Delta }}_k}{N}_{i,k}{Z}_{i,k}^2+\frac{1}{4}{\mathrm{\Delta }}_k+{\mathrm{\Gamma }}_{\mathit{ni1}}^{-1}{\tilde{N}}_{i,k}{\dot{\widehat{N}}}_{i,k}\hfill \\ \hfill & =\hfill & -{\displaystyle \sum _{j=1}^i}{\eta }_j{Z}_{j,k}^2+\frac{i}{4}{\mathrm{\Delta }}_k+Z_{i,k}{Z}_{i+1,k}\hfill \\ \hfill & \hfill & +{\tilde{W}}_{fi,k}^T{\mathrm{\Gamma }}_{\mathit{fi1}}^{-1}\left({\mathrm{\Gamma }}_{\mathit{fi1}}\left(S_{fi}\left({\bar{x}}_{i,k},{\widehat{M}}_{i,k}^T{\mathrm{\Phi }}_i\left(t\right)\right)-{\widehat{S}}_{fi,k}^{\prime }{\widehat{M}}_{i,k}^T{\mathrm{\Phi }}_i\left(t\right)\right)Z_{i,k}+{\dot{\widehat{W}}}_{fi,k}\right)\hfill \\ \hfill & \hfill & -{\tilde{W}}_{gi,k}^T{\mathrm{\Gamma }}_{\mathit{gi1}}^{-1}\left({\mathrm{\Gamma }}_{\mathit{gi1}}{S}_{gi}\left({\bar{x}}_{i,k}\right)Z_{i,k}-{\dot{\widehat{W}}}_{gi,k}\right)\hfill \\ \hfill & \hfill & +{\tilde{M}}_{i,k}^T{\mathrm{\Gamma }}_{\mathit{mi1}}^{-1}\left({\mathrm{\Gamma }}_{\mathit{mi1}}{\mathrm{\Phi }}_i\left(t\right){\widehat{W}}_{fi,k}^T{\widehat{S}}_{fi,k}^{\prime }{Z}_{i,k}+{\dot{\widehat{M}}}_{i,k}\right)\hfill \\ \hfill & \hfill & -{\tilde{N}}_{i,k}{\mathrm{\Gamma }}_{\mathit{ni1}}^{-1}\left({\mathrm{\Gamma }}_{\mathit{ni1}}\frac{1}{{\mathrm{\Delta }}_k}{Z}_{i,k}^2-{\dot{\widehat{N}}}_{i,k}\right).\hfill \end{array}(56)$

We choose

$\begin{array}{ccc}\hfill {\dot{\widehat{W}}}_{fi,k}& =\hfill & -{\mathrm{\Gamma }}_{\mathit{fi1}}\left(S_{fi}\left({\bar{x}}_{i,k},{\widehat{M}}_{i,k}^T{\mathrm{\Phi }}_i\left(t\right)\right)-{\widehat{S}}_{fi,k}^{\prime }{\widehat{M}}_{i,k}^T{\mathrm{\Phi }}_i\left(t\right)\right)Z_{i,k}\hfill \\ \hfill {\dot{\widehat{W}}}_{gi,k}& =\hfill & {\mathrm{\Gamma }}_{\mathit{gi1}}{S}_{gi}\left({\bar{x}}_{i,k}\right)Z_{i,k}\hfill \\ \hfill {\dot{\widehat{M}}}_{i,k}& =\hfill & -{\mathrm{\Gamma }}_{\mathit{mi1}}{\mathrm{\Phi }}_i\left(t\right){\widehat{W}}_{fi,k}^T{\widehat{S}}_{fi,k}^{\prime }{Z}_{i,k}\hfill \\ \hfill {\dot{\widehat{N}}}_{i,k}& =\hfill & {\mathrm{\Gamma }}_{\mathit{ni1}}\frac{1}{{\mathrm{\Delta }}_k}{Z}_{i,k}^2.\hfill \end{array}(57)$

Then, Equation 56 can be written as

${\dot{V}}_{2,k}\le -{\displaystyle \sum _{j=1}^i}{\eta }_j{Z}_{j,k}^2+\frac{i}{4}{\mathrm{\Delta }}_k+Z_{i,k}{Z}_{i+1,k},(58)$

Step n: Denote $N_n={\omega }_{Mn}^2$, which will be defined later. Because there exist initial state errors and gradient explosion, the function $Z_{n,k}$, denoting the error, is defined as

$\begin{array}{ccc}\hfill Z_{n,k}& =\hfill & z_{n\varphi ,k}-{\zeta }_{n,k}\hfill \\ \hfill z_{n\varphi ,k}& =\hfill & z_{n,k}-{\varphi }_{n,k}\left(t\right)sat\left(\frac{z_{n,k}}{{\varphi }_{n,k}\left(t\right)}\right)\hfill \\ \hfill z_{n,k}& =\hfill & x_{n,k}-{\beta }_{n-1,k}\hfill \\ \hfill {\varphi }_{n,k}\left(t\right)& =\hfill & {ϵ}_{n,k}{e}^{-{\eta }_{n}t}.\hfill \end{array}(59)$

The derivative of $Z_{i,k}$ with respect to time is expressed as

$\begin{array}{ccc}\hfill {\dot{Z}}_{n,k}& =\hfill & {\dot{z}}_{n,k}-sgn\left(z_{n\varphi ,k}\left(t\right)\right){\dot{\varphi }}_{n,k}-{\dot{\zeta }}_{n,k}\hfill \\ \hfill & =\hfill & u_k+f_n\left({\bar{x}}_{n,k},{\theta }_n\left(t\right)\right)+g_n\left({\bar{x}}_{n,k}\right)\hfill \\ \hfill & \hfill & -{\dot{\beta }}_{n-1,k}-sgn\left(z_{n\varphi ,k}\right){\dot{\varphi }}_{n,k}-{\dot{\zeta }}_{n,k}.\hfill \end{array}(60)$

Let the error compensation mechanism be defined as

${\dot{\zeta }}_{n,k}=-{\eta }_n{\zeta }_{n,k}-{\zeta }_{n-1,k}.(61)$

Using Equation 61, we can obtain the time derivative of the error function as

$\begin{array}{ccc}\hfill {\dot{Z}}_{n,k}& =\hfill & u_k+{\eta }_{n,k}{\zeta }_{n,k}+{\zeta }_{n-1,k}-{\dot{\beta }}_{n-1,k}\hfill \\ \hfill & \hfill & +f_n\left({\bar{x}}_{n,k},{\theta }_n\left(t\right)\right)+g_n\left({\bar{x}}_{n,k}\right)-sgn\left(z_{n\varphi ,k}\right){\dot{\varphi }}_{n,k}.\hfill \end{array}(62)$

The overall approximation capability of the RBFNN asserts that the unknown nonlinear functions $f_n({\bar{x}}_{n,k},{\theta }_n(t))$ and $G_n({\bar{x}}_{n,k})$ are capable of approximation within a defined scope by FSE-RBFNN and RBFNN, respectively, and reconstruction errors ${\delta }_{fn}$ and ${\delta }_{gn}$ are as follows:

$\begin{array}{ccc}\hfill f_n\left({\bar{x}}_{n,k},{\theta }_n\left(t\right)\right)& =\hfill & W_{fn}^T{S}_{fn}\left({\bar{x}}_{n,k},M_n^T{\mathrm{\Phi }}_n\left(t\right)\right)+{\delta }_{fn}\hfill \\ \hfill G_n\left({\bar{x}}_{n,k}\right)& =\hfill & W_{gn}^T{S}_{gn}\left({\bar{x}}_{n,k}\right)+{\delta }_{gn},\hfill \end{array}(63)$

where ${\delta }_{fn}$ and ${\delta }_{gn}$ are the approximation errors and $W_{fn}$ and $W_{gn}$ are ideal weight vectors.

Define ${\mathrm{\Delta }}_k=\frac{a}{k^l}$,where $a$ is any arbitrary number such that $a>0$; meanwhile, $l\ge 2$. Let the virtual control be defined as

$\begin{array}{ccc}\hfill u_k& =\hfill & -{\widehat{W}}_{fn,k}^T{S}_{fn}\left({\bar{x}}_{n,k},{\widehat{M}}_{n,k}^T{\mathrm{\Phi }}_n\left(t\right)\right)-{\widehat{W}}_{gn,k}^T{S}_{gn}\left({\bar{x}}_{n,k}\right)\hfill \\ \hfill & \hfill & -{\widehat{N}}_{n,k}\frac{1}{{\mathrm{\Delta }}_k}{Z}_{n,k}+{\dot{\beta }}_{n-1,k}-{\eta }_n{z}_{n,k}-z_{n-1\varphi ,k}.\hfill \end{array}(64)$

By substituting Equations 63, 64 into Equation 62, we can conclude that

$\begin{array}{ccc}\hfill {\dot{Z}}_{n,k}& =\hfill & -z_{n-1\varphi ,k}+{\zeta }_{n-1,k}-{\eta }_n{z}_{n,k}+{\eta }_n{\zeta }_{n,k}-sgn\left(z_{n\varphi ,k}\right){\dot{\varphi }}_{n,k}\hfill \\ \hfill & \hfill & +W_{fn}^T{S}_{fn}\left({\bar{x}}_{n,k},M_n^T{\mathrm{\Phi }}_n\left(t\right)\right)+{\delta }_{fn}-{\widehat{W}}_{fn,k}^T{S}_{fn}\left({\bar{x}}_{n,k},{\widehat{M}}_{n,k}^T{\mathrm{\Phi }}_n\left(t\right)\right)\hfill \\ \hfill & \hfill & +W_{gn}^T{S}_{gn}\left({\bar{x}}_{n,k}\right)+{\delta }_{gn}-{\widehat{W}}_{gn,k}^T{S}_{gn}\left({\bar{x}}_{n,k}\right)-{\widehat{N}}_{n,k}\frac{1}{{\mathrm{\Delta }}_k}{z}_{n\varphi ,k}\hfill \\ \hfill & =\hfill & W_{fn}^T{S}_{fn}\left({\bar{x}}_{n,k},M_n^T{\mathrm{\Phi }}_n\left(t\right)\right)+{\delta }_{fn}-{\widehat{W}}_{fn,k}^T{S}_{fn}\left({\bar{x}}_{n,k},{\widehat{M}}_{n,k}^T{\mathrm{\Phi }}_n\left(t\right)\right)\hfill \\ \hfill & \hfill & +W_{gn}^T{S}_{gn}\left({\bar{x}}_{n,k}\right)+{\delta }_{gn}-{\widehat{W}}_{gn,k}^T{S}_{gn}\left({\bar{x}}_{n,k}\right)-{\widehat{N}}_{n,k}\frac{1}{{\mathrm{\Delta }}_k}{z}_{n\varphi ,k}\hfill \\ \hfill & \hfill & -Z_{n-1,k}-{\eta }_n{z}_{n,k}+{\eta }_n{\zeta }_{n,k}-sgn\left(z_{n\varphi ,k}\right){\dot{\varphi }}_{n,k},\hfill \end{array}(65)$

where ${\widehat{W}}_{fn,k}$, ${\widehat{W}}_{gn,k}$, ${\widehat{M}}_{n,k}$, and ${\widehat{N}}_{n,k}$ are the estimations of $W_{fn}$, $W_{gn}$, $M_n$, and $N_n$, respectively. ${\tilde{W}}_{fn,k}={\widehat{W}}_{fn,k}-W_{fn}$, ${\tilde{W}}_{gn,k}={\widehat{W}}_{gn,k}-W_{gn}$, ${\tilde{M}}_{n,k}={\widehat{M}}_{n,k}-M_n$, and ${\tilde{N}}_{n,k}={\widehat{N}}_{n,k}-N_n$ are estimation errors. We can rephrase the final three components on the right side of Equation 65 as

$\begin{array}{ccc}\hfill -{\eta }_n{z}_{n,k}-sgn\left(z_{n\varphi ,k}\right){\dot{\varphi }}_{n,k}\left(t\right)+{\eta }_n{\zeta }_{n,k}& =\hfill & -{\eta }_n{z}_{n\varphi ,k}-{\eta }_n{\varphi }_{n,k}\left(t\right)sat\left(\frac{z_{n,k}}{{\varphi }_{n,k}\left(t\right)}\right)\hfill \\ \hfill & \hfill & -sgn\left(z_{n\varphi ,k}\right){\dot{\varphi }}_{n,k}\left(t\right)+{\eta }_n{\zeta }_{n,k}\hfill \\ \hfill & =\hfill & -{\eta }_n{z}_{n\varphi ,k}+{\eta }_n{\zeta }_{n,k}\hfill \\ \hfill & \hfill & -sgn\left(z_{n\varphi ,k}\right)\left({\dot{\varphi }}_{n,k}\left(t\right)+{\eta }_n{\varphi }_{n,k}\left(t\right)\right)\hfill \\ \hfill & =\hfill & -{\eta }_n{z}_{n\varphi ,k}+{\eta }_n{\zeta }_{n,k}\hfill \\ \hfill & =\hfill & -{\eta }_n\left(z_{n\varphi ,k}-{\zeta }_{n,k}\right)\hfill \\ \hfill & =\hfill & -{\eta }_n{Z}_{n,k}.\hfill \end{array}(66)$

Using Equations 7, 66, Equation 65 can be reformulated as

$\begin{array}{ccc}\hfill {\dot{Z}}_{n,k}& =\hfill & -Z_{n-1,k}-{\widehat{N}}_{n,k}\frac{1}{{\mathrm{\Delta }}_k}{z}_{n\varphi ,k}-{\eta }_n{Z}_{n,k}\hfill \\ \hfill & \hfill & +{\tilde{W}}_{fn}^T\left(S_{fn}\left({\bar{x}}_{n,k},{\widehat{M}}_{n,k}^T{\mathrm{\Phi }}_n\left(t\right)\right)-{\widehat{S}}_{fn,k}^{\prime }{\widehat{M}}_{n,k}^T{\mathrm{\Phi }}_n\left(t\right)\right)\hfill \\ \hfill & \hfill & +{\widehat{W}}_{fn,k}^T{\widehat{S}}_{fn,k}^{\prime }{\tilde{M}}_{n,k}^T{\mathrm{\Phi }}_n\left(t\right)-{\tilde{W}}_{gn}^T{S}_{gn}\left({\bar{x}}_{n,k}\right)\hfill \\ \hfill & \hfill & +d_n+{\delta }_{fn}+{\delta }_{gn}.\hfill \end{array}(67)$

Let ${\omega }_n=d_n+{\delta }_{fn}+{\delta }_{gn}$, then Equation 67 becomes

$\begin{array}{ccc}\hfill {\dot{Z}}_{n,k}& =\hfill & -Z_{n-1,k}-{\widehat{N}}_{n,k}\frac{1}{{\mathrm{\Delta }}_k}{Z}_{n,k}-{\eta }_n{Z}_{n,k}+{\omega }_n\hfill \\ \hfill & \hfill & +{\tilde{W}}_{fn,k}^T\left(S_{fn}\left({\bar{x}}_{n,k},{\widehat{M}}_{n,k}^T{\mathrm{\Phi }}_n\left(t\right)\right)-{\widehat{S}}_{fn,k}^{\prime }{\widehat{M}}_{n,k}^T{\mathrm{\Phi }}_n\left(t\right)\right)\hfill \\ \hfill & \hfill & +{\widehat{W}}_{fn,k}^T{\widehat{S}}_{fn,k}^{\prime }{\tilde{M}}_{n,k}^T{\mathrm{\Phi }}_n\left(t\right)-{\tilde{W}}_{gn}^T{S}_{gn}\left({\bar{x}}_{n,k}\right).\hfill \end{array}(68)$

Assumption 4: The remainder ${\omega }_n$ is bounded with $|{\omega }_n|\le {\omega }_{Mn}$ and ${\omega }_{Mn}>0$.

Remark 2: This assumption is reasonable because 1) $d_n$, ${\delta }_{fn}$, and ${\delta }_{gn}$ are constrained within the specified area by Equations 6, 8.

Let the following non-negative function be defined as

$\begin{array}{ccc}\hfill V_{n,k}& =\hfill & V_{n-1,k}+\frac{1}{2}{Z}_{n,k}^2+\frac{1}{2}{\tilde{W}}_{fn,k}^T{\mathrm{\Gamma }}_{\mathit{fn1}}^{-1}{\tilde{W}}_{fn,k}+\frac{1}{2}{\tilde{W}}_{gn,k}^T{\mathrm{\Gamma }}_{\mathit{gn1}}^{-1}{\tilde{W}}_{gn,k}\hfill \\ \hfill & \hfill & +\frac{1}{2}{\tilde{M}}_{n,k}^T{\mathrm{\Gamma }}_{\mathit{mn1}}^{-1}{\tilde{M}}_{n,k}+\frac{1}{2}{\mathrm{\Gamma }}_{\mathit{Nn1}}^{-1}{\tilde{N}}_{n,k}^2,\hfill \end{array}(69)$

where ${\mathrm{\Gamma }}_{\mathit{fn1}}$, ${\mathrm{\Gamma }}_{\mathit{gn1}}$, ${\mathrm{\Gamma }}_{\mathit{mn1}}$, and ${\mathrm{\Gamma }}_{\mathit{Nn1}}$ are adjustable, positive, definite, and symmetric matrices. The derivative of $V_{n,k}$ is considered as follows (Equation 68):

$\begin{array}{ccc}\hfill {\dot{V}}_{n,k}& =\hfill & {\dot{V}}_{n-1,k}+Z_{n,k}{\dot{Z}}_{n,k}+{\tilde{W}}_{fn,k}^T{\mathrm{\Gamma }}_{\mathit{fn1}}^{-1}{\dot{\widehat{W}}}_{fn,k}\hfill \\ \hfill & \hfill & +{\tilde{W}}_{gn,k}^T{\mathrm{\Gamma }}_{\mathit{gn1}}^{-1}{\dot{\widehat{W}}}_{gn,k}+{\tilde{M}}_{n,k}^T{\mathrm{\Gamma }}_{\mathit{mn1}}^{-1}{\dot{\widehat{M}}}_{n,k}+{\mathrm{\Gamma }}_{\mathit{Nn1}}^{-1}{\tilde{N}}_{n,k}{\dot{\widehat{N}}}_{n,k}\hfill \\ \hfill & \le \hfill & Z_{n-1,k}{Z}_{n,k}-{\displaystyle \sum _{j=1}^{n-1}}{\eta }_j{Z}_{j,k}^2+\frac{n-1}{4}{\mathrm{\Delta }}_k-Z_{n-1,k}{Z}_{n,k}-{\eta }_i{Z}_{i,k}^2\hfill \\ \hfill & \hfill & +{\tilde{W}}_{fn,k}^T{\mathrm{\Gamma }}_{\mathit{fn1}}^{-1}\left({\mathrm{\Gamma }}_{\mathit{fn1}}\left(S_{fn}\left({\bar{x}}_{n,k},{\widehat{M}}_{n,k}^T{\mathrm{\Phi }}_n\left(t\right)\right)\right.\right.\hfill \\ \hfill & \hfill & \left.\left.-{\widehat{S}}_{fn,k}^{\prime }{\widehat{M}}_{n,k}^T{\mathrm{\Phi }}_n\left(t\right)\right)Z_{n,k}+{\dot{\widehat{W}}}_{fn,k}\right)\hfill \\ \hfill & \hfill & -{\tilde{W}}_{gn,k}^T{\mathrm{\Gamma }}_{\mathit{gn1}}^{-1}\left({\mathrm{\Gamma }}_{\mathit{gn1}}{S}_{gn}\left({\bar{x}}_{n,k}\right)Z_{n,k}-{\dot{\widehat{W}}}_{gn,k}\right)\hfill \\ \hfill & \hfill & +{\tilde{M}}_{n,k}^T{\mathrm{\Gamma }}_{\mathit{mn1}}^{-1}\left({\mathrm{\Gamma }}_{\mathit{mn1}}{\mathrm{\Phi }}_n\left(t\right){\widehat{W}}_{fn,k}^T{\widehat{S}}_{fn,k}^{\prime }{Z}_{n,k}+{\dot{\widehat{M}}}_{n,k}\right)\hfill \\ \hfill & \hfill & -{\widehat{N}}_{n,k}\frac{1}{{\mathrm{\Delta }}_k}{Z}_{n,k}^2+{\omega }_n{Z}_{n,k}+{\mathrm{\Gamma }}_{\mathit{Nn1}}^{-1}{\tilde{N}}_{n,k}{\dot{\widehat{N}}}_{n,k}\hfill \\ \hfill & \le \hfill & -{\displaystyle \sum _{j=1}^{n-1}}{\eta }_j{Z}_{j,k}^2+\frac{n-1}{4}{\mathrm{\Delta }}_k-{\eta }_n{Z}_{n,k}^2\hfill \\ \hfill & \hfill & +{\tilde{W}}_{fn,k}^T{\mathrm{\Gamma }}_{\mathit{fn1}}^{-1}\left({\mathrm{\Gamma }}_{\mathit{fn1}}\left(S_{fn}\left({\bar{x}}_{n,k},{\widehat{M}}_{n,k}^T{\mathrm{\Phi }}_n\left(t\right)\right)\right.\right.\hfill \\ \hfill & \hfill & \left.\left.-{\widehat{S}}_{fn,k}^{\prime }{\widehat{M}}_{n,k}^T{\mathrm{\Phi }}_n\left(t\right)\right)Z_{n,k}+{\dot{\widehat{W}}}_{fn,k}\right)\hfill \\ \hfill & \hfill & -{\tilde{W}}_{gn,k}^T{\mathrm{\Gamma }}_{\mathit{gn1}}^{-1}\left({\mathrm{\Gamma }}_{\mathit{gn1}}{S}_{gn}\left({\bar{x}}_{n,k}\right)Z_{n,k}-{\dot{\widehat{W}}}_{gn,k}\right)\hfill \\ \hfill & \hfill & +{\tilde{M}}_{n,k}^T{\mathrm{\Gamma }}_{\mathit{mn1}}^{-1}\left({\mathrm{\Gamma }}_{\mathit{mn1}}{\mathrm{\Phi }}_n\left(t\right){\widehat{W}}_{fn,k}^T{\widehat{S}}_{fn,k}^{\prime }{Z}_{n,k}+{\dot{\widehat{M}}}_{n,k}\right)\hfill \\ \hfill & \hfill & -{\widehat{N}}_{n,k}\frac{1}{{\mathrm{\Delta }}_k}{Z}_{n,k}^2+\frac{1}{{\mathrm{\Delta }}_k}{\omega }_{Mn}^2{Z}_{n,k}^2+\frac{1}{4}{\mathrm{\Delta }}_k+{\mathrm{\Gamma }}_{\mathit{Nn1}}^{-1}{\tilde{N}}_{n,k}{\dot{\widehat{N}}}_{n,k}\hfill \\ \hfill & =\hfill & -{\displaystyle \sum _{j=1}^n}{\eta }_j{Z}_{j,k}^2+\frac{n-1}{4}{\mathrm{\Delta }}_k\hfill \\ \hfill & \hfill & +{\tilde{W}}_{fn,k}^T{\mathrm{\Gamma }}_{\mathit{fn1}}^{-1}\left({\mathrm{\Gamma }}_{\mathit{fn1}}\left(S_{fn}\left({\bar{x}}_{n,k},{\widehat{M}}_{n,k}^T{\mathrm{\Phi }}_n\left(t\right)\right)\right.\right.\hfill \\ \hfill & \hfill & \left.\left.-{\widehat{S}}_{fn,k}^{\prime }{\widehat{M}}_{n,k}^T{\mathrm{\Phi }}_n\left(t\right)\right)Z_{n,k}+{\dot{\widehat{W}}}_{fn,k}\right)\hfill \\ \hfill & \hfill & -{\tilde{W}}_{gn,k}^T{\mathrm{\Gamma }}_{\mathit{gn1}}^{-1}\left({\mathrm{\Gamma }}_{\mathit{gn1}}{S}_{gn}\left({\bar{x}}_{n,k}\right)Z_{n,k}-{\dot{\widehat{W}}}_{gn,k}\right)\hfill \\ \hfill & \hfill & +{\tilde{M}}_{n,k}^T{\mathrm{\Gamma }}_{\mathit{mn1}}^{-1}\left({\mathrm{\Gamma }}_{\mathit{mn1}}{\mathrm{\Phi }}_n\left(t\right){\widehat{W}}_{fn,k}^T{\widehat{S}}_{fn,k}^{\prime }{Z}_{n,k}+{\dot{\widehat{M}}}_{n,k}\right)\hfill \\ \hfill & \hfill & -{\widehat{N}}_{n,k}\frac{1}{{\mathrm{\Delta }}_k}{Z}_{n,k}^2+\frac{1}{{\mathrm{\Delta }}_k}{N}_{n,k}{Z}_{n,k}^2+\frac{1}{4}{\mathrm{\Delta }}_k+{\mathrm{\Gamma }}_{\mathit{Nn1}}^{-1}{\tilde{N}}_{n,k}{\dot{\widehat{N}}}_{n,k}\hfill \\ \hfill & =\hfill & -{\displaystyle \sum _{j=1}^n}{\eta }_j{Z}_{j,k}^2+\frac{n}{4}{\mathrm{\Delta }}_k\hfill \\ \hfill & \hfill & +{\tilde{W}}_{fn,k}^T{\mathrm{\Gamma }}_{\mathit{fn1}}^{-1}\left({\mathrm{\Gamma }}_{\mathit{fn1}}\left(S_{fn}\left({\bar{x}}_{n,k},{\widehat{M}}_{n,k}^T{\mathrm{\Phi }}_n\left(t\right)\right)\right.\right.\hfill \\ \hfill & \hfill & \left.\left.-{\widehat{S}}_{fn,k}^{\prime }{\widehat{M}}_{n,k}^T{\mathrm{\Phi }}_n\left(t\right)\right)Z_{n,k}+{\dot{\widehat{W}}}_{fn,k}\right)\hfill \\ \hfill & \hfill & -{\tilde{W}}_{gn,k}^T{\mathrm{\Gamma }}_{\mathit{gn1}}^{-1}\left({\mathrm{\Gamma }}_{\mathit{gn1}}{S}_{gn}\left({\bar{x}}_{n,k}\right)Z_{n,k}-{\dot{\widehat{W}}}_{gn,k}\right)\hfill \\ \hfill & \hfill & +{\tilde{M}}_{n,k}^T{\mathrm{\Gamma }}_{\mathit{mn1}}^{-1}\left({\mathrm{\Gamma }}_{\mathit{mn1}}{\mathrm{\Phi }}_n\left(t\right){\widehat{W}}_{fn,k}^T{\widehat{S}}_{fn,k}^{\prime }{Z}_{n,k}+{\dot{\widehat{M}}}_{n,k}\right)\hfill \\ \hfill & \hfill & -{\tilde{N}}_{n,k}{\mathrm{\Gamma }}_{\mathit{Nn1}}^{-1}\left({\mathrm{\Gamma }}_{\mathit{Nn1}}\frac{1}{{\mathrm{\Delta }}_k}{Z}_{n,k}^2-{\dot{\widehat{N}}}_{n,k}\right).\hfill \end{array}(70)$

We choose

$\begin{array}{ccc}\hfill {\dot{\widehat{W}}}_{fn,k}& =\hfill & -{\mathrm{\Gamma }}_{\mathit{fn1}}\left(S_{fn}\left({\bar{x}}_{n,k},{\widehat{M}}_{n,k}^T{\mathrm{\Phi }}_n\left(t\right)\right)-{\widehat{S}}_{fn,k}^{\prime }{\widehat{M}}_{n,k}^T{\mathrm{\Phi }}_n\left(t\right)\right)Z_{n,k}\hfill \\ \hfill {\dot{\widehat{W}}}_{gn,k}& =\hfill & {\mathrm{\Gamma }}_{\mathit{gn1}}{S}_{gn}\left({\bar{x}}_{n,k}\right)Z_{n,k}\hfill \\ \hfill {\dot{\widehat{M}}}_{n,k}& =\hfill & -{\mathrm{\Gamma }}_{\mathit{mn1}}{\mathrm{\Phi }}_n\left(t\right){\widehat{W}}_{fn,k}^T{\widehat{S}}_{fn,k}^{\prime }{Z}_{n,k}\hfill \\ \hfill {\dot{\widehat{N}}}_{n,k}& =\hfill & {\mathrm{\Gamma }}_{\mathit{Nn1}}\frac{1}{{\mathrm{\Delta }}_k}{Z}_{n,k}^2.\hfill \end{array}(71)$

Then, Equation 70 can be written as

${\dot{V}}_{n,k}\le -{\displaystyle \sum _{j=1}^n}{\eta }_j{Z}_{j,k}^2+\frac{n}{4}{\mathrm{\Delta }}_k.(72)$

For the initial state, we rely on the following set of assumed conditions:

Assumption 2: When $t=0$, ${\widehat{W}}_{fi,k}(0)={\widehat{W}}_{fi,k-1}(T)$, ${\widehat{W}}_{gi,k}(0)={\widehat{W}}_{gi,k-1}(T)$, ${\widehat{N}}_{i,k}(0)={\widehat{N}}_{i,k-1}(T)$, and ${\widehat{M}}_{i,k}(0)={\widehat{M}}_{i,k-1}(T)(i=1,\dots ,n)$ holds true for all values of $k$.

3.2 Stability and convergence analysis

Theorem 1: For nonlinear system (1) with assumptions 2, 3, and 4, if we design virtual controllers (21), (35), (50), controller (64), and parameter updating laws (28), (42), (57), (71),then all signals in the closed-loop system are bounded within the interval [0, T]. We obtain

$li{m}_{k\to \infty }{Z}_{j,k}\left(t\right)=0,j=\mathrm{1,2},\dots ,n.(73)$

In other words, $li{m}_{k\to \infty }|z_{1\varphi ,k}(t)|=li{m}_{k\to \infty }\Vert {\zeta }_{1,k}(t)\Vert \le \frac{\sqrt{2}{\aleph }_1}{{\eta }_1}(1-e^{-{\eta }_1(t-T)})$, and then $li{m}_{k\to \infty }|z_{1,k}(t)|\le {\varphi }_{1,\infty }(t)+\frac{\sqrt{2}{\aleph }_1}{{\eta }_1}(1-e^{-{\eta }_1(t-T)})$, where ${\aleph }_1$ is the boundary of the difference between ${\beta }_1$ and ${\alpha }_1$. Let ${\eta }_1$ be chosen sufficiently large, ensuring that ${\varphi }_{1,\infty }(t)$ and $\frac{\sqrt{2}{\aleph }_1}{{\eta }_1}(1-e^{-{\eta }_1(t-T)})$ can be minimized as much as possible throughout the entire time interval [0, T].

Proof: In accordance with Assumption 2, we find that $\Vert Z_k(0){\Vert }^2=0\le \Vert Z_k(T){\Vert }^2$. Consider that $V_{n,k}^{\prime }=V_{n,k}(Z_k(0),{\widehat{W}}_{fk}(T),{\widehat{W}}_{gk}(T),{\widehat{N}}_k(T),{\widehat{M}}_k(T))$. Using Equation 69, we obtain $Z_k={[Z_{1,k},Z_{2,k},\dots ,Z_{n,k}]}^T$, ${\widehat{W}}_{fk}={[{\widehat{W}}_{f1,k},{\widehat{W}}_{f2,k},\dots ,{\widehat{W}}_{fn,k}]}^T$,${\widehat{W}}_{gk}={[{\widehat{W}}_{g1,k},{\widehat{W}}_{g2,k},\dots ,{\widehat{W}}_{gn,k}]}^T$, ${\widehat{M}}_k={[{\widehat{M}}_{1,k},{\widehat{M}}_{2,k},\dots ,{\widehat{M}}_{n,k}]}^T$, and${\widehat{N}}_k={[{\widehat{N}}_{1,k},{\widehat{N}}_{2,k},\dots ,{\widehat{N}}_{n,k}]}^T$. Using Equation 72,

$\begin{array}{ccc}\hfill V_{n,k}^{\prime }& \le \hfill & V_{n,k}\left(Z_{,k}\left(0\right),{\widehat{W}}_{fk}\left(0\right),{\widehat{W}}_{gk}\left(0\right),{\widehat{N}}_k\left(0\right),{\widehat{M}}_k\left(0\right)\right)-\hfill \\ \hfill & \hfill & {\mathrm{\Sigma }}_{i=1}^k{\mathrm{\Sigma }}_{j=1}^n{\int }_0^T{\eta }_j{\left(Z_{j,i}\right)}^{2}dt+n\left(\frac{1}{4}\right)T\left({\mathrm{\Sigma }}_{i=1}^k{\mathrm{\Delta }}_i\right).\hfill \end{array}(74)$

Let $V_0(k)=V_{n,1}(Z_1(0),{\widehat{W}}_{f1}(0),{\widehat{W}}_{g1}(0),{\widehat{N}}_1(0),{\widehat{M}}_1(0))+n(\frac{1}{4})T({\mathrm{\Sigma }}_{i=1}^k{\mathrm{\Delta }}_i)$, then Equation 74 can be rewritten as

${\mathrm{\Sigma }}_{i=1}^k{\mathrm{\Sigma }}_{j=1}^n{\int }_0^T{\eta }_j{\left(Z_{j,i}\right)}^{2}dt\le V_0\left(k\right)-V_{n,k}^{\prime }.(75)$

Using Equation 9, we obtain $li{m}_{k\to \infty }{V}_0(k)\le V_{n,1}+2an(\frac{1}{4})T$ and $V_0(k)$ is bounded. $V_{n,k}(Z_k(0),{\widehat{W}}_{fk}(T),{\widehat{W}}_{gk}(T),{\widehat{N}}_k(T),{\widehat{M}}_k(T))\ge 0$, so

$li{m}_{k\to \infty }{\mathrm{\Sigma }}_{j=1}^n{\int }_0^T{\eta }_j{\left(Z_{j,k}\right)}^{2}dt=0.(76)$

Based on Equation 69, for any given value of $k$, $V_{n,k}(t)=V_{n,k}(0)+{\int }_0^t{\dot{V}}_{m,k}(\tau )d\tau$; substituting Equation 72 obtain

$V_{n,k}\left(t\right)\le V_{n,k}\left(0\right)-{\mathrm{\Sigma }}_{j=1}^n{\int }_0^t{\eta }_j{\left(Z_{j,k}\left(\tau \right)\right)}^{2}d\tau +tn\left(\frac{1}{4}\right){\mathrm{\Delta }}_k.(77)$

Based on Equation 76, ${\mathrm{\Sigma }}_{j=1}^n{\int }_0^t{\eta }_j{(Z_{j,k}(\tau ))}^{2}d\tau$ is bounded. According to definition 1, ${\mathrm{\Delta }}_k$ is bounded and $t\in [0,T]$, so $tn(\frac{1}{4}){\mathrm{\Delta }}_k$ is also bounded. In addition, ${\widehat{W}}_{fk}(0)={\widehat{W}}_{f(k-1)}(T)$, ${\widehat{W}}_{gk}(0)={\widehat{W}}_{g(k-1)}(T)$, ${\widehat{M}}_k(0)={\widehat{M}}_{k-1}(T)$, and ${\widehat{N}}_k(0)={\widehat{N}}_{k-1}(T)$; based on Equation 77, for any given value of $k$, $V_{n,k}(Z_k(0),{\widehat{W}}_{fk}(T),{\widehat{W}}_{gk}(T),{\widehat{N}}_k(T),{\widehat{M}}_k(T))$ is bounded. So, $V_{n,k}(0,{\widehat{W}}_{fk}(0),{\widehat{W}}_{gk}(0),{\widehat{N}}_k(0),{\widehat{M}}_k(0))=V_{n,k-1}(0,{\widehat{W}}_{f(k-1)}(T),{\widehat{W}}_{g(k-1)}(T),{\widehat{N}}_{k-1}(T),{\widehat{M}}_{k-1}(T))$ is also bounded; from above all, for any given value of $k$, if $V_{n,k}(t)$ is bounded, then we can deduce that $x_{i,k}$, ${\widehat{W}}_{fk}(t)$, ${\widehat{W}}_{gk}(t)$, ${\widehat{N}}_k(t)$, and ${\widehat{M}}_k(t)$ are bounded. According to Equation 64, $u_k$ is bounded. According to Equation 53, ${\dot{Z}}_{i,k}$ is bounded, so $Z_{i,k}$ is continuous uniformly. Thus, we can deduce Equation 73.

Then, we need to prove that ${\aleph }_1$ will converge to a neighborhood that approaches 0. Initially, let ${\alpha }_{i,k}(t)$ be a signal satisfying $|{\alpha }_{i,k}(t)|<\bar{\alpha }$ and $|{\dot{\alpha }}_{i,k}(t)|<\hslash$ for all $t\ge 0$. The compensation error within the compensation system is defined as

${\varrho }_{i,k}={\beta }_{i,k}-{\alpha }_{i,k}.(78)$

With specified initial conditions, ${\beta }_{i,0}={\alpha }_{i,0}$, i.e., ${\varrho }_{i,0}=0,i=\mathrm{1,2},\dots ,n-1$. From (11), we obtain

$\begin{array}{ccc}\hfill {\dot{\varrho }}_{i,k}& =\hfill & -{\xi }_{i,k}\left({\beta }_{i,k}-{\alpha }_{i,k}\right)-{\alpha }_{i,k}\hfill \\ \hfill & =\hfill & -{\xi }_{i,k}{\varrho }_{i,k}-{\dot{\alpha }}_{i,k}\hfill \\ \hfill {\varrho }_{i,k}\left(t\right)& =\hfill & -{\int }_0^t{\dot{\alpha }}_{i,k}{e}^{-{\xi }_{i,k}\left(t-\tau \right)}d\tau \hfill \\ \hfill |{\varrho }_{i,k}\left(t\right)|& =\hfill & |-{\int }_0^t{\dot{\alpha }}_{i,k}\left(\tau \right)e^{-{\xi }_{i,k}\left(t-\tau \right)}d\tau |\hfill \\ \hfill & =\hfill & |{\dot{\alpha }}_{i,k}\left(\tau \right)|{\int }_0^t{e}^{-{\xi }_{i,k}\left(t-\tau \right)}d\tau |\hfill \\ \hfill & \le \hfill & \max |{\dot{\alpha }}_{i,k}\left(\tau \right)|{\int }_0^t{e}^{-{\xi }_{i,k}\left(t-\tau \right)}d\tau |\hfill \\ \hfill & \le \hfill & \frac{\hslash }{{\xi }_{i,k}}\left(1-e^{-{\xi }_{i,k}t}\right)\hfill \\ \hfill & \le \hfill & \frac{\hslash }{{\xi }_{i,k}}={\aleph }_i.\hfill \end{array}(79)$

As shown in Equation 79, choosing an appropriate value for ${\xi }_{i,k}$ confines the error ${\varrho }_{i,k}$ within a narrow range, approximately equating ${\alpha }_{i,k}$ to ${\beta }_{i,k}$. In addition, based on the compensation system, the Lyapunov function is defined on the interval $[0,T]$ as follows:

$V_{\zeta ,k}={\displaystyle \sum _{i=1}^n}\frac{1}{2}{\zeta }_{i,k}^2.(80)$

The derivative of $V_{\zeta ,k}$ along systems (78) with respect to time is expressed as

$\begin{array}{ccc}\hfill {\dot{V}}_{\zeta ,k}& =\hfill & {\displaystyle \sum _{i=1}^n}{\zeta }_{i,k}{\dot{\zeta }}_{i,k}\hfill \\ \hfill & =\hfill & -{\displaystyle \sum _{i=1}^n}{\eta }_i{\zeta }_{i,k}^2+{\displaystyle \sum _{i=1}^{n-1}}{\zeta }_{i,k}\left({\beta }_{i,k}-{\alpha }_{i,k}\right)\hfill \\ \hfill & \le \hfill & -{\displaystyle \sum _{i=1}^n}{\eta }_i{\zeta }_{i,k}^2+{\displaystyle \sum _{i=1}^{n-1}}|{\zeta }_{i,k}\Vert \left({\beta }_{i,k}-{\alpha }_{i,k}\right)|\hfill \\ \hfill & =\hfill & -{\displaystyle \sum _{i=1}^n}{\eta }_i{\zeta }_{i,k}^2+{\displaystyle \sum _{i=1}^{n-1}}|{\zeta }_{i,k}\Vert \left({\beta }_{i,k}-{\alpha }_{i,k}\right)|+0|{\zeta }_{n,k}|\hfill \\ \hfill & \le \hfill & -{\eta }_0{\displaystyle \sum _{i=1}^n}{\zeta }_{i,k}^2+\aleph {\displaystyle \sum _{i=1}^n}|{\zeta }_{i,k}|\hfill \\ \hfill & \le \hfill & -{\eta }_0\Vert {\zeta }_{i,k}{\Vert }^2+\sqrt{2}\aleph \Vert {\zeta }_{i,k}\Vert ,\hfill \end{array}(81)$

where$\aleph =\max {\aleph }_i,{\eta }_0=\min {\eta }_i$. To ensure the stability of the compensation system, it is sufficient to satisfy

$\Vert {\zeta }_{i,k}\Vert \le \frac{\sqrt{2}\aleph }{{\eta }_0}\left(1-e^{-{\eta }_0\left(t-T\right)}\right).(82)$

Equation 82 leads to the conclusion that $\Vert {\zeta }_{i,k}\Vert$ is bounded. Hence, ${\zeta }_{i,k}$ is also bounded. Moreover, we can choose a parameter ${\xi }_{i,k}>0$ to arbitrarily reduce ${\aleph }_i$, thereby causing the compensation ${\zeta }_{i,k}$ of the system to approach 0. In this way, by ensuring that the error $Z_k$ approaches 0, $z_{\varphi ,k}$ will converge to the neighborhood approaching 0. Thus, we conclude Theorem 1.

4 Illustrative examples

4.1 Number simulation

This section includes an example illustrating the effectiveness of the proposed adaptive iterative learning controller.

The second-order pure-feedback nonlinear system described is considered as follows:

$\begin{array}{ccc}\hfill {\dot{x}}_{1,k}& =\hfill & x_{2,k}+\frac{r_1{x}_{1,k}+r_1^2{x}_{1,k}^2}{1+r_1^2{x}_{1,k}^2}\hfill \\ \hfill {\dot{x}}_{2,k}& =\hfill & u_k+sin\left(r_2{x}_{1,k}{x}_{2,k}\right)e^{-r_2^2{x}_{1,k}^2{x}_{2,k}^2}\hfill \\ \hfill y_k& =\hfill & x_{1,k},\hfill \end{array}(83)$

where $t\in [\mathrm{0,5}]$, $x_{1,k}$, and $x_{2,k}$ are state variables and $u_k$ is the input variable. Utilizing the widely recognized van der Pol oscillator as the reference model, we obtain

$\begin{array}{ccc}\hfill {\dot{x}}_{d1}& =\hfill & x_{d2}\hfill \\ \hfill {\dot{x}}_{d2}& =\hfill & -9x_{d1}-6x_{d2}+2\hfill \\ \hfill y_{d1}& =\hfill & x_{d1},\hfill \end{array}(84)$

where $x_{d1}$ and $x_{d2}$ are state variables. The primary control objective is to synchronize the output of systems (82) with the reference trajectory $y_{d1}$ generated by system (84) over the interval [0,5] under the condition $k\to \infty$.

In accordance with Theorem 1, the adaptive iterative learning controller is chosen as

$\begin{array}{ccc}\hfill {\alpha }_{1,k}& =\hfill & -{\widehat{W}}_{1,k}^T{S}_1\left({\bar{x}}_{1,k},{\widehat{M}}_{1,k}^T{\mathrm{\Phi }}_1\left(t\right)\right)-{\widehat{N}}_{1,k}\frac{1}{{\mathrm{\Delta }}_k}{z}_{1\varphi ,k}+{\dot{y}}_r-{\eta }_1{z}_{1,k}\hfill \\ \hfill u_k& =\hfill & -{\widehat{W}}_{f2,k}^T{S}_{f2}\left({\bar{x}}_{2,k},{\widehat{M}}_{2,k}^T{\mathrm{\Phi }}_2\left(t\right)\right)-{\widehat{N}}_{2,k}\frac{1}{{\mathrm{\Delta }}_k}{Z}_{2,k}\hfill \\ \hfill & \hfill & +{\dot{\beta }}_{1,k}-{\eta }_n{z}_{2,k}-z_{1\varphi ,k}.\hfill \end{array}(85)$

The error compensation mechanism is

$\begin{array}{ccc}\hfill {\dot{\zeta }}_{1,k}& =\hfill & {\beta }_{1,k}+{\zeta }_{2,k}-{\eta }_1{\zeta }_{1,k}-{\alpha }_{1,k}\hfill \\ \hfill {\dot{\zeta }}_{2,k}& =\hfill & -{\eta }_2{\zeta }_{2,k}-{\zeta }_{1,k},\hfill \end{array}(86)$

where ${\dot{\beta }}_{1,k}=-\xi ({\beta }_{1,k}-{\alpha }_{1,k})$.

The parameter adaptive iterative learning laws are provided by (57):

$\begin{array}{ccc}\hfill {\dot{\widehat{W}}}_{fi,k}& =\hfill & -{\mathrm{\Gamma }}_{\mathit{fi1}}\left(S_{fi}\left({\bar{x}}_{i,k},{\widehat{M}}_{i,k}^T{\mathrm{\Phi }}_i\left(t\right)\right)-{\widehat{S}}_{fi,k}^{\prime }{\widehat{M}}_{i,k}^T{\mathrm{\Phi }}_i\left(t\right)\right)Z_{i,k}\hfill \\ \hfill {\dot{\widehat{M}}}_{i,k}& =\hfill & -{\mathrm{\Gamma }}_{\mathit{mi1}}{\mathrm{\Phi }}_i\left(t\right){\widehat{W}}_{fi,k}^T{\widehat{S}}_{fi,k}^{\prime }{Z}_{i,k}\hfill \\ \hfill {\dot{\widehat{N}}}_{i,k}& =\hfill & {\mathrm{\Gamma }}_{\mathit{ni1}}\frac{1}{{\mathrm{\Delta }}_k}{Z}_{i,k}^2,\hfill \end{array}(87)$

where $i=\mathrm{1,2}$, $c_1=5$, $c_2=10,{\mathrm{\Delta }}_k=a/k^2$, $a=50000$, ${\mathrm{\Gamma }}_{11}=diag\{\mathrm{1,1,1,1,1}\}$, ${\mathrm{\Gamma }}_{21}=10$, ${\mathrm{\Gamma }}_{12}=diag\{\mathrm{1,1,1,1,1}\}$, ${\mathrm{\Gamma }}_{22}=1$, and $\xi =1$.

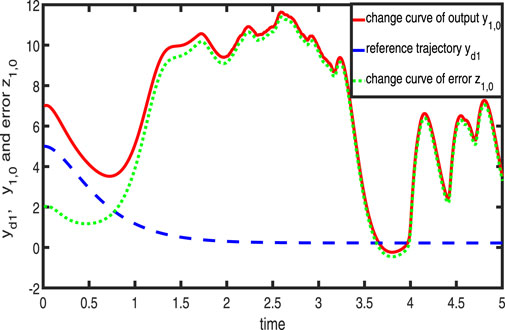
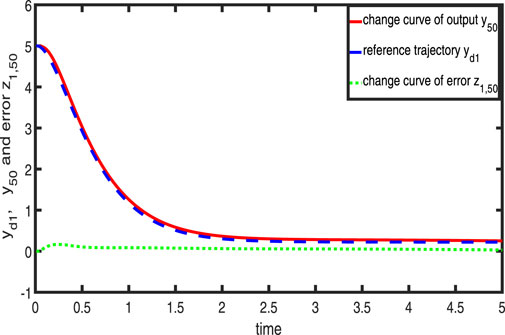
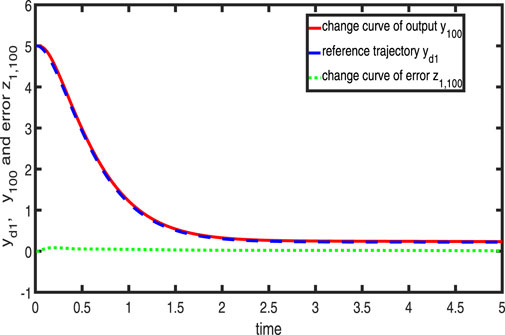
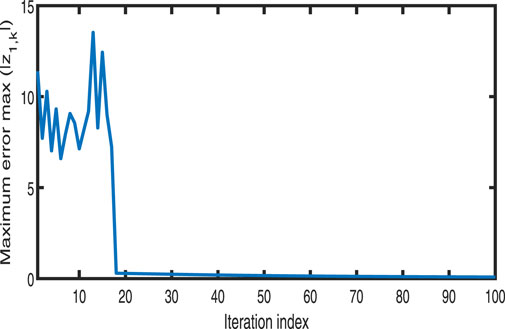
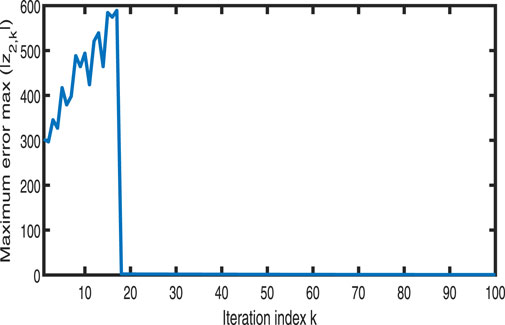
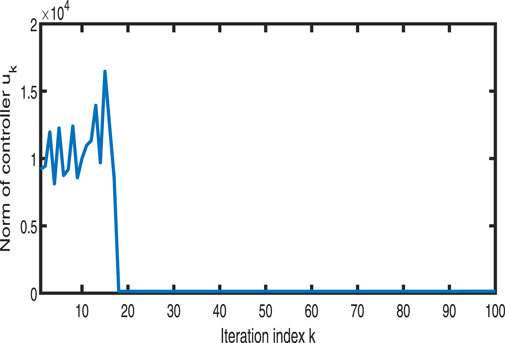
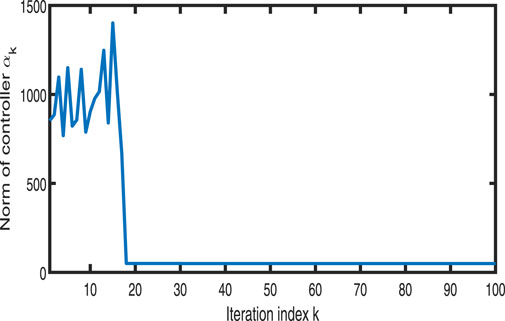
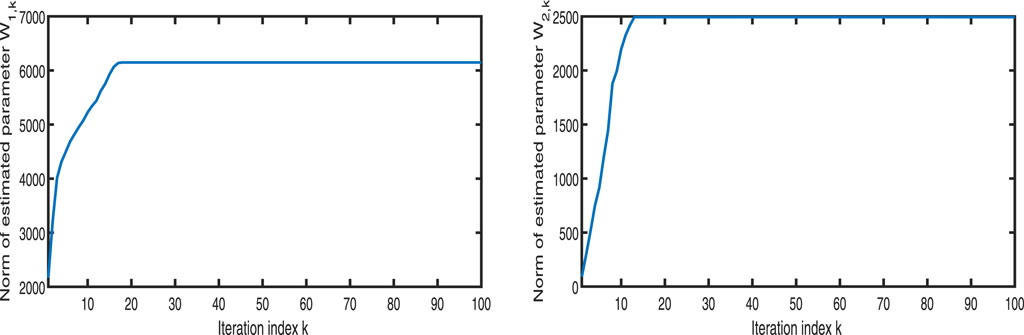
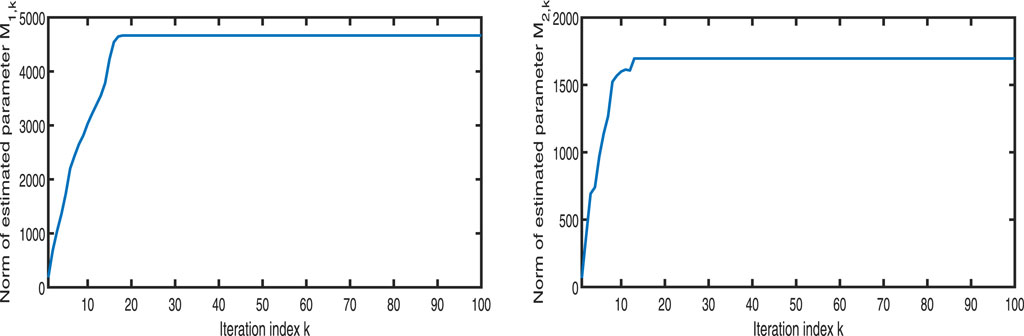
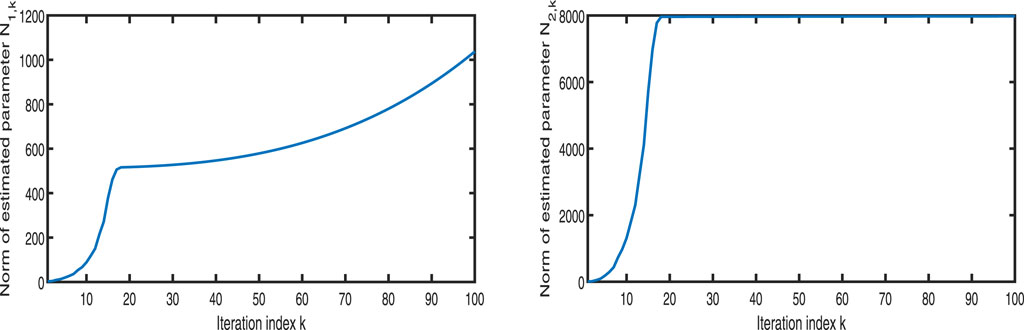
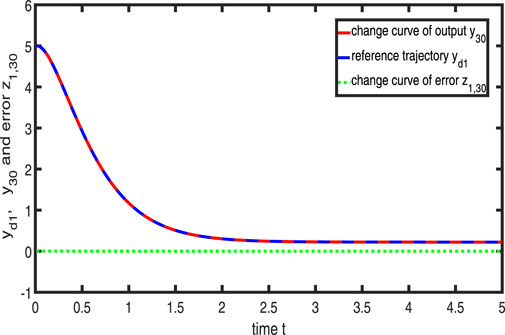
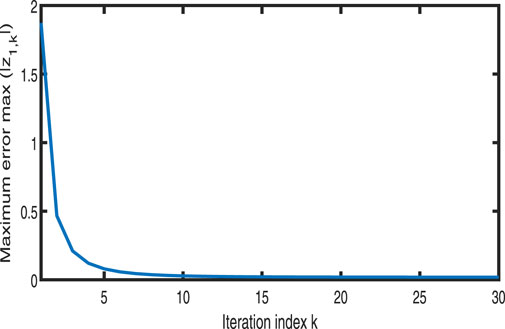
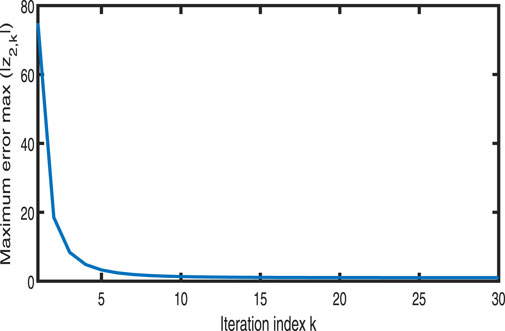
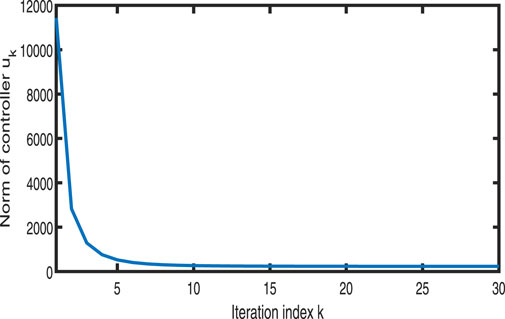
Figures 1–3 show the tracking performance of the system output and expected output without iteration and at 50th and 100th iterations, respectively. Figures 4, 5 show that as the number of iterations increases, the system error may converge to a small region near the zero point. Furthermore, observations shown in Figures 6–10 confirm that both control signals $\Vert u_k\Vert$ and $\Vert {\alpha }_k\Vert$ and estimated parameters, $\Vert {\widehat{W}}_{1,k}\Vert$, $\Vert {\widehat{W}}_{2,k}\Vert$, $\Vert {\widehat{M}}_{1,k}\Vert$, $\Vert {\widehat{M}}_{2,k}\Vert$, $\Vert {\widehat{N}}_{1,k}\Vert$,and $\Vert {\widehat{N}}_{2,k}\Vert$, exhibit bounded behavior within the [0,5] range. The validity of the control strategy presented in this research is reaffirmed by the simulation results shown in Figures 11–20 over the interval $[0,T]$.

Figure 1

Figure 1. Variation in $y_0,y_{d1},z_{\mathrm{1,0}}$ over time without iteration.

Figure 2

Figure 2. Variation in $y_{50},y_{d1},z_{\mathrm{1,50}}$ over time during the 50th iteration.

Figure 3

Figure 3. Variation in $y_{100},y_{d1},z_{\mathrm{1,100}}$ over time during the 100th iteration.

Figure 4

Figure 4. Variation in $max(|z_{1,k}|)$ according to the iteration index.

Figure 5

Figure 5. Variation in $max(|z_{2,k}|)$ according to the iteration index.

Figure 6

Figure 6. Variation in $\Vert u_k\Vert$ according to the iteration index.

Figure 7

Figure 7. Variation in $\Vert {\alpha }_k\Vert$ according to the iteration index.

Figure 8

Figure 8. Variation in $\Vert {\widehat{W}}_{1,k}\Vert$ and $\Vert {\widehat{W}}_{2,k}\Vert$ according to the iteration index.

Figure 9

Figure 9. Variation in $\Vert {\widehat{M}}_{1,k}\Vert$ and $\Vert {\widehat{M}}_{2,k}\Vert$ according to the iteration index.

Figure 10

Figure 10. Variation in $\Vert {\widehat{N}}_{1,k}\Vert$ and $\Vert {\widehat{N}}_{2,k}\Vert$ according to the iteration index.

Figure 11

Figure 11. Variation in $y_0,y_{d1},z_{\mathrm{1,0}}$ over time without iteration.

Figure 12

Figure 12. Variation in $y_{15},y_{d1},z_{\mathrm{1,15}}$ over time during the 15th iteration.

Figure 13

Figure 13. Variation in $y_{30},y_{d1},z_{\mathrm{1,30}}$ over time during the 30th iteration.

Figure 14

Figure 14. Variation in $max(|z_{1,k}|)$ according to the iteration index.

Figure 15

Figure 15. Variation in $max(|z_{2,k}|)$ according to the iteration index.

Figure 16

Figure 16. Variation in $\Vert u_k\Vert$ according to the iteration index.

Figure 17

Figure 17. Variation in $\Vert {\alpha }_k\Vert$ according to the iteration index.

Figure 18

Figure 18. Variation of $\Vert {\widehat{W}}_k\Vert$ according to the iteration index.

Figure 19

Figure 19. Variation in $\Vert {\widehat{M}}_k\Vert$ according to the iteration index.

Figure 20

Figure 20. Variation in $\Vert {\widehat{N}}_{1,k}\Vert$ and $\Vert {\widehat{N}}_{2,k}\Vert$ according to the iteration index.

4.2 Simulation of a single-joint robotic arm

In this section, we conducted simulation verification on a single degree-of-freedom robotic arm system to assess the performance of the proposed control method. The dynamic equation of a single degree-of-freedom robotic arm is

$\frac{{\partial }^2\theta }{\partial t^2}=-10\sin \theta -2\frac{\partial \theta }{\partial t}+u,(88)$

where $\theta$ is the angle between the robotic arm and the reference frame.$u$ is the input of the DC motor.

$\frac{{\partial }^2{y}_{d1}}{\partial t^2}=-9y_{d1}-6\frac{\partial y_{d1}}{\partial t}+2r,(89)$

where $y_{d1}$ is the output of the reference model. $r$ is the reference input signal. According to Equations 88, 89, the state equation of the system is derived as

$\begin{array}{ccc}\hfill {\dot{x}}_{1,k}& =\hfill & x_{2,k}\hfill \\ \hfill {\dot{x}}_{2,k}& =\hfill & -10\sin \left(x_{1,k}\right)-2x\left(2,k\right)+u_k\hfill \\ \hfill y_k& =\hfill & x_{1,k},\hfill \end{array}(90)$

and its reference model is derived as

$\begin{array}{ccc}\hfill {\dot{x}}_{d1}& =\hfill & x_{d2}\hfill \\ \hfill {\dot{x}}_{d2}& =\hfill & -9x_{d1}-6x_{d2}+2r\hfill \\ \hfill y_{d1}& =\hfill & x_{d1},\hfill \end{array}(91)$

where $x_{1,k}$ equals to $\theta$ can be defined as the angle between the robotic arm and the reference frame. $x_{2,k}$ is the time derivative of $\theta$, i.e., $\dot{\theta }$. The primary control objective is to synchronize the output of systems (88) with the reference trajectory $y_{d1}$ generated by system (89) over the interval [0,5] under the condition $k\to \infty$.

In accordance with Theorem 1, the adaptive iterative learning controller is chosen as

$\begin{array}{ccc}\hfill {\alpha }_{1,k}& =\hfill & -{\widehat{N}}_{1,k}\frac{1}{{\mathrm{\Delta }}_k}{z}_{1\varphi ,k}+{\dot{y}}_{d1}-{\eta }_1{z}_{1,k}\hfill \\ \hfill u_k& =\hfill & -z_{1\varphi ,k}-c_2{z}_{2,k}-{\widehat{W}}_{2,k}^T{S}_2\left({\bar{x}}_{2,k},{\widehat{M}}_{2,k}^T{\mathrm{\Phi }}_2\left(t\right)\right)-{\widehat{N}}_{2,k}\frac{1}{{\mathrm{\Delta }}_k}{z}_{2\varphi ,k}\hfill \\ \hfill & \hfill & +{\dot{\beta }}_{1,k}.\hfill \end{array}(92)$

The error compensation mechanism is

$\begin{array}{ccc}\hfill {\dot{\zeta }}_{1,k}& =\hfill & {\beta }_{1,k}+{\zeta }_{2,k}-{\eta }_1{\zeta }_{1,k}-{\alpha }_{1,k}\hfill \\ \hfill {\dot{\zeta }}_{2,k}& =\hfill & -{\eta }_2{\zeta }_{2,k}-{\zeta }_{1,k},\hfill \end{array}(93)$

where ${\beta }_{1,k}=-\xi ({\beta }_{1,k}-{\alpha }_{1,k})$.

The parameter adaptive iterative learning laws are provided by (57).

${\dot{\widehat{W}}}_k={\mathrm{\Gamma }}_f\left(S\left({\bar{x}}_{2,k},{\widehat{M}}_k^T\mathrm{\Phi }\left(t\right)\right)-{\widehat{S}}_k^{\prime }{\widehat{M}}_k^T{\mathrm{\Phi }}_2\left(t\right)\right)z_{2\varphi ,k},(94)$

${\dot{\widehat{N}}}_{i,k}={\mathrm{\Gamma }}_{Ni}\frac{1}{{\mathrm{\Delta }}_k}{z}_{i\varphi ,k}^2,i=\mathrm{1,2},(95)$

${\dot{\widehat{M}}}_k={\mathrm{\Gamma }}_m\mathrm{\Phi }\left(t\right){\widehat{W}}_k^T{\widehat{S}}_k^{\prime }{z}_{2\varphi ,k},(96)$

where $c_1=50$, $c_2=150,{\mathrm{\Delta }}_k=a/k^2$, $a=50000$, ${\mathrm{\Gamma }}_{11}=diag\{\mathrm{1,1,1,1,1}\}$, ${\mathrm{\Gamma }}_{21}=10$, ${\mathrm{\Gamma }}_{12}=diag\{\mathrm{1,1,1,1,1}\}$, ${\mathrm{\Gamma }}_{22}=1,and\xi =10$.

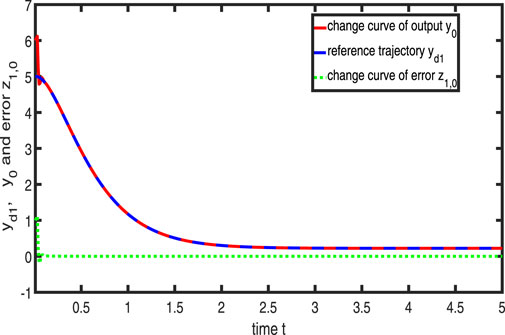
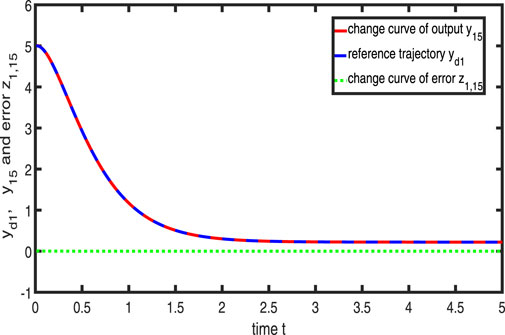
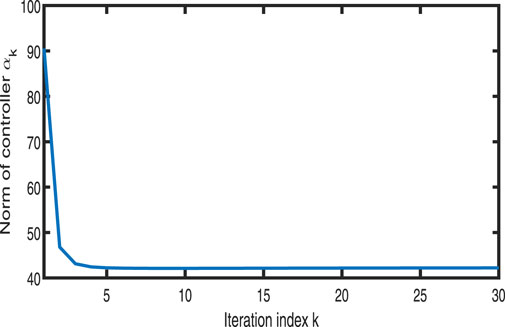
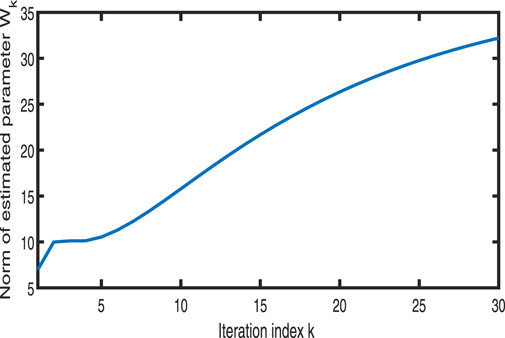
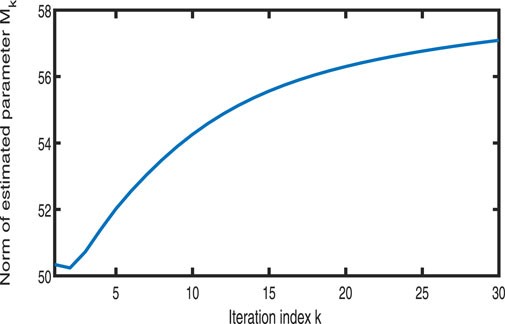
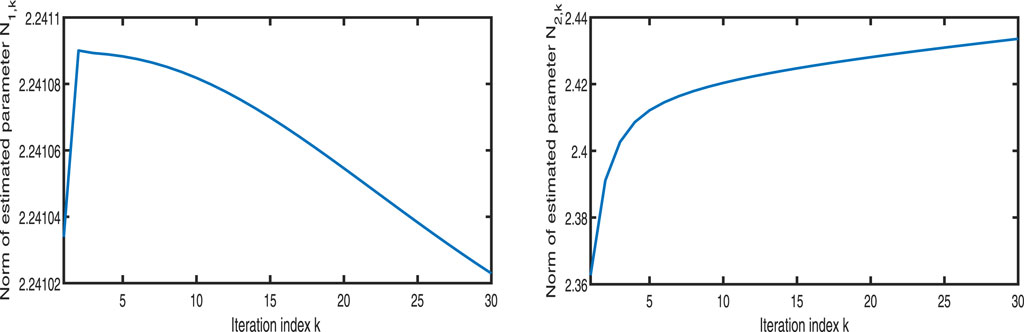
Figures 11–13 show the tracking performance of the system output and expected output without iteration and at 15th and 30th iterations, respectively. Figures 14, 15 show that as the number of iterations increases, the system error may converge to a small region near the zero point. Furthermore, observations from Figures 16–20 confirm that both control signals $\Vert u_k\Vert$ and $\Vert {\alpha }_k\Vert$ and estimated parameters, $\Vert {\widehat{W}}_k\Vert$, $\Vert {\widehat{M}}_k\Vert$, $\Vert {\widehat{N}}_{1,k}\Vert$, and $\Vert {\widehat{N}}_{2,k}\Vert$, exhibit bounded behavior within the [0,5] range. The validity of the control strategy presented in this research is reaffirmed by the simulation results shown in Figures 11–20 over the interval $[0,T]$.

5 Conclusion

This article presents a solution to the complete trajectory, following challenges within a finite time frame for a category of nonlinearly parameterized systems characterized by time-varying disturbed functions and initial state errors. A new FSE neural network is used to learn the time-varying, nonlinearly parameterized term. Based on this and Lyapunov theory, we proposed the new LPF-AILC method. A low-pass filter is used to solve the problem of parameter explosion after obtaining the derivative of the virtual controller. The unmatched uncertainties, nonlinear parameterization, and initial state errors are well considered. Two simulation examples have proven the feasibility of the control approach. This article does not mention time-delay issues, but they often exist in practical systems. Our future work should consider solving the complete tracking problem on a finite time interval for these complex systems with time delays. This is a more interesting issue. In addition, there are two deficiencies in the controller design process: the assumption of time-varying parameters being periodic and the jitter issues caused by the low-pass filter. These challenges will be carefully considered and addressed in our future work.

Data availability statement

The raw data supporting the conclusions of this article will be made available by the authors, without undue reservation.

Author contributions

CZ: conceptualization, funding acquisition, investigation, methodology, and writing–review and editing. LY: formal analysis, software, writing–original draft, and writing–review and editing. YG: investigation, validation, and writing–original draft. JY: funding acquisition, supervision, and writing–review and editing. FQ: funding acquisition, supervision, and writing–review and editing.

Funding

The authors declare that financial support was received for the research, authorship, and/or publication of this article. This work is supported by the National Natural Science Foundation (NNSF) of China (grants 62073259 and 61973094), the Natural Science Basis Research Plan in Shaanxi Province of China (2023-JC-QN-0752), the Science and Technology Plan Project of Xi’an City (No. 23GXFW0062), and the Shaanxi Provincial Key R& D Program General Project (No. 2024GX-YBXM-106).

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors, and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

1. Arimoto S, Kawamura S, Miyazaki F. Bettering operation of robots by learning. J Robot Syst (1984) 1(2):123–40. doi:10.1002/rob.4620010203

CrossRef Full Text | Google Scholar

2. Moore KL. Iterative learning control for Deterministic. London: Springer-Verlag (1993).

Google Scholar

3. Ahn HS, Chen YQ, Moore KL. Iterative learning control: brief survey and categorization. IEEE Trans Syst Man Cybernetics-C, Appl Rev (2007) 37(6):1099–121. doi:10.1109/tsmcc.2007.905759

CrossRef Full Text | Google Scholar

4. Xu J-X, Yan R, Chen Y-Q. “On initial conditions in iterative learning control,” in 2006 American Control Conference, Minneapolis, MN, United States (2006). doi:10.1109/ACC.2006.1655358

CrossRef Full Text | Google Scholar

5. Chen Y, Huang D, Xu C, Dong H. Iterative learning tracking control of high-speed trains with nonlinearly parameterized uncertainties and multiple time-varying delays. IEEE Trans Intell Transportation Syst (2022) 23(11):20476–88. doi:10.1109/tits.2022.3183608

CrossRef Full Text | Google Scholar

6. Zhang C, Yan L, Gao Y, Wang W, Li K, Wang D, et al. A new adaptive iterative learning control of finite-time hybrid function projective synchronization for unknown time-varying chaotic systems. Front Phys (2023) 11:1127884. doi:10.3389/fphy.2023.1127884

CrossRef Full Text | Google Scholar

7. Lu Y. Adaptive-Fuzzy control compensation design for direct adaptive fuzzy control. IEEE Trans Fuzzy Syst (2018) 26(6):3222–31. doi:10.1109/tfuzz.2018.2815552

CrossRef Full Text | Google Scholar

8. Yang Z, Wang S. Adaptive prescribed performance control for nonlinear robotic systems. J Franklin Inst (2023) 360(2):1378–94. doi:10.1016/j.jfranklin.2022.10.044

CrossRef Full Text | Google Scholar

9. Kong X, Yu F, Yao W, Cai S, Zhang J, Lin H. Memristor-induced hyperchaos, multiscroll and extreme multistability in fractional-order HNN: image encryption and FPGA implementation. Neural Networks (2024) 171:85–103. doi:10.1016/j.neunet.2023.12.008

PubMed Abstract | CrossRef Full Text | Google Scholar

10. Yu F, Kong X, Yao W, Zhang J, Cai S, Lin H, et al. Dynamics analysis, synchronization and FPGA implementation of multiscroll Hopfield neural networks with non-polynomial memristor. Chaos, Solitons & Fractals (2024) 179:114440. Article ID 114440. doi:10.1016/j.chaos.2023.114440

CrossRef Full Text | Google Scholar

11. Hu X, Xu B, Hu C. Robust adaptive fuzzy control for HFV with parameter uncertainty and unmodeled dynamics. IEEE Trans Ind Electronics (2018) 65(11):8851–60. doi:10.1109/tie.2018.2815951

CrossRef Full Text | Google Scholar

12. Liu Z, Shi J, Zhao X, Zhao Z, Li H -X. Adaptive fuzzy event-triggered control of aerial refueling hose system with actuator failures. IEEE Trans Fuzzy Syst (2022) 30(8):2981–92. doi:10.1109/tfuzz.2021.3098733

CrossRef Full Text | Google Scholar

13. Hu X, Li Y -X, Tong S, Hou Z. Event-triggered adaptive fuzzy asymptotic tracking control of nonlinear pure-feedback systems with prescribed performance. IEEE Trans Cybernetics (2023) 53(4):2380–90. doi:10.1109/tcyb.2021.3118835

CrossRef Full Text | Google Scholar

14. Zhang C, Tian X, Yan L. Adaptive iterative learning control method for finite-time tracking of an aircraft track angle system based on a neural network. Front Phys (2022) 10:1048942. doi:10.3389/fphy.2022.1048942

CrossRef Full Text | Google Scholar

15. Pang N, Wang X, Wang Z. Event-triggered adaptive control of nonlinear systems with dynamic uncertainties: the switching threshold case. IEEE Trans Circuits Syst Express Briefs (2022) 69(8):3540–4. doi:10.1109/tcsii.2022.3164572

CrossRef Full Text | Google Scholar

16. Liu X, Xu B, Cheng Y, Wang H, Chen W. Adaptive control of uncertain nonlinear systems via event-triggered communication and NN learning. IEEE Trans Cybernetics (2023) 53(4):2391–401. doi:10.1109/tcyb.2021.3119780

CrossRef Full Text | Google Scholar

17. Yang X, Zheng X. Gradient descent algorithm-based adaptive NN control design for an induction motor. IEEE Trans Syst Man, Cybernetics: Syst (2021) 51(2):1027–34. doi:10.1109/tsmc.2019.2894661

CrossRef Full Text | Google Scholar

18. Li K, Li Y. Adaptive neural network finite-time dynamic surface control for nonlinear systems. IEEE Trans Neural Networks Learn Syst (2021) 32(12):5688–97. doi:10.1109/tnnls.2020.3027335

CrossRef Full Text | Google Scholar

19. Lin H, Deng X, Yu F, Sun Y. Grid multi-butterfly memristive neural network with three memristive systems: modeling, dynamic analysis, and application in police IoT. IEEE Internet Things J (2024) 1. doi:10.1109/jiot.2024.3409373

CrossRef Full Text | Google Scholar

20. Li J, Wang C, Deng Q. Symmetric multi-double-scroll attractors in Hopfield neural network under pulse controlled memristor. Nonlinear Dyn (2024) 112:14463–77. doi:10.1007/s11071-024-09791-6

CrossRef Full Text | Google Scholar

21. Chien CJ. A combined adaptive law for fuzzy iterative learning control of nonlinear systems with varying control tasks. IEEE Trans Fuzzy Syst (2008) 16(1):40–51. doi:10.1109/tfuzz.2007.902021

CrossRef Full Text | Google Scholar

22. Xu JX, Yan R. Adaptive learning control for finite interval tracking based on constructive function approximation and wavelet. IEEE Trans Neural Networks (2011) 22(6):893–905. doi:10.1109/tnn.2011.2132143

PubMed Abstract | CrossRef Full Text | Google Scholar

23. Taybi A, Chien CJ. A unified adaptive iterative learning control framework for uncertain nonlinear systems. IEEE Trans Automatic Control (2007) 52(10):1907–13. doi:10.1109/TAC.2007.906215

CrossRef Full Text | Google Scholar

24. Ji H, Hou Z, Zhang R. Adaptive iterative learning control for high-speed trains with unknown speed delays and input saturations. IEEE Trans Automation Sci Eng (2016) 13(1):260–73. doi:10.1109/tase.2014.2371816

CrossRef Full Text | Google Scholar

25. Li JM, Wang YL, Li XM. Adaptive iterative learning control for nonlinear parameterized-systems with unknown time-varying delays. Control Theor Appl (2011) 28(6):861–8. doi:10.7641/j.issn.1000-8152.2011.6.ccta091224

CrossRef Full Text | Google Scholar

26. Zhang C-L, Li J-M. Adaptive iterative learning control for nonlinear time-delay systems with periodic disturbances using FSE-neural network. Int J Automation Comput (2011) 8(4):403–10. doi:10.1007/s11633-011-0597-x

CrossRef Full Text | Google Scholar

27. Park BH, Kuc TY, Lee JS. Adaptive learning of uncertain robotic systems. Int J Control (1996) 65(5):725–744. doi:10.1080/00207179608921719

CrossRef Full Text | Google Scholar

28. Choi JY, Lee JS. Adaptive iterative learning control of uncertain robotic systems. Proc Inst Elect Eng D (2000) 147(2):217–23. doi:10.1049/ip-cta:20000138

CrossRef Full Text | Google Scholar

29. Liu G, Hou Z. Adaptive iterative learning control for subway trains using multiple-point-mass dynamic model under speed constraint. IEEE Trans Intell Transportation Syst (2021) 22(3):1388–400. doi:10.1109/tits.2020.2970000

CrossRef Full Text | Google Scholar

30. Ji H, Hou Z, Zhang R. Adaptive iterative learning control for high-speed trains with unknown speed delays and input saturations. IEEE Trans Automation Sci Eng (2016) 13(1):260–73. doi:10.1109/tase.2014.2371816

CrossRef Full Text | Google Scholar

31. Geng Y, Ruan X, Xu J. Adaptive iterative learning control of switched nonlinear discrete-time systems with unmodeled dynamics. IEEE Access (2019) 7:118370–80. doi:10.1109/access.2019.2936763

CrossRef Full Text | Google Scholar

32. Heinzinger G, Fenwick D, Paden B, Miyazaki F. Stability of learning control with disturbances and uncertain initial conditions. IEEE Trans Automat Contr (1992) 37:110–4. doi:10.1109/9.109644

CrossRef Full Text | Google Scholar

33. Chien CJ, Liu JS. AP-type iterative learning controller for robust output tracking of nonlinear time-varying systems. Int J Control (1996) 64(2):319–34. doi:10.1080/00207179608921630

CrossRef Full Text | Google Scholar

34. Park KH, Bien Z, Hwang DH. A study on the robustness of a PID-type iterative learning controller against initial state error. Int J Syst Sci (1999) 30(1):49–59. doi:10.1080/002077299292669

CrossRef Full Text | Google Scholar

35. Sun M, Wang D. Iterative learning control with initial rectifying action. Automatica (2002) 38:1177–82. doi:10.1016/s0005-1098(02)00003-1

CrossRef Full Text | Google Scholar

36. Chien CJ, Hsu CT, Yao CY. Fuzzy system based adaptive iterative learning control for nonlinear plants with initial state errors. IEEE Trans Fuzzy Syst (2004) 12(5):724–32. doi:10.1109/tfuzz.2004.834806

CrossRef Full Text | Google Scholar

37. Wu XJ, Wu XL, Ran Zhen XY, Luo XJ, Zhu QM. Adaptive control for time-delay non-linear systems with non-symmetric input non-linearity. Int J Model Identification Control (2011) 13(3):152–60. doi:10.1504/ijmic.2011.041302

CrossRef Full Text | Google Scholar

38. Luo XY, Wu XJ, Guan XP. Adaptive backstepping fault-tolerant controlfor unmatched non-linear systems against actuator dead-zone. IET Control Theor Appl. (2010) 4(5):879–88. doi:10.1049/iet-cta.2009.0086

CrossRef Full Text | Google Scholar

39. Wu X, Wu X, Luo X, Zhu Q, Guan X. Neural network-based adaptive tracking control for nonlinearly parameterized systems with unknown input nonlinearities. Neurocomputing (2012) 82:127–42. doi:10.1016/j.neucom.2011.10.019

CrossRef Full Text | Google Scholar

40. Chen WS. Adaptive backstepping dynamic surface control for systems with periodic disturbances using neural networks. IET Control Theor Appl (2009) 3(10):1383–94. doi:10.1049/iet-cta.2008.0322

CrossRef Full Text | Google Scholar

41. Zhu S, Ming-Xuan SUN, Xiong-Xiong HE. Iterative learning control of strict-feedback nonlinear time-varying systems. ACTA AUTOMATICA SINICA (2010) 36(3):454–8. doi:10.3724/SP.J.1004.2010.00454

CrossRef Full Text | Google Scholar

42. Yu H, Li Y. Adaptive obstacle avoidance control based on first-order low-pass filter for cleaning robots. Marseille, France: OCEANS 2019 - Marseille (2019). p. 1–6.

Google Scholar

43. Zhang C, Tian X, Gao Y, Qian F. Command filter AILC for finite time accurate tracking of aircraft track angle system based on fuzzy logic. Adv Math Phys (2023) 2023:11. Article ID 4744873. doi:10.1155/2023/4744873

CrossRef Full Text | Google Scholar

44. Huang J -T, Pham T -P. Differentiation-free multiswitching neuroadaptive control of strict-feedback systems. IEEE Trans Neural Networks Learn Syst (2017) 29(4):1095–107. doi:10.1109/tnnls.2017.2651903

CrossRef Full Text | Google Scholar