Periodic motion of macro- and/or micro-scale cantilevered fluid-conveying pipes with O(2) symmetry: a finite dimensional analysis

Introduction: In this study, the spatial bending vibration of macro- and/or micro-scale cantilevered fluid-conveying pipes is investigated through finite dimensional analysis.

Methods: Firstly, the Galerkin method is employed to discretize the partial differential equations of motion of the system into a system of ordinary differential equations. Then, the projection method based on center manifold-normal form theory is adopted to derive the coefficient formula that determines the pipe’s nonlinear dynamic behaviors, i.e., the change rate of the real part of the critical eigenvalue with respect to the flow velocity and the nonlinear resonance term, thereby obtaining reduced-order equations. Compared to previous studies that relied on the numerical solution of ordinary differential equations to determine the existence and stability of periodic motion, this paper concludes the existence and stability of periodic motion by utilizing the coefficients of the Galerkin discretized equations and the reduced-order equations, significantly saving time in determining the dynamic properties of pipes.

Results and discussion: Subsequently, by investigating the reduced-order equations under specific parameters, the existence and stability of the two types of periodic motion of the pipe are studied. For macro pipes, the truncated mode numbers are set incrementally to calculate the coefficients of the reduced-order equations, investigate the distribution of the stability of the two types of periodic motions with the mass ratio, and carry out a longitudinal comparison (i.e., the comparison between the results obtained under different truncated mode numbers) as well as a horizontal comparison (i.e., the comparison of results between the finite dimensional analysis and the infinite dimensional analysis). It is found that the reasonable truncated mode number required to study this type of system is 15. Previous studies primarily focused on the convergence of frequency and amplitude when determining the truncated mode numbers. On this basis, our study further examines the convergence of motion forms with respect to the truncated mode numbers. Finally, based on the Galerkin discretization equations of 15 modes, the distribution of the stability of two types of the periodic motion of micro pipes with the mass ratio is analyzed. For macro- and micro-scale pipes, when the truncated mode number is 15, the error between the finite dimensional analysis results and the infinite dimensional analysis results is calculated to be about 7%. The above results are verified by obtaining the numerical solution to Galerkin discretization equations.

1 Introduction

Fluid-conveying pipe is an important engineering structure, and its dynamic behaviors have been extensively and deeply studied. Early studies mainly focused on the establishment of motion equations and the linear vibration of pipelines [1–5]. Holmes was the first to investigate the nonlinear vibration of fluid-conveying pipes [6, 7]; in this literature, the processing method based on Galerkin discretization was called “finite dimensional analysis” [6], and the processing method based on function space projection was called “infinite dimensional analysis” [8]. The terms “finite dimensional analysis” and “infinite dimensional analysis” used in our study are derived from the definition given by Holmes. Rousselet and Herrmann [9] used the Krylov-Bogoliubov method to investigate the coupled nonlinear vibration of the cantilevered fluid-conveying pipe and the fluid in the pipes and analyze the variation law of the periodic motion amplitude of the pipe with the mass ratio. Based on the n-mode (n = 1, 2, or 3) discrete system of the motion equation of fluid-conveying pipes, Namchchivaya and Tien [10], Jayaraman and Narayaman [11], and Namchchivaya [12] studied the nonlinear parametric vibration of simply supported pipes at both ends; Chang and Chen [13], Li and Paidoussis [14] investigated the nonlinear parametric vibration of cantilevered pipes. Paidoussis et al. [15] considered the cantilevered fluid-conveying pipe subject to motion constraints; these motion constraints were simplified to a cubic nonlinear spring, which is the source of the nonlinear term of the system. In their study, the chaotic motion of the pipe was studied by the 2-mode Galerkin discretization of the original motion equation. Based on [15], Paidoussis and Semler [16] added the geometric nonlinearity caused by a large amplitude and used 2, 3, and 4 modes to discretize the original vibration equation; it was found that 2-mode Galerkin discretization equations can produce qualitatively accurate results, and 4-mode Galerkin discretization equations can produce quantitatively accurate results. Based on [15], Jin [17] added linear spring constraints and analyzed the influence of linear spring stiffness on the chaotic motion of the system by using 2-mode Galerkin discretization equations. Paidoussis and Semler [18] considered the nonlinear vibration of a cantilevered fluid-conveying pipe with an intermediate support spring, where the “nonlinear term” originating from the geometric nonlinearity was due to a large amplitude motion. In their study, based on 2-mode Galerkin discretization equations, various bifurcation phenomena of the system were investigated with the center manifold-normal form theory. Paidoussis and Semler [19] presented a general process of using the center manifold-normal form method to study the dynamic behavior of cantilevered fluid-conveying pipes, and numerical calculations were conducted by using Galerkin discretization equations of 2, 3, and 4 modes respectively. Subsequently, Paidoussis and Semler [19] found that the impact of truncation mode numbers on the calculation results was not obvious, and it was considered the essential dynamic characteristics of the system can be only extracted with low-order discretization equations. Until 2006, in the literature using the Galerkin method to investigate fluid-conveying pipes, the number of truncation modes generally did not exceed 4 [20–23]. It worths mentioning that the above-mentioned references are all studies on two-dimensional (2D) motions of fluid-conveying pipes.

Since the study by Wadham-Gagnon et al. [24], great attention was paid to the dynamics of three-dimensional (3D) vibrations of cantilevered fluid-conveying pipes. Following the modified Hamilton principle [1], Wadham-Gagnon et al. [24] derived a new 3D version of nonlinear governing equations for cantilevered fluid-conveying pipes by incorporating an additional mass at the free end of the pipe and springs support. Note that this equation is consistent with the equation derived by Lundgren et al. [25] using the force balance method when factors such as terminal mass and intermediate spring support are not considered. Based on this new 3D model, Modarres-Sadeghi et al. [26] investigated the motion switches of cantilevered fluid-conveying pipes between 2D and 3D with increasing flow velocity, where 8-mode Galerkin discretization equations were used at most. Additionally, the 3D motion of cantilevered fluid-conveying pipes with additional intermediate springs support [27], with an end mass [28], or with both an end mass and springs support [29] was been studied. In Ref. [27], using 4-mode Galerkin discretization equations, Païdoussis et al. conducted a theoretical and experimental study of 3D nonlinear dynamics of cantilevered pipes with external springs, involving five different cases in terms of attachment, spring configurations, and stiffnesses. Results indicated that the system may lose stability either via flutter or divergence, depending on the specific case of spring support. Compared to Ref. [27], a more complete (chaotic motion and far more extensive experimental investigation), accurate (a larger number of Galerkin’s truncation modes, where 8-mode Galerkin discretization equations were used at most), and interesting (richer dynamical behaviors) work was completed by Ghayesh and Païdoussis [30]. In Refs. [28, 29], to achieve the convergence of calculation, up to 10-mode Galerkin discretization equations were used. For pipes with a large end-mass, the resulting dynamics becomes much richer than that of pipes without any external attachments. Furthermore, it was found that for a very large end-mass, many Galerkin’s truncation modes (where 12-mode Galerkin discretization equations were used at most) are required to obtain convergent results [31]. By introducing a lateral base excitation, Chang and Modarres-Sadeghi [32] extended the equations proposed by Wadham-Gagnon et al. [24] and applied them to investigate the possibility of controlling the pipe’s 3D motion and/or limiting it to a 2D motion in a pre-defined direction by changing the base excitation frequency and amplitude, where 8-mode Galerkin discretization equations were used at most.

Due to the recent technological development in engineering practice, the characteristic size of structures become smaller and smaller [33–36], including the micro beam [37–39] with Winkler elastic foundation [40], micro torus plate [41], micro cylindrical shell [42, 43], micro-structure on elastic foundation [44], and fluid-conveying micro pipe [45]. The study of micro-scale pipes is an important research direction of the dynamics of fluid-conveying pipes. Yang et al. [46] discussed the geometric nonlinearity caused by axial stretching and investigated the free vibration of micropipes based on the modified couple stress theory (MCST), where the number of truncation modes was 1. Dai et al. [47] studied the buckling and post-buckling vibrations of carbon nanotubes (CNTs), calculated the buckling configuration of the tube when the fluid velocity in the pipe exceeded a critical value using a theoretical method, and derived a differential equation for the vibration of the pipe under this configuration. The post-buckling vibration of the pipe was studied by using the Galerkin method, and the number of truncation modes was 2. Bahaadini and Hosseini [48] examined the fluid-conveying CNTs in a magnetic field and investigated the buckling and vibration of the tube under different boundary conditions, where the number of truncation modes was 8. Bahaadini and Hosseini [49] studied the effect of dissipation on the stability of viscoelastic CNTs and comprehensively determined the viscosity coefficient and microscale effect on the system frequency and critical flow velocity, where the number of truncation modes was 8. Hu et al. [50] considered micro-scale cantilevered fluid-conveying pipes subject to motion constraints that were simplified into a smoothed-trilinear cubic model, where based on 4-mode Galerkin discretization equations, the impact of micro-scale effects and motion constraints on the dynamic behavior of the pipe was studied. It was found that the micro-scale parameters can make the pipe more stable, and the motion constraints make the system exhibit richer dynamic phenomena. Dai et al. [51] established a completely nonlinear vibration equation of cantilever fluid-conveying pipes under the action of electrostatic force, in which the nonlinear term was included by a nonlinear electrostatic force and geometric nonlinearity caused by a large amplitude. Based on Galerkin discretization equations of 4 modes, the impact of voltage on the stability boundary of the pipe was investigated. Ghayesh et al. [52] investigated the parametric vibration of CNTs fixed at both ends. By analyzing Galerkin discretization equations of 8 modes, it was found that the average flow velocity and amplitude of the fluid in the pipe significantly affect the path of the pipe to chaotic vibration. Zhu et al. [53] investigated the impact of viscoelastic foundation and partially distributed tangential force on the dynamics of cantilever CNTs, where the number of truncation modes was 8. In the comprehensive study by Sarparast et al. [54], the effects of various parameters, including magnetic flow, scale parameters, flow velocity, axial spin speed, Y-shaped downstream elbow angle, concentrated masses, attached springs, surface effects, and complex environments on the vibration characteristics of the cantilevered pipe and pinned-pinned pipe were analyzed, where the number of truncation modes was 7.

For the dynamics of fluid-conveying pipes, some studies do not perform Galerkin discretization on partial differential equations but directly use other methods. By using the perturbation method for analysis, Bajaj et al. investigated the Hopf bifurcation of planar cantilevered fluid-conveying pipes [55] and parametric vibration [56] and studied the type and stability of the periodic motion of symmetrical and asymmetric spatial cantilevered fluid-conveying pipes [57, 58] and spatial parametric vibration [59]. Yamashita et al. considered the interaction between the second-order and third-order modes of a cantilevered fluid-conveying pipe with a concentrated mass [60] and a spring constrained [61] attached to its free end under planar vibration. At this time, the complex frequencies corresponding to the second- and third-order modes had positive real parts, and these two modes were excited to perform interactions. Yamashita et al. [62] considered the spatial vibration of a cantilevered fluid-conveying pipe with a concentrated mass attached to the free end and investigated the “in-plane and out-of-plane” interactions of its second- and third-order modes based on the results reported in Ref. [60]. The methods used in references [60–62] were all projection methods [63], and the coefficients of the reduced-order equations were all determined by numerical calculations. Zhang and Huang [64] adopted a mode analysis method to study the effect of Poisson, junction, and friction couplings on the stability of cantilevered fluid-conveying pipes. Amiri et al. [65] studied the planar linear vibration of a micro-scale cantilevered fluid-conveying pipe in a spring-damper environment and subjected to temperature and magnetic loads. They used the extended Galerkin method (i.e., mode analysis method) to analyze the critical flow velocity and flutter frequency of the pipe by considering the boundary value problem of the differential equation. In references [66, 67] by Jin and Ren, the post-buckling equilibrium configuration was obtained by the two-step perturbation technique, and it was used as the initial configuration to establish a differential equation of perturbation motion for forced vibration analysis and parametric resonance study of FG nanotubes, where the effects of the flow velocity, material gradient, and different scales on the nonlinear dynamic behaviors were discussed. In another paper by Jin et al. [68], the analogous method was applied to obtain the amplitude-frequency response curves for pulsatile fluid-conveying FG nanopipes with movable boundary. The static deformation and flutter for cantilevered fluid-conveying curved pipes were studied experimentally by Chehreghani et al. [69]. Guo et al. applied the center manifold-normal form method to study the symmetric bifurcation [70] and asymmetric bifurcation [71] of the micro-scale cantilevered fluid-conveying pipe. The differential quadrature method was also widely used in the vibration research of fluid-conveying pipes [72, 73]. Incidentally, other methods applied to investigate the dynamics of structures, e.g., the Navier discretization method [74], eigenvalue and eigenvector method [75–77], successive approximation method [78], Fourier series method [79], compact analytical method [80], may also be suitable for the analysis of fluid-conveying pipe’s dynamics.

The literature review above indicates that most studies on the dynamics of fluid-conveying pipes adopt the Galerkin method. However, there is no unified conclusion on how many truncation modes should be taken. Among the majority of literatures, the truncated mode numbers generally do not exceed 8. Although some literature has conducted convergence analysis based on frequency or amplitude, the corresponding motion form of the same frequency or amplitude may also be different, i.e., it may be planar motion or spatial motion. Thus, it is necessary to examine the convergence of motion with respect to the number of truncation modes. Meanwhile, the mass ratio has an important impact on the dynamic characteristics of fluid-conveying pipes. However, most of the existing studies using the Galerkin method investigate the convergence of the calculation results at one or a few specific mass ratios. The number of truncation modes obtained in this way cannot be extended to a wide range of mass ratios. In view of this, in almost the entire mass ratio interval, by investigating the change law of the “distribution of periodic motion stability along the mass ratio” with the number of truncation modes and combined with infinite dimensional analysis results, this study summarizes the reasonable truncation mode numbers required when investigating the dynamics of macro- and/or micro-cantilevered fluid-conveying pipes with the Galerkin method, thus making the truncation modes applicable to a wide range of mass ratios while ensuring the convergence of motion forms.

The rest of this paper is organized as follows. In Section 2, the 3D bending vibration equation of a macro- and/or micro-cantilevered fluid-conveying pipe with O (2) symmetry is given based on previous studies. In Section 3, by using the Galerkin technique, the original vibration equation is discretized into a set of ordinary differential equations. Then, by utilizing the projection method based on the center manifold and normal form theory, the discretized systems are reduced to a two-degree-of-freedom nonlinear ordinary differential equation. It is worth mentioning that previous studies mainly relied on the numerical resolutions of Galerkin discretized equations for pipe. However, when the numbers of mode truncation are considerable, the numerical resolutions of these ordinary differential equations become exceedingly time-consuming. If the periodic motion patterns of the pipe can be determined based on the coefficients of the discretized equations, it would expedite the determination of the dynamic properties of pipes. The reduced-order equations proposed here precisely fulfill this research requirement. In Section 4, the truncation mode numbers are taken incrementally for a macro pipe. The convergence of the linear term coefficients of the reduced-order equations is analyzed, and the stability of the periodic motion determined by the nonlinear term coefficients of the reduced-order equations is investigated. By comparing the results given by different truncation mode numbers and the results of infinite dimensional analysis, the reasonable truncation mode numbers needed to study this type of system are summarized and applied to the study of micro-scale pipes. The reasonable numbers of mode truncation summarized through the aforementioned process ensures the convergence of frequency, amplitude, and motion forms. For macro- and/or micro-cantilevered fluid-conveying pipes, the errors between the finite dimensional analysis results and the infinite dimensional analysis results are calculated. Finally, some conclusions are drawn in Section 5.

2 Mechanics models and differential equations of motion

The motions equations [70] are derived on the basis of the following assumptions [24, 81]:

(1) the fluid is incompressible;

(2) the fluid is plug-flow and the flow velocity is constant;

(3) the pipe is modelled as a nonlinear Euler-Bernoulli beam;

(4) the transverse deflections of the pipe could be large, but the strains in the pipe are small;

(5) rotatory inertia and shear deformation are neglected;

(6) the centroid line of the pipe is inextensible;

(7) for micro-scale pipe, the pipe is made of materials of which size-dependent behaviors can be predicted by the MCST [82].

As shown in Figure 1A, the macro- and micro-scale cantilevered fluid-conveying pipe with a length of $L$ has a cross-sectional area of $A_p$, a bending stiffness of $EI$, and a mass per unit length of $m$. The mass of fluid conveyed per unit length is $M$, and the velocity $V$ is constant relative to the pipe centerline (i.e., axis). The cross-section of the pipe is circular with $\mathrm{O}\left(2\right)$ symmetry (Figure 1D). The general spatial flexural vibration of the pipe is considered in this study (Figure 1B).

Figure 1

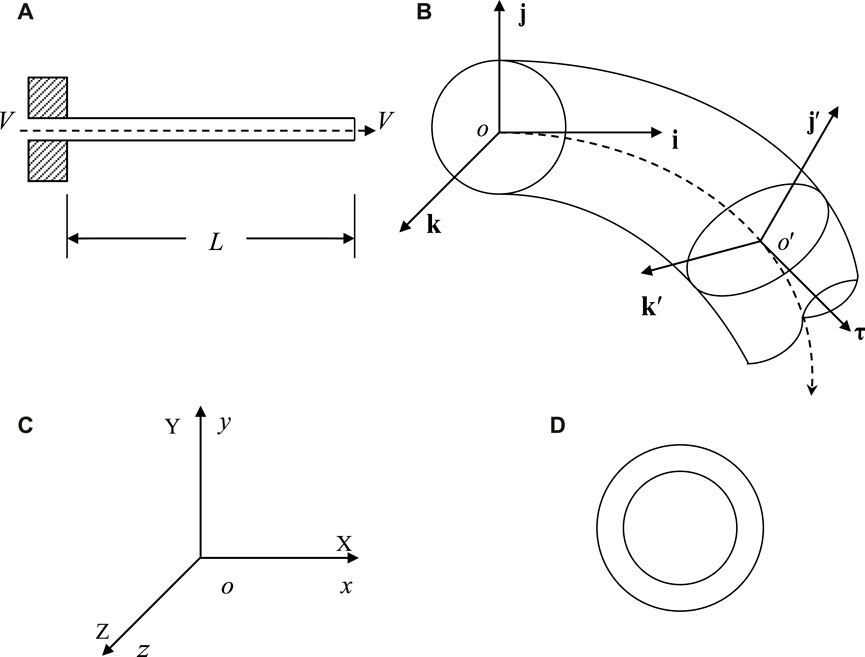
Figure 1. (A) The schematic of the macro- and micro-scale cantilevered fluid-conveying pipe; (B) 3D flexural vibration; (C) Coordinate systems; (D) The circular cross-section of the macro- and micro-scale pipe.

As shown in Figure 1C, when the pipe is not deformed, the straight line where the pipe centerline is located is the $X$ axis; the fluid velocity direction in the pipe is the positive direction of the $X$ axis; the surface of the cantilevered end is the $YZ$ plane; the intersection point of the pipe centerline and the $YZ$ plane is the origin $O$. Based on this, the reference system $O-XYZ$ is established, i.e., the Lagrange coordinate system, which is used to specify the position of the material point on the pipe when it is not deformed. After the pipe is deformed, another coordinate system $o-xyz$ is taken, i.e., the Euler coordinate system, which coincides with $O-XYZ$ and is used to describe the instantaneous position of the material point on the pipe. The displacement of any point on the pipe can be described by the relationship between the coordinates of the same mass point in the undeformed state and the deformed state of the pipe [83]. Before deformation, the initial position of a certain mass point of the pipe is denoted as $\left(X,Y,Z\right)$. After deformation, the position of the same mass point at time $t$ is represented as $\left(x,y,z\right)$. Then, the displacement $u_1\left(X,Y,Z,t\right)$, $u_2\left(X,Y,Z,t\right)$ and $u_3\left(X,Y,Z,t\right)$ of any material point of the pipe at moment t in the x, y and z directions can be described as

$u_1\left(X,Y,Z,t\right)=x-X,u_2\left(X,Y,Z,t\right)=y-Y,u_3\left(X,Y,Z,t\right)=z-Z(1)$

In the following, a curvilinear coordinate $s$ along the length of the pipe centerline is introduced. Generally, the cantilevered fluid-conveying pipes are assumed to be inextensible, $s$ is equal to $X$ [24], as shown in Figure 2 [71].

Figure 2

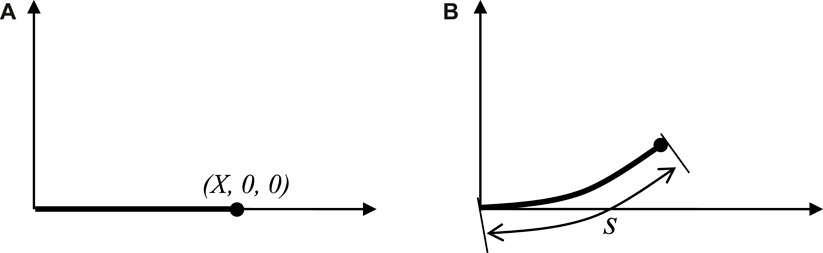
Figure 2. The centroid line of the pipe is not stretchable: (A) before the deformation; (B) after the deformation.

At moment t, it is assumed that the position of one point on the centerline of the pipe $\left(X,0,0\right)$ which can be represented as $\left(s,0,0\right)$ is

$\mathbf{r}=\mathbf{r}\left(s,t\right)=\left(s+u,v,w\right)(2)$

where $u=u_1\left(s,0,0,t\right)$, $v=u_2\left(s,0,0,t\right)$ and $w=u_3\left(s,0,0,t\right)$. The inextensibility condition can be written as follows [24]:

${\left(1+\frac{\partial u}{\partial s}\right)}^2+{\left(\frac{\partial v}{\partial s}\right)}^2+{\left(\frac{\partial w}{\partial s}\right)}^2=1(3)$

For the vibration of a slender pipe, the Euler-Bernoulli beam model can be adopted. The resulting dimensionless form of the motions equations and boundary conditions is shown below [70]:

$\begin{array}{l}\ddot{\eta }+{\nu }^2{\eta }^{″}+2\sqrt{\beta }\nu {\dot{\eta }}^{\prime }+\left(2l_0+1\right){\eta }^{\left(4\right)}+\frac{3}{2}\left[{{\eta }^{″}}^3+{\eta }^{″}{{\zeta }^{″}}^2+2{\eta }^{\prime }{\eta }^{″}{\eta }^{‴}+2{\eta }^{\prime }{\zeta }^{″}{\zeta }^{‴}\right]\\ -{\eta }^{″}{\int }_{\xi }^1{\int }_0^{\xi }\left[{{\dot{\eta }}^{\prime }}^2+2\sqrt{\beta }\nu {\dot{\eta }}^{\prime }{\eta }^{″}+{{\dot{\zeta }}^{\prime }}^2+2\sqrt{\beta }\nu {\dot{\zeta }}^{\prime }{\zeta }^{″}+{\nu }^2\left({{\eta }^{″}}^2+{{\zeta }^{″}}^2\right)+{\eta }^{″}{\eta }^{\left(4\right)}+{\zeta }^{″}{\zeta }^{\left(4\right)}\right]\mathrm{d}\xi \mathrm{d}\xi \\ +{\eta }^{\prime }{\int }_0^{\xi }\left[{{\dot{\eta }}^{\prime }}^2+2\sqrt{\beta }\nu {\dot{\eta }}^{\prime }{\eta }^{″}+{{\dot{\zeta }}^{\prime }}^2+2\sqrt{\beta }\nu {\dot{\zeta }}^{\prime }{\zeta }^{″}+{\nu }^2\left({{\eta }^{″}}^2+{{\zeta }^{″}}^2\right)+{\eta }^{″}{\eta }^{\left(4\right)}+{\zeta }^{″}{\zeta }^{\left(4\right)}\right]\mathrm{d}\xi \\ +l_0[-{{\eta }^{\prime }}^2{\eta }^{\left(4\right)}+2{\eta }^{\prime }{\eta }^{″}{\eta }^{‴}+2{{\eta }^{″}}^3+2{\eta }^{″}{{\zeta }^{″}}^2-{\eta }^{″}{\zeta }^{\prime }{\zeta }^{‴}+3{\eta }^{\prime }{\zeta }^{″}{\zeta }^{‴}-{\eta }^{\prime }{\zeta }^{\prime }{\zeta }^{\left(4\right)}\\ +2{\eta }^{\prime }{\int }_0^{\xi }\left({\eta }^{″}{\eta }^{\left(4\right)}+{\zeta }^{″}{\zeta }^{\left(4\right)}\right)\mathrm{d}\xi -2{\eta }^{″}{\int }_{\xi }^1{\int }_0^{\xi }\left({\eta }^{″}{\eta }^{\left(4\right)}+{\zeta }^{″}{\zeta }^{\left(4\right)}\right)\mathrm{d}\xi \mathrm{d}\xi ]=0\end{array}(\mathrm{4a})$

$\begin{array}{l}\ddot{\zeta }+{\nu }^2{\zeta }^{″}+2\sqrt{\beta }\nu {\dot{\zeta }}^{\prime }+\left(2l_0+1\right){\zeta }^{\left(4\right)}+\frac{3}{2}\left[{{\zeta }^{″}}^3+{{\eta }^{″}}^2{\zeta }^{″}+2{\zeta }^{\prime }{\zeta }^{″}{\zeta }^{‴}+2{\zeta }^{\prime }{\eta }^{″}{\eta }^{‴}\right]\\ -{\zeta }^{″}{\int }_{\xi }^1{\int }_0^{\xi }\left[{{\dot{\zeta }}^{\prime }}^2+2\sqrt{\beta }\nu {\dot{\zeta }}^{\prime }{\zeta }^{″}+{{\dot{\eta }}^{\prime }}^2+2\sqrt{\beta }\nu {\dot{\eta }}^{\prime }{\eta }^{″}+{\nu }^2\left({{\eta }^{″}}^2+{{\zeta }^{″}}^2\right)+{\eta }^{″}{\eta }^{\left(4\right)}+{\zeta }^{″}{\zeta }^{\left(4\right)}\right]\mathrm{d}\xi \mathrm{d}\xi \\ +{\zeta }^{\prime }{\int }_0^{\xi }\left[{{\dot{\zeta }}^{\prime }}^2+2\sqrt{\beta }\nu {\dot{\zeta }}^{\prime }{\zeta }^{″}+{{\dot{\eta }}^{\prime }}^2+2\sqrt{\beta }\nu {\dot{\eta }}^{\prime }{\eta }^{″}+{\nu }^2\left({{\eta }^{″}}^2+{{\zeta }^{″}}^2\right)+{\eta }^{″}{\eta }^{\left(4\right)}+{\zeta }^{″}{\zeta }^{\left(4\right)}\right]\mathrm{d}\xi \\ +l_0[-{{\zeta }^{\prime }}^2{\zeta }^{\left(4\right)}+2{\zeta }^{\prime }{\zeta }^{″}{\zeta }^{‴}+2{{\zeta }^{″}}^3+2{\zeta }^{″}{{\eta }^{″}}^2-{\zeta }^{″}{\eta }^{\prime }{\eta }^{‴}+3{\zeta }^{\prime }{\eta }^{″}{\eta }^{‴}-{\zeta }^{\prime }{\eta }^{\prime }{\eta }^{\left(4\right)}\\ +2{\zeta }^{\prime }{\int }_0^{\xi }\left({\eta }^{″}{\eta }^{\left(4\right)}+{\zeta }^{″}{\zeta }^{\left(4\right)}\right)\mathrm{d}\xi -2{\zeta }^{″}{\int }_{\xi }^1{\int }_0^{\xi }\left({\eta }^{″}{\eta }^{\left(4\right)}+{\zeta }^{″}{\zeta }^{\left(4\right)}\right)\mathrm{d}\xi \mathrm{d}\xi ]=0\end{array}(\mathrm{4b})$

$\eta \left(0,\tau \right)={\eta }^{\prime }\left(0,\tau \right)={\eta }^{″}\left(1,\tau \right)={\eta }^{‴}\left(1,\tau \right)=0(\mathrm{5a})$

$\zeta \left(0,\tau \right)={\zeta }^{\prime }\left(0,\tau \right)={\zeta }^{″}\left(1,\tau \right)={\zeta }^{‴}\left(1,\tau \right)=0(\mathrm{5b})$

where

$\xi =\frac{s}{L},\eta =\frac{w}{L},\zeta =\frac{v}{L},\tau ={\left(\frac{EI}{m+M}\right)}^{\frac{1}{2}}\frac{t}{L^2},\nu ={\left(\frac{M}{EI}\right)}^{\frac{1}{2}}VL,\beta =\frac{M}{m+M},l_0=\frac{A_p{l}^{2}G}{2EI}(6)$

are all dimensionless quantities. In Eq. 6, G is the Lamé’s constant and l is a material length scale parameter date from MCST [82], which has been used to analyze various micro-structures [84–86]. The dimensionless parameter $l_0=\frac{A_p{l}^{2}G}{2EI}$ represents the size effect on the equations of motions of the system, and its impact on the pipe’s responses will be given later. For macro-pipes, it is obvious that $l=0$ or $l_0=0$. l₀ may have different dimensionless form for different structures [85, 86]. Incidentally, there exists other nonlocal elasticity theory which can capture the small size effects of microstructures and has been used to study the vibration characteristics of nanorod [87, 88] and nanotube [89].

3 Galerkin discretization and reduced-order equations

3.1 Galerkin discreted equations

Given that the mode functions of the cantilever beam satisfy boundary condition (5), they can be selected as basis functions [2, 16, 17, 90]. According Galerkin method, let the solutions to Eqs. 4a and 4b be

$\eta \left(\xi ,\tau \right)={\displaystyle \sum _{i=1}^n}{\varphi }_i\left(\xi \right)q_i\left(\tau \right)(\mathrm{7a})$

$\zeta \left(\xi ,\tau \right)={\displaystyle \sum _{i=1}^n}{\psi }_i\left(\xi \right)p_i\left(\tau \right)(\mathrm{7b})$

where

$\left\{\begin{array}{l}{\varphi }_i\left(\xi \right)={\psi }_i\left(\xi \right)=\cosh {\lambda }_i\xi -\cos {\lambda }_i\xi -{\sigma }_i\left(\sinh {\lambda }_i\xi -\sin {\lambda }_i\xi \right),\\ {\sigma }_i=\left(\sinh {\lambda }_i-\sin {\lambda }_i\right)/\left(\cosh {\lambda }_i+\cos {\lambda }_i\right),\left(i=1,2,...,n\right)\end{array}\right.(8)$

$q_i\left(\tau \right)$ and $p_i\left(\tau \right)$ are the generalized coordinates corresponding to the vibration of the pipe in two transverse directions; ${\varphi }_i\left(\xi \right)$ and ${\psi }_i\left(\xi \right)$ are the i-th order eigenfunctions of the cantilever beam; n is the number of truncation modes; ${\lambda }_i$ is the i-th order eigenvalue of the cantilever beam. According to the Galerkin method, Eq. 7 is substituted into Eq. 4 and multiplied by ${\phi }_i\left(\xi \right)$ or ${\psi }_i\left(\xi \right)$ at both sides. Then, by conducting integration from 0 to 1, a system of second-order ordinary differential equations about $q_i,p_i$ can be obtained.

$\{\begin{array}{l}{\ddot{q}}_i+c_{ij}{\dot{q}}_j+k_{ij}{q}_j+A_{ijkl}{q}_j{q}_k{q}_l+B_{ijkl}{q}_j{q}_k{\dot{q}}_l+C_{ijkl}{q}_j{\dot{q}}_k{\dot{q}}_l\\ +L_{ijkl}{q}_j{p}_k{p}_l+M_{ijkl}{q}_j{p}_k{\dot{p}}_l+N_{ijkl}{q}_j{\dot{p}}_k{\dot{p}}_l=0\\ {\ddot{p}}_i+c_{ij}{\dot{p}}_j+k_{ij}{p}_j+A_{ijkl}{p}_j{p}_k{p}_l+B_{ijkl}{p}_j{p}_k{\dot{p}}_l+C_{ijkl}{p}_j{\dot{p}}_k{\dot{p}}_l\\ +L_{ijkl}{p}_j{q}_k{q}_l+M_{ijkl}{p}_j{q}_k{\dot{q}}_l+N_{ijkl}{p}_j{\dot{q}}_k{\dot{q}}_l=0\end{array}(9)$

where

$\left\{\begin{array}{l}{c}_{ij}=2\nu \sqrt{\beta }{\int }_0^1{\varphi }_i{\varphi }_j^{\prime }\mathrm{d}\xi ,k_{ij}=\left(1+2l_0\right){\int }_0^1{\varphi }_i^{\left(4\right)}{\varphi }_j\mathrm{d}\xi +{\nu }^2{\int }_0^1{\varphi }_i{\varphi }_j^{″}\mathrm{d}\xi \\ A_{ijkl}={\int }_0^1{\varphi }_i\cdot [l_0\left(2{\varphi }_j^{\prime }{\varphi }_k^{″}{\varphi }_l^{‴}+2{\varphi }_j^{″}{\varphi }_k^{″}{\varphi }_l^{″}-{\varphi }_j^{\prime }{\varphi }_k^{\prime }{\varphi }_l^{\left(4\right)}+2{\varphi }_j^{\prime }{\int }_0^{\xi }{\varphi }_k^{″}{\varphi }_l^{\left(4\right)}\mathrm{d}\xi -2{\varphi }_j^{″}{\int }_{\xi }^1{\int }_0^{\xi }{\varphi }_k^{″}{\varphi }_l^{\left(4\right)}\mathrm{d}\xi \mathrm{d}\xi \right)\\ +{\nu }^2\left({\varphi }_j^{\prime }{\int }_0^{\xi }{\varphi }_k^{″}{\varphi }_l^{″}d\xi -{\varphi }_j^{″}{\int }_{\xi }^1{\int }_0^{\xi }{\varphi }_k^{″}{\varphi }_l^{″}\mathrm{d}\xi \mathrm{d}\xi \right)\\ +\frac{3}{2}\left(2{\varphi }_j^{\prime }{\varphi }_k^{″}{\varphi }_l^{‴}+{\varphi }_j^{″}{\varphi }_k^{″}{\varphi }_l^{″}\right)+{\varphi }_j^{\prime }{\int }_0^{\xi }{\varphi }_k^{″}{\varphi }_l^{\left(4\right)}\mathrm{d}\xi -{\varphi }_j^{″}{\int }_{\xi }^1{\int }_0^{\xi }{\varphi }_k^{″}{\varphi }_l^{\left(4\right)}\mathrm{d}\xi \mathrm{d}\xi ]\mathrm{d}\xi \\ B_{ijkl}={\int }_0^1{\varphi }_i\cdot 2\nu \sqrt{\beta }\left({\varphi }_j^{\prime }{\int }_0^{\xi }{\varphi }_k^{″}{\varphi }_l^{\prime }\mathrm{d}\xi -{\varphi }_j^{″}{\int }_{\xi }^1{\int }_0^{\xi }{\varphi }_k^{″}{\varphi }_l^{\prime }\mathrm{d}\xi \mathrm{d}\xi \right)\mathrm{d}\xi \\ C_{ijkl}={\int }_0^1{\varphi }_i\cdot \left({\varphi }_j^{\prime }{\int }_0^{\xi }{\varphi }_k^{\prime }{\varphi }_l^{\prime }\mathrm{d}\xi -{\varphi }_j^{″}{\int }_{\xi }^1{\int }_0^{\xi }{\varphi }_k^{\prime }{\varphi }_l^{\prime }\mathrm{d}\xi \mathrm{d}\xi \right)\mathrm{d}\xi \\ L_{ijkl}={\int }_0^1{\varphi }_i\cdot [l_0(2{\varphi }_j^{″}{\psi }_k^{″}{\psi }_l^{″}-{\varphi }_j^{″}{\psi }_k^{\prime }{\psi }_l^{‴}+3{\varphi }_j^{\prime }{\psi }_k^{″}{\psi }_l^{‴}-{\varphi }_j^{\prime }{\psi }_k^{\prime }{\psi }_l^{\left(4\right)}+\\ \left.2{\varphi }_j^{\prime }{\int }_0^{\xi }{\psi }_k^{″}{\psi }_l^{\left(4\right)}\mathrm{d}\xi -2{\varphi }_j^{″}{\int }_{\xi }^1{\int }_0^{\xi }{\psi }_k^{″}{\psi }_l^{\left(4\right)}\mathrm{d}\xi \mathrm{d}\xi \right)\\ +{\nu }^2\left({\varphi }_j^{\prime }{\int }_0^{\xi }{\psi }_k^{″}{\psi }_l^{″}\mathrm{d}\xi -{\varphi }_j^{″}{\int }_{\xi }^1{\int }_0^{\xi }{\psi }_k^{″}{\psi }_l^{″}\mathrm{d}\xi \mathrm{d}\xi \right)\\ +\frac{3}{2}\left({\varphi }_j^{″}{\psi }_k^{″}{\psi }_l^{″}+2{\varphi }_j^{\prime }{\psi }_k^{″}{\psi }_l^{‴}\right)+{\varphi }_j^{\prime }{\int }_0^{\xi }{\psi }_k^{″}{\psi }_l^{\left(4\right)}\mathrm{d}\xi -{\varphi }_j^{″}{\int }_{\xi }^1{\int }_0^{\xi }{\psi }_k^{″}{\psi }_l^{\left(4\right)}\mathrm{d}\xi \mathrm{d}\xi ]\mathrm{d}\xi \\ M_{ijkl}={\int }_0^1{\varphi }_i\cdot 2\nu \sqrt{\beta }\left({\varphi }_j^{\prime }{\int }_0^{\xi }{\psi }_k^{″}{\psi }_l^{\prime }\mathrm{d}\xi -{\varphi }_j^{″}{\int }_{\xi }^1{\int }_0^{\xi }{\psi }_k^{″}{\psi }_l^{\prime }\mathrm{d}\xi \mathrm{d}\xi \right)\mathrm{d}\xi \\ N_{ijkl}={\int }_0^1{\varphi }_i\cdot \left({\varphi }_j^{\prime }{\int }_0^{\xi }{\psi }_k^{\prime }{\psi }_l^{\prime }\mathrm{d}\xi -{\varphi }_j^{″}{\int }_{\xi }^1{\int }_0^{\xi }{\psi }_k^{\prime }{\psi }_l^{\prime }\mathrm{d}\xi \mathrm{d}\xi \right)\mathrm{d}\xi \end{array}\right.(10)$

and $j,k,l$ run from 1 to n.

Let [15–17].

$q_i=x_i,{\dot{q}}_i=x_{i+n},p_i=x_{i+2n},{\dot{p}}_i=x_{i+3n}(11)$

Transform Eq. 9 into a first-order form:

$\dot{\mathbf{X}}=\mathbf{\text{LX}}+\mathbf{N}\left(\mathbf{X}\right)(12)$

In Eq. 12

$\mathbf{L}=\left[\begin{array}{cc}\begin{array}{cc}\mathbf{0}& \mathbf{I}\\ -\mathbf{K}& -\mathbf{C}\end{array}& \begin{array}{cc}\mathbf{0}& \mathbf{0}\\ \mathbf{0}& \mathbf{0}\end{array}\\ \begin{array}{cc}\mathbf{0}& \mathbf{0}\\ \mathbf{0}& \mathbf{0}\end{array}& \begin{array}{cc}\mathbf{0}& \mathbf{I}\\ -\mathbf{K}& -\mathbf{C}\end{array}\end{array}\right](13)$

where $\mathbf{K}$ is an n-order matrix whose elements are $k_{ij}$; $\mathbf{C}$ is an n-order matrix whose elements are $c_{ij}$; $\mathbf{I}$ is an n-order unit matrix; $\mathbf{0}$ is a n-order matrix whose elements are all zeros. $\mathbf{N}\left(\mathbf{X}\right)$ represents the nonlinear term in Eq. 12:

$\mathbf{N}\left(\mathbf{X}\right)={\left[\underset{1--n}{\underbrace{0,\cdots 0}},N_1\left(\mathbf{X}\right),\cdots ,N_n\left(\mathbf{X}\right),\underset{1--n}{\underbrace{0,\cdots 0}},N_{1+n}\left(\mathbf{X}\right),\cdots ,N_{2n}\left(\mathbf{X}\right)\right]}^{\mathrm{{\rm T}}}(14)$

where $N_i\left(\mathbf{X}\right)$ and $N_{i+n}\left(\mathbf{X}\right)$ are shown below.

$\begin{array}{l}{N}_i\left(\mathbf{X}\right)=-A_{ijkl}{x}_j{x}_k{x}_l-B_{ijkl}{x}_j{x}_k{x}_{l+n}-C_{ijkl}{x}_j{x}_{k+n}{x}_{l+n}\\ -L_{ijkl}{x}_j{x}_{k+2n}{x}_{l+2n}-M_{ijkl}{x}_j{x}_{k+2n}{x}_{l+3n}-N_{ijkl}{x}_j{x}_{k+3n}{x}_{l+3n}\end{array}(15)$

$\begin{array}{l}{N}_{i+n}\left(\mathbf{X}\right)=-A_{ijkl}{x}_{j+2n}{x}_{k+2n}{x}_{l+2n}-B_{ijkl}{x}_{j+2n}{x}_{k+2n}{x}_{l+3n}-C_{ijkl}{x}_{j+2n}{x}_{k+3n}{x}_{l+3n}\\ -L_{ijkl}{x}_{j+2n}{x}_k{x}_l-M_{ijkl}{x}_{j+2n}{x}_k{x}_{l+n}-N_{ijkl}{x}_{j+2n}{x}_{k+n}{x}_{l+n}\end{array}(16)$

3.2 Reduced-order equations

3.2.1 Critical flow velocity

By examining the degeneracy of the linear part of Eq. 12, the critical flow velocity can be given.

$\dot{\mathbf{X}}=\mathbf{\text{LX}}(17)$

Eq. 17 can be written as

$\left[\begin{array}{l}{\dot{\mathbf{X}}}_1\\ {\dot{\mathbf{X}}}_2\end{array}\right]=\left[\begin{array}{cc}{\mathbf{L}}_1& \mathbf{0}\\ \mathbf{0}& {\mathbf{L}}_2\end{array}\right]\left[\begin{array}{l}{\mathbf{X}}_1\\ {\mathbf{X}}_2\end{array}\right](18)$

where “$\mathbf{0}$” is a 2n-order matrix whose elements are all zeros, and ${\mathbf{L}}_1={\mathbf{L}}_2=\left[\begin{array}{cc}\mathbf{0}& \mathbf{I}\\ -\mathbf{K}& -\mathbf{C}\end{array}\right]$,

In Eq. 18, “$\mathbf{0}$” in L₁ and L₂ are n-order matrices whose elements are all zero, and X₁ and X₂ are given below.

${\mathbf{X}}_1={\left[\underset{n}{\underbrace{q_1,\cdots q_n}},\underset{n}{\underbrace{{\dot{q}}_1,\cdots {\dot{q}}_n}}\right]}^{\mathrm{{\rm T}}}={\left[x_1,\cdots ,x_{2n}\right]}^{\mathrm{{\rm T}}},{\mathbf{X}}_2={\left[\underset{n}{\underbrace{p_1,\cdots p_n}},\underset{n}{\underbrace{{\dot{p}}_1,\cdots {\dot{p}}_n}}\right]}^{\mathrm{{\rm T}}}={\left[x_{2n+1},\cdots ,x_{4n}\right]}^{\mathrm{{\rm T}}}$

It can be seen that ${\mathbf{X}}_1$ and ${\mathbf{X}}_2$ are non-coupling, and they can be written as

${\dot{\mathbf{X}}}_1={\mathbf{L}}_1{\mathbf{X}}_1(19)$

${\dot{\mathbf{X}}}_2={\mathbf{L}}_2{\mathbf{X}}_2(20)$

Considering ${\mathbf{L}}_1={\mathbf{L}}_2$, Eqs 19, 20 have the same form. No matter how the parameters change, the eigenvalues of ${\mathbf{L}}_1,{\mathbf{L}}_2$ are identical, so Eqs 19, 20 degenerate at the same time. Because the instability mode of this type of cantilevered fluid-conveying pipe [Eqs. 19, 20] is the occurrence of flutter [50, 91], the degeneracy forms of Eqs 19, 20 are that ${\mathbf{L}}_1,{\mathbf{L}}_2$ have a pair of equivalent pure imaginary eigenvalues $\pm \mathrm{i}{\omega }_0$ at the same time, which is equivalent to the degeneracy form of the matrix $\mathbf{L}$ with two pairs of “semi-simple” pure imaginary eigenvalues $\pm \mathrm{i}{\omega }_0,\pm \mathrm{i}{\omega }_0$. Therefore, the critical flow velocity is defined as follows. At a given $l_0$ and mass ratio β, the critical flow velocity (denoted as ${\nu }_c$) is the one when matrix $\mathbf{L}$ has two pairs of pure imaginary eigenvalues. The imaginary part of the pure imaginary eigenvalues $\pm \mathrm{i}{\omega }_0$, i.e., ω₀, is called ‘critical frequency’, which represents the natural frequency of the pipe at ${\nu }_c$. For a processed pipe, $l_0$ is given, and the fluid in the pipe depends on the specific application scenario. Hence, when examining the critical flow velocity, the value of $l_0$ can be determined first; then, the variation of ${\nu }_c$ with the mass ratio β is studied, and the “critical flow velocity-mass ratio curve” is drawn. The pure imaginary eigenvalues $\pm \mathrm{i}{\omega }_0,\pm \mathrm{i}{\omega }_0$ are called critical eigenvalues of which real parts generally change to be non-zero when flow velocity has an increment around ${\nu }_c$. And the change rate of the real part of the critical eigenvalue with respect to the flow velocity will be investigated later.

3.2.2 Reduced-order equations

At a given $l_0$ and mass ratio $\beta$, when the flow velocity has a change of $\epsilon$ near the critical value ${\nu }_c$, the original equation can be written as

$\dot{\mathbf{X}}=\mathbf{L}\left({\upsilon }_c+\epsilon \right)\mathbf{X}+\mathbf{N}\left(\mathbf{X}\right)(21)$

Denote ${\mathbf{L}}_0=\mathbf{L}\left({\nu }_c\right)$. $<\cdot ,\cdot >$ is used to represent the inner product, defined as $<\mathbf{x},\mathbf{y}>={\mathbf{x}}^{\mathrm{{\rm T}}}\overline{\mathbf{y}}$. “$\mathrm{{\rm T}}$” and “$\overline{}$” represent the transpose and conjugate, respectively. ${\mathbf{L}}_0^{*}$ represents the conjugate operator of ${\mathbf{L}}_0$, and it satisfies $〈{\mathbf{L}}_0\mathbf{x},\mathbf{y}〉=〈\mathbf{x},\mathbf{L}{}_0{}^{*}\mathbf{y}〉$. For the matrix, ${\mathbf{L}}_0^{*}={{\overline{\mathbf{L}}}_0}^{\mathrm{{\rm T}}}$. The eigenvalues set of a linear operator is the same as that of its conjugate operator. However, the eigenvectors need to be discussed separately. Accordingly, this study further defines ${\mathbf{w}}_0^{\left(i\right)}$ (${\overline{\mathbf{w}}}_0^{\left(i\right)}$) and ${\mathbf{q}}_0^{\left(i\right)}$ (${\overline{\mathbf{q}}}_0^{\left(i\right)}$) as the characteristic eigenvectors of ${\mathbf{L}}_0$ and ${\mathbf{L}}_0^{*}$ corresponding to eigenvalues $\mathrm{i}{\omega }_0\left(-\mathrm{i}{\omega }_0\right),-\mathrm{i}{\omega }_0\left(\mathrm{i}{\omega }_0\right)$, respectively. These quantities are related as

$\begin{array}{l}{\mathbf{L}}_0{\mathbf{w}}_0^{\left(1\right)}=\mathrm{i}{\omega }_0{\mathbf{w}}_0^{\left(1\right)},{\mathbf{L}}_0{\overline{\mathbf{w}}}_0^{\left(1\right)}=-\mathrm{i}{\omega }_0{\overline{\mathbf{w}}}_0^{\left(1\right)},{\mathbf{L}}_0{\mathbf{w}}_0^{\left(2\right)}=\mathrm{i}{\omega }_0{\mathbf{w}}_0^{\left(2\right)},{\mathbf{L}}_0{\overline{\mathbf{w}}}_0^{\left(2\right)}=-\mathrm{i}{\omega }_0{\overline{\mathbf{w}}}_0^{\left(2\right)},\\ {\mathbf{L}}_0^{*}{\mathbf{q}}_0^{\left(1\right)}=-\mathrm{i}{\omega }_0{\mathbf{q}}_0^{\left(1\right)},{\mathbf{L}}_0^{*}{\overline{\mathbf{q}}}_0^{\left(1\right)}=\mathrm{i}{\omega }_0{\overline{\mathbf{q}}}_0^{\left(1\right)},{\mathbf{L}}_0^{*}{\mathbf{q}}_0^{\left(2\right)}=-\mathrm{i}{\omega }_0{\overline{\mathbf{q}}}_0^{\left(2\right)},{\mathbf{L}}_0^{*}{\mathbf{q}}_0^{\left(2\right)}=\mathrm{i}{\omega }_0{\overline{\mathbf{q}}}_0^{\left(2\right)}\end{array}(22)$

The high-dimensional (specifically, 4n-dimensional, where n is the number of truncation modes) ordinary differential system (12) can be reduced and simplified to a 4-dimensional equations according to the method described in [70] ($z_1,z_2$ are complex numbers).

$\left\{\begin{array}{l}{\dot{z}}_1=\mathrm{i}{\omega }_0{z}_1+\epsilon {\lambda }_{\epsilon }^{\prime }{z}_1\\ +F_{2100}{z}_1^2{\overline{z}}_1+F_{1011}{z}_1{z}_2{\overline{z}}_2+F_{0120}{\overline{z}}_1{z}_2^2+O\left(\cdots \right)\\ {\dot{z}}_2=\mathrm{i}{\omega }_0{z}_2+\epsilon {\lambda }_{\epsilon }^{\prime }{z}_2\\ +H_{0021}{z}_2^2{\overline{z}}_2+H_{1110}{z}_1{\overline{z}}_1{z}_2+H_{2001}{z}_1^2{\overline{z}}_2+O\left(\cdots \right)\end{array}\right.(23)$

where

${\lambda }_{\epsilon }^{\prime }=〈{\mathbf{L}}_{\epsilon }^{\prime }{\mathbf{w}}_0^{\left(1\right)},{\mathbf{q}}_0^{\left(1\right)}〉=〈{\mathbf{L}}_{\epsilon }^{\prime }{\mathbf{w}}_0^{\left(2\right)},{\mathbf{q}}_0^{\left(2\right)}〉(24)$

${\mathbf{L}}_{\epsilon }^{\prime }=\left[\begin{array}{cccc}\mathbf{0}& \mathbf{0}& \mathbf{0}& \mathbf{0}\\ -{\mathbf{K}}^{\prime }& -{\mathbf{C}}^{\prime }& \mathbf{0}& \mathbf{0}\\ \mathbf{0}& \mathbf{0}& \mathbf{0}& \mathbf{0}\\ \mathbf{0}& \mathbf{0}& -{\mathbf{K}}^{\prime }& -{\mathbf{C}}^{\prime }\end{array}\right]$

Both ${\mathbf{K}}^{\prime }$ and ${\mathbf{C}}^{\prime }$ are n-order matrices, and their elements are $k_{ij}^{\prime }=2{\nu }_c{\int }_0^1{\varphi }_i{\varphi }_j^{″}\mathrm{d}\xi ,c_{ij}^{\prime }=2\sqrt{\beta }{\int }_0^1{\varphi }_i{\varphi }_j^{\prime }\mathrm{d}\xi$, respectively.

The coefficients $F_{2100},F_{1011},F_{0120},H_{0021},H_{1110}$ and $H_{2001}$ are determined by Eq. 25.

$\begin{array}{l}{F}_{2100}=\frac{1}{2}<{\mathbf{q}}_0^{\left(1\right)},\mathbf{C}\left({\mathbf{w}}_0^{\left(1\right)},{\mathbf{w}}_0^{\left(1\right)},{\overline{\mathbf{w}}}_0^{\left(1\right)}\right)>,F_{1011}=<{\mathbf{q}}_0^{\left(1\right)},\mathbf{C}\left({\mathbf{w}}_0^{\left(1\right)},{\mathbf{w}}_0^{\left(2\right)},{\overline{\mathbf{w}}}_0^{\left(2\right)}\right)>,\\ F_{0120}=\frac{1}{2}<{\mathbf{q}}_0^{\left(1\right)},\mathbf{C}\left({\overline{\mathbf{w}}}_0^{\left(1\right)},{\mathbf{w}}_0^{\left(2\right)},{\mathbf{w}}_0^{\left(2\right)}\right)>,\\ H_{0021}=\frac{1}{2}<{\mathbf{q}}_0^{\left(2\right)},\mathbf{C}\left({\mathbf{w}}_0^{\left(2\right)},{\mathbf{w}}_0^{\left(2\right)},{\overline{\mathbf{w}}}_0^{\left(2\right)}\right)>,H_{1110}=<{\mathbf{q}}_0^{\left(2\right)},\mathbf{C}\left({\mathbf{w}}_0^{\left(1\right)},{\overline{\mathbf{w}}}_0^{\left(1\right)},{\mathbf{w}}_0^{\left(2\right)}\right)>,H_{2001}=\frac{1}{2}<{\mathbf{q}}_0^{\left(2\right)},\mathbf{C}\left({\mathbf{w}}_0^{\left(1\right)},{\mathbf{w}}_0^{\left(1\right)},{\overline{\mathbf{w}}}_0^{\left(2\right)}\right)>.\end{array}(25)$

where $\mathbf{C}\left(\cdot ,\cdot ,\cdot \right)$ denotes the multiple symmetric linear types determined by $\mathbf{N}\left(\mathbf{X}\right)$. For any 4n-dimensional vector

$\mathbf{\alpha }={\left[{\alpha }_1,\cdots ,{\alpha }_{4n}\right]}^{\mathrm{{\rm T}}},\mathbf{\beta }={\left[{\beta }_1,\cdots ,{\beta }_{4n}\right]}^{\mathrm{{\rm T}}},\mathbf{\gamma }={\left[{\gamma }_1,\cdots ,{\gamma }_{4n}\right]}^{\mathrm{{\rm T}}}.$

considering the form of $\mathbf{N}\left(\mathbf{X}\right)$ in Eq. 14 and according to the definition of multiple symmetric linear types [92], we have

$\mathbf{C}\left(\mathbf{\alpha },\mathbf{\beta },\mathbf{\gamma }\right)={\left[\underset{1--n}{\underbrace{0,\cdots 0}},C_1\left(\mathbf{\alpha },\mathbf{\beta },\mathbf{\gamma }\right),\cdots ,C_n\left(\mathbf{\alpha },\mathbf{\beta },\mathbf{\gamma }\right),\underset{1--n}{\underbrace{0,\cdots 0}},C_{1+n}\left(\mathbf{\alpha },\mathbf{\beta },\mathbf{\gamma }\right),\cdots ,C_{2n}\left(\mathbf{\alpha },\mathbf{\beta },\mathbf{\gamma }\right)\right]}^{\mathrm{{\rm T}}}(26)$

where

$\left\{\begin{array}{l}{C}_i\left(\mathbf{\alpha },\mathbf{\beta },\mathbf{\gamma }\right)={{\displaystyle \sum _{j,k,l=1}^{4n}}\left.\frac{{\partial }^3{N}_i\left(\mathbf{X}\right)}{\partial x_j\partial x_k\partial x_l}\right|}_{\mathbf{X}=\mathbf{0}}{\alpha }_j{\beta }_k{\gamma }_l\\ C_{i+n}\left(\mathbf{\alpha },\mathbf{\beta },\mathbf{\gamma }\right)={{\displaystyle \sum _{j,k,l=1}^{4n}}\left.\frac{{\partial }^3{N}_{i+n}\left(\mathbf{X}\right)}{\partial x_j\partial x_k\partial x_l}\right|}_{\mathbf{X}=\mathbf{0}}{\alpha }_j{\beta }_k{\gamma }_l\end{array}\right.(27)$

According to Eqs 15, 16, the following results can be obtained.

$\begin{array}{l}{C}_i\left(\mathbf{\alpha },\mathbf{\beta },\mathbf{\gamma }\right)=\\ -A_{ijkl}\left({\alpha }_j{\beta }_k{\gamma }_l+{\alpha }_j{\beta }_l{\gamma }_k+{\alpha }_k{\beta }_j{\gamma }_l+{\alpha }_l{\beta }_j{\gamma }_k+{\alpha }_k{\beta }_l{\gamma }_j+{\alpha }_l{\beta }_k{\gamma }_j\right)\\ -B_{ijkl}\left({\alpha }_j{\beta }_k{\gamma }_{l+n}+{\alpha }_j{\beta }_{l+n}{\gamma }_k+{\alpha }_k{\beta }_j{\gamma }_{l+n}+{\alpha }_{l+n}{\beta }_j{\gamma }_k+{\alpha }_k{\beta }_{l+n}{\gamma }_j+{\alpha }_{l+n}{\beta }_k{\gamma }_j\right)\\ -C_{ijkl}\left({\alpha }_j{\beta }_{k+n}{\gamma }_{l+n}+{\alpha }_j{\beta }_{l+n}{\gamma }_{k+n}+{\alpha }_{k+n}{\beta }_j{\gamma }_{l+n}+{\alpha }_{l+n}{\beta }_j{\gamma }_{k+n}+{\alpha }_{k+n}{\beta }_{l+n}{\gamma }_j+{\alpha }_{l+n}{\beta }_{k+n}{\gamma }_j\right)\\ -L_{ijkl}\left({\alpha }_j{\beta }_{k+2n}{\gamma }_{l+2n}+{\alpha }_j{\beta }_{l+2n}{\gamma }_{k+2n}+{\alpha }_{k+2n}{\beta }_j{\gamma }_{l+2n}+{\alpha }_{l+2n}{\beta }_j{\gamma }_{k+2n}+{\alpha }_{k+2n}{\beta }_{l+2n}{\gamma }_j+{\alpha }_{l+2n}{\beta }_{k+2n}{\gamma }_j\right)\\ -M_{ijkl}\left({\alpha }_j{\beta }_{k+2n}{\gamma }_{l+3n}+{\alpha }_j{\beta }_{l+3n}{\gamma }_{k+2n}+{\alpha }_{k+2n}{\beta }_j{\gamma }_{l+3n}+{\alpha }_{l+3n}{\beta }_j{\gamma }_{k+2n}+{\alpha }_{k+2n}{\beta }_{l+3n}{\gamma }_j+{\alpha }_{l+3n}{\beta }_{k+2n}{\gamma }_j\right)\\ -N_{ijkl}\left({\alpha }_j{\beta }_{k+3n}{\gamma }_{l+3n}+{\alpha }_j{\beta }_{l+3n}{\gamma }_{k+3n}+{\alpha }_{k+3n}{\beta }_j{\gamma }_{l+3n}+{\alpha }_{l+3n}{\beta }_j{\gamma }_{k+3n}+{\alpha }_{k+3n}{\beta }_{l+3n}{\gamma }_j+{\alpha }_{l+3n}{\beta }_{k+3n}{\gamma }_j\right)\end{array}(28)$

$\begin{array}{l}{C}_{i+n}\left(\mathbf{\alpha },\mathbf{\beta },\mathbf{\gamma }\right)=\\ -A_{ijkl}({\alpha }_{j+2n}{\beta }_{k+2n}{\gamma }_{l+2n}+{\alpha }_{j+2n}{\beta }_{l+2n}{\gamma }_{k+2n}+{\alpha }_{k+2n}{\beta }_{j+2n}{\gamma }_{l+2n}\\ \left.+{\alpha }_{l+2n}{\beta }_{j+2n}{\gamma }_{k+2n}+{\alpha }_{k+2n}{\beta }_{l+2n}{\gamma }_{j+2n}+{\alpha }_{l+2n}{\beta }_{k+2n}{\gamma }_{j+2n}\right)\\ -B_{ijkl}({\alpha }_{j+2n}{\beta }_{k+2n}{\gamma }_{l+3n}+{\alpha }_{j+2n}{\beta }_{l+3n}{\gamma }_{k+2n}+{\alpha }_{k+2n}{\beta }_{j+2n}{\gamma }_{l+3n}\\ \left.+{\alpha }_{l+3n}{\beta }_{j+2n}{\gamma }_{k+2n}+{\alpha }_{k+2n}{\beta }_{l+3n}{\gamma }_{j+2n}+{\alpha }_{l+3n}{\beta }_{k+2n}{\gamma }_{j+2n}\right)\\ -C_{ijkl}({\alpha }_{j+2n}{\beta }_{k+3n}{\gamma }_{l+3n}+{\alpha }_{j+2n}{\beta }_{l+3n}{\gamma }_{k+3n}+{\alpha }_{k+3n}{\beta }_{j+2n}{\gamma }_{l+3n}\\ \left.+{\alpha }_{l+3n}{\beta }_{j+2n}{\gamma }_{k+3n}+{\alpha }_{k+3n}{\beta }_{l+3n}{\gamma }_{j+2n}+{\alpha }_{l+3n}{\beta }_{k+3n}{\gamma }_{j+2n}\right)\\ -L_{ijkl}\left({\alpha }_{j+2n}{\beta }_k{\gamma }_l+{\alpha }_{j+2n}{\beta }_l{\gamma }_k+{\alpha }_k{\beta }_{j+2n}{\gamma }_l+{\alpha }_l{\beta }_{j+2n}{\gamma }_k+{\alpha }_k{\beta }_l{\gamma }_{j+2n}+{\alpha }_l{\beta }_k{\gamma }_{j+2n}\right)\\ -M_{ijkl}({\alpha }_{j+2n}{\beta }_k{\gamma }_{l+n}+{\alpha }_{j+2n}{\beta }_{l+n}{\gamma }_k+{\alpha }_k{\beta }_{j+2n}{\gamma }_{l+n}\\ \left.+{\alpha }_{l+n}{\beta }_{j+2n}{\gamma }_k+{\alpha }_k{\beta }_{l+n}{\gamma }_{j+2n}+{\alpha }_{l+n}{\beta }_k{\gamma }_{j+2n}\right)\\ -N_{ijkl}({\alpha }_{j+2n}{\beta }_{k+n}{\gamma }_{l+n}+{\alpha }_{j+2n}{\beta }_{l+n}{\gamma }_{k+n}+{\alpha }_{k+n}{\beta }_{j+2n}{\gamma }_{l+n}\\ \left.+{\alpha }_{l+n}{\beta }_{j+2n}{\gamma }_{k+n}+{\alpha }_{k+n}{\beta }_{l+n}{\gamma }_{j+2n}+{\alpha }_{l+n}{\beta }_{k+n}{\gamma }_{j+2n}\right)\end{array}(29)$

These Eqs 28 and 29 are the specific forms of Eq. 26, where $i$ run from 1 to n [see Eq. 8]. Eq. 28 are these terms from $C_1\left(\mathbf{\alpha },\mathbf{\beta },\mathbf{\gamma }\right)$ to $C_n\left(\mathbf{\alpha },\mathbf{\beta },\mathbf{\gamma }\right)$ in Eq. 26. Eq. 29 are these terms from $C_{1+n}\left(\mathbf{\alpha },\mathbf{\beta },\mathbf{\gamma }\right)$ to $C_{2n}\left(\mathbf{\alpha },\mathbf{\beta },\mathbf{\gamma }\right)$ in Eq. 26.

In this way, Eq. 26, i.e., the specific form of $\mathbf{C}\left(\mathbf{\alpha },\mathbf{\beta },\mathbf{\gamma }\right)$ is known. By combining the eigenvectors ${\mathbf{w}}_0^{\left(1\right)}$, ${\overline{\mathbf{w}}}_0^{\left(1\right)}$, ${\mathbf{w}}_0^{\left(2\right)}$, and ${\overline{\mathbf{w}}}_0^{\left(2\right)}$ of ${\mathbf{L}}_0$ as well as the eigenvectors ${\mathbf{q}}_0^{\left(1\right)}$, ${\overline{\mathbf{q}}}_0^{\left(1\right)}$, ${\mathbf{q}}_0^{\left(2\right)}$, and ${\overline{\mathbf{q}}}_0^{\left(2\right)}$ of ${\mathbf{L}}_0^{*}$, the specific coefficients shown in Eqs 24, 25 can be calculated, thereby obtaining the specific form of Eq. 23.

3.2.3 Periodic motion and its stability

For Eq. 23, by taking polar coordinate transformation $z_1=r_1{e}^{\mathrm{i}{\theta }_1},z_2=r_2{e}^{\mathrm{i}{\theta }_2}$, Eq. 23 can be written as [70]

$\left\{\begin{array}{l}{\dot{r}}_1=\epsilon \text{Re}\left({\lambda }_{\epsilon }^{\prime }\right)r_1+\text{Re}{F}_{2100}{r}_1^3+\text{Re}{F}_{1011}{r}_1{r}_2^2\\ +\left[\text{Re}{F}_{0120}\cos \left(2{\theta }_2-2{\theta }_1\right)-\text{Im}{F}_{0120}\sin \left(2{\theta }_2-2{\theta }_1\right)\right]r_1{r}_2^2\\ {\dot{r}}_2=\epsilon \text{Re}\left({\lambda }_{\epsilon }^{\prime }\right)r_2+\text{Re}{H}_{0021}{r}_2^3+\text{Re}{H}_{1110}{r}_2{r}_1^2\\ +\left[\text{Re}{H}_{2001}\cos \left(2{\theta }_2-2{\theta }_1\right)+\text{Im}{H}_{2001}\sin \left(2{\theta }_2-2{\theta }_1\right)\right]r_2{r}_1^2\\ {\dot{\theta }}_1={\omega }_0+\epsilon \text{Im}\left({\lambda }_{\epsilon }^{\prime }\right)+\text{Im}{F}_{2100}{r}_1^2+\text{Im}{F}_{1011}{r}_2^2\\ +\left[\text{Re}{F}_{0120}\sin \left(2{\theta }_2-2{\theta }_1\right)+\text{Im}{F}_{0120}\cos \left(2{\theta }_2-2{\theta }_1\right)\right]r_2^2\\ {\dot{\theta }}_2={\omega }_0+\epsilon \text{Im}\left({\lambda }_{\epsilon }^{\prime }\right)+\text{Im}{H}_{0021}{r}_2^2+\text{Im}{H}_{1110}{r}_1^2\\ +\left[-\text{Re}{H}_{2001}\sin \left(2{\theta }_2-2{\theta }_1\right)+\text{Im}{H}_{2001}\cos \left(2{\theta }_2-2{\theta }_1\right)\right]r_1^2\end{array}\right.(30)$

Only when $\epsilon \text{Re}\left({\lambda }_{\epsilon }^{\prime }\right)>0$, the vibration of the pipe does not disappear. The vibration amplitude is supposed to be “small”, so the following scale transformation is conducted $r_1\to \sqrt{\left|\epsilon \right|}{r}_1,r_2\to \sqrt{\left|\epsilon \right|}{r}_2$,

With this scale transformation, Eq. 30 becomes

$\left\{\begin{array}{l}{\dot{r}}_1=\left|\epsilon \right|\{\left|\text{Re}\left({\lambda }_{\epsilon }^{\prime }\right)\right|r_1+\text{Re}{F}_{2100}{r}_1^3+\text{Re}{F}_{1011}{r}_1{r}_2^2\\ \left.+\left[\text{Re}{F}_{0120}\cos \left(2{\theta }_2-2{\theta }_1\right)-\text{Im}{F}_{0120}\sin \left(2{\theta }_2-2{\theta }_1\right)\right]r_1{r}_2^2\right\}\\ {\dot{r}}_2=\left|\epsilon \right|\{\left|\text{Re}\left({\lambda }_{\epsilon }^{\prime }\right)\right|r_2+\text{Re}{H}_{0021}{r}_2^3+\text{Re}{H}_{1110}{r}_2{r}_1^2\\ \left.+\left[\text{Re}{H}_{2001}\cos \left(2{\theta }_2-2{\theta }_1\right)+\text{Im}{H}_{2001}\sin \left(2{\theta }_2-2{\theta }_1\right)\right]r_2{r}_1^2\right\}\\ {\dot{\theta }}_1={\omega }_0+\left|\epsilon \right|\left\{\text{sign}\right.\left(\epsilon \right)\text{Im}\left({\lambda }_{\epsilon }^{\prime }\right)+\text{Im}{F}_{2100}{r}_1^2+\text{Im}{F}_{1011}{r}_2^2\\ \left.+\left[\text{Re}{F}_{0120}\sin \left(2{\theta }_2-2{\theta }_1\right)+\text{Im}{F}_{0120}\cos \left(2{\theta }_2-2{\theta }_1\right)\right]r_2^2\right\}\\ {\dot{\theta }}_2={\omega }_0+\left|\epsilon \right|\left\{\text{sign}\right.\left(\epsilon \right)\text{Im}\left({\lambda }_{\epsilon }^{\prime }\right)+\text{Im}{H}_{0021}{r}_2^2+\text{Im}{H}_{1110}{r}_1^2\\ \left.+\left[-\text{Re}{H}_{2001}\sin \left(2{\theta }_2-2{\theta }_1\right)+\text{Im}{H}_{2001}\cos \left(2{\theta }_2-2{\theta }_1\right)\right]r_1^2\right\}\end{array}\right.(31)$

Then, variable substitution $\varphi ={\theta }_2-{\theta }_1$ is conducted and let $\mathbf{\rho }={\left[r_1,r_2,\varphi \right]}^{\mathrm{{\rm T}}}$, then Eq. 31 can be rewritten as

$\left[\begin{array}{c}\dot{\mathbf{\rho }}\\ {\dot{\theta }}_1\end{array}\right]=\left[\begin{array}{c}\mathbf{0}\\ {\omega }_0\end{array}\right]+\epsilon \left[\begin{array}{c}\mathbf{g}\left(\mathbf{\rho }\right)\\ \mathrm{\Omega }\left(\mathbf{\rho }\right)\end{array}\right](32)$

where

$\mathbf{g}\left(\mathbf{\rho }\right)=\left[\begin{array}{c}\left|\text{Re}\left({\lambda }_{\epsilon }^{\prime }\right)\right|r_1+\text{Re}{F}_{2100}{r}_1^3+\text{Re}{F}_{1011}{r}_1{r}_2^2+\left[\text{Re}{F}_{0120}\cos \left(2\varphi \right)-\text{Im}{F}_{0120}\sin \left(2\varphi \right)\right]r_1{r}_2^2\\ \left|\text{Re}\left({\lambda }_{\epsilon }^{\prime }\right)\right|r_2+\text{Re}{H}_{0021}{r}_2^3+\text{Re}{H}_{1110}{r}_2{r}_1^2+\left[\text{Re}{H}_{2001}\cos \left(2\varphi \right)+\text{Im}{H}_{2001}\sin \left(2\varphi \right)\right]r_2{r}_1^2\\ \begin{array}{l}\left\{\left[-\text{Re}{H}_{2001}\sin \left(2\varphi \right)+\text{Im}{H}_{2001}\cos \left(2\varphi \right)+\text{Im}{H}_{1110}-\text{Im}{F}_{2100}\right]r_1^2\right.\\ \left.+\left[\text{Im}{H}_{0021}-\text{Im}{F}_{1011}-\text{Re}{F}_{0120}\sin \left(2\varphi \right)-\text{Im}{F}_{0120}\cos \left(2\varphi \right)\right]r_2^2\right\}\end{array}\end{array}\right](33)$

and

$\mathrm{\Omega }\left(\mathbf{\rho }\right)=\text{sign}\left(\epsilon \right)\text{Im}\left({\lambda }_{\epsilon }^{\prime }\right)+\text{Im}{F}_{2100}{r}_1^2+\text{Im}{F}_{1011}{r}_2^2+\left[\text{Re}{F}_{0120}\sin \left(2\varphi \right)+\text{Im}{F}_{0120}\cos \left(2\varphi \right)\right]r_2^2(34)$

In Eq. 32, $\mathbf{\rho }={\left[r_1,r_2,\varphi \right]}^{\mathrm{{\rm T}}}$ are slow variables and ${\theta }_1$ is a fast variable of which configuration space is ${\mathrm{{\rm T}}}^1$. After introducing a time scale transformation $\tau \to \epsilon \tau$, the derivative of $\mathbf{\rho }$ with respect to slow time ετ are equal to the time averaging of $\mathbf{g}\left(\mathbf{\rho }\right)$, which are equal to the spatial averaging of $\mathbf{g}\left(\mathbf{\rho }\right)$ on the configuration space ${\mathrm{{\rm T}}}^1$ of the fast variable ${\theta }_1$, i.e.,

$\dot{\mathbf{\rho }}=\frac{1}{2\pi }{\int }_0^{2\pi }\mathbf{g}\left(\mathbf{\rho }\right)\mathrm{d}{\theta }_1=\mathbf{g}\left(\mathbf{\rho }\right)(35)$

Thus one can write Eq. 35 in the following form

$\{\begin{array}{l}{\dot{r}}_1=\left|\alpha \right|r_1+a_1{r}_1^3+a_2{r}_1{r}_2^2+\left[a_3\cos \left(2\varphi \right)-b_3\sin \left(2\varphi \right)\right]r_1{r}_2^2\\ {\dot{r}}_2=\left|\alpha \right|r_2+a_1{r}_2^3+a_2{r}_2{r}_1^2+\left[a_3\cos \left(2\varphi \right)+b_3\sin \left(2\varphi \right)\right]r_2{r}_1^2\\ \dot{\varphi }=\left[-a_3\sin \left(2\varphi \right)+b_3\cos \left(2\varphi \right)+b_2-b_1\right]r_1^2+\left[b_1-b_2-a_3\sin \left(2\varphi \right)-b_3\cos \left(2\varphi \right)\right]r_2^2\end{array}(36)$

where (·) denotes the derivative with respect to slow time ετ and

$\left\{\begin{array}{l}\alpha =\text{Re}\left({\lambda }_{\epsilon }^{\prime }\right),\\ a_1=\text{Re}{F}_{2100}=\text{Re}{H}_{0021},b_1=\text{Im}{F}_{2100}=\text{Im}{H}_{0021},\\ a_2=\text{Re}{F}_{1011}=\text{Re}{H}_{1110},b_2=\text{Im}{F}_{1011}=\text{Im}{H}_{1110},\\ a_3=\text{Re}{F}_{0120}=\text{Re}{H}_{2001},b_3=\text{Im}{F}_{0120}=\text{Im}{H}_{2001}.\end{array}\right.(37)$

The equilibrium points of the averaging Eq. 36 correspond to the periodic motions of the original Eq. 23, and the stability of the two equations corresponds to each other in the case of nondegeneracy.

Regardless of whether $\alpha$ is positive or negative, it is known from Ref. [70] that one of the eigenvalues of spatial periodic motions and planar periodic motions is negative and equal to $-2\alpha$ or $2\alpha$, and the motion stability depends on the remaining eigenvalues. For spatial periodic motion, it is stable when $a_3/a_2$ is positive and unstable when $a_3/a_2$ is negative; for planar periodic motion, it is unstable when $a_3/a_1$ is positive and stable when $a_3/a_1$ is negative.

4 The influences of mode truncation number and “reasonable mode truncation numbers”

This study considers the nonlinear dynamic characteristics of the macro pipe ($l_0=0$) and micro-scale pipes ($l_0=0.2$ and $l_0=0.5$). The key point is to summarize the “reasonable mode truncation numbers” needed to study the vibration of the fluid-conveying pipe with the Galerkin method. To improve the paper’s readability, the Galerkin method is first used to explore the nonlinear dynamic characteristics of the macro pipe (i.e., $l_0=0$). In detail, the truncation mode numbers are taken incrementally; the convergence of the dynamic characteristics with respect to the “mode truncation numbers” is investigated through longitudinal comparison; combined with the horizontal comparison, the “reasonable mode truncation numbers” needed to study the dynamics of this type of system is summarized. Then, a horizontal comparison is conducted between the results obtained based on “reasonable mode truncation numbers” and the results obtained based on infinite dimensional analysis [70], and the “error” is calculated. Subsequently, the nonlinear dynamics phenomena of the micro-scale pipes ($l_0=0.2$ and $l_0=0.5$) are investigated according to the “reasonable mode truncation numbers”. Finally, the obtained results are compared with those reported in Ref. [70].

4.1 Case of macro-pipes ($l_0=0$)

4.1.1 Influence of the mode truncation number on the critical flow velocity-mass ratio curve and the critical frequency-mass ratio curve

The critical flow velocity-mass ratio curves and the critical frequency-mass ratio curves obtained by different orders of Galerkin truncation are different. The curves are drawn for the mode truncation numbers of n = 2, n = 4, n = 6, n = 8, n = 9, n = 11, n = 13, and n = 15. Then, the curves are compared with the exact solution reported in Ref. [70].

As shown in Figure 3A, C, the critical flow velocity-mass ratio curves and the critical frequency-mass ratio curves obtained by the Galerkin method are almost consistent with the exact solution when the mode truncation number is 8 and 9. Meanwhile, Figure 3B and Figure 3D shows that the critical flow velocity-mass ratio curves and the critical frequency-mass ratio curves given by the Galerkin method show almost no change when the mode truncation number increases from 8. Thus, for the prediction of critical flow velocity and critical frequency, the Galerkin truncation using 8 modes can obtain quite accurate results. Then, when the actual flow velocity exceeds the critical flow velocity, what type of motion will occur for the pipe conveying fluid, and can the Galerkin discretization of the 8 modes accurately predict its dynamic characteristics? These issues are analyzed below. The analysis result indicates that, in the prediction of the dynamic behavior of the fluid-conveying pipe after instability occurs, the Galerkin discretization of 8 modes cannot provide accurate results, and more modes truncations are required for accurate predictions.

Figure 3

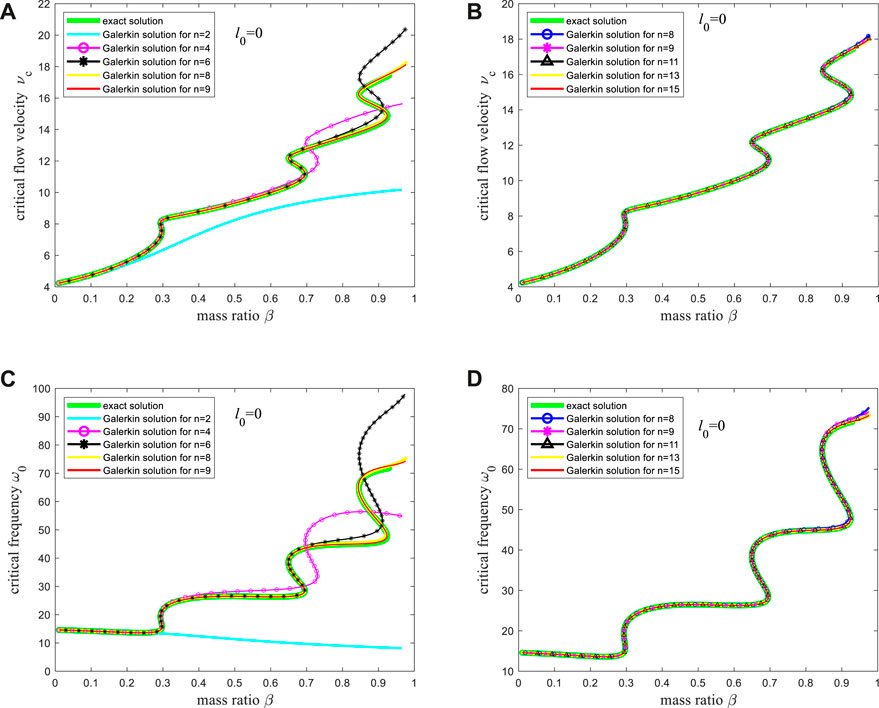
Figure 3. The critical flow velocity-mass ratio curve: (A) The exact solution and the solutions corresponding to the mode truncation numbers 2, 4, 6, 8, and 9; (B) The exact solution and the solutions corresponding to the mode truncation numbers 8, 9, 11, 13, and 15; The critical frequency-mass ratio curve: (C) The exact solution and the solutions corresponding to the mode truncation numbers 2, 4, 6, 8, and 9; (D) The exact solution and the solutions corresponding to the mode truncation numbers 8, 9, 11, 13, and 15.

4.1.2 Influences of the mode truncation number on periodic motion

Based on the above analysis, the following figures show the data (Eqs 24 and 25) required for the reduced-order Eq. 23 and the data [$a_3/a_2$ and $a_3/a_1$, shown in Eq. 37 required for determining the stability. Then, by comparing these figures with each other and with the infinite dimensional analysis results in Ref. [70], the number of modes truncations needed to accurately predict the system dynamics properties can be determined.

(a) The change rate of the real part of the critical eigenvalue under different mode truncation numbers, i.e., $\alpha$ or $\text{Re}\left({\lambda }_{\epsilon }^{\prime }\right)$, shown in Eqs 37, 24:

From Figure 4A, it can be seen that the change rate of the real part of the critical eigenvalue provided by the Galerkin method is highly consistent with the exact solution when the mode truncation number is 8 and 9. A more detailed comparison, as shown in Figure 4B, indicates that the exact solution of the change rate of the real part of the critical eigenvalue is completely consistent with the Galerkin solution when the mode truncation number is 9, 11, 13, and 15, respectively. In contrast, compared with the other solutions in Figure 4B, when the mode truncation number is 8, the Galerkin solution has a little deviation in the tail (i.e., the section where the mass ratio is greater than 0.9). Hence, for predicting the change rate of the real part of the critical eigenvalue, the Galerkin truncation of 9 modes can already obtain quite accurate results. The research in [70] indicates that (i) at $\text{Re}\left({\lambda }_{\epsilon }^{\prime }\right)>0$, flutter occurs in the pipe when the flow velocity increment is larger than zero, and the original straight configuration of the pipe is stable when the increment is smaller than zero; (ii) at $\text{Re}\left({\lambda }_{\epsilon }^{\prime }\right)<0$, flutter occurs in the pipe when the flow velocity increment is smaller than zero, and the original straight configuration of the pipe is stable when the increment is larger than zero. The following study demonstrates that the Galerkin discretization of 9 modes is insufficient to provide accurate qualitative dynamic characteristics of the pipe, but more mode truncation numbers are needed.

(b) The nonlinear resonance term (see Eqs 37, 25) and the stability criterion of periodic motion ($a_3/a_2$ and $a_3/a_1$) [see Eq. 37 for the definitions of $a_1,a_2,a_3$]:

Figure 4

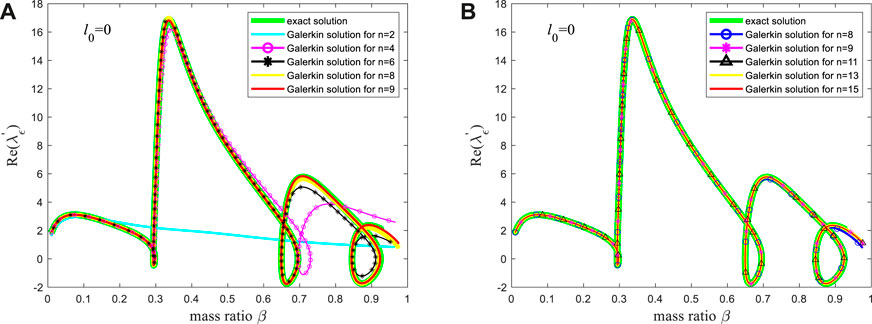
Figure 4. The rate of change of the real part of the critical eigenvalue: (A) The exact solution and the solutions corresponding to the mode truncation numbers as 2, 4, 6, 8, and 9, respectively; (B) The exact solution and the solutions corresponding to the mode truncation numbers as 8, 9, 11, 13, and 15, respectively.

Based on the above analysis about the effect of the mode truncation number on the critical flow velocity-mass ratio curve, the critical frequency-mass ratio curve and the change rate of the real part of the critical eigenvalue, let us start with n = 9 and take the truncation mode numbers incrementally to obtain the reasonable truncated mode number required to study this type of system. Subsequently, the resolutions of the ordinary differential equations set (9) are conducted using Runge-Kutta methods.

When n = 9, Figures 5A–C shows the variation curve of the high-order term coefficient with the mass ratio, and Figures 5D, E demonstrates the stability of the two types of periodic motion. A mass ratio of β = 0.92 [represented by “o” in Figures 5D,E] and a flow velocity of $\upsilon =17.42+0.18=17.6$ (17.42 is the critical flow velocity corresponding to the mass ratio β = 0.92 when n = 9, and 0.18 is the increment of flow velocity) are used to obtain the numerical solution to Eq. 9 and then substitute it into Eq. 7, thereby obtaining Figures 5F–I. Specifically, Figure 5F shows the relationship between the positions of the free ends of the pipe, and the pipe converges from the transient solution (in blue color) to the steady-state planar periodic motion (in red color). Figure 5G shows the relationship between displacement and velocity of the free ends of the pipe in one direction, and it is demonstrated that the system does not perform planar quasi-periodic motion or chaotic motion. Figure 5H, I show the motion configuration diagrams of the whole pipe. As time increases, the transient solution (in blue color) in Figure 5H gradually changes to the steady-state planar periodic motion (in red color) in Figure 5I, and the black line represents the trajectory of the free ends of the pipe. The figure presents stable planar periodic motion, which is consistent with the infinite dimensional analysis results in Ref. [70]. Furthermore, the Poincaré map (with $\dot{\eta }=0$ as the Poincaré section) is shown in Figure 5N.

Figure 5

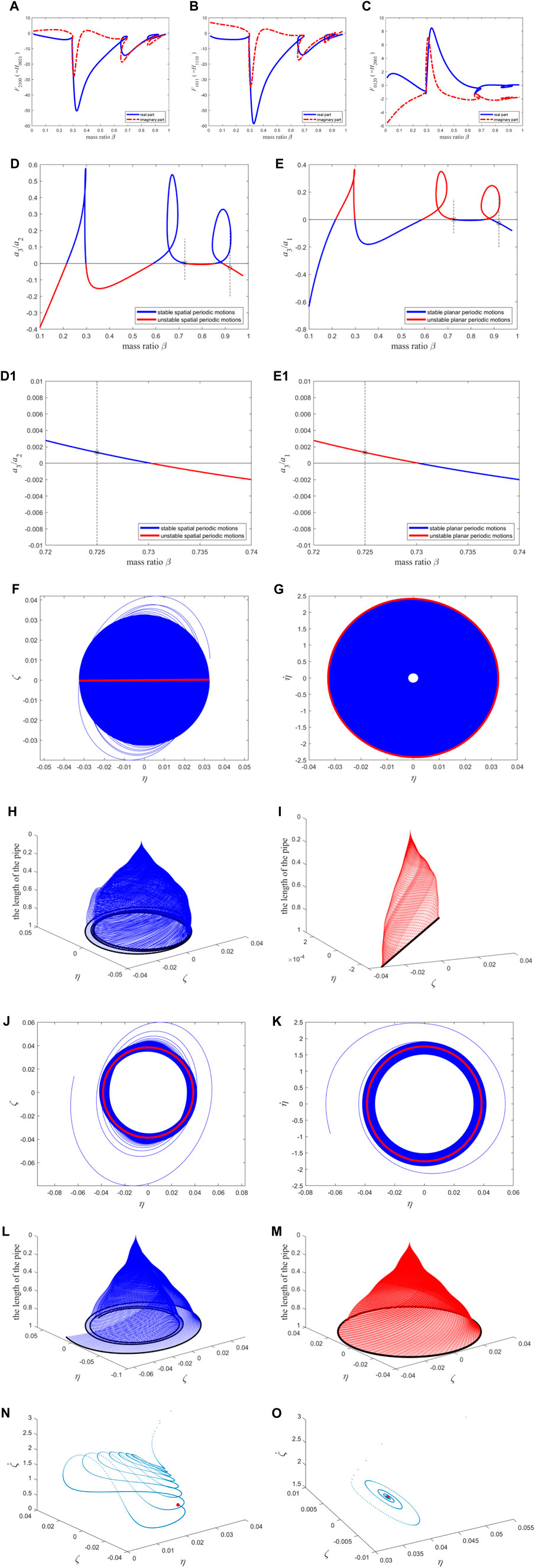
Figure 5. The resonance term coefficients of the second-order discretization equation of the macro pipe, the stability of two types of periodic motion, the phase diagram, and the configuration diagram: (A–C) The coefficients of the reduced-order equations; (D) the stability of spatial periodic motion; (E) the stability of planar periodic motion. (D1) and (E1) The enlarged version of (D, E) near the “*”. (F) the position relationship of the free ends of the pipe in two directions; (G) the velocity-displacement relationship diagram of the free ends of the pipe in one direction; (H) the transient process of the whole pipe vibration; (I) the steady-state vibration of the whole pipe. The blue (red) color represents the transient (steady-state) motion in (F–I). The interpretation of (J–M) is compared to (F–I); The Poincaré map: (N) corresponding to (F–I); (O) corresponding to (J–M). The blue points correspond to transient motion, and the red points correspond to steady-state motion (i.e., fixed point).

It needs to be explained that in the drawing of Figure 5H, I, the displacement of point $\left(\xi ,0,0\right)$ on the pipe centerline along the length direction can be determined using the inextensibility condition (Eq. 3) and the dimensionless process (Eq. 6). It is

${\int }_0^{\xi }\left[\sqrt{1-\left({{\eta }^{\prime }}^2+{{\zeta }^{\prime }}^2\right)}-1\right]\mathrm{d}\xi (38)$

It is significant that the nonlinear terms have an important influence on the dynamics of pipe. For the same parameters as Figures 5F-G, if only linear terms considered, the displacement and velocity of pipe will go toward infinity, as shown in Figure 6.

Figure 6

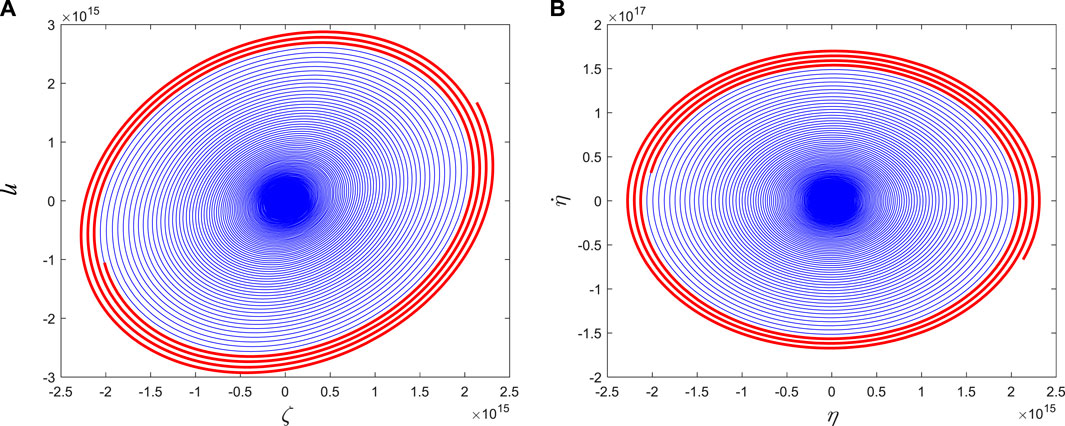
Figure 6. (A) The position relationship of the free ends of the pipe in two directions; (B) the velocity-displacement relationship diagram of the free ends of the pipe in one direction.

To compare with the results obtained when n = 11 in the following section, this study here sets the mass ratio β = 0.725 [represented by “*” in Figures 5D, E, and Figure 5(D1, E1) is the enlargement near the “*”] and the flow velocity $\upsilon =12.96+0.24=13.2$ (12.96 is the critical flow velocity corresponding to the mass ratio β = 0.725 when n = 9, and 0.24 is the increment of the flow velocity) to obtain the numerical solution to Eq. 9 and then substitute it into Eq. 7, thereby obtaining Figures 5J–M. The interpretations of Figures 5J–M can be compared to those of Figures 5F–I, respectively. According to the observation, the 9th-order truncation at this mass ratio gives the result that “the system performs stable spatial periodic motion”. The Poincaré map (with $\dot{\eta }=0$ as the Poincaré section) is shown in Figure 5O. In contrast, the analysis below demonstrates that the 11th-order truncation at this mass ratio yields the result that “the system performs stable planar periodic motion”. Meanwhile, the infinite dimensional analysis in [70] {see Figures 12A, B in Ref. [70] or Figures 12A, B in this study} also indicates that the pipe performs stable planar periodic motion at this time.

When n = 11, Figures 7A–C shows the variation curve of the high-order term coefficient with the mass ratio, and Figures 7D, E presents the stability of the two types of periodic motion.

Figure 7

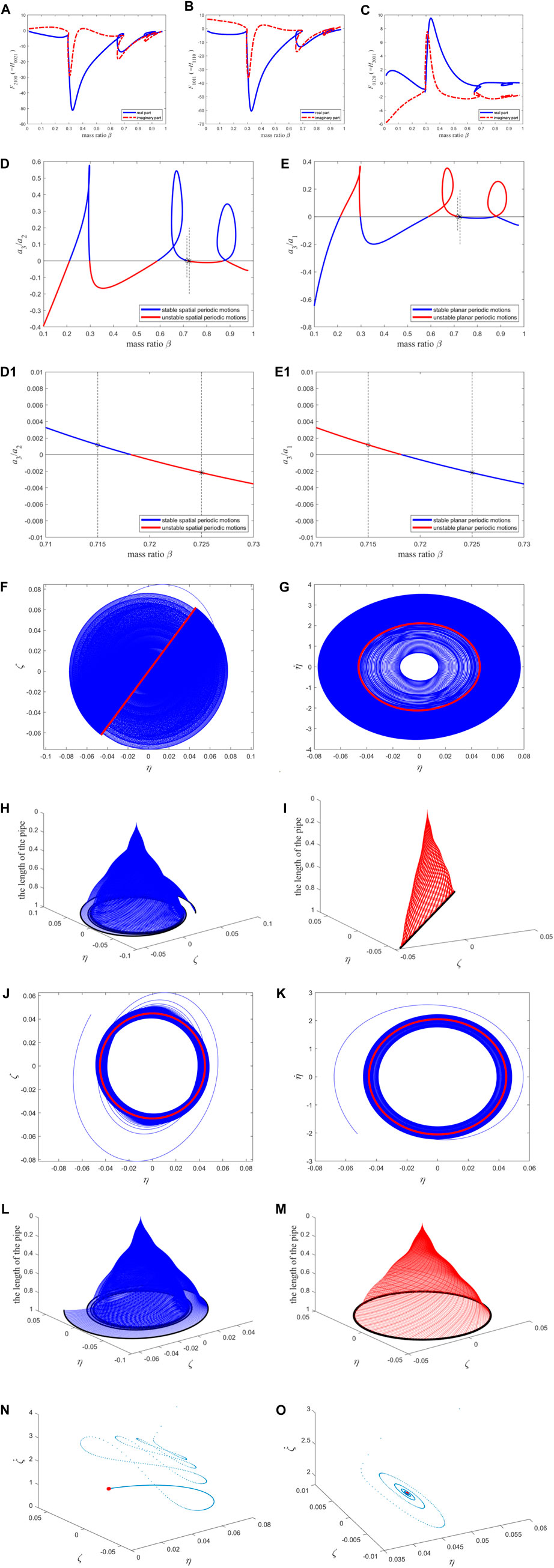
Figure 7. The resonance term coefficients of the second-order discretization equation of the macro pipe, the stability of two types of periodic motion, the phase diagram, and the configuration diagram: (A–C) The coefficients of the reduced-order equations; (D) the stability of spatial periodic motion; (E) the stability of planar periodic motion. (D1) and (E1) The enlarged version of (D) and (E) near the “*” and “o”. The interpretation of (F–I) is compared to Figures 5F–I. The interpretation of (j–m) is compared to Figures 5J–M; The Poincaré map: (N) corresponding to (F–I); (O) corresponding to (J–M). The blue points correspond to transient motion, and the red points correspond to steady-state motion (i.e., fixed point).

The results obtained when n = 11 have a minor correction to the results obtained when n = 9, as can be seen from the following comparison. This study sets a mass ratio of β = 0.725 again {represented by “*” in Figures 7D, E, and Figure 7(D1, E1) is the enlargement near the “*”} and a flow velocity of $\upsilon =12.96+0.24=13.2$ (12.96 is the critical flow velocity corresponding to the mass ratio β = 0.725 when n = 11, and 0.24 is the increment of flow velocity) to obtain the numerical solution to Eq. 9 and then substitute it into Eq. 7, thereby obtaining Figures 7F–I. Obviously, this figure represents stable planar periodic motion, which is consistent with the infinite dimensional analysis results in the [70]. Furthermore, the Poincaré map (with $\dot{\eta }=0$ as the Poincaré section) is shown in Figure 7N. The interpretations of Figures 7F–I can be compared to those of Figures 5F–I, respectively.

To compare with the results obtained when n = 13 in the following section, this study here sets the mass ratio β = 0.715 [represented by “_O” in Figures 7D, E, and Figure 7 (D1, E1) is the enlargement near the “_O”] and the flow velocity $\upsilon =12.88+0.32=13.2$ (12.88 is the critical flow velocity corresponding to the mass ratio β = 0.715 when n = 13, and 0.32 is the increment of the flow velocity) to obtain the numerical solution to Eq. 9 and then substitute it into Eq. 7, thereby obtaining Figures 7J–M. The interpretations of Figures 7J–M can be compared to those of Figures 5J–M, respectively. The observation indicates that the 11th-order truncation at this mass ratio gives the result that “the system performs stable spatial periodic motion”. The Poincaré map (with $\dot{\eta }=0$ as the Poincaré section) is shown in Figure 7O. In contrast, the analysis below demonstrates that the 13th-order truncation at this mass ratio yields the result that “the system performs stable planar periodic motion”. Meanwhile, the infinite dimensional analysis in Ref. [70] {see Figures 12A, B in Ref. [70] or Figures 12A,B in this study} also indicates that the pipe performs stable planar periodic motion at this time.

When n = 13, Figures 8A–C illustrates the variation curve of the high-order term coefficient with the mass ratio, and Figures 8D,E depicts the stability of the two types of periodic motion.

Figure 8

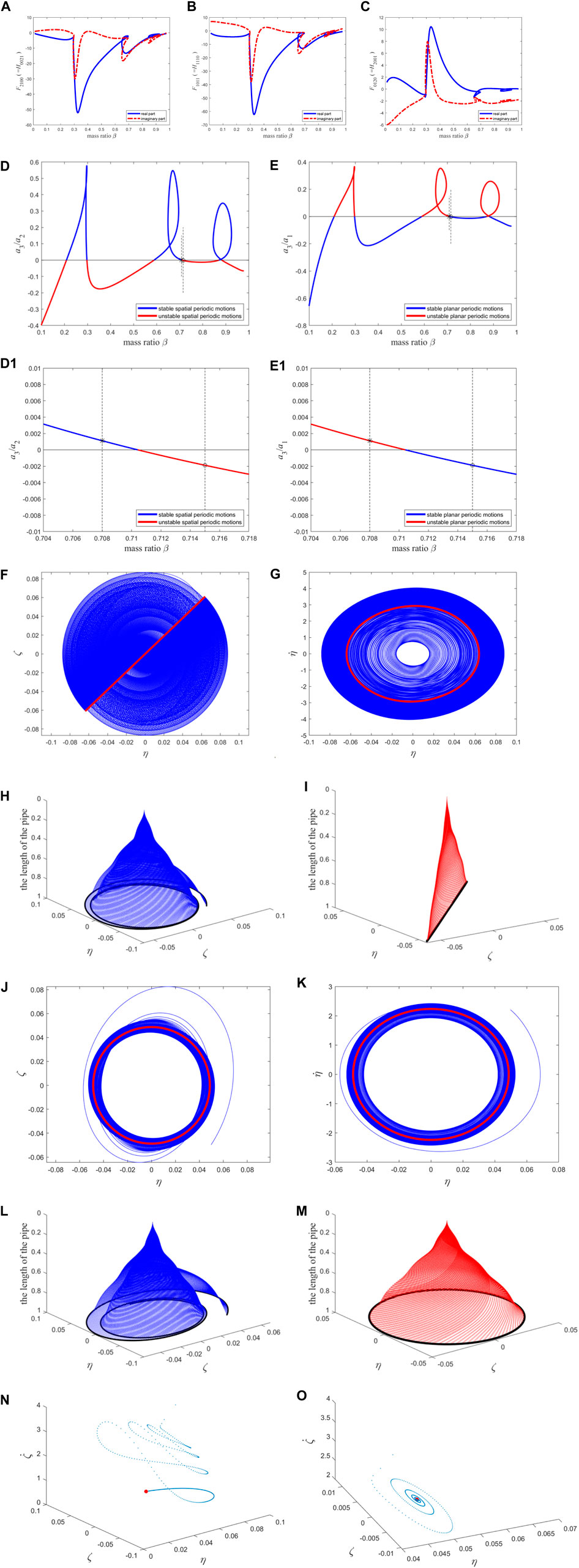
Figure 8. The resonance term coefficients of the second-order discretization equation of the macro pipe, the stability of two types of periodic motion, the phase diagram, and the configuration diagram: (A–C) The coefficients of the reduced-order equations; (D) the stability of spatial periodic motion; (E) the stability of planar periodic motion. (D1) and (E1) The enlarged version of (D) and (E) near the “*” and “o”. The interpretation of (F–I) is compared to Figures 5F–I. The interpretation of (J–M) is compared to Figures 5J–M; The Poincaré map: (N) corresponding to (F–I); (O) corresponding to (J–M). The blue points correspond to transient motion, and the red points correspond to steady-state motion (i.e., fixed point).

The results obtained when n = 13 have a minor correction to the results obtained when n = 11, as indicated by the comparison below. This study sets a mass ratio of β = 0.715 again [represented by “_O” in Figures 8D,E, and Figures 8(D1, E1) is the enlargement near the “_O”] and a flow velocity of $\upsilon =12.88+0.32=13.2$ (12.88 is the critical flow velocity corresponding to the mass ratio β = 0.715 when n = 13, and 0.32 is the increment of flow velocity) to obtain the numerical solution to Eq. 9 and then substitute it into Eq. 7, thereby obtaining Figures 8F–I. Obviously, the figure represents stable planar periodic motion, which is consistent with the infinite dimensional analysis results in [70]. Furthermore, the Poincaré map (with $\dot{\eta }=0$ as the Poincaré section) is shown in Figure 8N. The interpretations of Figures 8F–I can be compared to those of Figures 5F–I, respectively.

To compare with the results obtained when n = 15 in the following section, this study here sets the mass ratio β = 0.708 [represented by “*” in Figures 8D, E, and Figures 8(D1, E1) is the enlargement near the “*”] and the flow velocity $\upsilon =12.83+0.37=13.2$ (12.83 is the critical flow velocity corresponding to the mass ratio β = 0.708 when n = 13, and 0.37 is the increment of the flow velocity) to obtain the numerical solution of Eq. 9 and then substitute it into Eq. 7, thereby obtaining Figures 8J–M. The interpretations of Figures 8J–M can be compared to those of Figures 5J–M, respectively. The observation indicates that the 13th-order truncation at this mass ratio gives the result that “the system performs stable spatial periodic motion”. The Poincaré map (with $\dot{\eta }=0$ as the Poincaré section) is shown in Figure 8O. In contrast, the analysis below demonstrates that the 15th-order truncation at this mass ratio yields the result that “the system performs stable planar periodic motion”. Meanwhile, the infinite dimensional analysis in Ref. [70] {see Figures 12A,B in Ref. [70] or Figures 12A,B in this study} also indicates that the pipe performs stable planar periodic motion at this time.

When n = 15, Figures 9A–C shows the variation curve of the high-order term coefficient with the mass ratio, and Figures 9D, E demonstrates the stability of the two types of periodic motion.

Figure 9

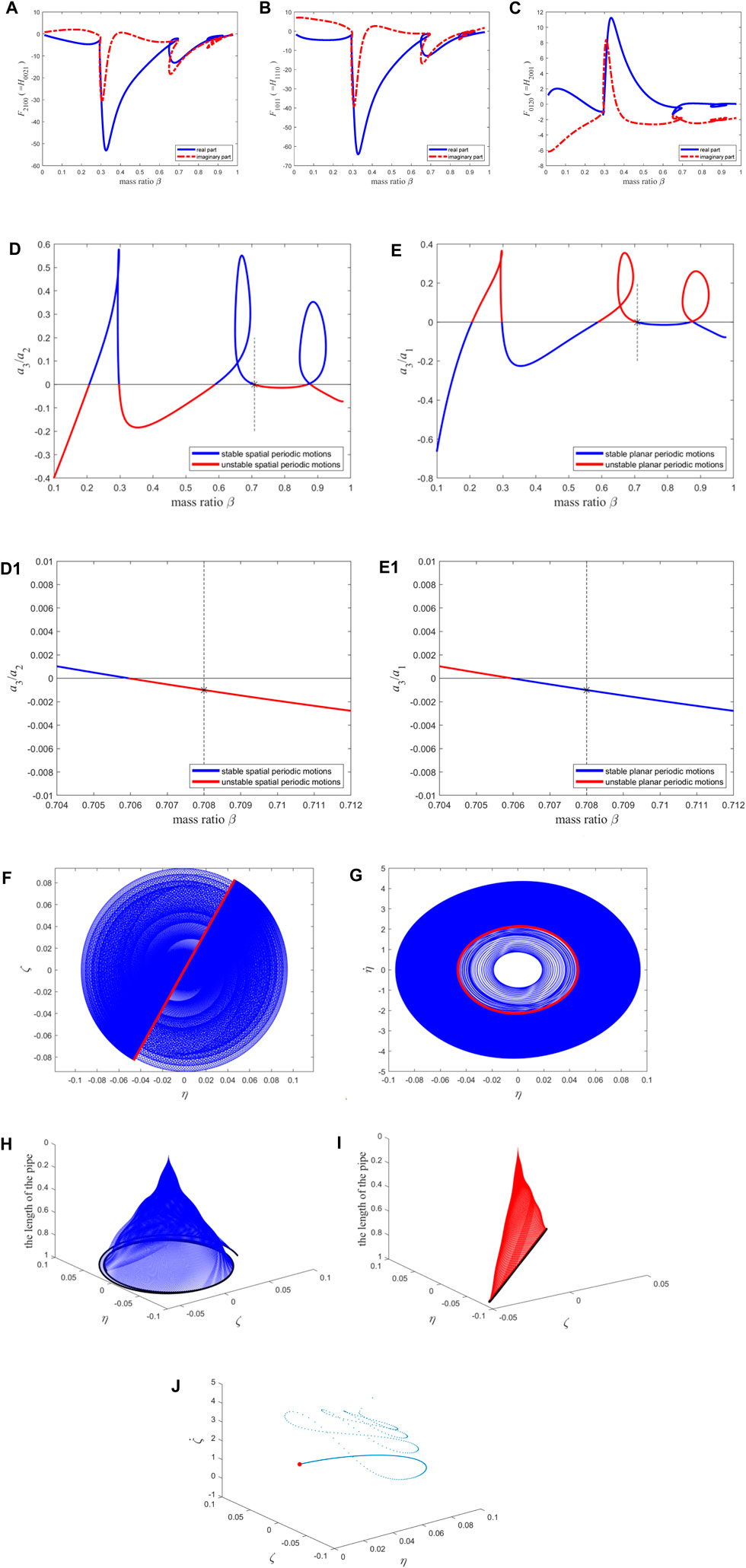
Figure 9. The resonance term coefficients of the second-order discretization equation of the macro pipe, the stability of two types of periodic motion, the phase diagram, and the configuration diagram: (A–C) The coefficients of the reduced-order equations; (D) the stability of spatial periodic motion; (E) the stability of planar periodic motion. (D1) and (E1) The enlarged version of (D) and (E) near the “*”. The interpretation of (F–I) is compared to Figures 5F–I; (J) The Poincaré map corresponding to (F–I). The blue points correspond to transient motion, and the red points correspond to steady-state motion (i.e., fixed point).

The results obtained when n = 15 have a minor correction to the results obtained when n = 13, as indicated by the following comparison. This study sets a mass ratio of β = 0.708 again [represented by “*” in Figures 9D, E, and Figures 9(D1, E1) is the enlargement near the “*”] and a flow velocity of $\upsilon =12.83+0.37=13.2$ (12.83 is the critical flow velocity corresponding to the mass ratio β = 0.708 when n = 15, and 0.37 is the increment of flow velocity) to obtain the numerical solution to Eq. 9 and then substitute it into Eq. 7, thereby obtaining Figures 9F–I. Obviously, this figure presents stable planar periodic motion, which is consistent with the infinite dimensional analysis results in Ref. [70]. Furthermore, the Poincaré map (with $\dot{\eta }=0$ as the Poincaré section) is shown in Figure 9J. The interpretations of Figures 9F–I can be compared to those of Figures 5F–I, respectively.

When n = 16, Figures 10A–C presents the variation curve of the high-order term coefficient with the mass ratio, and Figures 10D, E shows the stability of the two types of periodic motion.

Figure 10

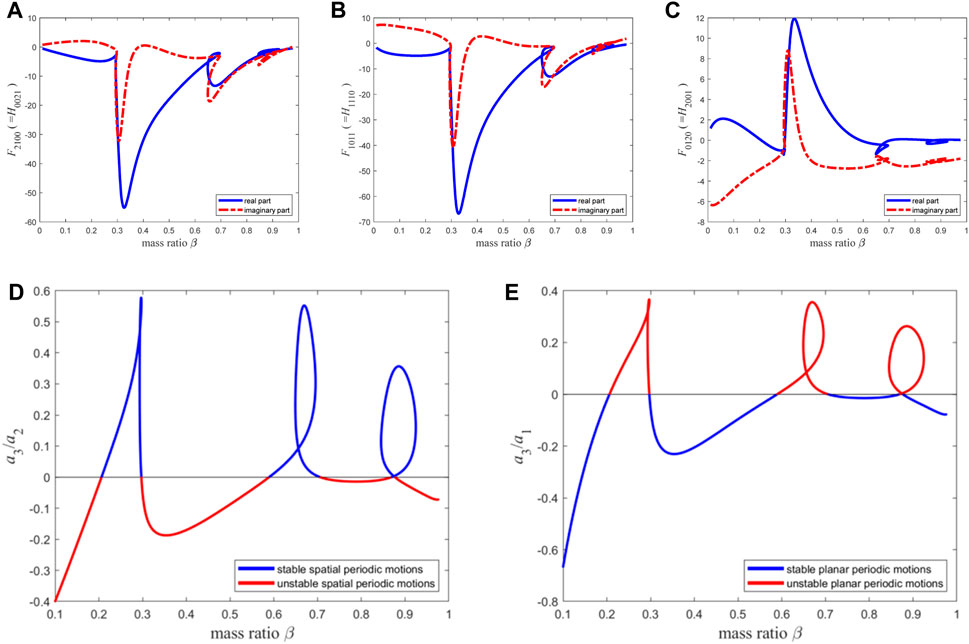
Figure 10. The resonance term coefficients of the second-order discretization equation of the macro pipe, the stability of two types of periodic motion: (A–C) The coefficients of the reduced-order equations; (D) the stability of spatial periodic motion; (E) the stability of planar periodic motion.

By comparing Figures 9D,E and Figures 10D, E, it is found that the two sets of figures are basically consistent in predicting the pipe’s periodic motion properties (as shown by Figure 11). Thus, when using the Galerkin method to investigate the qualitative dynamic behavior of this type of system, the reasonable mode truncation number should be set to 15, at which point the results have converged. Meanwhile, the results obtained at the mode truncation number of 15 are compared with those obtained based on infinite dimensional analysis in Ref. [70] (as shown in Figures 12A, B). It can be observed that in predicting the qualitative dynamic behavior of the system, the two sets of figures are also very close, and the difference lies in circles 1 to 5 and rectangles 1 to 5. Then, Figure 12(A1–A5) and Figure 12(B1–B5) are obtained by enlarging circles 1 to 5 and rectangles 1 to 5, respectively. The difference between the finite dimensional analysis results with the mode truncation number of 15 and that in Ref. [70] is represented by the black and magenta points in the figure. By calculating the distance between the black point and the magenta point in each figure in Figure 12(A1–A5), the sum of the distances is obtained as 0.0701. After conducting the same calculation for Figure 12(B1–B5), the sum of the distances is also 0.0701. Therefore, for this macro pipe, the error between the results of finite dimensional analysis and infinite dimensional analysis is only 7.01%, indicating a high level of coincidence. In the following section, for finite dimensional analysis of micro-scale pipes ($l_0=0.2$ and $l_0=0.5$), the mode truncation number is set to 15.

Figure 11

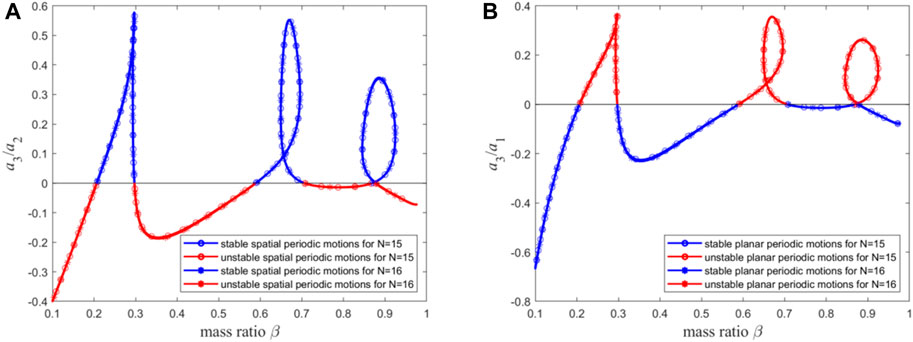
Figure 11. (A) The stability of spatial periodic motion for n = 15 and 16; (B) The stability of planar periodic motion for n = 15 and 16.

Figure 12

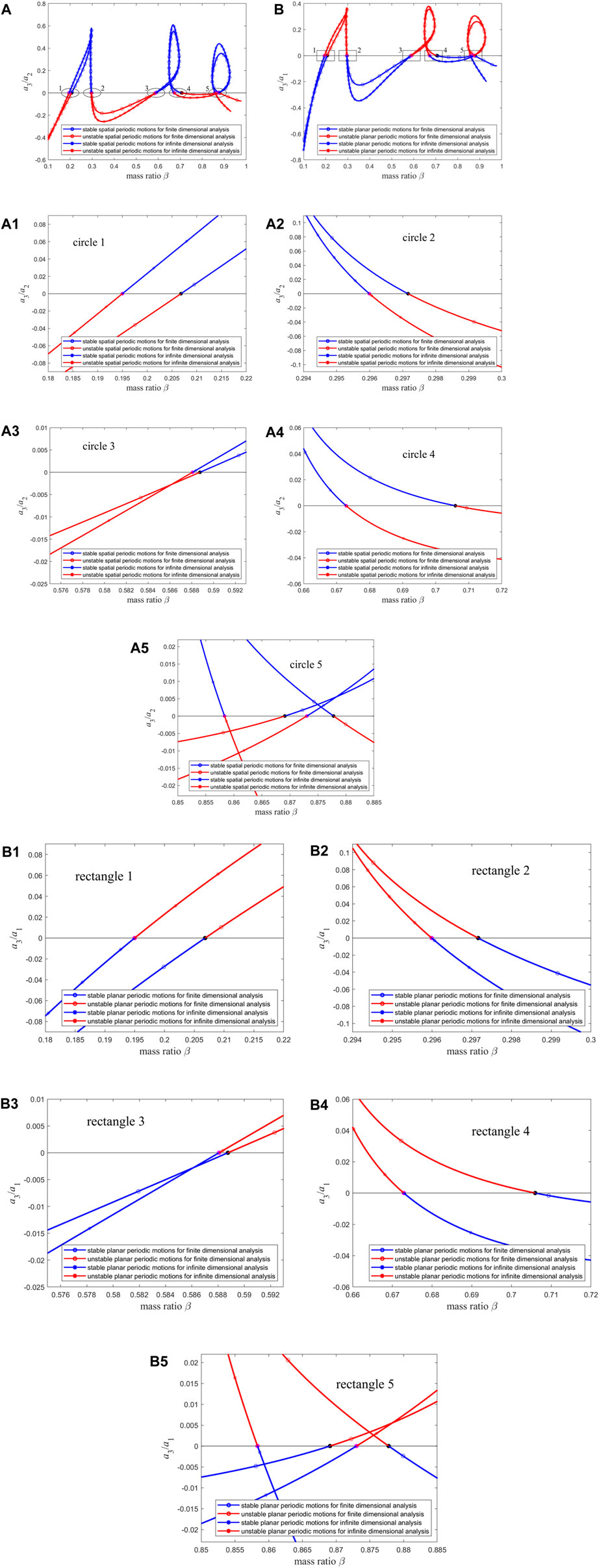
Figure 12. (A) The stability of spatial periodic motion for infinite dimensional analysis and finite dimensional analysis with n = 15; (B) The stability of planar periodic motion for infinite dimensional analysis and finite dimensional analysis with n = 15. (A1–A5) The enlarged version of circles 1 to 5 in (A); (B1–B5) The enlarged version of rectangles 1 to 5 in (B).

4.2 Case of micro-scale pipes ($l_0=0.2$ and $l_0=0.5$)

The values of characteristic length l in Eq. 6 are dependent on the materials made of pipes, which are given by [93].

$b_h^2=3\left(1-\mu \right)l^2(39)$

where μ is the Poisson’s ratio and $b_h$ is a higher-order bending parameter. For epoxy beams, $b_h$ is 24 μm [93]. For polypropylene beams, $b_h$ is 32 μm or 53.7 μm [94]. For steel or aluminum materials, $b_h\sim 10\mu \mathrm{m}$ [95]. As a matter of fact, the microscale effects of micropipes are hinged on the dimensionless material length scale parameter $l_0=\frac{A_p{l}^{2}G}{2EI}$, which encompasses not only material length scale parameter l but also involves the tension elastic modulus E, shear elastic modulus G, as well as the cross-sectional area A_p of the pipe and the moment of inertia I relative to its diameter.

When the mode truncation number is set to 15, the critical flow velocity-mass ratio curves and the critical frequencies-mass ratio curves of the two types of micro-scale pipes are illustrated in Figures 13A,C, and the variation curve regarding the change rate of the real part of the critical eigenvalue [i.e., $\alpha$ or $\text{Re}\left({\lambda }_{\epsilon }^{\prime }\right)$ in Eqs. 37, 24] with the mass ratio is presented in Figure 13B. By combining Figure 3B and Figure 4B, it can be seen that a larger $l_0$ corresponds to a larger critical flow velocity; however, $l_0$ does not affect the change rate of the real part of the critical eigenvalue.

Figure 13

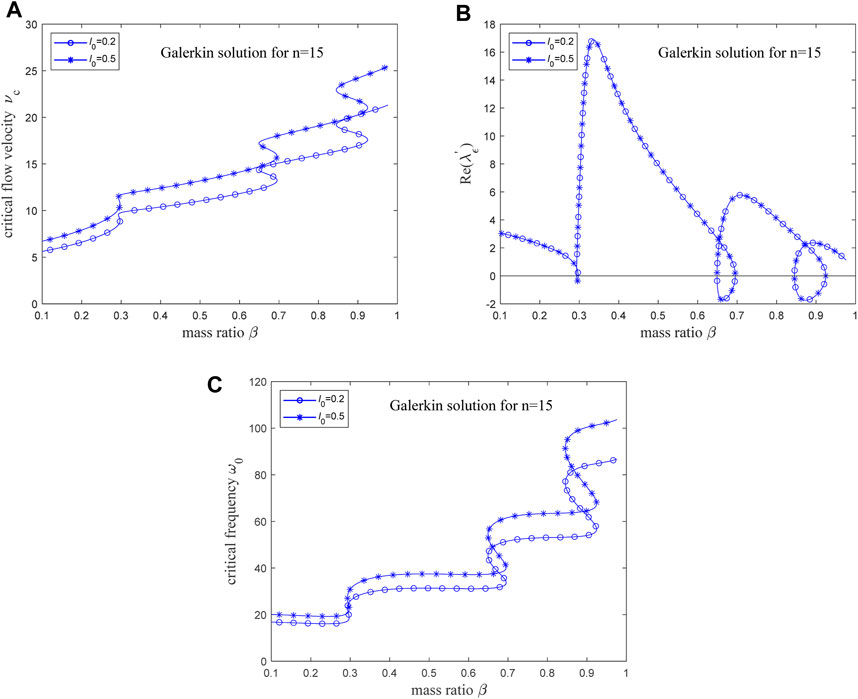
Figure 13. (A) The critical flow velocity-mass ratio curve for micro-scale pipes; (B) The rate of change of the real part of the critical eigenvalue for micro-scale pipes; (C) The critical frequencies-mass ratio curve for micro-scale pipes.

Reference [91] investigated the linear vibration characteristics of microscale cantilevered fluid-conveying pipes, in which the material and geometrical properties for micro-scale pipe constituents and fluid are taken as: l = 17.6 μm, E = 1.44 GPa, mass of pipe per unit volume ρ_p = 1000 kg/m, mass of fluid per unit volume ρ_f = 1000 kg/m, Poisson’s ration μ = 0.35, d/D = 0.8. Here, d and D are the inside and outside diameters, respectively. And then, the flutter boundaries as a function of D are shown by the red curves in Figure 14. For the aforementioned parameters, the mass ratio β = 0.64 is calculated; at D = 52.9 μm, l₀ = 0.2, and at D = 33.43 μm, l₀ = 0.5. Critical flow velocities at β = 0.64 in Figure 13A are 12.2041 and 14.5867, respectively, while in Figure 14A, the critical flow velocities for D = 52.9 μm and D = 33.43 μm are roughly 12.2041 and 14.5867; critical frequencies at β = 0.64 in Figure 13C are 31.1832和37.2710, and in Figure 14B, the critical frequencies for D = 52.9 μm and D = 33.43 μm are approximately 31.1832 and 37.2710. This demonstrates that when the model in this paper is simplified to a linear scenario, the results are consistent with those reported in the existing literature.

Figure 14

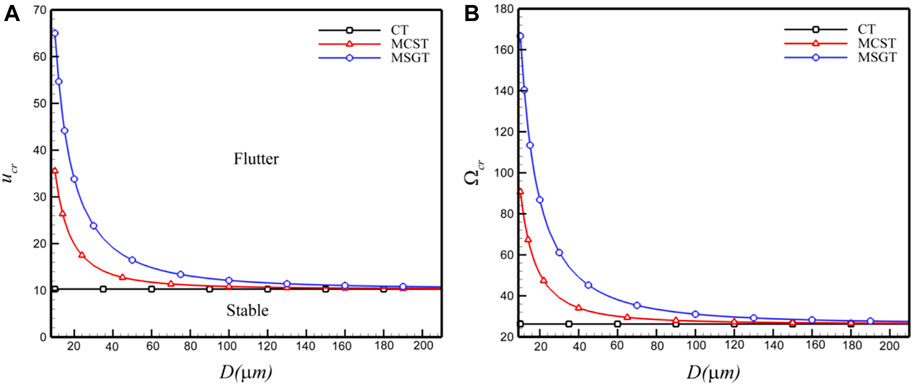
Figure 14. Flutter boundaries as a function of outside diameter D, (A) critical speed and (B) critical frequencies [91].

When the material length parameter is set to $l_0=0.2$, Figures 15A–C shows the variation curve of the high-order term coefficient with the mass ratio, and Figures 15D, E demonstrates the stability of the two types of periodic motion.

Figure 15

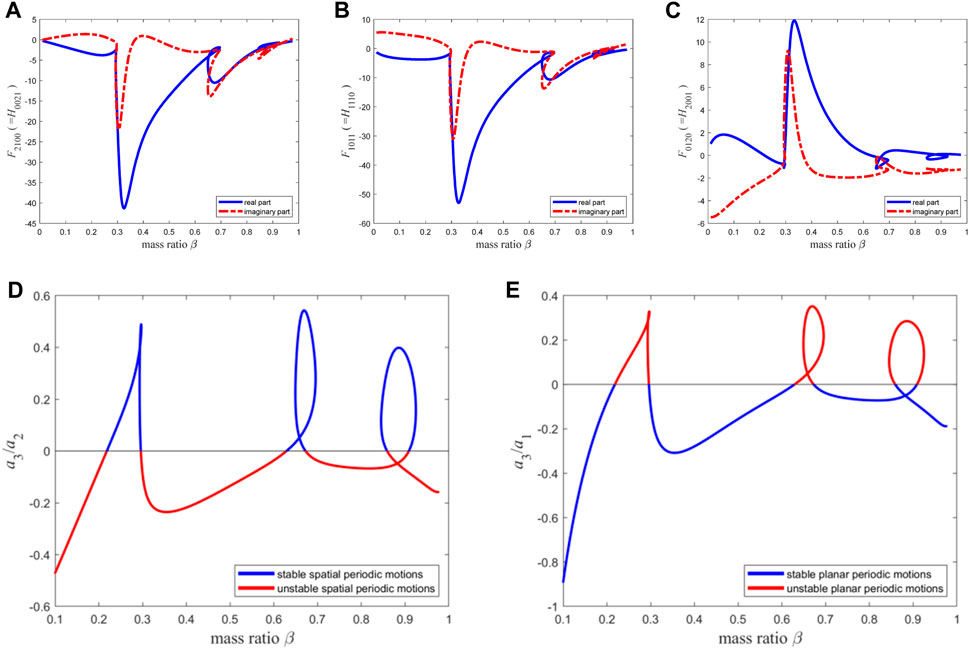
Figure 15. The resonance term coefficients of the second-order discretization equation of the micro pipe with $l_0=0.2$, the stability of two types of periodic motion: (A–C) The coefficients of the reduced-order equations; (D) the stability of spatial periodic motion; (E) the stability of planar periodic motion.

When the material length parameter is set to $l_0=0.5$, Figures 16A–C presents the variation curve of the high-order term coefficient with the mass ratio, and Figures 16D, E shows the stability of the two types of periodic motion.

Figure 16

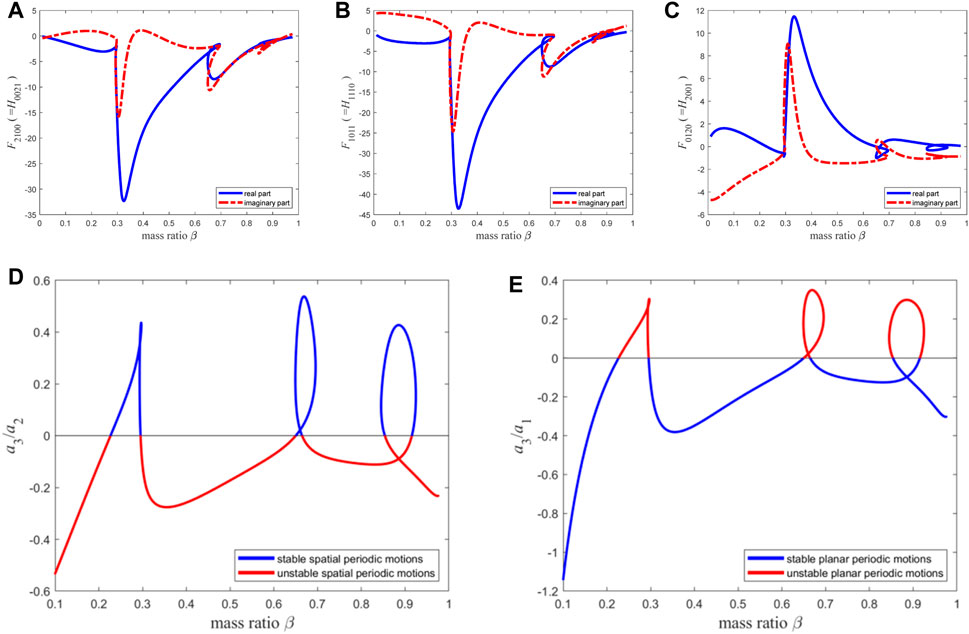
Figure 16. The resonance term coefficients of the second-order discretization equation of the micro pipe with $l_0=0.5$, the stability of two types of periodic motion: (A–C) The coefficients of the reduced-order equations; (D) the stability of spatial periodic motion; (E) the stability of planar periodic motion.

When $l_0$ is set to 0.2, the comparison between finite dimensional analysis and infinite dimensional analysis results is shown in Figures 17A, B. After calculation, the error in predicting the qualitative dynamic behavior of the pipe between the two methods is 0.0746, i.e., 7.46%. When $l_0$ is set to 0.5, the comparison between finite dimensional analysis and infinite dimensional analysis results is illustrated in Figures 17C, D. Through calculation, the error in predicting the qualitative dynamic behavior of the pipe between the two methods is 0.0669, i.e., 6.69%. For the macro pipe, the error is calculated to be 0.0701 (i.e., 7.01%), as mentioned in the previous section. Overall, whether it is a macro pipe or a micro pipe, the error between the results obtained using the mode truncation number of 15 and those obtained based on infinite dimensional analysis is very small. That is, it is reasonable to use 15 modes for Galerkin discretization.

Figure 17

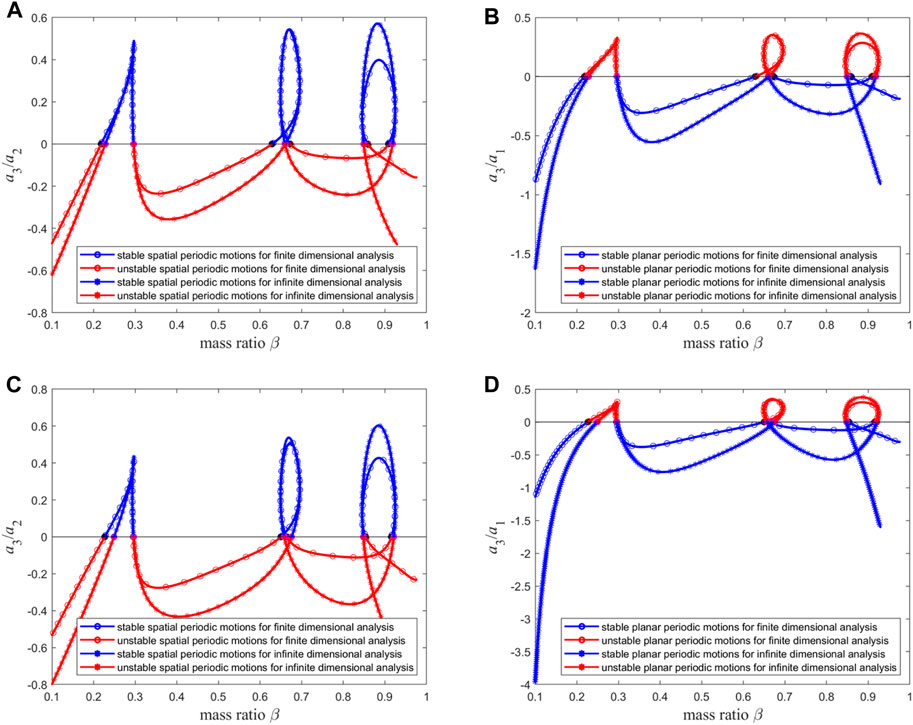
Figure 17. The stabilities of (A) spatial and (B) planar periodic motion for infinite dimensional analysis and finite dimensional analysis with n = 15 when $l_0=0.2$; The stabilities of (C) spatial and (D) planar periodic motion for infinite dimensional analysis and finite dimensional analysis with n = 15 when $l_0=0.5$.

5 Discussions

When the mode truncation number is set to 15, the stability comparison of the two types of periodic motion for $l_0$ values of 0 and 0.2 is shown in Figures 18A, B; for $l_0$ values of 0.2 and 0.5, the stability comparison of the two types of periodic motion is shown in Figures 18C, D. It can be seen that with the increase in $l_0$, the region corresponding to the stable planar periodic motion increases, and the region corresponding to the stable spatial periodic motion decreases. Meanwhile, the addition of micro-scale effects can change the stable spatial periodic motion into stable planar periodic motion, as shown by the black point in Figures 18A, B [Figures 18(A1, B1) is the enlargement near the black point]. At a mass ratio of 0.61, when $l_0$ is 0, the pipe performs stable spatial periodic motion, as shown in Figures 19A–D; at this time, the flow velocity is $\upsilon =10.07+0.33=10.4$, where 10.07 is the critical flow velocity, and 0.33 is the increment of flow velocity; the interpretation of the subfigures in Figures 19A–D can be compared to those in Figures 5J–M. The Poincaré map (with $\dot{\eta }=0$ as the Poincaré section) is shown in Figure 19I. However, when $l_0$ is 0.2, the pipe performs stable planar periodic motion, as shown in Figures 19E–H; at this time, the flow velocity is $\upsilon =11.915+0.285=12.2$, where 11.915 is the critical flow velocity, and 0.285 is the increment of flow velocity; the interpretation of the subfigures in Figures 19E–H can be compared to those in Figures 5F–I. The Poincaré map (with $\dot{\eta }=0$ as the Poincaré section) is shown in Figure 19J. This is consistent with the results of the infinite dimensional analysis in Ref. [70].

Figure 18

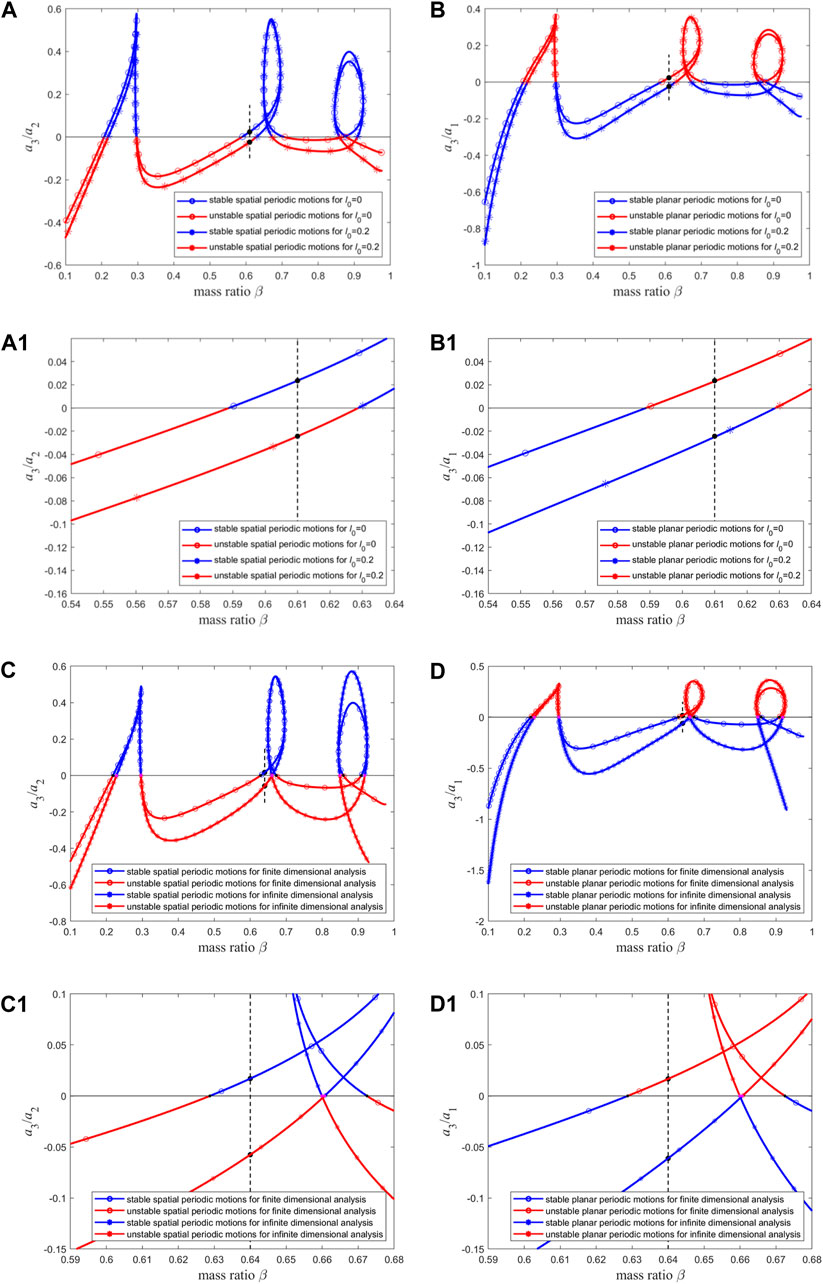
Figure 18. The stabilities of (A) spatial and (B) planar periodic motion for macro pipe (i.e., $l_0=0$) and micro pipe with $l_0=0.2$; The stabilities of (C) spatial and (D) planar periodic motion for infinite dimensional analysis and finite dimensional analysis with n = 15 when $l_0=0.2$. (A1) and (B1) The enlarged version of (A) and (B) near the black point; (C1) and (D1) The enlarged version of (C) and (D) near the black point.

Figure 19

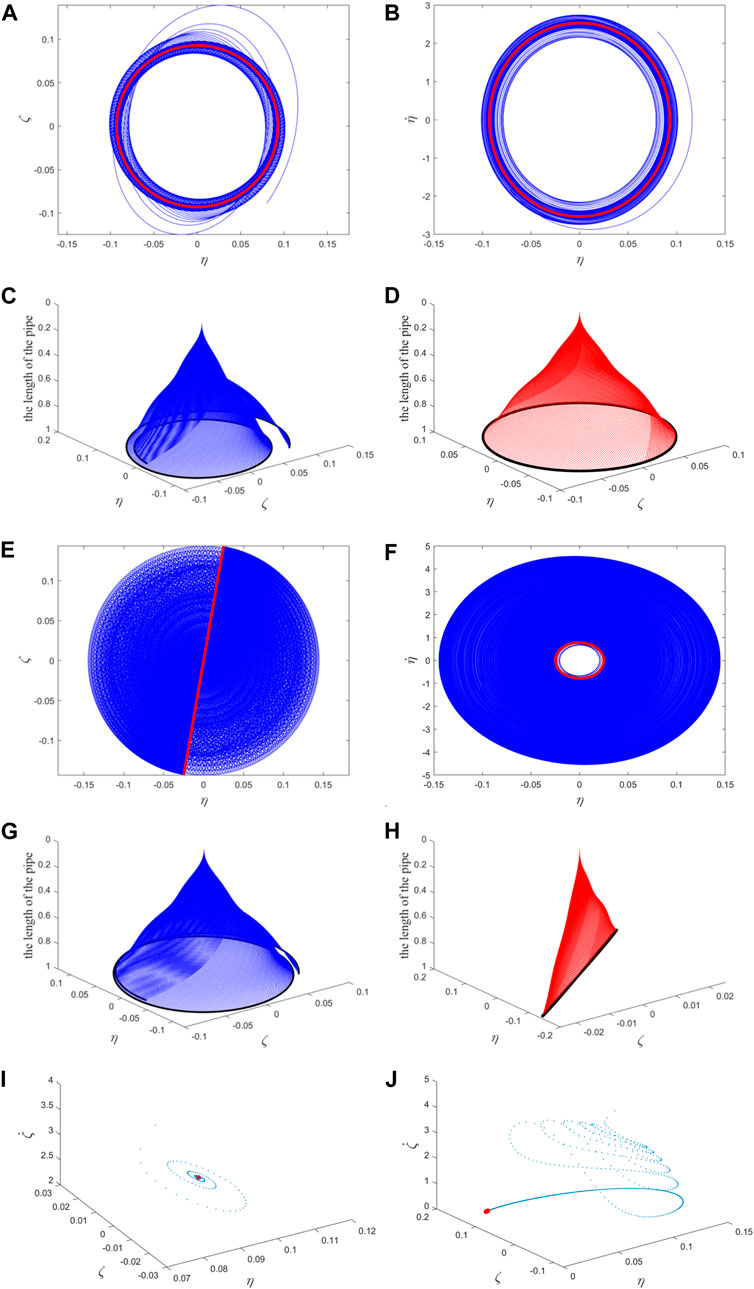
Figure 19. (A) and (E) the position relationship of the free ends of the pipe in two directions; (B) and (F) the velocity-displacement relationship diagram of the free ends of the pipe in one direction; (C) and (G) the transient process of the whole pipe vibration; (D) and (H) the steady-state vibration of the whole pipe. The blue (red) color represents the transient (steady-state) motion in (A–H); The Poincaré map: (I) corresponding to (A–D); (J) corresponding to (E–H). The blue points correspond to transient motion, and the red points correspond to steady-state motion (i.e., fixed point).

According to Eq. 4a, the dimensionless material length scale parameter l₀ is positively correlated with the bending stiffness of pipe, which implies that a larger l₀ leads to a higher bending stiffness. As shown in Figure 3B, Figure 13A, Figure 3D and Figure 13C larger l₀ leads to higher critical flow velocities and frequencies. In summary, a larger bending stiffness leads to higher critical flow velocities and critical frequencies, and makes it more likely for the pipe to exhibit stable planar periodic motion after losing stability.

For the truncated mode numbers n = 9 and n = 11, as shown in Figure 3D, the critical frequencies corresponding to β = 0.725 all are 44.2565. When a small increase in flow velocity causes vibrations as shown in Figures 5J–M, the actual frequency is 45.4974, close to the critical frequency. When a small increase in flow velocity causes vibrations shown in Figures 7F–I, the actual frequency is 45.3660, also close to the critical frequency. This indicates that the vibration frequencies in both Figures 7F–I and Figures 5J–M are near the critical frequency, yet their motion forms differ due to different numbers of mode truncation.

For the truncated mode numbers n = 11 and n = 13, as shown in Figure 3D, the critical frequencies corresponding to β = 0.715 all are 44.0148. When a small increase in flow velocity causes vibrations as shown in Figures 7J–M, the actual frequency is 45.7292, close to the critical frequency. When a small increase in flow velocity causes vibrations shown in Figures 8F–I, the actual frequency is 45.5303, also close to the critical frequency. This indicates that the vibration frequencies in both Figures 8F–I and Figures 7J–M are near the critical frequency, yet their motion forms differ due to different numbers of mode truncation.

For the truncated mode numbers n = 13 and n = 15, as shown in Figure 3D, the critical frequencies corresponding to β = 0.708 all are 43.8340. When a small increase in flow velocity causes vibrations as shown in Figures 8J–M, the actual frequency is 45.8627, close to the critical frequency. When a small increase in flow velocity causes vibrations shown in Figures 9F–I, the actual frequency is 45.6627, also close to the critical frequency. This indicates that the vibration frequencies in both Figures 9F–I and Figures 8J–M are near the critical frequency, yet their motion forms differ due to different numbers of mode truncation.

This paper demonstrates that for a wide range of mass ratio β, the spatial flexural vibrations of the fluid-conveying pipe shown in Figure 1 can be precisely described by the Galerkin discretized ordinary differential equations set of 15 truncated mode numbers. These ordinary differential equations are obtained by discretizing the original motions equations Eq. 4 by using the first 15 mode functions of a cantilever beam, effectively capturing the pipe’s dynamic properties, including critical flow velocity, frequency, amplitude, and motion form. Notably, the types of periodic motion of the pipe (including planar and spatial periodic motions) and their stability can be determined from the coefficients of the Galerkin discretized equations, specifically Eqs 10 and 23, 24, 25, 26, 28, 29, 37. Accurate prediction of the motion form assists in adopting appropriate vibration control measures, whether for stable planar or spatial periodic motions. For instance, stable planar periodic motion may be managed by integrating an energy sink within a specific plane, while managing a stable spatial periodic motion may necessitate the addition of energy sinks encircling the pipe. The projection method used in this paper (based on the Center Manifold-Normal Form Theory) can also be applied to other types of fluid-conveying pipe models, such as those without O (2) symmetry in their cross-sections. However, in such cases, the calculations of the center manifold and reduced-order equations become extremely complex due to the inability to apply ‘symmetry’ to simplifying, it is a matter that the author will seriously consider in future research.

The presence of errors between finite dimensional analysis and infinite dimensional analysis results is proven by taking the mass ratio β = 0.64 and $l_0=0.2$ as an example. According to the finite dimensional analysis {see the higher black points in Figures 18C, D [Figures 18(C1, D1) is the enlargement near the black point]}, the pipe performs stable spatial periodic motion, as shown in Figures 20A–D. Here, the flow velocity is $\upsilon =12.205+0.295=12.5$ (12.205 is the critical flow velocity, and 0.295 is the increment of flow velocity). The interpretation of the subfigures in Figures 20A–D can be compared to those in Figures 5J–M. The Poincaré map (with $\dot{\eta }=0$ as the Poincaré section) is shown in Figure 20E. However, according to infinite dimensional analysis {see Figures 13, 14 in Ref. [70] or Figure 17 and the lower black points in Figures 18C, D [Figure 18(C1, D1) is the enlargement near the black point] in this study}, stable planar periodic motion occurs here. Thus, there is an error between finite dimensional analysis and infinite dimensional analysis results, and how to reconcile this error is an open question.

Figure 20

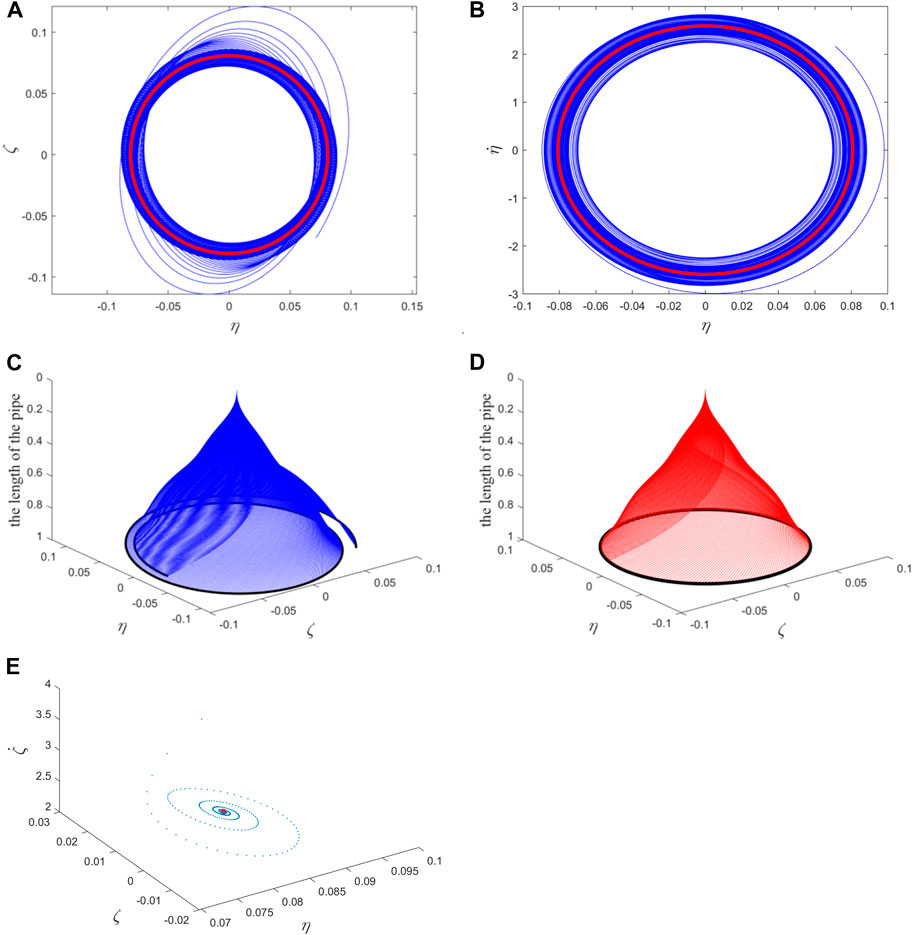
Figure 20. (A) The position relationship of the free ends of the pipe in two directions; (B) the velocity-displacement relationship diagram of the free ends of the pipe in one direction; (C) the transient process of the whole pipe vibration; (D) the steady-state vibration of the whole pipe. The blue (red) color represents the transient (steady-state) motion in (A–D); (E) The Poincaré map corresponding to (A–D). The blue points correspond to transient motion, and the red points correspond to steady-state motion (i.e., fixed point).

Galerkin method is also suitable for motions equations with large nonlinear terms, even though the flow velocity is far away from the instability threshold. Generally, more truncated mode numbers produce more accurate results. However, the center manifold theory and normal form method are applicable only close to the bifurcation point, i.e., for flow velocity not far away from the critical value. This is the limitation of the present reduced two-degree-of-freedom model. When the flow velocity is gradually increased beyond the instability threshold, the types, stabilities, and bifurcations of periodic motions of fluid-conveying cantilevered micropipes, e.g., the occurrence of torus motions or chaos, are still some of the open questions.

In practical applications, two considerations are proposed. Firstly, if the actual pipe model closely resembles that shown in Figure 1, then based on the specific mass ratio β and l₀, Eqs 10 and 23, 24, 25, 26, 28, 29, 37 can be calculated to determine the type of motion that the pipe will undergo after instability, either stable planar or spatial periodic motion, thereby selecting appropriate control strategies. Additionally, adjustments to the values of β and l₀ can facilitate these two types of motion for the pipe. Secondly, if the actual pipe model differs from that in Figure 1, the numbers of mode truncation n when using Galerkin method should be 15 or more to ensure the convergence of dynamic properties such as critical flow velocity, frequency, amplitude, and motion form.

6 Conclusion

In this study, by using the Galerkin method, the spatial vibration Eq. 4 of the macro- and micro-scale cantilevered fluid-conveying pipe is discretized into a system of ordinary differential Eq. 9. Meanwhile, the reduced-order Eq. 23 of the system of ordinary differential equations and associated coefficients (24) and (25) are calculated with the projection method. Based on this, two types of periodic motion and their stability within the system are investigated. The results of various mode truncation numbers are compared longitudinally and transversely with infinite dimensional analysis results by setting the modal truncation number incrementally. The following conclusions are obtained.

(1) For the linear vibration characteristics of pipes, which includes the critical flow velocity, the critical frequency and the change rate of the real part of the critical eigenvalue, the 9-mode Galerkin discretization equations can obtain results relatively close to those of the infinite dimensional analysis. As shown by Figure 3 and Figure 4. However, the 9-mode Galerkin discretization equations cannot give convergent results for the nonlinear vibration characteristics of pipes.

(2) As the mode truncation number n continues to increase, the results about the nonlinear vibration characteristics of pipes (i.e., the planar and spatial periodic motions) obtained when n = 11 have a minor correction to the results obtained when n = 9; there are similar minor corrections for the results of n = 13 to those of n = 11, results of n = 15 to those of n = 13, until the results of n = 16 are almost the same as those of n = 15. That is, when n = 15, the result converges, so this is a reasonable mode truncation number.

(3) With a mode truncation number of 15, the differences between the results of the finite dimensional and infinite dimensional analysis are calculated for macro- ($l_0=0$) and micro-scale pipes ($l_0$ = 0.2 and 0.5), respectively. It is found that the errors are 7.01%, 7.46%, and 6.69%, respectively, indicating a very small difference. This further verifies that the reasonable mode truncation number is 15. How to properly deal with these sources of error remains an open question.

Data availability statement

The original contributions presented in the study are included in the article/supplementary material, further inquiries can be directed to the corresponding author.

Author contributions

YG: Writing–original draft, Writing–review and editing, Writing–original draft, Writing–review and editing.

Funding

The author(s) declare that financial support was received for the research, authorship, and/or publication of this article. The supports from the National Natural Science Foundation of China (No, 12002096) and the 2022 Doctoral Foundation of Anshun University (No, asxybsjj202201) are acknowledged.

Conflict of interest

The author declares that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

1. Benjamin TB. Dynamics of a system of articulated pipes conveying fluid: I. Theory. Proc R Soc Lond Ser A, Math Phys Sci (1961) 261:457–86.

Google Scholar

2. Gregory RW, Païdoussis MP. Unstable oscillation of tubular cantilevers conveying fluid I. Theory. Proc R Soc Lond Ser A. Math Phys Sci (1966) 293:512–27. doi:10.1098/rspa.1966.0187

CrossRef Full Text | Google Scholar

3. Chen SS. Forced vibration of a cantilevered tube conveying fluid. The J Acoust Soc America (1970) 48:773–5. doi:10.1121/1.1912205

CrossRef Full Text | Google Scholar

4. Ginsberg JH. The dynamic stability of a pipe conveying a pulsating flow. Int J Eng Sci (1973) 11:1013–24.

CrossRef Full Text | Google Scholar

5. Païdoussis MP, Issid NT. Dynamic stability of pipes conveying fluid. J Sound Vibration (1974) 33:267–94. doi:10.1016/s0022-460x(74)80002-7

CrossRef Full Text | Google Scholar

6. Holmes PJ. Bifurcations to divergence and flutter in flow-induced oscillations: a finite dimensional analysis. J Sound Vibration (1977) 53:471–503. doi:10.1016/0022-460x(77)90521-1

CrossRef Full Text | Google Scholar

7. Holmes PJ. Pipes supported at both ends cannot flutter. J Appl Mech (1978) 45:619–22. doi:10.1115/1.3424371

CrossRef Full Text | Google Scholar

8. Holmes P, Marsden J. Bifurcation to Divergence and flutter in flow-induced oscillations: an infinite dimensional analysis. Automatica (1978) 14:367–84. doi:10.1016/0005-1098(78)90036-5

CrossRef Full Text | Google Scholar

9. Rousselet J, Herrmann G. Dynamic behavior of continuous cantilevered pipes conveying fluid near critical velocities. J Appl Mech (1981) 48:943–7. doi:10.1115/1.3157760

CrossRef Full Text | Google Scholar

10. Namchchivaya NS, Tien WM. Non-linear dynamics of supported pipe conveying pulsating fluid-II. Combination resonance. Int J Non-linear Mech (1989) 24:197–208. doi:10.1016/0020-7462(89)90038-3

CrossRef Full Text | Google Scholar

11. Jayaraman K, Narayaman S. Chaotic oscillations in pipes conveying pulsating fluid. Nonlinear Dyn (1996) 10:333–57.

CrossRef Full Text | Google Scholar

12. Namchchivaya NS. Non-linear dynamics of supported pipe conveying pulsating fluid-I. Subharmonic resonance. Int J Non-linear Mech (1989) 24:185–96.

CrossRef Full Text | Google Scholar

13. Chang CO, Chen KC. Dynamics and stability of pipes conveying fluid. J Press Vessel Technol (1994) 116:57–66. doi:10.1115/1.2929559

CrossRef Full Text | Google Scholar

14. Li GX, Païdoussis MP. Stability, double degeneracy and chaos in cantilevered pipes conveying fluid. Int J Non-Linear Mech (1994) 29:83–107. doi:10.1016/0020-7462(94)90054-x

CrossRef Full Text | Google Scholar

15. Païdoussis MP, Li GX, Moon FC. Chaotic oscillations of the autonomous system of a constrained pipe conveying fluid. J Sound Vibration (1989) 135:1–19. doi:10.1016/0022-460x(89)90750-5

CrossRef Full Text | Google Scholar

16. Païdoussis MP, Semler C. Nonlinear and chaotic oscillations of a constrained cantilevered pipe conveying fluid: a full nonlinear analysis. Nonlinear Dyn (1993) 4:655–70.

Google Scholar

17. Jin JD. Stability and chaotic motions of a restrained pipe conveying fluid. J Sound Vibration (1997) 208:427–39. doi:10.1006/jsvi.1997.1195

CrossRef Full Text | Google Scholar

18. Paidoussis MP, Semler C. Nonlinear dynamics of a fluid-conveying cantilevered pipe with an intermediate spring support. J Fluids Structures (1993) 7:269–98.

Google Scholar

19. Païdoussis MP, Semler C. Nonlinear analysis of the parametric resonances of a planar fluid-conveying cantilevered pipe. J Fluids Structures (1996) 10:787–825. doi:10.1006/jfls.1996.0053

CrossRef Full Text | Google Scholar

20. Jin JD, Zou GS. Bifurcations and chaotic motions in the autonomous system of a restrained pipe conveying fluid. J Sound Vibration (2003) 260:783–805. doi:10.1016/s0022-460x(02)00982-3

CrossRef Full Text | Google Scholar

21. Jin JD, Song ZY. Parametric resonances of supported pipes conveying pulsating fluid. J Fluids Structures (2005) 20:763–83. doi:10.1016/j.jfluidstructs.2005.04.007

CrossRef Full Text | Google Scholar

22. Szabό Z. Nonlinear analysis of a cantilever pipe containing pulsatile flow. Meccanica (2003) 38:161–72.

Google Scholar

23. Nikolić M, Rajković M. Bifurcations in nonlinear models of fluid-conveying pipes supported at both ends. J Fluids Structures (2006) 22:173–95. doi:10.1016/j.jfluidstructs.2005.09.009

CrossRef Full Text | Google Scholar

24. Wadham-Gagnon M, Païdoussis MP, Semler C. Dynamics of cantilevered pipes conveying fluid. Part 1: nonlinear equations of three-dimensional motion. J Fluids Structures (2007) 23:545–67. doi:10.1016/j.jfluidstructs.2006.10.006

CrossRef Full Text | Google Scholar

25. Lundgren TS, Sethna PR, Bajaj AK. Stability boundaries for flow induced motions of tubes with an inclined terminal nozzle. J Sound Vibration (1979) 64:553–71. doi:10.1016/0022-460x(79)90804-6

CrossRef Full Text | Google Scholar

26. Modarres-Sadeghi Y, Païdoussis MP, Semler C. Three-dimensional oscillations of a cantilever pipe conveying fluid. Int J Non-Linear Mech (2008) 43:18–25. doi:10.1016/j.ijnonlinmec.2007.09.005

CrossRef Full Text | Google Scholar

27. Païdoussis MP, Semler C, Wadham-Gagnon M, Saaid S. Dynamics of cantilevered pipes conveying fluid. Part 2: dynamics of the system with intermediate spring support. J Fluids Structures (2007) 23:569–87. doi:10.1016/j.jfluidstructs.2006.10.009

CrossRef Full Text | Google Scholar

28. Modarres-Sadeghi Y, Semler C, Wadham-Gagnon M, Païdoussis MP. Dynamics of cantilevered pipes conveying fluid. Part 3: three-dimensional dynamics in the presence of an end-mass. J Fluids Structures (2007) 23:589–603. doi:10.1016/j.jfluidstructs.2006.10.007

CrossRef Full Text | Google Scholar

29. Ghayesh MH, Païdoussis MP, Modarres-Sadeghi Y. Three-dimensional dynamics of a fluid-conveying cantilevered pipe fitted with an additional spring-support and an end-mass. J Sound Vibration (2011) 330:2869–99. doi:10.1016/j.jsv.2010.12.023

CrossRef Full Text | Google Scholar

30. Ghayesh MH, Païdoussis MP. Three-dimensional dynamics of a cantilevered pipe conveying fluid, additionally supported by an intermediate spring array. Int J Non-Linear Mech (2010) 45:507–24. doi:10.1016/j.ijnonlinmec.2010.02.001

CrossRef Full Text | Google Scholar

31. Modarres-Sadeghi Y, Païdoussis MP. Chaotic oscillations of long pipes conveying fluid in the presence of a large end-mass. Comput Structures (2013) 122:192–201. doi:10.1016/j.compstruc.2013.02.005

CrossRef Full Text | Google Scholar

32. Chang GH, Modarres-Sadeghi Y. Flow-induced oscillations of a cantilevered pipe conveying fluid with base excitation. J Sound Vibration (2014) 333:4265–80. doi:10.1016/j.jsv.2014.03.036

CrossRef Full Text | Google Scholar

33. Alsaud H, Alshehri MH. Continuum modeling for lithium storage inside nanotubes. Front Phys (2023) 11. doi:10.3389/fphy.2023.1221720

CrossRef Full Text | Google Scholar

34. Yun C, Wu Y, Liang Z, Yang W, Du H, Liu S, et al. Magnetic anisotropy-controlled vortex nano-oscillator for neuromorphic computing. Front Phys (2022) 10. doi:10.3389/fphy.2022.1019881

CrossRef Full Text | Google Scholar

35. Wang Y, Zhang X, Zhou T, Zhu Y, Cui Z, Zhang K. Properties and sensing performance of THz metasurface based on carbon nanotube and microfluidic channel. Front Phys (2021) 9. doi:10.3389/fphy.2021.749501

CrossRef Full Text | Google Scholar

36. Shephard JD, Urich A, Carter RM, Jaworski P, Maier RRJ, Belardi W, et al. Silica hollow core microstructured fibers for beam delivery in industrial and medical applications. Front Phys (2015) 3. doi:10.3389/fphy.2015.00024

CrossRef Full Text | Google Scholar

37. Tadi Beni Y, Karimipour I, Abadyan M. Modeling the instability of electrostatic nano-bridges and nano-cantilevers using modified strain gradient theory. Appl Math Model (2015) 39:2633–48. doi:10.1016/j.apm.2014.11.011

CrossRef Full Text | Google Scholar

38. Arefi M, Zenkour AM. Influence of micro-length-scale parameters and inhomogeneities on the bending, free vibration and wave propagation analyses of a FG Timoshenko’s sandwich piezoelectric microbeam. J Sandwich Structures Mater (2017) 21:1243–70. doi:10.1177/1099636217714181

CrossRef Full Text | Google Scholar

39. Arefi M, Zenkour AM. Transient analysis of a three-layer microbeam subjected to electric potential. Int J Smart Nano Mater (2017) 8:20–40. doi:10.1080/19475411.2017.1292967

CrossRef Full Text | Google Scholar

40. Yayli MÖ. Buckling analysis of a microbeam embedded in an elastic medium with deformable boundary conditions. Micro Nano Lett (2016) 11:741–5. doi:10.1049/mnl.2016.0257

CrossRef Full Text | Google Scholar

41. Karimipour I, Tadi Beni Y, Akbarzadeh AH. Modified couple stress theory for three-dimensional elasticity in curvilinear coordinate system: application to micro torus panels. Meccanica (2020) 55:2033–73. doi:10.1007/s11012-020-01220-3

CrossRef Full Text | Google Scholar

42. Arefi M, Moghaddam SK, Bidgoli EM-R, Kiani M, Civalek O. Analysis of graphene nanoplatelet reinforced cylindrical shell subjected to thermo-mechanical loads. Compos Structures (2021) 255:112924. doi:10.1016/j.compstruct.2020.112924

CrossRef Full Text | Google Scholar

43. Heidari Y, Arefi M, Irani Rahaghi M. Nonlocal vibration characteristics of a functionally graded porous cylindrical nanoshell integrated with arbitrary arrays of piezoelectric elements. Mech Based Des Structures Machines (2020) 50:4246–73. doi:10.1080/15397734.2020.1830799

CrossRef Full Text | Google Scholar

44. Mohammadi M, Arefi M, Dimitri R, Tornabene F. Higher-order thermo-elastic analysis of FG-CNTRC cylindrical vessels surrounded by a pasternak foundation. Nanomaterials (2019) 9:79. doi:10.3390/nano9010079

PubMed Abstract | CrossRef Full Text | Google Scholar

45. Zeighampour H, Beni YT, Karimipour I. Wave propagation in double-walled carbon nanotube conveying fluid considering slip boundary condition and shell model based on nonlocal strain gradient theory. Microfluidics and Nanofluidics (2017) 21:85. doi:10.1007/s10404-017-1918-3

CrossRef Full Text | Google Scholar

46. Yang T-Z, Ji Sd., Yang X-D, Fang B. Microfluid-induced nonlinear free vibration of microtubes. Int J Eng Sci (2014) 76:47–55. doi:10.1016/j.ijengsci.2013.11.014

CrossRef Full Text | Google Scholar

47. Dai HL, Wang L, Abdelkefi A, Ni Q. On nonlinear behavior and buckling of fluid-transporting nanotubes. Int J Eng Sci (2015) 87:13–22. doi:10.1016/j.ijengsci.2014.11.005

CrossRef Full Text | Google Scholar

48. Bahaadini R, Hosseini M. Nonlocal divergence and flutter instability analysis of embedded fluid-conveying carbon nanotube under magnetic field. Microfluidics and Nanofluidics (2016) 20:108. doi:10.1007/s10404-016-1773-7

CrossRef Full Text | Google Scholar

49. Bahaadini R, Hosseini M. Effects of nonlocal elasticity and slip condition on vibration and stability analysis of viscoelastic cantilever carbon nanotubes conveying fluid. Comput Mater Sci (2016) 114:151–9. doi:10.1016/j.commatsci.2015.12.027

CrossRef Full Text | Google Scholar

50. Hu K, Wang YK, Dai HL, Wang L, Qian Q. Nonlinear and chaotic vibrations of cantilevered micropipes conveying fluid based on modified couple stress theory. Int J Eng Sci (2016) 105:93–107. doi:10.1016/j.ijengsci.2016.04.014

CrossRef Full Text | Google Scholar

51. Dai H-L, Wu P, Wang L. Nonlinear dynamic responses of electrostatically actuated microcantilevers containing internal fluid flow. Microfluidics and Nanofluidics (2017) 21:162. doi:10.1007/s10404-017-1999-z

CrossRef Full Text | Google Scholar

52. Ghayesh MH, Farokhi H, Farajpour A. Chaotic oscillations of viscoelastic microtubes conveying pulsatile fluid. Microfluidics and Nanofluidics (2018) 22:72. doi:10.1007/s10404-018-2091-z

CrossRef Full Text | Google Scholar

53. Zhu B, Chen X, Dong Y, Li Y. Stability analysis of cantilever carbon nanotubes subjected to partially distributed tangential force and viscoelastic foundation. Appl Math Model (2019) 73:190–209. doi:10.1016/j.apm.2019.04.018

CrossRef Full Text | Google Scholar

54. Sarparast H, Alibeigloo A, Kesari SS, Esfahani S. Size-dependent dynamical analysis of spinning nanotubes conveying magnetic nanoflow considering surface and environmental effects. Appl Math Model (2022) 108:92–121. doi:10.1016/j.apm.2022.03.017

CrossRef Full Text | Google Scholar

55. Bajaj AK, Sethna PR, Lundgren TS. Hopf bifurcation phenomena in tubes carrying a fluid. Soc Ind Appl Maths (1980) 39:213–30. doi:10.1137/0139019

CrossRef Full Text | Google Scholar

56. Bajaj AK. Bifurcations in a parametrically excited non-linear oscillator. Int J Non-Linear Mech (1987) 22:47–59. doi:10.1016/0020-7462(87)90048-5

CrossRef Full Text | Google Scholar

57. Bajaj AK, Sethna PR. Flow induced bifurcations to three-dimensional oscillatory motions in continuous tubes, Society for Industrial and Applied Mathematics. J Appl Maths (1984) 44:270–86.

CrossRef Full Text | Google Scholar

58. Bajaj AK, Sethna PR. Effect of symmetry-breaking perturbations on flow-induced oscillations in tubes. J Fluids Structures (1991) 5:651–79. doi:10.1016/0889-9746(91)90344-o

CrossRef Full Text | Google Scholar

59. Folley CN, Bajaj AK. Spatial nonlinear dynamics near principal parametric resonance for a fluid-conveying cantilever pipe. J Fluids Structures (2005) 21:459–84. doi:10.1016/j.jfluidstructs.2005.08.014

CrossRef Full Text | Google Scholar

60. Yamashita K, Yagyu T, Yabuno H. Nonlinear interactions between unstable oscillatory modes in a cantilevered pipe conveying fluid. Nonlinear Dyn (2019) 98:2927–38. doi:10.1007/s11071-019-05236-7

CrossRef Full Text | Google Scholar

61. Yamashita K, Nishiyama N, Katsura K, Yabuno H. Hopf-Hopf interactions in a spring-supported pipe conveying fluid. Mech Syst Signal Process (2021) 152:107390. doi:10.1016/j.ymssp.2020.107390

CrossRef Full Text | Google Scholar

62. Yamashita K, Kitaura K, Nishiyama N, Yabuno H. Non-planar motions due to nonlinear interactions between unstable oscillatory modes in a cantilevered pipe conveying fluid. Mech Syst Signal Process (2022) 178:109183. doi:10.1016/j.ymssp.2022.109183

CrossRef Full Text | Google Scholar

63. Furuya H, Yamashita K, Yabuno H. Nonlinear stability of a fluid-conveying cantilevered pipe with end mass in case of horizontal excitation at the upper end. Proc ASME 2010 3rd Jt US-European Fluids Eng Summer Meet 8th Int Conf Nanochannels, Microchannels, Minichannels (2010) 1–9. doi:10.1115/FEDSM-ICNMM2010-31239

CrossRef Full Text | Google Scholar

64. Zhang L-x., Huang W-h. ANALYSIS OF NONLINEAR DYNAMIC STABILITY OF LIQUID-CONVEYING PIPES. Appl Maths Mech (2002) 23:1071–80.

Google Scholar

65. Amiri A, Masoumi A, Talebitooti R. Flutter and bifurcation instability analysis of fluid-conveying micro-pipes sandwiched by magnetostrictive smart layers under thermal and magnetic field. Int J Mech Mater Des (2020) 16:569–88. doi:10.1007/s10999-020-09487-w

CrossRef Full Text | Google Scholar

66. Jin Q, Ren Y. Nonlinear size-dependent bending and forced vibration of internal flow-inducing pre- and post-buckled FG nanotubes. Commun Nonlinear Sci Numer Simulation (2022) 104:106044. doi:10.1016/j.cnsns.2021.106044

CrossRef Full Text | Google Scholar

67. Jin Q, Ren Y. Dynamic instability mechanism of post-buckled FG nanotubes transporting pulsatile flow: size-dependence and local/global dynamics. Appl Math Model (2022) 111:139–59. doi:10.1016/j.apm.2022.06.025

CrossRef Full Text | Google Scholar

68. Jin Q, Ren Y, Yuan F-G. Combined resonance of pulsatile flow-transporting FG nanotubes under forced excitation with movable boundary. Nonlinear Dyn (2022) 111:6157–78. doi:10.1007/s11071-022-08148-1

CrossRef Full Text | Google Scholar

69. Chehreghani M, Shaaban A, Misra AK, Païdoussis MP. Experimental investigation of the dynamics of slightly curved cantilevered pipes conveying fluid. Nonlinear Dyn (2023) 111:22101–17. doi:10.1007/s11071-023-08384-z

CrossRef Full Text | Google Scholar

70. Guo Y, Xie Jh., Wang L. Three-dimensional vibration of cantilevered fluid-conveying micropipes—types of periodic motions and small-scale effect. Int J Non-Linear Mech (2018) 102:112–35. doi:10.1016/j.ijnonlinmec.2018.04.001

CrossRef Full Text | Google Scholar

71. Guo Y. Periodic motion of microscale cantilevered fluid-conveying pipes with symmetric breaking on the cross-section. Appl Math Model (2023) 116:277–326. doi:10.1016/j.apm.2022.11.023

CrossRef Full Text | Google Scholar

72. Ma Y, You Y, Chen K, Hu L, Feng A. Application of harmonic differential quadrature (HDQ) method for vibration analysis of pipes conveying fluid. Appl Maths Comput (2023) 439:127613. doi:10.1016/j.amc.2022.127613

CrossRef Full Text | Google Scholar

73. Mao X-Y, Jing J, Ding H, Chen L-Q. Dynamics of axially functionally graded pipes conveying fluid. Nonlinear Dyn (2023) 111:11023–44. doi:10.1007/s11071-023-08470-2

CrossRef Full Text | Google Scholar

74. Arefi M, Karroubi R, Irani-Rahaghi M. Free vibration analysis of functionally graded laminated sandwich cylindrical shells integrated with piezoelectric layer. Appl Maths Mech (2016) 37:821–34. doi:10.1007/s10483-016-2098-9

CrossRef Full Text | Google Scholar

75. Arefi M, Faegh RK, Loghman A. The effect of axially variable thermal and mechanical loads on the 2D thermoelastic response of FG cylindrical shell. J Therm Stresses (2016) 39:1539–59. doi:10.1080/01495739.2016.1217178

CrossRef Full Text | Google Scholar

76. Arefi M, Abbasi AR, Vaziri Sereshk MR. Two-dimensional thermoelastic analysis of FG cylindrical shell resting on the Pasternak foundation subjected to mechanical and thermal loads based on FSDT formulation. J Therm Stresses (2016) 39:554–70. doi:10.1080/01495739.2016.1158607

CrossRef Full Text | Google Scholar

77. Arefi M, Rahimi GH. The effect of nonhomogeneity and end supports on the thermo elastic behavior of a clamped–clamped FG cylinder under mechanical and thermal loads. Int J Press Vessels Piping (2012) 96-97:30–7. doi:10.1016/j.ijpvp.2012.05.009

CrossRef Full Text | Google Scholar

78. Saeedi S, Kholdi M, Loghman A, Ashrafi H, Arefi M. Thermo-elasto-plastic analysis of thick-walled cylinder made of functionally graded materials using successive approximation method. Int J Press Vessels Piping (2021) 194:104481. doi:10.1016/j.ijpvp.2021.104481

CrossRef Full Text | Google Scholar

79. Loghman A, Nasr M, Arefi M. Nonsymmetric thermomechanical analysis of a functionally graded cylinder subjected to mechanical, thermal, and magnetic loads. J Therm Stresses (2017) 40:765–82. doi:10.1080/01495739.2017.1280380

CrossRef Full Text | Google Scholar

80. Yayli MÖ. A compact analytical method for vibration of micro-sized beams with different boundary conditions. Mech Adv Mater Structures (2016) 24:496–508. doi:10.1080/15376494.2016.1143989

CrossRef Full Text | Google Scholar

81. Semler C, Li GX, Païdoussis MP. The non-linear equations of motion of pipes conveying fluid. J Sound Vibration (1994) 169:577–99.

CrossRef Full Text | Google Scholar

82. Yang F, Chong ACM, Lam DCC, Tong P. Couple stress based strain gradient theory for elasticity. Int J Sol Structures (2002) 39:2731–43. doi:10.1016/s0020-7683(02)00152-x

CrossRef Full Text | Google Scholar

83. Xu J, Wang L. Dynamics and control of fluid-conveying pipe systems. Beijing: Science Press (2015).

Google Scholar

84. Dehsaraji ML, Arefi M, Loghman A. Size dependent free vibration analysis of functionally graded piezoelectric micro/nano shell based on modified couple stress theory with considering thickness stretching effect. Defence Technol (2021) 17:119–34. doi:10.1016/j.dt.2020.01.001

CrossRef Full Text | Google Scholar

85. Beni YT, Karimipöur I, Abadyan M. Modeling the effect of intermolecular force on the size-dependent pull-in behavior of beam-type NEMS using modified couple stress theory. J Mech Sci Technol (2014) 28:3749–57. doi:10.1007/s12206-014-0836-5

CrossRef Full Text | Google Scholar

86. Karimipour I, Beni YT, Akbarzadeh AH. Size-dependent nonlinear forced vibration and dynamic stability of electrically actuated micro-plates. Commun Nonlinear Sci Numer Simulation (2019) 78:104856. doi:10.1016/j.cnsns.2019.104856

CrossRef Full Text | Google Scholar

87. Yayli MÖ. Free longitudinal vibration of a nanorod with elastic spring boundary conditions made of functionally graded material. Micro Nano Lett (2018) 13:1031–5. doi:10.1049/mnl.2018.0181

CrossRef Full Text | Google Scholar

88. Yayli MÖ. Axial vibration analysis of a Rayleigh nanorod with deformable boundaries. Microsystem Tech (2020) 26:2661–71. doi:10.1007/s00542-020-04808-7

CrossRef Full Text | Google Scholar

89. Yayli MÖ. Free vibration analysis of a rotationally restrained (FG) nanotube. Microsystem Tech (2019) 25:3723–34. doi:10.1007/s00542-019-04307-4

CrossRef Full Text | Google Scholar

90. Wang Y, Tang M, Yang M, Qin T. Three-dimensional dynamics of a cantilevered pipe conveying pulsating fluid. Appl Math Model (2023) 114:502–24. doi:10.1016/j.apm.2022.10.023

CrossRef Full Text | Google Scholar

91. Hosseini M, Bahaadini R. Size dependent stability analysis of cantilever micro-pipes conveying fluid based on modified strain gradient theory. Int J Eng Sci (2016) 101:1–13. doi:10.1016/j.ijengsci.2015.12.012

CrossRef Full Text | Google Scholar

92. Kuznetsov YA. Elements of applied bifurcation theory. 3rd ed. ed. New York: Springer-Verlag (2004).

Google Scholar

93. Lam DCC, Yang F, Chong ACM, Wang J, Tong P. Experiments and theory in strain gradient elasticity. J Mech Phys Sol (2003) 51:1477–508. doi:10.1016/s0022-5096(03)00053-x

CrossRef Full Text | Google Scholar

94. McFarland AW, Colton JS. Role of material microstructure in plate stiffness with relevance to microcantilever sensors. J Micromechanics Microengineering (2005) 15:1060–7. doi:10.1088/0960-1317/15/5/024

CrossRef Full Text | Google Scholar

95. Ellis SRW, Smith CW. A thin plate analysis and experimental evaluation of couple stress effects. Exp Mech (1968) 7:372–80. doi:10.1007/bf02326308

CrossRef Full Text | Google Scholar