- 1Department of Basic Sciences, Preparatory Year, King Faisal University, Al-Ahsa, Saudi Arabia
- 2Department of Mathematics, Faculty of Science, King Khalid University, Abha, Saudi Arabia
- 3Department of Computer Science and Mathematics, Lebanese American University, Beirut, Lebanon
- 4Basic Science Department, College of Science and Theoretical Studies, Saudi Electronic University, Riyadh, Saudi Arabia
- 5Department of Mathematics, Faculty of Science, AL-Azhar University, Assiut, Egypt
In this study, we employ the effective iterative method to address the fractional Wu-Zhang Equation within the framework of the Caputo Derivative. The effective iterative method offers a practical approach to obtaining approximate solutions for fractional differential equations. We seek to provide insights into its solution and behavior by applying this method to the Wu-Zhang Equation. Through numerical analysis and the presentation of relevant tables and Figures, we demonstrate the accuracy and efficiency of this method in solving the fractional Wu-Zhang Equation. This research contributes to the understanding and solution of fractional-order differential equations and their applications in various scientific and engineering domains.
1 Introduction
In mathematics, fractional calculation is a generalization of classical calculus. During the last few decades, researchers have paid much more attention to fractional calculus. Several fields have benefited from the application of fractional calculus, including physics, engineering, biology, medicine, hydrology, economics and finance [1–8]. In differential equations, linear models can be solved by different methods and do not require excessive effort to obtain their exact solutions. Non-linear models are more difficult to solve. It’s hard to solve most problems in the real world because they’re non-linear. There is no exact solution to the majority of non-linear problems. To solve these problems, researchers use a variety of approaches [9–15]. In recent years, the exploration of advanced mathematical methods and novel approaches has significantly impacted the domain of fractional calculus. A series of publications by notable researchers Tao, He, Anjum, Yang, and others have introduced pioneering concepts, unveiling the potential of transformative methodologies in the field. Among these, the Aboodh transformation-based homotopy perturbation method, highlighted in the work by [16] in Frontiers in Physics, presents a new ray of hope for the application of fractional calculus. He, Anjum, and others also, in their 2023 publication in Therm. Sci. has illuminated the challenges and prospects beyond Laplace and Fourier transforms, setting the stage for a broader understanding of mathematical transformations [17]. Exploring applications, Anjum, Ain, Din, and their team have undertaken an insightful analysis of Caputo fractional order dynamics, particularly in the context of the Middle East Lungs Coronavirus (MERS-CoV) model, as revealed in their 2022 [18]. Furthermore, the work of Anjum, He, He, and collaborators (2021) in Fractals introduces the intriguing concept of two-scale fractal theory in population dynamics [19]. In contrast, Anjum, Ain, Li, and others (2021) present a groundbreaking two-scale mathematical model for tsunami waves in the GEM-International Journal on Geo mathematics [20].
Coastal and harbor design is often influenced by the Wu-Zhang system of equations, which describes the non-linear water wave availability in the ocean. To obtain the exact solution, this is one of the most critical topics in mathematical physics. Several authors have recently used various numerical and analytical approaches to find the numerical and analytical solution to the WZ equations, for example, using the first integral method [21], the modified Adomian decomposition method [22], the homotopy perturbation method [23], the extended Tanh method and the exp-function method [24], the exponential rational function method [25], the successive approximation method [26], the modified variation iteration method [27], the extended trial equation method [28] and the dynamic system method [29]. In addition, more solitonic solutions were extracted using the mapping method. According to [30], the extended trial equation method, Lie symmetry analysis, and mapping method are used to obtain solutions for solitary, shock, and singular solitary waves. According to [31], the 3-component Wu-Zhang equation is solved using the ansatz method, followed by a one-solution solution. Several methods have been used recently to enhance these equations, including Backlund transformations [32], Darboux transformations [33–35], asymptotic analysis methods [36], Painleve analyses [37] and extended Painleve expansions [38].
The new iterative method (NIM) was introduced in 2006 by Daftardar-Gejji and Jafari for solving linear and non-linear equations [39]. A straightforward method is proposed for handling linear and non-linear equations. In contrast to ADM and numerical methods, NIM doesn’t require the calculation of tedious Adomian polynomials in non-linear terms like ADM, a Lagrange multiplier like VIM, or discretization like numerical methods. A significant advantage of this method is that it does not require small parameter assumptions, unlike regular perturbation methods. Its primary disadvantage lies in the fact that NIM is an iterative method requiring an initial condition. An iterative method was developed in [40] to solve linear and non-linear fractional diffusion-wave equations on finite domains with Dirichlet boundary conditions. In this study, the New Iterative Method [41] has been applied to linear and non-linear fractional diffusion-wave equations. It has been reported in [42] that new iterative methods were used to study a fractional version of a logistic equation. The scientific landscape in recent publications showcases diverse research spanning various disciplines. Among these, significant contributions emerge in physics, fluid dynamics, material science, and mathematical engineering [43–47]. Notably, [48] have made strides in particle physics by establishing the first hidden-charm pentaquark with strangeness. Concurrently, [49] delve into the characteristics of cavity dynamics in water entries with paired spheres, contributing insights into fluid behavior. Yang and Kai [50] explore the dynamical properties and chaotic behaviors of non-linear coupled Schrodinger equations in fiber Bragg gratings, while [51] propose a Dilatancy Equation for Geomaterials based on property-dependent plastic potential theory. Furthermore, [52] present an Iterative Threshold Algorithm for Sparse Problems, and [53] focus on aerial target threat assessment using improved methods in mathematical biosciences and engineering. These diverse studies underscore the multidisciplinary nature and broad scope of recent scientific endeavors [54–56].
The Wu-Zhang equation is a nonlinear partial differential equation that describes the (1 + 1)-dimensional dispersive long wave in two horizontal directions on shallow waters. It has been applied in various fields, including engineering and coastal design. The equation has been extended to include time-fractional and space-fractional derivatives, leading to the time-fractional (2 + 1)-dimensional Wu-Zhang system and the space-fractional (2 + 1)-dimensional Wu-Zhang system. The Wu-Zhang equation and its generalizations have found applications in various fields, such as ocean engineering, coastal design, and the study of nonlinear waves. The equation has also been used to model nonlinear and dispersive waves in other contexts, such as conformable time-fractional systems and time-fractional (2 + 1)-dimensional systems. Throughout the paper, a fractional approach will be used to solve the Wu-Zhang equation and analyze the behavior that lies behind the phenomenon in a fractional model. This research aims to extend the implementation of NIM to solve time-fractional partial differential equations, including systems of two or more partial differential equations, which are applied in engineering and science. Moreover, the study explores various fractional order values across three distinct situations, examining 3D and contour plots to determine the physical characteristics of the solution. A comparison between the approximate and exact solution is done to ensure the model is accurate. Physical problems with fractional orders can be solved using the New Iterative Method (NIM), which can be applied to both linear and non-linear fractional order problems. Three main sections in the article are arranged as follows: Section 2 represents some definitions, and Section 3 shows the methodology of the New Iterative Method (NIM). Section 4 discusses the problem’s solution. Section 5 provides the numerical results and discussions and the last Section 6 shows the short conclusion.
2 Preliminaries
In this section, we will discuss several basic definitions and conclusions relating to the Caputo fractional derivative.
Definition 1. The formula for the Riemann fractional integral is as follows [57]:
Definition 2. The fractional derivative of f according to the Caputo formula is defined as [57]:
Lemma 1. For n − 1 < σ ≤ n, p > − 1, t ≥ 0 and λ ∈ R, we have:
1.
2.
3.
4.
3 General procedure for the proposed methods
3.1 General procedure of new iterative method
For the basic idea of the new iterative method, we consider the general functional equation:
where N is non linear operator and K is unknown function. We have been looking for a solution of Eq. 1 having the series form
The nonlinear term can be decomposed as
From 4 to 5, 3 is equivalent to
We define the following recurrence relation:
Then
3.1.1 Basic road map of NIM
In this section, we discuss basic idea for solving fractional-order nonlinear PDE using the NIM. Consider the following fractional-order PDE:
where A is non linear function of ν and ∂ν (partial derivative of ν with respect to ν) and B is the source function. In view of the new iterative method, the intimal value problem Eqs 2, 3 is equivalent to the integral equation
where
4 Solution of Wu-Zhang (WZ) equation by NIM
In this section, we apply NIM to understand the anomalous behavior of the fractional-order Wuâ“Zhang (WZ) equation, which is given by
Subject to initial condition
in Eq. 4, γ(f, g, ϵ) represent the elevation of the water wave, α(f, g, ϵ) represent the surface velocity of water along the x-axis, and β(f, g, ϵ) represents the surface velocity of water along the y-axis. In Eq. 5 a0, a1, a2, and a3 are arbitrary constant.
Now using the NIM procedure, we get the following few terms for α(f, g, ϵ)
Now for β(f, g, ϵ) the zeroth, first and second order approximation is
Similarly the same procedure for γ(f, g, ϵ) we will get
According to Nim procedure we will get solution of the system is
Solution for α(f, g, ϵ)
Solution for β(f, g, ϵ)
Similarly solution for γ(f, g, ϵ)
5 Results and discussions
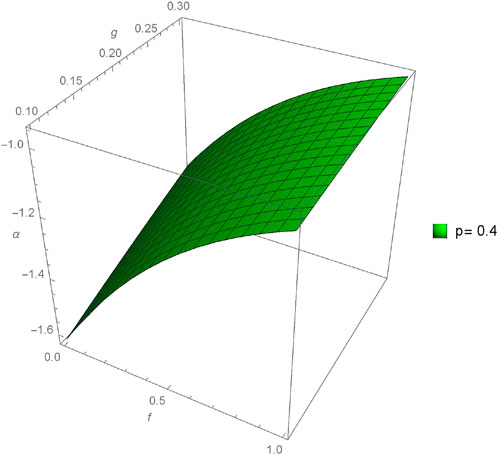
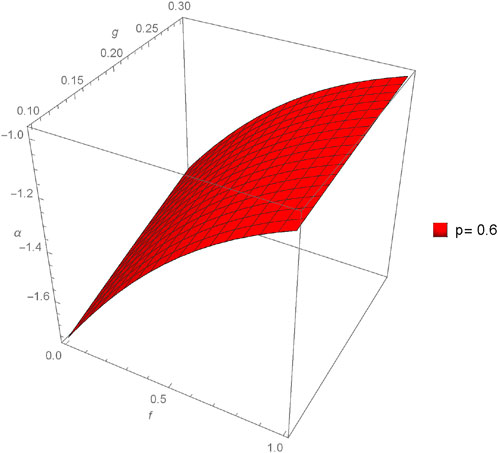
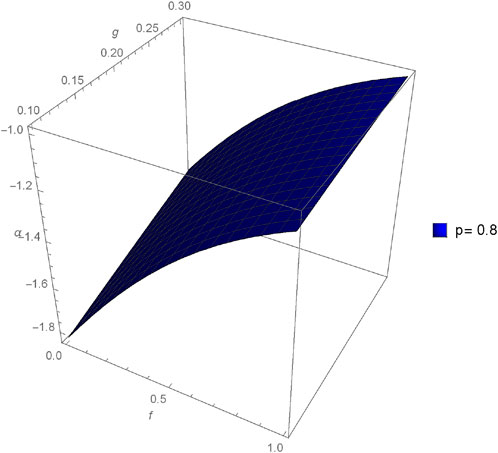
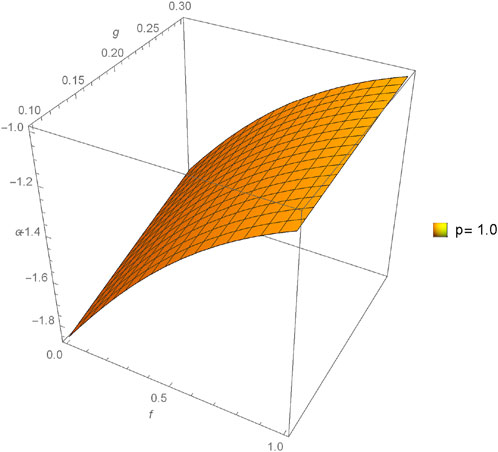
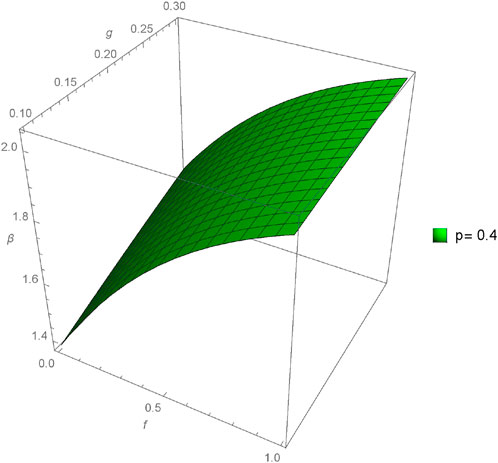
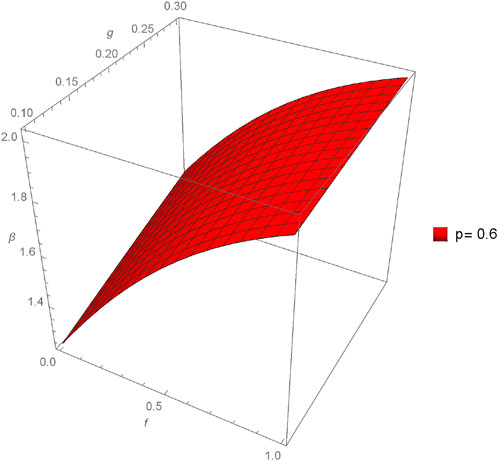
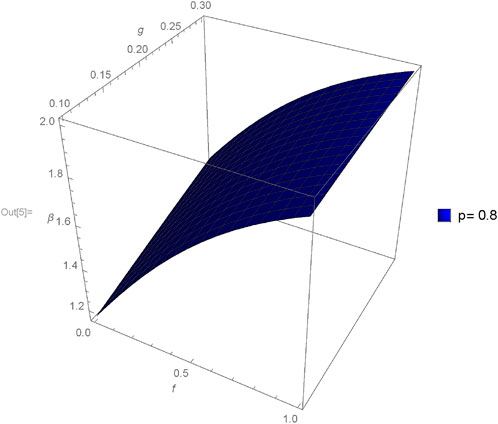
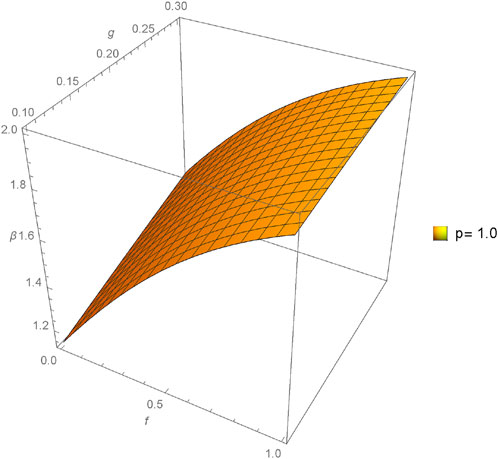
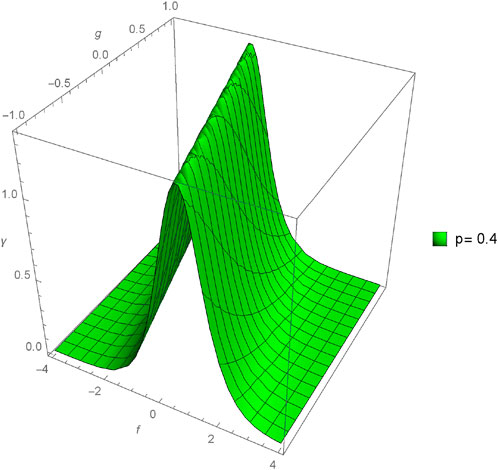
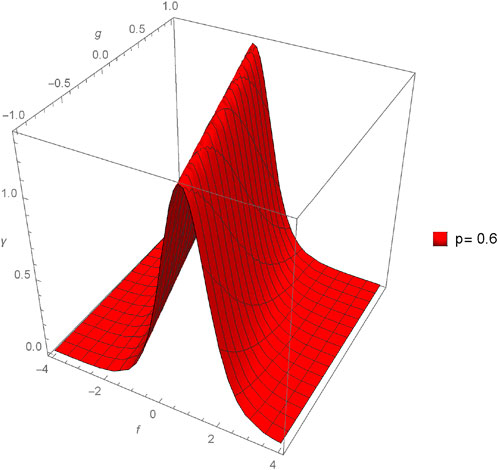
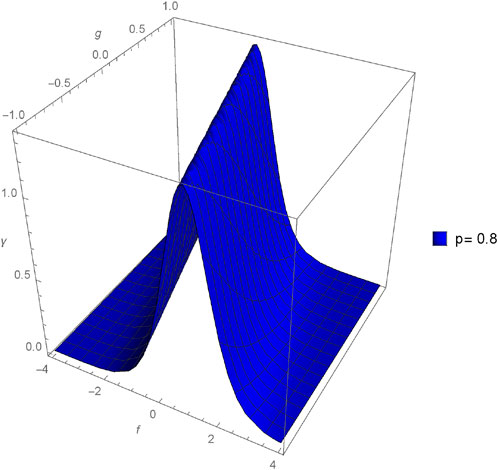
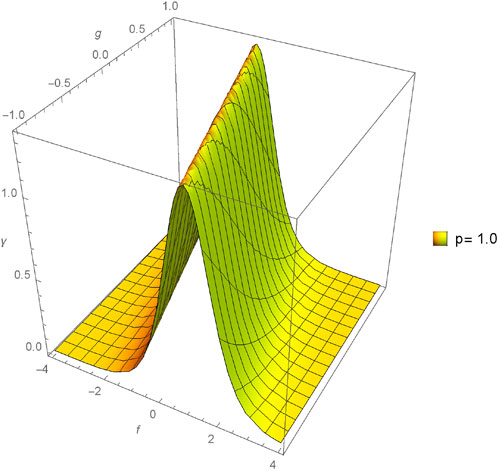
The graphical analysis presented in this section offers a comparative study between the approximate and exact solutions derived through the proposed method, shedding light on the method’s accuracy and practical utility. Figures 1–4 showcase three-dimensional plots depicting the approximate solutions α(f, g, h, ϵ) across different values of fractional orders (p). Notably, an observable trend emerges as the fractional orders (p) increase, corresponding to an increment in the plotted graphs, implying a relationship between the solutions and the variation in fractional orders. Furthermore, Figures 5–12 present three-dimensional plots of the approximate solutions β(f, g, h, ϵ) and γ(f, g, h, ϵ) concerning varied fractional orders (p) at a fixed value of ϵ = 0.02. These visual representations offer insights into the influence of fractional orders on the solutions, revealing potential patterns or dependencies within the system at constant values of other parameters.
Figures 13–15 provide a comparison between the 3D plots of α(f, g, h, ϵ), β(f, g, h, ϵ), and γ(f, g, h, ϵ), respectively, illustrating the discrepancies and agreements between the approximate solutions and the exact solution across different fractional orders (p). Similarly, Figures 16–18 focus on the comparison of two-dimensional plots for α(f, g, h, ϵ), β(f, g, h, ϵ), and γ(f, g, h, ϵ), utilizing the New Iterative Method (NIM). These comparisons aim to highlight the closeness or divergence between the approximate solutions obtained through the proposed method and the exact solutions, offering a comprehensive understanding of the method’s efficacy in capturing the intricate dynamics of the system under varied fractional orders.
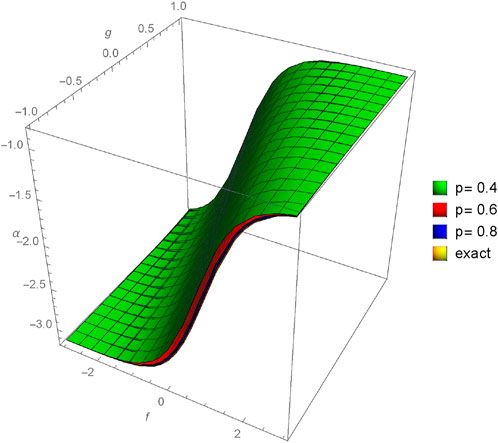
FIGURE 13. Comparison between exact and NIM solution for 3D plot α(f, g, h, ϵ) for different fractional order values of p = 0.4, 0.6, 0.8, 1.0.
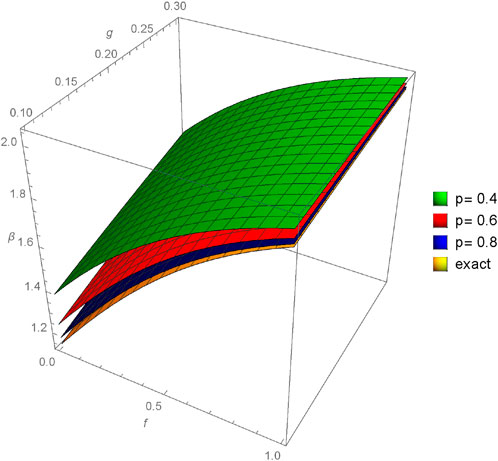
FIGURE 14. Comparison between exact and NIM solution for 3D plot β(f, g, h, ϵ) for different fractional order values of p = 0.4, 0.6, 0.8, 1.0.
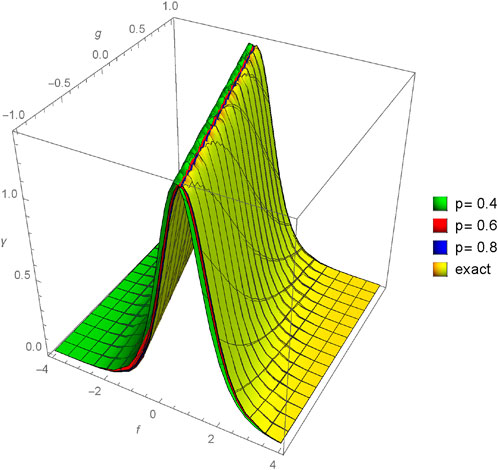
FIGURE 15. Comparison between exact and NIM solutions for a 3D plot γ(f, g, h, ϵ) for different fractional order values of p = 0.4, 0.6, 0.8, 1.0.
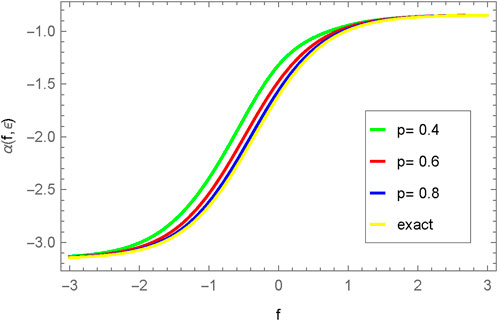
FIGURE 16. Comparison between exact and NIM solution for 2D plot γ(f, g, h, ϵ) for different fractional order values of p = 0.4, 0.6, 0.8, 1.0.
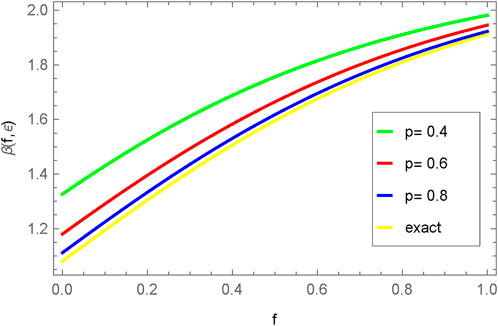
FIGURE 17. Comparison between exact and NIM solution for 2D plot γ(f, g, h, ϵ) for different fractional order values of p = 0.4, 0.6, 0.8, 1.0.
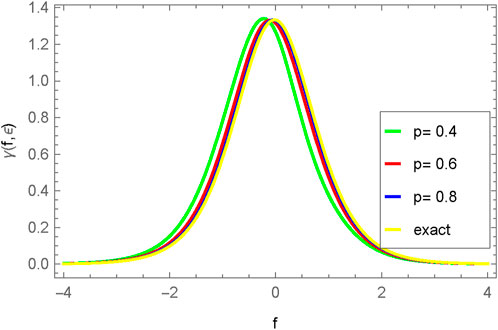
FIGURE 18. Comparison between exact and NIM solution for 2D plot γ(f, g, h, ϵ) for different fractional order values of p = 0.4, 0.6, 0.8, 1.0.
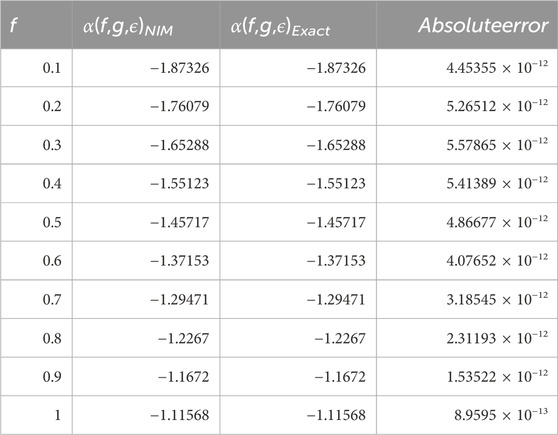
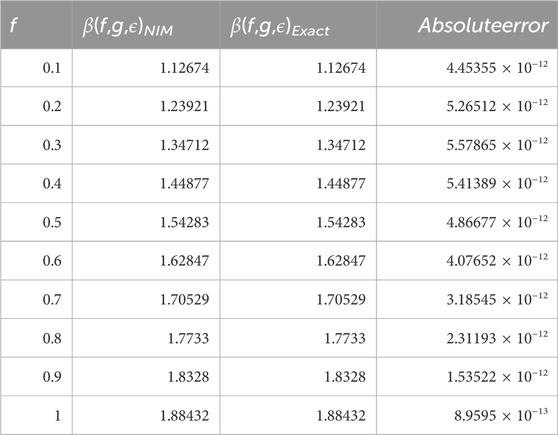
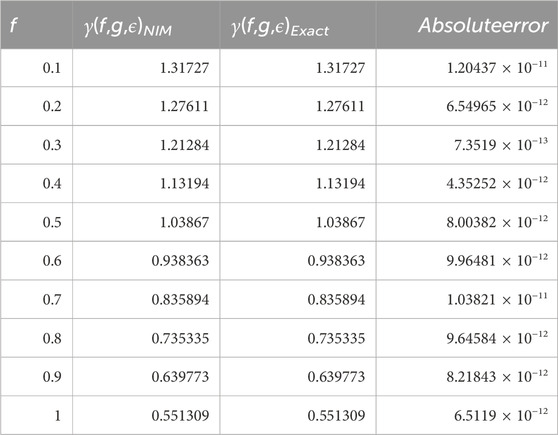
The tables provided in this discussion serve to compare the numerical solutions derived from the New Iterative Method (NIM) with the exact solution of the fractional-order nonlinear Wu-Zhang equation, demonstrating the method’s efficacy in solving nonlinear partial differential equations plagued by scaling issues. Tables 1–3 exhibit the obtained solutions and compare them to the exact solutions while evaluating their absolute error for a fractional integer order (p = 1). These tables offer a quantitative assessment of the accuracy and closeness of the NIM-derived solutions to the exact solutions, providing insights into the method’s performance under specific fractional orders.
On the other hand, Tables 4–6 provide a comparative analysis of α(f, g, h, ϵ), β(f, g, h, ϵ), and γ(f, g, h, ϵ), respectively, for varying fractional orders (p = 0.4, 0.6, 0.8, 1.0) at a fixed value of ϵ = 0.2. These tables facilitate a comprehensive examination of the solutions obtained through the NIM method across different fractional orders, enabling researchers to discern any patterns or variations in the solutions concerning changes in the fractional parameters. By comparing the solutions across various fractional orders, the tables offer insights into how the method performs under different degrees of fractional derivatives, aiding in understanding the behavior and dependency of the solutions on fractional order variations.
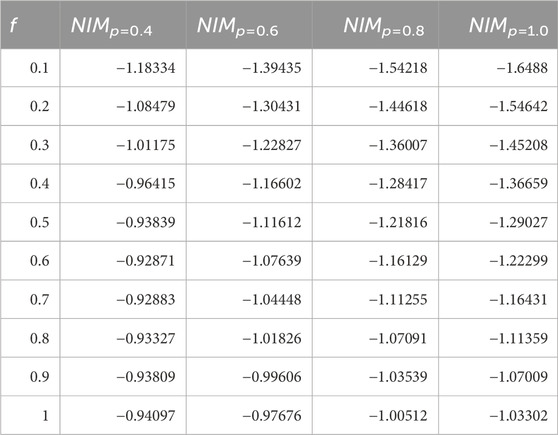
TABLE 4. Numerical values of α(f, g, ϵ) using the NIM solution for different values of fractional order of p.
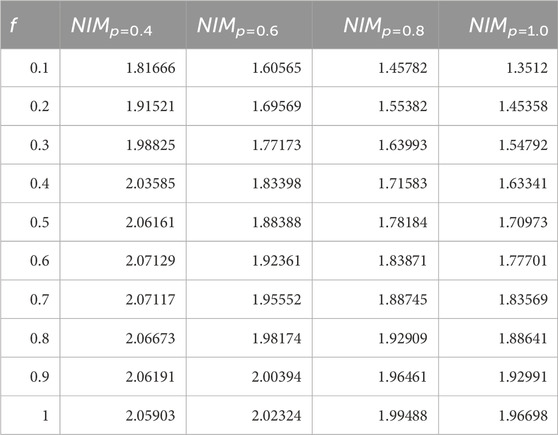
TABLE 5. Numerical values of β(f, g, ϵ) using the NIM solution for different values of fractional order of p.
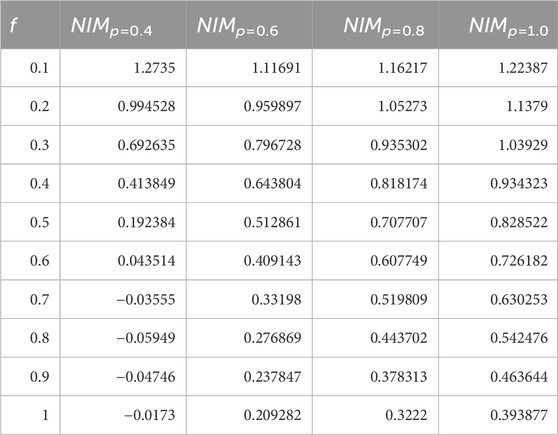
TABLE 6. Numerical values of γ(f, g, ϵ) using the NIM solution for different values of fractional order of ν.
Additionally, the visualization of the solutions in 3D and 2D plots for various fractional order values complements the tables, allowing for a comprehensive assessment of the method’s performance through both numerical data and graphical representations. In Table 7, comparison of the present solution (NIM) with the HPM solution for the Wu-Zhang equation. Together, these tables and plots serve as invaluable tools in evaluating the NIM’s efficiency in handling fractional-order nonlinear equations, providing a detailed understanding of the method’s accuracy and performance under different fractional orders and parameter settings.
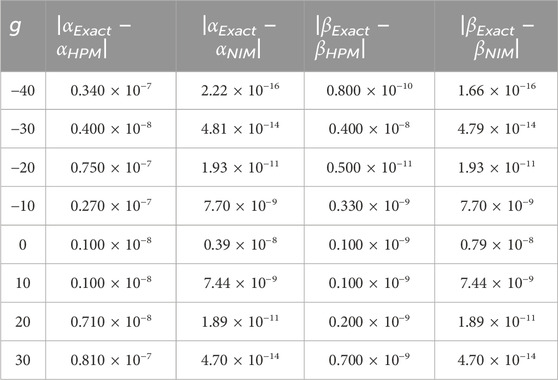
TABLE 7. Comparison of the present solution (NIM) with the HPM solution [58] for the Wu-Zhang equation.
6 Conclusion
In conclusion, we have successfully applied the New Iterative Method to solve the fractional Wu-Zhang Equation within the Caputo Derivative framework. The method has demonstrated its efficacy in providing approximate solutions to this complex fractional differential equation. Through our numerical analysis and the presentation of pertinent tables and figures, we have showcased the accuracy and reliability of the method in addressing the Wu-Zhang Equation. This research highlights the significance of the New Iterative Method as a valuable tool for solving fractional-order differential equations, contributing to the broader field of mathematics and its applications. It opens up opportunities for further exploration and application in various scientific and engineering disciplines.
Data availability statement
The original contributions presented in the study are included in the article/Supplementary material, further inquiries can be directed to the corresponding authors.
Author contributions
HY: Writing–original draft, Formal Analysis, Investigation, Methodology, Visualization. AA: Project administration, Conceptualization, Methodology, Software, Data curation, Writing–review and editing. RS: Investigation, Writing–review and editing, Formal Analysis, Funding acquisition, Methodology, Supervision. AH: Conceptualization, Resources, Software, Supervision, Validation, Writing–original draft. SA: Methodology, Software, Writing–review and editing.
Funding
The authors declare financial support was received for the research, authorship, and/or publication of this article. The authors extend their appreciation to the Deanship of Scientific Research at King Khalid University for funding this work through the Small Group Research Project under grant number RGP1/216/44. This work was supported by the Deanship of Scientific Research, the Vice Presidency for Graduate Studies and Scientific Research, King Faisal University, Saudi Arabia (Grant No. 5717).
Acknowledgments
The authors extend their appreciation to the Deanship of Scientific Research at King Khalid University for funding this work through the Small Group Research Project under grant number RGP1/216/44. This work was supported by the Deanship of Scientific Research, the Vice Presidency for Graduate Studies and Scientific Research, King Faisal University, Saudi Arabia (Grant No. 5717).
Conflict of interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Publisher’s note
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
References
1. Baleanu D, Hasanabadi M, Vaziri AM, Jajarmi A. A new intervention strategy for an HIV/AIDS transmission by a general fractional modeling and an optimal control approach. Chaos, Solitons Fractals (2023) 167:113078. doi:10.1016/j.chaos.2022.113078
2. Defterli O, Baleanu D, Jajarmi A, Sajjadi SS, Alshaikh N, Asad J. Fractional treatment: an accelerated mass-spring system. Rom Rep Phys (2022) 74(4):1–13.
3. Baleanu D, Arshad S, Jajarmi A, Shokat W, Ghassabzade FA, Wali M. Dynamical behaviours and stability analysis of a generalized fractional model with a real case study. J Adv Res (2023) 48:157–73. doi:10.1016/j.jare.2022.08.010
4. Ali M, Alquran M, Jaradat I. Asymptotic-sequentially solution style for the generalized Caputo time-fractional Newell–Whitehead–Segel system. Adv Difference Equations (2019) 2019(1):70–9. doi:10.1186/s13662-019-2021-8
5. Alquran M, Ali M, Al-Khaled K, Grossman G. Simulations of fractional time-derivative against proportional time-delay for solving and investigating the generalized perturbed-KdV equation. Nonlinear Eng (2023) 12(1):20220282. doi:10.1515/nleng-2022-0282
6. Alquran MARWAN. Investigating the revisited generalized stochastic potential-KdV equation: fractional time-derivative against proportional time-delay. Rom J Phys (2023) 68:106.
7. Alquran M, Al-Khaled K, Sivasundaram S, Jaradat HM. Mathematical and numerical study of existence of bifurcations of the generalized fractional Burgers-Huxley equation. Nonlinear Stud (2017) 24(1):235–44.
8. Alquran M. The amazing fractional Maclaurin series for solving different types of fractional mathematical problems that arise in physics and engineering. Partial Differential Equations Appl Math (2023) 7:100506. doi:10.1016/j.padiff.2023.100506
9. Farman M, Akgul A, Garg H, Baleanu D, Hincal E, Shahzeen S. Mathematical analysis and dynamical transmission of monkeypox virus model with fractional operator. Expert Syst (2023):e13475. doi:10.1111/exsy.13475
10. Farman M, Akgul A, Alshaikh N, Azeem M, Asad J. Fractional-order Newton–raphson method for nonlinear equation with convergence and stability analyses. Fractals (2023) 31. doi:10.1142/s0218348x23400790
11. Ali R, Akgul A. A new matrix splitting generalized iteration method for linear complementarity problems. Appl Math Comput (2024) 464:128378. doi:10.1016/j.amc.2023.128378
12. Jamil S, Farman M, Akgul A, Saleem MU, Hincal E, El Din SM. Fractional order age dependent Covid-19 model: an equilibria and quantitative analysis with modeling. Results Phys (2023) 53:106928. doi:10.1016/j.rinp.2023.106928
13. Farman M, Shehzad A, Akgul A, Baleanu D, Attia N, Hassan AM. Analysis of a fractional order Bovine Brucellosis disease model with discrete generalized Mittag–Leffler kernels. Results Phys (2023) 52:106887. doi:10.1016/j.rinp.2023.106887
14. Akram G, Sadaf M, Zainab I, Abbas M, Akgul A. A comparative study of time fractional nonlinear drinfeld–sokolov–wilson system via modified auxiliary equation method. Fractal and Fractional (2023) 7(9):665. doi:10.3390/fractalfract7090665
15. Jamil S, Farman M, Akgul A. Qualitative and quantitative analysis of a fractal fractional HIV/AIDS model. Alexandria Eng J (2023) 76:167–77. doi:10.1016/j.aej.2023.06.021
16. Tao H, Anjum N, Yang YJ. The Aboodh transformation-based homotopy perturbation method: new hope for fractional calculus. Front Phys (2023) 11:310. doi:10.3389/fphy.2023.1168795
17. He JH, Anjum N, He CH, Alsolami AA. Beyond laplace and fourier transforms: challenges and future prospects. Therm Sci (2023) 27(6B):5075–89. doi:10.2298/tsci230804224h
18. Ain QT, Anjum N, Din A, Zeb A, Djilali S, Khan ZA. On the analysis of Caputo fractional order dynamics of Middle East Lungs Coronavirus (MERS-CoV) model. Alexandria Eng J (2022) 61(7):5123–31. doi:10.1016/j.aej.2021.10.016
19. Anjum N, He CH, He JH. Two-scale fractal theory for the population dynamics. Fractals (2021) 29(07):2150182. doi:10.1142/s0218348x21501826
20. Anjum N, Ain QT, Li XX. Two-scale mathematical model for tsunami wave. GEM-International J Geomathematics (2021) 12(1):10. doi:10.1007/s13137-021-00177-z
21. Baleanu D, Kılıç B, Inç M. The first integral method for Wu-Zhang nonlinear system with time-dependent coefficients (2015).
22. Qasim AF, Ali ZY. Application of modified Adomian decomposition method to (2+1)-dimensional non-linear Wu-Zhang system. J Al-qadisiyah Comput Sci Math (2018) 10(1):40. doi:10.29304/jqcm.2018.10.1.340
23. Ma ZY. Homotopy perturbation method for the Wu-Zhang equation in fluid dynamics. In: Journal of physics: conference series, vol. 96 012182. IOP Publishing (2008).
24. Asgari A, Ganji DD, Davodi AG. Extended tanh method and exp-function method and its application to (2+1)-dimensional dispersive long wave nonlinear equations. J Appl Math Stat Inf (Jamsi) (2010) 6:61–72.
25. Kaur B, Gupta RK. Time fractional (2+1)-dimensional Wu–Zhang system: dispersion analysis, similarity reductions, conservation laws, and exact solutions. Comput Math Appl (2020) 79(4):1031–48. doi:10.1016/j.camwa.2019.08.014
26. Al-Rozbayani AM, Shammar AH. Successive approximation method for solving Wu-zhang systems of (1 1) dimensional. Open Access Libr J (2020) 7(08):1–7. doi:10.4236/oalib.1106601
27. Zayed EME, Rahman HM-A. On solving the Kay-Burger’s equation and the Wu-Zhang equations using the modified variational iteration method. Int J Nonlinear Sci Numer Simul (2009) 10(9):1093–104. doi:10.1515/ijnsns.2009.10.9.1093
28. Mirzazadeha M, Ekicib M, Eslamic M, Krishnand EV, Kumar S, Biswas A. Solitons and other solutions to Wu–Zhang system (2017).
29. Zheng H, Xia Y, Bai Y, Lei G. Travelling wave solutions of Wu–Zhang system via dynamic analysis. Discret Dyn Nat Soc (2020) 2020:1–9. doi:10.1155/2020/2845841
30. Mirzazadeh M, Ekici M, Eslami M, Krishnan EV, Kumar S, Biswas A. Solitons and other solutions to Wu–Zhang system. Nonlinear Anal Model (2017) 22:441–58. doi:10.15388/na.2017.4.2
31. Triki H, Hayat T, Aldossary OM, Biswas A. Soliton solution of the three component system of Wu-Zhang equations, Hacet. Hacet J Math Stat (2012) 41:537.
32. Du Z, Tian B, Xie XY, Chai J, Wu XY. Bäcklund transformation and soliton solutions in terms of the Wronskian for the Kadomtsev–Petviashvili-based system in fluid dynamics. J Phys (2018) 90:45. doi:10.1007/s12043-018-1532-2
33. Li YS, Ma WX, Zhang JE. Darboux transformations of classical Boussinesq system and its new solutions. Phys Lett A (2000) 275:60–6. doi:10.1016/s0375-9601(00)00583-1
34. Li YS, Zhang JE. Darboux transformations of classical Boussinesq system and its multi-soliton solutions. Phys Lett A (2001) 284:253–8. doi:10.1016/s0375-9601(01)00331-0
35. Matveev VB, Salle MA. Darboux transformation and soliton Vol. 8. Berlin: Springer-Verlag (1991). p. 120.
36. Sun HQ, Chen AH. Exact solutions of the classical Boussinesq system. Arab J Basic Appl Sci (2018) 25:85–91. doi:10.1080/25765299.2018.1449416
37. Tang XY, Lou SY. Extended multilinear variable separation approach and multivalued localized excitations for some (2+1)-dimensional integrable systems. J Math Phys (2003) 44:4000–25. doi:10.1063/1.1598619
38. Chen C, Lou S. Soliton excitations and periodic waves without dispersion relation in shallow water system. Chaos Solitons Fractals (2003) 16:27–35. doi:10.1016/s0960-0779(02)00148-0
39. Daftardar-Gejji V, Jafari H. An iterative method for solving nonlinear functional equations. J Math Anal Appl (2006) 316(2), 753–63. doi:10.1016/j.jmaa.2005.05.009
40. Daftardar-Gejji V, Bhalekar S Solving fractional boundary value problems with Dirichlet boundary conditions using a new iterative method. Comput Math Appl (2010) 59(5), 1801–9. doi:10.1016/j.camwa.2009.08.018
41. Daftardar-Gejji V, Bhalekar S. Solving fractional diffusion-wave equations using a new iterative method. Fract Calc Appl Anal (2008) 11(2), 193–202.
42. Bhalekar S, Daftardar-Gejji V. Solving fractional-order logistic equation using a new iterative method. Int J Differ Equ (2012) 2012:1–12. doi:10.1155/2012/975829
43. Kbiri Alaoui M, Nonlaopon K, Zidan AM, Khan A, Shah R. Analytical investigation of fractional-order Cahn–Hilliard and gardner equations using two novel techniques. Mathematics (2022) 10(10):1643. doi:10.3390/math10101643
44. Botmart T, Agarwal RP, Naeem M, Khan A, Shah R. On the solution of fractional modified Boussinesq and approximate long wave equations with non-singular kernel operators. AIMS Math (2022) 7:12483–513. doi:10.3934/math.2022693
45. Yasmin H, Aljahdaly NH, Saeed AM, Shah R. Probing families of optical soliton solutions in fractional perturbed radhakrishnan–kundu–lakshmanan model with improved versions of extended direct algebraic method. Fractal and Fractional (2023) 7(7):512. doi:10.3390/fractalfract7070512
46. Yasmin H, Aljahdaly NH, Saeed AM, Shah R. Investigating families of soliton solutions for the complex structured coupled fractional biswas–arshed model in birefringent fibers using a novel analytical technique. Fractal and Fractional (2023) 7(7):491. doi:10.3390/fractalfract7070491
47. Yasmin H, Aljahdaly NH, Saeed AM, Shah R. Investigating symmetric soliton solutions for the fractional coupled konno–onno system using improved versions of a novel analytical technique. Mathematics (2023) 11(12):2686. doi:10.3390/math11122686
48. Chen H, Chen W, Liu X, Liu X. Establishing the first hidden-charm pentaquark with strangeness. The Eur Phys J C (2021) 81(5):409. doi:10.1140/epjc/s10052-021-09196-4
49. Lyu X, Wang X, Qi C, Sun R. Characteristics of cavity dynamics, forces, and trajectories on vertical water entries with two spheres side-by-side. Phys Fluids (2023) 35(9):92101. doi:10.1063/5.0166794
50. Yang R, Kai Y Dynamical properties, modulation instability analysis and chaotic behaviors to the nonlinear coupled Schrödinger equation in fiber Bragg gratings. Mod Phys Lett B (2023) 38:2350239. doi:10.1142/S0217984923502391
51. Li X, Zhu H, Yuan Q. Dilatancy equation based on the property-dependent plastic potential theory for geomaterials. Fractal and Fractional (2023) 7(11):824. doi:10.3390/fractalfract7110824
52. Zhou X, Liu X, Zhang G, Jia L, Wang X, Zhao Z. An iterative Threshold Algorithm of log-sum regularization for Sparse problem. IEEE Trans Circuits Syst Video Tech (2023) 33(9):4728–40. doi:10.1109/TCSVT.2023.3247944
53. Yin Y, Zhang R, Su Q. Threat assessment of aerial targets based on improved GRA-TOPSIS method and three-way decisions. Math Biosciences Eng (2023) 20(7):13250–66. doi:10.3934/mbe.2023591
54. Mukhtar S, Noor S. The numerical investigation of a fractional-order multi-dimensional Model of Navier–Stokes equation via novel techniques. Symmetry (2022) 14(6):1102. doi:10.3390/sym14061102
55. Noor S, Alshehry AS, Aljahdaly NH, Dutt HM, Khan I, Shah R. Investigating the impact of fractional non-linearity in the Klein–Fock–Gordon equation on quantum dynamics. Symmetry (2023) 15(4):881. doi:10.3390/sym15040881
56. Noor S, Alshehry AS, Dutt HM, Nazir R, Khan A, Shah R. Investigating the dynamics of time-fractional Drinfeld–Sokolov–Wilson system through analytical solutions. Symmetry (2023) 15(3):703. doi:10.3390/sym15030703
57. Odibat Z. Approximations of fractional integrals and Caputo fractional derivatives. Appl Math Comput (2006) 178(2):527–33. doi:10.1016/j.amc.2005.11.072
Keywords: effective iterative method, Wu-Zhang equation, fractional calculus, fractional partial difference equation, Caputo derivative
Citation: Yasmin H, Alderremy AA, Shah R, Hamid Ganie A and Aly S (2024) Iterative solution of the fractional Wu-Zhang equation under Caputo derivative operator. Front. Phys. 12:1333990. doi: 10.3389/fphy.2024.1333990
Received: 06 November 2023; Accepted: 29 January 2024;
Published: 21 February 2024.
Edited by:
Vijay Kumar Yadav, Amity University Gurgaon, IndiaReviewed by:
Marwan Alquran, Jordan University of Science and Technology, JordanAli Akgül, Siirt University, Türkiye
Amin Jajarmi, University of Bojnord, Iran
Naveed Anjum, Government College University, Faisalabad, Pakistan
Copyright © 2024 Yasmin, Alderremy, Shah, Hamid Ganie and Aly. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Humaira Yasmin, aGhhc3NhaW5Aa2Z1LmVkdS5zYQ==; Rasool Shah, cmFzb29sLnNoYWhAbGF1LmVkdS5sYg==
 Humaira Yasmin
Humaira Yasmin A. A. Alderremy2
A. A. Alderremy2 Rasool Shah
Rasool Shah Abdul Hamid Ganie
Abdul Hamid Ganie