- 1Graduate School of Integrated Sciences for Life, Hiroshima University, Hiroshima, Japan
- 2Organization for the Strategic Coordination of Research and Intellectual Properties, Meiji University, Tokyo, Japan
- 3Meiji Institute for Advanced Study of Mathematical Sciences (MIMS), Meiji University, Tokyo, Japan
- 4Graduate School of Arts and Sciences, The University of Tokyo, Tokyo, Japan
- 5Department of Physics, Institute of Physics, Budapest University of Technology and Economics, Budapest, Hungary
- 6HU-REN−BME Condensed Matter Physics Research Group, Budapest University of Technology and Economics, Budapest, Hungary
- 7Graduate School of Advanced Mathematical Sciences, Meiji University, Tokyo, Japan
1 Introduction
The self-propelled motion in inanimate systems is one of the fascinating manifestations of life-like behavior [1]. The size of these objects can range from molecular level- (e.g., photochemical oscillator [2] and chemo-hydrodynamic pulsations [3]) to macro- (e.g., droplets) [4–6] via microscales (e.g., Janus particles) [7–9], and the underlying mechanisms of the self-propelled motion can be diversified. It can be passive (the particles generate their motion along the gradient generated in the environment through thermophoresis, electrophoresis, or diffusiophoresis) and active (the objects also create a fluid flow, Marangoni flow, inside them which contributes to the motion). The BZ reaction has been studied theoretically and experimentally as a chemical oscillatory reaction that exhibits nonlinear phenomena, e.g., synchronization [10–15], bifurcation [16, 17], and pattern formation [18–21]. Repetition between swelling and contraction of a gel loaded with the catalyst of the BZ reaction was reported [10, 22, 23]. The periodic motion of a w/o emulsion droplet consisting of the BZ solution has been demonstrated [1, 24, 25]. However, there are no reports on self-propelled systems in which the BZ reaction-produced bubble generates the driving force. In this study, we developed a self-propelled bead that exhibited repetition between up-and-down motion and synchronization between the periodic motion of the bead and the BZ chemical oscillation via the CO2 bubble produced during the oxidation of malonic acid in the BZ reaction.
2 Experiments
The reagents used in the experiments were the same as those in a previous report [19]. Ferroin, as the metal catalyst of the BZ reaction, was adsorbed into cation exchange resin beads (Strong Acidic Cation Exchange 50Wx4 200–400 Mesh, H Form) in a similar manner to previous protocols [19]. 5.4 nmol ferroin was adsorbed per one bead (called a “BZ bead”). The BZ solution whose total volume was 1.0 mL composed of 0.75 M NaBrO3, 1.3 M malonic acid, and 0.95 M H2SO4 was poured into a glass vessel (diameter: 13 mm, height: 40 mm) and then a BZ bead was put into the solution. One hour after soaking, the vessel was placed on a Peltier device (Matsuo Electric Co., LTD., MET III, Japan) to control the temperature of the solution. Temperature was monitored with a thermometer (AS ONE Co., 1-5455–02 Digital Thermometer IT-2000, Japan). The chemical oscillation and motion of the bead were monitored with a digital video camera (SONY, HDR−CX590V, Japan) from the side view. The resulting movies were analyzed with ImageJ software (National Institutes of Health, Bethesda, MD).
3 Results
At first, we investigated the motion of a BZ bead in the BZ solution. Figure 1A shows an image sequence of up-and-down motion of the BZ bead. The BZ bead generated the bubble on the top of its surface (Figure 1A1) increasing the buoyancy. The object floated to the air/aqueous interface with the bubble once the buoyancy overcame the gravitational force acting on the BZ bead and bubble (Figures 1A2, 1A3). After reaching the interface, the bubble bursted, and the BZ bead came back to the bottom of the vessel driven by the gravitational force (see Figures 1A4, 1A5). Figure 1B shows the time-variation of the position of the BZ bead and the volume of the bubble generated on the BZ bead. The BZ bead started floating when the size of the bubble reached ∼2.4 × 10−2 mm3 (see Figure 1B). Supplementary Figure S1 shows the thermal gradients in the BZ solution. A cation exchange bead without adsorbing ferroin in the BZ solution with the thermal gradients exhibited no up-and-down motion (data not shown).
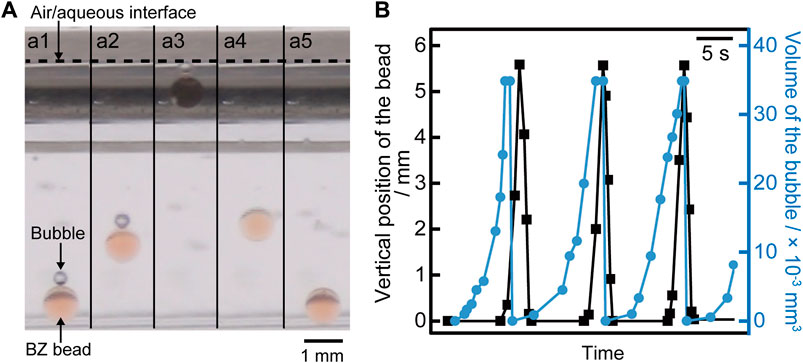
FIGURE 1. (A) Snapshots of vertical motion (side view) of the BZ bead when the temperature of the solution was 35°C. The time interval was 1.0 s. (B) Time-variation of the position of the BZ bead measured from the bottom of the vessel (filled black square) and the volume of the bubble on the bead (filled blue circle). The data corresponds to the Movie S1 in the Supplementary Material.
We also measured the period of up-and-down motion of the BZ bead (Tm) under various periods of the oscillatory reaction (Tr). Tr was adjusted by the temperature of the solution. Figure 2A shows the relationship between Tm and Tr at different temperatures. The relationship between Tm and Tr was linear, and the slope was approximately 3. We also measured the time elapsed between the latest oxidation of ferroin in the BZ bead and the time when the BZ bead left the bottom of the vessel as Δt at 30°C–35°C. Oxidations of ferroin were detected as the peak of the gray value on the center of the BZ bead (see Supplementary Figure S2). The reason for the temperature limit in this measurement was to accurately observe Δt at 40°C–45°C were difficult to observe accurately. Figure 2B shows the distribution on the phase difference between motion and oscillation, Δt/Tr. Smaller values of Δt/Tr was observed rather than lager ones.
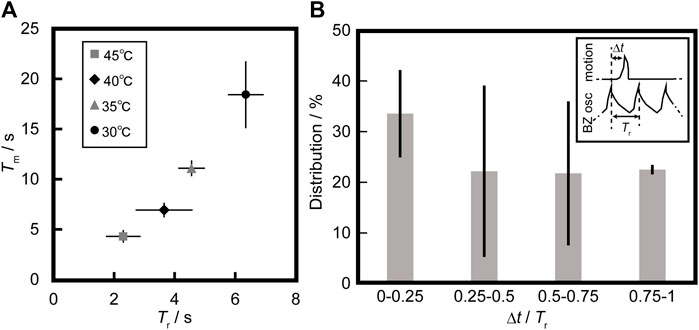
FIGURE 2. (A) Relationship between the average value of the period of up-and-down motion of the BZ bead (Tm) and period of the oscillatory reaction (Tr) at different temperatures. Tm and Tr were calculated from 10 cycles of oscillations under different temperatures and the error bars represent the standard deviations. (B) The distribution of Δt/Tr at 30°C–35°C, where Δt corresponds to the time elapsed between the latest oxidation of ferroin in the BZ bead and the time when the BZ bead left the bottom of the vessel, Tr was the latest period of oscillatory reaction before up-and-down motion. The data sets were 17, 18 and 23 obtained from three experiments. The error bars represent the standard deviations.
4 Discussion
We discuss the relationship between up-and-down motion of the bead and gas production in the BZ oscillatory reaction in relation to the previous study [26]. Figures 1A,B suggest that the driving force of the up motion is buoyancy due to the bubble, and it starts after inflating the bubble to a constant size. This bubble is composed of CO2, which is produced by oxidizing malonic acid in the reduction using a metal catalyst [26]. The bead with the bubble moves up once the overall density of the bead and bubble reaches the density of the solution. We assume that the density of the solution is equal to the density of the water (at 35°C), which is 9.94 × 10−4 g/mm−3. Based on the measurement, the mass of the bead is 4.71 × 10−4 g. To start the lift of the bubble, the total volume of the system should be 9.94 × 10−4 g/mm−3/4.71 × 10−4 g = 0.474 mm3. The volume of the bead is 0.454 mm3. Therefore, the volume of the bubble should be 0.020 mm3. Using the image analysis, the volume of the bubble was obtained as 0.024 mm3, which is close to the value that was estimated based on hydrostatics. CO2 bubble is released at the air/aqueous interface, and the BZ bead comes back to the bottom of the vessel because of gravity. Figure 2A shows that three cycles of BZ oscillations are necessary to float the BZ bead regardless of the period of BZ oscillations. This may be because the volume of CO2 produced by one BZ oscillation was constant. Figure 2B suggests that the BZ bead tends to float relatively early after the reduction phase in the BZ reaction. This may be because more CO2 is produced by oxidizing malonic acid when the metal catalyst of the BZ reaction is reduced from Fe3+ to Fe2+.
5 Conclusion
In this study, we reported up-and-down motion synchronized with the BZ reaction. The bubble of CO2 was generated from a ferroin-loaded bead called BZ bead. The bead and the bubble float to the air/aqueous interface because of the buoyancy of the bubble and release CO2. After that, the BZ bead is back to the bottom of the vessel because of the gravity. The synchronized ratio of the chemical oscillation and up-and-down motion is constant regardless of the period of BZ oscillation. In addition, floating BZ bead tended to occur relatively soon after the reduction of the BZ reaction. The up-and-down BZ beads propose the utility of BZ reaction for a periodic mass transport system. Such a mass transport system is expected to provide a novel platform for a more complex and organized mass transport system by applying pattern formation, optical control, and synchronous phenomena of BZ reaction-based systems.
Author contributions
YK: Data curation, Formal Analysis, Investigation, Methodology, Software, Visualization, and Writing–original draft. MK: Data curation, Investigation and Writing–review and editing. KK: Data curation and Formal Analysis. MM: Validation and Writing–review and editing. IL: Formal Analysis, Validation and Writing–review and editing. NJS: Resources, Validation and Writing–review and editing. SN: Conceptualization, Project administration, Resources, Supervision, Validation, Visualization, and Writing–review and editing.
Funding
The author(s) declare financial support was received for the research, authorship, and/or publication of this article. This study was supported by JSPS KAKENHI (Grant Nos. JP20H02712, JP20H01871, and JP21H00996), the Cooperative Research Program of “Network Joint Research Center for Materials and Devices” (No. 20211061) to SN and JSPS Japan–Hungary Bilateral Joint Research Project (JPJSBP 120213801).
Acknowledgments
We acknowledge the financial support from JSPS Japan–Hungary Bilateral Joint Research Project (JPJSBP 120213801).
Conflict of interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Publisher’s note
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
Supplementary material
The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/fphy.2023.1306533/full#supplementary-material
References
1. Suematsu NJ, Nakata S. Evolution of self-propelled objects: from the viewpoint of nonlinear science. Chem Eur J (2018) 24:6308–24. doi:10.1002/chem.201705171
2. Gentili PL, Dolnik M, Epstein IR. “Photochemical oscillator”: colored hydrodynamic oscillations and waves in a photochromic system. J Phys Chem C (2014) 118:598–608. doi:10.1021/jp407393h
3. Budroni MA, Polo A, Upadhyay V, Bigaj A, Rongy L. Chemo-hydrodynamic pulsations in simple batch A + B → C systems. J Chem Phys (2021) 154:114501. doi:10.1063/5.0042560
4. Lagzi I., Soh S., Wesson P. J., Browne K. P., Grzybowski B. A. (2010). Maze solving by chemotactic droplets. J Am Chem Soc. 132, 1198–9. doi:10.1021/ja9076793
5. Holler S, Hanczyc M. M. Droplet based synthetic biology: chemotaxis and interface with biology. In The 2019 Conference on Artificial Life (2019) Cambridge, MA: MIT Press, 650–1. doi:10.1162/isal_a_00234
6. Čejková J., Novák M., Štěpánek F., Hanczyc M. M. Dynamics of chemotactic droplets in salt concentration gradients. Langmuir. (2014) 30, 11937–44. doi:10.1021/la502624f
7. Paxton W. F., Kistler K. C., Olmeda C. C., Sen A., Angelo S. K., Cao Y., et al. Catalytic nanomotors: autonomous movement of striped nanorods. J Am Chem Soc (2004) 126, 13424–31. doi:10.1021/ja047697z
8. Liu R., Sen A. Autonomous nanomotor based on copper-platinum segmented nanobattery. J Am Chem Soc. 2011 133, 20064–7. doi:10.1021/ja2082735
9. Pavlick R. A., Sengupta S., McFadden T., Zhang H., Sen A. A polymerization-powered motor. Angew Chem Int Ed (2011) 50:9374–7. doi:10.1002/anie.201103565
10. Yoshimoto M, Yoshikawa K, Mori Y, Hanazaki I. Asymmetric coupling stabilizes the out-of-phase mode: experimental evidence in the Belousov—zhabotinsky reaction. Chem Phys Lett (1992) 189:18–22. doi:10.1016/0009-2614(92)85146-2
11. Ito K, Ezaki T, Suzuki S, Kobayashi R, Hara Y, Nakata S. Synchronization of two self-oscillating gels based on chemo-mechanical coupling. J Phys Chem B (2016) 120:2977–83. doi:10.1021/acs.jpcb.6b00873
12. Horvath V, Gentili PL, Vanag VK, Epstein IR. Pulse-coupled chemical oscillators with time delay. Angew Chem Int Ed (2012) 51:6878–81. doi:10.1002/anie.201201962
13. Crowley MF, Field RJ. Electrically coupled Belousov-Zhabotinskii oscillators. 1. Experiments and simulations. J Phys Chem (1986) 90:1907–15. doi:10.1021/j100400a033
14. Hohmann W, Kraus M, Scheneider FW. Pattern recognition by electrical coupling of eight chemical reactors. J Phys Chem A (1999) 103:7606–11. doi:10.1021/jp991480n
15. Gentili PL, Micheau JC. Light and chemical oscillations: review and perspectives. J Photochem Photobiol C: Photochem Rev (2020) 43:100321. doi:10.1016/j.jphotochemrev.2019.100321
16. Maselko J. Determination of bifurcation in chemical systems. An experimental method. Chem Phys (1982) 67:17–26. doi:10.1016/0301-0104(82)88054-3
17. Noszticzius Z, Stirling P, Wittmann M. Measurement of bromine removal rate in the oscillatory BZ reaction of oxalic acid. Transition from limit cycle oscillations to excitability via saddle-node infinite period bifurcation. J Phys Chem (1985) 89:4914–21. doi:10.1021/j100269a007
18. Zaikin AN, Zhabotinsky AM. Concentration wave propagation in two-dimensional liquid-phase self-oscillating system. Nature (1970) 225:535–7. doi:10.1038/225535b0
19. Kuze M, Kitahata H, Steinbock O, Nakata S. Distinguishing the dynamic fingerprints of two- and three-dimensional chemical waves in microbeads. J Phys Chem A (2018) 122:1967–71. doi:10.1021/acs.jpca.7b12210
20. Matsuo M, Yasuda K, Nishi K, Kuze M, Kitahata H, Nishiura Y, et al. Originating point of traveling waves on a spherical field dependent on the nature of substrate surface. J Phys Chem C (2023) 127:1841–7. doi:10.1021/acs.jpcc.2c08041
21. Bánsági T, Vanag VK, Epstein IR. Tomography of reaction-diffusion microemulsions reveals three-dimensional turing patterns. Science (2011) 331:1309–12. doi:10.1126/science.1200815
22. Yoshida R, Takahashi T, Yamaguchi T, Ichijo H. Self-Oscillating gel. J Am Chem Soc (1996) 118:5134–5. doi:10.1021/ja9602511
23. Yoshida R. Self-oscillating gels driven by the belousov-zhabotinsky reaction as novel smart materials. Adv Mater (2010) 22:3463–83. doi:10.1002/adma.200904075
24. Suematsu NJ, Mori Y, Amemiya T, Nakata S. Oscillation of speed of a self-propelled belousov-zhabotinsky droplet. J Phys Chem Lett (2016) 7:3424–8. doi:10.1021/acs.jpclett.6b01539
25. Suematsu NJ, Udagawa S. Real-time mode-switching of a self-propelled droplet controlled by the photosensitive belousov-zhabotinsky reaction. Chem Lett (2023) 52:110–2. doi:10.1246/cl.220513
Keywords: self-propelled object, Belousov-Zhabotinsky reaction, up-and-down motion, bubble, buoyancy
Citation: Kubodera Y, Kuze M, Kagawa K, Muneyuki M, Lagzi I, Suematsu N and Nakata S (2023) Up-and-down motion of a Belousov-Zhabotinsky bead in couple with chemical oscillation. Front. Phys. 11:1306533. doi: 10.3389/fphy.2023.1306533
Received: 04 October 2023; Accepted: 28 November 2023;
Published: 22 December 2023.
Edited by:
Adriano Tiribocchi, National Research Council (CNR), ItalyReviewed by:
Pier Luigi Gentili, Università degli Studi di Perugia, ItalyKonrad Giżyński, Polish Academy of Sciences, Poland
Copyright © 2023 Kubodera, Kuze, Kagawa, Muneyuki, Lagzi, Suematsu and Nakata. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Satoshi Nakata, nakatas@hiroshima-u.ac.jp; Masakazu Kuze, kuzem1234@gmail.com
 Yujin Kubodera1
Yujin Kubodera1