
95% of researchers rate our articles as excellent or good
Learn more about the work of our research integrity team to safeguard the quality of each article we publish.
Find out more
ORIGINAL RESEARCH article
Front. Phys. , 21 June 2023
Sec. Interdisciplinary Physics
Volume 11 - 2023 | https://doi.org/10.3389/fphy.2023.1236828
 Yulu Zhang1*
Yulu Zhang1* Hua Lu1,2
Hua Lu1,2With the development of quantum computing, the application of quantum neural networks will be more and more extensive, and its security will also face more challenges. Although quantum communication has high security, quantum neural networks may have many internal and external insecure factors in the process of information transmission, such as noise impact during the preparation of input quantum states, privacy disclosure during transmission, and external attacks on the network structure, which may cause major security incidents. Because of the possible insecurity factors of quantum neural networks, this paper proposes a quantum sampling method to detect the state of quantum neural networks at each stage, so as to judge whether there are security risks in quantum neural networks and thus ensure their security. The method also provides a safe basis for further research on the stability and reliability of quantum neural networks.
The principles of artificial neural networks (ANNs) and quantum neural networks (QNNs) are simulations of the working mechanism of biological neural networks, and many of their functions come from parallel information processing capabilities. Compared with the QNN, ANN’s simulation of the human brain is relatively simple. It uses simplified neuron models and learning methods to solve problems or make certain decisions. Up to now, neural network theory has achieved extensive success in many research fields, such as pattern recognition, automatic control, signal processing, assistant decision-making, artificial intelligence, processing big data, and so on. However, compared with the human brain, the existing artificial neural network theory still has many defects, mainly reflected in the following aspects: 1) Learning in the traditional sense is a sequential processing mode and the processing speed slows down gradually with the increase of the amount of information, which is not in line with the characteristics of real-time response and large-capacity work of the human brain. 2) The human brain takes memory and recalls information as a part of learning. But for neural networks, the trained samples are only used to change the connection weights and will be immediately forgotten and not stored. 3) The neural network needs repeated training and continuous learning, but the human brain can learn once. 4) The neural network will have a catastrophic forgetting phenomenon when receiving new information. Therefore, to further develop the neural network theory, new theories, and new ideas must be introduced. The combination of quantum theory and neural networks is a useful attempt.
QNN combines the basic knowledge of neural networks with quantum computing and makes use of quantum computing theory, which shows great advantages over traditional neural networks in terms of parallel processing capacity and storage capacity. In 1995, Kak published the paper “On Quantum Neural Computing” and put forward the concept of quantum neural computing for the first time [1]. In the same year, Chrisley proposed the concept of quantum learning and proposed the quantum neural network model of a non-superposition state and the corresponding learning algorithm. Narayanan proposed a quantum-inspired neural network model [2]. In 1996, Toth proposed a quantum cellular neural network model. The performance of the network is investigated for the two-state cell model [3]. In the same year, Perus proposed that there is an interesting similarity between quantum parallelism and neural networks [4]. The collapse of the quantum wave function is very similar to the phenomenon of neural pattern reconstruction in human memory. In 1997, Gopathy et al proposed a quantum neural network model based on a multi-layer excitation function which was studied from the idea of quantum state superposition [5]. In the same year, Lagaris et al proposed an artificial neuron model with quantum mechanical properties to solve the initial value problem of partial differential equations and successfully applied it to solve the Schrodinger equation [6]. Dan proposed the algorithm of quantum associative storage. Compared with traditional storage, quantum associative storage has exponential storage capacity [7, 8]. In 1998, Menneer comprehensively and deeply discusses how to introduce quantum computing into an artificial neural network from the point of view of a multi-universe. It was proved that quantum neural network is more effective than traditional neural network for classification problem [9]. In 1999, Li published a paper on the quantum parallel SOM algorithm and applied it to satellite remote sensing image recognition [10]. In the same year, Berhman et al constructed quantum neural networks of time and space based on the molecular model of quantum dots [11]. In 2000, Ajit et al studied the structure and model of quantum neural networks and put forward the idea of constructing a superimposed multi-universe quantum neural network model from the point of view of multi-universe quantum theory [12]. In the same year, Matsui et al of Japan proposed a new method of quantum states as neuron states and constructed a quantum neuron model based on qubit description on the basis of the traditional neural network topology. According to the characteristics of a one-bit quantum revolving gate and two controlled non-gates, a learning algorithm based on the complex operation is constructed, and the performance of the model is tested by 4-bit parity and function approximation problem [13]. In 2001, Altaisky proposed a quantum neural network model based on the principle of quantum information processing. In this model, the input and output are realized by photon beams with different polarization directions, and the connection weights are realized by beam splitters and phase shifters [14]. In 2005, Matsui et al summarized their previous work and verified the performance of their proposed model in more detail with 6-bit parity problems [15]. In 2007, Maeda M and others continued to conduct in-depth research on quantum neural networks and proposed a quantum neural learning algorithm for solving XOR problems according to the quantum circuit structure [16]. In the same year, Shafee pointed out that quantum neural networks were similar to biological neural networks, and quantum neural networks can be constructed by AND gates and controlled non-gates [17].
In 2014, Schuld et al introduced a systematic approach to the study of quantum neural networks, mainly about Hopfield networks and associative memory tasks. They also summarized the difficulties of combining the nonlinearity of neural computing with the linearity of quantum computing [18]. In 2018, Steinbrecher et al proposed a quantum optical neural network. Experimental results showed that it is a powerful quantum optical system design tool [19]. Beer et al proposed a real quantum simulation of classical neurons, which can form a quantum feed forward neural network capable of general quantum computation [20]. In 2021, Kashif et al proposed a method of designing quantum layers in hybrid quantum-classical neural networks. The experimental results show that, compared with the traditional model, the addition of the quantum layer in the mixed variant provides a significant computational advantage [21]. Fard et al proposed a quantum neural network with multi-neuron interaction and applied it to pattern recognition tasks [22]. Silva et al proposed a quantum neural network model [23], which is directly extended by classical perceptrons, which can solve some problems in the existing quantum perceptron models. To apply random quantum circuits to medical image detection, Houssein et al proposed a hybrid quantum-classical convolution neural network model [24].
Generally speaking, the current research in the field of QNN is mainly focused on the following aspects: 1) To study the problems in quantum computing through the neural network model. 2) To make full use of the ultra-high-speed, super-parallel, and exponential storage capacity of quantum computing to improve the structure and performance of the neural network. 3) By introducing quantum theory into the traditional neural network, a new network model is constructed, and an efficient learning algorithm is designed to improve the intelligence level of the network.
However, when developing QNN, we should also consider the security problems of QNN itself and the security problems that QNN may cause to the outside world. For example, QNN’s own structure is damaged, information leaks and attacks, which may cause major security incidents in the future. Another problem is the “quantum advantage” of quantum computers, that is, the ability of quantum computers to handle some problems that conventional computers cannot. This capability can pose a threat to current information security technologies such as encryption algorithms and digital signatures. Therefore, in the development of quantum computing and quantum neural networks, security issues must be paid attention to.
This paper enumerates a quantum neural network model and takes this model as an example. Zhou and Ding [25] proposed a quantum M-P neural network model based on the traditional M-P neural network and using the quantum linear superposition property. They not only give the working principle of the quantum neural networks but also give examples to describe the weight updating algorithm when the input state is orthogonal and non-orthogonal basis set, respectively.
The inner product of two quantum states,
The above is the inner product of a continuous function, which can be simplified to a discrete function:
If the
Based on the analysis and summary of the basic characteristics of neurons, McCulloch and Pitts first proposed the M-P model [26], the model is shown in Figure 1. This model had a great influence on the research in the fields of brain models, automata, and artificial intelligence, which leads the era of neuroscience theoretical research. In Figure 1, each input of a neuron has a weighting coefficient, the weight
The above can be expressed in mathematical expressions as follows:
where
Quantum M-P neural network model is an artificial neural network model based on quantum computing, which uses quantum superposition and entanglement properties to process information and learning. Its basic structure is similar to the traditional M-P neural networks, while its neurons and connection weights are expressed in qubits as shown in Figure 2.
The expression is
where
The output can be expressed as:
The expression can also be expressed as:
where
In the quantum field, the quantum state output of the quantum M-P neural network model is expressed as follows:
That is,
If
In the analysis of the previous section, it was assumed that states
where
Similar to the traditional learning mechanism, the neural network usually has a weight set, which is constantly modified and updated through learning in the training process, so that the error between the actual output of the network and the target output is acceptable. Zhou and Ding proposed a weight-updating algorithm for a quantum M-P network [25]. The input-output relationship of the quantum M-P network model can be simplified as follows:
The process of the weight learning algorithm is as follows:
a. Initialize a weight matrix
b. A pair of actual input and output values
c. Calculate the actual output
d. Update the network weight
e. Repeat steps c and d until the error of the output is within an acceptable range.
In the quantum M-P neural network model, the input data is encoded as qubits and then operated through a series of quantum gates. Each quantum neuron can perform certain calculations and transformations, and the final output is also in the form of qubits. Through the combination and adjustment of multiple quantum neurons, we can realize the classification, recognition, regression, and other tasks of input data. Compared with the traditional M-P neural network model based on classical computation, quantum M-P neural network model has more powerful computing power and higher learning efficiency. However, due to the limitations of current quantum computing technology, it is still a great challenge to realize large-scale quantum M-P neural network models. At the same time, the network model also has a lot of security problems, such as external intrusion when the weight is updated, environmental noise impact, etc., will seriously affect the performance of the network.
The development of artificial neural network is earlier than quantum neural network, and it is widely used in all walks of life. Although the technology is becoming more mature, ANN still faces significant security problems. Similarly, with the development of quantum computing, the application of quantum neural network will be more and more extensive, and its security will also face more challenges. In particular, due to the special working mechanism of QNN, there may be more security issues involved. One of the major security concerns is the potential for privacy breaches of data when using quantum neural networks for machine learning. Because quantum neural networks can process data through properties such as superposition and entanglement of quantum states, there may be a risk that some private information will be leaked. Another security issue is the “quantum advantage” of quantum computers, that is, the ability of quantum computers to handle some problems that conventional computers cannot. This capability can pose a threat to current information security technologies such as encryption algorithms and digital signatures.
In addition to the two main security issues mentioned above, there are also external security factors that may be suffered:
Malicious use: Hackers and other bad actors are beginning to use quantum neural networks to attack systems and networks. For example, hackers can use neural networks to forge identity information, gain access to protected systems, and steal sensitive information.
Adversarial attacks: Adversarial attacks are attacks against quantum neural networks in which an attacker tricks the neural network by adding noise or deleting data. Such attacks can lead to model inaccuracies or miscalculations.
Data privacy: Neural networks require a lot of training data, but this data often contains sensitive information. Attackers can steal training data by attacking neural networks, thereby compromising personal privacy.
Backdoor attacks: An attacker can embed a backdoor in a neural network to perform malicious actions while performing certain specific tasks. This type of attack can allow an attacker to take control of a system remotely, steal sensitive information or compromise the system.
Adversarial example: An adversarial example is an attack against a neural network in which the attacker tricks the neural network by using special techniques to generate misleading samples.
In general, in the application of quantum computers and quantum neural networks, security issues need to be highly valued and guaranteed.
A quantum neural network is not the same as the traditional neural network, it does not use weighted and biased neurons but encodes the input data into a series of qubits. QNN applies a series of quantum gates and then changes the parameters of the gate to minimize the loss function. In quantum neural networks, the quantum circuit structure usually consists of three parts, and the basic structure is shown in Figure 4.
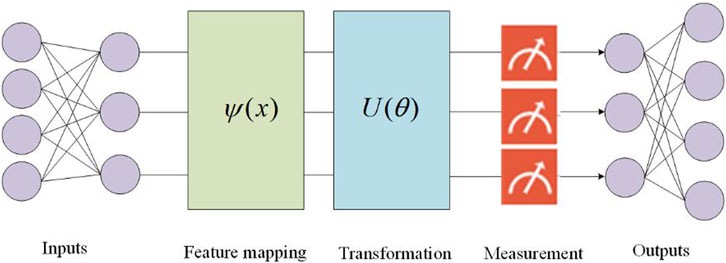
FIGURE 4. The basic structure of the quantum neural network mainly consists of three parts, feature mapping, transformation, and measurement, and the left and right ends of the structure can be the classical network as the input and output.
The feature mapping part is the coding circuit, which is used to encode the classical data into quantum data; the transformation part is the training circuit, which is used to train the parameters with a parametric quantum gate; and the measurement part is used to detect whether the measured value is close to the expected value of the target.
In order to further study the security performance of each part of the quantum neural network, this paper combined with the performance of the quantum M-P neural network model, firstly from the coding part of the neural network structure, the stability of the data processed by the coding part is discussed: Any given input is randomly sampled at the output end after passing through the coded circuit, so as to simulate the original distribution of the quantum states at the input end. At this time, the training circuit does not contain reference quantum gates.
Quantum neural networks include quantum states and quantum gate manipulation processes, which can describe the evolution of quantum states through operations in the form of their matrices:
We can simply understand this process as a matrix and a vector performing a point multiplication operation to obtain an updated state vector:
Under the framework of quantum computing, since the general quantum gate operations are unitary, whether it is a pre-update or post-update operation, the resulting state vector is always normalized:
When considering sampling in this paper, in order to facilitate calculation, we convert the state vector to a probability vector first, and then sample. The characteristics of the probability vector are as follows:
where
After conversion to a probability amplitude vector, each element represents the probability of obtaining the current binary quantum state. In this way, when obtaining the state vector or probability amplitude vector of a quantum state, it is actually obtaining the probability distribution of the system. Through this probability distribution, we can perform Monte Carlo simulation: first perform uniform random scattering points on [0, 1), while converting the probability amplitude vector into its corresponding cumulative distribution map, and finally calculate the position of the cumulative distribution map corresponding to the randomly scattered points, we can obtain the simulation sampling under the current probability, which is implemented as follows.
Assume the distribution of a probability amplitude and then sample it. Given the distribution of probability amplitudes for an exponential descent, select a probability distribution function
Next, a uniform random number between [0, 1) is generated as shown in Figure 6, and the more scattered points, the more obvious the uniformly distributed result presented.
Then, the cumulative distribution function is used to do a cumulative superposition operation on the probability vector obtained earlier, and the corresponding calculation method is as follows:
It is easy to predict that the end point of the cumulative distribution function must be 1, because of the previous definition
Finally, the quantum state sampling process directly compares the probability distribution function and the analog sampling results together, as shown in Figure 8:
The simulation results are already very close, and if you continue to increase the number of samples, the results will be closer to the true distribution, as shown in Figure 9:
Therefore, after obtaining the probability amplitude, we can sample the probability amplitude according to the precision requirements of the scene, and all the functions are completed here.
Next up is the transformation part. Quantum circuits constructed in quantum neural networks contain parametric gates, whose parameter values can be adjusted according to needs after the circuits are established. This part of the quantum circuit can not only be transmitted forward, but also can be propagated back: the gradient of each parameter relative to the objective function (generally the expected value of a mechanical quantity in a quantum state) can be obtained by derivation methods such as “central difference,” and then the parameters can be updated with an optimizer. After training, the model learns a set of parameters for a quantum circuit, which it controls to make accurate categorical predictions about unknown inputs. This is much like a classic neural network: you define a variable name and then update its parameters according to the back propagation algorithm. At present, there are many quantum computing frameworks for studying quantum neural networks, and the deep integration with classical machine learning frameworks makes the updating of quantum circuit parameters more convenient. This paper does not conduct simulation training for a certain kind of quantum neural network.
In this section, we simulate the original distribution of quantum states at the input of the quantum neural network by sampling quantum data at the output. The sampling results show that with the increase of the number of iterations, QNN can almost completely approximate the real distribution of the input values. Each part of QNN is randomly sampled by quantum sampling to judge whether there are security risks in the quantum neural network and ensure its security.
In this paper, a protection method is proposed to solve the possible security problems of quantum neural networks. The quantum sampling algorithm is used to randomly sample the structure of each part of the quantum neural network. The sampling results show that the probability distribution of the data processed by the quantum neural network is almost identical to that of the original data, which also shows that the method provides security for the quantum neural network. Although the above security issues are real, researchers are constantly looking for solutions to ensure the security of neural networks. For example, they are developing adversarial training techniques to help neural networks better cope with adversarial attacks and researching encryption technology to ensure secure communication.
The original contributions presented in the study are included in the article/supplementary material, further inquiries can be directed to the corresponding author.
YZ: methodology, writing—original draft, formal analysis. HL: writing—review and editing. All authors contributed to the article and approved the submitted version.
The work described in this paper was supported by the National Natural Science Foundation of China (No. 12175057).
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
1. Kak S. On quantum neural computing. Inf Sci (1995) 83(3-4):143–60. doi:10.1016/0020-0255(94)00095-s
3. Tóth G, Lent CS, Tougaw PD, Brazhnik Y, Weng W, Porod W. Quantum cellular neural networks[J]. Superlattices Microstruct (1996) 20(4):473–478.
5. Purushothaman G, Karayiannis NB. Quantum neural networks (QNNs): Inherently fuzzy feedforward neural networks. IEEE Trans Neural Networks (1997) 8(3):679–93. doi:10.1109/72.572106
6. Lagaris IE, Likas A, Fotiadis D. Artificial neural network methods in quantum mechanics. Comp Phys Commun (1997) 104:1–14. doi:10.1016/s0010-4655(97)00054-4
7. Ventura D, Martinez T. Quantum associative memory with exponential capacity. In: Proceeding of the IEEE World Congress on IEEE International Joint Conference on Neural Networks; May 1998; Anchorage, AK, USA. IEEE Xplore (1998).
8. Dan V, Martinez T. Quantum associative memory. Inf Sci (2000) 124(1-4):273–96. doi:10.1016/s0020-0255(99)00101-2
10. Weigang L, da Silva NC. A study of parallel neural networks[C]//IJCNN'99. In: International Joint Conference on Neural Networks. Proceedings (Cat. No. 99CH36339). IEEE (1999) 2:1113–1116.
11. Behrman EC, Steck JE, Skinner SR. A spatial quantum neural computer. In: Proceeding of the IJCNN'99. International Joint Conference on Neural Networks. Proceedings (Cat. No.99CH36339); July 1999; Washington, DC, USA. IEEE (1999).
12. Ajit N, Tammy M. Quantum artificial neural network architectures and components. Inf Sci (2000) 128:231–55. doi:10.1016/S0020-0255(00)00055-4
13. Matsui N, Kouda N, Nishimura H. Neural network based on QBP and its performance. In: Proceedings of the IEEE-INNS-ENNS International Joint Conference on Neural Networks. IJCNN 2000. Neural Computing: New Challenges and Perspectives for the New Millennium; July 2000; Como, Italy. IEEE (2000).
15. Kouda N, Matsui N, Nishimura H, Peper F. Qubit neural network and its learning efficiency. Neural Comput Appl (2005) 14(2):114–21. doi:10.1007/s00521-004-0446-8
16. Maeda M, Suenaga M, Miyajima H. Qubit neuron according to quantum circuit for XOR problem. Appl Math Comput (2007) 185(2):1015–25. doi:10.1016/j.amc.2006.07.046
17. Shafee F. Neural networks with quantum gated nodes. Eng Appl Artif Intelligence (2007) 20(4):429–37. doi:10.1016/j.engappai.2006.09.004
18. Schuld M, Sinayskiy I, Petruccione F. The quest for a quantum neural network. Quan Inf Process (2014) 13(11):2567–86. doi:10.1007/s11128-014-0809-8
19. Steinbrecher GR, Olson JP, Englund D, Carolan J. Quantum optical neural networks[J]. npj Quantum Information (2019) 5(1):60.
20. Beer K, Bondarenko D, Osborne TJ, Salzmann R, Scheiermann D, Farrelly T, Wolf R. Training deep quantum neural networks. Nat Commun (2020) 11:808. doi:10.1038/s41467-020-14454-2
21. Kashif M, Al-Kuwari S. Design space exploration of hybrid quantum–classical neural networks. Electronics (2021) 10(23):2980. doi:10.3390/electronics10232980
22. Fard ER, Aghayar K, Amniat-Talab M. Quantum pattern recognition with multi-neuron interactions. Quan Inf Process (2018) 17:42. doi:10.1007/s11128-018-1816-y
23. Silva A, Ludermir TB, Oliveira WD. Quantum perceptron over a field and neural network architecture selection in a quantum computer. Neural Networks (2016) 76:55–64. doi:10.1016/j.neunet.2016.01.002
24. Houssein EH, Abohashima Z, Elhoseny M, Mohamed WM. Hybrid quantum convolutional neural networks model for COVID-19 prediction using chest X-Ray images. J Comput Des Eng (2021) 9:343. doi:10.1093/jcde/qwac003
25. Zhou RG, Ding QL. Quantum M-P neural network. Int J Theor Phys (2007) 46(12):3209–15. A Journal of Original Research and Reviews in Theoretical Physics and Related Mathematics, Dedicated to the Unification of Physics. doi:10.1007/s10773-007-9437-8
Keywords: quantum computing, quantum neural network, security studies, quantum sampling, artificial neural network
Citation: Zhang Y and Lu H (2023) Protecting security of quantum neural network with sampling checks. Front. Phys. 11:1236828. doi: 10.3389/fphy.2023.1236828
Received: 08 June 2023; Accepted: 13 June 2023;
Published: 21 June 2023.
Edited by:
Ma Hongyang, Qingdao University of Technology, ChinaCopyright © 2023 Zhang and Lu. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Yulu Zhang, eWx6QGhhaW5hbnUuZWR1LmNu
Disclaimer: All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article or claim that may be made by its manufacturer is not guaranteed or endorsed by the publisher.
Research integrity at Frontiers

Learn more about the work of our research integrity team to safeguard the quality of each article we publish.