- 1Institute of Computing Science and Technology, Guangzhou University, Guangzhou, China
- 2Department of Mathematics, University of Mazandaran, Babolsar, Iran
- 3Department of Mathematics, Prince Sattam Bin Abdulaziz University, Al-Kharj, Saudi Arabia
The cubic fuzzy graph structure is a tool for modeling problems, in which there are two fuzzy values for each variable and the relationships between them that cannot be expressed as a single fuzzy number. Inducing the same relationship among different subjects has an important effect on the understanding of uncertain problems. This is especially ambiguous and complicated when we are dealing with two different fuzzy values. With the aim of explaining edge regular in relationships among vertices, the current research has introduced this concept in the cubic fuzzy graph structure and expressed some of its characteristics. The edge regular and the total edge regularity are described in relation to several relationships. This concept has been applied in some special types such as the complete cubic fuzzy graph structure, and its results have been reviewed. Moreover, the vertex regular and its relationship with the edge regularity have been discussed. This study showed that the degree of vertices is effective in the edge adjustment process. In the end, an application of the topic under discussion is presented.
1 Introduction
In today’s world, a graph is a well-known mathematical model for a set whose members are related in some way. Mathematicians are particularly interested in understanding how many vertices and edges a graph can have before various substructures appear. They eagerly look for a set of vertices that are all connected by edges of the same color after certain coloring procedures. In social networks, edges that do not belong to any cluster or that connect different clusters are important in detecting anomalies. In similar cases, especially in weighted graphs, the idea of regularity of vertices and edges in a graph was gradually proposed.
In dealing with some events, classical graphs showed that they are not able to accurately describe and model uncertain problems. The theory of fuzzy set (FS) proposed by Zadeh [1] tried to model human reasoning, and in this process, it used approximate information and inaccurate data to make decisions under uncertain conditions. Actually, these systems mathematically model the existing inaccuracy and provide a suitable tool for real problems. With the introduction of the fuzzy graph (FG) based on fuzzy sets by Rosenfeld [2], a new perspective in the field of weighted graphs was opened to researchers. Gradually, different types of FGs were proposed by researchers. Talebi [3] studied the Cayley fuzzy graph. A generalization of fuzzy sets called the intuitionistic fuzzy set (IFS) was explained by Atanassov [4]. Borzooei et al. [5] presented properties of the product on the intuitionistic fuzzy graph (IFG). In 2011, Akram and Dudek [6] proposed an interval of fuzzy numbers instead of a fuzzy number by introducing the interval-valued fuzzy graph (IVFG). Concepts of the interval-valued intuitionistic fuzzy graph (IVIFG) were introduced by Talebi et al. [7, 8]. Rashmanlou et al. [9] explained some concepts of the bipolar fuzzy graph. Some properties of the single-valued neutrosophic graph were studied by Zeng et al. [10]. Certain concepts of vague graphs were studied by Kosari et al. [11–13]. Akram et al. [14–16] investigated concepts of connectivity in the m-polar fuzzy network model. The connectivity index in a directed rough fuzzy graph was studied by Ahmad et al. [17]. An extension of the fuzzy competition graph and its applications was presented by Pramanik et al. [18].
In 2006, Sampathkumar [19] established a new concept of graphs called the graph structure (GS) by generalizing signed or colored graphs. Since uncertainty and ambiguity in many phenomena often occur in the form of two or more separate relationships, therefore, a large part of problems can be modeled with the fuzzy graph structure (FGS). The idea of the FGS was first presented by Dinesh [20]. This concept was later developed by Ramakrishnan and Dinesh [21]. The progress of the FGS was further completed by the introduction of the intuitionistic fuzzy graph structure (IFGS) and m-polar FGS by Akram et al. [22, 23]. Kou et al. [24] researched the vague graph structure. Some decision-making based on the FGS was presented by Akram et al. [25, 26].
In general, in all types of FGs, most of the membership values of vertices and edges are in the form of one or more fuzzy numbers or one or more interval-valued fuzzy numbers. In fuzzy research studies, it was found that it was not possible to assign a fuzzy number to all graph vertices, especially when the membership value cannot be expressed with a fuzzy number. Jun et al. [27] tried to use two fuzzy values and interval fuzzy values in assigning the membership of graph vertices. By introducing the cubic fuzzy set (CFS), they were able to label the vertices of an FG with two fuzzy and interval values by combining FS and IVFS. With the flexibility of this concept, various problems arising from uncertainties can be solved. June et al. [28] also combined the neutrosophic set with CFS and presented a new set called neutrosophic CFS. Novel neutrosophic cubic graph structures were introduced by Gulistan et al. [29]. Muhiuddin et al. [30] studied graphs based on m-polar cubic structures. New types of CFGs and their applications are categorized in the studies of Rashid et al. [31]. Muhiuddin et al. [32] presented a new definition of CFG. Rashmanlou et al. [33] explained some of the concepts of the CFG.
The concept of the regular FG was first mentioned in the research by Ghani and Radha [34]. Pal et al. [35, 36] introduced the concept of the irregular and regular FGs. The irregularity concept, total irregularity, and total degree in an FG were defined by Gani and Lathi [37]. The degree and the total degree of an edge were introduced by Radha and Kumaravel [38]. Cary [39] initiated the idea of perfectly regular and perfectly edge regular FGs. Karunambigai et al. [40] introduced the concept of edge regular IFGs. Kumar et al. [41] investigated the regularity concept in CFGs.
As a combination of FGS and CFG, the cubic fuzzy graph structure (CFGS) is considered a more developed CFG model. Maximal product concepts in CFGS were reviewed by Rao et al. [42]. Some concepts of connectivity in CFGS were described by Shi et al. [43]. It is important to study the regularity in CFGS that supports multiple relationships. The necessity of examining the regularity in a CFGS is because in most cases, we face more than one relationship among objects for modeling. Li et al. [44] investigated the concept of vertex regularity in a CFGS.
This paper investigates the edge regularity in a CFGS. We examined some related features by defining the edge degree and total edge degree. In the following, by introducing the order and size in the CFGS, some related results were investigated. Moreover, a study on the edge regular in the complete CFGS is carried out. Vertex regularity and its relationship with an edge regular were discussed. At the end, an application of a CFGS in the field of goods and passenger transportation was presented.
2 Preliminaries
At the beginning of the discussion, we have to go over some basic definitions to enter the main concepts.
A graph in the form of G = (V, E) is a set of vertices V surrounded by a set of relations E. A graph structure (GS) X = (V, E1, E2, …, Ek) is introduced from the set V with a set of mutual relationship of E1, E2, …, Ek on V that every Ei is non-reflective and symmetric for 1 ≤ i ≤ k [19].
A fuzzy graph (FG) on V is a pair G = (ς, ϑ), where ς is a fuzzy subset (FS) of V and ϑ is a fuzzy relation on ς, so that ϑ(x, y) ≤ ς(x) ∧ ς(y) and ∀x, y ∈ V.
A cubic fuzzy set (CFS) of
where [μ(z), ν(z)] is an interval-valued fuzzy number and η(z) is a fuzzy number as the membership value of z, so that μ, ν, η: V → [0, 1] [29].
Definition 2.1. [21] Consider Z = (V, E1, E2, …, Ek) as a GS. Then,
Definition 2.2. [32] The pair
Definition 2.3. [42] Consider
Definition 2.4. [42] A CFGS
Example 2.5. The CFGS of
Definition 2.6. [44] Consider
Definition 2.7. [44] Consider
3 The edge regularity in cubic fuzzy graph structures
In this section, we introduce the edge regularity in a CFGS and examine some of its properties.
Definition 3.1. Let
This definition is equivalent to
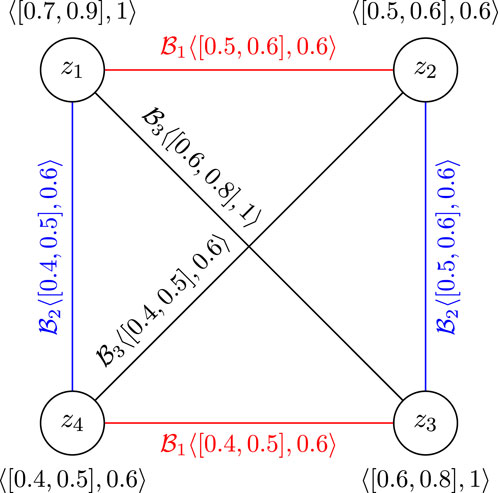
Example 3.2. Consider CFGS
The
Therefore,
Remark 3.3. For any CFGS of
Definition 3.4. Let
This is equivalent to
Example 3.5. Consider CFGS
Therefore,
Definition 3.6. Consider
Definition 3.7. Consider
Furthermore, the minimum total
Definition 3.8. Consider
Furthermore, the maximum total
Remark 3.9. A CFGS
Moreover,
Example 3.10. Consider CFGS
The total degree of
Theorem 3.11. Consider
Proof. Suppose that
Thus, by definition
Therefore,
Hence,
Remark 3.12. The total
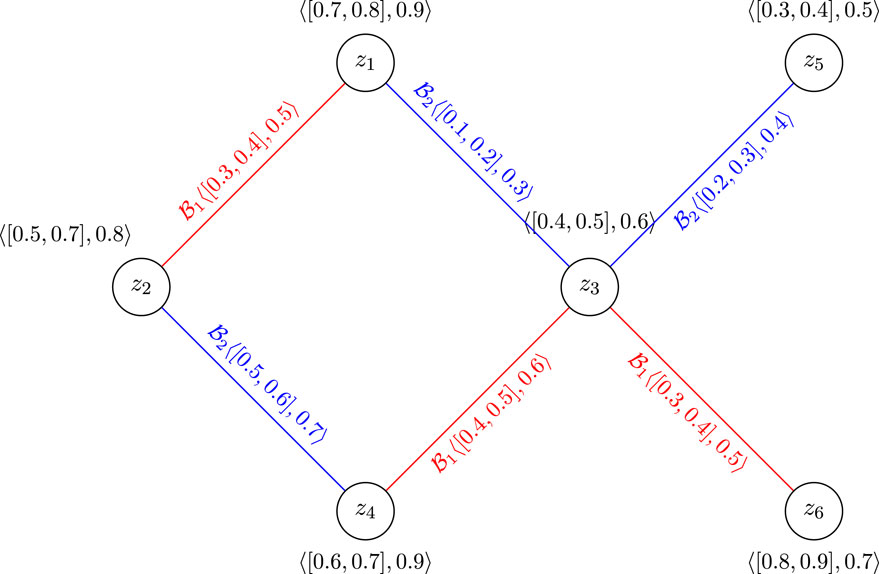
Example 3.13. Consider the CFGS
Theorem 3.14. Consider
(i)
(ii)
Proof. Suppose
(i) ⇒ (ii) Consider
On the other hand, we have
Thus,
Therefore,
Then,
Since
Theorem 3.15. Consider
Proof. Let
Suppose that
for all wz ∈ Ei. Then,
Theorem 3.16. Consider
Proof. The proof is the same as the previous theorem, except that
for all wz ∈ Ei and 1 ≤ i ≤ k. Therefore,
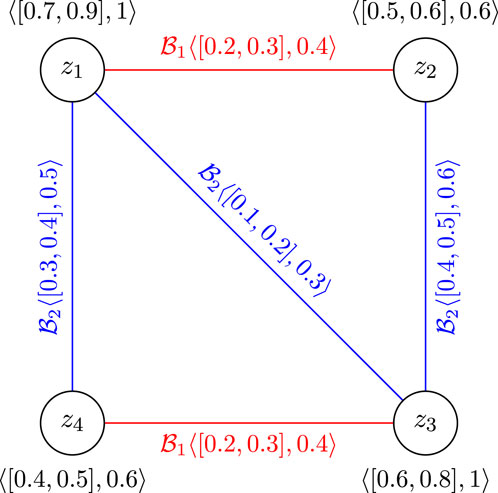
Example 3.17. Consider the complete CFGS of
Definition 3.18. Consider
Example 3.19. The CFGS
Theorem 3.20. If
Proof. Suppose that
According to the definition of the total
Therefore,
Hence,
Definition 3.21. The order of a CFGS
The
The size of a CFGS
Theorem 3.22. If
Proof. According to the definition of CFGS,
Thus, we have
Therefore,
Theorem 3.23. If
Proof. The proof is obvious.
In the following theorem, we examine the relationship between a
Theorem 3.24. Consider
Proof. Suppose that
On the other hand, for all wz ∈ Ei,
Moreover, by the definition of total
Then,
Theorem 3.25. Consider
Proof. Suppose that
Therefore,
4 Application
The transportation sector has its own importance in the economy of every country, which is well felt with the expansion of economic activities, the increase in national production, and the need to develop and improve transportation networks. Transportation in today’s human life is responsible for the safe, fast, economic movement of cargo, passengers, or information according to the environmental model. Transportation is one of the inevitable necessities of every human society, which causes the dynamics of economic and social development. The transportation component can and should be presented as a tool to achieve sustainable development. The transportation network importance in the social, economic, and even political and military structure of today’s societies is so urgent that experts consider it the foundation of sustainable development of any society. The transportation system is a set of devices, facilities, routes, rules, and regulations that are used to move people and goods.
All kinds of daily transportation methods are progressing, and their safety and comfort are improving. As you know, there are three methods of transportation including land, air, and sea, and the land-based transportation is divided into two branches of rail and road. Usually, most people use road transport to travel or move their cargo because it is both more economical and safer, but it takes more time than other methods.
Air-based transportation is a fast approach to move cargo and passengers that can make transfers in less than a few hours. However, the air-based transportation is less secure than other types of transportation methods and costs more. In the sea-based transportation that we often deal with ships and vessels, the security is well provided and the costs are reasonable, but the speed of the arrival of passengers or goods is very long. Usually, most people use the land and air to transfer cargo or travel.
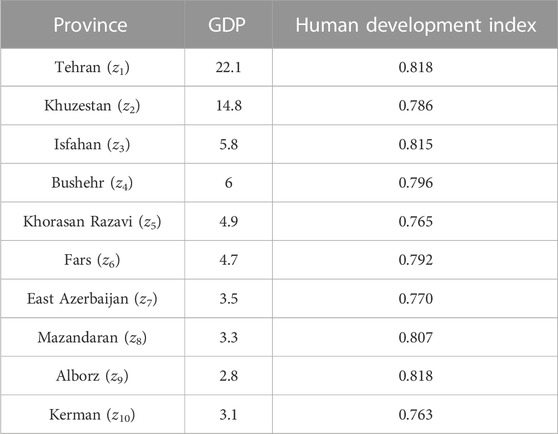
According to the data by Iran’s Statistics Center in 2018, more than 70% of the gross domestic product (GDP) was produced in the provinces of Tehran, Khuzestan, Isfahan, Bushehr, Khorasan Razavi, Fars, East Azerbaijan, Mazandaran, Alborz, and Kerman. The GDP and human development indexes are two factors that can determine the power of provinces in terms of capacity to accept goods and passengers. Table 2 shows the percentage of GDP and human development indexes in the mentioned provinces.
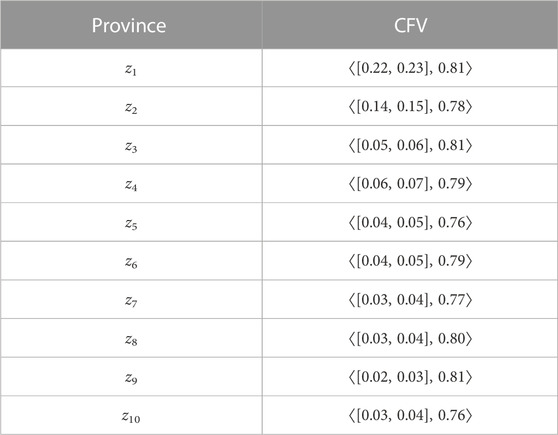
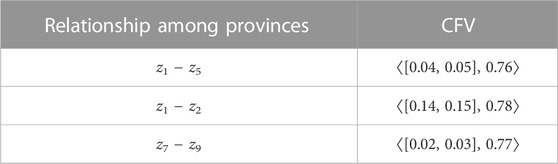
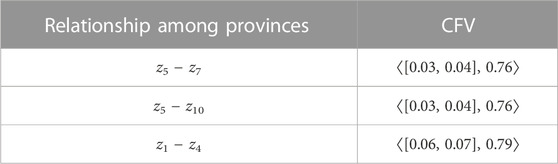
Table 3 shows the cubic fuzzy values (CFVs) of the mentioned provinces, which are expressed in the GDP with an interval-valued fuzzy number and the human development index with a fuzzy number.
Considering the provinces as the vertices of a graph, we define the relationships between the vertices as follows:
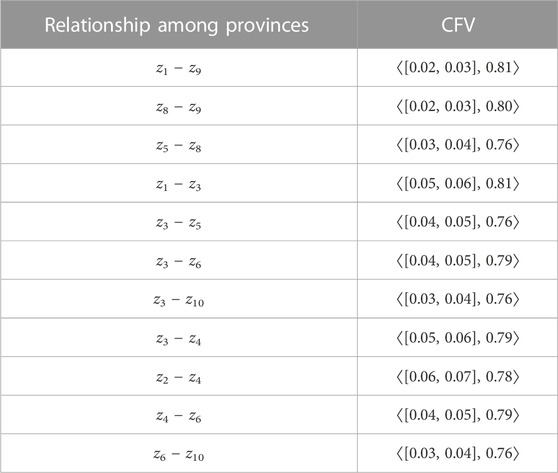
The CFVs of the connection between provinces corresponding to
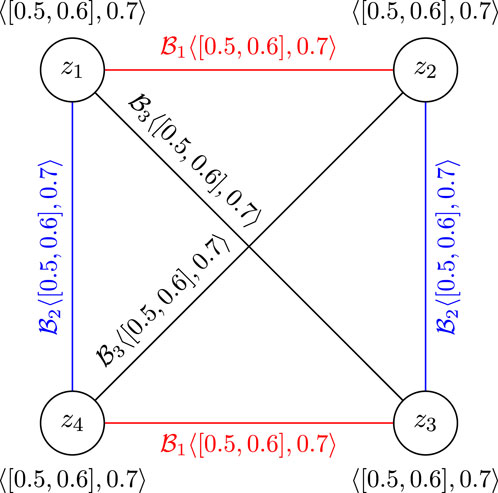
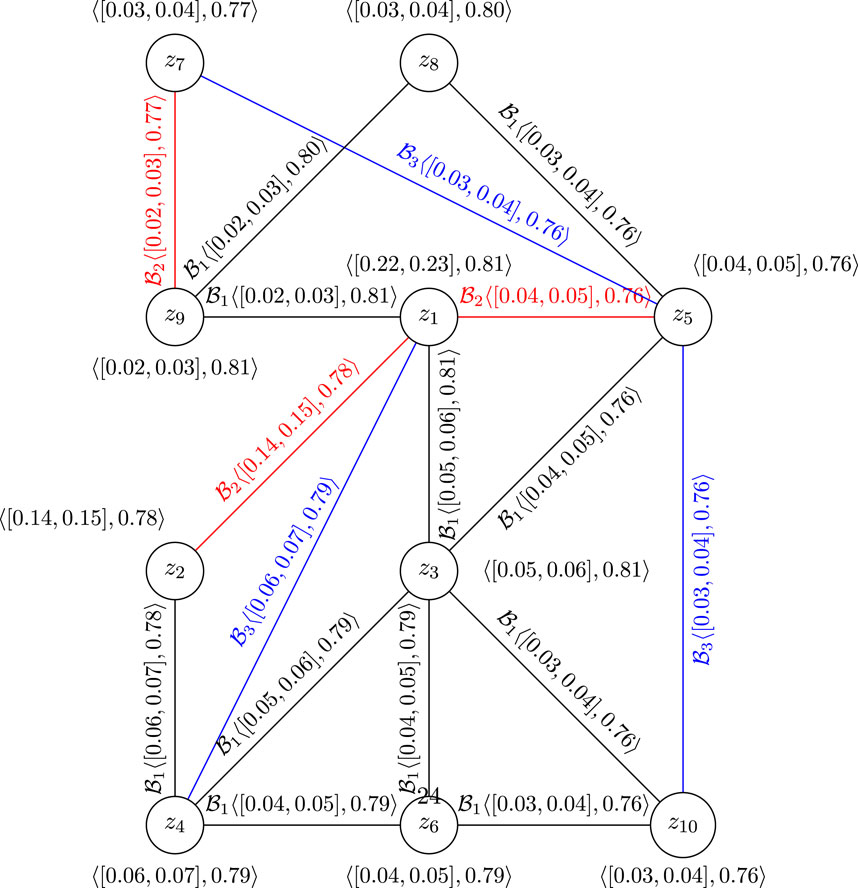
Now, we can explain the situation of passenger and goods transportation among the mentioned provinces by a CFGS, as shown in Figure 5.
In Figure 5, by removing the z1z4 edge, we will have a
5 Conclusion
The cubic fuzzy graph structure (CFGS) is an opportunity to model problems that have two values of the fuzzy and interval membership in uncertain issues and have a variety of relationships among them. The lack of research on the concepts of edge regularity in graphs led us to investigate the edge regularity in the CFGS and to study some of its properties. In this context, a comparative study between edge regular and total edge regularity in a CFGS with necessary and sufficient conditions is provided. All the results are expressed in the form of a cubic fuzzy number in order to provide the possibility of comparison to different degrees. The results show that there is a direct relationship between the regularity of the edges and the membership value of the vertices. The observations indicate a direct relationship between the edge membership functions and edge regularity. The obtained results show that the constancy of the membership functions of the edge results in the edge regularity of the CFGS and vice versa. Meanwhile, some properties are not always true. In the presented application, it was found that a
Data availability statement
The original contributions presented in the study are included in the article/Supplementary Material; further inquiries can be directed to the corresponding author.
Author contributions
XS and SK conceived and designed the experiments; AT performed the experiments; SS and AT analyzed the data; SK and SS contributed reagents/materials/analysis tools; XS wrote the paper. All authors contributed to the article and approved the submitted version.
Funding
This work was supported by the National Key R&D Program of China (grant no. 2019YFA0706402) and the National Natural Science Foundation of China under grant nos 62172302, 62072129, and 61876047.
Conflict of interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Publisher’s note
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors, and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
References
2. Rosenfeld A. Fuzzy graphs, fuzzy sets and their applications. New York, NY, USA: Academic Press (1975). p. 77–95.
3. Talebi AA. Cayley fuzzy graphs on the fuzzy groups. Comput Appl Math (2018) 37(4):4611–32. doi:10.1007/s40314-018-0587-5
4. Atanassov K. Intuitionistic fuzzy sets. Fuzzy Sets Syst (1986) 20:87–96. doi:10.1016/s0165-0114(86)80034-3
5. Borzooei RA, Rashmanlou H. Ring sum in product intuitionistic fuzzy graphs. J Adv Res Pure Math (2015) 7(1):16–31. doi:10.5373/jarpm.1971.021614
6. Akram M, Dudek WA. Interval-valued fuzzy graphs. Comput Math Appl (2011) 61(2):289–99. doi:10.1016/j.camwa.2010.11.004
7. Talebi AA, Rashmanlou H, Sadati SH. New concepts on m-polar interval-valued intuitionistic fuzzy graph. TWMS J Appl Eng Math (2020) 10(3):808–16.
8. Talebi AA, Rashmanlou H, Sadati SH. Interval-valued intuitionistic fuzzy competition graph. J Multiple-Valued Logic Soft Comput (2020) 34:335–64.
9. Rashmanlou H, Jun YB, Borzooei RA. More results on highly irregular bipolar fuzzy graphs. Ann Fuzzy Math Inform (2014) 8(1):149–68.
10. Zeng S, Shoaib M, Ali S, Smarandache F, Rashmanlou H, Mofidnakhaei F. Certain properties of single-valued neutrosophic graph with application in food and agriculture organization. Int J Comput Intell Syst (2021) 14(1):1516–40. doi:10.2991/ijcis.d.210413.001
11. Kosari S, Rao Y, Jiang H, Liu X, Wu P, Shao Z. Vague graph structure with application in medical diagnosis. Symmetry (2020) 12(10):1582. doi:10.3390/sym12101582
12. Rao Y, Kosari S, Shao Z. Certain properties of vague graphs with a novel application. Mathematics (2020) 8(10):1647. doi:10.3390/math8101647
13. Shi X, Kosari S. Certain properties of domination in product vague graphs with an application in medicine. Front Phys (2021) 9:680634. doi:10.3389/fphy.2021.680634
14. Akram M, Siddique S, Alcantud JCR. Connectivity indices of m-polar fuzzy network model, with an application to a product manufacturing problem. Artif Intelligence Rev (2022) 1–44. doi:10.1007/s10462-022-10360-9
15. Akram M, Siddique S, Alharbi MG. Clustering algorithm with strength of connectedness for m-polar fuzzy network models. Math Biosciences Eng (2022) 19(1):420–55. doi:10.3934/mbe.2022021
16. Akram M, Zafar F. A new approach to compute measures of connectivity in rough fuzzy network models. J Intell Fuzzy Syst (2019) 36(1):449–65. doi:10.3233/jifs-181751
17. Ahmad U, Nawaz I, Broumi S. Connectivity index of directed rough fuzzy graphs and its application in traffic flow network. Granular Comput (2023) 1–22. doi:10.1007/s41066-023-00384-z
18. Pramanik T, Muhiuddin G, Alanazi AM, Pal M. An extension of fuzzy competition graph and its uses in manufacturing industries. Mathematics (2020) 8(6):1008. doi:10.3390/math8061008
21. Dinesh T, Ramakrishnan T. On generalised fuzzy graph structures. Appl Math Sci (2011) 5(4):173–80.
22. Akram M, Akram M. m–Polar fuzzy graph structures. In: M– polar fuzzy graphs: Theory, methods and applications (2019). p. 209–33.
23. Akram M, Akmal R. Intuitionistic fuzzy graph structures. Kragujevac J Math (2017) 41(2):219–37. doi:10.5937/kgjmath1702219a
24. Kou Z, Akhoundi M, Chen X, Omidi S. A study on vague graph structures with an application. Adv Math Phys (2022) 2022, 1–14. doi:10.1155/2022/3182116
25. Akram M, Sitara M. Decision-making with q-rung orthopair fuzzy graph structures. Granular Comput (2022) 7(3):505–26. doi:10.1007/s41066-021-00281-3
26. Koam AN, Akram M, Liu P. Decision-making analysis based on fuzzy graph structures. Math Probl Eng (2020) 2020:1–30. doi:10.1155/2020/6846257
28. Jun YB, Smarandache F, Kim CS. Neutrosophic cubic sets. New Math Nat Comput (2017) 13(01):41–54. doi:10.1142/s1793005717500041
29. Gulistan M, Ali M, Azhar M, Rho S, Kadry S. Novel neutrosophic cubic graphs structures with application in decision making problems. IEEE access (2019) 7:94757–78. doi:10.1109/access.2019.2925040
30. Muhiuddin G, Alanazi AM, Mahboob A, Alkhaldi AH, Alatwai W. A Novel Study of Graphs Based on -Polar Cubic Structures. J Funct Spaces (2022) 2022, 1–12. doi:10.1155/2022/2643575
31. Rashid S, Yaqoob N, Akram M, Gulistan M. Cubic graphs with application. Int J Anal Appl (2018) 16(5):733–50.
32. Muhiuddin G, Takallo MM, Jun YB, Borzooei RA. Cubic graphs and their application to a traffic flow problem. Int J Comput Intelligence Syst (2020) 13(1):1265–80. doi:10.2991/ijcis.d.200730.002
33. Rashmanlou H, Muhiuddin G, Amanathulla SK, Mofidnakhaei F, Pal M. A study on cubic graphs with novel application. J Intell Fuzzy Syst (2021) 40(1):89–101. doi:10.3233/jifs-182929
36. Borzooei RA, Rashmanlou H, Samanta S, Pal M. Regularity of vague graphs. J Intell Fuzzy Syst (2016) 30(6):3681–9. doi:10.3233/ifs-162114
37. Nagooani A, Latha SR. Isomorphism on irregular fuzzy graphs. Int J Math Sci Eng Appl (2012) 6(3):193–208.
39. Cary M. Perfectly regular and perfectly edge-regular fuzzy graphs. Ann Pure Appl Math (2018) 16(2):461–9. doi:10.22457/apam.v16n2a24
40. Karunambigai MG, Sivasankar S, Palanivel K. Some properties of a regular intuitionistic fuzzy graph. Int J Math Comput (2015) 26(4):53–61.
41. Krishna KK, Rashmanlou H, Talebi AA, Mofidnakhaei F. Regularity of cubic graph with application. J Indonesian Math Soc (2019) 1–15. doi:10.22342/jims.25.1.607.1-15
42. Rao Y, Akhoundi M, Talebi AA, Sadati SH. The maximal product in cubic fuzzy graph structures with an application. Int J Comput Intelligence Syst (2023) 16(1):18. doi:10.1007/s44196-023-00193-x
43. Shi X, Akhoundi M, Talebi AA, Sadati SH. Some properties of cubic fuzzy graphs with an application. Symmetry (2022) 14(12):2623. doi:10.3390/sym14122623
Keywords: cubic fuzzy graph structure, Bi-vertex regular, Bi-edge regular, total Bi-edge regular, perfect Bi-edge regular
Citation: Shi X, Kosari S, Sadati SH, Talebi AA and Khan A (2023) Special concepts of edge regularity in the cubic fuzzy graph structure environment with an application. Front. Phys. 11:1222150. doi: 10.3389/fphy.2023.1222150
Received: 13 May 2023; Accepted: 14 June 2023;
Published: 08 August 2023.
Edited by:
Yilun Shang, Northumbria University, United KingdomReviewed by:
Muhammad Akram, University of the Punjab, PakistanSaid Broumi, University of Hassan II Casablanca, Morocco
G. Muhiuddin, University of Tabuk, Saudi Arabia
Copyright © 2023 Shi, Kosari, Sadati, Talebi and Khan. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Saeed Kosari, c2FlZWRrb3NhcmkzOEBnemh1LmVkdS5jbg==
 Xiaolong Shi
Xiaolong Shi Saeed Kosari
Saeed Kosari Seyed Hossein Sadati2
Seyed Hossein Sadati2