- 1School of Mathematical Sciences, Zhejiang Normal University, Jinhua, Zhejiang, China
- 2Department of Mathematics and Statistics, University of South Florida, Tampa, FL, United States
- 3School of Mathematical and Statistical Sciences, North-West University, Mmabatho, South Africa
- 4Department of Mathematics, University of Management and Technology, Lahore, Pakistan
- 5Faculty of Engineering, Future University in Egypt, Cairo, Egypt
- 6Department of Statistics and Operations Research, College of Science, King Saud University, Riyadh, Saudi Arabia
The Landau–Ginzburg–Higgs equation (LGHE) is a mathematical model used to describe nonlinear waves that exhibit weak scattering and long-range connections in the tropical and mid-latitude troposphere as interactions between equatorial and mid-latitude Rossby waves. This study assessed the fractional Landau–Ginzburg–Higgs model, previously introduced in truncated M-fractional derivatives utilizing the
1 Introduction
Non-linear partial differential equations (NLPDEs) play significant roles in physics, mathematical engineering, and other phenomena such as heat flow, plasma physics, wave propagation, shallow water waves, chemically dispersed electricity, quantum mechanics, fluid dynamics, and reactive materials. NLPDEs also play substantial roles in nonlinear optical fibers and quantum fields, such as nonlinear wave equations, Monge–Ampere equations, Burgers equations, Liouville equations, Fisher equations, and Kolmogorov–Petrovskii–Piskunov equations [1–4]. These equations assist in the implementation of essential parts of the soliton solution. The soliton is stimulated during diffusion by eliminating the effects of diffusion. Now, soliton assessment is very common [5]. Solitons are solutions to large, weakly detached partial differential equations (PDEs) for physical structures. Nowadays, many models are considered for computing the soliton solutions (SS) [6–8]. Among these, the Landau–Ginzburg–Higgs (LGH) model [9, 10] is one of the most considered in recent years, as follows:
where
For two centuries, fractional calculus has fascinated many intellectuals’ curiosity. Use them to develop many nonlinear aspects, inclosing bioprocesses, chemical processes, fluid mechanics, etc. In the traditional integer order, the fractional-order PDEs are used to generalize PDEs. Several definitions of the fractional derivative exist in the literature, such as Riemann–Liouville [17], Caputo [18], Caputo–Fabrizio [19], conformable fractional derivative (FD) [20], and beta-derivative [21] to solve non-integer-order models. Studies have shown that these definitions of FD do not meet some of the basic assets of derivatives, such as product and chain rules. Sousa and Oliveira [22] developed a novel truncated-M fractional derivative that meets numerous properties considered to be the FD’ boundary. This derivative has interesting results in different areas, such as chaos theory, biological modeling, circuit analysis, optical physics, and disease analysis.
The core aim of this study was to explore the space-time fractional LGH model [23], symbolized as
where
The fundamental consideration of this exploration was to take advantage of the novel indication of fractional-order derivatives, called truncated truncated-M fractional derivatives [22, 24, 25], for space-time fractional LGHE [23], and to use the
Moreover, the planned technique has been used to solve various models. For instance, Hafiz [28] employed the
This work is structured into six sections. Section 2 presents the truncated M-fractional derivative and its properties, which is the foundation of the proposed methods. The methodologies of the three proposed approaches are discussed in Section 3, where we explain how to use the truncated M-fractional derivative to solve mathematical models. Section 4 involves a mathematical examination of the models we have presented and the solutions we have obtained using the proposed methods. We compare them with existing methods in the literature. Section 5 provides a graphical representation of the obtained solutions for each analyzed model. Finally, Section 6 provides the study conclusion by summarizing the key findings and their implications.
2 Truncated M-fractional derivative and its properties
The following section will discuss the truncated M-fractional derivative (TMFD) of order
Definition 2.1. Let
where
Properties 2.2. Let
1.
2.
3.
4.
5. If
6.
3 General form of the methods
3.1
The core steps of the
where
Case 1:. When
and we have
where
Case 2:. When
and we have
where
Case 3:. When
and we have
where
The unfamiliar function
Step 1:. By coordinate transformation
where
where
Step 2:. Assume that a polynomial can express the solutions of Eq. 14 in two variables
To determine the values of the constants
Step 3:. Substitute Eq. 15 into Eq. 14 along with Eqs 5 and 7, reducing the left-hand side of the ODE into a polynomial in terms of
Step 4:. Substitute the values obtained for ai (i = 0, 1, …, m), bi (i = 1, …, m), c, μ, λ(λ<0), A1 and A2 in Eq. 15 to determine the traveling wave solutions in terms of hyperbolic functions, as expressed in Eq. 14.
Step 5:. Similarly, substitute Eq. 15 into Eq. 14 along with Eq. 5 and either Eq. 9 or Eq. 11 to obtain exact traveling wave solutions expressed in terms of trigonometric or rational functions, respectively.
3.2 The modified
We outline the fundamental steps of the modified
Step 1:. Start by considering Eqs 12–14.
Step 2:. Extend the solutions to Eq. 14 as follows:
where
where
When
When
where
Step 3:. If we substitute Eq. 16 and Eq. 17 into Eq. 14 and equate the coefficients of each power of
Step 4:. Replacing Eq. 16 of which
3.3 The new auxiliary equation method
Now, we will designate the elementary steps of the new auxiliary equation method [39, 40].
Step 2:. Subsequently determine the solutions of Eq. 14:
which satisfies the auxiliary equation:
where
Family-2 When
Family-3 When
Family-4 When
Family-5 When
Family-6 When
Family-7 When
Family-8 When
Family-9 When
Family-10 When
Family-11 When
Family-12 When
Family-13 When
Family-14 When
Family-15 When
Family-16 When
Family-17 When
Family-18 When
Family-19 When
Family-20 When
4 Mathematical analyses of the models and their solutions
Assuming the transformations:
where
The subsequent sections employ the planned techniques to obtain the desired solutions.
4.1 Solutions with the
Using the homogenous balance technique to the highest-order derivative with the nonlinear term in Eq. 24, we get
where
Case 1:. The obtained Eq. 25 is substituted into Eq. 24 with the use of Eqs 5 and 7 to result in a polynomial equation. A system of algebraic equations is obtained by setting each polynomial coefficient to zero
The hyperbolic traveling wave solutions of Eq. 24 can be obtained by substituting Eq. 26 into Eq. 25:
where
Family 1.2: If
Case 2:. By substituting Eq. 25 into Eq. 24 along with Eqs 5 and 9 for
The periodic trigonometric traveling wave solution of Eq. 24 can be obtained by substituting Eq. 30 into Eq. 25, as follows:
where
4.2 Solutions with the modified
Using the homogenous balance technique to the highest order derivatives with the nonlinear term in Eq. 24, we get
where
By substituting Eqs 35, 18, and 19 into Eq. 34 and considering the following cases, if
4.3 Solutions with the new auxiliary equation method
Using the homogenous balance technique to the highest order derivative with the nonlinear term in Eq. 24, we obtain
where
Switching Eq. 10 into Eq. 24 with Eq. 22, we obtain the algebraic equations involving
Using mathematical software (Mathematica) to solve the aforementioned system of algebraic equations, we obtain the subsequent solution:
where
Substituting the attained solution Eq. 40 into Eq. 38, we obtain the following:
Substituting the solution stated by Eq. 22 into Eq. 41, the solutions regained are:
For Family 1: When
For Family 2: When
For Family 3: When
For Family 4: When
For Family 5: When
For Family 6: When
For Family 7: When
For Family 8: When
For Family 9: When
For Family 13: When
For Family 14: When
For Family 15: When
For Family 16: When
For Family 18: When
For Family 19: When
5 Graphical demonstration and explanation
To demonstrate the dynamics and behavior of our solutions, we used Eqs 32, 36, 42, and 17 to graphically represent the solutions in 3D, 2D, and contour graphs, which are shown in Figures 1–4. To illustrate the variation over time or to compare multiple wave items, 3D plots are often used. In this study, the wave points were arranged in a series with evenly spaced breaks and connected by a line to emphasize their relationships. In contrast, 2D line plots demonstrate very high and low frequency and amplitude. The authors note that the plots show the different natures of the solutions, such as periodic, singular-kink type, singular-bell shaped, and bright singular wave solutions. Furthermore, the authors emphasize that the correct physical description of the solutions can be generated by choosing distinct values for the fractional parameter

FIGURE 1. Influence of fractional order by 2D, 3D, and corresponding contours of Eq. 32 for
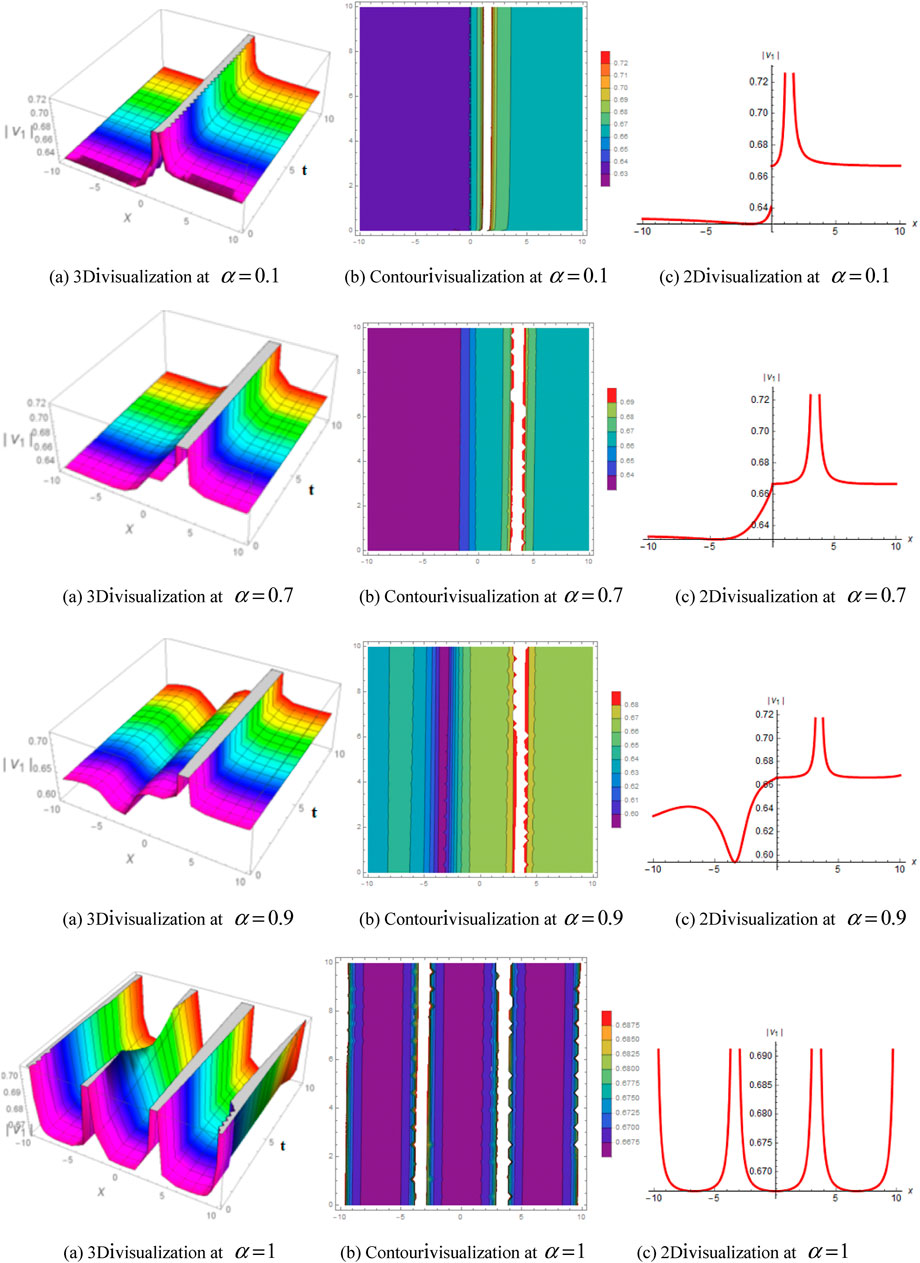
FIGURE 2. Influence of fractional order by 2D, 3D, and corresponding contours of Eq. 36 for
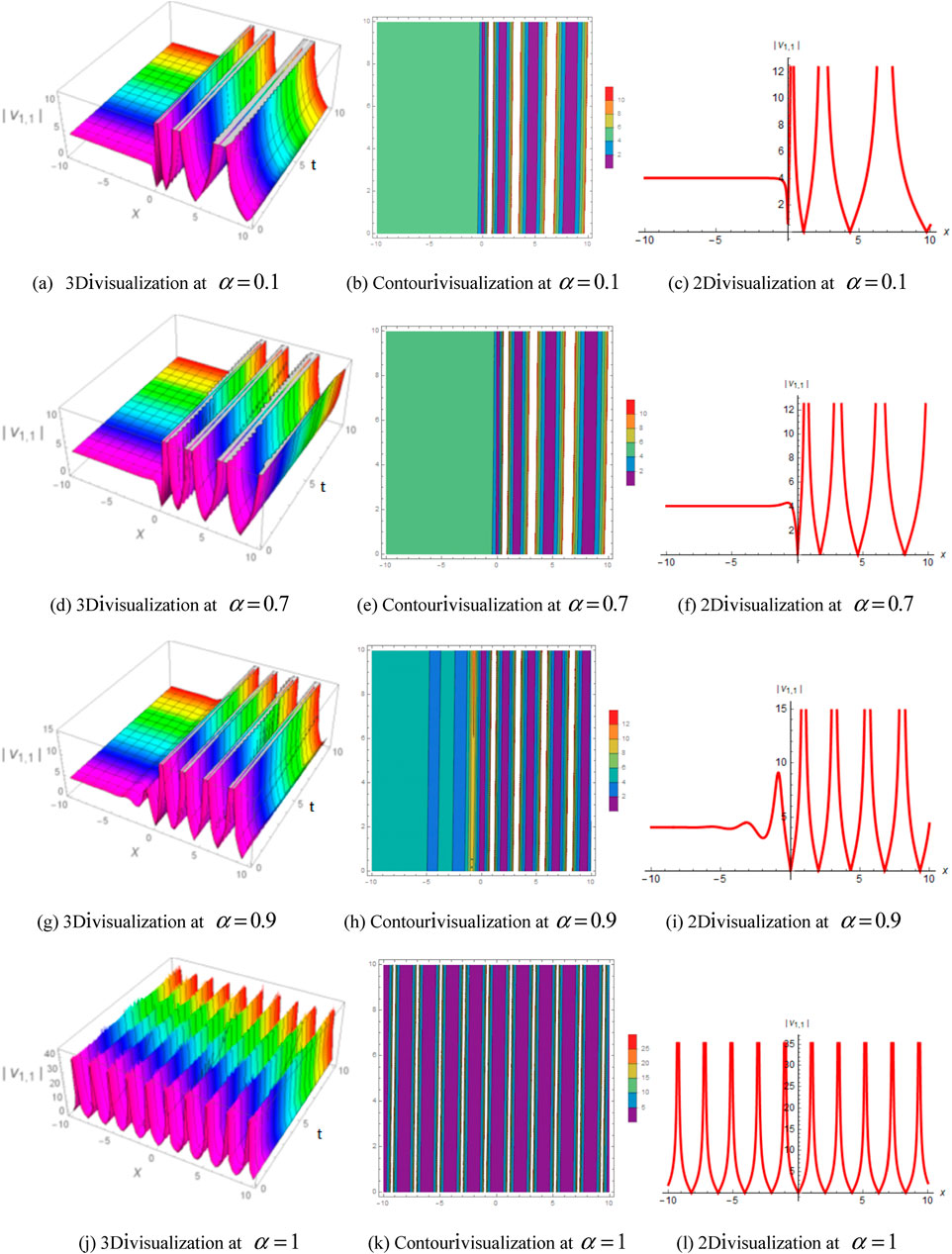
FIGURE 3. Influence of fractional order by 2D, 3D, and corresponding contours of Eq. 42 for
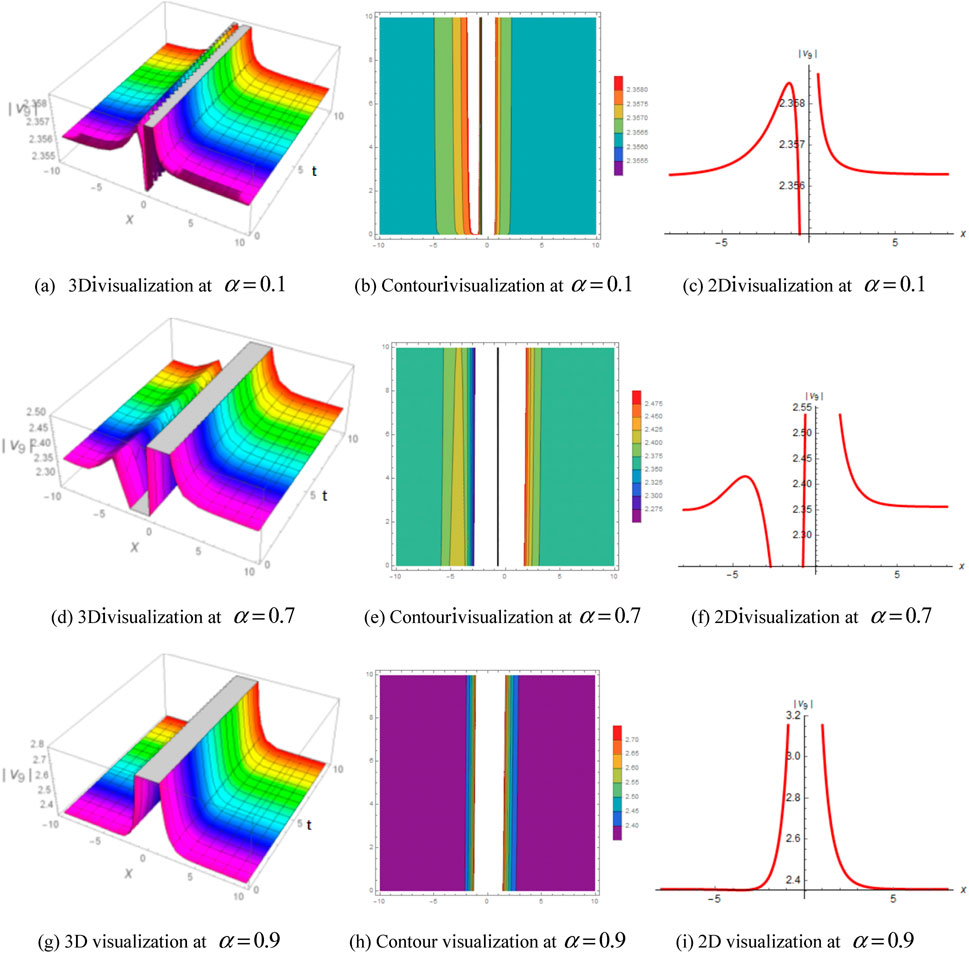
FIGURE 4. Influence of fractional order by 2D, 3D, and corresponding contours of Eq. 57 for
6 Conclusion
In this work, we applied the
Data availability statement
The original contributions presented in the study are included in the article/Supplementary Material. Further inquiries can be directed to the corresponding author.
Author contributions
RZ, W-XM, SA, and IS contributed to the study conception and design. IS and AH organized the database. AH and SA performed the statistical analysis. RZ and KM wrote the first draft of the manuscript. W-XM, IS, and AH wrote sections of the manuscript. SA and AH writing-review and editing. SA is the project administrative. All authors contributed to the article and approved the submitted version.
Funding
This Project is funded by King Saud University, Riyadh, Saudi Arabia.
Acknowledgments
Research Supporting Project number (RSP2023R167), King Saud University, Riyadh, Saudi Arabia.
Conflict of interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Publisher’s note
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors, and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
References
1.Wazwaz. Partial differential equations and solitary wave theory. Berlin, Germany: Springer (2009).
3. Wazwaz AM. The extended tanh method for abundant solitary wave solutions of nonlinear wave equations. Appl Math Comput (2007) 187:1131–42. doi:10.1016/j.amc.2006.09.013
4. Raza N, Zubair A. Bright, dark and dark-singular soliton solutions of nonlinear Schrödinger's equation with spatio-temporal dispersion. J Mod Opt (2018) 65:1975–82. doi:10.1080/09500340.2018.1480066
5. Seadawy AR. Two-dimensional interaction of a shear flow with a free surface in a stratified fluid and its solitary-wave solutions via mathematical methods. Eur Phys J Plus (2017) 132:518. doi:10.1140/epjp/i2017-11755-6
6. Hosseini K, Sadri K, Mirzazadeh M, Chu YM, Ahmadian A, Pansera BA, et al. A high-order nonlinear Schrödinger equation with the weak non-local nonlinearity and its optical solitons. Results Phys (2021) 23:104035. doi:10.1016/j.rinp.2021.104035
7. Hoan LVC, Owyed S, Inc M, Ouahid L, Abdou MA, Chu YM. New explicit optical solitons of fractional nonlinear evolution equation via three different methods. Phys (2020) 18:103209. doi:10.1016/j.rinp.2020.103209
8. Rezazadeh H, Ullah N, Akinyemi L, Shah A, Alizamin SMM, Chu YM, et al. Optical soliton solutions of the generalized non-autonomous nonlinear Schrödinger equations by the new Kudryashov’s method. Phys (2021) 24:104179. doi:10.1016/j.rinp.2021.104179
9. Hu WP, Deng ZC, Han SM, Fa W. Multi-symplectic Runge-Kutta methods for Landau-Ginzburg-Higgs equation. Appl Math Mech (2009) 30(8):1027–34. doi:10.1007/s10483-009-0809-x
10. Bekir1 A, Unsal O. Exact solutions for a class of nonlinear wave equations by using First Integral Method. Int J Nonlinear Sci (2013) 15(2):99–110.
11. Cyrot M. Ginzburg-Landau theory for superconductors. Rep Prog Phys (1973) 36(2):103–58. doi:10.1088/0034-4885/36/2/001
12. Bekir A, Unsal O. Exact solutions for a class of nonlinear wave equations by using the first integral method. Int J Nonlinear Sci (2013) 15(2):99–110.
13. Iftikhar A, Ghafoor A, Jubair T, Firdous S, Mohyud-Din ST. The expansion method for travelling wave solutions of (2+1)-dimensional generalized KdV, sine Gordon and Landau-Ginzburg-Higgs equation. Sci Res Essays (2013) 8:1349–859.
14. Barman HK, Akbar MA, Osman MS, Nisar KS, Zakarya M, Abdel-Aty AH, et al. Solutions to the Konopelchenko-Dubrovsky equation and the Landau-Ginzburg-Higgs equation via the generalized Kudryashov technique. Results Phys (2021) 24:104092. doi:10.1016/j.rinp.2021.104092
15. Barman HK, Aktar MS, Uddin MH, Akbar MA, Baleanu D, Osman MS. Physically significant wave solutions to the Riemann wave equations and the Landau-Ginsburg-Higgs equation. Results Phys (2021) 27:104517. doi:10.1016/j.rinp.2021.104517
16. Islam ME, Akbar MA. Stable wave solutions to the Landau-Ginzburg-Higgs equation and the modified equal width wave equation using the IBSEF method. Arab J Basic Appl Sci (2020) 27(1):270–8. doi:10.1080/25765299.2020.1791466
17. Kilbas AA, Srivastava HM, Trujillo JJ. Theory and applications of fractional differential equations. Amsterdam: Elsevier (2006).
18. Miller S, Ross B. An introduction to the fractional calculus and fractional differential equations. New York, NY: Wiley (1993).
19. Caputo M, Fabrizio M. A new definition of Fractional differential without singular kernel. Prog Fract Differ Appl (2015) 1(2):1–13.
20. Khalil R, Horani MA, Yousef A, Sababheh M. A new definition of fractional derivativefinition of fractional derivative. J Compu Appl Math (2014) 264:65–70. doi:10.1016/j.cam.2014.01.002
21. Atangana A, Baleanu D, Alsaedi A. Analysis of time-fractional hunter-saxton equation: A model of neumatic liquid crystal. Open Phys (2016) 14:145–9. doi:10.1515/phys-2016-0010
22. Vanterler D, Sousa JC, Capelas deOliveira E. A new truncated M-fractional derivative type unifying some fractional derivative types with classical properties. Int J Anal Appli (2018) 16(1):83–96.
23. Deng SX, Ge XX. Analytical solution to local fractional Landau-Ginzburg-Higgs equation on fractal media. Therm Sci (2021) 25(6B):4449–55. doi:10.2298/tsci2106449d
24. Siddique I, Zafar A, Bukht Mehdi K, Osman M, Jaradat A, Zafar KB, et al. Exact traveling wave solutions for two prolific conformable M-Fractional differential equations via three diverse approaches. Results Phys (2021) 28:104557. doi:10.1016/j.rinp.2021.104557
25. Siddique I, Mehdi KB, Jaradat MMM, Zafar A, Elbrolosy ME, Elmandouh AA, et al. Bifurcation of some new traveling wave solutions for the time–space M-fractional MEW equation via three altered methods. Results Phys (2022) 41:105896. doi:10.1016/j.rinp.2022.105896
26. Sirendaoreji S. Auxiliary equation method and new solutions of Klein–Gordon equations. Chaos Solitons Fractals (2007) 31(4):943–50. doi:10.1016/j.chaos.2005.10.048
27. Rezazadeh H, Adel W, Tebue ET, Yao SW, Inc M. Bright and singular soliton solutions to the Atangana-Baleanu fractional system of equations for the ISALWs. J King Saud Univ – Sci (2021) 33:101420. doi:10.1016/j.jksus.2021.101420
28. Zayed EME, Abdelaziz MAM. The two variable G'G, 1G-expansion method for solving the nonlinear KdVmKdV equation. Math Prob Engr., ID (2012) 725061:14.
29. Zhang Y, Zhang L, pang J. Application of G'G2expansion method for solving Schrodinger’s equation with three-order dispersion. Adv Appl Math (2017) 6(2):212–7.
30. Demiray S, Unsal O, Bekir A. New exact solutions for boussinesq type equations by using (G'/G, 1/G) and (1/G')-Expansion MethodsG'G, 1Gand 1G'expansion method. Acta Phys Pol A (2014) 125(5):1093–8. doi:10.12693/aphyspola.125.1093
31. Hafiz Uddin M. Close form solutions of the fractional generalized reaction duffing model and the density dependent fractional diffusion reaction equation. Fractional Diffusion React Equation (2017) 6(4):177–84. doi:10.11648/j.acm.20170604.13
32. Wazwaz AM. Couplings of a fifth order nonlinear integrable equation: Multiple kink solutions. Comput Fluids (2013) 84:97–9. doi:10.1016/j.compfluid.2013.05.020
33. Wazwaz AM. Kink solutions for three new fifth-order nonlinear equations. Appl Math Model (2014) 38:110–8. doi:10.1016/j.apm.2013.06.009
34. Sirisubtawee S, Koonprasert S, Sungnul S. Some applications of the (G′/G,1/G)-Expansion method for finding exact traveling wave solutions of nonlinear fractional evolution EquationsG'G,1Gexpansion method for finding exact traveling wave solutions of nonlinear fractional evolution equations. Symmetry (2019) 11:952. doi:10.3390/sym11080952
35. Mahak N, Akram G. Exact solitary wave solutions of the (1+1)-dimensional Fokas-Lenells equation. Optik (2020) 208:164459. doi:10.1016/j.ijleo.2020.164459
36. Noufe Aljahdaly H. Some applications of the modified G'G2expansion method in mathematical physics. Results Phys (2019) 13:102272. doi:10.1016/j.rinp.2019.102272
37. Daghan D, Donmez O. Exact solutions of the gardner equation and their applications to the different physical plasmas. Braz J Phys (2016) 46:321–33. doi:10.1007/s13538-016-0420-9
38. Ali MN, Husnine SM, Saha A, Bhowmik SK, Dhawan S, Ak T. Exact solutions, conservation laws, bifurcation of nonlinear and super nonlinear traveling waves for Sharma-Tasso-Olver equation. Nonlinear Dyn (2018) 94:1791–801. doi:10.1007/s11071-018-4457-x
39. Jhangeer A, Almusawa H, Rahman RU. Fractional derivative-based performance analysis to caudrey–dodd–gibbon–sawada–kotera equation. Results Phys (2022) 36:105356. doi:10.1016/j.rinp.2022.105356
40. Raza N, Jhangeer A, Rahman R, Butt AR, Chu YM. Sensitive visualization of the fractional wazwaz-benjamin-bona-mahony equation with fractional derivatives: A comparative analysis. Results Phys (2021) 25:104171. doi:10.1016/j.rinp.2021.104171
Keywords: Ginzburg–Higgs equation, truncated M-fractional derivative, the (Gʹ/G,1/G)-expansion method, modified (Gʹ/G2)-expansion method, new auxiliary equation method, exact solitary wave solutions
Citation: Zulqarnain RM, Ma W-X, Mehdi KB, Siddique I, Hassan AM and Askar S (2023) Physically significant solitary wave solutions to the space-time fractional Landau–Ginsburg–Higgs equation via three consistent methods. Front. Phys. 11:1205060. doi: 10.3389/fphy.2023.1205060
Received: 13 April 2023; Accepted: 05 May 2023;
Published: 25 May 2023.
Edited by:
Gangwei Wang, Hebei University of Economics and Business, ChinaReviewed by:
Xinyue Li, Shandong University of Science and Technology, ChinaJunchao Chen, Lishui University, China
Copyright © 2023 Zulqarnain, Ma, Mehdi, Siddique, Hassan and Askar. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Wen-Xiu Ma, d21hQHVzZi5lZHU=; Imran Siddique, aW1yYW5zbXNyYXppQGdtYWlsLmNvbQ==
 Rana Muhammad Zulqarnain
Rana Muhammad Zulqarnain Wen-Xiu Ma1,2,3*
Wen-Xiu Ma1,2,3*