Temporal-spatial perception adjustment to fitness enhances the cooperation in the spatial prisoner’s dilemma game

The exploration of real-world cooperative behavior is essential for societal development. In real life, the surrounding social environment and past experiences often influence individuals’ assessment of their self-fitness. Based on this phenomenon, we propose a novel model that explores the effect of subjective human perceptions on the evolution of cooperation, combining temporal and spatial dimensions into individual fitness. In this model, strategy persistence is used as a proxy for the temporal dimension. Strategy popularity, on the other hand, is portrayed to characterize the subjective influence of the spatial dimension. The weight distribution between the temporal perception and the spatial perception can be controlled by the parameter α, and the intensity of the subjective perception can be regulated by the parameter β. Numerical experiments show that when spatial perception is fully considered, the system tends to reach a fully cooperative state via network reciprocity. Conversely, fully considering the temporal state allows some cooperators to maintain cooperative behavior even under more unfavorable conditions (i.e., larger temptation). Notably, an intermediate state α exists when both temporal and spatial perceptions are considered, resulting in a higher level of cooperation compared to α = 0 or 1. Micro-analysis of the evolution of cooperation in temporal or spatial perception has been investigated to reveal the mechanism of macroscopic phenomena. Additionally, the robustness of the mechanism is discussed by varying the intensity of subjective perception β and the upper limit of strategy age A_max. Similarly, we explore the validity of our work to different network structures, the different numbers of agents, and the real social network. Overall, this study contributes to understanding the impact of individual subjective factors, such as temporal-spatial perception, on the evolution of cooperation in society.

1 Introduction

According to Darwin’s theory of natural selection, cooperative groups may be eliminated in the iterative process, while only betrayers will survive for an extended period [1,2]. This is because rational selfish groups tend to maximize their individual interests based on the fact that defection is more profitable than cooperation [3–5]. However, despite this theory, cooperation is widespread in the animal kingdom and human society, playing a crucial role in the development of our society [6–9]. This raises a conflict, and as a result, the origin of self-interested individuals’ spontaneous participation in cooperation has been extensively explored [10]. Evolutionary game theory was then developed as a mathematical framework to explore the popularity of cooperative behavior [11–13]. Using this framework, various game strategies have evolved to study the evolution of cooperation under pairwise interactions, such as the prisoner’s dilemma game (PDG) [14,15], the public goods game (PGG) [16], and the snowdrift game (SDG) [17,18]. Additionally, with the introduction of complex networks, such as scale-free networks [19,20], square-lattice networks [21], and small-world networks [22], related studies have demonstrated those network topologies also profoundly influence the emergence of cooperation. Furthermore, Nowak summarized five typical mechanisms that increase the frequency of cooperators, including direct reciprocity, indirect reciprocity, kin selection, group selection, and network reciprocity [23]. To make this approach more realistic, observable phenomena from real life, such as rewards [24,25], punishments [26], reputation [27,28], and others [29–33], are introduced into the mechanism to further expand the approach of promoting cooperation.

In addition to the aforementioned mechanisms, recent research has uncovered that herd imitation in the individual spatial state plays a significant role in the evolutionary dynamics of human societies [34]. Individuals often observe and imitate strategies that are popular among their peers [35,36]. This phenomenon of pursuing popularity, similar to the popularity of fashion trends, is ubiquitous in daily life, reflecting the human preference for high-popularity strategies from a spatial perspective. Thus, this popularity-based strategy mechanism has been extensively studied to explore the emergence of cooperation through fitness calculations, strategy update rules, and network reciprocity. Szolnoki et al. [37] found that an individual’s popularity strongly influences cooperative behavior, with wider knowledge leading to defectors being penalized. [38] introduced a parameter α to adjust the influence of popularity and investigated its impact on individual behavior. Their results indicated that α can accelerate the emergence of cooperative clusters. These studies provide evidence for the effectiveness of popularity in promoting cooperation under specific circumstances. While the subjective perception of space by players also leads to a biased objective evaluation of returns for different strategies. Some researchers have incorporated popularity into individual fitness, whereby some players adjust their utility functions by evaluating the popularity of their strategies in the environment. [39] incorporated popularity as a coefficient into the calculation of individual fitness using a single parameter α, and their findings suggest that positive α values promote the evolution of cooperation. [40] considered local and global popularity as components of self-fitness to provide a comprehensive understanding of the influence of popularity.

Temporal perception plays a crucial role in individuals’ decision-making processes, as past experiences can guide them toward making wiser choices. Consequently, memory has been introduced as a vital mechanism to enhance the dynamic game model, and numerous researchers have investigated this concept [41–45]. In Lu et al.’s study [41], players were asked to memorize their historical strategies and evaluate the impact of memory length on their cooperation levels. [42] incorporated the accumulated income into the game and tested the robustness of cooperation following the introduction of the memory mechanism. However, memory content does not solely consist of the payoff of each game round but also includes strategy persistence. [46] focused on the stability of their neighbors’ strategies and introduced the level of strategy persistence into strategy updates to modify the probability of learning their neighbors’ strategies. They found that their model improved network reciprocity. Strategy persistence has a direct effect on individuals’ confidence in their current strategies.

The previous studies have focused solely on specific aspects, such as the popularity or persistence of a strategy. However, there is a lack of exploration of the influence of subjective factors in both the temporal and spatial dimensions. To address this gap, we propose incorporating subjective perception of temporal and spatial dimensions to regulate individual fitness, which aligns with human behavior that involves observing the environment and reflecting on past experiences. The most similar work to ours is a study by [47], where they integrated memory and conformity into the strategy update rule to address the effect of integrative effects on the emergence of cooperation. However, the innovation in their work, combining memory and conformity into the strategy update rule, enforces learning behavior on players, which is unnatural and does not reflect the self-interested and rational qualities of intelligent agents. In our work, we focus on adjusting individual fitness based on subjective perceptions, which are more akin to human cognition. Thus, our study investigates the impact of individual fitness with subjective perceptions of temporal and spatial dimensions on cooperation in the prisoner’s dilemma.

The rest of this article is structured as follows: Section 2 outlines our proposed model for integrating temporal and spatial perspectives. In Section 3, we present the results of our simulations and provide an analysis of the findings. Finally, Section 4 offers a summary of the conclusions drawn from our study, as well as a discussion of the potential implications.

2 Model

In this section, we focus on the game model of players based on perception with both temporal and spatial perspectives, the calculation of player payoff and fitness, and the strategy update rule.

2.1 The game model

A square lattice with periodic boundary conditions is considered to construct the WPDG (weak prisoner’s dilemma game) model. Each player in the lattice can interact with their four nearest neighbors with certain information. Each player has only two strategies to choose from: cooperation and defection, and at initialization, the player selects a strategy with equal probability. The player’s strategy attributes can also be represented by the following vectors:

${\mathrm{S}}_x=C={\left(\mathrm{1,0}\right)}^{T}or{\mathrm{S}}_x=D={\left(\mathrm{0,1}\right)}^T.$

Based on previous research, we aim to explore the effects of temporal and spatial mechanisms on cooperation by considering the prisoner’s dilemma game. The prisoner’s dilemma game represents an acute contradiction in society, where both players receive a reward of R if they cooperate with each other, but they receive a penalty of P if they betray each other. However, the different choices give the cooperator the sucker’s payoff of S, and the defector the temptation to defect of T. These gains satisfy T > R > P > S and 2R > T + S. To begin from a general point of view, we consider the weak prisoner’s dilemma to simplify the model. At this point, we have R = 1, S = P = 0, and T = b > 1. From this, we can represent it in the following matrix:

$M_{PD}=\left(\begin{array}{cc}\hfill R\hfill & \hfill S\hfill \\ \hfill T\hfill & \hfill P\hfill \end{array}\right)=\left(\begin{array}{cc}\hfill 1\hfill & \hfill 0\hfill \\ \hfill b\hfill & \hfill 0\hfill \end{array}\right).(1)$

2.2 Fitness evaluation

For a player x, it plays with all four of its nearest neighbors and then calculates the cumulative payoffs P_x based on Eq. 1. The P_x is as follows:

$P_x=\sum _{y\in {\mathrm{\Omega }}_x}{\mathrm{S}}_x{M}_{PD}{{\mathrm{S}}_y}^T,(2)$

where Ω_x represents the set of neighbors of player x. S_x and S_y represent the strategies of players x and y. Similarly, other players have to calculate their payoffs in this way.

In actuality, individuals evaluate their strategies not solely on the basis of the payoffs they receive through objective comparisons with others’ strategies, they also adapt their strategies based on their perceptions of the world. On the one hand, individuals assess the strategies of nearby neighbors in order to gauge the popularity of their strategies. On the other hand, the persistence of strategies in their memory also influences individuals’ confidence in them. As a result, diverse perspectives can impact a player’s level of fitness. Then, we set the player’s perception to have two dimensions and consider the mixed effects of spatial and temporal perceptions on cooperative behavior.

• Spatial perspective: from a spatial perspective, players assess their fitness based on the popularity of their strategies. The strategy popularity, represented by $\frac{k_i}{N}$, is based on the number of people with the same strategy as player x and its neighbors, divided by the total number of people in their cliques. Here, N denotes the total number of players in player x’s cliques (including player x), and k_i denotes the number of people with the same strategy as player x in those cliques. Even if all of the player x’s neighbors have different strategies from S_x, the strategy popularity of player x can still reach 1/5.

• Temporal perspective: from a temporal perspective, players incorporate strategy persistence into adjusting their fitness according to their memory. In this case, the strategy persistence $\frac{A_x}{A_{\max }}$ is the ratio of one’s strategy age to the strategy age limit. Here, A_max denotes the upper limit of a player’s strategy age, which is usually a constant. On the other hand, A_x represents a player’s current strategy age, i.e., the length of time that their current strategy remains unchanged. The upper limit of A_x is A_max. After a game, if a player’s strategy changes, its strategy age is reset to 1. Otherwise, it increases by 1. If the strategy age reaches the upper limit A_max, it remains unchanged unless the current strategy changes.

ALGORITHM 1

Algorithm 1 Monte Carlo simulation.

We integrate strategy popularity and persistence by weighted summation [40] to obtain the overall perception formula, and then use the index [39] to adjust its overall effect of perception on individual fitness. Finally, we give the following fitness function:

$F_x={\left[\left(1-\alpha \right)\cdot \frac{k_i}{N}+\alpha \cdot \frac{A_x}{A_{\max }}\right]}^{\beta }{P}_x.(3)$

F_x is the individual fitness of player x. P_x is the objective payoff of player x, which is calculated by Eq. 2. $\frac{k_i}{N}$ and $\frac{A_x}{A_{\max }}$ represent the strategy popularity and strategy persistence of players, respectively. α ∈ [0, 1], denotes the intensity distribution of temporal and spatial perspectives. β denotes the scaling index of perceptual factors, which takes values in the range (−1, 1). It is easy to see that when β = 0, the whole model degenerates to the conventional WPDG. And, when β is positive, player fitness is proportional to perception. Conversely, it is inversely proportional.

2.3 The strategy update rule

After engaging in a game with their neighbors, players often re-evaluate their strategies. Typically, they will imitate the strategies of the better-adapted players to put themselves at an advantage. Then we use the fitness considering temporal-spatial perception to calculate the imitation probability. One of the four neighbors y is chosen at random and if the neighbor’s strategy is different from its own, the probability that player x imitates neighbor y can be given by the Fermi function [21]:

$W\left(s_x\to s_y\right)=\frac{1}{1+e^{\left(F_x-F_y\right)/K}},(4)$

where F_x and F_y denote the current fitness of the player x and its neighbor y, respectively, and the parameter K denotes the uncertainty or introduced random noise. For the sake of exploring generality, we set K to 0.1 [48].

2.4 Simulation procedure

The asynchronous Monte Carlo simulation method is adopted in this paper. The simulations were performed on a 50 * 50 square-lattice network, and the fraction of cooperation F_c was determined by averaging the last 100 rounds over a total of 10,000 Monte Carlo simulations, which were conducted 50 times to minimize randomness.

In summary, the specific Monte Carlo process of the evolutionary game model is shown by Algorithm 1.

3 Result and discussion

To investigate the impact of individual fitness, as influenced by the perception in both temporal and spatial dimensions, on bursts of cooperation, this section presents the findings of our simulation and corresponding explanations. Our main parameters, α and b, were investigated to determine how different allocations of temporal and spatial dimensions in the model influenced the promotion of cooperation. Additionally, the robustness analysis explored the effects of parameters A_max and β on cooperation. The effect of network structure and the number of agents on cooperation are also discussed. In addition, the real network structure is also considered in the discussion.

To comprehensively elucidate the influences of α and b on cooperation, we constructed a heat map representing the fraction of cooperators in the α-b plane, with β set to 1, as depicted in Figure 1A. In the left region of the plot, roughly confined within the bounds of α = 0.4, the colour spectrum predominantly exhibits shades of dark blue and dark yellow, denoting a prevailing state of complete cooperation or complete defection within the system. Furthermore, the critical value for transitioning from full cooperation to partial cooperation, denoted as b_r, exhibits a declining trend followed by an increase as α increases, peaking at approximately α = 0 and α = 0.4. This indicates that these specific values of α (0 and 0.4) endow cooperators in the system with enhanced resistance to temptation. In the right region of the graph, as α increases, the distinct boundary between full cooperation and full defection becomes blurred, and the color spectrum shifts from the aforementioned dark blue and dark yellow to green, indicating a greater prevalence of coexistence between cooperators and defectors. To delve into the influence of the distribution of temporal and spatial perceptions, represented by the parameter α, on cooperation within the system, we specifically selected several α values (0, 0.2, 0.4, 0.6, 0.8, 1) for analysis and plotted Figure 1B. This figure illustrates the variation in the proportion of cooperation with respect to the temptation value b, for different α values. Evidently, distinct disparities in the shape of the curves emerge between smaller and larger values of α, and an intermediate value of α (0.4) demonstrates heightened resistance to temptation. For the purpose of comprehensive comprehension, we initially discuss the impact of solely considering spatial or temporal perceptual dimensions on cooperation, subsequently exploring their underlying microscopic mechanisms. Finally, we revert to investigating the effect resulting from the combination of both spatial and temporal dimensions on cooperation, aiming to provide a more comprehensive analysis.

FIGURE 1

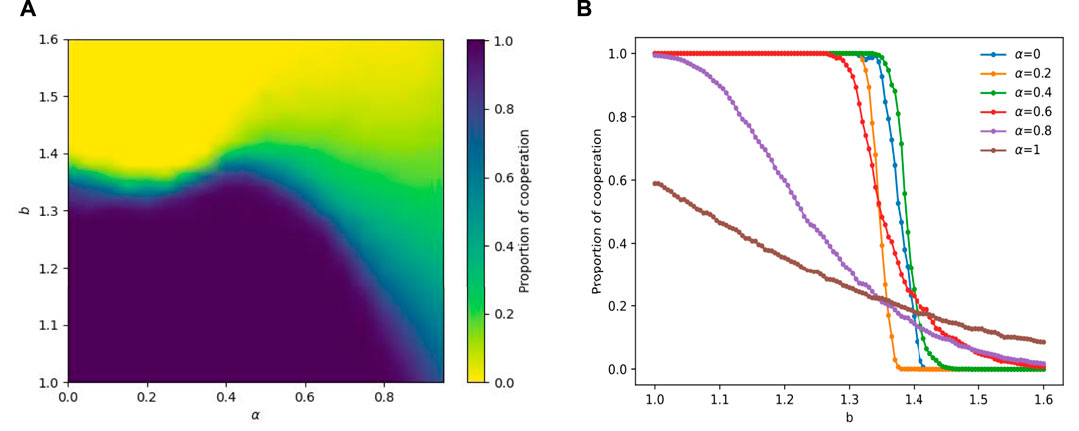
FIGURE 1. For the case of β = 1, the heat map (A) with parameter b and α shows the change in the percentage of collaborators. Graph (B) presents the change in the fraction of cooperators F_c as b increases from 1 to 1.6 for different α, where α is set to 0, 0.2, 0.4, 0.6, 0.8, and 1, respectively. α = 0 means that perception is completely dependent on the spatial perspective, and α = 1 means that perception is entirely dependent on the temporal perspective.

3.1 Effect of temporal or spatial dimension on the cooperation level

To investigate the impact of temporal or spatial dimension on cooperative behavior, we first investigate the relationship between the fraction of cooperators F_c and the betrayal temptation b under the conditions of α = 0 and α = 1. To ensure that the perception, including both dimensions, is proportional to individual fitness, we set β to 1. A higher level of individual strategy persistence or popularity corresponds to greater individual fitness, consistent with most reality. In addition, we set the maximum age that a strategy can achieve, A_max, to 50.

As shown in Figure 1B, we can observe that as the value of defection temptation b increases, for α = 0, i.e., fully considering the spatial perspective, the system rapidly turns from a state of complete cooperation at the beginning to a state of complete defection (when b increases to about 1.41). The curve takes on a radical state. However, for α = 1, which fully considers the temporal perspective, the curve for the cooperators’ fraction declines steadily (from approximately 0.6 to 0.1) as b increases, yet still maintains a coexistence between cooperators and defectors. The curve for the cooperators’ fraction remains flat. Thus, for lower b values, the α = 0 strategy leads to a higher degree of cooperation, since it induces all players to cooperate. However, as b increases to about 1.4, the α = 1 strategy promotes better cooperation than α = 0 does. Although defectors exist, some cooperators remain steadfast in their strategy, thereby enabling the cooperators to maintain a certain proportion.

3.2 Analyses of evolutionary strategy when α = 0 and 1

To investigate the mechanism of cooperative evolution, we focus on the microprocesses from a temporal or spatial perspective. Specifically, the effect of space on individual fitness is considered when α = 0. The formation of cooperative clusters is facilitated by the popularity of the strategy space, which is a typical network reciprocity process. The core view of network reciprocity is introduced, dividing the time evolution process of cooperation into two periods: the END period and the EXP period [49]. During the END period (presented to the left of the dotted line), cooperators must endure the invasion of defectors, which leads to a rapid decrease in the number of cooperators. If some cooperators manage to survive, they expand their clusters during the EXP period to reach the final full cooperation. As illustrated in Figure 2 (blue curve), the percentage of cooperators initially falls to a certain level before rapidly rising to reach the fully cooperative state. Moreover, from the snapshot plot in Figure 3 with α = 0, the number of cooperators rapidly decreases and clumps together to form a cluster of cooperators. During the EXP period (presented on the right side of the dotted line), the cluster expands to ultimately reach the cooperative state. In contrast, when α = 1, the proportion of the cooperative population first decreases, and cooperators eventually reach a steady state of coexistence with defectors, where the defector population dominates, as indicated by the yellow curve in Figure 2. In the snapshot plot of α = 1 in Figure 3, it can be seen that the cooperative clusters are smaller and scattered in the steady state, but they are still not easily destroyed by defectors.

FIGURE 2

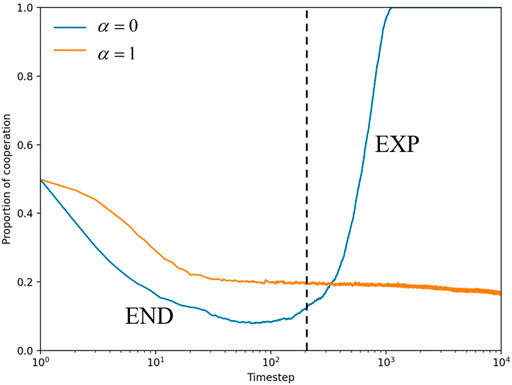
FIGURE 2. When b = 1.34, time evolution of the proportion of cooperators P_c for α = 0 and α = 1. Based on the nature of network reciprocity, the left side of the dotted line is roughly the END period and the right side is the EXP period.

FIGURE 3

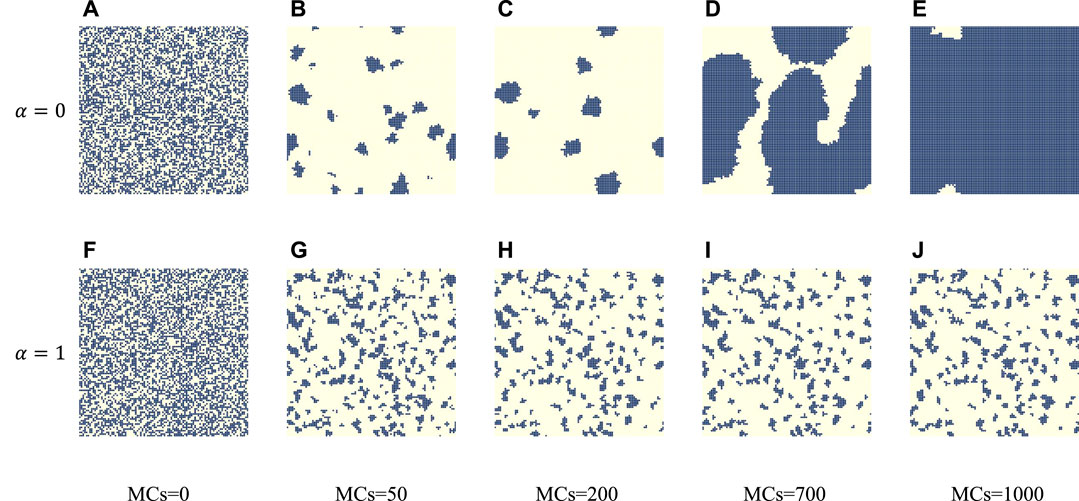
FIGURE 3. For α = 0 [panel (A–E)] and 1 [panel (F–J)], the panel depicts the characteristic snapshots of cooperators (blue) and defectors (yellow) at different time steps, which are obtained for fixed b = 1.34. From left to right, the time steps are 200, 400, 1,000, and 2,500, respectively, and from the top row to bottom, the value of α is 0, 1.

With α = 0 in cooperative evolution, the generation of cooperative clusters serves as the foundation for cooperative expansion. To understand the formation of cooperative clusters from an individual perspective, we present a micro-level diagram of the game in Figure 4, which consists of two sides: the cooperator C′ and the defector D′. In Figure 4A, when a cooperator is surrounded by multiple defectors, the fitness of C′ is 0, while the fitness of D′ is 0.8 × b. Therefore, D′ has greater fitness, resulting in the disappearance of cooperation. In Figure 4B, when two cooperators stick together, the fitness of C′ is 0.4 × 1, while the fitness of D′ is still 0.8 × b. Consequently, the cooperator changes its strategy. However, when the number of cooperators increases to three (as shown in Figure 4C), the fitness of C′ (0.6 × 2 = 1.2) exceeds the fitness of D′ for b < 1.5, enabling the cooperative cluster to expand. For values of b between 1.5 and 3, at least four cooperators are required to form a cluster for cooperative expansion (as shown in Figure 4D). Notably, when the temptation value b is small, cases that reach the cooperative state of Figure 4C easily transition to the state of Figure 4D, leading to the formation of larger cooperative clusters and the prosperity of cooperation. However, for sufficiently large values of b, only a few cases (e.g., Figure 4D) can achieve cooperative expansion, and most cases of defectors invading cooperative clusters are highly likely to result in the extinction of cooperation. The value of b = 1.5 serves as the demarcation point that produces the cases in Figures 4C, D, and to some extent, it verifies the turning point of b = 1.4 where cooperation completely dies out when α = 0 in Figure 1. This reflects a degree of consistency between the microevolution of cooperation and the macroscopic simulation.

FIGURE 4

FIGURE 4. Diagram of cooperative expansion. Light and dark yellow circles represent cooperators. The light blue and dark blue circles represent defectors. Dark blue and dark yellow represent both sides of the game. Panels (A-D) show the situation where the cooperator's neighbors have four defectors, three defectors, two defectors, and one defector.

To elucidate the coexistence of cooperators and defectors under the condition of α = 1, we present Figure 5, which captures the dynamic characteristics of cooperators during stable evolution (as demonstrated by the convergence of the proportion of cooperators in Figure 2). Figure 5 provides an enlarged view of the same region depicted in Figure 3 for α = 1, where defectors are represented by yellow squares, cooperators by blue squares, and the numbers on the squares indicate the current strategic age of the players. The figure illustrates an unfavorable scenario for the survival of cooperators, where they form a back-to-back cluster, relying solely on each other. As the evolutionary process reaches stability, an observation can be made from Figures 5A–D: the two middle committed cooperators, characterized by a maximum strategy age, remain steadfast, maintaining their strategies for an extended duration, while the surrounding six players, possessing younger strategy ages, continue to modify their own strategies. The area between the cluster of committed cooperators and the cluster of committed defectors, comprising several players of younger strategic age, is referred to as the swing zone. Players in this zone are highly susceptible to changing their strategies and are easily attracted by the committed cooperators to become cooperators of younger strategic age, while they are also easily tempted by the surrounding cluster of defectors to become defectors. Thus, they are constantly wavering in their choice of strategy. The swing zone acts as a barrier, preventing the cluster of committed cooperators from reaching out to the cluster of committed defectors and from being attracted to the lure of the committed defectors. With the support of their partners and trust in their strategies, the committed cooperator clusters can achieve greater fitness and always win when playing against the uncommitted swing zone. Therefore, even with only one partner, committed cooperators can maintain their cluster in the event of a defector siege.

FIGURE 5

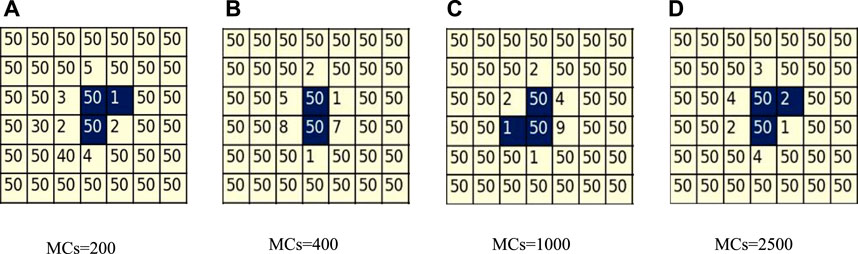
FIGURE 5. Zoomed-in image of the same area in the characteristic snapshots when α = 1 and b = 1.34, from panel (A-D), with time steps of 200, 400, 1,000 and 2,500. The numbers on the squares indicate the age of the players. The yellow and blue areas represent defectors and cooperators, respectively.

3.3 Effect of the different ratios of temporal and spatial dimension on the cooperation level

In our study, we are particularly interested in how the combination of temporal and spatial perspectives affects cooperative bursts within our model. Therefore, we pay attention to the change in cooperator fraction P_c with changes in the value of b under various intermediate states α. The results are shown in Figure 1B. As α increases, we observe a shift in the curve from a radical to a flat state. To assess the overall effectiveness of the curve, we define the cooperator area S as the area enclosed by the curve and the x- and y-axes in Figure 1B. A larger cooperator area S indicates that more players can reach a cooperative state within the range of b from 1 to 1.6. Using this definition, we calculated the cooperator area S for the curve at different values of α, specifically 0, 0.2, 0.4, 0.6, 0.8, and 1, resulting in values of 0.3742, 0.3464, 0.3897, 0.3677, 0.2507, and 0.1720, respectively. It can be seen that with the increase of α, the cooperator area S first decreases, then increases, and then decreases again, indicating that α has a nonlinear relationship with the cooperator area S of the curve. In addition, for these intermediate states α, there exists an optimal α (around 0.4) that maximizes the cumulative cooperative occupancy when b is in the range of 1–1.6. In a way, this shows that comprehensive consideration of temporal-spatial perception can enhance the prevalence of cooperation more than single consideration, which explains the reality that the overall consideration is more conducive to success.

3.4 Robustness analysis of the model

After discussing the impact of the parameter α on cooperation, we conduct a robustness analysis of the parameters A_max, β, the number of agents, network structures, and the real network.

3.4.1 Effect of the parameter A_max on the cooperation frequency

Here, A_max represents the upper limit of an individual’s strategy age, and the ratio of an individual’s strategy age to A_max directly reflects the persistence of individual strategies and the degree of trust that players have in their strategies. To investigate the effect of A_max on the intermediate state of α, we plot the heat maps of cooperators in b—A_max panel when α = 0.2, 0.4, and 0.8, as shown in Figure 6. For smaller values of α (specifically, α = 0.2), the heat map is divided by the line b = 1.34 into two parts, dark yellow on the upper side and dark blue on the lower side. We found that the variation in the value of A_max had little effect on change in cooperative population with b. This may be due to the fact that A_max primarily affects the perception of time, but time perception plays a smaller role in the model when α = 0.2. For the intermediate state (α = 0.4), there is also a less volatile splitting boundary between full cooperation and full defection, but around A_max = 25 the cooperative population is significantly more resistant to temptation than the smaller and larger A_max, suggesting that a moderate A_max strengthens the cooperative population’s resistance to temptation. For larger values of α (α = 0.8), it can be seen that as the A_max increases, the cooperative population becomes more resistant to temptation, although full cooperation cannot be achieved, it can maintain the coexistence of cooperators and defectors for larger temptation values. Since smaller values of A_max lower the upper age limit of the strategy, making even the most committed cooperators vulnerable to invasion by the fringe. At larger b, cooperative clusters become vulnerable to invasion by defectors, leading to the complete disappearance of cooperation.

FIGURE 6

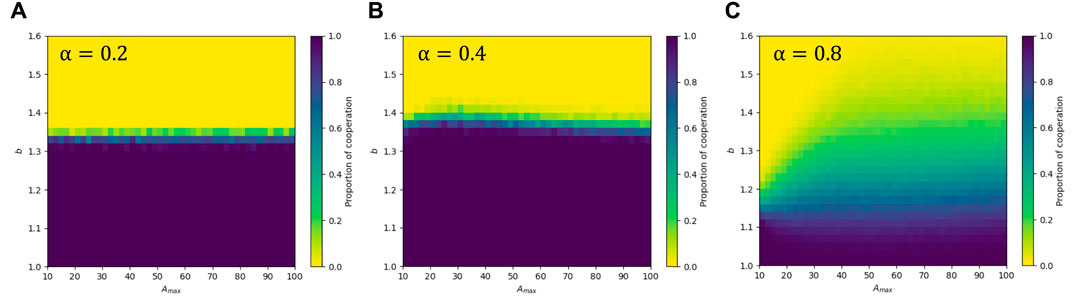
FIGURE 6. The heat map of the fraction of cooperators in the b—A_max panel with β = 1. In panels (A–C), parameter α = 0.2, 0.4, and 0.8, respectively.

3.4.2 Effect of the parameter β on the cooperation frequency

There is another parameter β, which represents the intensity of the subjective perception of individual fitness. Above we set the value of β to 1 and analyze the impact of other parameters on the model. Now we fix the intermediate state of α and vary the value of β to investigate its effect on the model dynamics. Figure 7 shows that the proportion of the cooperative population decreases as the temptation b increases for either β curve. When β = 0, the model reduces to the conventional prisoner’s dilemma game on a lattice network, without considering the subjective perception of individual fitness. Figure 7 indicates that cooperation disappears when b > 1.04, and cooperators struggle to resist defectors. For a positive value of β (β = 1), players with higher temporal-spatial scores will receive higher fitness and cooperation becomes more advantageous. With smaller b, the system can reach a fully cooperative state. However, at b > 1.35, there is also a rapid decline in the percentage of cooperators. For negative values of β (β = −1), the temporal score is inversely proportional to the player’s fitness, meaning that individuals with higher popularity and persistence in a specific strategy have a lower chance of achieving higher fitness. Under this condition, cooperation and defection coexist, but cooperators can still survive even in challenging situations (i.e., high values of b).

FIGURE 7

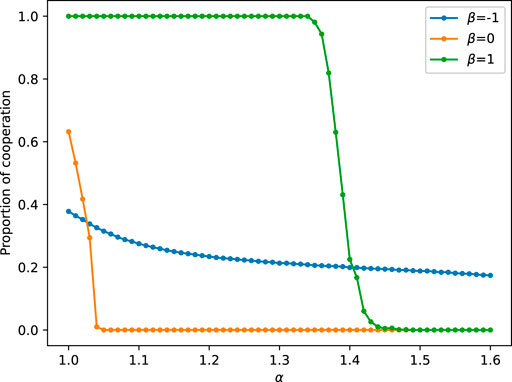
FIGURE 7. The graphs of the cooperator proportion with increasing b for three intermediate states of α = 0.2, 0.4, and 0.8 are discussed separately for different A_max cases.

3.4.3 Effect of the number of agents and network structures on the cooperation frequency

In the above argumentation, we only talk about exploring the effect of the temporal-spatial fitness mechanism on cooperation in a 50*50 square-lattice network. Then we apply this mechanism to different numbers of agents and network structures for robustness verification. Heat maps of the corresponding cooperation levels are provided under different α and b cooperative behaviors in the square-lattice network (Figure 8A), the scale-free network (Figure 8B) and the small-world network (Figure 8C), respectively, and give the results under different numbers of agents in each network structure. When considering the square-lattice network (Figure 8A) and the small-world network (Figure 8C), it becomes evident that variations in the number of agents have minimal impact on the proportion of cooperation. Consequently, the number of agents exhibits negligible influence on the resulting characteristics. However, for the scale-free network, an increase in the number of agents results in a larger scope of cooperation and an enhanced degree of cooperation within the network. This phenomenon can be attributed to the inherent network properties of scale-free networks, which amplify the influence of the high number of nodes, thus establishing cooperative behavior as the dominant feature [3].

FIGURE 8

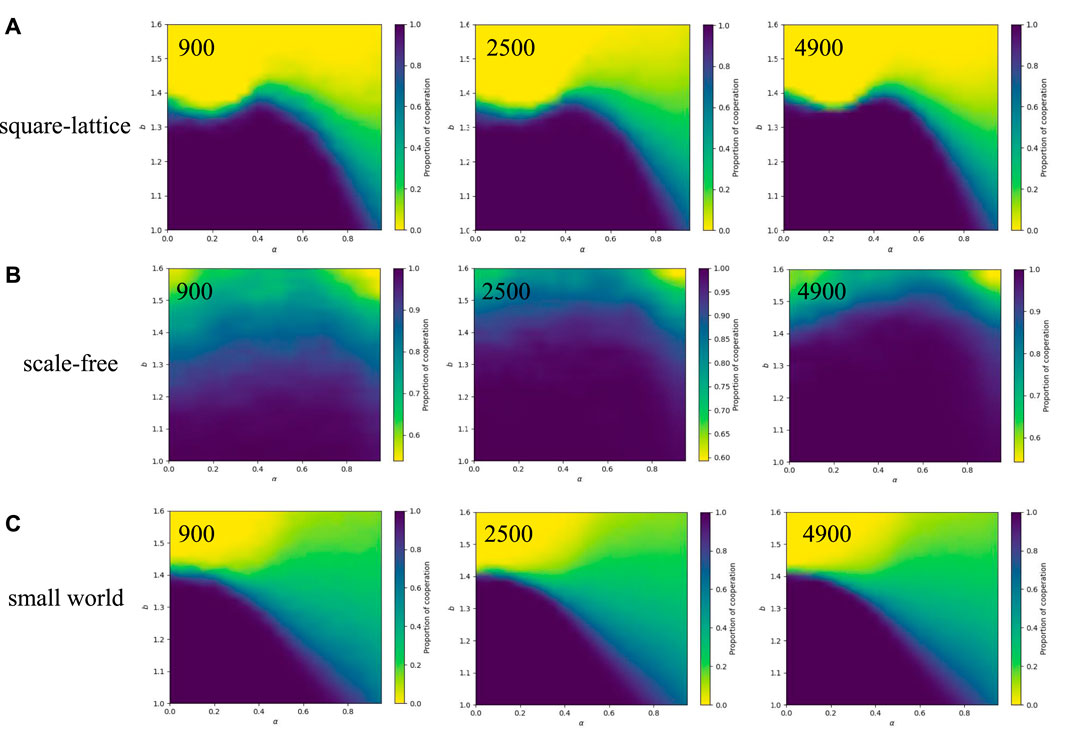
FIGURE 8. Different network structures and the number of agents act on the heat map. Each heat map represents the number of cooperators under the influence of different α and temptations b with fixed β = 1. From (A-C), they are the square-lattice network, the scale-free network, and the small-world network. From left to right, the number of agents is 900, 2,500, and 4,900, respectively.

In terms of network structure, the heat map of the scale-free network (Figure 8B) reveals a higher level of cooperation compared to the other two networks when the number of agents is fixed at 4900. However, when solely considering either the temporal state or the spatial state, the system tends towards complete extinction under higher temptation levels. Nevertheless, when an intermediate value of α is employed, the system exhibits significantly stronger cooperation, indicating that the combination of temporal and spatial mechanisms is more effective in promoting cooperation. Regarding the small-world network (Figure 8C), an increase in α leads to a progressive reduction in the b_r value, which represents the threshold for transitioning from full cooperation to partial cooperation. This shift enables a higher coexistence state within the system and empowers the partial cooperators to withstand the invasion of defections at higher temptation values b. The introduction of temporal-spatial mechanisms seems to reconcile the system’s ability to reach high cooperation proportions and resist high temptations.

3.4.4 Applicability in the real social network

To validate our model with real data, we introduce the real Facebook social network [50] as our network structure to explore the effect of temporal-spatial mechanisms on facilitating cooperative behavior. In this network, each user and his friends are considered as nodes, and the connections between friends constitute edges. The specific results are presented in Figure 9. The proportion of the cooperators is not as significantly influenced by α. However, at the same temptation (b > 1.3), it presents a higher level of cooperation at the moderate α value (about 0.45). It is somewhat similar to the results presented by the scale-free network but with an overall decrease in the resistance of the cooperative population to high temptations. However, it is still evident from this real network that a combination of temporal and spatial mechanisms would promote the prevalence of cooperation better than a single mechanism.

FIGURE 9

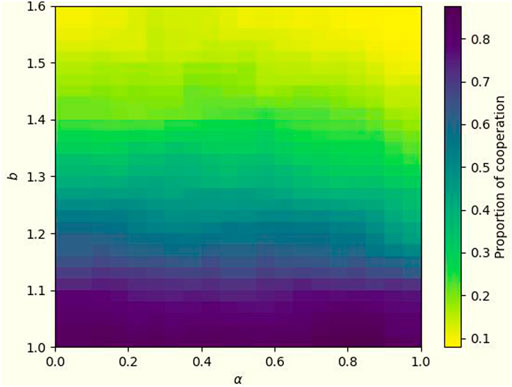
FIGURE 9. The social network among users on Facebook was selected, with a total number of 4,039 nodes and 88,233 edges. Based on this network structure, a cooperative population heat map is constructed to portray the cooperation in the system with different α and temptation b. Also fix β as 1.

4 Conclusion

In this work, we propose to adjust individual fitness from a temporal-spatial perspective to explore the evolution of cooperation in networks. In our model, each player has two dimensions of subjective perception: the temporal and spatial dimensions. They can observe their neighbors’ strategy states in spatial dimension to assess their strategy popularity and to memorize the current length of their strategy persistence in the temporal dimension. When players perform the strategy update at the current game round, they refer to both strategy popularity and strategy persistence to adjust their fitness based on objective payoffs. Numerous simulations show that when the perceptual impact β on objective payoff is 1 (i.e., perception and individual fitness are proportional), the system can achieve full cooperation under the perceptual impact of fully considering space at b approximately less than 1.4, which is corroborated by further inquiry. However, fully considering temporal perception allows cooperators to survive in more difficult situations. We also explain several of these phenomena from the microevolution diagram. It is worth noting that the existence of an optimal trade-off point makes the cooperative state optimal when spatial and temporal perceptions are combined. This coincides with the realistic situation where humans tend to consider temporal-spatial factors comprehensively before making a better choice. Finally, we perform a sensitivity analysis in terms of both perceptual impact β and maximum strategy age A_max. Robustness analysis regarding the network structure and the number of agents is also further investigated. Finally, we use the Facebook social network structure to check the applicability of our work in real situations.

We hope that the findings of this paper will provide new insights into the evolution of cooperation from individual fitness. Of course, from a realistic perspective, the perception that humans are subjected to in temporal space is not limited to strategy persistence and strategy popularity. Related experiments based on other human behaviors are also worth further investigation in the future.

Data availability statement

The original contributions presented in the study are included in the article/supplementary material, further inquiries can be directed to the corresponding author.

Author contributions

Conceptualization: XY, JW, XJ, and ZW. Methodology: CW, XY, XJ, and ZW. Software: XY, JW, and ZZ. Visualization: XY, CW, and ZZ. Formal analysis: XJ, JW, and ZW. Writing: XY, JW, and XJ. Funding acquisition: XJ, CW, ZZ, and ZW. All authors listed have made a substantial, direct, and intellectual contribution to the work and approved it for publication.

Funding

This work was supported by the National Natural Science Foundation of China under Grant Nos. 62002092, 62176080, and 42201510, and Zhejiang Provincial Natural Science Foundation of China under Grant No. LTGG23F030004, and Zhejiang Lab (2022PG0AC03).

Conflict of interest

Author ZZ is employed by Zhejiang Zhike Yunchuang Digital Technology Co., LTD., China.

The remaining authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

1. Darwin C. On the origin of the species and the voyage of the beagle. Berkeley: Graphic Arts Books (2012).

Google Scholar

2. Sachs JL, Mueller UG, Wilcox TP, Bull JJ. The evolution of cooperation. Q Rev Biol (2004) 79:135–60. doi:10.1086/383541

PubMed Abstract | CrossRef Full Text | Google Scholar

3. Santos FC, Pacheco JM. Scale-free networks provide a unifying framework for the emergence of cooperation. Phys Rev Lett (2005) 95:098104. doi:10.1103/PhysRevLett.95.098104

PubMed Abstract | CrossRef Full Text | Google Scholar

4. Rubinstein A, Kuhn HW, Morgenstern O, Von Neumann J. Theory of games and economic behavior: 60th anniversary. Commemorative Edition. Princeton: Princeton university press (2007).

Google Scholar

5. Colman AM. Game theory and its applications in the social and biological sciences. London: Psychology Press (1995).

Google Scholar

6. Dugatkin LA. Cooperation among animals: An evolutionary perspective. Oxford: Oxford University Press on Demand (1997).

Google Scholar

7. Turner PE, Chao L. Prisoner’s dilemma in an rna virus. Nature (1999) 398:441–3. doi:10.1038/18913

PubMed Abstract | CrossRef Full Text | Google Scholar

8. Macy MW, Flache A. Learning dynamics in social dilemmas. Proc Natl Acad Sci (2002) 99:7229–36. doi:10.1073/pnas.092080099

PubMed Abstract | CrossRef Full Text | Google Scholar

9. Perc M, Szolnoki A, Szabo G. Restricted connections among distinguished players support cooperation. Phys Rev E (2008) 78:066101. doi:10.1103/PhysRevE.78.066101

PubMed Abstract | CrossRef Full Text | Google Scholar

10. Perc M, Jordan JJ, Rand DG, Wang Z, Boccaletti S, Szolnoki A. Statistical physics of human cooperation. Phys Rep (2017) 687:1–51. doi:10.1016/j.physrep.2017.05.004

CrossRef Full Text | Google Scholar

11. Nowak M, May R. Evolutionary games and spatial chaos. Nature (1992) 359:826–9. doi:10.1038/359826a0

CrossRef Full Text | Google Scholar

12. Axelrod R, Hamilton WD. The evolution of cooperation. science (1981) 211:1390–6. doi:10.1126/science.7466396

PubMed Abstract | CrossRef Full Text | Google Scholar

13. Ritzberger K, Weibull JW. Evolutionary selection in normal-form games. Econometrica (1995) 63:1371. doi:10.2307/2171774

CrossRef Full Text | Google Scholar

14. Tucker AW. A two-person dilemma. Prisoner’s Dilemma (1950).

Google Scholar

15. Milinski M. Tit for tat in sticklebacks and the evolution of cooperation. nature (1987) 325:433–5. doi:10.1038/325433a0

PubMed Abstract | CrossRef Full Text | Google Scholar

16. Szolnoki A, Perc M, Szabó G. Topology-independent impact of noise on cooperation in spatial public goods games. Phys Rev E (2009) 80:056109. doi:10.1103/physreve.80.056109

PubMed Abstract | CrossRef Full Text | Google Scholar

17. Hauert C, Doebeli M. Spatial structure often inhibits the evolution of cooperation in the snowdrift game. Nature (2004) 428:643–6. doi:10.1038/nature02360

PubMed Abstract | CrossRef Full Text | Google Scholar

18. Gore J, Youk H, Van Oudenaarden A. Snowdrift game dynamics and facultative cheating in yeast. Nature (2009) 459:253–6. doi:10.1038/nature07921

PubMed Abstract | CrossRef Full Text | Google Scholar

19. Barabási AL, Albert R, Jeong H. Mean-field theory for scale-free random networks. Physica A: Stat Mech its Appl (1999) 272:173–87. doi:10.1016/s0378-4371(99)00291-5

CrossRef Full Text | Google Scholar

20. Barabási AL, Albert R. Emergence of scaling in random networks. science (1999) 286:509–12. doi:10.1126/science.286.5439.509

PubMed Abstract | CrossRef Full Text | Google Scholar

21. Szabó G, Tőke C. Evolutionary prisoner’s dilemma game on a square lattice. Phys Rev E (1998) 58:69–73. doi:10.1103/physreve.58.69

CrossRef Full Text | Google Scholar

22. Watts DJ, Strogatz SH. Collective dynamics of ‘small-world’networks. nature (1998) 393:440–2. doi:10.1038/30918

PubMed Abstract | CrossRef Full Text | Google Scholar

23. Nowak MA. Five rules for the evolution of cooperation. science (2006) 314:1560–3. doi:10.1126/science.1133755

PubMed Abstract | CrossRef Full Text | Google Scholar

24. Jiménez R, Lugo H, Cuesta JA, Sánchez A. Emergence and resilience of cooperation in the spatial prisoner’s dilemma via a reward mechanism. J Theor Biol (2008) 250:475–83. doi:10.1016/j.jtbi.2007.10.010

PubMed Abstract | CrossRef Full Text | Google Scholar

25. Szolnoki A, Perc M. Reward and cooperation in the spatial public goods game. Europhysics Lett (2010) 92:38003. doi:10.1209/0295-5075/92/38003

CrossRef Full Text | Google Scholar

26. Fehr E, Gächter S. Altruistic punishment in humans. Nature (2002) 415:137–40. doi:10.1038/415137a

PubMed Abstract | CrossRef Full Text | Google Scholar

27. Chen M, Wang L, Sun S, Wang J, Xia C. Evolution of cooperation in the spatial public goods game with adaptive reputation assortment. Phys Lett A (2016) 380:40–7. doi:10.1016/j.physleta.2015.09.047

CrossRef Full Text | Google Scholar

28. Dong Y, Sun S, Xia C, Perc M. Second-order reputation promotes cooperation in the spatial prisoner’s dilemma game. IEEE Access (2019) 7:82532–40. doi:10.1109/access.2019.2922200

CrossRef Full Text | Google Scholar

29. Qin J, Chen Y, Kang Y, Perc M. Social diversity promotes cooperation in spatial multigames. Europhysics Lett (2017) 118:18002. doi:10.1209/0295-5075/118/18002

CrossRef Full Text | Google Scholar

30. Danku Z, Perc M, Szolnoki A. Knowing the past improves cooperation in the future. Scientific Rep (2019) 9:262. doi:10.1038/s41598-018-36486-x

PubMed Abstract | CrossRef Full Text | Google Scholar

31. Capraro V, Perc M. Mathematical foundations of moral preferences. J R Soc Interf (2021) 18:20200880. doi:10.1098/rsif.2020.0880

CrossRef Full Text | Google Scholar

32. Zeng Z, Li Y, Feng M. The spatial inheritance enhances cooperation in weak prisoner’s dilemmas with agents’ exponential lifespan. Physica A: Stat Mech its Appl (2022) 593:126968. doi:10.1016/j.physa.2022.126968

CrossRef Full Text | Google Scholar

33. Zeng Z, Li Q, Feng M. Spatial evolution of cooperation with variable payoffs. Chaos: Interdiscip J Nonlinear Sci (2022) 32:073118. doi:10.1063/5.0099444

CrossRef Full Text | Google Scholar

34. Boyd R, Richerson PJ. Culture and the evolutionary process. Chicago: University of Chicago press (1988).

Google Scholar

35. Liu C, Shen C, Geng Y, Li S, Xia C, Tian Z, et al. Popularity enhances the interdependent network reciprocity. New J Phys (2018) 20:123012. doi:10.1088/1367-2630/aaf334

CrossRef Full Text | Google Scholar

36. Shen C, Chu C, Geng Y, Jin J, Chen F, Shi L. Cooperation enhanced by the coevolution of teaching activity in evolutionary prisoner’s dilemma games with voluntary participation. PLOS ONE (2018) 13:e0193151. doi:10.1371/journal.pone.0193151

PubMed Abstract | CrossRef Full Text | Google Scholar

37. Szolnoki A, Wang Z, Perc M. Wisdom of groups promotes cooperation in evolutionary social dilemmas. Scientific Rep (2012) 2:576. doi:10.1038/srep00576

PubMed Abstract | CrossRef Full Text | Google Scholar

38. Zhang H-F, Jin Z, Wang Z. Cooperation and popularity in spatial games. Physica A: Stat Mech its Appl (2014) 414:86–94. doi:10.1016/j.physa.2014.07.013

CrossRef Full Text | Google Scholar

39. Li S, Hong L, Geng Y, Shen C. Popularity-driven fitness calculation promotes cooperation in spatial prisoner’s dilemma game. Chaos, Solitons & Fractals (2020) 134:109701. doi:10.1016/j.chaos.2020.109701

CrossRef Full Text | Google Scholar

40. Liao HM, Hao QY, Qian JL, Wu CY, Guo N, Ling X. Cooperative evolution under the joint influence of local popularity and global popularity. Appl Math Comput (2023) 439:127635. doi:10.1016/j.amc.2022.127635

CrossRef Full Text | Google Scholar

41. Lu W, Wang J, Xia C. Role of memory effect in the evolution of cooperation based on spatial prisoner’s dilemma game. Phys Lett A (2018) 382:3058–63. doi:10.1016/j.physleta.2018.07.049

CrossRef Full Text | Google Scholar

42. Ren G, Wang X. Robustness of cooperation in memory-based prisoner’s dilemma game on a square lattice. Physica A: Stat Mech its Appl (2014) 408:40–6. doi:10.1016/j.physa.2014.04.022

CrossRef Full Text | Google Scholar

43. Luo C, Zhang X, Liu H, Shao R. Cooperation in memory-based prisoner’s dilemma game on interdependent networks. Physica A: Stat Mech its Appl (2016) 450:560–9. doi:10.1016/j.physa.2016.01.032

CrossRef Full Text | Google Scholar

44. Liu C, Wang J, Li X, Xia C. The link weight adjustment considering historical strategy promotes the cooperation in the spatial prisoner’s dilemma game. Physica A: Stat Mech its Appl (2020) 554:124691. doi:10.1016/j.physa.2020.124691

CrossRef Full Text | Google Scholar

45. Sun C, Luo C. Co-evolution of limited resources in the memory-based spatial evolutionary game. Chaos, Solitons & Fractals (2020) 131:109504. doi:10.1016/j.chaos.2019.109504

CrossRef Full Text | Google Scholar

46. Wang J, Dai W, He J, Yu F, Shen X. Persistent imitation paves the way for cooperation in public goods game. Phys Lett A (2022) 447:128302. doi:10.1016/j.physleta.2022.128302

CrossRef Full Text | Google Scholar

47. Pi B, Li Y, Feng M. An evolutionary game with conformists and profiteers regarding the memory mechanism. Physica A: Stat Mech its Appl (2022) 597:127297. doi:10.1016/j.physa.2022.127297

CrossRef Full Text | Google Scholar

48. Tanimoto J. Fundamentals of evolutionary game theory and its applications. Berlin: Springer (2015).

Google Scholar

49. Wang Z, Kokubo S, Tanimoto J, Fukuda E, Shigaki K. Insight into the so-called spatial reciprocity. Phys Rev E (2013) 88:042145. doi:10.1103/physreve.88.042145

PubMed Abstract | CrossRef Full Text | Google Scholar

50. Leskovec J, Mcauley J. Learning to discover social circles in ego networks. In: Proceedings of the 25th International Conference on Neural Information Processing Systems; December 3 - 6, 2012; Lake Tahoe Nevada (2012).

Google Scholar