Exact solutions and Darboux transformation for the reverse space–time non-local fifth-order non-linear Schrödinger equation

In this paper, the non-local reverse space−time fifth-order non-linear Schrödinger(NLS) equation has been investigated, which is proposed by the non-local reduction of Ablowitz–Kaup–Newell–Segur (AKNS) scattering problems. The determinant representation of the Nth Darboux transformation for the non-local reverse space−time fifth-order NLS equation is obtained. Some interesting non-linear wave solutions, including soliton, complexiton, and rogue wave solutions, are derived by the Darboux transformation. Moreover, the dynamics of non-linear wave solutions are illustrated with the corresponding evolution plots, and the results show that the non-local fifth-order NLS equation has new different properties from the local case.

1 Introduction

Integrable systems play an important role in non-linear science fields such as non-linear optics [1, 2], ocean physics [3], Bose–Einstein condensates [4], and even financial markets [5]. The investigation of various physically meaningful non-linear wave solutions is still one of the active areas of research in the field of integrable systems. In the past decades, many powerful methods and techniques have been proposed to construct various non-linear wave solutions and to study their underlying dynamics, such as Darboux transformation [6, 7], inverse scattering [8, 9], bilinear transformation [10], and Riemann–Hilbert approaches [11, 12]. Recently, Ablowitz and Musslimani proposed a new integrable non-local non-linear Schrödinger (NLS) equation under a reduction of the Ablowitz–Kaup–Newell–Segur (AKNS) system, and some non-linear wave solutions are constructed by the inverse scattering method [13]. Subsequently, much more non-local integrable systems including reverse space–time and reverse time cases are further investigated [14]. At the same time, the physical background of non-local integrable equations is also investigated from various related fields, such as multi-place systems [15], magnetic structures [16], nanomagnetic artificial materials [17], and loop quantum cosmology [18] [19, 20].

The NLS equation [21] is a fundamental prototype and plays a pivotal role in many fields of physics, such as fluid mechanics [22], plasmas [23], Bose–Einstein condensates [24], and deep water waves [25]. However, the NLS equation only contains the lowest-order dispersion term and the lowest-order non-linear effect. Under the necessary physical conditions, various higher-order dispersions and non-linear effects must be taken into account, such as ultrashort pulses in optical fibers [26], where the effects of higher-order dispersions should be considered. Therefore, some higher-order NLS equations, including Hirota [27], Lakshmanan–Porsezian–Daniel (LPD) [21, 28], and quintic NLS equations [29], have been constructed, and their corresponding integrable properties and dynamics have been studied.

In this paper, we consider the scattering problem as follows:

$\begin{array}{cc}\hfill {\mathrm{\Phi }}_x& =U\mathrm{\Phi },\hfill \\ \hfill {\mathrm{\Phi }}_t& =V\mathrm{\Phi }=\left(\lambda U+V_0+\alpha L+\omega M+\delta N\right)\mathrm{\Phi },\hfill \end{array}(1)$

where $\mathrm{\Phi }={\left({\varphi }_1\left(x,t\right),{\varphi }_2\left(x,t\right)\right)}^T$, λ is the spectral parameter, and U, V₀, L, M, and N are given by

$\begin{array}{cc}\hfill U& =\left[\begin{array}{cc}\hfill i\lambda \hfill & \hfill ir\hfill \\ \hfill iq\hfill & \hfill -i\lambda \hfill \end{array}\right],V_0=\frac{1}{2}\left[\begin{array}{cc}\hfill -iqr\hfill & \hfill r_x\hfill \\ \hfill -q_x\hfill & \hfill iqr\hfill \end{array}\right]\hfill \\ \hfill L& =-4\left({\lambda }^{2}U+\lambda V_0\right)+L_0,M=2\lambda L+M_0,N=-2\lambda M+N_0,\hfill \end{array}(2)$

where

$\begin{array}{cc}\hfill L_0& =\left[\begin{array}{cc}\hfill q{r}_x-r{q}_x\hfill & \hfill i\left(2r^{2}q+r_{xx}\right)\hfill \\ \hfill i\left(2q^{2}r+q_{xx}\right)\hfill & \hfill r{q}_x-q{r}_x\hfill \end{array}\right],\hfill \\ \hfill M_0& =\left[\begin{array}{cc}\hfill m_1\hfill & \hfill m_2\hfill \\ \hfill m_3\hfill & \hfill -m_1\hfill \end{array}\right],N_0=\left[\begin{array}{cc}\hfill n_1\hfill & \hfill n_2\hfill \\ \hfill n_3\hfill & \hfill -n_1\hfill \end{array}\right],\hfill \\ \hfill m_1& =i\left(-3q^2{r}^2-q{r}_{xx}+q_x{r}_x-r{q}_{xx}\right),\hfill \\ \hfill m_2& =6qr{r}_x+r_{xxx},\hfill \\ \hfill m_3& =-6qr{q}_x-q_{xxx},\hfill \\ \hfill n_1& =q{r}_{xxx}-r{q}_{xxx}+q_{xx}{r}_x-q_x{r}_{xx}+6qr\left(q{r}_x-r{q}_x\right),\hfill \\ \hfill n_2& =i{r}_{xxxx}+2i{r}^2{q}_{xx}+8iqr{r}_{xx}+4ir{r}_x{q}_x+6iq{r}_x^2+6i{r}^3{q}^2,\hfill \\ \hfill n_3& =i{q}_{xxxx}+2i{q}^2{r}_{xx}+8iqr{q}_{xx}+4iq{r}_x{q}_x+6ir{q}_x^2+6i{q}^3{r}^2.\hfill \end{array}(3)$

Under the symmetry reduction q (x, t) = r*(x, t), the generalized integrable fifth-order NLS equation [30],

$i{q}_t+S\left(q,r\right)-i\alpha H\left(q,r\right)+\omega P\left(q,r\right)-i\delta Q\left(q,r\right)=0,(4)$

where

$S\left(q,r\right)=\frac{1}{2}{q}_{xx}+q^{2}r,$

$H\left(q,r\right)=q_{xxx}+6q{q}_{x}r,$

$P\left(q,r\right)=q_{xxxx}+8qr{q}_{xx}+6q^3{r}^2+4q{q}_x{r}_x+6q_x^{2}r+2q^2{r}_{xx},$

$Q\left(q,r\right)=q_{xxxxx}+10qr{q}_{xxx}+10{\left(q{q}_x{r}_x\right)}_x+20r{q}_x{q}_{xx}+30q^2{r}^2{q}_x,$

can be obtained from the compatibility condition of the linear spectral problem (1), i.e., the zero-curvature equation, $U_t-V_x+\left[U,V\right]=0$. However, a new integrable reverse space–time non-local fifth-order NLS equation,

$\begin{array}{ll}\hfill & ir{\left(-x,-t\right)}_t+S\left(-r\left(-x,-t\right),r\left(x,t\right)\right)-i\alpha H\left(-r\left(-x,-t\right),r\left(x,t\right)\right)\hfill \\ \hfill & +\omega P\left(-r\left(-x,-t\right),r\left(x,t\right)\right)-i\delta Q\left(-r\left(-x,-t\right),r\left(x,t\right)\right)=0,\hfill \end{array}(5)$

can be obtained under the symmetry reduction,

$q\left(x,t\right)=-r\left(-x,-t\right).(6)$

Considering the importance of such non-local equations in multi-place physical systems [15], it is significant and has far-reaching importance in constructing exact solutions to the equations and aids in studying the dynamical properties of the solutions. To the best of our knowledge, such reverse space–time non-local equations have not been investigated. This paper is organized as follows: in Section 2, the one-fold and N-fold Darboux transformation of Eq. 5 are presented; in Section 3, soliton, complexiton, and rogue wave solutions are derived through the Darboux transformation and their corresponding dynamical properties and evolutions are discussed; and in Section 4, some conclusions and discussions are drawn.

2 Darboux transformation for the reverse space–time non-local fifth-order NLS equation

The Darboux transformation method is a very effective tool for constructing exact solutions of integrable non-linear equations in the soliton theory. In order to derive the Darboux transformation of the reverse space–time non-local fifth-order NLS in Eq. 5, we first introduce a gauge transformation of the linear spectral problem (1),

${\mathrm{\Phi }}^{\left[1\right]}=T^{\left[1\right]}\mathrm{\Phi },(7)$

under which the linear spectral problem (1) can be deformed as follows:

$\begin{array}{cc}\hfill {\mathrm{\Phi }}_x^{\left[1\right]}& =U^{\left[1\right]}{\mathrm{\Phi }}^{\left[1\right]}=\left(T_x^{\left[1\right]}+T^{\left[1\right]}U\right){\left(T^{\left[1\right]}\right)}^{-1}{\mathrm{\Phi }}^{\left[1\right]},\hfill \\ \hfill {\mathrm{\Phi }}_t^{\left[1\right]}& =V^{\left[1\right]}{\mathrm{\Phi }}^{\left[1\right]}=\left(T_t^{\left[1\right]}+T^{\left[1\right]}V\right){\left(T^{\left[1\right]}\right)}^{-1}{\mathrm{\Phi }}^{\left[1\right]}.\hfill \end{array}(8)$

The next pivotal step is to construct the Darboux matrix T^[1] in such a form that $U^{\left[1\right]},V^{\left[1\right]}$ in Equation 8 have the same form as U and V in (1) and the old potentials r and q are replaced by the new potentials $r^{\left[1\right]},q^{\left[1\right]}$. Suppose

$T^{\left[1\right]}=\lambda I+B^{\left[1\right]}=\left(\begin{array}{cc}\hfill \lambda +b_{11}^{\left[1\right]}\hfill & \hfill b_{12}^{\left[1\right]}\hfill \\ \hfill b_{21}^{\left[1\right]}\hfill & \hfill \lambda +b_{22}^{\left[1\right]}\hfill \end{array}\right),(9)$

where $b_{ij}^{\left[1\right]}\left(i,j=\mathrm{1,2}\right)$ are functions of x and t. Substituting Eq. 9 into Eq. 8, it is evident that the relationships between two potentials in the two linear spectral problems (1, 8) can be given as

$\begin{array}{cc}\hfill r^{\left[1\right]}& =r-2b_{12}^{\left[1\right]},\hfill \\ \hfill q^{\left[1\right]}& =q+2b_{21}^{\left[1\right]}.\hfill \end{array}(10)$

In addition, combined with symmetry reduction (6), there is

$b_{12}^{\left[1\right]}\left(x,t\right)=b_{21}^{\left[1\right]}\left(-x,-t\right).(11)$

We see that $f({\lambda }_j)={\left(f_1({\lambda }_j),f_2({\lambda }_j)\right)}^T$ and $g({\lambda }_j)={\left(g_1({\lambda }_j),g_2({\lambda }_j)\right)}^T$ are two eigenfunctions corresponding to the eigenvalue λ = λ_j (j = 1, 2). From the gauge transformation, there exist constants ${\gamma }_j,j=\left(\mathrm{1,2}\right)$ such that

$\begin{array}{cc}\hfill {\lambda }_j+b_{11}^{\left[1\right]}+{\sigma }_j{b}_{12}^{\left[1\right]}& =0,\hfill \\ \hfill b_{21}^{\left[1\right]}+{\sigma }_j\left({\lambda }_j+b_{22}^{\left[1\right]}\right)& =0,\hfill \end{array}(12)$

where

${\sigma }_j=\frac{f_2\left({\lambda }_j\right)+{\gamma }_j{g}_2\left({\lambda }_j\right)}{f_1\left({\lambda }_j\right)+{\gamma }_j{g}_1\left({\lambda }_j\right)},\left(j=\mathrm{1,2}\right).(13)$

Then, the gauge transformation $T^{\left[1\right]}$ can be given as follows:

$T^{\left[1\right]}=\left(\begin{array}{cc}\hfill \lambda \hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill \lambda \hfill \end{array}\right)+\frac{1}{{\sigma }_2-{\sigma }_1}\left(\begin{array}{cc}\hfill {\lambda }_2{\sigma }_1-{\lambda }_1{\sigma }_2\hfill & \hfill {\lambda }_1-{\lambda }_2\hfill \\ \hfill {\sigma }_1{\sigma }_2\left({\lambda }_2-{\lambda }_1\right)\hfill & \hfill {\lambda }_1{\sigma }_1-{\lambda }_2{\sigma }_2\hfill \end{array}\right),(14)$

where ${\sigma }_j,\left(j=\mathrm{1,2}\right)$ can satisfy

$\begin{array}{cc}\hfill {\sigma }_{jx}& =-2i{\sigma }_j{\lambda }_j-ir{\sigma }_j^2+iq,\hfill \\ \hfill {\sigma }_{jt}& =\left(\left(-2i{r}^2{q}_{xx}-4ir{q}_x{r}_x-6iq{r}_x^2-i{r}_{\mathit{xxxx}}\right)\delta +2{\chi }_d{r}_{\mathit{xxx}}-\frac{{\chi }_d}{2}{r}_{xx}\right.\hfill \\ \hfill & +\left(12qr{\chi }_d+2{\chi }_c\right)r_x\left.+4i{\chi }_{a}r\right){\sigma }_j^2+\left(\left(4r{q}^2{r}_x-4r^{2}q{q}_x+2r{q}_{\mathit{xxx}}\right.\right.\hfill \\ \hfill & -2q{r}_{\mathit{xxx}}-2q_{xx}{r}_x+2q_x{r}_{xx}\delta -4ir{q}_{xx}{\chi }_d\left.-4iq{r}_{xx}{\chi }_d\right)\hfill \\ \hfill & +\left(4i{r}_x{\chi }_d-ir{\chi }_b\right)q_x+iq{r}_x{\chi }_b-12i{r}^2{q}^2{\chi }_d+8i{\lambda }_j^2{\chi }_c-4iqr{\chi }_c{\sigma }_j\hfill \\ \hfill & +2\left(2i{q}^2{r}_{xx}\right.\left.+4iq{r}_x{q}_x+6ir{q}_x^2+i{q}_{\mathit{xxxx}}\right)\delta \hfill \\ \hfill & +2{\chi }_d{q}_{\mathit{xxx}}+\frac{{\chi }_d}{2}{q}_{xx}+\left(12qr{\chi }_d+2{\chi }_c\right)q_x-4iq{\chi }_a,\hfill \end{array}(15)$

along with

$\begin{array}{cc}\hfill {\chi }_a& =-\frac{3\delta q^2{r}^2}{2}-4\delta {\lambda }_j^4+2\omega {\lambda }_j^3+\alpha {\lambda }_j^2-\frac{{\lambda }_j}{4}-\frac{\left(-4\delta {\lambda }_j^2+2\omega {\lambda }_j+\alpha \right)qr}{2},\hfill \\ \hfill {\chi }_b& =4i{\lambda }_j\omega +2i\alpha +16iqr\delta -8i\delta {\lambda }_j^2,\hfill \\ \hfill {\chi }_c& =-4\delta {\lambda }_j^3+2\omega {\lambda }_j^2+\alpha {\lambda }_j-\frac{1}{4},\hfill \\ \hfill {\chi }_d& =\delta {\lambda }_j-\frac{\omega }{2},j=\mathrm{1,2}.\hfill \end{array}(16)$

By tedious calculations and using the identities (15), it can be verified that $U^{\left[1\right]},V^{\left[1\right]}$ have the same forms as U and V under the symmetry reduction (6). To construct the N-fold Darboux transformation of Eq. 5, a more generalized higher-order gauge transformation can be given as follows:

${\mathrm{\Phi }}^{\left[N\right]}=T_N\mathrm{\Phi },(17)$

where

$T_N=\prod _{k=1}^N{T}^{\left[k\right]}=\prod _{k=1}^N\left(\lambda I+B^{\left[k\right]}\right)=\prod _{k=1}^N\left(\begin{array}{cc}\hfill \lambda +b_{11}^{\left[k\right]}\hfill & \hfill b_{12}^{\left[k\right]}\hfill \\ \hfill b_{21}^{\left[k\right]}\hfill & \hfill \lambda +b_{22}^{\left[k\right]}\hfill \end{array}\right),(18)$

from which the following relationships can be obtained:

$\begin{array}{cc}\hfill r^{\left[N\right]}\left(x,t\right)& =r\left(x,t\right)-2\sum _{k=1}^N{b}_{12}^{\left[k\right]}\left(x,t\right),\hfill \\ \hfill q^{\left[N\right]}\left(x,t\right)& =q\left(x,t\right)+2\sum _{k=1}^N{b}_{21}^{\left[k\right]}\left(x,t\right).\hfill \end{array}(19)$

Combined with symmetry reduction (6), there is

$b_{12}^{\left[k\right]}\left(x,t\right)=b_{21}^{\left[k\right]}\left(-x,-t\right).(20)$

Similar to the case of one-fold Darboux transformation, we construct the following equations:

$\begin{array}{cc}\hfill {\left.\left({\left(T_N\right)}_{11}+{\sigma }_j{\left(T_N\right)}_{12}\right)\right|}_{\lambda ={\lambda }_j}& =0,\hfill \\ \hfill {\left.\left({\left(T_N\right)}_{21}+{\sigma }_j{\left(T_N\right)}_{22}\right)\right|}_{\lambda ={\lambda }_j}& =0,\hfill \end{array}(21)$

with

${\sigma }_j=\frac{f_2\left({\lambda }_j\right)+{\gamma }_j{g}_2\left({\lambda }_j\right)}{f_1\left({\lambda }_j\right)+{\gamma }_j{g}_1\left({\lambda }_j\right)},j=\mathrm{1,2},\dots ,2N.(22)$

From algebraic Eq. 21, the determinant representation of the N-fold Darboux matrix T_N can be derived by Cramer’s rule, from which the determinant representations of $r^{\left[N\right]}$ and $q^{\left[N\right]}$ can be given as follows:

$r^{\left[N\right]}=r-2\frac{W_{2N}}{Q_{2N}},q^{\left[N\right]}=q+2\frac{{\widehat{W}}_{2N}}{Q_{2N}}.(23)$

Here,

$Q_{2N}=\left[\begin{array}{ccccccc}\hfill 1\hfill & \hfill {\sigma }_1\hfill & \hfill {\lambda }_1\hfill & \hfill {\lambda }_1{\sigma }_1\hfill & \hfill \dots \hfill & \hfill {\lambda }_1^{N-1}\hfill & \hfill {\sigma }_1{\lambda }_1^{N-1}\hfill \\ \hfill 1\hfill & \hfill {\sigma }_2\hfill & \hfill {\lambda }_2\hfill & \hfill {\lambda }_2{\sigma }_2\hfill & \hfill \dots \hfill & \hfill {\lambda }_2^{N-1}\hfill & \hfill {\sigma }_2{\lambda }_2^{N-1}\hfill \\ \hfill 1\hfill & \hfill {\sigma }_3\hfill & \hfill {\lambda }_3\hfill & \hfill {\lambda }_3{\sigma }_3\hfill & \hfill \dots \hfill & \hfill {\lambda }_3^{N-1}\hfill & \hfill {\sigma }_3{\lambda }_3^{N-1}\hfill \\ \hfill 1\hfill & \hfill {\sigma }_4\hfill & \hfill {\lambda }_4\hfill & \hfill {\lambda }_4{\sigma }_4\hfill & \hfill \dots \hfill & \hfill {\lambda }_4^{N-1}\hfill & \hfill {\sigma }_4{\lambda }_4^{N-1}\hfill \\ \hfill ⋮\hfill & \hfill ⋮\hfill & \hfill ⋮\hfill & \hfill ⋮\hfill & \hfill \ddots \hfill & \hfill ⋮\hfill & \hfill ⋮\hfill \\ \hfill 1\hfill & \hfill {\sigma }_{2N-1}\hfill & \hfill {\lambda }_{2N-1}\hfill & \hfill {\lambda }_{2N-1}{\sigma }_{2N-1}\hfill & \hfill \dots \hfill & \hfill {\lambda }_{2N-1}^{N-1}\hfill & \hfill {\sigma }_{2N-1}{\lambda }_{2N}^{N-1}\hfill \\ \hfill 1\hfill & \hfill {\sigma }_{2N}\hfill & \hfill {\lambda }_{2N}\hfill & \hfill {\lambda }_{2N}{\sigma }_{2N}\hfill & \hfill \dots \hfill & \hfill {\lambda }_{2N}^{N-1}\hfill & \hfill {\sigma }_{2N}{\lambda }_{2N}^{N-1}\hfill \end{array}\right],(24)$

$W_{2N}=\left[\begin{array}{ccccccc}\hfill 1\hfill & \hfill {\sigma }_1\hfill & \hfill {\lambda }_1\hfill & \hfill {\lambda }_1{\sigma }_1\hfill & \hfill \dots \hfill & \hfill {\lambda }_1^{N-1}\hfill & \hfill -{\lambda }_1^N\hfill \\ \hfill 1\hfill & \hfill {\sigma }_2\hfill & \hfill {\lambda }_2\hfill & \hfill {\lambda }_2{\sigma }_2\hfill & \hfill \dots \hfill & \hfill {\lambda }_2^{N-1}\hfill & \hfill -{\lambda }_2^N\hfill \\ \hfill 1\hfill & \hfill {\sigma }_3\hfill & \hfill {\lambda }_3\hfill & \hfill {\lambda }_3{\sigma }_3\hfill & \hfill \dots \hfill & \hfill {\lambda }_3^{N-1}\hfill & \hfill -{\lambda }_3^N\hfill \\ \hfill 1\hfill & \hfill {\sigma }_4\hfill & \hfill {\lambda }_4\hfill & \hfill {\lambda }_4{\sigma }_4\hfill & \hfill \dots \hfill & \hfill {\lambda }_4^{N-1}\hfill & \hfill -{\lambda }_4^N\hfill \\ \hfill ⋮\hfill & \hfill ⋮\hfill & \hfill ⋮\hfill & \hfill ⋮\hfill & \hfill \ddots \hfill & \hfill ⋮\hfill & \hfill ⋮\hfill \\ \hfill 1\hfill & \hfill {\sigma }_{2N-1}\hfill & \hfill {\lambda }_{2N-1}\hfill & \hfill {\lambda }_{2N-1}{\sigma }_{2N-1}\hfill & \hfill \dots \hfill & \hfill {\lambda }_{2N-1}^{N-1}\hfill & \hfill -{\lambda }_{2N-1}^N\hfill \\ \hfill 1\hfill & \hfill {\sigma }_{2N}\hfill & \hfill {\lambda }_{2N}\hfill & \hfill {\lambda }_{2N}{\sigma }_{2N}\hfill & \hfill \dots \hfill & \hfill {\lambda }_{2N}^{N-1}\hfill & \hfill -{\lambda }_{2N}^N\hfill \end{array}\right],(25)$

${\widehat{W}}_{2N}=\left[\begin{array}{ccccccc}\hfill 1\hfill & \hfill {\sigma }_1\hfill & \hfill {\lambda }_1\hfill & \hfill {\lambda }_1{\sigma }_1\hfill & \hfill \dots \hfill & \hfill -{\lambda }_1^N{\sigma }_1\hfill & \hfill {\sigma }_1{\lambda }_1^{N-1}\hfill \\ \hfill 1\hfill & \hfill {\sigma }_2\hfill & \hfill {\lambda }_2\hfill & \hfill {\lambda }_2{\sigma }_2\hfill & \hfill \dots \hfill & \hfill -{\lambda }_2^N{\sigma }_2\hfill & \hfill {\sigma }_2{\lambda }_2^{N-1}\hfill \\ \hfill 1\hfill & \hfill {\sigma }_3\hfill & \hfill {\lambda }_3\hfill & \hfill {\lambda }_3{\sigma }_3\hfill & \hfill \dots \hfill & \hfill -{\lambda }_3^N{\sigma }_3\hfill & \hfill {\sigma }_3{\lambda }_3^{N-1}\hfill \\ \hfill 1\hfill & \hfill {\sigma }_4\hfill & \hfill {\lambda }_4\hfill & \hfill {\lambda }_4{\sigma }_4\hfill & \hfill \dots \hfill & \hfill -{\lambda }_4^N{\sigma }_4\hfill & \hfill {\sigma }_4{\lambda }_4^{N-1}\hfill \\ \hfill ⋮\hfill & \hfill ⋮\hfill & \hfill ⋮\hfill & \hfill ⋮\hfill & \hfill \ddots \hfill & \hfill ⋮\hfill & \hfill ⋮\hfill \\ \hfill 1\hfill & \hfill {\sigma }_{2N-1}\hfill & \hfill {\lambda }_{2N-1}\hfill & \hfill {\lambda }_{2N-1}{\sigma }_{2N-1}\hfill & \hfill \dots \hfill & \hfill -{\lambda }_{2N-1}^N{\sigma }_{N-1}\hfill & \hfill {\sigma }_{2N-1}{\lambda }_{2N-1}^{N-1}\hfill \\ \hfill 1\hfill & \hfill {\sigma }_{2N}\hfill & \hfill {\lambda }_{2N}\hfill & \hfill {\lambda }_{2N}{\sigma }_{2N}\hfill & \hfill \dots \hfill & \hfill -{\lambda }_{2N}^N{\sigma }_N\hfill & \hfill {\sigma }_{2N}{\lambda }_{2N}^{N-1}\hfill \end{array}\right].(26)$

This is the N-fold Darboux transformation of Eq. 5. Moreover, the existence of the symmetry reduction condition Eq. 6 implies that the Darboux transformation of the non-local reverse space−time fifth-order NLS Eq. 5 is very different from the Darboux transformation of the classical fifth-order NLS Eq. 4, although both of them have the same form.

3 Non-linear wave solutions of the reverse space–time non-local fifth-order NLS equation

3.1 One-soliton solutions from zero seed solution

To construct a soliton solution of the non-local Eq. 5, we take a zero seed solution, under which the corresponding eigenfunctions of the linear spectral problem (1) can be given as follows:

$f^{\left[1\right]}\left(\lambda \right)=\left(\begin{array}{c}\hfill e^{i\lambda x-i{\lambda }^2\left(-16\delta {\lambda }^3+8\omega {\lambda }^2+4\alpha \lambda -1\right)t}\hfill \\ \hfill 0\hfill \end{array}\right),g^{\left[1\right]}\left(\lambda \right)=\left(\begin{array}{c}\hfill 0\hfill \\ \hfill e^{-i\lambda x+i{\lambda }^2\left(-16\delta {\lambda }^3+8\omega {\lambda }^2+4\alpha \lambda -1\right)t}\hfill \end{array}\right).(27)$

Then, the following relationships can be obtained:

${\sigma }_j={\gamma }_j{e}^{{\xi }_j}\left(j=\mathrm{1,2}\right),(28)$

$b_{12}^{\left[1\right]}\left(x,t\right)=\frac{{\lambda }_1-{\lambda }_2}{{\gamma }_2{e}^{{\xi }_2}-{\gamma }_1{e}^{{\xi }_1}},b_{21}^{\left[1\right]}\left(x,t\right)=\frac{\left({\lambda }_2-{\lambda }_1\right){\gamma }_1{\gamma }_2{e}^{{\xi }_1+{\xi }_2}}{{\gamma }_2{e}^{{\xi }_2}-{\gamma }_1{e}^{{\xi }_1}},(29)$

${\xi }_j=8i\left(-4\delta {\lambda }_j^{4}t+2{\lambda }_j^3\omega t+\alpha {\lambda }_j^{2}t-\frac{1}{4}{\lambda }_{j}t-\frac{1}{4}x\right){\lambda }_j,(30)$

under which the conditions for symmetry reduction (6) can be obtained as follows:

${\gamma }_1\left({\gamma }_2^2-1\right)=0,{\gamma }_2\left(1-{\gamma }_1^2\right)=0.(31)$

Without the loss of generality, we take γ₁ = −1 and γ₂ = 1 and ${\lambda }_j=k_j+i{w}_j,\left(j=\mathrm{1,2}\right)$, and the solution can be simplified as follows:

$r^{\left[1\right]}=-\left(\left(k_1-k_2\right)+i\left(w_1-w_2\right)\right)\mathrm{s}\mathrm{e}\mathrm{c}\mathrm{h}\left(\frac{1}{2}\left(\left({\xi }_{1R}-{\xi }_{2R}\right)+i\left({\xi }_{1I}-{\xi }_{2I}\right)\right)\right)e^{-\frac{1}{2}\left(\left({\xi }_{1R}+{\xi }_{2R}\right)+i\left({\xi }_{1I}+{\xi }_{2I}\right)\right)},(32)$

where

$\begin{array}{c}{\xi }_{jR}=\mathfrak{R}\left({\xi }_j\right)=160w_j(\left(\delta k_j^4-\frac{2k_j^3\omega }{5}+\left(-2w_j^2\delta -\frac{3\alpha }{20}\right)k_j^2+\left(\frac{2w_j^2\omega }{5}+\frac{1}{40}\right)k_j+\frac{w_j^2\left(w_j^2\delta +\frac{\alpha }{4}\right)}{5}\right)t+\frac{x}{80}),\hfill \\ \hfill {\xi }_{jI}=\mathfrak{I}\left({\xi }_j\right)=\left(8\left(k_j^3-3k_j{w}_j^2\right)\alpha +32\left(10k_j^3-k_j^5-5k_j{w}_j^4\right)\delta +16\left(k_j^4-6k_j^2{w}_j^2+w_j^4\right)\omega 2w_j^2-2k_j^2\right)t-2x{k}_j.\end{array}(33)$

The soliton solution can be obtained as follows:

$r^{\left[1\right]}=\frac{-2i{w}_1{e}^{2i\left(16k_1^5\delta -160\delta k_1^3{w}_1^2+80\delta k_1{w}_1^4-8k_1^4\omega +48\omega k_1^2{w}_1^2-8w_1^4\omega -4\alpha k_1^3+12\alpha k_1{w}_1^2+k_1^2-w_1^2\right)t+2i{k}_{1}x}}{\cosh \left(160w_1\left(\left(\delta k_1^4-\frac{2k_1^3\omega }{5}+\left(-2w_1^2\delta -\frac{3\alpha }{20}\right)k_1^2+\left(\frac{2w_1^2\omega }{5}+\frac{1}{40}\right)k_1+\frac{w_1^2\left(w_1^2\delta +\frac{\alpha }{4}\right)}{5}\right)t+\frac{x}{80}\right)\right)}.(34)$

This is under the condition that k₁ = k₂ and w₁ = −w₂. Evidently, the propagation direction of a soliton (34) is determined by the value of $\left(\delta k_1^4-\frac{2k_1^3\omega }{5}+\left(-2w_1^2\delta -\frac{3\alpha }{20}\right)k_1^2+\left(\frac{2w_1^2\omega }{5}+\frac{1}{40}\right)k_1+\frac{w_1^2\left(w_1^2\delta +\frac{\alpha }{4}\right)}{5}\right)$. In Figure 1A, the evolution of a soliton solution (34) is illustrated, and the corresponding evolution profiles of the real and imaginary parts are shown in Figures 1B, C, which exhibit the characteristics of a breather. On the other hand, by taking k₂ = −2k₁ and w₂ = 0, the complexiton solution can be given as follows:

$r^{\left[1\right]}=\left(-3k_1-i{w}_1\right)\mathrm{s}\mathrm{e}\mathrm{c}\mathrm{h}\left(\frac{1}{2}\left({\xi }_{1R}+i\left({\xi }_{1I}-{\xi }_{2I}\right)\right)\right)e^{-\frac{1}{2}\left({\xi }_{1R}+i\left({\xi }_{1I}+{\xi }_{2I}\right)\right)},(35)$

where

$\begin{array}{cc}\hfill \frac{1}{2}i\left({\xi }_{1I}-{\xi }_{2I}\right)& =i\left(-\left(12w_1^2{k}_1-36k_1^3\right)\alpha -\left(528k_1^5-160k_1^3{w}_1^2+80k_1{w}_1^4\right)\delta -\left(-3k_1^2-w_1^2\right)\right.\hfill \\ \hfill & \left.-\left(120k_1^4+48k_1^2{w}_1^2-8w_1^4\right)\omega \right)t-3ix{k}_1,\hfill \\ \hfill -\frac{1}{2}i\left({\xi }_{1I}+{\xi }_{2I}\right)& =-i\left(\left(-28k_1^3-12k_1{w}_1^2\right)\alpha +\left(496k_1^5+160k_1^3{w}_1^2-80k_1{w}_1^4\right)\delta +\left(w_1^2-5k_1^2\right)\right.\left.+\left(136k_1^4-48k_1^2{w}_1^2+8w_1^4\right)\omega \right)t-i{k}_{1}x.\hfill \end{array}(36)$

FIGURE 1

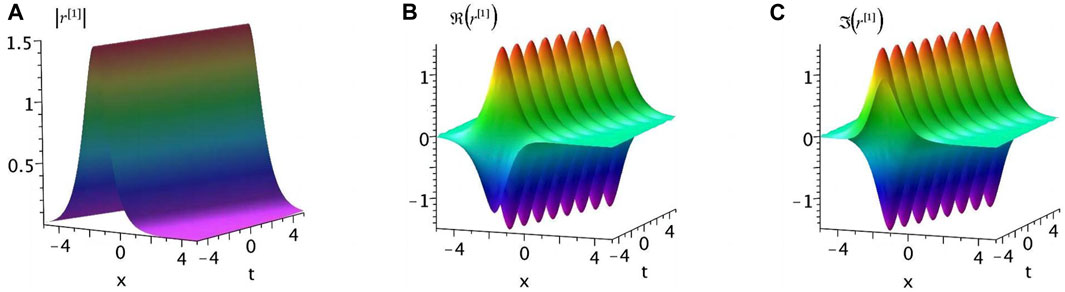
FIGURE 1. (Color online). (A) Density evolution of the one-soliton solution; (B) evolution of the real part; (C) evolution of the imaginary part of the soliton solution (34) under the parameters $\alpha =\frac{1}{2},\delta =\frac{1}{5},\omega =\frac{1}{3},k_1=-\frac{1}{5},w_1=-\frac{3}{4},\left(\delta k_1^4-\frac{2k_1^3\omega }{5}+\left(-2w_1^2\delta -\frac{3\alpha }{20}\right)k_1^2+\left(\frac{2w_1^2\omega }{5}+\frac{1}{40}\right)k_1+\frac{w_1^2\left(w_1^2\delta +\frac{\alpha }{4}\right)}{5}\right)<0$.

It can be seen from Figure 2A that the solution (35) propagates to the left along the x-axis under the condition that $\left(\delta k_1^4-\frac{2k_1^3\omega }{5}+\left(-2w_1^2\delta -\frac{3\alpha }{20}\right)k_1^2+\left(\frac{2w_1^2\omega }{5}+\frac{1}{40}\right)k_1+\frac{w_1^2\left(w_1^2\delta +\frac{\alpha }{4}\right)}{5}\right)>0$. Figures 2B, C show the evolution characteristics of the real and imaginary parts of the solution (35). The propagation states of the solution (35) at three different times are shown in Figure 2D.

FIGURE 2

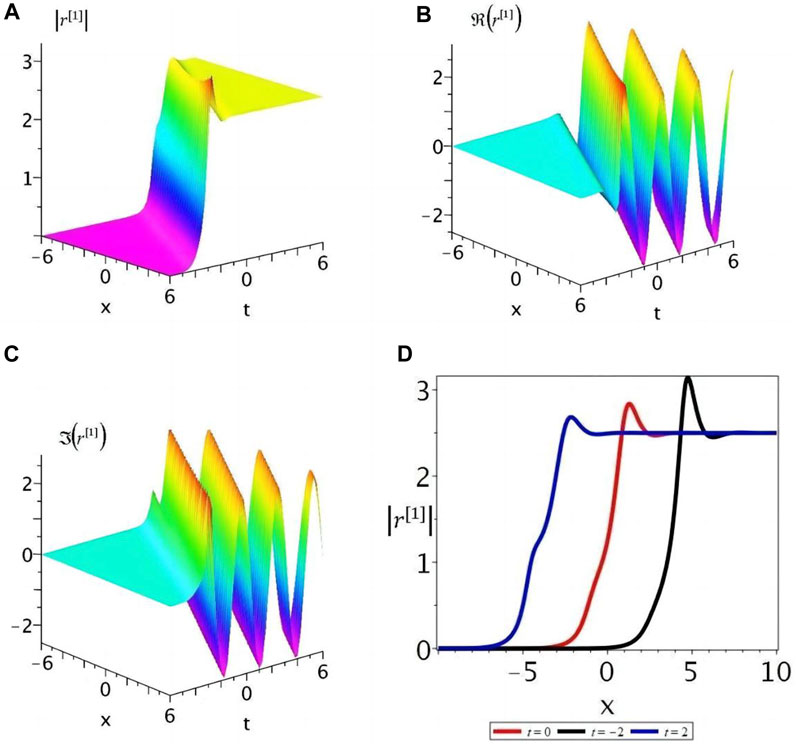
FIGURE 2. (Color online). (A) Density evolution of the complexiton solution; (B) evolution of the real part; (C) evolution of the imaginary part; (D) three evolution states at t =−2,0,2 for the solution (35) under the parameters $\alpha =-\frac{1}{5},\delta =\frac{1}{4},\omega =\frac{1}{2},k_1=\frac{1}{3},w_1=-\frac{3}{4},\left(\delta k_1^4-\frac{2k_1^3\omega }{5}+\left(-2w_1^2\delta -\frac{3\alpha }{20}\right)k_1^2+\left(\frac{2w_1^2\omega }{5}+\frac{1}{40}\right)k_1+\frac{w_1^2\left(w_1^2\delta +\frac{\alpha }{4}\right)}{5}\right)>0$.

3.2 Two-soliton solutions from zero seed solution

Two-fold exact solutions of Eq. 5 can be derived from the Darboux transformation (23) by taking N = 2. In order to satisfy the constraint condition (20), we take γ₁ = −1, γ₂ = 1, γ₃ = −1, and γ₄ = 1 and consider the case that the eigenvalues are two pairs of conjugate complexes, i.e., ${\lambda }_1={\lambda }_2^{*}=k_1+i{w}_1,{\lambda }_3={\lambda }_4^{*}=k_2+i{w}_2$. Then, the solution can be obtained as

$r^{\left[2\right]}=\frac{G_1\left(x,t\right)}{H_1\left(x,t\right)},(37)$

where

$\begin{array}{cc}\hfill G_1\left(x,t\right)& =4i\left(\left(\frac{w_1^2}{2}-\frac{w_2^2}{2}+\frac{{\left(k_1-k_2\right)}^2}{2}\right)\cosh \left({\xi }_{2R}\right)+i{w}_2\left(k_1-k_2\right)\sinh \left({\xi }_{2R}\right)\right)w_1{e}^{-i{\xi }_{1I}}\hfill \\ \hfill & -4i\left(\left(\frac{w_1^2}{2}-\frac{w_2^2}{2}-\frac{{\left(k_1-k_2\right)}^2}{2}\right)\cosh \left({\xi }_{1R}\right)+i{w}_1\left(k_1-k_2\right)\sinh \left({\xi }_{1R}\right)\right)w_2{e}^{-i{\xi }_{2I}},\hfill \\ \hfill H_1\left(x,t\right)& =2w_1{w}_2\cos \left({\xi }_{1I}-{\xi }_{2I}\right)-\left(w_1^2+w_2^2+{\left(k_1-k_2\right)}^2\right)\cosh \left({\xi }_{1R}\right)\cosh \left({\xi }_{2R}\right)\hfill \\ \hfill & +2w_1{w}_2\sinh \left({\xi }_{1R}\right)\sinh \left({\xi }_{2R}\right),\hfill \end{array}(38)$

and ξ_jR and ξ_jI are defined by (33) previously. In Figure 3A, the two-soliton solution behaves as an interaction of two bright solitons; after that, they stably propagate with original shapes and velocities. The corresponding evolutions of real and imaginary parts of the solution are shown in Figures 3B, C, which are all two-order breather solutions.

FIGURE 3

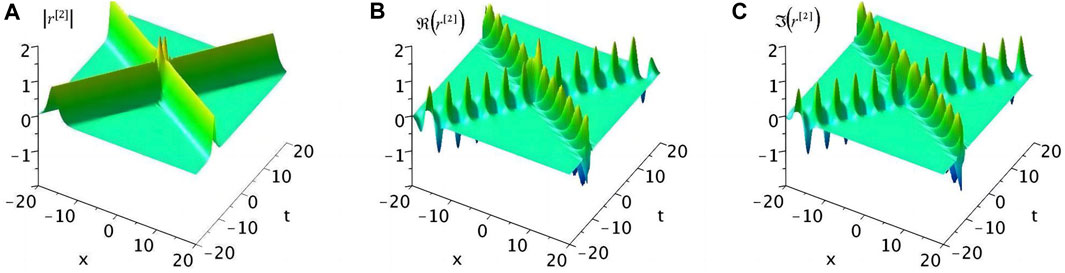
FIGURE 3. (Color online). (A) Density evolution of the two-soliton solution; (B) evolution of the real part; (C) evolution of the imaginary part of the solution (37) under the parameters $k_1=-\frac{1}{2},w_1=-\frac{1}{2}.k_2=\frac{11}{20},w_2=\frac{11}{20},\alpha =\frac{1}{2},\delta =-\frac{3}{10},\omega =\frac{3}{10}$.

3.3 One-soliton solutions from non-zero seed solution

In order to construct the rogue wave solution of Eq. 5 by the Darboux transformation (10), the seed solution is taken as the plane wave solution,

$r=-ic{e}^{-i\left(ax+\eta t\right)},q=ic{e}^{i\left(ax+\eta t\right)},(39)$

where a and c are an arbitrary constant and $\eta =\left(-a^3+6a{c}^2\right)\alpha +\left(a^5-20a^3{c}^2+30a{c}^4\right)\delta +\left(-a^4+12a^2{c}^2-6c^4\right)\omega +\frac{a^2}{2}-c^2$, respectively. Substituting the seed solution (39) into the linear spectral problem (1) with $\lambda =\frac{a}{2}-ic$ or $\lambda =\frac{a}{2}+ic$, the eigenfunctions can be obtained as follows:

$\mathrm{\Phi }\left(\lambda \right)=\left(\begin{array}{c}\hfill \left(C_1\left(cx-{\mathrm{\Delta }}_{1}t+1\right)+c{C}_2\right)e^{\frac{i}{2}\left(ax+\eta t\right)}\hfill \\ \hfill \left(C_1\left(-cx+{\mathrm{\Delta }}_{1}t\right)-c{C}_2\right)e^{-\frac{i}{2}\left(ax+\eta t\right)}\hfill \end{array}\right),(40)$

or

$\mathrm{\Phi }\left(\lambda \right)=\left(\begin{array}{c}\hfill \left(C_3\left(-cx+{\mathrm{\Delta }}_{2}t+1\right)-c{C}_4\right)e^{\frac{i}{2}\left(ax+\eta t\right)}\hfill \\ \hfill \left(C_3\left(-cx+{\mathrm{\Delta }}_{2}t\right)-c{C}_4\right)e^{-\frac{i}{2}\left(ax+\eta t\right)}\hfill \end{array}\right),(41)$

where

$\begin{array}{cc}\hfill {\mathrm{\Delta }}_1& =-c\left(-3a^2+6c^2\right)\alpha -c\left(5a^4-60a^2{c}^2+30c^4\right)\delta -c\left(-4a^3+24a{c}^2\right)\omega -ac\hfill \\ \hfill & +i{c}^2\left(20a^3\delta -60a{c}^2\delta -12\omega a^2+12c^2\omega -6a\alpha +1\right),\hfill \\ \hfill {\mathrm{\Delta }}_2& =-c\left(-3a^2+6c^2\right)\alpha -c\left(5a^4-60a^2{c}^2+30c^4\right)\delta -c\left(-4a^3+24a{c}^2\right)\omega -ac\hfill \\ \hfill & -i{c}^2\left(20a^3\delta -60a{c}^2\delta -12\omega a^2+12c^2\omega -6a\alpha +1\right),\hfill \end{array}(42)$

and C₁, C₂, C₃, and C₄ are arbitrary constants. For simplicity, taking $\{C_1=1,C_2=-\frac{1}{c}\}$ and $\{C_3=-1,C_4=-\frac{1}{c}\}$ and considering their relationship (13), we have the following:

$\begin{array}{cc}\hfill & {\sigma }_1=\left(-1+\frac{1+{\gamma }_1}{1+\left(cx-{\mathrm{\Delta }}_{1}t\right)\left({\gamma }_1+1\right)}\right)e^{-i\left(ax+\eta t\right)},\hfill \\ \hfill & {\sigma }_2=\left(1+\frac{{\gamma }_2-1}{1+\left(cx-{\mathrm{\Delta }}_{2}t\right)\left({\gamma }_2-1\right)}\right)e^{-i\left(ax+\eta t\right)}.\hfill \end{array}(43)$

To satisfy the constraint condition (11), we take γ₁ = 1 and γ₂ = −1. Then, the rogue wave solution can be given as follows:

$r^{\left[1\right]}=ic{e}^{i\left(ax+\eta t\right)}\left(1+\frac{G_2\left(x,t\right)}{H_2\left(x,t\right)}\right),(44)$

where

$\begin{array}{cc}\hfill G_2\left(x,t\right)& =-4+i\left(8c^2+160a^3{c}^2\delta -480a{c}^4\delta -96a^2{c}^2\omega -48a\alpha c^2+96c^4\omega \right)t,\hfill \\ \hfill H_2\left(x,t\right)& =4c^2\left(\left(a^4+4c^4\right){\alpha }^2+\left(30\left(a^6+6a^4{c}^2-6a^2{c}^4+12c^6\right)\delta +24\left(a^5-2a^3{c}^2+6a{c}^4\right)\omega \right)\alpha -6a^3\alpha \right.\hfill \\ \hfill & +25\left(a^8-8a^6{c}^2+60a^4{c}^4+36c^8\right){\delta }^2+40a^3\left(-a^4+6a^2{c}^2-30c^4\right)\omega \delta \hfill \\ \hfill & +10a\left(a^4-8a^2{c}^2-6c^4\right)\delta +16\left(a^6-3a^4{c}^2+18a^2{c}^4+9c^6\right){\omega }^2\hfill \\ \hfill & +8\left(-a^4+3a^2{c}^2+3c^4\right)\omega \left.+a^2+c^2\right)t^2+\left(24c^2\left(2c^2-a^2\right)\alpha \right.\hfill \\ \hfill & +40c^2\left({\left(6c^2-a^2\right)}^2-30c^4\right)\delta +32a{c}^2\left(6c^2-a^2\right)\omega \left.+8a{c}^2\right)xt+4c^2{x}^2+1.\hfill \end{array}(45)$

The density evolution and 2D contour plots for the rogue wave solution (45) under appropriate parameters are shown in Figures 4A, B, and the typical amplitude |r^[1]| profile with t = 0 is illustrated in Figure 4C.

FIGURE 4

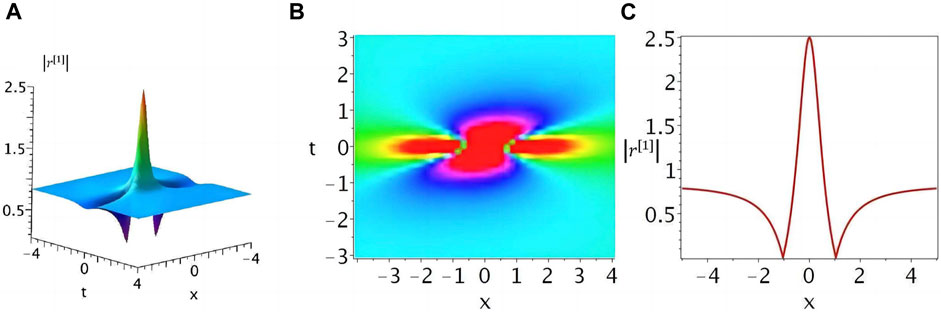
FIGURE 4. (Color online). The rogue wave solution given by (45) with $a=-\frac{9}{10},c=-\frac{5}{6},\alpha =-\frac{1}{4},\delta =-\frac{1}{6},\omega =\frac{1}{6}$: (A) density evolution; (B) 2D contour plot; (C) amplitude |r^[1]| profile with t = 0 of the rogue wave.

4 Conclusion

In this paper, the reverse space–time non-local fifth-order NLS Eq. 5 is studied by Darboux transformations. Based on the scattering problem, the N-fold Darboux transformation of the equation is constructed. By selecting different seed solutions, we have presented soliton, complexiton, and rogue wave solutions of Eq. 5, whose non-linear dynamics and evolutions are discussed. However, the computational effort increases rapidly due to the increase of the order of the Darboux transformation and the presence of the symmetric reduction condition; so, more interesting and physically meaningful non-linear wave solutions are difficult to be derived, such as breather and higher-order rogue wave solutions. At the same time, whether the equation has other integrable properties, such as Bäcklund transformations, Hamilton structures, and infinite conservation laws, will be studied in the near future.

Data availability statement

The raw data supporting the conclusion of this article will be made available by the authors, without undue reservation.

Author contributions

XS: conceptualization, formal analysis, investigation, methodology, and writing—original draft. YY: conceptualization, methodology, and writing—review and editing. All authors contributed to the article and approved the submitted version.

Funding

This work is supported by the Zhoushan Science and Technology Program (No. 2021C21023).

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors, and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

1. Soli DR, Ropers C, Koonath P, Jalali B. Optical rogue waves. Nature (2007) 450:1054–7. doi:10.1038/nature06402

PubMed Abstract | CrossRef Full Text | Google Scholar

2. Hasegawa A. Optical soliton theory and its applications in communication. Berlin: Springer (2003).

Google Scholar

3. Li J, Xu T, Meng XH, Zhang YX, Zhang HQ, Tian B. Lax pair, Bäcklund transformation and N-soliton-like solution for a variable-coefficient Gardner equation from nonlinear lattice, plasma physics and ocean dynamics with symbolic computation. J Math Anal Appl (2007) 336:1443–55. doi:10.1016/j.jmaa.2007.03.064

CrossRef Full Text | Google Scholar

4. Yan ZY, Konotop VV, Akhmediev N. Three-dimensional rogue waves in nonstationary parabolic potentials. Phys Rev E (2010) 82:036610. doi:10.1103/PhysRevE.82.036610

CrossRef Full Text | Google Scholar

5. Yan ZY. Vector financial rogue waves. Phys Lett A (2011) 375:4274–9. doi:10.1016/j.physleta.2011.09.026

CrossRef Full Text | Google Scholar

6. Li YS, Zhang JE. Darboux transformations of classical Boussinesq system and its multi-soliton solutions. Phys Lett A (2001) 284:253–8. doi:10.1016/S0375-9601(01)00331-0

CrossRef Full Text | Google Scholar

7. Feng BF, Ling LM. Darboux transformation and solitonic solution to the coupled complex short pulse equation. Physica D: Nonlinear Phenomena (2022) 437:133332. doi:10.1016/j.physd.2022.133332

CrossRef Full Text | Google Scholar

8. Weng WF, Zhang GQ, Zhou ZJ, Yan ZY. Semi-rational vector rogon–soliton solutions of the five-component Manakov/NLS system with mixed backgrounds. Appl Maths Lett (2022) 125:107735. doi:10.1016/j.aml.2021.107735

CrossRef Full Text | Google Scholar

9. Ma WX. Inverse scattering and soliton solutions of nonlocal complex reverse-spacetime mKdV equations. J Geometry Phys (2020) 157:103845. doi:10.1016/j.geomphys.2020.103845

CrossRef Full Text | Google Scholar

10. Hu XB, Ma WX. Application of hirota’s bilinear formalism to the toeplitz lattice—Some special soliton-like solutions. Phys Lett A (2002) 293:161–5. doi:10.1016/S0375-9601(01)00850-7

CrossRef Full Text | Google Scholar

11. Geng XG, Wu JP. Riemann–Hilbert approach and N-soliton solutions for a generalized Sasa–Satsuma equation. Wave Motion (2016) 60:62–72. doi:10.1016/j.wavemoti.2015.09.003

CrossRef Full Text | Google Scholar

12. Xu J, Fan EG. A Riemann-Hilbert approach to the initial-boundary problem for derivative nonlinear Schrödinger equation. Acta Mathematica Scientia (2014) 34:973–94. doi:10.1016/S0252-9602(14)60063-1

CrossRef Full Text | Google Scholar

13. Ablowitz MJ, Musslimani ZH. Integrable nonlocal nonlinear schrödinger equation. Phys Rev Lett (2013) 110:064105. doi:10.1103/PhysRevLett.110.064105

PubMed Abstract | CrossRef Full Text | Google Scholar

14. Ablowitz MJ, Musslimani ZH. Integrable nonlocal nonlinear equations. Stud Appl Maths (2017) 139:7–59. doi:10.1111/sapm.12153

CrossRef Full Text | Google Scholar

15. Lou SY. Alice-Bob systems, P^-T^-Ĉ symmetry invariant and symmetry breaking soliton solutions. J Math Phys (2018) 59:083507. doi:10.1063/1.5051989

CrossRef Full Text | Google Scholar

16. Gadzhimuradov TA, Agalarov AM. Towards a gauge-equivalent magnetic structure of the nonlocal nonlinear Schrödinger equation. Phys Rev A (2016) 93:062124. doi:10.1103/PhysRevA.93.062124

CrossRef Full Text | Google Scholar

17. Rybakov FN, Borisov AB, Blügel S, Kiselev NS. New type of stable particlelike states in chiral magnets. Phys Rev Lett (2015) 115:117201. doi:10.1103/PhysRevLett.115.117201

PubMed Abstract | CrossRef Full Text | Google Scholar

18. Dantas CC. An inhomogeneous space-time patching model based on a nonlocal and nonlinear Schrödinger equation. Foundations Phys (2016) 46:1269–92. doi:10.1007/s10701-016-0019-6

CrossRef Full Text | Google Scholar

19. Tang XY, Liang ZF, Hao XZ. Nonlinear waves of a nonlocal modified KdV equation in the atmospheric and oceanic dynamical system. Commun Nonlinear Sci Numer Simulation (2018) 60:62–71. doi:10.1016/j.cnsns.2017.12.016

CrossRef Full Text | Google Scholar

20. Zhang XE, Chen Y, Zhang Y. Breather, lump andXsoliton solutions to nonlocal KP equation. Comput Maths Appl (2017) 74:2341–7. doi:10.1016/j.camwa.2017.07.004

CrossRef Full Text | Google Scholar

21. Lakshmanan M, Porsezian K, Daniel M. Effect of discreteness on the continuum limit of the Heisenberg spin chain. Phys Lett A (1988) 133:483–8. doi:10.1016/0375-9601(88)90520-8

CrossRef Full Text | Google Scholar

22. Wen XY, Yan ZY. Higher-order rational solitons and rogue-like wave solutions of the (2 + 1)-dimensional nonlinear fluid mechanics equations. Commun Nonlinear Sci Numer Simulation (2017) 43:311–29. doi:10.1016/j.cnsns.2016.07.020

CrossRef Full Text | Google Scholar

23. Moslem WM. Langmuir rogue waves in electron-positron plasmas. Phys Plasmas (2011) 18:032301. doi:10.1063/1.3559486

CrossRef Full Text | Google Scholar

24. He JS, Charalampidis E, Kevrekidis P, Frantzeskakis D. Rogue waves in nonlinear Schrödinger models with variable coefficients: Application to Bose–Einstein condensates. Phys Lett A (2014) 378:577–83. doi:10.1016/J.PHYSLETA.2013.12.002

CrossRef Full Text | Google Scholar

25. Benney DJ, Newell AC. The propagation of nonlinear wave envelopes. J Maths Phys (1967) 46:133–9. doi:10.1002/sapm1967461133

CrossRef Full Text | Google Scholar

26. Dudley JM, Tarlor JR. Supercontinuum generation in optical fibers. Cambridge: Cambridge University Press (2010).

Google Scholar

27. Li LJ, Wu ZW, Wang LH, He JS. High-order rogue waves for the Hirota equation. Ann Phys (2013) 334:198–211. doi:10.1016/j.aop.2013.04.004

CrossRef Full Text | Google Scholar

28. Yang YQ, Suzuki T, Cheng XP. Darboux transformations and exact solutions for the integrable nonlocal Lakshmanan−Porsezian−Daniel equation. Appl Maths Lett (2020) 99:105998. doi:10.1016/j.aml.2019.105998

CrossRef Full Text | Google Scholar

29. Yang YQ, Wang X, Cheng XP. Higher-order rational solutions for a new integrable nonlocal fifth-order nonlinear Schrödinger equation. Wave Motion (2018) 77:1–11. doi:10.1016/j.wavemoti.2017.10.012

CrossRef Full Text | Google Scholar

30. Chowdury A, Kedziora DJ, Ankiewicz A, Akhmediev N. Soliton solutions of an integrable nonlinear Schrödinger equation with quintic terms. Phys Rev E (2014) 90:032922. doi:10.1103/PhysRevE.90.032922

CrossRef Full Text | Google Scholar