Applications of the invariant subspace method on searching explicit solutions to certain special-type non-linear evolution equations

We extend the invariant subspace method (ISM) to a class of Hamilton–Jacobi equations (HJEs) and a family of third-order time-fractional dispersive PDEs with the Caputo fractional derivative in this letter. More precisely, the complete classification is presented for such HJEs that admit invariant subspaces governed by solutions of the second-order and third-order linear ordinary differential equations (ODEs). Meanwhile, some concrete equations are derived for the construction of new exact solutions $u(x,t)={\sum }_{i=1}^n{C}_i(t)f_i(x)$. Then a set of invariant subspaces of the considered third-order time-fractional non-linear dispersive equations are obtained. Based on the Laplace transform method (LTM) and applying several properties of the well known Mitta-Leffer (ML) function, the different types of explicit solutions of a family of third-order time-fractional dispersive PDEs are finally derived.

1 Introduction

One of the recently invented methods to derive the explicit solution of NPDE is ISM, which was initiated by Galaktionov and Svirshchevskii in [1] and many researchers have illustrated its applicability in Refs. [2–6]. Specifically, Refs. [2, 3, 5, 6] have addressed the basic question of the dimension of invariant subspaces, which in addition to ISM is also relevant to Lie-B$\ddot{a}$cklund symmetry (LBS) and the conditional Lie-B$\ddot{a}$cklund symmetry (CLBS) [7–14]. Very recently, Refs. [15–23] generalized this method to resolve fractional non-linear partial differential equations (fNPDEs). It is verified that by applying ISM, a fNPDE can be reduced to a system of fractional non-linear ordinary differential equations (fNODEs), which can be solved by known analytical approaches.

In this paper, we analyze the following two families of special-type non-linear evolution equations.

1.1 Hamilton–Jacobi equations

Hamilton–Jacobi equations (HJEs) can be regarded as models for various processes in theoretical physics, quantum mechanics and contemporary problems of control, etc. In Refs. [24–28], the authors analyzed HJEs in different directions. References [29–32] have also indicated that these equations can be used to depict several properties including blow up behavior and the long time action of non-linear diffusion equations. We will consider the following HJEs

$u_t=u_x^{m+2}+p\left(x\right)B\left(u\right)u_x^{m+1}+Q\left(x,u\right),t\in {\mathbb{R}}^{+},x\in \mathbb{R},(1.1)$

where u = u(t, x) and p(x), B(u), Q(x, u) are sufficiently smooth functions of indicated variables. Here we suppose that m ≠ − 1, −2. This assumption means that Eq. 1.1 is a fully non-linear HJE. In Ref. [7], Qu showed that Eq. 1.1 preserves the second-order CLBS with $\eta =u_{xx}+H(u)u_x^2+G(u)u_x+F(u)$ and classified the solutions for Eq. 1.1.

1.2 Third-order time-fractional dispersive PDEs

The concept of fractional order derivative was initiated with the half-order derivative as considered by Leibniz and L’Hopital and many authors have generalized it to an arbitrary order derivative. Different concepts of fractional derivatives were proposed in [33–36]. Now fNPDEs have gained much attention because they can be utilized to represent a large number of physical processes. Some techniques have been employed to solve fNPDEs, but the study of fNPDEs has been still handicapped due to the limitations on dealing with more complex fNODEs.

We will study a family of third-order time-fractional dispersive PDEs

$\frac{{\partial }^{\alpha }}{\partial t^{\alpha }}\left[u-{\delta }^2\frac{{\partial }^{2}u}{\partial x^2}\right]+\sigma \frac{\partial u}{\partial x}+\gamma \frac{{\partial }^{3}u}{\partial x^3}=F\left[u\right]=\frac{\partial }{\partial x}\left[b_1{u}^2+b_2{\left(\frac{\partial u}{\partial x}\right)}^2+b_{3}u\frac{{\partial }^{2}u}{\partial x^2}\right],(1.2)$

where u = u(t, x), 0 < α ≤ 1, t > 0, and $\frac{{\partial }^{\alpha }u}{\partial t^{\alpha }}$ is the Caputo fractional derivative of u with respect to t. The ordinary case α = 1 of Eq. 1.2 was first introduced in [37] and has been discussed in depth by many researchers [38, 39]. In fact, when α = 1, δ = b₂ = b₃ = 0, Eq. 1.2 becomes the KdV equation. If we take $\alpha ={\delta }^2=b_3=1,b_1=-\frac{3}{2},b_2=\frac{1}{2}$, Eq. 1.2 becomes the Camassa–Holm equation [40]:

$u_t+\sigma u_x+\gamma u_{xxx}-u_{\mathit{xxt}}+3u{u}_x=2u_x{u}_{xx}+u{u}_{xxx}.(1.3)$

If $\alpha ={\delta }^2=b_2=b_3=-\frac{b_1}{2}=1,\sigma =\gamma =0$, Eq. 1.2 is the Degasperis–Procesi equation [41, 42]:

$u_t-u_{\mathit{xxt}}+4u{u}_x=3u_x{u}_{xx}+u{u}_{xxx}.(1.4)$

If α = δ² = 2b₂ = b₃ = 1, σ = γ = b₁ = 0, Eq. 1.2 becomes the Hunter-Saxton equation [1]:

$u_t-u_{\mathit{xxt}}=2u_x{u}_{xx}+u{u}_{xxx}.(1.5)$

These equations arise as asymptotic models in the theory of shallow water waves. Many authors have concentrated on studying the above special cases of Eq. 1.2.

The major contents of this paper are as follows. We recall the method of the invariant subspace, and also introduce several definitions and fundamental theorems on fractional derivatives and integrals in Section 2. In Section 3 we obtain the complete invariant subspace classification of Eq. 1.1 and derive the reductions and explicit solutions of several examples by utilizing ISM. In Section 4, combined with LTM and inspired by several properties of the well known ML function, we investigate exact solutions of different cases for Eq. 1.2. In the last section, we make some concluding remarks.

2 Preliminaries

First, we introduce ISM. Then, we give several definitions and properties.

2.1 Invariant subspace method

Now, we will present brief details of ISM for a kth-order NPDE

$u_t=F\left(x,u,u_x,\dots ,u_{kx}\right)\equiv F\left[u\right],(2.1)$

where $u_{jx}=\frac{{\partial }^{j}u}{\partial x^j}(j=1,\dots ,k)$.

In [15], Gazizov and Kasatkin demonstrated that ISM can be used to reduce a fNPDE to a system of fNODEs.

We focus on the fNPDE of the form

$\frac{{\partial }^{\alpha }u}{\partial t^{\alpha }}=F\left(x,u,u_x,\dots ,u_{kx}\right)\equiv F\left[u\right],(2.2)$

where $\frac{{\partial }^{\alpha }}{\partial t^{\alpha }}$ is the time-fractional Caputo derivative. Let f₁(x), f₂(x), …, f_n(x) be linearly independent functions and their linear span over $\mathbb{R}$ be W_n, namely,

$W_n=\mathcal{L}\left\{f_1\left(x\right),f_2\left(x\right),\dots ,f_n\left(x\right)\right\}\equiv \left\{\sum _{i=1}^n{C}_i{f}_i\left(x\right),C_i\in \mathbb{R}\right\}.$

Definition 2.1. If differential operator F satisfies F[W_n] ⊆ W_n, the subspace W_n is invariant under F.Let us suppose Eq. 2.2 preserves the subspace W_n, then

$F\left[\sum _{i=1}^n{C}_i{f}_i\left(x\right)\right]=\sum _{i=1}^n{\mathrm{\Psi }}_i\left(C_1,C_2,\dots ,C_n\right)f_i\left(x\right)$

$(C_1,C_2,\dots ,C_n)\in {\mathbb{R}}^n$. Thus Eq. 2.2 has the solution

$u\left(x,t\right)=\sum _{i=1}^n{C}_i\left(t\right)f_i\left(x\right),$

{C_i(t), (i = 1, 2, …, n)} satisfy the n-dimensional dynamical system

$\frac{{\partial }^{\alpha }{C}_i\left(t\right)}{\partial t^{\alpha }}=\mathrm{\Psi }\left(C_1\left(t\right),C_2\left(t\right),\dots ,C_n\left(t\right)\right),i=\mathrm{1,2},\dots ,n.$

Observing that the subspace W_n is determined by a basic solution set of a linear nth-order ODE,

$L\left[y\right]\equiv y^{\left(n\right)}+a_{n-1}\left(x\right)y^{\left(n-1\right)}+\cdots +a_1\left(x\right)y^{\prime }+a_0\left(x\right)y=0.(2.3)$

Therefore, the invariant condition F is

$L\left[F\left[u\right]\right]{\left|\right.}_{\left[H\right]}=0.(2.4)$

2.2 Some results on fractional calculus

Definition 2.2. The Riemann–Liouville fractional integral operator of order α > 0 is represented as the following expression:

$I_{a^{+}}^{\alpha }f\left(t\right)=\frac{1}{\mathrm{\Gamma }\left(\alpha \right)}{\int }_a^t{\left(t-\tau \right)}^{\alpha -1}f\left(\tau \right)d\tau ,t>a.(2.5)$

Where $\mathrm{\Gamma }(p)={\int }_0^{\infty }{e}^{-x}{x}^{p-1}dx$ is the Euler Gamma function. Note that $I_{a^{+}}^{0}f(t)=f(t)$.

Definition 2.3. The Caputo fractional differential operator of order α > 0 is represented as the following expression:

$D_{a^{+}}^{\alpha }f\left(t\right)=I_{a^{+}}^{n-\alpha }{D}^{n}f\left(t\right)=\left\{\begin{array}{cc}\hfill & \frac{1}{\mathrm{\Gamma }\left(n-\alpha \right)}{\int }_a^t{\left(t-\tau \right)}^{n-\alpha -1}{f}^{\left(n\right)}\left(\tau \right)d\tau ,\alpha \in \left(n-1,n\right),n\in \mathbb{N},\hfill \\ \hfill & f^{\left(n\right)}\left(t\right),\alpha =n\in \mathbb{N}.\hfill \end{array}\right.(2.6)$

When $\alpha =0,D_{a^{+}}^{\alpha }f(t)=f(t)$.We can replace operators $D_{0^{+}}^{\alpha }f(t)$ and $I_{0^{+}}^{\alpha }f(t)$ by D^αf(t) and I^αf(t) respectively. The following properties are true for fractional integral and derivative:

$\begin{array}{ccc}\hfill & \hfill & D^{\alpha }\left[f\left(t\right)+g\left(t\right)\right]=D^{\alpha }f\left(t\right)+D^{\alpha }g\left(t\right),\hfill \\ \hfill & \hfill & D^{\alpha }{I}^{\alpha }f\left(t\right)=f\left(t\right),\hfill \\ \hfill & \hfill & I^{\alpha }{D}^{\alpha }f\left(t\right)=f\left(t\right)-\sum _{k=0}^{n-1}\frac{f^{\left(k\right)}\left(0\right)}{k!}{t}^k,\alpha >0,t>0,\hfill \\ \hfill & \hfill & I^{\alpha }{t}^{\beta }=\frac{\mathrm{\Gamma }\left(\beta +1\right)}{\mathrm{\Gamma }\left(\beta +\alpha +1\right)}{t}^{\beta +\alpha },\alpha >0,t>0,\beta >-1,\hfill \\ \hfill & \hfill & D^{\alpha }{t}^{\beta }=\frac{\mathrm{\Gamma }\left(\beta +1\right)}{\mathrm{\Gamma }\left(\beta -\alpha +1\right)}{t}^{\beta -\alpha },\beta >0.\hfill \end{array}$

When α ∈ (0, 1], the LT of Caputo fractional derivative has the following expression

$\mathrm{L}\left\{\frac{d^{\alpha }f\left(t\right)}{d{t}^{\alpha }}\right\}=s^{\alpha }\bar{f}\left(s\right)-s^{\alpha -1}f\left(0\right),$

where $\bar{f}(s)={\int }_0^{\infty }{e}^{-st}f(t)dt$.

Definition 2.4. A ML function is

$E_{\alpha ,\beta }\left(z\right)=\sum _{k=0}^{\infty }\frac{z^k}{\mathrm{\Gamma }\left(\alpha k+\beta \right)},\mathrm{R}\mathrm{e}\left(\alpha \right)>0,\mathrm{R}\mathrm{e}\left(\beta \right)>0.$

Also, E_α,1(z) = E_α(z).We can see the γth order Caputo derivatives of the ML function are:

$\begin{array}{ccc}\hfill & \hfill & D^{\gamma }\left[t^{\beta -1}{E}_{\alpha ,\beta }\left(a{t}^{\alpha }\right)\right]=t^{\beta -\gamma -1}{E}_{\alpha ,\beta -\gamma }\left(a{t}^{\alpha }\right),\hfill \\ \hfill & \hfill & D^{\gamma }\left[E_{\alpha }\left(a{t}^{\alpha }\right)\right]=a{E}_{\alpha }\left(a{t}^{\alpha }\right),\hfill \end{array}$

$a\in \mathbb{R},\gamma >0,\alpha >0$, and the following presentation gives the LT of function $t^{\alpha k+\beta -1}{E}_{\alpha ,\beta }^{(k)}(\pm a{t}^{\alpha })$, that is

$\begin{array}{ccc}\hfill & \hfill & \mathrm{L}\left\{t^{\alpha k+\beta -1}{E}_{\alpha ,\beta }^{\left(k\right)}\left(\pm a{t}^{\alpha }\right)\right\}={\int }_0^{\infty }{t}^{\alpha k+\beta -1}{e}^{-st}{E}_{\alpha ,\beta }^{\left(k\right)}\left(\pm a{t}^{\alpha }\right)dt\hfill \\ \hfill & \hfill & =\frac{k!s^{\alpha -\beta }}{{\left(s^{\alpha }\mp a\right)}^{k+1}},\mathrm{R}\mathrm{e}\left(s\right)>|a{|}^{\frac{1}{\alpha }}.\hfill \end{array}$

3 Exact solutions of HJEs

3.1 Invariant subspace classification of Eq. 1.1

For Eq. 1.1, we write it in the form $u_t=F[u]=u_x^{m+2}+p(x)B(u)u_x^{m+1}+Q(x,u)$. By the maximal dimension n ≤ 2k + 1, we consider the following cases for n = 2, 3.

We investigate n = 2 first. After a straightforward calculation, we obtain that

$J_1{u}_x^{m+3}+J_2{u}_x^{m+2}+J_3{u}_x^{m+1}+J_4{u}_x^m+J_5{u}_x^{m-1}+J_6{u}_x^2+J_7{u}_x+J_8=0,(3.1)$

where J_i(i = 1, 2, …, 8) have the following expressions:

$\begin{array}{ccc}\hfill & \hfill & J_1=p{B}^{″},\hfill \\ \hfill & \hfill & J_2=\left(m+1\right)\left(m+2\right)a_1^2-\left(m+1\right)a_0-\left(m+2\right)a_1^{\prime }\hfill \\ \hfill & \hfill & +2p^{\prime }{B}^{\prime }-2\left(m+1\right)p{a}_1{B}^{\prime },\hfill \\ \hfill & \hfill & J_3=p^{″}B-\left(2m+3\right)p{a}_0{B}^{\prime }u-\left(2m+1\right)a_1{p}^{\prime }B\hfill \\ \hfill & \hfill & +\left[m\left(m+1\right)a_1^2-\left(m+1\right)a_1^{\prime }-m{a}_0\right]pB\hfill \\ \hfill & \hfill & +2\left(m+1\right)\left(m+2\right)a_1{a}_{0}u-\left(m+2\right)a_0^{\prime }u,\hfill \\ \hfill & \hfill & J_4=\left(m+1\right)\left[\left(m+2\right)a_0^{2}u+\left(2m{a}_1{a}_0-a_0^{\prime }\right)pB-2a_0{p}^{\prime }B\right]u,\hfill \\ \hfill & \hfill & J_5=m\left(m+1\right)p{a}_0^2{u}^{2}B,\hfill \\ \hfill & \hfill & J_6=Q_{uu},\hfill \\ \hfill & \hfill & J_7=2Q_{xu},\hfill \\ \hfill & \hfill & J_8=a_{0}Q+a_1{Q}_x-a_{0}u{Q}_u+Q_{xx}.\hfill \end{array}$(3.2)

Observing the above expression Eq. 3.1, we shall discuss four possibilities: m = −3, 1, 2 and m ≠ − 3, 1, 2. For the case of m = −3, we derive the following system

$\begin{array}{ccc}\hfill & \hfill & 2a_0+2a_1^2+a_1^{\prime }+2\left(p^{\prime }+2a_{1}p\right)B^{\prime }=0,\hfill \\ \hfill & \hfill & p^{″}B+5a_1{p}^{\prime }B+\left(3a_0+6a_1^2+2a_1^{\prime }\right)pB\hfill \\ \hfill & \hfill & +\left(3a_{0}p{B}^{\prime }+4a_0{a}_1+a_0^{\prime }\right)u=0,\hfill \\ \hfill & \hfill & a_0^{2}u+\left(a_0^{\prime }+6a_0{a}_1\right)pB+2a_0{p}^{\prime }B=0,\hfill \\ \hfill & \hfill & p{a}_0^{2}B=0,\hfill \\ \hfill & \hfill & Q_{xu}=0,\hfill \\ \hfill & \hfill & Q_{uu}=0,\hfill \\ \hfill & \hfill & p{B}^{″}+a_{0}Q+a_1{Q}_x-a_{0}u{Q}_u+Q_{xx}=0.\hfill \end{array}$(3.3)

From the first equation of Eq. 3.3, it is apparent that B(u) = b₁u + b₂. By solving the fifth and sixth equations of Eq. 3.3, we obtain Q(x, u) = q₁u + Q₁(x), where b₁, b₂ and q₁ are arbitrary constants and Q₁(x) is a function of x. Inserting B(u) = b₁u + b₂ and Q(x, u) = q₁u + Q₁(x) into system Eq. 3.3, we have

$\begin{array}{ccc}\hfill & \hfill & 2a_1^2+4b_1{a}_{1}p+a_1^{\prime }+2a_0+2b_1{p}^{\prime }=0,\hfill \\ \hfill & \hfill & 6b_1{a}_1^{2}p+\left(4a_0+5b_1{p}^{\prime }\right)a_1+2b_1{a}_1^{\prime }p+6b_1{a}_{0}p+a_0^{\prime }+b_1{p}^{″}=0,\hfill \\ \hfill & \hfill & 6b_2{a}_1^{2}p+5b_2{a}_1{p}^{\prime }+2b_2{a}_1^{\prime }p+3b_2{a}_{0}p+b_2{p}^{″}=0,\hfill \\ \hfill & \hfill & 6b_1{a}_0{a}_{1}p+a_0^2+2b_1{a}_0{p}^{\prime }+b_1{a}_0^{\prime }p=0,\hfill \\ \hfill & \hfill & 6b_2{a}_0{a}_{1}p+2b_2{a}_0{p}^{\prime }+b_2{a}_0^{\prime }p=0,\hfill \\ \hfill & \hfill & b_1{a}_0^{2}p=0,\hfill \\ \hfill & \hfill & b_2{a}_0^{2}p=0.\hfill \\ \hfill & \hfill & a_1{Q}_1^{\prime }+a_0{Q}_1+Q_1^{″}=0.\hfill \end{array}$(3.4)

Taking into account the assumption p(x) ≠ 0 and solving the system (3.4), the corresponding classifying equations and two-dimensional invariant subspaces are listed as the first three lines in Table 1 with the case m = −3. The cases of m = 1, 2 and m ≠ − 3, 1, 2 can be dealt in a similar way; therefore, we obtain the invariant subspace classification results, which are presented in Table 1.

TABLE 1

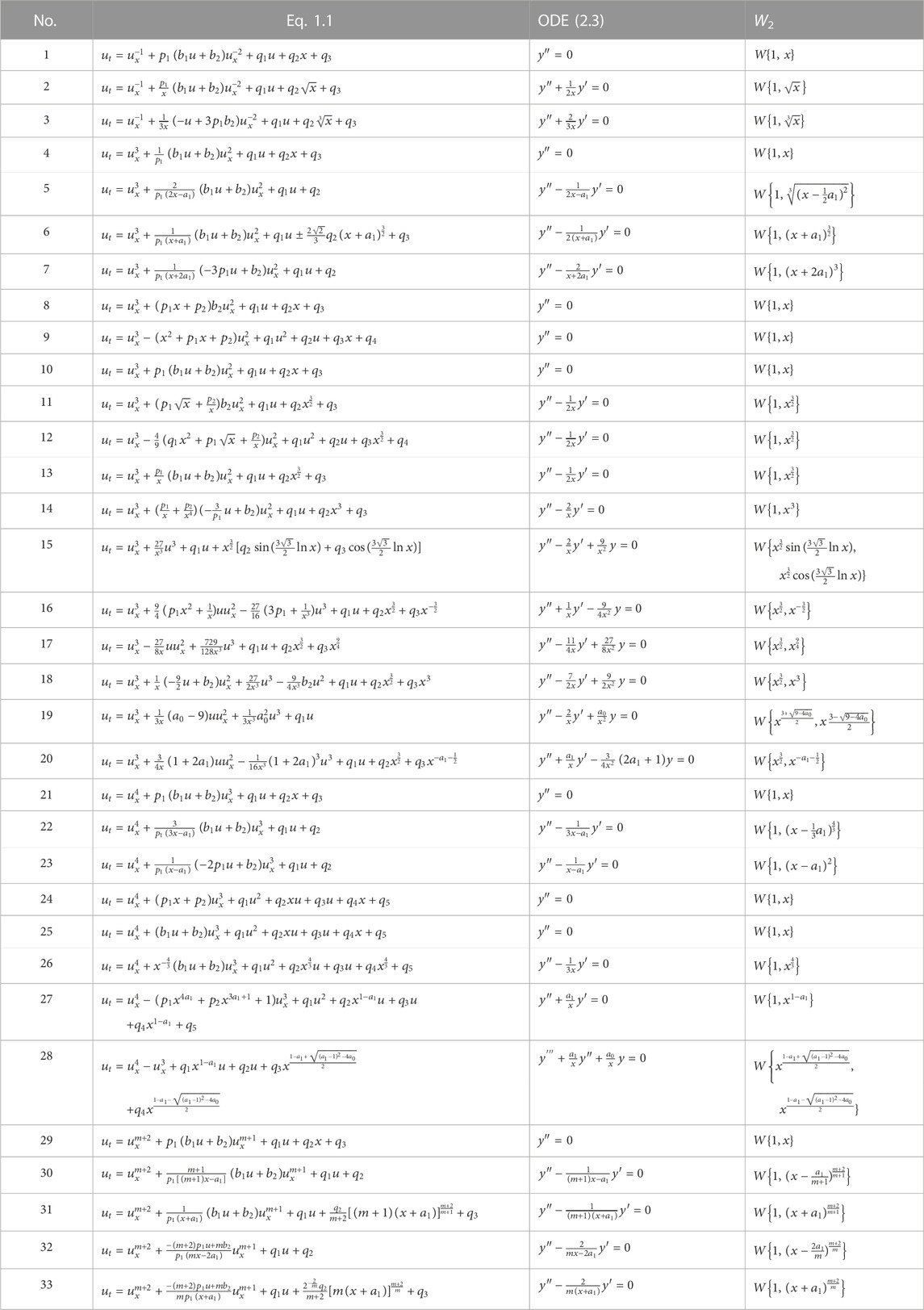
TABLE 1. Classifications of W₂ governed by linear ODEs (2.3) of Eq. 1.1.

When n = 3, we find there is only one case: m = 0, and the corresponding results are listed in Table 2.

TABLE 2

TABLE 2. Classifications of W₃ governed by linear ODEs (2.3) of Eq. 1.1.

3.2 Applications

In this section, we provide a further discussion for addressing with the explicit solutions using the above classification results.

Example 1: The equation

$u_t=u_x^3+\frac{9}{4x}u{u}_x^2-\frac{27}{16x^3}{u}^3+q_{1}u(3.5)$

admits the two-dimensional invariant subspace $W\left\{x^{\frac{3}{2}},x^{-\frac{3}{2}}\right\}$ generated by ODE

$y^{″}+\frac{1}{x}{y}^{\prime }-\frac{9}{4x^2}y=0.$

As a result, we derive that

$u\left(x,t\right)=C_1\left(t\right)x^{\frac{3}{2}}+C_2\left(t\right)x^{-\frac{3}{2}},$

Substituting the above solution into Eq. 3.5, we obtain

$\begin{array}{ccc}\hfill & \hfill & C_1^{\prime }=q_1{C}_1+\frac{27}{4}{C}_1^3,\hfill \\ \hfill & \hfill & C_2^{\prime }=-\frac{81}{4}{C}_1^2{C}_2+q_1{C}_2,\hfill \end{array}$

For q₁ = 0, we can see that

$\begin{array}{ccc}\hfill & \hfill & C_1=\frac{2}{\sqrt{4c_1-54t}},\hfill \\ \hfill & \hfill & C_2=c_2{\left(27t-2c_1\right)}^{\frac{3}{2}}.\hfill \end{array}$

For q₁ ≠ 0, we have

$\begin{array}{ccc}\hfill & \hfill & C_1=\frac{2}{\sqrt{4c_1{q}_1{e}^{-2q_{1}t}-27}},\hfill \\ \hfill & \hfill & C_2=c_2{\left(4c_1{q}_1{e}^{-2q_{1}t}-27\right)}^{\frac{3}{2}}{e}^{4q_{1}t}.\hfill \end{array}$

The corresponding solution shown in Figure 1

FIGURE 1

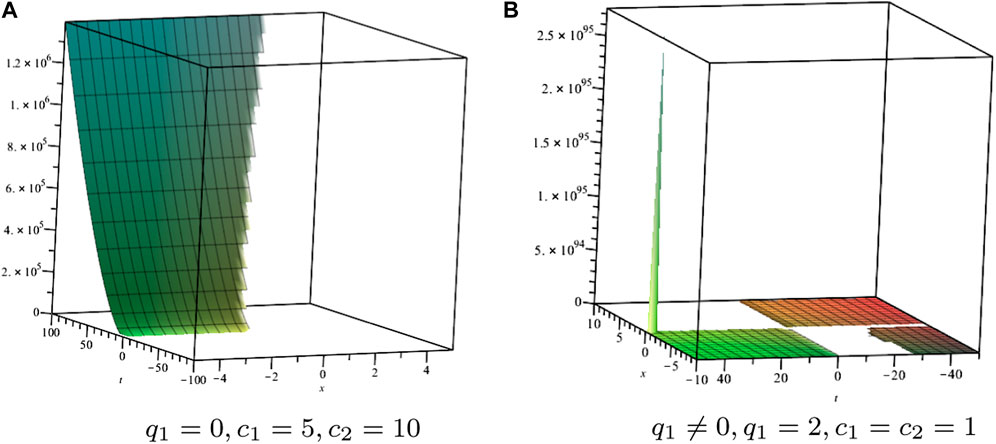
FIGURE 1. Solution profile of Eq. 3.5.

Example 2: The equation

$u_t=u_x^4+q_{1}u(3.6)$

admits the invariant subspace $W\left\{1,{(x-\frac{1}{3}{a}_1)}^{\frac{4}{3}}\right\}$ governed by ODE

$y^{″}-\frac{1}{3x-a_1}{y}^{\prime }=0.$

Then, we arrive at

$u\left(x,t\right)=C_1\left(t\right)+C_2\left(t\right){\left(x-\frac{1}{3}{a}_1\right)}^{\frac{4}{3}},$

Inserting the above solution into Eq. 3.6, we obtain

$\begin{array}{ccc}\hfill & \hfill & C_1^{\prime }=q_1{C}_1,\hfill \\ \hfill & \hfill & C_2^{\prime }=\frac{256}{81}{C}_2^4+q_1{C}_2,\hfill \end{array}$

For q₁ = 0, we obtain

$\begin{array}{ccc}\hfill & \hfill & C_1=c_1,\hfill \\ \hfill & \hfill & C_2=\frac{3}{\sqrt[3]{27c_2-256t}}.\hfill \end{array}$

For q₁ ≠ 0, we have

$\begin{array}{ccc}\hfill & \hfill & C_1=c_1{e}^{q_{1}t},\hfill \\ \hfill & \hfill & C_2=3\sqrt[3]{\frac{3q_1}{81c_2{q}_1{e}^{-3q_{1}t}-256}}.\hfill \end{array}$

The corresponding solution shown in Figure 2

FIGURE 2

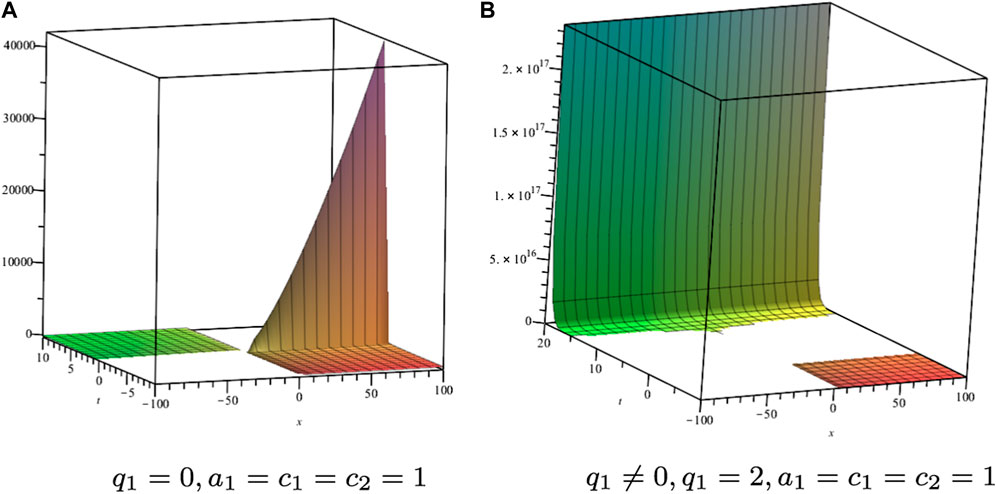
FIGURE 2. Solution profile of Eq. 3.6.

Example 3: The equation

$u_t=u_x^{m+2}-\frac{m+2}{mx}u{u}_x^{m+1}(3.7)$

admits the two-dimensional invariant subspace $W\left\{1,x^{\frac{m+2}{m}}\right\}$ governed by ODE

$y^{″}-\frac{2}{mx}{y}^{\prime }=0.$

Then we arrive at

$u\left(x,t\right)=C_1\left(t\right)+C_2\left(t\right)x^{\frac{m+2}{m}},$

Inserting the above solution into Eq. 3.7, we obtain

$\begin{array}{ccc}\hfill & \hfill & C_1^{\prime }=0,\hfill \\ \hfill & \hfill & C_2^{\prime }=-{\left(\frac{m+2}{m}\right)}^{m+2}{C}_1{C}_2^{m+1},\hfill \end{array}$

we can see that

$\begin{array}{ccc}\hfill & \hfill & C_1=c_1,\hfill \\ \hfill & \hfill & C_2=\frac{1}{\sqrt[m]{m{\left(\frac{m+2}{m}\right)}^{m+2}{c}_{1}t+c_2}}.\hfill \end{array}$

The corresponding solution shown in Figure 3

FIGURE 3

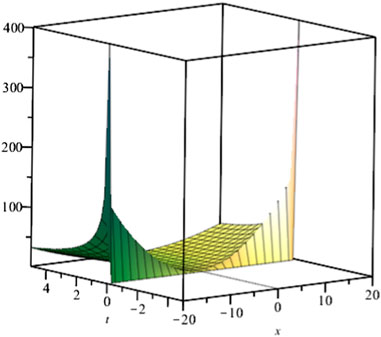
FIGURE 3. Solution profile of Eq. 3.7 with m = 2, c₁ = c₂ = 1.

Example 4: The equation

$u_t=u_x^2+\frac{4}{3}{a}_{2}u{u}_x+\frac{4}{9}{a}_2^2{u}^2+q_{2}u(3.8)$

admits the three-dimensional trigonometric invariant subspace $W\left\{1,e^{-\frac{1}{3}{a}_{2}x},e^{-\frac{2}{3}{a}_{2}x}\right\}$ governed by ODE

$y^{\prime \prime \prime }+a_2{y}^{″}+\frac{2}{9}{a}_2^2{y}^{\prime }=0.$

Then we arrive at

$u\left(x,t\right)=C_1\left(t\right)+C_2\left(t\right)e^{-\frac{1}{3}{a}_{2}x}+C_3\left(t\right)e^{-\frac{2}{3}{a}_{2}x},$

Inserting the above solution into Eq. 3.8, we obtain

$\begin{array}{ccc}\hfill & \hfill & C_1^{\prime }=\frac{4}{9}{a}_2^2{C}_1^2+q_2{C}_1,\hfill \\ \hfill & \hfill & C_2^{\prime }=\frac{4}{9}{a}_2^2{C}_1{C}_2+q_2{C}_2,\hfill \\ \hfill & \hfill & C_3^{\prime }=\frac{1}{9}{a}_2^2{C}_2^2+q_2{C}_3,\hfill \end{array}$

For q₂ = 0, we can see that

$\begin{array}{ccc}\hfill & \hfill & C_1=\frac{9}{9c_1-4a_2^{2}t},\hfill \\ \hfill & \hfill & C_2=\frac{c_2}{9c_1-4a_2^{2}t},\hfill \\ \hfill & \hfill & C_3=\frac{c_2^2}{36\left(9c_1-4a_2^{2}t\right)}+c_3.\hfill \end{array}$

For q₂ ≠ 0, we have

$\begin{array}{ccc}\hfill & \hfill & C_1=\frac{9q_2}{9c_1{q}_2{e}^{-q_{2}t}-4a_2^2},\hfill \\ \hfill & \hfill & C_2=\frac{c_2}{9c_1{q}_2{e}^{-q_{2}t}-4a_2^2},\hfill \\ \hfill & \hfill & C_3=\left[\frac{a_2^2{c}_2^2}{81c_1{q}_2^2\left(9c_1{q}_2{e}^{-q_{2}t}-4a_2^2\right)}+c_3\right]e^{q_{2}t}.\hfill \end{array}$

The corresponding solution shown in Figure 4

FIGURE 4

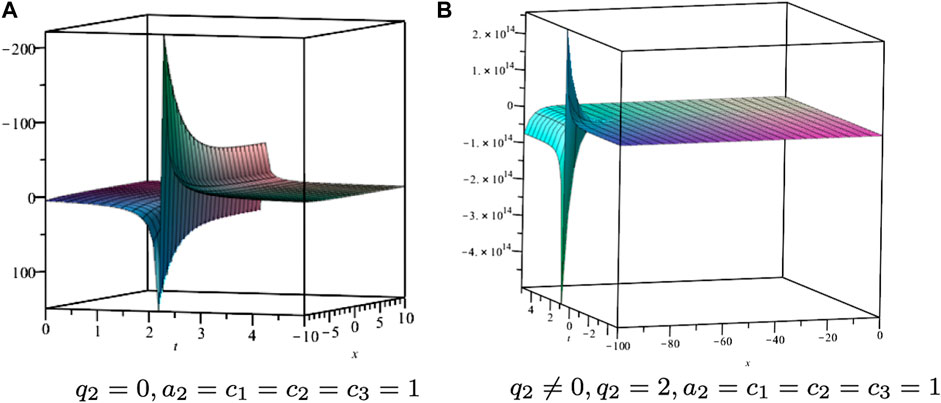
FIGURE 4. Solution profile of Eq. 3.8.

4 Exact solutions of a family of third-order time-fractional dispersive PDEs

Now, we will investigate the different invariant subspaces of non-linear differential operator F[u] and discuss explicit solutions of Eq. 1.2, see the following discussions.

Case 1. Let us consider the following equation

$\frac{{\partial }^{\alpha }u}{\partial t^{\alpha }}+\gamma \frac{{\partial }^{3}u}{\partial x^3}-{\delta }^2\frac{{\partial }^2}{\partial x^2}\left(\frac{{\partial }^{\alpha }u}{\partial t^{\alpha }}\right)=F\left[u\right]=\frac{\partial }{\partial x}\left[b_1{u}^2+b_2{\left(\frac{\partial u}{\partial x}\right)}^2+b_{3}u\frac{{\partial }^{2}u}{\partial x^2}\right].(4.1)$

Here $\alpha \in (\mathrm{0,1})-\left\{\frac{1}{2}\right\}$, Eq. 4.1 admits the invariant subspace $W_2=\mathcal{L}\left\{1,x\right\}$, the reason is that

$F\left[C_1+C_{2}x\right]=2b_1{C}_1{C}_2+2b_1{C}_2^{2}x\in W_2.$

This means that Eq. 4.1 has the following explicit solution:

$u\left(x,t\right)=C_1\left(t\right)+C_2\left(t\right)x,$

Substituting the solution into Eq. 4.1, we have

$\frac{d^{\alpha }{C}_1\left(t\right)}{d{t}^{\alpha }}=2b_1{C}_1\left(t\right)C_2\left(t\right),(4.2)$

$\frac{d^{\alpha }{C}_2\left(t\right)}{d{t}^{\alpha }}=2b_1{C}_2^2\left(t\right).(4.3)$

Eqs 4.2, 4.3 provide

$C_2\left(t\right)=\frac{1}{2b_1}\frac{\mathrm{\Gamma }\left(1-\alpha \right)}{\mathrm{\Gamma }\left(1-2\alpha \right)}{t}^{-\alpha },$

and

$C_1\left(t\right)=t^{-\alpha }.$

Then

$u\left(x,t\right)=t^{-\alpha }+\frac{1}{2b_1}\frac{\mathrm{\Gamma }\left(1-\alpha \right)}{\mathrm{\Gamma }\left(1-2\alpha \right)}{t}^{-\alpha }x.$

The corresponding solution shown in Figure 5

FIGURE 5

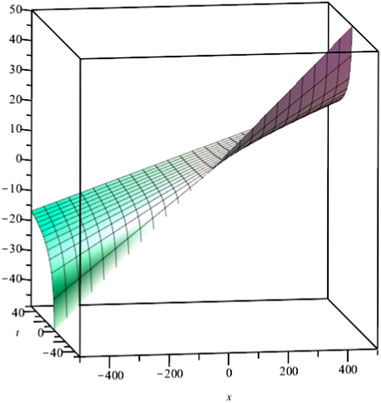
FIGURE 5. Solution profile of Eq. 4.1 with α = 1/3, b₁ = 2.

Case 2. We consider the equation

$\frac{{\partial }^{\alpha }u}{\partial t^{\alpha }}+\sigma \frac{\partial u}{\partial x}+\gamma \frac{{\partial }^{3}u}{\partial x^3}-{\delta }^2\frac{{\partial }^2}{\partial x^2}\left(\frac{{\partial }^{\alpha }u}{\partial t^{\alpha }}\right)=F\left[u\right]=\frac{\partial }{\partial x}\left[-a_1^2\left(b_2+b_3\right)u^2+b_2{\left(\frac{\partial u}{\partial x}\right)}^2+b_{3}u\frac{{\partial }^{2}u}{\partial x^2}\right],(4.4)$

α ∈ (0, 1], Eq. 4.4 preserves invariant subspace $W_2=\mathcal{L}\left\{1,e^{-a_{1}x}\right\}$, since

$F\left[C_1+C_2{e}^{-a_{1}x}\right]=a_1^3\left(2b_2+b_3\right)C_1{C}_2{e}^{-a_{1}x}\in W_2,$

which means that Eq. 4.4 has the solution

$u\left(x,t\right)=C_1\left(t\right)+C_2\left(t\right)e^{-a_{1}x}.$

Plugging the solution into Eq. 4.4, we find

$\frac{d^{\alpha }{C}_1\left(t\right)}{d{t}^{\alpha }}=0,(4.5)$

$\left(1-a_1^2{\delta }^2\right)\frac{d^{\alpha }{C}_2\left(t\right)}{d{t}^{\alpha }}=a_1\left(\sigma +\gamma a_1^2\right)C_2\left(t\right)+a_1^3\left(2b_2+b_3\right)C_1\left(t\right)C_2\left(t\right).(4.6)$

Solving Eq. 4.5, C₁(t) = c₁, c₁ is an arbitrary constant, and when $a_1^2{\delta }^2\ne 1$, letting

$\mu =\frac{a_1\left[\sigma +\gamma a_1^2+a_1^2\left(2b_2+b_3\right)c_1\right]}{1-a_1^2{\delta }^2}.$

Therefore, Eq. 4.6 becomes

$\frac{d^{\alpha }{C}_2\left(t\right)}{d{t}^{\alpha }}=\mu C_2\left(t\right).(4.7)$

Applying the LT to Eq. 4.7, we have

$s^{\alpha }\mathrm{L}\left\{C_2\left(t\right)\right\}-s^{\alpha -1}{C}_2\left(0\right)=\mu \mathrm{L}\left\{C_2\left(t\right)\right\},$

namely,

${\bar{C}}_2\left(s\right)=\mathrm{L}\left\{C_2\left(t\right)\right\}=a\frac{s^{\alpha -1}}{s^{\alpha }-\mu }.$

Here C₂(0) = a, its inverse LT is

$C_2\left(t\right)=a{E}_{\alpha ,1}\left(\mu t^{\alpha }\right),\alpha \in \left(\mathrm{0,1}\right].$

where E_α,1(.) is the ML function

$E_{\alpha ,1}\left(\mu t^{\alpha }\right)=\sum _{k=0}^{\infty }\frac{{\left(\mu t^{\alpha }\right)}^k}{\mathrm{\Gamma }\left(\alpha k+1\right)}.$

Hence, we derive that

$u\left(x,t\right)=c_1+a{E}_{\alpha ,1}\left(\mu t^{\alpha }\right)e^{-a_{1}x}.$

In the case of α = 1, it is a traveling wave solution

$u\left(x,t\right)=c_1+a{e}^{\mu t-a_{1}x}.$

The corresponding solution shown in Figure 6

FIGURE 6

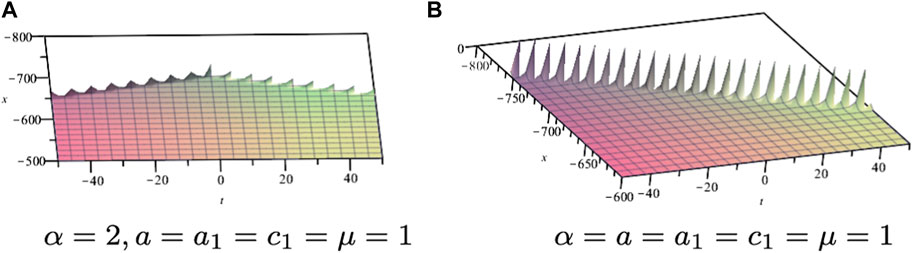
FIGURE 6. Solution profile of Eq. 4.4.

Case 3. We consider the equation

$\frac{{\partial }^{\alpha }u}{\partial t^{\alpha }}+\sigma \frac{\partial u}{\partial x}+\gamma \frac{{\partial }^{3}u}{\partial x^3}-{\delta }^2\frac{{\partial }^2}{\partial x^2}\left(\frac{{\partial }^{\alpha }u}{\partial t^{\alpha }}\right)=F\left[u\right]=\frac{\partial }{\partial x}\left[a_0\left(b_2+b_3\right)u^2+b_2{\left(\frac{\partial u}{\partial x}\right)}^2+b_{3}u\frac{{\partial }^{2}u}{\partial x^2}\right],(4.8)$

α ∈ (0, 1], Eq. 4.8 admits the two-dimensional invariant subspace $W_2=\mathcal{L}\left\{\cos (\sqrt{a_0}x),\sin (\sqrt{a_0}x)\right\}$, since

$F\left[C_1\cos \left(\sqrt{a_0}x\right)+C_2\sin \left(\sqrt{a_0}x\right)\right]=0\in W_2.$

This indicates that Eq. 4.8 has the solution

$u\left(x,t\right)=C_1\cos \left(\sqrt{a_0}x\right)+C_2\sin \left(\sqrt{a_0}x\right).$

Substituting the solution into Eq. 4.8, we have

$\frac{d^{\alpha }{C}_1\left(t\right)}{d{t}^{\alpha }}=\lambda C_2\left(t\right),(4.9)$

$\frac{d^{\alpha }{C}_2\left(t\right)}{d{t}^{\alpha }}=-\lambda C_1\left(t\right).(4.10)$

Here, $\lambda =\frac{\sqrt{a_0}(\sigma -a_0\gamma )}{1+a_0{\delta }^2}$. By applying the time-fractional derivative $\frac{d^{\alpha }}{d{t}^{\alpha }}$ to Eq. 4.9, we derive that

$\frac{d^{\alpha }}{d{t}^{\alpha }}\frac{d^{\alpha }{C}_1\left(t\right)}{d{t}^{\alpha }}=-{\lambda }^2{C}_1\left(t\right).$

Now we discuss the following Cauchy problem:

$\left\{\begin{array}{cc}\hfill & \frac{d^{\alpha }}{d{t}^{\alpha }}\frac{d^{\alpha }{C}_1\left(t\right)}{d{t}^{\alpha }}=-{\lambda }^2{C}_1\left(t\right),\hfill \\ \hfill & C_1\left(0\right)=a,\hfill & \hfill \\ \hfill & \frac{d^{\alpha }{C}_1\left(t\right)}{d{t}^{\alpha }}{|}_{t=0}=0.\hfill \end{array}\right.(4.11)$

Then, define $g(t)=\frac{d^{\alpha }{C}_1(t)}{d{t}^{\alpha }}$, and utilizing the LT to this equation, we can see

$\bar{g}\left(s\right)=s^{\alpha }{\bar{C}}_1\left(s\right)-a{s}^{\alpha -1}.(4.12)$

At the same time, applying LT to the first equation of Eq. 4.11, we obtain

$\mathrm{L}\left\{\frac{d^{\alpha }}{d{t}^{\alpha }}\frac{d^{\alpha }{C}_1\left(t\right)}{d{t}^{\alpha }}\right\}=\mathrm{L}\left\{\frac{d^{\alpha }g\left(t\right)}{d{t}^{\alpha }}\right\}=s^{\alpha }\bar{g}\left(s\right)-s^{\alpha -1}g\left(0\right),(4.13)$

Inserting Eq. 4.12 into Eq. 4.13, we find

${\bar{C}}_1\left(s\right)=a\frac{s^{2\alpha -1}}{s^{2\alpha }+{\lambda }^2}.$

whose inverse LT is

$C_1\left(t\right)=a{E}_{2\alpha ,1}\left(-{\lambda }^2{t}^{2\alpha }\right),\alpha \in \left(\mathrm{0,1}\right].(4.14)$

where E_2α,1(.) is the ML function

$E_{2\alpha ,1}\left(-{\lambda }^2{t}^{2\alpha }\right)=\sum _{k=0}^{\infty }\frac{{\left(-1\right)}^k{\lambda }^{2k}{t}^{2\alpha k}}{\mathrm{\Gamma }\left(2\alpha k+1\right)}.$

Substituting Eq. 4.14 in Eq. 4.10, we get

$\frac{d^{\alpha }{C}_2\left(t\right)}{d{t}^{\alpha }}=-\lambda a{E}_{2\alpha ,1}\left(-{\lambda }^2{t}^{2\alpha }\right).(4.15)$

By applying I^α on both sides of Eq. 4.15, we obtain

$C_2\left(t\right)=-a\lambda t^{\alpha }{E}_{2\alpha ,\alpha +1}\left(-{\lambda }^2{t}^{2\alpha }\right).$

For the sake of simplicity, we set the integration constant to zero. Assuming a = 1, the solution of Eq. 4.8 is

$u\left(x,t\right)=E_{2\alpha ,1}\left(-{\lambda }^2{t}^{2\alpha }\right)\cos \left(\sqrt{a_0}x\right)-\lambda t^{\alpha }{E}_{2\alpha ,\alpha +1}\left(-{\lambda }^2{t}^{2\alpha }\right)\sin \left(\sqrt{a_0}x\right).$

Note that for α = 1,

$\begin{array}{ccc}\hfill & \hfill & E_{\mathrm{2,1}}\left(-{\lambda }^2{t}^2\right)=\sum _{k=0}^{\infty }\frac{{\left(-{\lambda }^2{t}^2\right)}^k}{\mathrm{\Gamma }\left(2k+1\right)}=\cos \left(\lambda t\right),\hfill \\ \hfill & \hfill & \lambda t{E}_{\mathrm{2,2}}\left(-{\lambda }^2{t}^2\right)=\lambda t\sum _{k=0}^{\infty }\frac{{\left(-{\lambda }^2{t}^2\right)}^k}{\mathrm{\Gamma }\left(2k+2\right)}=\sin \left(\lambda t\right),\hfill \end{array}$

and the solution becomes

$u\left(x,t\right)=\cos \left(\lambda t\right)\cos \left(\sqrt{a_0}x\right)-\sin \left(\lambda t\right)\sin \left(\sqrt{a_0}x\right)=\cos \left(\lambda t+\sqrt{a_0}x\right).$

The corresponding solution shown in Figure 7

FIGURE 7

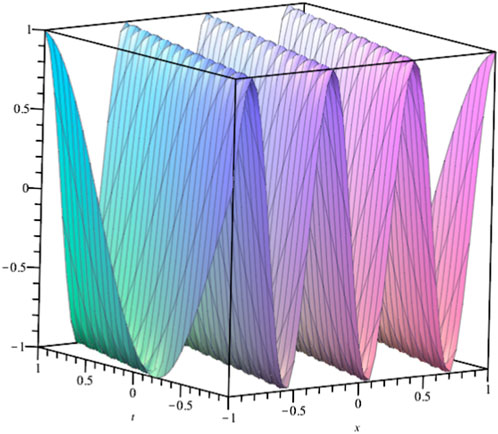
FIGURE 7. Solution profile of Eq. 4.8 with a₀ = 100, σ = γ = 1, δ = 2.

Case 4. We consider the equation

$\frac{{\partial }^{\alpha }u}{\partial t^{\alpha }}-\frac{4}{9}\gamma a_1^2\frac{\partial u}{\partial x}+\gamma \frac{{\partial }^{3}u}{\partial x^3}-{\delta }^2\frac{{\partial }^2}{\partial x^2}\left(\frac{{\partial }^{\alpha }u}{\partial t^{\alpha }}\right)=F\left[u\right]=\frac{\partial }{\partial x}\left[-\frac{1}{9}{a}_1^2{u}^2-\frac{3}{4}{\left(\frac{\partial u}{\partial x}\right)}^2+u\frac{{\partial }^{2}u}{\partial x^2}\right],(4.16)$

α ∈ (0, 1], Eq. 4.16 admits the two-dimensional invariant subspace $W_2=\mathcal{L}\left\{e^{-\frac{1}{3}{a}_{1}x},e^{-\frac{2}{3}{a}_{1}x}\right\}$, since

$F\left[C_1{e}^{-\frac{1}{3}{a}_{1}x}+C_2{e}^{-\frac{2}{3}{a}_{1}x}\right]=\frac{1}{18}{a}_1^3{C}_1^2{e}^{-\frac{2}{3}{a}_{1}x}\in W_2.$

This means that the explicit solution has the following form

$u\left(x,t\right)=C_1\left(t\right)e^{-\frac{1}{3}{a}_{1}x}+C_2\left(t\right)e^{-\frac{2}{3}{a}_{1}x}.$

Substituting the solution into Eq. 4.16, we have

$\frac{d^{\alpha }{C}_1\left(t\right)}{d{t}^{\alpha }}={\lambda }_1{C}_1\left(t\right),(4.17)$

$\frac{d^{\alpha }{C}_2\left(t\right)}{d{t}^{\alpha }}={\lambda }_2{\left[C_1\left(t\right)\right]}^2,(4.18)$

where ${\lambda }_1=\frac{a_1^3\gamma }{a_1^2{\delta }^2-9},{\lambda }_2=\frac{a_1^3}{18-8a_1^2{\delta }^2}$. Setting C₁(0) = 1 and employing the LT of both sides of Eq. 4.17, we have

${\bar{C}}_1\left(s\right)=\frac{s^{\alpha -1}}{s^{\alpha }-{\lambda }_1}.$

Its inverse LT is

$C_1\left(t\right)=E_{\alpha ,1}\left({\lambda }_1{t}^{\alpha }\right),\alpha \in \left(\mathrm{0,1}\right].$

Utilizing C₁(t) in Eq. 4.18, we obtain

$\frac{d^{\alpha }{C}_2\left(t\right)}{d{t}^{\alpha }}={\lambda }_2{\left(E_{\alpha ,1}\left({\lambda }_1{t}^{\alpha }\right)\right)}^2.$

However, while the ML function does not fulfill the following composition property

$E_{\alpha }\left(x\right)E_{\alpha }\left(y\right)\ne E_{\alpha }\left(x+y\right),$

it should be noted that

$E_{\alpha }\left(x^{\alpha }\right)=\sum _{k=0}^{\infty }\frac{x^{\alpha k}}{\mathrm{\Gamma }\left(\alpha k+1\right)}$

which satisfies the composition property, that is,

$E_{\alpha }\left(x^{\alpha }\right)E_{\alpha }\left(y^{\alpha }\right)=E_{\alpha }\left({\left(x+y\right)}^{\alpha }\right),\alpha >0.$

Thus, we find

$\frac{d^{\alpha }{C}_2\left(t\right)}{d{t}^{\alpha }}={\lambda }_2{E}_{\alpha ,1}\left.\left({\lambda }_1{\left(2t\right)}^{\alpha }\right)\right).(4.19)$

Taking I^α on Eq. 4.19 and applying the integration of the ML function relation, we derive the following result:

$C_2\left(t\right)={\lambda }_2{\left(2t\right)}^{\alpha }{E}_{\alpha ,\alpha +1}\left.\left({\lambda }_1{\left(2t\right)}^{\alpha }\right)\right).$

Here, we set C₂(0) = 0. Hence, the exact solution of Eq. 4.16 associated with $W_2=\mathcal{L}\left\{e^{-\frac{1}{3}{a}_{1}x},e^{-\frac{2}{3}{a}_{1}x}\right\}$ reads

$u\left(x,t\right)=E_{\alpha ,1}\left({\lambda }_1{t}^{\alpha }\right)e^{-\frac{1}{3}{a}_{1}x}+{\lambda }_2{\left(2t\right)}^{\alpha }{E}_{\alpha ,\alpha +1}\left.\left({\lambda }_1{\left(2t\right)}^{\alpha }\right)\right)e^{-\frac{2}{3}{a}_{1}x}.$

Note that for α = 1,

$\begin{array}{ccc}\hfill & \hfill & E_{\mathrm{1,1}}\left({\lambda }_{1}t\right)=\sum _{k=0}^{\infty }\frac{{\left({\lambda }_{1}t\right)}^k}{\mathrm{\Gamma }\left(k+1\right)}=e^{{\lambda }_{1}t},\hfill \\ \hfill & \hfill & E_{\mathrm{1,2}}\left({\lambda }_1\left(2t\right)\right)=\sum _{k=0}^{\infty }\frac{{\left(2{\lambda }_{1}t\right)}^k}{\mathrm{\Gamma }\left(k+2\right)}=\frac{e^{2{\lambda }_{1}t}-1}{2{\lambda }_{1}t},\hfill \end{array}$

$u\left(x,t\right)=e^{{\lambda }_{1}t-\frac{1}{3}{a}_{1}x}+\frac{{\lambda }_2}{{\lambda }_1}\left(e^{2{\lambda }_{1}t}-1\right)e^{-\frac{2}{3}{a}_{1}x}.$

The corresponding solution shown in Figure 8

FIGURE 8

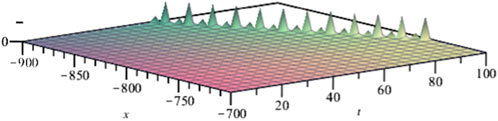
FIGURE 8. Solution profile of Eq. 4.16 with a₁ = 1, λ₁ = 1, λ₂ = 2, δ = 2.

Case 5. We consider the equation

$\frac{{\partial }^{\alpha }u}{\partial t^{\alpha }}+\sigma \frac{\partial u}{\partial x}+\gamma \frac{{\partial }^{3}u}{\partial x^3}-{\delta }^2\frac{{\partial }^2}{\partial x^2}\left(\frac{{\partial }^{\alpha }u}{\partial t^{\alpha }}\right)=F\left[u\right]=\frac{\partial }{\partial x}\left[\left(b_2+b_3\right)u^2+b_2{\left(\frac{\partial u}{\partial x}\right)}^2+b_{3}u\frac{{\partial }^{2}u}{\partial x^2}\right],(4.20)$

α ∈ (0, 1], Eq. 4.20 admits the three-dimensional invariant subspace $W_3=\mathcal{L}\left\{1,\cos x,\sin x\right\}$, since

$F\left[C_1+C_2\cos x+C_3\sin x\right]=\left(2b_2+b_3\right)C_1{C}_3\cos x-\left(2b_2+b_3\right)C_1{C}_2\sin x\in W_3.$

This means that the exact solution has the following form:

$u\left(x,t\right)=C_1\left(t\right)+C_2\left(t\right)\cos x+C_3\left(t\right)\sin x.$

Substituting the solution into Eq. 4.20, we obtain

$\frac{d^{\alpha }{C}_1\left(t\right)}{d{t}^{\alpha }}=0,(4.21)$

$\left(1+{\delta }^2\right)\frac{d^{\alpha }{C}_2\left(t\right)}{d{t}^{\alpha }}=\left(\gamma -\sigma \right)C_3\left(t\right)+\left(2b_2+b_3\right)C_1\left(t\right)C_3\left(t\right),(4.22)$

$\left(1+{\delta }^2\right)\frac{d^{\alpha }{C}_3\left(t\right)}{d{t}^{\alpha }}=\left(\sigma -\gamma \right)C_2\left(t\right)-\left(2b_2+b_3\right)C_1\left(t\right)C_2\left(t\right).(4.23)$

Solving Eq. 4.21, we obtain C₁(t) = c₁, inserting it into Eq. 4.22 and Eq. 4.23, we find

$\begin{array}{ccc}\hfill & \hfill & \frac{d^{\alpha }{C}_2\left(t\right)}{d{t}^{\alpha }}=\lambda C_3\left(t\right),\hfill \\ \hfill & \hfill & \frac{d^{\alpha }{C}_3\left(t\right)}{d{t}^{\alpha }}=-\lambda C_2\left(t\right),\hfill \end{array}$

where $\lambda =\frac{\gamma -\delta +c_1(2b_2+b_3)}{1+{\delta }^2}$, Following the procedure described in case 3, we obtain the exact solution

$u\left(x,t\right)=c_1+E_{2\alpha ,1}\left(-{\lambda }^2{t}^{2\alpha }\right)\cos x-\lambda t^{\alpha }{E}_{2\alpha ,\alpha +1}\left(-{\lambda }^2{t}^{2\alpha }\right)\sin x.$

Note that for α = 1,

$\begin{array}{ccc}\hfill & \hfill & E_{\mathrm{2,1}}\left(-{\lambda }^2{t}^2\right)=\sum _{k=0}^{\infty }\frac{{\left(-1\right)}^k{\left(\lambda t\right)}^{2k}}{\mathrm{\Gamma }\left(2k+1\right)}=\cos \left(\lambda t\right),\hfill \\ \hfill & \hfill & \lambda t{E}_{\mathrm{2,2}}\left(-{\lambda }^2{t}^2\right)=\lambda t\sum _{k=0}^{\infty }\frac{{\left(-1\right)}^k{\left(\lambda t\right)}^{2k+1}}{\mathrm{\Gamma }\left(2k+1\right)}=\sin \left(\lambda t\right),\hfill \end{array}$

and the solution is

$u\left(x,t\right)=c_1+\cos \left(\lambda t\right)\cos x-\sin \left(\lambda t\right)\sin x=c_1+\cos \left(\lambda t+x\right),$

which is a compacton solution.The corresponding solution shown in Figure 9

FIGURE 9

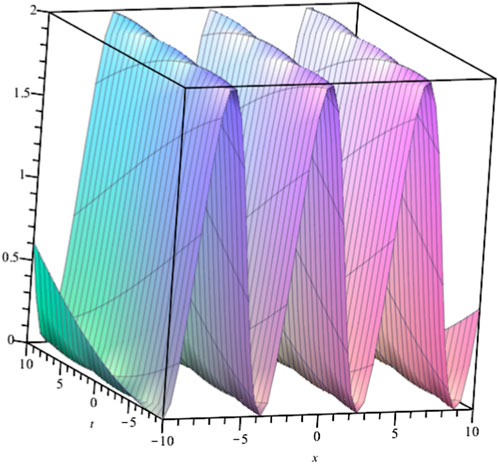
FIGURE 9. Solution profile of Eq. 4.20 with α = γ = b₂ = b₃ = c₁ = 1, δ = 10.

Case 6. We consider the equation

$\frac{{\partial }^{\alpha }u}{\partial t^{\alpha }}-{\delta }^2\frac{{\partial }^2}{\partial x^2}\left(\frac{{\partial }^{\alpha }u}{\partial t^{\alpha }}\right)=F\left[u\right]=\frac{\partial }{\partial x}\left[b_2{\left(\frac{\partial u}{\partial x}\right)}^2+b_{3}u\frac{{\partial }^{2}u}{\partial x^2}\right],(4.24)$

$\alpha \in (\mathrm{0,1})-\left\{\frac{1}{2}\right\}$, Eq. 4.24 admits the four-dimensional invariant subspace $W_4=\mathcal{L}\left\{1,x,x^2,x^3\right\}$, since

$\begin{array}{ccc}\hfill & \hfill & F\left[C_1+C_{2}x+C_3{x}^2+C_4{x}^3\right]=6b_3{C}_1{C}_4+\left(4b_2+2b_3\right)C_2{C}_3+\left[\left(8b_2+4b_3\right)C_3^2\right.\hfill \\ \hfill & \hfill & \left.+12\left(b_2+b_3\right)C_2{C}_4\right]x+12\left(3b_2+2b_3\right)C_3{C}_4{x}^2\hfill \\ \hfill & \hfill & +12\left(3b_2+2b_3\right)C_4^2{x}^3\in W_4.\hfill \end{array}$

This means that the exact solution has the following form

$u\left(x,t\right)=C_1\left(t\right)+C_2\left(t\right)x+C_3\left(t\right)x^2+C_4\left(t\right)x^3.$

Substituting the solution into (4.24), we have

$\begin{array}{ccc}\hfill & \hfill & \frac{d^{\alpha }{C}_1\left(t\right)}{d{t}^{\alpha }}-2{\delta }^2\frac{d^{\alpha }{C}_3\left(t\right)}{d{t}^{\alpha }}=6b_3{C}_1\left(t\right)C_4\left(t\right)+\left(4b_2+2b_3\right)C_2\left(t\right)C_3\left(t\right),\hfill \\ \hfill & \hfill & \frac{d^{\alpha }{C}_2\left(t\right)}{d{t}^{\alpha }}-6{\delta }^2\frac{d^{\alpha }{C}_4\left(t\right)}{d{t}^{\alpha }}=\left(8b_2+4b_3\right)C_3^2\left(t\right)+12\left(b_2+b_3\right)C_2\left(t\right)C_4\left(t\right),\hfill \\ \hfill & \hfill & \frac{d^{\alpha }{C}_3\left(t\right)}{d{t}^{\alpha }}=12\left(3b_2+2b_3\right)C_3\left(t\right)C_4\left(t\right),\hfill \\ \hfill & \hfill & \frac{d^{\alpha }{C}_4\left(t\right)}{d{t}^{\alpha }}=12\left(3b_2+2b_3\right)C_4^2\left(t\right).\hfill \end{array}$

Solving this system, we derive that

$\begin{array}{ccc}\hfill & \hfill & C_1\left(t\right)=\frac{2\left(3b_2+2b_3\right)}{2b_2+b_3}{\delta }^2{t}^{-\alpha }+\frac{16}{3}{\left(3b_2+2b_3\right)}^2{\left[\frac{\mathrm{\Gamma }\left(1-2\alpha \right)}{\mathrm{\Gamma }\left(1-\alpha \right)}\right]}^2{t}^{-\alpha },\hfill \\ \hfill & \hfill & C_2\left(t\right)=\left[\frac{{\delta }^2}{2\left(2b_2+b_3\right)}\frac{\mathrm{\Gamma }\left(1-\alpha \right)}{\mathrm{\Gamma }\left(1-2\alpha \right)}+4\left(3b_2+2b_3\right)\frac{\mathrm{\Gamma }\left(1-2\alpha \right)}{\mathrm{\Gamma }\left(1-\alpha \right)}\right]t^{-\alpha },\hfill \\ \hfill & \hfill & C_3\left(t\right)=t^{-\alpha },\hfill \\ \hfill & \hfill & C_4\left(t\right)=\frac{1}{12\left(3b_2+2b_3\right)}\frac{\mathrm{\Gamma }\left(1-\alpha \right)}{\mathrm{\Gamma }\left(1-2\alpha \right)}{t}^{-\alpha }.\hfill \end{array}$

Thus, Eq. 4.24 has the solution

$\begin{array}{ccc}\hfill & \hfill & u\left(x,t\right)=\left(3b_2+2b_3\right)\left[\frac{2}{2b_2+b_3}{\delta }^2+\frac{16}{3}\left(3b_2+2b_3\right){\eta }^2\right]t^{-\alpha }\hfill \\ \hfill & \hfill & +\left[4\left(3b_2+2b_3\right)\eta +\frac{1}{2\left(2b_2+b_3\right)\eta }{\delta }^2\right]t^{-\alpha }x+t^{-\alpha }{x}^2+\frac{1}{12\left(3b_2+2b_3\right)\eta }{t}^{-\alpha }{x}^3.\hfill \end{array}$

where $\eta =\frac{\mathrm{\Gamma }(1-2\alpha )}{\gamma (1-\alpha )}$.The corresponding solution shown in Figure 10

FIGURE 10

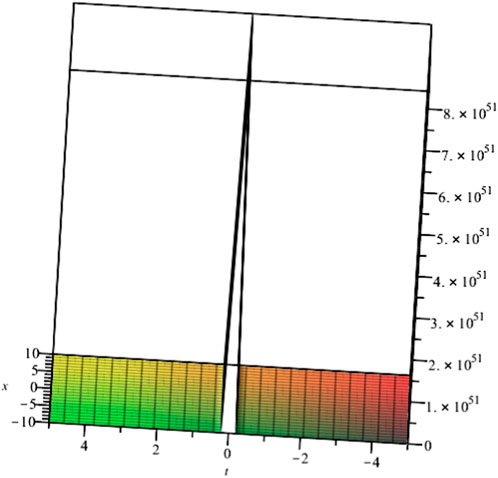
FIGURE 10. Solution profile of Eq. 4.24 with α = 1/3, b₂ = b₃ = 1, δ = 10.

5 Conclusion

In this work, a class of HJEs (1.1) and a family of third-order time-fractional dispersive PDEs (1.2) are investigated by utilizing ISM. All invariant subspaces for the considered HJEs are derived and displayed in Table 1 and Table 2. Meanwhile, some exact solutions to the equations are obtained due to the corresponding symmetry reductions. For the third-order time-fractional dispersive PDEs, the right-hand side of Eq. 1.2 is the derivative of a quadratic differential polynomial, therefore they preserve more than one invariant subspace, each of which generates a solution. Then, by employing the LT method and applying several properties of the well known ML function, the different kinds of explicit solutions of Eq. 1.2 are derived.

There are still some important problems to be considered. For instance, how does one use ISM to resolve initial value problems? How can we develop this method to investigate higher-dimensional non-linear equations and their discrete versions? This will be considered in the future. Moreover, in the extended version of this work, we will discuss more complicated fractional differential equations by using ISM.

Data availability statement

The original contributions presented in the study are included in the article/supplementary material, further inquiries can be directed to the corresponding authors.

Author contributions

GQ: Investigation, methodology, software, writing—original draft. MW: Writing—review and editing, software. SS: Formal analysis, writing—review and editing, supervision. All authors contributed to the article and approved the submitted version.

Funding

The work was supported by the National Natural Science Foundation of China (Grant No. 11501419), the Natural Science Foundation of Shaanxi Province, China (Grant No. 2021JM-521) and the Key Research Foundation of Weinan City, China (Grant No. 2019ZDYF-JCYJ-118).

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

1. Galaktionov VA, Svirshchevskii SR. Exact solutions and invariant subspaces of nonlinear partial differential equations in mechanics and physics. London: Chapman and Hall/CRC (2007).

Google Scholar

2. Qu CZ, Zhu CR. Classification of coupled systems with two-component nonlinear diffusion equations by the invariant subspace method. J Phys A Math Theor (2009) 42:475201. [27pp]. doi:10.1088/1751-8113/42/47/475201

CrossRef Full Text | Google Scholar

3. Zhu CR, Qu CZ. Maximal dimension of invariant subspaces admitted by nonlinear vector differential operators. J Math Phys (2011) 52:043507. [15pp]. doi:10.1063/1.3574534

CrossRef Full Text | Google Scholar

4. Ma WX. A refined invariant subspace method and applications to evolution equations. Sci China Math (2012) 55:1769–78. doi:10.1007/s11425-012-4408-9

CrossRef Full Text | Google Scholar

5. Song JQ, Shen SF, Jin YY, Zhang J. New maximal dimension of invariant subspaces to coupled systems with two-component equations. Commun Nonlinear Sci Numer Simulat (2013) 18:2984–92. doi:10.1016/j.cnsns.2013.03.019

CrossRef Full Text | Google Scholar

6. Shen SF, Qu CZ, Jin YY, Ji LN. Maximal dimension of invariant subspaces to systems of nonlinear evolution equations. Chin Ann Math Ser B (2012) 33:161–78. doi:10.1007/s11401-012-0705-4

CrossRef Full Text | Google Scholar

7. Qu CZ. Conditional Lie Bäcklund symmetries of Hamilton-Jacobi equations. Nonlinear Anal (2009) 71:e243–e258.doi:10.1016/j.na.2008.10.045

CrossRef Full Text | Google Scholar

8. Svirshchevskii SR. Lie Bäcklund symmetries of linear ODEs and generalized separation of variables in nonlinear equations. Phys Lett A (1995) 99:344–8.

CrossRef Full Text | Google Scholar

9. King JR. Exact polynomial solutions to some nonlinear diffusion equations. Phys D (1993) 64:35–65. doi:10.1016/0167-2789(93)90248-y

CrossRef Full Text | Google Scholar

10. Fokas AS, Liu QM. Nonlinear interaction of traveling waves of nonintegrable equations. Phys Rev Lett (1994) 72:3293–6. doi:10.1103/physrevlett.72.3293

PubMed Abstract | CrossRef Full Text | Google Scholar

11. Zhdanov RZ. Conditional Lie-Bäcklund symmetry and reductions of evolution equations. J Phys A Math Gen (1995) 28:3841–50.

CrossRef Full Text | Google Scholar

12. Qu CZ. Group classification and generalized conditional symmetry reduction of the nonlinear diffusion-convection equation with a nonlinear source. Stud Appl Math (1997) 99:107–36. doi:10.1111/1467-9590.00058

CrossRef Full Text | Google Scholar

13. Qu CZ. Exact solutions to nonlinear diffusion equations obtained by a generalized conditional symmetry method. IMA J Appl Math (1999) 62:283–302. doi:10.1093/imamat/62.3.283

CrossRef Full Text | Google Scholar

14. Ji LN, Qu CZ. Conditional Lie Bäcklund symmetries and solutions to (n+1)-dimensional nonlinear diffusion equationscklund symmetries and solutions to (n + 1)-dimensional nonlinear diffusion equations. J Math Phys (2007) 48:103509. doi:10.1063/1.2795216

CrossRef Full Text | Google Scholar

15. Gazizov RK, Kasatkin AA. Construction of exact solutions for fractional order differential equations by invariant subspace method. Comput Math Appl (2013) 66:576–84.doi:10.1016/j.camwa.2013.05.006

CrossRef Full Text | Google Scholar

16. Sahadevan R, Bakkyaraj T. Invariant subspace method and exact solutions of certain nonlinear time fractional partial differential equations. Fract Calc Appl Anal (2015) 18:146–62. doi:10.1515/fca-2015-0010

CrossRef Full Text | Google Scholar

17. Harris PA, Garra R. Analytic solution of nonlinear fractional Burgers-type equation by invariant subspace method. Nonlinear Stud (2013) 20:471–81. doi:10.48550/arXiv.1306.1942

CrossRef Full Text | Google Scholar

18. Prakash P, Priyendhu KS, Lakshmanan M. Invariant subspace method for (m+1)-dimensional non-linear time-fractional partial differential equations. Commun Nonlinear Sci Numer Simulat (2022) 111:106436.doi:10.1016/j.cnsns.2022.106436

CrossRef Full Text | Google Scholar

19. Prakash P, Priyendhu KS, Anjitha KM. Initial value problem for the (2+1)-dimensional time-fractional generalized convection-reaction-diffusion wave equation:invariant subspace and exact solutions. Comput Appl Math (2022) 41:1–55.

CrossRef Full Text | Google Scholar

20. Sahadevan R, Prakash P. Exact solutions and maximal dimension of invariant subspaces of time fractional coupled nonlinear partial differential equations. Commun Nonlinear Sci Numer Simulat (2017) 42:158–77. doi:10.1016/j.cnsns.2016.05.017

CrossRef Full Text | Google Scholar

21. Rui WG. Idea of invariant subspace combined with elementary integral method for investigating exact solutions of time-fractional NPDEs. Appl Math Comput (2018) 339:158–71. doi:10.1016/j.amc.2018.07.033

CrossRef Full Text | Google Scholar

22. Feng W, Zhao SL. Time-fractional inhomogeneous nonlinear diffusion equation: Symmetries, conservation laws, invariant subspaces, and exact solutions. Mod Phys Lett B (2018) 32:1850401. doi:10.1142/s0217984918504018

CrossRef Full Text | Google Scholar

23. Choudhary S, Prakash P, Varsha DG. Invariant subspaces and exact solutions for a system of fractional PDEs in higher dimensions. Comput Appl Math (2019) 38:126. doi:10.1007/s40314-019-0879-4

CrossRef Full Text | Google Scholar

24. Crandall MG, Lions PL. Viscosity solutions of Hamilton-Jacobi equations. Trans Amer Math Soc (1983) 277:1–42. doi:10.1090/s0002-9947-1983-0690039-8

CrossRef Full Text | Google Scholar

25. Crandall MG, Evans LC, Lions PL. Some properties of viscosity solutions of Hamilton-Jacobi equations. Trans Amer Math Soc (1984) 282:487–502. doi:10.1090/s0002-9947-1984-0732102-x

CrossRef Full Text | Google Scholar

26. Crandall MG, Lions PL. On existence and uniqueness of solutions of Hamilton-Jacobi equations. Nonlinear Anal TMA (1986) 10:353–70. doi:10.1016/0362-546x(86)90133-1

CrossRef Full Text | Google Scholar

27. Evans LC. Partial differential equations. In: Graduate studies in mathematics. Providence, RI: American Mathematical Society (1998).

Google Scholar

28. Wei QL. Viscosity solution of the Hamilton-Jacobi equation by a limiting minimax method. Nonlinearity (2014) 27:17–41. doi:10.1088/0951-7715/27/1/17

CrossRef Full Text | Google Scholar

29. Galaktionov VA. Gemetric sturmian theory of nonlinear parabolic equations and applications. Boca Raton, FL: Chapman and Hall/CRC (2004).

Google Scholar

30. Galaktionov VA. Vẚzquez jl. A stability technique for evolution partial differential equations. In: A dynamical systems approach. Boston, MA: Birkhauser Boston, Inc (2004).

Google Scholar

31. Galaktionov VA, Vazquez JL. Blow-up for quasilinear heat equations described by means of nonlinear Hamilton–Jacobi equationszquez JL. Blow-Up for quasilinear heat equations described by means of nonlinear Hamilton-Jacobi equations. J Differential Equations (1996) 127:1–40. doi:10.1006/jdeq.1996.0059

CrossRef Full Text | Google Scholar

32. Galaktionov VA, Vazquez JL. Geometrical properties of the solutions of one-dimensional nonlinear parabolic equationszquez JL. Geometrical properties of the solutions of one-dimensional nonlinear parabolic equations. Math Ann (1995) 303:741–69. doi:10.1007/bf01461014

CrossRef Full Text | Google Scholar

33. Podlubny I. Fractional differential equations: An introduction to fractional derivatives, fractional differential equations, to methods of their solution and some of their applications. New York: Academic Press (1999).

Google Scholar

34. Oldham KB, Spanier J. The fractional calculus. New York: Academic Press (1974).

Google Scholar

35. Miller KS, Ross B. An introduction to the fractional calculus and fractional differential equations. New York: John Wiley and Sons (1993).

Google Scholar

36. Kilbas AA, Trujillo JJ, Srivastava HM. Theory and applications of fractional differential equations. Amsterdam: Elseiver (2006).

Google Scholar

37. Degasperis A, Holm DD, Hone ANW. A new integrable equation with peakon solutions. Theor Math Phys (2002) 133:1463–74. doi:10.48550/arXiv.nlin/0205023

CrossRef Full Text | Google Scholar

38. Rui WG, He B, Long Y, Chen C. The integral bifurcation method and its application for solving a family of third-order dispersive PDEs. Nonlinear Anal (2008) 69:1256–67. doi:10.1016/j.na.2007.06.027

CrossRef Full Text | Google Scholar

39. Johnson RS. Camassa-Holm, Korteweg-de Vries and related models for water waves. J Fluid Mech (2002) 455:63–82. doi:10.1017/s0022112001007224

CrossRef Full Text | Google Scholar

40. Camassa R, Holm D. An integrable shallow water equation with peaked solitons. Phys Rev Lett (1993) 71:1661–4. doi:10.1103/physrevlett.71.1661

PubMed Abstract | CrossRef Full Text | Google Scholar

41. Chen C, Tang M. A new type of bounded waves for Degasperis-Procesi equation. Chaos Soliton Fract (2006) 27:698–704. doi:10.1016/j.chaos.2005.04.040

CrossRef Full Text | Google Scholar

42. Coclite GM, Karlsen KH. On the well-posedness of the Degasperis-Procesi equation. J Funct Anal (2006) 233:60–91. doi:10.1016/j.jfa.2005.07.008

CrossRef Full Text | Google Scholar