Lie symmetries and reductions via invariant solutions of general short pulse equation

Around 1880, Lie introduced an idea of invariance of the partial differential equation (PDE) under one-parameter Lie group of transformation to find the invariant, similarity, or auto-model solutions. Lie symmetry analysis (LSA) provides us an algorithm to search for point symmetries for solving related linear systems for infinitesimal generators. Actually, point symmetries lead us to one-parameter family of solutions from a known solution. LSA is a program that provides us the exact solutions for the non-linear differential equations (DEs) in analogy of the program designed by Galois for algebraic polynomial equations. In this paper, we have carried out the LSA for computing the similarity solutions (symmetries) of the non-linear short pulse equation (SPE) for the cases when h(u) = e^u, k(u) = u_xx, $h(u)=e^{u^n}$, and k(u) = u_xx. In addition, an optimal system of one-dimensional sub-algebra has been set up. The reductions and invariant solutions for the generalized SPE are calculated corresponding to this optimal system as well. Reductions reduce the non-linear PDE or system of PDEs into non-linear reduced ordered ODE or system of PDEs. This helps to solve these systems of PDEs to reduced form. Graphical behavior of the transformed points of the 1-parameter solution functions have drawn.

1 Introduction

Galois used the group theory to discuss the solvability of algebraic polynomial equations. Sophus Lie used the same idea foe differential equations and devised a comprehensive program now known as Lie symmetry analysis (LSA). In his attempt, he also developed the theory of Lie groups with broad applications in many areas of mathematics, physics, and in applied sciences [1, 2]. [3] have explained the procedure of symmetry reductions and exact solutions for the non-linear PDEs using three different methods that are direct, classical, and non-classical. [4] used LSA for systems of non-linear PDEs including the solutions, for system of non-linear coupled PDEs in real physical application, for the unsteady liquid and gas flow in long pipelines, for approximated long wave equations in shallow water and for the general dispersive long-wave equation.

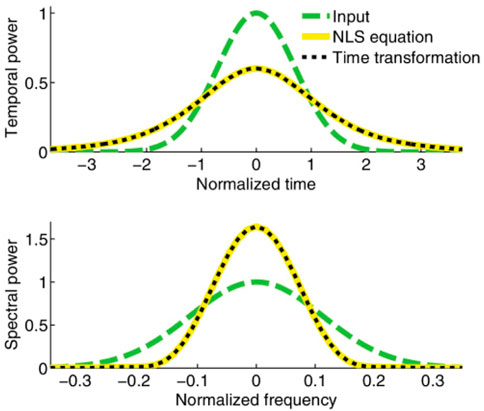
Non-linear short pulse equation (SPE) represents the propagation of ultra-short pulses (light pulses) in optical fibers of silica [5]. Propagation of pulses in optical fibers was first depicted by the cubic non-linear Schrodinger equation (NLSE) which are used to provide the actual fiber connections and refer new systems of fiber communication to attain very high data transmission [6, 7]. Research studies on a large scale have been performed for the propagation of ultra-short pulses (very narrow pulses) that permit high quality fast data transmission [6, 8]. In case of short pulses (or ultra-short pulses), the rationality of NLSE lacks due to the breakdown, [9]. Also, the higher order terms that are involved in cubic NLSE cause difficulties, see Figure 1, for the behavior of NLSE as an output [10]. Therefore, determined the SPE which provides more accurate approximation of the solution of Maxwell’s equation in non-linear media rather than the NLSE [6]. The SPE has vast applications in many applied fields such as systems of impulse, mechanics, neural networks, and in many other fields of sciences. Determined the symmetries of SPE and travelling wave solution by parametric representation and power series process, respectively, [11]. Evaluated the symmetry reductions and conservation laws by using the direct method for SPE, [12]. Authors also determined the Lie symmetries for SPE through the non-local system. Established the results for well-posedness of solutions which are bounded for homogenous IBVP and Cauchy problem connected with SPE, [5]. Matsuno constructed multiple exact solutions by using the direct method for three novel PDEs related with generalizations of SPE that are integrable, [13]. He gave the parametric representation of multi-soliton solutions of generalized SPE. LSA has been used by many mathematicians to explore the results related to the exact solutions of non-linear PDEs which depict physical phenomena [14]. Discussed the class of non-linear PDEs having an arbitrary order [15]. Authors estimated the determining equations for non-classical symmetries by using compatibility of original equations with invariant surface conditions.

FIGURE 1

FIGURE 1. Pulse propagation in NL-dispersive optics.

In this article, we have discussed the LSA for one of the modified form of SPE and see graphical behavior of the functions depending upon 1-parameter (ϵ) Lie groups. The non-linear SPE is as follows:

$u_{xt}=\alpha u+\frac{1}{3}\beta {\left(u^3\right)}_{xx},(1)$

where u(x, t) is the magnitude of electric field. α and β are the real parameters. Considering the SPE of the following form

$u_{xt}=\alpha h\left(u\right)+\frac{1}{3}\beta k^3\left(u\right),(2)$

where we let the general functions h(u) and k(u) as:

• h(u) = e^u and k(u) = u_xx,

• $h(u)=e^{u^n}$ for n ∈ N, (n > 1) and k(u) = u_xx.

It is worth mentioning that the case h(u) = uⁿ and k(u) = u_xx for Eq. 2 has been recently discussed in the article [16]. We will find Lie point symmetries corresponding to the aforementioned cases and the optimal system with reductions and see their graphical behavior corresponding to the Lie symmetries.

2 Results

In the present section, we give our main results with computations.

2.1 Lie symmetries of SPE for the case of h(u) = e^u and k(u) = u_xx

Eq. 2 becomes

$u_{xt}=\alpha e^u+\frac{1}{3}\beta u_{xx}^3,(3)$

Consider the one parameter Lie group of point transformations for Eq. 3.

$\begin{array}{ll}\hfill x^{*}& =x+ϵ\lambda \left(x,t,u\right)+O\left({ϵ}^2\right),\hfill \\ \hfill t^{*}& =t+ϵ\mu \left(x,t,u\right)+O\left({ϵ}^2\right),\hfill \\ \hfill u^{*}& =u+ϵ\nu \left(x,t,u\right)+O\left({ϵ}^2\right),\hfill \end{array}(4)$

where ϵ ∈ R is the group parameter.The group generator of (4) is defined in the following vector form as:

$W=\lambda \left(x,t,u\right)\frac{\partial }{\partial x}+\mu \left(x,t,u\right)\frac{\partial }{\partial t}+\nu \left(x,t,u\right)\frac{\partial }{\partial u},(5)$

where λ, μ and ν are infinitesimal functions of group variables. The second prolongation of the infinitesimal generator along with coefficients has the following form:

$\begin{array}{ll}\hfill {\mathit{Pr}}^{\left(2\right)}W& =W+{\nu }^x\frac{\partial }{\partial u_x}+{\nu }^t\frac{\partial }{\partial u_t}+{\nu }^{xx}\frac{\partial }{\partial u_{xx}}+{\nu }^{xt}\frac{\partial }{\partial u_{xt}}+{\nu }^{tt}\frac{\partial }{\partial u_{tt}},\hfill \\ \hfill {\nu }^{xx}& =D_x{D}_x\left(\nu -\lambda u_x-\mu u_t\right)+\lambda u_{\mathit{xxx}}+\mu u_{\mathit{xxt}},\hfill \\ \hfill {\nu }^{xt}& =D_x{D}_t\left(\nu -\lambda u_x-\mu u_t\right)+\lambda u_{\mathit{xtx}}+\mu u_{\mathit{xtt}}.\hfill \end{array}(6)$

where D_x and D_t are the total derivatives.

Apply the second prolongation of the infinitesimal generator Eq. 5 onto Eq. 3. Then, in order to calculate symmetry of Eq. 3, we have the equation of the following form:

${\mathit{Pr}}^{\left[2\right]}W\left(u_{xt}-\alpha e^u-\frac{1}{3}\beta u_{xx}^3\right){|}_{u_{xt}=\alpha e^u+\frac{1}{3}\beta u_{xx}^3}=0.(7)$

Solving this equation

$\left[-\alpha \nu e^u-\beta {\nu }^{xx}{\left(u^2\right)}_{xx}+{\nu }^{xt}\right]{|}_{u_{xt}=\alpha e^u+\frac{1}{3}\beta u_{xx}^3}=0.(8)$

Substitute the values of ν^xx, ν^xt and Eq. 3 which leads to an under-determined system of equations given as:

$\begin{array}{ll}\hfill {\mu }_{xx}& =0,{\mu }_{xu}=0,{\mu }_{uu}=0,{\lambda }_{uu}=0,{\mu }_u=0,{\lambda }_u=0,\hfill \\ \hfill {\lambda }_{tu}& =0,{\mu }_x=0,{\nu }_{uu}=0,{\nu }_{xu}=0,{\nu }_{xx}=0,{\nu }_{tu}=0,\hfill \\ \hfill {\lambda }_t& =0,{\lambda }_{xx}=0,\hfill \\ \hfill & -\alpha \nu e^u+{\nu }_{xt}+\alpha \left({\nu }_u-{\lambda }_x-{\mu }_t\right)e^u=0,\hfill \\ \hfill & -\frac{2}{3}{\nu }_u+\frac{5}{3}{\lambda }_x-\frac{1}{3}{\mu }_t=0.\hfill \end{array}(9)$

The solution of the aforementioned determining equations gives the coefficient functions in the form of

$\begin{array}{ll}\hfill \lambda \left(x\right)& =\frac{1}{5}{c}_1^{\prime }x+c_3^{\prime },\hfill \\ \hfill \mu \left(t\right)& =c_1^{\prime }t+c_2^{\prime },\hfill \\ \hfill \nu \left(x,t,u\right)& =-\frac{6}{5}{c}_1^{\prime }.\hfill \end{array}(10)$

$c_1^{\prime },c_2^{\prime }$ and $c_3^{\prime }$ are arbitrary constants. Thus, the Lie algebra of the infinitesimal symmetries for the case n = 1 is

$\begin{array}{ll}\hfill W_1& =\frac{1}{5}x{\partial }_x+t{\partial }_t-\frac{6}{5}{\partial }_u,\hfill \\ \hfill W_2& ={\partial }_t,\hfill \\ \hfill W_3& ={\partial }_x.\hfill \end{array}(11)$

Theorem 3.1 The set of these generators is closed under the one parameter Lie groups $H_i^{ϵ}$ which are generated by infinitesimal generators W_i for i = 1, 2, and 3 are given in the following table. The entries give the transformed points exp(ϵW_i)(x, t, u) = (x*, t*, u*).

$\begin{array}{ll}\hfill H_1^{ϵ}& :\left(x,t,u\right)\to \left(e^{\frac{1}{5}ϵ}x,e^{ϵ}t,u-\frac{6}{5}ϵ\right),\hfill \\ \hfill H_2^{ϵ}& :\left(x,t,u\right)\to \left(x,t+ϵ,u\right),\hfill \\ \hfill H_3^{ϵ}& :\left(x,t,u\right)\to \left(x+ϵ,t,u\right).\hfill \end{array}(12)$

where ϵ ∈ R is the group parameter.Theorem 3.2 If $u=\mathbb{B}(x,t)$ satisfies Eq. 3, then, u⁽ⁱ⁾(i = 1, 2, and 3) are solutions of Eq. 3:

$\begin{array}{ll}\hfill u^{\left(1\right)}& =-\frac{6}{5}ϵ\mathbb{B}\left(e^{-\frac{1}{5}ϵ}x,e^{-ϵ}t\right),\hfill \\ \hfill u^{\left(2\right)}& =\mathbb{B}\left(x,t-ϵ\right),\hfill \\ \hfill u^{\left(3\right)}& =\mathbb{B}\left(x-ϵ,t\right).\hfill \end{array}(13)$

where $u^i=H_i^{ϵ}.{\mathbb{B}}^i(x,t)$, (i = 1,2, and 3), ϵ ≪ 1 is any positive number.

The Eq. 13 provides a class of solutions for Eq. 3 depending upon the parameter ϵ and general function ${\mathbb{B}}^i$ where (i = 1, 2, 3). The Figures 2–5 show the graphical view of the functions uⁱ, (i = 1, 2, 3) where uⁱ attained from Lie symmetry groups W_i. These graphs are formed by letting different general functions in place of ${\mathbb{B}}^i$ in Eq. 13. The graphs are constructed from the maple.

FIGURE 2

FIGURE 2. For $u^{(1)}=-\frac{6}{5}ϵ[\cos (e^{-\frac{1}{5}ϵ}x+e^{-ϵ}t)]$ and ϵ =0.000005.

FIGURE 3

FIGURE 3. For $u^{(1^{*})}=-\frac{6}{5}ϵ[\cos ({ϵ}^{-\frac{1}{5}ϵ}x)+\sin (e^{-ϵ}t)]$ and ϵ = 0.000005.

FIGURE 4

FIGURE 4. For u⁽²⁾ = x³+2(t − ϵ) and ϵ = 0.000005.

FIGURE 5

FIGURE 5. For u⁽³⁾=2t ln (x − ϵ).

For first equation in Eq. 13, letting the general trigonometric function in place of $\mathbb{B}(x,t)$

$u^{\left(1\right)}=-\frac{6}{5}ϵ\left[\cos \left(e^{-\frac{1}{5}ϵ}x+e^{-ϵ}t\right)\right],(14)$

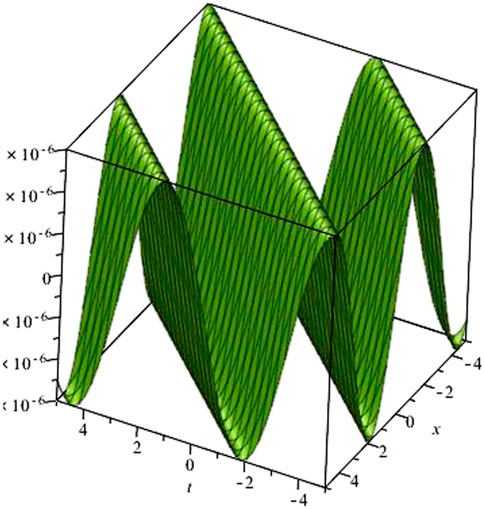
along-with ϵ = 0.000005 and abscissa x = −5 to 5, ordinate t = −5 to 5.

$u^{\left(1\right)}=-0.000006\left[\cos \left(e^{-0.000001}x+e^{-0.000005}t\right)\right].(15)$

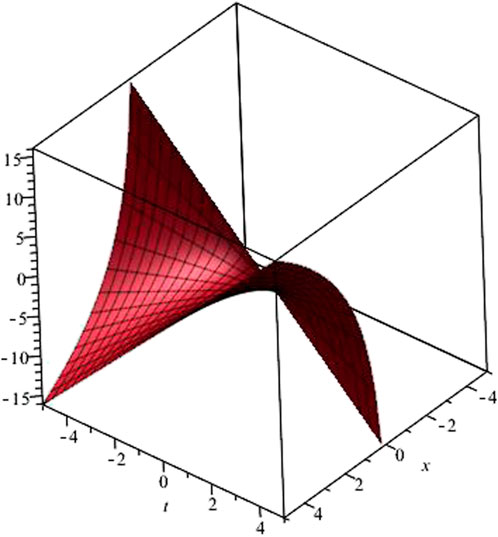
Figure 2 shows the graphical behavior of Eq. 15.letting another general value of function $\mathbb{B}(x,t)=\cos ({ϵ}^{-\frac{1}{5}ϵ}x)+\sin (e^{-ϵ}t)$. The function becomes

$u^{\left(1^{*}\right)}=-0.000006\left[\cos \left(e^{-0.000001}x\right)+\sin \left(e^{-0.000005}t\right)\right].(16)$

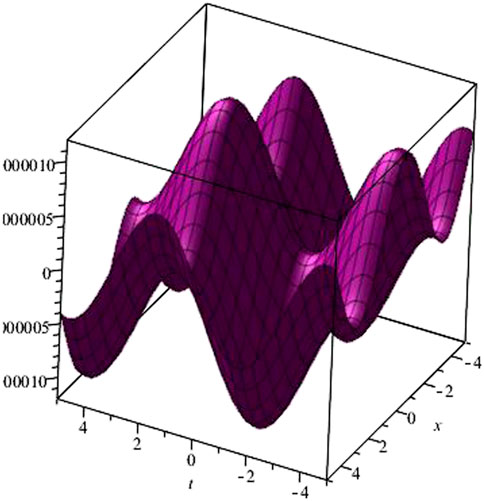
Figure 3 shows the graphical view of Eq. 16.

For second equation of Eq. 13, considering a general function $\mathbb{B}(x,t)=x^3+2(t-ϵ)$ for the same values of ϵ = 0.000005 and aforementioned coordinates for Eq. 14.

$u^{\left(2\right)}=x^3+2\left(t-0.000005\right),(17)$

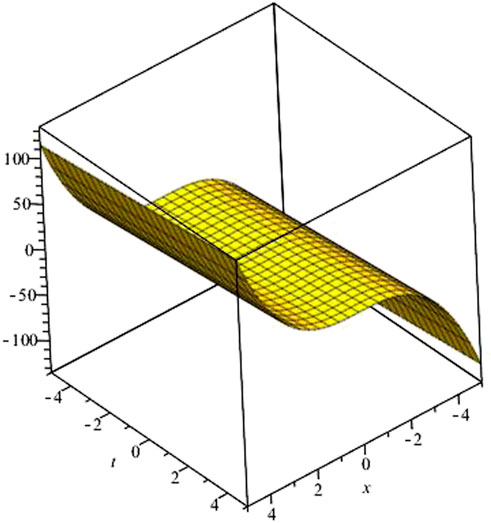
Figure 4 shows its graphical view.

For last equation of Eq. 13, we let a general logarithmic function $\mathbb{B}=2t\ln (x-ϵ)$ and for similar values of ϵ, x, and t coordinates.

$u^{\left(3\right)}=2t\ln \left(x-0.000005\right).(18)$

Its graph is in Figure 5.

2.2 Optimal system of subalgebras

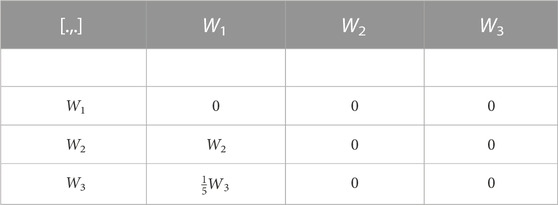
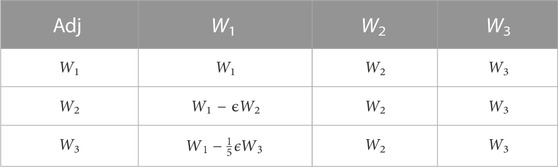
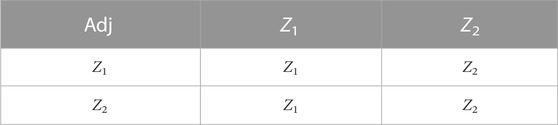
In this part, we will find the optimal system of one dimensional Lie subalgebras for Eq. 3 by using the adjoint representation. The corresponding commutator table and the adjoint table are as follows:Commutator Table: Adjoint Table:

Let us take a generator

$W={\beta }_1{W}_1+{\beta }_2{W}_2+{\beta }_3{W}_3,(19)$

Case No.1 For β₁ ≠ 0, the generator turns to

$W=W_1+{\beta }_2{W}_2+{\beta }_3{W}_3.(20)$

Applying $Ad{j}_{e^{{\beta }_2{W}_2}}$ on Y gives

$W^{\prime }=W_1+{\beta }_3{W}_3,(21)$

furthermore, proceeding in the same way

$W^{″}=Ad{j}_{e^{5{\beta }_3{W}_3}}\left(W_3\right)=W_1,(22)$

which successively makes the coefficients β₂ and β₃ equal to 0and implies that W ≃ W₁.Case No.2 Without loss of generality, here we take β₁ = 0 and β₂ = 1, the generator becomes

$W=W_2+{\beta }_3{W}_3,(23)$

Now, act $Ad{j}_{e^{{\beta }_3{W}_3}}$ on the aforementioned W,

$W^{\prime }=W_2+{\beta }_3{W}_3,(24)$

Subcase No.2.1 If β₃ < 0, then

$W^{\prime }=W_2-W_3.(25)$

Subcase No.2.2 If β₃ > 0, then

$W^{\prime }=W_2+W_3.(26)$

Case No.3 For β₁ = β₂ = 0 and β₃ = 1. Thus, in the meanwhile we have W ≃ W₃.Case No.4 Let consider β₁ = 0 = β₃ and β₂ ≠ 0. In this case, the generator is W ≃ W₂.

The optimal system of one-dimensional subalgebras admitted by Eq. 3) is as follows:

$W=\left\{\begin{array}{c}{W}_1,\hfill \\ W_2,\hfill \\ W_3,\hfill \\ W_2\pm W_3.\hfill \end{array}\right.(27)$

2.3 Reductions and invariant solutions

2.3.1 Reduction by W₂

The invariants for corresponding characteristic equation are as follows:

$x=a,u=b,(28)$

where a and b are arbitrary constants.

The invariant solution can be written in the form of b = f(a), implies that

$u=f\left(a\right),(29)$

substituting this value in Eq. 3), we obtain

$\Rightarrow \beta {\left(f^{″}\left(a\right)\right)}^3+3\alpha e^{f\left(a\right)}=0.(30)$

The solution of this reduced equation for β = 1 is given in the form of solution set as.

${\int }^{f\left(a\right)}\frac{\mp 1}{\sqrt{6\left(-3\alpha e^b\right)-k_1}}db-x-k_2=0,$

$\mp 6k_1\arctan \left(\sqrt{-3I{3}^{\frac{5}{6}}-33^{\frac{1}{3}}{\left(-\alpha e^{f\left(a\right)}\right)}^{\frac{1}{3}}+\frac{1}{k_1^2}}{k}_1\right)-x-k_2=0,$

$\mp 6k_1\arctan \left(\sqrt{3I{3}^{\frac{5}{6}}-33^{\frac{1}{3}}{\left(-\alpha e^{f\left(a\right)}\right)}^{\frac{1}{3}}-\frac{1}{k_1^2}}{k}_1\right)-x-k_2=0.$

2.3.2 Reduction by W₃

The corresponding characteristic equation to this generator is as follows:

$\frac{dx}{1}=\frac{dt}{0}=\frac{du}{0},(31)$

this gives two invariants

$t=a_1,u=b_1,(32)$

where a₁ and b₁ are arbitrary constants. It implies

$u=f\left(t\right),(33)$

putting this in Eq. 3, we obtain

$\alpha e^u=0,(34)$

which gives a trivial solution for u = f(x).

2.3.3 Reduction by W₁

The characteristic equation is

$5\frac{dx}{x}=\frac{dt}{t}=-\frac{5}{6}du,(35)$

solving this, we obtain corresponding invariants of the form

$r=\frac{t}{x^5},s=e^u{x}^6,(36)$

from this

$u=\ln \left[x^{-6}f\left(t{x}^{-5}\right)\right],(37)$

where we obtain

$\begin{array}{ll}\hfill u_x& =-\frac{1}{xf\left(r\right)}\left[5r{f}^{\prime }\left(r\right)+6f\left(r\right)\right],\hfill \\ \hfill u_{xx}& =\frac{f\left(r\right)\left[25r^2{f}^{″}\left(r\right)+6f\left(r\right)+30r{f}^{\prime }\left(r\right)\right]-25r^2{f}^{\prime 2}\left(r\right)}{x^2{f}^{2\left(r\right)}},\hfill \\ \hfill u_{xt}& =\frac{f\left(r\right)\left[-5r{f}^{″}\left(r\right)-5f^{\prime }\left(r\right)\right]+5r{f}^{\prime 2}\left(r\right)}{x^6{f}^2\left(r\right)}.\hfill \end{array}(38)$

substituting these derivatives into Eq. 3, we obtain

$\begin{array}{ll}\hfill & 3f^5\left(r\right)\left[-5r{f}^{″}\left(r\right)-5r{f}^{\prime }\left(r\right)\right]+15r{f}^4\left(r\right)f^{\prime 2}\left(r\right)-3\alpha f^7\left(r\right)+\beta \left[f\left(r\right)\left[6f\left(r\right)+25r^2{f}^{″}\left(r\right)\right.\right.\hfill \\ \hfill & +{\left.\left.30r{f}^{\prime }\left(r\right)\right]-25r^2{f}^{\prime 2}\left(r\right)\right]}^3=0.\hfill \end{array}(39)$

Thus, non-linear PDE (3) reduces to a non-linear ODE.

2.3.4 Reduction by W₂ + W₃

The invariants that we gain by solving characteristic equation are as follows:

$a_3=x-t,u=b_3,(40)$

a₃ and b₃ are arbitrary constants. The invariant solution corresponding to them is u = f (a₃). Inserting this solution into Eq. 3 will give us a non-linear ODE of the form

$3f^{″}\left(a_3\right)+\beta {\left(f^{″}\left(a_3\right)\right)}^3+3\alpha e^{f\left(a_3\right)}=0.(41)$

2.3.5 Reduction by W₂ − W₃

The invariants corresponding to characteristic equation for this case are a₄ = x + t and b₄ = u. Furthermore, its invariant solution is given as u = f (a₄). Therefore, the Eq. 3 will be converted into an ODE of the form

$3f^{″}\left(a_4\right)-\beta {\left(f^{″}\left(a_4\right)\right)}^3-3\alpha e^{f\left(a_4\right)}=0.(42)$

2.4 Determining lie symmetry of SPE for the case $h(u)=e^{u^n}$ and k(u) = u_xx (n > 1)

The equation becomes

$u_{xt}=\alpha e^{u^n}+\frac{1}{3}\beta u_{xx}^3.(43)$

The one-parameter Lie group of transformations and the second prolongation with coefficients are given in Eqs 4, 6, respectively for Eq. 43. Let the generator be

$Z=\lambda \left(x,t,u\right){\partial }_x+\mu \left(x,t,u\right){\partial }_t+\nu \left(x,t,u\right){\partial }_u,(44)$

Therefore, we have

${\mathit{Pr}}^{\left[2\right]}Z\left(u_{xt}-\alpha e^{u^n}-\frac{1}{3}\beta u_{xx}^3\right){|}_{u_{xt}=\alpha e^{u^n}+\frac{1}{3}\beta u_{xx}^3}=0,(45)$

simplification gives the following equation:

$-\alpha n\nu e^{u^n}{u}^{n-1}-\beta {\nu }^{xx}{u}_{xx}^2+{\nu }^{xt}=0,(46)$

which is solved for the values of ν^xx and ν^xt, will give us the equation involving derivatives of infinitesimals with respect to dependent and independent variables and also the derivatives of dependent variable w.r.to independent variables. Substituting Eq. 43 and comparing the values of coefficients on both sides gives an under-determined system of equations

$\begin{array}{ll}\hfill {\mu }_{xx}& =0{\mu }_{xu}=0,{\mu }_{uu}=0,{\lambda }_{uu}=0,{\mu }_u=0,{\lambda }_u=0,\hfill \\ \hfill {\lambda }_{tu}& =0,{\mu }_x=0,{\nu }_{uu}=0,{\nu }_{xu}=0,{\nu }_{xx}=0,{\nu }_{tu}=0,\hfill \\ \hfill {\lambda }_t& =0,{\lambda }_{xx}=0,-\frac{2}{3}{\nu }_u+\frac{5}{3}{\lambda }_x-\frac{1}{3}{\mu }_t=0,\hfill \\ \hfill & -\alpha n\nu e^{u^n}{u}^{n-1}+{\nu }_{xt}+\alpha \left({\nu }_u-{\lambda }_x-{\mu }_t\right)e^{u^n}=0.\hfill \end{array}(47)$

To solve this system, we consider ν as:

$\nu =L\left(t\right)x+Mu+N\left(t\right),(48)$

which satisfies the aforementioned equations and then by solving the aforementioned system, we obtain

$\begin{array}{ll}\hfill \lambda \left(x\right)& ={\mathrm{c}}_2,\hfill \\ \hfill \mu \left(t\right)& ={\mathrm{c}}_1,\hfill \\ \hfill \nu \left(x,t,u\right)& =0.\hfill \end{array}(49)$

c₁ and c₂ are any arbitrary constants. The infinitesimal generators for the one-parameter of Lie groups of transformations admitted in Eq. 43) are given by

$\begin{array}{ll}\hfill Z_1& ={\partial }_t,\hfill \\ \hfill Z_2& ={\partial }_x.\hfill \end{array}(50)$

These symmetry generators give us the symmetry groups $Q_i^{ϵ}$ for i = 1, 2:

$\begin{array}{ll}\hfill Q_1^{ϵ}& =\left(x,t+ϵ,u\right),\hfill \\ \hfill Q_2^{ϵ}& =\left(x+ϵ,t,u\right).\hfill \end{array}(51)$

If u = R (x,t) is a solution of Eq. 43), then uⁱ for i = 1, 2, and 3 and ϵ ≪ 1 also satisfies Eq. 43,

$\begin{array}{ll}\hfill u^{\left(1\right)}& =R\left(x,t-ϵ\right),\hfill \\ \hfill u^{\left(2\right)}& =R\left(x-ϵ,t\right).\hfill \end{array}(52)$

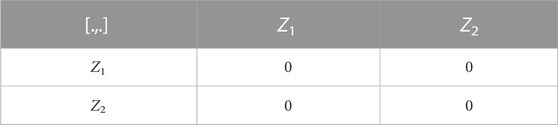
Commutator Table:also,

Adjoint Table.

Proposition 5.1: The generators Z₁ = ∂_t and Z₂ = ∂_x form a two-dimensional abelian Lie symmetry algebra.

2.5 Optimal system, reductions and invariant solutions

Considering a generator Z = b₁Z₁ + b₂Z₂. This generator will established a set of optimal system comprising of Lie algebra

$Z=\left\{Z_1,Z_2,b_1{Z}_1+b_2{Z}_2\right\}(53)$

where b₁, and b₂ are arbitrary constants. The reduction of PDE Eq. 39 by using the generator Z₁ leads to an invariant solution u = f (c₁). The reduced non-linear ODE will be

$3\alpha e^{u^n}+\beta u^{\prime \prime 3}=0(54)$

The reduction through Z₂ generates a trivial case for Eq. 39.

3 Conclusion

In this paper, we have carried out the LSA for computing the similarity solutions (symmetries) of the non-linear SPE for the cases when h(u) = e^u and k(u) = u_xx and $h(u)=e^{u^n}$ and k(u) = u_xx in SPE (2). In addition, an optimal system of one-dimensional subalgebra has been set up. The reductions and invariant solutions for the generalized SPE are calculated corresponding to this optimal system as well. The graphs are formed by the maple for the functions obtained from the transformed points of one-parameter Lie groups.

Data availability statement

The original contributions presented in the study are included in the article/Supplementary Material; further inquiries can be directed to the corresponding author.

Author contributions

Article has been concieved by MM, drafted by HB and MA. All authors contributed to the article and approved the submitted version.

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors, and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

1. Oliveri F. Lie symmetries of differential equations: Classical results and recent contributions. Symmetry (2010) 2(2):658–706. doi:10.3390/sym2020658

CrossRef Full Text | Google Scholar

2. Knight JC, Broeng J, Birks TA, Russell PSJ. Photonic band gap guidance in optical fibers. Science (1998) 282(5393):1476–8. doi:10.1126/science.282.5393.1476

PubMed Abstract | CrossRef Full Text | Google Scholar

3. Clarkson PA, Ludlow DK, Priestley TJ. The classical, direct, and nonclassical methods for symmetry reductions of nonlinear partial differential equations. Methods Appl Anal (1997) 4(2):173–95. doi:10.4310/maa.1997.v4.n2.a7

CrossRef Full Text | Google Scholar

4. Liu H, Zhang L. Symmetry reductions and exact solutions to the systems of nonlinear partial differential equations. Physica Scripta (2018) 94(1):015202. doi:10.1088/1402-4896/aaeeff

CrossRef Full Text | Google Scholar

5. Coclite GM, di Ruvo L. Well-posedness results for the short pulse equation. Z für Angew Mathematik Physik (2015) 66(4):1529–57. doi:10.1007/s00033-014-0478-6

CrossRef Full Text | Google Scholar

6. Schäfer T, Wayne CE. Propagation of ultra-short optical pulses in cubic nonlinear media. Physica D: Nonlinear Phenomena (2004) 196(1-2):90–105. doi:10.1016/j.physd.2004.04.007

CrossRef Full Text | Google Scholar

7. Agrawal GP. Nonlinear fiber optics. In: Nonlinear science at the dawn of the 21st century. Berlin, Heidelberg: Springer (2000). p. 195–211.

Google Scholar

8. Karasawa N, Nakamura S, Nakagawa N, Shibata M, Morita R, Shigekawa H, et al. Comparison between theory and experiment of nonlinear propagation for a-few-cycle and ultrabroadband optical pulses in a fused-silica fiber. IEEE J Quan Electron (2001) 37(3):398–404. doi:10.1109/3.910449

CrossRef Full Text | Google Scholar

9. Moloney JV, Newell AC. Nonlinear optics. Physica D: Nonlinear Phenomena (1990) 44(1-2):1–37. doi:10.1016/0167-2789(90)90045-q

CrossRef Full Text | Google Scholar

10. Xiao Y, Maywar DN, Agrawal GP. New approach to pulse propagation in nonlinear dispersive optical media. JOSA B (2012) 29(10):2958–63. doi:10.1364/josab.29.002958

CrossRef Full Text | Google Scholar

11. Liu H, Li J. Lie symmetry analysis and exact solutions for the short pulse equation. Nonlinear Anal Theor Methods Appl (2009) 71(5-6):2126–33. doi:10.1016/j.na.2009.01.075

CrossRef Full Text | Google Scholar

12. Fakhar K, Wang G, Kara AH. Symmetry reductions and conservation laws of the short pulse equation. Optik (2016) 127(21):10201–7. doi:10.1016/j.ijleo.2016.08.013

CrossRef Full Text | Google Scholar

13. Matsuno Y. Parametric solutions of the generalized short pulse equations. J Phys A: Math Theor (2020) 53(10):105202. doi:10.1088/1751-8121/ab6f18

CrossRef Full Text | Google Scholar

14. Ali AT. New generalized Jacobi elliptic function rational expansion method. J Comput Appl Math (2011) 235(14):4117–27. doi:10.1016/j.cam.2011.03.002

CrossRef Full Text | Google Scholar

15. El-Sabbagh MF, Ali AT. New generalized Jacobi elliptic function expansion method. Commun Nonlinear Sci Numer Simulation (2008) 13(9):1758–66. doi:10.1016/j.cnsns.2007.04.014

CrossRef Full Text | Google Scholar

16. Zhao W, Munir MM, Bashir H, Ahmad D, Athar M. Lie symmetry analysis for generalized short pulse equation. Open Phys (2022) 20(1):1185–93. doi:10.1515/phys-2022-0212

CrossRef Full Text | Google Scholar