
94% of researchers rate our articles as excellent or good
Learn more about the work of our research integrity team to safeguard the quality of each article we publish.
Find out more
ORIGINAL RESEARCH article
Front. Phys., 21 March 2023
Sec. Mathematical Physics
Volume 11 - 2023 | https://doi.org/10.3389/fphy.2023.1133550
This article is part of the Research TopicSymmetry and Exact Solutions of Nonlinear Mathematical Physics EquationsView all 20 articles
 Muhammad Sohail1*
Muhammad Sohail1* Umar Nazir2
Umar Nazir2 Kanit Mukdasai2
Kanit Mukdasai2 Manoj Singh3
Manoj Singh3 Abha Singh4
Abha Singh4 Chandika Rama Mohan5
Chandika Rama Mohan5 Ahmed M. Galal6,7
Ahmed M. Galal6,7 Sayed M. Eldin8*
Sayed M. Eldin8*This developing study is focused on mass diffusion and thermal energy enhancement in Reiner–Philippoff martial across a vertical-surface under an exposed Lorentz force. Characterization of the thermal energy and mass diffusion are modified utilizing non-Fourier’s theory in the presence of a heat source. Three types of nanoparticles—
Non-Newtonian fluids have numerous applications and are used extensively in many materials. This investigation deals with Sutterby nanofluid boundary-layer flow in a stretched cylinder by including updated models for mass and heat transfers and applying the Cattaneo–Christov theory. Boundary-layer analysis leads to the creation of a mathematical model. By utilizing conservation principles, the physical phenomena are first generated in terms of PDEs. The penetrating medium is influenced by the advanced Darcy’s law. The suggested model’s non-linear equations are optimally and dynamically investigated. By establishing the conservation rules for mass, momentum, energy, and concentration, non-linear partial differential equations (PDEs) are created. The OHAM is adopted and aims to develop numerical solutions for non-linear systems, as previously discussed [1]. Nanofluids are the newest category of fluids, and Choi first described them at the beginning of 1995. Akbar et al. [2] formulated a model of peristaltic transport in the presence of thermal conductive using variable viscosity-based temperature with carbon nanoparticles; the authors found the exact solution of the developed model. Akram et al. [3] utilized curved microchannels to investigate heat transfer and flow behavior in the presence of titanium dioxide in Carneau fluid rheology; the authors estimated the motion of nanoparticles using mechanisms of thermophoretic and Brownian motion via an exact solution technique. Maraj et al. [4] discovered the consequences of Lorentz force, including CNTs and thermal deposition in the channel, utilizing exact closed-form solutions involving radiation and magnetic field. Akram et al. [5] studied thermal features of peristaltic transport involving Lorentz force and electroosmosis with SWCNTs in aqueous diagrams. Multiple industrial and technological implications, including wire drawing, glass fiber production, assembly of particularly elastic sheets, and cooling of concerning metallic plates are among the pertinent themes investigated previously [6] regarding the study of fluid attributes in multiple mathematical models. When a fixed magnetic field was supplied, Bhandari and Husain carefully examined the combined impacts particularly of rotating viscosity and magnetized force subjected to a 2D Ferro hydrodynamic non-conductor nanoliquid flow across a stretched surface. To explore the hybrid nanomaterials’ flow demeanor when subjected to a stretched sheet, Gul et al. presented a computer model. Fractional calculus ideas have been widely used in different areas in recent years. This topic has recently expanded in several different directions, including fractional-order multipoles influenced by electromagnetism and in the field of electrochemistry. Moreover, tracer is used within the fluid flow demeanor, the neuron model in the field of biology, finance, and signal processing. The Riemann–Liouville and Caputo fractional derivatives are the most popular applications discussed by Shah and Khan [7]. Biomedical engineering and medical care greatly benefit from the radiation and magnetic field impacts appertaining to nanofluids. Khan et al. [8] examined gold particle performance toward the blood flow demeanor (Sisko fluid flow) through a penetrating, slick, curvy surface. Partial slip impacts were considered in thoroughly analyzing the properties referring to nanofluidic flow. After Choi’s original study, a significant advancement in this field was made. In an experimental study, Eastman et al. examined heat transfer in the presence of Al2O3 and CuO particles, synthesized using ethylene glycol and water, respectively. Investigation based on blood flow demeanor in small arteries involves many variable features. Understanding the rheological behavior of blood and other biological fluids, namely urine, spermatozoa, and eye drops, requires accounting for heat conductivity and viscosity change. In the current work, which was motivated by these applications, we describe the peristaltic flow demeanor—particularly Ree–Eyring liquid via a uniform compliant channel—while accounting for the influence of varying thermal conductivity and viscosity, as described previously [9]. Recent studies have shown a particular interest in dusty fluid model flows due to their two-phase nature. This effect occurs when solid particles are dispersed in fluid (gas or liquid) flows. As an example, consider the chemical process that results in droplet formation when relatively small dust particles agglomerate, leading to high dusty-air velocity. Cosmic dust, a mixture of gas and dust particles, is the essential precursor for planetary systems, as expressed previously [10]. In tabular and graphical formats, Khan and Pop [11] examined fluctuation in declining Nusselt and reduced Sherwood numbers. Falkner–Skan flow is one of the most well-known motives for investigating magnetohydrodynamics, on account of its applications in the field of fluid dynamics and heat transfer. In the scientific community, conventional flow behavior, specifically Newtonian and non-Newtonian fluids subjected to a moving wedge, is very popular right now. Lin et al. investigated the properties of heat transmission within the static wedge flow demeanor. The authors examined the model particularly for every conceivable finite Prandtl number value. Watanabe and Watanabe and Pop, respectively, researched forced and free-convection Falkner–Skan flow. Akbar et al. [12] discussed investigations into shape factors associated with SiO2/MoS2 nanoparticles in a base fluid in a channel including a temperature gradient (oscillatory). Convection may occur in three different ways in heat transfer flows: naturally, forcibly, and mixed. The last of these has uses in a variety of industrial and natural phenomena, including nuclear reactor cooling, electronic systems, and heat exchangers used to heat or cool fluids in the food industry and in compact heat exchangers, as studied previously [13]. In numerous systems pertaining to heating and cooling, fluids including water and kerosene oil, ethylene, and glycol are frequently utilized. Most of these fluids, which are sometimes referred to as the basic fluids, are poor heat conductors. We must address the issues caused by these systems' weak conductivities in order to improve their performance. Nowadays, a relatively novel approach is being used to increase thermal conductivity and other thermal characteristics. Habib et al. [14] discussed a new discovery regarding nanofluid behavior in clinical isolates of Staphylococcus aureus using gold nanoparticles. Alghamdi et al. [15] favored adopting non-linear stretching sheets. These crucial industrial applications drove researchers to carefully examine boundary-layer flow demeanor over linear and non-linear prolonged sheets of a range of geometric thicknesses. Micropolar nanofluidic flow demeanor embedded with buoyancy force, along with magnetic field subjected to an enclosure, has been studied for its heat and mass transmission mechanism. The proposed mathematical model needed to assess effectiveness, particularly nanoparticle thermal efficiency, must be built using mass and energy and must be within the momentum equations. This study aims to increase the effectiveness of heat and mass transmission within the heat transport machinery and heat-ameliorated units used in engineering and industrial operations. The proposed dimensionless 2D model given the significance of dimensional analysis analyzed previously [16]. The substandard thermal conductivity of operating liquids, which constrains high solidity and performance appertaining to thermal production within heat exchanges, is currently a serious worldwide problem. Most frequently, ethanol and water, as well as an acetone and an ethylene–glycol combination, are used as working fluids, as discussed previously [17]. Additionally, in response to this issue, numerous scientists and engineers have demonstrated the essential principles of improving thermal properties, specifically for energy-transported liquids, and efficiency, particularly of heat transfer in industrial appliances.
Examining entropy production in catalytic and non-linear thermal radiative impacts involves assessing the hydromagnetic stagnation point flow demeanor of a micropolar nanofluid. A water nanofluid is created by mixing in the magnetite nanoparticles. The time-independent, significant 2D flow demeanor is supposed to start with a vertically stretchable sheet. When creating the governing equations for the relevant issue, the Joule heating and viscous dissipation impacts are considered, as described previously [18]. Using updated heat and mass flux models, the entropy production approach is subjected to Maxwell nanofluid incorporated with gyrotactic microorganisms influenced by homogeneous–heterogeneous processes. Amended models are provided using the dual diffusive theory and the generalized Fick’s equation. According to boundary-layer theory, derived equations that depict the flow situation under consideration are modeled as PDEs. An appropriate transformation is then applied to alter the resulting PDEs toward the transformed ODEs and is subsequently solved using a powerful technique called the optimal homotopy analysis approach. Special instances of certain previously published research are in close accordance with our findings. Graphs are used to describe the effects, specifically of physical factors within the velocity, as well as temperature, concentration, reaction rate, the concentration of motile bacteria, and entropy production, as examined in an earlier study [19]. Based on the three-dimensional and steady power-law for nanofluidic flow demeanor close to the stagnation point area, the MHD and non-linear thermal radiative impacts included in penetrable material are applied to conduct an entropy generation study. The heat transformation phenomena inside the boundary layer configured by the stretchy moving disc are investigated and accompanied by non-uniformly thermal radiative heat source/sink exposed to convective boundary circumstances. The basic fluid ethylene glycol (C2H6O2) is combined with multi-wall carbon nanotubes (MWCNTs). The suggested fluid flow issue is analytically modeled, as discussed previously [20]. Incompressible viscous hybrid nanofluid flow is analyzed in three dimensions in a rotating frame. The basic liquid is ethylene glycol, and the nanoparticles are copper and silver. Fluid flows within the dual parallel surfaces, with the bottom surface extending linearly. Since fluid conducts, a consistent magnetic field is applied. We consider the viscous dissipation impacts and Joule heating and non-linear thermal radiations. The Nusselt number and surface drag force are addressed as interesting quantities. Xia et al. [21] examined the rate of entropy formation. Because of their significant industrial applications and high heat transfer rates, nanofluids are of great importance to scientists. Hybrid nanofluids, a brand-new form of nanofluid, have lately been employed to accelerate heat transfer even further. The current phenomena focus particularly on the investigation of SWCNT–MWCNT/water hybrid nanofluidic flow demeanor and on heat transmission subjected to a moving wedge. The flow demeanor in the porosity media is described by the Darcy–Forchheimer relationship. In addition, Ahmad et al. [22] covered in depth the effect of varying viscosity and velocity, as well as thermal slip, thermal radiation, and heat production. By performing a theoretical study, peculiarly viscous three-dimensional fluid flow demeanor incorporated with gyrotactic microorganisms across a non-linear stretchy surface, heat mechanisms, and mass transmission may be understood. To regulate the flow of fluid, the fluctuating magnetic field is thought to be normal toward the stretchy surface. The varying thermal conductivity prompts a discussion of thermal transportation. Mass transportation incorporates chemical processes and variable mass diffusion properties. The porous medium is defined using the Darcy–Forchheimer equation. To improve diffusion, Abdelsalam and Sohail [23] included Brownian motion and thermophoresis. The current study investigates viscous fluid flow in three dimensions when specific heat (PHF) and concentration (PCF) fluxes are present. Chemical reactions, viscosity dissipation, and Joule heating impacts are all considered when the mathematical formulation is being constructed. Fluid becomes electrically conductive when influenced by the applied magnetic field, whereas the non-linear system referring to ordinary differential equations is obtained by appropriate transformations. The resultant non-linear system determines the solution. To investigate the effects, particularly the physical factors, of the temperature and concentration distributions, graphs are plotted. Maraj et al. [24] estimated rotational flow and motion of hybrid nanoparticles with Hall currents in a vertical channel using conditions of thermal periodic and velocity slip via closed-form solutions. Saleem et al. [25] adopted FEM for statistical solutions, referring to a set of ODEs. Damaged arteries with stenosis have reduced blood flow; the accumulation of plaque within the artery walls, brought on by fats and oils, leads to the development of this stenosis. Multiple stenoses may exist in an artery that has severe stenosis. Multiple stenoses cause the artery to narrow, which restricts blood flow across it. Many academics have recently been interested in examining this particular kind of stenotic artery. Blood flows through tiny channels, with non-Newtonian behavior in big vessels and Newtonian behavior in smaller vessels. Owing to various peculiarities, particularly blood circulation along with the mechanical characteristics of the vessel walls, it is essential to examine the blood flow through a stenotic channel. Shahzad et al. [26] determined the location of stenosis on the vessel wall and the flow behavior through sick blood arteries by observing blood flow across a stenotic artery. In this investigation, the contributions of viscous dissipation and thermophoresis, as well as Brownian motion, gravitational effects, and stratification impacts, were examined. Physical events are derived as linked systems of partial differential equations. An appropriate transformation converts the model’s equation system into straightforward ordinary differential equations (ODEs). Naz et al. [27] used an ideal homotopy analysis approach and an improvised system that relies on coupled non-linear ODEs solved in Mathematica. Due to its use in several sectors, heat transfer is crucial. Hybrid nanofluidic flow, a novel manner of nanofluids with a greater heat exponent in comparison to the nanofluids, is being utilized to improve the ability of regular fluids to transport heat. In a base fluid, two-element nanoparticles are known as hybrid nanofluids (HNFs). Jamshed et al. [28] demonstrated the properties of steady hybrid nanofluidic flow and thermal transfer over a slippery surface. Convection, whether forced or natural, is more significant in the context of fluid dynamics than the other two well-known heat transfer processes, conduction and radiation. It happens because of differences in the thermal energy that is applied differently to various parts of the fluid under examination. Akram et al. [29] discussed theoretical investigations of thermal transfer based on Au and Ag hybrid water-based nanoparticles induced by electroosmotic pumping in a microchannel. Due to their poor heat conductivity, pure liquids like water and oil have proven to be problematic in this respect. To improve heat transmission and modify the carrier fluid’s thermal characteristics, nanoparticles with an approximate diameter of less than 100 nm, materials with intensified thermal conductivities, are mixed along with the fluid, as discussed previously [30]. This analysis emphasizes the importance of radiation and Joule heating effects, particularly for Casson liquid-boundary layer flow (BLF) configured by a linearly elongating surface, as well as the properties of momentum and entropy production. Likewise, species and thermal dissemination are also considered. Thermal conductivity and mass diffusion coefficient models that vary with temperature are used to provide thermal and species transportation. Emerging issues take the non-linear partial differential equations form, in opposition to the principles governing the movement of mass, momentum, heat, and species. The exhibited issue may be transformed into ordinary differential equations with the proper modification. Sohail et al. [31] used the optimal homotopy analysis method (OHAM) as a competent and dependable approach for obtaining numerical solutions, specifically for upgraded boundary-layer ordinary differential equations (ODEs). Due to its applicability, heat transfer analysis in two-dimensional flows has drawn the interest of several academics in recent years. Akram et al. [32] derived features of electroosmotic flow by inserting silver nanoparticles and solving using two various approaches. Applications like drawing wire, making plastic and rubber sheets, cooling electric plates enclosed by a bath, melt spinning, and hot rolling, among others, all benefit from fluid passage over elongating sheets. Because a plate expands at a specific rate, Sakiadis was the first to examine fluid flow. Crane then concentrated on the laminar flow demeanor, specifically two-dimensional, incompressible, and viscous fluid subjected to a stretching plate. There is a precise closed-form solution to this problem. Following the above-mentioned studies, many researchers (see, for instance, [33]) concentrated on fluid flow caused by stretched plates. These researchers investigated flow demeanor across an exponentially stretching sheet with the impacts of MHD and radiation, and discovered that the magnetic and radiation parameters are what reduce the heat transmission rate. The authors looked across the Eyring–Powell fluid boundary-layer fluid flow configured by a linearly stretching sheet and computed the findings for velocity profiles using the collocation method.
Two-dimensional consequences of mass diffusion and thermal fields of a complex fluid (Reiner–Philippoff) were investigated under conditions of EMHD on a vertical plate. Three phases of hybrid nanomaterial are implemented in the presence of engine oil. Fields associated with mass diffusion and thermal conductivity are carried out by heat sink and non-Fourier’s theory, as well as variable properties pertaining to mass diffusion and thermal conductivity. A flow diagram with boundary conditions and suspension of ternary hybrid nanoparticles is shown in Figure 1. Conservation laws have been implemented to obtain distributions for motion, concentration, and thermal conductivity, as listed below. The thermophysical properties of different used materials are depicted in Table 1.
The reduced form of PDEs [34–36] is derived as
and subjected to the desired boundary conditions
Similarity, the variables of temperature-dependent concentration and temperature-dependent thermal conductivity are defined as
The system of ODEs [34] is formulated as
Equation 5 in dimensionless form [34] is defined as
The defined correlations associated with tri-hybrid nanoparticles [36] are
The mathematical expressions of Sherwood number and temperature gradient [34] are
where (Reynolds number)
The current model in terms of ODEs is numerically handled by a finite element approach based on the following steps:
The computational form domain has been discretized into elements, and weighted residuals are derived as
The assembly process is implemented to derive a global stiffness matrix. In this step, the boundary vector, source vector, and stiffness matrix are obtained as.
Error analysis is estimated as
Table 2 shows mesh-free simulations and convergence analysis, while criteria regarding convergence are defined as
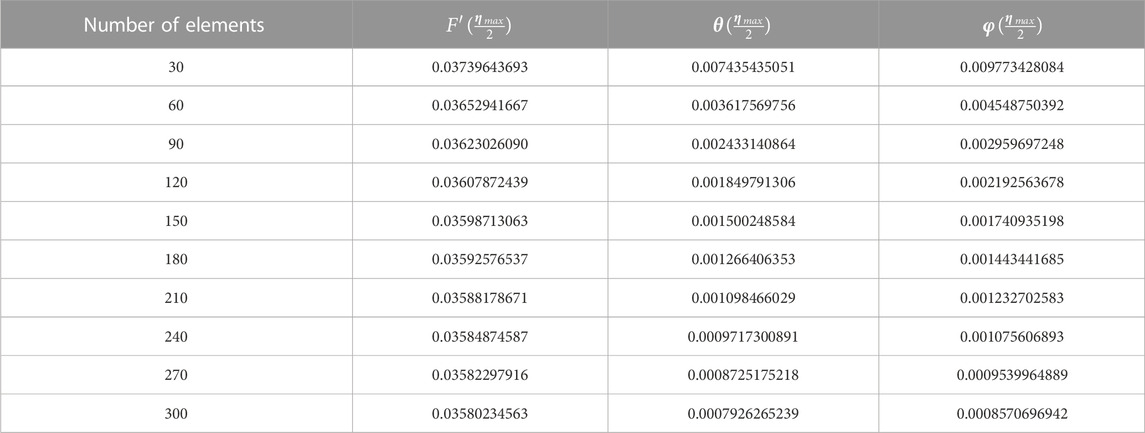
TABLE 2. Analysis of the grid-independent study carried out for 300 elements for concentration, velocity, and temperature profiles.
The code for FEM was designed in MAPLE 18. Table 3 illustrates the present validation in view of temperature gradient, with an already-published study [38] having different values of
The development of a two-dimensional model is formulated in view of Reiner–Philippoff toward a surface involving buoyancy forces and electric field. Energy transfer and mass species are carried out in the presence. Dispersions of tiny nanoparticles are incorporated using generalized theory. Mass diffusion (variable) and thermal conductivity (variable) are inserted into the concentration and energy equations. A finite element scheme has been utilized to simulate numerical study of the present problem. Graphical explanations regarding flow, solute, and thermal energy versus various parameters are displayed in the following sections.
In this subsection, graphs related to velocity curves are plotted versus electric magnetic (
Figures 5–7 show the role of fluidic temperature against changes in
Figures 8–10 determine the characterizations of fluidic concentration versus impacts of
The impact of
Features of fluidic motion, fluidic thermal energy, and fluidic concentration are determined in a two-dimensional model under non-Fourier’s law with variable properties. A heat source and chemical reactions are also taken out into a mixture of nanoparticles. A strong scheme, termed a finite element method, is utilized. The main findings of the problem are summarized as follows:
➢ Velocity field has been enhanced against changes in
➢ Heat energy increases against changes in relaxation number, heat source number, and variable thermal conductivity parameter.
➢ Fluidic concentration declines against changes in Schmidt number and chemical reaction parameter.
➢ The cooling process can be improved by adding ternary hybrid nano-structures rather than other nanoparticles.
➢ The highest production of thermal energy can be achieved utilizing tri-hybrid nanoparticles as compared with hybrid nanofluids and nanofluids.
➢ Thermal gradient and mass diffusion gradient are higher for
The raw data supporting the conclusion of this article will be made available by the authors, without undue reservation.
All authors listed have made a substantial, direct, and intellectual contribution to the work and approved it for publication.
This study was supported by funding from Prince Sattam bin Abdulaziz University (project number PSAU/2023/R/1444).
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors, and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
1. Sohail M, Naz R. Modified heat and mass transmission models in the magnetohydrodynamic flow of Sutterby nanofluid in stretching cylinder. Physica A: Stat Mech its Appl (2020) 549:124088. doi:10.1016/j.physa.2019.124088
2. Akbar NS, Maraj EN, Noor NFM, Habib MB. Exact solutions of an unsteady thermal conductive pressure driven peristaltic transport with temperature-dependent nanofluid viscosity. Case Stud Therm Eng (2022) 35:102124. doi:10.1016/j.csite.2022.102124
3. Akram J, Akbar NS, Alansari M, Tripathi D. Electroosmotically modulated peristaltic propulsion of TiO2/10W40 nanofluid in curved microchannel. Int Commun Heat Mass Transfer (2022) 136:106208. doi:10.1016/j.icheatmasstransfer.2022.106208
4. Maraj EN, Akbar NS, Iqbal Z, Azhar E. Framing the MHD mixed convective performance of CNTs in rotating vertical channel inspired by thermal deposition: Closed form solutions. J Mol Liquids (2017) 233:334–43. doi:10.1016/j.molliq.2017.03.041
5. Akram J, Akbar NS, Tripathi D. Electroosmosis augmented MHD peristaltic transport of SWCNTs suspension in aqueous media. J Therm Anal Calorim (2022) 147(3):2509–26. doi:10.1007/s10973-021-10562-3
6. Saeed A, Bilal M, Gul T, Kumam P, Khan A, Sohail M. Fractional order stagnation point flow of the hybrid nanofluid towards a stretching sheet. Scientific Rep (2021) 11(1):20429–15. doi:10.1038/s41598-021-00004-3
7. Shah NA, Khan I. Heat transfer analysis in a second grade fluid over and oscillating vertical plate using fractional Caputo–Fabrizio derivatives. The Eur Phys J C (2016) 76(7):362–11. doi:10.1140/epjc/s10052-016-4209-3
8. Khan U, Zaib A, Ishak A. Magnetic field effect on Sisko fluid flow containing gold nanoparticles through a porous curved surface in the presence of radiation and partial slip. Mathematics (2021) 9(9):921. doi:10.3390/math9090921
9. Rajashekhar C, Mebarek-Oudina F, Vaidya H, Prasad KV, Manjunatha G, Balachandra H. Mass and heat transport impact on the peristaltic flow of a Ree–Eyring liquid through variable properties for hemodynamic flow. Heat Transfer (2021) 50(5):5106–22. doi:10.1002/htj.22117
10. Rehman SU, Fatima N, Ali B, Imran M, Ali L, Shah NA, et al. The Casson dusty nanofluid: Significance of Darcy–forchheimer law, magnetic field, and non-Fourier heat flux model subject to stretch surface. Mathematics (2022) 10(16):2877. doi:10.3390/math10162877
11. Khan WA, Pop I. Boundary-layer flow of a nanofluid past a stretching sheet. Int J Heat mass transfer (2010) 53(11-12):2477–83. doi:10.1016/j.ijheatmasstransfer.2010.01.032
12. Akbar NS, Iqbal Z, Ahmad B, Maraj EN. Mechanistic investigation for shape factor analysis of SiO2/MoS2–ethylene glycol inside a vertical channel influenced by oscillatory temperature gradient. Can J Phys (2019) 97(9):950–8. doi:10.1139/cjp-2018-0717
13. Laouira H, Mebarek-Oudina F, Hussein AK, Kolsi L, Merah A, Younis O. Heat transfer inside a horizontal channel with an open trapezoidal enclosure subjected to a heat source of different lengths. Heat Transfer—asian Res (2020) 49(1):406–23. doi:10.1002/htj.21618
14. Habib MB, Akbar NS. New trends of nanofluids to combat Staphylococcus aureus in clinical isolates. J Therm Anal Calorim (2021) 143(3):1893–9. doi:10.1007/s10973-020-09502-4
15. Alghamdi M, Wakif A, Thumma T, Khan U, Baleanu D, Rasool G. Significance of variability in magnetic field strength and heat source on the radiative-convective motion of sodium alginate-based nanofluid within a Darcy-Brinkman porous structure bounded vertically by an irregular slender surface. Case Stud Therm Eng (2021) 28:101428. doi:10.1016/j.csite.2021.101428
16. Batool S, Rasool G, Alshammari N, Khan I, Kaneez H, Hamadneh N. Numerical analysis of heat and mass transfer in micropolar nanofluids flow through lid driven cavity: Finite volume approach. Case Stud Therm Eng (2022) 37:102233. doi:10.1016/j.csite.2022.102233
17. Khan U, Zaib A, Shah Z, Baleanu D, Sherif ESM. Impact of magnetic field on boundary-layer flow of Sisko liquid comprising nanomaterials migration through radially shrinking/stretching surface with zero mass flux. J Mater Res Technol (2020) 9(3):3699–709. doi:10.1016/j.jmrt.2020.01.107
18. Ishtiaq B, Zidan AM, Nadeem S, Alaoui MK. Analysis of entropy generation in the nonlinear thermal radiative micropolar nanofluid flow towards a stagnation point with catalytic effects. Physica Scripta (2022) 97(8):085204. doi:10.1088/1402-4896/ac79d7
19. Sohail M, Naz R, Abdelsalam SI. On the onset of entropy generation for a nanofluid with thermal radiation and gyrotactic microorganisms through 3D flows. Physica Scripta (2020) 95(4):045206. doi:10.1088/1402-4896/ab3c3f
20. Ghaffari A, Mustafa I, Muhammad T, Altaf Y. Analysis of entropy generation in a power-law nanofluid flow over a stretchable rotatory porous disk. Case Stud Therm Eng (2021) 28:101370. doi:10.1016/j.csite.2021.101370
21. Xia WF, Hafeez MU, Khan MI, Shah NA, Chung JD. Entropy optimized dissipative flow of hybrid nanofluid in the presence of non-linear thermal radiation and Joule heating. Scientific Rep (2021) 11(1):16067–16. doi:10.1038/s41598-021-95604-4
22. Ahmad S, Nadeem S, Ullah N. Entropy generation and temperature-dependent viscosity in the study of SWCNT–MWCNT hybrid nanofluid. Appl Nanoscience (2020) 10(12):5107–19. doi:10.1007/s13204-020-01306-0
23. Abdelsalam SI, Sohail M. Numerical approach of variable thermophysical features of dissipated viscous nanofluid comprising gyrotactic micro-organisms. Pramana (2020) 94(1):67–12. doi:10.1007/s12043-020-1933-x
24. Maraj EN, Zehra I, SherAkbar N. Rotatory flow of MHD (MoS2-SiO2)/H2O hybrid nanofluid in a vertical channel owing to velocity slip and thermal periodic conditions. Colloids Surf A: Physicochemical Eng Aspects (2022) 639:128383. doi:10.1016/j.colsurfa.2022.128383
25. Saleem S, Gopal D, Shah NA, Feroz N, Kishan N, Chung JD, et al. Modelling entropy in magnetized flow of eyring–powell nanofluid through nonlinear stretching surface with chemical reaction: A finite element method approach. Nanomaterials (2022) 12(11):1811. doi:10.3390/nano12111811
26. Shahzad MH, Awan AU, Akhtar S, Nadeem S. Entropy and stability analysis on blood flow with nanoparticles through a stenosed artery having permeable walls. Sci Prog (2022) 105(2):003685042210960. doi:10.1177/00368504221096000
27. Naz R, Noor M, Shah Z, Sohail M, Kumam P, Thounthong P. Entropy generation optimization in MHD pseudoplastic fluid comprising motile microorganisms with stratification effect. Alexandria Eng J (2020) 59(1):485–96. doi:10.1016/j.aej.2020.01.018
28. Jamshed W, Prakash M, Hussain SM, Eid MR, Nisar KS, Muhammad T, et al. Entropy amplified solitary phase relative probe on engine oil based hybrid nanofluid. Chin J Phys (2022) 77:1654–81. doi:10.1016/j.cjph.2021.11.009
29. Akram J, Akbar NS, Tripathi D. A theoretical investigation on the heat transfer ability of water-based hybrid (Ag–Au) nanofluids and Ag nanofluids flow driven by electroosmotic pumping through a microchannel. Arabian J Sci Eng (2021) 46(3):2911–27. doi:10.1007/s13369-020-05265-0
30. Alsabery AI, Hashim I, Hajjar A, Ghalambaz M, Nadeem S, Saffari Pour M. Entropy generation and natural convection flow of hybrid nanofluids in a partially divided wavy cavity including solid blocks. Energies (2020) 13(11):2942. doi:10.3390/en13112942
31. Sohail M, Shah Z, Tassaddiq A, Kumam P, Roy P. Entropy generation in MHD Casson fluid flow with variable heat conductance and thermal conductivity over non-linear bi-directional stretching surface. Scientific Rep (2020) 10(1):12530–16. doi:10.1038/s41598-020-69411-2
32. Akram J, Akbar NS, Tripathi D. Analysis of electroosmotic flow of silver-water nanofluid regulated by peristalsis using two different approaches for nanofluid. J Comput Sci (2022) 62:101696. doi:10.1016/j.jocs.2022.101696
33. Sohail M, Ali U, Al-Mdallal Q, Thounthong P, Sherif ESM, Alrabaiah H, et al. Theoretical and numerical investigation of entropy for the variable thermophysical characteristics of couple stress material: Applications to optimization. Alexandria Eng J (2020) 59(6):4365–75. doi:10.1016/j.aej.2020.07.042
34. Xiu W, Saleem S, Weera W, Nazir U. Cattaneo-Christove thermal flux in Reiner–Philippoff martial under action of variable Lorentz force employing tri-hybrid nanomaterial approach. Case Stud Therm Eng (2022) 38:102267. doi:10.1016/j.csite.2022.102267
35. Hou E, Wang F, Nazir U, Sohail M, Jabbar N, Thounthong P. Dynamics of tri-hybrid nanoparticles in the rheology of pseudo-plastic liquid with dufour and soret effects. Micromachines (2022) 13(2):201. doi:10.3390/mi13020201
36. Nazir U, Saleem S, Al-Zubaidi A, Shahzadi I, Feroz N. Thermal and mass species transportation in tri-hybridized Sisko martial with heat source over vertical heated cylinder. Int Commun Heat Mass Transfer (2022) 134:106003. doi:10.1016/j.icheatmasstransfer.2022.106003
37. Nazir U, Mukdasai K. Combine influence of Hall effects and viscous dissipation on the motion of ethylene glycol conveying alumina, silica and titania nanoparticles using the non-Newtonian Casson model. AIMS Maths (2023) 8(2):4682–99. doi:10.3934/math.2023231
38. Sajid T, Sagheer M, Hussain S. Impact of temperature-dependent heat source/sink and variable species diffusivity on radiative Reiner–Philippoff fluid. Math Probl Eng (2020) 2020:9701860. doi:10.1155/2020/9701860
PDEs partial differential equations
EO engine oil
MHD magneto-hydrodynamics
FEM finite element method
ODEs ordinary differential equations
EO engine oil
EMHD electric magneto-hydrodynamic
Keywords: EMHD, three-phase simulations, buoyancy forces, thermal properties, two-dimensional plate, Galerkin algorithm
Citation: Sohail M, Nazir U, Mukdasai K, Singh M, Singh A, Mohan CR, Galal AM and Eldin SM (2023) Transportation of
Received: 29 December 2022; Accepted: 22 February 2023;
Published: 21 March 2023.
Edited by:
Samir A. El-Tantawy, Port Said University, EgyptReviewed by:
Md. Golam Hafez, Chittagong University of Engineering & Technology, BangladeshCopyright © 2023 Sohail, Nazir, Mukdasai, Singh, Singh, Mohan, Galal and Eldin. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Muhammad Sohail, bXVoYW1tYWRfc29oYWlsMTExQHlhaG9vLmNvbQ==; Sayed M. Eldin, c2F5ZWQuZWxkaW4yMkBmdWUuZWR1LmVn
Disclaimer: All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article or claim that may be made by its manufacturer is not guaranteed or endorsed by the publisher.
Research integrity at Frontiers

Learn more about the work of our research integrity team to safeguard the quality of each article we publish.