Lie symmetry analysis and exact solutions of the (3+1)-dimensional generalized Shallow Water-like equation

In this article, (3+1)-dimensional generalized Shallow Water-like (gSWl) equation is discussed. The infinitesimal generators of the equation are derived by using the Lie symmetry analysis method. The optimal system is obtained based on the adjoint table of the generators of the equation. Exact solutions of the equation are constructed by applying symmetry reduction, Exp$\left(-\varphi (\xi )\right)$ expansion method, Exp-function expansion method, Riccati equation method, and $\left(G^{\prime }/G\right)$ expansion method. For analyzing the dynamical behavior of the solutions, we derive the physical structures of dark soliton, kink wave, and periodic solutions via numerical simulations.

1 Introduction

Non-linear phenomena are widespread in the life of the world, such as marine engineering, hydrodynamics, chemical physics, etc [1–3]. To investigate exact solutions of any complex non-linear partial differential equations and examine the behavior of the solutions is very interesting. Many effective methods for constructing the exact solutions are proposed, including Bäcklund transformation method [4] (G′/G) expansion method [5, 6], Hirota bilinear method [7], Homogeneous balance method [8, 9], Lie symmetry method [10–12], Inverse scattering method [13], F-expansion method [14], Exp-function method [15, 16], Darboux transformation method [17], Riemann-Hilbert method [18, 19] and so on.

The following (3 + 1)-dimensional generalized Shallow Water equation

$\begin{array}{c}{u}_{\mathit{xxxy}}-3u_{xx}{u}_y-3u_x{u}_{xy}+u_{yt}-u_{xz}=0,\hfill \end{array}$(1.1)

has been studied by many approaches. Huang and Gao [20] derived the one-, two- and three-soliton solutions of the equation by the Hirota method, and deduced the propagation and interaction of the soliton solutions. In [21], Huang studied the stability of solitons by numerical methods and noticed that the soliton amplitude magnitude is affected by the spectral parameters. In [22], the closed-form solutions of the equation were derived by Lie symmetry, and the soliton solutions were found through the optimal system. Based on the auto-Bäcklund transformation, Li and Liu [23] constructed the multi-periodic solitons of Eq. 1.1 through the variable-coefficient homogeneous balance method and investigated the propagation and interactions of the solutions. In [24], Liu deduced the new periodic solitary solutions of Eq. 1.1 by the direct test function method, and the validity of the direct test function method was shown. Liu and Zhu [25] investigated the variable coefficients of the gSW equation by the Hirota bilinear method and constructed a large number of breather wave solutions.

Tang, Ma and Xu [26] proposed the (3 + 1)-dimensional generalized Shallow Water-like (gSWl) equation

$\begin{array}{c}{u}_{\mathit{xxxy}}+3u_{xx}{u}_y+3u_x{u}_{xy}-u_{yt}-u_{xz}=0,\hfill \end{array}$(1.2)

which can be derived by rewriting Eq. 1.1 on the scale x → −x. In [26], the Grammian and Pfaffian solutions of Eq. 1.2 were obtained and the equations were extended with the Pfaffianization method. Kumar et al. [27] derived the multi-stripe and breathing wave solutions of Eq. 1.2 by the bilinear method, combining the quadratic function and hyperbolic cosine method, the behavior between the one-block and multi-stripe solutions were obtained. Sadat et al. [28] applied symbolic calculations to yield lump-type and stripe solutions of Eq. 1.2. Zhang et al. [29] applied the generalized bilinear operator method and obtained the rational and lump solutions of Eq. 1.2.

The shallow water wave equation plays an essential role in marine engineering, environmental problems, and ecology, so it is valuable to derive the exact solutions of the shallow water wave equation. Employing the Lie symmetry method to yield exact solutions of the (3 + 1)-dimensional gSWl equation has not been studied. In this paper, the Lie symmetry analysis method is applied to investigate the solutions of Eq. 1.2. Lie symmetry method [30–34] has an important significance for solving partial differential equations (PDEs). Applying the Lie symmetry method, the symmetry group of the equation can be derived, furthermore, the equation can be similarly reduced and the new solutions of the equation can be yielded by the symmetry transformation. The Lie symmetry method can reduce the order of the equation when solving with higher order equations, which is difficult to accomplish by other methods.

The structure of the rest of the paper is as follows: In Sect 2, the infinitesimal generators are obtained by applying the Lie group transformation to the (3 + 1)-dimensional gSWl equation. In Sect 3, the optimal system for Eq. 1.2 is derived under the basis of the adjoint table. The periodic wave, kink wave and soliton solutions of the equation are derived by Exp$\left(-\varphi (\xi )\right)$ expansion method, Exp-function expansion method, Riccati equation method, and $\left(G^{\prime }/G\right)$ expansion method in Sect 4. The dynamical behavior of the soliton wave solutions of the gSWl equation are analyzed in Sect 5. The conclusions are given in Sect 6.

2 Lie symmetry analysis for the (3 + 1) gSWl equation

The key step for solving non-linear PDEs by Lie symmetry group method is to obtain Lie algebra of the equation. Consider the following one-parameter Lie group transformation:

$\begin{array}{c}\widehat{x}=x+\epsilon \xi +O\left({\epsilon }^2\right),\hfill \\ \widehat{y}=y+\epsilon \eta +O\left({\epsilon }^2\right),\hfill \\ \widehat{z}=z+\epsilon \phi +O\left({\epsilon }^2\right),\hfill \\ \widehat{t}=t+\epsilon \tau +O\left({\epsilon }^2\right),\hfill \\ \widehat{u}=u+\epsilon \varphi +O\left({\epsilon }^2\right),\hfill \end{array}$(2.1)

where ɛ is a parameter, and ɛ ≪ 1. ξ, η, φ, τ, and ϕ are infinitesimal generators concerning x, y, z, t and u. The one-parameter vector field V of gSWl equation can be written as

$\begin{array}{c}V=\xi \frac{\partial }{\partial x}+\eta \frac{\partial }{\partial y}+\phi \frac{\partial }{\partial z}+\tau \frac{\partial }{\partial t}+\varphi \frac{\partial }{\partial u}.\hfill \end{array}$(2.2)

The vector field V satisfies

$\begin{array}{c}{\left.p{r}^{\left(4\right)}V\left(\mathrm{\Delta }\right)\right|}_{\mathrm{\Delta }=0}=0,\hfill \end{array}$(2.3)

in which Δ = u_xxxy + 3u_xxu_y + 3u_xu_xy − u_yt − u_xz and $p{r}^{\left(4\right)}$ is the fourth prolongation of V. The fourth prolongation of Eq. 1.2 can be derived as

$\begin{array}{c}p{r}^{\left(4\right)}V=V+{\varphi }^x\frac{\partial }{\partial u_x}+{\varphi }^y\frac{\partial }{\partial u_y}+{\varphi }^{xx}\frac{\partial }{\partial u_{xx}}+{\varphi }^{xz}\frac{\partial }{\partial u_{xz}}+{\varphi }^{xy}\frac{\partial }{\partial u_{xy}}+{\varphi }^{yt}\frac{\partial }{\partial u_{yt}}+{\varphi }^{\mathit{xxxy}}\frac{\partial }{\partial u_{\mathit{xxxy}}}.\hfill \end{array}$(2.4)

The invariant condition can be given as

$\begin{array}{c}{\varphi }^{\mathit{xxxy}}+3{\varphi }^{xx}{u}_y+3u_x{\varphi }^{xy}-{\varphi }^{yt}-{\varphi }^{xz}+3u_{xx}{\varphi }^y+3{\varphi }^x{u}_{xy}=0.\hfill \end{array}$(2.5)

Based on Eq. 2.5, the system of determining equations can be given by

$\begin{array}{c}{\varphi }_u=-\frac{1}{3}{\tau }_t,{\varphi }_x=-\frac{1}{3}{\eta }_z-\frac{1}{3}{\xi }_t,{\varphi }_y=-\frac{1}{3}{\xi }_z,{\varphi }_t=0,\hfill \\ {\tau }_x=0,{\tau }_y=0,{\tau }_z=0,{\tau }_{tt}=0,{\xi }_u=0,{\xi }_x=\frac{1}{3}{\tau }_t,{\xi }_y=0,\hfill \\ {\eta }_t=0,{\eta }_u=0,{\eta }_x=0,{\eta }_y={\phi }_z-\frac{2}{3}{\tau }_t,{\phi }_t=0,\hfill \\ {\phi }_u=0,{\phi }_x=0,{\phi }_y=0,{\phi }_{zz}=0,{\xi }_{tz}=-\frac{1}{2}{\eta }_{zz}.\hfill \end{array}$(2.6)

By solving the above equations we can derive

$\begin{array}{c}\varphi =-\frac{1}{3}{c}_{3}u-\frac{1}{6}\left\{{F^{\prime }}_1\left(z\right)+2{F^{\prime }}_2\left(t\right)\right\}x+\frac{1}{6}\left\{{F^{″}}_1\left(z\right)t-2{F^{\prime }}_3\left(z\right)\right\}y+F_4\left(z,t\right),\tau =c_{3}t+c_4,\hfill \\ \xi =\frac{1}{3}{c}_{3}x+F_3\left(z\right)+F_2\left(t\right)-\frac{1}{2}t{F^{\prime }}_1\left(z\right),\eta =F_1\left(z\right)+\frac{1}{3}\left(3c_1-2c_3\right)y,\phi =c_{1}z+c_2,\hfill \end{array}$(2.7)

where c_i and F_i (i = 1, 2, 3, 4) are arbitrary constants and functions, respectively.

Assume that $F_1\left(z\right)=0,F_2\left(t\right)=c_5,F_3\left(z\right)=0,F_4\left(z,t\right)=c_6$. The infinitesimal generators have new forms

$\begin{array}{c}\xi =c_{3}x+c_5,\eta =\left(c_1-2c_3\right)y,\phi =c_{1}z+c_2,\tau =3t{c}_3+c_4,\varphi =-u{c}_3+c_6.\hfill \end{array}$(2.8)

Thus, Lie algebras of infinitesimal symmetry of Eq. 1.2 can be spanned by the following six vector fields

$\begin{array}{c}{v}_1=y\frac{\partial }{\partial y}+z\frac{\partial }{\partial z},v_2=\frac{\partial }{\partial z},v_3=x\frac{\partial }{\partial x}+3t\frac{\partial }{\partial t}-2y\frac{\partial }{\partial y}-u\frac{\partial }{\partial u},\hfill \\ v_4=\frac{\partial }{\partial t},v_5=\frac{\partial }{\partial x},v_6=\frac{\partial }{\partial u}.\hfill \end{array}$(2.9)

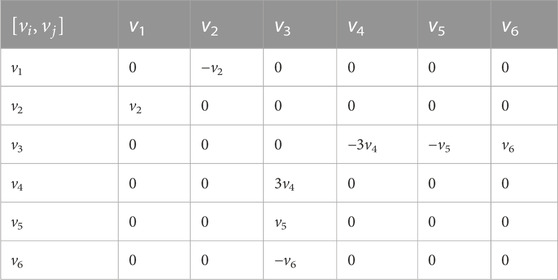
The commutator table derived for the gSWl equation by the action of Lie brackets is shown in Table 1, where $\left[v_i,v_j\right]=v_i{v}_j-v_j{v}_i$.

TABLE 1

TABLE 1. Commutator table.

3 Optimal systems of one-dimensional subalgebras

Based on the Lie brackets, the optimal system of one-dimensional subalgebras of the equation can be deduced. By the linear combination of subalgebras, a new form is given by

$\begin{array}{c}V=a_1{v}_1+a_2{v}_2+a_3{v}_3+a_4{v}_4+a_5{v}_5+a_6{v}_6.\hfill \end{array}$(3.1)

By Olver theory [30], using symbolic calculations

$Ad\left(\exp \left(\epsilon V_i\right)\right)V_j=V_j-\epsilon \left[V_i,V_j\right]+\frac{1}{2}{\epsilon }^2\left[V_i,\left[V_i,V_j\right]\right]-\cdots .$

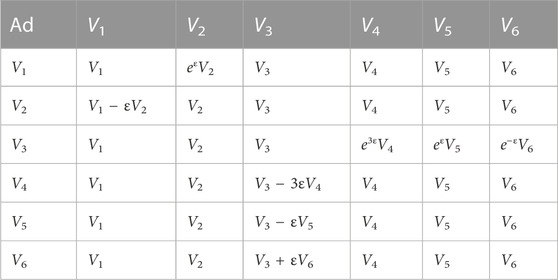
The adjoint table is shown in Table 2.

TABLE 2

TABLE 2. Adjoint table.

3.1 Construction of group invariants

The exchange and adjoint relations of the six-dimensional Lie algebras are given in Table 1 and Table 2, respectively. Assume that the vectors $V=\sum _{i=1}^6{a}_i{v}_i$ and $R=\sum _{i=1}^6{s}_i{v}_i$ satisfy

$\begin{array}{c}\mathrm{A}\mathrm{d}\left(\exp \left(\epsilon R\right)V\right)\hfill \\ =V-\epsilon \left[R,V\right]+\frac{1}{2}{\epsilon }^2\left[R,\left[R,V\right]\right]-\cdots \hfill \\ =\left(a_1{v}_1+\cdots +a_6{v}_6\right)-\epsilon \left[s_1{v}_1+\cdots +s_6{v}_6,a_1{v}_1+\cdots +a_6{v}_6\right]+O\left({\epsilon }^2\right)\hfill \\ =\left(a_1{v}_1+\cdots +a_6{v}_6\right)-\epsilon \left[k_1{v}_1+\cdots +k_6{v}_6\right]+O\left({\epsilon }^2\right),\hfill \end{array}$(3.2)

in which $k=k\left(a_1,\cdots a_6,s_1,\dots ,s_6\right)$ can be derived from Table 1. The values of k were calculated from Table 1 as follows

$\begin{array}{c}{k}_1=0,k_2=-a_2{s}_1+a_1{s}_2,k_3=0,\hfill \\ k_4=-3a_4{s}_3+3a_3{s}_4,k_5=-a_5{s}_3+a_3{s}_5,k_6=a_6{s}_3-a_3{s}_6.\hfill \end{array}$(3.3)

For any s_j (j = 1, 2, 3, 4, 5, 6), it have required

$\begin{array}{c}{k}_1\frac{\partial \chi }{\partial a_1}+k_2\frac{\partial \chi }{\partial a_2}+k_3\frac{\partial \chi }{\partial a_3}+k_4\frac{\partial \chi }{\partial a_4}+k_5\frac{\partial \chi }{\partial a_5}+k_6\frac{\partial \chi }{\partial a_6}=0.\hfill \end{array}$(3.4)

Gather the coefficients containing s_j in the above equation, the following system of differential equations are deduced as

$\begin{array}{c}{s}_1:-a_2\frac{\partial \chi }{\partial a_2}=0,\hfill \\ s_2:a_1\frac{\partial \chi }{\partial a_2}=0,\hfill \\ s_3:-3a_4\frac{\partial \chi }{\partial a_4}-a_5\frac{\partial \chi }{\partial a_5}+a_6\frac{\partial \chi }{\partial a_6}=0,\hfill \\ s_4:3a_3\frac{\partial \chi }{\partial a_4}=0,\hfill \\ s_5:a_3\frac{\partial \chi }{\partial a_5}=0,\hfill \\ s_6:-a_3\frac{\partial \chi }{\partial a_6}=0.\hfill \end{array}$(3.5)

After analyzing the above system of PDEs (3.5), it is not difficult to yield that the invariant function as $\chi \left(a_1,a_2,a_3,a_4,a_5,a_6\right)=F\left(a_1,a_3\right)$.

3.2 One-dimensional optimal system

For $J_n^{\epsilon }:\dot{j}\to \dot{j}$ defined by $l\to \mathrm{A}\mathrm{d}\left(\exp \left({\epsilon }_i{l}_i\right)s\right)$ is a linear map [35], in which n = 1, … , 6. The matrix $M_n^{\epsilon }$ of $J_n^{\epsilon }$ with respect to basis to $\left\{v_1,\dots ,v_6\right\}$ are deduced below

$\begin{array}{c}{M}_1^{\epsilon }=\left[\begin{array}{cccccc}\hfill 1\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill e^{\epsilon }\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill 0\hfill & \hfill 1\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 1\hfill & \hfill 0\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 1\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 1\hfill \end{array}\right],M_2^{\epsilon }=\left[\begin{array}{cccccc}\hfill 1\hfill & \hfill -{\epsilon }_2\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill 1\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill 0\hfill & \hfill 1\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 1\hfill & \hfill 0\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 1\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 1\hfill \end{array}\right],M_3^{\epsilon }=\left[\begin{array}{cccccc}\hfill 1\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill 1\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill 0\hfill & \hfill 1\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill e^{3{\epsilon }_3}\hfill & \hfill 0\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill e^{{\epsilon }_3}\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill e^{-{\epsilon }_3}\hfill \end{array}\right],\hfill \\ M_4^{\epsilon }=\left[\begin{array}{cccccc}\hfill 1\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill 1\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill 0\hfill & \hfill 1\hfill & \hfill -3{\epsilon }_4\hfill & \hfill 0\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 1\hfill & \hfill 0\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 1\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 1\hfill \end{array}\right],M_5^{\epsilon }=\left[\begin{array}{cccccc}\hfill 1\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill 1\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill 0\hfill & \hfill 1\hfill & \hfill 0\hfill & \hfill -{\epsilon }_5\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 1\hfill & \hfill 0\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 1\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 1\hfill \end{array}\right],M_6^{\epsilon }=\left[\begin{array}{cccccc}\hfill 1\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill 1\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill 0\hfill & \hfill 1\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill {\epsilon }_6\hfill \\ \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 1\hfill & \hfill 0\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 1\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 1\hfill \end{array}\right].\hfill \end{array}$(3.6)

Then, the matrix M can be yielded by

$\begin{array}{c}M=M_1^{\epsilon }\ast M_2^{\epsilon }\ast M_3^{\epsilon }\ast M_4^{\epsilon }\ast M_5^{\epsilon }\ast M_6^{\epsilon }.\hfill \end{array}$(3.7)

The matrix M can be written as

$M=\left[\begin{array}{cccccc}\hfill 1\hfill & \hfill -{\epsilon }_2\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill e^{{\epsilon }_1}\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill 0\hfill & \hfill 1\hfill & \hfill -3{\epsilon }_4\hfill & \hfill -{\epsilon }_5\hfill & \hfill {\epsilon }_6\hfill \\ \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill e^{3{\epsilon }_3}\hfill & \hfill 0\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill e^{{\epsilon }_3}\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill e^{-{\epsilon }_3}\hfill \end{array}\right].$(3.8)

The adjoint transformation equation for Eq. 1.2 is

$\begin{array}{cc}\hfill \left({\rho }_1,{\rho }_2,\cdots ,{\rho }_6\right)& =\left(a_1,a_2,\dots ,a_6\right)\cdot M\hfill \\ \hfill & =a_1{v}_1+\left(-a_1{\epsilon }_2+a_2{e}^{{\epsilon }_1}\right)v_2+a_3{v}_3+\left(-3a_3{\epsilon }_4+a_4{e}^{3{\epsilon }_3}\right)v_4\hfill \\ \hfill & +\left(-a_3{\epsilon }_5+a_5{e}^{{\epsilon }_3}\right)v_5+\left(a_3{\epsilon }_6+a_6{e}^{-{\epsilon }_3}\right)v_6.\hfill \end{array}$(3.9)

By applying the invariants a₁ and a₃, discuss the situations of the following Lie algebras.

Case 1 Assume that a₁ ≠ 0 and a₃ = 0. Let a₁ = 1. Making ρ₂ = 0, ρ₃ = 0 through

$\begin{array}{c}{\epsilon }_1=0,{\epsilon }_2=\frac{a_2}{a_1},{\epsilon }_3=0,\hfill \end{array}$(3.10)

and ɛ₄, ɛ₅, ɛ₆ are constants. In other words, all v₁ + a₂v₂ + a₃v₃ + a₄v₄ + a₅v₅ + a₆v₆ can be replaced by v₁ + ς₄v₄ + ς₅v₅ + ς₆v₆, where ς₄, ς₅ and ς₆ are constants.

Case 2 Assume that a₃ ≠ 0 and a₁ = 0. Let a₃ = 1. Making ρ₁ = 0, ρ₄ = 0, ρ₅ = 0, ρ₆ = 0 through

$\begin{array}{c}{\epsilon }_1=0,{\epsilon }_3=0,{\epsilon }_4=\frac{a_4}{3a_3},{\epsilon }_5=\frac{a_5}{a_3},{\epsilon }_6=-\frac{a_6}{a_3},\hfill \end{array}$(3.11)

and ɛ₂ is an arbitrary constant. In other words, all a₁v₁ + a₂v₂ + v₃ + a₄v₄ + a₅v₅ + a₆v₆ can be replaced by ς₂v₂ + v₃, where ς₂ is a constant.

Case 3 Assume that a₁ ≠ 0 and a₃ ≠ 0. Let a₁ = 1 and a₃ = 1. Making ρ₂ = 0, ρ₄ = 0, ρ₅ = 0, ρ₆ = 0 through

$\begin{array}{c}{\epsilon }_1=0,{\epsilon }_2=\frac{a_2}{a_1},{\epsilon }_3=0,{\epsilon }_4=\frac{a_4}{3a_1},{\epsilon }_5=\frac{a_5}{a_1},{\epsilon }_6=-\frac{a_6}{a_1}.\hfill \end{array}$(3.12)

In other words, all v₁ + a₂v₂ + v₃ + a₄v₄ + a₅v₅ + a₆v₆ can be replaced with v₁ + v₃.

Case 4 Replacing a₁ = a₃ = 0 into (3.9). By solving (3.9) for ɛ_i, we get ɛ₁ = 0, ɛ₃ = 0 and ɛ₂, ɛ₄, ɛ₅, ɛ₆ are arbitrary constants. In other words, all v₁ + a₂v₂ + v₃ + a₄v₄ + a₅v₅ + a₆v₆ can be replaced by ς₂v₂ + ς₄v₄ + ς₅v₅ + ς₆v₆, where ς₂, ς₄, ς₅ and ς₆ are constants.

Similarly, the other terms of the optimal system of Eq. 1.2 can be obtained by the above method. All of them are listed below.Single vector fields: v₁, v₂, v₃, v₄, v₅, v₆.Dual vector fields: v₁ + v₃, v₁ + v₄, v₁ + v₅, v₁ + v₆, v₂ + v₃, v₂ + v₄, v₂ + v₅, v₂ + v₆, v₄ + v₅, v₄ + v₆, v₅ + v₆.Triple vector fields: v₁ + v₄ + v₅, v₁ + v₄ + v₆, v₁ + v₅ + v₆, v₂ + v₄ + v₅, v₂ + v₄ + v₆, v₄ + v₅ + v₆.Quadruple vector fields: v₁ + v₄ + v₅ + v₆, v₂ + v₄ + v₅ + v₆.

4 Exact solutions of the gSWl equation

Next, the exact solutions of the gSWl equation are derived by employing the optimal system. The similarity solutions for arbitrary vector field v in the optimal system can be solved by the Lagrange’s system.

$\begin{array}{c}\frac{dx}{\xi }=\frac{dy}{\eta }=\frac{dz}{\phi }=\frac{dt}{\tau }=\frac{du}{\varphi }.\hfill \end{array}$(4.1)

4.1 Vector field v₁

The characteristic equation can be composed as

$\begin{array}{c}\frac{dx}{0}=\frac{dy}{y}=\frac{dz}{z}=\frac{dt}{0}=\frac{du}{0}.\hfill \end{array}$(4.2)

(Eq. 4.2) has the following form similarity solution.

U (x, y, z, t) = F (α, β, δ).in which α = x, $\beta =\frac{y}{z}$, δ = t.

Taking the above similarity solution into Eq. 1.2, the reduced NLPDE is given as

$\begin{array}{c}3F_{\alpha \alpha }{F}_{\beta }+3F_{\alpha }{F}_{\alpha \beta }+F_{\alpha \alpha \alpha \beta }+\beta F_{\alpha \beta }-F_{\beta \delta }=0.\hfill \end{array}$(4.3)

Similarly, applying the Lie symmetry method, the infinitesimal generators of Eq. 4.3 can be derived

$\begin{array}{c}{\xi }_{\alpha }=\frac{1}{3}{c}_1\alpha +g_1\left(\delta \right),{\xi }_{\beta }=-\frac{2}{3}{c}_1\beta +c_3,{\xi }_{\delta }=c_1\delta +c_2,{\eta }_F=-\frac{1}{3}{c}_{1}F-\frac{1}{3}\left(c_3+g_1{\left(\delta \right)}_{\delta }\right)\alpha +g_2\left(\delta \right).\hfill \end{array}$(4.4)

Let c₁ = 0,₁(δ) = d,₂(δ) = d, c₂ = d, c₃ = 3d, and take these values into (4.4), we get

$\begin{array}{c}\frac{d\alpha }{d}=\frac{d\beta }{3d}=\frac{d\delta }{d}=\frac{dF}{-\alpha +d},\hfill \end{array}$(4.5)

which has the similarity solutions from

$\begin{array}{c}F\left(\alpha ,\beta ,\delta \right)=\alpha -\frac{1}{2}{\alpha }^2+h\left(P,Q\right),\hfill \end{array}$(4.6)

where P = α − δ and Q = 3α − β.

Putting it into Eq. 4.3, the following reduced equation can be yield

$\begin{array}{c}-3h_Q{h}_{PP}-27h_Q{h}_{PQ}-3h_P{h}_{PQ}+Q{h}_{PQ}-54h_Q{h}_{QQ}-9h_P{h}_{QQ}\hfill \\ +3Q{h}_{QQ}-4h_{PQ}-9h_{QQ}+3h_Q-h_{\mathit{PPPQ}}-9h_{\mathit{PPQQ}}-27h_{\mathit{PQQQ}}-27h_{\mathit{QQQQ}}=0.\hfill \end{array}$(4.7)

Repeating the above steps, we get

$\begin{array}{c}{\xi }_P=c_1,{\xi }_Q=c_2,{\eta }_h=\frac{1}{3}{c}_{2}P+c_3.\hfill \end{array}$(4.8)

Substituting c₁ = d, c₂ = 3d, c₃ = d into (4.8). The new characteristic equation is given as

$\begin{array}{c}\frac{dP}{d}=\frac{dQ}{3d}=\frac{dh}{dP+1}.\hfill \end{array}$(4.9)

The new similarity solutions from

$\begin{array}{c}h\left(P,Q\right)=\frac{1}{2}{P}^2+P+k\left(\varpi \right),\hfill \end{array}$(4.10)

where ϖ = 3P − Q. Replacing (4.10) into Eq. 4.7, we get 3k_ϖϖ = 0. The solution of Eq. 1.2 via the above method can be given as

$\begin{array}{c}u=2x-t+\frac{1}{2}{t}^2-xt+\frac{c_{1}y}{z}-3c_{1}t+c_2,\hfill \end{array}$(4.11)

in which c₁ and c₂ are constants.

4.2 Vector field v₃

The characteristic equation can be composed as

$\begin{array}{c}\frac{dx}{x}=\frac{dy}{-2y}=\frac{dz}{0}=\frac{dt}{3t}=\frac{du}{-u}.\hfill \end{array}$(4.12)

The derived similarity solution has the form as.

$u\left(x,y,z,t\right)=F\left(\alpha ,\beta ,\theta \right)$.where $\alpha =\frac{x}{t^{\frac{1}{3}}}$, $\beta =y{t}^{\frac{2}{3}}$, θ = z. Hence, the following (2 + 1)-dimensional equation can be given as

$\begin{array}{c}2\beta F_{\beta \beta }-9F_{\alpha \alpha }{F}_{\beta }-9F_{\alpha }{F}_{\alpha \beta }-3F_{\alpha \alpha \alpha \beta }+F_{\beta }+3F_{\alpha \theta }-\alpha F_{\alpha \beta }=0.\hfill \end{array}$(4.13)

Then, the new infinitesimal generators of Eq. 4.13 can be yielded

$\begin{array}{c}{\xi }_{\alpha }=c_3,{\xi }_{\beta }=c_1\beta ,{\xi }_{\theta }=c_1\theta +c_2,{\eta }_F=-\frac{1}{9}{c}_3\alpha +g_1\left(\theta \right).\hfill \end{array}$(4.14)

Let c₁ = 0, c₂ = 0, c₃ = 0, g₁(z) = θ, and take these values into (4.14), the corresponding characteristic equation is reduced as

$\begin{array}{c}\frac{d\alpha }{0}=\frac{d\beta }{\beta }=\frac{d\theta }{\theta }=\frac{dF}{\theta },\hfill \end{array}$(4.15)

which has the similarity solutions from

$\begin{array}{c}F\left(\alpha ,\beta ,\theta \right)=\theta +h\left(P,Q\right),\hfill \end{array}$(4.16)

in which P = α, $Q=\frac{\beta }{\theta }$. Substituting F (α, β, θ) into Eq. 4.13 results

$\begin{array}{c}-9h_{PP}{h}_Q-9h_P{h}_{PQ}-P{h}_{PQ}+2Q{h}_{QQ}+h_Q-3Q{h}_{PQ}-3h_{\mathit{PPPQ}}=0.\hfill \end{array}$(4.17)

Equations 4.17 satisfies infinitesimal as follows

$\begin{array}{c}{\xi }_P=c_1,{\xi }_Q=0,{\eta }_h=-P+c_2,\hfill \end{array}$(4.18)

assume that c₁ = 9, c₂ = 1 and its characteristic equation is

$\begin{array}{c}\frac{dP}{9}=\frac{dQ}{0}=\frac{dh}{-P+1}.\hfill \end{array}$(4.19)

The similarity solution is

$\begin{array}{c}h\left(P,Q\right)=-\frac{1}{18}{P}^2+\frac{P}{8}+k\left(\varpi \right),\hfill \end{array}$(4.20)

where ϖ = Q. Then the ODE can be reduced as

$\begin{array}{c}2k_{\mathit{\varpi }}+2\mathit{\varpi }{k}_{\mathit{\varpi }\mathit{\varpi }}=0.\hfill \end{array}$(4.21)

By solving the above equation, we get

$\begin{array}{c}u=\frac{z+\frac{x}{9t^{\frac{1}{3}}}-\frac{x^2}{18t^{\frac{2}{3}}}+c_2\ln \left(\frac{y{t}^{\frac{2}{3}}}{z}\right)+c_1}{t^{\frac{1}{3}}}.\hfill \end{array}$(4.22)

4.3 Vector field v₂ + v₅

The characteristic equation can be composed as

$\begin{array}{c}\frac{dx}{1}=\frac{dy}{0}=\frac{dz}{1}=\frac{dt}{0}=\frac{du}{0}.\hfill \end{array}$(4.23)

(4.23) has the following form similarity solution

$\begin{array}{c}u\left(x,y,z,t\right)=F\left(\alpha ,\beta ,\delta \right),\hfill \end{array}$(4.24)

in which α = x − z, β = y, δ = z. Then Eq. 1.2 can be reduced to the following (2 + 1)-dimensional equation

$\begin{array}{c}{F}_{\alpha \alpha \alpha \beta }+3F_{\alpha \alpha }{F}_{\beta }+3F_{\alpha }{F}_{\alpha \beta }-F_{\beta \delta }+F_{\alpha \alpha }=0.\hfill \end{array}$(4.25)

The solution of Eq. 4.25 is more difficult to be derived, hence we use the Exp$\left(-\varphi \left(\xi \right)\right)$ expansion method to find its solution. Considering the following traveling wave transformation

$\begin{array}{c}F\left(\alpha ,\beta ,\delta \right)=h\left(\upsilon \right),\upsilon =k\alpha +l\beta +m\delta ,\hfill \end{array}$(4.26)

where k, l, m are constants. Replacing (4.26) into Eq. 4.25 and integrate the derived equation with respect to υ once, we get

$\begin{array}{c}l{k}^3{h}_{\upsilon \upsilon \upsilon }+3l{k}^2{h}_{\upsilon }^2-lm{h}_{\upsilon }+k^2{h}_{\upsilon }=0.\hfill \end{array}$(4.27)

Suppose that Eq. 4.27 can be solved in the following form

$\begin{array}{c}h\left(\upsilon \right)=a_j{\left(\exp \left(-\vartheta \left(\upsilon \right)\right)\right)}^j,\hfill \end{array}$(4.28)

in which j can be determined later and ϑ satisfies

$\begin{array}{c}{\vartheta }^{\prime }\left(\upsilon \right)=\exp \left(-\varphi \left(\upsilon \right)\right)+\mu \exp \left(\vartheta \left(\upsilon \right)\right)+\lambda .\hfill \end{array}$(4.29)

When λ² − 4μ > 0 and μ ≠ 0, (4.29) has a solution given by

$\begin{array}{c}\vartheta \left(\upsilon \right)=\ln \left(\frac{-\sqrt{{\lambda }^2-4\mu }\tanh \left(\frac{\sqrt{{\lambda }^2-4\mu }}{2}\left(\upsilon +{\epsilon }_0\right)\right)-\lambda }{2\mu }\right).\hfill \end{array}$(4.30)

When λ² − 4μ < 0, (4.29) has a solution given by

$\begin{array}{c}\vartheta \left(\upsilon \right)=\ln \left(\frac{\sqrt{4\mu -{\lambda }^2}\tan \left(\frac{\sqrt{4\mu -{\lambda }^2}}{2}\left(\upsilon +{\epsilon }_0\right)\right)-\lambda }{2\mu }\right).\hfill \end{array}$(4.31)

By balancing Eq. 4.27, j = 1. Hence (4.28) can be rewritten

$\begin{array}{c}h\left(\upsilon \right)=a_0+a_1{e}^{-\vartheta \left(\upsilon \right)}.\hfill \end{array}$(4.32)

Taking (4.32) along with Eq. 4.29 into Eq. 4.27, a series of algebraic equations about a₀, a₁, k, l and m can be deduced. Select a set from these to discuss the solution of the equations, we get

$\begin{array}{c}k=k,l=\frac{k^2}{k^3{\lambda }^2-4k^3\mu -m},m=m,a_0=a_0,a_1=2k.\hfill \end{array}$(4.33)

If λ² − 4μ > 0 and μ ≠ 0, the kink wave solution of Eq. 1.2 is

$\begin{array}{c}u=a_0+\frac{4k\mu }{-\tanh \left(\frac{1}{2}{c}_1\sqrt{{\lambda }^2-4\mu }+\frac{1}{2}\left(mt+k\left(x-z\right)-\frac{k^{2}y}{k^3{\lambda }^2-4k^3\mu -m}\right)\sqrt{{\lambda }^2-4\mu }\right)\sqrt{{\lambda }^2-4\mu }-\lambda }.\hfill \end{array}$(4.34)

If λ² − 4μ < 0, the periodic wave solution of Eq. 1.2 can be given by

$\begin{array}{c}u=a_0+\frac{4k\mu }{\tan \left(\frac{1}{2}{c}_1\sqrt{-{\lambda }^2+4\mu }+\frac{1}{2}\left(mt+k\left(x-z\right)-\frac{k^{2}y}{k^3{\lambda }^2-4k^3\mu -m}\right)\sqrt{-{\lambda }^2+4\mu }\right)\sqrt{-{\lambda }^2+4\mu }-\lambda }.\hfill \end{array}$(4.35)

4.4 Vector field v₄ + v₆

The characteristic equation can be composed as

$\begin{array}{c}\frac{dx}{0}=\frac{dy}{0}=\frac{dz}{0}=\frac{dt}{1}=\frac{du}{1}.\hfill \end{array}$(4.36)

We derive $u\left(x,y,z,t\right)=t+F\left(\alpha ,\beta ,\theta \right)$, where α = x, β = y and θ = z as the similarity variables. Taking it into Eq. 1.2, the following reduced equation can be obtained

$\begin{array}{c}{F}_{\alpha \alpha \alpha \beta }+3F_{\alpha \alpha }{F}_{\beta }+3F_{\alpha }{F}_{\alpha \beta }-F_{\alpha \theta }=0.\hfill \end{array}$(4.37)

In the following (G′/G) method is applied to solve Eq. 4.37. Considering the following traveling wave transform

$\begin{array}{c}F\left(\alpha ,\beta ,\theta \right)=h\left(\upsilon \right),\upsilon =k\alpha +l\beta +m\theta ,\hfill \end{array}$(4.38)

in which k, l, m are constants. Putting (4.38) into Eq. 4.37 yields

$\begin{array}{c}l{k}^3{h}_{\upsilon \upsilon \upsilon \upsilon }+6l{k}^2{h}_{\upsilon \upsilon }{h}_{\upsilon }-mk{h}_{\upsilon \upsilon }=0,\hfill \end{array}$(4.39)

then integrate once, we yield

$\begin{array}{c}{k}^3{h}_{\upsilon \upsilon \upsilon }+3l{k}^2{h}_{\upsilon \upsilon }-mk{h}_{\upsilon }=0.\hfill \end{array}$(4.40)

Assume that Eq. 4.40 has solutions of the following form

$\begin{array}{c}h\left(\upsilon \right)=\sum _{j=0}^p{\alpha }_j{\left(\frac{G^{\prime }}{G}\right)}^j,\hfill \end{array}$(4.41)

in which b_j (j = 0, … , p) are constants which can be derived later and $h\left(\upsilon \right)$ satisfies the equation

$\begin{array}{c}{G}^{″}+\lambda G^{\prime }+\mu G=0.\hfill \end{array}$(4.42)

Exploiting the principle of homogeneous balance, p = 1. Hence (4.41) can be rewritten as

$\begin{array}{c}h\left(\upsilon \right)={\alpha }_0+{\alpha }_1\left(\frac{G^{\prime }}{G}\right).\hfill \end{array}$(4.43)

Substituting (4.42) and Eq. 4.43 into Eq. 4.40 and putting the same power combination of (G′/G)^j. Then make these coefficients be zero, and a series of algebraic equations about k, l, m, α₁, α₂ can be yielded. By solving the above equations, we obtain

$\begin{array}{c}k=k,l=\frac{m}{k^2\left(\lambda -4\mu \right)},m=m,{\alpha }_0={\alpha }_0,{\alpha }_1={\alpha }_1,\hfill \end{array}$(4.44)

where k ≠ 0 and λ − 4μ ≠ 0. With these parameters, we can yield the following forms of solutions:

For λ² > 4μ,

$\begin{array}{c}u=\frac{k\sqrt{{\lambda }^2-4\mu }\left(c_1\sinh \kappa \right)+c_2\cosh \kappa }{c_1\cosh \kappa +c_2\sinh \kappa }-k\lambda +{\alpha }_0,\hfill \end{array}$(4.45)

where $\kappa =\left(\frac{1}{2}\left(kx+\frac{my}{k^2\left({\lambda }^2-4\mu \right)}+mz\right)\sqrt{{\lambda }^2-4\mu }\right)$ and c₁, c₂, α₀, k, λ, μ are constants.

For λ² < 4μ,

$\begin{array}{c}u=\frac{k\sqrt{-{\lambda }^2+4\mu }\left(c_1\sin \chi \right)+c_2\cos \chi }{c_1\cos \chi +c_2\sin \phi }-k\lambda +{\alpha }_0,\hfill \end{array}$(4.46)

where $\chi =\left(\frac{1}{2}\left(kx+\frac{my}{k^2\left({\lambda }^2-4\mu \right)}+mz\right)\sqrt{-{\lambda }^2+4\mu }\right)$ and c₁, c₂, α₀, k, λ, μ are constants.

4.5 Vector field v₂ + v₄ + v₅ + v₆

The characteristic equation can be composed as

$\begin{array}{c}\frac{dx}{1}=\frac{dy}{0}=\frac{dz}{1}=\frac{dt}{1}=\frac{du}{1}.\hfill \end{array}$(4.47)

Solving (4.47), we derived the similarity solution

$\begin{array}{c}u\left(x,y,z,t\right)=F\left(\alpha ,\beta ,\theta \right),\hfill \end{array}$(4.48)

in which α = x − t, β = y and θ = z − t are similarity variables. Taking (4.48) into Eq. 1.2, the (2 + 1)-dimensional equation can be yielded

$\begin{array}{c}{F}_{\alpha \alpha \alpha \beta }+3F_{\alpha \alpha }{F}_{\beta }+3F_{\alpha }{F}_{\alpha \beta }+F_{\alpha \beta }+F_{\beta \theta }-F_{\alpha \theta }=0.\hfill \end{array}$(4.49)

Next, applying the Riccati equation method, different forms of solutions of Eq. 4.49 can be deduced. Taking the following traveling wave transform

$\begin{array}{c}F\left(\alpha ,\beta ,\theta \right)=h\left(\upsilon \right),\upsilon =k\alpha +l\beta +m\theta ,\hfill \end{array}$(4.50)

where k, l, m are constants. Substituting (Eq. 4.50) into Eq. 4.49 and integrating once yields

$\begin{array}{c}l{k}^3{h}_{\upsilon \upsilon \upsilon }+3l{k}^2{h}_{\upsilon }^2+lk{h}_{\upsilon }+lm{h}_{\upsilon }-mk{h}_{\upsilon }=0.\hfill \end{array}$(4.51)

Suppose that Eq. 4.51 has solutions of the following form

$\begin{array}{c}h\left(\upsilon \right)=\sum _{j=0}^p{a}_j{\varphi }^j,\hfill \end{array}$(4.52)

where a_j (j = 1 p) are constants which can be obtained later and $h\left(\upsilon \right)$ satisfies the equation

$\begin{array}{c}{\varphi }^{\prime }={\varphi }^2+\omega ,\hfill \end{array}$(4.53)

in which ω is an constant. The form of the solutions of Eq. 4.53 are as follows

$\begin{array}{c}\varphi =\left\{\begin{array}{c}-\sqrt{\omega }\tanh \left(\sqrt{-\omega }\upsilon \right),\omega <0,\hfill \\ -\frac{1}{\upsilon },\omega =0,\hfill \\ \sqrt{\omega }\tan \left(\sqrt{\omega }\upsilon \right),\omega >0.\hfill \end{array}\right.\hfill \end{array}$(4.54)

By balancing Eq. 4.51, we get p = 1. Hence, (Eq. 4.52) can be rewritten as

$\begin{array}{c}h=a_0+a_1\varphi .\hfill \end{array}$(4.55)

Replacing (Eq. 4.53) along with Eq. 4.55 into Eq. 4.51, letting the same coefficients and a series of algebraic equations about a₀, a₁ and l can be yielded. Solving the above equations, we obtain

$\begin{array}{c}l=\frac{mk}{-4k^3\omega +m+k},k=k,m=m,a_0=a_0,a_1=-2k.\hfill \end{array}$(4.56)

On the basis of Eq. 4.56, we derive the solution of Eq. 1.2 as follows:

For ω < 0,

$\begin{array}{c}u=t+2k\sqrt{-\omega }\tanh \left(\sqrt{-\omega }\left(k\left(x-t\right)+\frac{mky}{-4k^3\omega +k+m}+m\left(z-t\right)\right)\right)+a_0,\hfill \end{array}$(4.57)

where k, m, a₀, ω, y, z are constants.

For ω > 0,

$\begin{array}{c}u=t-2k\sqrt{\omega }\tan \left(\left(k\left(x-t\right)+\frac{mky}{-4k^3\omega +k+m}+m\left(z-t\right)\right)\sqrt{\omega }\right)+a_0,\hfill \end{array}$(4.58)

where k, m, a₀, ω, y, z are constants.

4.6 Vector field v₂ + v₄

The characteristic equation can be composed as

$\begin{array}{c}\frac{dx}{0}=\frac{dy}{0}=\frac{dz}{1}=\frac{dt}{1}=\frac{du}{0}.\hfill \end{array}$(4.59)

Solving (Eq. 4.59), we derived the similarity solution

$\begin{array}{c}u\left(x,y,z,t\right)=F\left(\alpha ,\beta ,\theta \right),\hfill \end{array}$(4.60)

where α = x, β = y and θ = z − t are similarity variables. Taking (Eq. 4.60) into Eq. 1.2, the (2 + 1)-dimensional equation can be obtained by

$\begin{array}{c}{F}_{\alpha \alpha \alpha \beta }+3F_{\alpha \alpha }{F}_{\beta }+3F_{\alpha }{F}_{\alpha \beta }+F_{\beta \theta }-F_{\alpha \theta }=0.\hfill \end{array}$(4.61)

Taking the traveling wave transform

$\begin{array}{c}F\left(\alpha ,\beta ,\theta \right)=h\left(\upsilon \right),\upsilon =k\alpha +l\beta +m\theta ,\hfill \end{array}$(4.62)

where k, l and m are constants. Putting (Eq. 4.62) into Eq. 4.61 and integrate once, we derive

$\begin{array}{c}l{k}^3{h}_{\upsilon \upsilon \upsilon }+3l{k}^2{h_{\upsilon }}^2+lm{h}_{\upsilon }-mk{h}_{\upsilon }=0.\hfill \end{array}$(4.63)

Suppose the solution of Eq. 4.63 is given by

$\begin{array}{c}h\left(\upsilon \right)=\frac{\sum _{j=0}^{2p}{s}_j{e}^{i\upsilon }}{\sum _{j=0}^{2p}{r}_j{e}^{i\upsilon }},\hfill \end{array}$(4.64)

where s_j, r_j are constants to be obtained. By balancing Eq. 4.63, p = 1. Therefore, Eq. 4.64 is written as

$\begin{array}{c}h\left(\upsilon \right)=\frac{s_0+s_1{e}^{\upsilon }+s_2{e}^{2\upsilon }}{r_0+r_1{e}^{\upsilon }+r_2{e}^{2\upsilon }}.\hfill \end{array}$(4.65)

Replacing (Eq. 4.63) along with Eq. 4.65 and making the same coefficient be zero, a family of algebraic equations about s₀, s₁, s₂, r₀, r₁, r₂, k, l and m can be yielded. Solving the above equations, we obtain:

$\begin{array}{c}k=0,l=0,m=m,s_0=s_0,s_1=s_1,s_2=s_2,r_0=r_0,r_1=r_1,r_2=r_2.\hfill \end{array}$(4.66)

Then the solution of Eq. 1.2 is given by:

$\begin{array}{c}u=\frac{s_0}{r_0+r_1{e}^{\left(z-t\right)m}+r_2{e}^{{\left(\left(z-t\right)m\right)}^2}}+\frac{s_1{e}^{\left(z-t\right)m}}{r_0+r_1{e}^{\left(z-t\right)m}+r_2{e}^{{\left(\left(z-t\right)m\right)}^2}}+\frac{s_2{e}^{{\left(\left(z-t\right)m\right)}^2}}{r_0+r_1{e}^{\left(z-t\right)m}+r_2{e}^{{\left(\left(z-t\right)m\right)}^2}},\hfill \end{array}$(4.67)

where m, s₀, s₁, s₂, r₀, r₁ and r₂ are constants. Based on Eq. 4.67, replacing the parameter k = ik, l = il, m = im and picking the real part, the following periodic wave solution can be given

$\begin{array}{c}u=\frac{s_0}{r_0+r_1\cos \left(\left(z-t\right)m\right)+r_2\cos \left(2\left(z-t\right)m\right)}+\frac{s_1\cos \left(\left(z-t\right)m\right)}{r_0+r_1\cos \left(\left(z-t\right)m\right)+r_2\cos \left(2\left(z-t\right)m\right)}\hfill \\ +\frac{s_2\cos \left(2\left(z-t\right)m\right)}{r_0+r_1\cos \left(\left(z-t\right)m\right)+r_2\cos \left(2\left(z-t\right)m\right)}.\hfill \end{array}$(4.68)

5 Analysis and discussion

In this part, the geometric representation of the solution of Eq. 1.2 is discussed by employing graphical description. The physical phenomena of the solutions can be seen more obviously via numerical simulation. The solutions of the gSWl equation yielded from the above process include periodic, dark soliton, kink wave and annihilation structures of solutions. The dynamic structure of the solutions is investigated below.

Figure 1 depicts the physical structure of the singular solution when the parameter c₁ = 1, = 1, x = 1, y = 1. (B) Indicates the density plot of the corresponding solution.

FIGURE 1

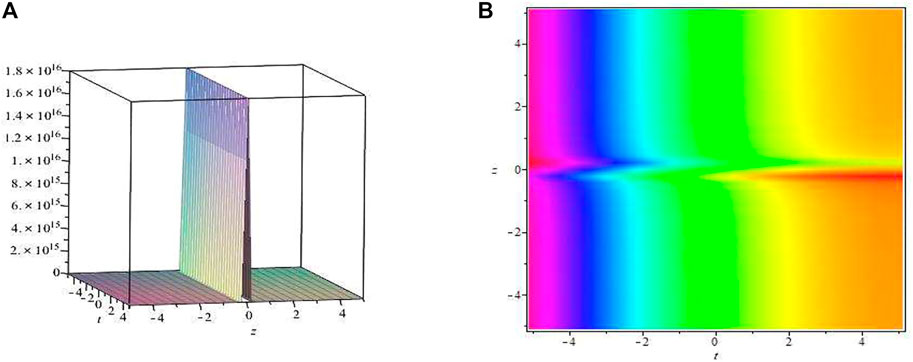
FIGURE 1. Singularity profile of (4.11).

Figure 2 describes the physical structure of the kink solution when t = 1, and the rest of the parameters take the value of y = 1, = 3, = 1, k = 1, l = 1, m = 1, = 1, = 1. When the time increases from t = 1 to t = 28, the energy of the wave is gradually depleted and eventually becomes a plane wave.

FIGURE 2

FIGURE 2. Annihilation of the kink wave solution of (4.34) at y =1.

The physical structure of the antisymmetric periodic solution (4.35) is shown in Figure 3. The 3-D plot of the antisymmetric periodic solution is described when the parameter is taken as z = 0, y = 0, = 1, = 1, k = 1, l = 1, m = 1, = 1, = −1. (B) show the density plot of the solution.

FIGURE 3

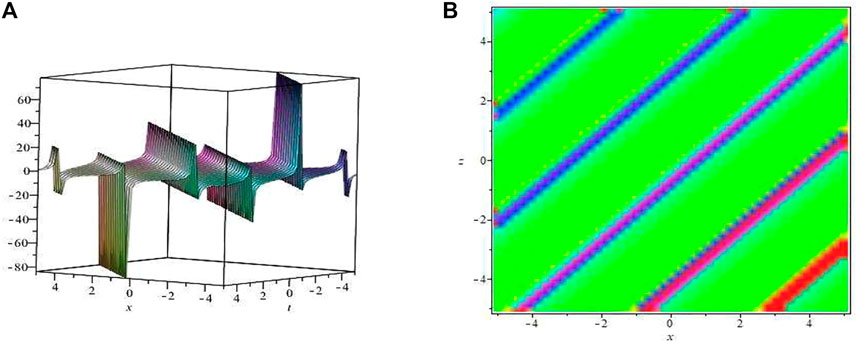
FIGURE 3. Multi period solution of (4.35).

The dynamics structure of the kink wave solution at z = 0 is plotted in Figure 4. When k = −10, c = 10, = 1, = −10, y = 1. (A) shows the 3-D plot of the solution and (B) depicts the spread route of the solution along the x-axis when t = 0, t = 1, t = 2 and t = 3, respectively.

FIGURE 4

FIGURE 4. The kink wave solution of (4.57) at z =0.

It is shown in Figure 5 and Figure 6 that the physical structure of the periodic wave solutions (4.58) and (4.68). (A) Is the corresponding 3D structure, (B) is the track of the solution along the x-axis, which is given when the parameterk = 1, = −1, = 1, r = 1, y = 0, z = 0 (4.68) shows the 3-D structure of the symmetric two-period wave solution, with the corresponding parameter a₀ = 1, = 1, = 1, = 5, = 1, = 1, m = 1. (B) Depicts the spread route of the solution along the z-axis at t = 0.

FIGURE 5

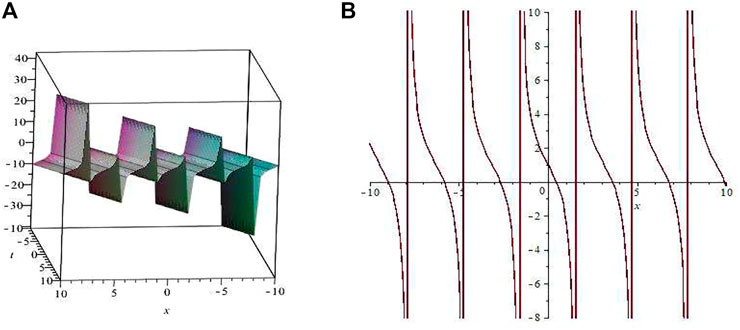
FIGURE 5. The periodic solution of (4.58) at z =0.

FIGURE 6

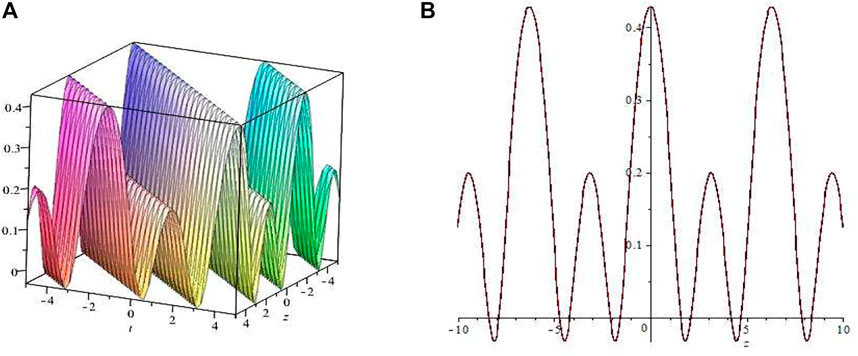
FIGURE 6. The symmetric two-periodic solution of (4.68).

A structure of the dynamics of the dark soliton (4.67) is depicted in Figure 7. The 3-D plot of the dark soliton is obtained when the parameter is selected as a₀ = 1, = 1, = 1, = 1, = 2, = 1, m = 1. The spread route behavior of the dark soliton along the z-axis can be derived by choosing t = 0, t = 1, t = 2 and t = 3.

FIGURE 7

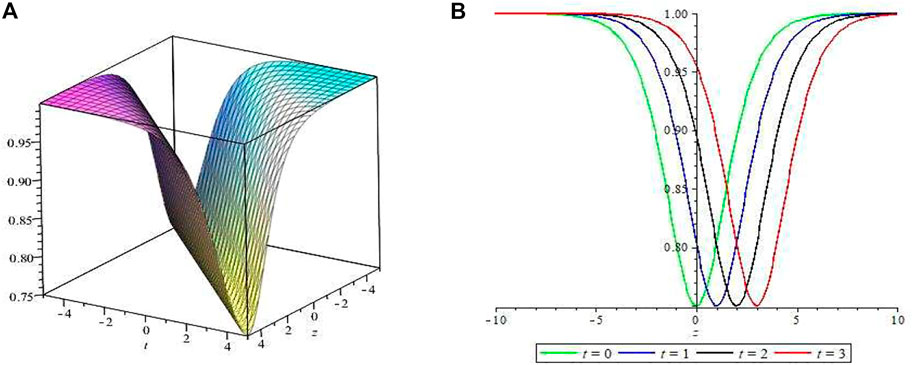
FIGURE 7. Dark soliton solution of (4.67).

6 Conclusion

In summary, the (3 + 1)-dimensional generalized Shallow Water-like wave equation is shown in this paper which is studied based on the Lie symmetry method and the symbolic calculation. By the adjoint table of the infinitesimal generators, a one-dimensional optimal system is formulated. In terms of the optimal system, some new solutions of the gSWl equation are derived by Exp$\left(-\varphi (\xi )\right)$ expansion method, Riccati equation method, Exp-function expansion method, and $\left(G^{\prime }/G\right)$ expansion method. In particular, the physical structures of the detected dark soliton, kink wave, and periodic solutions are investigated to make this study more credible.

In this work, a situation of the (3 + 1)-dimensional gSWl equation has been investigated based on the Lie symmetry method, and the rest of the latter cases are presented in other subsequent papers. More work needs to be done in the future. Firstly, in this paper, the exact solutions of the equation are derived richly with the Lie symmetry method, and other methods can be employed for the solutions of the equation, such as the numerical analysis method [36–38]. Secondly, the natural properties of the solutions to the equation can be investigated further in subsequent studies through the generalized multi-symplectic method and the structure-preserving method [39–42].

Data availability statement

The original contributions presented in the study are included in the article/Supplementary Material, further inquiries can be directed to the corresponding author.

Author contributions

BY: Conceptualization, Methodology, Investigation, Formal analysis, Writing–original draft. YS: Software, Formal analysis. ZW: Conceptualization, Funding acquisition, Resources, Supervision, Writing–review and editing.

Funding

This work was supported by Natural Science Foundation of Shandong Province (Grant ZR2021MA084), the Natural Science Foundation of Liaocheng University (318012025), and Discipline with Strong Characteristics of Liaocheng University—Intelligent Science and Technology (319462208).

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

1. Eslami M. Soliton-like solutions for the coupled Schrodinger-Boussinesq equation. Optik (2015) 126(23):3987–91. doi:10.1016/j.ijleo.2015.07.197

CrossRef Full Text | Google Scholar

2. Eslami M, Mirzazadeh MA, Neirameh A. New exact wave solutions for Hirota equation. Pramana (2015) 84(1):3–8. doi:10.1007/s12043-014-0837-z

CrossRef Full Text | Google Scholar

3. Gao XY, Guo YJ, Shan WR. Beholding the shallow water waves near an ocean beach or in a lake via a Boussinesq-Burgers system. Chaos, Solitons & Fractals (2021) 147:110875. doi:10.1016/j.chaos.2021.110875

CrossRef Full Text | Google Scholar

4. Lan ZZ, Gao YT, Yang JW, Su CQ, Solitons BQM. Solitons, Bäcklund transformation and Lax pair for a (2+1)-dimensional Broer-Kaup-Kupershmidt system in the shallow water of uniform depth. Commun Nonlinear Sci Numer Simulation (2017) 44:360–72. doi:10.1016/j.cnsns.2016.07.013

CrossRef Full Text | Google Scholar

5. Iqbal MA, Wang Y, Miah MM, Osman MS. Study on date-Jimbo-Kashiwara-Miwa equation with conformable derivative dependent on time parameter to find the exact dynamic wave solutions. Fractal and Fractional (2021) 6(1):4. doi:10.3390/fractalfract6010004

CrossRef Full Text | Google Scholar

6. Yokus A, Durur H, Ahmad H, Yao SW. Construction of different types analytic solutions for the Zhiber-Shabat equation. Mathematics (2020) 8(6):908. doi:10.3390/math8060908

CrossRef Full Text | Google Scholar

7. Chen SJ, Ma WX, Lü X. Bäcklund transformation, exact solutions and interaction behaviour of the (3+1)-dimensional Hirota-Satsuma-Ito-like equation. Commun Nonlinear Sci Numer Simulation (2020) 83:105135. doi:10.1016/j.cnsns.2019.105135

CrossRef Full Text | Google Scholar

8. Rady ASA, Osman ES, Khalfallah M. The homogeneous balance method and its application to the Benjamin-Bona-Mahoney (BBM) equation. Appl Math Comput (2010) 217(4):1385–90. doi:10.1016/j.amc.2009.05.027

CrossRef Full Text | Google Scholar

9. Bhutani G, Brito-Parada PR. Analytical solution for a three-dimensional non-homogeneous bivariate population balance equation-A special case. Int J Multiphase Flow (2017) 89:413–6. doi:10.1016/j.ijmultiphaseflow.2016.11.005

CrossRef Full Text | Google Scholar

10. Kumar S, Kumar D, Kumar A. Lie symmetry analysis for obtaining the abundant exact solutions, optimal system and dynamics of solitons for a higher-dimensional Fokas equation. Chaos, Solitons & Fractals (2021) 142:110507. doi:10.1016/j.chaos.2020.110507

CrossRef Full Text | Google Scholar

11. Ghanbari B, Kumar S, Niwas M, Baleanu D. The Lie symmetry analysis and exact Jacobi elliptic solutions for the Kawahara-KdV type equations. Results Phys (2021) 23:104006. doi:10.1016/j.rinp.2021.104006

CrossRef Full Text | Google Scholar

12. Benoudina N, Zhang Y Y, Khalique CM. Lie symmetry analysis, optimal system, new solitary wave solutions and conservation laws of the Pavlov equation. Commun Nonlinear Sci Numer Simulation (2021) 94:105560. doi:10.1016/j.cnsns.2020.105560

CrossRef Full Text | Google Scholar

13. Ma WX. Inverse scattering for nonlocal reverse-time nonlinear Schrddotodinger equations. Appl Math Lett (2020) 102:106161. doi:10.1016/j.aml.2019.106161

CrossRef Full Text | Google Scholar

14. Ali Akbar M, Ali NHM. The improved F-expansion method with Riccati equation and its applications in mathematical physics. Cogent Math (2017) 4(1):1282577. doi:10.1080/23311835.2017.1282577

CrossRef Full Text | Google Scholar

15. Akbulut A, Kaplan M, Tascan F. The investigation of exact solutions of nonlinear partial differential equations by using exp method. Optik (2017) 132:382–7. doi:10.1016/j.ijleo.2016.12.050

CrossRef Full Text | Google Scholar

16. Hafez MG. Exact solutions to the (3+1)-dimensional coupled Klein-Gordon-Zakharov equation using exp xi-expansion method. Alexandria Eng J (2016) 55(2):1635–45. doi:10.1016/j.aej.2016.02.010

CrossRef Full Text | Google Scholar

17. Li HM, Tian B, Xie XY, Chai J, Liu L, Gao YT. Soliton and rogue-wave solutions for a (2+1)-dimensional fourth-order nonlinear Schrodinger equation in a Heisenberg ferromagnetic spin chain. Nonlinear Dyn (2016) 86(1):369–80. doi:10.1007/s11071-016-2894-y

CrossRef Full Text | Google Scholar

18. Peng WQ, Tian SF, Wang XB, Zhang TT, Fang Y. Riemann-Hilbert method and multi-soliton solutions for three-component coupled nonlinear Schrodinger equations. J Geometry Phys (2019) 146:103508. doi:10.1016/j.geomphys.2019.103508

CrossRef Full Text | Google Scholar

19. Wang DS, Wang X. Long-time asymptotics and the bright N-soliton solutions of the Kundu–Eckhaus equation via the Riemann–Hilbert approach. Nonlinear Anal Real World Appl (2018) 41:334–61. doi:10.1016/j.nonrwa.2017.10.014

CrossRef Full Text | Google Scholar

20. Huang QM, Gao YT, Jia SL, DengBilinear GF. Bilinear Bäcklund transformation, soliton and periodic wave solutions for a $$\varvec{(3 + 1)}$$ (3 + 1) -dimensional variable-coefficient generalized shallow water wave equation. Nonlinear Dyn (2017) 87(4):2529–40. doi:10.1007/s11071-016-3209-z

CrossRef Full Text | Google Scholar

21. Huang QM, Gao YT. Bilinear form, bilinear Bäcklund transformation and dynamic features of the soliton solutions for a variable-coefficient (3+1)-dimensional generalized shallow water wave equation. Mod Phys Lett B (2017) 31(22):1750126. doi:10.1142/s0217984917501263

CrossRef Full Text | Google Scholar

22. Kumar D, Kumar S. Some new periodic solitary wave solutions of (3+1)-dimensional generalized shallow water wave equation by Lie symmetry approach. Comput Math Appl (2019) 78(3):857–77. doi:10.1016/j.camwa.2019.03.007

CrossRef Full Text | Google Scholar

23. Li YZ, Liu JG. Multiple periodic-soliton solutions of the (3+1)-dimensional generalised shallow water equation. Pramana (2018) 90(6):1–11.

CrossRef Full Text | Google Scholar

24. Liu JG, He Y. New periodic solitary wave solutions for the (3+1)-dimensional generalized shallow water equation. Nonlinear Dyn (2017) 90(1):363–9. doi:10.1007/s11071-017-3667-y

CrossRef Full Text | Google Scholar

25. Liu JG, Zhu WH. Breather wave solutions for the generalized shallow water wave equation with variable coefficients in the atmosphere, rivers, lakes and oceans. Comput Math Appl (2019) 78(3):848–56. doi:10.1016/j.camwa.2019.03.008

CrossRef Full Text | Google Scholar

26. Tang YN, Ma WX, Xu W. Grammian and Pfaffian solutions as well as Pfaffianization for a (3+1)-dimensional generalized shallow water equation. Chin Phys B (2012) 21(7):070212. doi:10.1088/1674-1056/21/7/070212

CrossRef Full Text | Google Scholar

27. Kumar D, Raju I, Paul GC, Ali ME, Haque MD. Characteristics of lump-kink and their fission-fusion interactions, rogue, and breather wave solutions for a (3+1)-dimensional generalized shallow water equation. Int J Comp Math (2022) 99(4):714–36. doi:10.1080/00207160.2021.1929940

CrossRef Full Text | Google Scholar

28. Sadat R, Kassem M, Ma WX. Abundant lump-type solutions and interaction solutions for a nonlinear (3+1)-dimensional model. Adv Math Phys (2018) 2018:1–8. doi:10.1155/2018/9178480

CrossRef Full Text | Google Scholar

29. Zhang Y, Dong H, Zhang X, Yang H. Rational solutions and lump solutions to the generalized (3+1)-dimensional Shallow Water-like equation. Comput Math Appl (2017) 73(2):246–52. doi:10.1016/j.camwa.2016.11.009

CrossRef Full Text | Google Scholar

30. Olver PJ. Applications of Lie groups to differential equations. Springer Science & Business Media (1993).

Google Scholar

31. Ovsjannikov LV. Group properties of differential equations. Novosibirsk: Siberian Section of the Academy of Science of USSR (1962).

Google Scholar

32. Wang GW. Symmetry analysis, analytical solutions and conservation laws of a generalized KdV-Burgers-Kuramoto equation and its fractional version. Fractals (2021) 29(04):2150101. doi:10.1142/s0218348x21501012

CrossRef Full Text | Google Scholar

33. Wang GW. A new (3+1)-dimensional schrödinger equation: Derivation, soliton solutions and conservation laws. Nonlinear Dyn (2021) 104(2):1595–602. doi:10.1007/s11071-021-06359-6

CrossRef Full Text | Google Scholar

34. Wang GW. A novel (3+1)-dimensional sine-gorden and a sinh-gorden equation: Derivation, symmetries and conservation laws. Appl Math Lett (2021) 113:106768. doi:10.1016/j.aml.2020.106768

CrossRef Full Text | Google Scholar

35. Hu X, Li Y, Chen Y. A direct algorithm of one-dimensional optimal system for the group invariant solutions. J Math Phys (2015) 56(5):053504. doi:10.1063/1.4921229

CrossRef Full Text | Google Scholar

36. Hu WP, Deng ZC, Han S, Zhang WR. Generalized multi-symplectic integrators for a class of Hamiltonian nonlinear wave PDEs. J Comput Phys (2013) 235:394–406. doi:10.1016/j.jcp.2012.10.032

CrossRef Full Text | Google Scholar

37. Hu WP, Wang Z, Zhao YP, Deng ZC. Symmetry breaking of infinite-dimensional dynamic system. Appl Math Lett (2020) 103:106207. doi:10.1016/j.aml.2019.106207

CrossRef Full Text | Google Scholar

38. Hu WP, Ye J, Deng ZC. Internal resonance of a flexible beam in a spatial tethered system. J Sound Vibration (2020) 475:115286. doi:10.1016/j.jsv.2020.115286

CrossRef Full Text | Google Scholar

39. Hu WP, Zhang CZ, Deng ZC. Vibration and elastic wave propagation in spatial flexible damping panel attached to four special springs. Commun Nonlinear Sci Numer Simulation (2020) 84:105199. doi:10.1016/j.cnsns.2020.105199

CrossRef Full Text | Google Scholar

40. Hu WP, Huai YL, Xu MB, Feng XQ, Jiang RS, Zheng YP, et al. Mechanoelectrical flexible hub-beam model of ionic-type solvent-free nanofluids. Mech Syst Signal Process (2021) 159:107833. doi:10.1016/j.ymssp.2021.107833

CrossRef Full Text | Google Scholar

41. Hu WP, Huai YL, Xu MB, Deng ZC. Coupling dynamic characteristics of simplified model for tethered satellite system. Acta Mechanica Sinica (2021) 37(8):1245–54. doi:10.1007/s10409-021-01108-9

CrossRef Full Text | Google Scholar

42. Hu WP, Xu MB, Zhang F, Xiao C, Deng ZC. Dynamic analysis on flexible hub-beam with step-variable cross-section. Mech Syst Signal Process (2022) 180:109423. doi:10.1016/j.ymssp.2022.109423

CrossRef Full Text | Google Scholar