Optical solitons in birefringent fibers with the generalized coupled space–time fractional non-linear Schrödinger equations

The nonlinear Schrödinger (NLS) equation is an ideal model for describing optical soliton transmission. This paper first introduces an integer-order generalized coupled NLS equation describing optical solitons in birefringence fibers. Secondly, the semi-inverse and fractional variational method is used to extend the integer-order model to the space–time fractional order. Moreover, various nonlinear forms of fractional NLS equations are discussed, including the Kerr, power, parabolic, dual-power, and log law. The exact soliton solutions, such as bright, dark, and singular solitons, are given. Finally, the behavior of the solution is shown by three-dimensional figures with different fractional orders, which reveals the propagation characteristics of optical solitons in birefringence fibers described by the generalized coupled space–time fractional NLS equation.

1 Introduction

With the great progress of the information technology and the increase in market demand, especially with the outbreak of COVID-19 in recent years, modern society relies more and more on communication, forcing optical fiber communication to develop to high-speed and large capacity. Optical fiber communication has become the main transmission mode of communication network due to its high transmission capacity, low loss, and wide frequency band. Optical soliton is the most ideal information carriers in fiber optic communications. From the perspective of physics, optical solitons can keep the waveform and speed of optical fiber transmission unchanged, which is a special product of non-linear effects in optics. It is considered one of the most promising transmission modes in the next generation [1]. From the perspective of mathematics, optical solitons are integrable solutions of some non-linear partial differential equations. Studying the exact solution of these mathematical models has become a great significant frontier in this field [2, 3].

In the field of optical fiber communication, NLS-type equations have attracted great attention from researchers [4–6]. In the 1850s and 1860s, the NLS equation was introduced to study the two-dimensional self-focusing phenomenon of strong beams in weakly interacting non-ideal Bose gases and non-linear media. As a general equation to reveal the propagation of wave packets in weakly non-linear medium, the NLS equation is of great significance to the study of non-linear physics. With further research, the NLS equation has been extended to the equations of the variable coefficient, complex coefficient, multi-dimensional, higher order, non-local, and fractional order, which contain various physical effects [7, 8]. The standard NLS equation contains a second-order dispersion term and a third-order non-linear term [9–11], in the form of

$i{u}_t+p{u}_{xx}+q|u{|}^{2}u=0.$

The aforementioned equation describes the picosecond pulse propagation in a single-mode fiber without ignoring the optical loss. Here, u = u(x, t) represents the complex function of the real variables x and t. Both p and q are non-zero real numbers, representing the group velocity dispersion coefficient and self-phase modulation coefficient, respectively. The subscripts represent the corresponding partial derivatives.

Introducing birefringence, a natural phenomenon in fiber optics, into fiber optics will contribute to improve the research and development of high-birefringence fibers. The Kerr, power, parabola, and dual-power non-linearity laws are considered to study solitons in birefringent fibers. These criteria for the existence of solitons are also regarded as constraints [12, 13]. In birefringent fibers, the basic theoretical model of optical pulse transmission is coupled NLS equations [14, 15]. The classical coupled NLS equations have the following form:

$\begin{array}{cc}\hfill & i{u}_{1t}+\frac{1}{2}{u}_{1xx}+\left(|u_1{|}^2+|u_2{|}^2\right)u_1=0,\hfill \\ \hfill & i{u}_{2t}+\frac{1}{2}{u}_{2xx}+\left(|u_1{|}^2+|u_2{|}^2\right)u_2=0,\hfill \end{array}$

where u₁ and u₂ represent the slow-varying amplitude of two interacting fiber modes; the coupled NLS equations include not only self-similar modulation |u₁|²u₁ and |u₂|²u₂ but also cross-phase modulation |u₁|²u₂ and |u₂|²u₁.

Fractional calculus plays an important role in physics and engineering. Fractional derivatives have been successfully used to describe fractal problems in engineering, such as the heat transfer in fractal medium [16], fractal hydrodynamic equations [17], fractal electrostatics [18], fractal Fokker–Planck equations [19], fractal description of stress, and strain in elasticity [20] [21–23].

In 2000, Laskin first proposed fractional quantum mechanics [24], which replaced the traditional NLS equation with a fractional NLS equation of the generalized second-order partial differential equation with a fractional order. The fractional NLS equation has attracted extensive attention in the field of physics [25, 26]. It has important implications for theoretical research in the field of fraction and fractional spin particle dynamics [27]. The theory of fractional NLS equations is difficult to advance due to the influence of its inherent non-local operators and the connection between fractional derivatives. Until 2015, Longhi considered the similarity between the Schrodinger equation and the paraxial wave equation. Then, the fractional NLS equation is introduced into optics, and the quantum harmonic oscillator is simulated by optical methods [28]. The field of optics provides a wealth of possibilities for the realization of the fractional NLS equation theory and the study of fractional transmission dynamics of light beams [29–31].

This paper is organized as follows: in Section 2, the generalized coupled spatiotemporal fractional NLS equations are derived using the semi-inverse and Agrawal’s method [32, 33]. Kerr, power, parabolic, dual-power, and log laws of this equations are discussed, and bright, dark, and singular solitons are obtained by changing the amplitude components of the function [34–37]; in Section 3, the behaviors of the obtained solutions are shown by three-dimensional graphics with four different fractional orders; and in Section 4, we elaborate the conclusion of this paper.

2 Formulation of coupled fractional NLS equations

In this section, with a fractional derivative theory, we derive the two-dimensional coupled fractional NLS equations in the fractal domain by the Euler–Lagrange equation, and semi-inverse and Agrawal’s variation methods. The generalized coupled NLS equations under the rigid-lid assumption are

$\begin{array}{ccc}\hfill i{u}_t& +a_1{u}_{xx}+b_1{u}_{xt}+F\left(c_1|u{|}^2+d_1|v{|}^2\right)u\hfill & \hfill +i\left\{{\lambda }_1|u{|}^2{u}_x+{\theta }_1{u}_{\mathit{xxx}}\right\}=0,\\ \hfill i{v}_t& +a_2{v}_{xx}+b_2{v}_{xt}+F\left(d_2|u{|}^2+c_2|v{|}^2\right)v\hfill & \hfill +i\left\{{\lambda }_2|v{|}^2{v}_x+{\theta }_2{v}_{\mathit{xxx}}\right\}=0,\end{array}(1)$

where u(x, t) and v(x, t) are complex valued functions that denote the soliton profiles for the two components in birefringent fibers, F is a non-linear function, a_l(l = 1, 2) denotes the group velocity dispersion coefficients, b_l(l = 1, 2) denotes the space–time dispersion terms, and c_l and d_l(l = 1, 2) denote the self-phase and cross-phase modulation terms, respectively. In the perturbation terms, λ_l(l = 1, 2) denotes non-linear dispersion and θ_l(l = 1, 2) represents the third-order dispersion which should be considered when the situation of the group velocity dispersion is small.

The coupled space–time fractional NLS equations can be represented by the following equations. We assume the potential function u(x, t) = f(x, t) + ig(x, t) and v(x, t) = p(x, t) + iq(x, t) accordingly that Eq. 1 has the following form:

$\begin{array}{cc}\hfill & i\left[f_t+i{g}_t\right]+a_1\left[f_{xx}+i{g}_{xx}\right]+b_1\left[f_{xt}+i{g}_{xt}\right]+F\left[f+ig\right]\hfill \\ \hfill & +i\left\{{\lambda }_1|u{|}^2\left[f_x+i{g}_x\right]+{\theta }_1\left[f_{\mathit{xxx}}+i{g}_{\mathit{xxx}}\right]\right\}=0,\hfill \\ \hfill & i\left[p_t+i{q}_t\right]+a_2\left[p_{xx}+i{q}_{xx}\right]+b_2\left[p_{xt}+i{q}_{xt}\right]+F\left[p+iq\right]\hfill \\ \hfill & +i\left\{{\lambda }_2|v{|}^2\left[p_x+i{q}_x\right]+{\theta }_2\left[p_{\mathit{xxx}}+i{q}_{\mathit{xxx}}\right]\right\}=0,\hfill \end{array}(2)$

where the subscripts represent the partial differential function with parameters.

The function of the potential Eq. 2 can be expressed as

$\begin{array}{cc}\hfill J\left(f,g,p,q\right)=& {\int }_{R}dx{\int }_{T}dt\left\{f\left[c_1{g}_t-c_2{a}_1{f}_{xx}-c_3{b}_1{f}_{xt}-c_{4}Ff+c_5{\lambda }_1|u{|}^2{g}_x+c_6{\theta }_1{g}_{\mathit{xxx}}\right]+\right.\hfill \\ \hfill & g\left[d_1{f}_t+d_2{a}_1{g}_{xx}+d_3{b}_1{g}_{xt}+d_{4}Fg+d_5{\lambda }_1|u{|}^2{f}_x+d_6{\theta }_1{f}_{\mathit{xxx}}\right]+\hfill \\ \hfill & p\left[m_1{q}_t-m_2{a}_2{q}_{xx}-m_3{b}_2{p}_{xt}-m_{4}Fp+m_5{\lambda }_2|v{|}^2{q}_x+m_6{\theta }_2{q}_{\mathit{xxx}}\right]+\hfill \\ \hfill & \left.q\left[n_1{p}_t+n_2{a}_2{q}_{xx}+n_3{b}_2{q}_{xt}+n_{4}Fq+n_5{\lambda }_2|v{|}^2{p}_x+n_6{\theta }_2{p}_{\mathit{xxx}}\right]\right\}.\hfill \end{array}(3)$

The coefficients c_i, d_i, m_i, and n_i (i = 1, 2, …, 6) are Lagrange multipliers. The integral shown in Eq. 3 can be calculated by f_x|_R = f_x|_T = 0, g_x|_R = g_x|_T = 0, p_x|_R = p_x|_T = 0, and q_x|_R = q_x|_T = 0, respectively. |u|² and |v|² and the function F is treated as a fixed function.

On the basis of the function conversion, we get the following relationship by using variational optimization conditions and δJ(f, g, p, q) = 0 for piecewise integration:

$\begin{array}{cc}\hfill & \left[2c_1{g}_t-2c_2{a}_1{f}_{xx}-2c_3{b}_1{f}_{xt}-2c_{4}Ff+2c_5{\lambda }_1|u{|}^2{g}_x+2c_6{\theta }_1{g}_{\mathit{xxx}}\right]+\left[2d_1{f}_t+2d_2{a}_1{g}_{xx}\right.\hfill \\ \hfill & +\left.2d_3{b}_1{g}_{xt}+2d_{4}Fg+2d_5{\lambda }_1|u{|}^2{f}_x+2d_6{\theta }_1{f}_{\mathit{xxx}}\right]+\left[2m_1{q}_t-2m_2{a}_2{p}_{xx}-2m_3{b}_2{p}_{xt}\right.\hfill \\ \hfill & -2m_{4}Fp\left.+2m_5{\lambda }_2|v{|}^2{q}_x+2m_6{\theta }_2{q}_{\mathit{xxx}}\right]+\left[2n_1{q}_t+2n_2{a}_2{q}_{xx}+2n_3{b}_2{q}_{xt}+2n_{4}Fq+2n_5{\lambda }_2|v{|}^2{p}_x\right.\hfill \\ \hfill & +\left.2n_6{\theta }_2{p}_{\mathit{xxx}}\right]=0.\hfill \end{array}(4)$

Compared with Eq. 3, in the aforementioned Eq. 4, we get $c_i=d_i=m_i=n_i=\frac{1}{2}(i=1,\dots ,6)$. We substitute the c_i, d_i, m_i, and n_i into Eq. 3. The Lagrangian form of the NLS equations is

$\begin{array}{cc}\hfill & L\left(f,f_x,f_t,f_{xx},g,g_x,g_t,g_{xx},p,p_x,p_t,p_{xx},q,q_x,q_t,q_{xx}\right)=\left[-\frac{1}{2}{f}_{t}g+\frac{1}{2}{a}_1{f}_x^2+\frac{1}{2}{b}_1{f}_t{f}_x-\frac{1}{2}F{f}^2\right.\hfill \\ \hfill & \left.-\frac{1}{2}{\lambda }_1|u{|}^2{f}_{x}g-\frac{1}{2}{\theta }_1{f}_x{g}_{xx}\right]+\left[\frac{1}{2}{g}_{t}f-\frac{1}{2}{a}_1{g}_x^2-\frac{1}{2}{b}_1{g}_t{g}_x+\frac{1}{2}F{g}^2-\frac{1}{2}{\lambda }_1|u{|}^2{g}_{x}f-\frac{1}{2}{\theta }_1{g}_x{f}_{xx}\right]+\hfill \\ \hfill & \left[-\frac{1}{2}{p}_{t}q+\frac{1}{2}{a}_2{p}_x^2+\frac{1}{2}{b}_2{p}_t{p}_x-\frac{1}{2}F{p}^2+\left[\frac{1}{2}{q}_{t}p-\frac{1}{2}{\lambda }_2|v{|}^2{p}_{x}q-\frac{1}{2}{\theta }_2{p}_x{q}_{xx}\right]-\frac{1}{2}{a}_2{q}_x^2-\frac{1}{2}{b}_2{q}_t{q}_x+\right.\left.\frac{1}{2}F{q}^2-\frac{1}{2}{\lambda }_2|v{|}^2{q}_{x}p-\frac{1}{2}{\theta }_2{q}_x{p}_{xx}\right].\hfill \end{array}(5)$

Similarly, the Lagrangian form of the coupled space–time fractional NLS equations can be converted as

$\begin{array}{cc}\hfill F=& \left[-\frac{1}{2}g{D}_t^{\alpha }f+\frac{1}{2}{a}_1{\left(D_x^{\beta }f\right)}^2+\frac{1}{2}{b}_1{D}_t^{\alpha }f{D}_x^{\beta }f-\frac{1}{2}F{f}^2-\frac{1}{2}{\lambda }_1|u{|}^{2}g{D}_x^{\beta }f-\frac{1}{2}{\theta }_1{D}_x^{\beta }f{D}_x^{2\beta }\right]+\hfill \\ \hfill & \left[\frac{1}{2}f{D}_t^{\alpha }g-\frac{1}{2}{a}_1{\left(D_x^{\beta }g\right)}^2-\frac{1}{2}{b}_1{D}_t^{\alpha }g{D}_x^{\beta }g+\frac{1}{2}F{g}^2-\frac{1}{2}{\lambda }_1|u{|}^{2}f{D}_x^{\beta }g-\frac{1}{2}{\theta }_1{D}_x^{\beta }g{D}_x^{2\beta }f\right]+\hfill \\ \hfill & \left[\frac{1}{2}{a}_2{\left(D_x^{\beta }p\right)}^2-\frac{1}{2}q{D}_t^{\alpha }p-\frac{1}{2}{\lambda }_2|v{|}^{2}q{D}_x^{\beta }p-\frac{1}{2}{\theta }_2{D}_x^{\beta }p{D}_x^{2\beta }q+\frac{1}{2}{b}_2{D}_t^{\alpha }p{D}_x^{\beta }p-\frac{1}{2}F{p}^2\right]+\hfill \\ \hfill & \left[\frac{1}{2}p{D}_t^{\alpha }q-\frac{1}{2}{a}_2{\left(D_x^{\beta }q\right)}^2+\frac{1}{2}F{q}^2-\frac{1}{2}{b}_2{D}_t^{\alpha }q{D}_x^{\beta }q-\frac{1}{2}{\lambda }_2|v{|}^{2}p{D}_x^{\beta }q-\frac{1}{2}{\theta }_2{D}_x^{\beta }q{D}_x^{2\beta }p\right],\hfill \end{array}(6)$

where $D_x^{2\beta }f=D_x^{\beta }[D_x^{\beta }f]$ and $D_x^{\beta }f(x)$ represent the mRL fractional derivative [39].

$\begin{array}{cc}\hfill D_x^{\beta }f\left(x\right)=\frac{1}{\mathrm{\Gamma }\left(1-\beta \right)}& \frac{d}{dx}\left\{{\int }_a^{x}d\zeta \frac{\left[f\left(\zeta \right)-f\left(a\right)\right]}{{\left(x-\zeta \right)}^{\beta }}\right\},\hfill \\ \hfill & 0\le \beta <1.\hfill \end{array}(7)$

Here, Γ(x) is the standard Euler’s gamma function.

The functional form of the coupled fractional NLS equations is

$\begin{array}{cc}\hfill J\left(A,B,M,N\right)=& {\int }_R{\left(dx\right)}^{\beta }{\int }_T{\left(dt\right)}^{\alpha }F\left(A,D_x^{\beta }A,D_t^{\alpha }A,D_x^{2\beta }A,B,D_x^{\beta }B,D_t^{\alpha }B,D_x^{2\beta }B,M,D_x^{\beta }M,\right.\hfill \\ \hfill & \left.D_t^{\alpha }M,D_x^{2\beta }M,N,D_x^{\beta }N,D_t^{\alpha }N,D_x^{2\beta }N\right),\hfill \end{array}(8)$

in which

${\int }_a^t{\left(d\tau \right)}^{\gamma }f\left(\tau \right)=\gamma {\int }_a^{t}d\tau {\left(t-\tau \right)}^{\gamma }f\left(\tau \right).(9)$

The relationship can be obtained by integration by parts [40].

$\begin{array}{cc}\hfill {\int }_a^b{\left(d\tau \right)}^{\gamma }f\left(x\right)D_x^{\gamma }g\left(x\right)=\mathrm{\Gamma }\left(1+\gamma \right)& \left[g\left(x\right)f\left(x\right){|}_a^b-{\int }_a^b{\left(dx\right)}^{\gamma }g\left(x\right)D_x^{\gamma }f\left(x\right)\right],\hfill \\ \hfill & f\left(x\right),g\left(x\right)\in \left[a,b\right].\hfill \end{array}(10)$

With δJ(A, B, M, N) = 0, we obtain the Euler–Lagrangian equations of coupled NLS equations in the form

$\begin{array}{cc}\hfill & \left(\frac{\partial F}{\partial A}\right)A+\left(\frac{\partial F}{\partial D_x^{\beta }A}\right)D_x^{\beta }A+\left(\frac{\partial F}{\partial D_t^{\alpha }A}\right)D_t^{\alpha }A+\left(\frac{\partial F}{\partial D_x^{2\beta }A}\right)D_x^{2\beta }A+\left(\frac{\partial F}{\partial D_x^{\beta }B}\right)D_x^{\beta }B+\hfill \\ \hfill & \left(\frac{\partial F}{\partial D_t^{\alpha }B}\right)D_t^{\alpha }B+\left(\frac{\partial F}{\partial D_x^{2\beta }B}\right)D_x^{2\beta }B+\left(\frac{\partial F}{\partial B}\right)B+\left(\frac{\partial F}{\partial M}\right)M+\left(\frac{\partial F}{\partial D_x^{\beta }M}\right)D_x^{\beta }M+\hfill \\ \hfill & \left(\frac{\partial F}{\partial N}\right)+\left(\frac{\partial F}{\partial D_t^{\alpha }M}\right)D_t^{\alpha }M+\left(\frac{\partial F}{\partial D_x^{2\beta }M}\right)D_x^{2\beta }M+\left(\frac{\partial F}{\partial D_x^{\beta }N}\right)D_x^{\beta }N+\hfill \\ \hfill & \left(\frac{\partial F}{\partial D_t^{\alpha }N}\right)D_t^{\alpha }N+\left(\frac{\partial F}{\partial D_x^{2\beta }N}\right)D_x^{2\beta }N=0.\hfill \end{array}(11)$

Substituting the Lagrange form of the NLS equations (Eq. 6) into the Euler–Lagrange formula (Eq. 11) and defining u(x, t) = A(x, t) + iB(x, t) and v(x, t) = M(x, t) + iN(x, t) according to the definition of the fractional potential function yields

$\begin{array}{cc}\hfill & i{D}_t^{\alpha }u+a_1{D}_x^{2\beta }u+b_1{D}_x^{\beta }{D}_t^{\alpha }u+F\left(c_1|u{|}^2+d_1|v{|}^2\right)u+i\left\{{\lambda }_1|u{|}^2{D}_x^{\beta }u+{\theta }_1{D}_x^{3\beta }u\right\}=0,\hfill \\ \hfill & i{D}_t^{\alpha }v+a_2{D}_x^{2\beta }v+b_2{D}_x^{\beta }{D}_t^{\alpha }v+F\left(d_2|u{|}^2+c_2|v{|}^2\right)v+i\left\{{\lambda }_2|v{|}^2{D}_x^{\beta }v+{\theta }_2{D}_x^{3\beta }v\right\}=0,\hfill \end{array}(12)$

where α and β are fractal dimensions and u(x, t) and v(x, t) denote the fractal wave functions for space x and time t. Equation 12 is the generalized coupled space–time fractional NLS equations.

3 Mathematical analysis

We obtain the soliton solution of the equation by using the solitary wave ansatz to perform the integration of the coupled fractional NLS equations (Eq. 12) in this section. It is considered that the four types of non-linear conditions of the equation are the Kerr, power, parabolic, dual-power, and log power non-linearity laws.

Introducing the fractional transforms yields

$T=\frac{m_1{t}^{\alpha }}{\mathrm{\Gamma }\left(1+\alpha \right)},X=\frac{m_2{x}^{\beta }}{\mathrm{\Gamma }\left(1+\beta \right)},(13)$

where m₁ and m₂ are constants. With the aforementioned conversions, the fractional derivatives are transformed into the classic derivatives [41] as

$\frac{{\partial }^{\alpha }u}{\partial t^{\alpha }}=m_1\frac{\partial u}{\partial T},\frac{{\partial }^{\beta }u}{\partial x^{\beta }}=m_2\frac{\partial u}{\partial X}.(14)$

According to Eqs 12–14, it becomes

$\begin{array}{cc}\hfill & i{u}_T+a_1{u}_{XX}+b_1{u}_{XT}+F\left(c_1|u{|}^2+d_1|v{|}^2\right)u+i\left\{{\lambda }_1|u{|}^2{u}_X+{\theta }_1{u}_{\mathit{XXX}}\right\}=0,\hfill \\ \hfill & i{v}_T+a_2{v}_{XX}+b_2{v}_{XT}+F\left(d_2|u{|}^2+c_2|v{|}^2\right)v+i\left\{{\lambda }_2|v{|}^2{v}_X+{\theta }_2{v}_{\mathit{XXX}}\right\}=0.\hfill \end{array}(15)$

3.1 Kerr law

The Kerr law non-linearity is also called cubic non-linear. This non-linearity occurs when the light wave in the fiber is subjected to a non-linear response. According to the Kerr law non-linearity F(s) = s, Eq. 15 describes the propagation of dispersive solitons and can be rewritten as

$\begin{array}{cc}\hfill & i{u}_T+a_1{u}_{XX}+b_1{u}_{XT}+\left(c_1|u{|}^2+d_1|v{|}^2\right)u+i\left\{{\lambda }_1|u{|}^2{u}_X+{\theta }_1{u}_{\mathit{XXX}}\right\}=0,\hfill \\ \hfill & i{v}_T+a_2{v}_{XX}+b_2{v}_{XT}+\left(d_2|u{|}^2+c_2|v{|}^2\right)v+i\left\{{\lambda }_2|v{|}^2{v}_X+{\theta }_2{v}_{\mathit{XXX}}\right\}=0.\hfill \end{array}(16)$

We obtain the exact bright, dark, and singular 1-soliton solutions of the coupling equations by the ansatz method, respectively. To set the starting point, we write the solitons as the phase-amplitude form, similar to [38].

$\begin{array}{cc}\hfill & u\left(X,T\right)=P_1\left(X,T\right)e^{i\varphi \left(X,T\right)},\hfill \\ \hfill & v\left(X,T\right)=P_2\left(X,T\right)e^{i\varphi \left(X,T\right)},\hfill \end{array}(17)$

where P_l(X, T)(l = 1, 2) denotes the amplitude components of the soliton solution. The phase component ϕ(X, T) is

$\varphi \left(X,T\right)=-\kappa X+\omega T+\sigma ,(18)$

where κ represents the frequency, and ω and σ denote the wave number and phase constant, respectively. Substituting Eq. 17 into Eq. 16 and decomposing this equation into real and imaginary parts yield

$\left(\omega +a_l{k}^2-b_l\kappa \omega +{\theta }_l{k}^3\right)P_l-d_l{P}_l{P}_{\bar{l}}^2-\left(\lambda \kappa +c_l\right)P_l^3-\left(a_l+3{\theta }_l\kappa \right)P_{\mathit{lXX}}-b_l{P}_{\mathit{lXT}}=0(19)$

and

$\left(1-b_l\kappa \right)P_{lT}-\left(2a_l\kappa -b_l\omega +3{\theta }_l{\kappa }^2\right)P_{lx}+{\lambda }_l{P}_l^2{P}_{lX}+{\theta }_l{P}_{\mathit{lXXX}}=0,(20)$

respectively, with l = 1, 2 and $\bar{l}=3-l$, and the profile function P_l(X, T) is converted to f(X − vT). According to Eq. 20, the soliton velocity v is calculated as

$v=\frac{b_l\omega -2a_l\kappa }{1-b_l\kappa },(21)$

provided

${\theta }_l={\lambda }_l=0.(22)$

It is important to note a special situation where θ_l = λ_l = 0. One study on recovering from a non-dispersive situation was reported in 2014 [22].

The coefficients of the linear components in Eq. 16 can be calculated by comparing the two result values of the soliton velocities as follows:

$a_1=a_2,b_1=b_2.(23)$

Eq. 21 becomes

$v=\frac{b\omega -2a\kappa }{1-b\kappa }.(24)$

Without considering the non-linearity, Eqs 19, 20 take the following new form as

$\left(\omega +a{k}^2-b\kappa \omega \right)P_l-d_l{P}_l{P}_{\bar{l}}^2-c_l{P}_l^3-a{P}_{\mathit{lXX}}-b{P}_{\mathit{lXT}}=0(25)$

and

$\left(1-b\kappa \right)P_{lT}-\left(2a\kappa -b\omega \right)P_{lX}=0.(26)$

3.1.1 Bright solitons

To solve the bright solitons, the starting assumption is [42]

$P_l\left(X,T\right)=A_l{\mathrm{s}\mathrm{e}\mathrm{c}\mathrm{h}}^{p_l}\tau ,(27)$

with l = 1, 2 and

$\tau =B\left(X-vT\right),(28)$

where A_l and B represent the amplitude and inverse width of the solitons, respectively; v is the soliton velocity, which is considered to be the same along the two components. Substituting Eq. 27 into Eq. 25 yields

$\begin{array}{cc}\hfill & A_l{\mathrm{s}\mathrm{e}\mathrm{c}\mathrm{h}}^{p_l}\tau \left[\omega \left(b\kappa -1\right)-a{\kappa }^2+p_l^2\left(a-vb\right)B^2\right]-p_l\left(p_l+1\right)B^2\left(a-bv\right)A_l{\mathrm{s}\mathrm{e}\mathrm{c}\mathrm{h}}^{2+p_l}\tau \hfill \\ \hfill & +d_l{A}_{\bar{l}}^2{A}_l{\mathrm{s}\mathrm{e}\mathrm{c}\mathrm{h}}^{2p_{\bar{l}}+p_l}\tau +c_l{A}_l^3{\mathrm{s}\mathrm{e}\mathrm{c}\mathrm{h}}^{3p_l}\tau =0.\hfill \end{array}(29)$

On account of the equilibrium principle [38] and applying it to the real part, Eq. 29 can be transformed into

$3p_l=2+p_l.(30)$

Thus,

$p_l=1,(31)$

with l = 1, 2. Considering the linearly independent functions sech^jτ with zero coefficients, when j = 1, 3, the velocity and wave numbers of the resulting bright solitons are

$v=\frac{2a{B}^2-c_l{A}_l^2-d_l{A}_{\bar{l}}^2}{2b{B}^2},(32)$

$\omega =\frac{2a{\kappa }^2-d_l{A}_{\bar{l}}^2-c_l{A}_l^2}{2\left(b\kappa -1\right)}.(33)$

When bB ≠ 0 and bκ ≠ 1, it is noted that the two replacement expressions of the soliton velocity v are equal to l = 1, 2 in Eq. 32; the relationship between A_l and A₂ is

$\frac{A_1}{A_2}=\sqrt{\frac{c_2-d_1}{c_1-d_2}},(34)$

constrained by

$\left(c_2-d_1\right)\left(c_1-d_2\right)>0.(35)$

With Eq. 34, comparing Eqs 24–33 yields

$A_l=\sqrt{\frac{2\left[a{\kappa }^2-\left(b\kappa -1\right)\omega \right]\left(d_l-c_{\bar{l}}\right)}{d_l{d}_{\bar{l}}-c_l{c}_{\bar{l}}}}.(36)$

With l = 1, 2 and $\bar{l}=3-l$, the following formula holds

$\left[a{\kappa }^2-\left(b\kappa -1\right)\omega \right]\left(d_l-c_{\bar{l}}\right)\times \left[d_l{d}_{\bar{l}}-c_l{c}_{\bar{l}}\right]>0.(37)$

Therefore, the bright soliton solutions for the Kerr law non-linearity of the generalized coupled fractional NLS equations are

$\begin{array}{cc}\hfill & u_{k1}\left(x,t\right)=A_1\mathrm{s}\mathrm{e}\mathrm{c}\mathrm{h}\left\{B\left[\frac{x^{\beta }}{\mathrm{\Gamma }\left(1+\beta \right)}-v\frac{t^{\alpha }}{\mathrm{\Gamma }\left(1+\alpha \right)}\right]\right\}{e}^{i\left[-\kappa \frac{x^{\beta }}{\mathrm{\Gamma }\left(1+\beta \right)}+\omega \frac{t^{\alpha }}{\mathrm{\Gamma }\left(1+\alpha \right)}+\sigma \right]},\hfill \\ \hfill & v_{k1}\left(x,t\right)=A_2\mathrm{s}\mathrm{e}\mathrm{c}\mathrm{h}\left\{B\left[\frac{x^{\beta }}{\mathrm{\Gamma }\left(1+\beta \right)}-v\frac{t^{\alpha }}{\mathrm{\Gamma }\left(1+\alpha \right)}\right]\right\}{e}^{i\left(-\kappa \frac{x^{\beta }}{\mathrm{\Gamma }\left(1+\beta \right)}+\omega \frac{t^{\alpha }}{\mathrm{\Gamma }\left(1+\alpha \right)}+\sigma \right)}.\hfill \end{array}(38)$

The parameters and corresponding constraints in the formula are consistent with the aforementioned discussion.

Figure 1 shows the 3D plots of bright soliton solutions for the Kerr law non-linearity with the four different fractional values: 0.15, 0.45, 0.75, and 1. Bright solitons depict solitary waves with peak intensities higher than those on the ground. Moreover, it can be clearly found that when changing the values of the fractional orders α and β, the contours and widths of the soliton solutions all change. With the increase of α and β, the widths of the solitons change irregularly and the plots gradually become smooth.

FIGURE 1

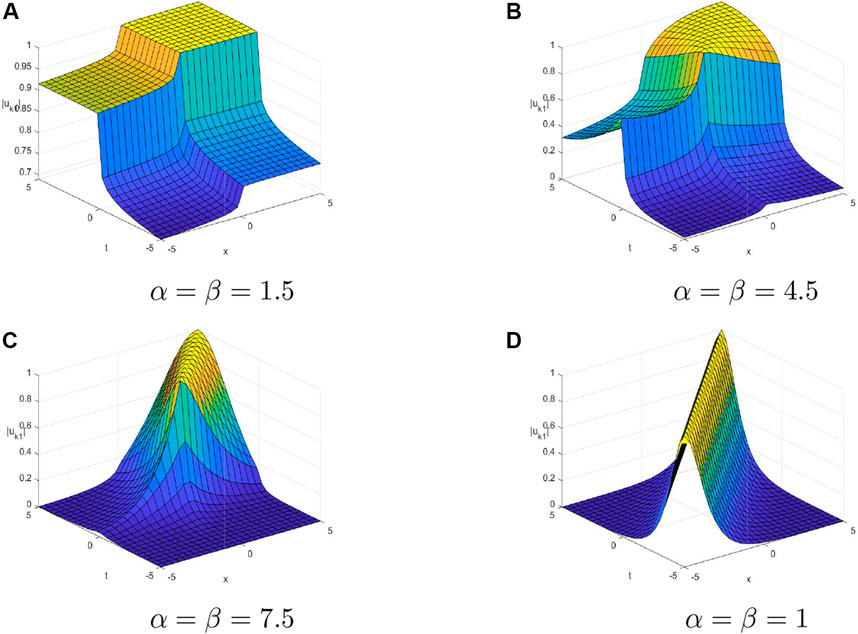
FIGURE 1. 3D plots of bright soliton solutions for the Kerr law non-linearity with the four different fractional values by considering the values A₁ = 1, B = −1, v = 1, κ = −1, ω = 3, and δ = 1. (A) α = β = 1.5. (B) α = β = 4.5. (C) α = β = 7.5. (D) α = β = 1.

3.1.2 Dark solitons

To solve the dark solitons, from the assumption [36],

$P_l\left(X,T\right)=A_l{\tanh }^{p_l}\tau ,(39)$

where the argument τ is given in Eq. 28. The substitution of Eq. 39 into Eq. 16 leads to

$\begin{array}{cc}\hfill & \left[\omega \left(b\kappa -1\right)-a{\kappa }^2-2p_l^2\left(a-bv\right)B^2\right]A_l{\tanh }^{p_l}\tau +d_l{A}_{\bar{l}}^2{A}_l{\tanh }^{2p_{\bar{l}}+p_l}\tau +c_l{A}_l^3{\tanh }^{3p_l}\tau +\hfill \\ \hfill & \left[p_l\left(p_l+1\right)B^2\left(a-bv\right)\right]A_l{\tanh }^{p_l+2}\tau +\left[p_l\left(p_l-1\right)\left(a-bv\right)B^2\right]A_l{\tanh }^{p_l-2}\tau =0.\hfill \end{array}(40)$

The equilibrium principle reveals the same values of p_l with l = 1, 2 as Eq. 31. Analogously, as to bright solitons, considering the coefficients of the linearly independent functions of Eq. 40 yields

$v=\frac{2a{B}^2-c_l{A}_l^2-d_l{A}_{\bar{l}}^2}{2b{B}^2},(41)$

$\omega =\frac{a{\kappa }^2-d_l{A}_{\bar{l}}^2-c_l{A}_l^2}{\left(b\kappa -1\right)}.(42)$

It should be noted that in Eq. 41, the specific value between amplitudes shows the same relationship given in Eqs 34, 35 by contrasting the wave velocity v with l = 1, 2.

Considering Eq. 34, two possible expressions of the velocity in Eqs 24, 42 are jointly evaluated for either value of l, and we get

$A_l=\sqrt{\frac{\left[a{\kappa }^2-\left(b\kappa -1\right)\omega \right]\left(d_l-c_{\bar{l}}\right)}{d_l{d}_{\bar{l}}-c_l{c}_{\bar{l}}}},(43)$

as long as

$\left[a{\kappa }^2-\left(b\kappa -1\right)\omega \right]\left(d_l-c_{\bar{l}}\right)\times \left[d_l{d}_{\bar{l}}-c_l{c}_{\bar{l}}\right]>0.(44)$

Therefore, the dark soliton solutions for Kerr law non-linearity are

$\begin{array}{cc}\hfill & u_{k2}\left(x,t\right)=A_1\tanh \left\{B\left[\frac{x^{\beta }}{\mathrm{\Gamma }\left(1+\beta \right)}-v\frac{t^{\alpha }}{\mathrm{\Gamma }\left(1+\alpha \right)}\right]\right\}{e}^{i\left(-\kappa \frac{x^{\beta }}{\mathrm{\Gamma }\left(1+\beta \right)}+\omega \frac{t^{\alpha }}{\mathrm{\Gamma }\left(1+\alpha \right)}+\sigma \right)},\hfill \\ \hfill & v_{k2}\left(x,t\right)=A_2\tanh \left\{B\left[\frac{x^{\beta }}{\mathrm{\Gamma }\left(1+\beta \right)}-v\frac{t^{\alpha }}{\mathrm{\Gamma }\left(1+\alpha \right)}\right]\right\}{e}^{i\left(-\kappa \frac{x^{\beta }}{\mathrm{\Gamma }\left(1+\beta \right)}+\omega \frac{t^{\alpha }}{\mathrm{\Gamma }\left(1+\alpha \right)}+\sigma \right)},\hfill \end{array}(45)$

where Eq. 43 describes the soliton amplitudes, Eqs 41, 42 describe the velocity and the wave numbers, and Eq. 34 describes the frequency accompanied by corresponding constraints.

Figure 2 shows dark soliton solutions for Kerr law non-linearity with the four different fractional values. Dark solitons depict solitary waves whose intensity is lower than that of the background. As can be seen from Figures 2A–D, with the increase of α and β, the amplitudes of solitons increase, while their widths change irregularly. When α = β = 1, the soliton has the largest amplitude.

FIGURE 2

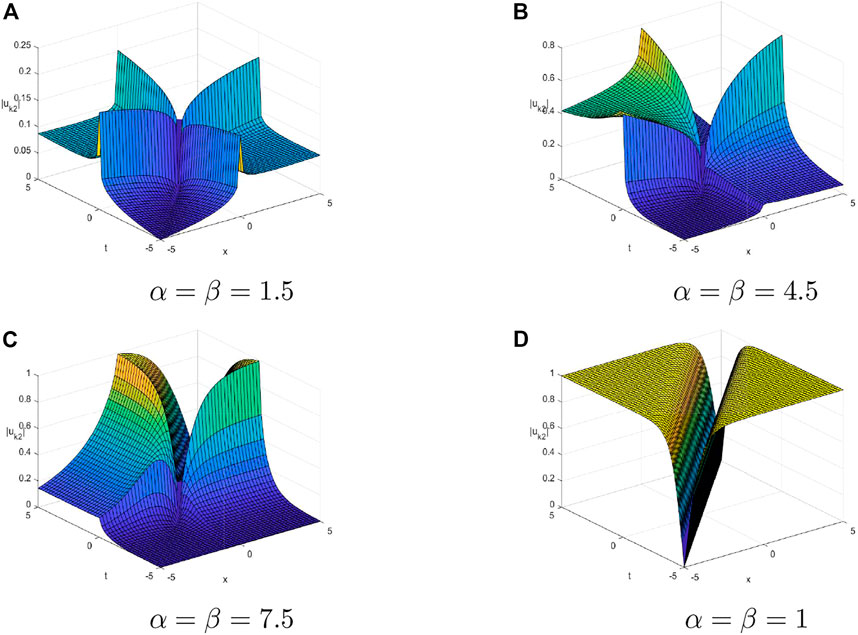
FIGURE 2. 3D plots of dark soliton solutions for the Kerr law non-linearity with the four different fractional values by considering the values A₁ = 1, B = −1, v = 1, κ = −1, ω = 3, and δ = 1. (A) α = β = 1.5. (B) α = β = 4.5. (C) α = β = 7.5. (D) α = β = 1.

3.1.3 Singular solitons

To solve the singular solitons, the assumption is [36]

$P_l\left(X,T\right)=A_l{\mathrm{c}\mathrm{s}\mathrm{c}\mathrm{h}}^{p_l}\tau ,(46)$

where A_l denotes the pulse amplitude and p_l is a free parameter to be evaluated by the equilibrium non-linearity and will be revealed in the following. Substituting Eq. 46 into Eq. 16 leads to

$\begin{array}{cc}\hfill & A_l{\mathrm{c}\mathrm{s}\mathrm{c}\mathrm{h}}^{p_l}\tau \left[\omega \left(b\kappa -1\right)-a{\kappa }^2+p_l^2\left(a-bv\right)B^2\right]+p_l\left(p_l+1\right)B^2\left(a-bv\right)A_l{\mathrm{c}\mathrm{s}\mathrm{c}\mathrm{h}}^{2+p_l}\tau \hfill \\ \hfill & +d_l{A}_l{A}_{\bar{l}}^2{\mathrm{c}\mathrm{s}\mathrm{c}\mathrm{h}}^{2p_{\bar{l}}+p_l}\tau +c_l{A}_l^3{\mathrm{c}\mathrm{s}\mathrm{c}\mathrm{h}}^{3p_l}\tau =0.\hfill \end{array}(47)$

After the equilibrium program, we get the values of the parameter p_l in Eq. 31. It can also be evaluated in coefficients of independent elements ${\mathrm{c}\mathrm{s}\mathrm{c}\mathrm{h}}^{p_l-2}\tau$. Substituting p_l = 1 with l = 1, 2 into Eq. 47, the linearly independent function csch^jτ, j = 1, 3 with zero coefficients to recover the soliton velocity in the dark soliton (Eq. 41) and the wave numbers translate to

$\omega =\frac{c_l{A}_l^2+2a{\kappa }^2+d_l{A}_{\bar{l}}^2}{2\left(bk-1\right)}.(48)$

Considering Eq. 34 and equalizing the two possible velocity expressions Eqs. 24, 48, we obtain

$A_l=\sqrt{\frac{2\left[\left(b\kappa -1\right)\omega -a{\kappa }^2\right]\left(d_l-c_{\bar{l}}\right)}{d_l{d}_{\bar{l}}-c_l{c}_{\bar{l}}}},(49)$

with l = 1, 2 and $\bar{l}=3-l$. When the following formula holds

$\left[\left(b\kappa -1\right)\omega -a{\kappa }^2\right]\left(d_l-c_{\bar{l}}\right)\times \left[d_l{d}_{\bar{l}}-c_l{c}_{\bar{l}}\right]>0.(50)$

The singular 1-soliton solutions for Kerr law non-linearity are

$\begin{array}{cc}\hfill & u_{k3}\left(x,t\right)=A_1\mathrm{c}\mathrm{s}\mathrm{c}\mathrm{h}\left\{B\left[\frac{x^{\beta }}{\mathrm{\Gamma }\left(1+\beta \right)}-v\frac{t^{\alpha }}{\mathrm{\Gamma }\left(1+\alpha \right)}\right]\right\}{e}^{i\left(-\kappa \frac{x^{\beta }}{\mathrm{\Gamma }\left(1+\beta \right)}+\omega \frac{t^{\alpha }}{\mathrm{\Gamma }\left(1+\alpha \right)}+\sigma \right)},\hfill \\ \hfill & v_{k3}\left(x,t\right)=A_2\mathrm{c}\mathrm{s}\mathrm{c}\mathrm{h}\left\{B\left[\frac{x^{\beta }}{\mathrm{\Gamma }\left(1+\beta \right)}-v\frac{t^{\alpha }}{\mathrm{\Gamma }\left(1+\alpha \right)}\right]\right\}{e}^{i\left(-\kappa \frac{x^{\beta }}{\mathrm{\Gamma }\left(1+\beta \right)}+\omega \frac{t^{\alpha }}{\mathrm{\Gamma }\left(1+\alpha \right)}+\sigma \right)}.\hfill \end{array}(51)$

If the corresponding constraints, as described previously are satisfied, the singular soliton solution will persist.

3.2 Power law

In physics research, various materials exhibit power law non-linearities, such as semiconductors. This non-linear law occurs in non-linear plasmas and can solve the small K-condensation problem theory in weak turbulence. The general form of a non-linear function is F(s) = sⁿ, where n denotes a parameter of power law non-linear. We restrict 0 < n < 2 to ensure the wave stability and n ≠ 2 to avoid self-focusing singularities, the initial system Eq. 15 can be rewritten as

$\begin{array}{cc}\hfill & i{u}_T+a_1{u}_{XX}+b_1{u}_{XT}+\left(c_1|u{|}^{2n}+d_1|v{|}^{2n}\right)u+i\left\{{\lambda }_1|u{|}^2{u}_X+{\theta }_1{u}_{\mathit{XXX}}\right\}=0,\hfill \\ \hfill & i{v}_T+a_2{v}_{XX}+b_2{v}_{XT}+\left(c_2|v{|}^{2n}+d_2|u{|}^{2n}\right)v+i\left\{{\lambda }_2|v{|}^2{v}_X+{\theta }_2{v}_{\mathit{XXX}}\right\}=0.\hfill \end{array}(52)$

Substituting Eq. 17 into Eq. 52 and transforming the real part Eq. 19 into

$\left(b_l\kappa \omega -\omega -a_l{k}^2-{\theta }_l{k}^3\right)P_l+\left(c_l{P}_l^{2n}+d_l{P}_{\bar{l}}^{2n}\right)p_l+\left(a_l+3{\theta }_l\kappa \right)P_{\mathit{lXX}}+b_l{P}_{\mathit{lXT}}=0.(53)$

The imaginary part takes the form as

$\left(1-b_l\kappa \right)P_{lT}+\left(b_l\omega -2a_l\kappa -3{\theta }_l{\kappa }^2\right)P_{lX}+\left(2n+1\right){\lambda }_l{P}_l^2{P}_{lX}+{\theta }_l{P}_{\mathit{lXXX}}=0.(54)$

The real part of Eq. 53 can be simply written as

$\left[\omega \left(b\kappa -1\right)-a{k}^2\right]P_l+\left(c_l{p}_l^{2n}+d_l{p}_{\bar{l}}^{2n}\right)p_l+a{P}_{\mathit{lXX}}+b{P}_{\mathit{lXT}}=0.(55)$

3.2.1 Bright solitons

We use the same starting assumption as the cubic nonlinearity given by Eqs 27, 28 to conduct research on the bright soliton solutions on the system (Eq. 52). Substituting Eq. 27 into Eq. 55 yields

$\begin{array}{cc}\hfill & A_l{\mathrm{s}\mathrm{e}\mathrm{c}\mathrm{h}}^{p_l}\tau \left[\omega \left(b\kappa -1\right)-a{\kappa }^2+p_l^2\left(a-vb\right)B^2\right]+d_l{A}_{\bar{l}}^{2n}{A}_l{\mathrm{s}\mathrm{e}\mathrm{c}\mathrm{h}}^{2n{p}_{\bar{l}}+p_l}\tau +c_l{A}_l^{2n+1}{\mathrm{s}\mathrm{e}\mathrm{c}\mathrm{h}}^{\left(2n+1\right)p_l}\tau \hfill \\ \hfill & -p_l\left(p_l+1\right)B^2\left(a-bv\right)A_l{\mathrm{s}\mathrm{e}\mathrm{c}\mathrm{h}}^{2+p_l}\tau =0.\hfill \end{array}(56)$

From the equilibrium between nonlinearity and dispersion,

$\left(2n+1\right)p_l=p_l+2,(57)$

where

$p_l=\frac{1}{n},(58)$

with l = 1, 2. Substituting Eq. 58 into Eq. 56 and letting the coefficients set to zero of the linearly independent functions sech^jτ with $j=\frac{1}{n},\frac{1}{n}+1$, we obtain

$v=\frac{\left(n+1\right)a{B}^2-n^2\left[c_l{A}_l^{2n}+d_l{A}_{\bar{l}}^{2n}\right]}{\left(n+1\right)b{B}^2}(59)$

and

$\omega =\frac{\left(n+1\right)a{k}^2-c_l{A}_l^{2n}-d_l{A}_{\bar{l}}^{2n}}{\left(n+1\right)\left(b\kappa -1\right)},(60)$

when bB ≠ 0 and bκ ≠ 1; in Eq. 59, by equating the two alternative expressions for the soliton velocity v with 1 = 1, 2, the relation form between the amplitudes can be written as

$\frac{A_1}{A_2}={\left(\frac{c_2-d_1}{c_1-d_2}\right)}^{\frac{1}{2n}},(61)$

with l = 1, 2, $\bar{l}=3-l$, and condition Eq. 35. On the basis of Eq. 61, equating Eqs.24, 60 with l = 1, 2 yields

$A_l={\left[\frac{\left[\left(n+1\right)\left(a{\kappa }^2-\omega \left(b\kappa -1\right)\right)\right]\left(d_l-c_{\bar{l}}\right)}{\left[d_l{d}_{\bar{l}}-c_l{c}_{\bar{l}}\right]}\right]}^{\frac{1}{2n}},(62)$

whenever the inequality Eq. 37 holds. Hence, the bright soliton solutions for power law nonlinearity of the generalized coupled fractional NLS equations are

$\begin{array}{cc}\hfill & u_{po1}\left(x,t\right)=A_1{\mathrm{s}\mathrm{e}\mathrm{c}\mathrm{h}}^{\frac{1}{n}}\left\{B\left[\frac{x^{\beta }}{\mathrm{\Gamma }\left(1+\beta \right)}-v\frac{t^{\alpha }}{\mathrm{\Gamma }\left(1+\alpha \right)}\right]\right\}{e}^{i\left(-\kappa \frac{x^{\beta }}{\mathrm{\Gamma }\left(1+\beta \right)}+\omega \frac{t^{\alpha }}{\mathrm{\Gamma }\left(1+\alpha \right)}+\sigma \right)},\hfill \\ \hfill & v_{po1}\left(x,t\right)=A_2{\mathrm{s}\mathrm{e}\mathrm{c}\mathrm{h}}^{\frac{1}{n}}\left\{B\left[\frac{x^{\beta }}{\mathrm{\Gamma }\left(1+\beta \right)}-v\frac{t^{\alpha }}{\mathrm{\Gamma }\left(1+\alpha \right)}\right]\right\}{e}^{i\left(-\kappa \frac{x^{\beta }}{\mathrm{\Gamma }\left(1+\beta \right)}+\omega \frac{t^{\alpha }}{\mathrm{\Gamma }\left(1+\alpha \right)}+\sigma \right)}.\hfill \end{array}(63)$

The aforementioned conditions determine the perturbation of the bright soliton solutions.

3.2.2 Dark solitons

Dark solitons are applied to the same ansatz method in Eq. 39; the real part equation Eq. 55 can be transformed into

$\begin{array}{cc}\hfill & \left\{\left[\omega \left(b\kappa -1\right)-a{\kappa }^2\right]-2p_l^2\left(a-bv\right)B^2\right\}{A}_l{\tanh }^{p_l}\tau +p_l\left(p_l-1\right)\left(a-bv\right)B^2{A}_l{\tanh }^{p_l-2}\tau +\hfill \\ \hfill & d_l{A}_l{A}_{\bar{l}}^{2n}{\tanh }^{p_l+2n{p}_{\bar{l}}}\tau +c_l{A}_l^{2n+1}{\tanh }^{\left(2n+1\right)p_l}\tau +p_l\left(p_l+1\right)\left(a-bv\right)B^2{A}_l{\tanh }^{p_l+2}\tau =0.\hfill \end{array}(64)$

The equilibrium principle can calculate the value of p_l, as shown in Eq. 58. However, the independent element ${\tanh }^{p_l-2}$ results in p_l, as given in Eq. 31, forcing n = 1. Then, the system (Eq. 52) reduces to Eq. 16, and the dark soliton solutions will exist when the power law non-linearity folds to Kerr law. Our results are the same as Eqs 40–45, which is the same for cubic non-linear dark solitons, which means u_po2(x, t) = u_k2(x, t) and v_po2(x, t) = v_k2(x, t).

3.2.3 Singular solitons

In order to study the first type of the singular soliton solution of the system (Eq. 52), we readopt the guess function (Eq. 46). The real part of Eq. 55 is

$\begin{array}{cc}\hfill & A_l{\mathrm{c}\mathrm{s}\mathrm{c}\mathrm{h}}^{p_l}\tau \left[\omega \left(b\kappa -1\right)-a{\kappa }^2+p_l^2\left(a^2-bv\right)B^2\right]+d_l{A}_l{A}_{\bar{l}}^{2n}{\mathrm{c}\mathrm{s}\mathrm{c}\mathrm{h}}^{2n{p}_{\bar{l}}+p_l}\tau \hfill \\ \hfill & +c_l{A}_l^{2n+1}{\mathrm{c}\mathrm{s}\mathrm{c}\mathrm{h}}^{\left(2n+1\right)p_l}\tau +p_l\left(p_l+1\right)B^2\left(a-bv\right)A_l{\mathrm{c}\mathrm{s}\mathrm{c}\mathrm{h}}^{2+p_l}\tau =0.\hfill \end{array}(65)$

The proper equilibrium between dispersion and non-linear terms gives p_l in Eq. 58. Based on Eq. 65 and the coefficients of csch^jτ with $j=\frac{1}{n},\frac{1}{n}+1$, the soliton velocity and wave numbers are written as

$v=\frac{\left(n+1\right)a{B}^2-n^2\left[c_l{A}_l^{2n}+d_l{A}_{\bar{l}}^{2n}\right]}{\left(n+1\right)b{B}^2}(66)$

and

$\omega =\frac{\left(n+1\right)a{k}^2+c_l{A}_l^{2n}+d_l{A}_{\bar{l}}^{2n}}{\left(n+1\right)\left(b\kappa -1\right)}.(67)$

Substituting the expressions of v with l = 1, 2 into Eq. 66 yields the specific value (Eq. 61). A similar processing for ω of Eq. 67 will get the identical equation:

$\left(c_1-d_2\right)A_1^{2n}=\left(c_2-d_1\right)A_2^{2n}.(68)$

As to this variety of soliton and the non-linearity under power law, Eqs 24, 66 are set as l = 1, 2 and can obtain

$A_l={\left[\frac{\left[\left(n+1\right)\left(\omega \left(b\kappa -1\right)-a{\kappa }^2\right)\right]\left(d_l-c_{\bar{l}}\right)}{\left[d_l{d}_{\bar{l}}-c_l{c}_{\bar{l}}\right]}\right]}^{\frac{1}{2n}}.(69)$

Considering Eqs 61, 44, the singular soliton solutions for the power law non-linearity are

$\begin{array}{cc}\hfill & u_{po3}\left(x,t\right)=A_1{\mathrm{c}\mathrm{s}\mathrm{c}\mathrm{h}}^{\frac{1}{n}}\left\{B\left[\frac{x^{\beta }}{\mathrm{\Gamma }\left(1+\beta \right)}-v\omega \frac{t^{\alpha }}{\mathrm{\Gamma }\left(1+\alpha \right)}\right]\right\}{e}^{i\left(-\kappa \frac{x^{\beta }}{\mathrm{\Gamma }\left(1+\beta \right)}+\omega \frac{t^{\alpha }}{\mathrm{\Gamma }\left(1+\alpha \right)}+\sigma \right)},\hfill \\ \hfill & v_{po3}\left(x,t\right)=A_2{\mathrm{c}\mathrm{s}\mathrm{c}\mathrm{h}}^{\frac{1}{n}}\left\{B\left[\frac{x^{\beta }}{\mathrm{\Gamma }\left(1+\beta \right)}-v\omega \frac{t^{\alpha }}{\mathrm{\Gamma }\left(1+\alpha \right)}\right]\right\}{e}^{i\left(-\kappa \frac{x^{\beta }}{\mathrm{\Gamma }\left(1+\beta \right)}+\omega \frac{t^{\alpha }}{\mathrm{\Gamma }\left(1+\alpha \right)}+\sigma \right)}.\hfill \end{array}(70)$

The corresponding constraints parameters have been described in detail previously.

3.3 Parabolic law

Parabolic law, which is derived from the non-linear interaction between Langmuir waves and electrons, reveals the non-linear interaction between the high-frequency Langmuir and ionic sound waves through pondermotive forces [37].

Due to the lack of known analytical solutions and the difficulty of finding parameters with a significant fifth-order term [42], the propagation of beams in fifth-order non-linear media has little attention. However, there have been some recent developments, and experiments have shown that the optical sensitivity of CdS_xSe_1−x-doped glass has a considerable χ⁽⁵⁾, that is, fifth-order sensitivity. In the strong fem pulse of 620 nm, there is an obvious non-linear effect of χ⁽⁵⁾ in the transparent glass. When establishing the theory of self-trapping beam diameter, knowledge of the aforementioned third-order non-linearity needs to be considered. In the 1960s and 1970s, it was recognized that non-linear refractive index saturation played an important role in self-trapping. By retaining the higher-order terms in the non-linear polarization tensor [42], higher order non-linearities can be produced.

For the parabolic law non-linearity, F(s) = s + k₁s², the equations (Eq. 15) describing the dispersive soliton propagation are

$\begin{array}{cc}\hfill i{u}_T& +a_1{u}_{XX}+b_1{u}_{XT}+\left(c_1|u{|}^2+d_1|v{|}^2\right)u+\left({\xi }_1|u{|}^4+{\eta }_1|u{|}^2|v{|}^2+{\zeta }_1|v{|}^4\right)u\hfill \\ \hfill & +i\left\{{\lambda }_1|u{|}^2{u}_X+{\theta }_1{u}_{\mathit{XXX}}\right\}=0,\hfill \\ \hfill i{v}_T& +a_2{v}_{XX}+b_2{v}_{XT}+\left(c_2|v{|}^2+d_2|u{|}^2\right)v+\left({\xi }_2|v{|}^4+{\eta }_2|v{|}^2|u{|}^2+{\zeta }_2|u{|}^4\right)v\hfill \\ \hfill & +i\left\{{\lambda }_2|v{|}^2{v}_X+{\theta }_2{v}_{\mathit{XXX}}\right\}=0,\hfill \end{array}(71)$

where terms with ξ, η, and ζ are connected with the quintic of the cubic-quintic non-linear law. Other terms are interpreted as the Kerr law non-linearity in the same way.

Substituting Eq. 17 into Eq. 71 and converting to real and imaginary terms, we can get the same imaginary of Eq. 20; therefore, the results for this subsection will be the same as Eqs. 21–26 for the Kerr law non-linearity as well. The real part of the equation is

$\left(\omega +a{\kappa }^2-b\kappa \omega \right)P_l-c_l{P}_l^3-d_l{P}_l{P}_{\bar{l}}^2-\xi P_l^5-{\eta }_l{P}_l^3{P}_{\bar{l}}^2-{\zeta }_l{P}_l{P}_{\bar{l}}^4-a_l{P}_{\mathit{lXX}}-b_l{P}_{\mathit{lXT}}=0.(72)$

3.3.1 Bright solitons

To solve the bright solitons, starting with the assumption [42]

$P_l\left(X,T\right)=\frac{A_l}{{\left(D_l+\cosh \tau \right)}^{p_l}},(73)$

where the definition of τ is consistent with Eq. 28, A_l denotes the amplitudes of the solitons, and D_l represents the two newly introduced parameters with l = 1, 2. Substituting Eq. 73 into Eq. 72 yields

$\begin{array}{c}\left[\omega \left(bk-1\right)-a{\kappa }^2-p_l^2\left(bv-a\right)B^2\right]+\frac{p_l\left(2p_l+1\right)\left(bv-a\right)D_l{B}^2}{D_l+\cosh \tau }-\frac{p_l\left(p_l+1\right)\left(bv-a\right)B^2\left(D_l^2-1\right)}{{\left(D_l+\cosh \tau \right)}^2}\hfill \\ +\frac{c_l{A}_l^2}{{\left(D_l+\cosh \tau \right)}^{2p_l}}+\frac{d_l{A}_{\bar{l}}^2}{{\left(D_l+\cosh \tau \right)}^{2p_{\bar{l}}}}+\frac{{\xi }_l{A}_l^4}{{\left(D_l+\cosh \tau \right)}^{4p_l}}+\frac{{\eta }_l{A}_l^2{A}_{\bar{l}}^2}{{\left(D_l+\cosh \tau \right)}^{2p_l}{\left(D_{\bar{l}}+\cosh \tau \right)}^{2p_{\bar{l}}}}\hfill \\ +\frac{{\xi }_l{A}_{\bar{l}}^4}{{\left(D_{\bar{l}}+\cosh \tau \right)}^{4p_{\bar{l}}}}=0.\hfill \end{array}(74)$

According to the equilibrium principle, equating the exponents $(4p_l=4p_{\bar{l}}=2)$ or $(2p_l=2p_{\bar{l}}=1)$, we get

$p_l=p_{\bar{l}}=\frac{1}{2}.(75)$

Setting the coefficients of the linearly independent functions to zero, we have

$\omega =\frac{4{\kappa }^{2}a+\left(bv-a\right)B^2}{4\left(bk-1\right)},(76)$

$A_l=B\sqrt{\frac{D_l\left(a-bv\right)}{c_l}},(77)$

and

$D_l=\frac{1}{B}\sqrt{\frac{3B^2\left(a-bv\right)-4{\xi }_l{A}_l^4}{3\left(a-bv\right)}}.(78)$

When bκ ≠ 1, other constraint conditions are

$c_l{D}_l\left(a-bv\right)>0(79)$

and

$\left(a-bv\right)\left[B^2\left(a-bv\right)-{\xi }_l{A}_l^4\right]>0.(80)$

Hence, the bright soliton solutions of the parabolic law non-linearity for the generalized coupled fractional NLS equations are

$\begin{array}{cc}\hfill & u_{pa1}\left(x,t\right)=\frac{A_1}{\sqrt{D_1+\cosh \left\{B\left[\frac{x^{\beta }}{\mathrm{\Gamma }\left(1+\beta \right)}-v\frac{t^{\alpha }}{\mathrm{\Gamma }\left(1+\alpha \right)}\right]\right\}}}{e}^{i\left(-\kappa \frac{x^{\beta }}{\mathrm{\Gamma }\left(1+\beta \right)}+\omega \frac{t^{\alpha }}{\mathrm{\Gamma }\left(1+\alpha \right)}+\sigma \right)},\hfill \\ \hfill & v_{pa1}\left(x,t\right)=\frac{A_2}{\sqrt{D_2+\cosh \left\{B\left[\frac{x^{\beta }}{\mathrm{\Gamma }\left(1+\beta \right)}-v\frac{t^{\alpha }}{\mathrm{\Gamma }\left(1+\alpha \right)}\right]\right\}}}{e}^{i\left(-\kappa \frac{x^{\beta }}{\mathrm{\Gamma }\left(1+\beta \right)}+\omega \frac{t^{\alpha }}{\mathrm{\Gamma }\left(1+\alpha \right)}+\sigma \right)}.\hfill \end{array}(81)$

Figure 3 shows bright soliton solutions for parabolic law non-linearity with the four different fractional values.

FIGURE 3

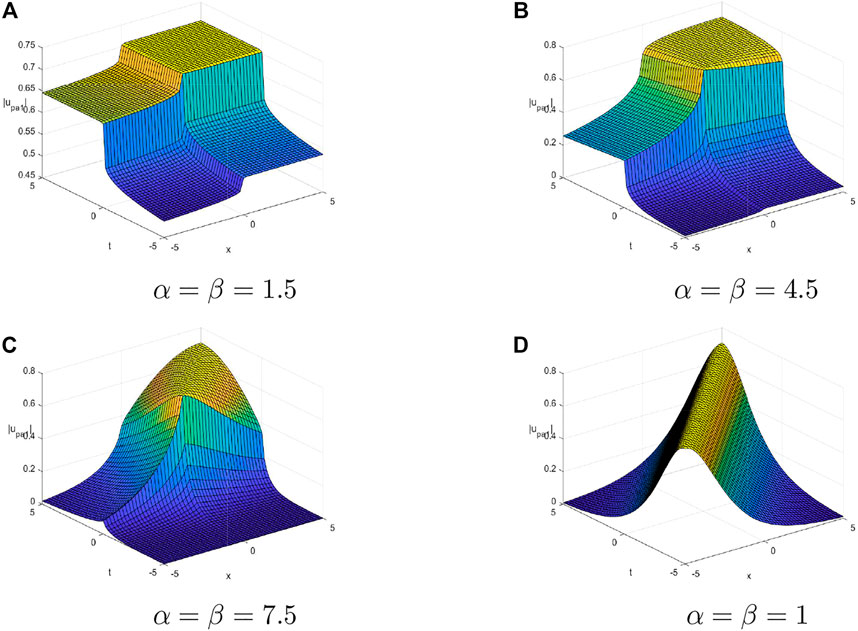
FIGURE 3. 3D plots of bright soliton solutions for the parabolic law non-linearity with the four different fractional values by considering the values A₁ = 1, B = −1, v = 1, κ = −1, ω = 3, and δ = 1. (A) α = β = 1.5. (B) α = β = 4.5. (C) α = β = 7.5. (D) α = β = 1.

3.3.2 Dark solitons

To solve the dark solitons, starting the hypothesis [43]

$P_l\left(X,T\right)={\left(A_l+B_l\tanh \tau \right)}^{p_l},(82)$

where A_l and B_l represent the free parameters. Substituting Eq. 82 into Eq. 26, we obtain

$B_l^2\left[\left(b\kappa -1\right)v-2a\kappa +b\omega \right]{\left(A_l+B_l\tanh \tau \right)}^2=0.(83)$

The linearly independent function requires the third-order dispersion value to be zero. In addition,

$A_l=B_l.(84)$

Take A_l > 0, and the linearly independent function gives the soliton velocity v, as shown in Eq. 24, and gives the constraint condition Eq. 22. For l = 1, 2, substituting Eq. 82 into Eq. 72, we get

$\begin{array}{cc}\hfill & B^2{p}_l\left(p_l+1\right)\left(a-bv\right){\left(A_l+B_l\tanh \tau \right)}^2-2B^2{A}_l{p}_l\left(2p_l+1\right)\left(a-bv\right){\left(A_l+B_l\tanh \tau \right)}^3\hfill \\ \hfill & +\left\{B_l^2\left[{\omega }_l\left(b\kappa -1\right)-a{\kappa }^2\right]+2p_l^2{B}^2\left(3A^2-B^2\right)\left(a-bv\right)\right\}{\left(A_l+B_l\tanh \tau \right)}^2+2p_l\left(2p_l-1\right)\hfill \\ \hfill & B^2{A}_l\left(a-bv\right)\left(B_l^2-A_l^2\right)\left(A_l+B_l\tanh \tau \right)+B^2{p}_l\left(p_l-1\right)\left(a-bv\right){\left(B_l^2-A_l^2\right)}^2\hfill \\ \hfill & +c_l{\left(A_l+B_l\tanh \tau \right)}^{2p_l+2}+d_l{\left(A_l+B_l\tanh \tau \right)}^2{\left(A_{\bar{l}}+B_{\bar{l}}\tanh \tau \right)}^{2p_{\bar{l}}}+{\xi }_l{\left(A_l+B_l\tanh \tau \right)}^{4p_l+2}\hfill \\ \hfill & +{\eta }_l{\left(A_l+B_l\tanh \tau \right)}^{2p_l+2}{\left(A_{\bar{l}}+B_{\bar{l}}\tanh \tau \right)}^{2p_{\bar{l}}}+{\zeta }_l{\left(A_l+B_l\tanh \tau \right)}^2{\left(A_{\bar{l}}+B_{\bar{l}}\tanh \tau \right)}^{4p_{\bar{l}}}=0.\hfill \end{array}(85)$

The equilibrium principle gives

$p_l=\frac{1}{2}.(86)$

The other parameter values from Eq. 85 are

$\omega =\frac{a{\kappa }^2+\left(bv-a\right)B^2}{b\kappa -1},(87)$

$A_l=B\sqrt{\frac{2\left(a-bv\right)}{c_l}},(88)$

and

$v=\frac{a+{\xi }_{\bar{l}}}{b}.(89)$

The relation is obtained by equalizing the two values of the velocity

${\xi }_l={\xi }_{\bar{l}}.(90)$

Eqs 87–89 introduced the condition bκ ≠ 1 and

$c_l\left(a-bv\right)>0.(91)$

Dark soliton solutions for the parabolic law non-linearity are

$\begin{array}{cc}\hfill u_{pa2}\left(x,t\right)=& \sqrt{A_1+A_1\tanh \left\{B\left[\frac{x^{\beta }}{\mathrm{\Gamma }\left(1+\beta \right)}-v\frac{t^{\alpha }}{\mathrm{\Gamma }\left(1+\alpha \right)}\right]\right\}}{e}^{i\left(-\kappa \frac{x^{\beta }}{\mathrm{\Gamma }\left(1+\beta \right)}+\omega \frac{t^{\alpha }}{\mathrm{\Gamma }\left(1+\alpha \right)}+\sigma \right)},\hfill \\ \hfill v_{pa2}\left(x,t\right)=& \sqrt{A_2+A_2\tanh \left\{B\left[\frac{x^{\beta }}{\mathrm{\Gamma }\left(1+\beta \right)}-v\frac{t^{\alpha }}{\mathrm{\Gamma }\left(1+\alpha \right)}\right]\right\}}{e}^{i\left(-\kappa \frac{x^{\beta }}{\mathrm{\Gamma }\left(1+\beta \right)}+\omega \frac{t^{\alpha }}{\mathrm{\Gamma }\left(1+\alpha \right)}+\sigma \right)}.\hfill \end{array}(92)$

Figure 4 shows dark soliton solutions for parabolic law non-linearity with the four different fractional values.

FIGURE 4

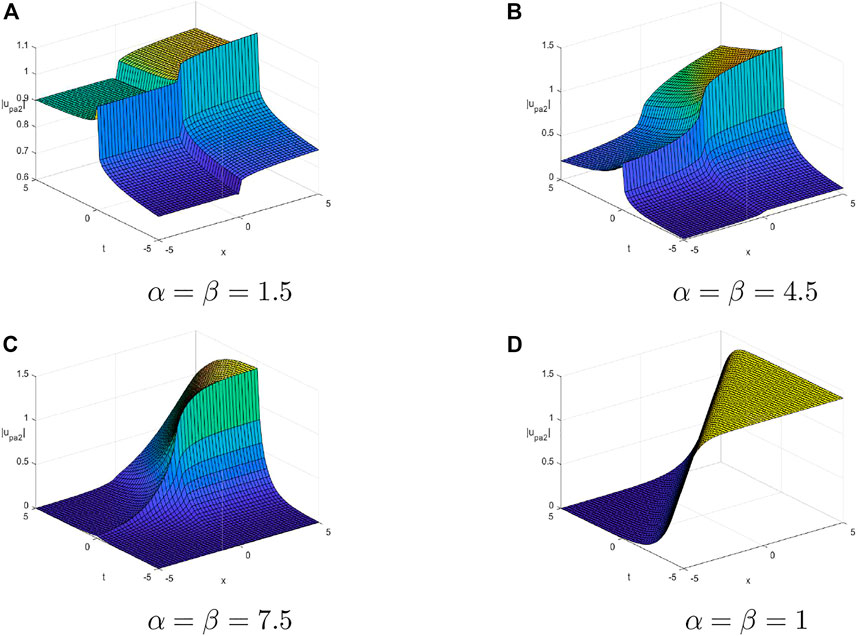
FIGURE 4. 3D plots of dark soliton solutions for the parabolic law non-linearity with the four different fractional values by considering the values A₁ = 1, B = −1, v = 1, κ = −1, ω = 3, and δ = 1. (A) α = β = 1.5. (B) α = β = 4.5. (C) α = β = 7.5. (D) α = β = 1.

3.3.3 Singular solitons

To solve the singular solitons, starting with the assumption [36]

$P_l\left(X,T\right)=\frac{A_l}{{\left(D_l+\sinh \tau \right)}^{p_l}}.(93)$

Combining Eq. 26 with Eq. 93, we get

$v=\frac{b\omega -2a\kappa }{1-bk},(94)$

with the constraint relation bκ ≠ 1.

From the real part, substituting Eq. 93 into Eq. 72, we get

$\begin{array}{cc}\hfill & \left[\omega \left(b\kappa -1\right)-a{\kappa }^2-p_l^2\left(bv-a\right)B^2\right]+\frac{p_l\left(2p_l+1\right)\left(bv-a\right)D_l{B}^2}{D_l+\sinh \tau }-\hfill \\ \hfill & \frac{p_l\left(p_l+1\right)\left(bv-a\right)B^2\left(D_l^2-1\right)}{{\left(D_l+\sinh \tau \right)}^2}+\frac{c_l{A}_l^2}{{\left(D_l+\sinh \tau \right)}^{2p_l}}+\frac{d_l{A}_{\bar{l}}^2}{{\left(D_l+\sinh \tau \right)}^{2p_{\bar{l}}}}+\hfill \\ \hfill & \frac{{\eta }_l{A}_l^2{A}_{\bar{l}}^2}{{\left(D_l+\sinh \tau \right)}^{2p_l}{\left(D_{\bar{l}}+\sinh \tau \right)}^{2p_{\bar{l}}}}+\frac{{\xi }_l{A}_l^4}{{\left(D_l+\sinh \tau \right)}^{4p_l}}+\frac{{\zeta }_l{A}_{\bar{l}}^4}{{\left(D_{\bar{l}}+\sinh \tau \right)}^{4p_{\bar{l}}}}=0.\hfill \end{array}(95)$

The value of p_l with l = 1, 2 is consistent in Eq. 75. According to Eq. 95, linearly independent functions with zero coefficients can get ω, B, and D_l consistent with the parameters given by Eqs 76–78. The corresponding constraints 79, 80 and bκ ≠ 1 still exist. Thus, the parabolic non-linear singular soliton solutions are obtained as

$\begin{array}{cc}\hfill u_{pa3}\left(x,t\right)=& \frac{A_1}{\sqrt{D_1+\sinh \left\{B\left[\frac{x^{\beta }}{\mathrm{\Gamma }\left(1+\beta \right)}-v\frac{t^{\alpha }}{\mathrm{\Gamma }\left(1+\alpha \right)}\right]\right\}}}{e}^{i\left(-\kappa \frac{x^{\beta }}{\mathrm{\Gamma }\left(1+\beta \right)}+\omega \frac{t^{\alpha }}{\mathrm{\Gamma }\left(1+\alpha \right)}+\sigma \right)},\hfill \\ \hfill v_{pa3}\left(x,t\right)=& \frac{A_2}{\sqrt{D_2+\sinh \left\{B\left[\frac{x^{\beta }}{\mathrm{\Gamma }\left(1+\beta \right)}-v\frac{t^{\alpha }}{\mathrm{\Gamma }\left(1+\alpha \right)}\right]\right\}}}{e}^{i\left(-\kappa \frac{x^{\beta }}{\mathrm{\Gamma }\left(1+\beta \right)}+\omega \frac{t^{\alpha }}{\mathrm{\Gamma }\left(1+\alpha \right)}+\sigma \right)}.\hfill \end{array}(96)$

3.4 Dual-power law

The dual-power law is applied to reveal the saturation in the non-linear refractive index. It is a description of the soliton dynamics in photoelectric photorefractive substances, for example, LiNbO₃. For the dual-power law non-linear F(s) = k₁sⁿ + k₂s²ⁿ, Eq. 15 describing the propagation of dispersive solitons can be rewritten as

$\begin{array}{cc}\hfill & i{u}_T+a_1{u}_{XX}+b_1{u}_{XT}+\left(c_1|u{|}^{2n}+d_1|v{|}^{2n}\right)u\hfill \\ \hfill & +\left({\xi }_1|u{|}^{4n}+{\eta }_1|u{|}^{2n}|v{|}^{2n}+{\zeta }_1|v{|}^{4n}\right)u+i\left\{{\lambda }_1|u{|}^{2n}{u}_X+{\theta }_1{u}_{\mathit{XXX}}\right\}=0,\hfill \\ \hfill & i{v}_T+a_2{v}_{XX}+b_2{v}_{XT}+\left(c_2|v{|}^{2n}+d_2|u{|}^{2n}\right)v\hfill \\ \hfill & +\left({\xi }_2|v{|}^{4n}+{\eta }_2|v{|}^{2n}|u{|}^{2n}+{\zeta }_2|u{|}^{4n}\right)v+\left\{i{\lambda }_2|v{|}^{2n}{v}_X+{\theta }_2{v}_{\mathit{XXX}}\right\}=0.\hfill \end{array}(97)$

Substituting the same hypothesis as in Eq. 17 into Eq. 97 and converting to real and imaginary terms, we can get the same imaginary part of Eq. 20. Therefore, the results for this subsection will be the same as Eqs 21–26 for the Kerr law non-linearity as well. The equation for the real part is

$\begin{array}{cc}\hfill & \left(\omega +a{\kappa }^2-b\kappa \omega \right)P_l-c_l{P}_l^{2n+1}-d_l{P}_l{P}_{\bar{l}}^{2n}-\xi P_l^{4n+1}\hfill \\ \hfill & -{\eta }_l{P}_l^{2n+1}{P}_{\bar{l}}^{2n}-{\zeta }_l{P}_l{P}_{\bar{l}}^{4n}-a_l{P}_{\mathit{lXX}}-b_l{P}_{\mathit{lXT}}=0.\hfill \end{array}(98)$

3.4.1 Bright solitons

Substituting Eq. 73 into Eq. 98, we get

$\begin{array}{cc}\hfill & \left[\omega \left(bk-1\right)-a{\kappa }^2-p_l^2\left(bv-a\right)B^2\right]+\frac{p_l\left(2p_l+1\right)\left(bv-a\right)D_l{B}^2}{D_l+\cosh \tau }\hfill \\ \hfill & -\frac{p_l\left(p_l+1\right)\left(bv-a\right)B^2\left(D_l^2-1\right)}{{\left(D_l+\cosh \tau \right)}^2}+\frac{c_l{A}_l^{2n}}{{\left(D_l+\cosh \tau \right)}^{2n{p}_l}}+\frac{{\xi }_l{A}_l^{4n}}{{\left(D_l+\cosh \tau \right)}^{4n{p}_l}}\hfill \\ \hfill & +\frac{{\eta }_l{A}_l^{2n}{A}_{\bar{l}}^{2n}}{{\left(D_l+\cosh \tau \right)}^{2n{p}_l}{\left(D_{\bar{l}}+\cosh \tau \right)}^{2n{p}_{\bar{l}}}}+\frac{{\xi }_l{A}_{\bar{l}}^{4n}}{{\left(D_{\bar{l}}+\cosh \tau \right)}^{4n{p}_{\bar{l}}}}+\frac{d_l{A}_{\bar{l}}^{2n}}{{\left(D_l+\cosh \tau \right)}^{2n{p}_{\bar{l}}}}=0.\hfill \end{array}(99)$

Similarly, based on the equilibrium principle, equating the exponents $(4n{p}_l=4n{p}_{\bar{l}}=2)$ or $(2n{p}_l=2n{p}_{\bar{l}}=1)$ gives

$p_l=p_{\bar{l}}=\frac{1}{2n}.(100)$

From Eq. 99, the coefficients are set to zero, and we get

$\omega =\frac{4n^2{\kappa }^{2}a+\left(bv-a\right)B^2}{4n^2\left(bk-1\right)},(101)$

$A_l={\left[\frac{2B^2{n}^2\left(a-bv\right)D_l}{c_l\left(n+1\right)}\right]}^{\frac{1}{2n}},(102)$

and

$D_l=\frac{1}{B}\sqrt{\frac{\left(2n+1\right)B^2\left(a-bv\right)-4n^2{\xi }_l{A}_l^{4n}}{\left(2n+1\right)\left(a-bv\right)}}.(103)$

When bκ ≠ 1, other constraint conditions are

$c_l{D}_l\left(a-bv\right)>0(104)$

and

$\left(a-bv\right)\left[\left(2n+1\right)B^2\left(a-bv\right)-4n^2{\xi }_l{A}_l^4\right]>0.(105)$

Bright soliton solutions of the dual-power law non-linearity for the generalized coupled fractional NLS equations (Eq. 97) are

$\begin{array}{cc}\hfill u_{d1}\left(x,t\right)=& \frac{A_1}{{\left\{D_1+\cosh \left[B\left(\frac{x^{\beta }}{\mathrm{\Gamma }\left(1+\beta \right)}-v\frac{t^{\alpha }}{\mathrm{\Gamma }\left(1+\alpha \right)}\right)\right]\right\}}^{\frac{1}{2n}}}{e}^{i\left(-\kappa \frac{x^{\beta }}{\mathrm{\Gamma }\left(1+\beta \right)}+\omega \frac{t^{\alpha }}{\mathrm{\Gamma }\left(1+\alpha \right)}+\sigma \right)},\hfill \\ \hfill v_{d1}\left(x,t\right)=& \frac{A_2}{{\left\{D_2+\cosh \left[B\left(\frac{x^{\beta }}{\mathrm{\Gamma }\left(1+\beta \right)}-v\frac{t^{\alpha }}{\mathrm{\Gamma }\left(1+\alpha \right)}\right)\right]\right\}}^{\frac{1}{2n}}}{e}^{i\left(-\kappa \frac{x^{\beta }}{\mathrm{\Gamma }\left(1+\beta \right)}+\omega \frac{t^{\alpha }}{\mathrm{\Gamma }\left(1+\alpha \right)}+\sigma \right)}.\hfill \end{array}(106)$

3.4.2 Dark solitons

Substituting Eq. 82 into Eq. 98, we get

$\begin{array}{cc}\hfill & B^2{p}_l\left(p_l+1\right)\left(a-bv\right){\left(A_l+B_l\tanh \tau \right)}^2-2B^2{A}_l{p}_l\left(2p_l+1\right)\left(a-bv\right){\left(A_l+B_l\tanh \tau \right)}^3+\hfill \\ \hfill & \left\{B_l^2\left[{\omega }_l\left(b\kappa -1\right)-a{\kappa }^2\right]+2p_l^2{B}^2\left(3A^2-B^2\right)\left(a-bv\right)\right\}{\left(A_l+B_l\tanh \tau \right)}^2+\hfill \\ \hfill & 2p_l\left(2p_l-1\right)B^2{A}_l\left(a-bv\right)\left(B_l^2-A_l^2\right)\left(A_l+B_l\tanh \tau \right)+B^2{p}_l\left(p_l-1\right)\left(a-bv\right){\left(B_l^2-A_l^2\right)}^2+\hfill \\ \hfill & c_l{\left(A_l+B_l\tanh \tau \right)}^{2n{p}_l+2}+d_l{\left(A_l+B_l\tanh \tau \right)}^2{\left(A_{\bar{l}}+B_{\bar{l}}\tanh \tau \right)}^{2n{p}_{\bar{l}}}+{\xi }_l{\left(A_l+B_l\tanh \tau \right)}^{4n{p}_l+2}\hfill \\ \hfill & +{\eta }_l{\left(A_l+B_l\tanh \tau \right)}^{2n{p}_l+2}{\left(A_{\bar{l}}+B_{\bar{l}}\tanh \tau \right)}^{2n{p}_{\bar{l}}}+{\zeta }_l{\left(A_l+B_l\tanh \tau \right)}^2{\left(A_{\bar{l}}+B_{\bar{l}}\tanh \tau \right)}^{4n{p}_{\bar{l}}}=0.\hfill \end{array}(107)$

Similarly, based on the equilibrium principle, equating the exponents (2np_l + 2 = 3) gives

$p_l=\frac{1}{2n}.(108)$

From Eq. 107, letting the coefficients to zero yields

$\omega =\frac{n^{2}a{\kappa }^2+\left(bv-a\right)B^2}{n^{2}b\kappa -1},(109)$

$A_l=B\sqrt{\frac{\left(n+1\right)\left(a-bv\right)}{n^2{c}_l}},(110)$

where other constraint conditions are bκ ≠ 1 and Eqs 84–91.

Dark soliton solutions for the dual-power law non-linearity are

$\begin{array}{cc}\hfill u_{d2}\left(x,t\right)=& {\left\{A_1+A_1\tanh \left[B\left(\frac{x^{\beta }}{\mathrm{\Gamma }\left(1+\beta \right)}-v\frac{t^{\alpha }}{\mathrm{\Gamma }\left(1+\alpha \right)}\right)\right]\right\}}^{\frac{1}{2n}}{e}^{i\left(-\kappa \frac{x^{\beta }}{\mathrm{\Gamma }\left(1+\beta \right)}+\omega \frac{t^{\alpha }}{\mathrm{\Gamma }\left(1+\alpha \right)}+\sigma \right)},\hfill \\ \hfill v_{d2}\left(x,t\right)=& {\left\{A_2+A_2\tanh \left[B\left(\frac{x^{\beta }}{\mathrm{\Gamma }\left(1+\beta \right)}-v\frac{t^{\alpha }}{\mathrm{\Gamma }\left(1+\alpha \right)}\right)\right]\right\}}^{\frac{1}{2n}}{e}^{i\left(-\kappa \frac{x^{\beta }}{\mathrm{\Gamma }\left(1+\beta \right)}+\omega \frac{t^{\alpha }}{\mathrm{\Gamma }\left(1+\alpha \right)}+\sigma \right)}.\hfill \end{array}(111)$

3.4.3 Singular solitons

Substituting Eq. 93 into Eq. 98 yields

$\begin{array}{cc}\hfill & \left[\omega \left(b\kappa -1\right)-a{\kappa }^2-p_l^2\left(bv-a\right)B^2\right]+\frac{p_l\left(2p_l+1\right)\left(bv-a\right)D_l{B}^2}{D_l+\sinh \tau }-\hfill \\ \hfill & \frac{p_l\left(p_l+1\right)\left(bv-a\right)B^2\left(D_l^2-1\right)}{{\left(D_l+\sinh \tau \right)}^2}+\frac{c_l{A}_l^{2n}}{{\left(D_l+\sinh \tau \right)}^{2n{p}_l}}+\frac{{\xi }_l{A}_l^{4n}}{{\left(D_l+\sinh \tau \right)}^{4n{p}_l}}+\hfill \\ \hfill & \frac{{\eta }_l{A}_l^{2n}{A}_{\bar{l}}^{2n}}{{\left(D_l+\sinh \tau \right)}^{2n{p}_l}{\left(D_{\bar{l}}+\sinh \tau \right)}^{2n{p}_{\bar{l}}}}+\frac{{\zeta }_l{A}_{\bar{l}}^{4n}}{{\left(D_{\bar{l}}+\sinh \tau \right)}^{4n{p}_{\bar{l}}}}+\frac{d_l{A}_{\bar{l}}^{2n}}{{\left(D_l+\sinh \tau \right)}^{2n{p}_{\bar{l}}}}=0.\hfill \end{array}(112)$

Singular soliton solutions for the dual-power law non-linearity of the coupled fractional NLS equations Eq. 97 are

$\begin{array}{cc}\hfill u_{d3}\left(x,t\right)=& \frac{A_1}{{\left\{D_1+\sinh \left[B\left(\frac{x^{\beta }}{\mathrm{\Gamma }\left(1+\beta \right)}-v\frac{t^{\alpha }}{\mathrm{\Gamma }\left(1+\alpha \right)}\right)\right]\right\}}^{\frac{1}{2n}}}{e}^{i\left(-\kappa \frac{x^{\beta }}{\mathrm{\Gamma }\left(1+\beta \right)}+\omega \frac{t^{\alpha }}{\mathrm{\Gamma }\left(1+\alpha \right)}+\sigma \right)},\hfill \\ \hfill v_{d3}\left(x,t\right)=& \frac{A_2}{{\left\{D_2+\sinh \left[B\left(\frac{x^{\beta }}{\mathrm{\Gamma }\left(1+\beta \right)}-v\frac{t^{\alpha }}{\mathrm{\Gamma }\left(1+\alpha \right)}\right)\right]\right\}}^{\frac{1}{2n}}}{e}^{i\left(-\kappa \frac{x^{\beta }}{\mathrm{\Gamma }\left(1+\beta \right)}+\omega \frac{t^{\alpha }}{\mathrm{\Gamma }\left(1+\alpha \right)}+\sigma \right)}.\hfill \end{array}(113)$

3.5 Log law

There is no radiation in the case of log law non-linearity, that is to say, there is no energy loss, so it is the optimal mode of soliton communication. c is a constant in the log law non-linearity F(s) = c ln(s). Eq. 12, which describes the propagation of dispersion solitons, is rewritten as

$\begin{array}{cc}\hfill & i{u}_T+a{u}_{XX}+b{u}_{XT}+2\left(c_1\ln |u|+d_1\ln |v|\right)u+i\left\{{\lambda }_1|u{|}^2{u}_X+{\theta }_1{u}_{\mathit{XXX}}\right\}=0,\hfill \\ \hfill & i{v}_T+a{v}_{XX}+b{v}_{XT}+2\left(c_2\ln |v|+d_2\ln |u|\right)v+i\left\{{\lambda }_2|v{|}^2{v}_X+{\theta }_2{v}_{\mathit{XXX}}\right\}=0.\hfill \end{array}(114)$

Substitute the same hypothesis in Eq. 17 into Eq. 114 and convert it into real and imaginary numbers to obtain the same imaginary number as Eq. 20. The results of this section are the same as Kerr law non-linearity (Eqs 24–26). The real equation is

$\left(\omega +a{\kappa }^2-b\kappa \omega \right)P_l-2P_l\left[c_l\ln |P_l|+c_{\bar{l}}\ln |P_{\bar{l}}|\right]-a_l{P}_{\mathit{lXX}}-b_l{P}_{\mathit{lXT}}=0.(115)$

Since it is debatable whether the log law non-linearity supports dark solitons or singular solitons, only bright solitons (or Gaussian) can be used for log law.

3.5.1 Bright soliton

To solve the bright solitons, form the assumption

$P_l\left(X,T\right)=A_l{e}^{-{\tau }^2}.(116)$

Substituting Eq. 116 into Eq. 115 yields

$\begin{array}{cc}\hfill & \left(\omega +a{\kappa }^2-b\kappa \omega \right)+2B^2\left(a-bv\right)+2{\tau }^2\left(2bv{B}^2-2a{B}^2+c_l+c_{\bar{l}}\right)-2c_l\ln \left(A_l\right)-\hfill \\ \hfill & 2c_{\bar{l}}\ln \left(A_{\bar{l}}\right)=0.\hfill \end{array}(117)$

Letting the coefficients of the linearly independent functions τ^2j to zero with j = 0, 1, we get

$\begin{array}{c}\hfill \omega \left(1-b\kappa \right)+a{\kappa }^2+2B^2\left(a-bv\right)\\ \hfill -2c_l\ln \left(A_l\right)-2c_{\bar{l}}\ln \left(A_{\bar{l}}\right)=0\end{array}(118)$

and

$B=\sqrt{\frac{c_l+c_{\bar{l}}}{2\left(a-bv\right)}}.(119)$

Uncoupling Eqs 24, 118, we get

$v=\frac{a\left(b{\kappa }^2-2\kappa -2b{B}^2\right)+2b\left(c_l\ln \left(A_l\right)+c_{\bar{l}}\ln \left(A_{\bar{l}}\right)\right)}{{\left(b\kappa -1\right)}^2-2b^2{B}^2}(120)$

and

$\omega =\frac{a\left(b{\kappa }^3-b^2-2B^2+2b{B}^2\kappa \right)}{{\left(1-b\kappa \right)}^2-2b^2{B}^2}+\frac{2\left(1-b\kappa \right)\left(c_l\ln \left(A_l\right)+c_{\bar{l}}\ln \left(A_{\bar{l}}\right)\right)}{{\left(1-b\kappa \right)}^2-2b^2{B}^2}.(121)$

When bκ ≠ 1, constraint conditions are

$\left(c_l+c_{\bar{l}}\right)\left(a-bv\right)>0(122)$

and

${\left(1-b\kappa \right)}^2-2b^2{B}^2\ne 0.(123)$

Hence, the bright soliton solutions of the log law non-linearity for the generalized coupled fractional NLS equations are

$\begin{array}{cc}\hfill & u_L\left(x,t\right)=A_1{e}^{-B\left[\frac{x^{\beta }}{\mathrm{\Gamma }\left(1+\beta \right)}-v\frac{t^{\alpha }}{\mathrm{\Gamma }\left(1+\alpha \right)}\right]+i\left[-\kappa \frac{x^{\beta }}{\mathrm{\Gamma }\left(1+\beta \right)}+\omega \frac{t^{\alpha }}{\mathrm{\Gamma }\left(1+\alpha \right)}+\sigma \right]},\hfill \\ \hfill & v_L\left(x,t\right)=A_2{e}^{-B\left[\frac{x^{\beta }}{\mathrm{\Gamma }\left(1+\beta \right)}-v\frac{t^{\alpha }}{\mathrm{\Gamma }\left(1+\alpha \right)}\right]+i\left[-\kappa \frac{x^{\beta }}{\mathrm{\Gamma }\left(1+\beta \right)}+\omega \frac{t^{\alpha }}{\mathrm{\Gamma }\left(1+\alpha \right)}+\sigma \right]}.\hfill \end{array}(124)$

4 Conclusion

In this paper, the generalized coupled space–time fractional NLS equations are constructed by the semi-inverse method and the Agrawal’s method. In the presence of spatio-temporal dispersion and birefringence, the Kerr, power, parabolic, dual-power, and log law non-linearity laws are studied. Then, we used the ansatz method to obtain the bright, dark, and singular soliton solution of the equations. At the same time, the constraints on the existence of these solitons are given. They can be further extended to other non-linear laws, such as the anti-cubic law, quadratic cubic laws, and cubic power law non-linearity.

Data availability statement

The original contributions presented in the study are included in the article/supplementary material; further inquiries can be directed to the corresponding author.

Author contributions

LF: investigation, methodology, writing—original draft, and writing—review and editing. JL: investigation, visualization, and resources. HY: conceptualization, investigation, methodology, and writing—review and editing. HD: investigation and result analysis. XH: investigation, supervision, methodology, validation, and writing—review and editing.

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors, and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

1. Agrawal GP. Nonlinear fiber optics. New York: Academic Press (2007).

Google Scholar

2. Ferreira MF, Facao MV, Latas SV, Sousa MH. Optical solitons in fibers for communication systems. Fiber Integrated Opt (2005) 24(3-4):287–313. doi:10.1080/01468030590923019

CrossRef Full Text | Google Scholar

3. Patel MG, Khant SB. Soliton transmission in fiber optics for long distance communication. Int Jounal Adv Res Electr Electron Instrumentation Eng (2014) 3(2):7100–7107.

Google Scholar

4. Chakraborty S, Nandy S, Barthakur A. Bilinearization of the generalized coupled nonlinear Schrödinger equation with variable coefficients and gain and dark-bright pair soliton solutions. Phys Rev E (2015) 91(2):023210. doi:10.1103/physreve.91.023210

PubMed Abstract | CrossRef Full Text | Google Scholar

5. Wazwaz AM, El-Tantawy SA. Gaussian soliton solutions to a variety of nonlinear logarithmic Schrödinger equation. J Electromagn Waves Appl (2016) 30(14):1909–17. doi:10.1080/09205071.2016.1222312

CrossRef Full Text | Google Scholar

6. Triki H, Wazwaz AM. Soliton solutions of the cubic-quintic nonlinear Schrödinger equation with variable coefficients. Rom J Phys (2016) 61:360366.

Google Scholar

7. Chen M, Li B, Yu YX. Darboux transformations, higher-order rational solitons and rogue wave solutions for a (2+1)-dimensional nonlinear Schrödinger equation. Commun Theor Phys (2019) 71(1):027–36. doi:10.1088/0253-6102/71/1/27

CrossRef Full Text | Google Scholar

8. Wang MM, Chen Y. Dynamic behaviors of general N-solitons for the nonlocal generalized nonlinear Schrödinger equation. Nonlinear Dyn (2021) 104:2621–38. doi:10.1007/s11071-021-06421-3

CrossRef Full Text | Google Scholar

9. Taghizadeh N, Mirzazadeh M, Frarhrooz F. Exact solutions of the nonlinear Schrödinger equation by the first integral method. Joural Math Anal Appl (2011) 374:549–53. doi:10.1016/j.jmaa.2010.08.050

CrossRef Full Text | Google Scholar

10. Aktosun T, Busse T, Demontis F, Mee C. Exact solutions to the nonlinear Schrödinger equation. J Phys A: Math Theor (2010) 43(2):1–14. doi:10.1007/978-3-0346-0161-0_1

CrossRef Full Text | Google Scholar

11. Feng BF, Ling L, Takahashi DA. Multi-breather and high-order rogue waves for the nonlinear Schrödinger equation on the elliptic function background. Stud Appl Math (2020) 144(1):46–101. doi:10.1111/sapm.12287

CrossRef Full Text | Google Scholar

12. Wang DS, Wang XL. Long-time asymptotics and the bright N-soliton solutions of the Kundu–Eckhaus equation via the Riemann–Hilbert approach. Nonlinear Anal Real World Appl (2018) 41:334–61. doi:10.1016/j.nonrwa.2017.10.014

CrossRef Full Text | Google Scholar

13. Nonlaopon K, Kumar S, Rezaei S, Bayones FS, Elagan SK. Some optical solutions to the higher-order nonlinear Schrödinger equation with Kerr nonlinearity and a local fractional derivative. Results Phys (2022) 36:105430. doi:10.1016/j.rinp.2022.105430

CrossRef Full Text | Google Scholar

14. Sun WR, Tian B, Wang YF, Zhen HL. Soliton excitations and interaction for the three-coupled fourth-order nonlinear Schrödinger equations in the alpha helical proteins. Eur Phys J D (2015) 69(146):1–9. doi:10.1140/epjd/e2015-60027-6

CrossRef Full Text | Google Scholar

15. Kanna T, Lakshmanan M. Exact soliton solutions of coupled nonlinear schrödinger equations: Shape-changing collisions, logic gates, and partially coherent solitons. Phys Rev E (2003) 67(4):046617–2. doi:10.1103/physreve.67.046617

PubMed Abstract | CrossRef Full Text | Google Scholar

16. West B, Bologna M, Grigolini P. Physics of fractal operators. San Diego: Institute for Nonlinear Science (2003).

Google Scholar

17. Tarasov VE. Fractional hydrodynamic equations for fractal media. Ann Phys (2005) 318:286–307. doi:10.1016/j.aop.2005.01.004

CrossRef Full Text | Google Scholar

18. Baskin E, Iomin A. Electrostatics in fractal geometry: Fractional calculus approach. Chaos, Solitons and Fractals (2011) 44:335–41. doi:10.1016/j.chaos.2011.03.002

CrossRef Full Text | Google Scholar

19. Tarasov VE. Fractional fokker-planck equation for fractal media. Chaos: Interdiscip J Nonlinear Sci (2005) 15:023102. doi:10.1063/1.1886325

PubMed Abstract | CrossRef Full Text | Google Scholar

20. Carpinteri A, Cornetti P. A fractional calculus approach to the description of stress and strain localization in fractal media. Chaos, Solitons and Fractals (2002) 13:85–94. doi:10.1016/s0960-0779(00)00238-1

CrossRef Full Text | Google Scholar

21. Tarasov VE. Fractional dynamics: Applications of fractional calculus to dynamics of particles, fields and media. Beijing: Higher Education Press (2010).

Google Scholar

22. Savescu M, Bhrawy A, Hilal E, Alshaery A, Biswas A. Optical solitons in magneto-optic waveguides with spatio-temporal dispersion. Frequenz (2014) 68:445–451. doi:10.1515/freq-2013-0164

CrossRef Full Text | Google Scholar

23. Younas U, Younis M, Seadawy AR, Rizvi STR, Althobaiti S, Sayed S. Diverse exact solutions for modified nonlinear Schrödinger equation with conformable fractional derivative. Results Phys (2021) 20:103766–10. doi:10.1016/j.rinp.2020.103766

CrossRef Full Text | Google Scholar

24. Laskin N. Fractional quantum mechanics and Lévy path integrals. Phys Lett A (2000) 268:298–305. doi:10.1016/s0375-9601(00)00201-2

CrossRef Full Text | Google Scholar

25. Laskin N. Fractional quantum mechanics. Phys Rev E (2000) 62:3135–45. doi:10.1103/physreve.62.3135

CrossRef Full Text | Google Scholar

26. Laskin N. Fractional schrödinger equation. Phys Rev E (2002) 66:056108. doi:10.1103/physreve.66.056108

CrossRef Full Text | Google Scholar

27. Herrmann R. Fractional calculus: An introduction for physicists. Singapore: World Scientific (2001).

Google Scholar

28. Longhi S. Fractional Schrödinger equationin optics. Opt Lett (2015) 40:1117–1120. doi:10.1364/ol.40.001117

PubMed Abstract | CrossRef Full Text | Google Scholar

29. Wang FZ, Salama SA, Khater MA. Optical wave solutions of perturbed time-fractional nonlinear Schrödinger equation. J Ocean Eng Sci (2022). doi:10.1016/j.joes.2022.03.014

CrossRef Full Text | Google Scholar

30. Okposoa NI, Veereshab P, Okposo EN. Solutions for time-fractional coupled nonlinear Schrödinger equations arising in optical solitons. Chin J Phys (2022) 77:965–84. doi:10.1016/j.cjph.2021.10.014

CrossRef Full Text | Google Scholar

31. Han TY, Li Z, Zhang X. Bifurcation and new exact traveling wave solutions to time-space coupled fractional nonlinear Schrödinger equation. Phys Lett A (2021) 395:127217. doi:10.1016/j.physleta.2021.127217

CrossRef Full Text | Google Scholar

32. Agrawal OP. Formulation of Euler–Lagrange equations for fractional variational problems. J Math Anal Appl (2002) 272:368–79. doi:10.1016/s0022-247x(02)00180-4

CrossRef Full Text | Google Scholar

33. Agrawal OP. A general formulation and solution scheme for fractional optimal control problems. Nonlinear Dyn (2004) 38:323–37. doi:10.1007/s11071-004-3764-6

CrossRef Full Text | Google Scholar

34. Bhrawy A, Alshaery A, Hilal E, Savescu M, Milovic D, Khan KR, et al. Optical solitons in birefringent fibers with spatio-temporal dispersion. Optik-international J Light Electron Opt (2014) 125:4935–44. doi:10.1016/j.ijleo.2014.04.025

CrossRef Full Text | Google Scholar

35. Vega-Guzman J, Ullah MZ, Asma M, Zhou Q, Biswas A. Dispersive solitons in magneto-optic waveguides. Superlattices and Microstructures (2017) 103:161–70. doi:10.1016/j.spmi.2017.01.020

CrossRef Full Text | Google Scholar

36. Savescu M, Khan KR, Kohl RW, Moraru L, Yildirim A, Biswas A. Optical soliton perturbation with improved nonlinear Schrödinger’s equation in nano fibers. J Nanoelectronics Optoelectronics (2013) 8:208–20. doi:10.1166/jno.2013.1459

CrossRef Full Text | Google Scholar

37. Biswas A, Milovic D. Bright and dark solitons of the generalized nonlinear Schrödinger’s equation. Commun Nonlinear Sci Numer Simulation (2010) 15:1473–84. doi:10.1016/j.cnsns.2009.06.017

CrossRef Full Text | Google Scholar

38. Biswas A, Khan KR, Rahman A, Yildirim A, Hayat T, Aldossary OM. Bright and dark optical solitons in birefringent fibers with Hamiltonian perturbations and kerr law nonlinearity. J Optoelectronics Adv Mater (2012) 14:571.

Google Scholar

39. Jumarie G. Table of some basic fractional calculus formulae derived from a modified Riemann–Liouville derivative for non-differentiable functions. Appl Math Lett (2009) 22:378–85. doi:10.1016/j.aml.2008.06.003

CrossRef Full Text | Google Scholar

40. Gazizov R, Kasatkin A, Lukashchuk SY. Continuous transformation groups of fractional differential equations. Vestnik Usatu (2007) 9:21.

Google Scholar

41. Jaradat H. New solitary wave and multiple soliton solutions for the time-space fractional boussinesq equation. Ltalian J Pure Appl Math (2016) 36:367–376.

Google Scholar

42. Biswas A, Konar S. Introduction to non-Kerr law optical solitons. Boca Raton: Chapman and Hall/CRC (2006).

Google Scholar

43. Triki H, Biswas A. Dark solitons for a generalized nonlinear Schrödinger equation with parabolic law and dual-power law nonlinearities. Math Methods Appl Sci (2011) 34:958–62. doi:10.1002/mma.1414

CrossRef Full Text | Google Scholar