- Freiburg Center for Data Analysis and Modeling (FDM), University of Freiburg, Freiburg im Breisgau, Germany
This mini-review discusses agent-based models as modeling techniques for studying pattern formation of multi-cellular systems in biology. We introduce and compare different agent-based model frameworks with respect to spatial representation, microenvironment, intracellular and extracellular reactions, cellular properties, implementation, and practical use. The guiding criteria for the considered selection of agent-based model frameworks are that they are actively maintained, well documented, and provide a model development workflow.
1 Introduction
Interacting cellular biological systems, such as bacterial communities, tissues, organoids, exhibit a plethora of phenomena, which are often not easy to understand intuitively. To explore and analyse cellular systems mathematical equations and/or computer simulations can be powerful tools. Because the fundamental building blocks or units of biological systems are cells, agent-based models with cells as the individual agents are natural simulation tools to study such systems. Pattern formation in cellular systems requires interactions between cells, the exchange of information, and, in case of self-organisation, that cells respond in a sufficiently non-linear manner, including feedback loops [1, 2]. Exchange of information can occur in a multitude of different ways and on different length scales: (short range) mechanical forces [3] and cellular junctions [4], (medium range) diffusing chemicals [5], and (long range) hormones [6]. Due to the individual cell based perspective agent-based models make it easy to implement these interactions and also the signal processing and response of the cells. In this mini-review we consider agent-based software frameworks with individual cells as agents, which are actively maintained and developed, provide documentation beyond a minimum, and provide a model development workflow1.
Traditionally, pattern formation in biology is studied using Partial Differential Equations (PDEs) that model continuous distribution of cells [7–10]. There is a wealth of literature onhow to solve coupled non-linear PDEs, estimate the parameters from data, and how to explore their behavior, e.g., sensitivity analysis, bifurcation analysis, see, e.g., [11–16]. PDEs are powerful tools, however, in a PDE cells have no spatial extension, ignoring the underlying cellular spatial structure. Although it is possible in a PDE to distinguish between the inside of the cells and their micro-environment, there is no unique or canonical way to handle, e.g., cell proliferation, differentiation, internal cell structure and other properties of the cells, which may be relevant for the questions at hand. This problem can be solved by cellular Automata (CA) [17] which consist of a regular grid with a finite number of states at each grid point and rules, determining how to update them accordingly. A further development of CA introduced ABMs [18–20] where the modeling approach is to handle cells as individual agents with rules, potentially with an internal structure and/or moving in space. By using coarse-graining or homogenization techniques one could derive a system of coupled PDEs from an ABM; there is, however, no unique way to go from a PDE to an ABM [21].
2 Agent-based models
An ABM is a collection of autonomous agents with a predefined set of rules, which depend on the existing state of the agent and external factors [22–25]. The rules can be discrete following logical if-else statements, continuous, i.e., Ordinary Differential Equations (ODEs) for intra-cellular reactions or a combination of both. Also, graphs, neural networks and other intricate algorithms can be implemented [26]. Nevertheless, one usually strives to employ the most simple set of rules sufficient to accurately describe the complexity of the desired system. Compared to macroscopic PDE models, ABMs are considered microscopic modeling, since they deal with agents directly and are thus more common in a bottom-up approach [27]. ABMs should not be seen as a technologically distinct toolset but rather as a mindset for researchers by modeling complex systems from the perspective of individual constituents.
Historically, precursors to ABMs were cellular Automata, which were developed by [17]. They reached widespread recognition even in the general public with the introduction of Conway’s “Game of Life” [28, 29]. Not long after, the first ABMs were being envisioned to study a biological system [18]. Up until the break of the century, ABMs were used in many fields of research such as modeling human crowd stampedes [30], bird flocks [19] or the prediction of financial markets [31]. With the rapidly growing accessibility and power of modern computer hardware, the popularity of ABMs kept on increasing, where tools such as NanoHUB [32] or the Systems Biology Markup Language (SBML) [33] further helped to share computational models between researchers. In order to study complex phenomena such as pattern formation ABMs must be able to capture cell-cell communication and cellular response mechanisms [10, 34–37]. In the next section we will compare the available ABM frameworks and discuss how they cover different cellular properties.
2.1 Comparison of ABMs
The effort of writing efficient solving algorithms and data structures in a usable fashion is considerable. Therefore, agent-based model frameworks (ABMFs) have emerged that define a certain workflow and implement a set of features, so that users of the frameworks can focus on their research question instead of having to spend a significant amount of time for design and implementation.
The majority of cell-agent-based model frameworks (CABMFs) evolved as generalizations of solutions to specific problems. BSim [38] was specifically designed to model bacterial populations and has been used to study gene regulatory control [39] and bacterial biofilms [40]. Chaste2 was designed as a Cancer, Heart and Soft Tissue Environment [41] and has been used in studying growth of epithelial monolayers [42]. CompuCell3D [43] originated from CompuCell [44], which was one of the first frameworks created and originally used to model only simple reaction-diffusion (RD) systems but was since extended considerably to cover a wider range of topics such as angiogenesis [45], cancer [46] and tissue engineering [47]. EPISIM was used to understand how varying proportions of T Cells emerge in different vertebrate taxa [48]. Morpheus [49] was applied to self-organization in neural stem cell divisions in adult zebrafish [50] and polarization of the multiciliated planarian epidermis [51]. MultiCellSim [52] resulted from the in-depth analysis of cell-cell communication and was since applied to Immuno-Oncology [53]. PhysiCell [54] is mainly used modeling cancer and tumor dynamics [55, 56]. TiSim/CellSys [57] was applied to liver regeneration processes [58]. VirtualLeaf [59] was specifically designed for modeling plants and emphasizes intercellular connections and details of the mechanical properties of the cell wall. Table 1 displays general characteristics of these modeling frameworks.
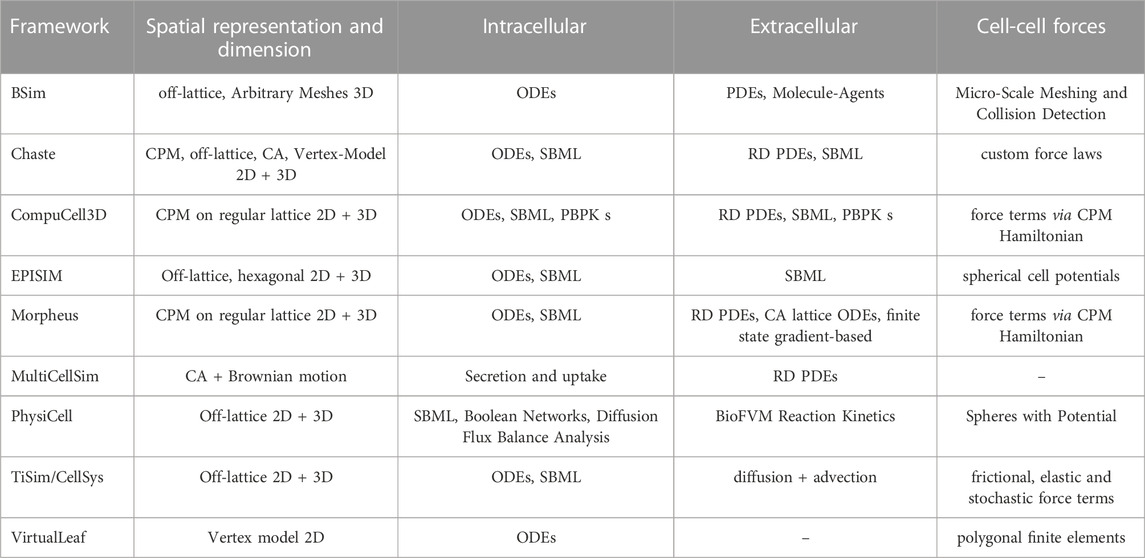
TABLE 1. Comparison of CABMFs in alphabetical order with respect to implementations of spatial representation, dimension, intra- and extracellular processes and cell-cell forces (Supplementary Table S1).
2.1.1 Spatial representation
A key distinction between ABMs is given by the difference of the spatial representation of cells and chemicals. ABMs can be separated into lattice-based and lattice-free, the former meaning that cells can only migrate between predefined lattice nodes, while the later permits free movement of cells in a given domain. Frameworks such as Chaste, PhysiCell, TiSim/CellSys and VirtualLeaf utilize off-lattice motion. Chaste3, CompuCell3D and Morpheus utilize lattice-based methods for cell-migration. This also means that no particular cellular shape is modeled explicitly, but rather cells follow rules (often potentials) to determine their respective quantity on lattice points. The disadvantage of the lattice-based approach is that it is limited in the spatial resolution, but in turn as an advantage it can yield considerable performance improvements. Off-lattice models often take a cell centre [60] approach meaning, a cell is defined by a single location vector and a shape (such as sphere, ellipsoid or cylinder) that governs interactions. BSim additionally has the ability to represent microbes as meshed objects thus offering a much higher resolution at micro-scale although at increased computational cost. Another less common modeling choice is to use a vertex model [61, 62] that represents each cell by a polygon, determined by a number of vertices, which can be subject to external forces, pressure, friction, adhesion, chemotaxis and other external and internal contributing factors. Lattice-bound models can utilize different discretizations such as regular Cartesian meshes, hexagonal or triangulated ones. Most of the presented frameworks in Table 1 can be used to simulate two-dimensional (2D) as well as three-dimensional (3D) scenarios. The Cellular Potts Model, also known as Glazier-Graner-Hogeweg (GGH) model [63, 64], is a common choice for many frameworks. Typically, in a Cellular Potts Model a Hamiltonian is formulated which describes the phenomenological “energy” of a given configuration of the system on a Euclidean lattice. Subsequently, the systems is evolved by minimizing the energy. LBIBCell modifies the classical Cellular Potts Model (CPM) approach by representing cells as evolving polygons with the immersed boundary method and thus obtains off-lattice cellular representations [65, 66].
2.1.2 External microenvironment
Transport processes of chemicals typically involve numerically solving (convection-) diffusion equations (67) and (68) with cell to extracellular matrix interaction nodes at the positions of the cellular agents on a (often euclidean) mesh. One exception is presented by VirtualLeaf where intracellular compartments are connected via membranes to adjacent cells and model transport through membrane-potentials [59]. Many ABMs utilize PDEs to model intracellular or extracellular transport processes such as convection and diffusion and allow for custom forms of reactions either via well-defined user-interfaces like Morpheus [49] or direct implementation into the source code.
2.1.3 Cellular processes
In an agent-based approach the processes occuring inside a cell can naturally be described by giving the agents the required set of functions. Each framework mentioned in Table 1 implements proliferation and cell-death mechanisms as key components. However, predefined and detailed cell-cycle routines such as utilized in PhysiCell [54] are less common, but are important to consider if, e.g., external factors such as growth hormones affect the cell-cycle [69]. In addition, internal chemicals may be released upon cell death. In order to model developmental processes such as embryogenesis, the framework needs to support cell-differentiation with dynamic modifications of the phenotype. Cell polarity can play an important role in many phenomena such as in ciliary rootlets in planarian epidermis [51]. Many frameworks like CompuCell3D, Chaste, Morpheus, VirtualLeaf support this feature. The geometry of the cell includes its spatial representation together with mechanical features such as adhesion and repulsion. PhysiCell utilize spheroid/ellipsoid cellular geometries, meaning each cell is represented by a sphere or ellipsoid and a corresponding potential. Further, adhesion plays an important role in cell-cell interactions and communication. Lattice-free frameworks often model it by choosing a particular form of interaction potential. One sophisticated example is the experimental Johnson-Kendall-Roberts (JKR) potential [70], which was derived from the Hertz contact model [71]. It also models cell separation and is implemented by CellSys. Other frameworks that implement a CPM treat adhesion via interaction terms in its Hamiltonian Formulation [72]. In the context of vertex models, force potentials can also be utilized although the implementation is often more complex. All of the above ABMs are able to model stochastic cell migration, excluding VirtualLeaf since almost all plant cells are non-motile. Collectively arising forces and friction which can play an important role in early embryonic development [73] may be harder to simulate if the geometry of the cells is solely implemented as spheroid/ellipsoid. For frameworks such as PhysiCell and TiSim/CellSys who additionally do not support polarity, modeling of force-mitigated spatial effects is difficult. Chemotaxis is a key concept in cell-sorting [74] and can be implemented by any framework that supports migration and can calculate reactant gradients. All of the presented frameworks can capture intracellular reactions by using ODEs ignoring the internal spatial structure of the cells; different reaction compartments can be easily introduced by coupling of ODEs. Some (e.g., Chaste, EPISIM) can also handle intracellular stochastic reactions, using the Gillespie algorithm [75].
2.2 Implementational details
2.2.1 Development, standards and features
Development and design of efficient algorithms and their implementation require knowledge in software engineering and in writing maintainable code, as these frameworks are usually developed by teams rather than by individuals and consist of many thousands of lines of code. The Chaste framework was one of the first projects to follow agile coding principles and other best-practice workflows such as rigorous unit-testing [76]. All presented CABMFs are written in C++ which together with the C and Fortran language have historically served as the de facto languages for high-performance software development. In addition to CABMFs, researchers have over the last two decades developed internationally recognized formats to seamlessly share model details (e.g., SMBL). This is utilized in Chaste, CompuCell3D, Morpheus and PhysiCell4 and allows for rapid model development, implementation and comparison to classical ODE and PDE solvers. CompuCell3D is also able to model physiologically based pharmacokinetics (PBPKs). Additionally, many frameworks come with dedicated [sometimes graphical user interfaces (GUIs)] tools for configuration, analysis, batch-processing, visualization and other workflow-aiding features which are valuable additions. In this regard, EPISIM is special as it utilizes the popular COPASI [77] and Mason [78] software and plugins for the eclipse code editor [79] to build the application.
3 Studying pattern formation with agent-based models
3.1 Applications
Pattern formation in cellular biological systems can occur via self-assembly or self-organization and ABMs have been applied to investigate both aspects. Chaste was used to study cell migration in the crypt [80]. Furthermore, CompuCell3D provided examples for self-organization in work on polarization [81] and studies of physical forces [82] in migrating cells. Morpheus was used to describe pattern formations in the telencephalon of adult zebrafish [83] and was also used to study growth of the Drosophila wing via cell recruitment [84]. PhysiCell recently provided insights to formation of patterns in tumour spheroids [56]. Pattern formation in dicot leaves was modeled using VirtualLeaf [85]. ABMs allow researchers to examine complicated models which would otherwise be hard to study and interpret with classical PDEs.
Figure 1 shows results of a multi-scale model using PhysiCell [54]. We can observe that the pattern changes as the number of patterning cells (type I) increases. This simple example shows, how to readily formulate and explore models in an ABM mindset - by increasing the cell number in this case. Constructing a corresponding PDE model is much harder and not uniquely defined.
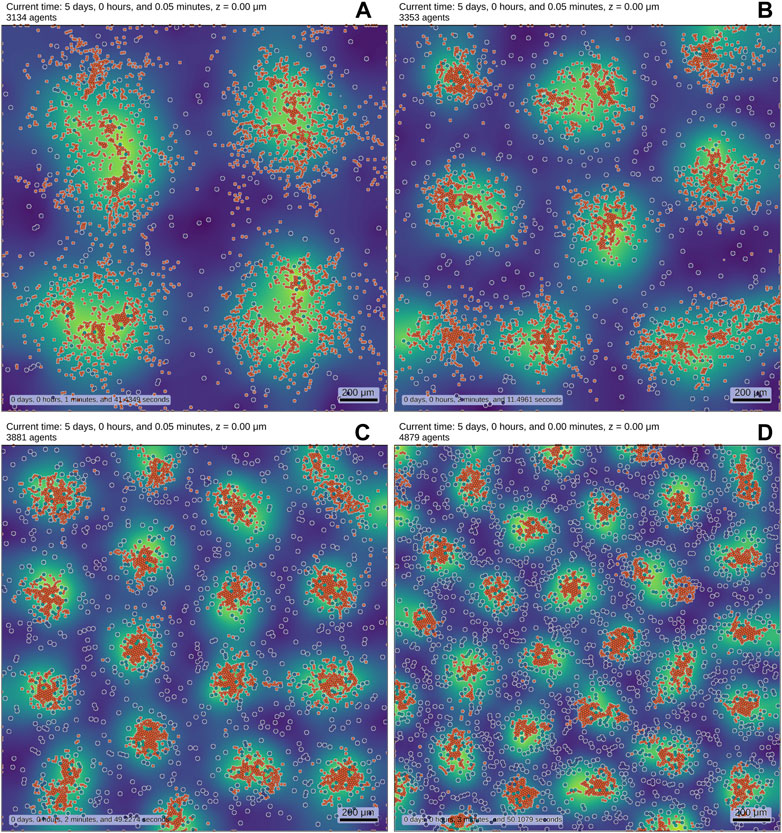
FIGURE 1. We implemented a RD system (see also Supplementary Equation SB1-SB4–Equations) in an ABM to showcase results. The simulation contains two distinct cell types, which are both motile and initially randomly distributed. Cell type I (blue-shaded, white border) obey reaction equations given by a substrate-depletion system [36] and are colored by their internal concentration of the activator. Cell type II (orange) is smaller than cell type I and is chemotactically attracted by the activator which is secreted by cell type I. The background displays the density profile of the secreted activator molecule (yellow: high density, blue: low density). The number of cells I is increased from (A–D) (256, 484, 1,024, 2,025), while the number of cells II remains fixed to 3,000. Cell death reduces the overall number of agents. The pictures show the final state of the simulation after reaching (up to statistical fluctuations) a steady-state. The variations in cell number alone lead to different emerging patterns. While these results may be obtainable by a modified purely PDE-based approach, they are much easier to interpret and develop in an ABM. The simulations were carried out using PhysiCell [54].
3.2 Techniques and challenges
CABMFs allow researchers to investigate biological systems on the cellular level with the option to implement many details, with the downside of substantial computational cost. To combat this issue, all presented frameworks are of multi-scale nature.
The relevant time- and length-scales are identified and the corresponding sub-processes are modeled and updated according to their scales. This can greatly improve performance as for example diffusion-driven processes tend to be much faster than cell migrational or phenotypical processes [86]. Other techniques to improve performance are efficient
4 Discussion
This review introduced the concepts of agent-based models in cellular systems. We compared different frameworks with respect to their conceptual and implementational differences. To date, a large number of different agent-based model frameworks with different strengths and weaknesses exist and are openly available. The multitude of options is a clear indication for the overall interest in the subject. ABMs provide a unique tool to integrate combinations of processes and study their respective dynamics. Even for the exploration of systems that lack sufficient data, ABMs can be used as they can be developed initially with rather simplified rule sets, by means of which researchers can generate hypotheses, which can in turn guide the design of laboratory experiments. By this cycle of experimental and computational methods, the model and the experiments can be improved and finally increase the conceptual knowledge about the system. Due to this, it is important to understand the challenges of ABMs and their limitations. ABMs can be seen as a mapping of specific rules to spatial configurations. This mapping is non-unique, and the question arises, how the results of the ABM depend on the set of rules and the used parameters. How are the values (or distributions) of the parameters estimated? How does the uncertainty in the system parameters affect the predictions of the simulations? In particular, when analyzing the (often stochastic) results of a simulation, one needs to quantify the influence of the parameter uncertainty which is a considerable challenge. Besides these questions and challenges it can be expected that ABMs are quickly becoming mainstream tools in biology.
Author contributions
CF and JP devised the study. JP wrote the first draft of the manuscript. JP and CF revised, read, and approved the submitted version.
Funding
CF and JP received funding from FET-Open research and innovation actions grant under the European Union’s Horizon 2020 (CyGenTiG; grant agreement 801041).
Conflict of interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Publisher’s note
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
Supplementary material
The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/fphy.2022.968409/full#supplementary-material
Footnotes
1An extended list of other agent-based models (ABMs) can be found in the Supplementary material.
2We only consider here the cell-based part of the chaste software environment.
3Cell-based Chaste supports off-lattice as well as on-lattice representations.
4Via an addon libroadrunner and only for intracellular reactions.
References
1. Mitrophanov AY, Groisman EA. Positive feedback in cellular control systems. BioEssays : News Rev Mol Cell Dev Biol (2008) 30:542–55. doi:10.1002/bies.20769
2. Deritei D, Rozum J, Ravasz Regan E, Albert R. A feedback loop of conditionally stable circuits drives the cell cycle from checkpoint to checkpoint. Scientific Rep (2019) 9:16430. doi:10.1038/s41598-019-52725-1
3. Vining KH, Mooney DJ. Mechanical forces direct stem cell behaviour in development and regeneration. Nat Rev Mol Cel Biol (2017) 18:728–42. doi:10.1038/nrm.2017.108
4. Bloemendal S, Kück U. Cell-to-cell communication in plants, animals, and fungi: A comparative review. Naturwissenschaften (2013) 100:3–19. doi:10.1007/s00114-012-0988-z
5. Duester G. Retinoic acid synthesis and signaling during early organogenesis. Cell (2008) 134:921–31. doi:10.1016/j.cell.2008.09.002
6. Greenwood FC, Landon J. Growth hormone secretion in response to stress in man. Nature (1966) 210:540–1. doi:10.1038/210540a0
7. Kolmogorov A, Petrovsky L, Piskunov N. An investigation of the diffusion equation combined with an increase in mass and its application to a biological problem. Bull Uni Mosc Ser Int A (1937) 1:1–26.
8. Turing AM. The chemical basis of morphogenesis. Philos Trans R Soc Lond Ser B, Biol Sci (1952) 237:37–72.
9. Koch A, Meinhardt H. Biological pattern formation: From basic mechanisms to complex structures. Rev Mod Phys (1994) 66:1481–507. doi:10.1103/revmodphys.66.1481
10. Gierer A, Meinhardt H. A theory of biological pattern formation. Kybernetik (1972) 12:30–9. doi:10.1007/bf00289234
11. Browder F. Partial differential equations in the 20th century. Adv Maths (1998) 135:76–144. doi:10.1006/aima.1997.1713
12. Müller TG, Timmer J. Parameter identification techniques for partial differential equations. Int J Bifurcation Chaos (2004) 14:2053–60. doi:10.1142/S0218127404010424
13. Stavroulakis IP, Tersian SA. Partial differential equations. An introduction with mathematica and MAPLE. World Scientific (2004). doi:10.1371/journal.pone.0197666
14. Baker RE, Gaffney EA, Maini PK. Partial differential equations for self-organization in cellular and developmental biology. Nonlinearity (2008) 21:R251–90. doi:10.1088/0951-7715/21/11/R05
15. Saltelli A, editor. Global sensitivity analysis: The primer. Chichester, England ; Hoboken, NJ: John Wiley (2008).
16. Kielhöfer H. Bifurcation theory, applied mathematical sciences, 156. New York, NY: Springer New York (2012). doi:10.1007/978-1-4614-0502-3
17. Von Neumann J, Burks AWAW. Theory of self-reproducing Automata. Urbana: University of Illinois Press (1966).
18. Schelling TC. Dynamic models of segregation. J Math Sociol (1971) 1:143–86. doi:10.1080/0022250X.1971.9989794
19. Reynolds CW. Flocks, herds and schools: A distributed behavioral model. ACM SIGGRAPH Comput Graphics (1987) 21:25–34. doi:10.1145/37402.37406
20. Glen CM, Kemp ML, Voit EO. Agent-based modeling of morphogenetic systems: Advantages and challenges. PLOS Comput Biol (2019) 15:e1006577. doi:10.1371/journal.pcbi.1006577
22. Bodine EN, Panoff RM, Voit EO, Weisstein AE. Agent-based modeling and simulation in mathematics and biology education. Bull Math Biol (2020) 82:101. doi:10.1007/s11538-020-00778-z
23. Metzcar J, Wang Y, Heiland R, Macklin P. A review of cell-based computational modeling in cancer biology. JCO Clin Cancer Inform (2019) 3:1–13. doi:10.1200/CCI.18.00069
24. Tomlin CJ, Axelrod JD. Biology by numbers: Mathematical modelling in developmental biology. Nat Rev Genet (2007) 8:331–40. doi:10.1038/nrg2098
25. Nagarajan K, Ni C, Lu T. Agent-based modeling of microbial communities. ACS Synth Biol (2022) 11:3564–74. doi:10.1021/acssynbio.2c00411
26. Haynes T, Sen S. Evolving behavioral strategies in predators and prey. In: Weiß G, Sen S, editors. Adaption and learning in multi-agent systems. Berlin, Heidelberg: SpringerLecture Notes in Computer Science (1996). p. 113–26. doi:10.1007/3-540-60923-7_22
27. Bonabeau E. Agent-based modeling: Methods and techniques for simulating human systems. Proc Natl Acad Sci (2002) 99:7280–7. doi:10.1073/pnas.082080899
28. Gardner M. Mathematical games. Scientific Am (1970) 223:120–3. doi:10.1038/scientificamerican1070-120
29. Berlekamp ER, Conway JH, Guy RK, Peters AK. Winning Ways for Your Mathematical Plays. 2nd ed. edn. (Wellesley, MA: A.K. Peters) (2001).
30. Helbing D, Farkas I, Vicsek T. Simulating dynamical features of escape panic. Nature (2000) 407:487–90. doi:10.1038/35035023
31. Kephart JO, Hanson JE, Greenwald AR. Dynamic pricing by software agents. Computer Networks (2000) 32:731–52. doi:10.1016/S1389-1286(00)00026-8
32. Klimeck G, McLennan M, Brophy SP, Adams GB, Lundstrom MS. nanoHUB.org: Advancing education and research in nanotechnology. Comput Sci Eng (2008) 10:17–23. doi:10.1109/MCSE.2008.120
33. Keating SM, Waltemath D, König M, Zhang F, Dräger A, Chaouiya C, et al. SBML Level 3: An extensible format for the exchange and reuse of biological models. Mol Syst Biol (2020) 16:e9110. doi:10.15252/msb.20199110
34. Bajpai S, Prabhakar R, Chelakkot R, Inamdar MM. Role of cell polarity dynamics and motility in pattern formation due to contact-dependent signalling. J R Soc Interf (2021) 18:20200825. doi:10.1098/rsif.2020.0825
35. Nakamasu A, Takahashi G, Kanbe A, Kondo S. Interactions between zebrafish pigment cells responsible for the generation of Turing patterns. Proc Natl Acad Sci (2009) 106:8429–34. doi:10.1073/pnas.0808622106
36. Schnakenberg J. Simple chemical reaction systems with limit cycle behaviour. J Theor Biol (1979) 81:389–400. doi:10.1016/0022-5193(79)90042-0
37. Wolpert L, Wolpert EPBL, Tickle C, Arias AM. Principles of development. USA): Oxford University Press (2015).
38. Gorochowski TE, Matyjaszkiewicz A, Todd T, Oak N, Kowalska K, Reid S, et al. BSim: An agent-based tool for modeling bacterial populations in systems and synthetic biology. PLOS ONE (2012) 7:e42790. doi:10.1371/journal.pone.0042790
39. Martinelli V, Salzano D, Fiore D, di Bernardo M. Multicellular PI control for gene regulation in microbial consortia. IEEE Control Syst Lett (2022) 6:3373–8. doi:10.1109/LCSYS.2022.3184922
40. Jin X, Marshall JS. Influence of cell interaction forces on growth of bacterial biofilms. Phys Fluids (2020) 32:091902. doi:10.1063/5.0021126
41. Cooper F, Baker R, Bernabeu M, Bordas R, Bowler L, Bueno-Orovio A, et al. Chaste: Cancer, Heart and Soft tissue environment. J Open Source Softw (2020) 5:1848. doi:10.21105/joss.01848
42. Dunn SJ, Fletcher AG, Chapman SJ, Gavaghan DJ, Osborne JM. Modelling the role of the basement membrane beneath a growing epithelial monolayer. J Theor Biol (2012) 298:82–91. doi:10.1016/j.jtbi.2011.12.013
43. Swat MH, Thomas GL, Belmonte JM, Shirinifard A, Hmeljak D, Glazier JA. Chapter 13 - multi-scale modeling of tissues using CompuCell3D. In: Methods in cell biology Asthagiri AR, Arkin AP, editors, 110. Academic PressComputational Methods in Cell Biology (2012). p. 325–66. doi:10.1016/B978-0-12-388403-9.00013-8
44. Izaguirre JA, Chaturvedi R, Huang C, Cickovski T, Coffland J, Thomas G, et al. CompuCell, a multi-model framework for simulation of morphogenesis. Bioinformatics (2004) 20:1129–37. doi:10.1093/bioinformatics/bth050
45. Nivlouei SJ, Soltani M, Carvalho J, Travasso R, Salimpour MR, Shirani E. Multiscale modeling of tumor growth and angiogenesis: Evaluation of tumor-targeted therapy. PLOS Comput Biol (2021) 17:e1009081. doi:10.1371/journal.pcbi.1009081
46. Asadullah KS, Saxena N, Sarkar M, Barai A, Sen S. Combined heterogeneity in cell size and deformability promotes cancer invasiveness. J Cel Sci (2021) 134:jcs250225. jcs250225. doi:10.1242/jcs.250225
47. Moldovan NI. Position of the kenzan method in the space-time of tissue engineering. In: Nakayama K, editor. Kenzan method for scaffold-free biofabrication. Cham: Springer International Publishing (2021). p. 17–31. doi:10.1007/978-3-030-58688-1_2
48. Aghaallaei N, Dick AM, Tsingos E, Inoue D, Hasel E, Thumberger T, et al. Aβ/Γδ T cell lineage outcome is regulated by intrathymic cell localization and environmental signals. Sci Adv (2021) 7:eabg3613. eabg3613. doi:10.1126/sciadv.abg3613
49. Starruß J, de Back W, Brusch L, Morpheus DA. Morpheus: A user-friendly modeling environment for multiscale and multicellular systems biology. Bioinformatics (2014) 30:1331–2. doi:10.1093/bioinformatics/btt772
50. Mulberry N, Edelstein-Keshet L. Self-organized multicellular structures from simple cell signaling: A computational model. Phys Biol (2020) 17:066003. doi:10.1088/1478-3975/abb2dc
51. Vu HTK, Mansour S, Kücken M, Blasse C, Basquin C, Azimzadeh J, et al. Dynamic polarization of the multiciliated planarian epidermis between body plan landmarks. Develop Cel (2019) 51:526–42.e6. e6. doi:10.1016/j.devcel.2019.10.022
52. Dang Y, Grundel DAJ, Youk H. Cellular dialogues: Cell-cell communication through diffusible molecules yields dynamic spatial patterns. Cel Syst (2020) 10:82–98.e7. e7. doi:10.1016/j.cels.2019.12.001
53. Karolak A, Branciamore S, McCune JS, Lee PP, Rodin AS, Rockne RC. Concepts and applications of information theory to immuno-oncology. Trends Cancer (2021) 7:335–46. doi:10.1016/j.trecan.2020.12.013
54. Ghaffarizadeh A, Heiland R, Friedman SH, Mumenthaler SM, PhysiCell MP. PhysiCell: An open source physics-based cell simulator for 3-D multicellular systems. PLOS Comput Biol (2018) 14:e1005991. doi:10.1371/journal.pcbi.1005991
55. Ponce-de-Leon M, Montagud A, Akasiadis C, Schreiber J, Ntiniakou T, Valencia A. Optimizing dosage-specific treatments in a multi-scale model of a tumor growth. Front Mol Biosciences (2022) 9:836794. doi:10.3389/fmolb.2022.836794
56. Gonçalves IG, Garcia-Aznar JM. Extracellular matrix density regulates the formation of tumour spheroids through cell migration. PLOS Comput Biol (2021) 17:e1008764. doi:10.1371/journal.pcbi.1008764
57. Hoehme S, Drasdo D. A cell-based simulation software for multi-cellular systems. Bioinformatics (2010) 26:2641–2. doi:10.1093/bioinformatics/btq437
58. Hoehme S, Brulport M, Bauer A, Bedawy E, Schormann W, Hermes M, et al. Prediction and validation of cell alignment along microvessels as order principle to restore tissue architecture in liver regeneration. Proc Natl Acad Sci (2010) 107:10371–6. doi:10.1073/pnas.0909374107
59. Merks RM, Guravage M, Inzé D, Beemster GT. VirtualLeaf: An open-source framework for cell-based modeling of plant tissue growth and development. Plant Physiol (2011) 155:656–66. doi:10.1104/pp.110.167619
60. Drasdo D. Center-based single-cell models: An approach to multi-cellular organization based on a conceptual analogy to colloidal particles. In: Anderson ARA, Chaplain MAJ, Rejniak KA, editors. Single-cell-based Models in Biology and medicine (basel: Birkhäuser), mathematics and biosciences in interaction (Basel, CH: Birkhäuser) (2007). p. 171–96. doi:10.1007/978-3-7643-8123-3_8
61. Nagai T, Honda H. A dynamic cell model for the formation of epithelial tissues. Philosophical Mag B (2001) 81:699–719. doi:10.1080/13642810108205772
62. Smith C. On vertex-vertex systems and their use in geometric and biological modelling Ph.D. thesis, University of Calgary (2006). doi:10.11575/PRISM/439
63. Graner F, Glazier JA. Simulation of biological cell sorting using a two-dimensional extended Potts model. Phys Rev Lett (1992) 69:2013–6. doi:10.1103/PhysRevLett.69.2013
64. Savill NJ, Hogeweg P. Modelling morphogenesis: From single cells to crawling slugs. J Theor Biol (1997) 184:229–35. doi:10.1006/jtbi.1996.0237
65. Rejniak KA. An immersed boundary framework for modelling the growth of individual cells: An application to the early tumour development. J Theor Biol (2007) 247:186–204. doi:10.1016/j.jtbi.2007.02.019
66. Peskin CS. The immersed boundary method. Acta Numerica (2002) 11:479–517. doi:10.1017/S0962492902000077
67. Alberts B, Johnson A, Lewis J, Raff M, Roberts K, Walter P. Principles of membrane transport. In: Molecular Biology of the cell. 4th ed. (2002).
68. Chandrasekhar S. Stochastic problems in physics and astronomy. Rev Mod Phys (1943) 15:1–89. doi:10.1103/RevModPhys.15.1
69. Kassem M, Blum W, Ristelli J, Mosekilde L, Eriksen EF. Growth hormone stimulates proliferation and differentiation of normal human osteoblast-like cells in vitro. Calcified Tissue Int (1993) 52:222–6. doi:10.1007/BF00298723
70. Johnson KL, Kendall K, Roberts AD. Surface energy and the contact of elastic solids. Proc R Soc Lond A. Math Phys Sci (1971) 324:301–13. doi:10.1098/rspa.1971.0141
71. Hertz H. Ueber die Berührung fester elastischer Körper. J fur die reine und angewandte Mathematik (1882) 92:156–171. doi:10.1515/crll.1882.92.156
72. Marée AFM, Grieneisen VA, Hogeweg P. The cellular Potts model and biophysical properties of cells, tissues and morphogenesis. In: Anderson ARA, Chaplain MAJ, Rejniak KA, editors. Single-cell-based models in biology and medicine (Basel, CH: Birkha user, Mathematics and Biosciences in Interaction) (2007). p. 107–36. doi:10.1007/978-3-7643-8123-3_5
73. Smutny M, Ákos Z, Grigolon S, Shamipour S, Ruprecht V, Čapek D, et al. Friction forces position the neural anlage. Nat Cel Biol (2017) 19:306–17. doi:10.1038/ncb3492
74. Vasiev B, Weijer CJ. Modeling chemotactic cell sorting during Dictyostelium discoideum mound formation. Biophysical J (1999) 76:595–605. doi:10.1016/S0006-3495(99)77228-0
75. Gillespie DT. Stochastic simulation of chemical kinetics. Annu Rev Phys Chem (2007) 58:35–55. doi:10.1146/annurev.physchem.58.032806.104637
76. Pitt-Francis J, Bernabeu MO, Cooper J, Garny A, Momtahan L, Osborne J, et al. Chaste: Using agile programming techniques to develop computational biology software. Philos Trans R Soc A: Math Phys Eng Sci (2008) 366:3111–36. doi:10.1098/rsta.2008.0096
77. Hoops S, Sahle S, Gauges R, Lee C, Pahle J, Simus N, et al. COPASI—A COmplex PAthway SImulator. Bioinformatics (2006) 22:3067–74. doi:10.1093/bioinformatics/btl485
78. Luke S, Cioffi-Revilla C, Panait L, Sullivan K, Mason BG. Mason: A multiagent simulation environment. SIMULATION (2005) 81:517–27. doi:10.1177/0037549705058073
79. Burnette E. Eclipse IDE Pocket Guide: Using the Full-Featured IDE. Sebastopol, CA: O’Reilly Media, Inc. (2005).
80. Dunn SJ, Näthke IS, Osborne JM. Computational models reveal a passive mechanism for cell migration in the crypt. PLOS ONE (2013) 8:e80516. doi:10.1371/journal.pone.0080516
81. Thomas GL, Fortuna I, Perrone GC, Graner F, de Almeida RMC. Shape–velocity correlation defines polarization in migrating cell simulations. Physica A: Stat Mech its Appl (2022) 587:126511. doi:10.1016/j.physa.2021.126511
82. Pan M, Yang Y, Liu L. Physical forces influence the self-organization of the leader cell formation during collective cell migration. In: 2021 IEEE 16th International Conference on Nano/Micro Engineered and Molecular Systems (NEMS) (2021). p. 1923. doi:10.1109/NEMS51815.2021.9451315
83. Lupperger V, Marr C, Chapouton P. Reoccurring neural stem cell divisions in the adult zebrafish telencephalon are sufficient for the emergence of aggregated spatiotemporal patterns. PLOS Biol (2020) 18:e3000708. doi:10.1371/journal.pbio.3000708
84. Muñoz-Nava LM, Alvarez HA, Flores-Flores M, Chara O, Nahmad M. A dynamic cell recruitment process drives growth of the Drosophila wing by overscaling the vestigial expression pattern. Develop Biol (2020) 462:141–51. doi:10.1016/j.ydbio.2020.03.009
85. Holloway DM, Wenzel CL. Polar auxin transport dynamics of primary and secondary vein patterning in dicot leaves. silico Plants (2021) 3. diab030. doi:10.1093/insilicoplants/diab030
86. Keener JP, Keizer JE. Fast and slow time scales. In: Fall CP, Marland ES, Wagner JM, Tyson JJ, editors. Computational cell biology. New York, NY: SpringerInterdisciplinary Applied Mathematics (2002). p. 77–100. doi:10.1007/978-0-387-22459-6_4
87. Meagher D. Geometric modeling using octree encoding. Comput Graphics Image Process (1982) 19:129–47. doi:10.1016/0146-664X(82)90104-6
88. Chandra R, editor. Parallel programming in OpenMP. San Francisco, CA: Morgan Kaufmann Publishers (2001).
89. Steuwer M, Kegel P, Gorlatch S. SkelCL - a portable skeleton library for high-level GPU programming. In: 2011 IEEE International Symposium on Parallel and Distributed Processing Workshops and Phd Forum. Anchorage, AK, USA: IEEE (2011). p. 1176–82. doi:10.1109/IPDPS.2011.269
90. Efimenko M, Ignatev A, Koshechkin K. Review of medical image recognition technologies to detect melanomas using neural networks. BMC Bioinformatics (2020) 21:270. doi:10.1186/s12859-020-03615-1
91. Caicedo JC, Cooper S, Heigwer F, Warchal S, Qiu P, Molnar C, et al. Data-analysis strategies for image-based cell profiling. Nat Methods (2017) 14:849–63. doi:10.1038/nmeth.4397
92. Ker J, Wang L, Rao J, Lim T. Deep learning applications in medical image analysis. IEEE Access (2018) 6:9375–89. doi:10.1109/ACCESS.2017.2788044
93. Hoehme S, Friebel A, Hammad S, Drasdo D, Hengstler JG. Creation of three-dimensional liver tissue models from experimental images for systems medicine. In: Stock P, Christ B, editors. Hepatocyte transplantation: Methods and protocols. New York, NY: SpringerMethods in Molecular Biology (2017). p. 319–62. doi:10.1007/978-1-4939-6506-9_22
94. Chen SH, Londoño-Larrea P, McGough AS, Bible AN, Gunaratne C, Araujo-Granda PA, et al. Application of machine learning techniques to an agent-based model of pantoea. Front Microbiol (2021) 12:726409. doi:10.3389/fmicb.2021.726409
95. Sivakumar N, Mura C, Peirce SM. Combining machine learning and agent-based modeling to study biomedical systems. Front Sys Biol (2022) 2.
96. Kramer MA. Nonlinear principal component analysis using autoassociative neural networks. AIChE J (1991) 37:233–43. doi:10.1002/aic.690370209
97. Aguilar B, Gibbs DL, Reiss DJ, McConnell M, Danziger SA, Dervan A, et al. A generalizable data-driven multicellular model of pancreatic ductal adenocarcinoma. GigaScience (2020) 9:giaa075. giaa075. doi:10.1093/gigascience/giaa075
98. Kang S, Kahan S, McDermott J, Flann N, Shmulevich I. Biocellion : Accelerating computer simulation of multicellular biological system models. Bioinformatics (2014) 30:3101–8. doi:10.1093/bioinformatics/btu498
99. Wei G, Bogdan P, Marculescu R. Efficient modeling and simulation of bacteria-based nanonetworks with BNSim. IEEE J Selected Areas Commun (2013) 31:868–78. doi:10.1109/JSAC.2013.SUP2.12130019
100. Kaizu K, Nishida K, Sakamoto Y, Kato S, Niina T, Nishida N, et al. E-Cell System version 4. Zenodo (2020). doi:10.5281/ZENODO.3865614
101. Sütterlin T, Kolb C, Dickhaus H, Jäger D, Grabe N. Bridging the scales: Semantic integration of quantitative SBML in graphical multi-cellular models and simulations with EPISIM and COPASI. Bioinformatics (Oxford, England) (2013) 29:223–9. doi:10.1093/bioinformatics/bts659
102. Gutiérrez M, Gregorio-Godoy P, Pérez del Pulgar G, Muñoz LE, Sáez S, Rodríguez-Patón A. A new improved and extended version of the multicell bacterial simulator gro. ACS Synth Biol (2017) 6:1496–508. doi:10.1021/acssynbio.7b00003
103. Lardon LA, Merkey BV, Martins S, Dötsch A, Picioreanu C, Ju K, et al. iDynoMiCS: Next-generation individual-based modelling of biofilms. Environ Microbiol (2011) 13:2416–34. doi:10.1111/j.1462-2920.2011.02414.x
104. Tanaka S, Sichau D, Iber D. LBIBCell: A cell-based simulation environment for morphogenetic problems. Bioinformatics (2015) 31:2340–7. doi:10.1093/bioinformatics/btv147
105. Delile J, Herrmann M, Peyriéras N, Doursat R. A cell-based computational model of early embryogenesis coupling mechanical behaviour and gene regulation. Nat Commun (2017) 8:13929. doi:10.1038/ncomms13929
106. Letort G, Montagud A, Stoll G, Heiland R, Barillot E, Macklin P, et al. PhysiBoSS: A multi-scale agent-based modelling framework integrating physical dimension and cell signalling. Bioinformatics (2019) 35:1188–96. doi:10.1093/bioinformatics/bty766
107. Vladimirov N, Løvdok L, Lebiedz D, Sourjik V. Dependence of bacterial chemotaxis on gradient shape and adaptation rate. PLOS Comput Biol (2008) 4:e1000242. doi:10.1371/journal.pcbi.1000242
108. Milde F, Tauriello G, Haberkern H, Koumoutsakos P. SEM++: A particle model of cellular growth, signaling and migration. Comput Part Mech (2014) 1:211–27. doi:10.1007/s40571-014-0017-4
109. Angermann BR, Klauschen F, Garcia AD, Prustel T, Zhang F, Germain RN, et al. Computational modeling of cellular signaling processes embedded into dynamic spatial contexts. Nat Methods (2012) 9:283–9. doi:10.1038/nmeth.1861
110. Canela-Xandri O, Anbari S, TiFoSi BJ. TiFoSi: An efficient tool for mechanobiology simulations of epithelia. Bioinformatics (2020) 36:4525–6. doi:10.1093/bioinformatics/btaa592
111. Cytowski M, Szymanska Z. Large-scale parallel simulations of 3D cell colony dynamics: The cellular environment. Comput Sci Eng (2015) 17:44–8. doi:10.1109/MCSE.2015.66
112. Hamant O, Heisler MG, Jönsson H, Krupinski P, Uyttewaal M, Bokov P, et al. Developmental patterning by mechanical signals in arabidopsis. Science (2008) 322:1650–5. doi:10.1126/science.1165594
113. Jönsson H, Heisler MG, Shapiro BE, Meyerowitz EM, Mjolsness E. An auxin-driven polarized transport model for phyllotaxis. Proc Natl Acad Sci (2006) 103:1633–8. doi:10.1073/pnas.0509839103
114. Resasco DC, Gao F, Morgan F, Novak IL, Schaff JC, Slepchenko BM. Virtual Cell: Computational tools for modeling in cell biology. WIREs Syst Biol Med (2012) 4:129–40. doi:10.1002/wsbm.165
Keywords: agent-based models (ABM), computer simulation, biological cellular systems, pattern formation, developmental biology
Citation: Pleyer J and Fleck C (2023) Agent-based models in cellular systems. Front. Phys. 10:968409. doi: 10.3389/fphy.2022.968409
Received: 13 June 2022; Accepted: 09 December 2022;
Published: 04 January 2023.
Edited by:
Pau Formosa-Jordan, Max Planck Institute for Plant Breeding Research, GermanyReviewed by:
Yiteng Dang, Max Planck Institute for the Physics of Complex Systems, GermanyH. Ariel Alvarez, Universidad Nacional de La Plata, Argentina
Copyright © 2023 Pleyer and Fleck. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Christian Fleck, Y2hyaXN0aWFuLmZsZWNrQGZkbS51bmktZnJlaWJ1cmcuZGU=
 Jonas Pleyer
Jonas Pleyer Christian Fleck
Christian Fleck