The modeling of free-fall arch formation in granular flow through an aperture

In this study, to predict the formation of the free-fall arch via granular flow through an aperture, an analytical model has been developed based on the particle-scale force equilibrium. This model calculates the size and location of the meta-stable arch and can be extended to predict the granular flow rate. According to the developed analytical model, the formation of a free-fall arch is independent of granular height and stress state above the arch, where only granular particle size, aperture size, and granular friction influence the development of the arch. Besides, this proposed model can predict the formation of the meta-stable arch without empirical parameters. In comparison with experimental results, the predicted granular flow rate based on the model exhibits high accuracy for uniform-sized granular flow. According to numerical simulations, the free-fall arch appears above the aperture; however, the particle velocity at the arch is low and can be considered negligible. Gravity will cause the granular particles under the arch to fall freely. This mathematical model offers an efficient method to predict the formation of the free-fall arch and calculate the granular flow rate through an aperture.

Introduction

In nature, granular materials exist in various forms, so studies in both science and engineering have been conducted to investigate granular flow. Because of its extensive application space, granular flow through an aperture has been explored as a classic problem in past many decades. Recently, a frequently reported hazard, the urban sinkhole, has been modeled and simplified as granular flow through an opening on damaged underground pipes [1,2].

The characteristics of granular flow are quite different from fluid flow, in which the rate of granular flow through an orifice is independent of its height, as Janssen [3] initially explained. Due to this characteristic of granular material, the hourglass has been used to measure the passage of time for centuries. Based on experimental results, Beverloo et al. [4] proposed an empirical correlation to predict the granular flow rate through an opening. Beverloo’s equation was shown to be valid under conditions restricted by granular particle size [5], and various studies have been conducted to extend the application of Beverloo’s correlation [6–9]. Although Beverloo’s formula and other improved Beverloo-type formulas may effectively estimate the granular flow rate under certain situations, the mechanism and physical basis are unknown. Continuum models have been used to depict granular flow [10–14] by incorporating the mass conservation equation and momentum equation with material yield criteria. Although the continuum approach was developed based on sound mathematical formulations, it cannot describe the flow process microscopically at the particle level.

To explain the mechanics of granular flow, Brown [15] presented the minimum energy hypothesis. The energy within granular material is thought to diminish throughout a granular flow stream tube, reaching a minimum value at the outlet, where the particles then fall freely due to gravity. Brown and Richards [16] named this minimal energy boundary the free-fall arch. Other researchers have adopted these assumptions, and an ‘hourglass theory’ was proposed to predict the granular flow rate and stress distribution in hopper flow [17]. Because of the simplicity, the free-fall arch hypothesis was introduced to determine the granular flow rate [7,18–24]. It is true that granular particles may not fall freely below the arch, and particles could not lose all the kinetic energy at the arch [19], which is an oversimplification of the original free fall arch hypothesis. Therefore, from current studies, the term, free fall arch, may not literally describe free falling of the material which may be more appropriate to define it as a transition zone in granular flow [25-26]. In particular, the existence of this transition zone close to the aperture has been widely confirmed by experimental and theoretical studies [20,27]. From the picture of the free fall arch, although there is stress/velocity discontinuity it is difficult to confirm the existing of the arch with certainty [26,28]. Various approaches, such as the self-similar method, have been introduced to improve the free fall arch theory in calculating the granular mass flow rate [7,29]. Particularly, a novel approach based on the energy balance of the system has been proposed by Darias et al. [30]. Various studies have been conducted to interpret the “transition region”, such as the study by Rubio-Largo et al. [19] who proposed the significance of the kinetic pressure. Although different arguments exist on the free fall arch hypothesis, it is still the key to explain the granular flow rate through an aperture. Particularly, the free fall arch hypothesis is supported by the similar expressions to calculate mass flow rate in comparison with Beverloo’s formula [31–33]. Therefore, it becomes much clearer that a transition zone/region is formed when granular material flow through the aperture, at which the kinetic energy is significantly reduced (not necessarily zero). Besides, particle interaction is reduced or some particles are not in contact below this region with particles accelerating under gravity [27,34]. These arguments suggest the existence of a transition zone while the flow mechanism in this transition zone is still unclear. The mechanism of granular flow has been well-explained in principle by the free-fall arch hypothesis; however, locating the free-fall arch lacks an analytical model, whereas the free-fall arch’s location and dimensions are typically assumed and simplified.

This study develops a novel analytical model to predict the development of the meta-stable arch during granular flow through an aperture, which was then introduced to predict the granular mass flow rate. Experiments were used to validate the analytical model, and numerical simulations using the discrete element method were conducted to verify this proposed model.

Formulation of the analytical model

Model of the free-fall arch formation in granular flow

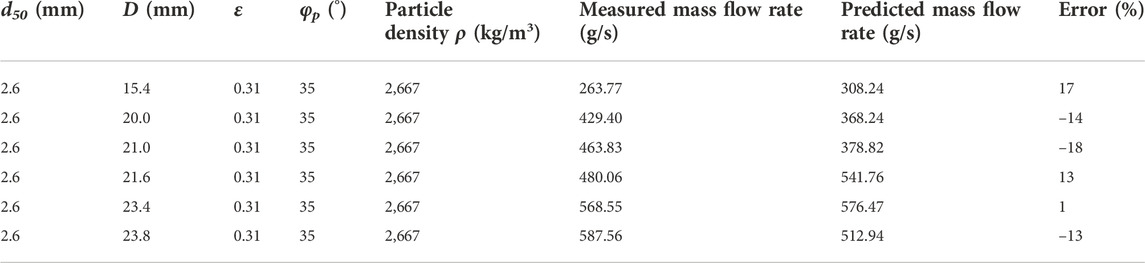
As grains flow through an aperture, the movement transforms from dense flow to diluted flow because of the changes in frictional forces between granular particles until reaching the free-fall arch. This arch is not a static structure, as the particles forming the arch only stop or slow down momentarily. In other words, the arch forms and breaks continuously during the flow process. Based on experimental observations, the two edges of the arch do not necessarily rest on the ends of the opening. As shown in Figure 1A, various potential arches might develop close to the opening. In contrast to the fluid flow, the friction between granules is a critical factor affecting the flow characteristics. From the previous studies [35-36], a stagnant zone exists between the active flowing zone and the base outside the opening. The slopes of the stagnant zones are steeper than the angle of repose of the granular material.

FIGURE 1

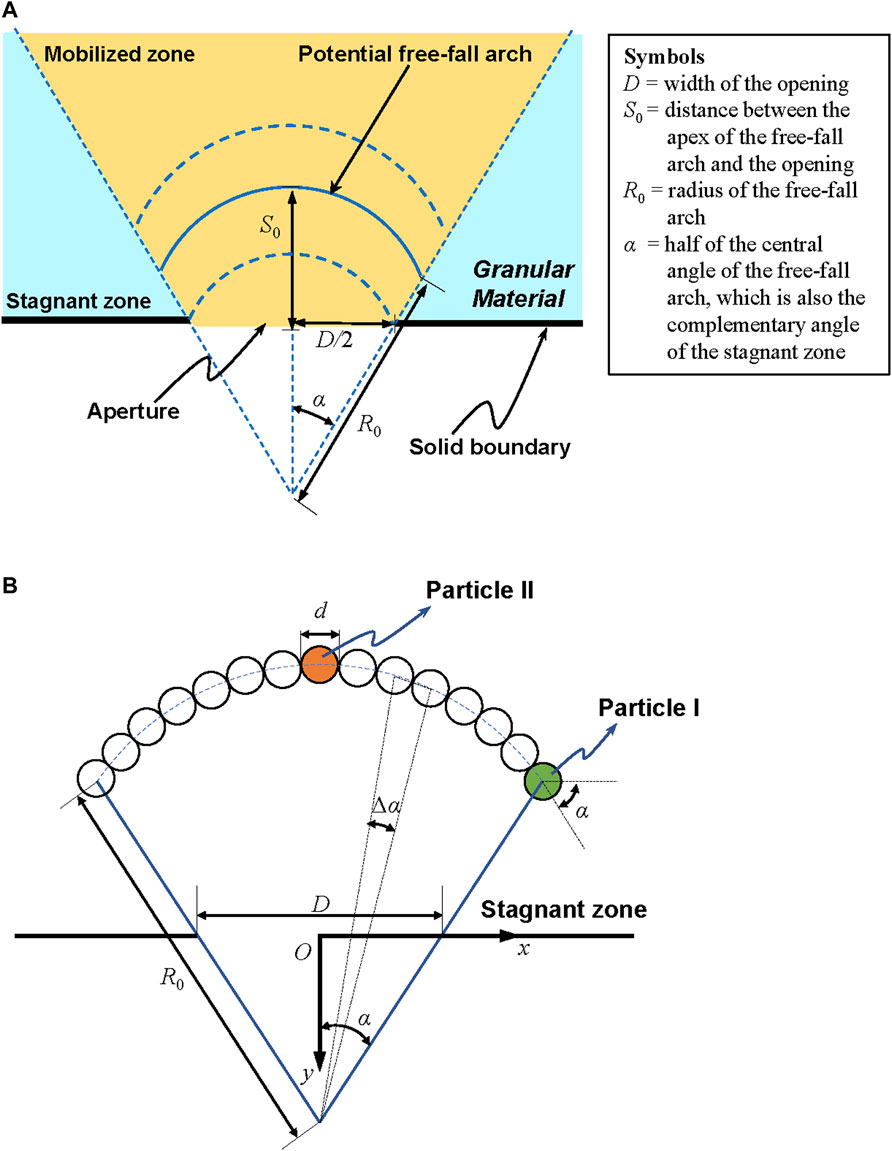
FIGURE 1. Schematic of the free-arch formation via granular flow through an aperture: (A) sketch of the potential free-fall arch; (B) schematic of the analytical model for the free-fall arch.

The free-fall arch model diagram is shown in Figure 1B. D represents the two-dimensional aperture width, while the particle size of granules forming the arch in this model is the same. Furthermore, the friction between particles is consistent with Coulomb’s friction theory [37]. Based on previous research, it is assumed that the arch is circular [16,31], which is also supported by the studies of Li et al. [38]. Although the other shapes of the arch structures were also used and observed [7,24,27]. Considering the introduction of the stagnant zone in the granular domain of this model, the circular-shaped arch was used for the simplicity. Furthermore, other shapes could also be introduced in this proposed model since only the terms related to the geometry need to be modified and revised.

The location of the arch and the number of particles that make up the arch are unknown. As seen in Figure 1B, α denotes half of the center angle of this arch, and Δα is the angle between any neighboring particles. The motion of two particles at two locations on the arch will be analyzed, which are the particle at the end (particle I) and the particle at the center of the arch (particle II). If the number of particles making up the arch is odd, particle II will be a single particle in this analytical model. When the number of particles is even, particle II is made up of two particles at the apex of the arch. The detailed development of this proposed analytical model can be found in the supplementary material. After that, the governing equation of this proposed model, which is in the supplementary material, can be obtained:

$\frac{\sqrt{2}\left(\cos \Delta \alpha +\tan {\phi }_p\sin \Delta \alpha \right)}{\left(M-2\right)\left(\sin \Delta \alpha +\tan {\phi }_p\cos \Delta \alpha \right)}=\frac{\left(\cos \alpha -\tan {\phi }_p\sin \alpha \right)}{\left(\sin \alpha +\tan {\phi }_p\cos \alpha \right)}(1)$

Δα is the only unknown in Eq. 1. Even though it is difficult to find an explicit solution, it can be solved numerically using an iterative technique. After determining Δα from Eq. 1, the radius of the arch structure, R₀, can be determined by. Using Beverloo’s modification, the aperture width D₀ can be modified to account for the effect of displacement thickness, indicating that D₀ = D-k_pd, in which k_p is about 1.5. Consequently, the distance between the arch apex and the aperture, S₀, may be estimated using geometry:

$S_0=R_0-\frac{D_0}{2\tan \alpha }(2)$

The size of the free-fall arch is determined to be independent of the force W in this proposed model, indicating that granular height and stress state on the arch do not affect its formation. This conclusion is in accordance with the classical theory of granular flow, which states that the granular flow rate through an orifice is unaffected by granular height.

Rate of granular flow through an aperture

From the free-fall arch theory, granules fall freely from the arch apex to the aperture under the effect of gravity. Using this proposed free-fall arch model, the particle velocity at the aperture may be calculated if the particle velocity at the arch is negligible. As the granular particle passes through the aperture, its velocity can be determined as:

$v_p=\sqrt{2gS}(3)$

where S is the distance from the free-fall arch to the aperture. Other scholars also used a similar equation to determine the particle velocity passing the opening [31,32]. The difference between Eq. 3 and other studies is the distance S in this proposed model, which is determined by the arch size. In previous studies, the distance was simply related to the aperture size by assuming the shape of the arch, while the discrepancy between modeling and measurement was corrected by introducing a fitting parameter [7,29, 39]. We proposed this model to predict the formation of the arch structure based on granular mechanics, which can account for the effects of particle size, particle friction, and aperture size without fitting parameters. The distance S can be determined as:

$S=\sqrt{{R_0}^2-x^2}-\frac{D_0}{2\tan \theta },x\in \left[0,D_0/2\right](4)$

The volumetric flow rate per unit width through the opening is equal to:

$Q=2\left(1-\epsilon \right){{\displaystyle \int }}_0^{D_0/2}{v}_p\mathrm{d}x=2\left(1-\epsilon \right){{\displaystyle \int }}_0^{D_0/2}\sqrt{2g\left(\sqrt{{R_0}^2-x^2}-\frac{D_0}{2\tan \alpha }\right)}\mathrm{d}x(5)$

where ε is the porosity of granular flow at the aperture. As the granular particle flow through the outlet, a transition zone/region is formed, while the soil porosity below this free-fall arch should be greater than the initial value because of the reduction of the particle interaction. From the experimental studies [40-41], the difference in the porosity between the packing bed and granular flow below the arch can be neglected. Therefore, the porosity at the aperture is assumed to be the same as the granular porosity, which was also used by other scholars [4,31].

If D₀<<R₀, S can be assumed to be a constant equal to S₀. It is possible to estimate the volumetric rate of granular flow through the aperture utilizing Eq. 6:

$Q=\left(1-\epsilon \right)D_0\sqrt{2g{S}_0}(6)$

Results and discussions

Model verification by experimental results

The experimental data taken from Mamtani [42], which are given in Table 1, were analyzed using this proposed model. In the experiment, the flow rate of uniform-sized glass beads through a slot was recorded, and the predictions using this proposed model were shown to agree with the experimental data. In Mamtani’s [42] study, the Fowler-Glastonbury Equation [43] and modified Beverloo’s Equation (35) was used to predict the experiments. The deviation between calculations and measurements was over 10%, while the discrepancy could be reduced to around 5% using this method. Therefore, the accuracy of the flow rate estimation is improved using this proposed method.

TABLE 1

TABLE 1. Comparison of uniform-sized granular flow rates between experimental and analytical results.

Granular flow experiments on a vertical plane with a slot as the outlet were conducted by Ostadi [44] using non-uniform quartz sand, and the details of the experiments can be found in supplementary material of Supplementary Figure S5. A comparison between calculated and measured flow rates is shown in Table 2 with detailed material properties. This proposed free-fall arch model was developed based on uniform-sized particles, and the mean particle size, d₅₀, is used in the calculation of granular flow rate when compared with the experimental results by Ostadi [44]. The modified Berverloo’s Equation [35] was also used to predict the flow rate of narrow-graded sand particles [44], while the prediction could be over 1.5 times the measurements. Although the deviation between the estimations and measurements is around 15% as listed in Table 2, the prediction accuracy is significantly improved using this proposed method, which exhibits the reasonable accuracy of this proposed model for non-uniform-sized particles. It is worth noting that the particle size distribution in the experiment is quite narrow with a uniformity coefficient (C_u = d₆₀/d₁₀) of four, where a model considering the effects of particle size distribution should be developed in further studies. Since the length of the slot in the perpendicular to the flow direction is much larger than the width (four times in Ostadi’s experiment), the arch induced by the continuous force chain can hardly form in the third dimension. The arch can mainly form in a two-dimensional plane from previous experimental observations of the granular flow through a slot [45]. Thus, this proposed model can be applied to predict Ostadi’s experimental measurements.

TABLE 2

TABLE 2. Comparison of non-uniform granular flow rates between experimental and analytical results.

Although the analytical results of granular flow rates agree reasonably well with the experimental measurements, the details of the particle behavior (such as the particle velocity, acceleration, and contact force) are difficult to be captured from experiments. Therefore, the discrete element method (DEM) is used to analyze the development of a free-fall arch and trace the fluctuation of particle velocity during granular flow, which can evaluate the flow process microscopically.

Micromechanical modeling and formation of the free-fall arch

In this study, Mamtani’s experiment (2011) was simulated by DEM. The theoretical basis of DEM is Newton’s second law and the force-displacement law at the contact. In this study, the linear contacts and spherical particles with uniform size were used for the two-dimensional numerical simulation. The details of the numerical simulation can be found in the supplementary material. Supplementary Figure S6 shows the numerical model of the granular assembly used to model the experiment [42], in which the particle size is 2.27 mm. A linear contact model between particle contacts is used in DEM. The model parameters are determined using a calibration process to match the measured granular flow rate, as shown in Supplementary Figure S8. In particular, the particle density in the simulation is 2,580 kg/m³, and the friction coefficient between particles is set to be 0.5. Furthermore, the normal stiffness is equal to 1 × 10⁵ N/m in the simulation, while the shear stiffness between particles is set to be equal to the normal stiffness. The damping force in the dashpot provides the mechanism for energy dissipation. The damping coefficient is set to be 0.1 in this study. The calculated particle flow rate reaches a steady-state volumetric flow rate of about 0.00625 m³/s, as shown in Supplementary Figure S8, which is consistent with the experiments. When the hopper becomes empty, the flow rate drops after about 4 s. The movements of four particular particles (Particles A, B, C, and D) at different places were monitored to offer insights into the flow mechanism, as illustrated in Supplementary Figure S8.

Figure 2 depicts the time-dependent fluctuations of particle velocities in the y direction. For particle A, its original location is at the top of the granular model. When the flow begins, the velocity of particle A increases significantly from 0 to around 0.15 m/s. The movement of this particle approaches a quasi steady-state afterwards, where velocity fluctuations are witnessed only due to particle collisions. From Figure 2A, the velocity of particle A tends to increase before 2.5 s. But then at around 2.75 s, there is a dramatic reduction in the velocity of particle A, which is followed by a rapid increase. This change in particle velocity in Figure 2A supports the development of a free-fall arch due to a momentary decrease in particle velocity. As the particle approaches the aperture, an arch is built up, and the particle velocity reaches a minimum or even becomes zero. Figure 2 demonstrates that the velocity fluctuations of particles B, C, and D follow a pattern similar to that of particle A.

FIGURE 2

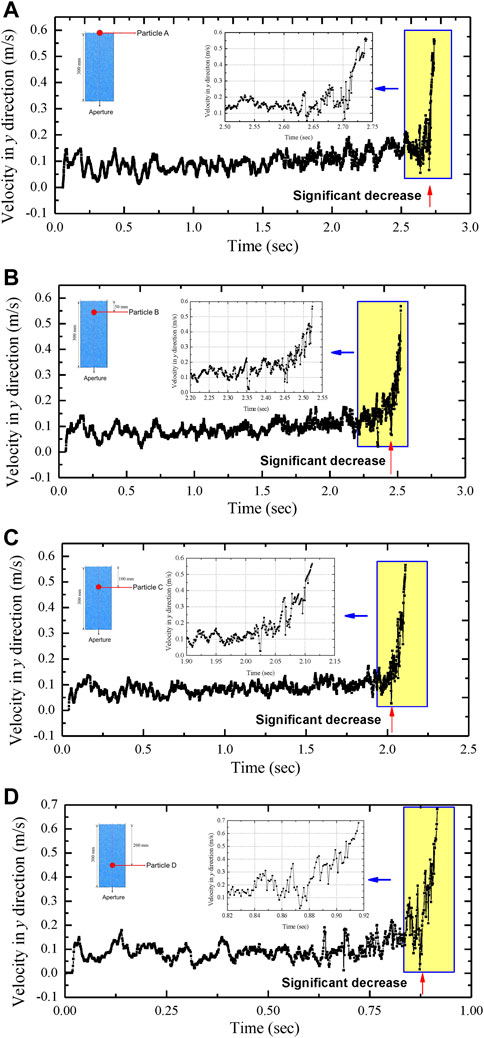
FIGURE 2. Variation of particle velocities with time from numerical simulations:(A) particle A; (B) particle B; (C) particle C; (D) particle D.

Figure 3A shows the variation of particle velocity with respect to its vertical position. The velocities fluctuate for all tracked particles, which exhibits a slight increase at y < -0.075 m. As illustrated in Figure 3A, the particle velocity greatly decreases and then grows abruptly in the region above the aperture (-0.075 m < y < -0.0125 m). Figure 3B illustrates the variance in particle acceleration at various points along the y-axis. If the particle is located at a far distance from the aperture (y < -0.075 m), its vertical acceleration is weak and fluctuating. The vertical acceleration changes dramatically when the particle approaches the opening (-0.075 m < y < -0.0125 m). Figure 3B demonstrates that as the particle goes beyond this zone (y > -0.0125 m), its vertical acceleration approaches gravitational acceleration (g = -9.81 m²/s), indicating free-fall motion. Due to collisions between particles, the acceleration will not exactly equal gravitational acceleration. According to the proposed model, the distance between the apex of the free-fall arch and the aperture is roughly 0.04 m, which agrees with the numerical results, as seen in Figure 4A. Because of particle collisions, the arch size in the numerical simulation is somewhat less than the analytical prediction. This proposed model assumes that the particles forming the arch are in a condition of static equilibrium, with no consideration of the dynamic pattern of granular flow. As illustrated in Figure 3B, the arch size from the numerical simulation is greater than the estimated size, while the particle acceleration in the freely-falling region is greater than the gravitational acceleration due to particle collisions. Therefore, the differences in granular flow rate between theoretical calculation and numerical simulation are compensated with improved accuracy, as shown in Table 1.

FIGURE 3

FIGURE 3. Particle velocity and acceleration in y direction during the discharge: (A) particle velocity; (B) particle acceleration.

FIGURE 4

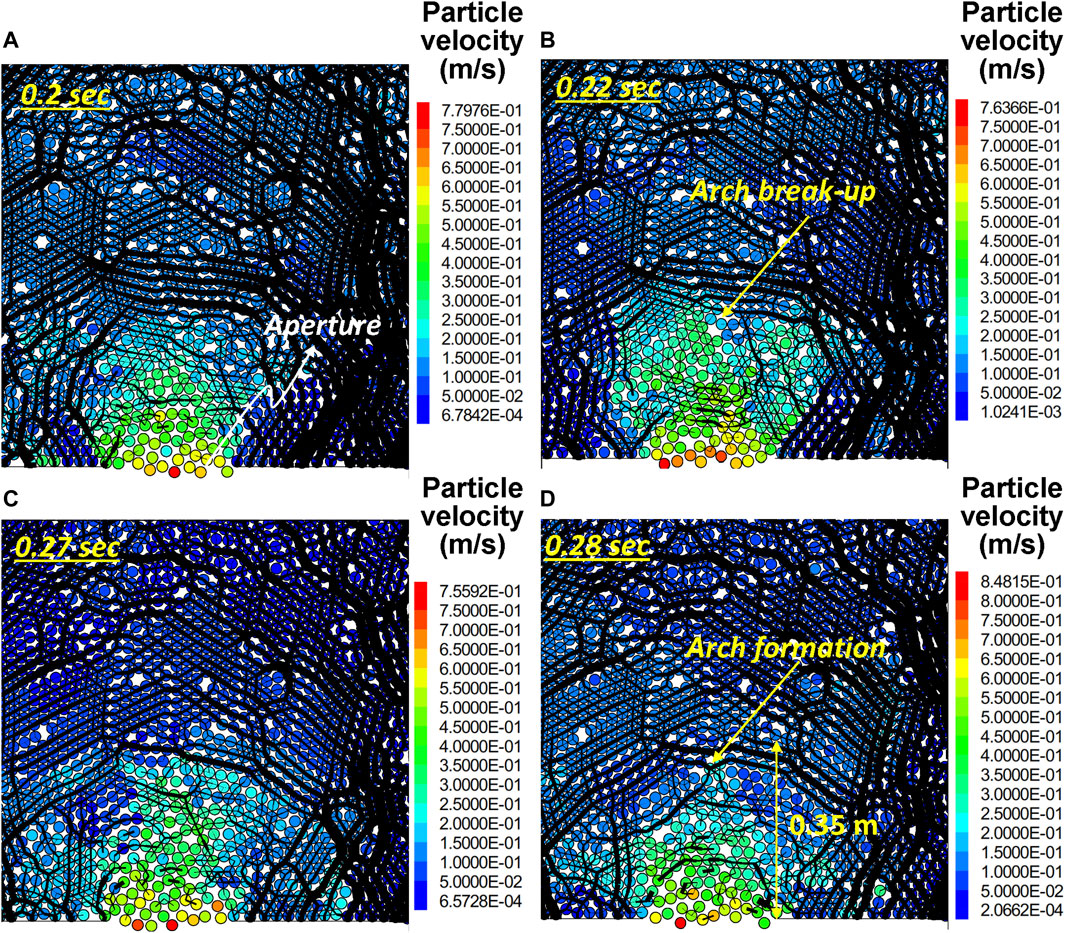
FIGURE 4. Force chain development in the granular flow through a two-dimensional aperture (the black curve shows the force between particles and thickness indicates the magnitude): (A) time = 0.20 s; (B) time = 0.22 s; (C) time = 0.27 s; (D) time = 0.28 s.

As shown in Figure 3, the movement of the granular particle goes through different stages. When particles are far from the aperture, their velocity increases slowly as they approach the opening. As granules move closer to the aperture, the free-fall arch is developed, and their velocity quickly decreases to a much lower value. The particles then fall freely through the aperture due to gravity. Since the velocity of particles at the free-fall arch can be negligible, the distance between the free-fall arch and the aperture largely determines the particle velocity as it passes through. This distance can be determined using this proposed model, which is unaffected by granular height and only dependent on particle size, opening size, and particle friction.

Based on numerical simulations, the evolution of the force chain as the grains discharge is shown in Figure 4. The black curves indicate the forces between particles, and the thickness of the curve is directly proportional to the magnitudes of the forces. As granules pass the aperture, an arch resembled by the force chain forms above the aperture. The force chain below this arch is discontinuous. Moreover, the free-fall arch breaks up during the flow process, as shown in Figure 4B. The arch reforms as particles approach the aperture from Figures 4C,D. An arch-shaped force chain is roughly 0.035 m away from the aperture, which agrees with the observed and anticipated free-fall arch position, as seen in Figure 4.

This analytical model was developed based on micro-granular mechanics and the formation of a free-fall arch in the granular assembly from a perspective of the particle-scale force equilibrium, which provides a theoretical explanation for the phenomenon of granular flow, such as the hourglass, silo flow, etc. Although the assumptions (zero particle velocity at the arch, free-falling of the particle below the arch) to estimate the mass flow rate are based on the original free fall arch theory, the proposed mathematical model for predicting the arch formation is original and novel, which is developed by introducing the meta-stable arch based on the particle-scale granular mechanics. Besides, the prediction accuracy of granular flow rate could be improved using this proposed arch model. It should be noted that sliding particles outside the arch zone contribute to granular flow through the aperture, resulting in underestimated granular flow in this model. The assumption of free-fall neglects the congestion effect of particle motion below the arch and above the opening, which can somehow compensate for the underestimation of the flow rate of this model. Besides, the volume fraction is important in granular flow. As the material flows through the aperture, the volume fraction increase, particularly in the region below the arch, which could be one factor leading to the discrepancy between the predictions and the measurements. Considering this study is aimed to propose a model to predict the size/location of the arch, the changes in volume fraction can be introduced in Eq. 5 in further studies.

Conclusion

A model was proposed to predict the arch formation as the granular flow through an aperture based on the particle-scale force equilibrium, which can be used to predict the mass flow rate by introducing the free-fall arch hypothesis. Following conclusions can be obtained from this study:

1) A mathematical model to predict the formation of the meta-stable arch is developed from particle-scale granular mechanics, which can account for the effects of particle size, particle friction, and aperture size without the empirical parameters. In this proposed model, the distance between the arch and aperture is unaffected by the granular height or stress above the arch. This proposed model can be used to predict the mass flow rate through the aperture by introducing the free-fall arch hypothesis.

2) The motion of the granular particle exhibits three stages, starting from the top surface of the granular assembly to the outlet. The granules flow downwards into the aperture with little acceleration from the top surface to an area above the arch. As the particle approaches the arch, its velocity dramatically decreases to a minimum. The particle velocity increases significantly after free-falling below the arch, under the forces of gravity, until it passes the aperture. Free-fall then continues below the opening.

3) The proposed analytical model may be utilized to compute the flow rate for non-uniform size particles with acceptable accuracy. However, the experimental results are based on a material with a narrow grain-size distribution. A model considering the effects of particle size distribution should be developed in further studies

Data availability statement

The original contributions presented in the study are included in the article/Supplementary Material, further inquiries can be directed to the corresponding author.

Author contributions

YT, writing, modeling, calculation DC, editing, supervision DZ, editing, supervision.

Funding

This work was supported by the National Natural Science Foundation of China (Grant Nos. 51908493, and 41961144018), Laboratory of Sustainable Urban Drainage of Ningbo University, and National Key R&D Program of China (2022YFC3203200). Financial supports from the Chinese Program of Introducing Talents of Discipline to University (the 111 Project, B18047) are also acknowledged. Open access publication fees will be funded by the National Natural Science Foundation of China (Grant Nos. 51908493 and 41961144018) and Zhejiang University.

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

Supplementary material

The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/fphy.2022.963495/full#supplementary-material

References

1. Tang Y., Zhu D. Z., Chan D. H. Experimental study on submerged sand erosion through a slot on a defective pipe. J Hydraul Eng (2017) 143:4017026. doi:10.1061/(asce)hy.1943-7900.0001326

CrossRef Full Text | Google Scholar

2. Mohamed H. I., Rabey S. H., Darweesh M. S. Laboratory investigation of ground surface settlement caused by erosion around a leaking pipe. J Pipeline Syst Eng Pract (2022) 13:13. doi:10.1061/(asce)ps.1949-1204.0000629

CrossRef Full Text | Google Scholar

3. Janssen H. A. Versuche über Getreidedruck in Silozellen, Zeitschrift des Vereins. Dtsch Ingenieure (1895) 39:1045–9.

Google Scholar

4. Beverloo W. A., Leniger H. A., van de Velde J. The flow of granular solids through orifices. Chem Eng Sci (1961) 15:260–9. doi:10.1016/0009-2509(61)85030-6

CrossRef Full Text | Google Scholar

5. Nedderman R. M., Tüzün U., Savage S. B., Houlsby G. T. The flow of granular materials-I. Discharge rates from hoppers. Chem Eng Sci (1982) 37:1597–1609. doi:10.1016/0009-2509(82)80029-8

CrossRef Full Text | Google Scholar

6. Mankoc C., Janda A., Arévalo R., Pastor J. M., Zuriguel I., Garcimartín A., et al. The flow rate of granular materials through an orifice. Granul Matter (2007) 9:407–14. doi:10.1007/s10035-007-0062-2

CrossRef Full Text | Google Scholar

7. Janda A., Zuriguel I., Maza D. Flow rate of particles through apertures obtained from self-similar density and velocity profiles. Phys Rev Lett (2012) 108:248001. doi:10.1103/PhysRevLett.108.248001

PubMed Abstract | CrossRef Full Text | Google Scholar

8. Hu G., Lin P., Zhang Y., Li L., Yang L., Chen X. Size scaling relation of velocity field in granular flows and the Beverloo law. Granul Matter (2019) 21:21. doi:10.1007/s10035-019-0872-z

CrossRef Full Text | Google Scholar

9. Anyam V. K. R., Anki Reddy K. Granular mixtures discharging through a silo with lateral orifice. Phys Fluids (1994) (2022) 34:43319. doi:10.1063/5.0086936

CrossRef Full Text | Google Scholar

10. Savage S. B. The mass flow of granular materials derived from coupled velocity-stress fields. Br J Appl Phys (1965) 16:1885–8. doi:10.1088/0508-3443/16/12/313

CrossRef Full Text | Google Scholar

11. Sanad A. M., Ooi J. Y., Holst J. M. F. G., Rotter J. M. Computations of granular flow and pressures in a flat-bottomed silo. J Eng Mech (2001) 127:1033–43. doi:10.1061/(asce)0733-9399(2001)127:10(1033)

CrossRef Full Text | Google Scholar

12. Xiao H., Fan Y., Jacob K. V., Umbanhowar P. B., Kodam M., Koch J. F., et al. Continuum modeling of granular segregation during hopper discharge. Chem Eng Sci (2019) 193:188–204. doi:10.1016/j.ces.2018.08.039

CrossRef Full Text | Google Scholar

13. Lin C. C., Yang F. L. Continuum simulation of non-local effects in a granular silo discharge flow using a regularized μ (I) rheology model. Phys Fluids (1994) (2021) 33:093302. doi:10.1063/5.0057598

CrossRef Full Text | Google Scholar

14. Barker T., Zhu C., Sun J. Exact solutions for steady granular flow in vertical chutes and pipes. J Fluid Mech (2022) 930:A21. doi:10.1017/jfm.2021.909

CrossRef Full Text | Google Scholar

15. Brown R. L. Minimum energy theorem for flow of dry granules through apertures. Nature (1961) 191:458–61. doi:10.1038/191458a0

CrossRef Full Text | Google Scholar

16. Brown R. L., Richards J. C. Kinematics of the flow of dry powders and bulk solids. Rheol Acta (1965) 4:153–65. doi:10.1007/BF01969251

CrossRef Full Text | Google Scholar

17. Davidson J. F., Nedderman R. M. The Hour-Glass theory of hopper flow. Trans Instn Chem Engrs (1973) 51:29–35.2. doi:10.1007/BF01969251

CrossRef Full Text | Google Scholar

18. Le Pennec T., Måløy K. J., Hansen A., Ammi M., Bideau D., Wu X. Ticking hour glasses: Experimental analysis of intermittent flow. Phys Rev E (1996) 53:2257–64. doi:10.1103/PhysRevE.53.2257

CrossRef Full Text | Google Scholar

19. Rubio-Largo S. M., Janda A., Maza D., Zuriguel I., Hidalgo R. C. Disentangling the free-fall arch paradox in silo discharge. Phys Rev Lett (2015) 114:238002. doi:10.1103/PhysRevLett.114.238002

PubMed Abstract | CrossRef Full Text | Google Scholar

20. Tian Y., Lin P., Zhang S., Wang C. L., Wan J. F., Yang L. Study on free fall surfaces in three-dimensional hopper flows. Adv Powder Technol (2015) 26:1191–9. doi:10.1016/j.apt.2015.05.015

CrossRef Full Text | Google Scholar

21. Koivisto J., Korhonen M., Alava M., Ortiz C. P., Durian D. J., Puisto A. Friction controls even submerged granular flows. Soft Matter (2017) 13:7657–64. doi:10.1039/c7sm00806f

PubMed Abstract | CrossRef Full Text | Google Scholar

22. Gella D., Maza D., Zuriguel I. Role of particle size in the kinematic properties of silo flow. Phys Rev E (2017) 95:052904. doi:10.1103/PhysRevE.95.052904

PubMed Abstract | CrossRef Full Text | Google Scholar

23. Zhang D., Yang X., Zhan J., Liu X., Yue C., Ayala J., et al. Mortality analysis of captive red panda cubs within Chengdu, China. BMC Vet Res (2022) 68:68. doi:10.1186/s12917-022-03170-2

PubMed Abstract | CrossRef Full Text | Google Scholar

24. Wang Q., Chen Q., Li R., Zheng G., Han R., Yang H. Shape of free-fall arch in quasi-2D silo. Particuology (2021) 55:62–9. doi:10.1016/j.partic.2020.10.001

CrossRef Full Text | Google Scholar

25. Tuzun U. Statistics and kinematics of granular materials. In: RM Nedderman, editor, 75. Cambridge, UK: Cambridge University Press (1993). p. 103–4. Bypublished by1992352pp.£50ISBN 0-521-40435.Powder Technol

Google Scholar

26. Xiao Y., Han Y., Jia F., Liu H., Li G., Chen P., et al. Experimental study of granular flow transition near the outlet in a flat-bottomed silo. Biosyst Eng (2021) 202:16–27. doi:10.1016/j.biosystemseng.2020.11.013

CrossRef Full Text | Google Scholar

27. Vivanco F., Rica S., Melo F. Dynamical arching in a two dimensional granular flow. Granul Matter (2012) 14:563–76. doi:10.1007/s10035-012-0359-7

CrossRef Full Text | Google Scholar

28. Rubio-Largo S. M., Maza D., Hidalgo R. C. Large-scale numerical simulations of polydisperse particle flow in a silo. Comput Part Mech (2017) 4:419–27. doi:10.1007/s40571-016-0133-4

CrossRef Full Text | Google Scholar

29. Alonso-Marroquin F., Mora P. Beverloo law for hopper flow derived from self-similar profiles. Granul Matter (2021) 23:7. doi:10.1007/s10035-020-01067-1

CrossRef Full Text | Google Scholar

30. Darias J. R., Madrid M. A., Pugnaloni L. A. Differential equation for the flow rate of discharging silos based on energy balance. Phys Rev E (2020) 101:052905. doi:10.1103/PhysRevE.101.052905

PubMed Abstract | CrossRef Full Text | Google Scholar

31. Hilton J. E., Cleary P. W. Granular flow during hopper discharge. Phys Rev E (2011) 84:011307. doi:10.1103/PhysRevE.84.011307

PubMed Abstract | CrossRef Full Text | Google Scholar

32. Oldal I., Keppler I., Csizmadia B., Fenyvesi L. Outflow properties of silos: The effect of arching. Adv Powder Technol (2012) 23:290–7. doi:10.1016/j.apt.2011.03.013

CrossRef Full Text | Google Scholar

33. Peng Z., Zhou J., Zhou J., Miao Y., Cheng L., Jiang Y., et al. External pressure dependence of granular orifice flow: Transition to Beverloo flow. Phys Fluids (1994) (2021) 33:043313. doi:10.1063/5.0048357

CrossRef Full Text | Google Scholar

34. Lin P., Zhang S., Qi J., Xing Y. M., Yang L. Numerical study of free-fall arches in hopper flows. Physica A: Stat Mech its Appl (2015) 417:29–40. doi:10.1016/j.physa.2014.09.032

CrossRef Full Text | Google Scholar

35. Nedderman R. M. Statics and kinematics of granular materials (1992). doi:10.1017/cbo9780511600043

CrossRef Full Text | Google Scholar

36. Samadani A., Mahadevan L., Kudrolli A. Shocks in sand flowing in a silo. J Fluid Mech (2002) 452:293–301. doi:10.1017/S0022112001006991

CrossRef Full Text | Google Scholar

37. Rao K. K., Nott P. R. An introduction to granular flow (2008). doi:10.1017/CBO9780511611513

CrossRef Full Text | Google Scholar

38. Li C., Li X., Jiao T., Hu F., Sun M., Huang D. Influence of grain bidispersity on dense granular flow in a two-dimensional hopper. Powder Technol (2022) 401:117271. doi:10.1016/j.powtec.2022.117271

CrossRef Full Text | Google Scholar

39. Li C., Li X., Jiao T., Hu F., Sun M., Huang D. Influence of grain bidispersity on dense granular flow in a two-dimensional hopper. Powder Technol (2022) 401:117271. doi:10.1016/j.powtec.2022.117271

CrossRef Full Text | Google Scholar

40. Crewdson B. J., Ormond A. L., Nedderman R. M. Air-impeded discharge of fine particles from a hopper. Powder Technol (1977) 16:197–207. doi:10.1016/0032-5910(77)87007-1

CrossRef Full Text | Google Scholar

41. Donsi G., Ferrari G., Poletto M. Distribution of gas pressure inside a hopper discharging fine powders. Chem Eng Sci (1997) 52:4291–302. doi:10.1016/S0009-2509(97)00163-2

CrossRef Full Text | Google Scholar

42. Mamtani K. Effect of particle shape on hopper discharge rate. Florida, FL, USA: Univ Florida (2011) (MSc thesis).

Google Scholar

43. Fowler R. T., Glastonbury J. R. The flow of granular solids through orifices. Chem Eng Sci (1959) 10:150–6. doi:10.1016/0009-2509(59)80042-7

CrossRef Full Text | Google Scholar

44. Ostadi M. Mechanics of dry granular flow through an opening. Edmonton, Canada: Univ Alberta (2019) (MSc thesis).

Google Scholar

45. Sun G., Chen Q., Li R., Zheng Z., Xin Y. J., Yang H. A parabola-shaped free-fall arch in silos with centric and eccentric outlets. Powder Technol (2022) 409:117770. doi:10.1016/j.powtec.2022.117770

CrossRef Full Text | Google Scholar