- 1Theoretical Physics Group, Department of Physics, University of Uyo, Uyo, Nigeria
- 2Department of Physics, University of Ilorin, Ilorin, Nigeria
- 3Department of Physics, Federal University of Petroleum Resources, Effurun, Nigeria
- 4Department of Physical Sciences, Landmark University, Omu-Aran, Nigeria
- 5Physics Programme, Department of Physics, University of Uyo, Uyo, Nigeria
- 6Instituto Federal do Sudeste de Minas Gerais, Juiz de Fora, Brazil
In this study, we apply the parametric Nikiforov-Uvarov method to obtain the bound state solution of Schrödinger wave equation in the presence of Kratzer plus generalized Morse potential (KPGM). The energy eigen equation and the corresponding normalised wave function were obtained in closed form. The resulting energy eigen equation was used to study partition function and other thermodynamic properties such as vibrational mean energy, vibrational specific heat capacity, vibrational mean free energy and vibrational entropy for the proposed potential as applied to lithium hydride diatomic molecule. The thermodynamic plots obtained were in excellent agreement to work of existing literatures. The wave function and probability density plots for the diatomic molecules were obtained through a well designed and implemented maple programme.
1 Introduction
The exact solutions of Schrödinger wave equation is one of the essential part in quantum mechanics, this is because Schrödinger wave equation is used to describe non-relativistic spinless particles and also has many applications in atomic, nuclear and high energy Physics [1–9]. This has prompted many researchers over the years to search for the solution of Schrödinger wave equation with different potentials [10–15]. However, different methods have been used to obtain approximate solution of Schrödinger wave equation, they include Nikiforov-Uvarov method (NU) [16–22], Supersymmetry quantum mechanics (SUSY) [23–28], Asymtotic Iteration method (AIM) [29, 30], Factorization method [31, 32], Exact and proper quantization method [33–36]. In solving the wave equation, the results obtained for various potential models are vastly applied [4, 31, 37, 38, 38, 39, 39–41]. A lot of researchers have studied bound state solutions of Schrödinger wave equation as applicable to different field of physical and chemical sciences including molecular spectroscopy and quauntum information. Ahmadov et al. [42] studied bound state solution to the Schrodinger equation at finite temperature with the sum of Cornell and Inversely quadratic potential with developed approximation to the centrifugal term using Nikiforov-Uvarov method. Their energy eigenvalues were applied to study charmonium and bottomium masses at finite and zero temperature in which their theoretical results were in total agreement with the experimental results. Ahmadov et al. [43] also studied finite temperature dependent Schrodinger equation with the sum of Cornell, Inversely quadratic and harmonic type potential. They obtained analytical expression for the energy eigenvalues and applied it to study heavy quarkonia and messon masses at different temperatures. Considering the application of bound state solutions of Schrödinger equation to quantum information; Shi et al. [44] evaluated Shannon information entropies in position and monentum spaces for an infinite spherical potential well where their result satisfies Beckner, Bialynicki-Birula and Mycieslki (BBM) inequality. Okon et al. [45] studied Fisher and Shannon information entropies for a noncentral Inversely quadratic plus exponential Mie-Type potential using parametric Nikiforov-Uvarov method where the evaluated Fisher and Shannon Information entropies for position and momemtum spaces.
The thermodynamic properties of a particular system is studied by finding the partition function which is a function of temperature. Other thermodynamic properties such as entropy, specific heat capacity, mean free energy and others are easily obtained using the partition function, which is widely applied in molecular physics and statistical physics [46–48].
In this research article, we solve the bound state solution of Schrödinger wave equation with Kratzer plus generalized Morse potential using the parametric Nikiforov-Uvarov method. We also extend our work to study the thermodynamic properties of the system as applied to lithium hydride (LIH) molecules. Hydride compound are most oftenly used as a portable sources of hydrogen gas [49]. Hydrides compound are used for advance fuel cells and battery applications. meanwhile, hydrogen can be stored as compressed hydrogen, liquid hydrogen as well as chemical storage [50]. Lithium hydride has high density hydrogen storage and serve as a precausor for building complex hydrides for industrial usage [51]. Lithium hydride is hetero diatomic molecule with applications in molecular spectroscopy. Evaluating the thermodynamic properties of this molecule will further reveals its statistical behaviour as well as its intrinsic properties. The Kratzer potential is a potential model that is used to described the internuclear vibration of diatomic molecules [52]. Kratzer potential is importance in the description of molecular structures and interraction existing between diatomic molecules and at the same time played a vital role in quantum chemistry [53] Kratzer potential is a limiting case of exponential type potentials [54]. Because of the Coulomb and the inverse square term present in Kratzer potential model, Kratzer potential can therefore be used to described molecules with short and long intermolecular distance. A lot of research work has been carried out using Kratzer potential within relativistic and nonrelativistic quantum mechanics. Such work can be find in Refs. [55–57]. Kratzer potential model is only characterised with dissociation energy De and equilibrium bond length re without the potential screening parameter α which characterises the strength of the potential. Morse potential has proved to be one of the most successful in explaining rotational and vibrational structure of diatomic molecules. As the internuclear distance gets larger, the potential vanishes to zero. Meanwhile, the combination of Kratzer and generalised Morse potential will provide a macroscopic description of the molecular interaction existing between diatomic molecules and incorporate all the experimental spectroscopic parameters needed for complete discription of molecular interaction. The Kratzer plus generalized Morse potential takes the form
where De is dissociation energy, re is the equilibrium bond length, r represent the interatomic distance, α is the screening parameter. This article is organised as follows: Section 1 is the introduction of the article, The Parametric Nikiforov-Uvarov method and the non-relativistic solution is presented in section 2, Thermodynamic properties is expressed in section 3, while the numerical solution is shown in section 4. The article is concluded in section 5.
2 The Parametric Nikiforov-Uvarov Method
In the parametric NU method, the second order linear differential equation is reduced to a generalised equation of hyper-geometric type which provides exact solutions interms of special orthogonal functions and the corresponding energy eigenvalues of the form. With the appropriate coordinate transformation S = S(x) the equation can be written as [17, 58–63].
where
The parametric constants are obtained as follows
The eigen energy equation is given as
The corresponding total wave function is then given as
2.1 Non-Relativistic Solution With KPGMP
The Schrödinger wave equation for an arbitrary external potential V(r) in spherical coordinate is written as [4].
where E is the exact bound state energy eigenvalues, Rnℓ(r) is the eigenfunction,
Also, on substituting Eq. 1 into Eq. 6, the radial part of the Schrödinger equation for the KPGM is given as
The Green-Aldrich approximation is given as [64].
On Substituting the transformation s = eαr and applying the Green-Aldrich approximation into Eq. 7 yields
where
Comparing Eq. 9 with the standard parametric NU differential equation of (2), the parameters are obtained as follows:
By substituting the appropriate parameters of Eq. 11 into equations (?) and equation (?), then simplify gives the respective wave function and energy eigenvalue equation for the KPGMP as
and
where
The normalization constant in Eq. 12 can be obtain using the normalization condition [1, 4].
the wavefunction is assumed to be in the bound at r ɛ (0, ∞) and s = eαr ɛ (1, 0) Eq. 15 becomes
Let z = 1 − 2s thus, the limit of integration of Eq. 16 changes from s ɛ(1, 0) to z ɛ(−1, 1). Then Eq. 16 reduces to
Applying the standard integral [1, 4].
Also, let z = w, x = 2γ − 1, y = 2δ. Then the normalization constant can be obtained as
therefore, the total normalized wave function is given as
3 Thermodynamic Properties for the Potential Model
The thermodynamic properties for KPGM will be studied by first obtaining the vibrational partition function defined as
where λ is an upper bound of the vibrational quantum number obtain from the numerical solution of
The energy equation of Eq. 13 can be simplified to
where
The energy Eq. 23 can then be express in the form
Hence, the partition function Eq. 22 can be express in the classical limit as
where
Using the partition function 27, other thermodynamic properties are obtain as follows.
a) Vibrational mean energy:
where
b) Vibrational specific heat capacity:
where
(c) Vibrational entropy
where
(c) Vibrational free energy
4 Results and Discussion
The thermodynamics properties of KPGM was studied, the plots of the wavefunction and thermodynamics properties as a function of the inverse temperature parameter β and λ for Lithium hydride (LiH) diatomic molecule are shown in Figures 1–4 and Figures 5–9 respectively. The spectroscopic parameter for Lithium hydride is adopted from Ref. [54]. Figure 1A is the wave function plot for fixed l = 0 which begins with a commom origin and proceed to a continous sinusoidal curve with various maximum and minimum turning points for Lithium hydride molecule. From the graph, it can be observed that the peaks of the turning points increases with increase in the principal quantum number (n), as such n = 0 has the lowest peak. The probability density curve for fixed l = 0 is displayed in Figure 1B. This plot follows normal distribution with several maximum points which also increases with an increase in the principal quantum number. The probability density curve completely describe the localization of electrons of LiH molecule, hence electron is more localized at n = 3 which has the highest maximum point. The same description of Figure 1A is applicable to Figures 2A, 4A while Figures 2B, 4B also have the same description as Figure 1B. The wavefunction graph in Figure 3A has maximum and minimum turning points at higher quantum states except at the ground state (n = 0) where there is a divergence in the curve. In Figure 3B, the probability density plot is sinusoidal in nature which shows the localization of electrons for higher quantum state while diverges at the ground state.
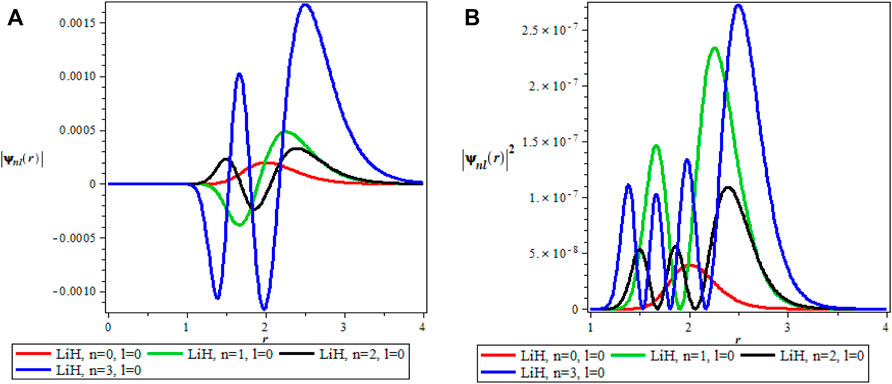
FIGURE 1. (A) Wavefunction plot for fixed l = 0 for LiH molecule. (B) Probabilty density plot for fixed l = 0 for LiH molecule.
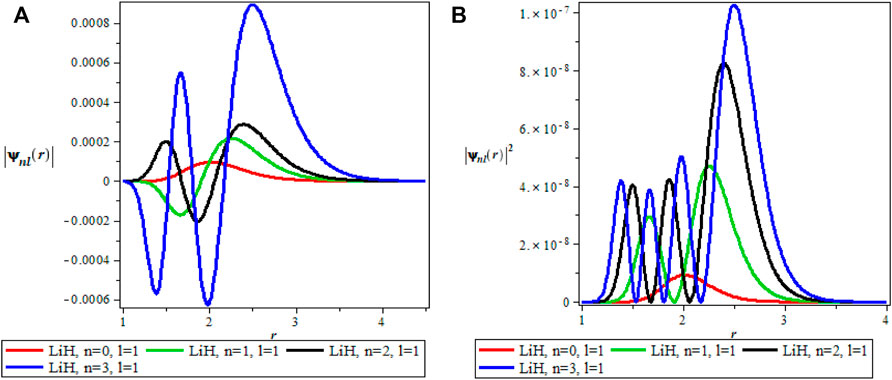
FIGURE 2. (A) Wavefunction plot for fixed l = 1 for LiH molecule. (B) Probabilty density plot for fixed l = 1 for LiH molecule.
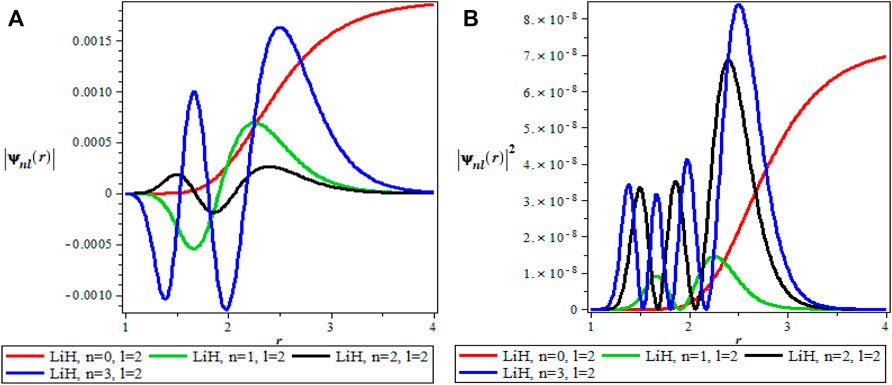
FIGURE 3. (A) Wavefunction plot for fixed l = 2 for LiH molecule. (B) Probabilty density plot for fixed l = 2 for LiH molecule.
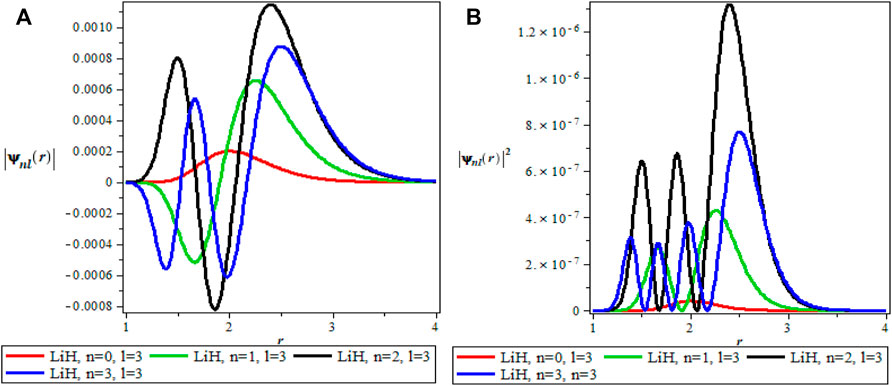
FIGURE 4. (A) Wavefunction plot for fixed l = 3 for LiH molecule. (B) Probabilty density plot for fixed l = 3 for LiH molecule.
Figures 5A,B show the variation of the vibrational partition function. It is observed in Figure 5A that the partition function Z(β) increases exponentially from the origin with increase in the inverse temperature parameter (β) but the partition function Z(λ) decreases with increase in λ as presented in Figure 5B for LiH diatomic molecule. The mean vibrational energy U(β) as displayed in Figure 6A increases monotonically with increase in the values of β with slight maximum turning points. The plot of U(λ) against λ has a hyperbolic nature. From Figure 7A, The vibrational specific heat capacity C(β) first decreases with an increase in inverse temperature parameter to a minimum value and then increase monotonically. However, the graph of vibrational specific heat capacity (C(β)) as a function of β has various minimum turn points that touch the horizontal axis. C(λ) decreases exponentially with λ in Figure 7B. Plots of the vibrational entropy with different values of β and λ is shown in Figures 8A,B respectively. As seen in Figure 8A, the vibrational entropy C(β) increases linearly with increasing values of β while S(λ) decreases with increasing values of λ. Plots of the mean free energy F(β) as a function of β increases monotonically with an increase in β for various values of λ as presented in Figure 9A. In Figure 9B, the vibrational free energy exhibited an hyperborlic nature which increases with an increase in λ. In order to prove the accuracy of work, the thermodynamic plots for this present work as applied to lithium hydride molecule are in excellent agreement to work of Okorie et al. [65] using improved deformed exponential type potential.
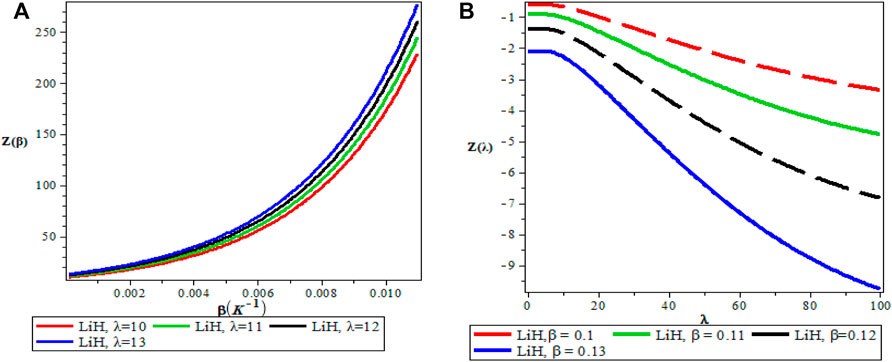
FIGURE 5. (A) Variation of Partition Function With Respect to β (B) Variation of Partition Function With Respect to λ.
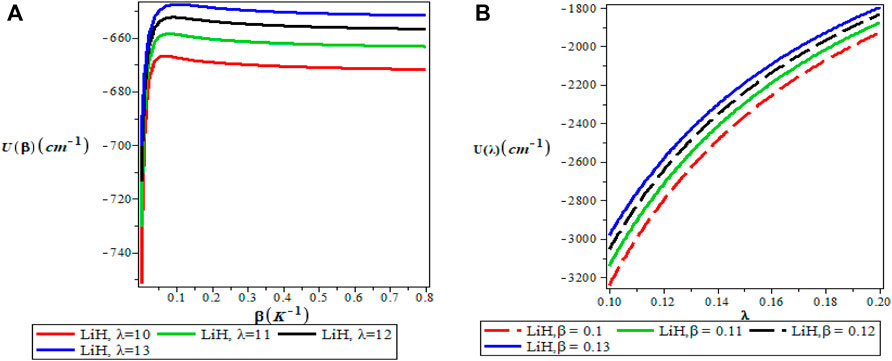
FIGURE 6. (A) Variation of Vibrational Mean Energy With Respect to β (B) Variation of Vibrational Mean Energy With Respect to λ.
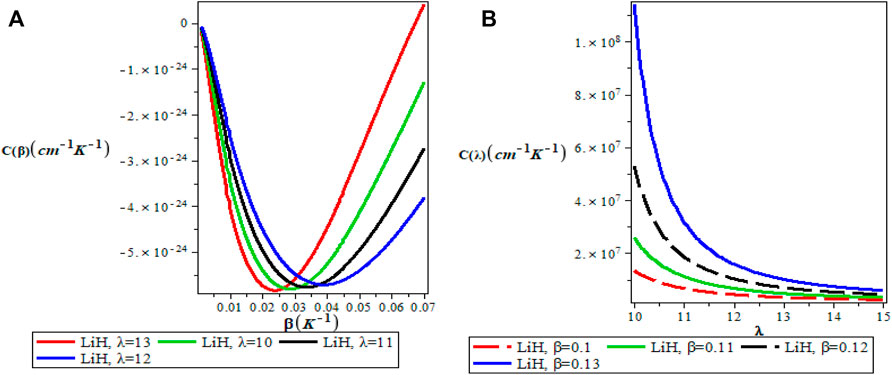
FIGURE 7. (A) Variation of Specific Heat Capacity With Respect to β (B) Variation of Specific Heat Capacity With Respect to λ.
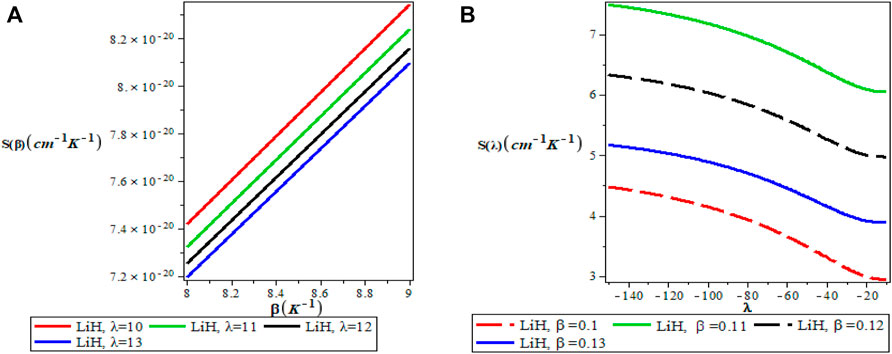
FIGURE 8. (A) Variation of Vibrational Entropy With Respect to β (B) Variation of Vibrational Entropy With Respect to λ.
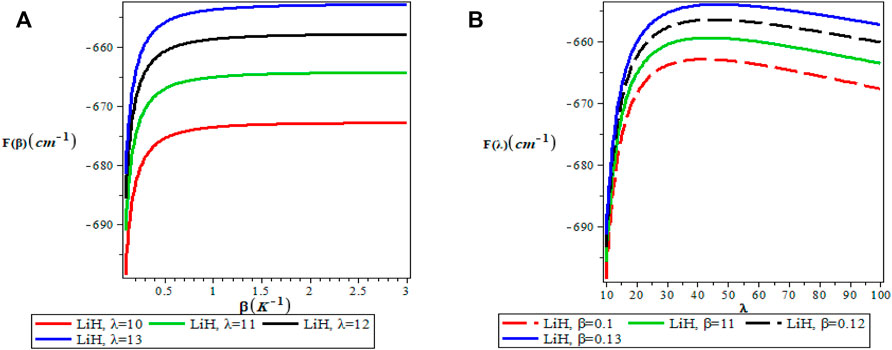
FIGURE 9. (A) Variation of Vibrational Free Energy With Respect to β (B) Variation of Vibrational Free Energy With Respect to λ.
5 Conclusion
In this work, we have solved the Schrödinger wave equation in the presence of Kratzer plus generalized Morse potential (KPGM) using Parametric Nikiforov-Uvarov method. The energy eigenvalues and the corresponding normalised wave function were obtained and presented in a closed and compact form. However, we studied the thermodynamics properties of KPGM which are: vibrational partition (Z), vibrational mean energy(U), specific heat capacity(C), vibrational entropy (s), and mean free energy (F). Also, we have plotted the variation of these thermodynamic functions as a function of inverse temperature parameter(β) and upper bound vibrational quantum number (λ) for Lithium hydride diatomic molecule. We analytically obtained the normalised wave function expressed in terms of hypergeometric function of Jacobi polynomial. The normalised wave function and probability density plots for the Lithium hydride molecule were obtained through a well designed Maple programming. This research work has application in molecular spectroscopy. Lithium hydride is heteronuclear diatomic molecule which has high density hydrogen storage and serve as a precausor for building complex hydrides. The thermodynamic plots obtained are in excellent agreement to work of an existing literature. Further research work can be carried out with Kratzer plus generalised Morse potential using other methods like the supersymmetric quantum mechanics approach to investigate other properties like expectation values as well as superstatistic formulation.
Data Availability Statement
The raw data supporting the conclusion of this article will be made available by the authors, without undue reservation.
Author Contributions
CI, IO, AA, and KO, conceived the original idea and wrote the first draft. EO, CO, and RJ carried out the thermodynamic plots. MU, EI, and JA carried out literature searches and editing of the final manuscript. All authors contributed to the manuscript.
Conflict of Interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Publisher’s Note
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
Acknowledgments
The authors sincerely appreciates the editorial team of Frontiers of Physics as well as the reviewers for their invaluable comments which we have used to further optimised and improved the quality of the manuscript.
References
2. Eshghi M, Mehraban H. Non-relativistic Continuous States in Arbitrary Dimension for a Ring-Shaped Pseudo-coulomb and Energy-dependent Potentials. Math Meth Appl Sci (2016) 39:1599–606. doi:10.1002/mma.3592
3. Dong SH, Lozada-Cassou M. Scattering of the Dirac Particle by a Coulomb Plus Scalar Potential in Two Dimensions. Phys Lett A (2004) 330:168–72. doi:10.1016/j.physleta.2004.08.008
6. Chen G. The Exact Solutions of the Schrödinger Equation with the Morse Potential via Laplace Transforms. Phys Lett A (2004) 326:55–7. doi:10.1016/j.physleta.2004.04.029
7. Ikhdair S, Sever R. Exact Polynomial Eigensolutions of the Schrödinger Equation for the Pseudoharmonic Potential. J Mol Struct THEOCHEM (2007) 806:155–8. doi:10.1016/j.theochem.2006.11.019
8. Arda A, Sever R. Exact Solutions of the Morse-like Potential, Step-Up and Step-Down Operators via Laplace Transform Approach. Commun Theor Phys (2012) 58:27–30. doi:10.1088/0253-6102/58/1/05
9. Zhang MC, Sun GH, Dong SH. Exactly Complete Solutions of the Schrödinger Equation with a Spherically Harmonic Oscillatory Ring-Shaped Potential. Phys Lett A (2010) 374:704–8. doi:10.1016/j.physleta.2009.11.072
10. Bayrak O, Boztosun I. Bound State Solutions of the Hulthén Potential by Using the Asymptotic Iteration Method. Phys Scr (2007) 76:1. doi:10.1088/0031-8949/76/1/016
12. Onate CA, Oyewumi KJ, Falaye BJ. Approximate Solutions of the Schrödinger Equation with the Hyperbolical Potential: Supersymmetric Approach. Few-body Syst (2014) 55:61–7. doi:10.1007/s00601-013-0731-0
13. Hamzavi M, Thylwe KE, Rajabi AA. Approximate Bound States Solution of the Hellmann Potential. Commun Theor Phys (2013) 60:1–8. doi:10.1088/0253-6102/60/1/01
14. Ikhdair SM, Falaye BJ. Approximate Analytical Solutions to Relativistic and Nonrelativistic Pöschl-Teller Potential with its Thermodynamic Properties. Chem Phys (2013) 421:84–95. doi:10.1016/j.chemphys.2013.05.021
15. Falaye BJ, Oyewumi KJ, Abbas M. Exact Solution of Schrödinger Equation with Q -deformed Quantum Potentials Using Nikiforov-Uvarov Method. Chin Phys. B (2013) 22:110301. doi:10.1088/1674-1056/22/11/110301
16. Antia AD, Isonguyo CN, Ikot AN, Hassanabadi H, Obong HP, Maghsoodi E. Afri Rev Phys (2017) 13:0003.
18. Ikot AN, Hassanabadi H, Abbey TM. Spin and Pseudospin Symmetries of Hellmann Potential with Three Tensor Interactions Using Nikiforov-Uvarov Method. Commun Theor Phys (2015) 64:637–43. doi:10.1088/0253-6102/64/6/637
19. Zhang MC, Sun GH, Dong SH. Exactly Complete Solutions of the Schrödinger Equation with a Spherically Harmonic Oscillatory Ring-Shaped Potential. Phys Lett A (2010) 374:704–8. doi:10.1016/j.physleta.2009.11.072
20. Eshghi M, Mehraban H, Ikhdair SM. Bound States of (1+1)-dimensional Dirac Equation with Kink-like Vector Potential and delta Interaction. Acta Math Appl Sin Engl Ser (2015) 31:1131–40. doi:10.1007/s10255-015-0521-1
21. Miranda MG, Sun GH, Dong SH. The Solution of the Second Pöschl-Teller like Potential by Nikiforov-Uvarov Method. Int J Mod Phys E (2010) 19:123–9. doi:10.1142/s0218301310014704
22. Okon IB, Popoola O, Isonguyo CN. Bound State Solution to Schrodinger Equation with Modified Hylleraas Plus Inversely Quadratic Potential Using Supersymmetric Quantum Mechanics Approach. Int J Recent Adv Phys (2014) 4:3. doi:10.14810/ijrap.2015.4403
23. Onate CA, Ojonubah JO. Eigensolutions of the Schrödinger Equation with a Class of Yukawa Potentials via Supersymmetric Approach. J Theor Appl Phys (2016) 10:21–6. doi:10.1007/s40094-015-0196-2
24. Ikot AN, Obong HP, Abbey TM, Zare S, Ghafourian M, Hassanabadi H. Bound and Scattering State of Position Dependent Mass Klein-Gordon Equation with Hulthen Plus Deformed-type Hyperbolic Potential. Few-body Syst (2016) 57:807–22. doi:10.1007/s00601-016-1111-3
26. Gendenstein LE. Derivation of Exact Spectra of the Schrödinger Equation by Means of Supersymmetry. J Exp Theor Phys Lett (1983) 38:356.
27. Cooper F, Freedman B. Aspects of Supersymmetric Quantum Mechanics. Ann Phys (1983) 146:262–88. doi:10.1016/0003-4916(83)90034-9
29. Ciftci H, Hall RL, Saad N. Perturbation Theory in a Framework of Iteration Methods. J Phys Lett A (2005) 340:288. doi:10.1016/j.physleta.2005.04.030
30. Bayrak O, Boztosun I, Ciftci H. Exact Analytical Solutions to the Kratzer Potential by the Asymptotic Iteration Method. Int J Quan Chem. (2007) 107:540–4. doi:10.1002/qua.21141
32. Oyewumi KJ. Realization of the Spectrum Generating Algebra for the Generalized Kratzer Potentials. Int J Theor Phys (2010) 49:1302–16. doi:10.1007/s10773-010-0311-8
34. Qiang WC, Dong SH. Proper Quantization Rule. Europhys Lett (2010) 89:10003. doi:10.1209/0295-5075/89/10003
35. Serrano FA, Cruz-Irisson M, Dong S-H. Proper Quantization Rule as a Good Candidate to Semiclassical Quantization Rules. Ann Phys (2011) 523:771–82. doi:10.1002/andp.201000144
36. Falaye BJ, Ikhdair SM, Hamzavi M. Spectroscopic Study of Some Diatomic Molecules via the Proper Quantization Rule. J Math Chem (2015) 53:1325–50. doi:10.1007/s10910-015-0491-9
37. Kestner NR, Sinanoglu O. Study of Electron Correlation in Helium-like Systems Using an Exactly Soluble Model. Phys Rev (1962) 128:2687. doi:10.1103/PhysRev.128.2687
38. Stahlhofen AA. Susy, Gauss, Heun and Physics: a Magic Square? J Phys A: Math Gen (2004) 37:10129–38. doi:10.1088/0305-4470/37/43/008
39. Karwowski J, Witek HA. Biconfluent Heun Equation in Quantum Chemistry: Harmonium and Related Systems. Theor Chem Acc (2014) 133:1494. doi:10.1007/s00214-014-1494-5
40. Slavyanov SY, Lay W, Seeger A. Special Functions, A Unifield Theory Based on Singularities. New-York: Oxford University Press (2000).
42. Ahmadov AI, Aydin C, Uzun O. Bound State Solution of the Schrödinger Equation at Finite Temperature. J Phys Conf Ser (2019) 1194:012001. doi:10.1088/1742-6596/1194/1/012001
43. Ahmadov AI, Abasova KH, Orucova MS. Bound State Solution Schrödinger Equation for Extended Cornell Potential at Finite Temperature. Adv.High Ener Phys (2021) 2021:1861946. doi:10.1155/2021/1861946
44. Shi Y-J, Sun G-H, Tahir F, Ahmadov AI, He B, Dong S-H. Quantum Information Measures of Infinite Spherical Well. Mod Phys Lett A (2018) 33:1850088. doi:10.1142/s0217732318500888
45. Okon IB, Isonguyo CN, Antia AD, Ikot AN, Popoola OO. Fisher and Shannon Information Entropies for a Noncentral Inversely Quadratic Plus Exponential Mie-type Potential. Commun Theor Phys (2020) 72:065104. doi:10.1088/1572-9494/ab7ec9
46. Kuhler KM, Truhlar DG, Isaacson AD. General Method for Removing Resonance Singularities in Quantum Mechanical Perturbation Theory. J Chem Phys (1996) 104:4664–71. doi:10.1063/1.471161
47. Issacson AD. Removing Resonance Effects from Quantum Mechanical Vibrational Partition Functions Obtained from Perturbation Theory. J Chem Phys (1998) 108:9978. doi:10.1063/1.476496
48. Strekalov ML. An Accurate Closed-form Expression for the Partition Function of Morse Oscillators. Chem Phys Lett (2007) 439:209–12. doi:10.1016/j.cplett.2007.03.052
50. Banger S, Nayak V, Verma UP. Hydrogen Storage in Lithium Hydride: A Theoretical Approach. J Phys Chem Sol (2018) 115:17. doi:10.1016/j.jpcs.2017.11.027
52. Ikot AN, Okorie US, Ngiangia AT, Onate CA, Edet CO, Akpan IO, et al. Electical Quimica J (2020) 45:76. doi:10.26850/1678-4618eqj.v45.1.2020.p65-77
54. Ravelo JG, Memendez A, Garcia J M, Halberg AS. Effective Kratzer and Coulomb Potentials as Limit Cases of a Multiparameter Exponential-type Potential. Phys Lett A (2014) 378:31. doi:10.1016/j.physleta.2014.05.023
56. Hassanabadi H, Rahimov H, Zarrinkamar S. Approximate Solutions of Klein-Gordon Equation with Kratzer Potential. Adv High Energ Phys (2011) 2011:458087. doi:10.1155/2011/458087
57. Bayrak O, Boztosun I, Ciftci H. Exact Analytical Solutions to the Kratzer Potential by the Asymptotic Iteration Method. Int J Quant Chem (2007) 107:544. doi:10.1002/qua.21141
58. Tezcan C, Sever R. A General Approach for the Exact Solution of the Schrödinger Equation. Int J Theor Phys (2009) 48:337–50. doi:10.1007/s10773-008-9806-y
59. Jia CS, Liu JY, Wang PQ. A New Approximation Scheme for the Centrifugal Term and the Hulthén Potential. Phys Lett A (2008) 372:4779–82. doi:10.1016/j.physleta.2008.05.030
60. Ikhdair SM. An Improved Approximation Scheme for the Centrifugal Term and the Hulthén Potential. Eur Phys J A (2009) 39:307–14. doi:10.1140/epja/i2008-10715-2
61. Varshni YP. Eigenenergies and Oscillator Strengths for the Hulthén Potential. Phys Rev A (1990) 41:4682–9. doi:10.1103/physreva.41.4682
62. Stanek J. Approximate Analytical Solutions for Arbitrary L-State of the Hulthén Potential with an Improved Approximation of the Centrifugal Term. Cent Eur J Chem (2011) 9:737–42. doi:10.2478/s11532-011-0050-6
63. Okon IB, Popoola OO, Isonguyo CN. Approximate Solutions of Schrodinger Equation with Some Diatomic Molecular Interactions Using Nikiforov-Uvarov Method. Adv High Ener Phys (2017) 2017:9671816. doi:10.1155/2017/9671816
64. Greene RL, Aldrich C. Variational Wave Functions for a Screened Coulomb Potential. Phys Rev A (1976) 14:263. doi:10.1103/physreva.14.2363
Keywords: nikiforov-uvarov method, kratzer plus generalised morse potential, thermodynamic properties, schrodinger wave equation, diatomic molecules
Citation: Isonguyo CN, Okon IB, Antia AD, Oyewumi KJ, Omugbe E, Onate CA, Joshua RU, Udoh ME, Ituen EE and Araujo JP (2022) Eigensolutions and Thermodynamic Properties of Kratzer Plus Generalized Morse Potential. Front. Phys. 10:962717. doi: 10.3389/fphy.2022.962717
Received: 06 June 2022; Accepted: 22 June 2022;
Published: 22 July 2022.
Edited by:
Akpan Ndem Ikot, University of Port Harcourt, NigeriaReviewed by:
Ramazan Sever, Middle East Technical University, TurkeyAzar Ahmadov, Baku Slavic University, Azerbaijan
Uduakobong Okorie, Akwa Ibom State University, Nigeria
Copyright © 2022 Isonguyo, Okon, Antia, Oyewumi, Omugbe, Onate, Joshua, Udoh, Ituen and Araujo. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Ituen B. Okon, aXR1ZW5va29uQHVuaXV5by5lZHUubmc=
 Cecilia N. Isonguyo1
Cecilia N. Isonguyo1 Ituen B. Okon
Ituen B. Okon Ekwevugbe Omugbe
Ekwevugbe Omugbe Judith P. Araujo
Judith P. Araujo