Thermodynamics of second-grade nanofluid over a stretchable rotating porous disk subject to Hall current and cubic autocatalysis chemical reactions

Homogeneous–heterogeneous chemical reactions for second-grade nanofluid and gyrotactic microorganisms in a rotating system with the effects of magnetic fields and thermal radiation are examined. The boundary layer equations of the problem in a non-dimensional form are evaluated by a strong technique, namely, the homotopy analysis method (HAM). The rates of flow, heat, mass, and gyrotactic microorganism motion are obtained for the augmentations in the pertinent parameters. The graphical pictures of the results are described by the physical significance. The Hall current effect decreases the azimuthal velocity, the axial velocity increases with the injection of mass, the Biot number leads to enhanced heat transfer and gyrotactic microorganisms, the concentration diffusion rate decreases with the Peclet number, and the concentration of the chemical reaction reduces with the Schmidt number. Excellent agreement of the present work is found with the previously published work. The present study has applications in the hydromagnetic lubrication, semiconductor crystal growth control, austrophysical plasmas, magnetic storage disks, computer storage devices, care and maintenance of turbine engines, aeronautical, mechanical, and architectural engineering, metallurgy, polymer industry, hydromagnetic flows in porous media, and food processing and preservation processes.

1 Introduction

Bioconvection has applications in medical sciences [1]. Bioconvection is the macroscopic motion of fluid generated due to density gradients and collective upward swimming of motile microorganisms in the presence of light or chemical attraction and gravity. This is due to the result of the self-propulsion of motile microorganisms. Bioconvection has a special role in the creation of energy and mechanical capability. It is dependent on the species of microorganisms that affects the direction of cell swimming. Due to the motion of microorganisms in each direction, the thickness of fluid increases which has vast applications in biology and biotechnology. Bioconvection causes the structures in microorganisms and has a wide range of applications in nuclear and medical engineering, fuel cell technology, bioreactors, and biodiesel fuels, etc. Shah et al. [2] scrutinized the bioconvection water-based nanofluid flow-containing carbon nanotubes through a vertical cone, in addition to microorganisms, entropy generation, Joule heating, heat generation/absorption, and chemical reaction. Waqas et al. [3] investigated the MHD flow of Burgers nanofluid with motile microorganisms, thermal radiation, and activation energy by using the bvp4c program to show the impact on medications for the treatment of arterial diseases. Waqas et al. [4] evaluated the second-order slip effects, activation energy, and Cattaneo–Christov heat and mass flux model with the melting phenomenon on the bioconvection flow of viscoelastic nanofluid. Farooq et al. [5] analyzed the three-dimensional bioconvectional flow of viscoelastic nanofluids past an elongated surface with motile microorganisms, thermal radiation, and solutal boundary conditions. Waqas et al. [6] disclosed the effects of Brownian motion, thermophoresis, thermal radiation, and Arrhenius activation energy on the bioconvection flow of Burgers nanofluid. Dawar et al. [7] presented the magnetized and non-magnetized Casson fluid flows with gyrotactic microorganisms past a stretching cylinder using the homotopy analysis method. Waqas et al. [8] performed a study on bioconvection Darcy–Forchheimer flow of MHD viscous fluid with thermal radiation, heat source, and Arrhenius activation energy past a rotating disk of variable thickness. Dawar et al. [9] attempted to solve the problem of two-dimensional electrically conducting MHD fluid with thermal radiation, Arrhenius activation energy, and binary chemical reaction. Khan et al. [10] analyzed the bioconvection flow of Oldroyd-B nanofluid in a porous medium with heat transfer. Some other studies regarding bioconvection can be seen in references [11–15].

Viscoelastic fluids are related to non-Newtonian fluids, which show viscous and elastic characteristics in the light of deformation. Second-grade fluid is a type of viscoelastic fluid [16]. Khan et al. [17] analyzed the second-grade fluid with temperature-dependent thermal conductivity and viscosity. Adeniyan et al. [18] studied the flow and heat transfer features of an incompressible second-grade fluid past a stretched porous vertical slender with viscous dissipation and convection heat at the wall with the surroundings in conjunction with far-field conditions. Adigun et al. [19] discussed the MHD stagnation point flow of a viscoelastic nanofluid past an inclined stretching cylinder with modified Darcy’s law and an Arrhenius activation energy effect. Concentrating on the other non-Newtonian fluids, Usman et al. [20] investigated the Oldroyd-B nanoliquid film with the spraying phenomena, heat transfer, nanoparticle concentration, and gyrotactic microorganisms. Yusuf et al. [21] examined the entropy generation in a steady, gravity-driven thin film flow of a micropolar fluid by implementing the differential transformation method. Hussain and Xu [22] performed the numerical analysis of the incompressible, time-dependent electrically conducting squeezing flow of micropolar nanofluid in rotating disks by using the Buongiorno nanofluid model and gyrotactic microorganisms. Hussain et al. [23] presented the convective heat transfer of MHD mixed convection flow past a stretching wedge with ohmic heating and thermal radiation by using the bvp4c method in MATLAB software. Shah et al. [24] examined the slip flow of upper-convected Maxwell nanofluid, taking into account the inclined stretching sheet, magnetic field, and porous medium. The non-Newtonian behaviors and other characteristics of fluids can be seen in references [25–31].

Nanofluids have important engineering and industrial applications due to their better heat transfer characteristics. Nanofluids are used in solar collectors, for heating and for cooling purposes like ventilation, air conditioning, and refrigeration. Choi [32] observed that nanofluids have a significant enhancement in thermal conductivity compared to ordinary base fluids. Khan et al. [33] presented the model of bioconvective cross diffusion flow of magnetized viscous nanofluid over the cone, wedge, and plate under convective boundary conditions and Cattaneo–Christov heat and mass flux with activation energy and thermal radiation. Dawar et al. [34] studied the convective flow of Williamson nanofluid over the cone and wedge under variable non-isosolutal and non-isothermal conditions by showing that flow is higher on the cone than the wedge. Cae et al. [35] reported forced, free, and mixed convection in the colloidal mixture of water with platelet alumina, spherical carbon nanotubes, and cylindrical graphene. Alrabaiah et al. [36] addressed the silver–magnesium oxide hybrid nanofluid flow inside the conical space between the disk and cone with gyrotactic microorganisms using the parametric continuation method. Nazir et al. [37] investigated the Carreau–Yasuda-based hybrid nanofluid past a porous rotating cone with Hall and ion slip forces, generalized Ohm’s law, heat generation, Joule heating, and viscous dissipation. Shahid et al. [38] used the Chebyshev spectral collocation method to solve the MHD nanofluid flow containing gyrotactic microorganisms through a porous sheet. The nanofluids and other studies can be seen in references [39–56].

Revolving surfaces in fluid dynamics are the transcendent research areas. Hafeez et al. [57] studied the upper convected Oldroyd-B fluid with homogeneous–heterogeneous chemical reactions using the BVP Midrich scheme. Acharya et al. [58] investigated the hybrid nanofluid flow over a spinning disk with Hall current and thermal radiation. Ariel [59] considered the time-independent laminar flow of a second-grade fluid past a revolving disk in which the viscoelasticity of the fluid causes a boundary value problem. Acharya [60] enlightened the hydrothermal characteristics of chemically reactive nanofluid past an inclined rotating porous disk in which he showed that the normalized thickness parameter enhances the radial velocity and nanoparticle concentration. Naqvi et al. [61] analyzed the Reiner-Rivlin fluid over a rotating disk under various slip conditions in which they performed the calculations for surface heat transfer and wall skin friction through a wide range of parameters. Khan et al. [62] studied the hybrid nanofluid flow through a porous medium with gyrotactic microorganisms, double diffusion, chemical reaction, Joule heating, and multiple slip boundary conditions. Beg et al. [63] focused on the time-independent MHD flow past a spinning porous disk with slip conditions, injection, thermal radiation, and variable thermophysical properties using the network simulation method.

Chemical reactions have important applications in chemical and food processing, polymer and ceramics, hydrometallurgical industry, crops damage due to freezing, groves of fruit trees, atmospheric flows, air, and water pollution, and flows in desert cooler and moisture. In most cases, chemical reactions involve homogeneous–heterogeneous reactions, whose examples are combustion, catalysis, and biochemical systems. Numerous researchers are working on investigations into flow behaviors due to chemical reactions. Chaudhary and Merkin [64] analyzed a simple model for homogeneous–heterogeneous reactions in stagnation-point boundary-layer flow in which the homogeneous reaction is assumed to be given by isothermal cubic autocatalator kinetics and the heterogeneous reaction by first-order kinetics. They considered the possible steady states of this system in detail in the case when the diffusion coefficients of both the reactant and autocatalyst are equal. Sajid et al. [65] examined the MHD Blasius flow with homogeneous–heterogeneous chemical reactions and thermal radiation using the shooting method for the computational work. Sravanthi et al. [66] considered the homogeneous–heterogeneous chemical reactions in nanofluid in a porous medium with variable magnetic field and non-linear thermal radiation, in which the non-linear thermal radiation has a high impact on heat transfer compared to that of linear thermal radiation. Alzahrani et al. [67] investigated the Oldroyd-B nanofluid past a porous boundary with homogeneous–heterogeneous chemical reactions, thermosolutal Marangoni convection, and heat source/sink in a revised model for thermal conductivity and dynamic viscosity. Khan et al. [68] investigated stagnation point time-dependent Oldroyd-B fluid flow with homogeneous–heterogeneous chemical reactions, thermal and solutal transportation, variable heat source/sink, Joule heating, and thermal radiation. Sunthrayuthet al. [69] focused on the study of second-grade nanofluid through a stretching cylinder with homogeneous–heterogeneous chemical reactions.

Due to the inspiration of the aforementioned published articles, the present study objective is to examine the homogeneous–heterogeneous chemical reactions and gyrotactic microorganism motion in a rotating porous system for MHD second-grade nanofluid with Hall current effect, thermal radiation, and mixed convection and convective conditions. The homotopy analysis method [70] is used to evaluate the non-dimensional problem.

2 Methods

2.1 Basic equations

An incompressible three-dimensional second-grade nanofluid flow with heat transfer, homogeneous–heterogeneous chemical reactions, and bioconvection due to motile gyrotactic microorganisms in the presence of Hall current effect and thermal radiation is considered. The porous disk flow in the upper plane z ≥ 0 has the uniform angular velocity, stretching rate, constant temperature, and motile gyrotactic microorganism concentration as Ω, c₁, T_w, and N_w, while at the free stream, the temperature and motile gyrotactic microorganism concentration are T_∞ and N_∞, respectively. The disk surface is porous and bears the velocity w₀. w₀ $>$ 0 shows the injection and w₀ $<$ 0 shows the suction of the mass. The convective heat transfer conditions are used. A simple model is considered for the interaction between a homogeneous reaction and a heterogeneous reaction involving two chemical species, A and B [64]. A magnetic field is applied in the z-direction (please see Figure 1). The given problem has the governing equations as in [8, 57, 64].

$\frac{\partial u}{\partial r}+\frac{u}{r}+\frac{\partial w}{\partial z}=0,(1)$

$\begin{array}{ll}\hfill {\rho }_f\left(\begin{array}{c}\hfill u\frac{\partial u}{\partial r}+w\frac{\partial u}{\partial z}-\frac{v^2}{r}\hfill \end{array}\right)& ={\mu }_f\frac{{\partial }^{2}u}{\partial z^2}-\frac{{\sigma }_f{B}_0^2\left(u-mv\right)}{1+m^2}+g_1\beta \left(T-T_{\infty }\right)\hfill \\ \hfill & +{\alpha }_1\left[\begin{array}{c}\hfill u\frac{{\partial }^{3}u}{\partial r\partial z^2}-\frac{1}{r}{\left(\frac{\partial u}{\partial z}\right)}^2+2\frac{\partial u}{\partial r}\frac{{\partial }^{2}u}{\partial z^2}+w\frac{{\partial }^{3}u}{\partial z^3}+\frac{\partial v}{\partial r}\frac{{\partial }^{2}v}{\partial z^2}+\frac{{\partial }^{2}u}{\partial z^2}\frac{\partial w}{\partial z}+\frac{\partial v}{\partial z}\frac{{\partial }^{2}v}{\partial r\partial z}+3\frac{\partial u}{\partial z}\frac{{\partial }^{2}u}{\partial r\partial z}-\frac{\partial v}{\partial r}\frac{{\partial }^{2}v}{\partial z^2}\hfill \end{array}\right],\hfill \end{array}(2)$

${\rho }_f\left(u\frac{\partial v}{\partial r}+w\frac{\partial v}{\partial z}+\frac{1}{r}uv\right)={\mu }_f\frac{{\partial }^{2}v}{\partial z^2}+{\alpha }_1\left[\begin{array}{c}\hfill u\frac{{\partial }^{3}v}{\partial r\partial z^2}+w\frac{{\partial }^{3}v}{\partial z^3}-2\frac{\partial v}{\partial z}\frac{{\partial }^{2}u}{\partial r\partial z}+\frac{u}{r}\frac{{\partial }^{2}v}{\partial z^2}-\frac{1}{r}\frac{\partial u}{\partial z}\frac{\partial v}{\partial z}\hfill \end{array}\right]-\frac{{\sigma }_f{B}_0^2\left(v+mu\right)}{1+m^2},(3)$

$\begin{array}{l}\hfill \left(\begin{array}{c}\hfill u\frac{\partial T}{\partial r}+w\frac{\partial T}{\partial z}\hfill \end{array}\right){\left(\rho c_p\right)}_f=k_f\left(\begin{array}{c}\hfill \frac{{\partial }^{2}T}{\partial z^2}+\frac{{\partial }^{2}T}{\partial r^2}+\frac{1}{\partial r}\frac{\partial T}{\partial r}\hfill \end{array}\right)+2{\mu }_f\left[\begin{array}{c}\hfill {\left(\frac{\partial u}{\partial r}\right)}^2+{\left(\frac{\partial w}{\partial z}\right)}^2+\frac{u^2}{r^2}\hfill \end{array}\right]+\frac{\partial q_r}{\partial z}+\frac{{\sigma }_f{B}_0^2\left(u^2+v^2\right)}{1+m^2}+{\mu }_f\left[{\left(\frac{\partial v}{\partial z}\right)}^2+{\left(\frac{\partial u}{\partial z}+\frac{\partial w}{\partial r}\right)}^2+{\left(r\frac{\partial }{\partial r}\left(\frac{v}{r}\right)\right)}^2\right],\end{array}(4)$

$u\frac{\partial N}{\partial r}+w\frac{\partial N}{\partial z}+\frac{\partial \left(N\stackrel{\sim }{v}\right)}{\partial z}=D_n\left[\begin{array}{c}\hfill \frac{{\partial }^{2}N}{\partial r^2}+\frac{1}{r}\frac{\partial N}{\partial r}+\frac{{\partial }^{2}N}{\partial z^2}\hfill \end{array}\right],(5)$

$u\frac{\partial a}{\partial r}+w\frac{\partial a}{\partial z}=D_A\left(\begin{array}{c}\hfill \frac{{\partial }^{2}a}{\partial z^2}\hfill \end{array}\right)-k_{c}a{b}^2,(6)$

$u\frac{\partial b}{\partial r}+w\frac{\partial b}{\partial z}=D_B\left(\begin{array}{c}\hfill \frac{{\partial }^{2}b}{\partial z^2}\hfill \end{array}\right)+k_{c}a{b}^2.(7)$

The boundary conditions are used as

$u=r{c}_1,v=r\mathrm{\Omega },w=w_0,-k\frac{\partial T}{\partial z}=h_f\left(T_f-T\right),D_A\frac{\partial a}{\partial z}=k_{s}a,D_B\frac{\partial b}{\partial z}=-k_{s}a,N=N_{w}atz=0,(8)$

$u\to 0,v\to 0,w\to 0,T\to T_{\infty },a\to a_0,b\to b_0,N\to N_{\infty },asz\to \infty ,(9)$

where u(r, ϑ, z), v(r, ϑ, z), and w(r, ϑ, z) are the velocity components, p is the pressure, and m is the Hall parameter [64]. α₁ is the material parameter, γ_av is the average volume of microorganisms, β is the coefficient of volumetric volume expansion of a second-grade nanofluid, g₁ is the acceleration due to gravity, and k_f is the thermal diffusivity of the nanofluid. ρ_f, μ_f, σ_f, and ${(c_p)}_f$ are the density, effective dynamic viscosity, electrical conductivity, and heat capacitance of the nanofluid, respectively. h_f is the convective heat transfer coefficient, ν_f = $\frac{{\mu }_f}{{\rho }_f}$ is the kinematic viscosity, $\stackrel{\sim }{v}$ = $\left[\begin{array}{c}\hfill \frac{b_1{W}_{ce}}{\mathrm{\Delta }a}\hfill \end{array}\right]\frac{\partial a}{\partial z}$ is the average swimming velocity vector of the oxytactic microorganisms in which b₁ is the chemotaxis constant, W_ce is the maximum cell swimming speed [8], and D_n is the diffusivity of microorganisms. a is the concentration of chemical species A, b is the concentration of chemical species B, and D_A and D_B are the diffusion coefficients. The rates of homogeneous and heterogeneous chemical reactions are denoted by k_c and k_s, respectively. The radiation heat flux is expressed by q_r for which the relation is given by

$q_r=-\left(\begin{array}{c}\hfill \frac{16{\sigma }^{\ast }{T_{\infty }}^3}{3k_e}\frac{\partial T}{\partial z}\hfill \end{array}\right),(10)$

where the Stefan–Boltzmann constant is σ* and the mean absorption coefficient is k_e.

FIGURE 1

FIGURE 1. Physical configuration of the problem.

The following transformations are used [57]:

$\begin{array}{ll}\hfill & u=r\mathrm{\Omega }f\left(\zeta \right),v=r\mathrm{\Omega }g\left(\zeta \right),w={\left(\mathrm{\Omega }{\nu }_f\right)}^{\frac{1}{2}}h\left(\zeta \right),\theta \left(\zeta \right)=\frac{T-T_{\infty }}{T_w-T_{\infty }},\varphi \left(\zeta \right)=\frac{a}{a_0},{\varphi }_1\left(\zeta \right)=\frac{b}{a_0},\hfill \\ \hfill & \chi \left(\zeta \right)=\frac{N-N_{\infty }}{N_w-N_{\infty }},\zeta ={\left[\frac{\mathrm{\Omega }}{{\nu }_f}\right]}^{\frac{1}{2}}z.\hfill \end{array}(11)$

Substituting the values from Eq. 11 in Eqs 1–9, the following nine Eqs 12–20 are obtained

$2f+h^{\prime }=0,(12)$

$f\prime \prime -f^2+g^2-f\prime h+{\beta }_1\left(\begin{array}{c}\hfill hf\prime \prime \prime +2ff\prime \prime -f{\prime }^2-g{\prime }^2\hfill \end{array}\right)-\frac{M\left(f^{\prime }-mg\right)}{1+m^2}-Gr\theta =0,(13)$

$g^{\prime \prime }-g^{\prime }h-2fg+{\beta }_1\left(\begin{array}{c}\hfill g^{\prime \prime }h+2f{g}^{\prime \prime }\hfill \end{array}\right)-\frac{M\left(m{f}^{\prime }+g\right)}{1+m^2}=0,(14)$

$\frac{1+Rd}{Pr}{\theta }^{\prime \prime }-h{\theta }^{\prime }+2\frac{Ec}{Re}\left[\begin{array}{c}\hfill {\left(\begin{array}{c}\hfill h^{\prime }\hfill \end{array}\right)}^2+2f^2\hfill \end{array}\right]+\frac{MEc}{1+m^2}\left(\begin{array}{c}\hfill f^2+g^2\hfill \end{array}\right)+Ec\left[\begin{array}{c}\hfill {\left(\begin{array}{c}\hfill f^{\prime }\hfill \end{array}\right)}^2+{\left(\begin{array}{c}\hfill g^{\prime }\hfill \end{array}\right)}^2\hfill \end{array}\right]=0,(15)$

${\chi }^{\prime \prime }-Lbh{\chi }^{\prime }-Pe\left(\begin{array}{c}\hfill {\chi }^{\prime }{\varphi }^{\prime }+{\varphi }^{\prime \prime }\left({\gamma }_1+\chi \right)\hfill \end{array}\right)=0,(16)$

$\frac{1}{Sc}{\varphi }^{\prime \prime }-h{\varphi }^{\prime }-k_1\varphi {\varphi }_1^2=0,(17)$

$\frac{\delta }{Sc}{\varphi }_1^{\prime \prime }-h{\varphi }_1^{\prime }+k_1\varphi {\varphi }_1^2=0,(18)$

$f=s_1,g=1,h=h_w,{\theta }^{\prime }=-Bi\left(1-\theta \right),{\varphi }^{\prime }=k_2\varphi ,\delta {\varphi }_1^{\prime }=-k_2\varphi ,\chi =1at\zeta =0,(19)$

$f\to 0,g\to 0,h\to 0,\theta \to 0,\varphi \to 1,\chi \to 0,as\zeta \to \infty ,(20)$

where (^‘) represents the differentiability through ζ. β₁ = $\frac{{\alpha }_1\mathrm{\Omega }}{{\mu }_f}$ is the dimensionless measure of non-Newtonian second-grade nanofluid parameter, $M=\frac{{\sigma }_f{B}_0^2}{{\rho }_f\mathrm{\Omega }}$ is the magnetic field parameter, $Gr=\frac{g_{1\beta }(T_w-T_{\infty })}{{\nu }_f\mathrm{\Omega }}$ is the modified Grashof number, $Rd=\frac{16{\sigma }^{*}{T_{\infty }}^3}{3k_e{k}_f}$ is the thermal radiation parameter, $Pr=\frac{{\nu }_f}{k_f}$ is the Prandtl number, $Ec=\frac{r^2{\mathrm{\Omega }}^2}{c_P(T_w-T_{\infty })}$ is the Eckert number, $Re=\frac{r^2\mathrm{\Omega }}{{\nu }_f}$ is the local rotational Reynolds number, $Lb=\frac{{\nu }_f}{D_n}$ is the bioconvection Lewis number, $Pe=\frac{b{W}_{\mathit{ce}}}{D_n}$ is the Peclet number, and γ₁ = $\frac{N_{\infty }}{N_w-N_{\infty }}$ is the microorganism concentration difference parameter. $Sc=\frac{{\nu }_f}{D_A}$ is the Schmidt number, $k_1=\frac{k_c{a}_0^2}{\mathrm{\Omega }}$ is the homogeneous chemical reaction rate, $k_2=\frac{k_s}{D_A}{\left[\begin{array}{c}\hfill \frac{{\nu }_f}{\mathrm{\Omega }}\hfill \end{array}\right]}^{\frac{1}{2}}$ is the heterogeneous chemical reaction rate, $s_1=\frac{c_1}{\mathrm{\Omega }}$ is the stretching parameter, $h_w=\frac{w_0}{{\left[\begin{array}{c}\hfill {\nu }_f\mathrm{\Omega }\hfill \end{array}\right]}^{\frac{1}{2}}}$ is the suction/injection parameter, $Bi=\frac{h_f}{k_f}{\left[\begin{array}{c}\hfill \frac{{\nu }_f}{\mathrm{\Omega }}\hfill \end{array}\right]}^{\frac{1}{2}}$ is the Biot number, and δ = $\frac{D_B}{D_A}$ is the ratio of diffusion coefficients. In many applications, the diffusion coefficients A and B of the chemical species can be comparable in size which leads to the assumption that the diffusion coefficients D_A and D_B are equal. By the Chaudhary and Merkin [64] study, assuming δ = 1 which provides the following equation:

$\varphi \left(\zeta \right)+{\varphi }_1\left(\zeta \right)=1.(21)$

So Eqs 17, 18 finally result in

$\frac{1}{Sc}{\varphi }^{\prime \prime }-h{\varphi }^{\prime }-k_1\varphi {\left[1-\varphi \right]}^2=0,(22)$

with the boundary conditions as

${\varphi }^{\prime }=k_2\varphi at\zeta =0and\varphi \to 1as\zeta \to \infty .(23)$

The physical quantities such as coefficient of skin friction C_F, local Nusselt number $N_{u_r}$, and local motile density number $N_{n_r}$ are defined as

$C_F=\frac{\tau {|}_{z=0}}{{\rho }_f{\left(r\mathrm{\Omega }\right)}^2},(24)$

where

$\tau =\sqrt{{\left({\tau }_r\right)}^2+{\left({\tau }_{\vartheta }\right)}^2}(25)$

denotes the square root of the sum of shear stresses τ_r and τ_ϑ in a squaring form along radial and transverse directions.

$N{u}_r=\frac{-r{q}_1}{k_f\left(T_w-T_{\infty }\right)},N{n}_r=\frac{-r{q}_2}{D_m\left(N_w-N_{\infty }\right)},(26)$

where q₁ and q₂ are the heat and motile microorganism fluxes at the surface of the rotating disk, respectively, and are defined as

$q_1=-k_f{T}_z{|}_{z=0},q_2=D_m{N}_z{|}_{z=0}.(27)$

Using the information from Eq. 11, Eq. 24 proceeds to

$C_F=R{e}_r^{\frac{-1}{2}}\left[\begin{array}{c}\hfill {\left(\begin{array}{c}\hfill f^{\prime }\left(0\right)\hfill \end{array}\right)}^2+{\left(\begin{array}{c}\hfill g^{\prime }\left(0\right)\hfill \end{array}\right)}^2\hfill \end{array}\right],(28)$

where Re_r = $\frac{r^2\mathrm{\Omega }}{{\nu }_f}$ is the Reynolds number. Similarly by applying values from Eq. 11 in Eq. 26, it is obtained that

$N{u}_r=-R{e}_r^{0.5}{\theta }^{\prime }\left(0\right),N{n}_r=-R{e}_r^{0.5}{\chi }^{\prime }\left(0\right).(29)$

3 Computational framework

Following the homotopy analysis method (HAM) [70], the initial approximations and auxiliary linear operators are

$\begin{array}{ll}\hfill & f_0\left(\zeta \right)=s_1\exp \left(-\zeta \right),g_0\left(\zeta \right)=\exp \left(-\zeta \right),h_0\left(\zeta \right)=h_w\exp \left(-\zeta \right),{\theta }_0\left(\zeta \right)=\frac{Bi}{1+Bi}\exp \left(-\zeta \right),\hfill \\ \hfill & {\chi }_0\left(\zeta \right)=\exp \left(-\zeta \right),{\varphi }_0\left(\zeta \right)=\exp \left(-\zeta \right),\hfill \end{array}(30)$

${\mathit{L}}_h=h^{\prime },{\mathit{L}}_f=f^{\prime \prime }-f,{\mathit{L}}_g=g^{\prime \prime }-g^{\prime },{\mathit{L}}_{\theta }={\theta }^{\prime \prime }-\theta ,{\mathit{L}}_{\chi }={\chi }^{\prime \prime }-\chi ,{\mathit{L}}_{\varphi }={\varphi }^{\prime \prime }-\varphi .(31)$

The following properties are satisfied with the linear operators:

$\begin{array}{ll}\hfill {\mathit{L}}_h\left[\begin{array}{c}\hfill C_1\hfill \end{array}\right]& =0,{\mathit{L}}_f\left[\begin{array}{c}\hfill C_2\exp \left(\zeta \right)+C_3\exp \left(-\zeta \right)\hfill \end{array}\right]=0,{\mathit{L}}_g\left[\begin{array}{c}\hfill C_4\exp \left(\zeta \right)+C_5\exp \left(-\zeta \right)\hfill \end{array}\right]=0,{\mathit{L}}_{\theta }\left[\begin{array}{c}\hfill C_6\exp \left(\zeta \right)+C_7\exp \left(-\zeta \right)\hfill \end{array}\right]\hfill \\ \hfill & =0,{\mathit{L}}_{\chi }\left[\begin{array}{c}\hfill C_8\exp \left(\zeta \right)+C_9\exp \left(-\zeta \right)\hfill \end{array}\right]=0,{\mathit{L}}_{\varphi }\left[\begin{array}{c}\hfill C_{10}\exp \left(\zeta \right)+C_{11}\exp \left(-\zeta \right)\hfill \end{array}\right]=0,\hfill \end{array}(32)$

where C_i(i = 1–11) are the arbitrary constants.

3.1 Zeroth order deformation problems

The zeroth order form of the present problem is

$\left(1-q\right){\mathit{L}}_{\mathit{h}}\left[h\left(\zeta ,q\right)-h_0\left(\zeta \right)\right]=q{\mathit{\hslash }}_h{\aleph }_h\left[f\left(\zeta ,q\right),h\left(\zeta ,q\right)\right],(33)$

$\left(1-q\right){\mathit{L}}_{\mathit{f}}\left[f\left(\zeta ,q\right)-f_0\left(\zeta \right)\right]=q{\hslash }_f{\aleph }_f\left[f\left(\zeta ,q\right),g\left(\zeta ,q\right),h\left(\zeta ,q\right),\theta \left(\zeta ,q\right)\right],(34)$

$\left(1-q\right){\mathit{L}}_{\mathit{g}}\left[g\left(\zeta ,q\right)-g_0\left(\zeta \right)\right]=q{\hslash }_g{\aleph }_g\left[f\left(\zeta ,q\right),g\left(\zeta ,q\right),h\left(\zeta ,q\right)\right],(35)$

$\left(1-q\right){\mathit{L}}_{\mathit{\theta }}\left[\theta \left(\zeta ,q\right)-{\theta }_0\left(\zeta \right)\right]=q{\hslash }_{\theta }{\aleph }_{\theta }\left[f\left(\zeta ,q\right),g\left(\zeta ,q\right),h\left(\zeta ,q\right),\theta \left(\zeta ,q\right)\right],(36)$

$\left(1-q\right){\mathit{L}}_{\mathit{\chi }}\left[\chi \left(\zeta ,q\right)-{\chi }_0\left(\zeta \right)\right]=q{\hslash }_{\chi }{\aleph }_{\chi }\left[h\left(\zeta ,q\right),\chi \left(\zeta ,q\right),\varphi \left(\zeta ,q\right)\right],(37)$

$\left(1-q\right){\mathit{L}}_{\mathit{\varphi }}\left[\varphi \left(\zeta ,q\right)-{\varphi }_0\left(\zeta \right)\right]=q{\hslash }_{\varphi }{\aleph }_{\varphi }\left[h\left(\zeta ,q\right),\varphi \left(\zeta ,q\right)\right],(38)$

where q is an embedding parameter and ℏ_f, ℏ_g, ℏ_h, ℏ_θ, ℏ_χ, and ℏ_ϕ are the non-zero auxiliary parameters. ℵ_f, ℵ_g, ℵ_h, ℵ_θ, ℵ_χ, and ℵ_ϕ are the nonlinear operators and are given as

${\aleph }_h\left[f\left(\zeta ,q\right),h\left(\zeta ,q\right)\right]=2f\left(\zeta ,q\right)+\frac{\partial h\left(\zeta ,q\right)}{\partial \zeta },(39)$

$\begin{array}{ll}\hfill {\aleph }_f\left[f\left(\zeta ,q\right),g\left(\zeta ,q\right),h\left(\zeta ,q\right),\theta \left(\zeta ,q\right)\right]& =\frac{{\partial }^{2}f\left(\zeta ,q\right)}{\partial {\zeta }^2}-{\left(\begin{array}{c}\hfill f\left(\zeta ,q\right)\hfill \end{array}\right)}^2+{\left(\begin{array}{c}\hfill g\left(\zeta ,q\right)\hfill \end{array}\right)}^2-\frac{\partial f\left(\zeta ,q\right)}{\partial \zeta }h\left(\zeta ,q\right)\hfill \\ \hfill & +{\beta }_1\left[\begin{array}{c}\hfill h\left(\zeta ,q\right)\frac{{\partial }^{3}f\left(\zeta ,q\right)}{\partial {\zeta }^3}+2f\left(\zeta ,q\right)\frac{{\partial }^{2}f\left(\zeta ,q\right)}{\partial {\zeta }^2}-{\left(\begin{array}{c}\hfill \frac{\partial f\left(\zeta ,q\right)}{\partial \zeta }\hfill \end{array}\right)}^2-{\left(\begin{array}{c}\hfill \frac{\partial g\left(\zeta ,q\right)}{\partial \zeta }\hfill \end{array}\right)}^2\hfill \end{array}\right]\hfill \\ \hfill & -\frac{M}{1+m^2}\left[\begin{array}{c}\hfill \frac{\partial f\left(\zeta ,q\right)}{\partial \zeta }-mg\left(\zeta ,q\right)\hfill \end{array}\right]+Gr\theta \left(\zeta ,q\right),\hfill \end{array}(40)$

$\begin{array}{ll}\hfill {\aleph }_g\left[f\left(\zeta ,q\right),g\left(\zeta ,q\right),h\left(\zeta ,q\right)\right]& =\frac{{\partial }^{2}g\left(\zeta ,q\right)}{\partial {\zeta }^2}-\frac{\partial g\left(\zeta ,q\right)}{\partial \zeta }h\left(\zeta ,q\right)+{\beta }_1\left[\begin{array}{c}\hfill \frac{{\partial }^{2}f\left(\zeta ,q\right)}{\partial {\zeta }^2}h\left(\zeta ,q\right)+2f\left(\zeta ,q\right)\frac{{\partial }^{2}g\left(\zeta ,q\right)}{\partial {\zeta }^2}\hfill \end{array}\right]\hfill \\ \hfill & -\frac{M}{1+m^2}\left[\begin{array}{c}\hfill \frac{m\partial f\left(\zeta ,q\right)}{\partial \zeta }+g\left(\zeta ,q\right)\hfill \end{array}\right],\hfill \end{array}(41)$

$\begin{array}{ll}\hfill {\aleph }_{\theta }\left[f\left(\zeta ,q\right),g\left(\zeta ,q\right),h\left(\zeta ,q\right),\theta \left(\zeta ,q\right)\right]& =\frac{1+Rd}{Pr}\frac{{\partial }^2\theta \left(\zeta ,q\right)}{\partial {\zeta }^2}-h\left(\zeta ,q\right)\frac{\partial \theta \left(\zeta ,q\right)}{\partial \zeta }+2\frac{Ec}{Re}\left[\begin{array}{c}\hfill {\left(\begin{array}{c}\hfill \frac{\partial h\left(\zeta ,q\right)}{\partial \zeta }\hfill \end{array}\right)}^2+2{\left(\begin{array}{c}\hfill f\left(\zeta ,q\right)\hfill \end{array}\right)}^2\hfill \end{array}\right]\hfill \\ \hfill & +\frac{MEc}{1+m^2}\left[\begin{array}{c}\hfill {\left(\begin{array}{c}\hfill f\left(\zeta ,q\right)\hfill \end{array}\right)}^2+{\left(\begin{array}{c}\hfill g\left(\zeta ,q\right)\hfill \end{array}\right)}^2\hfill \end{array}\right]+Ec\left[\begin{array}{c}\hfill {\left(\begin{array}{c}\hfill \frac{\partial f\left(\zeta ,q\right)}{\partial \zeta }\hfill \end{array}\right)}^2+{\left(\begin{array}{c}\hfill \frac{\partial g\left(\zeta ,q\right)}{\partial \zeta }\hfill \end{array}\right)}^2\hfill \end{array}\right],\hfill \end{array}(42)$

$\begin{array}{ll}\hfill {\aleph }_{\chi }\left[h\left(\zeta ,q\right),\varphi \left(\zeta ,q\right),\chi \left(\zeta ,q\right)\right]& =\frac{{\partial }^2\chi \left(\zeta ,q\right)}{\partial {\zeta }^2}-Lbh\left(\zeta ,q\right)\frac{\partial \chi \left(\zeta ,q\right)}{\partial \zeta }\hfill \\ \hfill & -Pe\left[\begin{array}{c}\hfill \frac{\partial \varphi \left(\zeta ,q\right)}{\partial \zeta }\frac{\partial \chi \left(\zeta ,q\right)}{\partial \zeta }+\frac{{\partial }^2\varphi \left(\zeta ,q\right)}{\partial {\zeta }^2}\left(\begin{array}{c}\hfill {\gamma }_1+\chi \left(\zeta ,q\right)\hfill \end{array}\right)\hfill \end{array}\right],\hfill \end{array}(43)$

${\aleph }_{\varphi }\left[h\left(\zeta ,q\right),\varphi \left(\zeta ,q\right),\chi \left(\zeta ,q\right)\right]=\frac{1}{Sc}\frac{{\partial }^2\varphi \left(\zeta ,q\right)}{\partial {\zeta }^2}-h\left(\zeta ,q\right)\frac{\partial \varphi \left(\zeta ,q\right)}{\partial \zeta }-k_1\varphi \left(\zeta ,q\right){\left[\begin{array}{c}\hfill 1-\frac{\partial \varphi \left(\zeta ,q\right)}{\partial \zeta }\hfill \end{array}\right]}^2.(44)$

Eq. 33 has the boundary conditions

$h\left(0,q\right)=h_w.(45)$

Eq. 34 has the boundary conditions

$f\left(0,q\right)=s_1,f\left(\infty ,q\right)=0.(46)$

Eq. 35 has the boundary conditions

$g\left(0,q\right)=1,g\left(\infty ,q\right)=0.(47)$

Eq. 36 has the boundary conditions

${\theta }^{\prime }\left(0,q\right)=-Bi\left(1-\theta \left(0,q\right)\right),\theta \left(\infty ,q\right)=0.(48)$

Eq. 37 has the boundary conditions

$\chi \left(0,q\right)=1,\chi \left(\infty ,q\right)=0.(49)$

Eq. 38 has the boundary conditions

${\varphi }^{\prime }\left(0,q\right)=k_2\varphi \left(0,q\right),\varphi \left(\infty ,q\right)=0.(50)$

For q = 0 and q = 1, Eqs 33–38 provide

$q=0\Rightarrow h\left(\zeta ,0\right)=h_0\left(\zeta \right)andq=1\Rightarrow h\left(\zeta ,1\right)=h\left(\zeta \right),(51)$

$q=0\Rightarrow f\left(\zeta ,0\right)=f_0\left(\zeta \right)andq=1\Rightarrow f\left(\zeta ,1\right)=f\left(\zeta \right),(52)$

$q=0\Rightarrow g\left(\zeta ,0\right)=g_0\left(\zeta \right)andq=1\Rightarrow g\left(\zeta ,1\right)=g\left(\zeta \right),(53)$

$q=0\Rightarrow \theta \left(\zeta ,0\right)={\theta }_0\left(\zeta \right)andq=1\Rightarrow \theta \left(\zeta ,1\right)=\theta \left(\zeta \right),(54)$

$q=0\Rightarrow \chi \left(\zeta ,0\right)={\chi }_0\left(\zeta \right)andq=1\Rightarrow \chi \left(\zeta ,1\right)=\chi \left(\zeta \right),(55)$

$q=0\Rightarrow \varphi \left(\zeta ,0\right)={\varphi }_0\left(\zeta \right)andq=1\Rightarrow \varphi \left(\zeta ,1\right)=\varphi \left(\zeta \right).(56)$

Expanding h(ζ, q), f(ζ, q), g(ζ, q), θ(ζ, q), χ(ζ, q), and ϕ(ζ, q) through Taylor series, Eqs 51–56 generate

$h\left(\zeta ,q\right)=h_0\left(\zeta \right)+\sum _{m=1}^{\infty }{h}_m\left(\zeta \right)q^m,h_m\left(\zeta \right)=\frac{1}{m!}\frac{{\partial }^{m}h\left(\zeta ,q\right)}{\partial {\zeta }^m}{\mid }_{q=0},(57)$

$f\left(\zeta ,q\right)=f_0\left(\zeta \right)+\sum _{m=1}^{\infty }{f}_m\left(\zeta \right)q^m,f_m\left(\zeta \right)=\frac{1}{m!}\frac{{\partial }^{m}f\left(\zeta ,q\right)}{\partial {\zeta }^m}{\mid }_{q=0},(58)$

$g\left(\zeta ,q\right)=g_0\left(\zeta \right)+\sum _{m=1}^{\infty }{g}_m\left(\zeta \right)q^m,g_m\left(\zeta \right)=\frac{1}{m!}\frac{{\partial }^{m}g\left(\zeta ,q\right)}{\partial {\zeta }^m}{\mid }_{q=0},(59)$

$\theta \left(\zeta ,q\right)={\theta }_0\left(\zeta \right)+\sum _{m=1}^{\infty }{\theta }_m\left(\zeta \right)q^m,{\theta }_m\left(\zeta \right)=\frac{1}{m!}\frac{{\partial }^m\theta \left(\zeta ,q\right)}{\partial {\zeta }^m}{\mid }_{q=0},(60)$

$\chi \left(\zeta ,q\right)={\chi }_0\left(\zeta \right)+\sum _{m=1}^{\infty }{\chi }_m\left(\zeta \right)q^m,{\chi }_m\left(\zeta \right)=\frac{1}{m!}\frac{{\partial }^m\chi \left(\zeta ,q\right)}{\partial {\zeta }^m}{\mid }_{q=0},(61)$

$\varphi \left(\zeta ,q\right)={\varphi }_0\left(\zeta \right)+\sum _{m=1}^{\infty }\varphi \left(\zeta \right)q^m,\varphi \left(\zeta \right)=\frac{1}{m!}\frac{{\partial }^m\varphi \left(\zeta ,q\right)}{\partial {\zeta }^m}{\mid }_{q=0}.(62)$

From Eqs 57–62, the convergence of the series is obtained by taking q = 1 for the appropriate values of ℏ_f, ℏ_g, ℏ_h, ℏ_θ, ℏ_χ, and ℏ_ϕ, so

$h\left(\zeta \right)=h_0\left(\zeta \right)+\sum _{m=1}^{\infty }{h}_m\left(\zeta \right),(63)$

$f\left(\zeta \right)=f_0\left(\zeta \right)+\sum _{m=1}^{\infty }{f}_m\left(\zeta \right),(64)$

$g\left(\zeta \right)=g_0\left(\zeta \right)+\sum _{m=1}^{\infty }{g}_m\left(\zeta \right),(65)$

$\theta \left(\zeta \right)={\theta }_0\left(\zeta \right)+\sum _{m=1}^{\infty }{\theta }_m\left(\zeta \right),(66)$

$\chi \left(\zeta \right)={\chi }_0\left(\zeta \right)+\sum _{m=1}^{\infty }\chi \left(\zeta \right),(67)$

$\varphi \left(\zeta \right)={\varphi }_0\left(\zeta \right)+\sum _{m=1}^{\infty }\varphi \left(\zeta \right).(68)$

3.2 mth order deformation problems

The mth order deformation equations are

${\mathit{L}}_{\mathit{h}}\left[h_m\left(\zeta \right)-{\psi }_m{h}_{m-1}\left(\zeta \right)\right]={\hslash }_h{\mathfrak{R}}_m^h\left(\zeta \right),(69)$

${\mathit{L}}_{\mathit{f}}\left[f_m\left(\zeta \right)-{\psi }_m{f}_{m-1}\left(\zeta \right)\right]={\hslash }_f{\mathfrak{R}}_m^f\left(\zeta \right),(70)$

${\mathit{L}}_{\mathit{g}}\left[g_m\left(\zeta \right)-{\psi }_m{g}_{m-1}\left(\zeta \right)\right]={\hslash }_g{\mathfrak{R}}_m^g\left(\zeta \right),(71)$

${\mathit{L}}_{\theta }\left[{\theta }_m\left(\zeta \right)-{\psi }_m{\theta }_{m-1}\left(\zeta \right)\right]={\hslash }_{\theta }{\mathfrak{R}}_m^{\theta }\left(\zeta \right),(72)$

${\mathit{L}}_{\chi }\left[{\chi }_m\left(\zeta \right)-{\psi }_m{\chi }_{m-1}\left(\zeta \right)\right]={\hslash }_{\chi }{\mathfrak{R}}_m^{\chi }\left(\zeta \right),(73)$

${\mathit{L}}_{\varphi }\left[{\varphi }_m\left(\zeta \right)-{\psi }_m{\varphi }_{m-1}\left(\zeta \right)\right]={\hslash }_{\varphi }{\mathfrak{R}}_m^{\varphi }\left(\zeta \right),(74)$

$h_m\left(0\right)=0,(75)$

$f_m\left(0\right)=0,f_m\left(\infty \right)=0,(76)$

$g_m\left(0\right)=0,g_m\left(\infty \right)=0,(77)$

${\theta }_m^{\prime }\left(0\right)=0,{\theta }_m\left(\infty \right)=0,(78)$

${\chi }_m\left(0\right)=0,{\chi }_m\left(\infty \right)=0,(79)$

${\varphi }_m^{\prime }\left(0\right)=0,{\varphi }_m\left(\infty \right)=0,(80)$

where

${\mathfrak{R}}_m^h\left(\zeta \right)=h_{m-1}^{\prime }+2f_{m-1},(81)$

$\begin{array}{ll}\hfill {\mathfrak{R}}_m^f\left(\zeta \right)& =f_{m-1}\prime \prime -\sum _{k=o}^{m-1}{f}_{m-1-k}{f}_k+\sum _{k=o}^{m-1}{g}_{m-1-k}{g}_k-\sum _{k=o}^{m-1}{f}_{m-1-k}^{\prime }{h}_k\hfill \\ \hfill & +{\beta }_1\sum _{k=o}^{m-1}\left[\begin{array}{c}\hfill h_{m-1-k}{f}_k^{\prime \prime \prime }+2f_{m-1-k}{f}_k^{\prime \prime }-f_{m-1-k}^{\prime }{f}_k^{\prime }-g_{m-1-k}^{\prime }{g}_k^{\prime }\hfill \end{array}\right]\hfill \\ \hfill & -\frac{M}{1+m^2}\left[\begin{array}{c}\hfill f_{m-1}^{\prime }-m{g}_{m-1}\hfill \end{array}\right]-Gr{\theta }_{m-1},\hfill \end{array}(82)$

$\begin{array}{ll}\hfill {\mathfrak{R}}_m^g\left(\zeta \right)& =g_{m-1}\prime \prime -\sum _{k=o}^{m-1}{g}_{m-1-k}\prime h_k-2\sum _{k=o}^{m-1}{f}_{m-1-k}{g}_k+{\beta }_1\sum _{k=o}^{m-1}\left[\begin{array}{c}\hfill g_{m-1-k}\prime \prime h_k+2f_{m-1-k}{g}_k^{\prime \prime }\hfill \end{array}\right]\hfill \\ \hfill & -\frac{M}{1+m^2}\left[\begin{array}{c}\hfill m{f}_{m-1}^{\prime }+g_{m-1}\hfill \end{array}\right],\hfill \end{array}(83)$

$\begin{array}{ll}\hfill {\mathfrak{R}}_m^{\theta }\left(\zeta \right)& =\frac{1+Rd}{Pr}{\theta }_{m-1}\prime \prime -\sum _{k=o}^{m-1}{h}_{m-1-k}{\theta }_k^{\prime }+2\frac{Ec}{Re}\sum _{k=o}^{m-1}\left[\begin{array}{c}\hfill h_{m-1-k}^{\prime }{h}_k^{\prime }+2f_{m-1-k}{f}_k\hfill \end{array}\right]\hfill \\ \hfill & +\frac{MEc}{1+m^2}\sum _{k=o}^{m-1}\left[\begin{array}{c}\hfill f_{m-1-k}{f}_k+g_{m-1-k}{g}_k\hfill \end{array}\right]+Ec\sum _{k=o}^{m-1}\left[\begin{array}{c}\hfill f_{m-1-k}^{\prime }{f}_k^{\prime }+g_{m-1-k}^{\prime }{g}_k^{\prime }\hfill \end{array}\right],\hfill \end{array}(84)$

${\mathfrak{R}}_m^{\chi }\left(\zeta \right)={\chi }_{m-1}\prime \prime -Lb\sum _{k=o}^{m-1}{h}_{m-1-k}{\chi }_k^{\prime }-Pe\sum _{k=o}^{m-1}\left[\begin{array}{c}\hfill {\chi }_{m-1-k}^{\prime }{\varphi }_k^{\prime }+{\varphi }_{m-1-k}\prime \prime {\chi }_k\hfill \end{array}\right]-{\gamma }_{1}Pe{\varphi }_m\prime \prime ,(85)$

${\mathfrak{R}}_m^{\varphi }\left(\zeta \right)=\frac{1}{Sc}{\varphi }_{m-1}\prime \prime -\sum _{k=o}^{m-1}{h}_{m-1-k}{\varphi }_k^{\prime }-k_1\sum _{k=o}^{m-1}{\varphi }_{m-1-k}\sum _{l=o}^k\left(\begin{array}{c}\hfill {\varphi }_{k-l}{\varphi }_l\hfill \end{array}\right)+2k_1\sum _{k=o}^{m-1}{\varphi }_{m-1-k}{\varphi }_k-k_1{\varphi }_m,(86)$

${\psi }_m=\left\{\begin{array}{cc}0,\hfill & m⩽1,\hfill \\ 1,\hfill & m>1.\hfill \end{array}\right..(87)$

If $f_m^{*}(\zeta )$, $g_m^{*}(\zeta )$, $h_m^{*}(\zeta )$, ${\theta }_m^{*}$(ζ), ${\chi }_m^{*}$(ζ), and ${\varphi }_m^{*}$(ζ) are the particular solutions, then the general solutions of Eqs 69–74 are

$h_m\left(\zeta \right)=h_m^{\ast }\left(\zeta \right)+C_1,(88)$

$f_m\left(\zeta \right)=f_m^{\ast }\left(\zeta \right)+C_2\exp \left(-\zeta \right)+C_3\exp \left(\zeta \right),(89)$

$g_m\left(\zeta \right)=g_m^{\ast }\left(\zeta \right)+C_4\exp \left(-\zeta \right)+C_5\exp \left(\zeta \right),(90)$

${\theta }_m\left(\zeta \right)={\theta }_m^{\ast }\left(\zeta \right)+C_6\exp \left(-\zeta \right)+C_7\exp \left(\zeta \right),(91)$

${\chi }_m\left(\zeta \right)={\chi }_m^{\ast }\left(\zeta \right)+C_8\exp \left(-\zeta \right)+C_9\exp \left(\zeta \right),(92)$

${\varphi }_m\left(\zeta \right)={\varphi }_m^{\ast }\left(\zeta \right)+C_{10}\exp \left(-\zeta \right)+C_{11}\exp \left(\zeta \right).(93)$

4 Comparsion of the present work with the published work

Table 1 is constructed to verify the obtained results. The achieved results are compared with the published results [57] which are found in excellent agreement.

TABLE 1

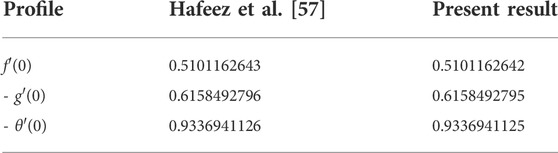
TABLE 1. Comparsion of the present results with [57].

5 Analysis and discussion of results

It is shown in Figure 2 that an increment in second-grade nanofluid parameter β₁ accelerates the radial velocity f(ζ). Figure 3 demonstrates that the azimuthal velocity g(ζ) has reducing features of flow. It is due to the fact that effective conductivity $\frac{{\sigma }_f}{1+m^2}$ is decreased with increasing values of Hall current parameter m which results in reducing the damping effect on g(ζ). It is detected in Figure 4 that azimuthal velocity g(ζ) increases due to the strong Lorentz force effect generated by the magnetic field. Physically, the term $\frac{M(m{f}^{\prime }+g)}{1+m^2}$ in Eq. 14 shows that g(ζ) achieves the maximum value at 0.30, 1.30, 2.30, and 3.30 for M and for the fixed value of m. Figure 5 anticipates the effect of the suction/injection parameter h_w on the axial velocity h(ζ). The values of h_w $<$ 0 correspond to injection of the fluid, and values of h_w $>$ 0 correspond to suction of the fluid. For h_w $>$ 0, it is shown in Figure 5 that the axial velocity h(ζ) acquires high value. It is due to the fact that on the non-dimensional axial coordinate ζ, h_w is defined as $\frac{w_0}{{\left[\begin{array}{c}\hfill {\nu }_f\mathrm{\Omega }\hfill \end{array}\right]}^{\frac{1}{2}}}$ which is the transpiration velocity at the surface of the disk. The centrifugal force due to the spinning disk flow results in the outward axial velocity. So the axial flow created from the disk surface, as proceeded in the axial direction, reaches to the maximum value. It is observed that with enhancing h_w for positive values, the highest value of h(ζ) is shown. Therefore, with higher disk injection, axial flow acceleration is higher further from the surface of the disk. It is evident that through injection, the involvement of mass transfer into the boundary layer exists. The stretching parameter s₁ influence on radial velocity f(ζ) is shown in Figure 6. The flow enhances in the radial direction. The reason is that the stretching rate increases in the radial direction as the stretching parameter is the ratio of c₁ (stretching rate) and Ω (angular velocity). The Biot number Bi role is discussed in Figure 7. It is observed that the Biot number raises the heat transfer. The boosting up phenomena of heat transfer is clear from its definition $\frac{h_f}{k_f}{\left[\begin{array}{c}\hfill \frac{{\nu }_f}{\mathrm{\Omega }}\hfill \end{array}\right]}^{\frac{1}{2}}$ which shows the convective heat transfer coefficient enhanced performance, and consequently, from the surface, more heat transfer is enhanced. Figure 8 depicts the influence of rotational Reynolds number Re on the temperature profile θ(ζ). Heat transfer increases with the increasing value of rotational Reynolds number Re. It is clear that the rotational Reynolds number quantifies the power of the rotation-induced flow and for higher values of Re, the flow is enhanced, as a result, the temperature field also increases with increasing flow of rotation. Figure 9 shows the influence of the Eckert number Ec on the temperature profile θ(ζ). Heat transfer decreases with increasing values of the Eckert number. Figure 10 illustrates the characteristics of heat transfer θ(ζ) and thermal radiation parameter Rd. An increase in Rd results in decline in the boundary layer of temperature near the surface. The behavior of gyrotactic microorganism concentration χ(ζ) due to bioconvection Lewis number Lb effect is visible in Figure 11. Due to the development of bioconvection Lewis number Lb, the gyrotactic microorganism concentration diffusion rate is enhanced. The decrease in gyrotactic microorganism concentration with enhanced values of the Peclet number Pe is seen in Figure 12. The reason is that rising values of Pe increase the cell swimming speed, which results in decreasing the microorganism density. Concentration of the chemical reaction ϕ(ζ) and homogeneous chemical reaction parameter k₁ are considered in Figure 13. It is scrutinized that ϕ(ζ) decreases as k₁ enhances. The heterogeneous chemical reaction parameter k₂ and the concentration of chemical reaction ϕ(ζ) are pictured in Figure 14. The graph shows a reduction trend for various values of k₂. The Schmidt number Sc effect and the concentration of the chemical reaction ϕ(ζ) are plotted in Figure 15. It is observed that ϕ(ζ) has a decreasing behavior for Sc = 1.10, 2.10, 3.10, and 4.10.

FIGURE 2

FIGURE 2. Role of the radial velocity profile and parameter.

FIGURE 3

FIGURE 3. Role of the azimuthal velocity profile and parameter.

FIGURE 4

FIGURE 4. Role of the azimuthal velocity profile and parameter.

FIGURE 5

FIGURE 5. Role of the axial velocity profile and parameter.

FIGURE 6

FIGURE 6. Role of the radial velocity profile and parameter.

FIGURE 7

FIGURE 7. Role of the heat transfer profile and parameter.

FIGURE 8

FIGURE 8. Role of the heat transfer profile and parameter.

FIGURE 9

FIGURE 9. Role of the heat transfer profile and parameter.

FIGURE 10

FIGURE 10. Role of the heat transfer profile and parameter.

FIGURE 11

FIGURE 11. Role of the gyrotactic microorganism concentration profile and parameter.

FIGURE 12

FIGURE 12. Role of the gyrotactic microorganism concentration profile and parameter.

FIGURE 13

FIGURE 13. Role of the chemical reaction concentration profile and parameter.

FIGURE 14

FIGURE 14. Role of the chemical reaction concentration profile and parameter.

FIGURE 15

FIGURE 15. Role of the chemical reaction concentration profile and parameter.

6 Conclusion

A porous spinning disk is studied in terms of second-grade nanofluid flow, heat and mass transfer with the flow of gyrotactic microorganisms incorporating the effects of Hall current, thermal radiation, and mixed convection under convective boundary conditions. The Homotopy analysis method (HAM) is used to obtain the solution of transformed equations.The concluding remarks are given as follows:

1) The radial velocity is increased with the increasing values of second-grade nanofluid and stretching parameters.

2) The azimuthal velocity is enhanced with the increasing values of the magnetic field and injection parameters.

3) The temperature is reduced with the increasing values of the thermal radiation parameter and Eckert number, while it is enhanced with the Biot and Reynolds numbers.

4) The gyrotactic microorganism concentration is enhanced with the increasing values of the bioconvection Lewis number and is reduced with the increasing values of the Peclet number.

5) The concentration of the chemical reaction is reduced with the increasing values of homogeneous–heterogeneous chemical reaction parameters and Schmidt number.

6) There exists excellent agreement between the previously published work and present work.

Data availability statement

The original contributions presented in the study are included in the article/Supplementary Material; further inquiries can be directed to the corresponding authors.

Author contributions

NK, UF-G, MK, WK, PK, and AG completed the research work.

Funding

The work of UF-G was supported by the Government of Basque Country for the ELKARTEK21/10KK-2021/00014 and ELKARTEK22/85 research programs.

Acknowledgments

The authors are thankful to the respectable reviewers for their comments and suggestions. The authors acknowledge the financial support provided by the Center of Excellence in Theoretical and Computational Science (TaCS-CoE), KMUTT. Moreover, this research was supported by the Science, Research, and Innovation Promotion Funding (TSRI) (Grant No. FRB650070/0168). WK was supported by Rajamangala University of Technology Thanyaburi (RMUTT). The first author is thankful to the Higher Education Commission (HEC), Pakistan, for providing the technical and financial support through the Startup Research Grant Program (SRGP) under Project No. 10534.

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors, and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

1. Zuhra S, Khan NS, Shah Z, Islam Z, Bonyah E. Simulation of bioconvection in the suspension of second grade nanofluid containing nanoparticles and gyrotactic microorganisms. AIP Adv (2018):105210.

CrossRef Full Text | Google Scholar

2. Shah Z, Alzahrani E, Jawad M, Khan U. Microstructure and inertial characteristics of MHD suspended SWCNTs and MWCNTs based Maxwell nanofluid flow with bio-convection and entropy generation past a permeable vertical cone. Coatings (2020) 10:998. doi:10.3390/coatings10100998

CrossRef Full Text | Google Scholar

3. Waqas H, Manzoor U, Shah Z, Arif M, Shutaywi M. Magneto-Burgers nanofluid stratified flow with swimming motile microorganisms and dual variables conductivity configured by a stretching cylinder/plate. Math Probl Eng (2021) 2021:1–16. doi:10.1155/2021/8817435

CrossRef Full Text | Google Scholar

4. Waqas H, Farooq U, Shah Z, Kumam P, Shutaywi M. Second-order slip effect on bio-convectional viscoelastic nanofluid flow through a stretching cylinder with swimming microorganisms and melting phenomenon. Sci Rep (2021) 11:11208. doi:10.1038/s41598-021-90671-z

PubMed Abstract | CrossRef Full Text | Google Scholar

5. Farooq U, Waqas H, Shah Z, Kumam P, Deebani W. On unsteady 3D bio-convection flow of viscoelastic nanofluid with radiative heat transfer inside a solar collector plate. Sci Rep (2022) 12:2952. doi:10.1038/s41598-022-06728-0

PubMed Abstract | CrossRef Full Text | Google Scholar

6. Waqas H, Farooq U, Ibrahim A, Alam MK, Shah Z, Kumam P. Numerical simulation for bioconvectional flow of burger nanofluid with effects of activation energy and exponential heat source/sink over an inclined wall under the swimming microorganisms. Sci Rep (2021) 11:14305. doi:10.1038/s41598-021-93748-x

PubMed Abstract | CrossRef Full Text | Google Scholar

7. Dawar A, Shah Z, Alshehri HM, Islam S, Kumam P. Magnetized and non-magnetized Casson fluid flow with gyrotactic microorganisms over a stratified stretching cylinder. Sci Rep (2021) 11:16376. doi:10.1038/s41598-021-95878-8

PubMed Abstract | CrossRef Full Text | Google Scholar

8. Waqas H, Yasmin S, Althobaiti N, Bonyah E, Alsehri A, Shah Z. Evaluating the higher-order slip consequence in bioconvection nanofluid flow configured by a variable thick surface of disk. J Nanomater (2022) 2022:1–13. doi:10.1155/2022/2766317

CrossRef Full Text | Google Scholar

9. Dawar A, Saeed A, Islam S, Shah Z, Kumam W, Kumam P. Electromagnetohydrodynamic bioconvective flow of binary fluid containing nanoparticles and gyrotactic microorganisms through a stratified stretching sheet. Sci Rep (2021) 11:23159. doi:10.1038/s41598-021-02320-0

PubMed Abstract | CrossRef Full Text | Google Scholar

10. Khan NS, Shah Q, Sohail A. Dynamics with Cattaneo–Christov heat and mass flux theory of bioconvection Oldroyd-B nanofluid. Adv Mech Eng (2020) 12(7):168781402093046–20. doi:10.1177/1687814020930464

CrossRef Full Text | Google Scholar

11. Khan NS, Humphries UW, Kumam W, Kumam P, Muhammad T. Bioconvection Casson nanoliquid film sprayed on a stretching cylinder in the portfolio of homogeneous-heterogeneous chemical reactions. ZAMM Angew Math Mech (2022) 101(102):e202000212. doi:10.1002/zamm.202000212

CrossRef Full Text | Google Scholar

12. Khan NS, Humphries UW, Kumam W, Kumam P, Muhammad T. Dynamic pathways for the bioconvection in thermally activated rotating system. Biomass Conver Bioref (2022):1–19. doi:10.1007/s13399-022-02961-9

CrossRef Full Text | Google Scholar

13. Khan NS, Shah Z, Islam S, Khan I, Alkanhal TA, Tlili I. Entropy generation in MHD mixed convection non-Newtonian second-grade nanoliquid thin film flow through a porous medium with chemical reaction and stratification. Entropy (2019) 21(2):139. doi:10.3390/e21020139

PubMed Abstract | CrossRef Full Text | Google Scholar

14. Zuhra S, Khan NS, Islam S. Magnetohydrodynamic second grade nanofluid flow containing nanoparticles and gyrotactic microorganisms. Comp Appl Math (2018) 37:6332–58. doi:10.1007/s40314-018-0683-6

CrossRef Full Text | Google Scholar

15. Palwasha Z, Islam S, Khan NS, Hayat H. Non-Newtonian nanoliquids thin film flow through a porous medium with magnetotactic microorganisms. Appl Nanosci (2018) 8:1523–44. doi:10.1007/s13204-018-0834-5

CrossRef Full Text | Google Scholar

16. Khan NS, Zuhra S, Shah Z, Bonyah E, Khan W, Islam S, et al. Hall current and thermophoresis effects on magnetohydrodynamic mixed convective heat and mass transfer thin film flow. J Phys Commun (2019) 3:035009. doi:10.1088/2399-6528/aaf830

CrossRef Full Text | Google Scholar

17. Khan NS, Gul T, Islam S, Khan W. Thermophoresis and thermal radiation with heat and mass transfer in a magnetohydrodynamic thin film second-grade fluid of variable properties past a stretching sheet. Eur Phys J Plus (2017) 132:11. doi:10.1140/epjp/i2017-11277-3

CrossRef Full Text | Google Scholar

18. Adeniyan A, Mabood F, Okoya SS. Effect of heat radiating and generating second-grade mixed convection flow over a vertical slender cylinder with variable physical properties. Int Commun Heat Mass Transfer (2021) 121:105110. doi:10.1016/j.icheatmasstransfer.2021.105110

CrossRef Full Text | Google Scholar

19. Adigun JA, Adeniyan A, Abiala IO. Stagnation point MHD slip-flow of viscoelastic nanomaterial over a stretched inclined cylindrical surface in a porous medium with dual stratification. Int Commun Heat Mass Transfer (2021) 126:105479. doi:10.1016/j.icheatmasstransfer.2021.105479

CrossRef Full Text | Google Scholar

20. Usman AH, Khan NS, Humphries UW, Ullah Z, Shah Q, Kumam P, et al. Computational optimization for the deposition of bioconvection thin Oldroyd-B nanofluid with entropy generation. Sci Rep (2021) 11(1):11641. doi:10.1038/s41598-021-91041-5

PubMed Abstract | CrossRef Full Text | Google Scholar

21. Yusuf TA, Kumar RN, Prasannakumara BC, Adesanya SO. Irreversibility analysis in micropolar fluid film along an incline porous substrate with slip effects. Int Commun Heat Mass Transfer (2021) 126:105357. doi:10.1016/j.icheatmasstransfer.2021.105357

CrossRef Full Text | Google Scholar

22. Hussain T, Xu H. Time-dependent squeezing bio-thermal MHD convection flow of a micropolar nanofluid between two parallel disks with multiple slip effects. Case Stud Therm Eng (2022) 31:101850. doi:10.1016/j.csite.2022.101850

CrossRef Full Text | Google Scholar

23. Hussain M, AliYao SW, Ghaffar A, Atif M. Numerical investigation of ohmically dissipated mixed convective flow. Case Stud Therm Eng (2022) 31:101809. doi:10.1016/j.csite.2022.101809

CrossRef Full Text | Google Scholar

24. Shah S, Rafiq N, Abdullah FA, Atif SM, Abbas M. Slip and radiative effects on MHD Maxwell nanofluid with non-Fourier and non-Fick laws in a porous medium. Case Stud Therm Eng (2022) 30:101779. doi:10.1016/j.csite.2022.101779

CrossRef Full Text | Google Scholar

25. Khan NS, Gul T, Kumam P, Shah Z, Islam S, Khan W, et al. Influence of inclined magnetic field on Carreau nanoliquid thin film flow and heat transfer with graphene nanoparticles. Energies (2019) 12:1459. doi:10.3390/en12081459

CrossRef Full Text | Google Scholar

26. Khan NS, Shah Q, Sohail A, Kumam P, Thounthong P, Muhammad T. Mechanical aspects of Maxwell nanofluid in dynamic system with irreversible analysis. Z Angew Math Mech (2021) 8:e202000212. doi:10.1002/zamm.202000212

CrossRef Full Text | Google Scholar

27. Khan NS, Kumam P, Thounthong P. Renewable energy technology for the sustainable development of thermal system with entropy measures. Int J Heat Mass Transf (2019) 145:118713. doi:10.1016/j.ijheatmasstransfer.2019.118713

CrossRef Full Text | Google Scholar

28. Khan NS. Bioconvection in second grade nanofluid flow containing nanoparticles and gyrotactic microorganisms. Braz J Phys (2018) 43:227–41. doi:10.1007/s13538-018-0567-7

CrossRef Full Text | Google Scholar

29. Khan NS, Gul T, Khan MA, Bonyah E, Islam S. Mixed convection in gravity-driven thin film non-Newtonian nanofluids flow with gyrotactic microorganisms. Results Phys (2017) 7:4033–49. doi:10.1016/j.rinp.2017.10.017

CrossRef Full Text | Google Scholar

30. Khan NS. Mixed convection in MHD second grade nanofluid flow through a porous medium containing nanoparticles and gyrotactic microorganisms with chemical reaction. Filomat (2019) 33:4627–53. doi:10.2298/fil1914627k

CrossRef Full Text | Google Scholar

31. Khan NS, Shah Z, Shutaywi M, Kumam P, Thounthong P. A comprehensive study to the assessment of Arrhenius activation energy and binary chemical reaction in swirling flow. Sci Rep (2020) 10:7868. doi:10.1038/s41598-020-64712-y

PubMed Abstract | CrossRef Full Text | Google Scholar

32. Choi SUS. Development and application of non-Newtonian flows. Amer Soc Mech Eng N Y FED (1995) 231:99–105.

Google Scholar

33. Khan SA, Waqas H, Naqvi SMRS, Alghamdi M, Al-Mdallal Q. Cattaneo-Christov double diffusions theories with bio-convection in nanofluid flow to enhance the efficiency of nanoparticles diffusion. Case Stud Therm Eng (2021) 26:101017. doi:10.1016/j.csite.2021.101017

CrossRef Full Text | Google Scholar

34. Dawar A, Shah Z, Tassaddiq A, Kumam P, Islam S, Khan W. A convective flow of Williamson nanofluid through cone and wedge with non-isothermal and non-isosolutal conditions: A revised buongiorno model. Case Stud Therm Eng (2021) 24:100869. doi:10.1016/j.csite.2021.100869

CrossRef Full Text | Google Scholar

35. Cao W, Lare AI, Yook SJ, V.a. O, Ji X. Simulation of the dynamics of colloidal mixture of water with various nanoparticles at different levels of partial slip: Ternary-hybrid nanofluid. Int Commun Heat Mass Transfer (2022) 135:106069. doi:10.1016/j.icheatmasstransfer.2022.106069

CrossRef Full Text | Google Scholar

36. Alrabaiah H, Bilal M, Khan MA, Muhammad T, Legas EY. Parametric estimation of gyrotactic microorganism hybrid nanofluid flow between the conical gap of spinning disk-cone apparatus. Sci Rep (2022) 12:59. doi:10.1038/s41598-021-03077-2

PubMed Abstract | CrossRef Full Text | Google Scholar

37. Nazir U, Sohail M, Selim MM, Alrabaiah H, Kumam P. Finite element simulations of hybrid nano-Carreau Yasuda fluid with hall and ion slip forces over rotating heated porous cone. Sci Rep (2021) 11:19604. doi:10.1038/s41598-021-99116-z

PubMed Abstract | CrossRef Full Text | Google Scholar

38. Shahid A, Huang H, Bhatti MM, Zhang L, Ellahi R. Numerical investigation on the swimming of gyrotactic microorganisms in nanofluids through porous medium over a stretched surface. Mathematics (2020) 8:380. doi:10.3390/math8030380

CrossRef Full Text | Google Scholar

39. Khan NS, Zuhra S, Shah Q. Entropy generation in two phase model for simulating flow and heat transfer of carbon nanotubes between rotating stretchable disks with cubic autocatalysis chemical reaction. Appl Nanosci (2019) 9:1797–822. doi:10.1007/s13204-019-01017-1

CrossRef Full Text | Google Scholar

40. Oke AS. Combined effects of Coriolis force and nanoparticle properties on the dynamics of gold-water nanofluid across nonuniform surface. ZAMM Angew Math Mech (2022) 2022:e202100113. doi:10.1002/zamm.202100113

CrossRef Full Text | Google Scholar

41. Liu B, Yang W, Liu Z. A PANS method based on rotation-corrected energy spectrum for efficient simulation of rotating flow. Front Energ Res (2022) 10:894258. doi:10.3389/fenrg.2022.894258

CrossRef Full Text | Google Scholar

42. Ali B, Shafiq A, Siddique I, Al-Madallal Q, Jarad F. Significance of suction/injection, gravity modulation, thermal radiation, and magnetohydrodynamic on dynamics of micropolar fluid subject to an inclined sheet via finite element approach. Case Stud Therm Eng (2021) 28:101537. doi:10.1016/j.csite.2021.101537

CrossRef Full Text | Google Scholar

43. Shahid N, Rana M, Siddique I. Exact solution for motion of an Oldroyd-B fluid over an infinite flat plate that applies an oscillating shear stress to the fluid. Bound Value Prob (2012) 2012:48. doi:10.1186/1687-2770-2012-48

CrossRef Full Text | Google Scholar

44. Lei T, Siddique I, Ashraf MK, Hussain S, Abdal S, Ali B. Computational analysis of rotating flow of hybrid nanofluid over a stretching surface. Proceed Inst Mechl Eng E: J Process Mech Eng (2022). doi:10.1177/09544089221100092

CrossRef Full Text | Google Scholar

45. Habib D, Salamat N, Abdal S, Siddique I, Salimi M, Ahmadian A. On time dependent MHD nanofluid dynamics due to enlarging sheet with bioconvection and two thermal boundary conditions. Microfluid Nanofluid (2022) 26:11. doi:10.1007/s10404-021-02514-y

CrossRef Full Text | Google Scholar

46. Hussain F, Nazeer M, Ghafoor I, Saleem A, Waris B, Siddique I. Perturbation solution of Couette flow of casson nanofluid with composite porous medium inside a vertical channel. Nano Sci Technol Int J (2022) 13(4):23–44. doi:10.1615/nanoscitechnolintj.2022038799

CrossRef Full Text | Google Scholar

47. Siddique I, Zulqarnain RM, Nadeem M, Jarad F. Numerical simulation of MHD Couette flow of a Fuzzy nanofluid through an inclined channel with thermal radiation effect. Comput Intell Neurosci (2021) 6608684:1–16. doi:10.1155/2021/6608684

CrossRef Full Text | Google Scholar

48. Abdal S, Siddique I, Saif Ud Din I, Ahmadian A, Hussain S, Salimi M. Significance of magnetohydrodynamic Williamson Sutterby nanofluid due to a rotating cone with bioconvection and anisotropic slip. ZAMM Angew Math Mech (2022) 2022:e202100503. doi:10.1002/zamm.202100503

CrossRef Full Text | Google Scholar

49. Sadiq K, Siddique I, Ali R, Jarad F. Impact of ramped concentration and temperature on MHD Casson nanofluid flow through a vertical channel. J Nanomater (2021) 3743876:1–17. doi:10.1155/2021/3743876

CrossRef Full Text | Google Scholar

50. Iqbal S, Siddique I, Siddiqui AM. OHAM and FEM solutions of concentric n-layer flows of incompressible third-grade fluids in a horizontal cylindrical pipe. J Braz Soc Mech Sci Eng (2019) 41:204. doi:10.1007/s40430-019-1687-x

CrossRef Full Text | Google Scholar

51. Song YQ, Obideyi BD, Shah NA, Animasaun IL, Mahrous YM, Chung JD. Significance of haphazard motion and thermal migration of alumina and copper nanoparticles across the dynamics of water and ethylene glycol on a convectively heated surface. Case Stud Therm Eng (2021) 26:101050. doi:10.1016/j.csite.2021.101050

CrossRef Full Text | Google Scholar

52. Oke AS, Animasaun IL, Mutuku WN, Kimathi M, Shah NA, Saleem S. Significance of Coriolis force, volume fraction, and heat source/sink on the dynamics of water conveying 47 nm alumina nanoparticles over a uniform surface. Chin J Phys (2021) 71:716–27. doi:10.1016/j.cjph.2021.02.005

CrossRef Full Text | Google Scholar

53. Khan NS, Shah Q, Bhaumik A, Kumam P, Thounthong P, Amiri I. Entropy generation in bioconvection nanofluid flow between two stretchable rotating disks. Sci Rep (2020) 10:4448. doi:10.1038/s41598-020-61172-2

PubMed Abstract | CrossRef Full Text | Google Scholar

54. Usman AH, Khan NS, Rano SA, Humphries UW, Kumam P. Computational investigations of Arrhenius activation energy and entropy generation in a viscoelastic nanofluid flow thin film sprayed on a stretching cylinder. J Adv Res Fluid Mech Therm Sci (2021) 86(1):27–51. doi:10.37934/arfmts.86.1.2751

CrossRef Full Text | Google Scholar

55. Ramzan M, Khan NS, Kumam P. Mechanical analysis of non-Newtonian nanofluid past a thin needle with dipole effect and entropic characteristics. Sci Rep (2021) 11(1):19378. doi:10.1038/s41598-021-98128-z

PubMed Abstract | CrossRef Full Text | Google Scholar

56. Khan NS, Humphries UW, Kumam W, Kumam P, Muhammad T. Bioconvection Casson nanoliquid film sprayed on a stretching cylinder in the portfolio of homogeneous-heterogeneous chemical reactions. Z Angew Math Mech (2022) 8:e2020000222. doi:10.1002/zamm.202000222

CrossRef Full Text | Google Scholar

57. Hafeez A, Khan M, Ahmed J. Thermal aspects of chemically reactive Oldroyd-B fluid flow over a rotating disk with Cattaneo-Christov heat flux theory. J Therm Anal Calorim (2021) 144:793–803. doi:10.1007/s10973-020-09421-4

CrossRef Full Text | Google Scholar

58. Acharya N, Bag R, Kundu PK. Influence of Hall current on radiative nanofluid flow over a spinning disk: A hybrid approach. Phys E: Low Dimen Sys Nanostructure (2019) 2019:1–39.

CrossRef Full Text | Google Scholar

59. Ariel PD. Computation of flow of a second grade fluid near a rotating disk. Int J Eng Sci (1997) 35(14):1335–57. doi:10.1016/s0020-7225(97)87427-7

CrossRef Full Text | Google Scholar

60. Acharya N. Spectral quasi linearization simulation on the radiative nanofluid spraying over a permeable inclined spinning disk considering the existence of heat source/sink. Appl Math Comput (2021) 411:126547. doi:10.1016/j.amc.2021.126547

CrossRef Full Text | Google Scholar

61. Naqvi SMRS, Kim HM, Muhammad T, Mallawi F, Ullah MZ. Numerical study for slip flow of Reiner-Rivlin nanofluid due to a rotating disk. Int Commun Heat Mass Transfer (2020) 116:104643. doi:10.1016/j.icheatmasstransfer.2020.104643

CrossRef Full Text | Google Scholar

62. Khan MN, Ahmad S, Ahammad NA, Alqahtani T, Algarni S. Numerical investigation of hybrid nanofluid with gyrotactic microorganism and multiple slip conditions through a porous rotating disk. Waves Random Complex Media (2022) 2022:1–15. doi:10.1080/17455030.2022.2055205

CrossRef Full Text | Google Scholar

63. Beg OA, Zueco J, Lopez-Ochoa LM. Network numerical analysis of optically thick hydromagnetic slip flow from a porous spinning disk with radiation flux, variable thermophysical properties, and surface injection effects. Chem Eng Commun (2011) 198:360–84. doi:10.1080/00986445.2010.512543

CrossRef Full Text | Google Scholar

64. Chaudhary MA, Merkin JH. A simple isothermal model for homogeneous-heterogeneous reactions in boundary-layer flow. I Equal diffusivities. Fluid Dyn Res (1995) 16(6):311–33. doi:10.1016/0169-5983(95)00015-6

CrossRef Full Text | Google Scholar

65. Sajid M, Iqbal SA, Naveed M, Abbas Z. Effect of homogeneous-heterogeneous reactions and magnetohydrodynamics on Fe₃O₄ nanofluid for the Blasius flow with thermal radiations. J Mol Liq (2017) 233:115–21. doi:10.1016/j.molliq.2017.02.081

CrossRef Full Text | Google Scholar

66. Sravanthi CS, Mabood F, Nabi SG, Shehzad SA. Heterogeneous and homogeneous reactive flow of magnetite-water nanofluid over a magnetized moving plate. Propulsion Power Res (2022) 11(2):265–75. doi:10.1016/j.jppr.2022.02.006

CrossRef Full Text | Google Scholar

67. Alzahrani F, Gowda RJP, Kumar RN, Khan MI. Dynamics of thermosolutal Marangoni convection and nanoparticle aggregation effects on Oldroyd-B nanofluid past a porous boundary with homogeneous-heterogeneous catalytic reactions. J Indian Chem Soc (2022) 99(6):100458. doi:10.1016/j.jics.2022.100458

CrossRef Full Text | Google Scholar

68. Khan M, Yasi M, Alshomrani AS, Sivasankaran S, Aladwani YR, Ahmed A. Variable heat source in stagnation-point unsteady flow of manetized Oldroyd-B fluid with cubic autocatalysis chemical reaction. Ain Shams Eng J (2022) 13:101610.

CrossRef Full Text | Google Scholar

69. Sunthrayuth P, Abdelmohsen SAM, Rekha MB, Raghunatha KR, Abdelbacki AMM, Gori MR, et al. Impact of nanoparticle aggregation on heat transfer phenomena of second grade nanofluid flow over melting surface subject to homogeneous-heterogeneous reactions. Case Stud Therm Eng (2022) 32:101897. doi:10.1016/j.csite.2022.101897

CrossRef Full Text | Google Scholar

70. Shijun L. On the homotopy analysis method for non-linear problems. Appl Math Comput (2004) 147:499–513. doi:10.1016/s0096-3003(02)00790-7

CrossRef Full Text | Google Scholar

Nomenclature

Abbreviations

m Hall parameter

(u, v, w) velocity components

(r, ϑ, z) cylindrical coordinates

c₁ stretching rate

v˜ average swimming velocity of oxytactic microorganisms

W_ce cell swimming speed

w₀ suction/injection parameter

Sc Schmidt number

M magnetic field parameter

Pr Prandtl number

Ec Eckert number

Lb bioconvection Lewis number

Pe Peclet number

C_i, i = 1, 2, 3..., 11 arbitrary constants

Re Reynolds number

Rd thermal radiation parameter

k thermal diffusivity

k_c, k_s chemical reactant rate constants

k₁ strength of the homogeneous chemical reaction

k₂ strength of the heterogeneous chemical reaction

k_e mean absorption coefficient

T temperature

N motile microorganism concentration

P pressure

Bi Biot number

c_P specific heat at constant pressure

s₁ non-dimensional stretching parameter

b₁ chemotaxis constant

h_w non-dimensional suction/injection parameter

D diffusivity

Gr Grashof number

A, B chemical species

a, b concentration of chemical species

f dimensionless radial velocity

g dimensionless tangential velocity

h dimensionless axial velocity

g₁ gravity acceleration

B₀ applied magnetic field strength

q_r radiation heat flux

h_f convective heat transfer

L linear operator

Greek symbols

Ω angular velocity

σ electrical conductivity

σ* Stefan–Boltzmann constant

ζ similarity variable

ϕ(ζ) concentration of the homogeneous chemical reaction

ϕ₁(ζ) concentration of the heterogeneous chemical reaction

θ(ζ) dimensionless temperature

χ(ζ) non-dimensional motile microorganism concentration

α₁ second-grade fluid parameter

γ₁ microorganism concentration difference parameter

δ ratio of diffusion coefficients

β coefficient of volumetric volume expansion

β₁ non-dimensional second-grade nanofluid parameter

ν kinematic viscosity

μ dynamic viscosity

ρ density

Subscripts

f base fluid

w condition at the wall

Superscripts

′ differentiation with respect to ζ