Consensus analysis of the weighted corona networks

The consensus of complex networks has attracted the attention of many scholars. The graph operation is a common method to construct complex networks, which is helpful in studying the consensus of complex networks. Based on the corona networks G₁◦G₂, this study gives different weights to the edges of G₁◦G₂ to obtain the weighted corona networks ${\tilde{G}}_1◦{\tilde{G}}_2$ and studies the consensus of ${\tilde{G}}_1◦{\tilde{G}}_2$. The consensus of the networks can be measured by coherence. First, the Laplacian polynomial of ${\tilde{G}}_1◦{\tilde{G}}_2$ is derived by using the properties of an orthogonal matrix. Second, the relationship between the first-order coherence of ${\tilde{G}}_1◦{\tilde{G}}_2$ and G₁ is deduced by using the relevant properties of the determinant and the conclusion of polynomial coefficients and the principal minors of the matrix. Third, the join operation is introduced to further simplify the analytical formula of network coherence. Finally, a specific network example is used to verify the validity of the conclusion.

1 Introduction

With the development of network science, the research of complex networks has been extended to many fields, such as technical networks and transportation networks. Nowadays, the relevant theoretical knowledge of complex networks has been widely used in physics, computer science, life science, and other fields, such as consensus [1–5], resistance distance and Kirchhoff index [6], robustness [7, 8], and network synchronization [9, 10].

As a method of constructing networks, the graph operation can be used to construct more complex networks. The common graph operations include corona operation, edge corona operation, and join operation. In recent years, graph operations have attracted extensive attention of scholars. Y. Shang used the edge corona product to construct a simplicial network and, based on the degree of network vertices, studied the recently widely concerned Sombor index [11]. J. Liu presented a kind of weighted edge corona networks and obtained the Laplacian and signless Laplacian spectra of the weighted edge corona networks, and a specific application example is given by calculating the number of spanning trees and the Kirchhoff index [12]. M. Dai used the eigenvector method to obtain the generalized adjacency and Laplacian spectra of the special weighted corona networks [13]. We considered the weighted corona networks that are more realistic as the research object to study the consensus of networks.

The consensus of the networks is the key to solve cooperative control among nodes in complex networks. The consensus of complex networks means that network nodes reach the same level in a certain state with the change of time. For example, the direction of unmanned aerial vehicle formation is consistent during flight. The research on the consensus of special networks has achieved many good results. E. Mackin took the network of networks as the object, investigated how to connect the subgraph to achieve the optimal consensus of the networks, and used a specific example to illustrate it [14]. T. Hu defined three types of tree models with the given parameters and obtained the leaderless and leader–follower coherence of three types of network models. The study found that the leader–follower coherence was weaker than the leaderless coherence [15]. J. Wang analyzed the consensus of three different types of weighted duplex networks and compared the consensus of the three types of networks [16]. J. Chen showed the consensus of a class of special topological networks and obtained the relationships between the network consensus and parameters [17]. X. Wang used the property of the determinant to calculate the Laplacian polynomial of 5-rose graphs and investigated the consensus of 5-rose graphs by using the relationships between polynomial coefficients and eigenvalues [18].

Compared with the aforementioned literature, the innovation of this study is as follows. This study defines the weighted corona network model based on the unweighted corona networks. We used the properties of the orthogonal matrix to transform a high-order determinant into a low-order determinant and deduced the Laplacian polynomial of the weighted corona networks. Finally, the specific analytical formula of the first-order coherence of the weighted corona networks is obtained according to the relationship between the coefficient and the principal minor, which provided a theoretical basis for studying the coherence of the arbitrary weighted corona network.

This study is arranged as follows. Section 2 introduces the preliminaries. The characteristic polynomial of ${\tilde{G}}_1◦{\tilde{G}}_2$ is given in Section 3. Section 4 obtains the first-order coherence of ${\tilde{G}}_1◦{\tilde{G}}_2$. In Section 5, the specific application example is shown. Section 6 gives the final conclusion.

2 Preliminaries

2.1 Definitions of the weighted graph operations

The topology of networks is the key to study the consensus of complex networks. It is a common method to construct complex networks by using graph operations. Next, we introduced two graph operations.

Definition 1 [19, 20]: Let G₁ and G₂ denote the two graphs with n₁ and n₂ vertices, respectively. The corona of G₁ and G₂ is described as the graph G₁◦G₂ obtained by taking one copy of G₁ and n₁ copies of G₂ and then joining the ith vertex of G₁ to every vertex in the ith copy of G₂ (i = 1, 2, 3, … , n₁).

The weighted corona graphs ${\tilde{G}}_1◦{\tilde{G}}_2$ mean that on the basis of G₁◦G₂, the edges of G₁ and G₂ have weights r₁ and r₂, respectively. The edges between G₁ and G₂ have weight r₃. ${\tilde{C}}_6◦{\tilde{K}}_2$ is shown in Figure 1.

Definition 2 [21]: Let the join of two disjoint graphs G₁ and G₂ be G₁ ∨ G₂, the vertex set of G₁ ∨ G₂ be V (G₁ ∨ G₂) = V (G₁) ∪ V (G₂), and the edge set of G₁ ∨ G₂ be E (G₁ ∨ G₂) = E (G₁) ∪ E (G₂) ∪ (xy) (x ∈ V (G₁), y ∈ V (G₂)).

FIGURE 1

FIGURE 1. (A) Circle graph C₆, (B) complete graph K₂, and (C) weighted corona graph ${\tilde{C}}_6◦{\tilde{K}}_2$.

The weighted join graphs ${\tilde{G}}_1\vee {\tilde{G}}_2$ mean that on the basis of G₁ ∨ G₂, the edges of G₁ and G₂ have weights r₁ and r₂, respectively. The edges between G₁ and G₂ have weight r₃.

2.2 Network coherence

The network model of the system with noise is defined as follows [4]:

$\frac{dx\left(t\right)}{dt}=-Lx\left(t\right)+\chi \left(t\right),(1)$

where L = D − A is the Laplacian matrix, D = diag (d₁, d₂, … , d_s) denotes the degree matrix, d_i (i = 1, 2, … , s) is the degree of the ith node of the network. $A={(a_{ij})}_{s\times s}$ is the adjacency matrix, where $a_{ij}=\left\{\begin{array}{cc}1,\hfill & \text{\hspace{0.17em}if}\text{i}\text{connected}\text{j}\hfill \\ 0,\hfill & \text{otherwise}\hfill \end{array}\right.$, and x(t) denotes the dynamic variable of the network nodes. χ(t) indicates that all nodes in the network are affected by Gaussian white noise at time t. The Gaussian white noise means that the instantaneous value of noise obeys Gaussian distribution. It is an ideal model for noise analysis.

Under the influence of noise, it is difficult for all nodes in the network to converge in a certain state. In order to describe the consensus of the networks, the concept of first-order coherence is introduced. It is defined as follows [4]:

$H^{\left(1\right)}=\frac{1}{s}\sum _{i=1}^s\underset{t\to \infty }{\lim }\mathit{var}\left\{x_i\left(t\right)-\frac{1}{s}\sum _{j=1}^s{x}_j\left(t\right)\right\}.(2)$

The output of system (1) is denoted as follows:

$y\left(t\right)=Kx\left(t\right),(3)$

where K is the projection operator, $K=I-\frac{1}{s}\mathit{1}{\mathit{1}}^{\mathit{T}}$, and 1 is the s-vector of all nodes. H⁽¹⁾ is given by the H₂ norm of the systems defined in Eqs 1 and 3.

$H^{\left(1\right)}=\frac{1}{s}tr\left({\int }_0^{\infty }{e}^{-L^{T}t}K{e}^{-Lt}dt\right).(4)$

The research shows that H⁽¹⁾ is closely related to the non-zero eigenvalues λ_i (i = 2, 3, … , s) of the Laplacian matrix L [18],

$H^{\left(1\right)}=\frac{1}{2s}\sum _{i=2}^s\frac{1}{{\lambda }_i}.(5)$

The Kirchhoff index (Kf) is also closely related to the non-zero eigenvalues of the Laplacian matrix L, $Kf=s{\sum }_{i=2}^s\frac{1}{{\lambda }_i}=2s^2{H}^{(1)}$.

3 Laplacian polynomial of ${\tilde{G}}_1◦{\tilde{G}}_2$

In this section, the Laplacian polynomial of ${\tilde{G}}_1◦{\tilde{G}}_2$ is obtained by using the properties of the orthogonal matrix.

Lemma 1: Let the Laplacian eigenvalues of G be 0 = v₁ < v₂ ≤ v₃ ≤ ⋯ ≤ v_n; there is an orthogonal matrix $P={(p_{ij})}_{n\times n},P^{T}L(G)P=\mathrm{diag}(v_1,v_2,\dots ,v_n)$. Then, $p_1=\sqrt{n},p_2=p_3=\cdots =p_n=0$, where p_i (i = 1, 2, … , n) is the sum of the ith column of the matrix P.

Proof: the Laplacian eigenvalues of G are 0 = v₁ < v₂ ≤ v₃ ≤ ⋯ ≤ v_n; then, there is an orthogonal matrix $P={(p_{ij})}_{n\times n},P^{T}L(G)P=\mathrm{diag}(v_1,v_2,\dots ,v_n)$. It is obvious that $\sqrt{n}{(1,\dots ,1)}^T$ is the unit eigenvector of the eigenvalue $v_1=0,p_1=\sqrt{n}$. Let ${\zeta }_i={(p_{1i},p_{2i},\dots ,p_{ni})}^T$ be the unit eigenvector corresponding to the eigenvalue v_i (i = 2, 3, … , n); from the orthogonality of the eigenvectors, we have (1, … , 1)ζ_i = 0 (i = 2, 3, … , n) and p₂ = p₃ = ⋯ = p_n = 0.Theorem 1: let the number of vertices of G₁ and G₂ be n₁ and n₂, respectively; the Laplacian eigenvalues of G₁ and G₂ are $0={\eta }_1<{\eta }_2\le {\eta }_3\le \cdots \le {\eta }_{n_1},0={\mu }_1<{\mu }_2\le {\mu }_3\le \cdots \le {\mu }_{n_2}$. Then, the Laplacian polynomial of ${\tilde{G}}_1◦{\tilde{G}}_2$ is

$\mathrm{\Phi }\left(\lambda \right)=\left[\prod _{i=2}^{n_2}{\left(\lambda -r_3-r_2{\mu }_i\right)}^{n_1}\right]\left|\begin{array}{cc}\hfill \left(\lambda -r_3{n}_2-r_3\right)I_{n_1}-r_1{L}_1\hfill & \hfill -r_1{L}_1\hfill \\ \hfill r_3{I}_{n_1}\hfill & \hfill \lambda I_{n_1}\hfill \end{array}\right|.(6)$

Proof: let A_i (i = 1, 2) be the adjacency matrices of G₁ and G₂; D_i (i = 1, 2) denotes the degree matrices of G₁ and G₂; $I_{n_1}$ is the identity matrix of order n₁; $J_{n_2}$ represents all 1 column vector of dimension n₂; and 0_m×n represents a zero matrix.

The adjacency matrix of ${\tilde{G}}_1◦{\tilde{G}}_2$ is

$A\left({\tilde{G}}_1◦{\tilde{G}}_2\right)={\left(\begin{array}{cc}\hfill r_1{A}_1\hfill & \hfill r_3{I}_{n_1}\otimes \underset{n_2}{\overset{T}{J}}\hfill \\ \hfill r_3{I}_{n_1}\otimes J_{n_2}\hfill & \hfill I_{n_1}\otimes r_2{A}_2\hfill \end{array}\right)}_{\left(n_1+n_1{n}_2\right)\times \left(n_1+n_1{n}_2\right)}.$

The degree matrix of ${\tilde{G}}_1◦{\tilde{G}}_2$ is

$D\left({\tilde{G}}_1◦{\tilde{G}}_2\right)={\left(\begin{array}{cc}\hfill r_1{D}_1+r_3{n}_2{I}_{n_1}\hfill & \hfill 0_{n_1\times \left(n_1{n}_2\right)}\hfill \\ \hfill 0_{n_1\times \left(n_1{n}_2\right)}^T\hfill & \hfill I_{n_1}\otimes \left(r_2{D}_2+r_3{I}_{n_2}\right)\hfill \end{array}\right)}_{\left(n_1+n_1{n}_2\right)\times \left(n_1+n_1{n}_2\right)}.$

The Laplacian matrix of ${\tilde{G}}_1◦{\tilde{G}}_2$ is

$L\left({\tilde{G}}_1◦{\tilde{G}}_2\right)={\left(\begin{array}{cc}\hfill r_1{L}_1+r_3{n}_2{I}_{n_1}\hfill & \hfill -r_3{I}_{n_1}\otimes \underset{n_2}{\overset{T}{J}}\hfill \\ \hfill -r_3{I}_{n_1}\otimes J_{n_2}\hfill & \hfill I_{n_1}\otimes \left(r_2{L}_2+r_3{I}_{n_2}\right)\hfill \end{array}\right)}_{\left(n_1+n_1{n}_2\right)\times \left(n_1+n_1{n}_2\right)}.$

Let the Laplacian eigenvalues of G₁ and G₂ be

$0={\eta }_1<{\eta }_2\le {\eta }_3\le \cdots \le {\eta }_{n_1},0={\mu }_1<{\mu }_2\le {\mu }_3\le \cdots \le {\mu }_{n_2}.$

Then, there are orthogonal matrices $M={(m_{ij})}_{n_1\times n_1},N={(n_{ij})}_{n_2\times n_2}$, and

$\left(\begin{array}{cc}\hfill M^T\hfill & \hfill \hfill \\ \hfill \hfill & \hfill I_{n_1}\otimes N^T\hfill \end{array}\right)\left(\begin{array}{cc}\hfill M\hfill & \hfill \hfill \\ \hfill \hfill & \hfill I_{n_1}\otimes N\hfill \end{array}\right)=I,(7)$

$M^{T}L\left(G_1\right)M=\mathit{diag}\left({\eta }_1,{\eta }_2,\dots ,{\eta }_{n_1}\right),N^{T}L\left(G_2\right)N=\mathit{diag}\left({\mu }_1,{\mu }_2,\dots ,{\mu }_{n_2}\right).(8)$

Because similar matrices have the same characteristic polynomials, the Laplacian polynomial of ${\tilde{G}}_1◦{\tilde{G}}_2$ is

$\mathrm{\Phi }\left(\lambda \right)=\left|\begin{array}{cc}\hfill M^T\left[\left(\lambda -r_3{n}_2\right)\left.I_{n_1}-r_1{L}_1\right)\right]M\hfill & \hfill r_3{M}^T{I}_{n_1}\otimes \left(\underset{n_2}{\overset{T}{J}}N\right)\hfill \\ \hfill r_3{I}_{n_1}\otimes \left(N^T{J}_{n_2}\right)M\hfill & \hfill I_{n_1}\otimes N^T\left[\left(\lambda -r_3\right)I_{n_2}-r_2{L}_2\right]N\hfill \end{array}\right|.(9)$

In order to find a specific expression for Φ(λ), we further investigated $r_3{M}^T{I}_{n_1}\otimes {(J_{n_2}^{T}N)}_{(n_1{n}_2)\times (n_1{n}_2)}$,

$r_3{M}^T{I}_{n_1}\otimes \left(\underset{n_2}{\overset{T}{J}}N\right)=r_3\left(\begin{array}{ccccccc}\hfill m_{11}{n}_1\hfill & \hfill \cdots \hfill & \hfill m_{11}{n}_{n_2}\hfill & \hfill \hfill & \hfill m_{n_{1}1}{n}_1\hfill & \hfill \cdots \hfill & \hfill m_{n_{1}1}{n}_{n_2}\hfill \\ \hfill ⋮\hfill & \hfill \ddots \hfill & \hfill ⋮\hfill & \hfill \cdots \hfill & \hfill ⋮\hfill & \hfill \ddots \hfill & \hfill ⋮\hfill \\ \hfill m_{1n_1}{n}_1\hfill & \hfill \cdots \hfill & \hfill m_{1n_1}{n}_{n_2}\hfill & \hfill \hfill & \hfill m_{n_1{n}_1}{n}_1\hfill & \hfill \cdots \hfill & \hfill m_{n_1{n}_1}{n}_{n_2}\hfill \end{array}\right),(10)$

where $n_j=\sum _{i=1}^{n_2}{n}_{ij}$ is the sum of the jth column of the orthogonal matrix N. By Lemma 1 and Eq. 10, we obtained

$r_3{M}^T{I}_{n_1}\otimes \left(\underset{n_2}{\overset{T}{J}}N\right)=r_3\left(\begin{array}{ccccccc}\hfill m_{11}\sqrt{n_2}\hfill & \hfill \cdots \hfill & \hfill 0\hfill & \hfill \hfill & \hfill m_{n_{1}1}\sqrt{n_2}\hfill & \hfill \cdots \hfill & \hfill 0\hfill \\ \hfill ⋮\hfill & \hfill \ddots \hfill & \hfill ⋮\hfill & \hfill \cdots \hfill & \hfill ⋮\hfill & \hfill \ddots \hfill & \hfill ⋮\hfill \\ \hfill m_{1n_1}\sqrt{n_2}\hfill & \hfill \cdots \hfill & \hfill 0\hfill & \hfill \hfill & \hfill m_{n_1{n}_1}\sqrt{n_2}\hfill & \hfill \cdots \hfill & \hfill 0\hfill \end{array}\right).(11)$

By Eq. 8,

$M^T\left[\left(\lambda -r_3{n}_2\right)\left.I_{n_1}-r_1{L}_1\right)\right]M={\left(\begin{array}{cccc}\hfill \lambda -r_3{n}_2\hfill & \hfill 0\hfill & \hfill \cdots \hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill \lambda -r_3{n}_2-r_1{\eta }_2\hfill & \hfill \cdots \hfill & \hfill 0\hfill \\ \hfill ⋮\hfill & \hfill ⋮\hfill & \hfill \ddots \hfill & \hfill ⋮\hfill \\ \hfill 0\hfill & \hfill 0\hfill & \hfill \cdots \hfill & \hfill \lambda -r_3{n}_2-r_1{\eta }_{n_1}\hfill \end{array}\right)}_{n_1\times n_1},(12)$

$N^T\left[\left(\lambda -r_3\right)\left.I_{n_2}-r_2{L}_2\right)\right]N={\left(\begin{array}{cccc}\hfill \lambda -r_3\hfill & \hfill 0\hfill & \hfill \cdots \hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill \lambda -r_3-r_2{\mu }_2\hfill & \hfill \cdots \hfill & \hfill 0\hfill \\ \hfill ⋮\hfill & \hfill ⋮\hfill & \hfill \ddots \hfill & \hfill ⋮\hfill \\ \hfill 0\hfill & \hfill 0\hfill & \hfill \cdots \hfill & \hfill \lambda -r_3-r_2{\mu }_{n_2}\hfill \end{array}\right)}_{n_2\times n_2}.(13)$

By formulas (9), (11), 12) and (13), the row and column of element λ − r₃ − r₂μ_i (i = 2, 3, … , n₂) are all 0 except itself. We expanded them according to the row; then,

$\mathrm{\Phi }(\lambda )=[n_2^{n_1}{\prod }_{i=2}^{n_2}{(\lambda -r_3-r_2{\mu }_i)}^{n_1}]\left|\begin{array}{cc}\hfill M^T[(\lambda -r_3{n}_2)I_{n_1}-r_1{L}_1\left.\right)]M\hfill & \hfill r_3{M}^T\hfill \\ \hfill r_{3}M\hfill & \hfill (\lambda -r_3)I_{n_1}/n_2\hfill \end{array}\right|$

$=\left[n_2^{n_1}\prod _{i=2}^{n_2}{\left(\lambda -r_3-r_2{\mu }_i\right)}^{n_1}\right]\left|\begin{array}{cc}\hfill \left(\lambda -r_3{n}_2\right)I_{n_1}-r_1{L}_1\hfill & \hfill r_3{I}_{n_1}\hfill \\ \hfill r_3{I}_{n_1}\hfill & \hfill \left(\lambda -r_3\right)I_{n_1}/n_2\hfill \end{array}\right|$

$=\left[\prod _{i=2}^{n_2}{\left(\lambda -r_3-r_2{\mu }_i\right)}^{n_1}\right]\left|\begin{array}{cc}\hfill \left(\lambda -r_3{n}_2-r_3\right)I_{n_1}-r_1{L}_1\hfill & \hfill -r_1{L}_1\hfill \\ \hfill r_3{I}_{n_1}\hfill & \hfill \lambda I_{n_1}\hfill \end{array}\right|.$

4 First-order coherence of ${\tilde{G}}_1◦{\tilde{G}}_2$

In this section, according to theorem 1, the first-order coherence of ${\tilde{G}}_1◦{\tilde{G}}_2$ is calculated by using the relationship between characteristic polynomial coefficients and the principal minors the of matrix.

Theorem 2: the first-order coherence of ${\tilde{G}}_1◦{\tilde{G}}_2$ can be described as follows:

$H^{\left(1\right)}\left({\tilde{G}}_1◦{\tilde{G}}_2\right)=\frac{1}{2n_1\left(n_2+1\right)}\left(\frac{1}{r_3{n}_2+r_3}+\frac{n_1-1}{r_3}+\frac{2n_1\left(n_2+1\right)}{r_1}{H}^{\left(1\right)}\left(G_1\right)+\sum _{i=2}^{n_2}\frac{n_1}{r_2{\mu }_i+r_3}\right).(14)$

Proof: according to theorem 1, the Laplacian polynomial of ${\tilde{G}}_1◦{\tilde{G}}_2$ is

$\mathrm{\Phi }\left(\lambda \right)=\left[\prod _{i=2}^{n_2}{\left(\lambda -r_3-r_2{\mu }_i\right)}^{n_1}\right]\left|\begin{array}{cc}\hfill \left(\lambda -r_3{n}_2-r_3\right)I_{n_1}-r_1{L}_1\hfill & \hfill -r_1{L}_1\hfill \\ \hfill r_3{I}_{n_1}\hfill & \hfill \lambda I_{n_1}\hfill \end{array}\right|.$

However, the Laplacian matrix of ${\tilde{G}}_1◦{\tilde{G}}_2$ must contain a zero eigenvalue, and r₃ + r₂μ_i ≠ 0 (i = 2, 3, … , n₂).

Therefore, let $0={\lambda }_1<{\lambda }_2\le {\lambda }_3\le \cdots \le {\lambda }_{2n_1}$ be the eigenvalues of ψ(λ),

$\psi \left(\lambda \right)=\left|\begin{array}{cc}\hfill \left(\lambda -r_3{n}_2-r_3\right)I_{n_1}-r_1{L}_1\hfill & \hfill -r_1{L}_1\hfill \\ \hfill r_3{I}_{n_1}\hfill & \hfill \lambda I_{n_1}\hfill \end{array}\right|$

$=a_{2n_1{\lambda }^{2n_1}}+a_{2n_1-1}{\lambda }^{2n_1-1}+\cdots +a_2{\lambda }^2+a_1\lambda .$

By [16], we have

$\sum _{i=2}^{2n_1}\frac{1}{{\lambda }_i}=-\frac{a_2}{a_1}.$

Just for the sake of calculation, let B*(i) and B*(i, j) be the submatrices of matrix B by removing the ith row, and ith and jth rows. B^†(i) and B^†(i, j) are the submatrices of matrix B by removing the ith column, and ith and jth columns.

$C=\left(\begin{array}{cc}\hfill (r_3{n}_2+r_3)I_{n_1}+r_1{L}_1\hfill & \hfill r_1{L}_1\hfill \\ \hfill -r_3{I}_{n_1}\hfill & \hfill 0_{n_1}\hfill \end{array}\right)$. Here, |C(i)| represents the (2n₁ − 1)-order principal minors of matrix C by removing the ith row and column, and |C (i, j)| represents the (2n₁ − 2)-order principal formula of matrix C by removing the ith and jth rows, and ith and jth columns. E_i is the diagonal matrix, where the ith element is r₃n₂ + r₃, and the remaining elements are all 0.

First, we calculated a₁, and we obtained it from algebra,

$a_1={\left(-1\right)}^{2n_1-1}\sum _{i=1}^{n_1}|C\left(i\right)|+{\left(-1\right)}^{2n_1-1}\sum _{i=n_1+1}^{2n_1}|C\left(i\right)|.$

When 1 ≤ i ≤ n₁, the (n₁ − 1 + i)-th row of |C(i)| is all 0; then, $\sum _{i=1}^{n_1}|C(i)|=0$,

$a_1=-\sum _{i=n_1+1}^{2n_1}|C\left(i\right)|=-\sum _{i=1}^{n_1}\left|\begin{array}{cc}\hfill \left(r_3{n}_2+r_3\right)I_{n_1}+r_1{L}_1\hfill & \hfill r_1{L}_1^{†}\left(i\right)\hfill \\ \hfill -r_3{I}_{n_1}^{\ast }\left(i\right)\hfill & \hfill 0_{n_1-1}\hfill \end{array}\right|$

$={\left(-1\right)}^{n_1}{\left(-1\right)}^{n_1-1}{r}_3^{n_1-1}\sum _{i=1}^{n_1}\left|\begin{array}{cc}\hfill \left(r_3{n}_2+r_3\right)I_{n_1}^{†}\left(i\right)+r_1{L}_1^{†}\left(i\right)\hfill & \hfill r_1{L}_1+E_i\hfill \\ \hfill I_{n_1-1}\hfill & \hfill 0_{n_1}^{\ast }\left(i\right)\hfill \end{array}\right|$

$\begin{array}{ll}\hfill & =-r_3^{n_1-1}\sum _{i=1}^{n_1}|r_1{L}_1+E_i|\hfill \\ \hfill & =-r_3^{n_1-1}\sum _{i=1}^{n_1}(|r_1{L}_1|+(r_3{n}_2+r_3)|r_1{L}_1(i)|)\hfill \\ \hfill & =-r_1^{n_1-1}{r}_3^{n_1-1}(r_3{n}_2+r_3)n_{1}t(G_1),\hfill \end{array}(15)$

where t (G₁) is the number of spanning trees of G₁.

Second, we calculated a₂,

$\begin{array}{ll}\hfill a_2& =\sum _{1\le i<j\le 2n_1}|C(i,j)|\hfill \\ \hfill & =\sum _{1\le i<j\le n_1}|C(i,j)|+\sum _{\begin{array}{c}\hfill 1\le i\le n_1\hfill \\ \hfill j>n_1,j\ne n_1+i\hfill \end{array}}|C(i,j)|+\sum _{\begin{array}{c}\hfill 1\le i\le n_1\hfill \\ \hfill j=n_1+i\hfill \end{array}}|C(i,j)|\hfill \\ \hfill & +\sum _{\begin{array}{c}\hfill n_1+1\le i<j\le 2n_1\hfill \end{array}}|C(i,j)|.\hfill \end{array}(16)$

If 1 ≤ i < j ≤ n₁, the (n₁ − 2 + i)-th and (n₁ − 2 + j)-th rows of |C (i, j)| are all 0; then, $\sum _{1\le i<j\le n_1}|C(i,j)|=0$.

If 1 ≤ i ≤ n₁, j > n₁, j ≠ n₁ + i and the (n₁ − 1 + i)-th row of |C (i, j)| is all 0, then $\sum _{\begin{array}{c}\hfill 1\le i\le n_1\hfill \\ \hfill j>n_1,j\ne n_1+i\hfill \end{array}}|C(i,j)|=0$.

By Eq. 16,

$a_2=\sum _{\begin{array}{c}\hfill 1\le i\le n_1\hfill \\ \hfill j=n_1+i\hfill \end{array}}|C\left(i,j\right)|+\sum _{\begin{array}{c}\hfill n_1+1\le i<j\le 2n_1\hfill \end{array}}|C\left(i,j\right)|,(17)$

where

$\sum _{\begin{array}{c}\hfill 1\le i\le n_1\hfill \\ \hfill j=n_1+i\hfill \end{array}}|C(i,j)|=\sum _{i=1}^{n_1}\left|\begin{array}{cc}\hfill (r_3{n}_2+r_3)I_{n_1-1}+r_1{L}_1(i)\hfill & \hfill r_1{L}_1(i)\hfill \\ \hfill -r_3{I}_{n_1-1}\hfill & \hfill 0_{n_1-1}\hfill \end{array}\right|$

$={(-1)}^{n_1-1}{r_3}^{n_1-1}\sum _{i=1}^{n_1}\left|\begin{array}{cc}\hfill (r_3{n}_2+r_3)I_{n_1-1}+r_1{L}_1(i)\hfill & \hfill r_1{L}_1(i)\hfill \\ \hfill I_{n_1-1}\hfill & \hfill 0_{n_1-1}\hfill \end{array}\right|.$.

By the properties of the determinant, we can obtain

$\begin{array}{ll}\hfill \sum _{\begin{array}{c}\hfill 1\le i\le n_1\hfill \\ \hfill j=n_1+i\hfill \end{array}}|C(i,j)|& ={(-1)}^{n_1-1}{r_3}^{n_1-1}\sum _{i=1}^{n_1}|-r_1{L}_1(i)|\hfill \\ \hfill & ={r_1}^{n_1-1}{r_3}^{n_1-1}\sum _{i=1}^{n_1}|L_1(i)|={r_1}^{n_1-1}{r_3}^{n_1-1}{n}_{1}t(G_1),\hfill \end{array}(18)$

$\begin{array}{ll}\hfill \sum _{\begin{array}{c}\hfill n_1+1\le i<j\le 2n_1\hfill \end{array}}|C(I,j)|& =\sum _{1\le i<j\le n_1}\left|\begin{array}{cc}\hfill (r_3{n}_2+r_3)I_{n_1}+r_1{L}_1\hfill & \hfill r_1{L}_1^{†}(i,j)\hfill \\ \hfill -r_3{I}_{n_1}^{\ast }(i,j)\hfill & \hfill 0_{n_1-2}\hfill \end{array}\right|\hfill \\ \hfill & ={(-1)}^{n_1-2}{r_3}^{n_1-2}\sum _{1\le i<j\le n_1}\left|\begin{array}{cc}\hfill (r_3{n}_2+r_3)I_{n_1}+r_1{L}_1\hfill & \hfill r_1{L}_1^{†}(i,j)\hfill \\ \hfill I_{n_1}^{\ast }(i,j)\hfill & \hfill 0_{n_1-2}\hfill \end{array}\right|.\hfill \end{array}$

By varying the determinant elementary column, we obtain

$\begin{array}{ll}\hfill & \sum _{\begin{array}{c}\hfill n_1+1\le i<j\le 2n_1\hfill \end{array}}|C(i,j)|\hfill \\ \hfill & ={(-1)}^{n_1-2}{r_3}^{n_1-2}\sum _{1\le i<j\le n_1}\left|\begin{array}{cc}\hfill (r_3{n}_2+r_3)I_{n_1}^{†}(i,j)+r_1{L}_1^{†}(i,j)\hfill & \hfill r_1{L}_1+E_i+E_j\hfill \\ \hfill I_{n_1-2}\hfill & \hfill 0_{n_1}^{\ast }(i,j)\hfill \end{array}\right|\hfill \\ \hfill & ={(-1)}^{n_1-2}{(-1)}^{n_1(n_1-2)}{r_3}^{n_1-2}\sum _{1\le i<j\le n_1}\left|\begin{array}{cc}\hfill r_1{L}_1+E_i+E_j\hfill & \hfill (r_3{n}_2+r_3)I_{n_1}^{†}(i,j)+r_1{L}_1^{†}(i,j)\hfill \\ \hfill 0_{n_1}^{*}(i,j)\hfill & \hfill I_{n_1-2}\hfill \end{array}\right|\hfill \\ \hfill & ={r_3}^{n_1-2}\sum _{1\le i<j\le n_1}|r_1{L}_1+E_i+E_j|\hfill \\ \hfill & ={r_3}^{n_1-2}\sum _{1\le i<j\le n_1}[|r_1{L}_1|+(r_3{n}_2+r_3)(|r_1{L}_1(i)|+|r_1{L}_1(j)|)+{(r_3{n}_2+r_3)}^2|r_1{L}_1(i,j)|].\hfill \end{array}$

Because |r₁L₁| = 0, then

$\begin{array}{ll}\hfill \sum _{\begin{array}{c}\hfill n_1+1\le i<j\le 2n_1\hfill \end{array}}|C(i,j)|& ={r_1}^{n_1-1}{r_3}^{n_1-2}{n}_1(n_1-1)(r_3{n}_2+r_3)t(G_1)\hfill \\ \hfill & +{r_1}^{n_1-2}{r_3}^{n_1-2}{(r_3{n}_2+r_3)}^2\sum _{1\le i<j\le n_1}|L_1(i,j)|.\hfill \end{array}(19)$

By formulas (15), (17), (18), and 19) and the literature [22], we obtain

$-\frac{a_2}{a_1}=\frac{1}{r_3{n}_2+r_3}+\frac{n_1-1}{r_3}+\frac{n_2+1}{r_1{n}_1}\frac{\sum _{1\le i<j\le n_1}|L_1\left(i,j\right)|}{t\left(G_1\right)}$

$=\frac{1}{r_3{n}_2+r_3}+\frac{n_1-1}{r_3}+\frac{n_2+1}{r_1{n}_1}Kf\left(G_1\right)$

$=\frac{1}{r_3{n}_2+r_3}+\frac{n_1-1}{r_3}+\frac{2n_1\left(n_2+1\right)}{r_1}{H}^{\left(1\right)}\left(G_1\right).$

From Eq. 5,

$H^{\left(1\right)}\left({\tilde{G}}_1◦{\tilde{G}}_2\right)=\frac{1}{2n_1\left(n_2+1\right)}\left(\frac{1}{r_3{n}_2+r_3}+\frac{n_1-1}{r_3}+\frac{2n_1\left(n_2+1\right)}{r_1}{H}^{\left(1\right)}\left(G_1\right)+\sum _{i=2}^{n_2}\frac{n_1}{r_2{\mu }_i+r_3}\right).$

Since the form of theorem 2 is complicated, we further optimized the conclusion to obtain theorem 3.

Theorem 3

$H^{\left(1\right)}\left({\tilde{G}}_1◦{\tilde{G}}_2\right)=\frac{n_2\left(n_1-1\right)}{2n_1{\left(n_2+1\right)}^2{r}_3}+H^{\left(1\right)}\left({\tilde{G}}_1\right)+H^{\left(1\right)}\left({\tilde{G}}_2\vee {\tilde{K}}_1\right).(20)$

Proof: the Laplacian eigenvalues of ${\tilde{G}}_1$ are

$0=r_1{\eta }_1<r_1{\eta }_2\le r_1{\eta }_3\le \cdots \le r_1{\eta }_{n_1}.$

By Eq. 5,

$H^{\left(1\right)}\left({\tilde{G}}_1\right)=\frac{1}{2n_1}\sum _{i=2}^{n_1}\frac{1}{r_1{\eta }_i}=\frac{1}{2n_1{r}_1}\sum _{i=2}^{n_1}\frac{1}{{\eta }_i}=\frac{1}{r_1}{H}^{\left(1\right)}\left(G_1\right).(21)$

Let K₁ be the complete graph of order 1. The adjacency matrix of ${\tilde{G}}_2\vee {\tilde{K}}_1$ is

$A\left({\tilde{G}}_2\vee {\tilde{K}}_1\right)={\left(\begin{array}{cc}\hfill r_2{A}_2\hfill & \hfill r_3{J}_{n_2}\hfill \\ \hfill r_3{J}_{n_2}^T\hfill & \hfill 0\hfill \end{array}\right)}_{\left(n_2+1\right)\times \left(n_2+1\right)}.$

The degree matrix of ${\tilde{G}}_2\vee {\tilde{K}}_1$ is

$D\left({\tilde{G}}_2\vee {\tilde{K}}_1\right)={\left(\begin{array}{cc}\hfill r_2{D}_2+r_3{I}_{n_2}\hfill & \hfill 0_{n_2\times 1}\hfill \\ \hfill 0_{1\times n_2}\hfill & \hfill n_2{r}_3\hfill \end{array}\right)}_{\left(n_2+1\right)\times \left(n_2+1\right)}.$

The Laplacian matrix of ${\tilde{G}}_2\vee {\tilde{K}}_1$ is

$L\left({\tilde{G}}_2\vee {\tilde{K}}_1\right)={\left(\begin{array}{cc}\hfill r_2{L}_2+r_3{I}_{n_2}\hfill & \hfill -r_3{J}_{n_2}\hfill \\ \hfill -r_3{J}_{n_2}^T\hfill & \hfill n_2{r}_3\hfill \end{array}\right)}_{\left(n_2+1\right)\times \left(n_2+1\right)}.$

Because of

$\left(\begin{array}{cc}\hfill N^T\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill 1\hfill \end{array}\right)\left(\begin{array}{cc}\hfill r_2{L}_2+r_3{I}_{n_2}\hfill & \hfill -r_3{J}_{n_2}\hfill \\ \hfill -r_3{J}_{n_2}^T\hfill & \hfill n_2{r}_3\hfill \end{array}\right)\left(\begin{array}{cc}\hfill N\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill 1\hfill \end{array}\right)$

$=\left(\begin{array}{cc}\hfill N^T\left(r_2{L}_2+r_3{I}_{n_2}\right)N\hfill & \hfill -r_3{N}^T{J}_{n_2}\hfill \\ \hfill -r_3{J}_{n_2}^{T}N\hfill & \hfill n_2{r}_3\hfill \end{array}\right).$

$|\lambda I-L({\tilde{G}}_2\vee {\tilde{K}}_1)|=\left|\begin{array}{cc}\hfill N^T(\lambda I-r_2{L}_2-r_3{I}_{n_2})N\hfill & \hfill r_3{N}^T{J}_{n_2}\hfill \\ \hfill r_3{J}_{n_2}^{T}N\hfill & \hfill \lambda -n_2{r}_3\hfill \end{array}\right|$

$=\left|\begin{array}{cccc}\hfill \lambda -r_3\hfill & \hfill 0\hfill & \hfill \cdots \hfill & \hfill r_3\sqrt{n_2}\hfill \\ \hfill 0\hfill & \hfill \lambda -r_3-r_2{\mu }_2\hfill & \hfill \cdots \hfill & \hfill 0\hfill \\ \hfill ⋮\hfill & \hfill ⋮\hfill & \hfill \ddots \hfill & \hfill ⋮\hfill \\ \hfill r_3\sqrt{n_2}\hfill & \hfill 0\hfill & \hfill \cdots \hfill & \hfill \lambda -r_3{n}_2\hfill \end{array}\right|.$

The Laplacian eigenvalues of ${\tilde{G}}_2\vee {\tilde{K}}_1$ are

$r_2{\mu }_i+r_3\left(i=\mathrm{2,3},\dots ,n_2\right),0,n_2{r}_3+r_3.$

Then,

$H^{\left(1\right)}\left({\tilde{G}}_2\vee {\tilde{K}}_1\right)=\frac{1}{2\left(n_2+1\right)}\left(\frac{1}{r_3{n}_2+r_3}+\sum _{i=2}^{n_2}\frac{1}{r_2{\mu }_i+r_3}\right).(22)$

By formulas (14), (21), and (22), we obtain

$H^{\left(1\right)}\left({\tilde{G}}_1◦{\tilde{G}}_2\right)=\frac{n_2\left(n_1-1\right)}{2n_1{\left(n_2+1\right)}^2{r}_3}+H^{\left(1\right)}\left({\tilde{G}}_1\right)+H^{\left(1\right)}\left({\tilde{G}}_2\vee {\tilde{K}}_1\right).$

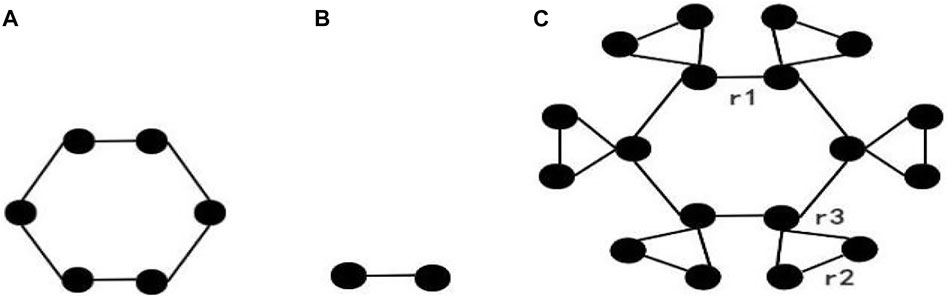
5 Actual example

Let $K_{m(n_1-m)}$ be the complete bipartite graph of order n₁ and $C_{n_2}$ be the cycle of order n₂.

The Laplacian spectrum of $K_{m(n_1-m)}$ is

$0,n_1,\underset{n_1-m-1}{\underbrace{m}},\underset{m-1}{\underbrace{n_1-m}}.$

The Laplacian spectrum of $C_{n_2}$ is

$\mathrm{0,4}si{n}^2\left(\frac{\alpha \pi }{2n_2}\right)\left(\alpha =\mathrm{1,2},\dots ,n_2-1\right).$

From Eq. 20,

$H^{\left(1\right)}\left({\tilde{K}}_{m\left(n_1-m\right)}◦{\tilde{C}}_{n_2}\right)=\frac{n_2\left(n_1-1\right)}{2n_1{\left(n_2+1\right)}^2{r}_3}+H^{\left(1\right)}\left({\tilde{K}}_{m\left(n_1-m\right)}\right)+H^{\left(1\right)}\left({\tilde{C}}_{n_2}\vee {\tilde{K}}_1\right).$

From Eq. 21,

$H^{\left(1\right)}\left({\tilde{K}}_{m\left(n_1-m\right)}\right)=\frac{1}{r_1}{H}^{\left(1\right)}\left(K_{m\left(n_1-m\right)}\right)=\frac{1}{2n_1{r}_1}\left(\frac{1}{n_1}+\frac{n_1-m-1}{m}+\frac{m-1}{n_1-m}\right).$

From Eq. 22,

$H^{\left(1\right)}\left({\tilde{C}}_{n_2}\vee {\tilde{K}}_1\right)=\frac{1}{2\left(n_2+1\right)}\left(\frac{1}{r_3{n}_2+r_3}+\sum _{\alpha =1}^{n_2-1}\frac{1}{4r_2{\mathit{sin}}^2\left(\frac{\alpha \pi }{2n_2}\right)+r_3}\right).$

Then,$H^{(1)}({\tilde{K}}_{m(n_1-m)}◦{\tilde{C}}_{n_2})=\frac{n_2(n_1-1)+n_1}{2n_1{(n_2+1)}^2{r}_3}+\frac{1}{2n_1{r}_1}(\frac{1}{n_1}+\frac{n_1-m-1}{m}+\frac{m-1}{n_1-m})+\frac{1}{2(n_2+1)}(\sum _{\alpha =1}^{n_2-1}\frac{1}{4r_2{\mathit{sin}}^2(\frac{\alpha \pi }{2n_2})+r_3})$.

6 Conclusion

For the unweighted corona networks G₁◦G₂, the corresponding Laplacian spectra can be obtained by the eigenvector method, and we can use the relationship between eigenvalues and coherence to get the network coherence of G₁◦G₂. For the weighted corona networks ${\tilde{G}}_1◦{\tilde{G}}_2$, due to the different weights, it is difficult to obtain the Laplacian spectra, that is, it is not easy to obtain the network coherence of ${\tilde{G}}_1◦{\tilde{G}}_2$ through the eigenvalue spectra. Based on the Laplacian matrix ${\tilde{G}}_1◦{\tilde{G}}_2$, the Laplacian characteristic polynomial of ${\tilde{G}}_1◦{\tilde{G}}_2$ is calculated by using the properties of matrix diagonalization and orthogonal matrix. We further used the relationship between eigenvalues and characteristic polynomial coefficients to obtain the network coherence of ${\tilde{G}}_1◦{\tilde{G}}_2$ and found the relationship between the network coherence of ${\tilde{G}}_1◦{\tilde{G}}_2$ and G₁. The Laplacian spectra of the weighted corona networks are not obtained in this study. We will conduct further research in future work. The research on the Sombor index and degree-related properties of simplicial networks is very meaningful, and we will try to obtain the Sombor index of the weighted corona networks.

Data availability statement

The original contributions presented in the study are included in the article/Supplementary Material; further inquiries can be directed to the corresponding author.

Author contributions

Conceptualization, HG and WD; methodology, HG and JZ; software, WD; validation, XL and JZ; formal analysis, HG and WD; writing—original draft preparation, HG and WD; writing—review and editing, JZ; supervision, XL; and project administration, HG. All authors contributed to manuscript revision, read, and approved the submitted version.

Funding

This work was supported by the National Natural Science Foundation of China (no.61802316), the School level project of the Xinjiang institute of Light industry Technology (no. XJQG2022S16), the Scientific Research and Education Project of Xinjiang Institute of Engineering (2020xgy372302), the National innovation and entrepreneurship training program for College Students (no. 202110994006), and the project of Key Laboratory of New Energy and Materials Research of Xinjiang Institute of Engineering.

Acknowledgments

The authors express their sincere gratitude to the people who gave valuable comments.

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors, and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

1. Mackin E, Patterson S. Optimizing the coherence of a network of networks. IEEE Trans Control Netw Syst (2020) 7(3):1465–75. doi:10.1109/tcns.2020.2979884

CrossRef Full Text | Google Scholar

2. Shang Y. Practical consensus for heterophilous multiagent networks with constrained states. J Franklin Inst (2022). doi:10.1016/j.jfranklin.2022.04.037

CrossRef Full Text | Google Scholar

3. Sun W, Li Y, Liu S. Noisy consensus dynamics in windmill-type graphs. Chaos (2020) 30(12):123131. Article ID 123131, 2020. doi:10.1063/5.0020696

PubMed Abstract | CrossRef Full Text | Google Scholar

4. Gao H, Zhu J, Chen X, Zhang L, Li X. Coherence analysis of symmetric star topology networks. Front Phys (2022) 10:876994. Article ID 876994. doi:10.3389/fphy.2022.876994

CrossRef Full Text | Google Scholar

5. Chen J, Li Y, Sun W. Network coherence in a family of bookgraphs. Front Phys (2020) 8:583603. Article ID 583603. doi:10.3389/fphy.2020.583603

CrossRef Full Text | Google Scholar

6. Liu J, Peng X, Gu J, Lin W. The (multiplicative degree-) Kirchhoff index of graphs derived from the cartesian product. J Math (2022) 2022:1–9. doi:10.1155/2022/1670984

CrossRef Full Text | Google Scholar

7. Yi Y, Zhang Z, Shan L, Chen G. Robustness of first-and second-order consensus algorithms for a noisy scale-free small-world koch network. IEEE Trans Control Syst Technol (2016) 25(1):342–50. doi:10.1109/tcst.2016.2550582

CrossRef Full Text | Google Scholar

8. Wang D, Huang L. Robust synchronization of discontinuous cohen-grossberg neural networks: Pinning control approach. J Franklin Inst (2018) 355(13):5866–92. doi:10.1016/j.jfranklin.2018.05.048

CrossRef Full Text | Google Scholar

9. Tang L, Wu X, Lu J, Lu JA, D’Souza RM. Master stability functions for complete, intra-layer, and inter-layer synchronization in multiplex networks of coupled Rossler oscillators. Phys Rev E (2019) 99(1):012304. Article ID 012304. doi:10.1103/physreve.99.012304

PubMed Abstract | CrossRef Full Text | Google Scholar

10. Gao H, Zhu J, Li X, Chen X (2021). Synchronizability of multi-layer coupled star-composed networks. Symmetry 13:2224. Article ID 2224. doi:10.3390/sym13112224

CrossRef Full Text | Google Scholar

11. Shang Y. Sombor index and degree-related properties of simplicial networks. Appl Math Comput (2022) 419:126881. Article ID 126881, 2022. doi:10.1016/j.amc.2021.126881

CrossRef Full Text | Google Scholar

12. Liu J, Zhao J, Cai Z. On the generalized adjacency, Laplacian and signless Laplacian spectra of the weighted edge corona networks. Physica A: Stat Mech its Appl (2019) 540:123073. Article ID 123073. doi:10.1016/j.physa.2019.123073

CrossRef Full Text | Google Scholar

13. Dai M, Shen J, Dai L, Ju T, Hou Y, Su W, et al. Generalized adjacency and laplacian spectra of the weighted corona graphs. Physica A: Stat Mech its Appl (2019) 528:121285. Article ID 121285. doi:10.1016/j.physa.2019.121285

CrossRef Full Text | Google Scholar

14. Mackin E, Patterson S. Submodular optimization for consensus networks with noise-corrupted leaders. IEEE Trans Automat Contr (2019) 64(7):3054–9. doi:10.1109/TAC.2018.2874306

CrossRef Full Text | Google Scholar

15. Hu T, Li L, Wu Y, Sun W. Consensus dynamics in noisy trees with given parameters. Mod Phys Lett B (2022) 36(7):2150608. Article ID 2150608, 2022. doi:10.1142/s0217984921506089

CrossRef Full Text | Google Scholar

16. Wang J, Chen J, Sun W. Network coherence of weighted duplex networks: Exact results. Int J Mod Phys C (2022) 2022:2250130. Article ID 2250130, 2022. doi:10.1142/s0129183122501303

CrossRef Full Text | Google Scholar

17. Chen J, Jing T, Sun W. Robustness of network coherence in asymmetric unicyclic graphs. Int J Mod Phys B (2021) 35(29):2150301. Article ID 2150301, 2021. doi:10.1142/s021797922150301x

CrossRef Full Text | Google Scholar

18. Wang X, Xu H, Dai M. First-order network coherence in 5-rose graphs. Physica A: Stat Mech its Appl (2019) 527:121129. Article ID 121129, 2019. doi:10.1016/j.physa.2019.121129

CrossRef Full Text | Google Scholar

19. Frucht R, Harary F. On the corona of two graphs. Aequ Math (1970) 4(1-2):264. doi:10.1007/bf01817769

CrossRef Full Text | Google Scholar

20. Liu Q. The Laplacian spectrum of corona of two graphs. Kragujevac J Math (2014) 38(1):163–70. doi:10.5937/kgjmath1401163l

CrossRef Full Text | Google Scholar

21. Bondy JA, Murty USR. Graph theory. Switzerland AG: Springer (2008).

Google Scholar

22. Bapat R, Gutman I, Xiao W. A simple method for computing resistance distance. Z Naturforschung A (2003) 58(9-10):494–8. doi:10.1515/zna-2003-9-1003

CrossRef Full Text | Google Scholar