Entropy Optimization and Thermal Behavior of a Porous System With Considering Hybrid Nanofluid

The aim of this research work is to study the performance of hybrid eclectically conducting nanofluid (MWCNT-Fe₃O₄) with entropy optimization impacts using the CVFEM approach. 3D and contour plots are two types of outcomes that extend the discrepancy of analyzed variables. The Newtonian liquid is presumed as a testing fluid, and the non-Darcy model is employed to simulate the permeable domain. The geometry has two adiabatic walls and one wavy hot wall with unvarying flux, and the other is kept at a constant temperature. The impact of Brownian motion in the hybrid nanofluid (MWCNT-Fe₃O₄) is considered. The irreversibility effect is also taken into account. This effect acts against the performance of the system and reduces the efficiency of the system. To solve the final equations with higher accuracy, we utilized the method of CVFEM. The validation of the results obtained through CVFEM is clearly and graphically presented with the available literature. The outputs of the simulation showed that there is an inverse relation between permeability and the Bejan Number, and the boundary layer thickness augments with intensification in Lorentz force. These variations in the form of streamline, isotherm, and various contour plots have been reported at $Ra={10}^3$ and $Ra={10}^5$ for different values of Da, Ha, and $\varphi .$

Introduction

Nanofluids have been investigated for the last decade with the giant potential to enrich the efficiency of the heat transfer features. Though, well-dispersed nanoparticles for nanofluids are very much expected to improve mechanical performance in many industries. The use of nanoparticles in engineering and technology has provided remarkable achievements, especially in heat transfer augmentation. The applications of these nanoparticles within the porous enclosure in the occurrence of heat transfer analysis are widely investigated by many researchers [1, 2]. Some of these applications are solar collectors, fuel cells, cooling of electronic accessories (on a small and large scale), and drying process. The augmentation of the heat transfer inside the square enclosure is not only related to the de-purification of the fluid inside but also related to the shape and nature of the walls of the square. For this purpose, Ghasemi et al. [3] analyzed the natural convective flow of the MHD fluid flow in the x-direction inside the square cavity. They reported that with a larger Rayleigh number and smaller values of the Hartmann number the heat transfer enhances. This enhancement may or may not occur when the nanofluid is added which affects the performance of the Hartmann and Rayleigh numbers. The thermal analysis of the nanofluid inside an inclined enclosure is reported by Abbassi [4]. The geometry was chosen in such a way that heat flows from left to right, where the right wall chosen was cool. The impact of the inclination angle and the aspect ratio has been studied in detail. The aspect ratio impact increases or decreases the Nusselt number due to its larger or smaller values. The influence of the magnetic parameter by the nanofluid flow inside an enclosure by considering the Brownian motion is reported by Mahmoudi et al. [5] and Ghasemi and Aminossadati [6]. The Al₂O₃ and CuO nanoparticles in a water-based mixture through a trapezium shape enclosure are numerically analyzed by Saleh et al. [7]. They constituted a new empirical formula for the Nusselt number and reported that CuO-water nanofluid has greater thermal conductivity as compared to that of Al₂O₃-water. The finite element analysis of the CuO-water nanofluid through a parallelogram shape enclosure is analyzed by Mustafa and Hussein [8]. The top wall of the enclosure was chosen open through which the thermally heated fluid flows. The walls are heated in such a way that the inclined walls are kept cool while partial heating to the enclosure is provided from the bottom. The impacts of the inclination angles of the cold walls, Rayleigh number, a source of heat in addition to the concentration of the nanofluid are reported in detail. They described that for the betterment of the heat transmission from the source of heat should be nearer to the left wall that is inclined at 60°. In their work, they showed that heat flux shows an increasing trend by the larger values of the Rayleigh parameter.

The entropy, as well as the influence of various nanoparticles (Cu, TiO₂, Al₂O_3, etc.) through different complex enclosures, are reported by Cho et al. [9]. They showed the impact of motion of the surface with its length and Rayleigh parameter over the heat transmission and fluid flow. They observed that the generation of entropy is very low for Cu nanoparticles as compared to the other nanoparticles chosen in the study. On the other hand, the transfer of heat has the maximum bound in the performance of heat transfer. The effects of the inclined magnetic field, as well as the internal heat source inside an enclosure for the natural convective flow of the Al₂O₃ nanofluid through an enclosure, are analyzed by Sadeghi et al. [10]. The enclosure was chosen in such a way that it has one cold wavy wall with a trapezium heat source. They numerically investigated the system for the influence of Rayleigh and Hartmann parameters together with the shape factor and the location of the heat source for the analysis of the fluid as well as the heat transfer. They reported that the magnetic parameter reduces the transfer of heat in the natural convection case when it acts horizontally. The saturation of nanofluids is recently studied with various models (Darcy model, LTE, Darcy–Brinkmann model, LTNE, etc.) by many researchers [11, 12]. In the same way, Rashed and Ahmed [13] numerically studied the internal source impact on the MHD nanofluid through a porous enclosure. Izadi et al. [14] analyzed the variable magnetic field effect for the fluid flows through semi-circular heated cylinders numerically. They used the non-equilibrium model for the hybrid nanofluid to fill in the gap. They reported the impacts of various important parameters like Rayleigh number, porosity coefficient, magnetic source, and the Hartmann number over the state variables. The Cu-Al₂O₃ hybrid nanofluid inside a wavy enclosure with the porous medium is analyzed by Kadhim et al. [15]. The Darcy–Brinkmann model is applied and the finite element method is used for solution purposes. They reported that Al₂O₃–water nanofluid impact over the heat flux is not very effective as compared to that of the Cu–water nanofluid. Apart from this, heat flux acts as a function of the Darcy and Rayleigh number. A similar analysis for the Ag-MgO–water nanofluid through a square enclosure is reported by Mehryan et al. [15]. More interesting results on square cavity can be found in [16–18].

The study of different geometries within an enclosure has been reported by many researchers. For instance, the inner body moving (in all directions) has been reported in [19–21]. Yoon et al. [22] studied the flow between two circular cylinders that were immersed in an enclosure. The flow had taken natural convective and the analysis of the flow pattern is investigated with the numerical scheme for various parameters over the state variables. Kefayati and Tang [23] reported the flow through the two different shape cylinders placed within a square enclosure by using LBM. The enclosure was chosen inclined and the impact of the inclination angle together with the inner body position and the Rayleigh number is analyzed for all the states variables. Rectangular, elliptical, and circular shape bodies within an enclosure filled with nanofluid by considering the natural convective flow are studied by Roy [24]. He showed that the impact of the circular shapes body inside the cavity is enhancing the transfer of heat effectively as compared to the other shapes considered in the study. Wang et al. [25] interrogated the vertical motion of the circular shaped object in an enclosure filled with nanofluid having transient convection. They showed that the position of the object highly influences the nanofluid and the heat transmission. Bhowmick et al. [26] considered the cylinders in pairs inside the porous enclosure and analyzed the magnetic effect and entropy generation for the natural convective flow inside the enclosure. They found that the heat augments with rising distance between the immersed cylinders. In the same way, Alsabery et al. [27] investigated the square shaped body effect inside an enclosure for the transfer of heat by considering the two-phase model. Despite its applications, geometries like, U, H, C, and I shape for the natural convective flow have not been widely studied by researchers [28–30]. One such study is reported by Armaghani et al. [32] by considering the shape porous enclosure filled with nanofluid. They concluded the impact of the magnetic field for the heat transfer analysis. Similar geometry is considered by Ma et al. [33] for the analysis of the multi-square nanofluid flow. For the analysis of the flow inside the square enclosure by considering various impacts of the nanofluid flow has been studied through innovative methods [34, 35]. The lattice Boltzmann equations for the three-dimensional flow are analyzed by Succi et al. [36]. In their work, they used Darcy’s law and analyzed the results for variations of the Reynolds number. Heat transfer analysis with the effect of a magnetic field for innumerable nanofluids with different properties in different geometries can be found in [37–47]. Recently, Rashidi et al. [41, 42] discussed the entropy generation by analyzing the stagnation point flow and the circular tube heat exchanger by utilizing the nanofluids. A more detailed survey on the entropy generation by using various approaches has been reported by Abbas et al. [48–59]. Thus, according to the literature, Table 1 presents the properties of hybrid MWCNT and Fe₃O₄. More development of simulating approaches were demonstrated in recent articles [60–71].

TABLE 1

TABLE 1. Properties of hybrid MWCNT and Fe₃O₄ [48].

From the aforementioned discussion, it is clear that the entropy generation inside a square enclosure has not been reported yet. In this work, we will investigate the hybrid nanofluid (MWCNT- Fe₃O₄) flow inside a permeable enclosure (tank). The influence of the magnetic field and entropy generation has been taken into account for the analysis of the heat transfer. The geometry is chosen in such a way that the two walls are adiabatic, and one wall is wavy. For simulation purposes, an advanced computational technique CVFEM is used. Through this technique, various parameters like, Hartmann number, Reynolds number, and volume fraction of the nanofluid have been studied in detail. The results are validated with the available literature through graph.

Physical and Mathematical Model

Geometric Model

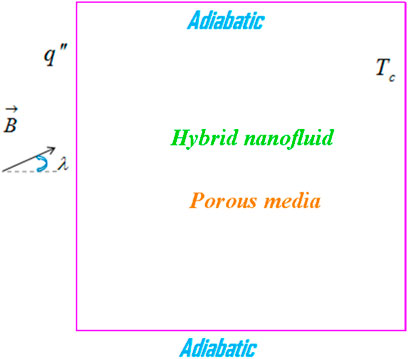
Assume a permeable geometry having one hot wavy wall (through which a uniform flux passes) and two horizontal adiabatic walls, while the rest of the wall (perpendicular) is kept at constant temperature T_c as shown in Figure 1. The testing fluid for the non-Darcy model through this geometry considered is Newtonian. The hybrid nanofluid is utilized and estimated for the correlation properties as per the procedure described in the Ref. [48]. The magnetic field is applied at an angle and it is presumed that the induced field produced is ignored. For the problem solution and utilization, the advanced numerical procedure CVFEM is used [49].

FIGURE 1

FIGURE 1. Porous zone with considering heat flux.

Governing Equations

For the assumptions and flow pattern through Figure 1, the basic model equations are constituted as follows [20–25]:

${\left(\rho C_p\right)}_{nf}\left(u\frac{\partial T}{\partial x}+\frac{\partial T}{\partial y}v\right)=k_{nf}\left(\frac{{\partial }^{2}T}{\partial x^2}+\frac{{\partial }^{2}T}{\partial y^2}\right)(1)$

$\begin{array}{l}{\mu }_{nf}\left(\frac{{\partial }^{2}v}{\partial y^2}+\frac{{\partial }^{2}v}{\partial x^2}\right)-\frac{\partial P}{\partial y}-\frac{{\mu }_{nf}}{K}v,\\ -B_{x}v{B}_x{\sigma }_{nf}+g\left(T-T_c\right){\rho }_{nf}{\beta }_{nf}+B_{x}u{\sigma }_{nf}{B}_y={\rho }_{nf}\left(v\frac{\partial v}{\partial y}+\frac{\partial v}{\partial x}u\right),\end{array}(2)$

$\begin{array}{l}\left({\rho }_{nf}\right)\left(\frac{\partial u}{\partial y}v+u\frac{\partial u}{\partial x}\right)={\sigma }_{nf}{B}_x{B}_{y}v-{\sigma }_{nf}{B}_y^{2}u+\left(\frac{{\partial }^{2}u}{\partial y^2}+\frac{{\partial }^{2}u}{\partial x^2}\right){\mu }_{nf},\\ -\frac{\partial P}{\partial x}-\frac{{\mu }_{nf}}{K}u,\left(B_y,B_x\right)=B_o\left(\sin \lambda ,\cos \lambda \right),\end{array}(3)$

$\frac{\partial v}{\partial y}+\frac{\partial u}{\partial x}=0.(4)$

Since the vorticity effect is affecting the flow, for this, we assume the following formulation in this work:

$\begin{array}{l}\frac{\partial \psi }{\partial y}=u,-\frac{\partial \psi }{\partial x}=v,u_y-v_x=-\omega .\\ \end{array}(5)$

The formulae describing the nanofluid and nanomaterial characteristics are outlined as follows [18–22]:

$\mathit{ }{\rho }_{nf}{\beta }_{nf}=\left(1-\phi \right){\left(\rho \beta \right)}_{bf}+\phi {\left(\rho \beta \right)}_{np}\text{, }{\beta }_{np}=\frac{{\beta }_{MWCNT}{\phi }_{MWCNT}+{\beta }_{F{e}_3{O}_4}{\phi }_{F{e}_3{O}_4}}{{\phi }_{MWCNT}+{\phi }_{F{e}_3{O}_4}}.$

To reduce the complexity, and transform the given PDEs system into a dimensional form, we assume the following important transformations [20, 26]:

$U=\frac{uL}{{\alpha }_f},V=\frac{vL}{{\alpha }_f},\Theta ={\left[q^{″}L/k_f\right]}^{-1}\left(T-T_c\right),\left(X,Y\right)=\frac{\left(x,y\right)}{L}.(6)$

Using Eq. 6 in the system of PDEs (1)–(4), we have [20–26]

$\left(\frac{{\partial }^2\Theta }{\partial Y^2}+\frac{{\partial }^2\Theta }{\partial X^2}\right)=V\frac{\partial \Theta }{\partial Y}+\frac{\partial \Theta }{\partial X}U,(7)$

$\frac{{\partial }^2\mathrm{\Psi }}{\partial Y^2}+\frac{{\partial }^2\mathrm{\Psi }}{\partial X^2}=-\mathrm{\Omega }(8)$

$\begin{array}{l}\mathrm{Pr}\left(\frac{A_3{A}_2^2}{A_1{A}_4^2}\right)Ra\left(\frac{\partial \Theta }{\partial X}\right)+H{a}^2\mathrm{Pr}\left(\left(\cos \lambda \right)\frac{\partial U}{\partial X}\left(\sin \lambda \right)-\left(0.5\sin 2\lambda \right)\frac{\partial V}{\partial Y}\right)\left[\frac{A_6{A}_2}{A_1{A}_4}\right]\\ +\mathrm{Pr}\left(\frac{A_5{A}_2}{A_1{A}_4}\right)\left(\frac{{\partial }^2\mathrm{\Omega }}{\partial Y^2}+\frac{{\partial }^2\mathrm{\Omega }}{\partial X^2}\right)\\ +\mathrm{Pr}\left[\frac{A_6{A}_2}{A_1{A}_4}\right]\left(-\frac{\partial V}{\partial X}{\left(\cos \lambda \right)}^2+{\left(\sin \lambda \right)}^2\frac{\partial U}{\partial Y}\right)H{a}^2\\ -\frac{\mathrm{Pr}}{Da}\mathrm{\Omega }\left(\frac{A_5{A}_2}{A_1{A}_4}\right)=\frac{\partial \mathrm{\Omega }}{\partial Y}V+U\frac{\partial \mathrm{\Omega }}{\partial X}.\end{array}(9)$

The dimensionless constants are defined as follows [20–24]:

$\begin{array}{l}{A}_6=\frac{{\sigma }_{nf}}{{\sigma }_f},A_2=\frac{{\left(\rho C_P\right)}_{nf}}{{\left(\rho C_P\right)}_f},A_1=\frac{{\rho }_{nf}}{{\rho }_f},A_3=\frac{{\left(\rho \beta \right)}_{nf}}{{\left(\rho \beta \right)}_f},A_4=\frac{k_{nf}}{k_f},Ha=L{B}_0\sqrt{{\sigma }_f/{\mu }_f},\\ Da=\frac{K}{L^2},Ra=g{\beta }_f{q}^{″}{L}^4/\left(k_f{\upsilon }_f{\alpha }_f\right),A_5=\frac{{\mu }_{nf}}{{\mu }_f},\mathrm{Pr}={\upsilon }_f/{\alpha }_f.\end{array}(10)$

Nusselt Number

For the hot body placed inside the enclosure, we use the following mathematical form for the computational purposes of the Nusselt number [20, 31]:

$N{u}_{ave}=\frac{1}{S}{\displaystyle \underset{0}{\overset{s}{\int }}N{u}_{loc}}ds,(11)$

where

$N{u}_{loc}=A_4\frac{1}{\Theta }.$

In the same way, the Nusselt number for the multiple bodies can be computed from the sum of all the Nusselt numbers for each hot body placed inside the enclosure.

Entropy Optimization

Entropy generation implies energy waste; henceforth, reducing entropy production is often a prime aim. It can be applied to recognize the source of wastefulness in any system and deliver opportunities for device or process design developments. The second Law of thermodynamics is used to scrutinize energy creating, changing, and consuming systems from a theoretical point of view. Because of irreversibility in the thermal dynamic process, entropy generation causes energy dissipation. Whenever heat and mass transfer are involved, entropy production minimization techniques are used in numerous sectors. The main goal is to save as much energy as possible while improving thermodynamic performance.

The entropy generated inside the enclosure is expressed in the following functional forms [43–45]:

$Be={\left(S_{gen,total}\right)}^{-1}{S}_{gen,th},(12)$

$X_d=T_0{S}_{gen,total},(13)$

$\begin{array}{l}{S}_{gen,total}=\underset{S_{gen,P}}{\underbrace{\frac{{\mu }_{nf}}{KT}\left(u^2+v^2\right)}}+\underset{S_{gen,M}}{\underbrace{\frac{{\sigma }_{nf}}{T}{B}_0^2{v}^2}}+\underset{S_{gen,f}}{\underbrace{\left[{\left(\frac{\partial v}{\partial x}+\frac{\partial u}{\partial y}\right)}^2+2\left({\left(\frac{\partial u}{\partial x}\right)}^2+{\left(\frac{\partial v}{\partial y}\right)}^2\right)\right]\frac{{\mu }_{nf}}{T}}}\\ +\underset{S_{gen,th}}{\underbrace{\left[{\left(T_y\right)}^2+{\left(T_x\right)}^2\right]T^{-2}{k}_{nf}}}.\end{array}(14)$

Numerical Technique and Validation of Results

Sheikholeslami [49] introduced a new technique Control Volume Finite Element Method (CVFEM) for the computation of numerical results. The consistency and reliability of this method has been reported in various references for different problems. In this study we have used the CVFEM procedure for the computation of the numerical results in which residual ranges up to 10⁻⁵. The results are obtained here are validated with Khanafer [72] shown in Figure 2. It is clear that as the values of $X$ increases from 0.018 up to 0.11 our results approaching towards the already available results, and at $X=0.26$ both the results are the same. The dimensionless temperature show an increase at the initial and intermediate values of $X$, while at the larger values of $X$ this effect is very small. Both the results show a good agreement.

FIGURE 2

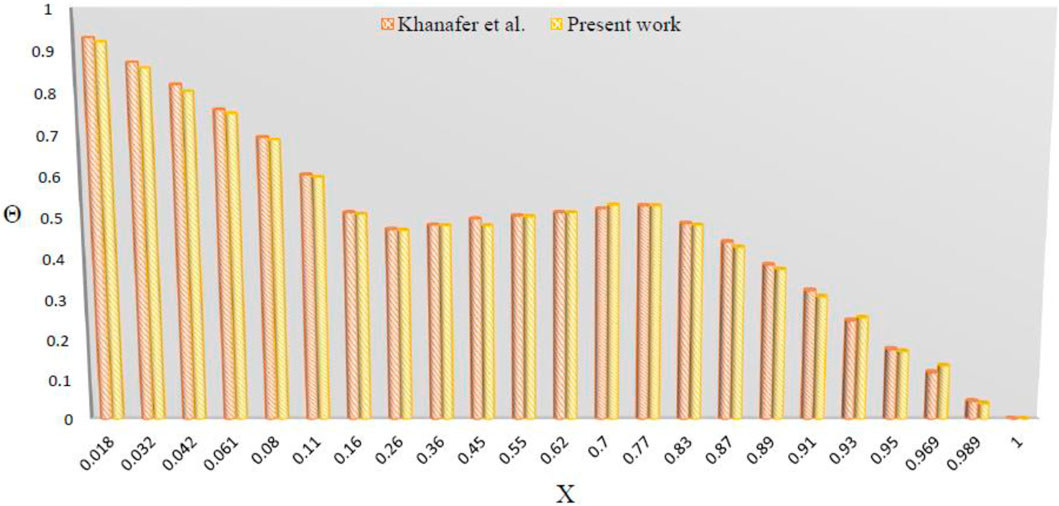
FIGURE 2. Code verification according to [31].

Results and Discussion

In the occurrence of a uniform magnetic field and irreversibility effect the heat transmission analysis has been studied through CVFEM. The validation of the results obtained is discussed in the above section. In this study we have used the range $Ra={10}^n\text{ for }n=\mathrm{3,4,5}$ for Rayleigh number, $Ha=n\left(10\right);\text{ for }n=\mathrm{0,2,4,6}$ for Hartmann number at $\varphi =0.04,Ha=1,Da=100,\varphi =0.04,Ra={10}^5,Da=100,$ and $Da=0.001\text{ to }100$ and $\varphi =0.04,Ra={10}^5,Ha=1,$ for the computation of the Nusselt number $N{u}_{ave}$ and the Bejan number $Be.$

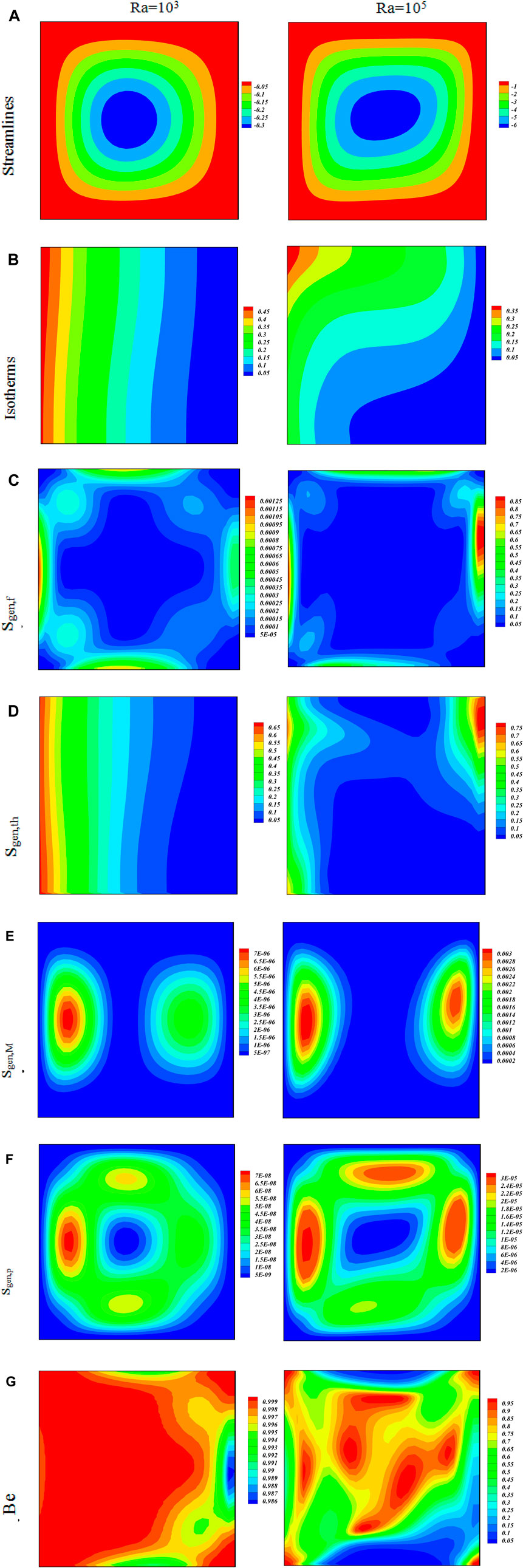
The variations in the Bejan number caused by the irreversibility effect under the impact of the Rayleigh parameter are plotted through isotherms and streamlines in Figures 3A–G. From these diagrams; it is clear that the nanofluid inside the enclosure is affected by the buoyancy and Lorentz forces. Figures 3A, B, consisting of four subplots, in the form of isotherms and streamlines during the nanofluid convective flow in the presence and absence of radiation effect for various values of the Rayleigh number (10³ and 10⁵). Graphs are plotted in the form of two columns; whereas column one graphs represent the convective flow in the absence of the radiation effect, while on the other hand, the second column show the radiation effect as well as the convection effect. The buoyancy forces are directly linked with the Raleigh number, as a result, the increasing values of $Ra$ show less strength in the contours as compared to the smaller values of Ra as shown in Figures 3A, B. It is observed that larger or smaller values of $Ra$ (associated with buoyancy forces) cause to decline in the temperature of the hot wall, that further makes the inner (center) temperature inside the enclosure approximately uniform. This effect of uniformity inside the enclosure is more strengthened when the thermal radiations are included for the nanofluid flow. The smaller values of $Ra$ causing the heat to flow fast as compared to the higher values as clear from the isotherm shapes. Physically, $Ra$ is the function of Pr and Gr; when $Ra$ declines the product of Pr and Gr also declines, and as a result, the Prandtl number jumps that further enhances the heat transfer. The stream functions show its maximum value at the high intensity of the cavity. When the natural convection becomes stronger the distortion in the isotherms becomes more powerful. Therefore, it is clear that $Ha$ is a function of the stream that directly affects the nanofluid as exposed in the figure. The convection rate of the current is increasing with larger values of $Ra$, due to the efficacy of the buoyancy forces over the viscous forces. Since we have considered the circulation impact in this work, this effect pushing the cold fluid underneath and the hot fluid came to the rescue of the empty spaces, and as a result, the transfer of heat becomes dominant. In Figures 3C–F the irreversibility effect is plotted. In these plots, the main two forces affecting the irreversibility are the Lorentz and buoyancy forces. The natural convective flow is dominating at higher values of the buoyancy forces. On the other hand, the Lorentz forces are acting against the natural convection at higher values. In the ratio $\frac{H{a}^2}{Ra}\approx 1$ one of these two forces will be effective. The buoyancy forces are very effective in the case $\frac{H{a}^2}{Ra}<<1$ while the Lorentz forces become dominant when $\frac{H{a}^2}{Ra}>>1$. The increasing values of $Ha$ for all the values of $Ra$ make the transfer pure conductive. We know that $Ra$ is the function of Pr and Gr, when $Ra$ declines the Pr or Gr will jump up and as a result the conduction will be higher. This effect causes due to the buoyancy and Lorentz forces; that interact and the fluid flow becomes dominant over the convection rate. The impact of the higher values of the Rayleigh number pushes for the pure convection rate. Physically, to slow down the impact of the convection rate a higher magnetic parameter is required. It is due to the physical significance of the magnetic parameter that disturbs the flow patterns, and further causes the reduction in convection in the heat transfer case. In addition to this $Ha$ declines the stream function strength. Since $Ha$ is in direct relation with the magnetic field strength and inversely related to the dynamic viscosity and as a result the higher values of $Ha$ and a small amount of the Rayleigh number the $x-$ direction elongated wall totally represents the kinetic energy. As the values of $Ra$ increase, new smaller circles are produced and the already available cells elongate on the y-axis. From this physically we can say that the kinetic energy goes up as the values of $Ha$ increase.

FIGURE 3

FIGURE 3. Contour of streamlines, isotherms, irreversibility, and the Bejan Number changes at $\varphi =0.04,Ha=1,Da=100.$

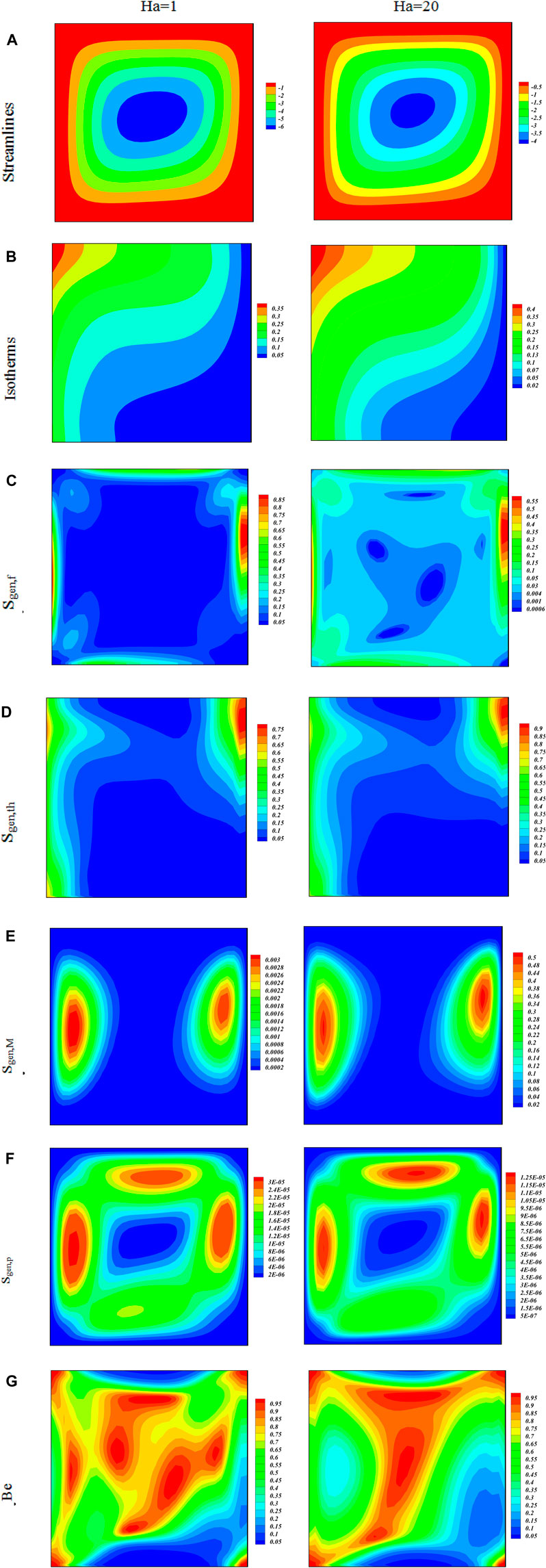
The variations in the Bejan number caused by the irreversibility effect under the impact of the Hartmann number with respect to the magnetic field influence on fluid flow and heat transfer are plotted through isotherms and streamlines in Figures 4A–G. The impact of the Hartmann number shows diverse shapes inside the body reported in Figure 4A. It is clear that the higher values of the Hartmann number reduce the strength of the nanofluid flow. The Isotherm effect of the Hartmann number on nanofluid flow is shown in Figure 4B. It shows that a higher value of Ha enhances the hybrid nanofluid flow motion. The effect of the Hartmann number on entropy generation is presented in Figures 3C–F. Graphs are plotted in the form of two columns, where different effects are observed for different values, and the results are clear from the graphs displayed. The entropy behavior with the effect of the Hartmann number is observed that entropy optimization is decreasing with higher values of the Hartmann number. The effect of the Bejan number weakens with a higher value of Ha, which is due to the reducing behavior of entropy.

FIGURE 4

FIGURE 4. Contour of streamlines, isotherms, irreversibility, and the Bejan Number changes at $\varphi =0.04,Ra={10}^5,Da=100.$

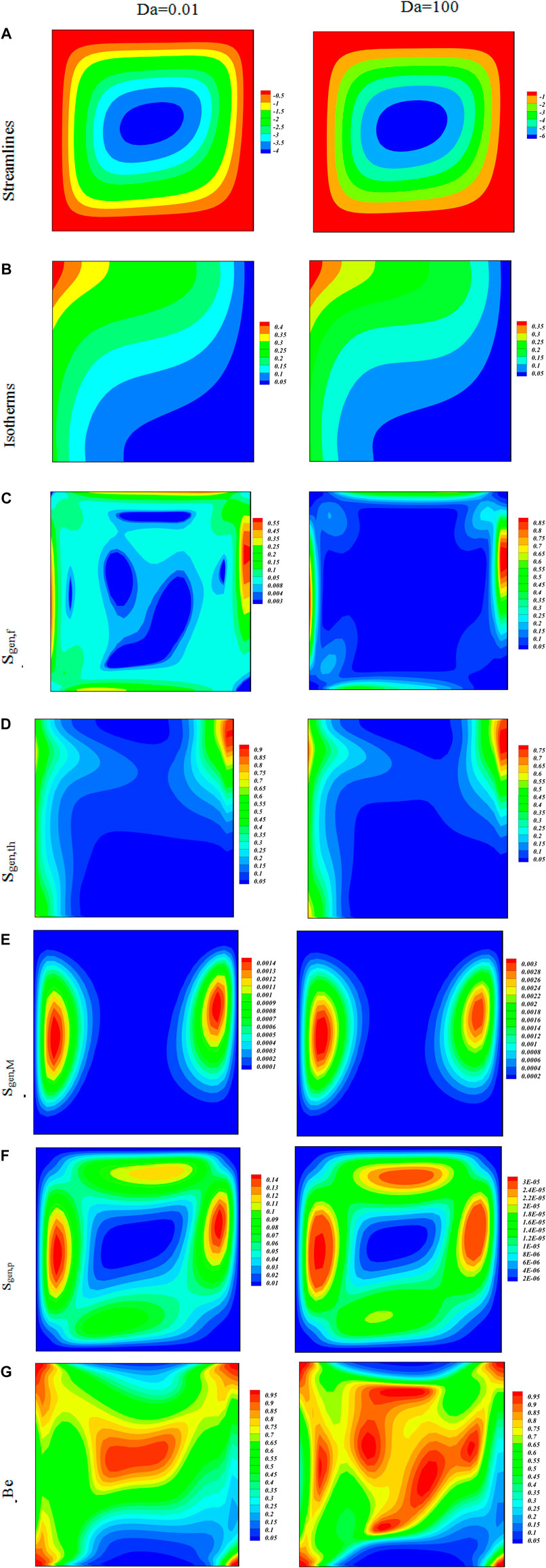
The variations in the Bejan number caused by the irreversibility effect under the impact of the Darcy number $Da=0.1$ and $Da=100$ are plotted through isotherms and streamlines in Figures 5A–G at $\varphi =0.04,Ra={10}^5,Ha=1$. The Streamlines and isotherms that are plotted show that the strength of vortexes augments with enhancing penetrability. Actually, the greater porous enclosure porousness permits the easy hybrid nanofluid movement, and hence the thermal energy transfer enhances. Darcy’s number is indirect relation to the permeability of the medium and is inversely related to the square of the characteristic length. This functional relation physically interprets that increasing the dimensionless value of Darcy’s number leads to an obvious increment in the permeability of the porous medium, which helps nanofluid to penetrate into the left layer leading to an increase in the convection heat transfer mode; because the conductive mode is dominant at low Darcy number. Also, it is obvious from the shape of the streamlines in the left layer as there are no inner cells that reflect low fluid flow strength. The fluid temperature drops with increasing medium porosity as displayed with isotherms plots. The entropy generation impact on Da is shown in different figures by their respective contours. It is observed that an increase in permeability enhances the entropy in different phases.

FIGURE 5

FIGURE 5. Contour of streamlines, isotherms, irreversibility, and the Bejan Number changes at $\varphi =0.04,Ra={10}^5,Ha=1.$

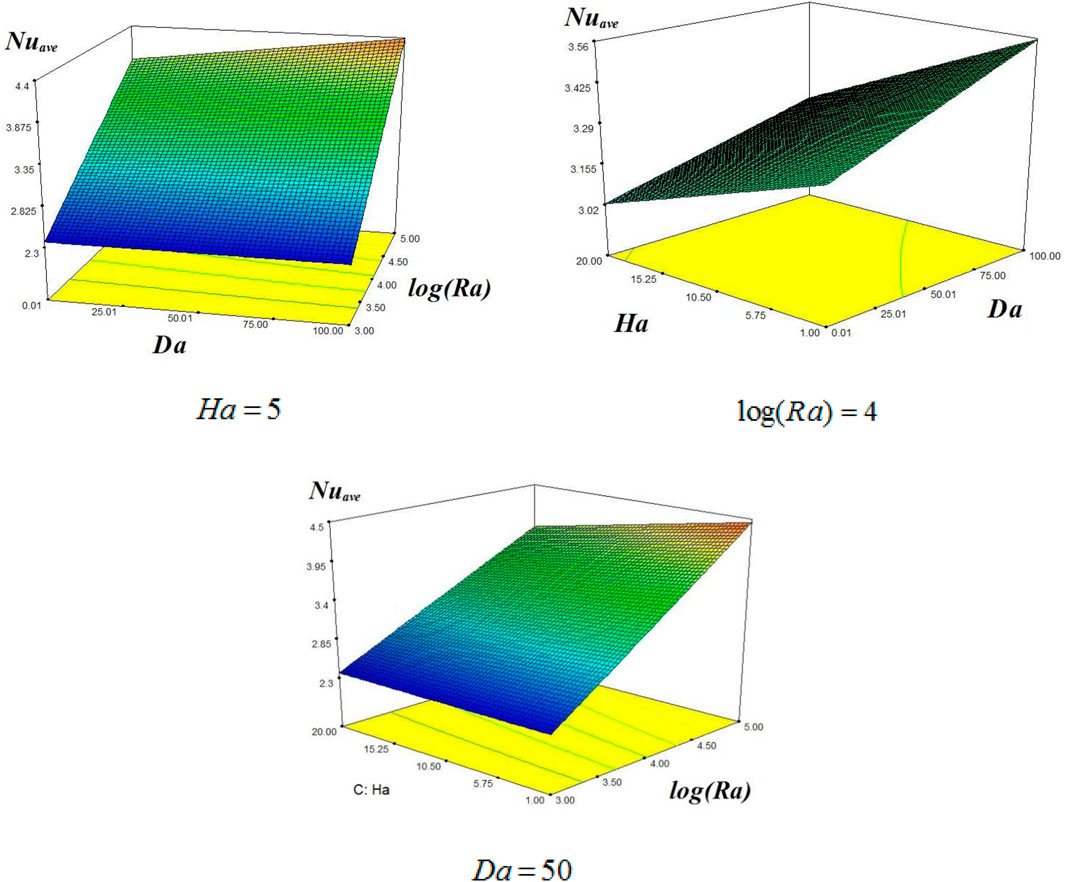
Figure 6 shows the local Nusselt number variation with the increasing distance along the y-direction at different values of Ra, Da, and Ha. This figure consists of three subfigures. The lowest value of $Ha$ and higher values of $Da$ it display concentric circles. When $Ha$ and $Da$ jumps up to $100$, these circles become flattened on both of the surfaces. It is clear that the presence of heat transfer augments the thermal energy transfer during the convective nanofluid motion. The subfigure shows that the value of the local Nusselt number is higher for larger values of Ra, as one moves away from the hotter wall. These relations are shown as

$\begin{array}{l}N{u}_{ave}=0.43\log \left(Ra\right)+0.37{\left\{\log \left(Ra\right)\right\}}^2-0.27Ha+0.18Da\\ -0.16\left(Ha\right)\left(Da\right)+0.23Da\left\{\log \left(Ra\right)\right\}-0.38Ha\left\{\log \left(Ra\right)\right\}+\mathrm{2.17.}\end{array}(15)$

FIGURE 6

FIGURE 6. Nu_ave values for different cases.

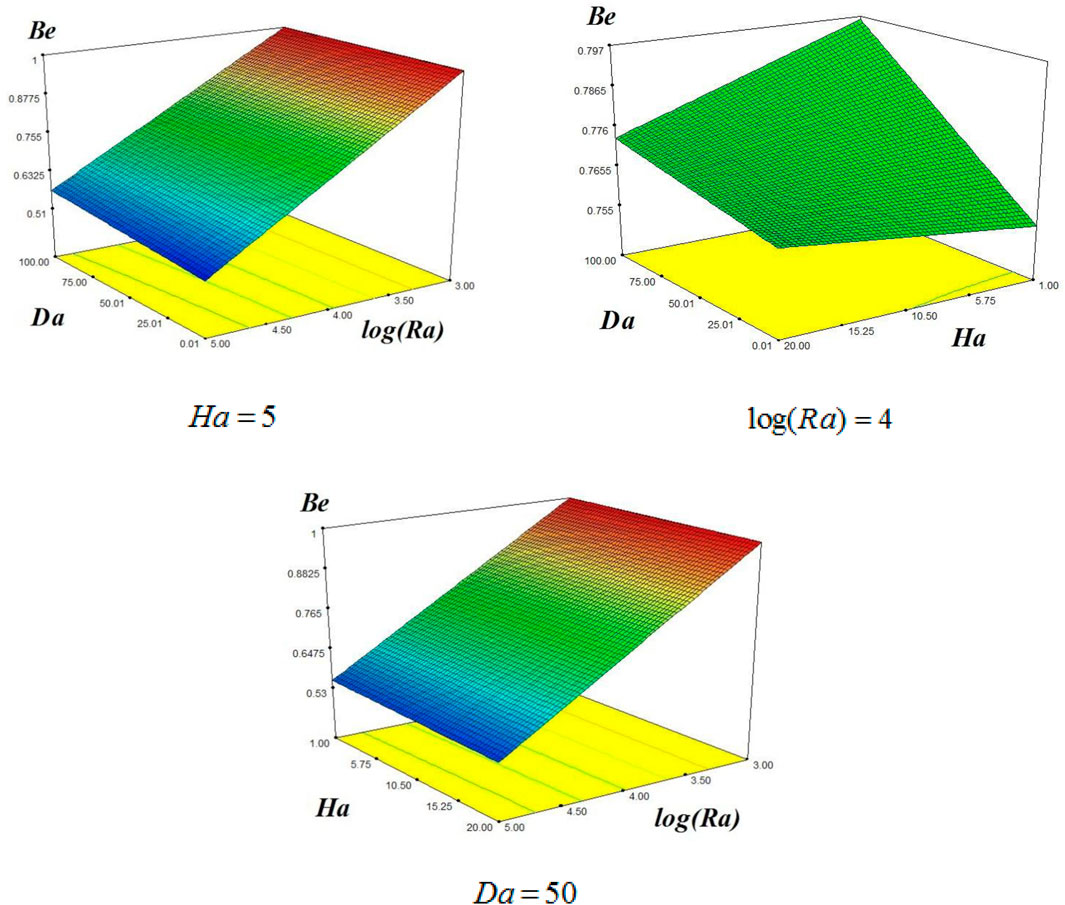
Figure 7 shows the Bejan number variation at different values of log(Ra) = 4, Da = 50 and Ha = 5. This figure consists of three subfigures. From these figures, it is observed that the higher Rayleigh number reduces the Bejan number, while there is no effect on Darcy’s number Da. In the second case, it is observed that the higher values of the Hartmann number enhance the Bejan number, while it reduces with Darcy’s number Da. In the third case, the Bejan number reduces with the enhancement of Ha at constant Ha.

FIGURE 7

FIGURE 7. Be values for different cases.

Conclusion

The main outcomes of this work are concluded as follows:

1. The heat transfer is enhanced with the increasing values of $Ra$ and nanofluid loading

2. The fluid flow is at its peak point when the inner object is placed near the down wall of the enclosure, but this effect is valid up to some threshold number

3. The entropy effect is mainly affected by the two forces: Lorentz and buoyancy

4. The buoyancy forces are very effective in the case $\raisebox{1ex}{$H{a}^2$}\!\left/ \!\raisebox{-1ex}{$Ra$}\right.<<1$, while Lorentz forces become dominant when $\raisebox{1ex}{$H{a}^2$}\!\left/ \!\raisebox{-1ex}{$Ra$}\right.>>1$

5. The increasing values of the magnetic parameter disturb the flow pattern that further affects the flow of the fluid in the heat transfer case

6. The Nusselt number variations along the y-axis near the hot wall enhance the heat transfer for the increasing values of $Ra$

7. Furthermore, the Nusselt number vary directly with the larger values of $Ra$ and inversely to $Ha$

8. The impact of the magnetic parameter inside the enclosure is fully influenced by the Rayleigh number, Nusselt number, and Hartmann number to fully control the convection

Data Availability Statement

The raw data supporting the conclusion of this article will be made available by the authors, without undue reservation.

Author Contributions

All authors listed have made a substantial, direct, and intellectual contribution to the work and approved it for publication.

Funding

This project was financed by Lucian Blaga University of Sibiu and Hasso Plattner Foundation research grants LBUS-IRG-2021-07.

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s Note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors, and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

1. Chu Y-M, Yadav D, Shafee A, Li Z, Bach Q-V. Influence of Wavy Enclosure and Nanoparticles on Heat Release Rate of PCM Considering Numerical Study. J Mol Liquids (2020) 319:114121. doi:10.1016/j.molliq.2020.114121

CrossRef Full Text | Google Scholar

2. Sheikholeslami M, Farshad SA. Nanoparticles Transportation with Turbulent Regime through a Solar Collector with Helical tapes. Adv Powder Tech (2022) 33(3):103510. doi:10.1016/j.apt.2022.103510

CrossRef Full Text | Google Scholar

3. Ghasemi B, Aminossadati SM, Raisi A. Magnetic Field Effect on Natural Convection in a Nanofluid-Filled Square Enclosure. Int J Therm Sci (2011) 50(9):1748–56. doi:10.1016/j.ijthermalsci.2011.04.010

CrossRef Full Text | Google Scholar

4. Bouhalleb M, Abbassi H. Natural Convection in an Inclined Rectangular Enclosure Filled by CuO-H2o Nanofluid, with Sinusoidal Temperature Distribution. Int J Hydrogen Energ (2015) 40(39):13676–84. doi:10.1016/j.ijhydene.2015.04.090

CrossRef Full Text | Google Scholar

5. Mahmoudi AH, Pop I, Shahi M. Effect of Magnetic Field on Natural Convection in a Triangular Enclosure Filled with Nanofluid. Int J Therm Sci (2012) 59:126–40. doi:10.1016/j.ijthermalsci.2012.04.006

CrossRef Full Text | Google Scholar

6. Ghasemi B, Aminossadati SM. Brownian Motion of Nanoparticles in a Triangular Enclosure with Natural Convection. Int J Therm Sci (2010) 49(6):931–40. doi:10.1016/j.ijthermalsci.2009.12.017

CrossRef Full Text | Google Scholar

7. Saleh H, Roslan R, Hashim I. Natural Convection Heat Transfer in a Nanofluid-Filled Trapezoidal Enclosure. Int J Heat Mass Transfer (2011) 54(1-3):194–201. doi:10.1016/j.ijheatmasstransfer.2010.09.053

CrossRef Full Text | Google Scholar

8. Hussein AK, Mustafa AW. Natural Convection in Fully Open Parallelogrammic Cavity Filled with Cu-Water Nanofluid and Heated Locally from its Bottom wall. Therm Sci Eng Prog (2017) 1:66–77. doi:10.1016/j.tsep.2017.03.002

CrossRef Full Text | Google Scholar

9. Cho C-C, Chen C-L, Chen Co.-K. Natural Convection Heat Transfer and Entropy Generation in Wavy-wall Enclosure Containing Water-Based Nanofluid. Int J Heat Mass Transfer (2013) 61:749–58. doi:10.1016/j.ijheatmasstransfer.2013.02.044

CrossRef Full Text | Google Scholar

10. Sadeghi MS, Tayebi T, Dogonchi AS, Armaghani T, Talebizadehsardari P. Analysis of Hydrothermal Characteristics of Magnetic Al2O3‐H2O Nanofluid within a Novel Wavy Enclosure during Natural Convection Process Considering Internal Heat Generation. Math Methods Appl Sci (2020):1–13. doi:10.1002/mma.6520

CrossRef Full Text | Google Scholar

11. You J, Lee KJ. Pore-Scale Study to Analyze the Impacts of Porous Media Heterogeneity on Mineral Dissolution and Acid Transport Using Darcy-Brinkmann-Stokes Method. Transp Porous Med (2021) 137(3):575–602. doi:10.1007/s11242-021-01577-3

CrossRef Full Text | Google Scholar

12. Sheikholeslami M, Said Z, Jafaryar M. Hydrothermal Analysis for a Parabolic Solar Unit with Wavy Absorber Pipe and Nanofluid. Renew Energ (2022) 188:922–32. doi:10.1016/j.renene.2022.02.086

CrossRef Full Text | Google Scholar

13. Ahmed SE, Rashed ZZ. MHD Natural Convection in a Heat Generating Porous Medium-Filled Wavy Enclosures Using Buongiorno's Nanofluid Model. Case Stud Therm Eng (2019) 14:100430. doi:10.1016/j.csite.2019.100430

CrossRef Full Text | Google Scholar

14. Izadi M, Mohebbi R, Sajjadi H, Delouei AA. LTNE Modeling of Magneto-Ferro Natural Convection inside a Porous Enclosure Exposed to Nonuniform Magnetic Field. Physica A: Stat Mech its Appl (2019) 535:122394. doi:10.1016/j.physa.2019.122394

CrossRef Full Text | Google Scholar

15. Kadhim HT, Jabbar FA, Rona A. Cu-Al2O3 Hybrid Nanofluid Natural Convection in an Inclined Enclosure with Wavy walls Partially Layered by Porous Medium. Int J Mech Sci (2020) 186:105889. doi:10.1016/j.ijmecsci.2020.105889

CrossRef Full Text | Google Scholar

16. Mehryan SAM, Ghalambaz M, Chamkha AJ, Izadi M. Numerical Study on Natural Convection of Ag-MgO Hybrid/water Nanofluid inside a Porous Enclosure: A Local thermal Non-equilibrium Model. Powder Tech (2020) 367:443–55. doi:10.1016/j.powtec.2020.04.005

CrossRef Full Text | Google Scholar

17. Mejri I, Mahmoudi A, Abbassi MA, Omri A. Magnetic Field Effect on Entropy Generation in a Nanofluid-Filled Enclosure with Sinusoidal Heating on Both Side walls. Powder Tech (2014) 266:340–53. doi:10.1016/j.powtec.2014.06.054

CrossRef Full Text | Google Scholar

18. Oztop HF, Oztop M, Varol Y. Numerical Simulation of Magnetohydrodynamic Buoyancy-Induced Flow in a Non-isothermally Heated Square Enclosure. Commun Nonlinear Sci Numer Simulation (2009) 14(3):770–8. doi:10.1016/j.cnsns.2007.11.005

CrossRef Full Text | Google Scholar

19. Kahveci K, Öztuna S. A Differential Quadrature Solution of MHD Natural Convection in an Inclined Enclosure with a Partition. J Fluids Eng (2008) 130(2). doi:10.1115/1.2829567

CrossRef Full Text | Google Scholar

20. Kim BS, Lee DS, Ha MY, Yoon HS. A Numerical Study of Natural Convection in a Square Enclosure with a Circular cylinder at Different Vertical Locations. Int J Heat mass transfer (2008) 51(7-8):1888–906. doi:10.1016/j.ijheatmasstransfer.2007.06.033

CrossRef Full Text | Google Scholar

21. Lee JM, Ha MY, Yoon HS. Natural Convection in a Square Enclosure with a Circular cylinder at Different Horizontal and diagonal Locations. Int J Heat Mass Transfer (2010) 53(25-26):5905–19. doi:10.1016/j.ijheatmasstransfer.2010.07.043

CrossRef Full Text | Google Scholar

22. Miles A, Bessaïh R. Heat Transfer and Entropy Generation Analysis of Three-Dimensional Nanofluids Flow in a Cylindrical Annulus Filled with Porous media. Int Commun Heat Mass Transfer (2021) 124:105240. doi:10.1016/j.icheatmasstransfer.2021.105240

CrossRef Full Text | Google Scholar

23. Yoon HS, Jung JH, Park YG. Natural Convection in a Square Enclosure with Two Horizontal Cylinders. Numer Heat Transfer, A: Appl (2012) 62(9):701–21. doi:10.1080/10407782.2012.709438

CrossRef Full Text | Google Scholar

24. Kefayati GR, Tang H. Lattice Boltzmann Simulation of Viscoplastic Fluids on Natural Convection in an Inclined Enclosure with Inner Cold Circular/elliptical Cylinders (Part I: One cylinder). Int J Heat mass transfer (2018) 123:1138–62. doi:10.1016/j.ijheatmasstransfer.2018.01.139

CrossRef Full Text | Google Scholar

25. Roy NC. Natural Convection of Nanofluids in a Square Enclosure with Different Shapes of Inner Geometry. Phys Fluids (2018) 30(11):113605. doi:10.1063/1.5055663

CrossRef Full Text | Google Scholar

26. Wang Z, Wang T, Xi G, Huang Z. Periodic Unsteady Natural Convection in Square Enclosure Induced by Inner Circular cylinder with Different Vertical Locations. Int Commun Heat Mass Transfer (2021) 124:105250. doi:10.1016/j.icheatmasstransfer.2021.105250

CrossRef Full Text | Google Scholar

27. Bhowmick D, Chakravarthy S, Randive PR, Pati S. Numerical Investigation on the Effect of Magnetic Field on Natural Convection Heat Transfer from a Pair of Embedded Cylinders within a Porous Enclosure. J Therm Anal Calorim (2020) 141(6):2405–27. doi:10.1007/s10973-020-09411-6

CrossRef Full Text | Google Scholar

28. Alsabery AI, Tayebi T, Kadhim HT, Ghalambaz M, Hashim I, Chamkha AJ. Impact of Two-phase Hybrid Nanofluid Approach on Mixed Convection inside Wavy Lid-Driven Cavity Having Localized Solid Block. J Adv Res (2021) 30:63–74. doi:10.1016/j.jare.2020.09.008

PubMed Abstract | CrossRef Full Text | Google Scholar

29. Keramat F, Azari A, Rahideh H, Abbasi M. A CFD Parametric Analysis of Natural Convection in an H-Shaped Cavity with Two-Sided Inclined Porous Fins. J Taiwan Inst Chem Eng (2020) 114:142–52. doi:10.1016/j.jtice.2020.09.011

CrossRef Full Text | Google Scholar

30. Ma Y, Mohebbi R, Rashidi MM, Yang Z. Effect of Hot Obstacle Position on Natural Convection Heat Transfer of MWCNTs-Water Nanofluid in U-Shaped Enclosure Using Lattice Boltzmann Method. Int J Numer Methods Heat Fluid flow (2018) 29(1):223–50. doi:10.1108/hff-01-2018-0004

CrossRef Full Text | Google Scholar

31. Mohebbi R, Izadi M, Chamkha AJ. Heat Source Location and Natural Convection in a C-Shaped Enclosure Saturated by a Nanofluid. Phys Fluids (2017) 29(12):122009. doi:10.1063/1.4993866

CrossRef Full Text | Google Scholar

32. Armaghani T, Chamkha A, Rashad AM, Mansour MA. Inclined Magneto: Convection, Internal Heat, and Entropy Generation of Nanofluid in an I-Shaped Cavity Saturated with Porous media. J Therm Anal Calorim (2020) 142(6):2273–85. doi:10.1007/s10973-020-09449-6

CrossRef Full Text | Google Scholar

33. Ma Y, Mohebbi R, Rashidi MM, Yang Z, Sheremet M. Nanoliquid thermal Convection in I-Shaped Multiple-Pipe Heat Exchanger under Magnetic Field Influence. Physica A: Stat Mech its Appl (2020) 550:124028. doi:10.1016/j.physa.2019.124028

CrossRef Full Text | Google Scholar

34. Sheikholeslami M, Ebrahimpour Z. Thermal Improvement of Linear Fresnel Solar System Utilizing Al2O3-Water Nanofluid and Multi-Way Twisted Tape. Int J Therm Sci (2022) 176:107505. doi:10.1016/j.ijthermalsci.2022.107505

CrossRef Full Text | Google Scholar

35. Chu Y-M, Salahshoor Z, Shahraki MS, Shafee A, Bach Q-V. Annulus Shape Tank with Convective Flow in a Porous Zone with Impose of MHD. Int J Mod Phys C (2020) 31:2050168. doi:10.1142/S0129183120501685

CrossRef Full Text | Google Scholar

36. Succi S, Foti E, Higuera F. Three-dimensional Flows in Complex Geometries with the Lattice Boltzmann Method. Europhys Lett (1989) 10(5):433–8. doi:10.1209/0295-5075/10/5/008

CrossRef Full Text | Google Scholar

37. Sheikholeslami M. Numerical Investigation of Solar System Equipped with Innovative Turbulator and Hybrid Nanofluid. Solar Energ Mater Solar Cell (2022) 243:111786. doi:10.1016/j.solmat.2022.111786

CrossRef Full Text | Google Scholar

38. Qu S, Zhao L, Xiong Z. Cross-layer Congestion Control of Wireless Sensor Networks Based on Fuzzy Sliding Mode Control. Neural Comput Applic (2020) 32(17):13505–20. doi:10.1007/s00521-020-04758-1

CrossRef Full Text | Google Scholar

39. Su F, Jia Q, Li Z, Wang M, He L, Peng D, Song Y, Zhang Z, Fang S. Aptamer-templated Silver Nanoclusters Embedded in Zirconium Metal-Organic Framework for Targeted Antitumor Drug Delivery. Microporous mesoporous Mater (2019) 275:152–62. doi:10.1016/j.micromeso.2018.08.026

CrossRef Full Text | Google Scholar

40. Wu C, Wang X, Chen M, Kim MJ. Differential Received Signal Strength Based RFID Positioning for Construction Equipment Tracking. Adv Eng Inform (2019) 42:100960. doi:10.1016/j.aei.2019.100960

CrossRef Full Text | Google Scholar

41. Rashidi MM, Mohammadi F, Abbasbandy S, Alhuthali MS. Entropy Generation Analysis for Stagnation point Flow in a Porous Medium over a Permeable Stretching Surface. Jafm (2015) 8(4):753–65. doi:10.18869/acadpub.jafm.67.223.22916

CrossRef Full Text | Google Scholar

42. Rashidi MM, Nasiri M, Shadloo MS, Yang Z. Entropy Generation in a Circular Tube Heat Exchanger Using Nanofluids: Effects of Different Modeling Approaches. Heat Transfer Eng (2017) 38(9):853–66. doi:10.1080/01457632.2016.1211916

CrossRef Full Text | Google Scholar

43. Ali Abbas M, Anwar Bég O, Zeeshan A, Hobiny A, Bhatti MM. Parametric Analysis and Minimization of Entropy Generation in Bioinspired Magnetized Non-newtonian Nanofluid Pumping Using Artificial Neural Networks and Particle Swarm Optimization. Therm Sci Eng Prog (2021) 24:100930. doi:10.1016/j.tsep.2021.100930

CrossRef Full Text | Google Scholar

44. Bhatti MM, Abbas MA, Rashidi MM. Entropy Generation for Peristaltic Blood Flow with Casson Model and Consideration of Magnetohydrodynamics Effects. Walailak J Sci Tech (Wjst) (2017) 14(6):451–61.

Google Scholar

45. Abbas MA, Ahmed B, Chen L, Rehman SU, Saleem M, Khudair WS. Analysis of Entropy Generation on Magnetohydrodynamic Flow with Mixed Convection through Porous Media. Energies (2022) 15(3):1206. doi:10.3390/en15031206

CrossRef Full Text | Google Scholar

46. Ahmed B, Abbas MA, Rehman SU, Saleem M. Numerical Investigation of Entropy Generation on MHD Flow of Micropolar Fluid over a Stretching Sheet in the Presence of a Porous Medium. Waves in Random and Complex Media (2022) 1–15. doi:10.1080/17455030.2022.2055202

CrossRef Full Text | Google Scholar

47. Abbas MA, Hussain I. Analysis of Regression and Correlation of Entropy Generation of Nanofluid in the MHD Peristaltic Flow. City Univ Int J Comput Anal (2017) 1(1):01–9.

Google Scholar

48. Abbas IA, El-Amin MF, Salama A. Effect of thermal Dispersion on Free Convection in a Fluid Saturated Porous Medium. Int J Heat Fluid Flow (2009) 30(2):229–36. doi:10.1016/j.ijheatfluidflow.2009.01.004

CrossRef Full Text | Google Scholar

49. Sheikholeslami M. New Computational Approach for Exergy and Entropy Analysis of Nanofluid under the Impact of Lorentz Force through a Porous media. Comp Methods Appl Mech Eng (2019) 344:319–33. doi:10.1016/j.cma.2018.09.044

CrossRef Full Text | Google Scholar

50. Chu Y-M, Hajizadeh MR, Li Z, Bach Q-V. Investigation of Nano Powders Influence on Melting Process within a Storage Unit. J Mol Liquids (2020) 318(15 November 2020):114321. doi:10.1016/j.molliq.2020.114321

CrossRef Full Text | Google Scholar

51. Luo Y, Xie Y, Jiang H, Chen Y, Zhang L, Sheng X, Xie D, Wu H, Mei Y. Flame-retardant and Form-Stable Phase Change Composites Based on MXene with High Thermostability and thermal Conductivity for thermal Energy Storage. Chem Eng J (20211996) 420:130466. doi:10.1016/j.cej.2021.130466

CrossRef Full Text | Google Scholar

52. Chu Y-M, Almusawi MB, Hajizadeh MR, Yao S-W, Bach Q-V. Hybrid Nanomaterial Treatment within a Permeable Tank Considering Irreversibility. Int J Mod Phys C (2021) 32:2150061. doi:10.1142/S0129183121500613

CrossRef Full Text | Google Scholar

53. Chu Y-M, Shankaralingappa BM, Gireesha BJ, Alzahrani F, Khan MI, Khan SU. Combined Impact of Cattaneo-Christov Double Diffusion and Radiative Heat Flux on Bio-Convective Flow of Maxwell Liquid Configured by a Stretched Nano-Material Surface. Appl Math Comput (2022) 419:126883. doi:10.1016/j.amc.2021.126883

CrossRef Full Text | Google Scholar

54. Chu YM, Bilal S, Hajizadeh MR. Hybrid Ferrofluid along with MWCNT for Augmentation of thermal Behavior of Fluid during Natural Convection in a Cavity. Math Meth Appl Sci (2020) 1–12. doi:10.1002/mma.6937

CrossRef Full Text | Google Scholar

55. Yang D-X, Wang P-F, Liu H-Y, Zhang Y-H, Sun P-P, Shi F-N. Facile Synthesis of Ternary Transition Metal-Organic Framework and its Stable Lithium Storage Properties. J Solid State Chem (2022) 309:122947. doi:10.1016/j.jssc.2022.122947

CrossRef Full Text | Google Scholar

56. Li J, Alawee WH, Rawa MJH, Dhahad HA, Chu Y-M, Issakhov A, et al. Heat Recovery Application of Nanomaterial with Existence of Turbulator. J Mol Liquids (2021) 326:115268. doi:10.1016/j.molliq.2020.115268

CrossRef Full Text | Google Scholar

57. Chu Y-M, Nazir U, Sohail M, Selim MM, Lee J-R. Enhancement in thermal Energy and Solute Particles Using Hybrid Nanoparticles by Engaging Activation Energy and Chemical Reaction over a Parabolic Surface via Finite Element Approach. Fractal Fract (2021) 5(3):119. doi:10.3390/fractalfract5030119

CrossRef Full Text | Google Scholar

58. Chu Y-M, Abu-Hamdeh NH, Ben-Beya B, Hajizadeh MR, Li Z, Bach Q-V. Nanoparticle Enhanced PCM Exergy Loss and thermal Behavior by Means of FVM. J Mol Liquids (2020) 320:114457. doi:10.1016/j.molliq.2020.114457

CrossRef Full Text | Google Scholar

59. Guo Z, Yang J, Tan Z, Tian X, Wang Q. Numerical Study on Gravity-Driven Granular Flow Around Tube out-wall: Effect of Tube Inclination on the Heat Transfer. Int J Heat mass transfer (2021) 174:121296. doi:10.1016/j.ijheatmasstransfer.2021.121296

CrossRef Full Text | Google Scholar

60. Chu Y-M, Salehi F, Jafaryar M, Bach Q-V. Simulation Based on FVM for Influence of Nanoparticles on Flow inside a Pipe Enhanced with Helical tapes. Appl Nanosci (2020). doi:10.1007/s13204-020-01583-9

CrossRef Full Text | Google Scholar

61. Chu YM, Bashir S, Ramzan M, Malik MY. Model‐based Comparative Study of Magnetohydrodynamics Unsteady Hybrid Nanofluid Flow between Two Infinite Parallel Plates with Particle Shape Effects. Math Methods App Sci (2022). doi:10.1002/mma.8234

CrossRef Full Text | Google Scholar

62. Wang T, Almarashi A, Al-Turki YA, Abu-Hamdeh NH, Hajizadeh MR, Chu Y-M. Approaches for Expedition of Discharging of PCM Involving Nanoparticles and Radial Fins. J Mol Liquids (2021) 329:115052. doi:10.1016/j.molliq.2020.115052

CrossRef Full Text | Google Scholar

63. Yu D, Wang R. An Optimal Investigation of Convective Fluid Flow Suspended by Carbon Nanotubes and Thermal Radiation Impact. Mathematics (2022) 10(9):1542. doi:10.3390/math10091542

CrossRef Full Text | Google Scholar

64. Chu Y-M, Li Z, Bach Q-V. Application of Nanomaterial for thermal Unit Including Tube Fitted with Turbulator. Appl Nanosci (2020). doi:10.1007/s13204-020-01587-5

CrossRef Full Text | Google Scholar

65. Xiong Q-M, Chen Z, Huang J-T, Zhang M, Song H, Hou X-F, Li X-B, Feng Z-J. Preparation, Structure and Mechanical Properties of Sialon Ceramics by Transition Metal-Catalyzed Nitriding Reaction. Rare Met (2020) 39(5):589–96. doi:10.1007/s12598-020-01385-6

CrossRef Full Text | Google Scholar

66. Chu Y-M, Kumar R, Bach Q-V. Water-based Nanofluid Flow with Various Shapes of Al2O3 Nanoparticles Owing to MHD inside a Permeable Tank with Heat Transfer. King Abdulaziz: Applied Nanoscience (2020). doi:10.1007/s13204-020-01609-2

CrossRef Full Text | Google Scholar

67. Iqbal SA, Hafez MG, Hafez MG, Chu Y-M, Park C. Dynamical Analysis of Nonautonomous Rlc Circuit with the Absence and Presence of Atangana-Baleanu Fractional Derivative. jaac (2022) 12(2):770–89. doi:10.11948/20210324

CrossRef Full Text | Google Scholar

68. Gong D, Wei C, Xie D, Tang Y. Ultrasmall Antimony Nanodots Embedded in Carbon Nanowires with Three-Dimensional Porous Structure for High-Performance Potassium Dual-Ion Batteries. Chem Eng J (2022) 431:133444. doi:10.1016/j.cej.2021.133444

CrossRef Full Text | Google Scholar

69. Li F, Almarashi A, Jafaryar M, Hajizadeh MR, Chu Y-M. Melting Process of Nanoparticle Enhanced PCM through Storage cylinder Incorporating Fins. Powder Tech (2021) 381:551–60.

CrossRef Full Text | Google Scholar

70. Yang S, Tan J, Chen B. Robust Spike-Based Continual Meta-Learning Improved by Restricted Minimum Error Entropy Criterion. Entropy (2022) 24(4):455. doi:10.3390/e24040455

PubMed Abstract | CrossRef Full Text | Google Scholar

71. Chu Y-M, Bach Q-V. Application of TiO2 Nanoparticle for Solar Photocatalytic Oxidation System. King Abdulaziz: Applied Nanoscience (2020). doi:10.1007/s13204-020-01614-5

CrossRef Full Text | Google Scholar

72. Khanafer K, Vafai K, Lightstone M. Buoyancy-driven Heat Transfer Enhancement in a Two-Dimensional Enclosure Utilizing Nanofluids. Int J Heat mass transfer (2003) 46(19):3639–53. doi:10.1016/s0017-9310(03)00156-x

CrossRef Full Text | Google Scholar