Underwater Transmitted Wavefront Manipulation Based on Bubble-Arrayed Acoustic Metasurfaces

Manipulating underwater acoustic waves along the prescribed trajectory has great potential for various applications. Traditional metasurfaces for underwater acoustic modulation usually have complex structural designs and are complicated to manufacture. Here, we propose a simple strategy of embedding air bubbles of different sizes inside the polymer to freely manipulate the transmitted underwater acoustic wavefields. The transmitted phase shift covers the entire $2\pi$ range by adjusting the diameter of the bubbles. Utilizing the air-bubble array with precisely designed phase profiles, the abnormal refraction, self-bending beams, and bottle beams are univocally demonstrated based on the generalized Snell’s law. Our study can be used for designing waterborne metasurfaces with simple structures to freely manipulate the transmitted wavefronts and inspire lots of applications for underwater explorations.

Introduction

As a kind of artificial microstructure material, metamaterial has exotic physical properties that are not seen in traditional materials, such as negative refractive index [1] and negative density [2]. Conventional metamaterials are usually limited by bulky structures and complicated manufacturing processes. To modulate waves in 2D scales, the concept of metasurfaces was proposed in optics [3] based on the generalized Snell’s law (GSL) [4]. With the advantage of ultrathin and lightweight compact structure, the acoustic metasurface has also attracted broad attention in the past decade [5–10]. By intriguingly designing the functional units, multiple functionalities can be realized, such as abnormal reflection [11, 12], negative refraction [13, 14], beam focusing [15], vortex sources and perfect absorption [16–19], and self-bending beams [20]. Li et al. [21] proposed the ultrathin planar acoustic metasurfaces with the phase shifts spanning over a full $2\pi$ range to realize the reflected wave manipulation, which expanded metasurfaces from the optics to the regime of acoustics. Subsequently, by coiling up the space, Xie et al. [22] presented a transmitted acoustic metasurface composed of tapered labyrinthine metamaterials maintaining a uniform subwavelength thickness, which realized complex modulations, beam-steering, and abnormal refraction through higher-order diffractions. Zhu et al. [23] introduced helical-structured metamaterials by adjusting the helicity of functional units to generate dispersion-free self-bending of sound beams. The helical-structured airborne metamaterials have successfully led to achievable enhanced wave–matter interaction. By designing the initial phase and the amplitude profiles of the speak array, Zhang et al. [24] also proposed a recipe to realize acoustic self-bending and bottle beams propagating along the prescribed trajectories in air. Recently, Li et al. [25] introduced metasurfaces into the water environment. They designed a 3D gradient-index phononic crystal (GRIN PC) lens with numerous concentric torus air holes. It was verified theoretically and experimentally that the GRIN PC could control the propagation of transmitted waves and realize the waves focusing in water. Combining the diffraction theory and an optimization method, Zhou et al. [26] proposed a high-efficiency ultrathin nonlocal waterborne acoustic metasurface to generalize anomalous reflection with different reflected angles. However, underwater acoustic metamaterials or metasurfaces are usually extremely complicated and difficult to manufacture. Thus, developing new methods for engineering underwater acoustic wavefronts with simple structures is significant and useful.

In this article, we propose the bubble-arrayed acoustic metasurface (BAAM) by introducing air holes into the functional unit to manipulate the transmitted wave. First, a perforated unit cell with an air bubble inside a square structure was constructed. Second, we designed a bubble array functional unit composed of nine air bubbles with a diameter D. By changing the diameter D, the phase shift of $2\pi$ can be covered with a high transmission ratio. Lastly, based on the GSL, we performed three cases of the transmitted wavefield manipulation: abnormal refraction, Bezier beams, and acoustic bottle beams. To explore the frequency response of the BAAM, the numerical simulations were conducted using finite element analysis, which showed good agreement with the theoretical results. Compared with the traditional transmitted waterborne metasurfaces, the BAAM has the advantages of simple design and a flexible fabrication process. The present study can provide a new method to achieve elegant modulation of the transmitted wavefront and underwater explorations with a simple metasurface structure.

Design of the BAAM With Perforated Functional Units

Theoretical Foundation

When an acoustic wave with an incident angle ${\theta }_i$ impinges on an arbitrary planar interface with two different media owning refractive indexes ($n_i$ and $n_t$), the reflected angle ${\theta }_r$ will be identical to ${\theta }_i$, and the refracted angle ${\theta }_t$ will be determined by ${\theta }_i$, $n_i$, and $n_t$, which is the classical Snell’s law. However, when there exists a phase gradient at the interface, one can obtain the generalized Snell’s law:

$\begin{array}{c}\sin \left({\theta }_r\right)-\sin \left({\theta }_i\right)=\frac{{\lambda }_i}{2\pi }\frac{d\phi \left(y\right)}{dy},\end{array}(1)$

$\begin{array}{c}\frac{\text{sin}\left({\theta }_t\right)}{{\lambda }_t}-\frac{\sin \left({\theta }_i\right)}{{\lambda }_i}=\frac{1}{2\pi }\frac{d\phi \left(y\right)}{dy},\end{array}(2)$

where ${\lambda }_i$ and ${\lambda }_t$ are the wavelengths of the incident and transmitted wave, respectively. $d\phi \left(y\right)/dy$ is the phase gradient along with the planar interface. ${\theta }_r$ and ${\theta }_t$ can be expressed as:

$\begin{array}{c}{\theta }_r=\mathrm{a}\mathrm{r}\mathrm{c}\mathrm{s}\mathrm{i}\mathrm{n}[\mathrm{s}\mathrm{i}\mathrm{n}\left({\theta }_i\right)+({\lambda }_i/2\pi )(d\phi \left(y\right)/dy)],\end{array}(3)$

$\begin{array}{c}{\theta }_t=\mathrm{a}\mathrm{r}\mathrm{c}\mathrm{s}\mathrm{i}\mathrm{n}[({\lambda }_t/{\lambda }_i)\mathrm{s}\mathrm{i}\mathrm{n}\left({\theta }_i\right)+({\lambda }_t/2\pi )(d\phi \left(y\right)/dy)].\end{array}(4)$

Equations 3 and 4 imply that ${\theta }_r$ and ${\theta }_t$ are determined by three factors: incident angle, phase gradient, and wavelength. Thus, it is possible to manipulate the reflected and transmitted wave freely by designing a suitable phase shift $\phi \left(y\right)$.

The BAAM

We consider a perforated unit cell composed of an air hole (the diameter being D) inside a square polymer (the width being a), as shown in Figure 1A. Figures 1B and C present the functional unit with nine periodically arrayed unit cells and BAAM, respectively. The blue medium indicates the water, and the gray and white medium are polymer and water. By arranging the functional unit with different diameters D, the metasurface can be constructed to steer the transmitted wave field. The material properties and geometric parameters of the BAAM are listed in Tables 1 and 2, respectively. In this article, the full-wave simulations are performed using commercial finite element software COMSOL Multiphysics with a preset Pressure Acoustic and Solid Mechanics module. Figure 2A illustrates the strip model with a functional unit. Continuous periodic boundary conditions are applied on the two sides of the strip model to simulate a periodically arranged structure. Perfectly matched layers (PMLs) are adopted at the upper end to absorb the reflection from the boundaries. The normally incident plane wave is employed at the bottom end of the strip model. To evaluate the phase shift and the transmission ratio, we set a probe line in the near area of the upper end, as shown in Figure 2A. The detected transmission ratio is defined as:

$\begin{array}{c}T=\frac{\left|P_{out}\right|}{\left|P_{in}\right|},\end{array}(5)$

where $p_{in}$ and $p_{out}$ are the amplitudes of the incident wave and the transmitted wave, respectively. Figure 2B shows the relationship between the phase shift and the diameter D. As D varies from 0 to 0.268 mm, the phase shift spans over a full 2π range, as shown with the black, and the transmittance exhibits a relatively high level, as shown with the color map. The number of air bubbles is an important variable for the functional unit. If the number of air bubbles is less than nine, it is impossible to achieve the phase shift covering an entire 2π range, and conversely, if the number of air bubbles is more than nine, the transmission ratio is affected, and the processing will be much more difficult.

FIGURE 1

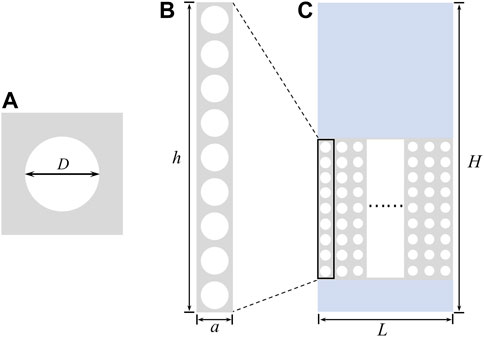
FIGURE 1. (A) The square unit cell with perforated air holes; (B) the functional unit with nine square units; and (C) the schematic diagrams of the bubble-arrayed metasurface.

TABLE 1

TABLE 1. Material properties.

TABLE 2

TABLE 2. Geometric parameters (unit: mm).

FIGURE 2

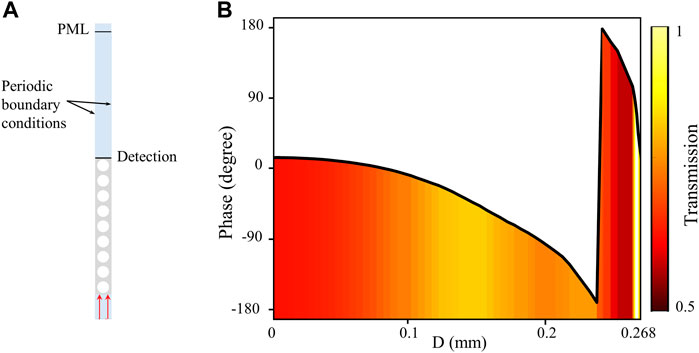
FIGURE 2. (A) The schematic diagrams of the functional model and (B) simulated phase shift and transmission ratio varying with the diameter D at f = 700 kHz.

Case Studies of the Metasurfaces for Modulation Refracted Wave and Discussion

From the GSL, we can conclude that the phase gradient plays a significant role in the wavefield manipulation. Thus, based on the relationship between the continuous phase shift and the diameter D, multiple functionalities of the proposed BAAM can be achieved, such as anomalous refraction and self-bending beams.

Abnormal Refraction

Assuming that the acoustic wave is normally incident on the designed structure, Eq. 3 can be rewritten as:

$\begin{array}{c}{\theta }_t=\mathrm{a}\mathrm{r}\mathrm{c}\mathrm{s}\mathrm{i}\mathrm{n}\left[({\lambda }_t/2\pi )(d\phi \left(y\right)/dy)\right].\end{array}(6)$

From Eq. 6, we can conclude that the transmitted angle varies with the phase shift, which indicates it is likely to steer the transmitted wave propagating along the direction as we want. Once we know the required phase shift and obtain the corresponding diameter D, the abnormal refraction will be achievable. This section performs the anomalous refraction effects of the proposed BAAM. Without loss of generality, we select three phase gradients: $d\phi =\frac{\pi }{6},\frac{2\pi }{15},\frac{\pi }{9}$. According to Eq. 6, we obtain the corresponding transmitted angles ${\theta }_t={20.9}^o,{16.6}^o,{13.8}^o$. For these three kinds of BAAM, Figures 3A–C illustrate the relationships between the phase shift and the diameter D. The blue dotted lines present the phase shift to manipulate the transmitted wave and determine the diameter D of each functional unit. The red dotted curves illustrate the diameter D corresponding to the phase shift. A Gaussian beam is normally applied to the bottom end of the metasurfaces as an initial incident at f = 700 kHz. As shown in Figures 3D–F, when the acoustic wave propagates through the metasurface, an apparent abnormal deflection of the acoustic wave can be observed in the transmitted field. The simulated results agree well with the theoretical results, which indicates the proposed metasurface shows an exceptional ability to manipulate the acoustic wave underwater. To verify the broadband feature of the proposed BAAM, we perform the full-wave manipulation at the frequencies of 694, 697, 700, 703, 706, and 709 kHz, respectively. Owing to limited space, we only demonstrate the simulated results of $d\phi =\frac{2\pi }{15}$ with the transmitted angle ${\theta }_t$ of 16.6°. As shown in Figures 4A–F, the proposed BAAM has the advantage of broadband in the abnormal refraction propagation.

FIGURE 3

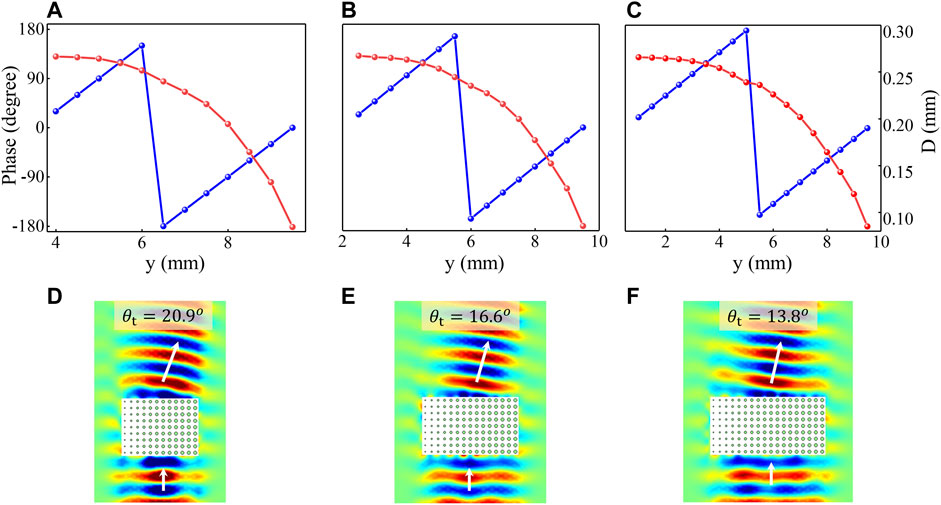
FIGURE 3. (A–C) The relationship between phase shift and air hole diameter D with phase gradient of π/6, 2π/15, and π/9. (D–F) The corresponding transmitted wavefields of abnormal refraction with the refracted angles of 20.9°, 16.6°, and 13.8°, respectively.

FIGURE 4

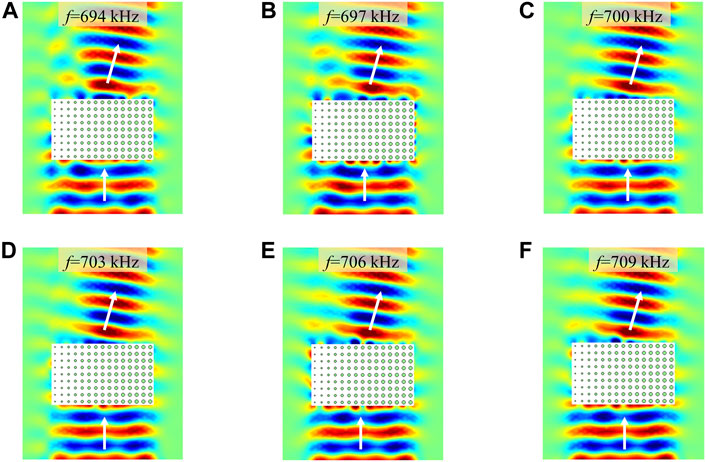
FIGURE 4. (A–F) Simulated pressure field of abnormal refraction with a phase shift $d\phi =\frac{2\pi }{15}$ at operating frequencies of 694, 697, 700, 703, 706, and 709 kHz, respectively.

The Generation of Self-Bending Beam

In order to further verify the feasibility of the proposed metasurface to manipulate the acoustic wave, two different cases of self-bending beam propagation trajectories will be presented: the Bezier beam and the bottle beam.

In this section, we use a third-order Bezier curve to designate the acoustic propagation path of the transmitted wavefield. The Bezier curve is a polynomial function concerning the parameter t, which is expressed as:

$\begin{array}{c}P\left(t\right)={\displaystyle \sum }_{i=0}^n{P}_i\frac{n!}{i!\left(n-i\right)!}{t}^i{\left(1-t\right)}^{n-i}\left(0\le t\le 1\right),\end{array}(7)$

where P(t) is the specific expression of a Bezier curve and n = 3 is the order. It can be found that once a series of points from $P_0$ to $P_n$ is selected, the trajectory of the curve will be determined. For a third-order Bezier curve, namely, a cubic Bezier curve, the expression will be obtained by defining four different points $P_0$, $P_1$, $P_2$, and $P_3$ on the XY plane. Thus, the cubic Bezier curve can be expressed as a cubic polynomial:

$\begin{array}{c}P\left(t\right)={\left(1-\text{t}\right)}^3{P}_0+3t{\left(1-\text{t}\right)}^2{P}_1+3\left(1-t\right)t^2{P}_2+t^3{P}_3 \\ ={\left(1-\text{t}\right)}^3\left(\begin{array}{c}0\\ -0.2311\end{array}\right)+3t{\left(1-\text{t}\right)}^2\left(\begin{array}{c}0.1\\ -0.2311\end{array}\right)+3t^2\left(\begin{array}{c}0.25\\ 0.1689\end{array}\right)\\ +t^3\left(\begin{array}{c}0.98\\ -0.3311\end{array}\right).\end{array}(8)$

Figure 5A illustrates the process of obtaining the phase profile in the y-direction. By substituting different parameter t into Eq. 8, we obtain the designed trajectory (red curve) owning the shape of the Bezier curve with $y=f\left(x\right)$. Since the acoustic wave propagates along the direction perpendicular to the wavefront, we construct an envelope of tangential rays (black lines) of the trajectory, which will be utilized to build the wavefront (black dash line).

FIGURE 5

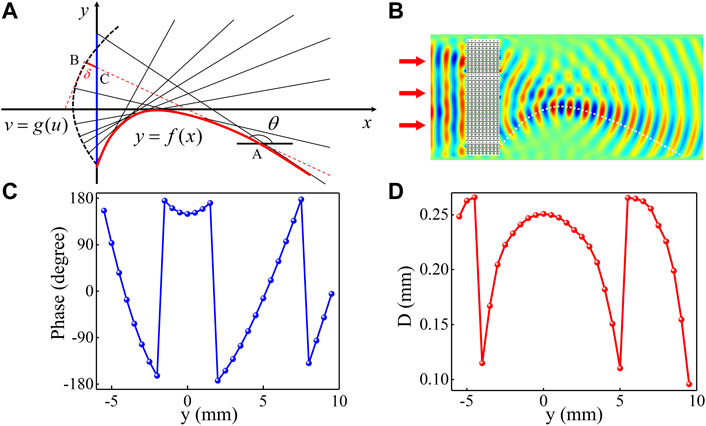
FIGURE 5. Self-bending beams for the Bezier curve trajectory at the frequency of 700 kHz. (A) Schematic illustrations of the self-bending beam; (B) numerically simulated sound pressure field of the Bezier beam; and (C–D) the theoretical phase shifts and the corresponding diameter D along the y-direction.

We present the tangential ray (red dash line) as an example, it intersects with the trajectory, wavefront, and y-axis at point $A(x,y)$, $B(u,v)$, and $C(0,\xi )$, respectively, where the distance of points B and C is $\delta$, and the relationship between the two points satisfies the equations as follows:

$\begin{array}{c}\delta =\frac{-u}{\text{cos}(\pi -\theta )}=\frac{u}{\text{cos}\left(\theta \right)},\end{array}(9)$

$\begin{array}{c}\xi =v-[-u\mathrm{t}\mathrm{a}\mathrm{n}(\pi -\theta )]=v-u\mathrm{t}\mathrm{a}\mathrm{n}\left(\theta \right).\end{array}(10)$

Since the acoustic rays are perpendicular to the wavefront, the relationship between the slope of points A and B can be expressed as:

$\begin{array}{c}\frac{dx}{dz}\cdot \frac{dv}{du}=-1.\end{array}(11)$

By simplifying Eq. 11, we can obtain:

$\begin{array}{c}\frac{du}{dv}=-\mathrm{t}\mathrm{a}\mathrm{n}\left(\theta \right),\end{array}(12)$

where $\theta$ is the angle between the ray and the transverse direction. Lastly, with existing equations, the phase shift (blue line) in the y-direction can be expressed as:

$\begin{array}{c}\phi \left(\xi \right)=k\delta .\end{array}(13)$

Combining Eqs 8–12, the relationship between the phase shift profile and the transmitted angle can be written as:

$\begin{array}{c}\frac{d\phi \left(\xi \right)}{d\xi }=-ksin\left(\theta \right)=\frac{-k{f}^{\prime }\left(x\right)}{\sqrt{1+f^{\prime }{\left(x\right)}^2}}.\end{array}(14)$

It can be found from Eq. 14 that once the desired beam path is determined, the phase shift to design the BAAM will be readily constructed. We use 31 functional units to build the BAAM to realize the Bezier beam effect. The simulated result of the acoustic pressure is provided in Figure 5B. The white dashed line represents the theoretical trajectory of the Bezier beam effect. It is easy to find that the simulated result is in good agreement with the theoretical value. Similar to the abnormal refracted, Figure 5C illustrates the desired phase distribution of 31 units obtained by Eq. 14. According to the relationship between the phase shift and the diameter D, the diameter D can be selected to design the BAAM consisting of 31 functional units. The distribution of the diameter D along the y-direction is shown in Figure 5D.

When the trajectory of the self-accelerating beam is a bottle trajectory, the transmitted acoustic wave propagates along a circular path, which is defined by:

$\begin{array}{c}{(x-x_0)}^2+{(y-y_0)}^2=r^2,\end{array}(15)$

where $(x_0,y_0)$ and r are the central and the radius of the circular trajectory, respectively. Substituting Eq. 15 into Eq. 14, we can obtain the phase profile of the bottle beam $\phi \left(y\right)$ along the y-direction:

$\begin{array}{c}\phi \left(y\right)=k_t[y-2r\mathrm{a}\mathrm{r}\mathrm{c}\mathrm{t}\mathrm{a}\mathrm{n}(y/r)],\end{array}(16)$

where $k_t$ denotes the wavenumber of the transmitted wave. For the predesigned acoustic bottle beam, we set the center of the circle at $(x_0,y_0)=(0.005,0)$ with the radius r being 5 mm. From Eq. 16, the phase shift of the circular trajectory can be further rewritten as $\phi \left(y\right)=k_t[y-0.01\text{arctan}(y/r)]$.

Figure 6 (A) illustrates the schematic diagram of the circular trajectory described by $y=\sqrt{{0.005}^2-{(x-0.005)}^2}$. Since the functional units are arranged in a way of mirror-symmetrically around the x axis, the phase shift ${\phi }_n={{\phi }^{\prime }}_n$. Next, we assemble the metasurface with 30 functional arrayed units and test its performance with normal incident plane waves. The acoustic intensity of the transmitted wavefield is shown in Figure 6B. As can be clearly observed that the acoustic bottle beam propagates along the designated trajectory (white dashed circle) with nearly no sound pressure inside the bottle. The simulation results coincide well with the theoretical results. The phase shift can be obtained with Eq. 16, and the phase profile is shown in Figure 6C. Similarly, on the basis of the calculated phase shift from ${\phi }_1$ to ${\phi }_{30}$, the diameter D can be selected to design the BAAM consisting of 30 functional units. The distribution of the diameter D along the y-direction is shown in Figure 6D.

FIGURE 6

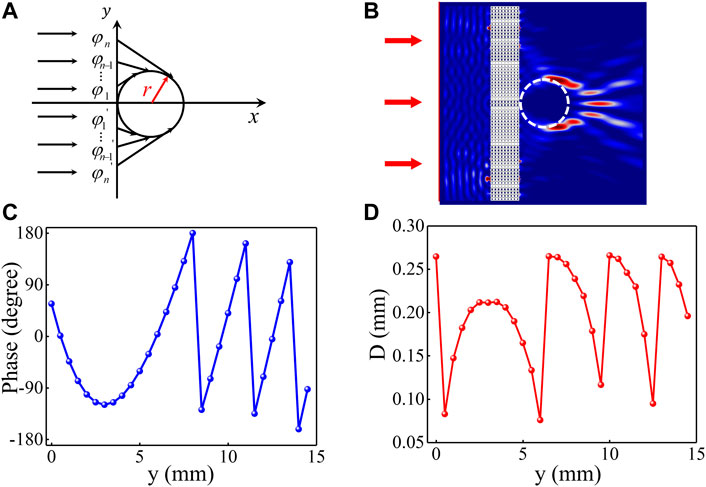
FIGURE 6. Self-bending beams for the acoustic bottle beam at f = 700 kHz. (A) Schematic illustrations of the acoustic bottom beam; (B) numerically simulated sound intensity field of the acoustic bottom beam; and (C–D) the theoretical phase shifts and the corresponding diameter D along the y-direction.

Conclusion

In summary, we numerically demonstrated a bubble-arrayed acoustic metasurface to manipulate the transmitted wave field by changing the diameter D of the air bubbles. The abnormal refraction, Bezier beams, and the acoustic bottle beam can be realized with the proposed metasurface, and the simulated results show good agreement with the theoretical predictions. The special feature of the BAAM is that air bubbles are introduced into the metasurface, which provides a unique design method to simplify the configurations with a relatively high transmission ratio. With the advantage of wavefield modulation of the transmitted wave over broadband frequencies, the compact and straightforward design of the proposed BAAM without complex manufacturing opens a new avenue for potential underwater applications in acoustic wave engineering manipulation and ultrasound imaging.

Data Availability Statement

The raw data supporting the conclusions of this article will be made available by the authors, without undue reservation.

Author Contributions

ZML: software, data curation, and writing—original draft. LSZ and HW: software and validation. ZBL and XFZ: supervised the study, funding acquisition, and writing—review and editing.

Funding

This work was supported by the National Key R&D Program of China (Grant Nos. 2020YFA0211400 and 2020YFA0211401).

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s Note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors, and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

1. Wen J, Shen H, Yu D, Wen X. Exploration of Amphoteric and Negative Refraction Imaging of Acoustic Sources via Active Metamaterials. Phys Lett A (2013) 377:2199–206. doi:10.1016/j.physleta.2013.06.016

CrossRef Full Text | Google Scholar

2. Li J, Chan CT. Double-negative Acoustic Metamaterial. Phys Rev E Stat Nonlin Soft Matter Phys (2004) 70:055602. doi:10.1103/PhysRevE.70.055602

PubMed Abstract | CrossRef Full Text | Google Scholar

3. Yu N, Capasso F. Flat Optics with Designer Metasurfaces. Nat Mater (2014) 13:139–50. doi:10.1038/nmat3839

PubMed Abstract | CrossRef Full Text | Google Scholar

4. Yu N, Genevet P, Kats MA, Aieta F, Tetienne J-P, Capasso F, et al. Light Propagation with Phase Discontinuities: Generalized Laws of Reflection and Refraction. Science (2011) 334:333–7. doi:10.1126/science.1210713

PubMed Abstract | CrossRef Full Text | Google Scholar

5. Assouar B, Liang B, Wu Y, Li Y, Cheng J-C, Jing Y. Acoustic Metasurfaces. Nat Rev Mater (2018) 3:460–72. doi:10.1038/s41578-018-0061-4

CrossRef Full Text | Google Scholar

6. Jia D, Wang Y, Ge Y, Yuan S-Q, Sun H-X. Tunable Topological Refractions in Valley Sonic Crystals with Triple Valley Hall Phase Transitions. Prog Electromagnetics Res (2021) 172. 13–22. doi:10.2528/pier21102002

CrossRef Full Text | Google Scholar

7. Tsang L, Liao T-H, Tan S. Calculations of Bands and Band Field Solutions in Topological Acoustics Using the Broadband Green's Function-KKR-Multiple Scattering Method. Pier (2021) 171:137–58. doi:10.2528/pier21081706

CrossRef Full Text | Google Scholar

8. Tang S, Ren B, Feng Y, Song J, Jiang Y. The Generation of Acoustic Airy Beam with Selective Band Based on Binary Metasurfaces: Customized on Demand. Appl Phys Lett (2021) 119:071907. doi:10.1063/5.0060032

CrossRef Full Text | Google Scholar

9. Lin Z, Xu W, Xuan C, Qi W, Wang W. Modular Elastic Metasurfaces with Mass Oscillators for Transmitted Flexural Wave Manipulation. J Phys D: Appl Phys (2021) 54:255303. doi:10.1088/1361-6463/abee47

CrossRef Full Text | Google Scholar

10. Zeng L-S, Shen Y-X, Fang X-S, Li Y, Zhu X-F. Experimental Realization of Ultrasonic Retroreflection Tweezing via Metagratings. Ultrasonics (2021) 117:106548. doi:10.1016/j.ultras.2021.106548

PubMed Abstract | CrossRef Full Text | Google Scholar

11. Li Y, Jiang X, Li R-q, Liang B, Zou X-y, Yin L-l, et al. Experimental Realization of Full Control of Reflected Waves with Subwavelength Acoustic Metasurfaces. Phys Rev Appl (2014) 2:064002. doi:10.1103/physrevapplied.2.064002

CrossRef Full Text | Google Scholar

12. Chen H. Anomalous Reflection of Acoustic Waves in Air with Metasurfaces at Low Frequency. Adv Condensed Matter Phys (2018) 2018:1–7. doi:10.1155/2018/5452071

CrossRef Full Text | Google Scholar

13. Mei J, Wu Y. Controllable Transmission and Total Reflection through an Impedance-Matched Acoustic Metasurface. New J Phys (2014) 16:123007. doi:10.1088/1367-2630/16/12/123007

CrossRef Full Text | Google Scholar

14. Zhu H, Semperlotti F. Anomalous Refraction of Acoustic Guided Waves in Solids with Geometrically Tapered Metasurfaces. Phys Rev Lett (2016) 117:034302. doi:10.1103/PhysRevLett.117.034302

PubMed Abstract | CrossRef Full Text | Google Scholar

15. Tang K, Qiu C, Lu J, Ke M, Liu Z. Focusing and Directional Beaming Effects of Airborne Sound through a Planar Lens with Zigzag Slits. J Appl Phys (2015) 117:024503. doi:10.1063/1.4905910

CrossRef Full Text | Google Scholar

16. Mei J, Ma G, Yang M, Yang Z, Wen W, Sheng P. Dark Acoustic Metamaterials as Super Absorbers for Low-Frequency Sound. Nat Commun (2012) 3:756–7. doi:10.1038/ncomms1758

PubMed Abstract | CrossRef Full Text | Google Scholar

17. Ye L, Qiu C, Lu J, Tang K, Jia H, Ke M, et al. Making Sound Vortices by Metasurfaces. Aip Adv (2016) 6:085007. doi:10.1063/1.4961062

CrossRef Full Text | Google Scholar

18. Li Z, Liu W, Li Z, Tang C, Cheng H, Li J, et al. Tripling the Capacity of Optical Vortices by Nonlinear Metasurface. Laser Photon Rev (2018) 12:1800164. doi:10.1002/lpor.201800164

CrossRef Full Text | Google Scholar

19. Fan S-W, Wang Y-F, Cao L, Zhu Y, Chen A-L, Vincent B, et al. Acoustic Vortices with High-Order Orbital Angular Momentum by a Continuously Tunable Metasurface. Appl Phys Lett (2020) 116:163504. doi:10.1063/5.0007351

CrossRef Full Text | Google Scholar

20. Li X-S, Zhou H-T, Wang Y-F, Wang Y-S. Modulation of Acoustic Self-Accelerating Beams with Tunable Curved Metasurfaces. Appl Phys Lett (2021) 118:023503. doi:10.1063/5.0035286

CrossRef Full Text | Google Scholar

21. Li Y, Liang B, Gu Z-m., Zou X-y., Cheng J-c. Reflected Wavefront Manipulation Based on Ultrathin Planar Acoustic Metasurfaces. Sci Rep (2013) 3:2546. doi:10.1038/srep02546

PubMed Abstract | CrossRef Full Text | Google Scholar

22. Xie Y, Wang W, Chen H, Konneker A, Popa BI, Cummer SA. Wavefront Modulation and Subwavelength Diffractive Acoustics with an Acoustic Metasurface. Nat Commun (2014) 5:5553–5. doi:10.1038/ncomms6553

PubMed Abstract | CrossRef Full Text | Google Scholar

23. Zhu X, Li K, Zhang P, Zhu J, Zhang J, Tian C, et al. Implementation of Dispersion-free Slow Acoustic Wave Propagation and Phase Engineering with Helical-Structured Metamaterials. Nat Commun (2016) 7:11731. doi:10.1038/ncomms11731

PubMed Abstract | CrossRef Full Text | Google Scholar

24. Zhang P, Li T, Zhu J, Zhu X, Yang S, Wang Y, et al. Generation of Acoustic Self-Bending and Bottle Beams by Phase Engineering. Nat Commun (2014) 5:4316. doi:10.1038/ncomms5316

PubMed Abstract | CrossRef Full Text | Google Scholar

25. Li Z, Yang S, Wang D, Shan H, Chen D, Fei C, et al. Focus of Ultrasonic Underwater Sound with 3D Printed Phononic crystal. Appl Phys Lett (2021) 119:073501. doi:10.1063/5.0058415

CrossRef Full Text | Google Scholar

26. Zhou H-T, Fu W-X, Wang Y-F, Wang Y-S. High-Efficiency Ultrathin Nonlocal Waterborne Acoustic Metasurface. Phys Rev Appl (2021) 15:044046. doi:10.1103/physrevapplied.15.044046

CrossRef Full Text | Google Scholar