A Theoretical Study of Tunable Brillouin Lasers Based on a Diamond Suspended Waveguide

In this work we detail the design of a novel, hybrid waveguide structure which enables independent control of phonon modes and optomechanical driving forces, thereby yielding customizable Brillouin coupling over a very broad bandwidth. The Brillouin gain reaches 4400 W⁻¹m⁻¹, with tunable phonon frequencies from 1–95 GHz. This hybrid waveguide relies on tuning of its width and enables photon-phonon conversion based on the Brillouin nonlinear effect, and importantly, it can guide and manipulate the phonons emitted by the Brillouin effect on a chip-level device. There is hence excellent potential for this technique to be applied in microwave sources using the on-chip Brillouin photoacoustic coupling mechanism.

Introduction

Stimulated Brillouin scattering (SBS) is a third-order nonlinear optical process that uses the interaction of two photons in a medium to generate new photons and phonons [1–3]. Therefore, the SBS effect can be used to force interaction between acoustic and optical waves, thereby generating higher frequency photons and phonons. Customizable slow light can be generated through techniques such as waveguide SBS photon-phonon coupling [4, 5], radio frequency (RF)-photon signal processing [6, 7], narrow linewidth laser sources [8–10], RF-waveform synthesis [11, 12] and optical frequency comb generators [11, 13, 14]. Silicon is the ideal platform for nanophotonic devices because it is compatible with complementary metal-oxide semi-conductors (CMOS). It enables nanoscale traveling-wave photon-phonon coupling through Brillouin interactions to achieve high-performance signals [1, 15–18]. In the case of nano-scale silicon-based optical waveguides, tight optical confinement results in significantly enhanced Raman and Kerr nonlinearities [19–21]. In 2013, Rakich’s group proposed a novel type of photon-phonon hybrid waveguide, which proved for the first time the process of forward SBS (FSBS) nonlinearity and gain in a silicon waveguide [22]. In their work, the structure comprised a suspended waveguide with Si₃N₄ on both sides and Si in the middle. Due to the significant difference in refractive index between silicon (n = 3.5) and silicon nitride (n = 2.0), the structure tightly confines the optical field mode to the central region of the silicon waveguide. The silicon nitride films on both sides guide the phonons to perform photon-phonon coupling within the silicon waveguide core. The SBS gain reached 2570 W⁻¹m⁻¹, and a tunable phonon range of 1–18 GHz was realized.

As diamond and silicon both belong to the fourth group of elements, they have many similar optical properties. Compared to silicon, diamond has lower loss and higher nonlinear coefficient across a wide range of operating wavelengths and can be used for highly accurate phase-matching [23]. In addition, diamond has excellent physical and chemical stability, especially with regard to its extremely high thermal stability, enabling it to overcome the inevitable thermal effect which can plague traditional laser gain media at high powers [24, 25]. Meanwhile, its wide spectral transmission range enables the operating wavelength of diamond lasers to cover the ultraviolet, visible to mid-infrared [24, 26]. Moreover, diamond has been proved to be a promising Brillouin material for its high Brillouin gain coefficient and large Brillouin frequency shift [27]. Currently, tens of watts of single-frequency and cascaded Brillouin lasing have been realized in diamond based on free-space structures [27, 28]. However, there are very few studies on the characteristics of diamond Brillouin lasers which employ a waveguide structure. Therefore, it is important to investigate schemes which will yield higher Brillouin gain, especially in the form of highly integrated and tunable on-chip Brillouin lasers.

In this brief report, we detail the design of a novel type of photon-phonon waveguide structure utilizing forward SBS (multi-mode SBS). Here, the optical field is coupled in different spatial modes to achieve the customizable FSBS of a traveling wave. The Brillouin gain reaches 4400 W⁻¹m⁻¹, and the generation of phonons with frequencies across the range 1–95 GHz is realized. The simulation results show that the nonlinear (Brillouin) enhancement caused by the radiation pressure due to the design of the structure far exceeds the nonlinear enhancement caused by the material. We believe that this enhanced broadband coherent phonon emission paves the way for hybrid on-chip CMOS signal processing technologies.

Theoretical Model

The FSBS process involves the interaction between pump, Stokes (or anti-Stokes) and acoustic waves [29, 30]. Specifically, in the FSBS process, the optical waves (pump and Stokes) propagate in the same direction while the acoustic (phonon) wave propagates perpendicular to the optical waves [31, 32]. Phase matching of the FSBS process requires the conservation of energy and momentum yielding the following conditions:

$\overrightarrow{k_A}=\overrightarrow{k_p}-\overrightarrow{k_s}(1)$

$\mathrm{\Omega }={\omega }_p-{\omega }_s(2)$

Where, ${\overrightarrow{k}}_A$, ${\overrightarrow{k}}_p$ and ${\overrightarrow{k}}_s$ represent pump, Stokes, and acoustic waves, respectively. Considering the propagation direction of optical waves, SBS can be categorized as FSBS and backward SBS (BSBS). In this paper, we only focus on the coupling between modes in FSBS.

For the FSBS process, let us assume that the propagation directions of the pump wave and Stokes wave are both along the z-axis, so the optical wave field of the pump wave and Stokes wave can be described as:

$E_P\left(z,t\right)={\tilde{E}}_p\left(x,y\right){\mathrm{e}}^{\mathrm{i}\left(k_{p}z-{\omega }_{p}t\right)}(3)$

$E_s\left(z,t\right)={\tilde{E}}_s\left(x,y\right){\mathrm{e}}^{\mathrm{i}\left(k_{s}z-{\omega }_{s}t\right)}(4)$

Where E_p (z, t) is the pump optical wave, and E_s (z, t) is the Stokes optical wave. Using small signals as an approximate replacement, when the power of the pump wave in the waveguide is greater than the power of the Stokes wave, the coupling between the two optical waves should meet the following conditions [33]:

$\frac{d{P}_p}{dz}=-\left(\alpha +\beta P_p+\gamma P_p^2\right)P_p(5)$

$\frac{d{P}_s}{dz}=\left(\alpha -g{P}_p+2\beta P_p+\gamma P_p^2\right)P_s(6)$

Where P_p and P_s are the power of the pump wave and the power of the Stokes wave respectively, α is the linear loss coefficient of optical wave caused by the structure, size, and other parameters of the material. β and γ are nonlinear loss coefficients (including two-photon absorption and free-carrier absorption). In Eqn. 6, g represents the Brillouin gain coefficient, which has a Lorentzian shape and can be expressed as [34]:

$g\left(\mathrm{\Omega }\right)={\displaystyle \sum _m{G}_m}\frac{{\left({\mathrm{\Gamma }}_m/2\right)}^2}{\left(\mathrm{\Omega }-{\mathrm{\Omega }}_m\right)+{\left({\mathrm{\Gamma }}_m/2\right)}^2}(7)$

Ω_m is the characteristic frequency that is satisfied by the total characteristic equation of the acoustic mode when the acoustic loss is ignored. ${\mathrm{\Gamma }}_m$ is the loss coefficient of acoustic mode when acoustic loss is taken into account [35], depending on the mechanical quality factor Q_m with the relation given as: $Q_m=\frac{{\mathrm{\Omega }}_{\mathrm{m}}}{{\mathrm{\Gamma }}_{\mathrm{m}}}$ [36]; subscript m is the mth acoustic mode (m = 1,2,3 … … ).

Considering the acoustic loss, the peak value of the SBS gain spectrum can be simplified as follows:

$G_m=\frac{2\omega Q_m}{{\mathrm{\Omega }}_{\mathrm{m}}^2{V}_{gp}{V}_{gs}}\frac{{\left|\langle f,u_m\rangle \right|}^2}{\langle E_p,\epsilon E_p\rangle \langle E_s,\epsilon E_s\rangle \langle u_m,\rho u_m\rangle }(8)$

Where V_g, ε, and ρ are the optical group velocity, conductivity and density, respectively. f is the total of the optical forces of the pump and Stokes waves. It is assumed that ${\omega }_m\approx {\omega }_s=\omega$ and $\langle X,Y\rangle ={\displaystyle \int X^{\ast }\cdot Yds}$ integrally cover the entire waveguide cross sectional. It is the overlap integral between the total optical force [37] and a single mth optical eigen-mode, and it represents the optical-mechanical coupling strength of the suspended waveguide [38].

The acoustic displacement field is included in the total optical force, satisfying the phase-matching conditions of Equations 1, 2 [35]. To facilitate the calculation u_m, the elastic loss in the isotropic medium can be ignored, and the ideal acoustic equation should satisfy:

$-\rho {\partial }_t^2{u}_i+{\displaystyle \sum _{jkl}{\partial }_j{c}_{ijkl}{\partial }_k{u}_l=-f_i}(9)$

Where C_ijkl denotes the photo-elastic tensor, and f_i is the ith component of the total optical force of the acoustic field ${\partial }_j$ is the derivative along the jth space direction of j, in which $j\in \left\{x,y,z\right\}$. When the driving force f_i is absent in Eqn. 9, the displacement component u_mi of the acoustic field in different modes can be obtained. Hybrid acoustic waves (HAW) include transverse waves and vertical displacement components which are excited in the waveguide structures.

To more clearly describe Eqn. 8 and 8 can be transformed into:

$G_m=C_{O{T}_m}{\left|Q_{C_m}\right|}^2(10)$

Where $Q_{Cm}=\langle f,u_m\rangle$ denotes the influence of optomechanical coupling on G_m, while $C_{O{T}_m}=C_{F{V}_m}{C}_{E{F}_m}$ is the influence of other factors (including optical group velocity, material quality factor, optical energy flow, and phonon energy flow) on G_m, where, $C_{F{V}_m}=\frac{2\omega Q_m}{{\mathrm{\Omega }}_{\mathrm{m}}^2{\nu }_{gp}{\nu }_{gs}}$, $C_{E{F}_m}=\frac{1}{\langle E_p,\epsilon E_p\rangle \langle E_s,\epsilon E_s\rangle \langle u_m,\rho u_m\rangle }$. From the two parameters in the above expression, we can see that in the waveguide structure, the angular frequency, the group velocity of the optical waves, the energy flow of the optical and acoustic waves, and the characteristics of the waveguide material are all related to C_OTm.

In the suspended waveguide structure, the linear sum of all overlap integrals between a single optical force and the mth acoustic eigenmode during the optical-mechanical coupling process can be expressed as:

$Q_{C_m}={\displaystyle \sum _n\langle f^n,u_m\rangle }(11)$

It is worth noting that the contribution of a single overlap integral depends on the optical force, and its relative phase is affected by interference effects. In a nano-level waveguide, the Brillouin gain coefficient in Eqn. 8 needs to consider two influencing factors: the electrostriction force and the radiation pressure, namely f ^Total = f ^PE + f ^MB. Electrostriction is the secondary response of mechanical strain excited by an external electric field. The ith component of the electrostriction force is defined as [39]:

$f_i^{PE}=-{\displaystyle \sum _{ij}\frac{\partial }{\partial j}{\sigma }_{ij}}(12)$

Where σ_ij is the electrostriction tensor that is given by:

${\sigma }_{ij}=-\frac{1}{4}{\epsilon }_0{\epsilon }_r^2{p}_{ijkl}\left(E_{pk}{E}_{sl}^{\ast }+E_{pl}{E}_{sk}^{\ast }\right)(13)$

Where $p_{ijkl}$ denotes the photo-elastic tensor, and ε_r and ε₀ are the relative permittivity and vacuum permittivity of the material respectively. Since common materials used in integrated photonics have either a cubic crystalline lattice (e.g., silicon) or are isotropic (e.g., silica glass), and most waveguide structures are fabricated to be aligned with the principal axes of the material, we consider the crystal material of the waveguide to have spatial symmetry. $p_{ijkl}$ is zero if it contains odd number of a certain component, and Eqn. 13 can be written as:

$\left[\begin{array}{c}{\sigma }_{xx}\\ {\sigma }_{yy}\\ {\sigma }_{zz}\\ {\sigma }_{yz}\\ {\sigma }_{xz}\\ {\sigma }_{xy}\end{array}\right]=-\frac{1}{2}{\epsilon }_0{n}^4\left[\begin{array}{cccccc}{p}_{11}& p_{12}& p_{13}& & & \\ p_{12}& p_{22}& p_{23}& & & \\ p_{13}& p_{23}& p_{33}& & & \\ & & & p_{44}& & \\ & & & & p_{55}& \\ & & & & & p_{66}\end{array}\right]\left[\begin{array}{c}{E}_{px}{E}_{sx}^{\ast }\\ E_{py}{E}_{sy}^{\ast }\\ E_{pz}{E}_{sz}^{\ast }\\ E_{py}{E}_{sz}^{\ast }+E_{pz}{E}_{sy}^{\ast }\\ E_{px}{E}_{sz}^{\ast }+E_{pz}{E}_{sx}^{\ast }\\ E_{px}{E}_{sy}^{\ast }+E_{py}{E}_{sx}^{\ast }\end{array}\right](14)$

When the acoustic wave with frequency Ω excited by the electrostriction body force propagates, the dielectric constant inside the bulk medium changes by Δε. In this process, the photon-phonon interaction mainly occurs inside the medium. The electrostriction force is generated by the dynamic mechanical response of the medium to the optical waves, and the relative permittivity inside the medium changes so that a complex spatial force distribution occurs inside the medium. Its magnitude and direction are determined by the photo-elasticity tensor of the material, and the electrostriction body force becomes f^PEe^i(qx−Ωt) according to Eqn. 14, with vector components:

$\begin{array}{l}{f}_x^{PE}=-iq{\sigma }_{xx}-{\partial }_y{\sigma }_{xy}-{\partial }_z{\sigma }_{xz}\\ f_y^{PE}=-iq{\sigma }_{xy}-{\partial }_y{\sigma }_{yy}-{\partial }_z{\sigma }_{yz}\\ f_z^{PE}=-iq{\sigma }_{xz}-{\partial }_y{\sigma }_{zy}-{\partial }_z{\sigma }_{zz}\end{array}(15)$

Radiation pressure acts only on boundaries where the gradient of ε_r is not equal to zero [40]. It can be derived from the Maxwell tensors between material 1 and 2, which can be written as:

$f_i^{\mathrm{MB}}=\left(T_{2ij}-T_{1ij}\right)n_j(16)$

$T_{ij}={\epsilon }_0{\epsilon }_r\left(E_i{E}_j-\frac{1}{2}{\sigma }_{ij}{E}^2\right)(17)$

Where n is the normal vector points from material one to material 2. For the waveguide with constant horizontal direction, only the transverse component of the force can contribute to the SBS gain coefficient.

Results

The factors affecting SBS gain mainly include electrostriction force and radiation pressure. Since waveguide size needs to reach the order of micrometers to nanometers, the SBS nonlinearity caused by the material will be weakened, resulting in lower SBS gain of the entire waveguide. So we need to design some specific structures to increase the SBS gain. At the micro-nanometer scale, the SBS nonlinearity caused by radiation pressure also plays a key role. Our waveguide model adds an air slot in the center of the waveguide, this results in an increase in the radiation pressure, and the contribution to the SBS nonlinearity caused by the radiation pressure is much higher than that from the material itself. In addition, the use of suspended waveguides better promote photon-phonon coupling because the suspended waveguide better confines the optical field and the acoustic field in the waveguide in comparison to a waveguide within the substrate [41].

As shown in Figure 1A, the Brillouin laser system is made from a diamond wafer. The diamond parameters are as follows: Young’s modulus E = 1,220 GPa, Poisson’s ratio v = 0.07, density ρ = 3515 kg/m³, photo-elastic tensor p₁₁ = −0.249, p₁₂ = 0.043, p₄₄ = −0.172, relative Permittivity ε = 5.86. The outline of the air slot is shown in Figure 1B. The thickness of the diamond wafer was t = 215 nm, wafer width w = 800 nm, and width of the air slot s = 2 nm. The waveguide width was variable with width w = 500–2,000 nm, and the displacement field associated with the waveguide mode satisfying the phase matching relationship is shown in Figure 1C. In the FSBS, the m = 0 order acoustic mode phase-matching conditions are shown in Eqs. 1, 2. This multi-mode, suspended waveguide provides low-loss guidance for different types of acoustic modes, resulting in higher mechanical quality factor (Q_m) cavity modes with altered free-spectral-range (FSR). As shown in Figure 1D, when the pump wave with frequency ω_p was injected into the slot waveguide, a beat frequency signal with frequency Ω was generated. Under the action of the beat frequency signal, an optical force was be generated in the waveguide, and the exciting optical force caused the waveguide material compress or expand, creating an acoustic signal:

FIGURE 1

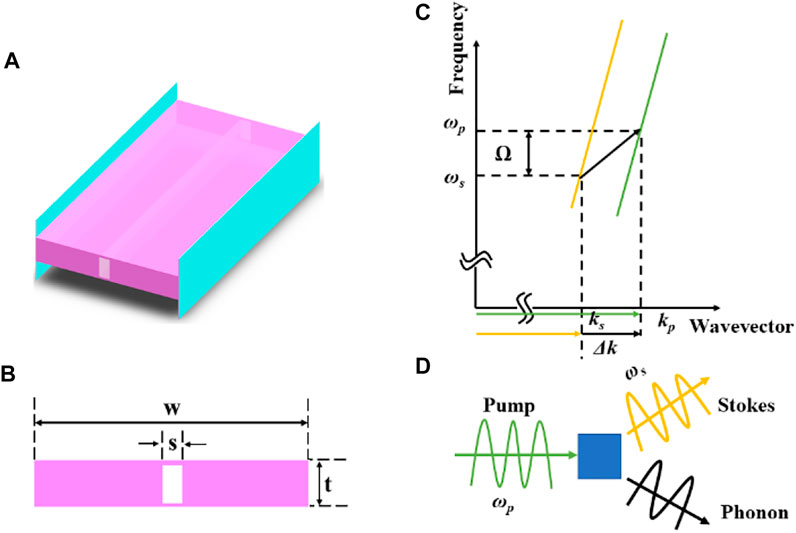
FIGURE 1. (A) Schematic diagram of the suspended waveguide structure. (B) Front view of the suspended waveguide highlighting the internal air slot; t = 215 nm, w = 800 nm, air slot length s = 2 nm. (C) Frequency-wavevector plot showing the interaction of the pump, Stokes and phonon waves in the FSBS process; the optical curves represent the optical resonances generated for different spatial modes. (D) Schematic diagram of the generation of Stokes and phonon waves produced by the annihilation of a pump wave.

Finite Element Simulation using COMSOL software was applied to examine the in the inter-mode FSBS; here the pump and the Stokes waves were injected into the optical waveguide as different modes. At the time, the incident pump frequency, Stokes frequency, and the generated phonon frequency satisfy Eqs. 1, 2 (s = 2 nm, w = 800 nm). To simplify the calculation, we assumed that the optical quality factor Q = 1,000 and the transformation of the eigenfrequency of the optical mode did not affect the optical quality factor Q. By examining the results shown in Figure 2A, it was found that the radiation pressure at the central air slot was significantly higher than that compared to other sections. Figure 2B shows the distribution diagram of the electric field components when m = 0 (basic optical mode). It can be observed that both optical and acoustic waves were guided in the thin film waveguide of Figure 1A. The optical wave was confined in the air slot by total internal reflection, guiding the TE-like optical mode. This produced strong Brillouin coupling, which significantly improved the photon-phonon coupling efficiency.

FIGURE 2

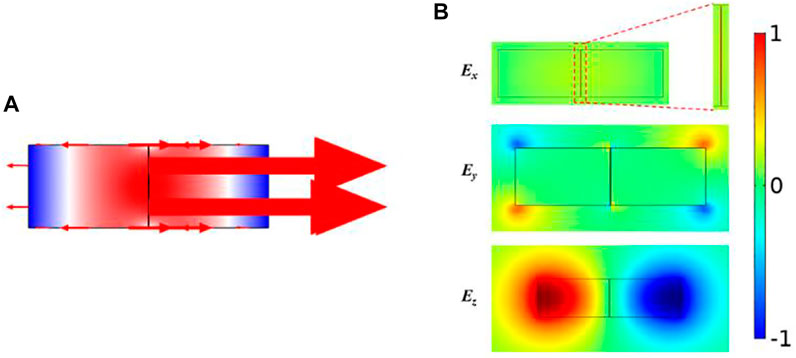
FIGURE 2. Data obtained showing the radiation pressure distribution of the designed waveguide in the case of an acoustic mode m = 0. (A) Schematic diagram showing the radiation pressure distribution of the slot waveguide. (B) The guiding lateral profile of the fundamental optical mode highlighting the E_x, E_y and E_z field components.

We calculated the total optical force as shown in Figure 3A. The result was consistent with the previous conjecture. Due to the existence of an air slot, most of the optical force was concentrated in the air slot. The acoustic displacement presented a symmetric and anti-symmetric spatial pattern in different directions for different acoustic modes. These are plotted in Figure 3B, and the pump wave is 1,550 nm. Efficient selection of waveguide and acoustic modes enables autonomous regulation of the photon-phonon coupling. As shown in Figure 3C, when the waveguide width was 800 nm, the slot waveguide exhibited five acoustic modes (m = 5) under the action of the PE and the MB effect. Especially between the first-order acoustic breathing mode and the TE optical mode, the strain component of the acoustic and the optical mode had a significant overlap integral, which significantly improved the photon-phonon coupling efficiency. Figure 3A and Figure 3B show that the higher the degree of agreement between the optical force and acoustic mode distribution, the higher the photon-phonon coupling efficiency. In the case of the first-order acoustic mode, the optical force and the acoustic displacement distribution in this mode had a very high degree of overlap. At the same time, with the increase of the mode order, the overlap integral of the optical force and the acoustic displacement became smaller, so the degree of Brillouin coupling gradually decreased. Since optical fields are symmetrically distributed in space, only the acoustic field modes with symmetry or anti-symmetry can produce effective Brillouin coupling with the optical field, as shown in Figure 3C. When the Brillouin spectrum changes with the size of the waveguide, a Brillouin resonance of 1–95 GHz is produced, achieving unprecedented nonlinear tunability. For example, in the case of the first-order acoustic mode, when the waveguide, initially 2000 nm wide, becomes 500 nm wide, the frequency of the acoustic wave shifts from 6.14 to 22.8 GHz, and a strong Brillouin resonance occurs at this frequency. In Figure 3D, it can be observed that in the case of the first-order acoustic mode, the photon-phonon coupling efficiency reaches the maximum, which is due to the optical force distribution mentioned above and the modal distribution of the acoustic wave being very consistent.

FIGURE 3

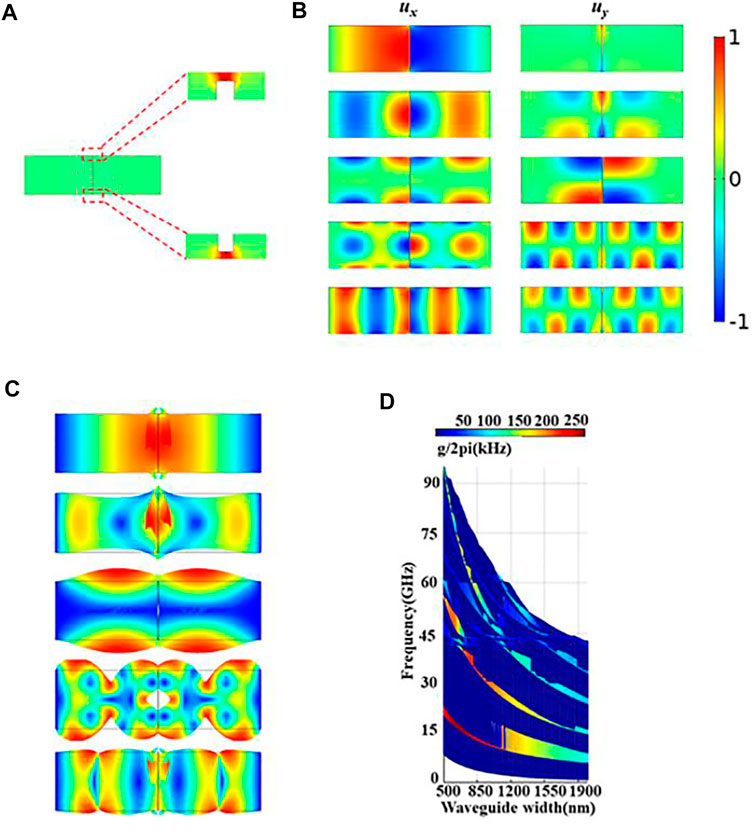
FIGURE 3. (A) Distribution diagram of the total optical force within the waveguide. (B) Displacement diagrams of phonons in the x and y directions for each mode. (C) Representations of the mode distribution diagram of each acoustic mode determined in b which satisfies phase matching when the waveguide width is 800 nm. (D) Finite element simulation of the photoacoustic coupling rate varying with the width of the waveguide in the slot waveguide structure. The depth of the color represents the coupling efficiency.

In the case where the optical quality factor was set to Q = 1,000 and the waveguide width was set to w = 800 nm, the resultant Brillouin gain is as shown in Figure 4A. In the case of a first-order mode, the Brillouin gain reaches a maximum of 4400 W⁻¹m⁻¹. It can be seen that the gain is mainly produced by the MB effect, while the Brillouin gain produced by the PE effect is minimal. With the increase in the mode order, the Brillouin gain gradually decreases. This is due to the mismatch of the optical force distribution due to the complicated profile of the model in space so that the rapid spatial oscillation of the elastic mode largely offsets the overlap integral. At the same time, it can be observed that in the case of the third-order acoustic mode, the partial gain (SBS nonlinearity caused by the radiation pressure) exceeds the total gain. This is due to the coupling between the third-order breathing mode and the surrounding TE modes, the competition between the photo-elastic effect, and the moving boundary effect [42]. The boundary and volume integrand have opposite phases for this geometry, causing a self-canceling effect.

FIGURE 4

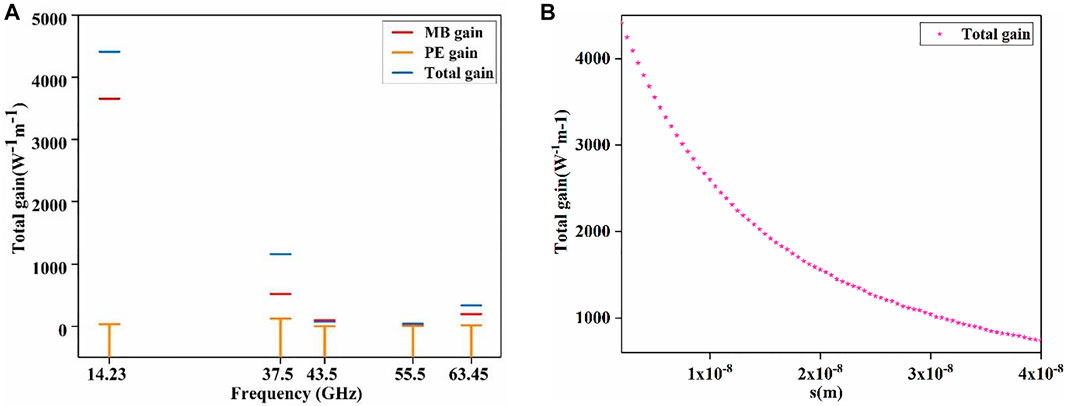
FIGURE 4. (A) Plot showing the Brillouin gain as a function of frequency with the waveguide width set to w = 800 nm; the red line represents the MB effect, the orange line the PE effect, and the blue line the total gain. (B) Calculated FSBS gain coefficients as the width of the air slot s is varied.

Next, the effect of the air slot width s on the FSBS gain coefficient was studied. We fixed the geometric size letting w = 800 nm and t = 215 nm. Then we varied s from 2 to 40 nm and calculated the FSBS gain coefficients. The corresponding FSBS gain coefficients are plotted in Figure 4B. The results show that as the air slot width S decreased, the total Brillouin gain decreased. This strong photon-phonon coupling phenomenon is produced by the combined action of electrostriction force and nanoscale radiation pressure, and the narrow air slot in the middle has considerable radiation pressure. The emergence of large radiation pressure-induced coupling represents a new form of boundary-induced Brillouin nonlinearity and a new form of boundary-mediated Brillouin coupling in subwavelength structures. This novel waveguide geometry enables independent control of acoustic modes and optomechanical driving forces, creating customizable Brillouin coupling over a 1–95 GHz bandwidth. The finite element simulations show that the FSBS effect is produced in the suspended slot waveguide and the obtained SBS gain reaches 4400 W⁻¹m⁻¹.

Conclusion

In this work, we designed a novel hybrid waveguide system. We demonstrated a Brillouin laser with a slot waveguide structure, which leveraged the favorable refractive index and the photo-elastic characteristics of diamond to generate a broad Brillouin frequency shift. The design uses the FSBS effect and by adjusting the cross-sectional width of the slot waveguide, achieves tuning of the frequency of the SBS acoustic wave. Multiphysics simulations reveal that the strength of photon-phonon coupling is dependent on the combined action of electrostriction force and nanoscale radiation pressure, with the narrow air slot in the middle of the waveguide generating considerable radiation pressure. The photon-phonon coupling induced by significant radiation pressure is a new form of Brillouin coupling which is induced by boundary-induced Brillouin nonlinearity and subwavelength structures. This suspended waveguide structure enables independent control of the acoustic wave and enables customizable Brillouin coupling over an ultra-wide bandwidth of 1–95 GHz. According to the PE and MB effect, the SBS laser of this slot waveguide shows an SBS gain of 4400 W⁻¹m⁻¹. At the same time, multiple transverse acoustic modes were coupled to produce relatively flat Brillouin gain across the 1–95 GHz frequency range. Therefore, this slot waveguide width tuning scheme can yield photon-phonon conversion based on the Brillouin nonlinear effect and guide and manipulate the phonons emitted by the Brillouin process on a chip. Therefore, we believe that this technique provides a means by which microwave sources can be produced via an on-chip Brillouin photoacoustic coupling mechanism.

Data Availability Statement

The raw data supporting the conclusions of this article will be made available by the authors, without undue reservation.

Author Contributions

WW: Investigation, Methodology, Writing—original draft, Writing—review and editing. YY: Conceptualization, Methodology, Writing—review and editing, Supervision, Funding acquisition. ZB: Investigation, Methodology, Writing—review and editing. YL: Writing—review and editing, Supervision. GW: Writing—review and editing, Supervision. KL: Investigation. CS: Investigation. ZW: Investigation. SL: Investigation. YL: Investigation. TL: Investigation. XY: Investigation. YW: Supervision, Funding acquisition. ZL: Supervision, Funding acquisition.

Funding

This work was supported by the National Natural Science Foundation of China (Grant No. 62005074, No. 61927815, No. 62075056, and No. 62004059), Natural Science Foundation of Hebei Province (No. F2021202002) and National Defense Science and Technology Key Laboratory Foundation (No. 61421070302).

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s Note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

1. Eggleton BJ, Poulton CG, Pant R. Inducing and Harnessing Stimulated Brillouin Scattering in Photonic Integrated Circuits. Adv Opt Photon (2013) 5(4):536–87. doi:10.1364/aop.5.000536

CrossRef Full Text | Google Scholar

2. Bai Z, Yuan H, Liu Z, Xu P, Gao Q, Williams RJ, et al. Stimulated Brillouin Scattering Materials, Experimental Design and Applications: A Review. Opt Mater (2018) 75:626–45. doi:10.1016/j.optmat.2017.10.035

CrossRef Full Text | Google Scholar

3. Cao C, Wang Y, Bai Z, Li Y, Yu Y, Lu Z. Developments of Picosecond Lasers Based on Stimulated Brillouin Scattering Pulse Compression. Front Phys (2021) 9:747272. doi:10.3389/fphy.2021.747272

CrossRef Full Text | Google Scholar

4. Okawachi Y, Bigelow MS, Sharping JE, Zhu Z, Schweinsberg A, Gauthier DJ, et al. Tunable All-Optical Delays via Brillouin Slow Light in an Optical Fiber. Phys Rev Lett (2005) 94:153902. doi:10.1103/physrevlett.94.153902

PubMed Abstract | CrossRef Full Text | Google Scholar

5. Song KY, Herraez MG, Thevenaz L. Observation of Pulse Delaying and Advancement in Optical Fibers Using Stimulated Brillouin Scattering. Opt Express (2005) 13:82–8. doi:10.1364/opex.13.000082

PubMed Abstract | CrossRef Full Text | Google Scholar

6. Zhu Z, Gauthier DJ, Boyd RW. Stored Light in an Optical Fiber via Stimulated Brillouin Scattering. Science (2007) 318:1748–50. doi:10.1126/science.1149066

PubMed Abstract | CrossRef Full Text | Google Scholar

7. Liu B, Geng Y, Zhang Q, Han X, Xu J, Zhou H, et al. All-optical Carrier Recovery for Self-Homodyne Detection via Injection Locked Brillouin Laser in Whispering-Gallery-Mode Microcavity. Chinese Optics Letters (2021) 19(11):111901. doi:10.3788/col202119.111901

CrossRef Full Text | Google Scholar

8. Kobyakov A, Sauer M, Chowdhury D. Stimulated Brillouin Scattering in Optical Fibers. Adv Opt Photon (2009) 2:1–59. doi:10.1364/aop.2.000001

CrossRef Full Text | Google Scholar

9. Lee H, Chen T, Li J, Yang KY, Jeon S, Painter O, et al. Chemically Etched Ultrahigh-Q Wedge-Resonator on a Silicon Chip. Nat Photon (2012) 6:369–73. doi:10.1038/nphoton.2012.109

CrossRef Full Text | Google Scholar

10. Grudinin IS, Matsko AB, Maleki L. Brillouin Lasing with a CaF2 Whispering Gallery Mode Resonator. Phys Rev Lett (2009) 102:043902. doi:10.1103/PhysRevLett.102.043902

PubMed Abstract | CrossRef Full Text | Google Scholar

11. Kang MS, Nazarkin A, Brenn A, Russell PSJ. Tightly Trapped Acoustic Phonons in Photonic crystal Fibres as Highly Nonlinear Artificial Raman Oscillators. Nat Phys (2009) 5:276–80. doi:10.1038/nphys1217

CrossRef Full Text | Google Scholar

12. Schneider T, Junker M, Hannover D. Generation of Millimetre-Wave Signals by Stimulated Brillouin Scattering for Radio over Fibre Systems. Electron Lett (2004) 40:1500–2. doi:10.1049/el:20046461

CrossRef Full Text | Google Scholar

13. Braje D, Hollberg L, Diddams S. Brillouin-Enhanced Hyperparametric Generation of an Optical Frequency Comb in a Monolithic Highly Nonlinear Fiber Cavity Pumped by a Cw Laser. Phys Rev Lett (2009) 102:193902. doi:10.1103/physrevlett.102.193902

PubMed Abstract | CrossRef Full Text | Google Scholar

14. Damzen MJ, Lamb RA, Wong GKN. Ultrashort Pulse Generation by Phase Locking of Multiple Stimulated Brillouin Scattering. Opt Commun (1991) 82:337–41. doi:10.1016/0030-4018(91)90470-x

CrossRef Full Text | Google Scholar

15. Lang Z, Qiao S, Ma Y. Acoustic Microresonator Based In-Plane Quartz-Enhanced Photoacoustic Spectroscopy Sensor with a Line Interaction Mode. Opt Lett (2022) 47(6):1295–8. doi:10.1364/ol.452085

PubMed Abstract | CrossRef Full Text | Google Scholar

16. Ma Y, He Y, Tong Y, Yu X, Tittel FK. Quartz-tuning-fork Enhanced Photothermal Spectroscopy for Ultra-high Sensitive Trace Gas Detection. Opt Express (2018) 26(24):32103–10. doi:10.1364/oe.26.032103

PubMed Abstract | CrossRef Full Text | Google Scholar

17. Pant R, Poulton CG, Choi D-Y, Mcfarlane H, Hile S, Li E, et al. On-chip Stimulated Brillouin Scattering. Opt Express (2011) 19:8285–90. doi:10.1364/oe.19.008285

PubMed Abstract | CrossRef Full Text | Google Scholar

18. Kang MS, Butsch A, Russell PSJ. Reconfigurable Light-Driven Opto-Acoustic Isolators in Photonic crystal Fibre. Nat Photon (2011) 5:549–53. doi:10.1038/nphoton.2011.180

CrossRef Full Text | Google Scholar

19. Jalali B, Raghunathan V, Shori R, Fathpour S, Dimitropoulos D, Stafsudd O. Prospects for Silicon Mid-IR Raman Lasers. IEEE J Select Top Quan Electron. (2006) 12:1618–27. doi:10.1109/jstqe.2006.885340

CrossRef Full Text | Google Scholar

20. Foster MA, Turner AC, Sharping JE, Schmidt BS, Lipson M, Gaeta AL. Broad-band Optical Parametric Gain on a Silicon Photonic Chip. Nature (2006) 441:960–3. doi:10.1038/nature04932

PubMed Abstract | CrossRef Full Text | Google Scholar

21. Rong H, Jones R, Liu A, Cohen O, Hak D, Fang A, et al. A Continuous-Wave Raman Silicon Laser. Nature (2005) 433:725–8. doi:10.1038/nature03346

PubMed Abstract | CrossRef Full Text | Google Scholar

22. Shin H, Qiu W, Jarecki R, Cox JA, Olsson RH, Starbuck A, et al. Tailorable Stimulated Brillouin Scattering in Nanoscale Silicon Waveguides. Nat Commun (2013) 4:1944. doi:10.1038/ncomms2943

PubMed Abstract | CrossRef Full Text | Google Scholar

23. Mildren R, Rabeau J, editors. Optical Engineering of diamond. John Wiley & Sons (2013). doi:10.1002/9783527648603

CrossRef Full Text | Google Scholar

24. Williams RJ, Kitzler O, Bai Z, Sarang S, Jasbeer H, McKay A, et al. High Power diamond Raman Lasers. IEEE J Selected Top Quan Electron (2018) 24(5):1602214. doi:10.1109/jstqe.2018.2827658

CrossRef Full Text | Google Scholar

25. Bai Z, Zhang Z, Wang K, Gao J, Zhang Z, Yang X, et al. Comprehensive thermal Analysis of diamond in a High-Power Raman Cavity Based on FVM-FEM Coupled Method. Nanomaterials (2021) 11(6):1572. doi:10.3390/nano11061572

PubMed Abstract | CrossRef Full Text | Google Scholar

26. Li Y, Bai Z, Chen H, Jin D, Yang X, Qi Y, et al. Eye-safe diamond Raman Laser. Results Phys (2020) 16:102853. doi:10.1016/j.rinp.2019.102853

CrossRef Full Text | Google Scholar

27. Bai Z, Williams RJ, Kitzler O, Sarang S, Spence DJ, Wang Y, et al. Diamond Brillouin Laser in the Visible. APL Photon (2020) 5(3):031301. doi:10.1063/1.5134907

CrossRef Full Text | Google Scholar

28. Chen H, Bai Z, Yang X, Ding J, Qi Y, Yan B, et al. Enhanced Stimulated Brillouin Scattering Utilizing Raman Conversion in diamond. Appl Phys Lett (2022) 120(18):181103. doi:10.1063/5.0087092

CrossRef Full Text | Google Scholar

29. Parameswaran KR, Route RK, Kurz JR, Roussev RV, Fejer MM, Fujimura M. Highly Efficient Second-Harmonic Generation in Buried Waveguides Formed by Annealed and Reverse Proton Exchange in Periodically Poled Lithium Niobate. Opt Lett (2002) 27(3):179–81. doi:10.1364/ol.27.000179

PubMed Abstract | CrossRef Full Text | Google Scholar

30. Miller GD, Batchko RG, Tulloch WM, Weise DR, Fejer MM, Byer RL. 42%-efficient Single-Pass Cw Second-Harmonic Generation in Periodically Poled Lithium Niobate. Opt Lett (1997) 22(24):1834–6. doi:10.1364/ol.22.001834

PubMed Abstract | CrossRef Full Text | Google Scholar

31. Eggleton BJ, Poulton CG, Rakich PT, Steel MJ, Bahl G. Brillouin Integrated Photonics. Nat Photon (2019) 13(15):1–14. doi:10.1038/s41566-019-0498-z

CrossRef Full Text | Google Scholar

32. Damzen MJ, Vlad V, Mocofanescu A. Stimulated Brillouin Scattering: Fundamentals and Applications. CRC Press (2010). doi:10.1201/9781420033465

CrossRef Full Text | Google Scholar

33. Mirnaziry SR, Wolff C, Steel MJ, Eggleton BJ, Poulton CG. Stimulated Brillouin Scattering in Silicon/chalcogenide Slot Waveguides. Opt Express (2016) 24(5):4786–800. doi:10.1364/oe.24.004786

PubMed Abstract | CrossRef Full Text | Google Scholar

34. Agrawal GP. Nonlinear Fiber Optics, IV. Academic Press (2006).

Google Scholar

35. Zhou L, Lu Y, Fu Y, Ma H, Du C. Design of a Hybrid On-Chip Waveguide with Giant Backward Stimulated Brillouin Scattering. Opt Express (2019) 27(18):24953. doi:10.1364/oe.27.024953

PubMed Abstract | CrossRef Full Text | Google Scholar

36. Qiu W, Rakich PT, Shin H, Dong H, Soljačić M, Wang Z. Stimulated Brillouin Scattering in Nanoscale Silicon Step-index Waveguides: A General Framework of Selection Rules and Calculating SBS Gain. Opt Express (2013) 21(25):31402–19. doi:10.1364/oe.21.031402

PubMed Abstract | CrossRef Full Text | Google Scholar

37. Aryanfar I, Wolff C, Steel MJ, Eggleton BJ, Poulton CG. Mode Conversion Using Stimulated Brillouin Scattering in Nanophotonic Silicon Waveguides. Opt Express (2014) 22:29270–82. doi:10.1364/oe.22.029270

PubMed Abstract | CrossRef Full Text | Google Scholar

38. Yu Z, Sun X. Giant Enhancement of Stimulated Brillouin Scattering with Engineered Phoxonic crystal Waveguides. Opt Express (2018) 26(2):1255–67. doi:10.1364/oe.26.001255

PubMed Abstract | CrossRef Full Text | Google Scholar

39. Rakich PT, Davids P, Wang Z. Tailoring Optical Forces in Waveguides through Radiation Pressure and Electrostrictive Forces. Opt Express (2010) 18(14):14439–53. doi:10.1364/oe.18.014439

PubMed Abstract | CrossRef Full Text | Google Scholar

40. Gordon JP. Radiation Forces and Momenta in Dielectric media. Phys Rev A (1973) 8(1):14–21. doi:10.1103/physreva.8.14

CrossRef Full Text | Google Scholar

41. Wang W, Yu Y, Li Y, Bai Z, Wang G, Li K, et al. Tailorable Brillouin Light Scattering in a Lithium Niobate Waveguide. Appl Sci (2021) 11(18):8390. doi:10.3390/app11188390

CrossRef Full Text | Google Scholar

42. Gao W, Chen L, Jiang W, Zhang Z, Zhang X, Gao P, et al. Stimulated Brillouin Scattering by the Interaction between Different-Order Optical and Acoustical Modes in an As2Se3 Photonic crystal Fiber. Chin Opt Lett (2020) 18(1):010602. doi:10.3788/col202018.010602

CrossRef Full Text | Google Scholar