Parameter Identification for Memristive Chaotic System Using Modified Sparrow Search Algorithm

A memristor is a non-linear element. The chaotic system constructed by it can improve its unpredictability and complexity. Parameter identification of a memristive chaotic system is the primary task to implement chaos control and synchronization. To identify the unknown parameters accurately and quickly, we introduce the Sine Pareto Sparrow Search Algorithm (SPSSA), a modified sparrow search algorithm (SSA). in this research. Firstly, we introduce the Pareto distribution to alter the scroungers’ location in the SSA. Secondly, we use a sine-cosine strategy to improve the producers’ position update. These measures can effectively accelerate the convergence speed and avoid local optimization. Thirdly, the SPSSA is used to identify the parameters of a memristive chaotic system. The proposed SPSSA exceeds the classic SSA, particle swarm optimization algorithm (PSO), and artificial bee colony algorithm (ABC) in simulations based on the five benchmark functions. The simulation results of parameter identification of a memristive chaotic system show that the method is feasible, and the algorithm has a fast convergence speed and high estimation accuracy.

1 Introduction

A memristor is the fourth fundamental circuit element except for resistance R, capacitance C, and inductance. L. Strukov et al [1]. realized the first memristor in the world in 2008. It has set off an upsurge of memristor research. In recent years, memristors have been intensely studied in many application fields, such as memory [2], neural networks [3, 4], and image processing [5]. A memristor is a non-linear element. A chaotic system constructed by the memristor can improve the unpredictability and complexity of the system [6–10]. Applying a memristive chaotic system is also one of the research hotspots [11–13].

In practical engineering applications, the parameter identification of chaotic systems is the primary problem in realizing chaos control and synchronization. The accuracy of the parameter identification will directly affect the control effect of a chaotic system. Therefore, it is essential to accurately identify the parameters of a chaotic system, which has crucial research significance. The parameter identification of a chaotic system is essentially a complex non-linear numerical optimization problem based on multi-dimensional search space. Because swarm intelligence (SI) optimization algorithm does not need the derivative information of objective function, it has more advantages than traditional optimization algorithm in parameter identification. At present, many research results have emerged for some classical continuous memristive chaotic systems, such as particle swarm optimization algorithm [14, 15], differential evolution algorithm [16, 17], artificial bee colony optimization algorithm [18], bird swarm algorithm [19], Jaya algorithm [20]. For a discrete memristive chaotic system, the swarm intelligence optimization algorithms also provide many practical solutions, such as an improved PSO algorithm [21], meta-heuristic algorithm [22], and enhanced differential evolution algorithm [23].

The Sparrow search algorithm (SSA) is one of SI optimization algorithms proposed in recent years [24]. It is created by imitating the foraging behavior of a group of sparrows. Compared with other SI optimization algorithms, SSA has the advantages of fewer parameters, simple calculation, and easy implementation in dealing with multi-dimensional problems and global search. Therefore, SSA is used to solve the problem of parameter identification in a chaotic system. However, the traditional SSA is also easy to fall into local optimization. To avoid this phenomenon, many researchers proposed some improved methods. For example, Xiong et al. [25] used a fractional-order chaotic sequence to increases the diversity of the population and used Pareto mutation to escape local best. These methods achieve better results than traditional SSA on 12 benchmark functions. But it is more time-consuming than SSA. In this study, we propose a modified SSA called Sine Pareto Sparrow Search Algorithm (SPSSA). The following are the primary contributions of this paper:

(1) We use a sine-cosine strategy to improve the producers’ position update.

(2) To improve the location of the scroungers, we employ Pareto distribution. This concept is useful for speeding up global convergence and avoiding local minimum points.

(3) A memristive chaotic system’s parameters are determined using the SPSSA.

In the following sections, Section 2 introduces preliminaries for parameter identification and some concepts of the SPSSA. Section 3 is the experimental results of the paper. Finally, our conclusions presented in Section 4.

2 Methods

2.1 Parameter Identification of the Chaotic System

Consider the n-dimensional original chaotic system with m parameters

$\dot{X}=F\left(X,X_0,\theta \right)(1)$

where, $X={\left(x_1,x_2,\cdots ,x_n\right)}^{\text{T}}\in R^n$ is the state vector, $\theta ={\left({\theta }_1,{\theta }_2,\cdots ,{\theta }_m\right)}^{\text{T}}\in R^m$ is system parameter vector, X₀ is the initial state of the system. $F:R^n\times R^m\to R^n$ is a given non-linear vector function.

Assuming that the system structure is known, the identified system can be defined as Eq. 2:

$\dot{Y}=F\left(Y,X_0,\widehat{\theta }\right)(2)$

where, $Y={\left(y_1,y_2,\cdots ,y_n\right)}^{\text{T}}\in R^n$ is the state vector of the identified system. $\widehat{\theta }={\left({\widehat{\theta }}_1,{\widehat{\theta }}_2,\cdots ,{\widehat{\theta }}_m\right)}^{\text{T}}\in R^m$ is the identified system parameter.

The parameter identified problem can be transformed into a Eq. 3

$\widehat{\theta }=\arg \underset{\theta }{\min }J\left(\theta \right)=\arg \underset{\theta }{\min }\frac{1}{D_n}{{\displaystyle \sum _{i=1}^{D_n}\Vert x_i-y_i\Vert }}^2(3)$

where, $D_n$ represents the data length used for state variables, x_i and y_i represent the actual value and estimated value of the system under their state variables, respectively. Through the above analysis, the parameter identification problem of a chaotic system can be transformed into a multivariable optimization problem, and the relevant variables can be adjusted to minimize the target value J. The optimization principle is shown in Figure 1.

FIGURE 1

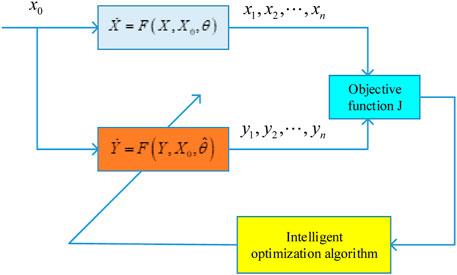
FIGURE 1. Identification principle of a chaotic system [20].

It is a multi-dimensional and multi-mode non-linear function, and the chaotic system is dynamically unstable and sensitive to initial parameters. Therefore, it is difficult to identify the parameters of a chaotic system effectively and accurately. The sparrow search algorithm is easy to realize in dealing with multi-dimensional problems, so this paper proposes a modified SSA and takes Eq. 3 as the objective function.

2.2 The Sparrow Search Algorithm

When a group of sparrows is searching for food, we can divide them into three roles: producers, scroungers, and scouts. Producers, also called finders, are some sparrows searching for food. Scroungers are some sparrows following the producers’ track to search for food. Scouts are sparrows watching for dangers. Producers usually account for 10%–20% of the population. Some sparrows will be selected randomly as scouts, which typically account for 10%–20% of the population.

In SSA, the behavior of sparrows searching for food can be simulated as the process of solving optimization problems. Consider that there exist N sparrows, the location of the ith sparrow is $X_i=\left[x_{i1},\dots ,x_{ij},\dots ,x_{iD}\right]$, where i = 1, 2, … , N, D is D-dimensional search space.

The formula for the location update of producers is described as below:

$x_{ij}^{\text{t}+1}=\{\begin{array}{l}{x}_{ij}^t·\exp \left(\frac{-i}{\alpha ·T_{\max }}\right),R_2<ST\hfill \\ x_{ij}^t+QL,R_2\mathrm{⩾}ST\hfill \end{array}(4)$

where, t presents the current iteration, j = 1,2, … D. T_max indicates the cycles number. $\alpha \in \left(\mathrm{0,1}\right]$ and $R_2\in \left[\mathrm{0,1}\right]$ are all random numbers . $ST\in \left[0.5,1\right]$ is the alarm value. Q is a random number subject to standard normal distribution; L is a matrix of $1\times D$. The initial values of all elements in the D are set to 1.

The location of scroungers is updated as follows:

$X_{ij}^{t+1}=\{\begin{array}{cc}Qexp\left(\frac{x_{\text{worst}}^t-x_{ij}^t}{i^2}\right)& \text{if}i>N/2\\ X_P^{t+1}+\left|X_{i,j}^t-X_P^{t+1}\right|\cdot A^{+}\cdot L& \text{otherwise}\end{array}(5)$

where, $X_P^{t+1}$ is the producers’ best location at iteration $t+1$, while $x_{\text{worst}}^t$ denotes the current global worst location. A is a matrix of $1\times D$. In A, all of the elements are initialized at random $A^{+}=A^T{\left(A{A}^T\right)}^{-1}$.

In addition, the position of the scouts is updated by (6)

$X_{i,j}^{t+1}=\{\begin{array}{cc}{X}_{\text{best}}^t+\beta \cdot \left|X_{i,j}^t-X_{\text{best}}^t\right|& \text{if}{f}_i>f_g\\ X_{i,j}^t+K\cdot \left(\frac{\left|X_{i,j}^t-X_{\text{worst}}^{t+1}\right|}{\left(f_i-f_w\right)+\epsilon }\right)& \text{if}{f}_i=f_g\end{array}(6)$

where, $X_{best}^t$ is the optimal place at iteration t. $\beta$ is a parameter that controls the size of the steps. It is a random number with a normal distribution, with a mean of 0 and a variance of 1. The current sparrow fitness value, the best fitness value, and the worst fitness value are f_i, f_g and f_w, respectively. K is a random number that ranges from -1 to 1. $\epsilon$ is a small constant that prevents zero-division-error.

2.3 The Modified Sparrow Search Algorithm

2.3.1 Updating Scroungers’ Locations

In the process of foraging, scroungers often forage around the best producer. During this process, the producers and the scroungers may switch roles with each other due to the competition for food. According to the optimization method proposed in [26], the Pareto distribution is introduced to improve scroungers’ location so that we can avoid the algorithm falling into local optimization.

A random variable is said to obey the Pareto distribution if its cumulative distribution function has the following equation [26].

$F\left(x_3\right)=\{\begin{array}{ll}1-{\left(\frac{k}{x_3}\right)}^h,\hfill & x_3\ge k\hfill \\ 0,\hfill & x_3<k\hfill \end{array}(7)$

where, k > 0 is the scale parameter, h > 0 is the shape parameter (Pareto’s index of inequality).

To avoid the local minimum points, the Pareto distribution is utilized [25]. As a result, the scroungers’ location update formula is changed by Eq. 8

$x_{ij}^{t+1}=\{\begin{array}{ll}Q\cdot \exp \left(\frac{x_{worst}^t-x_{ij}^t}{i^2}\right),\hfill & i>N/2\hfill \\ x_{ij}^t+\alpha \otimes Pareto\left(k,h\right)\otimes \left(x_i^t-x_{best}\right),\hfill & \text{otherwise}\hfill \end{array}(8)$

where, $Pareto\left(k,h\right)$ is a random number that follows the Pareto distribution. $\alpha$ is the step scale factor, and $\otimes$ is the point-to-point multiplication.

2.3.2 Updating Producers’ Locations

In the Eq. 4, when R₂ < ST, as the number of iterations increases, the producers gradually approach the local best location. Scroungers will also pour into that location, and the diversity of population locations will be decreased. The algorithm may inevitably fall into local optimum. To solve this problem, the idea of the sine cosine algorithm (SCA) is integrated into the producers’ location update method [27], and a learning factor is introduced. The learning factor has a bigger value in the early stage of the search, which is conducive to global exploration, and a smaller value in the later stage, which is conducive to improving local development ability and accuracy. The learning factor formula and the improved producers’ location formula are described as follows:

$\omega ={\omega }_{\max }-t\times \left({\omega }_{\max }/T_{\max }\right)(9)$

$X_{i,j}^{t+1}=\{\begin{array}{c}\left(1-\omega \right)\cdot X_{i,j}^t+\omega \cdot \sin \left(r_1\right)\cdot \left|r_2\cdot X_{\text{best}}^t-X_{i,j}^t\right|,R_2<ST\\ \left(1-\omega \right)\cdot X_{i,j}^t+\omega \cdot \cos \left(r_1\right)\cdot \left|r_2\cdot X_{\text{best}}^t-X_{i,j}^t\right|,R_2\mathrm{⩾}ST\end{array}(10)$

where, ${\omega }_{\max }$ is a constant, t indicates the current iteration, $r_1$ is a random number in [0,2π], and $r_2$ is a random number in [0, 2].

Implementation of an improved sparrow search algorithm for parameter identification of a memristive chaotic system.

Algorithm 1 shows the pseudo code for determining a memristive system’s parameters using the SPSSA.

ALGORITHM 1

Algorithm 1. Pseudo code of SPSSA in parameter identification.

3 Experiments and Discussions

To check the performance of SPSSA, we carry out some simulation experiments. The software platform is Windows 10 and MATLAB 2021b. The hardware platform is a desktop PC which a CPU is 3.20 GHz, and a memory size is 16 GB.

3.1 Benchmark Function Comparison Experiment

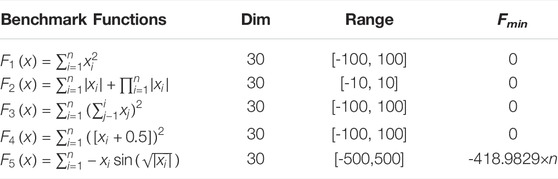
To prove the performance of the proposed SPSSA, we select five benchmark functions, which have been widely used to test the effectiveness of the SI algorithm [23]. Table 1 shows the name, range, and the minimum value of the benchmark test function.

TABLE 1

TABLE 1. Benchmark test functions.

In our experiment, we input the population number N = 50, Tmax = 500, ${\omega }_{\max }=0.6$, Fd = Sd = 0.2. The dimension and the search range are set according to the Table 1. The five benchmark functions are used as fitness functions. Each benchmark test function is run 30 times using four different SI algorithms. Table 2 contains the best value, average, standard deviation, and computation time. The best value reflects exploration ability, the average value demonstrates convergence accuracy, and the standard deviation depicts the SPSSA’s stability under the same benchmark test function [25].

TABLE 2

TABLE 2. Experiment results of benchmark functions.

In terms of the best value, average value, and standard deviation, the optimization accuracy of SPSSA is superior than the other three algorithms, as shown in Table 2. Especially for benchmark functions F5, only SPSSA converges to the optimal value. Although SPSSA is not the fastest, its accuracy and stability are the best. It shows that the SPSSA has a strong global search ability and better equilibrium. To further prove the dynamic convergence performance, four swarm intelligence techniques are utilized to show the convergence curves of the five benchmark functions (in Figure 2).

FIGURE 2

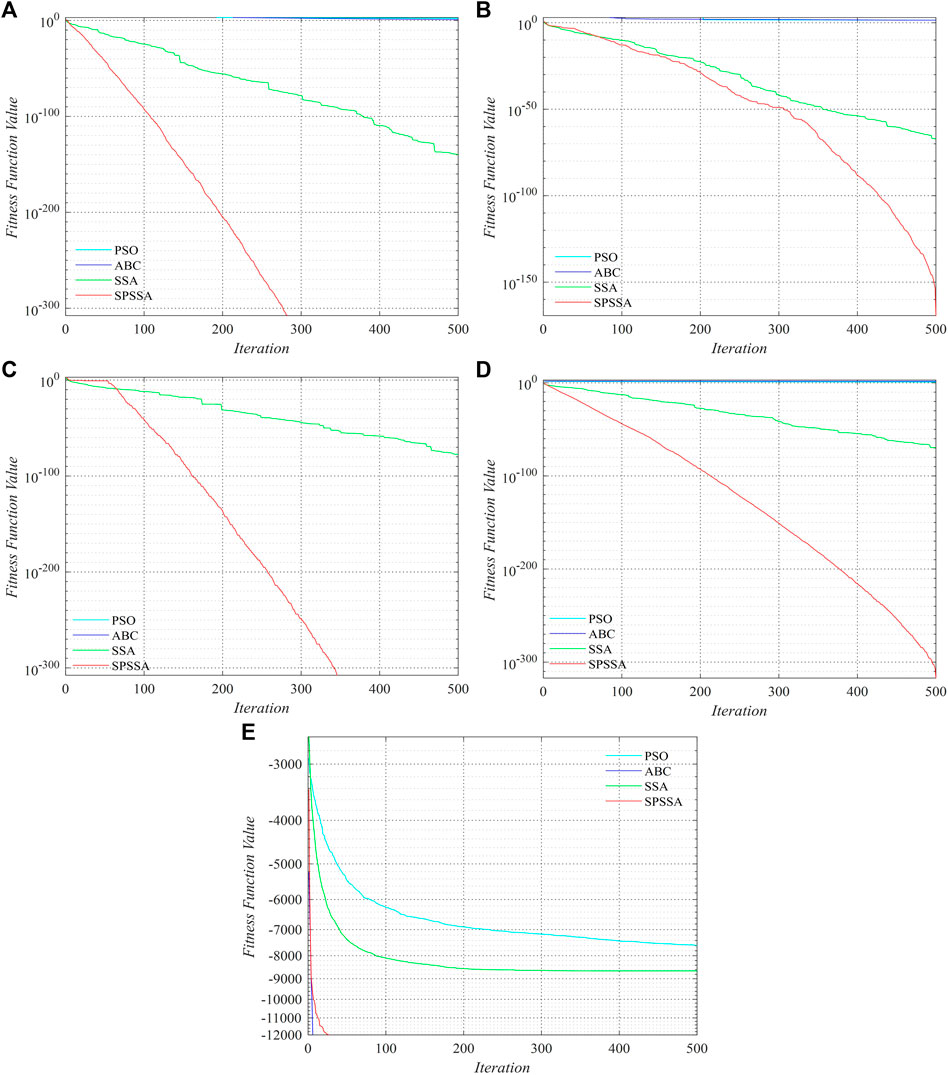
FIGURE 2. Four algorithms’ convergence curves on five benchmark functions. (A) F1; (B) F2; (C) F3; (D) F4; (E) F5.

From Figure 2, we can see that SPSSA proposed in this paper has a faster downward trend, steeper slope, and fewer iterations compared with the other three algorithms, obviously in Figure 2A,C, and Figure 2E. Figures 2B,D also show that SPSSA can get the best result. As a result, SPSSA outperforms PSO, ABC, and SSA in terms of convergence speed and optimization impact.This shows the feasibility and superiority of SPSSA.

3.2 Parameter Identification of a Memristive Chaotic System

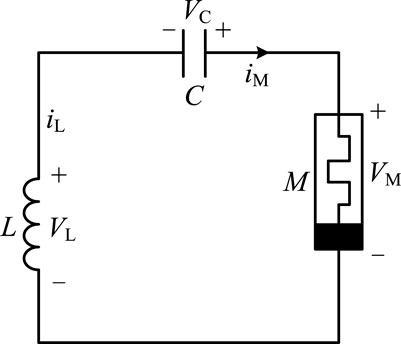
Figure 3 shows the simplest memristor chaotic circuit model. A linear passive inductor, a linear passive capacitor, and a non-linear active charge driven memristor make up the circuit [28].

FIGURE 3

FIGURE 3. The simplest memristor chaotic circuit.

The dimensionless equation of that simplest memristor circuit system can be described by Eq. 11

$\{\begin{array}{l}\dot{x}=ay\hfill \\ \dot{y}=-b\left(x+d\left(z^2-1\right)y\right)\hfill \\ \dot{z}=y-cz+yz\hfill \end{array}(11)$

where, $\dot{x}=\frac{\text{d}x}{\text{d}t},\dot{y}=\frac{\text{d}y}{\text{d}t},\dot{z}=\frac{\text{d}z}{\text{d}t}$. $a,b,c,d$ are system parameters. When the system parameters Eq. 11 are set to a = 1, b = 1/3, $c=0.6,d=1.5$ the system Eq. 11 exhibits hyperchaotic behavior. When the initial state values are set to x (0) = 0.1, y (0) = 0, z (0) = 0, we can use fourth-order Runge Kutta method to solve the differential Eq. 11. The phase diagrams of the hyperchaotic attractor are shown in Figure 4, in which the step length h = 0.1 and the sampling times Sn = 20000.

FIGURE 4

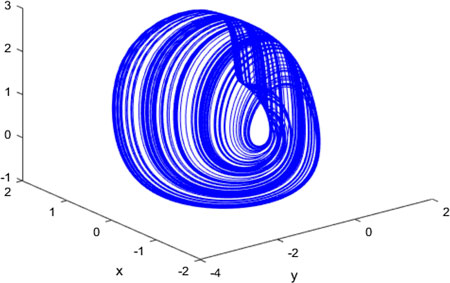
FIGURE 4. 3D diagram of the memristive chaotic system Eq. 11

In the following simulations, we set a = 1, b = 1/3, c = 0.6, d = 1.5. x (0) = 0.1, y (0) = 0, z (0) = 0 are initial value of the original system. The step length h is 0.01 and the sampling times Sn = 500. The parameters of the SPSSA are input as follows: N = 20, T_max = 100. Other parameters are same as those in Section 3.1. The range of the parameters of the memristive chaotic system is set to $0\le a\le \mathrm{3,0}\le b\le \mathrm{2,0}\le c\le \mathrm{3,0}\le d\le 2$.

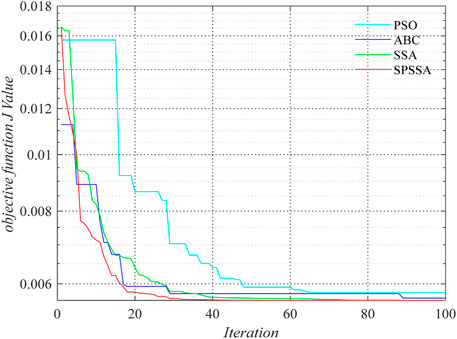
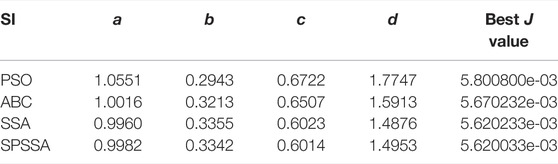
Figure 5 displays the convergence curve of the chaotic system Eq. 11. Figure 6 show the curve of parameters identification convergence. The final identified parameters of the PSO, ABC, SSA, and SPSSA are provided in Table 3.

FIGURE 5

FIGURE 5. The convergence curve of a memristive chaotic system.

FIGURE 6

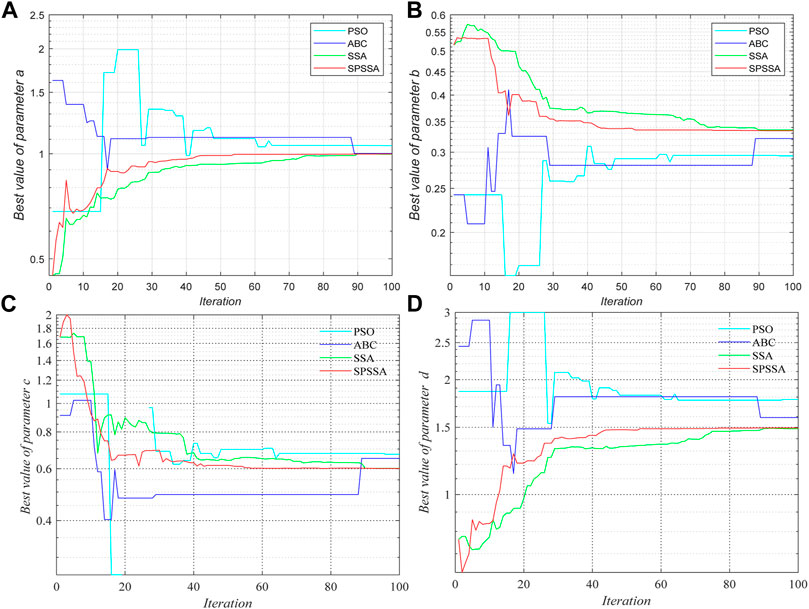
FIGURE 6. Convergence and optimization curve of parameter identification for a memristive chaotic system. (A) Optimization curve of parameter a. (B) Optimization curve of parameter b. (C) Optimization curve of parameter c. (D) Optimization curve of parameter d.

TABLE 3

TABLE 3. Identified parameters by PSO,ABC,SSA, and BSA algorithms.

As shown in Figure 5, it is obvious that the SPSSA has the fastest convergence speed and the smallest J value. Although SSA converges to the optimal value, its rate is significantly slower than SPSSA. This shows that among the four algorithms, SPSSA has the best performance. From Figure 6 we can see among the four algorithms, SPSSA always converges to the optimal value fastest. It is clear to see from Table 3 that the parameter values calculated by SPSSA are the closest to the actual value. All these show that the convergence and stability of SPSSA are better than the other three algorithms.

4 Conclusion

In this paper, a novel swarm intelligence optimization algorithm, the modified sparrow search algorithm, is used for the parameter estimation of a memristive chaotic system. The proposed algorithm, SPSSA, uses a sine cosine method to the sparrow finders’ position to avoid falling into local optimization in the later search stage. Pareto distribution is used to adjust the current individual position, to improve the speed and the global optimization accuracy. Five standard test functions are used to verify the algorithm, and the results show that the SPSSA has high search accuracy. The simulation results show that the SPSSA can identify the parameters of the simplest memristive chaotic system more accurately, more rapidly, and more stable than the PSO, the ABC, and the SSA. This proves that SPSSA has good effectiveness and robustness. Other memristive chaotic systems can benefit from the SPSSA. If we know the equation of other systems, we can identify the system parameters by the methods mentioned in the article.

Data Availability Statement

The original contributions presented in the study are included in the article/Supplementary Materials, further inquiries can be directed to the corresponding author.

Author Contributions

QX: system analysis, software design, and draft writing. JS: checking the whole analysis and manuscript revision. BT: numerical analysis. YX: checking the whole analysis.

Funding

This research was funded by the Natural Science Foundation of Hunan Province (No. 2021JJ50137), Doctoral research foundation program in Hunan University of arts and science (No.21BSQD30), the Scientific Research Project of Hunan University of arts and science (No. 21YB12).

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s Note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

1. Strukov DB, Snider GS, Stewart DR, Williams RS. The Missing Memristor Found. nature (2008) 453(7191):80–3. doi:10.1038/nature06932

PubMed Abstract | CrossRef Full Text | Google Scholar

2. Haj-Ali A, Ben-Hur R, Wald N, Ronen R, Kvatinsky S. Not in Name Alone: A Memristive Memory Processing Unit for Real In-Memory Processing. IEEE Micro (2018) 38(5):13–21. doi:10.1109/mm.2018.053631137

CrossRef Full Text | Google Scholar

3. Wang Y, Wang G, Shen Y, Iu HHC. A Memristor Neural Network Using Synaptic Plasticity and its Associative Memory. Circuits Syst Signal Process (2020) 39(7):3496–511. doi:10.1007/s00034-019-01330-8

CrossRef Full Text | Google Scholar

4. Zhang Y, Cui M, Shen L, Zeng Z. Memristive Fuzzy Deep Learning Systems[J]. IEEE Trans Fuzzy Syst (2020) 29(8):2224–38.

Google Scholar

5. Hu X, Feng G, Duan S, Liu L. A Memristive Multilayer Cellular Neural Network with Applications to Image Processing. IEEE Trans Neural Netw Learn Syst (2017) 28(8):1889–901. doi:10.1109/TNNLS.2016.2552640

PubMed Abstract | CrossRef Full Text | Google Scholar

6. Mannan ZI, Yang C, Kim H. Oscillation with 4-Lobe Chua Corsage Memristor. IEEE Circuits Syst Mag (2018) 18(2):14–27. doi:10.1109/mcas.2018.2821724

CrossRef Full Text | Google Scholar

7. Bao H, Jiang T, Chu K, Chen M, Xu Q, Bao B. Memristor-based Canonical Chua’s Circuit: Extreme Multistability in Voltage-Current Domain and its Controllability in Flux-Charge Domain[J]. Complexity (2018) 2018. doi:10.1155/2018/5935637

CrossRef Full Text | Google Scholar

8. Guo M, Yang W, Xue Y, Gao Z, Yuan F, Dou G, et al. Multistability in a Physical Memristor-Based Modified Chua's Circuit. Chaos (2019) 29(4):043114. doi:10.1063/1.5089293

PubMed Abstract | CrossRef Full Text | Google Scholar

9. Huang L, Yao W, Xiang J, Zhang Z. Heterogeneous and Homogenous Multistabilities in a Novel 4D Memristor-Based Chaotic System with Discrete Bifurcation Diagrams[J]. Complexity (2020) 2020:2408460. doi:10.1155/2020/2408460

CrossRef Full Text | Google Scholar

10. Ma X, Mou J, Liu J, Ma C, Yang F, Zhao X. A Novel Simple Chaotic Circuit Based on Memristor-Memcapacitor. Nonlinear Dyn (2020) 100(3):2859–76. doi:10.1007/s11071-020-05601-x

CrossRef Full Text | Google Scholar

11. Chen M, Wang Z, Nazarimehr F, Jafari S. A Novel Memristive Chaotic System without Any Equilibrium point. Integration (2021) 79:133–42. doi:10.1016/j.vlsi.2021.04.002

CrossRef Full Text | Google Scholar

12. Chen M, Wang Z, Nazarimehr F, Jafari S. A Novel Memristive Chaotic System without Any Equilibrium point. Integration (2021) 79:133–42. doi:10.1016/j.vlsi.2021.04.002

CrossRef Full Text | Google Scholar

13. Ostrovskii V, Fedoseev P, Bobrova Y, Butusov D. Structural and Parametric Identification of Knowm Memristors. Nanomaterials (2021) 12(1):63. doi:10.3390/nano12010063

CrossRef Full Text | Google Scholar

14. Lazzús JA, Vega-Jorquera P, López-Caraballo CH, Palma-Chilla L, Salfate I. Parameter Estimation of a Generalized Lotka-Volterra System Using a Modified PSO Algorithm. Appl Soft Comput (2020) 96:106606. doi:10.1016/j.asoc.2020.106606

CrossRef Full Text | Google Scholar

15. Peng Y, Sun K, He S, Yang X. Parameter Estimation of a Complex Chaotic System with Unknown Initial Values[J]. The Eur Phys J Plus (2018) 133(8):1–13. doi:10.1140/epjp/i2018-12091-1

CrossRef Full Text | Google Scholar

16. Du W, Miao Q, Tong L, Tang Y. Identification of Fractional-Order Systems with Unknown Initial Values and Structure. Phys Lett A (2017) 381(23):1943–9. doi:10.1016/j.physleta.2017.03.048

CrossRef Full Text | Google Scholar

17. Gu W, Yu Y, Hu W. Parameter Estimation of Unknown Fractional-Order Memristor-Based Chaotic Systems by a Hybrid Artificial Bee colony Algorithm Combined with Differential Evolution[J]. Nonlinear Dyn (2016) 84(2):779–95.

CrossRef Full Text | Google Scholar

18. Hu W, Yu Y, Zhang S. A Hybrid Artificial Bee colony Algorithm for Parameter Identification of Uncertain Fractional-Order Chaotic Systems[J]. Nonlinear Dyn (2015) 82(3):1441–56.

CrossRef Full Text | Google Scholar

19. Zhang P, Yang R, Yang R, Ren G, Yang X, Xu C, et al. Parameter Estimation for Fractional-Order Chaotic Systems by Improved Bird Swarm Optimization Algorithm. Int J Mod Phys C (2019) 30(11):1950086. doi:10.1142/s0129183119500864

CrossRef Full Text | Google Scholar

20. Chen F, Ding Z, Lu Z, Zeng X. Parameters Identification for Chaotic Systems Based on a Modified Jaya Algorithm. Nonlinear Dyn (2018) 94(4):2307–26. doi:10.1007/s11071-018-4490-9

CrossRef Full Text | Google Scholar

21. Peng Y, Sun K, He S, Peng D. Parameter Identification of Fractional-Order Discrete Chaotic Systems. Entropy (2019) 21(1):27. doi:10.3390/e21010027

PubMed Abstract | CrossRef Full Text | Google Scholar

22. Peng YX, Sun KH, He SB. Dynamics Analysis of Chaotic Maps: From Perspective on Parameter Estimation by Meta-Heuristic Algorithm*. Chin Phys. B (2020) 29(3):030502. doi:10.1088/1674-1056/ab695c

CrossRef Full Text | Google Scholar

23. Peng Y, He S, Sun K. Parameter Identification for Discrete Memristive Chaotic Map Using Adaptive Differential Evolution Algorithm. Nonlinear Dyn (2022) 107(1):1263–75. doi:10.1007/s11071-021-06993-0

CrossRef Full Text | Google Scholar

24. Xue J, Shen B. A Novel Swarm Intelligence Optimization Approach: Sparrow Search Algorithm. Syst Sci Control Eng (2020) 8:22–34. doi:10.1080/21642583.2019.1708830

CrossRef Full Text | Google Scholar

25. Xiong Q, Zhang X, He S, Shen J. A Fractional-Order Chaotic Sparrow Search Algorithm for Enhancement of Long Distance Iris Image. Mathematics (2021) 9(21):2790. doi:10.3390/math9212790

CrossRef Full Text | Google Scholar

26. Wei J, Chen Y, Yu Y, Chen Y. Optimal Randomness in Swarm-Based Search. Mathematics (2019) 7:828. doi:10.3390/math7090828

CrossRef Full Text | Google Scholar

27. Mirjalili S. SCA: A Sine Cosine Algorithm for Solving Optimization Problems. Knowledge-based Syst (2016) 96:120–33. doi:10.1016/j.knosys.2015.12.022

CrossRef Full Text | Google Scholar

28. Muthuswamy B. Implementing Memristor Based Chaotic Circuits. Int J Bifurcation Chaos (2010) 20(05):1335–50. doi:10.1142/s0218127410026514

CrossRef Full Text | Google Scholar