A New Four-Dimensional Chaotic System and its Circuit Implementation

A new four-dimensional chaotic system is designed in the paper. The equilibrium point and stability of the chaotic system are analyzed, and the dynamical behaviors of the system under different parameters are analyzed by using Lyapunov exponents, Bfurcation diagram, SE and C0 complexity algorithms. The special phenomenon of the coexistence of attractors is also found. Finally, the implementation of circuit of the new system is carried out using digital signal processing (DSP) technology, and the results are consistent with the numerical simulation results, which prove the validity of the theoretical analysis. Through analysis and simulation of the system, it can be found that it has relatively rich dynamic characteristics and can be applied in areas such as confidential communication and image encryption.

1 Introduction

In 1963, Lorenz proposed the famous Lorenz chaotic system [1], which has complex dynamical behavior although it is only three-dimensional. As an important branch of nonlinear systems, chaotic systems have good prospects for applications in secure communications, image encryption and neural networks because of their unique properties [2–24]. As the research progresses, chaotic systems have been expanded to the fractional-order domain [25–33], not only in the integer-order direction [34–40]. In both integer-order and fractional-order systems, some of them have the special phenomenon of hidden attractors.

The Sil’nikov criterion considers that a chaotic system requires at least one unstable equilibrium point [41]. However, the Sil’nikov criterion is a sufficient and unnecessary condition for the emergence of chaotic phenomena. A class of systems discovered in recent years may have only stable equilibrium points, no equilibrium points or infinitely many equilibrium points, the chaotic state is still apparent, with the attractor basin not meeting the adjacent domain of the equilibrium point, such fields of attraction are called hidden attractors [42–44].

For classical systems of chaos, such as Lorenz [1], Chen [45] and Lü [46] systems, the equilibrium points of these systems are unstable and therefore generate self-excited attractors. However, if the equilibrium point of the system is unstable, then hidden attractors may be created. Since the 21st century, more studies has been done on hidden attractors. In 2010, Vagaitsev et al. [47] discovered hidden attractors in generalized Chua’s circuits firstly, and since then there has been a boom in the study of hidden attractors. In 2012, G.A. Leonov et al. [48] studied hidden attractors in smooth Chua’s systems and proposed an algorithm for hidden attractors localization. In 2014, Lao et al. [49] introduced a cost function in chaotic systems with hidden attractors and used it for parameter estimation in chaotic circuit systems. In 2015, Chen et al. [50] discovered the coexistence of hidden attractors by improving the classical Chua’s circuit using memristors. In 2017, M. Borah et al. [51] proposed a fractional-order chaotic system and it does not have an equilibrium point, which is a system of chaos with hidden attractors. In 2019, Cang et al. [52] discovered the coexistence of hidden attractors under different parameters in a class of Lorenz-like systems. In the same year, Zhang et al. [53] introduced a multiscroll hyperchaotic system with hidden attractors based on the Jerk system. In 2020, Deng et al. [54] proposed a multi-wing system of hidden attractors with only a single stable equilibrium point. In addition, Mou et al. [55] presented a chaotic circuit based on memristor–memcapacitor, which is a circuit system with an abundance of hidden attractors.

In addition, the coexistence of attractors is an interesting phenomenon that occurs in some chaotic systems where the parameters remain the same and the system enters different orbits and thus forms different attractors under different initial conditions due to the properties of the chaotic system itself. In dynamical systems, the presence of this phenomenon can lead to very complex behavior of the system. In the article, a novel four-dimensional chaotic system is arised from a modification of Wei system [54]. It is found that the system has stable equilibrium points and can be classified as a chaotic system with hidden attractors, while the system also has complex dynamical phenomena, including the coexistence of periodic windows and attractors. The stability, interchangeability, and agility of system can be significantly improved by using software implementation, and therefore the effectiveness of the system is verified by execution onto a DSP platform.

The remainder of this article is presented below. In Section 2, the mathematical model of the system is presented and the type of equilibrium points and their stability are analyzed. In Section 3, the dynamical behavior of the 4-dimensional system is analyzed, including Lyapunov exponent spectrum (LEs) and bifurcation diagram (BD), coexistence of attractors, SE and C0 complexity. In Section 4, a circuit realization of the 4-dimensional chaotic system is performed through a DSP platform. Finally, conclusions are given in Section 5.

2 Mathematical Models

2.1 Analysis of Equilibrium Points

A new chaotic system is created by inserting extra variables w and a constant k into the three-dimensional system of chaos, as follows:

$\{\begin{array}{l}\dot{x}=a\left(y-x\right)\\ \dot{y}=-by+xz+k\\ \dot{z}=d-e^{xy}\\ \dot{w}=\text{c}zw\end{array}.(1)$

The dispersion of the system is obtained from the system dynamical equations and can be expressed as

$\nabla V=\frac{\partial \dot{x}}{\partial x}+\frac{\partial \dot{y}}{\partial y}+\frac{\partial \dot{z}}{\partial z}+\frac{\partial \dot{w}}{\partial w.}(2)$

Setting a = 2.6, b = 0.2, c = 5, d = 17, k = 3, and the initial conditions as (1, −3, 0.1, 7). And then

$\nabla V=\frac{\partial \dot{x}}{\partial x}+\frac{\partial \dot{y}}{\partial y}+\frac{\partial \dot{z}}{\partial z}+\frac{\partial \dot{w}}{\partial w}=-2.3<0,(3)$

Eq. 2 smaller than zero, it is proved that the system is dissipative and therefore may have chaotic attractors.

Setting $\dot{x}=\dot{y}=\dot{z}=\dot{w}=0$, it means that

$\{\begin{array}{l}a\left(y-x\right)=0\\ -by+xz+k=0.\\ d-e^{xy}=0\\ \text{c}zw=0\end{array}(4)$

It can be obtained that when d > 1, the system has two equilibrium points E₁ $\left(\sqrt{\ln d},\sqrt{\ln d},\frac{k}{\sqrt{\ln d}}+b,0\right)$ and E₂ $\left(\sqrt{\ln d},\sqrt{\ln d},\frac{k}{\sqrt{\ln d}}+b,0\right)$.

Let the set of equilibrium points be P. The Jacobian matrix of system 3) at the set of equilibrium points p is

$J=\left[\begin{array}{cccc}-a& a& 0& 0\\ z& -b& x& 0\\ -y{e}^{xy}& -x{e}^{xy}& 0& 0\\ 0& 0& cw& cz\end{array}\right],(5)$

and then the characteristic equation for point set

${\lambda }^4+a_1{\lambda }^3+a_2{\lambda }^2+a_3\lambda +a_4=0,(6)$

where a₁ = 3.3, a₂ = 2.2298, a₃ = 0.9327, and a₄ = 0.2589. The eigenvalues can be calculated from the characteristic equation as λ₁ = −2.5545, λ₂ = −0.5, λ₃ = −0.1227-0.4332i, λ₄ = −0.1227 + 0.4332i, λ₁ and λ₂ are negative real roots, and λ₃ and λ₄ are a pair of complex conjugate eigenvalues, so these two equilibrium points are saddle-focus equilibrium points, which are important for chaotic systems. According to the Routh-Hurwitz criterion, the real part of all roots is negative and satisfied with

${\mathrm{\Delta }}_1=a_1>0,(7)$

${\mathrm{\Delta }}_2=a_1{a}_2-a_0{a}_3>0,(8)$

${\mathrm{\Delta }}_3=a_1{a}_2{a}_3-a_1^2{a}_4-a_0{a}_3^3>0,(9)$

${\mathrm{\Delta }}_4=a_4{\mathrm{\Delta }}_3>0,(10)$

Thus, both equilibria E₁ and E₂ are asymptotically stable.

3 Dynamical Behaviors

3.1 Chaotic Attractor

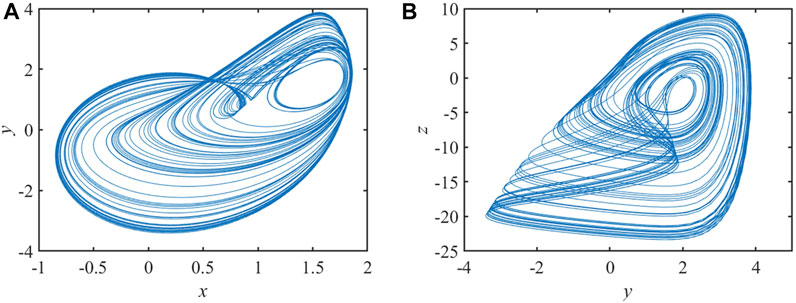
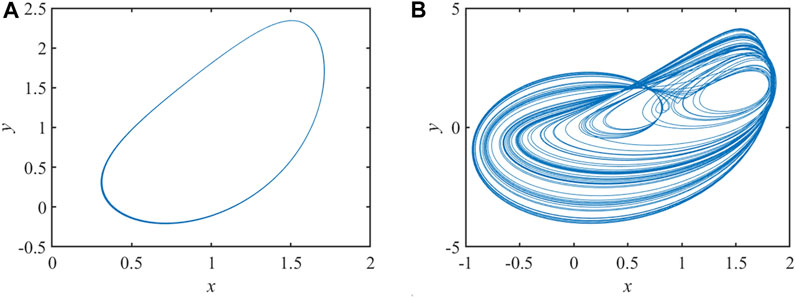
In system (1), let a = 2.6, b = 0.2, c = 5, d = 17, k = 3, and the initial values are (1, −3, −0.1, 7). The phase diagrams of chaotic attractors in the system in different phase planes are shown in Figure 1.

FIGURE 1

FIGURE 1. Hidden chaotic attractor of system (1), (A) x–y plane (B) y–z plane.

3.2 Lyapunov Exponents and Bifurcation Diagram of the System

In the system, which is a four-dimensional chaotic system, the BD is analyzed in combination with the LEs to obtain the states with different parameters. In the following, parameters a, b and d will be set as variables with initial values of (1, −3, −0.1, 7) and step size h = 0.01. Only parameters a, b and d will be changed, the rest will remain unchanged and the state of the system will be observed.

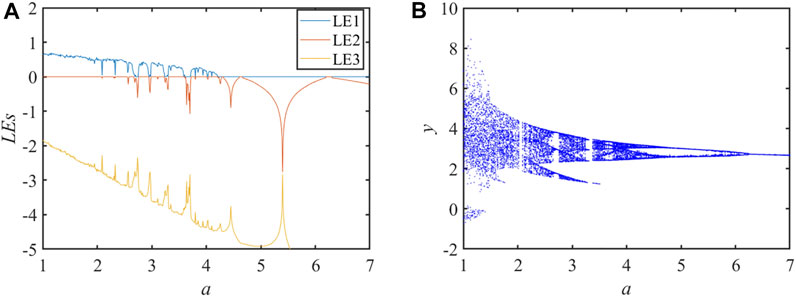
With the parameters a∈ [1, 7], let b = 0.2, c = 5, d = 17, k = 3, and initial values of (1, -3, −0.1, 7), the LEs and BD of the system are shown in Figure 2.

FIGURE 2

FIGURE 2. Dynamical analysis with parameter a, (A) LEs, (B) BD.

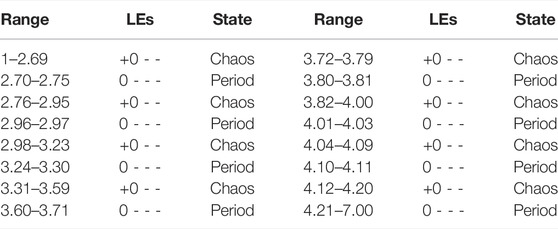
The LEs can clearly see the change of the system state when the parameter a changes, and the BD can be obtained from the multiplicative period bifurcation into chaos, and it is known after analysis that the BD corresponds exactly to the LEs. The system states are shown in Table 1, which gives a clear view of the range of parameters of the system in different states.

TABLE 1

TABLE 1. The state and LEs under the change of parameter a.

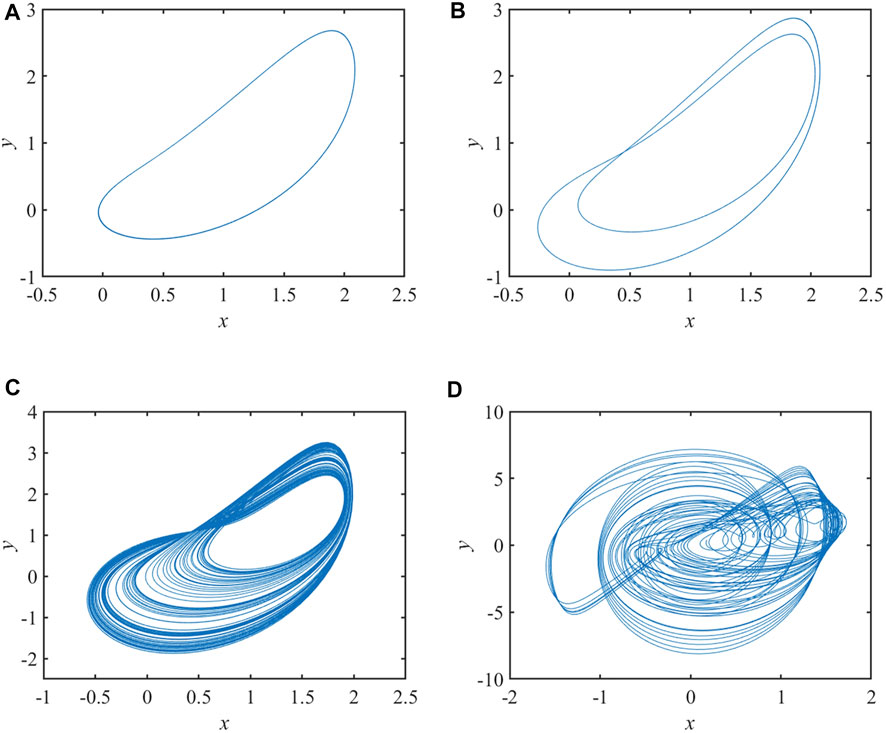
According to the data in Table 1, the cyclical and chaotic states of the system under the transformation of parameter a are shown in Figure 3.

FIGURE 3

FIGURE 3. Phase diagram of the system, (A) a = 6.8, (B) a = 5.8, (C) a = 4, (D) a = 1.2.

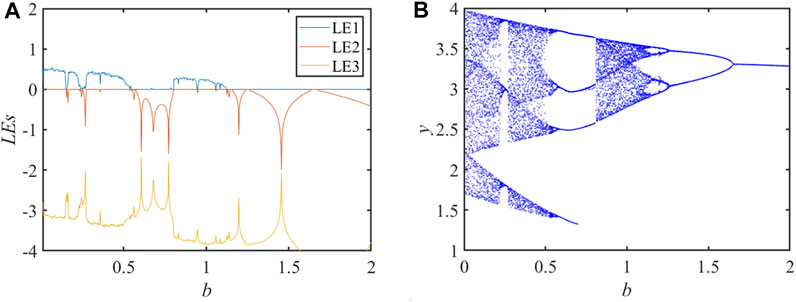
Taking the parameter b∈[0.01, 2], let a = 2.6, c = 5, d = 17, k = 3, and the initial values are (1, −3, −0.1, 7), the LEs and the BD under this condition are displayed at Figure 4. As the parameter b varies, cyclical and chaotic regions are evident in the system.

FIGURE 4

FIGURE 4. Dynamical analysis with parameter b, (A) LEs, (B) BD.

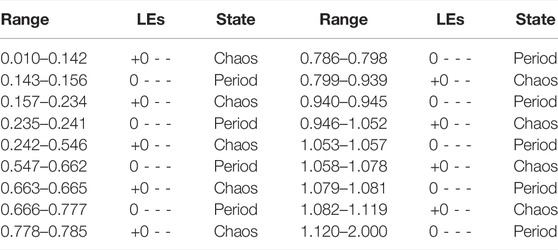
The state table of the system as the parameters b change is shown in Table 2. It is evident that the system undergoes another period-doubling bifurcation after going through a period-doubling bifurcation into chaos. The analysis shows that the BD corresponds exactly to the LEs.

TABLE 2

TABLE 2. The state and LEs under the change of parameter b.

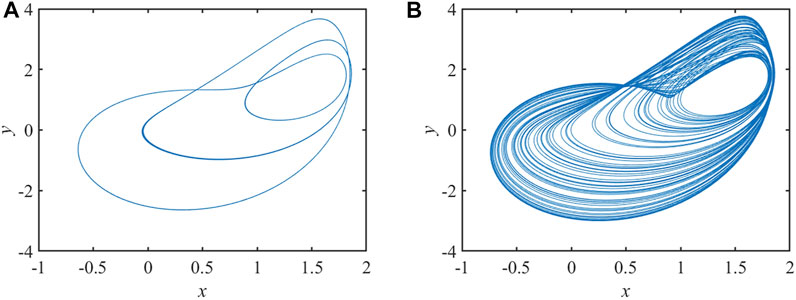
The state of the system with parameter b transformed is displayed at Figure 5.

FIGURE 5

FIGURE 5. Phase diagram of the system, (A) b = 0.70, (B) b = 0.46.

Taking the parameter d∈ [7, 20], setting a = 2.6, b = 0.2, c = 5, k = 3, and initial values of (1, −3, −0.1, 7), LEs and BD for this system are displayed at Figure 6. The system exhibits complex dynamics of chaos and alternating periods when the parameter d is varied.

FIGURE 6

FIGURE 6. Dynamical analysis with parameter d, (A) LEs, (B) BD.

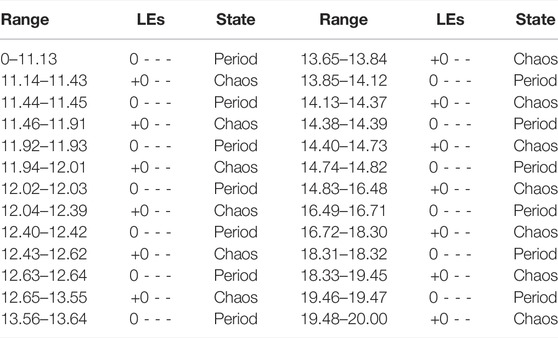
The state table of the system when the state varies with the parameter d is shown in Table 3. It can be seen that the chaotic range of the system is relatively large at this time, while there is a clear periodic window.

TABLE 3

TABLE 3. The state and Les under the change of parameter d.

When the parameter d is varied, the system produces the periodic and chaotic state displayed at Figure 7.

FIGURE 7

FIGURE 7. Phase diagram of the system, (A) d = 7.0, (B) d = 19.0.

3.3 Coexistence of Attractors

An interesting phenomenon that exists in chaotic systems, namely the coexistence of attractors. When the parameters of the system are constant and the initial values are varied, the trajectory of the system can gradually vary to a different state of motion. Setting a = 2.6, b = 0.2, c = 5, d = 17, k = 3. When the initial values are set to (1, −3, −0.4, 7) and (−0.1, 0.4, −0.1, 7), the coexistence of attractors of the system is displayed at Figure 8A, and when the initial values are set to (−2, 3.6, −0.1, 7) and (1, −3, −0.1, 7), the coexistence of attractors of the system is displayed at Figure 8B.

FIGURE 8

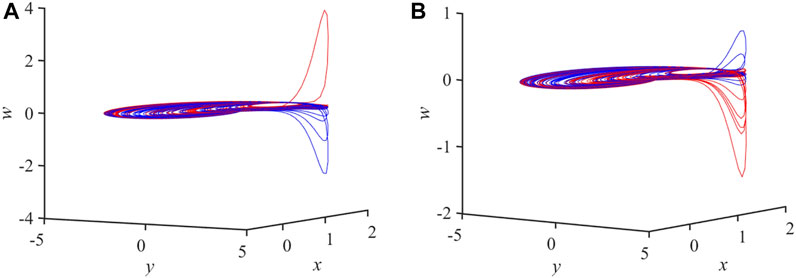
FIGURE 8. The phase diagram of coexistence attractor, (A) initial values are (1, −3, −0.4, 7) and (−0.1, 0.4, −0.1,7), (B) initial values are (−2, 3.6, −0.1, 7) and (1, −3, −0.1, 7).

3.4 Complexity Analysis

Another important aspect of the study of chaotic systems is the study of their complexity. The degree of closeness of a chaotic sequence to a random sequence, as shown using the corresponding algorithm, is the complexity of a chaotic system. The higher the value of complexity, the closer the system is to a random sequence and the safer it is [56, 57]. In this paper, the SE algorithm and the C0 algorithm are used to analyse the complexity of the structure.

The SE (spectral entropy) algorithm performs a Fourier transform on the sequence and then obtains the spectral entropy value by combining the energy density in the frequency domain with the Shannon entropy. The C0 algorithm, on the other hand, involves decomposing the sequence to produce two parts of regularity and irregularity, and then measuring the proportion of the irregular part to obtain the result.

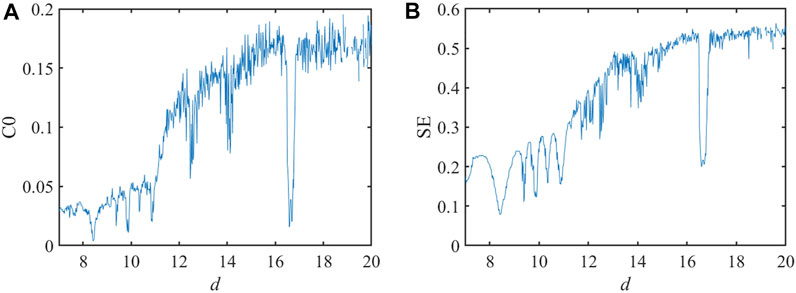
In the section, we will analyse the complexity of the system under the variation of parameter d. When taking parameters a = 2.6, b = 0.2, c = 5, k = 3, and d∈ [7, 20], the results obtained are shown in Figure 9.

FIGURE 9

FIGURE 9. Structural complexity curve with parameter d, (A) C0 Complexity, (B) SE Complexity.

As can be seen from Figure 9, the SE algorithm and the C0 algorithm are highly synchronized, and the system is in the limit ring state when d < 11.30, in the chaotic state when d∈[11.30, 12.43], in the limit ring state when d∈[12.44, 12.60], in the chaotic state when d∈[12.61, 14.01], in the limit ring state when d∈[ 14.02, 14.17], in the chaotic state when d∈[14.18, 16.48], in the limit ring state when d∈[16.49, 16.82], and when d > 16.83, the system enters the chaotic state again. By analyzing the SE complexity diagram and the C0 complexity diagram, it can be found that the complexity is at a low point when the system is in the periodic state and increases significantly when the system enters the chaotic state, and the presented results are consistent with the LEs and the BD displayed at Figure 6.

4 DSP Implementation

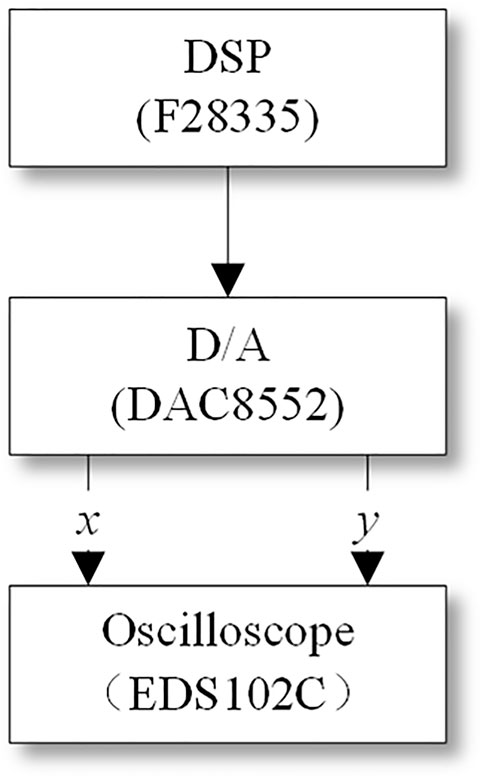
Since chaotic systems are susceptible to external perturbations when implemented using analog circuits, the relevant characteristic conditions in the actual circuit are more difficult to control accurately, so they can be implemented using DSP. The DSP chip F28335, with its fast computing speed, high accuracy and low environmental impact, was chosen as the empirical platform to validate the novel system of chaos. As software can only receive digital signals, a continuous chaotic system must be discretized in order to handle the system on a DSP platform firstly. Therefore, we discretize the continuous system of chaos and transform it into a discrete chaotic sequence by the approach of fourth-order Runge-Kutta, and then write into the DSP chip using a programming language. Here a stack operation is devised to make sure the data is not corrupted as much as possible. On the output side of the DSP, a D/A converter (DAC8552) is used to convert the digital sequence into an analogue sequence which is then sent to an oscilloscope (EDS102C) so that the oscilloscope can better capture the image. The overall workflow is shown in Figure 10.

FIGURE 10

FIGURE 10. The flow chart.

The parameters are given as a = 2.6, b = 0.2, c = 5, d = 17, k = 3, and the initial conditions as (1, −3, −0.1,7), the images are obtained as shown in Figure 11. By comparing with Figure 1, it is clear that the results obtained using DSP are consistent with the simulations carried out in MATLAB.

FIGURE 11

FIGURE 11. The phase diagram of DSP simulation, (A) x–y plane (B) y–z plane.

The f28335 chip, D/A converter and oscilloscope used for the system DSP simulation are shown in Figure 12.

FIGURE 12

FIGURE 12. DSP simulation physical picture.

5 Conclusion

The article proposes a new four-dimensional chaotic system and investigated its dynamic properties. In the study of this chaotic system, different chaotic attractors are found. By analysing the LEs, the BD and the complexity of this system, it can be understood that the system exhibits a dramatic degree of complexity in its dynamic properties as the parameters changed of the system. By numerical simulations, the peculiar phenomenon of the coexistence of chaotic attractors was observed by us. The results show that the chaotic system has very complex dynamic properties. Finally, the circuit was built and tested on a DSP platform, and a comparison of the test results with the numerical simulation results shows a high degree of consistency. The article provides a reference for the study of chaotic systems and circuit experiments, and has good prospects for applications in information encryption and secure communication.

Data Availability Statement

The original contributions presented in the study are included in the article/Supplementary Material, further inquiries can be directed to the corresponding author.

Author Contributions

XW built the system model, analysed the dynamics, performed the circuit implementation and wrote the manuscript. YF and YC supervised the work and revised the manuscript. Both authors read and approved the final manuscript.

Funding

Dalian Young Stars of Science and Technology Project (NO. 2021RQ088).

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s Note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

1. Lorenz EN. Deterministic Nonperiodic Flow. J Atoms (1963) 20. doi:10.1175/1520-0469(1963)020<0130:dnf>2.0.co;2

CrossRef Full Text | Google Scholar

2. Gao X, Mou J, Xiong L, Sha Y, Yan H, Cao Y. A Fast and Efficient Multiple Images Encryption Based on Single-Channel Encryption and Chaotic System. Nonlinear Dyn (2022) 108:613–36. doi:10.1007/s11071-021-07192-7

CrossRef Full Text | Google Scholar

3. Feki M. An Adaptive Chaos Synchronization Scheme Applied to Secure Communication. Chaos, Solitons & Fractals (2003) 18(1):141–8. doi:10.1016/s0960-0779(02)00585-4

CrossRef Full Text | Google Scholar

4. Zaher AA, Abu-Rezq A. On the Design of Chaos-Based Secure Communication Systems. Commun Nonlinear Sci Numer Simulation (2011) 16(9):3721–37. doi:10.1016/j.cnsns.2010.12.032

CrossRef Full Text | Google Scholar

5. Luo C, Wang X. Chaos Generated from the Fractional-Order Complex Chen System and its Application to Digital Secure Communication. Int J Mod Phys C (2013) 24(04):1350025. doi:10.1142/s0129183113500253

CrossRef Full Text | Google Scholar

6. Wang B, Zhang X, Dong X. Novel Secure Communication Based on Chaos Synchronization. IEICE Trans Fundamentalsa (2018) E101.A7:1132–5. doi:10.1587/transfun.e101.a.1132

CrossRef Full Text | Google Scholar

7. Xiu C, Zhou R, Zhao S, Xu G. Memristive Hyperchaos Secure Communication Based on Sliding Mode Control. Nonlinear Dyn (2021) 4:1–17. doi:10.1007/s11071-021-06302-9

CrossRef Full Text | Google Scholar

8. Yu F, Qian S, Chen X, Huang Y, Liu L, Shi C, et al. A New 4D Four-Wing Memristive Hyperchaotic System: Dynamical Analysis, Electronic Circuit Design, Shape Synchronization and Secure Communication. Int J Bifurcation Chaos (2020) 30(10). doi:10.1142/s0218127420501473

CrossRef Full Text | Google Scholar

9. Kamal FM, Elsonbaty A, Elsaid A. A Novel Fractional Nonautonomous Chaotic Circuit Model and its Application to Image Encryption. Chaos, Solitons & Fractals (2021) 144(3):110686. doi:10.1016/j.chaos.2021.110686

CrossRef Full Text | Google Scholar

10. Lin H, Wang C, Deng Q, Xu C, Deng Z, Zhou C. Review on Chaotic Dynamics of Memristive Neuron and Neural Network. Nonlinear Dyn (2021) 106(1):959–73. doi:10.1007/s11071-021-06853-x

CrossRef Full Text | Google Scholar

11. Man Z, Li J, Di X, Sheng Y, Liu Z. Double Image Encryption Algorithm Based on Neural Network and Chaos. Chaos, Solitons & Fractals (2021) 152(24):111318. doi:10.1016/j.chaos.2021.111318

CrossRef Full Text | Google Scholar

12. Li X, Mou J, Cao Y, Banerjee S. An Optical Image Encryption Algorithm Based on a Fractional-Order Laser Hyperchaotic System. Int J Bifurcation Chaos (2022) 32(03):2250035. doi:10.1142/s0218127422500353

CrossRef Full Text | Google Scholar

13. Li CL, Zhou Y, Li HM, Feng W, Du JR. Image Encryption Scheme with Bit-Level Scrambling and Multiplication Diffusion. Multimedia Tools Appl (2021) 80(3):1–23. doi:10.1007/s11042-021-10631-7

CrossRef Full Text | Google Scholar

14. Zhou Y, Li C, Li W, Li H, Feng W, Qian K. Image Encryption Algorithm with circle index Table Scrambling and Partition Diffusion. Nonlinear Dyn (2021) 103:2043–61. doi:10.1007/s11071-021-06206-8

CrossRef Full Text | Google Scholar

15. Yu F, Zhang Z, Shen H, Huang Y, Cai S, Du a. S. FPGA Implementation and Image Encryption Application of a New PRNG Based on a Memristive Hopfield Neural Network with a Special Activation Gradient. Chin Phys B (2022) 31(2):20505–020505. doi:10.1088/1674-1056/ac3cb2

CrossRef Full Text | Google Scholar

16. Yu F, Shen H, Zhang Z, Huang Y, Cai S, Du S. A New Multi-Scroll Chua's Circuit with Composite Hyperbolic tangent-cubic Nonlinearity: Complex Dynamics, Hardware Implementation and Image Encryption Application. Integration (2021) 81:71–83. doi:10.1016/j.vlsi.2021.05.011

CrossRef Full Text | Google Scholar

17. Yu F, Kong X, Chen H, Yu Q, Cai S, Huang Y, et al. A 6D Fractional-Order Memristive Hopfield Neural Network and its Application in Image Encryption. Front Phys (2022) 10109. doi:10.3389/fphy.2022.847385

CrossRef Full Text | Google Scholar

18. Yu F, Zhang Z, Shen H, Huang Y, Cai S, Jin J, et al. Design and FPGA Implementation of a Pseudo-random Number Generator Based on a Hopfield Neural Network under Electromagnetic Radiation. Front Phys (2021) 9:690651. doi:10.3389/fphy.2021.690651

CrossRef Full Text | Google Scholar

19. Li Y, Li C, Zhang S, Chen GR, Zeng Z. A Self-Reproduction Hyperchaotic Map with Compound Lattice Dynamics. IEEE Trans Ind Electron (2022) 1. doi:10.1109/TIE.2022.3144592

CrossRef Full Text | Google Scholar

20. Li Y, Li C, Zhao Y, Liu S. Memristor-type Chaotic Mapping. Chaos (2022) 32(2):021104. doi:10.1063/5.0082983

PubMed Abstract | CrossRef Full Text | Google Scholar

21. Li C, Yang Y, Yang X, Zi X, Xiao F. A Tristable Locally Active Memristor and its Application in Hopfield Neural Network. Nonlinear Dyn (2022) 108:1697–717. doi:10.1007/s11071-022-07268-y

CrossRef Full Text | Google Scholar

22. Gao X, Mou J, Banerjee S, Cao Y, Xiong L, Chen X. An Effective Multiple-Image Encryption Algorithm Based on 3D Cube and Hyperchaotic Map. J King Saud Univ - Comput Inf Sci (2022) 34(4):1535–51. doi:10.1016/j.jksuci.2022.01.017

CrossRef Full Text | Google Scholar

23. Zhou S, Wang X, Zhang Y, Ge B, Wang M, Gao S. A Novel Image Encryption Cryptosystem Based on True Random Numbers and Chaotic Systems. Multimedia Syst (2022) 28(1):95–112. doi:10.1007/s00530-021-00803-8

CrossRef Full Text | Google Scholar

24. Zhou S, Wang X, Wang M, Zhang Y. Simple Colour Image Cryptosystem with Very High Level of Security. Chaos, Solitons & Fractals (2020) 141:110225. doi:10.1016/j.chaos.2020.110225

CrossRef Full Text | Google Scholar

25. Liu T, Banerjee S, Yan H, Mou J. Dynamical Analysis of the Improper Fractional-Order 2D-SCLMM and its DSP Implementation. The Eur Phys J Plus (2021) 136(5):1–17. doi:10.1140/epjp/s13360-021-01503-y

CrossRef Full Text | Google Scholar

26. Ma C, Mou J, Li P, Liu T. Dynamic Analysis of a New Two-Dimensional Map in Three Forms: Integer-Order, Fractional-Order and Improper Fractional-Order. Eur Phys J Spec Top (2021) 230(7):1945–57. doi:10.1140/epjs/s11734-021-00133-w

CrossRef Full Text | Google Scholar

27. Xiong P-Y, Jahanshahi H, Alcaraz R, Chu Y-M, Gómez-Aguilar JF, Alsaadi FE. Spectral Entropy Analysis and Synchronization of a Multi-Stable Fractional-Order Chaotic System Using a Novel Neural Network-Based Chattering-free Sliding Mode Technique. Chaos, Solitons & Fractals (2021) 144:110576. doi:10.1016/j.chaos.2020.110576

CrossRef Full Text | Google Scholar

28. Liu T, Yan H, Banerjee S, Mou J. A Fractional-Order Chaotic System with Hidden Attractor and Self-Excited Attractor and its DSP Implementation. Chaos, Solitons & Fractals (2021) 145(2):110791. doi:10.1016/j.chaos.2021.110791

CrossRef Full Text | Google Scholar

29. Akgül A, Rajagopal K, Durdu A, Pala MA, Boyraz ÖF, Yildiz MZ. A Simple Fractional-Order Chaotic System Based on Memristor and Memcapacitor and its Synchronization Application. Chaos, Solitons & Fractals (2021) 152(3):111306. doi:10.1016/j.chaos.2021.111306

CrossRef Full Text | Google Scholar

30. Xie W, Wang C, Lin H. A Fractional-Order Multistable Locally Active Memristor and its Chaotic System with Transient Transition, State Jump. Nonlinear Dyn (2021) 104(4):4523–41. doi:10.1007/s11071-021-06476-2

CrossRef Full Text | Google Scholar

31. Jahanshahi H, Sajjadi SS, Bekiros S, Aly AA. On the Development of Variable-Order Fractional Hyperchaotic Economic System with a Nonlinear Model Predictive Controller. Chaos, Solitons & Fractals (2021) 144:110698. doi:10.1016/j.chaos.2021.110698

CrossRef Full Text | Google Scholar

32. Mathale D, Doungmo Goufo EF, Khumalo M. Coexistence of Multi-Scroll Chaotic Attractors for a Three-Dimensional Quadratic Autonomous Fractional System with Non-local and Non-singular Kernel. Alexandria Eng J (2021) 60(4):3521–38. doi:10.1016/j.aej.2021.02.024

CrossRef Full Text | Google Scholar

33. Yadav VK, Shukla VK, Das S. Exponential Synchronization of Fractional-Order Complex Chaotic Systems and its Application. Chaos, Solitons & Fractals (2021) 147(8):110937. doi:10.1016/j.chaos.2021.110937

CrossRef Full Text | Google Scholar

34. Yan M, Xu H. The Multi-Scroll Hyper-Chaotic Coexistence Attractors and its Application. Signal Processing: Image Commun (2021) 95:116210. doi:10.1016/j.image.2021.116210

CrossRef Full Text | Google Scholar

35. Sv A, As B, Atac D, Ss E. A New Multistable Plasma Torch Chaotic Jerk System, its Dynamical Analysis, Active Backstepping Control, and Circuit Design. Backstepping Control Nonlinear Dynamical Syst (2021) 191–214. doi:10.1016/B978-0-12-817582-8.00016-7

CrossRef Full Text | Google Scholar

36. Singh S, Mathpal S, Azar AT, Vaidyanathan S, Kamal NA. Multi-switching Synchronization of Nonlinear Hyperchaotic Systems via Backstepping Control. Backstepping Control Nonlinear Dynamical Syst (2021) 425–47. doi:10.1016/b978-0-12-817582-8.00024-6

CrossRef Full Text | Google Scholar

37. Yang J, Feng Z, Liu Z. A New Five-Dimensional Hyperchaotic System with Six Coexisting Attractors. Qual Theor Dynamical Syst (2021) 20(1). doi:10.1007/s12346-021-00454-0

CrossRef Full Text | Google Scholar

38. Llibre J, Tian Y. The Zero-Hopf Bifurcations of a Four-Dimensional Hyperchaotic System. J Math Phys (2021) 62(5):052703. doi:10.1063/5.0023155

CrossRef Full Text | Google Scholar

39. Li C, Li H, Xie W, Du J. A S-type Bistable Locally Active Memristor Model and its Analog Implementation in an Oscillator Circuit. Nonlinear Dyn (2021) 106:1041–58. doi:10.1007/s11071-021-06814-4

CrossRef Full Text | Google Scholar

40. Zhang X, Li C, Dong E, Zhao Y, Liu Z. A Conservative Memristive System with Amplitude Control and Offset Boosting. Int J Bifurcation Chaos (2022) 32(04):2250057. doi:10.1142/s0218127422500572

CrossRef Full Text | Google Scholar

41. Šil'nikov LP, Sil'nikov LP. A Contribution of the Problem of the Structure of an Extended Neighborhood of Rough Equilibrium State of Saddle-Focus Type. Math USSR Sbornikmathematics Ussr-sbornik (1970) 1010(1):9191–102. doi:10.1070/SM1970v010n01ABEH001588

CrossRef Full Text | Google Scholar

42. Leonov GA, Kuznetsov NV. IWCFTA2012 Keynote Speech I - Hidden Attractors in Dynamical Systems: From Hidden Oscillation in Hilbert-Kolmogorov, Aizerman and Kalman Problems to Hidden Chaotic Attractor in Chua Circuits. Int J Bifurcation Chaos (2012) 23(01). doi:10.1109/iwcfta.2012.8

CrossRef Full Text | Google Scholar

43. Wang N, Zhang G, Kuznetsov NV, Bao H. Hidden Attractors and Multistability in a Modified Chua's Circuit. Commun Nonlinear Sci Numer Simulation (2021) 92:105494. doi:10.1016/j.cnsns.2020.105494

CrossRef Full Text | Google Scholar

44. Kuznetsov NV, Vagaytsev VI, Leonov GA, Seledzhi SM, Localization of Hidden Attractors in Smooth Chua's Systems (2011). 26–33. doi:10.5555/2001305.2001309

CrossRef Full Text | Google Scholar

45. Ueta T, Chen G. Yet Another Chaotic Attractor. Int J Bifurcation Chaos (1999) 9(7):1465–6. doi:10.1142/S0218127499001024

CrossRef Full Text | Google Scholar

46. Lu J, Chen G. A New Chaotic Attractor Coined. Int J Bifurcation Chaos (2002) 12(3):659–61. doi:10.1142/s0218127402004620

CrossRef Full Text | Google Scholar

47. Vagaitsev VI, Kuznetsov NV, Leonov GA. Localization of Hidden Attractors of the Generalized Chua System Based on the Method of Harmonic Balance. Vestnik St.Petersb Univ.Math (2010) 43(4):242–55. doi:10.3103/s1063454110040096

CrossRef Full Text | Google Scholar

48. Leonov GA, Kuznetsov NV, Vagaitsev VI. Hidden Attractor in Smooth Chua System. Physica D Nonlinear Phenomena (2012) 241(18):1482–6. doi:10.1016/j.physd.2012.05.016

CrossRef Full Text | Google Scholar

49. Lao S-K, Shekofteh Y, Jafari S, Sprott JC. Cost Function Based on Gaussian Mixture Model for Parameter Estimation of a Chaotic Circuit with a Hidden Attractor. Int J Bifurcation Chaos (2014) 24(01):1450010. doi:10.1142/s0218127414500102

CrossRef Full Text | Google Scholar

50. Chen M, Li M, Yu Q, Bao B, Xu Q, Wang J. Dynamics of Self-Excited Attractors and Hidden Attractors in Generalized Memristor-Based Chua's Circuit. Nonlinear Dyn (2015) 81(1-2):215–26. doi:10.1007/s11071-015-1983-7

CrossRef Full Text | Google Scholar

51. Borah M, Roy BK. Hidden Attractor Dynamics of a Novel Non-equilibrium Fractional-Order Chaotic System and its Synchronisation Control. Guwahati: IEEE (2017). p. 450–5.

Google Scholar

52. Cang S, Yue L, Zhang R, Wang Z. Hidden and Self-Excited Coexisting Attractors in a Lorenz-like System with Two Equilibrium Points. Nonlinear Dyn (2019) 95(2). doi:10.1007/s11071-018-4570-x

CrossRef Full Text | Google Scholar

53. Zhang X, Wang C. Multiscroll Hyperchaotic System with Hidden Attractors and its Circuit Implementation. Int J Bifurcation Chaos (2019) 29(09):1157–71. doi:10.1142/s0218127419501177

CrossRef Full Text | Google Scholar

54. Deng Q, Wang C, Yang L. Four-Wing Hidden Attractors with One Stable Equilibrium Point. Int J Bifurcation Chaos (2020) 30(6):2050086. doi:10.1142/s0218127420500868

CrossRef Full Text | Google Scholar

55. Ma X, Mou J, Liu J, Ma C, Zhao X. A Novel Simple Chaotic Circuit Based on Memristor–Memcapacitor. Nonlinear Dyn (2020) 100(5):2859–76. doi:10.1007/s11071-020-05601-x

CrossRef Full Text | Google Scholar

56. Ma X, Mou J, Xiong L, Banerjee S, Cao Y, Wang J. A Novel Chaotic Circuit with Coexistence of Multiple Attractors and State Transition Based on Two Memristors. Chaos, Solitons & Fractals (2021) 152:111363. doi:10.1016/j.chaos.2021.111363

CrossRef Full Text | Google Scholar

57. Ma C, Mou J, Xiong L, Banerjee S, Han X. Dynamical Analysis of a New Chaotic System: Asymmetric Multistability, Offset Boosting Control and Circuit Realization. Nonlinear Dyn (2021) 103(6):1–14. doi:10.1007/s11071-021-06276-8

CrossRef Full Text | Google Scholar