Multiport Routing of Topologically Optical Transport Based on Merging of Valley-Dependent Edge States and Second-Order Corner States

Topological photonics provide a novel platform to robustly manipulate the flow of light and design high-performance nanophotonic devices. To do this, a fundamental mechanism is the flexible control of optical transport based on topological boundary states on edges or corners. In this work, we design a multiport device to route the topologically optical transport by using both valley-dependent edge states (VDESs) and second-order corner states (SOCSs). The VDESs are derived from sublattice symmetry breaking in a honeycomb lattice, while SOCSs are induced by the lattice deformation of Kagome lattice. In terms of unit cell, we find that both configurations can be reconsidered as the same triangular-lattice photonic crystal, which consists of a hexagon-profile air hole array in silicon background. Therefore, a four-port device is designed based on the two configurations. In simulation, we observe the frequency-dependent routing effect of the topologically optical transport by merging of VDESs and SOCSs. This work not only shows a novel platform to explore various topological phases in the photonic system but also provides guidance in the development of topological photonic integrated circuits with mode division multiplexing.

Introduction

Topology, a concept of mathematics that studies the invariant global properties under continuous deformation, has been introduced into the physics systems to explore the intriguing band structures in the momentum space [1, 2]. Due to tunable geometric structures and controllable band dispersions, photonic crystals (PCs) arouse a wide range of research interest to implement the topological concept in photonic systems [3–7]. The topological PCs have been used to demonstrate many topological physics with nontrivial phases, such as quantum Hall effect, quantum spin Hall effect, quantum valley Hall effect (QVHE), and 2D Zak phase [8–15, 42, 43]. By using the topologically protected states, topological PCs also provide a platform to design intriguing devices in integrated optics and nanophotonics [16–25].

For example, the QVHE of light can be demonstrated by a honeycomb-lattice PC with sublattice symmetry breaking, namely, valley photonic crystal (VPC) [19, 20, 26–29]. When two topologically distinct VPCs are placed side-by-side to form an interface, valley-dependent edge states (VDESs) will emerge and robustly propagate along the interface with backscattering-suppressed electromagnetic features. On the other hand, by lattice deformation in a Kagome-lattice PC, one can implement a second-order topological photonic crystal (SOTPC) with the nontrivial 2D Zak phase [30–34]. Such SOTPC supports in-plane-localized 0D state, i.e., second-order corner state (SOCS), which is derived from the topological nontrivial phase of 2D insulating bulk states. Based on those topological boundary states on edges or corners, optical transport can be controlled flexibly and various prototypes of novel photonic devices have been successfully demonstrated [19, 35, 36], such as topological photonic routing, slow light waveguide, and PC mirrors. Furthermore, it is interesting to merge different types of topological boundary states in a single PC platform [37, 38], which can be potential to develop mode-division multiplexing in the topological photonic integrated circuits.

In this work, we apply both VDESs and SOCSs to construct a frequency-dependent routing platform in a multiport device. For one, by breaking the sublattice symmetry in a honeycomb-lattice PC, the VDESs can be acquired in an interface between two topologically distinct VPCs. For another, the SOTPCs are designed by the lattice deformation of Kagome-lattice PC, and the localized SOCSs can be induced at the intersection of the interface between two SOTPCs with different 2D Zak phases. The unit cells for both configurations consist of hexagon-profile air holes in a triangular lattice, and the geometry of air holes has the same size. Therefore, both configurations can be reconsidered as a same triangular-lattice photonic crystal in silicon background. Therefore, a four-port device is designed based on the two configurations. By merging of VDESs and SOCSs, the simulation results of the four-port device demonstrate the frequency-dependent routing effect of topologically optical transport, which is potential for the mode-division multiplexing in the development of topological photonic integrated circuits.

Design of Valley Photonic Crystals in Honeycomb Lattice

To design a valley photonic crystal, we construct a two-dimensional honeycomb-lattice photonic crystal, whose unit cell contains two types of hexagon-profile air holes at the corners, i.e., hole A and hole B. As shown in Figure 1A, the air holes are embedded in the dielectric background (shaded in black) with a relative permittivity ε_eff. The side length of hole A (or B) is S_A (or S_B), and the lattice constant is a. Here, ε_eff = 8.12 is the effective permittivity of the dielectric background based on the TE₀ mode index of silicon slab with 0.55a thickness (corresponding to a 220-nm-thickness silicon slab when the operation wavelength is around 1,550 nm). When the two air holes have an equivalent side length that S_A = S_B = 0.198a, the transverse-electric (TE) photonic bands of honeycomb-lattice PC [left panel of Figure 1B] possess a Dirac cone around the K/K′ point due to the C_3v point group symmetry of the lattice. Note that the photonic bands and their eigenmodes in this work are calculated by the MIT photonic band (MPB) package [39]. If we increase (reduce) S_A and reduce (increase) S_B, the spatial inversion symmetry of honeycomb PC will be broken and thus a common TE-polarized band gap is opened, which is derived from the lift up and down of degenerate states at the K/K’ point. These configurations are both valley photonic crystals (VPCs), as described and demonstrated in previous works [19, 20, 28]. Note that the filling ratio of air holes maintains constant during the evolution, which ensures that the band structures of PCs do not change much in frequency.

FIGURE 1

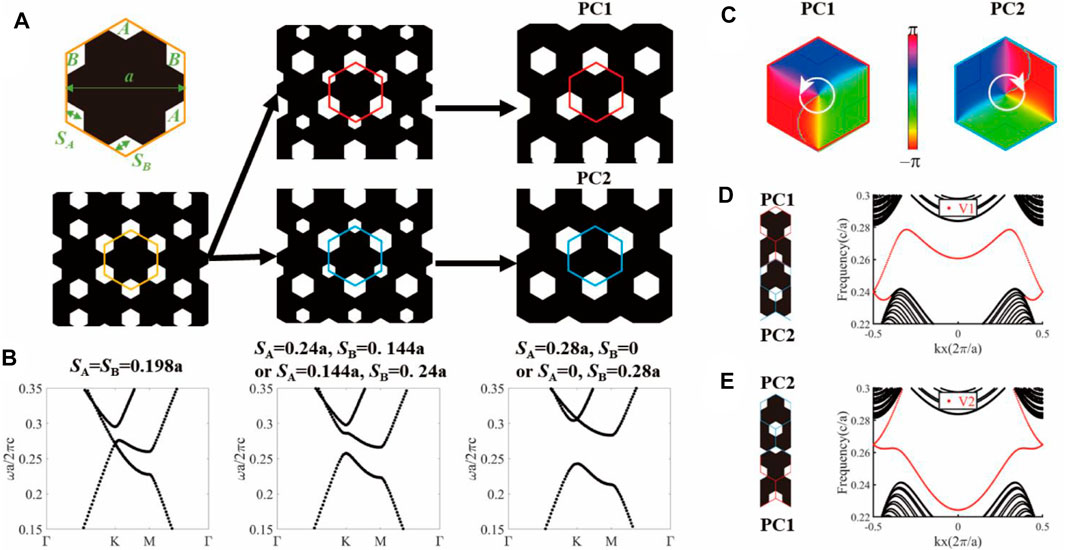
FIGURE 1. Design of valley photonic crystal in a honeycomb lattice. (A) The evolution of honeycomb-lattice photonic crystals (PCs) and (B) the corresponding TE-polarized band structures. The unit cell of honeycomb-lattice PC with lattice constant a consists of two hexagon-profile air holes at the corners, where the side length of hole A (or hole B) is S_A (or S_B). When the two air holes have equivalent side length that S_A = S_B = 0.198a (left panel), the TE-polarized photonic bands possess a Dirac cone around the K point. The spatial inversion symmetry of honeycomb PC is broken when S_A ≠ S_B, and thus the degenerate states at the K point are lifted to open a common TE band gap. Finally, we have two specific cases, i.e., PC1 with S_A = 0 and S_B = 0.28a and PC2 with S_A = 0.28a and S_B = 0. (C) Phase distribution of H_z eigenfields of the first TE bulk band at the K point. For PC1 (or PC2), we can observe that the phase vortex increases counterclockwise (or clockwise) by 2π around the center of unit cell, indicating the valley Chern index ${\text{C}}_K=-1/2$ (or ${\text{C}}_K=+1/2$). (D,E) Schematics of two types of valley-dependent interfaces and their edge dispersions (labeled as V1 and V2). The red points represent the edge states, while the black points represent bulk states.

As shown in the right panel of Figure 1A, we consider two specific configurations, i.e., PC1 that S_A = 0.28a and S_B = 0 and PC2 that S_A = 0 and S_B = 0.28a. Such a configuration can be reconsidered as a simple triangular-lattice PC with a hexagon-profile air hole at the corners. Both PC1 and PC2 possess the same band structures and a 15.2% band gap from 0.243 c/a to 0.283 c/a. Here, the band-gap size is expressed as a percentage of the gap-midgap ratio Δω/ω_m, where Δω is the frequency width of the band gap and ω_m is the frequency at the middle of the gap. It is a general and useful characterization, which is independent of the scale of PCs.

Although PC1 and PC2 have the same bulk band structures [i.e., the band structures in the right panel of Figure 1B], their topological properties are distinct and characterized by different valley Chern indices ${\text{C}}_{K/K\prime }$. For valley-contrasting physics [40–42], the valley Chern index is defined as

$C_{K/K^{\prime }}={\tau }_z\mathrm{sgn}\left(\text{Δ}\right)/2,(1)$

where ${\tau }_z$ is the z component of the Pauli matrix that ${\tau }_z=+1$ at the K valley and ${\tau }_z=-1$ at the K′ valley. $2\Delta$ denotes the frequency difference between two valley bulk modes. For another, modes at the two inequivalent valleys K/K′ are a pair of pseudospins, so they carry valley-dependent magnetic momentum,

$m\left(K,K^{\prime }\right)={\tau }_z{\mu }_B^{\ast },(2)$

where ${\mu }_B^{\ast }$ is the effective Bohr magneton at the bottom band and $sgn\left({\mu }_B^{\ast }\right)=sgn\left(\Delta \right)$ [40]. With regard to a PC, the effective “magnetic” momentum is related to the phase vortex of electromagnetic fields around the center of unit cell. When the phase vortex increases clockwise or counterclockwise by 2π, we can have ${\tau }_{z}sgn\left({\mu }_B^{\ast }\right)=$ +1 or −1. In other words, by observing the phase vortex of bulk modes at different valleys, it is easy to determine the valley Chern index. Figure 1C gives the phase distribution of H_z eigenfields of the first TE bulk band at K point. For PC1 (or PC2), we can observe that the phase vortex increases counterclockwise (or clockwise) by 2π around the center of the unit cell, indicating the valley Chern index ${\text{C}}_K=-1/2$ (or ${\text{C}}_K=+1/2$). Therefore, though one part of air holes (A or B) vanishes, PC1 and PC2 still maintain the topologically distinct features of valley-contrasting physics in a manner.

As band gaps of PC1 and PC2 are topologically distinct, the valley-dependent edge states (VDESs) can be obtained at the interface of domain walls between two VPCs with different valley indices. In Figures 1D,E, we show two types of interfaces (i.e., V1 and V2) constructed by PC1 and PC2 and their edge dispersions. The V1 case is PC1 at the upper domain and PC2 at the bottom, while V2 is PC2 at the upper domain and PC1 at the bottom. We calculate the edge dispersions for both two types of interfaces. The black points and red points represent bulk states and VDESs, respectively. The edge dispersions of V1-type and V2-type interfaces cover over the frequency range of the bulk band gap. Note that the group velocity direction of the V1-type (V2-type) VDES at the K valley is positive (negative) and vice versa for the K’ valley. It is in agreement with the bulk-edge correspondence, for example, that the difference of the valley-dependent topological index at the K valley crossing the domain wall of the V1-type interface (i.e., $C_K^{bottom}-C_K^{top}$) is +1.

Design of Second-Order Topological Photonic Crystals in Kagome Lattice

Except for VDES, another kind of topological boundary state in this work is the second-order corner state (SOCS). To implement SOCS, we will firstly design the second-order topological PC in Kagome lattice. As shown in Figure 2A, the unit cell is the assignment of Δ-shape cluster, consisting of three rhombic-profile air holes in a dielectric background. The side length of the rhombic hole d = 0.28a, where a is the lattice constant of Kagome PC. L₁ is the distance from the center of the rhombic hole to the center of the unit cell, such that the coupling length of the intra-cell cluster is $\sqrt{3}$ L₁. L₂ is the distance from the center of the rhombic hole to the vertex of the unit cell, and thus the coupling length of the inter-cell cluster is $\sqrt{3}$ L₂.

FIGURE 2

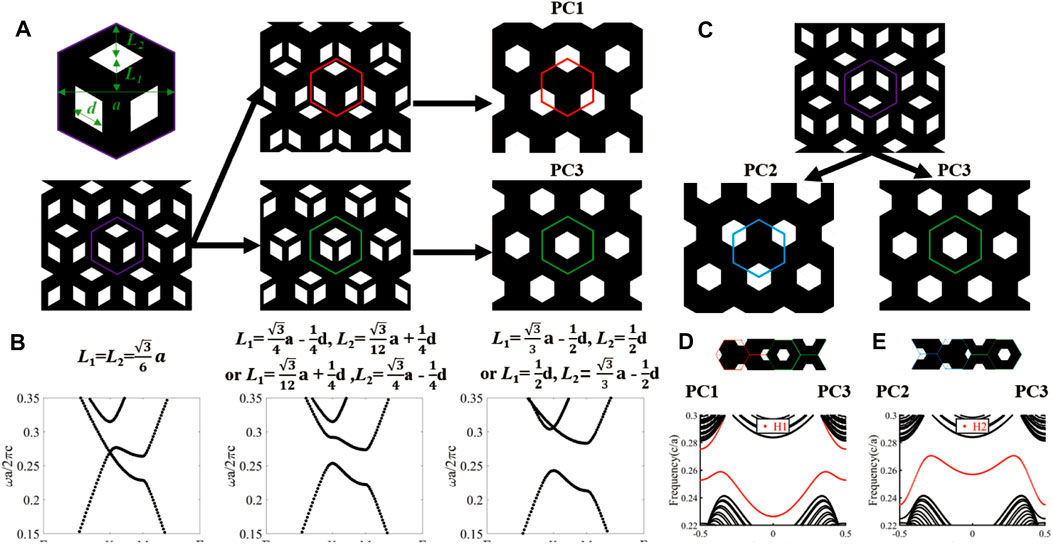
FIGURE 2. Design of the second-order topological photonic crystal in Kagome lattice. (A) The evolution of Kagome-lattice photonic crystals (PCs) with the assignment of Δ-shape cluster and (B) the corresponding TE-polarized band structures. The unit cell of Kagome-lattice PC with lattice constant a consists of three rhombic-profile air holes as a cluster, where the side length of the rhombic hole d = 0.28a. L₁ is the distance from the center of the rhombic hole to the center of the unit cell, and L₂ is the distance from the center of the rhombic hole to the vertex of the unit cell. Starting from L₁ = L₂, the intra-cluster coupling strength is equivalent to the inter-cluster case and there was a degenerate point around the K point of bulk band structures. With the expansion and shrinkage of clusters, the degenerate point disappears and the two bands gradually opened to form a TE-polarized gap. (C) The evolution of Kagome-lattice PCs with the assignment of ▽-shape cluster. We can have the same shrunken PC (i.e., PC3) and another expanded PC (i.e., PC2). (D,E) Schematics of two types of interfaces and their edge dispersions (labeled as H1 and H2). The red points represent the edge states, while the black points represent bulk states.

To approximately describe the topological properties of such PC, we can use the 2D Su–Schrieffer–Heeger (SSH) model [14, 15], which is determined by the relationship between L₁ and L₂. When L₁ = L₂, the strength of the intra-cluster coupling is equal to that of inter-cluster coupling, and there is a degeneracy point around the K point in the band structure, as shown in the left panel of Figure 2B. When we shrink the clusters with the decrease of L₁ (or expand the clusters with the increase of L₁), the balance of intra-coupling and inter-coupling is broken and thus open a TE-polarized band gap [as shown in the middle and right panels of Figure 2B]. The expanded case (i.e., red border with L₁ > L₂) shown in the top panel of Figure 2A is majorly dependent on inter-cluster coupling, while the shrunken structure (i.e., green border with L₁<L₂) shown in the bottom panel of Figure 2A is dominant for intra-cluster coupling. For the specific condition that L₁ = 0.5d (or L₂ = 0.5d), the intra- (or inter) clusters can be reconsidered as a new hexagon hole with side length equal to d. In this case, there is a 15.2% TE-polarized band gap from 0.243 c/a to 0.283 c/a for both PC1 and PC3. Based on the second-order topological physics [43, 44], it is easy to obtain the expanded PC that has a non-trivial phase and the shrunken PC that has a trivial phase. On the other hand, when we consider a ▽-shaped cluster as shown in Figure 2C, the shrunken case also changes to be PC3 (green border) and the expanded case can have another nontrivial second-order TPC (i.e., PC2 labeled as a blue border). More details about the discussions of the topological properties will be shown in the next section.

There are six types of the interfaces formed by two of these three PCs, and we have discussed two of them (i.e., V1 and V2) in the last section. Here, we show two types of second-order interfaces formed by the second-order topologically nontrivial case (i.e., PC1 or PC2) and the second-order topologically trivial case (i.e., PC3), which will be applied to design the multiport routing device in the following discussion. As shown in Figure 2D, one is the H1-type interface between PC1 in the left and PC3 in the right. The edge dispersion shows that there is an “edgeˮ band gap between the edge states (red dots) that does not support any bulk and edge state. As shown in Figure 2E, another one is the H2-type interface between PC2 in the left and PC3 in the right. There is an “edgeˮ band gap between the bulk states (black dots) and edge states (red dots). The second-order corner states we are interested in will fall in these “edgeˮ band gaps.

Two Types of Second-Order Corner States in the Topological Interfaces

To characterize the topological phases of the expanded and shrunken PCs in Kagome lattice, one can extract the bulk polarization $P=\left(p_1,p_2\right)$, where p_m is the bulk polarization component in the direction of the reciprocal vector b_m and m represents 1 or 2. In particular, the Kagome-lattice PCs have C₃ symmetry that constrains on P, so p₁ = p₂ and we can extract a simple form of the bulk polarization with respect to the parities at high-symmetry wavevector points (i.e. Γ and K) [43–45],

$p_m=\frac{-i}{2\pi }\ln \left[{\displaystyle {\prod }_{n\in occ}\frac{{\theta }_m^n\left(K\right)}{{\theta }_m^n\left(\text{Γ}\right)}}\right],(3)$

where

${\theta }_m^n\left(\text{k}\right)=\langle u_n\left(\text{k}\right)|R_3|u_n\left(\text{k}\right)\rangle /\langle u_n\left(\text{k}\right)|u_n\left(\text{k}\right)\rangle ,(4)$

is the expectation value of the three-fold symmetric operator R₃ in the b_m direction and $u_n\left(k\right)$ is the Bloch function of n-th-band eigenfields at a specific k point. The subscript “occ” in Eq. 3 implies the summation over the bands below the band gap. Note that the Kagome-lattice PCs in this work only have one TE-polarized bulk band below the topological band gap. At Γ point, the bulk state of the first TE band is a zero-frequency mode, which is always homogeneous in real space such that ${\theta }_m^1\left(\Gamma \right)\equiv 1$. Thus, the expression of bulk polarization can be simplified as,

$p_m=\frac{-i}{2\pi }\ln \left[{\theta }_m\left(K\right)\right],(5)$

Here, ${\theta }_m$ represents the expectation value of the threefold symmetric operator R₃ of the first band. In simulation, when we introduce the distribution of the Bloch mode at K $u_n\left(K\right)$ into Eq. 5, the bulk polarization can be estimated to determine the second-order topological phase. For the two types of expanded PCs, the PC1 [labeled as a red border in Figure 2A] has a non-trivial phase with nonzero bulk polarization P = (-1/3,-1/3), while the PC2 [labeled as a blue border in Figure 2C] has another type of nontrivial phase with nonzero bulk polarization P = (1/3,1/3). And the shrunken PC3 has a trivial phase with zero bulk polarization P = (0,0).

When PC1 and PC3 are spliced together that the topological non-trivial lattice is surrounded by the topological trivial lattice, the two H1-type boundaries are intersected at a corner (marked by a yellow star) and thus form a 120-deg-bending interface, as shown in Figure 3A. Next, we will compute the eigenmode spectrum of the interface by using the frequency-domain eigenvalue solution of COMSOL, in order to better understand the optical behavior. The PC1 [red border] is arranged as a rhombus shape with a side length of 20a, and the outer region is terminated with the topologically trivial PC3 [green border]. In the simulated model, the computational cell is a rhombus with the total side length of 40a and covers with a scattering boundary. Figure 3B shows the eigenmode spectrum of the H1-type interface with a 120-deg-bending geometry. Green and blue regions indicate the frequency range of bulk states and edge states, respectively. There are two eigenmodes (marked by red point) falling in the band gap and isolating from bulk and edge states, i.e., two types of SOCSs. In Figures 3C,D, we show the real part of H_z-field distributions of the two isolated modes, i.e., H1-type I and H1-type II corner states. With respect to mirror symmetry (the mirror planes are marked as white dashed lines), the lower-frequency one (around 0.262c/a) is an even mode derived from the nearest-neighboring hopping of SOTPC, while the higher-frequency one (around 0.263c/a) is an odd mode under the consideration of the next-nearest-neighboring hopping of SOTPC [46].

FIGURE 3

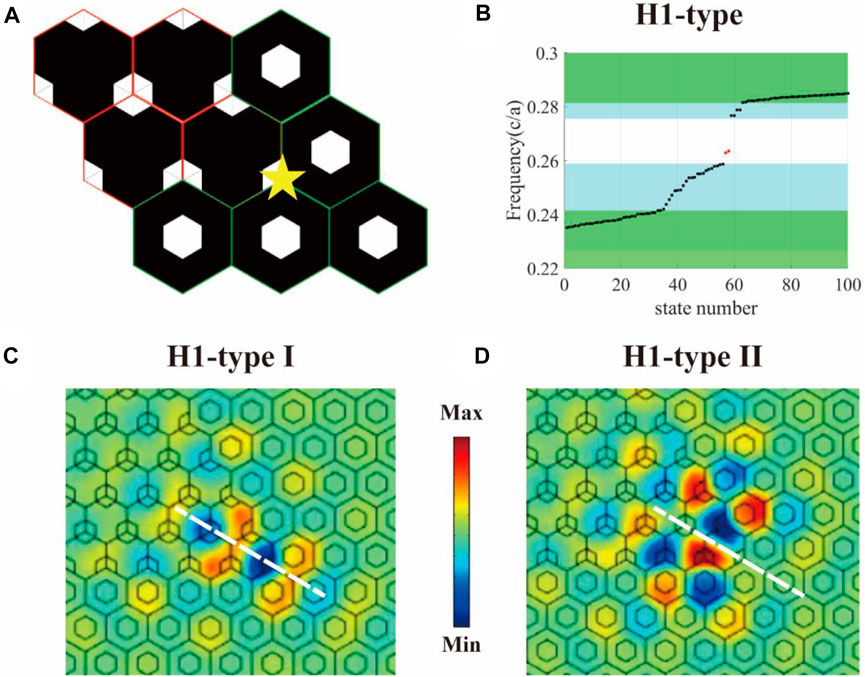
FIGURE 3. Two types of second-order corner states (SOCSs) in H1-type topological interfaces. (A) Schematic view and (B) eigenmode spectrum of the H1-type topological interface with a 120-deg-bending geometry. The interface is constructed by PC1 and PC3. Green and blue regions indicate the frequency range of bulk states and edge states, respectively. There are two eigenmodes (marked by red point) falling in the band gap and isolating from bulk and edge states, i.e. two types of SOCSs. (C) and (D) Distributions of real-part H_z fields for the two SOCSs. The SOCS with even symmetry (around 0.262c/a) is the type I corner state (labeled as H1-type-I), while the SOCS with odd symmetry (around 0.263c/a) is the type II corner state (labeled as H1-type-II). We use dashed white lines marking the mirror plane.

Proposal for Topological Photonic Crystal Routing Platform

In this section, based on the VDESs with robust transport and localized SOCSs, we will show the design of a multiport topological routing platform for the flexible control of topologically optical transport. As shown in Figure 4A, the platform is rhombus with a side length of 55a. There are four domains in the topological routing platform, which is constructed by PC1, PC2, and PC3. The boundaries formed by these topological PCs introduce three different edge states (V1, H1, and H2) along the interfaces and two corner states (H1-type I and H1-type II) at the intersection point [marked by a yellow star in Figure 3A]. The merging of different types of those topological boundary states can realize the frequency-dependent selection of transmission path. For incidence, a 4a-width waveguide-mode source with TE polarization is placed at the input terminal of port 1, depicted as purple arrows of Figure 4A. The incident source has the same amplitude for different frequencies. Three detectors with 4a width are placed at the output ends of ports 2–4 to measure the transmittance, shown as green, red, and cyan arrows in Figure 4A, respectively. In Figure 4B, we calculate the transmission spectrum of the four-port device when light is incident from port 1. The transmission intensities are described as arbitrary unit (a.u.) and normalized by the maximum intensity. We can see that the transmission of different paths obviously varies with frequency. With the increase of frequency, the excited waves change from bulk states to edge states and output to a certain port dependent on the selective excitation of those topological boundary states. Port 4 has the highest transmittance (cyan line) because the propagation light from port 1 to port 4 only experiences the coupling of V1 to H2 with a 120-deg detouring angle. On the contrary, port 2 has the lowest transmittance (green line). The propagation light from port 1 to port 2 involves the coupling of three types of edge states and two different angles, so that the high transmission should meet criteria that the boundary states of V1, H1, and H2 are all excited simultaneously. As for port 3, the transmission should mainly rely on the VDES of the V1 interface, but there is another interface (i.e., H1) in the middle that has an effect on its transmission efficiency.

FIGURE 4

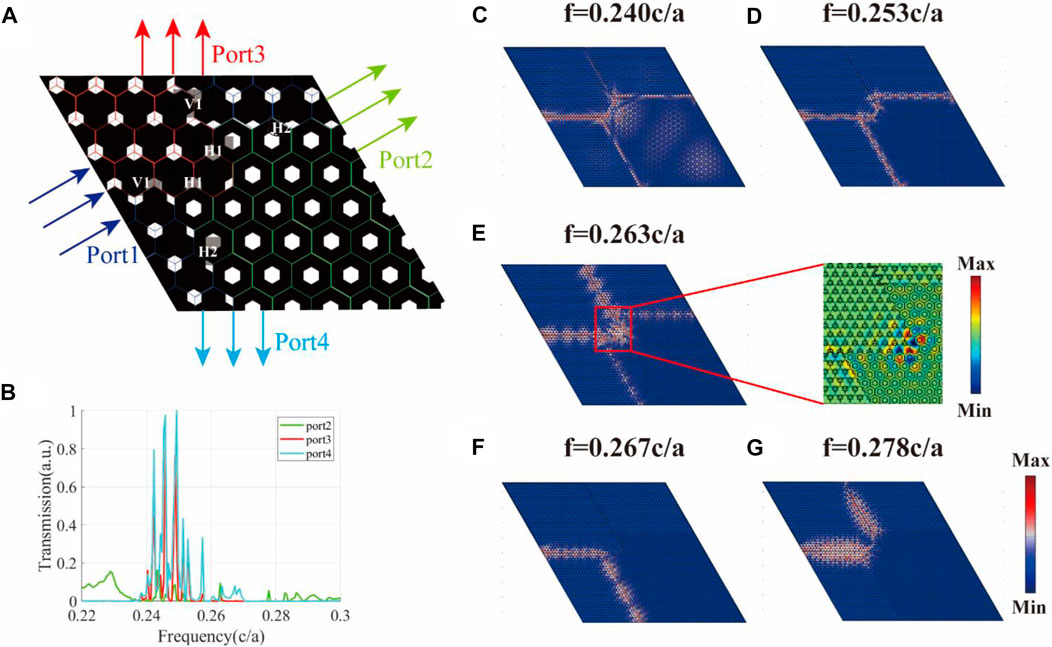
FIGURE 4. Design of a four-port routing platform based on topological photonic crystals. (A) Schematics of the multiport topological routing platform. There are four domains on the platform constructed by PC1, PC2, and PC3. The boundaries of these different topological photonic crystals introduce three different edge states (V1, H1, and H2) and two corner states (H1 type) at the intersection point. (B) Transmission spectrum of the four-port device when light is incident from port 1. The transmission intensity of different paths obviously varies with frequency. (C–G) Electric-field intensity distributions at the frequencies 0.240c/a, 0.253c/a, 0.263c/a, 0.267c/a, and 0.278c/a, respectively. The inset of panel (E) shows the real part of H_z field distribution at a frequency of 0.263c/a, indicating the excitation of the H1-type II corner state. Through the frequency-dependent selective excitation of different types of topological boundary states, such a four-port device provides a novel way to route the optical transport with topologically protected robustness.

To visually demonstrate the routing characteristics with the variation of frequency, we also calculate the distributions of electric-field intensity at several representative frequencies, as shown in Figures 4C–G. In Figure 4C, since the operation frequency of 0.240c/a is below the bulk band gap, both bulk states and edge states are excited and the propagation waves leak to the bulk crystal. At a frequency of 0.253c/a [Figure 4D], the propagation waves have mainly splitted to both port 2 and port 4, so the platform can act as an optical power splitter in this case. Although there is a lack of edge states in the H1 interface at a frequency of 0.263c/a, most of the propagation waves can output to port 3 with the aid of SOCS, as shown in Figure 4E. The inset gives the real part of H_z fields with odd symmetry that confirm the excitation of the type II corner state. Due to the absence of H1 edge states and SOCSs at a frequency of 0.267c/a [Figure 4F], the propagation waves incident from port 1 can only couple to the bottom-left H2 interface and output to port 4. At a frequency of 0.278c/a in Figure 4G, H2 edge states are absent but the channel supports both V1 and H1 edge states, so that the propagation waves can output to port 3. In a word, through the frequency-dependent selective excitation of different types of topological boundary states, such a four-port device provides a global method to route the optical transport with the topologically protected robustness. The global method means such robustness is one of the intrinsic properties of VDESs and SOCSs, which could be totally predicted by investigating the bulk topology, regardless of the local region around the corner. Therefore, some promising applications for light manipulation in topological nanophotonics (e.g., mode-division multiplexing) will benefit by the decrease of design complexity.

Conclusion

In summary, we have realized both VDESs and SOCSs based on two configurations of unit cell in the same triangular-lattice PC. The VDESs are derived from sublattice symmetry breaking in the honeycomb-lattice configuration, while SOCSs are induced by the lattice deformation of the Kagome-lattice configuration. We have designed a four-port device to selectively excite VDESs and SOCSs. Finally, the frequency-dependent routing effect of topological optical transport has been confirmed by simulation results. Our work explores various topological intriguing phases in a single photonic crystal platform, which will enrich the capability of light manipulation based on topological photonic systems. By merging of VDESs and SOCSs, the proposal of the multiport routing device provides a novel method to develop mode-division multiplexing in topological photonic integrated circuits.

Data Availability Statement

The original contributions presented in the study are included in the article/Supplementary Material; further inquiries can be directed to the corresponding authors.

Author Contributions

X-TH and J-WD initiated and supervised the project. M-YL and X-TH developed the theory. M-YL performed the numerical simulations. M-YL and X-TH wrote the draft. All authors contributed to the theoretical discussions, simulated data analysis, and article writing.

Funding

This work was supported by the National Key Research and Development Program of China (Grant No. 2019YFA0706302), the National Natural Science Foundation of China (Grant Nos. 62035016 and 11904421), the Basic and Applied Basic Research Foundation of Guangdong Province (Grant No. 2018B030308005), the Guangzhou Science, Technology and Innovation Commission (Grant No. 202002030322), and the Fundamental Research Funds for the Central Universities (Grant No. 20lgjc05).

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s Note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors, and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

1. Hasan MZ, Kane CL. Colloquium: Topological Insulators. Rev Mod Phys (2010) 82:3045–67. doi:10.1103/RevModPhys.82.3045

CrossRef Full Text | Google Scholar

2. Qi X-L, Zhang S-C. Topological Insulators and Superconductors. Rev Mod Phys (2011) 83:1057–110. doi:10.1103/RevModPhys.83.1057

CrossRef Full Text | Google Scholar

3. Haldane FDM, Raghu S. Possible Realization of Directional Optical Waveguides in Photonic Crystals with Broken Time-Reversal Symmetry. Phys Rev Lett (2008) 100:013904. doi:10.1103/PhysRevLett.100.013904

PubMed Abstract | CrossRef Full Text | Google Scholar

4. Lu L, Joannopoulos JD, Soljačić M. Topological Photonics. Nat Photon (2014) 8:821–9. doi:10.1038/nphoton.2014.248

CrossRef Full Text | Google Scholar

5. Khanikaev AB, Shvets G. Two-dimensional Topological Photonics. Nat Photon (2017) 11:763–73. doi:10.1038/s41566-017-0048-5

CrossRef Full Text | Google Scholar

6. Ozawa T, Price HM, Amo A, Goldman N, Hafezi M, Lu L, et al. Topological Photonics. Rev Mod Phys (2019) 91:015006. doi:10.1103/RevModPhys.91.015006

CrossRef Full Text | Google Scholar

7. Tang GJ, He XT, Shi FL, Liu JW, Chen XD, Dong JW. Topological Photonic Crystals: Physics, Designs, and Applications. Laser Photon Rev (2022) 16:2100300. doi:10.1002/lpor.202100300

CrossRef Full Text | Google Scholar

8. Wang Z, Chong Y, Joannopoulos JD, Soljačić M. Observation of Unidirectional Backscattering-Immune Topological Electromagnetic States. Nature (2009) 461:772–5. doi:10.1038/nature08293

PubMed Abstract | CrossRef Full Text | Google Scholar

9. Khanikaev AB, Hossein Mousavi S, Tse W-K, Kargarian M, MacDonald AH, Shvets G. Photonic Topological Insulators. Nat Mater (2012) 12:233–9. doi:10.1038/nmat3520

PubMed Abstract | CrossRef Full Text | Google Scholar

10. Chen W-J, Jiang S-J, Chen X-D, Zhu B, Zhou L, Dong J-W, et al. Experimental Realization of Photonic Topological Insulator in a Uniaxial Metacrystal Waveguide. Nat Commun (2014) 5:5782. doi:10.1038/ncomms6782

PubMed Abstract | CrossRef Full Text | Google Scholar

11. Wu L-H, Hu X. Scheme for Achieving a Topological Photonic Crystal by Using Dielectric Material. Phys Rev Lett (2015) 114:223901. doi:10.1103/PhysRevLett.114.223901

PubMed Abstract | CrossRef Full Text | Google Scholar

12. Dong J-W, Chen X-D, Zhu H, Wang Y, Zhang X. Valley Photonic Crystals for Control of Spin and Topology. Nat Mater (2017) 16:298–302. doi:10.1038/nmat4807

PubMed Abstract | CrossRef Full Text | Google Scholar

13. Yang Y, Xu YF, Xu T, Wang H-X, Jiang J-H, Hu X, et al. Visualization of a Unidirectional Electromagnetic Waveguide Using Topological Photonic Crystals Made of Dielectric Materials. Phys Rev Lett (2018) 120:217401. doi:10.1103/PhysRevLett.120.217401

PubMed Abstract | CrossRef Full Text | Google Scholar

14. Liu F, Wakabayashi K. Novel Topological Phase with a Zero Berry Curvature. Phys Rev Lett (2017) 118:076803. doi:10.1103/PhysRevLett.118.076803

PubMed Abstract | CrossRef Full Text | Google Scholar

15. Xie B-Y, Wang H-F, Wang H-X, Zhu X-Y, Jiang J-H, Lu M-H, et al. Second-order Photonic Topological Insulator with Corner States. Phys Rev B (2018) 98:205147. doi:10.1103/PhysRevB.98.205147

CrossRef Full Text | Google Scholar

16. Fu J-X, Lian J, Liu R-J, Gan L, Li Z-Y. Unidirectional Channel-Drop Filter by One-Way Gyromagnetic Photonic crystal Waveguides. Appl Phys Lett (2011) 98:211104. doi:10.1063/1.3593027

CrossRef Full Text | Google Scholar

17. Bahari B, Ndao A, Vallini F, El Amili A, Fainman Y, Kanté B. Nonreciprocal Lasing in Topological Cavities of Arbitrary Geometries. Science (2017) 358:636–40. doi:10.1126/science.aao4551

PubMed Abstract | CrossRef Full Text | Google Scholar

18. Barik S, Karasahin A, Flower C, Cai T, Miyake H, DeGottardi W, et al. A Topological Quantum Optics Interface. Science (2018) 359:666–8. doi:10.1126/science.aaq0327

PubMed Abstract | CrossRef Full Text | Google Scholar

19. He X-T, Liang E-T, Yuan J-J, Qiu H-Y, Chen X-D, Zhao F-L, et al. A Silicon-On-Insulator Slab for Topological valley Transport. Nat Commun (2019) 10:872. doi:10.1038/s41467-019-08881-z

PubMed Abstract | CrossRef Full Text | Google Scholar

20. Shalaev MI, Walasik W, Tsukernik A, Xu Y, Litchinitser NM. Robust Topologically Protected Transport in Photonic Crystals at Telecommunication Wavelengths. Nat Nanotech (2019) 14:31–4. doi:10.1038/s41565-018-0297-6

CrossRef Full Text | Google Scholar

21. Shao Z-K, Chen H-Z, Wang S, Mao X-R, Yang Z-Q, Wang S-L, et al. A High-Performance Topological Bulk Laser Based on Band-Inversion-Induced Reflection. Nat Nanotechnol (2020) 15:67–72. doi:10.1038/s41565-019-0584-x

PubMed Abstract | CrossRef Full Text | Google Scholar

22. Gao X, Yang L, Lin H, Zhang L, Li J, Bo F, et al. Dirac-vortex Topological Cavities. Nat Nanotechnol (2020) 15:1012–8. doi:10.1038/s41565-020-0773-7

PubMed Abstract | CrossRef Full Text | Google Scholar

23. Yang Y, Yamagami Y, Yu X, Pitchappa P, Webber J, Zhang B, et al. Terahertz Topological Photonics for On-Chip Communication. Nat Photon (2020) 14:446–51. doi:10.1038/s41566-020-0618-9

CrossRef Full Text | Google Scholar

24. Zeng Y, Chattopadhyay U, Zhu B, Qiang B, Li J, Jin Y, et al. Electrically Pumped Topological Laser with valley Edge Modes. Nature (2020) 578:246–50. doi:10.1038/s41586-020-1981-x

PubMed Abstract | CrossRef Full Text | Google Scholar

25. Chen Y, He X-T, Cheng Y-J, Qiu H-Y, Feng L-T, Zhang M, et al. Topologically Protected Valley-Dependent Quantum Photonic Circuits. Phys Rev Lett (2021) 126:230503. doi:10.1103/PhysRevLett.126.230503

PubMed Abstract | CrossRef Full Text | Google Scholar

26. Wu X, Meng Y, Tian J, Huang Y, Xiang H, Han D, et al. Direct Observation of valley-polarized Topological Edge States in Designer Surface Plasmon Crystals. Nat Commun (2017) 8:1304. doi:10.1038/s41467-017-01515-2

PubMed Abstract | CrossRef Full Text | Google Scholar

27. Gao F, Xue H, Yang Z, Lai K, Yu Y, Lin X, et al. Topologically Protected Refraction of Robust Kink States in valley Photonic Crystals. Nat Phys (2018) 14:140–4. doi:10.1038/nphys4304

CrossRef Full Text | Google Scholar

28. Ma J, Xi X, Sun X. Topological Photonic Integrated Circuits Based on Valley Kink States. Laser Photon Rev (2019) 13:1900087. doi:10.1002/lpor.201900087

CrossRef Full Text | Google Scholar

29. Han Y, Fei H, Lin H, Zhang Y, Zhang M, Yang Y. Design of Broadband All-Dielectric valley Photonic Crystals at Telecommunication Wavelength. Opt Commun (2021) 488:126847. doi:10.1016/j.optcom.2021.126847

CrossRef Full Text | Google Scholar

30. Chen X-D, Deng W-M, Shi F-L, Zhao F-L, Chen M, Dong J-W. Direct Observation of Corner States in Second-Order Topological Photonic Crystal Slabs. Phys Rev Lett (2019) 122:233902. doi:10.1103/PhysRevLett.122.233902

PubMed Abstract | CrossRef Full Text | Google Scholar

31. Xie B-Y, Su G-X, Wang H-F, Su H, Shen X-P, Zhan P, et al. Visualization of Higher-Order Topological Insulating Phases in Two-Dimensional Dielectric Photonic Crystals. Phys Rev Lett (2019) 122:233903. doi:10.1103/PhysRevLett.122.233903

PubMed Abstract | CrossRef Full Text | Google Scholar

32. Ota Y, Liu F, Katsumi R, Watanabe K, Wakabayashi K, Arakawa Y, et al. Photonic crystal Nanocavity Based on a Topological Corner State. Optica (2019) 6:786–9. doi:10.1364/OPTICA.6.000786

CrossRef Full Text | Google Scholar

33. Zhang W, Xie X, Hao H, Dang J, Xiao S, Shi S, et al. Low-threshold Topological Nanolasers Based on the Second-Order Corner State. Light Sci Appl (2020) 9:109. doi:10.1038/s41377-020-00352-1

PubMed Abstract | CrossRef Full Text | Google Scholar

34. He X-T, Li M-Y, Qiu H-Y, Ruan W-S, Zhou L-D, Liu L, et al. In-plane Excitation of a Topological Nanophotonic Corner State at Telecom Wavelengths in a Cross-Coupled Cavity. Photon Res (2021) 9:1423. doi:10.1364/prj.419569

CrossRef Full Text | Google Scholar

35. Yoshimi H, Yamaguchi T, Ota Y, Arakawa Y, Iwamoto S. Slow Light Waveguides in Topological valley Photonic Crystals. Opt Lett (2020) 45:2648–51. doi:10.1364/OL.391764

PubMed Abstract | CrossRef Full Text | Google Scholar

36. Yuan M, Xu T, Hang ZH. Construction of Optical Topological Cavities Using Photonic Crystals. Front Phys (2021) 9:9. doi:10.3389/fphy.2021.697719

CrossRef Full Text | Google Scholar

37. Zhu X, Wang H-X, Xu C, Lai Y, Jiang J-H, John S. Topological Transitions in Continuously Deformed Photonic Crystals. Phys Rev B (2018) 97. doi:10.1103/PhysRevB.97.085148

CrossRef Full Text | Google Scholar

38. Yang Y, Jia Z, Wu Y, Xiao R-C, Hang ZH, Jiang H, et al. Gapped Topological Kink States and Topological Corner States in Honeycomb Lattice. Sci Bull (2020) 65:531–7. doi:10.1016/j.scib.2020.01.024

CrossRef Full Text | Google Scholar

39. Johnson S, Joannopoulos J. Block-iterative Frequency-Domain Methods for Maxwell's Equations in a Planewave Basis. Opt Express (2001) 8:173–90. doi:10.1364/OE.8.000173

PubMed Abstract | CrossRef Full Text | Google Scholar

40. Xiao D, Yao W, Niu Q. Valley-contrasting Physics in Graphene: Magnetic Moment and Topological Transport. Phys Rev Lett (2007) 99:236809. doi:10.1103/PhysRevLett.99.236809

PubMed Abstract | CrossRef Full Text | Google Scholar

41. Ma T, Shvets G. All-Si valley-Hall Photonic Topological Insulator. New J Phys (2016) 18:025012. doi:10.1088/1367-2630/18/2/025012

CrossRef Full Text | Google Scholar

42. Chen X-D, Zhao F-L, Chen M, Dong J-W. Valley-contrasting Physics in All-Dielectric Photonic Crystals: Orbital Angular Momentum and Topological Propagation. Phys Rev B (2017) 96:020202. doi:10.1103/PhysRevB.96.020202

CrossRef Full Text | Google Scholar

43. Fang C, Gilbert MJ, Bernevig BA. Bulk Topological Invariants in Noninteracting point Group Symmetric Insulators. Phys Rev B (2012) 86:86. doi:10.1103/PhysRevB.86.115112

CrossRef Full Text | Google Scholar

44. Ni X, Weiner M, Alù A, Khanikaev AB. Observation of Higher-Order Topological Acoustic States Protected by Generalized Chiral Symmetry. Nat Mater (2019) 18:113–20. doi:10.1038/s41563-018-0252-9

PubMed Abstract | CrossRef Full Text | Google Scholar

45. Xue H, Yang Y, Gao F, Chong Y, Zhang B. Acoustic Higher-Order Topological Insulator on a Kagome Lattice. Nat Mater (2019) 18:108–12. doi:10.1038/s41563-018-0251-x

PubMed Abstract | CrossRef Full Text | Google Scholar

46. Li M, Zhirihin D, Gorlach M, Ni X, Filonov D, Slobozhanyuk A, et al. Higher-order Topological States in Photonic Kagome Crystals with Long-Range Interactions. Nat Photon (2019) 14:89–94. doi:10.1038/s41566-019-0561-9

CrossRef Full Text | Google Scholar