A Chaotic System With Infinite Attractors Based on Memristor

In this article, a memristor chaotic system is constructed by introducing a cosine function flux control memristor. By analyzing the balance of the system, it is found that there are coexisting attractors, and because of the periodicity of cosine function, the chaotic system has infinite coexisting attractors. The complexity analysis of Spectral Entropy (SE) and C0 is used in this paper to intuitively show the complex dynamic characteristics of the system. In addition, the introduction of paranoid propulsion also provides more possibilities for the system in engineering applications. Finally, the digital signal processing (DSP) experiment verifies the correctness of theoretical analysis and numerical analysis.

1 Introduction

In the 1960s, due to the birth of the Lorentz system [1], people started a period of a widespread upsurge in the study of chaos theory. Chaos is a physical phenomenon highly sensitive to initial values. Therefore, in the past decades, people have shown great interest in the creation of chaos. Chaos [2–10] has gradually developed from the study of climate to other fields, such as information science, biology, engineering, finance, and so on. So far, under the research of people, the chaotic system has been widely developed, from the original Lorentz system, to produce many different chaotic systems, including hyperchaotic system [11–17], discrete chaotic system [18–22], memristor chaotic system [23–25] and so on.

As the fourth basic circuit element, the memristor has aroused great interest in the nonlinear field since its birth. In 1971, Professor Chua made a prediction about the existence of the memristor based on the symmetrical structure of circuit elements. In 2008, HP company successfully developed a solid-state memristor that proved Chua’s prediction. Therefore, the study of memristor has become a new theoretical branch. In recent years, the combination of the memristor and chaotic system has formed a new memristor chaotic system [26–32], which is also called a new research hotspot.

In addition, the multi-steady state [33–37] of dynamic systems has aroused considerable interest in the nonlinear field. When the chaotic system has the property of a periodic state, the system may have periodic attractor pairs, which are constantly shifted in the same direction, so as to achieve an infinite multi-steady state. This discovery provides a new method for studying the multi-steady state of dynamic systems in the future.

In this paper, we choose an offset boosting [38–43] chaotic system as the basis, and introduce a memristor based on the cosine function to construct a new 5-D chaotic system, which has the following properties: 1) chaos generation; 2) infinite coexistence attractor; 3) and ffset boosting. In Section 2, the memristor in this system is analyzed, and obtain the “8” curve of proving the memristor. In Section 3, the corresponding chaotic phase diagram of the system is obtained through simulation analysis, and the related dynamics analysis of different parameters of the chaotic system is carried out, including the bifurcation diagram, Lyapunov exponential spectrum, infinite coexistence attractors, offset boosting, complexity analysis. In Section 4, the chaotic system is simulated by digital simulation and DSP experiment platform, and the reality of the physical existence of the system is verified. Finally, the conclusion of the study is given in Section 5.

2 Mathematical Model

2.1 Memristor Model

The memristor model is expressed as follows:

$\{\begin{array}{l}x=G\left(x,y,t\right)y\\ \dot{y}=H\left(x,y,t\right)\end{array},(1)$

where x is this output of the memristor, y represents the state of the memristor, and the functions G (.) and H (.) are particularly relevant to the memristor.

The flux-controlled memristor is from cosine function, and the specific equation is shown as follows:

$\{\begin{array}{l}W\left(w\right)=\frac{dq\left(w\right)}{d\left(w\right)}=\cos \left(w\right)\\ i=W\left(w\right)y=\cos \left(w\right)y\\ \frac{d\left(w\right)}{dt}=y^2-w\end{array},(2)$

Here, the following the “8” curve of the memristor is obtained by inputting different frequency parameters as shown in Figure 1.

FIGURE 1

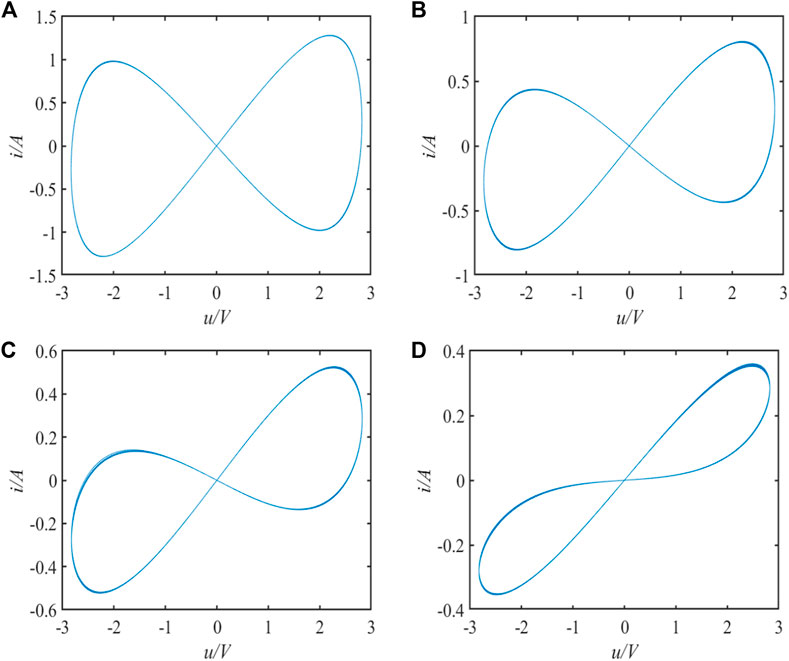
FIGURE 1. The u–i curve of memristor: (A) f = 0.5 kHz with u = 3 V, (B) f = 1 kHz with u = 3 V, (C) f = 2 kHz with u = 3 V, (D) f = 5 kHz with u = 3 V.

2.2 Equilibrium Points Set and Stability

By combining the memristor with the 4-D chaotic system, the specific expression of the chaotic system is shown below:

$\{\begin{array}{l}\dot{x}=ay-bz+\cos u\\ \dot{y}=cy\cos w-x^{2}z+k\\ \dot{z}=-dz+ex\\ \dot{u}=gy\\ \dot{w}=y^2-w\end{array}.(3)$

The divergence of the system is shown in Eq. 4,

$\nabla V=\frac{\partial \dot{x}}{\partial x}+\frac{\partial \dot{y}}{\partial y}+\frac{\partial \dot{z}}{\partial z}+\frac{\partial \dot{u}}{\partial u}+\frac{\partial \dot{w}}{\partial w},(4)$

when a = 9, b = 11, c = 15, d = 11, k = 1.5, e = 5, and g = 1, and this original conditions (1, 1, 1, 1, 1); $\nabla V$ not greater than zero; it is proved that the system is dissipative, there could be chaotic attractors in this system.

Setting $\dot{x}=\dot{y}=\dot{z}=\dot{u}=\dot{w}=0$, then lead to

$\{\begin{array}{l}ay-bz+\cos u=0\\ cy\cos w-x^{2}z+k=0\\ -dz+ex=0\\ gy=0\\ y^2-w=0\end{array},(5)$

from this the following equation can be obtained

$E^{\ast }=\{\begin{array}{l}None,k\ne 0\\ \left(\mathrm{0,0,0,0},n\pi +\frac{\pi }{2}\right)\text{,}k=0\end{array}.(6)$

If k = 0, the equilibrium set is set to O, Jacobi matrix J_E at the equilibrium points O

$J_E=\left[\begin{array}{ccccc}-a& z& y& b& 1\\ -z& c& -x& 0& 0\\ y& x& -d& 0& 0\\ z& 0& x& -e& 0\\ 0& g& 0& 0& 0\end{array}\right],(7)$

then, the secular equation set

${\lambda }^5+a_1{\lambda }^4+a_2{\lambda }^3+a_3{\lambda }^2+a_4\lambda +a_5=0,(8)$

where a₁ = 13.9, a₂ = -59.1, a₃ = 408.5, a₄ = 1,324.4, and a₅ = -39.5.

As shown in Eq. 6, the system is unstable according to the Rous criterion. Hence, when n be an any constant, and any equilibrium points within $O\left(\mathrm{0,0,0,0},n\pi +\frac{\pi }{2}\right)$, other parameters are n = 0, a = 9, b = 11, c = 15, d = 11, k = 1.5, e = 5, and g = 1, it results $a_2=-59.1<0$, $a_5=-39.5<0$, and λ₁ = -18.1636, λ₂ = 3.2391 + 4.7287i, λ₃ = 3.2391–4.7287i, λ₄ = -2.2397, λ₅ = 0.0296. At this point, the system is chaos.

3 Numerical Diagrams of the Dynamical Behavior

3.1 Chaotic Attractor

Let a = 9, b = 11, c = 15, d = 11, k = 3, e = 5, g = 1, and original conditions (1, 1, 1, 1, 1). Through simulation of the system, the phase diagrams of different chaotic attractors are shown in Figures 2, 3.

FIGURE 2

FIGURE 2. Chaotic attractor of system (3): (A) X-Y plane, (B) X-W plane.

FIGURE 3

FIGURE 3. (A) LEs, (B) bifurcation diagram.

3.2 LEs and Bifurcation Diagram of the System

System (3) sets three parameters, such as a, c, and d. The specific parameter range is as follows a ∈ [10, 15], c∈ [4, 6], and d∈ [3, 12].

After fixed the remaining parameters, set a, c, and d as variables, respectively, to determine their initial values. When analyzing the state of the system when the variable changes, the bifurcation diagram is usually combined with Lyapunov exponential spectrum, so that the changing state of the system can be analyzed more specifically.

Set a∈ [9, 15], b = 11, c = 15 d = 11, k = 1.5, e = 5, g = 1. The LEs and bifurcation diagram as shown in Figure 2 are obtained through software simulation. Meanwhile, smaller LEs are omitted below for easy observation. In the process of adjusting parameter a, it is found that the dynamical behavior of the system has complex dynamical characteristics, including a variety of states, such as period and chaos, and their mutual transformation. It can be observed from the figure that when parameter a ∈ [9, 11.2], and in the following range, the system slowly transforms from chaos to period and remains stable. In addition, parameter a ranges the corresponding system status can be clearly understood through the Table 1.

TABLE 1

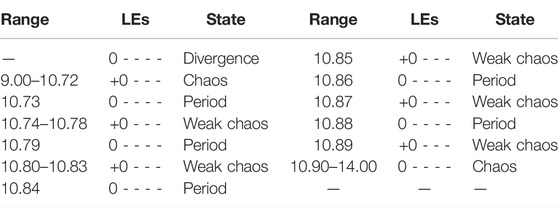
TABLE 1. System state corresponding to different parameter a when the original conditions is (1, 1, 1, 1, 1).

Set the parameter c∈ [10, 30] and keep the other unchanged. When c∈ [9, 9.12], the system is in a period, as shown in Figure 4. At the same time, the system changes rapidly from period to chaos in the following range. Specific numerical changes are shown in Table 2 and Figure 5.

FIGURE 4

FIGURE 4. (A) LEs, (B) bifurcation diagram.

TABLE 2

TABLE 2. System state corresponding to different parameter c when the original conditions is (1, 1, 1, 1, 1).

FIGURE 5

FIGURE 5. (A) LEs (B) bifurcation diagram.

Set d∈ [9, 18], and keep the other unchanged. In Figure 6, when d∈ [9, 9.43], at this point, the system LEs is 0, indicating that the system is in a periodic state, then the system changes to a chaos. When parameter d = 12.74 the system changes briefly to a periodic state. Table 3 clearly shows the process of system change within the range of parameter d.

FIGURE 6

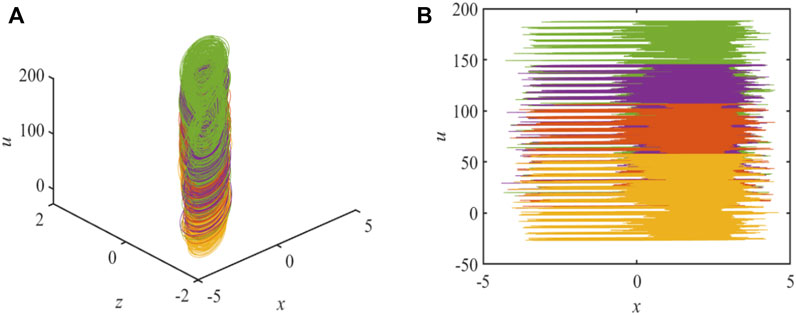
FIGURE 6. Coexisting attractors in system (3) with a = 9, b = 11, c = 15, d = 11, k = 1.5, e = 5, g = 1 under original conditions (1, 1, 1, 1, x₀), $x_0=-11\pi$ $x_0=-5\pi$ x₀ = 0 $x_0=-3\pi$ are for yellow, red, purple, and green correspondingly: (A) coexisting attractors in x–u plane (B) time-domain waveform.

TABLE 3

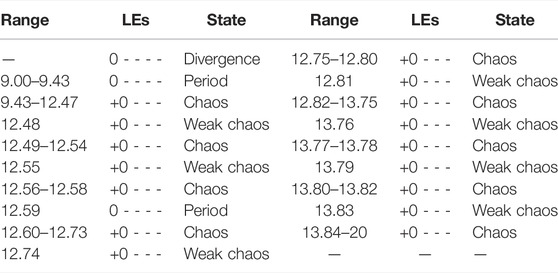
TABLE 3. System state corresponding to different parameter d when the original conditions is (1, 1, 1, 1, 1).

3.3 Infinite Coexisting Attractors

Coexistence attractor is a kind of phenomenon which mainly occurs in special nonlinear systems and has become a research hotspot. Because of the existence of trigonometric function in an equation, there exists the infinite coexisting attractor. The main phenomenon is that when parameters remain fixed and the initial values change, the trajectories could gradually tend to different states of motion. The phenomenon of the infinite coexisting attractor could be observed in Figure 6.

3.4 Offset Boosting Scheme

A new feedback state is introduced in the system to control the system flexibly so that the attractor and its attractor pool can move arbitrarily. This method is called offset boosting. By introducing a parameter q to boost the variable z, the system’s attractor and its attractor pool are controlled. The improved offset-boosted system is shown in Eq. 9:

$\{\begin{array}{l}x=ay-b\left(z-q\right)+\cos u\\ y=cy\cos w-x^2\left(z-q\right)+k\\ z=-d\left(z-q\right)+ex\\ u=gy\\ w=y^2-w\end{array}.(9)$

Let a = 9, b = 11, c = 15, d = 11, k = 1.5, e = 5, g = 1, when q is a constant. Figure 7A shows the 3D projection of the attractor with different offsets q, and with the increase of parameter q, the position of the attractor also shows a regular upward trend. Figure 7B shows the corresponding bifurcation diagram.

FIGURE 7

FIGURE 7. (A) The attractor at different offsets q (B) bifurcation diagram.

In Figures 7A,B, the local bifurcation diagram and the corresponding Lyapunov exponent spectrums are shown respectively. When parameter q ∈ [0, 2], the state variable z of the system augment with the augment of offset variable q, while the attractor LEs of the system does not change. In Figure 8B, the attractor is offset accordingly by introducing new variables, which have considerable practical application value in engineering.

FIGURE 8

FIGURE 8. (A) bifurcation diagram (B) Lyapunov exponent spectrum.

3.5 Complexity Analysis

The complexity analysis is one of the important methods to study chaotic system. In practical studies, complexity algorithms are generally introduced to measure chaotic sequences. In order to show the complexity of the chaotic system more clearly, as shown in Figure 9B, parameters b, c, b, and d are set respectively. When b∈ [10.5, 14] and d∈ [9, 18], it could be clearly observed that the region is dark, indicating that the system is in a chaotic state at this time. In this diagram, as the color gets darker, it also means that the system gets more complex. In addition, this multi-dimensional complexity analysis method also offers a deterministic foundation for the parameter pick of the systems.

FIGURE 9

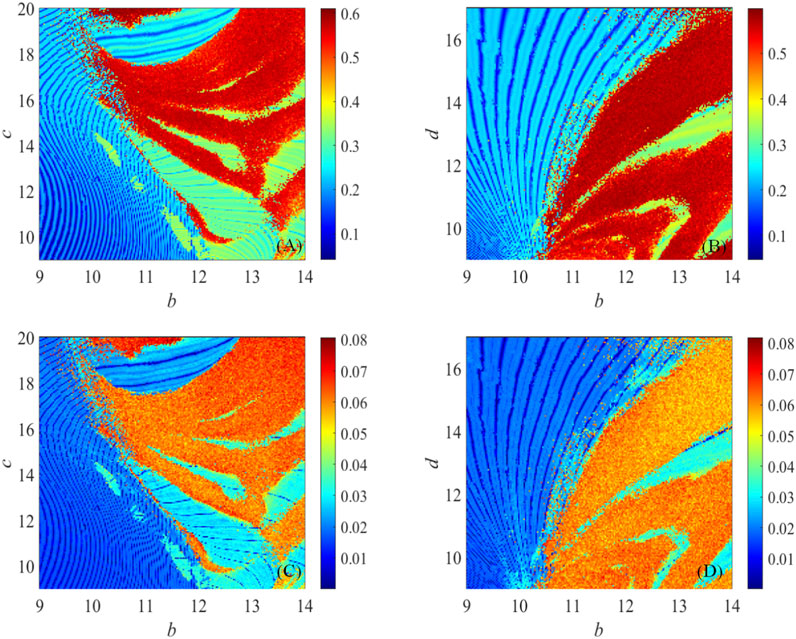
FIGURE 9. Complexity diagram with different parameter a d and e. (A) Parameters a d in SE complexity; (B) parameters a e in SE complexity; (C) parameters a d in C₀ complexity; (D) parameters a e in C₀ complexity.

4 Digital Circuit Platform Implementation

Fast speed, high accuracy, and low environmental impact are the characteristics of the DSP chip F28335. The chaos is confirmed on the experimental platform. The D/A converter needs to simulate and convert the sequence code generated by the DSP to snatch the output sequence displayed on the corresponding range (UTD7102H). By discretization of continuous chaos, correlation can be processed on DSP platform. Then, the fourth-order Runge-Kutta method is used to transform them into discrete chaotic sequences. Finally, the iterative relation is imported into DSP by C language and a corresponding simulation is carried out. The actual operation and experiment are shown in Figure 10.

FIGURE 10

FIGURE 10. Programming flow of DSP implementation.

The parameters were set as a = 9, b = 11, c = 15, d = 11, k = 1.5, e = 5, g = 1. The concrete experimental objects are shown in Figure 11, and the attractor shown in the figure corresponds to Figures 2A,B one by one.

FIGURE 11

FIGURE 11. Experimental platform for DSP implementation.

The phase diagram in Figure 12 shown on an oscilloscope is identical to the phase diagram simulated by the computer, The experiment proves that the digital simulation circuit is correct.

FIGURE 12

FIGURE 12. Chaotic attractor on the DSP platform: (A) X-Y plane, (B) X-W plane.

5 Conclusion

In this article, a memristor chaotic system is proposed and its dynamic behavior is analyzed. At the same time, it is proved that the appearance of infinite coexisting attractor caused by the periodicity of a trigonometric function is correct. By introducing the variable q into the variable z, the variable z changes parallel with the control variable q, while the value of LEs remains stable. It is proved that the method of flexibly changing the original sequence by introducing a new control variable is effective, and this method is called offset boosting. Finally, the corresponding digital circuit experiment is carried out, and the correctness of the experimental results is also verified. The influence of trigonometric function on memristor chaotic system is studied in this article, which provides a new reference and idea for the future study of the interaction between the chaotic system and periodic function.

Data Availability Statement

The original contributions presented in the study are included in the article/Supplementary Materials, further inquiries can be directed to the corresponding author.

Author Contributions

JW provided the idea of algorithm, carried out the simulations, arranged the architecture and drafted the manuscript. JW supervised the work and revised the manuscript. Both authors read and approved the final manuscript.

Funding

This research was financially supported by the Project for the National Natural Science Foundation of China (61402069), the 2017 Project for the Natural Science Foundation of Liaoning province (20170540059), and the General project of the National Social Science Fund (2019AG00482).

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s Note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors, and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

1. Lorenz EN. Deterministic Nonperiodic Flow. J Atmos Sci (1963) 20(2):130–41. doi:10.1175/1520-0469(1963)020<0130:dnf>2.0.co;2

CrossRef Full Text | Google Scholar

2. Liu T, Banerjee S, Yan H, Mou J. Dynamical Analysis of the Improper Fractional-Order 2D-SCLMM and its DSP Implementation. Eur Phys J Plus (2021) 136(5):506. doi:10.1140/epjp/s13360-021-01503-y

CrossRef Full Text | Google Scholar

3. Ma C, Mou J, Li P, Liu T. Dynamic Analysis of a New Two-Dimensional Map in Three Forms: Integer-Order, Fractional-Order and Improper Fractional-Order. Eur Phys J Spec Top (2021) 230(7):1945–57. doi:10.1140/epjs/s11734-021-00133-w

CrossRef Full Text | Google Scholar

4. Ma C, Mou J, Xiong L, Banerjee S, Liu T, Han X. Dynamical Analysis of a New Chaotic System: Asymmetric Multistability, Offset Boosting Control and Circuit Realization. Nonlinear Dyn (2021) 103(3):2867–80. doi:10.1007/s11071-021-06276-8

CrossRef Full Text | Google Scholar

5. Ma X, Mou J, Liu J, Ma C, Yang F, Zhao X. A Novel Simple Chaotic Circuit Based on Memristor-Memcapacitor. Nonlinear Dyn (2020) 100(3):2859–76. doi:10.1007/s11071-020-05601-x

CrossRef Full Text | Google Scholar

6. Mobayen S, Fekih A, Vaidyanathan S, Sambas A. Chameleon Chaotic Systems with Quadratic Nonlinearities: An Adaptive Finite-Time Sliding Mode Control Approach and Circuit Simulation. IEEE Access (2021) 9:64558–73. doi:10.1109/access.2021.3074518

CrossRef Full Text | Google Scholar

7. Sambas A, Vaidyanathan S, Bonny T, Zhang S, Sukono , Hidayat Y, et al. Mathematical Model and FPGA Realization of a Multi-Stable Chaotic Dynamical System with a Closed Butterfly-like Curve of Equilibrium Points. Appl Sci (2021) 11(2):788. doi:10.3390/app11020788

CrossRef Full Text | Google Scholar

8. Li X, Mou J, Cao Y, Banerjee S. An Optical Image Encryption Algorithm Based on a Fractional-Order Laser Hyperchaotic System. Int J Bifurcation Chaos (2022) 32(03):2250035. doi:10.1142/s0218127422500353

CrossRef Full Text | Google Scholar

9. Gao X, Mou J, Xiong L, Sha Y, Yan H, Cao Y. A Fast and Efficient Multiple Images Encryption Based on Single-Channel Encryption and Chaotic System. Nonlinear Dyn (2022) 108:613–636. doi:10.1007/s11071-021-07192-7

CrossRef Full Text | Google Scholar

10. Gao X, Mou J, Banerjee S, Cao Y, Xiong L, Chen X. An Effective Multiple-Image Encryption Algorithm Based on 3D Cube and Hyperchaotic Map. J King Saud University-Computer Inf Sci (2022) 34:1535–51. doi:10.1016/j.jksuci.2022.01.017

CrossRef Full Text | Google Scholar

11. Chen Z, Zhao H, Chen J. A Novel Image Encryption Scheme Based on Poker Cross-Shuffling and Fractional Order Hyperchaotic System. In: International Conference on Computer Engineering and Networks. Springer (2020). p. 818–25. doi:10.1007/978-981-15-8462-6_94

CrossRef Full Text | Google Scholar

12. Al-Azzawi SF, Al-Obeidi AS. Chaos Synchronization in a New 6D Hyperchaotic System with Self-Excited Attractors and Seventeen Terms. Asian-european J Math (2021) 14(05):2150085. doi:10.1142/s1793557121500856

CrossRef Full Text | Google Scholar

13. Yu F, Li L, He B, Liu L, Qian S, Zhang Z, et al. Pseudorandom Number Generator Based on a 5D Hyperchaotic Four-wing Memristive System and its FPGA Implementation. Eur Phys J Spec Top (2021) 230(7):1763–72. doi:10.1140/epjs/s11734-021-00132-x

CrossRef Full Text | Google Scholar

14. Chen X, Qian S, Yu F, Zhang Z, Shen H, Huang Y, et al. Pseudorandom Number Generator Based on Three Kinds of Four-wing Memristive Hyperchaotic System and its Application in Image Encryption. Complexity (2020) 2020:1–17. doi:10.1155/2020/8274685

CrossRef Full Text | Google Scholar

15. Huang W, Jiang D, An Y, Liu L, Wang X. A Novel Double-Image Encryption Algorithm Based on Rossler Hyperchaotic System and Compressive Sensing. IEEE Access (2021) 9:41704–16. doi:10.1109/access.2021.3065453

CrossRef Full Text | Google Scholar

16. Lai Q, Wan Z, Kamdem Kuate PD, Fotsin H. Dynamical Analysis, Circuit Implementation and Synchronization of a New Memristive Hyperchaotic System with Coexisting Attractors. Mod Phys Lett B (2021) 35(10):2150187. doi:10.1142/s0217984921501876

CrossRef Full Text | Google Scholar

17. Ahmad M, Doja MN, Beg MMS. Security Analysis and Enhancements of an Image Cryptosystem Based on Hyperchaotic System. J King Saud Univ - Comp Inf Sci (2021) 33(1):77–85. doi:10.1016/j.jksuci.2018.02.002

CrossRef Full Text | Google Scholar

18. Kumar D, Joshi AB, Singh S, Mishra VN, Rosales HG, Zhou L, et al. 6D-Chaotic System and 2D Fractional Discrete Cosine Transform Based Encryption of Biometric Templates. IEEE Access (2021) 9:103056–74. doi:10.1109/access.2021.3097881

CrossRef Full Text | Google Scholar

19. Peng Y, He S, Sun K. A Higher Dimensional Chaotic Map with Discrete Memristor. AEU - Int J Elect Commun (2021) 129:153539. doi:10.1016/j.aeue.2020.153539

CrossRef Full Text | Google Scholar

20. Chu Y-M, Bekiros S, Zambrano-Serrano E, Orozco-López O, Lahmiri S, Jahanshahi H, et al. Artificial Macro-Economics: A Chaotic Discrete-Time Fractional-Order Laboratory Model. Chaos, Solitons & Fractals (2021) 145:110776. doi:10.1016/j.chaos.2021.110776

CrossRef Full Text | Google Scholar

21. Alhadawi HS, Majid MA, Lambić D, Ahmad M. A Novel Method of S-Box Design Based on Discrete Chaotic Maps and Cuckoo Search Algorithm. Multimed Tools Appl (2021) 80(5):7333–50. doi:10.1007/s11042-020-10048-8

CrossRef Full Text | Google Scholar

22. Dai J-Y, Ma Y, Zhou N-R. Quantum Multi-Image Compression-Encryption Scheme Based on Quantum Discrete Cosine Transform and 4D Hyper-Chaotic Henon Map. Quan Inf Process (2021) 20(7):1–24. doi:10.1007/s11128-021-03187-w

CrossRef Full Text | Google Scholar

23. Liao K, Lei P, Tu M, Luo S, Jiang T, Jie W, et al. Memristor Based on Inorganic and Organic Two-Dimensional Materials: Mechanisms, Performance, and Synaptic Applications. ACS Appl Mater Inter (2021) 13(28):32606–23. doi:10.1021/acsami.1c07665

CrossRef Full Text | Google Scholar

24. Peng Y, He S, Sun K. Chaos in the Discrete Memristor-Based System with Fractional-Order Difference. Results Phys (2021) 24:104106. doi:10.1016/j.rinp.2021.104106

CrossRef Full Text | Google Scholar

25. Bao H, Hua Z, Li H, Chen M, Bao B. Discrete Memristor Hyperchaotic Maps. IEEE Trans Circuits Syst (2021) 68(11):4534–44. doi:10.1109/tcsi.2021.3082895

CrossRef Full Text | Google Scholar

26. Xie W, Wang C, Lin H. A Fractional-Order Multistable Locally Active Memristor and its Chaotic System with Transient Transition, State Jump. Nonlinear Dyn (2021) 104(4):4523–41. doi:10.1007/s11071-021-06476-2

CrossRef Full Text | Google Scholar

27. Akgül A, Rajagopal K, Durdu A, Pala MA, Boyraz ÖF, Yildiz MZ. A Simple Fractional-Order Chaotic System Based on Memristor and Memcapacitor and its Synchronization Application. Chaos, Solitons & Fractals (2021) 152:111306. doi:10.1016/j.chaos.2021.111306

CrossRef Full Text | Google Scholar

28. Sun S, Yan D, Ji’e M, Du X, Wang L, Duan S. Memristor-based Time-Delay Chaotic System with Hidden Extreme Multi-Stability and Pseudo-random Sequence Generator. Eur Phys J Spec Top (2021) 230(18):3481–91. doi:10.1140/epjs/s11734-021-00248-0

CrossRef Full Text | Google Scholar

29. Wang J, Mou J, Yan H, Liu X, Ma Y, Cao Y. A Three-Port Switch NMR Laser Chaotic System with Memristor and its Circuit Implementation. Eur Phys J Plus (2021) 136(11):1112. doi:10.1140/epjp/s13360-021-02097-1

CrossRef Full Text | Google Scholar

30. Wang Z, Qi G. Modeling and Analysis of a Three-Terminal-Memristor-Based Conservative Chaotic System. Entropy (2021) 23(1):71. doi:10.3390/e23010071

CrossRef Full Text | Google Scholar

31. Ma X, Mou J, Xiong L, Banerjee S, Cao Y, Wang J. A Novel Chaotic Circuit with Coexistence of Multiple Attractors and State Transition Based on Two Memristors. Chaos, Solitons & Fractals (2021) 152:111363. doi:10.1016/j.chaos.2021.111363

CrossRef Full Text | Google Scholar

32. Li C, Yang Y, Du J, Chen Z. A Simple Chaotic Circuit with Magnetic Flux-Controlled Memristor. Eur Phys J Spec Top (2021) 230(7):1723–36. doi:10.1140/epjs/s11734-021-00181-2

CrossRef Full Text | Google Scholar

33. Gu J, Li C, Chen Y, Iu HHC, Lei T. A Conditional Symmetric Memristive System with Infinitely many Chaotic Attractors. IEEE Access (2020) 8:12394–401. doi:10.1109/access.2020.2966085

CrossRef Full Text | Google Scholar

34. Yang T. Multistability in a 3D Autonomous System with Different Types of Chaotic Attractors. Int J Bifurcation Chaos (2021) 31(02):2150028. doi:10.1142/s0218127421500280

CrossRef Full Text | Google Scholar

35. Liu B, Ye X, Chen Q. Generating Infinitely many Coexisting Attractors via a New 3D Cosine System and its Application in Image Encryption. IEEE Access (2021) 9:136292–301. doi:10.1109/access.2021.3117570

CrossRef Full Text | Google Scholar

36. Cheng T, Zhang Y, Shen Y. Infinite Number of Parameter Regions with Fractal Nonchaotic Attractors in a Piecewise Map. Fractals (2021) 29(04):2150087. doi:10.1142/s0218348x21500870

CrossRef Full Text | Google Scholar

37. Li C, Peng Y, Tao Z, Sprott JC, Jafari S. Coexisting Infinite Equilibria and Chaos. Int J Bifurcation Chaos (2021) 31(05):2130014. doi:10.1142/s0218127421300147

CrossRef Full Text | Google Scholar

38. Sayed WS, Roshdy M, Said LA, Radwan AG. Design and FPGA Verification of Custom-Shaped Chaotic Attractors Using Rotation, Offset Boosting and Amplitude Control. IEEE Trans Circuits Syst (2021) 68(11):3466–70. doi:10.1109/tcsii.2021.3082271

CrossRef Full Text | Google Scholar

39. Li C, Wang R, Ma X, Jiang Y. A Class of Offset Boostable 3-D Memristive System. In: Proceeding of the 2021 International Conference on Neuromorphic Computing (ICNC); Oct. 2021; Wuhan, China. IEEE (2021). p. 53–60. doi:10.1109/icnc52316.2021.9608241

CrossRef Full Text | Google Scholar

40. Chen B, Xu Q, Chen M, Wu H, Bao B. Initial-condition-switched Boosting Extreme Multistability and Mechanism Analysis in a Memcapacitive Oscillator. Front Inform Technol Electron Eng (2021) 22(11):1517–31. doi:10.1631/fitee.2000622

CrossRef Full Text | Google Scholar

41. Kong S, Li C, He S, Çiçek S, Lai Q. A Memristive Map with Coexisting Chaos and Hyperchaos*. Chin Phys. B (2021) 30(11):110502. doi:10.1088/1674-1056/abf4fb

CrossRef Full Text | Google Scholar

42. Wen J, Feng Y, Tao X, Cao Y. Dynamical Analysis of a New Chaotic System: Hidden Attractor, Coexisting-Attractors, Offset Boosting, and DSP Realization. IEEE Access (2021) 9:167920–7. doi:10.1109/access.2021.3136249

CrossRef Full Text | Google Scholar

43. Reich S, Sporer M, Ortmanns M. A Chopped Neural Front-End Featuring Input Impedance Boosting with Suppressed Offset-Induced Charge Transfer. IEEE Trans Biomed Circuits Syst (2021) 15(3):402–11. doi:10.1109/tbcas.2021.3080398

PubMed Abstract | CrossRef Full Text | Google Scholar