- 1Physics and Chemistry of Materials Laboratory, Department of Physics, Faculty of Sciences, University of Monastir, Monastir, Tunisia
- 2Laboratory of Quantum and Statistical Physics, Department of Physics, Faculty of Sciences, University of Monastir, Monastir, Tunisia
The molecular geometries of the possible conformations of pyruvic acid–water complexes (PA-(H2O)n = 1–4) have been fully optimized at DFT/B3LYP/6-311G++ (d, p) levels of calculation. Among several optimized molecular clusters, we present here the most stable molecular arrangements obtained when one, two, three, and four water molecules are hydrogen-bonded to a central pyruvic acid molecule. Appropriate topological and geometrical parameters are considered primary indicators of H-bond strength. Atoms in molecules analysis shows that pyruvic acid can form a ring structure with water, and the molecular structures are stabilized by both strong O–H⋅⋅⋅O and C–H⋅⋅⋅O hydrogen bonds. In large clusters, classical O–H⋅⋅⋅O hydrogen bonds still exist between water molecules, and a cage-like structure is built around some parts of the central molecule of pyruvic acid.
Introduction
Pyruvic acid (CH3COCOOH, PA) is one of the important chemical components that exist in atmospheric aerosols, fog, and clouds. This organic substance is widely distributed in nature as a metabolic intermediate and supplies energy to living cells through the Krebs cycle when oxygen is present (aerobic respiration), and when oxygen is lacking, it ferments to produce lactic acid [1, 2]. It is also confirmed that the muscular contraction under physical efforts is associated with the level of both pyruvic and lactic acids [3].
The PA monomer has been the subject of many computational and experimental studies [4–14]. The PA molecule displays conformational complications in the gas and solution phases due to the possibility of intramolecular rotation around the C–C and C–O bonds. The most stable conformer is generally a labeled trans–cis eclipsed form (Tce isomer) and has a planar structure. This conformer has additional stabilization due to the intramolecular hydrogen bond between the acid hydrogen and the α-carbonyl [4–9]. The intramolecular hydrogen bond energy, Eintra-HB which is classically defined as the energy difference between the closed and open conformations of a PA molecule, is theoretically estimated to be about 8.80 kJ/mol, where a zero point in the energy scale is fixed [14].
Considerable effort has been devoted to the investigation of the structure and photochemistry of PA in an aqueous solution [14–26]. Fischer et al. demonstrate that PA prefers to stay as a monomer in nonpolar solvents, such as carbon tetrachloride, due to its ability to form intramolecular hydrogen bonds [15], and when it comes to the water atmosphere, hydrogen bonds C=O⋅⋅⋅H-O and O-H⋅⋅⋅O-H are established between pyruvic acid and water molecules [16]. The importance of intermolecular hydrogen bonds in the effective molecular recognition of pyruvic acid—water mixtures has been highlighted by Schnitzler et al. [17], where the rotational spectrum measurements confirm that the structure of pyruvic acid isomers is planar and the monohydrated clusters of PA. Strong hydrogen bonds are formed between pyruvic acid and water molecules where water acts as a hydrogen bond donor and acceptor. The non-covalent interactions (NCI) and the atoms—in—molecules (AIM) analysis [17] indicate that water rotation has little effect on the interactions between water and pyruvic acid molecules, and ring structures are formed where two hydrogen bonds connect the water and acid molecules. The tautomeric equilibrium remains in favor of the keto form, and the energy gap between the two isomers in solution is found to be smaller than that in the gas phase [18]. The pair correlation functions as determined by MD simulations show that important interactions between PA and water molecules exist and the distribution of water molecules around the PA anion is strongly dependent on the acid molar fraction [19]. DFT calculations on the monohydrated pyruvic acid complexes show that the intramolecular hydrogen bond within the PA molecule is broken and two intermolecular hydrogen bonds C=O⋅⋅⋅H–O and O–H⋅⋅⋅O–H are formed between pyruvic acid and water molecules and contribute to the stability of the Tce conformer [20]. H1NMR experiments and molecular dynamics simulations prove that small hydrate clusters of pyruvic acid with only four water molecules are able to reproduce the solvation effect of pyruvic acid [21].
The present study is considered a new contribution to the studies of intermolecular hydrogen bonds established between pyruvic acid and water molecules. With respect to the possible binding sites in the pyruvic acid monomer, a large number of possible molecular complexes are examined. In all considered PA-(H2O)n = 1–4 clusters, DFT calculations and AIM analysis were used to explore the geometrical properties and strength of the established C=O⋅⋅⋅H-O and O-H⋅⋅⋅O-H hydrogen bonds in the considered complexes. Several indicators of hydrogen bond strength such as the H-bond X-H⋅⋅⋅O-H (X = O, C) length, dO…H, H-bond energy, EHB, electron density at the bond critical point, ρBCP, and the Laplacian of the electron density, ∇2ρ, are considered in our calculations.
Theoretical Calculations
The structures of the PA molecule and the PA-(H2O)n = 1–4 were optimized using the GAUSSIAN 09 program [27]. To investigate the relative stability of considered pyruvic acid–water complexes, we have performed DFT/B3LYP calculations of the minimum energy structures of all considered species implemented in the Gaussian 09 using the 6-311++G(d,p) basis set [28, 29]. The initial configuration searches for the pyruvic acid–water complexes were based on two steps. First, the isomer component of the ABCluster software [30] was used to generate the initial structures of pyruvic acid–water complexes. Both 2D and 3D initial guess structures have been considered to make sure we get the true global minima of each structure. For each structure, more than 500 guess structures are generated. Second, each of the generated structures was then fully optimized by the DFT/B3LYP /6-311++G(d,p) method using the Gaussian 09 package. To eliminate BSSE error, we have applied the full counterpoise procedure in all the calculations [31]. The theory of atoms in molecules (AIM) of Bader was used to examine topological features of electron density on wave functions obtained at the B3LYP/6-311G++(d, p) level using the Multiwfn software package [32].
Results and Discussions
Structural Analysis
The main goal of our study is to investigate the interactions in the aqueous solutions of pyruvic acid. Many PA–water complexes were considered based on the ability of the pyruvic acid molecule to form hydrogen bonds with water, and only the most stable complexes were identified. The most stable structures of the pyruvic acid monomer and the pyruvic acid—water complexes, PA-(H2O)1, PA-(H2O)2, PA-(H2O)3, and PA-(H2O)4, were optimized at the B3LYP level of theory with the basis set 6-311G++ (d, p) and represented with atomic numbers in Figures 1A–E. One can easily see that in all considered structures, ring parts are formed between the acid and water molecules involving O-H⋅⋅⋅O and C-H⋅⋅⋅O hydrogen bonds. The intramolecular parameters such as bond lengths and bond angles within the pyruvic acid molecule alone and in PA-(H2O)1–4 complexes were obtained using the same method. The DFT calculations by Yang et al. [21] show that hydrogen bond formation in the monohydrated pyruvic acid has a weak effect on the intramolecular bond lengths, especially the O-H and C-C bonds. Our calculations strongly support this conclusion and show that the C1–C2 decrease from 1.551 Å in the free PA molecule to 1.541 Å in the PA-(H2O)4 complex and the C1-O5 bond length is shortened when more water molecules are linked to the PA molecule and various molecules from 1.340 Å in the PA molecule to 1.313 Å in the PA-(H2O)4 complex. It is worth noticing here that the hydrogen bond's effect on the other X-X (X = C and O) intramolecular bond lengths within the pyruvic acid molecule never exceeds 1% of their values in the free PA molecule.
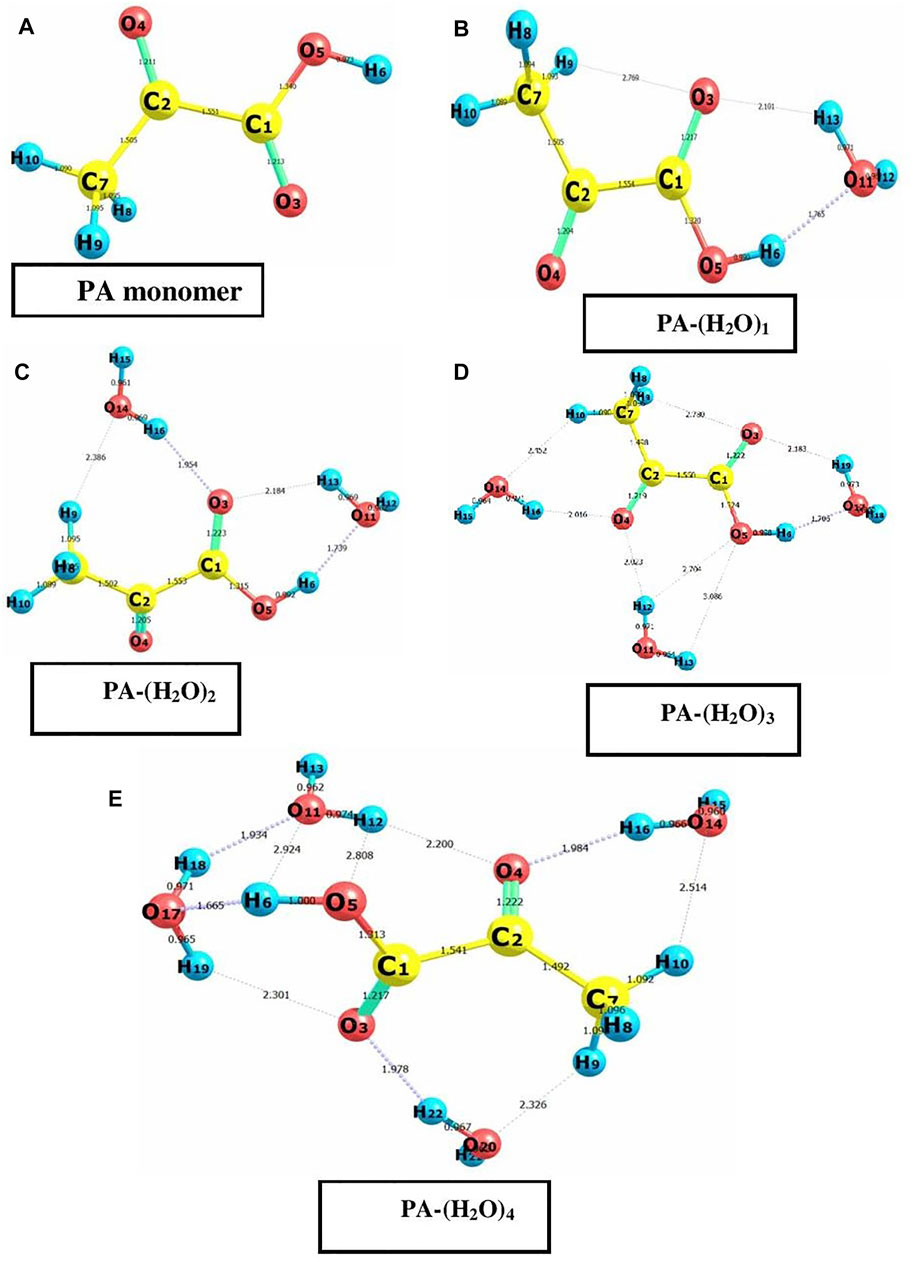
FIGURE 1. Optimized geometrics of pyruvic acid monomer and PA-(H2O)n = 1–4 (A–E) complexes with atom numbering using DFT/B3LYP calculations at the 6-311 G++(d, p) basic set.
The geometrical analysis of the structure of all the considered complexes shows that hydrogen bonds are established in aqueous solutions of pyruvic acid. The bond length between the donor and acceptor atoms of the hydrogen bonds and the bond angles are given in Table. 1 for PA-(H2O)n = 1–4 complexes. The energy of interaction of all the PA-(H2O)n = 1–4 complexes is calculated by the B3LYP/6- 311++G(d,p) method and listed in Table 2. The intermolecular hydrogen bonding energy largely contributes to the total energy of interaction inside each structure and is evaluated from the following equation:
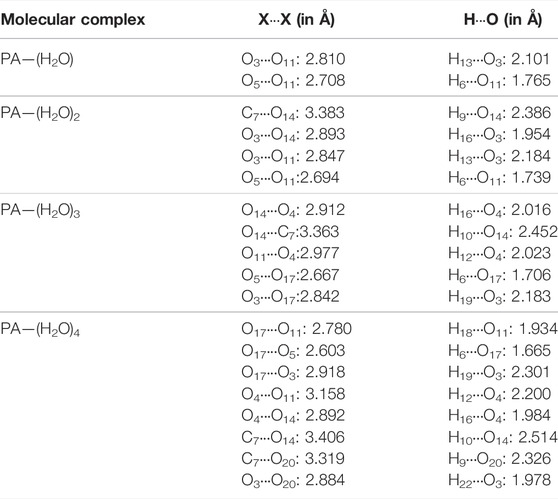
TABLE 1. Intermolecular hydrogen bond lengths (X∙∙∙X and X ∙∙∙H, where X = O and C) within the different molecular associations in the pyruvic acid–(H2O) n complexes.

TABLE 2. Energy spectrum of different pyruvic acid–water complexes calculated by the DFT/B3LYP method at the 6- 311++G(d, p) basis set.
The molecular complex formed between one pyruvic acid and one water molecule is treated previously by means of DFT calculations [20] and rotational spectroscopic analysis [17]. Our DFT calculations come to confirm the previously obtained results and show that if a pyruvic acid molecule is associated with only one water molecule, the most stable geometry of the PA-(H2O)1 is cyclic dimer–stabilized by the O11∙∙∙H6-O5 and O11-H13∙∙∙O3 hydrogen bonds, with bond lengths of 1.765 Å and 2.101 Å, respectively. These two H-bonds contribute by about—65.44 kcal/mol to the total energy of stabilization of the PA-(H2O)1 complex.
The interaction energy of the hydrogen network in the PA-(H2O)2 complex is -70.14 kcal/mol, and O-H∙∙∙O and C-H∙∙∙O hydrogen bonds are formed between water and acid molecules where the C-H∙∙∙O hydrogen bond is found to be longer than three O-H∙∙∙O bonds. The molecular structure of this complex is marked by two ring parts involving the O14-H16∙∙∙O3, O11-H13∙∙∙O3, O5-H6∙∙∙O11, and C7-H9∙∙∙O14 hydrogen bonds The H16∙∙∙O3, H13∙∙∙O3, H6∙∙∙O11, and H9∙∙∙O14 bond lengths are 1.954 Å, 2.184 Å, 1.739 Å, and 2.386 Å, respectively. It is important to note here that our calculations on the PA-(H2O)2 complex do not support the hydrogen bond formation between water molecules alone as previously published [18].
When a pyruvic acid molecule is linked to three water molecules, the most stable configuration is given in Figure 1D. The oxygen atom of pyruvic acid (O4) is hydrogen-bonded with two hydrogen atoms (H12 and H16) of two neighboring water molecules to form the O14-H16∙∙∙O4 and the O11-H12∙∙∙O4 intermolecular hydrogen bonds with 2.023 Å and 2.452 Å bond lengths, respectively. The oxygen atom, O17, of a water molecule serves as the acceptor and donor of hydrogen bonds in this complex. In fact, it is involved in the O17∙∙∙H6-O5 and O17-H19∙∙∙O3 H-bonds, where the bond lengths are found to be 1.706 Å and 2.183 Å, respectively. The C-H∙∙∙O hydrogen bond contributes also to the stability of the PA-(H2O)3 complex where a cyclic form is established between the methyl group of pyruvic acid and water molecules through the O14∙∙∙H10-C7 hydrogen bonded which is the longer one among all H-bonds in this complex. The energy of interactions including H-bonds is about -77.68 kcal/mol.
The large complex formed between pyruvic acid and water molecules is PA-(H2O)4. In this complex, five O-H∙∙∙O and two C-H∙∙∙O hydrogen bonds are established between acid and water molecules. The hydrogen bond lengths are 2.301 Å for H19∙∙∙O3, 1.978 Å for H22∙∙∙O3, 1.665 Å for H6∙∙∙O17, 2.200 Å for H12∙∙∙O4, and 1.984 Å for H16∙∙∙O4. The C-H∙∙∙O bonds are found to be longer than the O-H∙∙∙O bonds. In fact, the H9∙∙∙O20 and H10∙∙∙O14 bond lengths are about 2.326 Å and 2.514 Å, respectively. In this complex, new hydrogen bonds appear between water molecules alone which can form a cage-like structure around the hydroxyl group of the central pyruvic acid molecule. We note here that the H18-O17-H19 water molecule participates in the formation of three hydrogen bonds (O17-H18∙∙∙O11, O17-H19∙∙∙O3, and O17∙∙∙H6-O5). The water–water hydrogen bond, labeled O17-H18∙∙∙O11, has a bond length of about 1.934 Å, which is slightly shorter than that in pure water and very comparable to that of the other existing O-H∙∙∙O hydrogen bonds and consequently contributes to the stability of the molecular structure of the PA-(H2O)4 complex. The special structure of this complex has the largest energy of interactions by H-bonds (Eint =−81.28 kcal/mol) among all the considered structures. In this analysis of the UV spectrum of pyruvic acid in water, Shemesh et al. [21] show that small clusters such as PA-(H2O)4 are able to reproduce the solvation effect of pyruvic acid.
Topological Study of PA-(H2O)n = 1–4 Complexes
To gain a better insight into the intermolecular interactions between pyruvic acid and water, AIM analysis was performed on the optimized geometries. The AIM theory [33, 34], based on topological analysis of electron density at the bond critical point (ρBCP) and its Laplacian (∇2ρBCP) provides a universally applicable tool for the classification of the bonding interactions occurring in any molecular system, ranging from hydrogen bonds to van der Waals interactions [35–39]. In fact, large values of electronic density and Laplacian interactions are reliable with short distances, showing a clear relationship between the topological properties of the charge density with the interatomic distances within the systems and accordingly associated to the power of interactions such as hydrogen bonding [35, 36]. Furthermore, the positive sign of the Laplacian indicates the reduction of the charge in the internuclear zone if it is positive, and the strong covalent character is related to the negative sign [40].
The topological parameters calculated, in all the bond critical point (BCP) and ring critical point (RCP), for all the considered PA-(H2O)n = 1–4 complexes, such as electron density (ρ), Laplacian of electron density (∇2ρ), Lagrangian kinetic energy (G), Hamiltonian kinetic energy (H), potential energy density (V), the H-bond energy (EHB), and ellipticity of electron density (ε), are listed in Table 3. The molecular graph of the molecular complexes is shown in Figure 2, which shows the BCPs and RCP along with the bond path.
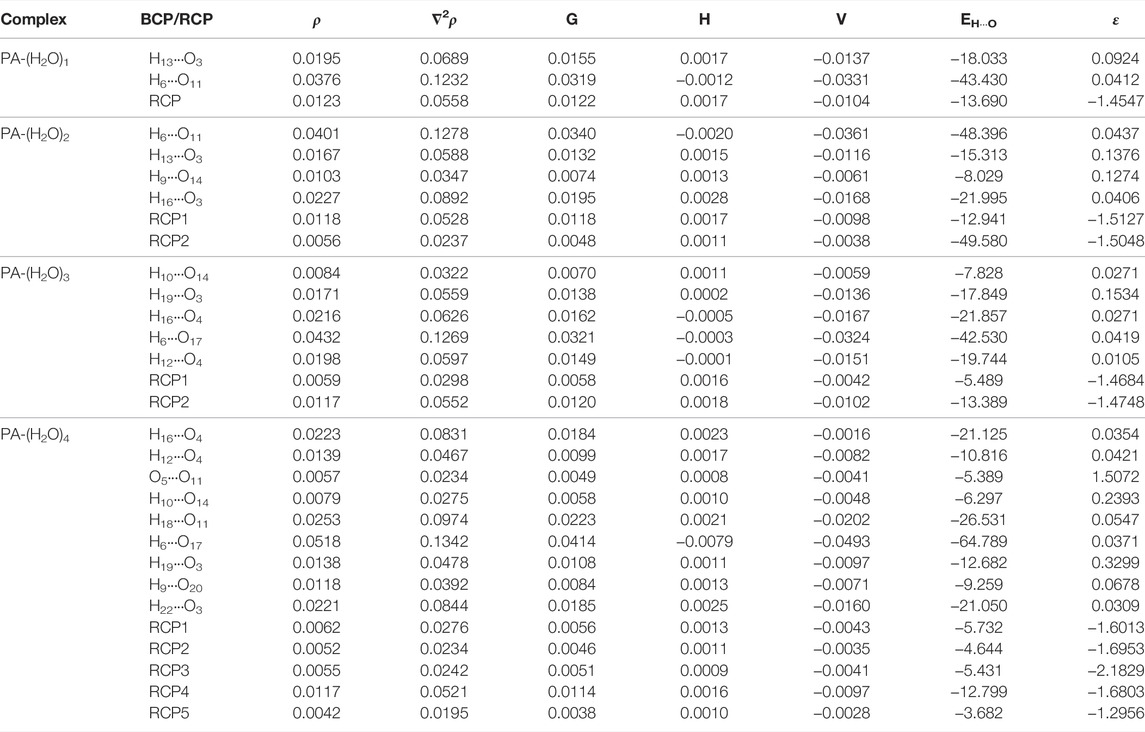
TABLE 3. Topological parameters obtained from AIM analysis for the considered molecular associations in the urea–water mixture (ρ: electron density (a.u.); ∇2ρ: Laplacian of electron density (a.u.); G: Lagrangian kinetic energy (a.u.); H: Hamiltonian kinetic energy (a.u.); V: potential energy density (a.u.); EH···O: H-bond energy (kJ/mol)), ε: ellipticity of electron density. BCP: bond critical point; RCP: ring critical point.
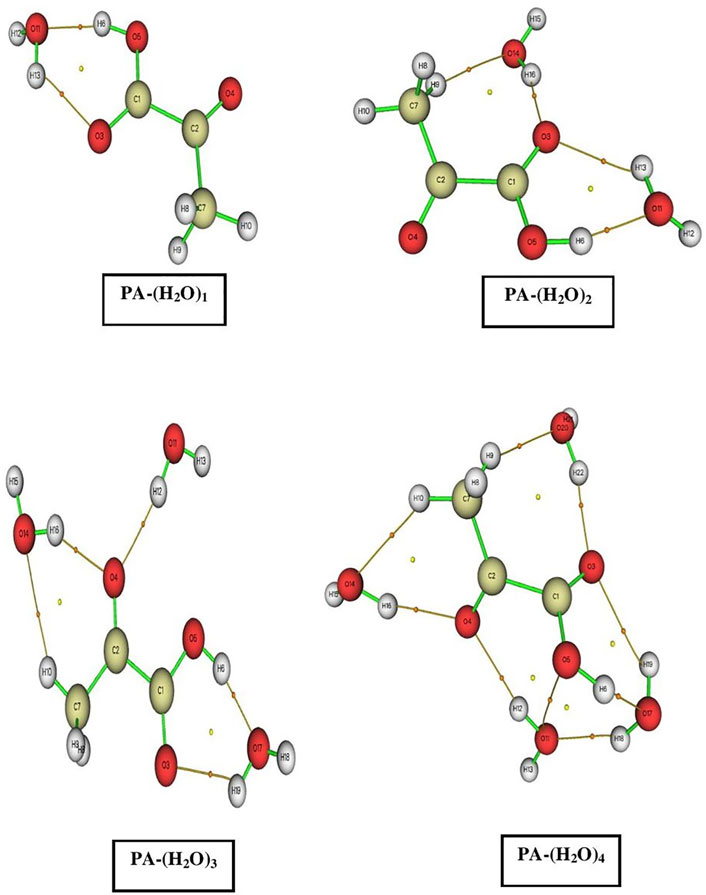
FIGURE 2. AIM molecular graphs of pyruvic acid–(H2O)n = 1–4 complexes. The BCP and RCP are marked by the small orange and yellow circles, respectively.
In the PA-(H2O)1 complex, the two C1-O3⋅⋅⋅H13 and O5-H6⋅⋅⋅O11 intermolecular interactions are retrieved, and the corresponding electron densities are 0.01949 a.u. and 0.03765 a.u. and the corresponding Laplacian are 0.06896 a.u. and 0.12325 a.u., respectively. The O-H⋅⋅⋅O and C-H⋅⋅⋅O interactions are found between water and pyruvic acid molecules in the PA-(H2O)2 complex. The large value of the electron density (ρ = 0.04011 a.u.) is observed for the O5-H6⋅⋅⋅O11, and the lowest one (ρ = 0.0103 a.u.) is obtained for the C7-H9⋅⋅⋅H14 interaction. The values of the corresponding Laplacian are 0.1278 a.u. and 0.03473 a.u., respectively. In the PA-(H2O)3 complex, we observed one C-H⋅⋅⋅O (C7-H10⋅⋅⋅O14) and four O-H⋅⋅⋅O (O3⋅⋅⋅H19-O17, O4⋅⋅⋅H16-O14, O5-H6⋅⋅⋅O17, and O4⋅⋅⋅H12-O11) types of interactions, where the electron density values are 0.00844 a.u., 0.01711 a.u., 0.02166 a.u., 0.04315 a.u., and 0.01983 a.u. respectively. The obtained values of the Laplacian of the corresponding electron densities are 0.03229 a.u., 0.05597 a.u., 0.06267 a.u., 0.12699 a.u., 0.05972 a.u., respectively.
In the largest complex considered in the present study, PA-(H2O)4, we observed two C-H⋅⋅⋅O (C7-H10⋅⋅⋅O14 and C7-H9⋅⋅⋅O20), six O-H…O (O4⋅⋅⋅H16-O14, O11-H12⋅⋅⋅O4, O17-H18⋅⋅⋅O11, O5-H6⋅⋅⋅O17, O17-H19⋅⋅⋅O3, and O3⋅⋅⋅H22-O20), and one O⋅⋅⋅O (O5⋅⋅⋅O11) type of interaction. The electron density values for all these interactions are varying from 0.0057 a.u. (O5⋅⋅⋅O11) to 0.0253 a.u. (O17-H18⋅⋅⋅O11), and all the corresponding values of Laplacian are positive varying from 0.0234 a.u. (O5⋅⋅⋅O11) to 0.0974 a.u. (O17-H18⋅⋅⋅O11).
In his topological analysis of the electron density in hydrogen bonds, Espinosa [38] postulated that if a hydrogen bond exists, the electron density and the Laplacian of the electron density will be in 0.002–0.035 a.u. and 0.024-0.139 a.u., respectively. The hydrogen bond energy is correlated with the potential electron energy at the critical point by the formula [37]:
In all considered complexes, hydrogen bonds form ring structures between acid and water molecules, and the obtained hydrogen bond energies (EHB) values vary in the range of −64.8 kJ/mol to −5.39 kJ/mol. A large energy value is found for the O5-H6⋅⋅⋅O17 hydrogen bond in the PA-(H2O)4 complex. We note that in this complex, hydrogen bonds between water molecules contribute to the stability of the molecular structure. In fact, the O17-H18⋅⋅⋅O11 is established between two water molecules and has an energy equal to −26.53 kJ/mol.
The relations between structural and topological parameters of hydrogen bonds are useful and can give rise to some important properties of the hydrogen bond network. For instance, the hydrogen bond strength is known to be related to its length. Therefore, it will be convenient to examine the relationship between the hydrogen bond length, dH⋅⋅⋅O, and some topological and energetic parameters such as electron density (ρBCP), Laplacian of electron density (∇2ρBCP), Lagrangian kinetic energy (GBCP), Hamiltonian kinetic energy (HBCP), and potential energy density (VBCP). Here, these correlations are examined for all considered acid—water complexes, except the PA- H2O cluster, where only two bond critical points are obtained from the AIM analysis, and this does not let us conclude about the relationship between topological and structural parameters of H-bonds. The variation of the electron density and the Laplacian of the hydrogen bonds formed in the PA-(H2O)4 versus their H⋅⋅⋅O lengths is presented in Figure 3 and those of the other complexes [PA-(H2O)2, PA-(H2O)3] are given in Figure S1A and Figure S2A, respectively.
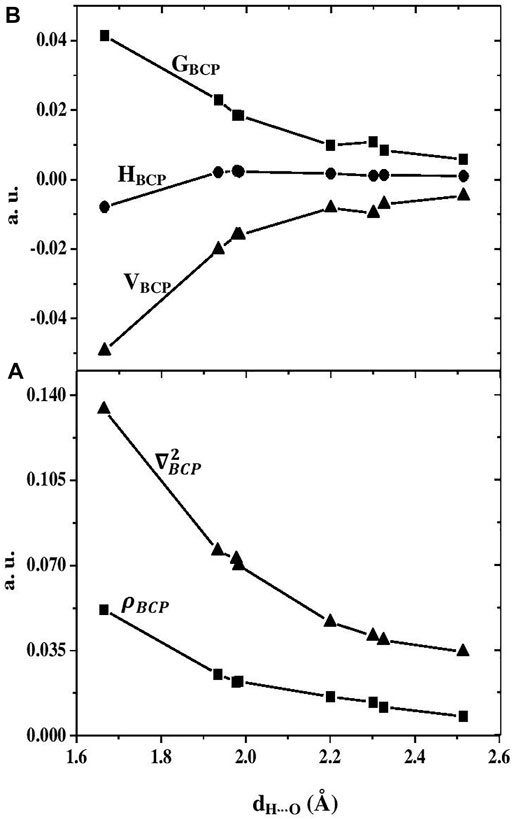
FIGURE 3. (A) Variation of the electron density (ρBCP in a. u. rectangle symbol) and its Laplacian, (∇2ρBCP in a. u., triangle symbol) of the hydrogen bonds formed in the PA-(H2O)4 versus their H∙∙∙O lengths, dH∙∙∙O in Å. (B) Hamiltonian kinetic energy (HBCPin a. u., circle symbol), the kinetic energy density (GBCP in a. u., rectangular symbol), and the potential energy density (VBCP in a. u., triangle symbol) at bond critical points in the PA-(H2O)4 as a function of the hydrogen bond lengths, dH∙∙∙O in Å.
The obtained results here are in good agreement with the empiric models developed by Tang [41] in 2005 and Vener [42] in 2007, where the relation between H-bond lengths and electron densities at the bond critical points in hydrogen-bonded systems is deeply considered. It is identified that the values of topological parameters in that reliance are defined by the nature of the heavy atom forming the hydrogen bond [42], and their variation with the hydrogen bond length gives rise to a classification of H-bonds in open and closed molecular structure, especially in crystalline phases. Similarly, to that obtained previously by Parra et al. [43] in their AIM study of polyols, our calculations show an exponential dependence of the ρBCP and the ∇2ρBCP on dH⋅⋅⋅O hydrogen bond length in the examined clusters [PA-(H2O)2, PA-(H2O)3, PA-(H2O)4]. The electron density (ρBCP) is analytically given by the following empiric formula:
The A, B, and C coefficients obtained for the considered complexes are listed in Table 4. In the largest complex PA-(H2O)4, these topological parameters (ρBCP and the ∇2ρBCP) vary with respect to the following regressions:
The covalent character of the interactions in the PA-(H2O)n is associated to the negative values of the Hamiltonian kinetic energy (HBCP) at bond critical points which becomes clear when the dH⋅⋅⋅O is smaller than 1.8 Å (Figure 3B). The dependence of the kinetic energy density (GBCP) and the potential energy density (VBCP) at the bond critical points in hydrogen-bonded systems is supported by the promolecule model, presented by Spackman in 1999 [37], which can explain the exponential variation of these energy densities on the H⋅⋅⋅O hydrogen bond length [35]. In Figure 3B, we present the variations of the GBCP and VBCP versus the dH⋅⋅⋅O distance for the PA-(H2O)4 complex. The relative variation of these topological functions with the hydrogen bond length for the other considered models (PA-(H2O)2 and PA-(H2O)3) is plotted in Figure S1B and Figure S2B, respectively. The exponential evolutions of GBCP and VBCP are confirmed in all clusters and more pronounced in the largest complex PA-(H2O)4 where they can analytically be expressed as follows:
AIM analysis allows classifying atomic interactions as covalent bonds (
Conclusion
The hydrogen-bonding network in the aqueous solutions of pyruvic acid is studied theoretically by means, especially, of the atoms-in-molecules approach. The geometry of a large number of molecular complexes where a central PA molecule is linked to one, two, three, and four water molecules is optimized at the DFT/B3LYP/6-311 G++ (d, p) level of theory, and only the more stable ones are presented in this study. O-H⋅⋅⋅O and C-H⋅⋅⋅O hydrogen bonds are formed between pyruvic acid and water molecules, and cyclic molecular arrangements are found in all PA-(H2O)n = 1–4. In the PA-(H2O)4 complex, water molecules form a cage-like structure around some parts of the central PA molecule, where the hydrogen bond length is very close to that of the bulk water ones. In this complex, topological AIM analysis confirms that the kinetic energy density (GBCP) and the potential energy density (VBCP) at the bond critical points and the electron density and the Laplacian of the electron density are strongly correlated to the hydrogen bond length. The electron density (ρBCP) is analytically given by the following empiric formula:
Data Availability Statement
The original contributions presented in the study are included in the article/Supplementary Material, further inquiries can be directed to the corresponding author.
Author Contributions
All authors listed have made a substantial, direct, and intellectual contribution to the work and approved it for publication.
Conflict of Interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Publisher’s Note
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors, and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
Supplementary Material
The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/fphy.2022.901736/full#supplementary-material
References
1. Richard K, Reinhard B. Degradation of Lactaminic Acid to Succinic Acid. Justus Liebigs Annalen der Chem (1959) 624:137–41.
2. Sloneker JH, Orentas DG. Pyruvic Acid, a Unique Component of an Exocellular Bacterial Polysaccharide. Nature (1962) 194:478–9. doi:10.1038/194478a0
3. Sacks J, Morton JH. Lactic and Pyruvic Acid Relations in Contracting Mammalian Muscle. Am J Physiology-Legacy Content (1956) 186:221–3. doi:10.1152/ajplegacy.1956.186.2.221
4. Kakkar R, Pathak M, Radhika NP. A DFT Study of the Structures of Pyruvic Acid Isomers and Their Decarboxylation. Org Biomol Chem (2006) 4:886–95. doi:10.1039/b516355b
5. Udagawa T, Sugiura K, Suzuki K, Tachikawa M. Unusual H/D Isotope Effect in Isomerization and Keto-Enol Tautomerism Reactions of Pyruvic Acid: Nuclear Quantum Effect Restricts Some Rotational Isomerization Reactions. RSC Adv (2017) 7:9328–37. doi:10.1039/c6ra28271g
6. Murto J, Raaska T, Kunttu H, Räsänen M. Conformers and Vibrational Spectra of Pyruvic Acid: an Ab Initio Study. J Mol Struct THEOCHEM (1989) 200:93–101. doi:10.1016/0166-1280(89)85046-8
7. Yang X., Orlova G., Zhou XJ, Leung KT. A DFT Study on the Radical, Monomer and Dimer of α-keto Pyruvic Acid: Equilibrium Structures and Vibrational Analysis of Stable Conformers. Chem Phys Lett (2003) 380:34–41.
8. Valadbeigi Y, Farrokhpour H. Theoretical Study on Keto-Enol Tautomerism and Isomerization in Pyruvic Acid. Int J Quan Chem. (2013) 113:2372–8. doi:10.1002/qua.24467
9. Raczynska ED, Duczmal K, Darowska M. Experimental (FT-IR) and Theoretical (DFT-IR) Studies of Keto-Enol Tautomerism in Pyruvic Acid. Vib Spectrosc (2005) 39:37–45.
10. Van Alsenoy C, Schäfer L, Siam K, Ewbank JD. Ab Initio studies of Structural Features Not Easily Amenable to experiment. J Mol Struct THEOCHEM (1989) 187:271–83. doi:10.1016/0166-1280(89)85167-x
11. Tarakeshwar P, Manogaran S, An ab initio study of pyruvic acid, J Mol Struct THEOCHEM (1998) 430: 51–6.doi:10.1016/s0166-1280(98)90215-9
12. Reva I, Nunes CM, Biczysko M, Fausto R. Conformational Switching in Pyruvic Acid Isolated in Ar and N2 Matrixes: Spectroscopic Analysis, Anharmonic Simulation, and Tunneling. J Phys Chem A (2015) 119:2614–27. doi:10.1021/jp509578c
13. Gordon BP, Moore FG, Scatena LF, Richmond GL. On the Rise: Experimental and Computational Vibrational Sum Frequency Spectroscopy Studies of Pyruvic Acid and its Surface-Active Oligomer Species at the Air-Water Interface. J Phys Chem A (2019) 123:10609–19. doi:10.1021/acs.jpca.9b08854
14. Buemi G. DFT Study of the Hydrogen Bond Strength and IR Spectra of Formic, Oxalic, Glyoxylic and Pyruvic Acids in Vacuum, Acetone and Water Solution. J Phys Org Chem (2009) 22:933–47. doi:10.1002/poc.1543
15. Fischer G, Flatau S, Schellenberger A, Zschunke A. Carbon-13 NMR Investigations on the Structure of .alpha.-keto Acids in Aqueous Solution. J Org Chem (1988) 53:214–6. doi:10.1021/jo00236a050
16. Maron MK, Takahashi K, Shoemaker RK, Vaida V. Hydration of Pyruvic Acid to its Geminal-Diol, 2,2-dihydroxypropanoic Acid, in a Water-Restricted Environment. Chem Phys Lett (2011) 513:184–90.
17. Schnitzler EG, Seifert N. A., Ghosh S., Thomas J, Xu Y, Jäger W. Hydration of the Simplest α-keto Acid: a Rotational Spectroscopic and Ab Initio Study of the Pyruvic Acid-Water Complex. Phys Chem Chem Phys (2017) 19:4440–6. doi:10.1039/c6cp08741h
18. Kakkar R, Pathak M, Gahlot P. Effect of Aqueous Solvation on the Structures of Pyruvic Acid Isomers and Their Reactions in Solution: A Computational Study. J Phys Org Chem (2008) 21:23–9. doi:10.1002/poc.1270
19. Matsunaga S. Structure, Transport Properties, and Dielectric Properties of Lactic Acid/pyruvic Acid Aqueous Solution in a Biofuel Cell: A Molecular Simulation Study. Polym Eng Sci (2019) 59:2474–8. doi:10.1002/pen.25244
20. Yang D, Zhang L. Excited-state Hydrogen Bonding Dynamics of Pyruvic Acid and Geminal-Diol, 2,2-dihydroxypropanoic Acid in Aqueous Solution: a DFT/TDDFT Study. J Phys Org Chem (2012) 25:1391–4. doi:10.1002/poc.3055
21. Shemesh D, Luo M, Grassian VH, Gerber RB. Absorption Spectra of Pyruvic Acid in Water: Insights from Calculations for Small Hydrates and Comparison to experiment. Phys Chem Chem Phys (2020) 22:12658–70. doi:10.1039/d0cp01810d
22. Blair SL, Reed Harris AE, Frandsen BN, Kjaergaard HG, Pangui E, Cazaunau M, et al. Conformer-specific Photolysis of Pyruvic Acid and the Effect of Water. J Phys Chem A (2020) 124:1240–52. doi:10.1021/acs.jpca.9b10613
23. Ray WJ, Katon JE, Phillips DB. Structure, Hydrogen Bonding and Vibrational Spectra of Pyruvic Acid. J Mol Struct (1981) 74:75–84. doi:10.1016/0022-2860(81)80009-9
24. Kappes KJ, Deal AM, Jespersen MF, Blair SL, Doussin J-F, Cazaunau M, et al. Chemistry and Photochemistry of Pyruvic Acid at the Air-Water Interface. J Phys Chem A (2021) 125:1036–49. doi:10.1021/acs.jpca.0c09096
25. Luo M, Shemesh D, Sullivan MN, Alves MR, Song M, Gerber RB, et al. Impact of pH and NaCl and CaCl2 Salts on the Speciation and Photochemistry of Pyruvic Acid in the Aqueous Phase. J Phys Chem A (2020) 124:5071–80. doi:10.1021/acs.jpca.0c01016
26. Guzman M I, Colussi A J, Hoffmann M R, Photoinduced Oligomerization of Aqueous Pyruvic Acid, J Phys Chem. A (2006) 110: 3619 – 26.
27. Frisch MJ, Trucks GW, Schlegel HB, Scuseria GE, Robb MA, Cheeseman JR. Gaussian. Wallingford CT: Gaussian, Inc. (2004).
28. Becke AD. Density‐functional Thermochemistry. III. The Role of Exact Exchange. J Chem Phys (1993) 98:5648–52. doi:10.1063/1.464913
29. Lee C, Yang W, Parr RG. Development of the Colle-Salvetti Correlation-Energy Formula into a Functional of the Electron Density. Phys Rev B (1988) 37:785–9. doi:10.1103/physrevb.37.785
30. Zhang J, Dolg MABCluster. ABCluster: the Artificial Bee colony Algorithm for Cluster Global Optimization. Phys Chem Chem Phys (2015) 17:24173–81. doi:10.1039/c5cp04060d
31. Boys SF, Bernardi F. The Calculation of Small Molecular Interactions by the Differences of Separate Total Energies. Some Procedures with Reduced Errors. Mol Phys (1973) 19:553–66.
32. Lu T, Chen F. Multiwfn: A Multifunctional Wavefunction Analyzer. J Comput Chem (2012) 33:580–92. doi:10.1002/jcc.22885
34. Poplier PLA, Badr RFW. The Existence of an Intramolecular C-H-O Hydrogen-Bond in Creatine and Carbamoyl Sarcosine. Chem Phys Lett (1992) 189:542–8.
35. Espinosa E, Lecomte C, Molins E. Experimental Electron Density Overlapping in Hydrogen Bonds: Topology vs. Energetics. Chem Phys Lett (1999) 300:745–8.
36. Espinosa E, Molinsa E, Lecomte C. Hydrogen Bond Strengths Revealed by Topological Analyses of Experimentally Observed Electron Densities. Chem Phys Lett (1998) 285:170–3.
37. Espinosa E, Souhassou M, Lachekar H, Lecomte C. Topological Analysis of the Electron Density in Hydrogen Bonds. Acta Crystallogr Sect Bcrystallogr B (1999) 55:563–72. doi:10.1107/s0108768199002128
38. Spackman MA, Hydrogen Bond Energetics from Topological Analysis of Experimental Electron Densities: Recognising the Importance of the Promolecule, Chem Phys Lett (1999) 301: 425–429.
39. Grabowski S. An Estimation of Strength of Intramolecular Hydrogen Bonds - Ab Initio and AIM Studies. J Mol Struct (2001) 562 137–43.
40. Johnson ER, Keinan S, Mori-Sánchez P, Contreras-García J, Cohen AJ, Yang W. Revealing Noncovalent Interactions. J Am Chem Soc (2010) 132:6498–506. doi:10.1021/ja100936w
41. Tang T-H, Deretey E, Knak Jensen SJ, Csizmadia IG. Hydrogen Bonds: Relation between Lengths and Electron Densities at Bond Critical Points. Eur Phys J D (2006) 37:217–22. doi:10.1140/epjd/e2005-00317-0
42. Vener MV, Manaev AV, Egorova AN, Tsirelson VG. QTAIM Study of Strong H-Bonds with the O−H···A Fragment (A = O, N) in Three-Dimensional Periodical Crystals. J Phys Chem A (2007) 111:1155–62. doi:10.1021/jp067057d
43. Parra RD, Streu K. Hydrogen Bond Cooperativity in Polyols. A DFT AIM Study, Comp Theo Chem (2011) 967:12–8.
44. Grabowski SJ, Hydrogen Bonding Strength—Measures Based on Geometric and Topological Parameters, J Phys Org Chem. (2004) 17: 18-31.
Keywords: pyruvic acid, PA–water complex, hydrogen bonding, DFT, AIM
Citation: Hammami F and Issaoui N (2022) A DFT Study of the Hydrogen Bonded Structures of Pyruvic Acid–Water Complexes. Front. Phys. 10:901736. doi: 10.3389/fphy.2022.901736
Received: 22 March 2022; Accepted: 22 April 2022;
Published: 31 May 2022.
Edited by:
Joydeep Chowdhury, Jadavpur University, IndiaReviewed by:
Bipan Dutta, Sammilani Mahavidyalaya, IndiaLuca Evangelisti, University of Bologna, Italy
Copyright © 2022 Hammami and Issaoui. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Ferid Hammami, ZmVyaWQuaGFtbWFtaUBpc2ltbS51LW1vbmFzdGlyLnRu, aGFtbWFtaWZlcmlkMUBnbWFpbC5jb20=
†These authors have contributed equally to this work
 Ferid Hammami
Ferid Hammami Noureddine Issaoui
Noureddine Issaoui