Coherent noise suppression in digital holographic microscopy based on label-free deep learning

Deep learning techniques can be introduced into the digital holography to suppress the coherent noise. It is often necessary to first make a dataset of noisy and noise-free phase images to train the network. However, noise-free images are often difficult to obtain in practical holographic applications. Here we propose a label-free training algorithms based on self-supervised learning. A dilated blind spot network is built to learn from the real noisy phase images and a noise level function network to estimate a noise level function. Then they are trained together via maximizing the constrained negative log-likelihood and Bayes’ rule to generate a denoising phase image. The experimental results demonstrate that our method outperforms standard smoothing algorithms in accurately reconstructing the true phase image in digital holographic microscopy.

Introduction

Digital holographic microscopy (DHM) is a non-invasive, highly precise and real-time quantitative phase measurement technology, and it has important applications in the fields of microsurface topography measurement, flow field measurement, biological cell measurement, and so on [1–4]. However, under high coherent illumination, uneven surfaces such as dust and scratches on the specimen will introduce random amplitude and phase fluctuations, and finally form speckle noise in the reconstructed holographic image [5]. And furthermore, the undesired diffraction and multiple reflections include the phase noise. They are all coherent noise because of the high coherence of optical field. Thus, the suppression of coherent noise is a key research subject, which is of great significance to improve the measurement accuracy and resolution of DHM.

The coherent noise suppression technologies can be classified into the optical approach and the digital image processing method. A light source with a low coherence length can prevent noise outside the coherence length from being imaged on the hologram, thus lowering the coherent noise [6, 7]. Multiple holograms with different incident angles [8, 9], polarization states [10] or wavelengths [11] can be collected and then superimposed to average the speckle noise. However, this increases the complexity of optical system, and can’t process holograms offline. In digital image processing, the median filtering and mean filtering are usually used for speckle noise suppressing, but high frequency details will inevitably be lost. The wiener filtering, blind convolution method and Block-matching and 3D filtering (BM3D) can also be used with the disadvantage that the parameter selection is difficult to determine [12]. The frequency-domain denoising assumes that the noise belongs to high-frequency information, so the denoising is accomplished by suppressing high-frequency information, such as windowed Fourier transform, wavelet transform, and so on [13]. The third type of digital image processing methods convert the denoising problem into an unconstrained optimization problem by building an optimization function such as a convex optimization form [14].

In recent years, the deep learning-based denoising methods have emerged. The work of Wang et al. demonstrated that the neural network can adapt to coherent noise on its own [15]. In most deep learning based coherent noise suppression methods, the training data pairs of noisy and noise-free phase images are first constructed using the noise model. The training data pairs are utilized to train a neural network capable mapping both the noisy and noise-free phase images [16–20]. However, these methods require paired data to train the neural network, which is difficult in practical holographic applications. Yin et al. used neural networks to learn common information from paired noisy phase images without noise-free data and achieved neural network denoising for noisy phase images [21]. However, this method still needs to obtain multiple noisy phase images while ensuring the consistency of the underlying sample.

We propose a label-free coherent noise suppression method based on deep learning, which realizes the self-supervised learning between the noise generation and suppression models by establishing the negative log-likelihood function of noise. The noise-free phase images are not necessary as labels, only the noisy phase images are needed to complete the network training. The trained network can achieve noise suppression for various noisy phase images, and the algorithm has remarkable generalization ability, which is of great significance for dynamic holographic imaging.

Methods

Physical generation of speckle noise

Assuming that the coordinates of the holographic recording plane is (x, y), the off-axis digital holographic intensity I (x, y) is expressed as [22].

$I\left(x,y\right)={\left|\mathit{O}\left(x,y\right)\right|}^2+{\left|\mathit{R}\left(x,y\right)\right|}^2+\mathit{O}\left(x,y\right){\mathit{R}}^{*}\left(x,y\right)+{\mathit{O}}^{*}\left(x,y\right)\mathit{R}\left(x,y\right)+n\left(x,y\right)(1)$

Where, O (x, y) and R (x, y) are the object wavefront and reference wavefronts at the recording plane, respectively. The third and fourth terms can be used to reconstruct the amplitude and phase of object wavefront, and the fifth term is speckle noise. For any scattering point source p of the imaging system, the coherent noise n (x, y) can be expressed as [5].

$n\left(x,y\right)={\left|{\displaystyle \sum }_1^{N}a\left(x_p,y_p\right)\exp \left[j\phi \left(x_p,y_p\right)\right]\exp \left[j\phi \left(x,y\right)\right]\right|}^2(2)$

Where, a (x_p, y_p) is the random intensity fluctuation, φ(x_p, y_p) is the random phase fluctuation, and φ(x,y) is the propagation phase of the light.

In the numerical reconstruction of the digital hologram, the reconstructed complex amplitude U (ξ, η) can be obtained by using the angular spectrum method [23]. Then, the phase of the sample can be calculated through

$\phi \left(\xi ,\eta \right)=\arctan \frac{\mathrm{I}\mathrm{m}\left[U\left(\xi ,\eta \right)\right]}{\mathrm{R}\mathrm{e}\left[U\left(\xi ,\eta \right)\right]}\left(\mathrm{mod}2\pi \right)(3)$

Where, Im ( ) and Re ( ) represent the operations of taking the complex imaginary part and the real part, respectively. Then the real phase of the sample can be obtained through the unwrapping operation. However, the obtained phase image will inevitably contain noise. Assuming that the noisy phase image can be expressed as

$\phi \left(\xi ,\eta \right)=\stackrel{\sim }{\phi }\left(\xi ,\eta \right)+n\left(\xi ,\eta \right)(4)$

Where, n (ξ, η) denotes the noise in φ(ξ, η), $\stackrel{\sim }{\phi }\left(\xi ,\eta \right)$ is the underlying noise-free phase image [24]. Assuming that the phase φ(ξ, η) is spatially correlated, the noise n (ξ, η) is a pixel-independent and signal-dependent Gaussian noise [25]. And then, the noise variance of pixel i var (n_i) is only determined by the underlying noise-free pixel value ${\stackrel{\sim }{\phi }}_i$ of pixel i. The noise variance var (n_i) can be regarded as a noise level function (NLF) $g\left({\stackrel{\sim }{\phi }}_i\right)$, which can be expressed as

$\mathrm{v}\mathrm{a}\mathrm{r}\left(n_i\right)=g\left({\stackrel{\sim }{\phi }}_i\right).(5)$

Label-free coherent noise suppression

The label-free coherent noise suppression method is composed of two steps, shown in Figure 1. In the first step, the object beam passes through the sample and the simulated coherent noise screen successively, and then interferes with the reference beam after the beam splitting prism (BS) to form the digital hologram. In this step, the coherent noise is introduced and a real holographic recording system is simulated. In the simulation process, the model of speckle-noise involves only phase distribution of object waves. The simulated coherent noise screen modulates the object beam in the form of an exponential term to simulate the random phase fluctuation of digital holography. In the second step, the noisy phase images will be processed by the trained neural network to reconstruct the clean phase images.

FIGURE 1

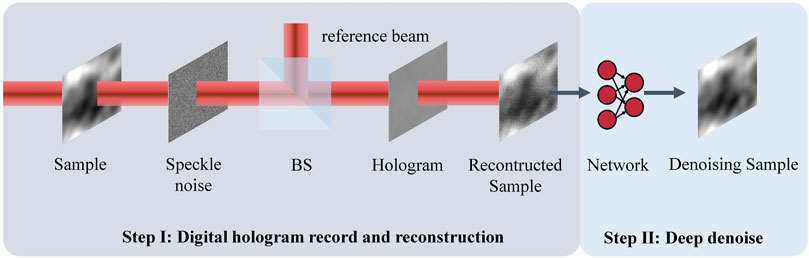
FIGURE 1. The schematic diagram for the label-free coherent noise suppression in digital holographic microscopy.

DBSN and NLFN

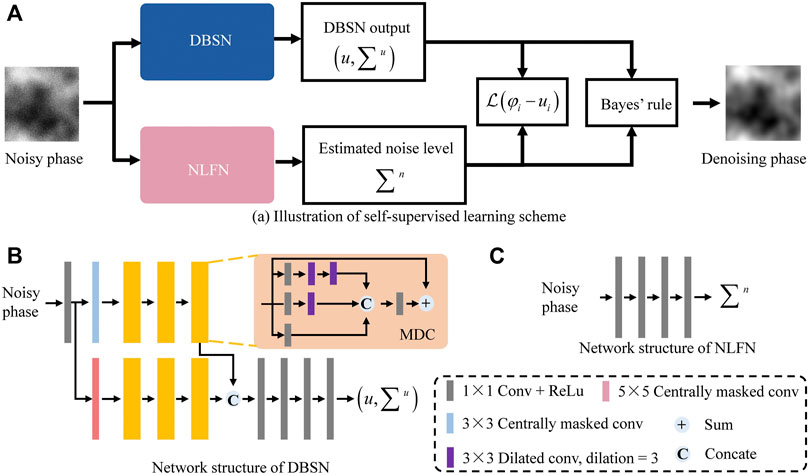
As shown in Figure 2A, the main structure is composed of the dilated blind spot network (DBSN) and the noise level function network (NLFN) [26]. Then, a self-supervised loss function is introduced to jointly train DBSN and NLFN by maximizing the constrained log-likelihood. For a given noisy phase image, DBSN and NLFN cooperate to produce a clean denoising phase image under a Bayes’ rules.

FIGURE 2

FIGURE 2. The framework for the label-free holographic phase noise suppression.

The structure of DBSN in Figure 2B is based on the blind spot network. DBSN starts with a 1 × 1 convolutional layer followed by two network branches. A 3 × 3 center-masked convolutional layer and six multi-dilated convolutional (MDC) modules make up each branch. The feature maps of the two branches are then concatenated, followed by the deployment of four 1 × 1 convolutional layers to yield the network output. The MDC module in Figure 2B utilizes a residual structure involving three sub-branches. In these branches, zero, one, and two 3 × 3 dilated convolutional layers are stacked on top of 1 × 1 convolutional layers, respectively. These branches’ outputs are then concatenated, followed by another 1 × 1 convolutional layer, and summed with the input of the MDC module. Finally, four 1 × 1 convolutional layers are further applied to produce the DBSN output by concatenating the feature maps from the two network branches.

To enhance the model’s flexibility, the noise is assumed as a signal-dependent multivariate Gaussian noise [25], with each noisy phase image being NLF-specific. The noise level will always be determined by input values at the same location. In the self-supervised learning, only noisy reconstructed phase images can be utilized. So NLFN learns NLF to approximate $g\left({\stackrel{\sim }{\phi }}_i\right)$ from the noisy phase image. The NLFN comprises five 1 × 1 convolutional layers with 16 channels, as shown in Figure 2C. Except for the final layer, the activation function ReLU applies to all convolutional layers.

In the proposed unpaired learning algorithms, the underlying noise-free image φ̃ and the NLF are not available. Therefore, self-supervised learning is used to train DBSN and NLFN. For a given position i, μ is set to be the clean image predicted directly by DBSN, which is closer to ${\stackrel{\sim }{\phi }}_i$ than φ_i. Then the assumption can be expressed as

$\{\begin{array}{l}{\phi }_i={\stackrel{\sim }{\phi }}_i+n_i,n_i\sim \mathrm{N}\left(0,{\sum }_i^{\mathbf{n}}\right)\\ {\mu }_i={\stackrel{\sim }{\phi }}_i+n_{\mathrm{i}}^{\mu },n_i^{\mathbf{\mu }}\sim \mathrm{N}\left(0,{\sum }_i^{\mathbf{u}}\right)\\ \left|{\sum }_i^{\mathbf{n}}\right|\gg \left|{\sum }_i^{\mathbf{u}}\right|\approx 0\end{array}(6)$

Among them, ${\phi }_i,{\stackrel{\sim }{\phi }}_i,n_i$ is constant. And further assume that n_i and µ_i are independent. Considering that ${\stackrel{\sim }{\phi }}_i$ is not available, the self-supervised loss function employs the negative log-likelihood of ${\phi }_i-u_i$, which can be written as [26]

$\mathit{L}\left({\phi }_i-u_i\right)={\sum }_i\frac{1}{2}{\left({\phi }_i-u_i\right)}^{\mathrm{T}}{\left({\sum }_i^{\mathbf{n}}+{\sum }_i^{\mathbf{u}}\right)}^{-1}\left({\phi }_i-u_i\right)+\log \left|{\sum }_i^{\mathbf{n}}\right|+\mathrm{t}\mathrm{r}\left({\left({\sum }_i^{\mathbf{n}}\right)}^{-1}{\sum }_i^{\mathbf{u}}\right)(7)$

where, $u_i,{\sum }_i^{\mathbf{u}}$ can be estimated from the output of the DBSN at location i, and ${\sum }_i^{\mathbf{n}}$ can be estimated from the output of the NLFN network at location i. After self-supervised learning, the denoising phase image can be obtained using the Bayes’ rule for each pixel

${\varphi }_i={\left({\sum }_i^{\mathbf{n}}+{\sum }_i^{\mathbf{u}}\right)}^{-1}\left({\sum }_i^{\mathbf{n}}{u}_i+{\sum }_i^{\mathbf{u}}{\phi }_i\right)(8)$

The following are the specifics of DBSN and NLFN self-supervised training. Noise-free phase images were obtained via using the power spectrum inversion method [27] to generate 10,000 images with 256 × 256 pixels. The holographic phase noise model in Figure 1 is used to generate noisy phase images. The test dataset consists of actual noisy phase images reconstructed from a DHM. The network is initialized with pre-trained parameters [26] throughout training and terminated after 100 epochs. DBSN and NLFN are trained using the Adam optimizer with a learning rate of 3 × 10^–4. The underlying noise-free image is first computed using DBSN, and then its noise level is estimated by NLF. Then, the loss function is calculated using Eq. 7, and then the parameters of DBSN and NLF are updated sequentially using the optimizer. The network is implemented by Pytorch 1.7 based on Python 3.7.1, which is performed on a PC with an Intel Core i7-10700K CPU, 32 GB of RAM, using NVIDIA GeForce GTX 2080Ti GPU.

Results and conclusion

The test dataset consists of 1,000 phase images from the real-world dataset [28] and 1,000 phase images simulated by the power spectrum inversion method [27]. Noisy phase images with atmospheric turbulence, fish and airplane patterns are shown in Figure 3A. The phase variation varies from 0 to 8 rad. The noisy phase images in Figure 3B are generated by the simulation method in Figure 1, simulating the phase reconstruction results of a DHM. It is worth emphasizing that the ground truth doesn’t participate in the network’s training process. It is simply utilized for comparing outcomes. A total of three sets of findings are shown in Figure 3. The mean relative phase error between denoising results and the real phase is 2.08%, which shows the self-supervised learning neural network can effectively suppress the noise of noisy phase images. The exact phase distribution at the red line on the left is shown in Figure 3D. The profile of network denoising result is shown by the red curve, while the profile of noise-free phase is represented by the blue curve. The two curves have a mean deviation error of 0.2838 rad, less than 0.1 wavelength. It demonstrates that the network denoising results accurately portray the samples’ real phase distribution.

FIGURE 3

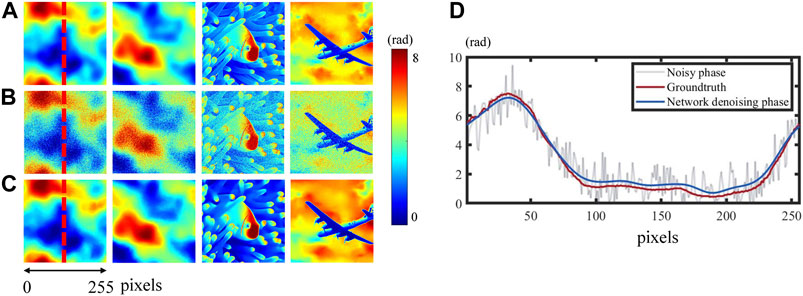
FIGURE 3. Neural network coherent noise suppression results on simulation data. (A) The noise-free phase images; (B) The noisy phase images reconstructed by a DHM; (C) The network denoising phase images; (D) The profile map along with the red lines.

The noise suppression test is conducted on the testing sample once finishing the network training. A series of digital holograms were recorded by using a DHM with a common-path and a wavelength of 532 nm [29, 30]. The phase images of the resolution board, HT22 cell and line board are numerically reconstructed in Figure 4A. Here, it is evident for the impact of coherent noise on quantitative phase measurements. To compare the noise suppression effect, median filter in a 6-by-6 neighborhood and BM3D with noise variance of 0.02 are employed. As shown in Figure 4, the proposed label-free self-supervised learning technique produces a smoother phase image with superior noise suppression than the BM3D and median filtering methods. Furthermore, the robustness of the proposed method may be proved since the feature space of phase images from a DHM and simulated turbulent phase images, which is the train dataset differ from each other significantly.

FIGURE 4

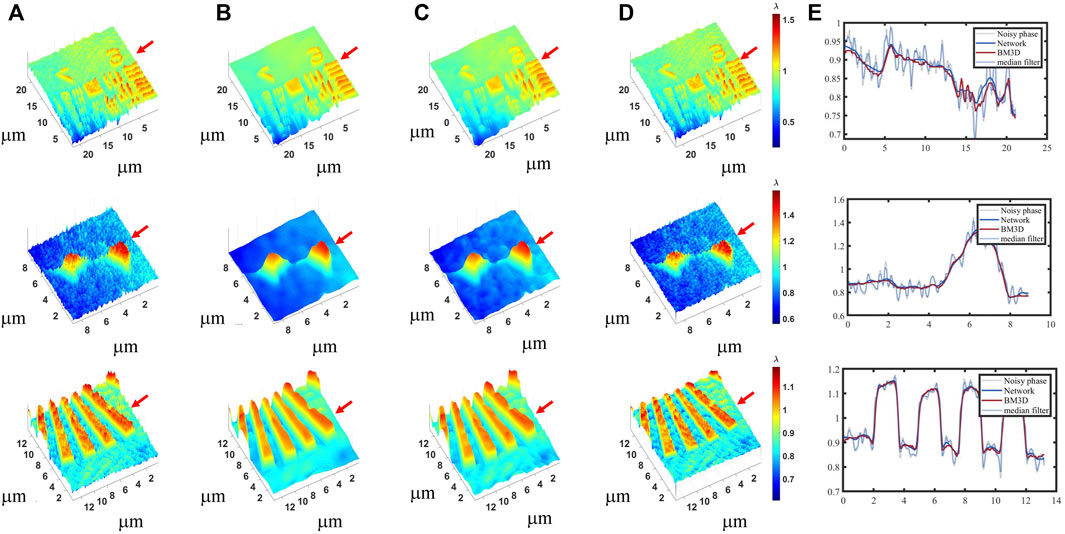
FIGURE 4. Comparison of noise suppression results on cell phase. The upper and lower rows are different cells. (A) The phase images of the resolution board, HT22 cell and line board; (B) The noise suppression phase by the network; (C) The noise suppression phase by median filter in a 6-by-6 neighborhood; (D) The noise suppression phase by BM3D with noise variance of 0.02; (E) The profile map along with the red at the red arrow.

In summary, we propose a label-free coherent noise suppression method based on self-supervised learning. The proposed method has excellent coherent noise suppression performance and good robustness. By constructing a negative log-likelihood loss function, we can complete the training of the denoising network without noise-free phase data. The mean relative phase error between denoising results and the real phase is 2.08%.

Data availability statement

The original contributions presented in the study are included in the article/Supplementary Material, further inquiries can be directed to the corresponding author.

Author contributions

JW wrote the draft of the manuscript and contributed to data analysis. JW, JT, and JZ performed experiments. JD conceived and supervised the project. All the authors edited the manuscript.

Funding

This work was supported by the National Natural Science Foundation of China (NSFC) (Grant No. 62075183).

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

1. Wang K, Dou J, Kemao Q, Di J, Zhao J. Y-Net: A one-to-two deep learning framework for digital holographic reconstruction. Opt Lett (2019) 44:4765. doi:10.1364/OL.44.004765

PubMed Abstract | CrossRef Full Text | Google Scholar

2. Di J, Li Y, Xie M, Zhang J, Ma C, Xi T, et al. Dual-wavelength common-path digital holographic microscopy for quantitative phase imaging based on lateral shearing interferometry. Appl Opt (2016) 55:7287. doi:10.1364/AO.55.007287

PubMed Abstract | CrossRef Full Text | Google Scholar

3. Sun W, Zhao J, Di J, Wang Q, Wang L. Real-time visualization of karman vortex street in water flow field by using digital holography. Opt Express (2009) 17:20342. doi:10.1364/OE.17.020342

PubMed Abstract | CrossRef Full Text | Google Scholar

4. Wang K, Zhang M, Tang J, Wang L, Hu L, Wu X, et al. Deep learning wavefront sensing and aberration correction in atmospheric turbulence. PhotoniX (2021) 2:8. doi:10.1186/s43074-021-00030-4

CrossRef Full Text | Google Scholar

5. Goodman JW. Speckle phenomena in optics: Theory and applications. Bellingham, Washington, United States: SPIE (2020).

Google Scholar

6. Bhaduri B, Pham H, Mir M, Popescu G. Diffraction phase microscopy with white light. Opt Lett (2012) 37:1094. doi:10.1364/OL.37.001094

PubMed Abstract | CrossRef Full Text | Google Scholar

7. Shan M, Kandel ME, Majeed H, Nastasa V, Popescu G. White-light diffraction phase microscopy at doubled space-bandwidth product. Opt Express (2016) 24:29033. doi:10.1364/OE.24.029033

PubMed Abstract | CrossRef Full Text | Google Scholar

8. Feng P, Wen X, Lu R. Long-working-distance synthetic aperture fresnel off-axis digital holography. Opt Express (2009) 17:5473. doi:10.1364/OE.17.005473

PubMed Abstract | CrossRef Full Text | Google Scholar

9. Wang Y, Meng P, Wang D, Rong L, Panezai S. Speckle noise suppression in digital holography by angular diversity with phase-only spatial light modulator. Opt Express (2013) 21:19568–78. doi:10.1364/OE.21.019568

PubMed Abstract | CrossRef Full Text | Google Scholar

10. Rong L, Xiao W, Pan F, Liu S, Li R. Speckle noise reduction in digital holography by use of multiple polarization holograms. Chin Opt Lett (2010) 8:653–5. doi:10.3788/col20100807.0653

CrossRef Full Text | Google Scholar

11. Turko NA, Eravuchira PJ, Barnea I, Shaked NT. Simultaneous three-wavelength unwrapping using external digital holographic multiplexing module. Opt Lett (2018) 43:1943. doi:10.1364/ol.43.001943

PubMed Abstract | CrossRef Full Text | Google Scholar

12. Dabov K, Foi A, Katkovnik V, Egiazarian K. Image denoising by sparse 3-d transform-domain collaborative filtering. IEEE Trans Image Process (2007) 16:2080–95. doi:10.1109/TIP.2007.901238

PubMed Abstract | CrossRef Full Text | Google Scholar

13. Kemao Q. Windowed Fourier transform method for demodulation of carrier fringes. Opt Eng (2004) 43:1472. doi:10.1117/1.1759333

CrossRef Full Text | Google Scholar

14. Rudin LI, Osher S, Fatemi E. Nonlinear total variation based noise removal algorithms. Physica D: Nonlinear Phenomena (1992) 60:259–68. doi:10.1016/0167-2789(92)90242-F

CrossRef Full Text | Google Scholar

15. Wang K, Li Y, Kemao Q, Di J, Zhao J. One-step robust deep learning phase unwrapping. Opt Express (2019) 27:15100. doi:10.1364/OE.27.015100

PubMed Abstract | CrossRef Full Text | Google Scholar

16. Jeon W, Jeong W, Son K, Yang H. Speckle noise reduction for digital holographic images using multi-scale convolutional neural networks. Opt Lett (2018) 43:4240. doi:10.1364/OL.43.004240

PubMed Abstract | CrossRef Full Text | Google Scholar

17. Tahon M, Montresor S, Picart P. Towards reduced cnns for de-noising phase images corrupted with speckle noise. Photonics (2021) 8:255. doi:10.3390/photonics8070255

CrossRef Full Text | Google Scholar

18. Yan K, Yu Y, Sun T, Asundi A, Kemao Q. Wrapped phase denoising using convolutional neural networks. Opt Lasers Eng (2020) 128:105999. doi:10.1016/j.optlaseng.2019.105999

CrossRef Full Text | Google Scholar

19. Yan K, Chang L, Andrianakis M, Tornari V, Yu Y. Deep learning-based wrapped phase denoising method for application in digital holographic speckle pattern interferometry. Appl Sci (2020) 10:4044. doi:10.3390/app10114044

CrossRef Full Text | Google Scholar

20. Jung K-J, Mandija S, Kim J-H, Ryu K, Jung S, Cui C, et al. Improving phase‐based conductivity reconstruction by means of deep learning–based denoising of phase data for 3T MRI. Magn Reson Med (2021) 86:2084–94. doi:10.1002/mrm.28826

PubMed Abstract | CrossRef Full Text | Google Scholar

21. Yin D, Gu Z, Zhang Y, Gu F, Nie S, Feng S, et al. Speckle noise reduction in coherent imaging based on deep learning without clean data. Opt Lasers Eng (2020) 133:106151. doi:10.1016/j.optlaseng.2020.106151

CrossRef Full Text | Google Scholar

22. Goodman JW. Introduction to fourier optics. New York, United States: McGraw-Hill (1968).

Google Scholar

23. Di J, Zhao J, Sun W, Jiang H, Yan X. Phase aberration compensation of digital holographic microscopy based on least squares surface fitting. Opt Commun (2009) 282:3873–7. doi:10.1016/j.optcom.2009.06.049

CrossRef Full Text | Google Scholar

24. Krull A, Buchholz T-O, Jug F. Noise2void - learning denoising from single noisy images. In: IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR); 5 Apr 2019; Dresden, Germany (20192019). p. 2124–32. doi:10.1109/CVPR.2019.00223

CrossRef Full Text | Google Scholar

25. Foi A, Trimeche M, Katkovnik V, Egiazarian K. Practical poissonian-Gaussian noise modeling and fitting for single-image raw-data. IEEE Trans Image Process (2008) 17:1737–54. doi:10.1109/TIP.2008.2001399

PubMed Abstract | CrossRef Full Text | Google Scholar

26. Wu X, Liu M, Cao Y, Ren D, Zuo W. Unpaired learning of deep image denoising. In: A Vedaldi, H Bischof, T Brox, and J-M Frahm, editors. Computer vision – eccv 2020. Cham: Springer International Publishing (2020). p. 352–68.

CrossRef Full Text | Google Scholar

27. Kaushal H, Kaddoum G. Optical communication in space: Challenges and mitigation techniques. IEEE Commun Surv Tutorials (2017) 19:57–96. doi:10.1109/COMST.2016.2603518

CrossRef Full Text | Google Scholar

28. Roth S, Black MJ. Fields of experts. Int J Comput Vis (2008) 82:205–29. doi:10.1007/s11263-008-0197-6

CrossRef Full Text | Google Scholar

29. Zhang J, Dai S, Ma C, Xi T, Di J, Zhao J, et al. A review of common-path off-axis digital holography: Towards high stable optical instrument manufacturing. gxjzz (2021) 2:1. doi:10.37188/lam.2021.023

CrossRef Full Text | Google Scholar

30. Di J, Wu J, Wang K, Tang J, Li Y, Zhao J, et al. Quantitative phase imaging using deep learning-based holographic microscope. Front Phys (2021) 9. doi:10.3389/fphy.2021.651313

CrossRef Full Text | Google Scholar