Coherent Control of Perfect Optical Vortex Through Four-Wave Mixing in an Asymmetric Semiconductor Double Quantum Well

A scheme for the coherent control of perfect optical vortex (POV) in an asymmetric semiconductor double quantum well (SDQW) nanostructure is proposed by exploiting the tunneling-induced highly efficient four-wave mixing (FWM). The orbital angular momentum (OAM) is completely transferred from a unique POV mode to the generated FWM field. Using experimentally achievable parameters, we identify the conditions under which resonant tunneling allows us to improve the quality of the vortex FWM field and engineer helical phase wave front beyond what is achievable in the absence of resonant tunneling. Furthermore, we find that the intensity and phase patterns of the vortex FWM field are sensitive to the detuning of the probe field but rather robust against the detuning of the coupling field. Subsequently, we perform the coaxial interference between the vortex FWM field and a same-frequency POV beam and show interesting interference properties, which allow us to measure the topological charge of the output POV beam. Our result may find potential applications in quantum technologies based on POV in solids.

1 Introduction

In the past several decades, the study of optical vortices has been one of the hot spots in optics due to their potential applications in particle manipulation [1, 2], optical communication [3, 4], and quantum information processing [5–16]. Note that an optical vortex beam with a helical phase factor e^ilθ carries OAM of lℏ per photon, where l and θ are the topological charge (TC) and azimuthal angle, respectively [17–19]. Conventional optical vortex beams such as Laguerre–Gaussian (LG) beam [20], Bessel–Gauss (BG) beam [21], and high-order Bessel beam [22] exhibit the concentric ring intensity pattern at the transverse distribution. However, the ring radii of this kind of optical vortices is proportional to TCs, which make them face difficulties in actual applications requiring a small vortex diameter and a large topological charge [3] or spatial superposition of vortex beams with different TCs [4]. In order to overcome this challenge, Ostrovsky et al. first proposed the concept of the POV beam, whose ring radius is completely independent of its TC [23]. Since then, significant efforts have been made to explore the generation and detection of the POV beam [24–28]. For instance, different kinds of POV beams have been experimentally generated via using spatial light modulator [28, 29], polymer-based phase plate [30], strongly scattering media [31], single-layer dielectric metasurface [32], etc. In situ measurements for TC of POV beams have been realized via exploiting the phase shift method [33], optical modal decomposition [34], and hybrid angular gradient phase grating [35]. Quite recently, Dai et al put forward a scheme for the fractional OAM conversion of an asymmetric POV beam by using second-harmonic generation [31].

On the other hand, based on the combination of electromagnetically induced transparency (EIT) and standing waves, spatially dependent light-matter interaction has led to many interesting quantum optical phenomena such as atom localization [36, 37], electromagnetically induced grating [38], and controllable photonic band gaps [39]. In 2015, Radwell et al experimentally observed spatially dependent electromagnetically induced transparency via utilizing optical vortex beams to drive cold rubidium atoms [40]. Subsequently, numerous schemes for the spatially dependent light-matter interaction induced by LG beams have been proposed in cold atomic ensembles [41], rare-earth–doped crystal [42], two-dimensional array of metal-coated dielectric nanosphere [43], semiconductor quantum dots [44], and molecular magnets [45]. Meanwhile, many intriguing quantum optical phenomena have been discovered such as vortex-induced spatial absorption [46, 47], spatially structured Kerr nonlinearity [39], ultraprecise Rydberg atomic localization [48], vortex four-wave mixing (FWM) [44, 45, 49, 50, 51, 52], and spatially dependent hyper Raman scattering [53]. Recently, semiconductor quantum wells (SQWs) have been exploited to explore the transfer and control of mid-infrared LG beams due to their inherent advantages such as high nonlinear optical coefficient and large electric dipole moments of intersubband transitions [54, 55, 56]. As far as we know, no reports have been proposed for the investigation of the conversion and manipulation of a POV beam in SDQWs.

In this study, we investigate the conversion and manipulation of a POV beam in an asymmetric SDQW nanostructure via resonant tunneling. The OAM of a unique POV mode can be completely transferred to the generated FWM field via the tunneling-induced highly efficient FWM process. Differing from previous studies in solids [44, 54, 55, 56], the distinguishing features of this scheme are given as follows: First and foremost, we are interested in showing the conversion and manipulation of the mid-infrared perfect optical vortex (POV) beam, which has different vortex characteristics from LG beams in Refs. [54, 55, 56]. Second, our scheme combines the advantages of the four-level ladder-type scheme [55] and tunneling-induced constructive interference [57, 58]. With resonant tunneling, the FWM field is closer to an ideal POV beam, which is a significant advantage of our scheme compared with Ref. [55]. Third, the detunings of probe and coupling fields have different influences on the intensity and phase of the FWM field. Differing from previous schemes [54, 55, 56], the vortex properties of the FWM field are rather robust against the detuning of the strong continuous-wave (CW) coupling field. Furthermore, we show the coaxial interference between the vortex FWM field and a same-frequency POV beam and focus on the influence of the TC of the vortex FWM field on the interference pattern. The interference results illustrate that the interference intensity and phase patterns are determined by the TC of the FWM field, which allows us to measure the TC of the generated POV field.

2 Models and Equations

As shown in Figure 1A, we consider an n-doped asymmetric SDQW nanostructure, which can be grown by molecular-beam epitaxy (MBE) on a semi-insulating GaAs substrate [59]. After a buffer layer, the active region shown in Figure 1A is grown. It consists of a 118 Å wide deep well layer (GaAs) and a 130 Å wider shallow well layer (Al_0.10Ga_0.90As). The two well layers are separated by a 32 Å wide thin potential barrier (Al_0.485Ga_0.515As). Then, the growth is finished with a thick capping layer. The corresponding electron wave functions are shown via color-coded solid lines, and the energy levels are shown via blue dashed lines. The electron motion in the z-direction is limited by the potential barrier of the SDQW and obeys the one-dimensional effective mass Schr$\ddot{\text{o}}$dinger equation, that is,$\left[\frac{{\hslash }^2}{2m^{*}}\frac{d^2}{d{z}^2}+V(z)\right]\psi (z)=E_z\psi (z)$, where m* and ψ(z) represent the effective mass and wave function of the moving electrons. It is worth noting that |ψ(z)|² represents the probability of finding the electrons. In this SDQW nanostructure, the energy of the ground subband |1⟩ in the right side of the deep well is 25.5 meV. Two closely spaced delocalized subbands |2⟩ and |3⟩ with energies 101.8 and 106.9 meV are separated by resonant tunneling. Their corresponding wave functions are asymmetric and symmetric combinations of |sg⟩ and |de⟩, that is, |2⟩ = (|sg⟩–|de⟩)/$\sqrt{2}$ and |3⟩ = (|sg⟩ + |de⟩)/$\sqrt{2}$. Two upper subbands |4⟩ and |5⟩ with eigen-energies of 259.5 and 374.1 meV are coupled by a continuous-wave (CW) driving field Ω_d (central frequency ω_d and wave vector ${\vec{k}}_d$). A weak probe field Ω_p (central frequency ω_p and wave vector ${\vec{k}}_p$) couples the ground subband |1⟩ and two short-lived subbands |2⟩ and |3⟩, while a CW control field Ω_c (central frequency ω_c and wave vector ${\vec{k}}_c$) couples the subband |4⟩ and the subbands |2⟩ and |3⟩, respectively. In this SDQW nanostructure, the pulse probe field and CW coupling and driving fields would induce two FWM processes |1⟩ → |2⟩ → |4⟩ → |5⟩ → |1⟩ and |1⟩ → |3⟩ → |4⟩ → |5⟩ → |1⟩, and then generate a pulse FWM field Ω_m (central frequency ω_m and wave vector ${\vec{k}}_m$) (see Figures 1B,C). In our proposal, the driving field Ω_d is a POV beam, which can be obtained through Fourier transformation of a BG beam [28]. Thus, the driving field Ω_d can be written as

${\mathrm{\Omega }}_d\left(r,\theta \right)={\mathrm{\Omega }}_{d0}\mathrm{\Omega }\left(r\right)e^{il\theta },(1)$

where $\mathrm{\Omega }(r)=i^{l-1}\frac{w_g}{w_0}{e}^{-{(r-R)}^2/{w_0}^2}$, Ω_d0 is the initial Rabi frequency of the driving field, r is the radius, and θ is the azimuthal angle. w₀ (= 2f/(k_dw_g)) and R are the half width and radius of the ring of the POV beam, respectively, f is the focal length of the Fourier lens, and w_g is the beam waist of the initial BG beam.

FIGURE 1

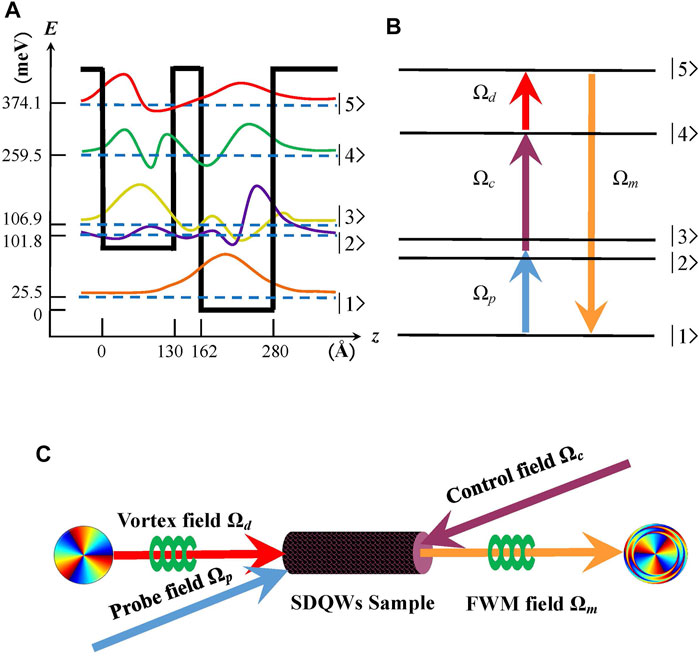
FIGURE 1. (A,B) Schematic of diagram of an asymmetric SDQW nanostructure with five subbands. The solid curves represent the schematics of the corresponding electronic wave functions. (C) A simple block diagram of the SDQW nanostructure sample with four optical fields, in which the driving field is a POV beam.

In the interaction picture and under the rotating-wave approximation, the Hamiltonian of this system is given by:

$H_I=-\hslash \left(\begin{array}{ccccc}\hfill 0\hfill & \hfill {\mathrm{\Omega }}_p^{*}{e}^{-i{k}_{p}z}\hfill & \hfill \alpha {\mathrm{\Omega }}_p^{*}{e}^{-i{k}_{p}z}\hfill & \hfill 0\hfill & \hfill {\mathrm{\Omega }}_m^{*}{e}^{-i{k}_{m}z}\hfill \\ \hfill {\mathrm{\Omega }}_p{e}^{i{k}_{p}z}\hfill & \hfill {\mathrm{\Delta }}_p\hfill & \hfill 0\hfill & \hfill {\mathrm{\Omega }}_c^{*}{e}^{-i{k}_{c}z}\hfill & \hfill 0\hfill \\ \hfill \alpha {\mathrm{\Omega }}_p{e}^{i{k}_{p}z}\hfill & \hfill 0\hfill & \hfill {\mathrm{\Delta }}_p-\delta \hfill & \hfill \beta {\mathrm{\Omega }}_c^{*}{e}^{-i{k}_{c}z}\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill {\mathrm{\Omega }}_c{e}^{i{k}_{c}z}\hfill & \hfill \beta {\mathrm{\Omega }}_c{e}^{i{k}_{c}z}\hfill & \hfill {\mathrm{\Delta }}_p+{\mathrm{\Delta }}_c\hfill & \hfill {\mathrm{\Omega }}_d^{*}{e}^{-i{k}_{d}z}\hfill \\ \hfill {\mathrm{\Omega }}_m{e}^{i{k}_{m}z}\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill {\mathrm{\Omega }}_d{e}^{i{k}_{d}z}\hfill & \hfill {\mathrm{\Delta }}_m\hfill \end{array}\right),(2)$

where${\mathrm{\Omega }}_p={\vec{\mu }}_{21}\cdot {\vec{E}}_p/(2\hslash ),{\mathrm{\Omega }}_c={\vec{\mu }}_{42}\cdot {\vec{E}}_c/(2\hslash ),{\mathrm{\Omega }}_d={\vec{\mu }}_{54}\cdot {\vec{E}}_d/(2\hslash )$, and ${\mathrm{\Omega }}_m={\vec{\mu }}_{51}\cdot {\vec{E}}_m/(2\hslash )$ represent one-half of the Rabi frequencies for the respective transitions. ${\vec{\mu }}_{21},{\vec{\mu }}_{42},{\vec{\mu }}_{54}$ and ${\vec{\mu }}_{51}$ are the corresponding dipole matrix elements. Δ_p(c,m) = ω_p(c,m) − (ω_2(4,5) − ω_1(2,1)) denote the detuning of the corresponding fields. $\delta \left(\right.\approx$ 5.1 meV indicates the strength of the resonant tunneling between subbands |3⟩ and |2⟩. $\alpha ={\vec{\mu }}_{31}/{\vec{\mu }}_{21}$ is the ratio between the subband transition dipole moments $\left\{\vec{\mu }\right\}\_\left\{31\right\}$ and $\left\{\vec{\mu }\right\}\_\left\{21\right\}$. $\beta ={\vec{\mu }}_{43}/{\vec{\mu }}_{42}$ is the ratio between the subband transition dipole moments $\left\{\vec{\mu }\right\}\_\left\{43\right\}$ and $\left\{\vec{\mu }\right\}\_\left\{42\right\}$.

Defining the electronic energy state as $\left|\mathrm{\Psi }(t)\right.⟩=A_1\left|1\right.⟩+A_2{e}^{i{k}_{p}z}\left|2\right.⟩+A_3{e}^{i{k}_{p}z}\left|3\right.⟩+A_4{e}^{i(k_p+k_c)z}\left|4\right.⟩+A_5{e}^{i{k}_{m}z}\left|5\right.⟩$, using the Schr$\ddot{\text{o}}$dinger equation $i\hslash \partial \left|\mathrm{\Psi }(t)\right.⟩/\partial t=H_I\left|\mathrm{\Psi }(t)\right.⟩$, the equations of motion for the probability amplitude A_j (j = 1 ∼ 5) of the electronic wave functions can be obtained as

$\frac{\partial A_2}{\partial t}=i\left({\mathrm{\Delta }}_p+i{\gamma }_2\right)A_2+i{\mathrm{\Omega }}_p{A}_1+i{\mathrm{\Omega }}_c^{*}{A}_4,(3)$

$\frac{\partial A_3}{\partial t}=i\left({\mathrm{\Delta }}_p-\delta +i{\gamma }_3\right)A_3+i\alpha {\mathrm{\Omega }}_p{A}_1+i\beta {\mathrm{\Omega }}_c^{*}{A}_4,(4)$

$\frac{\partial A_4}{\partial t}=i\left({\mathrm{\Delta }}_p+{\mathrm{\Delta }}_c+i{\gamma }_4\right)A_4+i{\mathrm{\Omega }}_c{A}_2+i\beta {\mathrm{\Omega }}_c{A}_3+i{\mathrm{\Omega }}_d^{*}{e}^{-i\mathrm{\Delta }kz}{A}_5,(5)$

$\frac{\partial A_5}{\partial t}=i\left({\mathrm{\Delta }}_m+i{\gamma }_5\right)A_5+i{\mathrm{\Omega }}_m{A}_1+i{\mathrm{\Omega }}_d{e}^{i\mathrm{\Delta }kz}{A}_4,(6)$

where γ_i (i = 2, 3, 4, 5) is added phenomenologically to describe the overall decay rate of the subbands |i⟩, (i = 2, 3, 4, 5). In order to simplify the calculation, we assume the phase matching condition, that is, $\mathrm{\Delta }\vec{k}={\vec{k}}_p+{\vec{k}}_c+{\vec{k}}_d-{\vec{k}}_m=0$, is satisfied.

The following Maxwell equations describe the propagation equations of the probe and FWM fields:

$\frac{\partial {\mathrm{\Omega }}_p\left(z,t\right)}{\partial z}+\frac{1}{c}\frac{\partial {\mathrm{\Omega }}_p\left(z,t\right)}{\partial t}=i\frac{c}{2{\omega }_p}{\nabla }_{\perp }^2{\mathrm{\Omega }}_p+i{\zeta }_p\left(A_2+\alpha A_3\right)A_1^{*},(7)$

$\frac{\partial {\mathrm{\Omega }}_m\left(z,t\right)}{\partial z}+\frac{1}{c}\frac{\partial {\mathrm{\Omega }}_m\left(z,t\right)}{\partial t}=i\frac{c}{2{\omega }_m}{\nabla }_{\perp }^2{\mathrm{\Omega }}_m+i{\zeta }_m{A}_5{A}_1^{*},(8)$

where ζ_p = ζ₂₁₍₃₁₎ = 2Nω_p|μ₂₁₍₃₁₎|²/(ℏɛ₀c), ζ_m = ζ₅₁ = 2Nω_m|μ₅₁|²/(ℏɛ₀c) are two constants, which are related to the frequently used oscillator strengths of the subband transitions |1⟩ ↔ |2 (3)⟩ and |1⟩ ↔ |5⟩. N is the electron sheet density. The transverse derivatives ${\nabla }_{\perp }^2{\mathrm{\Omega }}_{p(m)}$ on the right-hand sides of Eqs 7, 8 account for light diffraction [51]. When the propagation distance is much smaller than the Rayleigh length, that is, $\pi w_0^2/{\lambda }_m\gg L$, light diffraction can be neglected. In this study, w₀ ≈ 200 μm, λ_m = 3.56 μm, and L = 100 μm are chosen so that $\pi w_0^2/{\lambda }_m\approx 3.53\times 10^4\mu$m ≫ L. Therefore, it is reasonable to ignore diffraction in the following analysis.

In the limit of the weak probe and FWM fields, most of the electrons remain in the subband |1⟩, that is, |A₁|² ≈ 1. Taking Fourier transform of Eqs 3–6 and 7, 8, we obtain

$d_2{\tilde{A}}_2+{\mathrm{\Omega }}_c^{*}{\tilde{A}}_4+{\tilde{\mathrm{\Omega }}}_p=0,(9)$

$d_3{\tilde{A}}_3+\beta {\mathrm{\Omega }}_c^{*}{\tilde{A}}_4+\alpha {\tilde{\mathrm{\Omega }}}_p=0,(10)$

${\mathrm{\Omega }}_c{\tilde{A}}_2+\beta {\mathrm{\Omega }}_c{\tilde{A}}_3+d_4{\tilde{A}}_4+{\mathrm{\Omega }}_d^{*}{\tilde{A}}_5=0,(11)$

${\mathrm{\Omega }}_d{\tilde{A}}_4+d_5{\tilde{A}}_5+{\tilde{\mathrm{\Omega }}}_m=0,(12)$

$\frac{\partial {\tilde{\mathrm{\Omega }}}_p}{\partial z}-i\frac{\omega }{c}{\tilde{\mathrm{\Omega }}}_p=i{\zeta }_p\left({\tilde{A}}_2+\alpha {\tilde{A}}_3\right),(13)$

$\frac{\partial {\tilde{\mathrm{\Omega }}}_m}{\partial z}-i\frac{\omega }{c}{\tilde{\mathrm{\Omega }}}_m=i{\zeta }_m{\tilde{A}}_5,(14)$

where d₂ = ω + Δ_p + iγ₂, d₃ = ω + Δ_p − δ + iγ₃, d₄ = ω + Δ_p + Δ_c + iγ₄, d₅ = ω + Δ_m + iγ₅, ω is the Fourier variable. ${\tilde{A}}_j(j=\mathrm{2,3,4,5})$ and ${\tilde{\mathrm{\Omega }}}_{p(m)}$ are the Fourier transforms of A_j (j = 2, 3, 4, 5) and Ω_p(m), respectively. By solving Eqs 9–12, it is easy to obtain the following relations:

${\tilde{A}}_2+\alpha {\tilde{A}}_3=\left(D_{p1}{\tilde{\mathrm{\Omega }}}_p+D_{m1}{\tilde{\mathrm{\Omega }}}_m\right)/D,(15)$

${\tilde{A}}_5=\left(D_{p2}{\tilde{\mathrm{\Omega }}}_p+D_{m2}{\tilde{\mathrm{\Omega }}}_m\right)/D,(16)$

where D_p1 = D_p1(ω), D_p2 = D_p2(ω), D_m1 = D_m1(ω), D_m2 = D_m2(ω), D = D(ω), D_p1(ω) = d₅ (α − β)²|Ω_c|² − (d₂α² + d₃) (d₄d₅ − |Ω_d|²), D_p2(ω) = −(d₂αβ + d₃)Ω_cΩ_d, $D_{m1}(\omega )=-(d_2\alpha \beta +d_3){\mathrm{\Omega }}_c^{*}{\mathrm{\Omega }}_d^{*}$, $D_{m2}(\omega )=-d_2{d}_3{d}_4+\left(d_2{\beta }^2+d_3\right)|{\mathrm{\Omega }}_c{|}^2$, and D(ω) = d₂d₃ (d₄d₅ − |Ω_d|²) − d₅ (d₂β² + d₃)|Ω_c|².

By substituting Eqs 15, 16 into Eqs 13, 14 and using the initial condition ${\tilde{\mathrm{\Omega }}}_m(z=0,\omega ;x,y)=0$, the expression of the generated FWM field can be obtained as

${\tilde{\mathrm{\Omega }}}_m\left(z,\omega ;x,y\right)=\tilde{\mathrm{\Upsilon }}\left(\omega \right){\tilde{\mathrm{\Omega }}}_p\left(z=0,\omega ;x,y\right)\left[e^{i{K}_{+}\left(\omega \right)}z-e^{i{K}_{-}\left(\omega \right)}z\right],(17)$

where $K_{\pm }(\omega )=\omega /c+({\zeta }_p{D}_{p1}+{\zeta }_m{D}_{m2})/(2D)\pm \sqrt{G(\omega )}/(2D)=K_{\pm }(0)+K_{\pm }^{(1)}\omega +O\left({\omega }^2\right)$, $\tilde{\mathrm{\Upsilon }}(\omega )={\zeta }_m{D}_{p2}/\sqrt{G(\omega )}=\tilde{\mathrm{\Upsilon }}(0)+O(\omega )$ with $G(\omega )={({\zeta }_p{D}_{p1}-{\zeta }_m{D}_{m2})}^2+4{\zeta }_p{\zeta }_m{D}_{p2}{D}_{m1}$. From Eq. 17, we readily observe that there exist two modes described by the dispersion relations K₊(ω) and K₋(ω), respectively. By seeking the approximated inverse Fourier transform with the approximation of neglecting both O(ω) in $\tilde{\mathrm{\Upsilon }}(\omega )$ and O (ω²) in K_±(ω), it is straightforward to obtain

${\mathrm{\Omega }}_m\left(z,t;x,y\right)=\tilde{\mathrm{\Upsilon }}\left(0\right)\left[{\mathrm{\Omega }}_p\left({\eta }_{+}\right)e^{i{K}_{+}z}-{\mathrm{\Omega }}_p\left({\eta }_{-}\right)e^{i{K}_{-}z}\right],(18)$

where K_± = K_±(0), η_± = t − z/V_g±, and $V_{g\pm }=1/\mathrm{Re}[K_{\pm }^{(1)}]$ is the group velocity of K_± mode. Re(K_±) and Im (K_±) represent the phase shift per unit length and absorption coefficient of K_± mode, respectively. In the adiabatic regime, the absorption coefficient Im (K₋) is much greater than Im (K₊) [58], which indicates that the K₋ mode is absorbed quickly and only the K₊ mode remains after a short propagation distance L. Therefore, Re(K₊) and Im (K₊) are called as the modal phase shift per unit length and absorption coefficient for the remaining K₊ mode, respectively. By neglecting the K₋ mode, the generated FWM field after a short propagation distance L can be given as

${\mathrm{\Omega }}_m\left(L,t;x,y\right)=S{\mathrm{\Omega }}_c{\mathrm{\Omega }}_{d0}\mathrm{\Omega }\left(r\right){\mathrm{\Omega }}_p\left({\eta }_{+}\right)e^{il\theta }{e}^{i{K}_{+}L},(19)$

with

$S=-{\zeta }_m\left[\alpha \beta {\mathrm{\Delta }}_p+{\mathrm{\Delta }}_p-\delta +i\left(\alpha \beta {\gamma }_2+{\gamma }_3\right)\right]/\sqrt{G\left(0\right)}.(20)$

It is worth noting that the modulation term S, which is independent of the propagation distance L, can also influence the output of the FWM field, that is, the modulation term S appears once the FWM process takes place. Thus, S is the inherent attribute for the SDQW-based FWM system. S is a complex function of the radial position r due to the existence of the POV driving field and can modify the intensity and phase patterns of the generated FWM field. In order to compare with the modal phase shift Re(K₊) and modal absorption Im (K₊), we introduce a factor Q to replace S by setting S = e^iQL = e^{i Re(Q)L− Im(Q)L}. In this sense, the inherent phase shift and absorption induced by S can be represented by Re(Q) and Im(Q). Thus, Re(Q) and Im(Q) are called as the inherent phase shift per unit length and absorption coefficient of the SDQW-based FWM system. Using K₊ = Re(K₊) + i Im (K₊), Eq. 19 can be rewritten as

$\begin{array}{c}\hfill {\mathrm{\Omega }}_m\left(L,t;x,y\right)={\mathrm{\Omega }}_c{\mathrm{\Omega }}_{d0}\mathrm{\Omega }\left(r\right){\mathrm{\Omega }}_p\left({\eta }_{+}\right)e^{-\left[\mathrm{Im}\left(Q\right)+\mathrm{Im}\left(K_{+}\right)\right]L}{e}^{il\theta +i\left[\mathrm{Re}\left(Q\right)+\mathrm{Re}\left(K_{+}\right)\right]L},\hfill \end{array}(21)$

where the intensity of the vortex FWM field is $\propto |{\mathrm{\Omega }}_c{\mathrm{\Omega }}_{d0}\mathrm{\Omega }(r){\mathrm{\Omega }}_p({\eta }_{+})e^{-[\mathrm{Im}(Q)+\mathrm{Im}(K_{+})]L}{|}^2$, while the factor $e^{il\theta +i[\mathrm{Re}(Q)+\mathrm{Re}(K_{+})]L}$ reflects the phase wave front of the vortex FWM field. In Eq. 21, Im(K₊)L, Im(Q)L, and Re(Q)L should be dimensionless. In our proposal, the unit of the propagation distance L is μm. Therefore, the units of the absorption coefficients and the phase shifts per unit length are μm⁻¹.

3 Results and Discussions

In this section, the focus is on investigating the coherent control of the generated POV beam via FWM process in an asymmetric SDQW nanostructure. As we know, the structure of a SQW determines its properties such as resonant tunneling and subband decay rates. In other words, these properties of the SQW are determined once it is fabricated. Thus, the values of the decay rates may be different for the cases with and without resonant tunneling. In the proposed asymmetric SDQW nanostructure, resonant tunneling exists, that is, α = −0.11, β = 0.98, and δ = 5.1 meV, and the decay rates are γ₂ = γ₃ = 1 meV and γ₄ = γ₅ = 0.1 meV [58]. For comparative analysis, we consider the case without resonant tunneling by directly taking α = β = 0 and δ = 0. This approach has been used to investigate tunneling-induced highly efficient FWM [57,58].

The influence of the resonant tunneling on the intensity and phase of the generated FWM field is explored first. Here, the driving field Ω_d (r, θ) is a POV beam with the TC l = 3, and the corresponding intensity and phase profiles are plotted in Figures 2A,D, respectively. The intensity distribution of the driving field in Figure 2A exhibits a ring pattern at the radial position r = 2 mm with a full width at half maximum (FWHM) of Δω_H = 0.402 mm. Meanwhile, the helical phase profile in Figure 2D displays three periods along the azimuthal direction, and the phase of each period is 2π. Based on Eq. 21, the intensity and phase profiles of the generated FWM field are also plotted in Figure 2. As shown in Figures 2B,E, in the absence of resonant tunneling, that is, α = β = 0 and δ = 0, the intensity distribution also displays a ring pattern at r = 2 mm with an increased FWHM of Δω_H = 0.606 mm (see Figure 2B), while the helical phase twists in the clockwise direction [see Figure 2E]. When considering the existence of resonant tunneling, that is, α = −0.11, β = 0.98 and δ = 5.1 meV [58], as shown in Figures 2C,F, the intensity of the vortex FWM field is almost unchanged, and FWHM of the intensity pattern decreases from 0.606 to 0.384 mm, while the helical phase twists in the opposite direction compared with the case in Figures 2B,E. More interestingly, the phase distortion is significantly enhanced at two edges of the intensity pattern. For a POV beam, the FWHM of the intensity pattern can be adopted in appraising the quality of POV, where Δω_H = 0 corresponds to an ideal POV beam [23]. The direct comparison between the aforementioned two cases implies that the resonant tunneling makes the generated vortex FWM field closer to an ideal POV beam and modifies the wave front of the helical phase. Actually, the resonant tunneling can lead to the symmetric and asymmetric wave functions of subbands |2⟩ and |3⟩ in the SDQW nanostructure (i.e., αβ < 0). Therefore, the optical nonlinear properties of the SDQW nanostructure can be modified by the resonant tunneling, which results in the different findings in Figure 2.

FIGURE 2

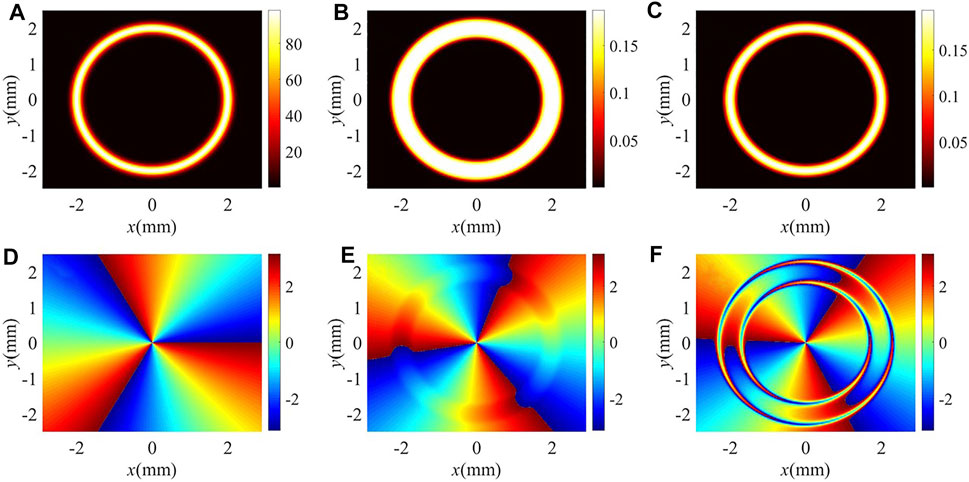
FIGURE 2. (A,D) Intensity and phase profiles of the drive field with POV. (B,C) Intensity and (E,F) phase profiles of the FWM field for different values of α, β, and δ: (B,E) α = β = 0, δ = 0 meV; (C,F) α = −0.11, β = 0.98, δ = 5.1 meV. The other parameters are ζ_p = ζ_m = 9.2 × 10^–3 meV/μm, L = 100 μm, l = 3, w_g = 200 μm, λ = 10.83 μm, R = 2 mm, f = 11.69 mm, Ω_p = 1 meV, Ω_c = 14 meV, Ω_d0 = 10 meV, Δ_p = 16 meV, and Δ_c = Δ_m = 0 meV.

In order to inspect the effect of the resonant tunneling, the radial distributions of the imaginary and real parts of Q and K₊ are plotted in Figure 3. Note that the inherent absorption Im(Q) and modal absorption Im (K₊) at r = 2 mm determine the output intensity of the vortex FWM field. Without and with resonant tunneling, the total absorption coefficients at r = 2 mm are 57.77 μm⁻¹ and 57.56 μm⁻¹, respectively. In the two cases, the total absorption coefficients are nearly equal so that the intensity of the FWM field remains nearly constant. In addition, the inherent absorption Im(Q) and modal absorption Im (K₊) determine the intensity distribution of the generated vortex FWM field, while the inherent phase shift Re(Q) and modal phase shift Re(K₊) determine the wave front distribution of the helical phase. Without the resonant tunneling, the inherent absorption Im(Q) dominates in tailoring the intensity profile of the FWM field [see blue lines in Figures 3A,C]. The ring pattern of the FWM field becomes flat in the vortex transfer processing due to the existence of the strong inherent absorption peak at r = 2 mm. Thus, the FWHM of the vortex FWM field increases compared with the driving field with POV. The appearance of peaks of both the inherent and modal phase shifts at r = 2 mm results in the helical phase twisted in the clockwise direction (see red lines in Figures 3A,C). With the resonant tunneling, the FWM field suffers stronger inherent and modal absorption at two edges of the intensity pattern (see blue lines in Figures 3B,D). In this case, the edge energy of the vortex FWM field can be easily dissipated, resulting in the width of the intensity pattern becoming narrower. The double-valley pattern of the dominated modal phase shift around r = 2 mm gives rise to two tremendous distortions in the anticlockwise direction (see red lines in Figures 3B,D).

FIGURE 3

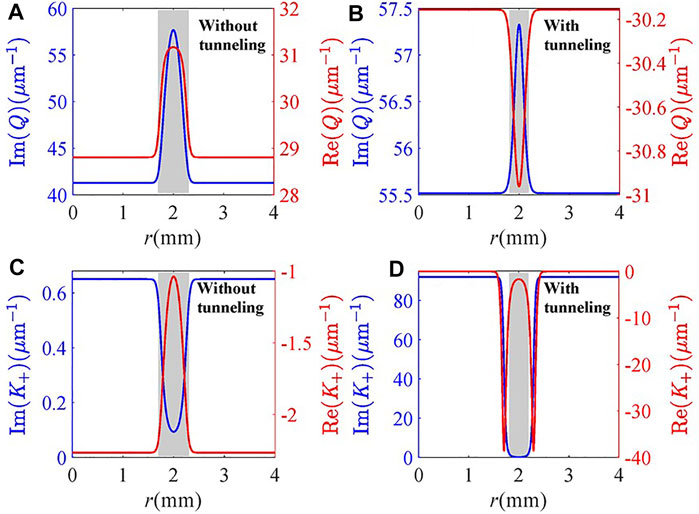
FIGURE 3. Real and imaginary parts of (A,B) Q and (C,D) K₊ versus radius r for different values of α, β, and δ: (A,C) α = β = 0, δ = 0 meV; (B,D) α = −0.11, β = 0.98, δ = 5.1 meV. Other parameters are the same as in Figure 2.

We then examine in Figure 4 the influence of the detuning Δ_p of the probe field on the intensity and helical phase of the vortex FWM field in the presence of the resonant tunneling. The corresponding radial distributions of the imaginary and real parts of Q and K₊ are shown in Figure 5. One can find that the total absorption (including inherent and modal absorption) at the center of the light ring increases when increasing Δ_p from −4 to 8 meV (see blue lines in Figure 5). Correspondingly, the intensity of the vortex FWM field decreases (see Figures 4A–C). In the case of Δ_p = −4 meV, one can find from Figures 4A,D that the FWHM of the light ring is wide (Δω_H = 0.416 mm) while the distortion of the helical phase is almost invisible. The reason is that the vortex FWM field suffers a strong inherent absorption at the center of the light ring and a small total phase shift (including inherent and modal phase shifts) (Figures 5A,D). When the probe detuning is varied from −4 to 4 meV, the vortex FWM field suffers stronger inherent and modal absorption at the edges of the intensity pattern (see Figure 5B), and there are single peaks of inherent phase shift and double peaks of modal phase shift (Figure 5E). Therefore, the FWHM of the intensity pattern decreases to 0.196 mm (Figure 4B), and the helical phase twists in the clockwise direction (Figure 4E). More importantly, the twisted helical phase wave front is flat because of complementation between inherent and modal phase shifts. As the probe detuning increases to 8 meV, as shown in Figures 4C,F, 5C,F, the FWHM of the intensity slightly increases to 0.264 mm due to the wider transparent window in modal absorption spectrum. Meanwhile, the helical phase twists anticlockwise because of the existence of a single valley of inherent phase shift and double valleys of modal phase shift. Therefore, one can conclude that the detuning of the probe field can manipulate the helical phase wave front of the generated FWM field in an effective manner.

FIGURE 4

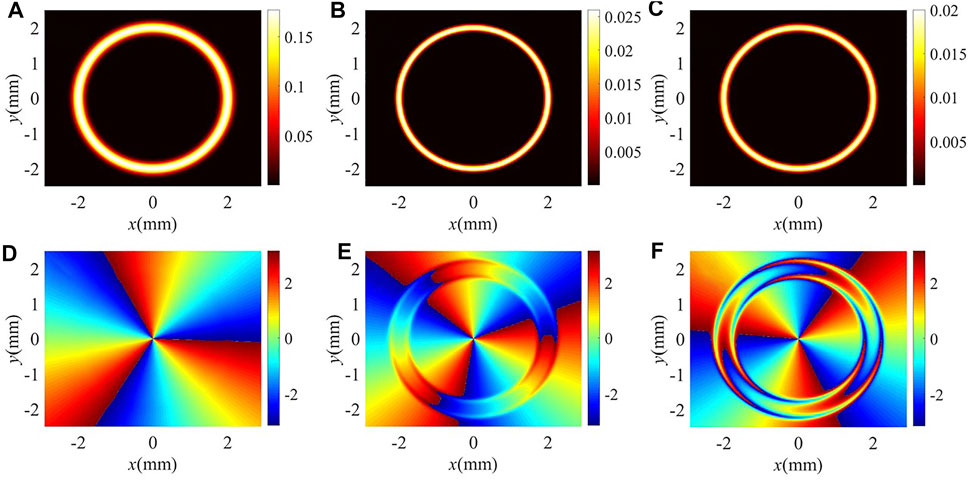
FIGURE 4. (A–C) Intensity and (D–F) phase profiles of the FWM field for different probe detuning Δ_p: (A,D) Δ_p = −4 meV; (B,E) Δ_p = 4 meV; (C,F) Δ_p = 8 meV. Other parameters are the same as in Figure 2C.

FIGURE 5

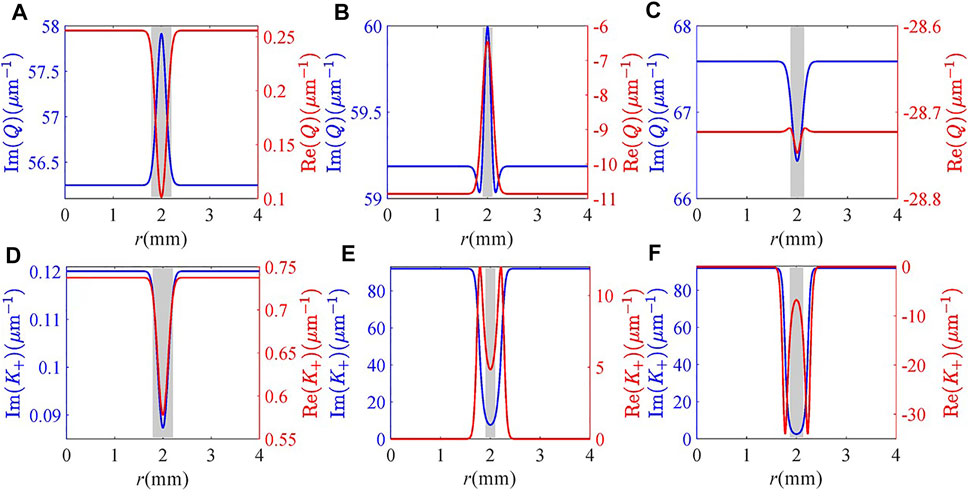
FIGURE 5. Real and imaginary parts of (A–C) Q and (D–F) K₊ versus radius r for different probe detuning Δ_p: (A,D) Δ_p = −4 meV; (B,E) Δ_p = 4 meV; (C,F) Δ_p = 8 meV. Other parameters are the same as in Figure 2C.

We further investigate the dependence of the intensity and helical phase of the vortex FWM field on the detuning Δ_c of the coupling field in Figures 6, 7. It can be seen from Figure 6 that the intensity, width, and phase of the vortex FWM field are not very sensitive to the coupling detuning Δ_c. The results can be explained that the impact of the coupling detuning on the absorption and phase properties of the FWM field is weak. At the center of the light ring, the modal absorption remains unchanged and the inherent absorption decreases slowly with the increase of Δ_c (see blue lines in Figure 7), so we can find that the intensity of the vortex FWM field increases limitedly in Figures 6A–C. However, the FWHM of the intensity pattern is kept at 0.216 mm because of the strong inherent and modal absorption at the two edges of the intensity pattern. At the same time, the modal phase shift dominates in modulating the helical phase wave front of the FWM field (see red lines in Figure 7). As shown in Figures 6D–F, the near-identical double valleys of the modal phase shift result in almost the same double distortions for the helical phase wave front. Therefore, the generated vortex FWM field has good robustness on the detuning of the coupling field.

FIGURE 6

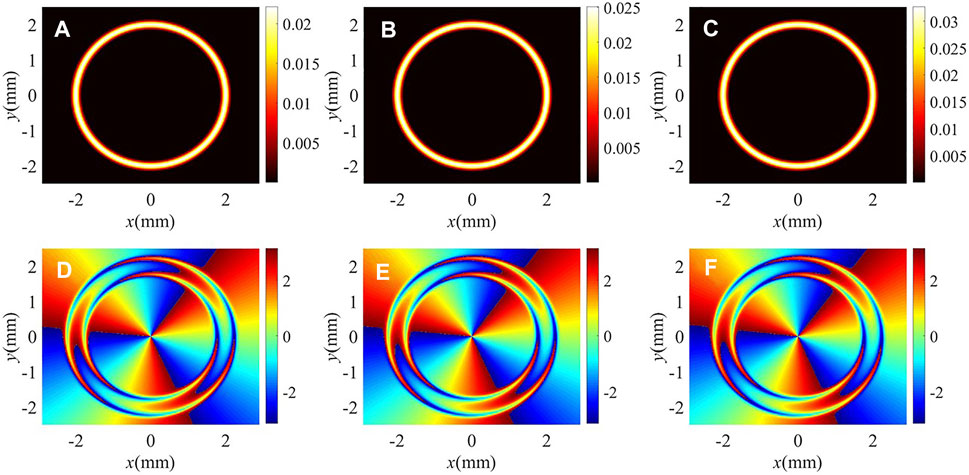
FIGURE 6. (A–C) Intensity and (D–F) phase profiles of the FWM field for different coupling detuning Δ_c: (A,D) Δ_c = 4 meV; (B,E) Δ_c = 8 meV; (C,F) Δ_c = 16 meV. Other parameters are the same as in Figure 4C.

FIGURE 7

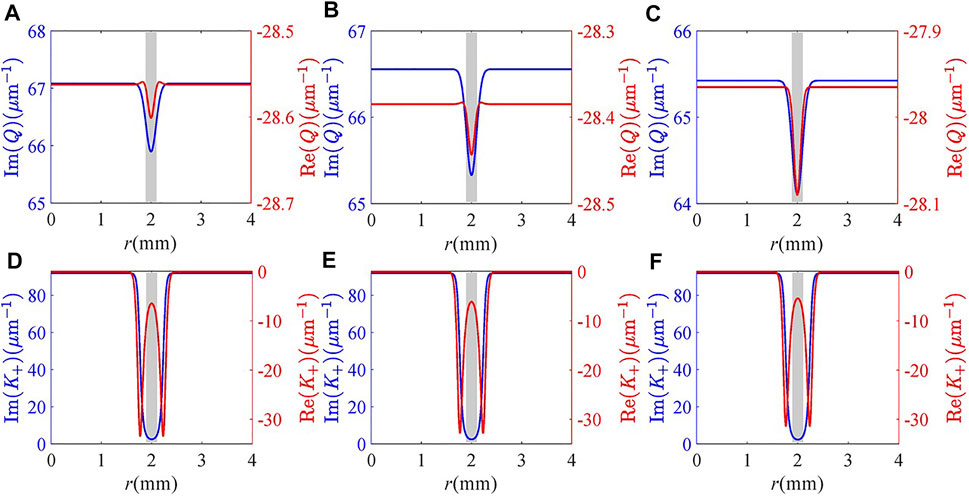
FIGURE 7. Real and imaginary parts of (A–C) Q and (D–F) K₊ versus radius r for different coupling detuning Δ_c: (A,D) Δ_c = 4 meV; (B,E) Δ_c = 8 meV; (C,F) Δ_c = 16 meV. Other parameters are the same as in Figure 4C.

Now, we analyze the influence of the conventional LG beam and POV beam with higher order TC on the intensity and phase patterns of the vortex FWM field in Figure 8. In the former case, we select the traditional single-ring LG beam ${\mathrm{\Omega }}_d={\mathrm{\Omega }}_{d0}\frac{1}{\sqrt{\left|l\right|!}}{(\frac{\sqrt{2r}}{w_{LG}})}^{\left|l\right|}{L}_p^{\left|l\right|}(\frac{2r^2}{w_{LG}^2})e^{-\frac{r^2}{w_{LG}^2}}{e}^{il\theta }$ with radial index p = 0 and TC l = 3 in Ref.[45] as the OAM driving field and plot the intensity and phase profiles of the FWM field in Figures 8A,C. Compared with the case shown in Figures 2C,F, we can find that both the intensity and ring radius of the FWM field greatly decrease (Figure 8A). In addition, the helical phase wave front also suffers double distortion at the two edges of the intensity pattern. However, the phase twist in the inner edge is much smaller than that in the outer edge (Figure 8C). In the latter case, a POV beam with TC l = 6 is treated as the OAM driving field. The intensity and phase profiles of the FWM field are plotted in Figures 8B,D, respectively. The direct comparison between Figures 2C,F, 8B,D implies that the intensity patterns and phase distortions of the FWM field remain unchanged, except for the fact that the helical phase profile in Figure 8D displays six periods along the azimuthal direction.

FIGURE 8

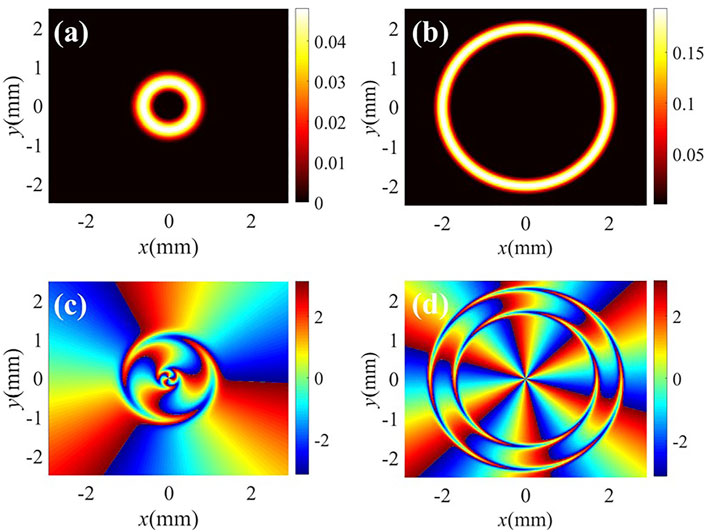
FIGURE 8. (A,B) Intensity and (C,D) phase profiles of the FWM field for different beams. (A,C) LG beam with p = 0, l = 3, and w_LG = 0.5 mm; (B,D) POV beam with l = 6. Other parameters are the same as in Figure 2C.

We note that, very recently, some theoretical schemes for exploring the vortex FWM process in SQWs have been proposed [54, 55, 56]. In these schemes, SQWs were used to explore the transfer and control of mid-infrared conventional LG beams [54, 55] and inner–outer ring LG beams [56]. In comparison with these schemes, the major differences in our proposal are the following: First, the main difference between our scheme and Refs. [54, 55, 56] is that we focus on the conversion and manipulation of the mid-infrared POV beam, while previous studies are focused on the control of the mid-infrared LG beams. Second, our scheme takes the advantages of the four-level ladder-type scheme [55] and tunneling-induced constructive interference [57, 58]. For example, resonant tunneling can effectively open the channel for the FWM process and modify the spatial distribution of the FWM field. Third, with the presence of resonant tunneling, both the intensity and phase patterns are insensitive to the detuning of the coupling field. The findings are quite different from the results obtained in Ref. [55], where the intensity pattern and phase distortion strongly depend on the detuning of the corresponding field.

Finally, we perform the coaxial interference between the vortex FWM field and a same-frequency POV beam ${\mathrm{\Omega }}_G(r,\theta )={\mathrm{\Omega }}_{G0}{i}^{(m-1)}\frac{w_g}{w_0}{e}^{im\theta }{e}^{-{(r-R)}^2/(4w_0^2)}$ with the topological charge m = 1. The interference intensity and phase patterns are displayed in Figure 9 for different TCs of the vortex FWM field. From Figure 9, one can find that the interference patterns are quite different from the case in Figures 4C,F. The interference intensity exhibits a double-ring pattern for l = m = 1 and a vortex petal-like pattern for l ≠ m = 1 (Figures 9A–C,G–I). Specifically, as TC increases from l = 1 to l = 3, the number of petals in the intensity pattern increases from 0 to 2, and the rotating direction of petals is clockwise. However, the number of petals increases from 2 to 4 with TC increasing from l = −1 to l = −3, where the petal-like pattern is rotated in the anticlockwise direction. Meanwhile, the interference phase at the radial position r = 2 mm twists in the clockwise direction for l = 1, 2, 3 and in the opposite direction for l = −1, −2, −3, while the interference phase in the other region is the same as the helical phase of the POV beam Ω_G. From Figure 9, one can conclude that the number of intensity petals in the interference intensity spectrum equals to the value of |l − m|, and the rotating direction of intensity petals reflects the sign of l − m (i.e., the clockwise and anticlockwise rotation of petals correspond to l − m > 0 and l − m < 0 , respectively). Therefore, we can efficiently realize the measurement for the value and sign of TC of the generated vortex FWM field (i.e., the vortex driving field) via observing the interference intensity spectrum.

FIGURE 9

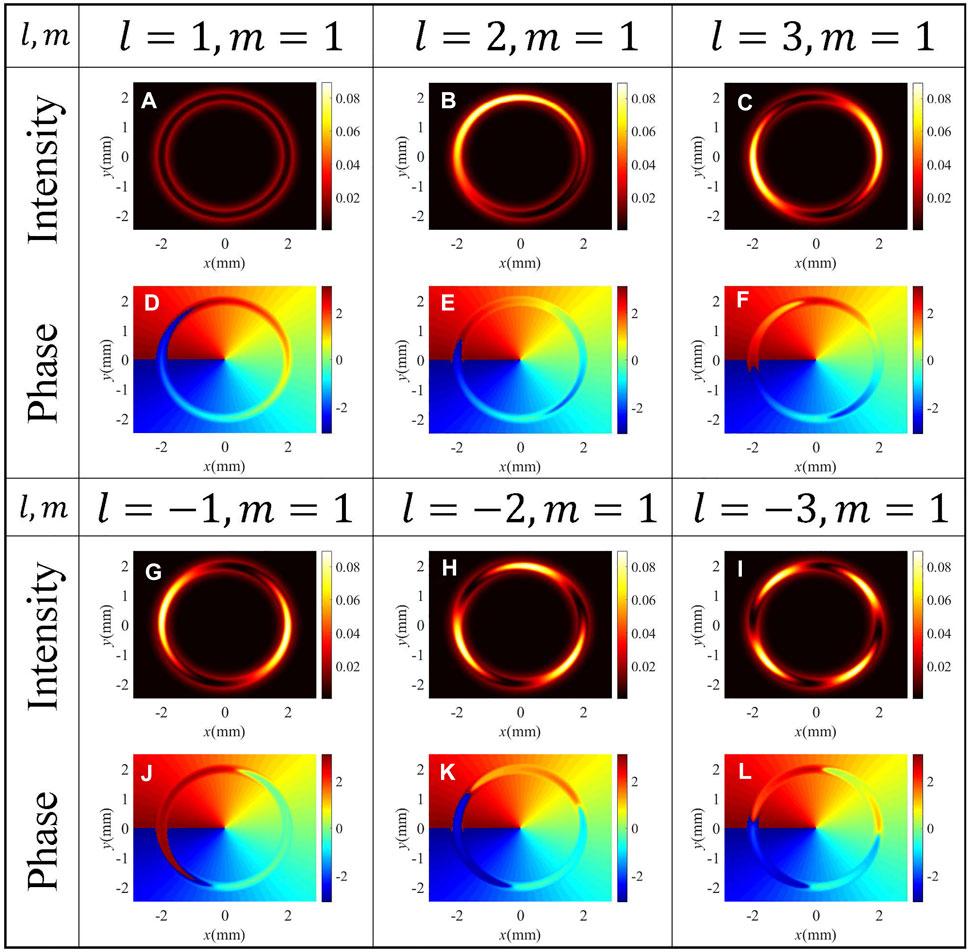
FIGURE 9. Interference intensity [(A–C) and (G–I)] and phase [(D–F) and (J–L)] profiles of different values of TC of the FWM field. Ω_G0 = 0.16 meV, m = 1, and other parameters are the same as in Figure 4C.

4 Conclusion

We mainly focus on the condition of low temperatures up to 10 K, and have neglected other many-body effects such as the depolarization effect, which renormalizes the free-carrier and carrier-field contributions. These contributions and their interplay have been investigated quite thoroughly in Ref. [60]. Note that due to the low electron sheet density considered here, these effects only give a negligible correction.

In conclusion, a scheme for transferring and manipulating POV in an asymmetric SDQW nanostructure is theoretically suggested. The OAM of a unique POV mode is completely transferred to the generated FWM field via a tunneling-induced highly efficient FWM process. It is demonstrated that resonant tunneling plays an important role in the manipulation of the intensity and phase distribution of the vortex FWM field. With the presence of resonant tunneling, the generated FWM field is closer to an ideal POV beam and exhibits an enhanced phase distortion at two edges of the intensity pattern. Furthermore, we find that the intensity and phase profiles of the vortex FWM field are sensitive to the detuning of the weak probe field but rather robust against the detuning of the strong coupling field. These results can be reasonably explained via the combination of inherent and modal dispersion relation. Subsequently, the coaxial interference between the vortex FWM field and a same-frequency POV beam is studied. It is found that the interference intensity and phase patterns are determined by TC of the vortex FWM field, which allows us to measure TC of the FWM field with POV. Our proposal may provide an avenue for the coherent control of POV and a possibility for the TC measurement of a POV beam.

Data Availability Statement

The raw data supporting the conclusion of this article will be made available by the authors, without undue reservation.

Author Contributions

The idea was first conceived by W-XY. XD was responsible for the physical model, numerical calculations, and writing most of the manuscript. TS contributed to writing the manuscript and verified the calculated results.

Funding

The National Natural Science Foundation of China (11774054, 12075036, 12104067); the Science and Technology Research Project of Education Department of Hubei Province (Q20211314).

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s Note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations or those of the publisher, the editors, and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

Acknowledgments

XD thanks Chun Meng, Yi Song, and Tong Zhang for helpful discussions.

References

1. Arita Y, Chen M, Wright EM, Dholakia K. Dynamics of a Levitated Microparticle in Vacuum Trapped by a Perfect Vortex Beam: Three-Dimensional Motion Around a Complex Optical Potential. J Opt Soc Am B (2017) 34:C14–C19. doi:10.1364/josab.34.000c14

CrossRef Full Text | Google Scholar

2. Liang Y, Lei M, Yan S, Li M, Cai Y, Wang Z, et al. Rotating of Low-Refractive-index Microparticles with a Quasi-Perfect Optical Vortex. Appl Opt (2018) 57:79–84. doi:10.1364/AO.57.000079

PubMed Abstract | CrossRef Full Text | Google Scholar

3. Yan H, Zhang E, Zhao B, Duan K. Free-space Propagation of Guided Optical Vortices Excited in an Annular Core Fiber. Opt Express (2012) 20:17904–15. doi:10.1364/OE.20.017904

PubMed Abstract | CrossRef Full Text | Google Scholar

4. Li S, Wang J. Multi-orbital-angular-momentum Multi-Ring Fiber for High-Density Space-Division Multiplexing. IEEE Photon J (2013) 5:7101007. doi:10.1109/jphot.2013.2272778

CrossRef Full Text | Google Scholar

5. Leach J, Jack B, Romero J, Jha A, Yao A, Franke-Arnold S, et al. Quantum Correlations in Optical Angle-Orbital Angular Momentum Variables. Science (2010) 329:662–5. doi:10.1126/science.1190523

PubMed Abstract | CrossRef Full Text | Google Scholar

6. Fickler R, Lapkiewicz R, Plick W, Krenn M, Schaeff C, Ramelow S, et al. Quantum Entanglement of High Angular Momenta. Science (2012) 338:640–3. doi:10.1126/science.1227193

PubMed Abstract | CrossRef Full Text | Google Scholar

7. Ding D, Zhou Z, Shi B, Guo G. Single-photon-level Quantum Image Memory Based on Cold Atomic Ensembles. Nat Commun (2013) 4:2527. doi:10.1038/ncomms3527

PubMed Abstract | CrossRef Full Text | Google Scholar

8. Nicolas A, Veissier L, Giner L, Giacobino E, Maxein D, Laurat J. Quantum Memory for Orbital Angular Momentum Photonic Qubits. Nat Photon (2014) 8:234–8. doi:10.1038/nphoton.2013.355

CrossRef Full Text | Google Scholar

9. Parigi V, D’Ambrosio V, Arnold C, Marrucci L, Sciarrino F, Laurat J. Storage and Retrieval of Vector Beams of Light in a Multiple-Degree-Of-freedom Quantum Memory. Nat Commun (2015) 6:706. doi:10.1038/ncomms8706

CrossRef Full Text | Google Scholar

10. Wang X, Luo Y, Huang H, Chen M, Su Z, Liu C, et al. 18-qubit Entanglement with Six Photons’ Three Degrees of freedom. Phys Rev Lett (2018) 120:260502. doi:10.1103/PhysRevLett.120.260502

PubMed Abstract | CrossRef Full Text | Google Scholar

11. Luo Y, Zhong H, Erhard M, Wang X, Peng L, Krenn M, et al. Quantum Teleportation in High Dimensions. Phys Rev Lett (2019) 123:070505. doi:10.1103/PhysRevLett.123.070505

PubMed Abstract | CrossRef Full Text | Google Scholar

12. Pan X, Yu S, Zhou Y, Zhang K, Zhang K, Lv S, et al. Orbital-angular-momentum Multiplexed Continuous-Variable Entanglement from Four-Wave Mixing in Hot Atomic Vapor. Phys Rev Lett (2019) 123:070506. doi:10.1103/PhysRevLett.123.070506

PubMed Abstract | CrossRef Full Text | Google Scholar

13. Zhang S, Zhou Y, Mei Y, Liao K, Wen Y, Li J, et al. δ-Quench Measurement of a Pure Quantum-State Wave Function. Phys Rev Lett (2019) 123:190402. doi:10.1103/PhysRevLett.123.190402

PubMed Abstract | CrossRef Full Text | Google Scholar

14. Li S, Pan X, Ren Y, Liu H, Yu S, Jing J. Deterministic Generation of Orbital-Angular-Momentum Multiplexed Tripartite Entanglement. Phys Rev Lett (2020) 124:083605. doi:10.1103/PhysRevLett.124.083605

PubMed Abstract | CrossRef Full Text | Google Scholar

15. Zhang K, Wang W, Liu S, Pan X, Du J, Lou Y, et al. Reconfigurable Hexapartite Entanglement by Spatially Multiplexed Four-Wave Mixing Processes. Phys Rev Lett (2020) 124:090501. doi:10.1103/PhysRevLett.124.090501

PubMed Abstract | CrossRef Full Text | Google Scholar

16. Liu S, Lou Y, Jing J. Orbital Angular Momentum Multiplexed Deterministic All-Optical Quantum Teleportation. Nat Commun (2020) 11:3875. doi:10.1038/s41467-020-17616-4

PubMed Abstract | CrossRef Full Text | Google Scholar

17. Allen L, Beijersbergen MW, Spreeuw RJC, Woerdman JP. Orbital Angular Momentum of Light and the Transformation of Laguerre-Gaussian Laser Modes. Phys Rev A (1992) 45:8185–9. doi:10.1103/physreva.45.8185

PubMed Abstract | CrossRef Full Text | Google Scholar

18. Padgett M, Courtial J, Allen L. Light’s Orbital Angular Momentum. Phys Today (2004) 57:35–40. doi:10.1063/1.1768672

CrossRef Full Text | Google Scholar

19. Molina-Terriza G, Torres J, Torner L. Twisted Photons. Nat Phys (2007) 3:305–10. doi:10.1038/nphys607

CrossRef Full Text | Google Scholar

20. Allen L, Padgett MJ, Babiker M. Iv the Orbital Angular Momentum of Light. Prog Opt (1999) 39:291–372. doi:10.1016/S0079-6638(08)70391-3

CrossRef Full Text | Google Scholar

21. Gori F, Guattari G, Padovani C. Bessel-gauss Beams. Opt Commun (1987) 64:491–5. doi:10.1016/0030-4018(87)90276-8

CrossRef Full Text | Google Scholar

22. Sepulveda K, Chávez V, Cerda S, Arlt J, Dholakia K. Orbital Angular Momentum of a High-Order Bessel Light Beam. J Opt B Quan Semiclass. Opt (2002) 4:S82. doi:10.1088/1464-4266/4/2/373

CrossRef Full Text | Google Scholar

23. Ostrovsky A, Rickenstorff-Parrao C, Arrizón V. Generation of the “Perfect” Optical Vortex Using a Liquid-crystal Spatial Light Modulator. Opt Lett (2013) 38:534–6. doi:10.1364/OL.38.000534

PubMed Abstract | CrossRef Full Text | Google Scholar

24. Kotlyar V, Kovalev A, Porfirev A. Optimal Phase Element for Generating a Perfect Optical Vortex. J Opt Soc Am (2016) 33:2376–84. doi:10.1364/JOSAA.33.002376

CrossRef Full Text | Google Scholar

25. Karahroudi M, Parmoon B, Qasemi M, Mobashery A, Saghafifar H. Generation of Perfect Optical Vortices Using a Bessel-Gaussian Beam Diffracted by Curved fork Grating. Appl Opt (2017) 56:5817–23. doi:10.1364/AO.56.005817

PubMed Abstract | CrossRef Full Text | Google Scholar

26. Jabir M, Chaitanya NA, Aadhi A, Samanta G. Generation of “Perfect” Vortex of Variable Size and its Effect in Angular Spectrum of the Down-Converted Photons. Sci Rep (2016) 6:21977. doi:10.1038/srep21877

PubMed Abstract | CrossRef Full Text | Google Scholar

27. Garcia-Garcia J, Rickenstorff-Parrao C, Ramos-Garcia R, Arrizon V, Ostrovsky A. Simple Technique for Generating the Perfect Optical Vortex. Opt Lett (2014) 39:5305–8. doi:10.1364/OL.39.005305

PubMed Abstract | CrossRef Full Text | Google Scholar

28. Vaity P, Rusch L. Perfect Vortex Beam: Fourier Transformation of a Bessel Beam. Opt Lett (2015) 40:597–600. doi:10.1364/OL.40.000597

PubMed Abstract | CrossRef Full Text | Google Scholar

29. Du Y, Liu D, Fu S, Wang Y, Qin Y. Reconfigurable Generation of Double-Ring Perfect Vortex Beam. Opt Express (2021) 29:17353–64. doi:10.1364/OE.424664

PubMed Abstract | CrossRef Full Text | Google Scholar

30. Guo Z, Liu H, Xiang L, Chen L, Yang J, Wen J, et al. Generation of Perfect V Ortex Beams with Polymer-Based Phase Plate. IEEE Photon Technol Lett (2020) 32:565–8. doi:10.1109/LPT.2020.2985745

CrossRef Full Text | Google Scholar

31. Dai K, Miller J, Li W, Watkins R, Johnson E. Fractional Orbital Angular Momentum Conversion in Second-Harmonic Generation with an Asymmetric Perfect Vortex Beam. Opt Lett (2021) 46:3332–5. doi:10.1364/OL.428859

PubMed Abstract | CrossRef Full Text | Google Scholar

32. Zhou Q, Liu M, Zhu W, Chen L, Ren Y, Lezec H, et al. Generation of Perfect Vortex Beams by Dielectric Geometric Metasurface for Visible Light. Laser Photon Rev (2021) 15:2100390. doi:10.1002/lpor.202100390

CrossRef Full Text | Google Scholar

33. Ma H, Li X, Tai Y, Li H, Wang J, Tang M, et al. In Situ measurement of the Topological Charge of a Perfect Vortex Using the Phase Shift Method. Opt Lett (2017) 42:135–8. doi:10.1364/OL.42.000135

PubMed Abstract | CrossRef Full Text | Google Scholar

34. Pinnell J, Rodríguez-Fajardo V, Forbes A. Quantitative Orbital Angular Momentum Measurement of Perfect Vortex Beams. Opt Lett (2019) 44:2736–9. doi:10.1364/ol.44.002736

CrossRef Full Text | Google Scholar

35. Chu C, Gao S, Liu Z, Tu J, Yang J, Hao C, et al. Hybrid Angular Gradient Phase Grating for Measuring the Orbital Angular Momentum of Perfect Optical Vortex Beams. IEEE Photon J (2020) 12:1. doi:10.1109/jphot.2020.2986266

CrossRef Full Text | Google Scholar

36. Jiang X, Li J, Sun X. Two-dimensional Atom Localization Based on Coherent Field Controlling in a Five-Level M-type Atomic System. Opt Express (2017) 25:31678–87. doi:10.1364/OE.25.031678

PubMed Abstract | CrossRef Full Text | Google Scholar

37. Tian Y, Wang X, Yang W, Shui T, Li L, Li X, et al. High-precision Three Dimensional Atom Localization via Multiphoton Quantum Destructive Interference. Opt Express (2020) 28:25308–18. doi:10.1364/OE.396973

PubMed Abstract | CrossRef Full Text | Google Scholar

38. Zhou F, Qi Y, Sun H, Chen D, Yang J, Niu Y, et al. Electromagnetically Induced Grating in Asymmetric Quantum wells via Fano Interference. Opt Express (2013) 21:12249–59. doi:10.1364/oe.21.012249

PubMed Abstract | CrossRef Full Text | Google Scholar

39. Che J, Zhao P, Ma D, Zhang Y. Kerr-nonlinearity-modulated Dressed Vortex Four-Wave Mixing from Photonic Band gap. Opt Express (2020) 28:18343–50. doi:10.1364/oe.395426

PubMed Abstract | CrossRef Full Text | Google Scholar

40. Radwell N, Clark T, Piccirillo B, Barnett S, Franke-Arnold S. Spatially Dependent Electromagnetically Induced Transparency. Phys Rev Lett (2015) 114:123603. doi:10.1103/PhysRevLett.114.123603

PubMed Abstract | CrossRef Full Text | Google Scholar

41. Han L, Cao M, Liu R, Liu H, Guo W, Wei D, et al. Identifying the Orbital Angular Momentum of Light Based on Atomic Ensembles. EPL (2012) 99:34003. doi:10.1209/0295-5075/99/34003

CrossRef Full Text | Google Scholar

42. Wang L, Zhang X, Li A, Kang Z, Wang H, Gao J. Controlled-Not Gate with Orbital Angular Momentum in a Rare-Earth-Ion-Doped Solid. J Lumin (2020) 228:117628. doi:10.1016/j.jlumin.2020.117628

CrossRef Full Text | Google Scholar

43. Hamedi H, Yannopapas V, Paspalakis E. Spatially Structured Optical Effects in a Four-Level Quantum System Near a Plasmonic Nanostructure. Ann Phys (2021) 533:2100117. doi:10.1002/andp.202100117

CrossRef Full Text | Google Scholar

44. Rahmatullah, , Abbas M, Ziauddin, , Qamar S. Spatially Structured Transparency and Transfer of Optical Vortices via Four-Wave Mixing in a Quantum-Dot Nanostructure. Phys Rev A (2020) 101:023821. doi:10.1103/PhysRevA.101.023821

CrossRef Full Text | Google Scholar

45. Mahdavi M, Sabegh Z, Hamedi H, Mahmoudi M. Orbital Angular Momentum Transfer in Molecular Magnets. Phys Rev B (2021) 104:094432. doi:10.1103/PhysRevB.104.094432

CrossRef Full Text | Google Scholar

46. Hamedi H, Kudriasov V, Ruseckas J, Juzeliunas G. Azimuthal Modulation of Electromagnetically Induced Transparency Using Structured Light. Opt Express (2018) 26:28249–62. doi:10.1364/OE.26.028249

PubMed Abstract | CrossRef Full Text | Google Scholar

47. Dai X, Hao X, Jin R, Peng C, Ding C. Controllable Probe Absorption Spectrum via Vortex Beams Excitation in a Cascaded Atomic System. J Appl Phys (2021) 129:224303. doi:10.1063/5.0050488

CrossRef Full Text | Google Scholar

48. Jia N, Qian J, Kirova T, Juzeliunas G, Hamedi H. Ultraprecise Rydberg Atomic Localization Using Optical Vortices. Opt Express (2020) 28:36936–52. doi:10.1364/OE.411130

PubMed Abstract | CrossRef Full Text | Google Scholar

49. Yu C, Wang Z. Engineering Helical Phase via Four-Wave Mixing in the Ultraslow Propagation Regime. Phys Rev A (2021) 103:013518. doi:10.1103/PhysRevA.103.013518

CrossRef Full Text | Google Scholar

50. Qiu J, Wang Z, Ding D, Huang Z, Yu B. Control of Space-dependent Four-Wave Mixing in a Four-Level Atomic System. Phys Rev A (2020) 102:033516. doi:10.1103/PhysRevA.102.033516

CrossRef Full Text | Google Scholar

51. Hamedi H, Ruseckas J, Juzeliūnas G. Exchange of Optical Vortices Using an Electromagnetically-Induced-Transparency–Based Four-Wave-Mixing Setup. Phys Rev A (2018) 98:013840. $\\bar{\\mathrm{u}}$. doi:10.1103/physreva.98.013840

CrossRef Full Text | Google Scholar

52. Hong Y, Wang Z, Ding D, Yu B. Ultraslow Vortex Four-Wave Mixing via Multiphoton Quantum Interference. Opt Express (2019) 27:29863–74. doi:10.1364/OE.27.029863

PubMed Abstract | CrossRef Full Text | Google Scholar

53. Chen J, Wang Z, Yu B. Spatially Dependent Hyper-Raman Scattering in Five-Level Cold Atoms. Opt Express (2021) 29:10914–22. doi:10.1364/oe.420015

PubMed Abstract | CrossRef Full Text | Google Scholar

54. Qiu J, Wang Z, Ding D, Li W, Yu B. Highly Efficient Vortex Four-Wave Mixing in Asymmetric Semiconductor Quantum wells. Opt Express (2020) 28:2975–86. doi:10.1364/OE.379245

PubMed Abstract | CrossRef Full Text | Google Scholar

55. Zhang Y, Wang Z, Qiu J, Hong Y, Yu B. Spatially Dependent Four-Wave Mixing in Semiconductor Quantum wells. Appl Phys Lett (2019) 115:171905. doi:10.1063/1.5121275

CrossRef Full Text | Google Scholar

56. Wang Z, Zhang Y, Paspalakis E, Yu B. Efficient Spatiotemporal-Vortex Four-Wave Mixing in a Semiconductor Nanostructure. Phys Rev A (2020) 102:063509. doi:10.1103/PhysRevA.102.063509

CrossRef Full Text | Google Scholar

57. Sun H, Fan S, Zhang H, Gong S. Tunneling-induced High-Efficiency Four-Wave Mixing in Asymmetric Quantum wells. Phys Rev B (2013) 87:235310. doi:10.1103/PhysRevB.87.235310

CrossRef Full Text | Google Scholar

58. Sun D, Zhang H, Sun H, Li X, Li H. Tunneling-induced Highly Efficient Four-Wave Mixing in Asymmetric Double Quantum wells. Laser Phys Lett (2018) 15:045208. doi:10.1088/1612-202X/aaa9c8

CrossRef Full Text | Google Scholar

59. Schmidt H, Campman K, Gossard A, Imamolu A. Tunneling Induced Transparency: Fano Interference in Intersubband Transitions. Appl Phys Lett (1997) 70:3455–7. doi:10.1063/1.119199

CrossRef Full Text | Google Scholar

60. Shih T, Reimann K, Woerner M, Elsaesser T, Waldmüller I, Knorr A, et al. Nonlinear Response of Radiatively Coupled Intersubband Transitions of Quasi-Two-Dimensional Electrons. Phys Rev B (2005) 72:195338. doi:10.1103/physrevb.72.195338

CrossRef Full Text | Google Scholar