Results on Resistance Distance and Kirchhoff Index of Graphs With Generalized Pockets

F, H_v are considered simple connected graphs on n and m + 1 vertices, and v is a specified vertex of H_v and u₁, u₂, … u_k ∈ F. The graph G = G[F, u₁, … , u_k, H_v] is called a graph with k pockets, obtained by taking one copy of F and k copies of H_v and then attaching the ith copy of H_v to the vertex u_i, i = 1, … , k, at the vertex v of H_v. In this article, the closed-form formulas of the resistance distance and the Kirchhoff index of G = G[F, u₁, … , u_k, H_v] are obtained in terms of the resistance distance and Kirchhoff index F and H_v.

1 Introduction

All graphs considered in this article are simple and undirected. The resistance distance between vertices u and v of G was defined by Klein and Randi$\acute{c}$ [1] to be the effective resistance between nodes u and v as computed with Ohm’s law when all the edges of G are considered to be unit resistors. The Kirchhoff index Kf(G) was defined in Ref. 1 as Kf(G) = ∑_u<vr_uv, where r_uv(G) denotes the resistance distance between u and v in G. Resistance distance are, in fact, intrinsic to the graph, with some nice purely mathematical interpretations and other interpretations. The Kirchhoff index was introduced in chemistry as a better alternative to other parameters used for discriminating different molecules with similar shapes and structures [1]. The resistance distance and Kirchhoff index have attracted extensive attention due to their wide applications in physics, chemistry, and other fields. Until now, many results on the resistance distance and Kirchhoff index are obtained. The references in [2–5] can be referred to know more. However, the resistance distance and Kirchhoff index of the graph is, in general, a difficult thing from the computational point of view. The bigger the graph, the more difficult it is to compute the resistance distance and Kirchhoff index; so a common strategy is to consider a complex graph as a composite graph and to find relations between the resistance distance and Kirchhoff index of the original graphs. Let G = (V(G), E(G)) be a graph with the vertex set V(G) and edge set E(G). Let d_i be the degree of vertex i in G and D_G = diag (d₁, d₂, ⋯d_|V(G)|) the diagonal matrix with all vertex degrees of G as its diagonal entries. For graph G, let A_G and B_G denote the adjacency matrix and vertex-edge incidence matrix of G, respectively. The matrix L_G = D_G − A_G is called the Laplacian matrix of G, where D_G is the diagonal matrix of vertex degrees of G. We use μ₁(G) ≥ u₂(G) ≥⋯ ≥ μ_n(G) = 0 to denote the spectrum of L_G. For other undefined notations and terminology from graph theory, the readers may refer to Ref. 6 and the references therein [7–23]. The computation of the resistance distance between two nodes in a resistor network is a classical problem in electric theory and graph theory. For certain families of graphs, it is possible to identify a graph by looking at the resistance distance and Kirchhoff index. More generally, this is not possible. In some cases, the resistance distance and Kirchhoff index of a relatively larger graph can be described in terms of the resistance distance and Kirchhoff index of some smaller (and simpler) graphs using some simple graph operations. There are results that discuss the resistance distance and Kirchhoff index of graphs obtained using some operations on graphs, such as join, graph products, corona, and many variants of corona, such as edge corona and neighborhood corona. For such operations, it is possible to describe the resistance distance and Kirchhoff index of the resulting graph using the resistance distance and Kirchhoff index of the corresponding constituting graph; Refs. 14 and 15 can be referred for reference. This article considers the resistance distance and Kirchhoff index of the graph operations as follows, obtained from Ref. 11.

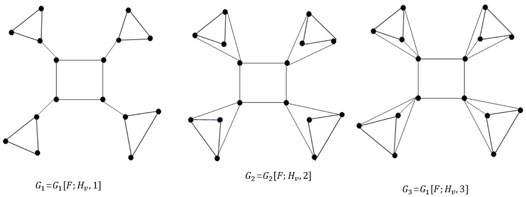
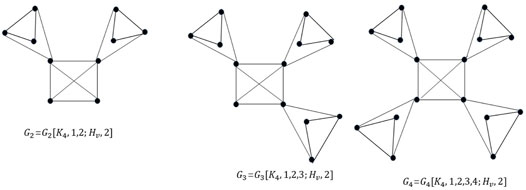
Definition 1. [11]: Let F, H_v be connected graphs, v be a specified vertex of H_v and u₁, u₂, … , u_k ∈ F. Let G = G[F, u₁, u₂, … , u_k, H_v] be the graph obtained by taking one copy of F and k copies of H_v and then attaching the ith copy of H_v to the vertex u_i, i = 1, 2, … , k, at the vertex v of H_v(identify u_i with the vertex v of the ith copy). Then, the copies of the graph H_v that are attached to the vertices u_i, i = 1, 2, … , k are referred to as pockets, and G is described as a graph with k pockets.Barik [11] has described the Laplacian spectrum of G = G [F, u₁, u₂, … , u_k, H_v] using the Laplacian spectrum of F and H_v in a particular case when deg(v) = m. Recently, Barik and Sahoo [12] have described the Laplacian spectrum of more such graphs’ relaxing condition deg(v) = m. Let deg(v) = l, 1 ≤ l ≤ m. In this case, we denoted G = G [F, u₁, u₂, … , u_k, H_v] more precisely by G = G [F, u₁, u₂, … , u_k; H_v, l]. When k = n, we denoted simply by G = G [F; H_v, l]. If deg(v) = l, 1 ≤ l ≤ m, let N(v) = {v₁, v₂, … , v_l} ⊂ V(H_v) be the neighborhood set of v in H_v. Let H₁ be the subgraph of H_v induced by the vertices in N(v) and H₂ be the subgraph of H_v induced by the vertices which are in V(H_v)\(N(v) ∪ {v}). When H_v = H₁ ∨ (H₂ + {v}), we described the resistance distance and Kirchhoff index of G = G[F, u₁, u₂, … , u_k, H_v]. The graphs F = C₄ and H − v = C₃ are considered. Taking l = 1, 2 and 3, we obtained graphs G₁ = G₁ [F; H_v, 1], G₂ = G₂ [F; H_v, 2], and G₃ = G₃ [F; H_v, 3], respectively. Figure 1 is referred. In this case, we described the resistance distance and Kirchhoff index of G = G [F; H_v, l] in terms of the resistance distance and Kirchhoff index of F and H_v. The results are contained in Section 3 of this article. Furthermore, when F = F₁ ∨ F₂, F₁ is the subgraph of F induced by the vertices u₁, u₂, … , u_k and F₂ is the subgraph of F induced by the vertices u_k+1, u_k+2, … , u_n. The considered three graphs G₂, G₃, and G₄ are shown in Figure 2, obtained from the two graphs F = K₄ and H_v such that H_v \{v} = K₃. It is observed that F = K₁ ∨ K₃, G₂, G₃, and G₄ are graphs with 2, 3, and 4 pockets, respectively. Figure 2 can be referred. In this case, we described the resistance distance and Kirchhoff index of G[F, u₁, u₂, … , u_k; H_v, l] in terms of the resistance distance and Kirchhoff index of F and H_v. These results are contained in Section 4.

FIGURE 1

FIGURE 1. [F; H_v, l] for different l.

FIGURE 2

FIGURE 2. Graphs having different numbers of pockets.

2 Preliminaries

The {1}-inverse of M is a matrix X such that MXM = M. If M is singular, then it has infinite {1}-inverse [16]. For a square matrix M, the group inverse of M, denoted by M^#, is the unique matrix X such that MXM = M, XMX = X, and MX = XM. It is known that M^# exists if and only if rank(M) = rank(M²) [16, 17]. If M is really symmetric, then M^# exists, and M^# is a symmetric {1}-inverse of M. Actually, M^# is equal to the Moore–Penrose inverse of M since M is symmetric [17].

It is known that the resistance distance in a connected graph G can be obtained from any {1}- inverse of G [13]. We used M⁽¹⁾ to denote any {1}-inverse of a matrix M, and (M)_uv denotes the (u, v)-entry of M.

Lemma 2.1. [17]: Let G be a connected graph, then

$\begin{array}{cc}\hfill r_{uv}\left(G\right)\hfill & \hfill ={\left(L_G^{\left(1\right)}\right)}_{uu}+{\left(L_G^{\left(1\right)}\right)}_{vv}-{\left(L_G^{\left(1\right)}\right)}_{uv}-{\left(L_G^{\left(1\right)}\right)}_{vu}\\ \hfill \hfill & \hfill ={\left(L_G^{\#}\right)}_{uu}+{\left(L_G^{\#}\right)}_{vv}-2{\left(L_G^{\#}\right)}_{uv}.\end{array}$

Let 1_n denote the column vector of dimension n with all the entries equal to one. We often use 1 to denote all-ones column vector if the dimension can be read from the context.

Lemma 2.2. [14]: For any graph, we have $L_G^{\#}1=0$.

Lemma 2.3. [18]: Let

$\begin{array}{c}\hfill M=\left(\begin{array}{cc}\hfill A\hfill & \hfill B\hfill \\ \hfill C\hfill & \hfill D\hfill \end{array}\right)\hfill \end{array}$

be a nonsingular matrix. If A and D are nonsingular, then

$\begin{array}{cc}\hfill M^{-1}\hfill & \hfill =\left(\begin{array}{cc}\hfill A^{-1}+A^{-1}B{S}^{-1}C{A}^{-1}\hfill & \hfill -A^{-1}B{S}^{-1}\hfill \\ \hfill -S^{-1}C{A}^{-1}\hfill & \hfill S^{-1}\hfill \end{array}\right)\\ \hfill \hfill & \hfill =\left(\begin{array}{cc}\hfill {\left(A-B{D}^{-1}C\right)}^{-1}\hfill & \hfill -A^{-1}B{S}^{-1}\hfill \\ \hfill -S^{-1}C{A}^{-1}\hfill & \hfill S^{-1}\hfill \end{array}\right),\end{array}$

where S = D − CA⁻¹B.

Lemma 2.4. [15]: Let L be the Laplacian matrix of a graph of order n. For any a > 0, we have

${\left(L+a{I}_n-\frac{a}{n}{J}_{n\times n}\right)}^{\#}={\left(L+aI\right)}^{-1}-\frac{1}{an}{J}_{n\times n}.$

Lemma 2.5. [5]: Let G be a connected graph on n vertices, then

$Kf\left(G\right)=ntr\left(L_G^{\left(1\right)}\right)-1^T{L}_G^{\left(1\right)}1=ntr\left(L_G^{\#}\right).$

Lemma 2.6. [19]: Let

$\begin{array}{c}\hfill L=\left(\begin{array}{cc}\hfill A\hfill & \hfill B\hfill \\ \hfill B^T\hfill & \hfill D\hfill \end{array}\right)\hfill \end{array}$

be the Laplacian matrix of a connected graph. If D is nonsingular, then

$\begin{array}{c}\hfill X=\left(\begin{array}{cc}\hfill H^{\#}\hfill & \hfill -H^{\#}B{D}^{-1}\hfill \\ \hfill -D^{-1}{B}^T{H}^{\#}\hfill & \hfill D^{-1}+D^{-1}{B}^T{H}^{\#}B{D}^{-1}\hfill \end{array}\right)\hfill \end{array}$

is a symmetric {1}-inverse of L, where H = A− BD⁻¹B^T.

3 The Resistance Distance and Kirchhoff Index of G [F; H_v, l]

Let F be a connected graph with the vertex set {u₁, u₂, … , u_n}. Let H_v be a connected graph on m + 1 vertices with a specified vertex v and V(H_v) = {v₁, v₂, … , v_m, v}. Let G = G[F; H_v, l]. It is noted that G has n(m + 1) vertices. Let deg(v) = l, 1 ≤ l ≤ m. With loss of generality, it is assumed that N(v) = {v₁, v₂, … , v_l}. Let H₁ be the subgraph of H_v induced by the vertices in {v₁, v₂, … , v_l} and H₂ be the subgraph of H_v induced by the vertices {v_l+1, v_l+2, … , v_m}. It is supposed that H_v = H₁ ∨ (H₂ + {v}). In this section, we focused on determining the resistance distance and Kirchhoff index of G[F; H_v, l] in terms of the resistance distance and Kirchhoff index of F, H₁ and H₂.

Theorem 3.1. Let G [F; H_v, l] be the graph, as described previously. It is supposed that H_v = H₁ ∨ (H₂ + {v}). Let the Laplacian spectrum of H₁ and H₂ be σ(H₁) = (0 = μ₁, μ₂, … μ_l) and σ(H₂) = (0 = ν₁, ν₂, … ν_m−l). Then, G [F; H_v, l] has the resistance distance and Kirchhoff index as follows:

(i) For any i, j ∈ V(F), we obtained

$r_{ij}\left(G\left[F;H_v,l\right]\right)={\left(L^{\#}\left(F\right)\right)}_{ii}+{\left(L^{\#}\left(F\right)\right)}_{jj}-2{\left(L^{\#}\left(F\right)\right)}_{ij}=r_{ij}\left(F\right).$

(ii) For any i ∈ V(F) and j ∈ V(H₁), we obtained

$\begin{array}{ccc}\hfill r_{ij}\left(G\left[F;H_v,l\right]\right)& =\hfill & {\left(L^{\#}\left(F\right)\right)}_{ii}+\left[{\left(L\left(H_1\right)+\left(m-l+1\right)I_l-\frac{m-l}{l}{J}_{l\times l}\right)}^{-1}\otimes I_n+\right.\hfill \\ \hfill & \hfill & {\left.\left(1_l\otimes I_n\right)L^{\#}\left(F\right)\left(1_l^T\otimes I_n\right)\right]}_{jj}-2L^{\#}\left(F\right){\left(1_l^T\otimes I_n\right)}_{ij}.\hfill \end{array}$

(iii) For any i ∈ V(F) and j ∈ V(H₂), we obtained

$\begin{array}{ll}\hfill r_{ij}\left(G\left[F;H_v,l\right]\right)=& {\left(L^{\#}\left(F\right)\right)}_{ii}+{\left[{\left(L\left(H_2\right)+l{I}_{m-l}-\frac{l}{m-l+1}{J}_{\left(m-l\right)\times \left(m-l\right)}\right)}^{-1}\otimes I_n\right]}_{jj}\hfill \\ \hfill & -2{\left(L^{\#}\left(F\right)\right)}_{ij}.\hfill \end{array}$

(iv) For any i ∈ V(H₁) and j ∈ V(H₂), we obtained

$\begin{array}{ccc}\hfill r_{ij}\left(G\left[F;H_v,l\right]\right)& =\hfill & {\left[{\left(L\left(H_1\right)+\left(m-l+1\right)I_l-\frac{m-l}{l}{J}_{l\times l}\right)}^{-1}\otimes I_n\right]}_{ii}+\hfill \\ \hfill & \hfill & \left[{\left(L\left(H_2\right)+l{I}_{m-l}-\frac{l}{m-l+1}{J}_{\left(m-l\right)\times \left(m-l\right)}\right)}^{-1}{\left.\otimes I_n\right]}_{jj}\right.\hfill \\ \hfill & \hfill & {\left.-2\left[{(L\left(H_1\right)+\left(m-l+1\right)I_l-\frac{m-l}{l}{J}_{l\times l})}^{-1}\otimes I_n\right.\right]}_{ij}.\hfill \end{array}$

(v) For any i ∈ V(H₂) and j ∈ V(H₁), we obtained

$\begin{array}{ccc}\hfill r_{ij}\left(G\left[F;H_v,l\right]\right)& =\hfill & {\left[{\left(L\left(H_2\right)+l{I}_{m-l}-\frac{l}{m-l+1}{J}_{\left(m-l\right)\times \left(m-l\right)}\right)}^{-1}\otimes I_n\right]}_{ii}\hfill \\ \hfill & \hfill & +\left[{\left(L\left(H_1\right)+\left(m-l+1\right)I_l-\frac{m-l}{l}{J}_{l\times l}\right)}^{-1}{\left.\otimes I_n\right]}_{jj}-2\right.\hfill \\ \hfill & \hfill & {\left.\left[{\left(L\left(H_2\right)+l{I}_{m-l}-\frac{l}{m-l+1}{J}_{\left(m-l\right)\times \left(m-l\right)}\right)}^{-1}\otimes I_n\right.\right]}_{ij}.\hfill \end{array}$

(vi) Let

$\begin{array}{ccc}\hfill Kf\left(G\left[F;H_v,l\right]\right)& =\hfill & n\left(m+1\right)\left(\frac{m+1}{n}Kf\left(F\right)+\left(n\sum _{i=2}^l\frac{1}{{\mu }_i\left(H_1\right)+\left(m-l+1\right)}+n\right)\right.\hfill \\ \hfill & \hfill & \left.+\left(n\sum _{i=2}^{m-l}\frac{1}{{\nu }_i\left(H_2\right)+l}+\frac{nl}{m-l+1}\right)\right)-\left({\left(m-l\right)}^2\frac{m-l+1}{l}+l^2\right).\hfill \end{array}$

Proof: Let $v_j^i$ denote the jth vertex of H in the ith copy of H_v in G, for i = 1, 2, … , n; j = 1, 2, … , m, and let $V_j(H_v)=\{v_j^1,v_j^2,\dots ,v_j^n\}$. Then, $V(F)\cup ({\cup }_{j=1}^m{V}_j(H_v))$ is a partition of V(G). Using this partition, the Laplacian matrix of G = G[F; H_v, l] can be expressed as

$\begin{array}{c}\hfill L\left(G\left[F;H_v,l\right]\right)=\left(\begin{array}{ccc}\hfill L\left(F\right)+l{I}_n\hfill & \hfill -1_l^T\otimes I_n\hfill & \hfill 0\hfill \\ \hfill -1_l\otimes I_n\hfill & \hfill \left(L\left(H_1\right)+\left(m-l+1\right)I_l\right)\otimes I_n\hfill & \hfill -J_{l\times \left(m-l\right)}\otimes I_n\hfill \\ \hfill 0\hfill & \hfill -J_{\left(m-l\right)\times l}\otimes I_n\hfill & \hfill \left(L\left(H_2\right)+l{I}_{m-l}\right)\otimes I_n\hfill \end{array}\right).\hfill \end{array}$

We began with the computation of {1}-inverse of the Laplacian matrix L(G) of G = G[F; H_v, l]. Let A = L(F) + lI_n, $B=\left(\begin{array}{cc}\hfill -1_l^T\otimes I_n\hfill & \hfill 0\hfill \end{array}\right)$, $B^T=\left(\begin{array}{cc}\hfill -1_l\otimes I_n\hfill & \hfill \hfill \\ \hfill 0\hfill \end{array}\right)$ and

$\begin{array}{c}\hfill D=\left(\begin{array}{cc}\hfill \left(L\left(H_1\right)+\left(m-l+1\right)I_l\right)\otimes I_n\hfill & \hfill -J_{l\times \left(m-l\right)}\otimes I_n\hfill \\ \hfill -J_{\left(m-l\right)\times l}\otimes I_n\hfill & \hfill \left(L\left(H_2\right)+l{I}_{m-l}\right)\otimes I_n\hfill \end{array}\right)\hfill \end{array}.$

First, we computed the D⁻¹. By Lemma 2.3, we obtained

$\begin{array}{ll}\hfill A_1-B_1{D}_1^{-1}{C}_1=& \left(L\left(H_1\right)+\left(m-l+1\right)I_l\right)\otimes I_n-\left(-J_{l\times \left(m-l\right)}\otimes I_n\right)\hfill \\ \hfill & \left({\left(L\left(H_2\right)+l{I}_{m-l}\right)}^{-1}\otimes I_n\right)\left(-J_{\left(m-l\right)\times l}\otimes I_n\right)\hfill \\ \hfill =& \left(L\left(H_1\right)+\left(m-l+1\right)I_l\right)\otimes I_n-1_l\left[1_{m-l}^T\left(L\left(H_2\right)\right.\right.\hfill \\ \hfill & \left.{\left.+l{I}_{m-l}\right)}^{-1}{1}_{m-l}\right]1_l^T\otimes I_n\hfill \\ \hfill =& \left(L\left(H_1\right)+\left(m-l+1\right)I_l\right)\otimes I_n-\frac{m-l}{l}{J}_{l\times l}\otimes I_n\hfill \\ \hfill =& \left[L\left(H_1\right)+\left(m-l+1\right)I_l-\frac{m-l}{l}{J}_{l\times l}\right]\otimes I_n,\hfill \end{array}$

so

$\begin{array}{cc}\hfill {\left(A_1-B_1{D}_1^{-1}{C}_1\right)}^{-1}\hfill & \hfill ={\left[\left(L\left(H_1\right)\right.+\left(m-l+1\right)I_l-\frac{m-l}{l}{J}_{l\times l}\right]}^{-1}\otimes I_n\end{array}.$

By Lemma 2.3, we obtained

$\begin{array}{ll}\hfill S^{-1}=& {\left(D_1-C_1{A}_1^{-1}{B}_1\right)}^{-1}\hfill \\ \hfill =& \left[\left(L\left(H_2\right)+l{I}_{m-l}\right)\otimes I_n-\left(-J_{\left(m-l\right)\times l}\otimes I_n\right)\left({\left(L\left(H_1\right)+\left(m-l+1\right)I_l\right)}^{-1}\otimes I_n\right)\right.\hfill \\ \hfill & {\left.\left(-J_{l\times \left(m-l\right)}\otimes I_n\right)\right]}^{-1}\hfill \\ \hfill =& {\left[\left(L\left(H_2\right)+l{I}_{m-l}\right)\otimes I_n-\left(J_{\left(m-l\right)\times l}{\left(L\left(H_1\right)+\left(m-l+1\right)I_l\right)}^{-1}{J}_{l\times \left(m-l\right)}\right)\otimes I_n\right]}^{-1}\hfill \\ \hfill =& {\left(L\left(H_2\right)+l{I}_{m-l}-\frac{l}{m-l+1}{J}_{\left(m-l\right)\times \left(m-l\right)}\right)}^{-1}\otimes I_n.\hfill \end{array}$

By Lemma 2.3, we obtained

$\begin{array}{ll}\hfill -A_1^{-1}{B}_1{S}^{-1}=& -\left[{\left(L\left(H_1\right)+\left(m-l+1\right)I_l\right)}^{-1}\otimes I_n\right]\left(-J_{l\times \left(m-l\right)}\otimes I_n\right)\hfill \\ \hfill & {\left[L\left(H_2\right)+l{I}_{m-l}-\frac{l}{m-l+1}{J}_{\left(m-l\right)\times \left(m-l\right)}\right]}^{-1}\otimes I_n\hfill \\ \hfill =& \left(\frac{1}{m-l+1}{1}_l\otimes I_n\right)\left(\frac{m-l+1}{l}{1}_{m-l}^T\otimes I_n\right)\hfill \\ \hfill =& \frac{1}{l}{J}_{l\times \left(m-l\right)}\otimes I_n.\hfill \end{array}$

Similarly, $-S^{-1}{C}_1{A}_1^{-1}={(-A_1^{-1}{B}_1{S}^{-1})}^T=\frac{1}{l}{J}_{(m-l)\times l}\otimes I_n$. So

$D^{-1}=\left(\begin{array}{cc}\hfill P_1\hfill & \hfill \frac{1}{l}{J}_{l\times \left(m-l\right)}\otimes I_n\hfill \\ \hfill \frac{1}{l}{J}_{\left(m-l\right)\times l}\otimes I_n\hfill & \hfill Q_1\hfill \end{array}\right),$

where $P_1={[\left(L(H_1)+(m-l+1)I_l-\frac{m-l}{l}{J}_{l\times l}\right.]}^{-1}\otimes I_n$, $Q_1={[(L(H_2)+l{I}_{m-l}-\frac{l}{m-l+1}{J}_{(m-l)\times (m-l)})]}^{-1}\otimes I_n$. Now, we computed the {1}-inverse of G[F; H_v, l]. By Lemma 2.6, we obtained

$\begin{array}{ll}\hfill H=& A-B{D}^{-1}{B}^T\hfill \\ \hfill =& L\left(F\right)+l{I}_n-\left(\begin{array}{cc}\hfill -1_l^T\otimes I_n\hfill & \hfill 0\hfill \end{array}\right)\left(\begin{array}{cc}\hfill P_1\hfill & \hfill \frac{1}{l}{J}_{l\times \left(m-l\right)}\otimes I_n\hfill \\ \hfill \frac{1}{l}{J}_{\left(m-l\right)\times l}\otimes I_n\hfill & \hfill Q_1\hfill \end{array}\right)\left(\begin{array}{c}\hfill -1_l\otimes I_n\hfill \\ \hfill 0\hfill \end{array}\right)\hfill \\ \hfill =& L\left(F\right)+l{I}_n-\left(1_l^T\otimes I_n\right)\left[L\left(H_1\right)+\left(m-l+1\right)I_l\right.\hfill \\ \hfill & {\left.-\frac{m-l}{l}{J}_{l\times l}\right]}^{-1}\left.\otimes I_n\right]\left(1_l\otimes I_n\right)\hfill \\ \hfill =& L\left(F\right)+l{I}_n-l{I}_n=L\left(F\right),\hfill \end{array}$

so H^# = L^#(F). According to Lemma 2.6, we calculated − H^#BD⁻¹ and − D⁻¹B^TH^#.

$\begin{array}{cc}\hfill -H^{\#}B{D}^{-1}\hfill & \hfill =-L^{\#}\left(F\right)\left(\begin{array}{cc}\hfill -1_l^T\otimes I_n\hfill & \hfill 0\hfill \end{array}\right)\left(\begin{array}{cc}\hfill P_1\hfill & \hfill \frac{1}{l}{J}_{l\times \left(m-l\right)}\otimes I_n\hfill \\ \hfill \frac{1}{l}{J}_{\left(m-l\right)\times l}\otimes I_n\hfill & \hfill Q_1\hfill \end{array}\right)\\ \hfill \hfill & \hfill =\left(L^{\#}\left(F\right)\left(1_l^T\otimes I_n\right),L^{\#}\left(F\right)\left(1_{m-l}^T\otimes I_n\right)\right)\end{array}$

and

$\begin{array}{cc}\hfill -D^{-1}{B}^T{H}^{\#}\hfill & \hfill =\left(\begin{array}{c}\hfill \left(1_l\otimes I_n\right)L^{\#}\left(F\right)\hfill \\ \hfill \left(1_{m-l}\otimes I_n\right)L^{\#}\left(F\right)\hfill \end{array}\right).\end{array}$

We are ready to compute the D⁻¹B^TH^#BD⁻¹.

$\begin{array}{ll}\hfill D^{-1}{B}^T{H}^{\#}B{D}^{-1}=& \left(\begin{array}{cc}\hfill \left(1_l\otimes I_n\right)L^{\#}\left(F\right)\hfill & \hfill \hfill \\ \hfill \left(1_{m-l}\otimes I_n\right)L^{\#}\left(F\right)\hfill & \hfill \hfill \end{array}\right)\left(\left(1_l^T\otimes I_n\right),\left(1_{m-l}^T\otimes I_n\right)\right)\hfill \\ \hfill =& \left(\begin{array}{cc}\hfill \left(1_l\otimes I_n\right)L^{\#}\left(F\right)\left(1_l^T\otimes I_n\right)\hfill & \hfill \left(1_l\otimes I_n\right)L^{\#}\left(F\right)\left(1_{m-l}^T\otimes I_n\right)\hfill \\ \hfill \left(1_{m-l}\otimes I_n\right)L^{\#}\left(F\right)\left(1_l^T\otimes I_n\right)\hfill & \hfill \left(1_{m-l}\otimes I_n\right)L^{\#}\left(F\right)\left(1_{m-l}^T\otimes I_n\right)\hfill \end{array}\right).\hfill \end{array}$

Let $P=[\left(L(H_1)+(m-l+1)I_l-\frac{m-l}{l}{J}_{l\times l}\right.]\otimes I_n$, $Q={(L(H_2)+l{I}_{m-l}-\frac{l}{m-l+1}{J}_{(m-l)\times (m-l)})}^{-1}\otimes I_n$, and $M=\frac{1}{l}{J}_{l\times (m-l)}\otimes I_n+(1_l\otimes I_n)L^{\#}(F)(1_{m-l}^T\otimes I_n)$; then, based on Lemma 2.6, the following matrix

$N=\left(\begin{array}{ccc}\hfill L^{\#}\left(F\right)\hfill & \hfill L^{\#}\left(F\right)\left(1_l^T\otimes I_n\right)\hfill & \hfill L^{\#}\left(F\right)\left(1_{m-l}^T\otimes I_n\right)\hfill \\ \hfill \left(1_l\otimes I_n\right)L^{\#}\left(F\right)\hfill & \hfill P_1\hfill & \hfill M\hfill \\ \hfill \left(1_{m-l}\otimes I_n\right)L^{\#}\left(F\right)\hfill & \hfill M^T\hfill & \hfill Q_1\hfill \end{array}\right),(1)$

is a symmetric {1}-inverse of G[F; H_v, l], where $P_1=P^{-1}+(1_l\otimes I_n)L^{\#}(F)(1_l^T\otimes I_n)$ and $Q_1=Q^{-1}+(1_{m-l}\otimes I_n)L^{\#}(F)(1_{m-l}^T\otimes I_n)$. For any i, j ∈ V(F), by Lemma 2.1 and Eq. 1, we obtained

$r_{ij}\left(G\left[F;H_v,l\right]\right)={\left(L^{\#}\left(F\right)\right)}_{ii}+{\left(L^{\#}\left(F\right)\right)}_{jj}-2{\left(L^{\#}\left(F\right)\right)}_{ij}=r_{ij}\left(F\right),$

as stated in (i). For any i ∈ V(F) and j ∈ V(H₁), by Lemma 2.1 and Eq. 1, we obtained

$\begin{array}{ccc}\hfill r_{ij}\left(G\left[F;H_v,l\right]\right)& =\hfill & {\left(L^{\#}\left(F\right)\right)}_{ii}+\left[{\left(L\left(H_1\right)+\left(m-l+1\right)I_l-\frac{m-l}{l}{J}_{l\times l}\right)}^{-1}\otimes I_n+\right.\hfill \\ \hfill & \hfill & {\left.\left(1_l\otimes I_n\right)L^{\#}\left(F\right)\left(1_l^T\otimes I_n\right)\right]}_{jj}-2L^{\#}\left(F\right){\left(1_l^T\otimes I_n\right)}_{ij},\hfill \end{array}$

as stated in (ii). For any i ∈ V(F) and j ∈ V(H₂), by Lemma 2.1 and Eq. 1, we obtained

$\begin{array}{ll}\hfill r_{ij}\left(G\left[F;H_v,l\right]\right)=& {\left(L^{\#}\left(F\right)\right)}_{ii}+{\left[{\left(L\left(H_2\right)+l{I}_{m-l}-\frac{l}{m-l+1}{J}_{\left(m-l\right)\times \left(m-l\right)}\right)}^{-1}\otimes I_n\right]}_{jj}\hfill \\ \hfill & -2{\left(L^{\#}\left(F\right)\right)}_{ij},\hfill \end{array}$

as stated in (iii). For any i ∈ V(H₁) and j ∈ V(H₂), by Lemma 2.1 and Eq. 1, we obtained

$\begin{array}{ccc}\hfill r_{ij}\left(G\left[F;H_v,l\right]\right)& =\hfill & \left[{\left(L\left(H_1\right)+\left(m-l+1\right)I_l-\frac{m-l}{l}{J}_{l\times l}\right)}^{-1}{\left.\otimes I_n\right]}_{ii}+\right.\hfill \\ \hfill & \hfill & \left[{\left(L\left(H_2\right)+l{I}_{m-l}-\frac{l}{m-l+1}{J}_{\left(m-l\right)\times \left(m-l\right)}\right)}^{-1}{\left.\otimes I_n\right]}_{jj}\right.\hfill \\ \hfill & \hfill & {\left.-2\left[{\left(L\left(H_1\right)+\left(m-l+1\right)I_l-\frac{m-l}{l}{J}_{l\times l}\right)}^{-1}\otimes I_n\right.\right]}_{ij},\hfill \end{array}$

as stated in (iv). For any i ∈ V(H₂) and j ∈ V(H₁), by Lemma 2.1 and Eq. 1, we obtained

$\begin{array}{ccc}\hfill r_{ij}\left(G\left[F;H_v,l\right]\right)& =\hfill & \left[{\left(L\left(H_2\right)+l{I}_{m-l}-\frac{l}{m-l+1}{J}_{\left(m-l\right)\times \left(m-l\right)}\right)}^{-1}{\left.\otimes I_n\right]}_{ii}\right.\hfill \\ \hfill & \hfill & +\left[{\left(L\left(H_1\right)+\left(m-l+1\right)I_l-\frac{m-l}{l}{J}_{l\times l}\right)}^{-1}{\left.\otimes I_n\right]}_{jj}-2\right.\hfill \\ \hfill & \hfill & {\left.\left[{\left(L\left(H_2\right)+l{I}_{m-l}-\frac{l}{m-l+1}{J}_{\left(m-l\right)\times \left(m-l\right)}\right)}^{-1}\otimes I_n\right.\right]}_{ij},\hfill \end{array}$

as stated in (v). Now, we computed the Kirchhoff index of G[F; H_v, l]. By Lemma 2.5, we obtained Kf(G[F; H_v, l])

$\begin{array}{ccc}\hfill & =\hfill & n\left(m+1\right)tr\left(N\right)-1^{T}N1\hfill \\ \hfill & =\hfill & n\left(m+1\right)\left[\left(tr\left(L^{\#}\left(F\right)\right)+tr\left({\left(L\left(H_1\right)+\left(m-l+1\right)I_l+\frac{m-l}{l}{J}_{l\times l}\right)}^{-1}\left.\otimes I_n\right)\right)+\right.\right.\hfill \\ \hfill & \hfill & \left.+tr\left({\left(L\left(H_2\right)+l{I}_{m-l}+\frac{l}{m-l+1}{J}_{\left(m-l\right)\times \left(m-l\right)}\right)}^{-1}\otimes I_n\right)\right)+\hfill \\ \hfill & \hfill & \left.tr\left(\left(1_l\otimes I_n\right)L^{\#}\left(F\right)\left(1_l^T\otimes I_n\right)\right)+tr\left(\left(1_{m-l}\otimes I_n\right)L^{\#}\left(F\right)\left(1_{m-l}^T\otimes I_n\right)\right)\right]-1^{T}N1.\hfill \end{array}$

It is noted that the eigenvalues of (L(H₂) + lI_m−l) are 0 + l, ν₂(H₂) + l, … , ν_m−l(H₂) + l and the eigenvalues of J_{(m−l)×(m−l)} are (m − l), 0^(m−l−1). Then,

$tr\left({\left(L\left(H_2\right)+l{I}_{m-l}-\frac{l}{m-l+1}{J}_{\left(m-l\right)}\right)}^{-1}\otimes I_n\right)=n\sum _{i=2}^{m-l}\frac{1}{{\nu }_i\left(H_2\right)+l}+\frac{n\left(m-l+1\right)}{l}.(2)$

Similarly,

$tr\left({\left(L\left(H_1\right)+\left(m-l+1\right)I_l-\frac{m-l}{l}{J}_{l\times l}\right)}^{-1}\left.\otimes I_n\right)\right)=n\sum _{i=2}^l\frac{1}{{\mu }_i\left(H_1\right)+\left(m-l+1\right)}+n.$

It is easily obtained

$tr\left(\left(1_l\otimes I_n\right)L^{\#}\left(F\right)\left(1_l^T\otimes I_n\right)\right)+tr\left(\left(1_{m-l}\otimes I_n\right)L^{\#}\left(F\right)\left(1_{m-l}^T\otimes I_n\right)\right)$

$=tr\left(J_{l\times l}\otimes L^{\#}\left(F\right)\right)+tr\left(J_{\left(m-l\right)\times \left(m-l\right)}\otimes L^{\#}\left(F\right)\right)$

$=ltr\left(L^{\#}\left(F\right)\right)+\left(m-l\right)tr\left(L^{\#}\left(F\right)\right)=mtr\left(L^{\#}\left(F\right)\right).(3)$

Let $P=\left(L(H_1)+(m-l+1)I_l-\frac{m-l}{l}{J}_{l\times l}\right)\otimes I_n$, then

$1^T{P}^{-1}1=\left(\begin{array}{cccc}\hfill 1_l^T\hfill & \hfill 1_l^T\hfill & \hfill \cdots \hfill & \hfill 1_l^T\hfill \end{array}\right)\left(\begin{array}{ccccc}\hfill P^{-1}\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill \dots \hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill P^{-1}\hfill & \hfill 0\hfill & \hfill \dots \hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill 0\hfill & \hfill \dots \hfill & \hfill \dots \hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill \dots \hfill & \hfill P^{-1}\hfill \end{array}\right)\left(\begin{array}{c}\hfill 1_l\hfill \\ \hfill 1_l\hfill \\ \hfill \cdots \hfill \\ \hfill 1_l\hfill \end{array}\right),(4)$

$=l{1}_l^T{\left(L\left(H_1\right)+\left(m-l+1\right)I_l-\frac{m-l}{l}{J}_{l\times l}\right)}^{-1}{1}_l=l^2.$

Let $Q=\left(L(H_2)+l{I}_{m-l}-\frac{l}{m-l+1}{J}_{(m-l)\times (m-l)}\right)\otimes I_n$, then

$1^T{Q}^{-1}1=\left(\begin{array}{cccc}\hfill 1_{m-l}^T\hfill & \hfill 1_{m-l}^T\hfill & \hfill \cdots \hfill & \hfill 1_{m-l}^T\hfill \end{array}\right)\left(\begin{array}{ccccc}\hfill Q^{-1}\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill \dots \hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill Q^{-1}\hfill & \hfill 0\hfill & \hfill \dots \hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill 0\hfill & \hfill \dots \hfill & \hfill \dots \hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill \dots \hfill & \hfill Q^{-1}\hfill \end{array}\right)\left(\begin{array}{c}\hfill 1_{m-l}\hfill \\ \hfill 1_{m-l}\hfill \\ \hfill \cdots \hfill \\ \hfill 1_{m-l}\hfill \end{array}\right),(5)$

$=\left(m-l\right)1_{m-l}^T{\left(L\left(H_2\right)+l{I}_{m-l}-\frac{l}{m-l+1}{J}_{\left(m-l\right)\times \left(m-l\right)}\right)}^{-1}{1}_{m-l}$

$={\left(m-l\right)}^2\frac{m-l+1}{l}.$

$1_{\mathit{ln}}^T\left(1_l\otimes I_n\right)L^{\#}\left(F\right)\left(1_l^T\otimes I_n\right)1_{\mathit{ln}}=\left(\begin{array}{cccc}\hfill 1_n^T\hfill & \hfill 1_n^T\hfill & \hfill \cdots \hfill & \hfill 1_n^T\hfill \end{array}\right)\left(\begin{array}{cc}\hfill I_n\hfill & \hfill \hfill \\ \hfill I_n\hfill & \hfill \hfill \\ \hfill \cdots \hfill & \hfill \hfill \\ \hfill I_n\hfill & \hfill \hfill \end{array}\right),(6)$

$L^{\#}\left(F\right)\left(\begin{array}{cccc}\hfill I_n\hfill & \hfill I_n\hfill & \hfill \cdots \hfill & \hfill I_n\hfill \end{array}\right)\left(\begin{array}{cc}\hfill 1_n\hfill & \hfill \hfill \\ \hfill 1_n\hfill & \hfill \hfill \\ \hfill \cdots \hfill & \hfill \hfill \\ \hfill 1_n\hfill & \hfill \hfill \end{array}\right)$

$=n^2{1}_n^T{L}^{\#}\left(F\right)1_n=0.$

Similarly, $1^T\left((1_l\otimes I_n)L^{\#}(F)\right.(1_{m-l}^T\otimes I_n)1=0,1^T\left((1_{m-l}\otimes I_n)L^{\#}(F)\right.(1_l^T\otimes I_n)1=0$ and $1^T\left((1_{m-l}\otimes I_n)L^{\#}(F)\right.(1_l^T\otimes I_n)1=0$Plugging Eqs 2–6 and the aforementioned equations into Kf(G[F; H_v, l]), we obtained the required result in (vi).

4 Resistance Distance and Kirchhoff Index of G [F, u₁, u₂, … , u_k; H_v, l]

In this section, we considered the case when F = F₁ ∨ F₂, where F₁ is the subgraph of F induced by the vertices u₁, u₂, … , u_k and F₂ is the subgraph of F induced by the vertices u_k+1, u_k+2, … , u_n. In this case, we indicated the explicit formulae of the resistance distance and Kirchhoff index of G = G[F, u₁, u₂, … , u_k; H_v, l] in terms of the resistance distance and Kirchhoff index of G and H_v.

Theorem 4.1. Let G = G [F, u₁, u₂, … , u_k; H_v, l] be the graph, as described previously. Let σ(F₁) = (0 = α₁, α₂, … α_k), σ(F₂) = (0 = β₁, β₂, … β_n−k), σ(H₁) = (0 = μ₁, μ₂, … μ_l), and σ(H₂) = (0 = ν₁, ν₂, … ν_m−l). Then, G has the resistance distance and Kirchhoff index as follows:

(i) For any i, j ∈ V(F₁), we obtained

$\begin{array}{ccc}\hfill r_{ij}\left(G\right)& =\hfill & {\left({\left(L\left(F_1\right)+\left(n-k\right)I_k\right)}^{-1}-\frac{n-k}{k}\right)}_{ii}+{\left({\left(L\left(F_1\right)+\left(n-k\right)I_k\right)}^{-1}-\frac{n-k}{k}\right)}_{jj}\hfill \\ \hfill & \hfill & -2{\left({\left(L\left(F_1\right)+\left(n-k\right)I_k\right)}^{-1}-\frac{n-k}{k}\right)}_{ij}.\hfill \end{array}$

(ii) For any i, j ∈ V(F₂), we obtained

$r_{ij}\left(G\right)={\left(L\left(F_2\right)+k{I}_{n-k}\right)}_{ii}^{-1}+{\left(L\left(F_2\right)+k{I}_{n-k}\right)}_{jj}^{-1}-2{\left(L\left(F_2\right)+k{I}_{n-k}\right)}_{ij}^{-1}.$

(iii) For any i, j ∈ V(H₁), we obtained

$\begin{array}{ccc}\hfill r_{ij}\left(G\right)& =\hfill & {\left(\left(L\left(H_1\right)+\left(m-l+1\right)I_l-\frac{m-l}{l}{J}_{l\times l}\right)\otimes I_k\right)}_{ii}\hfill \\ \hfill & \hfill & +\left(L\left(H_1\right)+\left(m-l+1\right)I_l-\frac{m-l}{l}{J}_{l\times l}\right){\left.\otimes I_k\right)}_{jj}\hfill \\ \hfill & \hfill & -2\left(L\left(H_1\right)+\left(m-l+1\right)I_l-\frac{m-l}{l}{J}_{l\times l}\right){\left.\otimes I_k\right)}_{ij}.\hfill \end{array}$

(iv) For any i, j ∈ V(H₂), we obtained

$\begin{array}{ll}\hfill r_{ij}\left(G\right)=& \left(L\left(H_2\right)+l{I}_{m-l}-\frac{l}{m-l+1}{J}_{\left(m-l\right)\times \left(m-l\right)}\right){\left.\otimes I_k\right)}_{ii}+\hfill \\ \hfill & \left(L\left(H_2\right)+l{I}_{m-l}-\frac{l}{m-l+1}{J}_{\left(m-l\right)\times \left(m-l\right)}\right){\left.\otimes I_k\right)}_{jj}\hfill \\ \hfill & -2\left(L\left(H_2\right)+l{I}_{m-l}-\frac{l}{m-l+1}{J}_{\left(m-l\right)\times \left(m-l\right)}\right){\left.\otimes I_k\right)}_{ij}.\hfill \end{array}$

(v) For any i ∈ V(F) and j ∈ V(H₁), we obtained

$r_{ij}\left(G\right)={\left(L^{\#}\left(F\right)\right)}_{ii}+{\left[\left(L\left(H_1\right)+\left(m-l+1\right)I_l-\frac{m-l}{l}{J}_{l\times l}\right)\right]}^{-1}\otimes I_n-2{\left(L^{\#}\left(F\right)\right)}_{ij}.$

(vi) For any i ∈ V(F) and j ∈ V(H₂), we obtained

$\begin{array}{ll}\hfill r_{ij}\left(G\right)=& {\left(L^{\#}\left(F\right)\right)}_{ii}+{\left[\left(L\left(H_2\right)+l{I}_{m-l}-\frac{l}{m-l+1}{J}_{\left(m-l\right)\times \left(m-l\right)}\right)\right]}^{-1}\otimes I_n\hfill \\ \hfill & -2{\left(L^{\#}\left(F\right)\right)}_{ij}.\hfill \end{array}$

(vii) For any i ∈ V(H₁) and j ∈ V(H₂), we obtained

$\begin{array}{ccc}\hfill r_{ij}\left(G\right)& =\hfill & {\left[{\left(L\left(H_1\right)+\left(m-l+1\right)I_l-\frac{m-l}{l}{J}_{l\times l}\right)}^{-1}\otimes I_n\right]}_{ii}+\hfill \\ \hfill & \hfill & {\left[{\left(L\left(H_2\right)+l{I}_{m-l}-\frac{l}{m-l+1}{J}_{\left(m-l\right)\times \left(m-l\right)}\right)}^{-1}\otimes I_n\right]}_{jj}\hfill \\ \hfill & \hfill & -2{\left[{\left(L\left(H_1\right)+\left(m-l+1\right)I_l-\frac{m-l}{l}{J}_{l\times l}\right)}^{-1}\otimes I_n\right]}_{ij}.\hfill \end{array}$

(viii) For any i ∈ V(H₂) and j ∈ V(H₁), we obtained

$\begin{array}{ll}\hfill r_{ij}\left(G\right)=& {\left[{\left(L\left(H_2\right)+l{I}_{m-l}-\frac{l}{m-l+1}{J}_{\left(m-l\right)\times \left(m-l\right)}\right)}^{-1}\otimes I_n\right]}_{ii}+\left[\left(L\left(H_1\right)+\left(m-l+1\right)I_l\right.\right.\hfill \\ \hfill & {\left.{\left.-\frac{m-l}{l}{j}_{l\times l}\right)}^{-1}\otimes I_n\right]}_{jj}-2{\left[{\left(L\left(H_2\right)+l{I}_{m-l}-\frac{l}{m-l+1}{J}_{\left(m-l\right)\times \left(m-l\right)}\right)}^{-1}\otimes I_n\right]}_{ij}.\hfill \end{array}$

(ix) Let

$\begin{array}{ll}\hfill Kf\left(G\right)=& \left(n+mk\right)\left[2\sum _{i=1}^k\left(\frac{1}{{\alpha }_i+\left(n-k\right)}-\frac{1}{\left(n-k\right)}\right)+\sum _{i=1}^{n-k}\frac{1}{{\beta }_i+k}\right.\hfill \\ \hfill & +\left(k\sum _{i=2}^l\frac{1}{{\mu }_i+\left(m-l+1\right)}+k\right)+\left(k\sum _{i=2}^{m-l}\frac{1}{{\nu }_i+l}+\frac{l\left(2m-2l+1\right)}{m-l+1}\right)\hfill \\ \hfill & \left.+k+\frac{k\left(m-l\right)}{l}\right]\hfill \\ \hfill & -\left(l^2+\frac{\left(m-l\right)\left(m-l+1\right)}{l}+2k\left(m-l\right)\right).\hfill \end{array}$

Proof: Let $v_j^i$ denote the jth vertex of H in the ith copy of H_v in G, for i = 1, 2, … , k, j = 1, 2, … , m, and let $V_j(H_v)=\{v_j^1,v_j^2,\dots ,v_j^k\}$. Then, $V(F_1)\cup V(F_2)\cup ({\cup }_{j=1}^m{V}_j(H_v))$ is a partition of the vertex set of G = G[F, u₁, u₂, … , u_k; H_v, l]. Using this partition, the Laplacian matrix of G can be expressed as

$\begin{array}{c}\hfill L\left(G\right)=\left(\begin{array}{cccc}\hfill L_1\hfill & \hfill -J_{k\times \left(n-k\right)}\hfill & \hfill -1_l^T\otimes I_k\hfill & \hfill 0\hfill \\ \hfill -J_{\left(n-k\right)\times k}\hfill & \hfill L_2\hfill & \hfill 0\hfill & \hfill 0\hfill \\ \hfill -1_l\otimes I_k\hfill & \hfill 0\hfill & \hfill L_3\hfill & \hfill -J_{l\times \left(m-l\right)}\otimes I_k\hfill \\ \hfill 0\hfill & \hfill 0\hfill & \hfill -J_{\left(m-l\right)\times l}\otimes I_k\hfill & \hfill L_4\hfill \end{array}\right)\hfill \end{array},$

where L₁ = L(F₁) + (n − k + l)I_k, L₂ = L(F₂) + kI_n−k, L₃ = (L(H₁) + (m − l + 1)I_l) ⊗ I_k, and L₄ = (L(H₂) + lI_m−l) ⊗ I_k. Let A = L₁, $B=\left(\begin{array}{ccc}\hfill -J_{k\times (n-k)}\hfill & \hfill -1_l^T\otimes I_k\hfill & \hfill 0\hfill \end{array}\right)$, $B^T=\left(\begin{array}{cc}\hfill -J_{(n-k)\times k}\hfill & \hfill \hfill \\ \hfill -1_l\otimes I_k\hfill & \hfill \hfill \\ \hfill 0\hfill & \hfill \hfill \end{array}\right)$, and

$\begin{array}{c}\hfill D=\left(\begin{array}{ccc}\hfill L_2\hfill & \hfill 0\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill L_3\hfill & \hfill -J_{l\times \left(m-l\right)}\otimes I_k\hfill \\ \hfill 0\hfill & \hfill -J_{\left(m-l\right)\times l}\otimes I_k\hfill & \hfill L_4\hfill \end{array}\right)\hfill \end{array}.$

First, we computed

$D_1^{-1}={\left(\begin{array}{cc}\hfill L_3\hfill & \hfill -J_{l\times \left(m-l\right)}\otimes I_k\hfill \\ \hfill -J_{\left(m-l\right)\times l}\otimes I_k\hfill & \hfill L_4\hfill \end{array}\right)}^{-1}.$

By Lemma 2.3, we obtained

$\begin{array}{ll}\hfill A_1-B_1{D}_1^{-1}{C}_1=& \left(L\left(H_1\right)+\left(m-l+1\right)I_l\right)\otimes I_k-\left(-J_{l\times \left(m-l\right)}\otimes I_k\right)\hfill \\ \hfill & \left({\left(L\left(H_2\right)+l{I}_{m-l}\right)}^{-1}\otimes I_k\right)\left(-J_{\left(m-l\right)\times l}\otimes I_k\right)\hfill \\ \hfill =& \left(L\left(H_1\right)+\left(m-l+1\right)I_l\right)\otimes I_k-1_l\left(1_{m-l}^T{\left(L\left(H_2\right)+l{I}_{m-l}\right)}^{-1}{1}_{m-l}\right)1_l^T\otimes I_k\hfill \\ \hfill =& \left(L\left(H_1\right)+\left(m-l+1\right)I_l\right)\otimes I_k-\frac{m-l}{l}{J}_{l\times l}\otimes I_k\hfill \\ \hfill =& \left[L\left(H_1\right)+\left(m-l+1\right)I_l-\frac{m-l}{l}{J}_{l\times l}\right]\otimes I_k,\hfill \end{array}$

so ${(A_1-B_1{D}_1^{-1}{C}_1)}^{-1}={[\left(L(H_1)+(m-l+1)\right.I_l-\frac{m-l}{l}{J}_{l\times l}]}^{-1}\otimes I_k$.By Lemma 2.3, we obtained

$\begin{array}{ll}\hfill S^{-1}=& {\left(D_1-C_1{A}_1^{-1}{B}_1\right)}^{-1}\hfill \\ \hfill =& \left[\left(L\left(H_2\right)+l{I}_{m-l}\right)\otimes I_k-\left(-J_{\left(m-l\right)\times l}\otimes I_k\right)\left({\left(L\left(H_1\right)+\left(m-l+1\right)I_l\right)}^{-1}\otimes I_k\right)\right.\hfill \\ \hfill & {\left.\left(-J_{l\times \left(m-l\right)}\otimes I_k\right.\right]}^{-1}\hfill \\ \hfill =& {\left[\left(L\left(H_2\right)+l{I}_{m-l}\right)\otimes I_k-\left(J_{\left(m-l\right)\times l}{\left(L\left(H_1\right)+\left(m-l+1\right)I_l\right)}^{-1}{J}_{l\times \left(m-l\right)}\right)\otimes I_k\right]}^{-1}\hfill \\ \hfill =& {\left[L\left(H_2\right)+l{I}_{m-l}-\frac{l}{m-l+1}{J}_{\left(m-l\right)\times \left(m-l\right)}\right]}^{-1}\otimes I_k.\hfill \end{array}$

By Lemma 2.3, we obtained

$\begin{array}{ll}\hfill -A_1^{-1}{B}_1{S}^{-1}=& -\left[{\left(L\left(H_1\right)+\left(m-l+1\right)I_l\right)}^{-1}\otimes I_k\right]\left(-J_{l\times \left(m-l\right)}\otimes I_k\right)\hfill \\ \hfill & {\left[L\left(H_2\right)+l{I}_{m-l}-\frac{l}{m-l+1}{J}_{\left(m-l\right)\times \left(m-l\right)}\right]}^{-1}\otimes I_k\hfill \\ \hfill =& \frac{1}{m-l+1}{1}_l\times \frac{m-l+1}{l}{1}_{m-l}^T\otimes I_k\hfill \\ \hfill =& \frac{1}{l}{J}_{l\times \left(m-l\right)}\otimes I_k.\hfill \end{array}$

Similarly, $-S^{-1}{C}_1{A}_1^{-1}={(-A_1^{-1}{B}_1{S}^{-1})}^T=\frac{1}{l}{J}_{(m-l)\times l}\otimes I_k$. So

$D_1^{-1}=\left(\begin{array}{cc}\hfill P_1\hfill & \hfill \frac{1}{l}{J}_{l\times \left(m-l\right)}\otimes I_k\hfill \\ \hfill \frac{1}{l}{J}_{\left(m-l\right)\times l}\otimes I_k\hfill & \hfill Q_1\hfill \end{array}\right),$

where $P_1={[\left(L(H_1)+(m-l+1)\right.I_l-\frac{m-l}{l}{J}_{l\times l}]}^{-1}\otimes I_n$, $Q_1={[(L(H_2)+l{I}_{m-l}-\frac{l}{m-l+1}{J}_{(m-l)\times (m-l)})]}^{-1}\otimes I_n$. Now, we computed the {1}-inverse of G[F, u₁, u₂, … , u_k; H_v, l]. Let $P=[\left(L(H_1)+(m-l+1)\right.I_l-\frac{m-l}{l}{J}_{l\times l}]\otimes I_k$ and $Q=[(L(H_2)+l{I}_{m-l}-\frac{l}{m-l+1}{J}_{(m-l)\times (m-l)})]\otimes I_k$. By Lemma 2.6, we obtained

$\begin{array}{ll}\hfill H=& A-B{D}^{-1}{B}^T\hfill \\ \hfill & =L\left(F_1\right)+\left(n-k+l\right)I_k-\left(\begin{array}{ccc}\hfill -J_{k\times \left(n-k\right)}\hfill & \hfill -1_l^T\otimes I_k\hfill & \hfill 0\hfill \end{array}\right)\hfill \\ \hfill & \left(\begin{array}{ccc}\hfill {\left(L\left(F_2\right)+k{I}_{n-k}\right)}^{-1}\hfill & \hfill 0\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill P^{-1}\hfill & \hfill \frac{1}{l}{J}_{l\times \left(m-l\right)}\otimes I_k\hfill \\ \hfill 0\hfill & \hfill \frac{1}{l}{J}_{\left(m-l\right)\times l}\otimes I_k\hfill & \hfill Q^{-1}\hfill \end{array}\right)\left(\begin{array}{c}\hfill -J_{\left(n-k\right)\times k}\hfill \\ \hfill -1_l\otimes I_k\hfill \\ \hfill 0\hfill \end{array}\right)\hfill \\ \hfill =& L\left(F_1\right)+\left(n-k+l\right)I_k-\frac{n-k}{k}{J}_{k\times k}-l{I}_k\hfill \\ \hfill =& L\left(F_1\right)+\left(n-k\right)I_k-\frac{n-k}{k}{J}_{k\times k},\hfill \end{array}$

so $H^{\#}={(L(F_1)+(n-k)I_k-\frac{n-k}{k}{J}_{k\times k})}^{\#}$. By Lemma 2.4, we obtained $H^{\#}={(L(F_1)+(n-k)I_k)}^{-1}-\frac{1}{k(n-k)}{J}_{k\times k}$.According to Lemma 2.6, we calculated − H^#BD⁻¹ and − D⁻¹B^TH^#.

$\begin{array}{ll}\hfill -H^{\#}B{D}^{-1}=& -H^{\#}\left(\begin{array}{ccc}\hfill -J_{k\times \left(n-k\right)}\hfill & \hfill -1_l^T\otimes I_k\hfill & \hfill 0\hfill \end{array}\right)\hfill \\ \hfill & \left(\begin{array}{ccc}\hfill {\left(L\left(F_2\right)+k{I}_{n-k}\right)}^{-1}\hfill & \hfill 0\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill P^{-1}\hfill & \hfill \frac{1}{l}{J}_{l\times \left(m-l\right)}\otimes I_k\hfill \\ \hfill 0\hfill & \hfill \frac{1}{l}{J}_{\left(m-l\right)\times l}\otimes I_k\hfill & \hfill Q^{-1}\hfill \end{array}\right)\hfill \\ \hfill =& \left(\begin{array}{ccc}\hfill \frac{1}{k}{H}^{\#}{J}_{k\times \left(n-k\right)}\hfill & \hfill H^{\#}\left(1_l^T\otimes I_k\right)\hfill & \hfill H^{\#}\left(1_{m-l}^T\otimes I_k\right)\hfill \end{array}\right)\hfill \end{array}$

and

$\begin{array}{cc}\hfill -D^{-1}{B}^T{H}^{\#}\hfill & \hfill =\left(\begin{array}{c}\hfill \frac{1}{k}{J}_{\left(n-k\right)\times k}{H}^{\#}\hfill \\ \hfill \left(1_l\otimes I_k\right)H^{\#}\hfill \\ \hfill \left(1_{m-l}\otimes I_k\right)H^{\#}\hfill \end{array}\right).\end{array}$

We are ready to compute the D⁻¹B^TH^#BD⁻¹.

$\begin{array}{ll}\hfill D^{-1}{B}^T{H}^{\#}B{D}^{-1}=& \left(\begin{array}{cc}\hfill \frac{1}{k}{J}_{\left(n-k\right)\times k}{H}^{\#}\hfill & \hfill \hfill \\ \hfill \left(1_l\otimes I_k\right)H^{\#}\hfill & \hfill \hfill \\ \hfill \left(1_{m-l}\otimes I_k\right)H^{\#}\hfill \end{array}\right)\left(\begin{array}{ccc}\hfill \frac{1}{k}{J}_{k\times \left(n-k\right)}\hfill & \hfill \left(1_l^T\otimes I_k\right)\hfill & \hfill \left(1_{m-l}^T\otimes I_k\right)\hfill \end{array}\right)\hfill \\ \hfill =& \left(\begin{array}{ccc}\hfill \frac{1}{k^2}J{H}^{\#}J\hfill & \hfill \frac{1}{k}J{H}^{\#}\left(1_l^T\otimes I_k\right)\hfill & \hfill \hfill \\ \hfill \frac{1}{k}\left(1_l\otimes I_k\right)H^{\#}{J}_{k\times \left(n-k\right)}\hfill & \hfill \left(1_l\otimes I_k\right)H^{\#}\left(1_l^T\otimes I_k\right)\hfill & \hfill \hfill \\ \hfill \frac{1}{k}\left(1_{m-l}\otimes I_k\right)H^{\#}{J}_{k\times \left(n-k\right)}\hfill & \hfill \left(1_{m-l}\otimes I_k\right)H^{\#}\left(1_l^T\otimes I_k\right)\hfill & \hfill \hfill \end{array}\right)\hfill \\ \hfill & \left(\begin{array}{c}\hfill \frac{1}{k}J{H}^{\#}\left(1_{m-l}^T\otimes I_k\right)\hfill \\ \hfill \left(1_l\otimes I_k\right)H^{\#}\left(1_{m-l}^T\otimes I_k\right)\hfill \\ \hfill \left(1_{m-l}\otimes I_k\right)H^{\#}\left(1_{m-l}^T\otimes I_k\right)\hfill \end{array}\right).\hfill \end{array}$

Let $M=1_{m-l}^T\otimes I_k$ and $N=1_l^T\otimes I_k$. Based on Lemma 2.6, the following matrix

$T=\left(\begin{array}{cccc}\hfill H^{\#}\hfill & \hfill \frac{1}{k}{H}^{\#}J\hfill & \hfill H^{\#}N\hfill & \hfill H^{\#}M\hfill \\ \hfill \frac{1}{k}J{H}^{\#}\hfill & \hfill {\left(L\left(F_2\right)+kI\right)}^{-1}\hfill & \hfill 0\hfill & \hfill 0\hfill \\ \hfill N^T{H}^{\#}\hfill & \hfill 0\hfill & \hfill P^{-1}+N^T{H}^{\#}N\hfill & \hfill N^T{H}^{\#}M+\frac{1}{l}J\otimes I_k\hfill \\ \hfill M^T{H}^{\#}\hfill & \hfill 0\hfill & \hfill M^T{H}^{\#}N+\frac{1}{l}J\otimes I_k\hfill & \hfill \left.Q^{-1}+M^T{H}^{\#}M\right)\hfill \end{array}\right)$,(7)

is a symmetric {1}-inverse of G = G[F, u₁, u₂, … , u_k; H_v, l], where $P=[\left(L(H_1)+(m-l+1)\right.I_l-\frac{m-l}{l}{J}_{l\times l}]\otimes I_k$ and $Q=[(L(H_2)+l{I}_{m-l}-\frac{l}{m-l+1}{J}_{(m-l)\times (m-l)})]\otimes I_k$. For any i, j ∈ V(F₁), by Lemma 2.1 and Eq. 7, we obtained

$\begin{array}{ll}\hfill r_{ij}\left(G\right)=& {\left({\left(L\left(F_1\right)+\left(n-k\right)I_k\right)}^{-1}-\frac{1}{k\left(n-k\right)}\right)}_{ii}+{\left({\left(L\left(F_1\right)+\left(n-k\right)I_k\right)}^{-1}-\frac{1}{k\left(n-k\right)}\right)}_{jj}\hfill \\ \hfill & -2{\left({\left(L\left(F_1\right)+\left(n-k\right)I_k\right)}^{-1}-\frac{1}{k\left(n-k\right)}\right)}_{ij},\hfill \end{array}$

as stated in (i). For any i, j ∈ V(F₂), by Lemma 2.1 and Eq. 7, we obtained

$r_{ij}\left(G\right)={\left(L\left(F_2\right)+k{I}_{n-k}\right)}_{ii}^{-1}+{\left(L\left(F_2\right)+k{I}_{n-k}\right)}_{jj}^{-1}-2{\left(L\left(F_2\right)+k{I}_{n-k}\right)}_{ij}^{-1},$

as stated in (ii). For any i, j ∈ V(H₁), by Lemma 2.1 and Eq. 7, we obtained

$\begin{array}{ccc}\hfill r_{ij}\left(G\right)& =\hfill & {\left(\left(L\left(H_1\right)+\left(m-l+1\right)I_l-\frac{m-l}{l}{J}_{l\times l}\right)\otimes I_k\right)}_{ii}^{-1}\hfill \\ \hfill & \hfill & +\left(L\left(H_1\right)+\left(m-l+1\right)I_l-\frac{m-l}{l}{J}_{l\times l}\right){\left.\otimes I_k\right)}_{jj}^{-1}\hfill \\ \hfill & \hfill & -2\left(L\left(H_1\right)+\left(m-l+1\right)I_l-\frac{m-l}{l}{J}_{l\times l}\right){\left.\otimes I_k\right)}_{ij}^{-1},\hfill \end{array}$

as stated in (iii). For any i, j ∈ V(H₂), by Lemma 2.1 and Eq. 7, we obtained

$\begin{array}{ccc}\hfill r_{ij}\left(G\right)& =\hfill & \left(L\left(H_2\right)+l{I}_{m-l}-\frac{l}{m-l+1}{J}_{\left(m-l\right)\times \left(m-l\right)}\right){\left.\otimes I_k\right)}_{ii}^{-1}\hfill \\ \hfill & \hfill & +\left(L\left(H_2\right)+l{I}_{m-l}-\frac{l}{m-l+1}{J}_{\left(m-l\right)\times \left(m-l\right)}\right){\left.\otimes I_k\right)}_{jj}^{-1}-2\left(L\left(H_2\right)+l{I}_{m-l}\right.\hfill \\ \hfill & \hfill & -\frac{l}{m-l+1}\left.J_{\left(m-l\right)\times \left(m-l\right)}\right){\left.\otimes I_k\right)}_{ij}^{-1},\hfill \end{array}$

as stated in (iv). For any i ∈ V(F) and j ∈ V(H₁) by Lemma 2.1 and Eq. 7, we obtained

$r_{ij}\left(G\right)={\left(L^{\#}\left(F\right)\right)}_{ii}+{\left[{\left(L\left(H_1\right)+\left(m-l+1\right)I_l-\frac{m-l}{l}{J}_{l\times l}\right)}^{-1}\otimes I_n\right]}_{jj}-2{\left(L^{\#}\left(F\right)\right)}_{ij},$

as stated in (v). For any i ∈ V(F) and j ∈ V(H₂), by Lemma 2.1 and Eq. 7, we obtained

$\begin{array}{ll}\hfill r_{ij}\left(G\right)=& {\left(L^{\#}\left(F\right)\right)}_{ii}+{\left[{\left(L\left(H_2\right)+l{I}_{m-l}-\frac{l}{m-l+1}{J}_{\left(m-l\right)\times \left(m-l\right)}\right)}^{-1}\otimes I_n\right]}_{jj}\hfill \\ \hfill & -2{\left(L^{\#}\left(F\right)\right)}_{ij},\hfill \end{array}$

as stated in (vi). For any i ∈ V(H₁) and j ∈ V(H₂), by Lemma 2.1 and Eq. 7, we obtained

$\begin{array}{ccc}\hfill r_{ij}\left(G\right)& =\hfill & {\left[{\left(L\left(H_1\right)+\left(m-l+1\right)I_l-\frac{m-l}{l}{J}_{l\times l}\right)}^{-1}\otimes I_n\right]}_{ii}\hfill \\ \hfill & \hfill & +{\left[{\left(L\left(H_2\right)+l{I}_{m-l}-\frac{l}{m-l+1}{J}_{\left(m-l\right)\times \left(m-l\right)}\right)}^{-1}\otimes I_n\right]}_{jj}\hfill \\ \hfill & \hfill & -2{\left[{\left(L\left(H_1\right)+\left(m-l+1\right)I_l-\frac{m-l}{l}{J}_{l\times l}\right)}^{-1}\otimes I_n\right]}_{ij},\hfill \end{array}$

as stated in (vii). For any i ∈ V(H₂) and j ∈ V(H₁), by Lemma 2.1 and Eq. 7, we obtained

$\begin{array}{ccc}\hfill r_{ij}\left(G\right)& =\hfill & {\left[{\left(L\left(H_2\right)+l{I}_{m-l}-\frac{l}{m-l+1}{J}_{\left(m-l\right)\times \left(m-l\right)}\right)}^{-1}\otimes I_n\right]}_{ii}\hfill \\ \hfill & \hfill & +{\left[{\left(L\left(H_1\right)+\left(m-l+1\right)I_l-\frac{m-l}{l}{J}_{l\times l}\right)}^{-1}\otimes I_n\right]}_{jj}\hfill \\ \hfill & \hfill & -2{\left[{\left(L\left(H_2\right)+l{I}_{m-l}-\frac{l}{m-l+1}{J}_{\left(m-l\right)\times \left(m-l\right)}\right)}^{-1}\otimes I_n\right]}_{ij},\hfill \end{array}$

as stated in (viii). Now, we computed the Kirchhoff index of $G\left[F,u_1,u_2,\dots \right.$ $\left.u_k;H_v,l\right]$ as Kf(G[F, u₁, u₂, … , u_k; H_v, l])

$\begin{array}{ll}\hfill =& \left(n+mk\right)tr\left(T\right)-1^{T}T1\hfill \\ \hfill =& \left(n+mk\right)\left(tr\left({\left(L\left(F_1\right)+\left(n-k\right)I_k\right)}^{-1}-\frac{1}{k\left(n-k\right)}{J}_{k\times k}\right)\right.\hfill \\ \hfill & +tr{\left(L\left(F_2\right)+k{I}_{n-k}\right)}^{-1}+ktr{\left(L\left(H_1\right)+\left(m-l+1\right)I_l-\frac{m-l}{l}{J}_{l\times l}\right)}^{-1}\hfill \\ \hfill & +ktr{\left(L\left(H_2\right)+l{I}_{m-l}-\frac{l}{m-l+1}{J}_{\left(m-l\right)\times \left(m-l\right)}\right)}^{-1}\hfill \\ \hfill & +\frac{1}{l}tr\left(J_{l\times \left(m-l\right)}\otimes I_k\right)+\frac{1}{l}tr\left(J_{\left(m-l\right)\times l}\otimes I_k\right)\hfill \\ \hfill & \left.+tr\left(N^T{H}^{\#}N\right)+tr\left(M^T{H}^{\#}M\right)\right)-1^{T}T1.\hfill \end{array}$

It is noted that the eigenvalues of (L(F₁) + (n − k)I_k) are α₁ + (n − k), α₂ + (n − k), …, α_k + (n − k). Then,

$tr\left({\left(L\left(F_1\right)+\left(n-k\right)I_k\right)}^{-1}-\frac{1}{k\left(n-k\right)}{J}_{k\times k}\right)$

$=\sum _{i=1}^k\frac{1}{{\alpha }_i+\left(n-k\right)}-\frac{k}{k\left(n-k\right)}.$

Similarly, $tr\left({(L(F_2)+k{I}_{n-k})}^{-1}\right)={\sum }_{i=1}^{n-k}\frac{1}{{\beta }_i+k}.$ It is noted that the eigenvalues of $\left(L(H_1)+(m-l+1)I_l\right.$ are 0 + (m − l + 1), μ₂(H₁) + (m − l + 1), …, μ_l(H₁) + (m − l + 1) and the eigenvalues of J_{(m−l)×(m−l)} are (m − l), 0^(m−l−1). Then,

$\begin{array}{l}\hfill tr{\left(L\left(H_1\right)+\left(m-l+1\right)I_l+\frac{m-l}{l}{\left.J_{l\times l}\right)}^{-1}\otimes I_k\right)}^{-1}\\ \hfill =k\sum _{i=2}^l\frac{1}{{\mu }_i+\left(m-l+1\right)}+k.\end{array}$

Similarly,

$tr{\left(\left(L\left(H_2\right)+l{I}_{m-l}-\frac{l}{m-l+1}{J}_{\left(m-l\right)\times \left(m-l\right)}\right)\otimes I_k\right)}^{-1}$

$=k\sum _{i=2}^{m-l}\frac{1}{{\nu }_i+l}+\frac{kl\left(2m-2l+1\right)}{m-l+1}.$

It is easily obtained that tr(J_l×(m−l) ⊗ I_k) = lk, tr(J_(m−l)×l ⊗ I_k) = (m − l)k and tr(N^TH^#N) + tr(M^TH^#M) = tr(J_l×l⊗H^#) + tr(J_{(m−l)×(m−l)}⊗H^#) = ltr(H^#) + (m − l)tr(H^#) = mtr(H^#). Since $1_k^T{H}^{\#}=1_k^T[{(L(F_1)+(n-k)I_k)}^{-1}-\frac{1}{k(n-k)}{J}_{k\times k}]=\frac{1}{n-k}{1}_k^T-\frac{1}{k(n-k)}{1}_k^T=0$, then

$\begin{array}{ll}\hfill 1^{T}N1=& 1^T{\left(L\left(F_2\right)+k{I}_{n-k}\right)}^{-1}1+1^T{P}^{-1}1+1^T{Q}^{-1}1+1^T{N}^T{H}^{\#}N1+1^T{N}^T{H}^{\#}M1\hfill \\ \hfill & +1^T{M}^T{H}^{\#}N1+1^T{M}^T{H}^{\#}M1+\frac{1}{l}{1}^T\left(J_{l\times \left(m-l\right)}\otimes I_k\right)1\hfill \\ \hfill & +\frac{1}{l}{1}^T\left(J_{\left(m-l\right)\times l}\otimes I_k\right)1.\hfill \end{array}$

By the process of Theorem 4.1, we obtained

$1^T{P}^{-1}1=l^2,1^T{Q}^{-1}1=\left(m-l\right)\frac{m-l+1}{l}.$

$\begin{array}{ll}\hfill 1^T\left(N^T{H}^{\#}N\right)1=& 1_{lk}^T\left(1_l\otimes I_k\right)H^{\#}\left(1_l^T\otimes I_k\right)1_{lk}\hfill \\ \hfill =& \left(\begin{array}{cccc}\hfill 1_k^T\hfill & \hfill 1_k^T\hfill & \hfill \cdots \hfill & \hfill 1_k^T\hfill \end{array}\right)\left(\begin{array}{cc}\hfill I_k\hfill & \hfill \hfill \\ \hfill I_k\hfill & \hfill \hfill \\ \hfill \cdots \hfill & \hfill \hfill \\ \hfill I_k\hfill & \hfill \hfill \end{array}\right)H^{\#}\left(\begin{array}{cccc}\hfill I_k\hfill & \hfill I_k\hfill & \hfill \cdots \hfill & \hfill I_k\hfill \end{array}\right)\left(\begin{array}{cc}\hfill 1_k\hfill & \hfill \hfill \\ \hfill 1_k\hfill & \hfill \hfill \\ \hfill \cdots \hfill & \hfill \hfill \\ \hfill 1_k\hfill & \hfill \hfill \end{array}\right)\hfill \\ \hfill =& k^2{1}_k^T{H}^{\#}{1}_k=0.\hfill \end{array}$

Similarly, 1^T(M^TH^#M)1 = 0, 1^TN^TH^#M1 = 0, and 1^TM^TH^#N1 = 0.

$\begin{array}{ll}\hfill 1^T\left(J_{l\times \left(m-l\right)}\otimes I_k\right)1=& \left(\begin{array}{cccc}\hfill 1_k^T\hfill & \hfill 1_k^T\hfill & \hfill \cdots \hfill & \hfill 1_k^T\hfill \end{array}\right)\left(\begin{array}{cccc}\hfill I_k\hfill & \hfill I_k\hfill & \hfill \cdots I_k\hfill & \hfill \hfill \\ \hfill I_k\hfill & \hfill I_k\hfill & \hfill \cdots I_k\hfill & \hfill \hfill \\ \hfill \cdots \hfill & \hfill \cdots \hfill & \hfill \hfill \\ \hfill I_k\hfill & \hfill I_k\hfill & \hfill \cdots I_k\hfill & \hfill \hfill \end{array}\right)\hfill \\ \hfill & \left(\begin{array}{cc}\hfill 1_k\hfill & \hfill \hfill \\ \hfill 1_k\hfill & \hfill \hfill \\ \hfill \cdots \hfill & \hfill \hfill \\ \hfill 1_k\hfill & \hfill \hfill \end{array}\right)=lk\left(m-l\right).\hfill \end{array}$

Similarly, 1^T(J_(m−l)×l ⊗ I_k) = lk(m − l). Applying the aforementioned equations into $Kf\left(G\left[F,u_1,u_2,\dots \right.\right.$, $\left.\left.u_k;H_v,l\right]\right)$, we obtained the required result in (ix).

Data Availability Statement

The original contributions presented in the study are included in the article/Supplementary Material, further inquiries can be directed to the corresponding author.

Author Contributions

All the authors listed have made a substantial, direct, and intellectual contribution to the work and approved it for publication.

Funding

This work was supported by the National Natural Science Foundation of China (no. 61963013), the Science and Technology Plan of Gansu Province(18JR3RG206), and the Research and Innovation Fund Project of President of Hexi University(XZZD2018003).

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s Note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors, and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

1. Klein DJ, Randić M. $acutec$Resistance Distance. J Math Chem (1993) 12:81–95. doi:10.1007/bf01164627

CrossRef Full Text | Google Scholar

2. Huang S, Zhou J, Bu C. Some Results on Kirchhoff index and Degree-Kirchhoff index. MATCH Commun Math Comput Chem (2016) 75:207–22.

Google Scholar

3. Cao J, Liu J, Wang S. Resistance Distances in corona and Neighborhood corona Networks Based on Laplacian Generalized Inverse Approach. J Algebra Appl (2019) 18(3):1950053. doi:10.1142/s0219498819500531

CrossRef Full Text | Google Scholar

4. Liu J-B, Pan X-F, Yu L, Li D. Complete Characterization of Bicyclic Graphs with Minimal Kirchhoff index. Discrete Appl Maths (2016) 200:95–107. doi:10.1016/j.dam.2015.07.001

CrossRef Full Text | Google Scholar

5. Sun L, Wang W, Zhou J, Bu C. Some Results on Resistance Distances and Resistance Matrices. Linear and Multilinear Algebra (2015) 63(3):523–33. doi:10.1080/03081087.2013.877011

CrossRef Full Text | Google Scholar

6. Bapat RB. Graphs and Matrices. London/New Delhi: Springer/Hindustan Book Agency (2010). Universitext.

Google Scholar

7. Chen H, Zhang F. Resistance Distance and the Normalized Laplacian Spectrum. Discrete Appl Maths (2007) 155:654–61. doi:10.1016/j.dam.2006.09.008

CrossRef Full Text | Google Scholar

8. Xiao W, Gutman I. Resistance Distance and Laplacian Spectrum. Theor Chem Acc Theor Comput Model (Theoretica Chim Acta) (2003) 110:284–9. doi:10.1007/s00214-003-0460-4

CrossRef Full Text | Google Scholar

9. Yang Y, Klein DJ. A Recursion Formula for Resistance Distances and its Applications. Discrete Appl Maths (2013) 161:2702–15. doi:10.1016/j.dam.2012.07.015

CrossRef Full Text | Google Scholar

10. Yang Y, Klein DJ. Resistance Distance-Based Graph Invariants of Subdivisions and Triangulations of Graphs. Discrete Appl Maths (2015) 181:260–74. doi:10.1016/j.dam.2014.08.039

CrossRef Full Text | Google Scholar

11. Barik S. On the Laplacian Spectra of Graphs with Pockets. Linear and Multilinear Algebra (2008) 56:481–90. doi:10.1080/03081080600906463

CrossRef Full Text | Google Scholar

12. Barik S, Sahoo G. Some Results on the Laplacian Spectra of Graphs with Pockets. Electron Notes Discrete Maths (2017) 63:219–28. doi:10.1016/j.endm.2017.11.017

CrossRef Full Text | Google Scholar

13. Bapat RB, Gupta S. Resistance Distance in Wheels and Fans. Indian J Pure Appl Math (2010) 41:1–13. doi:10.1007/s13226-010-0004-2

CrossRef Full Text | Google Scholar

14. Bu C, Yan B, Zhou X, Zhou J. Resistance Distance in Subdivision-Vertex Join and Subdivision-Edge Join of Graphs. Linear Algebra its Appl (2014) 458:454–62. doi:10.1016/j.laa.2014.06.018

CrossRef Full Text | Google Scholar

15. Liu X, Zhou J, Bu C. Resistance Distance and Kirchhoff index of R-Vertex Join and R-Edge Join of Two Graphs. Discrete Appl Maths (2015) 187:130–9. doi:10.1016/j.dam.2015.02.021

CrossRef Full Text | Google Scholar

16. Ben-Israel A, Greville TNE. Generalized Inverses: Theory and Applications. 2nd ed. New York: Springer (2003).

Google Scholar

17. Bu C, Sun L, Zhou J, Wei Y. A Note on Block Representations of the Group Inverse of Laplacian Matrices. Electron J Linear Algebra (2012) 23:866–76. doi:10.13001/1081-3810.1562

CrossRef Full Text | Google Scholar

18. Zhang FZ. The Schur Complement and its Applications. New York: Springer-Verlag (2005).

Google Scholar

19. Liu Q. Some Results of Resistance Distance and Kirchhoff index of Vertex-Edge corona for Graphs. Adv Mathematics(China) (2016) 45(2):176–83.

Google Scholar

20. Liu J-B, Pan X-F, Hu F-T. The {1}-inverse of the Laplacian of Subdivision-Vertex and Subdivision-Edge Coronae with Applications. Linear and Multilinear Algebra (2017) 65:178–91. doi:10.1080/03081087.2016.1179249

CrossRef Full Text | Google Scholar

21. Liu J-B, Cao J. The Resistance Distances of Electrical Networks Based on Laplacian Generalized Inverse. Neurocomputing (2015) 167:306–13. doi:10.1016/j.neucom.2015.04.065

CrossRef Full Text | Google Scholar

22. Xie P, Zhang Z, Comellas F. On the Spectrum of the Normalized Laplacian of Iterated Triangulations of Graphs. Appl Maths Comput (2016) 273:1123–9. doi:10.1016/j.amc.2015.09.057

CrossRef Full Text | Google Scholar

23. Xie P, Zhang Z, Comellas F. The Normalized Laplacian Spectrum of Subdivisions of a Graph. Appl Maths Comput (2016) 286:250–6. doi:10.1016/j.amc.2016.04.033

CrossRef Full Text | Google Scholar