Adaptive Sliding-Mode Synchronization of the Memristor-Based Sixth-Order Uncertain Chaotic System and Its Application in Image Encryption

This article presents a memristor-based sixth-order chaotic circuit which is designed based on Chua¡ ¯ s circuit using flux-controlled memristors and charge-controlled memristors. The chaotic characteristics are analyzed, and the chaotic phase diagrams are drawn. The specific upper bound information of the model uncertainty and external disturbance is unknown. We design an adaptive terminal sliding-mode control law for such chaotic systems, which not only compensates the influence of the uncertainty and disturbance but also ensures that the synchronization error system is fixed-time stable when the sliding motion takes place. Also, the accessibility of the sliding surface is guaranteed. Thus, the sufficient conditions for the synchronization of the considered systems are derived. Simulation examples show the significance and superiority of the control scheme. The synchronization strategy is applied to image encryption, and the results show that the encryption effect is excellent and has strong anti-disturbance ability.

1 Introduction

Chaos theory, one of the greatest scientific studies in the 20th century, establishes a link between determinism and probability theory and shows that even the simplest deterministic system also had randomness. Lorenz’s weather models [1] showed that small differences in the initial conditions of a system could make a tremendous effect on the final phenomenon. So, chaos was considered one of the most creative revolutions in the scientific world [2–6]. Lai et al. [7] presented the latest research progress in the field of chaotic systems. The memristor is a kind of nonlinear two-terminal device that expresses the relationship between the magnetic flux and charge. Compared with resistances, capacitances, and inductances, memristors have memory function and complex nonlinear characteristics [8], so they are an ideal component for designing complex nonlinear systems. Sun et al. [9–12] applied various memristors to the Pavlov associative memristor neural network circuit for enhancing the memory and learning ability of the circuit, which made progress in the research field of brain-like systems. Li et al. [13, 14] constructed a four-order memristor chaotic oscillator, which increased the amplitude and frequency of the output waveform and realized an analog circuit consistent with the theory. If it is introduced into chaos, the chaotic system will indicate more complex chaotic characteristics. In [15], the piecewise magnetically controlled memristor was used for the first time to replace Chua’s diode, and the memristor chaotic circuit was designed to obtain the third-order memristor chaotic system model, and the chaotic characteristics were analyzed. The results showed abundant chaotic characteristics.

At present, many scholars have improved the chaotic model with memristors [16, 17]. In [18], the three-dimensional Lorentzian system was improved to construct a new memory chaotic system. In [19], a new flux-controlled memristor with a hyperbolic cosine function for Chua’s circuit was designed. In [20], the adaptive projective synchronization of three chaotic systems with three unknown parameters was studied. However, their models are all chaotic systems of fifth-order or less, and there is little research on sixth-order chaotic systems. Compared with traditional chaotic circuits, memristor chaotic circuits have stronger randomness, which are more widely used. Hence, the first innovation of this article is to construct a novel memristor-based six-order chaotic system. At the same time, we can also find that it has great significance in solving the design and synchronization problems of high-dimensional chaotic systems.

Chaotic synchronization [21, 22] is an important research hotspot in complex system control and communication. In recent years, sliding-mode synchronization has attracted the attention of researchers. The sliding-mode control [23, 24] forces the synchronization error systems to move along the sliding surface. Adaptive control [25] could use the running data to make the estimated value closer to the unknown quantity, to solve the influence of internal uncertainty and external disturbance during the system operation. In [26], sliding-mode controllers and adaptive laws were designed to solve the transmission synchronization problem. In [27], a global nonlinear integral sliding-mode controller was designed, and the simulation results showed that the error convergence speed was improved. In [28], the synchronization problem of a class of nonlinear chaotic systems with mismatched disturbances was studied, and a new non-singular terminal sliding surface was designed. In addition, the traditional asymptotic synchronization time range is infinite, which does not meet the actual requirements.

Finite-time chaos synchronization [29] has attracted more and more interest due to its dynamic properties, which can reduce the cost, improve the robustness, and achieve fast convergence. In [30], a controller to satisfy the finite-time synchronization problem of chaotic systems was designed. In [31], a multi-switching rule was used to achieve finite-time hybrid synchronization for multi-systems. In [32], a finite-time continuous controller was designed to reduce the control cost of nonlinear systems. In addition, the setting time of the fixed-time synchronization is independent of the initial value but is affected by the system model and parameters, which is better than finite-time hybrid synchronization. In [33], the fixed-time synchronization was realized for the synchronization problem of the BAM neural network. Xu et al. [34] studied the finite-time and fixed-time synchronization of inertial neural networks and proved the difference between the two methods through simulation results. Wang et al. [35] realized the fixed-time and finite-time synchronization of the memristor chaotic system with sliding-mode control, and the superiority of fixed-time was proved by simulation. In summary, we will design an adaptive sliding-mode controller to realize the fixed-time synchronization of the new chaotic system.

For the application research of chaotic synchronization, it is known that the unpredictability of initial conditions made chaotic systems used in the field of image encryption [36, 37]. Lai et al. [38, 39] constructed and studied the image processing of non-equilibrium chaotic systems and memristor chaotic systems. In [40], the Lorenz system with an additional Fourier model was applied to the raster image encryption. In [41], a seventh-order memristor chaotic system was constructed, and a new and more complex algorithm was designed, which greatly enhances the effect of pixel encryption. In [42], a new four-dimensional chaotic system was constructed and applied to the field of image encryption. Then, we can use the theoretical results obtained in this article to apply the system to the application research of image encryption. This is the application innovation of this article. Event-triggered control [43–45] can save network resources and reduce energy consumption, which will become our next important research direction.

Inspired by the aforementioned contents, the contributions lie in the following three aspects:

1) A memristor-based sixth-order chaotic circuit is achieved by using flux-controlled memristors and charge-controlled memristors. Different from the third-order and fourth-order memristor chaotic systems described previously, this system has a higher order and a more complex model structure. The system model is analyzed by Kirchhoff’s law, and the chaotic characteristics and stability are analyzed.

2) A terminal sliding-mode surface and adaptive law are designed to solve the internal uncertainty and external disturbance. Different from the finite-time synchronization described previously, we realize the fixed-time synchronization scheme between sixth-order chaotic systems.

3) The synchronization method designed is applied to the image encryption algorithm based on obfuscation diffusion, and the image encryption process is realized. The results show that the better the encryption result, the higher the degree of anti-decryption.

2 Memristor-Based Sixth-Order Chaotic Circuits and Their Dynamics Analysis

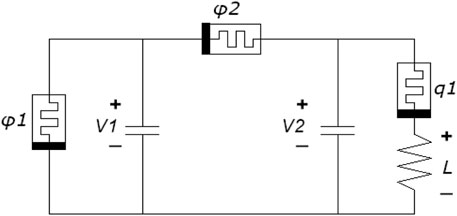
A memristor-based chaotic circuit based on Chua’s circuit is designed using two flux-controlled memristors and one charge-controlled memristor. The circuit diagram is described as follows:The flux-controlled memristor model used in this study is as follows:

$\begin{array}{c}q\left(\phi \right)=k\phi +l{\phi }^3\hfill \\ W\left(\phi \right)=\frac{dq\left(\phi \right)}{d\phi }=k+3l{\phi }^2,\hfill \end{array}(1)$

where q and φ are the charges and magnetic fluxs, respectively, k and l are constants, and W(φ) is conductance. Also, the charge-controlled memristor [46] used in this article is as follows:

$\begin{array}{c}M\left(q\right)=m+nq\hfill \\ \frac{dq}{dt}=\alpha i_M-\beta q-i_{M}q,\hfill \end{array}(2)$

where M(q) represents the resistance value. $\frac{dq}{dt}$ represents the internal state. i_M is the current flowing through the resistor, and m, n, α, and β are constants.

Remark 1. Compared with the aforementioned third-order and fourth-order memristor chaotic systems, our system is extended to the sixth-order, which has a more complex structure, and the three memristors make the model obtain rich chaotic dynamic characteristics.

In light of Kirchhoff’s voltage and current law analysis in Figure 1, the following equations can be obtained:

$\left\{\begin{array}{c}\frac{d{V}_1\left(t\right)}{dt}=-\frac{1}{C_1}\left[V_1\left(t\right)W\left({\phi }_1\left(t\right)\right)-\left(V_2\left(t\right)-V_1\left(t\right)\right)W\left({\phi }_2\left(t\right)\right)\right]\hfill \\ \frac{d{V}_2\left(t\right)}{dt}=-\frac{1}{C_2}\left[\left(\right.i_L\left(t\right)-\left(V_1\left(t\right)-V_2\left(t\right)\right)W\left({\phi }_2\left(t\right)\right)\right]\hfill \\ \frac{d{i}_L\left(t\right)}{dt}=\frac{1}{L}\left(V_2\left(t\right)+i_L\left(t\right)M\left(q\left(t\right)\right)\right)\hfill \\ \frac{d{\phi }_1\left(t\right)}{dt}=V_1\left(t\right)\hfill \\ \frac{d{\phi }_2\left(t\right)}{dt}=V_2\left(t\right)-V_1\left(t\right)\hfill \\ \frac{d{q}_1\left(t\right)}{dt}=-\alpha i_L\left(t\right)-\beta q_1\left(t\right)-i_L\left(t\right)q_1\left(t\right),\hfill \end{array}\right.(3)$

where i_L(t) is the current of L, V₁(t) and V₂(t) are the voltages of C₁ and C₂, respectively, φ₁(t), φ₁(t), and q₁(t) are the magnetic fluxes and charges of the three memristors, V₁(t) = x₁, V₂(t) = x₂, i_L(t) = x₃, φ₁(t) = x₄, φ₂(t) = x₅, q₁(t) = x₆, $\frac{1}{C_1}$= a, $\frac{1}{C_2}$= b, $\frac{1}{L}$=c, and i_M= − i_L(t). After normalization, the system equation is as follows:

$\left\{\begin{array}{c}{\dot{x}}_1=a\left[\left(x_2-x_1\right)\left(n_2+m_2{x_5}^2\right)-x_1\left(n_1+m_1{x_4}^2\right)\right]\hfill \\ {\dot{x}}_2=b\left[\left(x_1-x_2\right)\left(n_2+m_2{x_5}^2\right)-x_3\right]\hfill \\ {\dot{x}}_3=c\left(x_2+x_3\left(n_3+m_3{x}_6\right)\right)\hfill \\ {\dot{x}}_4=x_1\hfill \\ {\dot{x}}_5=x_2-x_1\hfill \\ {\dot{x}}_6=-\alpha x_3-\beta x_6-x_3{x}_6.\hfill \end{array}\right.(4)$

FIGURE 1

FIGURE 1. New memristor-based chaotic circuit.

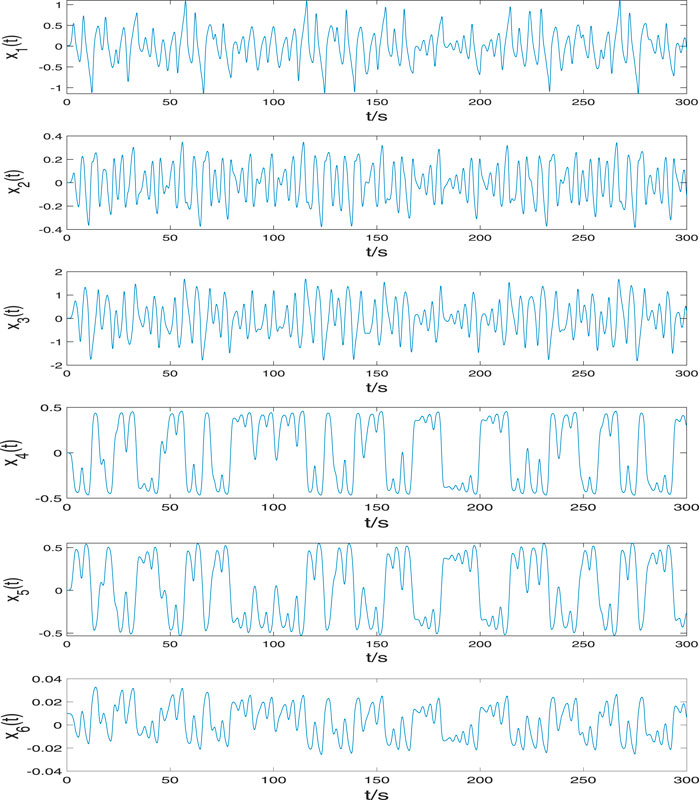
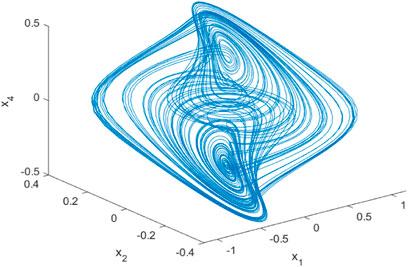
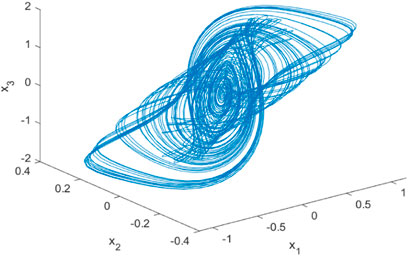
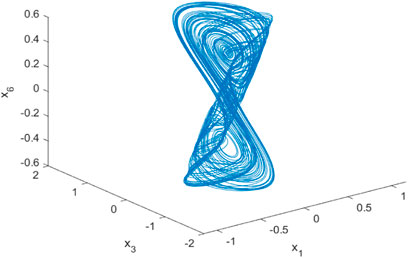
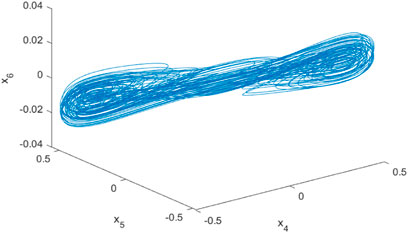
The next step is to analyze the dynamic characteristics. First, we investigate the chaotic characteristics. We choose a = 7, b = 1, c = 12, α = 0.3, β = 0.3, n₁ = −1.2, n₂ = 0.9, n₃ = 0.03, m₁ = 3.1, m₂ = 3.0, m₃ = 0.12, and then Figure 2 shows the state variables of Eq. 2. Figures 3–6 are the chaotic phase diagrams of x₁ − x₂ − x₄, x₁ − x₂ − x₃, x₁ − x₃ − x₅, x₄ − x₅ − x₆, which show the double vortex chaotic attractor.Second, the dissipation value of the calculated system is as follows:

$\begin{array}{cc}\hfill & \nabla V=\frac{\partial {\dot{x}}_1}{\partial x_1}+\frac{\partial {\dot{x}}_2}{\partial x_2}+\frac{\partial {\dot{x}}_3}{\partial x_3}+\frac{\partial {\dot{x}}_4}{\partial x_4}+\frac{\partial {\dot{x}}_5}{\partial x_5}+\frac{\partial {\dot{x}}_6}{\partial x_6}=-a\left(n_2+m_2{x_5}^2\right)\hfill \\ \hfill & -\left(n_1+m_1{x_4}^2\right)-b\left(n_2+m_2{x_5}^2\right)+c\left(n_3+m_3{x}_6\right)-\beta -x_3\hfill \\ \hfill & =-4.1116<0.\hfill \end{array}(5)$

The dissipation value of the system is less than zero, so the system is dissipative. Then, we calculate the following Lyapunov exponents of the memristor-based sixth-order chaotic L₁ = 0.2733, L₂ = 3.5526, L₃ = -9.4124, L₄ = -0.0071, L₅ = -0.0454, L₆ = -6.0755. Then, it can be found that two Lyapunov indices are greater than 0. Referring to the theory of [47], the system is a chaotic system.

FIGURE 2

FIGURE 2. Trajectories of the state variables x₁, x₂, x₃, x₄, x₅, x₆ of the system.

FIGURE 3

FIGURE 3. x₁ − x₂ − x₄.

FIGURE 4

FIGURE 4. x₁ − x₂ − x₃.

FIGURE 5

FIGURE 5. x₁ − x₃ − x₆.

FIGURE 6

FIGURE 6. x₄ − x₅ − x₆.

The next step is to analyze the stability of the system. The equilibrium point of Eq. 4 can be determined by the solution of Eq. 6,

$\left\{\begin{array}{c}0=a\left[\left(x_2-x_1\right)\left(n_2+m_2{x_5}^2\right)-x_1\left(n_1+m_1{x_4}^2\right)\right]\hfill \\ 0=b\left[\left(x_1-x_2\right)\left(n_2+m_2{x_5}^2\right)-x_3\right]\hfill \\ 0=c\left(x_2+x_3\left(n_3+m_3{x}_6\right)\right)\hfill \\ 0=x_1\hfill \\ 0=x_2-x_1\hfill \\ 0=-\alpha x_3-\beta x_6-x_3{x}_6.\hfill \end{array}\right.(6)$

The equilibrium solution is x₁ = x₂ = x₃ = x₆ = 0, x₄ = γ, x₅ = ɛ, where γ and ɛ are constants. It shows that the chaotic system has a plane equilibrium point corresponding to x₄ and x₅. The Jacobian matrix of the balanced set is shown as follows:

$J=\left[\begin{array}{cccccc}\hfill a\left[-\left(n_2+m_2{\epsilon }^2\right)-\left(n_1+m_1{\gamma }^2\right)\right]\hfill & \hfill a\left(n_2+m_2{\epsilon }^2\right)\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill \\ \hfill b\left(n_2+m_2{\epsilon }^2\right)\hfill & \hfill -b\left(n_2+m_2{\epsilon }^2\right)\hfill & \hfill -b\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill c\hfill & \hfill c{n}_3\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill \\ \hfill 1\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill \\ \hfill -1\hfill & \hfill 1\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill 0\hfill & \hfill -\alpha \hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill -\beta \hfill \end{array}\right].(7)$

The characteristic equation is obtained by the Jacobian matrix Eq. 7 as follows:

$\left[{\lambda }_1+a\left(n_1+m_1{\gamma }^2\right)\right]\left[{\lambda }_2+b\left(n_2+m_2{\epsilon }^2\right)-\frac{b}{n_3}\right]\left({\lambda }_3-c{n}_3\right){\lambda }_4{\lambda }_5\left({\lambda }_6+\beta \right)=0.(8)$

There are always two zero eigenvalues, and the other eigenvalues are determined by the system parameters. Because c, a, n₁, n₃ are positive, and λ₃ is greater than zero. According to the stability theory of chaotic systems, the aforementioned memristor-based chaotic system is unstable at such an equilibrium point.

3 Design of the Adaptive Sliding-Mode Synchronization Scheme

First, the drive system is Eq. 4, and the response system Eq. 9 is as follows:

$\left\{\begin{array}{c}{\dot{y}}_1=a\left[\left(y_2-y_1\right)\left(n_2+m_2{y_5}^2\right)-y_1\left(n_1+m_1{y_4}^2\right)\right]+{\varphi }_1\left(t\right)+f_1\left(t\right)+u_1\hfill \\ {\dot{y}}_2=b\left[\left(x_1-x_2\right)\left(n_2+m_2{y_5}^2\right)-y_3\right]+{\varphi }_2\left(t\right)+f_2\left(t\right)+u_2\hfill \\ {\dot{y}}_3=c\left(y_2+y_3\left(n_3+m_3{y}_6\right)\right)+{\varphi }_3\left(t\right)+f_3\left(t\right)+u_3\hfill \\ {\dot{y}}_4=y_1+{\varphi }_4\left(t\right)+f_4\left(t\right)+u_4\hfill \\ {\dot{y}}_5=y_2-y_1+{\varphi }_5\left(t\right)+f_5\left(t\right)+u_5\hfill \\ {\dot{y}}_6=-\alpha y_3-\beta y_6-y_3{y}_6+{\varphi }_6\left(t\right)+f_6\left(t\right)+u_6,\hfill \end{array}\right.(9)$

where ϕ_i(t) is the uncertain unknown model in Eq. 9, and f_i(t) is the external disturbance, and $\left|{\varphi }_i(t)\right|\le {\psi }_i,\left|f_i(t)\right|\le {\omega }_i$, ψ_i and ω_i are constants, and u_i(t) is the control input. Therefore, the error dynamic system can be expressed as:

$\left\{\begin{array}{c}{\dot{e}}_1=a\left[\left(y_2-y_1\right)\left(n_2+m_2{y_5}^2\right)-\left(x_2-x_1\right)\left(n_2+m_2{x_5}^2\right)\right.\hfill \\ \left.+x_1\left(n_1+m_1{x_4}^2\right)-y_1\left(n_1+m_1{y_4}^2\right)\right]+{\varphi }_1\left(t\right)+f_1\left(t\right)+u_1\hfill \\ {\dot{e}}_2=b\left[\left(x_1-x_2\right)\left(n_2+m_2{y_5}^2\right)-\left(x_1-x_2\right)\left(n_2+m_2{x_5}^2\right)-e_3\right]+{\varphi }_2\left(t\right)+f_2\left(t\right)+u_2\hfill \\ {\dot{e}}_3=c\left(e_2+y_3\left(n_3+m_3{y}_6\right)-x_3\left(n_3+m_3{x}_6\right)\right)+{\varphi }_3\left(t\right)+f_3\left(t\right)+u_3\hfill \\ {\dot{e}}_4=e_1+{\varphi }_4\left(t\right)+f_4\left(t\right)+u_4\hfill \\ {\dot{e}}_5=e_2-e_1+{\varphi }_5\left(t\right)+f_5\left(t\right)+u_5\hfill \\ {\dot{e}}_6=-\alpha e_3-\beta e_6-y_3{y}_6+x_3{x}_6+{\varphi }_6\left(t\right)+f_6\left(t\right)+u_6.\hfill \end{array}\right.(10)$

The next step is to design the synchronization controller u_i to realize the stability of the aforementioned error dynamic system. The sliding-mode control method is used to achieve the adaptive synchronization of memristor-based chaotic systems. The following lemmas will be used:

Lemma 1. [36] Consider the system $\dot{x}=f(x,t)$, when the continuous bounded functions V(x, t) satisfy the following conditions:

(i):V(0) = 0

(ii):V(t) ≤ −aV^χ(t) − bV^δ(t) − cV(t)where a > 0, b > 0, c > 0, 0 < χ < 1, δ > 1, and the system will achieve fixed-time stability and

$T_{\max }=\frac{1}{c\left(1-\chi \right)}\ln \left(1+\frac{c}{a}\right)+\frac{1}{c\left(\delta -1\right)}\ln \left(1+\frac{c}{b}\right).(11)$

Lemma 2. [48] For any real numbers ν₁, ν₂, …, ν_n and 0 < $g$₁ < 1, 1 < $g$₂, it satisfies that

$\begin{array}{c}\sum _{i=1}^n{\left|{\nu }_i\right|}^{g_1+1}\ge {\left(\sum _{i=1}^n{\left|{\nu }_i\right|}^2\right)}^{\left(g_{1+1}\right)/2}\hfill \\ \sum _{i=1}^n{\left|{\nu }_i\right|}^{g_2+1}\ge n^{\left(1-g_2\right)/2}{\left(\sum _{i=1}^n{\left|{\nu }_i\right|}^2\right)}^{\left(g_{2+1}\right)/2}\hfill \end{array}.(12)$

Then, we select the following sliding surface as:

$F_i\left(t\right)=e_i\left(t\right)+{\int }_0^t\left(j{\left|e_i\left(\tau \right)\right|}^{\frac{v}{b}}+k{\left|e_i\left(\tau \right)\right|}^{\frac{n}{m}}+l\left|e_i\left(\tau \right)\right|\right)\mathit{sgn}\left(e_i\left(\tau \right)\right)d\tau ,(13)$

where 0 < v < b, 0 < m < n, and j, k, l > 0, i = 1, …, 6, and we have

${\dot{F}}_i\left(t\right)={\dot{e}}_i\left(t\right)+\left(j{\left|e_i\left(t\right)\right|}^{\frac{v}{b}}+k{\left|e_i\left(t\right)\right|}^{\frac{n}{m}}+l\left|e_i\left(t\right)\right|\right)\mathit{sgn}\left(e_i\left(t\right)\right).(14)$

The adaptive sliding-mode controller is designated as:

$\left\{\begin{array}{c}{u}_1\left(t\right)=-\left(j{\left|e_1\left(t\right)\right|}^{\frac{v}{b}}+k{\left|e_1\left(t\right)\right|}^{\frac{n}{m}}+l\left|e_1\left(t\right)\right|\right)\mathit{sgn}\left(e_1\left(t\right)\right)-a\left[\left(y_2-y_1\right)\left(n_2+m_2{y_5}^2\right)-\left(x_2-x_1\right)\right.\hfill \\ \left.\left(n_2+m_2{x_5}^2\right)+x_1\left(n_1+m_1{x_4}^2\right)-y_1\left(n_1+m_1{y_4}^2\right)\right]-\left(\rho +{\left|F_1\left(t\right)\right|}^k\right)\mathit{sgn}\left(F_1\left(t\right)\right)\hfill \\ -\left({\widehat{\psi }}_1+{\widehat{\omega }}_1\right)\mathit{sgn}\left(F_1\left(t\right)\right)\hfill \\ u_2\left(t\right)=-\left(-j{\left|e_2\left(t\right)\right|}^{\frac{v}{b}}+k{\left|e_2\left(t\right)\right|}^{\frac{n}{m}}+l\left|e_2\left(t\right)\right|\right)\mathit{sgn}\left(e_2\left(t\right)\right)-b\left[\left(x_1-x_2\right)\left(n_2+m_2{y_5}^2\right)\right.\hfill \\ \left.-\left(x_1-x_2\right)\left(n_2+m_2{x_5}^2\right)-e_3\right]-\left(\rho +{\left|F_1\left(t\right)\right|}^k\right)\mathit{sgn}\left(F_2\left(t\right)\right)-\left({\widehat{\psi }}_2+{\widehat{\omega }}_2\right)\mathit{sgn}\left(F_2\left(t\right)\right)\hfill \\ u_3\left(t\right)=-\left(-j{\left|e_3\left(t\right)\right|}^{\frac{v}{b}}-k{\left|e_3\left(t\right)\right|}^{\frac{n}{m}}-l\left|e_3\left(t\right)\right|\right)\mathit{sgn}\left(e_3\left(t\right)\right)-c\left(e_2+y_3\left(n_3+m_3{y}_6\right)\right.\hfill \\ \left.-x_3\left(n_3+m_3{x}_6\right)\right)-\left(\rho +{\left|F_1\left(t\right)\right|}^k\right)\mathit{sgn}\left(F_3\left(t\right)\right)-\left({\widehat{\psi }}_3+{\widehat{\omega }}_3\right)\mathit{sgn}\left(F_3\left(t\right)\right)\hfill \\ u_4\left(t\right)=-\left(j{\left|e_4\left(t\right)\right|}^{\frac{v}{b}}+k{\left|e_4\left(t\right)\right|}^{\frac{n}{m}}+l\left|e_4\left(t\right)\right|\right)\mathit{sgn}\left(e_4\left(t\right)\right)-e_1-\left(\rho +{\left|F_1\left(t\right)\right|}^k\right)\mathit{sgn}\left(F_4\left(t\right)\right)\hfill \\ -\left({\widehat{\psi }}_4+{\widehat{\omega }}_4\right)\mathit{sgn}\left(F_4\left(t\right)\right)\hfill \\ u_5\left(t\right)=-\left(j{\left|e_5\left(t\right)\right|}^{\frac{v}{b}}+k{\left|e_5\left(t\right)\right|}^{\frac{n}{m}}+l\left|e_5\left(t\right)\right|\right)\mathit{sgn}\left(e_5\left(t\right)\right)-e_2-\left(\rho +{\left|F_1\left(t\right)\right|}^k\right)\mathit{sgn}\left(F_5\left(t\right)\right)\hfill \\ -\left({\widehat{\psi }}_5+{\widehat{\omega }}_5\right)\mathit{sgn}\left(F_5\left(t\right)\right)\hfill \\ u_6\left(t\right)=-\left(-j{\left|e_6\left(t\right)\right|}^{\frac{v}{b}}-k{\left|e_6\left(t\right)\right|}^{\frac{n}{m}}-l\left|e_6\left(t\right)\right|\right)\mathit{sgn}\left(e_6\left(t\right)\right)+\alpha e_3+\beta e_6+y_3{y}_6\hfill \\ -x_3{x}_6-\left(\rho +{\left|F_1\left(t\right)\right|}^k\right)\mathit{sgn}\left(F_6\left(t\right)\right)-\left({\widehat{\psi }}_6+{\widehat{\omega }}_6\right)\mathit{sgn}\left(F_6\left(t\right)\right),\hfill \end{array}\right.(15)$

where ρ, k are positive constants, and ${\widehat{\psi }}_i,{\widehat{\omega }}_i$ are estimates of ψ_i, ω_i. Also, the adaptive laws ${\widehat{\psi }}_i,{\widehat{\omega }}_i$ are selected as:

$\left\{\begin{array}{cc}\hfill & {\dot{\widehat{\psi }}}_i=\left|F_i\left(t\right)\right|\hfill \\ \hfill & {\dot{\widehat{\omega }}}_i=\left|F_i\left(t\right)\right|\hfill \end{array}\right.(16)$

Theorem 1. Under the influence of the controllers Eq. 13 and the adaptive laws Eq. 15, the error system Eq. 10 will reach sliding surfaces.

Proof. The following Lyapunov function is constructed:

$V_i\left(t\right)=\frac{1}{2}\sum _{i=1}^6\left(F_i^2\left(t\right)+\mathrm{\Delta }{{\psi }_i}^2+\mathrm{\Delta }{{\omega }_i}^2\right).(17)$

Taking the derivative of Eq. 17, one has

${\dot{V}}_i\left(t\right)=\sum _{i=1}^6\left(F_i\left(t\right){\dot{F}}_i\left(t\right)+\mathrm{\Delta }{\psi }_i{\dot{\widehat{\psi }}}_i+\mathrm{\Delta }{\omega }_i{\dot{\widehat{\omega }}}_i\right).(18)$

Substituting Eq. 14 into the aforementioned equation, we have

${\dot{V}}_i\left(t\right)=\sum _{i=1}^6{F}_i\left(t\right)\left[{\dot{e}}_i\left(t\right)+\left(j{\left|e_i\left(t\right)\right|}^{\frac{v}{b}}+k{\left|e_i\left(t\right)\right|}^{\frac{n}{m}}+l\left|e_i\left(t\right)\right|\right)\mathit{sgn}\left(e_i\left(t\right)\right)\right]+\sum _{i=1}^6\left({\widehat{\psi }}_i-{\psi }_i\right){\dot{\widehat{\psi }}}_i+\sum _{i=1}^6\left({\widehat{\omega }}_i-{\omega }_i\right){\dot{\widehat{\omega }}}_i.(19)$

Furthermore, we take the control scheme Eq. 13 into Eq. 10 and Eq. 18, we get

$\begin{array}{cc}\hfill & {\dot{V}}_i\left(t\right)=\sum _{i=1}^6{F}_i\left(t\right)\left[{\varphi }_i\left(t\right)+f_i\left(t\right)-\left(\rho +{\left|F_i\left(t\right)\right|}^k\right)\mathit{sgn}\left(F_i\left(t\right)\right)-\left({\widehat{\psi }}_i+{\widehat{\omega }}_i\right)\mathit{sgn}\left(F_i\left(t\right)\right)\right]+\sum _{i=1}^6\left({\widehat{\psi }}_i-{\psi }_i\right){\dot{\widehat{\psi }}}_i+\hfill \\ \hfill & \sum _{i=1}^6\left({\widehat{\omega }}_i-{\omega }_i\right){\dot{\widehat{\omega }}}_i\hfill \\ \hfill & =\sum _{i=1}^6\left({\varphi }_i\left(t\right)+f_i\left(t\right)\right)F_i\left(t\right)-\sum _{i=1}^6\left({\widehat{\psi }}_i+{\widehat{\omega }}_i\right)\left|F_i\left(t\right)\right|-\sum _{i=1}^6\rho \left|F_i\left(t\right)\right|+{\left|F_i\left(t\right)\right|}^{k+1}+\sum _{i=1}^6\left({\widehat{\psi }}_i\right.\hfill \\ \hfill & \left.-{\psi }_i\right){\dot{\widehat{\psi }}}_i+\sum _{i=1}^6\left({\widehat{\omega }}_i-{\omega }_i\right){\dot{\widehat{\omega }}}_i\hfill \end{array}.(20)$

According to the adaptive laws of Eq. 15, one has

$\begin{array}{cc}\hfill & {\dot{V}}_i\left(t\right)=\sum _{i=1}^6\left({\varphi }_i\left(t\right)+f_i\left(t\right)\right)F_i\left(t\right)-\sum _{i=1}^6\left({\widehat{\psi }}_i+{\widehat{\omega }}_i\right)\left|F_i\left(t\right)\right|-\sum _{i=1}^6\rho \left|F_i\left(t\right)\right|+{\left|F_i\left(t\right)\right|}^{k+1}+\sum _{i=1}^6\left({\widehat{\psi }}_i-{\psi }_i\right)\left|F_i\left(t\right)\right|+\hfill \\ \hfill & \sum _{i=1}^6\left({\widehat{\omega }}_i-{\omega }_i\right)\left|F_i\left(t\right)\right|\hfill \\ \hfill & \le \sum _{i=1}^6\left[\left({\varphi }_i\left(t\right)+f_i\left(t\right)\right)\left|F_i\left(t\right)\right|-\left({\psi }_i+{\omega }_i\right)\left|F_i\left(t\right)\right|-\rho \left|F_i\left(t\right)\right|-{\left|F_i\left(t\right)\right|}^{k+1}\right]\hfill \end{array}.(21)$

Due to $\left|{\varphi }_i(t)\right|\le {\psi }_i,\left|f_i(t)\right|\le {\omega }_i$, we obtain

$\begin{array}{cc}\hfill & {\dot{V}}_i\left(t\right)\le \sum _{i=1}^6\left[\left({\psi }_i+{\omega }_i\right)\left|F_i\left(t\right)\right|-\left({\psi }_i+{\omega }_i\right)\left|F_i\left(t\right)\right|-\left(\rho \left|F_i\left(t\right)\right|+{\left|F_1\left(t\right)\right|}^{k+1}\right)\right]\hfill \\ \hfill & \le \sum _{i=1}^6-\rho \left|F_i\left(t\right)\right|-{\left|F_i\left(t\right)\right|}^{k+1}\le 0.\hfill \end{array}(22)$

For the inequality (22), ${\dot{V}}_i(t)=0$ if and only if ${\dot{F}}_i(t)=0$; otherwise, ${\dot{V}}_i(t)<0$. According to the Lyapunov stability principle, the error system can move to the sliding surface.Theorem 2. After the error system Eq. 10 reaches the sliding surface, then the state variables of Eq. 10 will tend to zero in a fixed-time T₁, which means there will be fixed-time synchronization between the two chaotic systems Eqs 4, 9.

$T_1=\frac{v}{l\left(v-b\right)}\ln \left(1+\frac{2^{\frac{v-b}{2v}}l}{j}\right)+\frac{m}{l\left(n-m\right)}\ln \left(1+\frac{2^{\frac{m-n}{2m}}{6}^{\frac{n-m}{2m}}l}{k}\right).(23)$

Proof. The following Lyapunov function is constructed:

$V_i\left(t\right)=\frac{1}{2}\sum _{i=1}^6{e}_i^2\left(t\right).(24)$

When the system reaches the sliding surface, it will satisfy $F_i(t)=0,{\dot{F}}_i(t)=0,i=1,\dots ,6$, that is,

${\dot{F}}_i\left(t\right)={\dot{e}}_i\left(t\right)+\left(j{\left|e_i\left(t\right)\right|}^{\frac{v}{b}}+k{\left|e_i\left(t\right)\right|}^{\frac{n}{m}}+l\left|e_i\left(t\right)\right|\right)\mathit{sgn}\left(e_i\left(t\right)\right)=0.(25)$

Because the error systems satisfy

${\dot{e}}_i\left(t\right)=\left(-j{\left|e_i\left(t\right)\right|}^{\frac{v}{b}}-k{\left|e_i\left(t\right)\right|}^{\frac{n}{m}}-l\left|e_i\left(t\right)\right|\right)\mathit{sgn}\left(e_i\left(t\right)\right).(26)$

Therefore,

$\begin{array}{c}{\dot{V}}_i\left(t\right)=\sum _{i=1}^6{e}_i\left(t\right){\dot{e}}_i\left(t\right)\hfill \\ =\sum _{i=1}^6{e}_i\left(t\right)\left[\left(-j{\left|e_i\left(t\right)\right|}^{\frac{v}{b}}-k{\left|e_i\left(t\right)\right|}^{\frac{n}{m}}-l\left|e_i\left(t\right)\right|\right)\mathit{sgn}\left(e_i\left(t\right)\right)\right]\hfill \\ =\sum _{i=1}^6-j{\left|e_i\left(t\right)\right|}^{\frac{v}{b}+1}-k{\left|e_i\left(t\right)\right|}^{\frac{n}{m}+1}-l{\left|e_i\left(t\right)\right|}^2.\hfill \end{array}(27)$

According to Lemma 2, we continue to calculate Eq. 26 as

$\begin{array}{c}\hfill \\ {\dot{V}}_i\left(t\right)\le \sum _{i=1}^6\left[-j{\left({\left|e_i\left(t\right)\right|}^2\right)}^{\frac{v+b}{2b}}-6^{\frac{m-n}{2m}}k{\left({\left|e_i\left(t\right)\right|}^2\right)}^{\frac{n+m}{2m}}-l{\left|e_i\left(t\right)\right|}^2\right]\hfill \\ =-2^{\frac{v+b}{2b}}j{\left(V_i\left(t\right)\right)}^{\frac{v+b}{2b}}-2^{\frac{n+m}{2m}}{6}^{\frac{m-n}{2m}}k{\left(V_i\left(t\right)\right)}^{\frac{n+m}{2m}}-2l{V}_i\left(t\right).\hfill \end{array}(28)$

According to Lemma 1, we get that the error state variables of Eq. 10 will tend to zero in a fixed-time. Also, using Eq. 27, the setting time is

$T_1=\frac{v}{l\left(v-b\right)}\ln \left(1+\frac{2^{\frac{v-b}{2v}}l}{j}\right)+\frac{m}{l\left(n-m\right)}\ln \left(1+\frac{2^{\frac{m-n}{2m}}{6}^{\frac{n-m}{2m}}l}{k}\right).(29)$

Then, the proof of Theorem 2 is completed, which means that fixed-time synchronization is reached between the two chaotic systems Eqs 4,9.

Remark 2. Different from finite-time synchronization control, the bounds of fixed-time synchronization discussed in this article are only affected by system parameters, which are independent of the values of the initial time of the system.

In order to effectively verify the above theoretical results, a simulation example shows the significance of the adaptive sliding-mode synchronization scheme. We choose a = 7, b = 1, c = 12, α = 0.3, β = 0.3, n₁ = −1.2, n₂ = 0.9, n₃ = 0.03, m₁ = 3.1, m₂ = 3.0, m₃ = 0.12. Thus, the equation of the error system, Eq. 10 can be expressed as:

$\left\{\begin{array}{c}{\dot{e}}_1=21\left[\right.\left(y_2-y_1\right)\left({y_5}^2\right)-\left(x_2-x_1\right)\left({x_5}^2\right)+6.3e_2-5.1e_1+3.1\left(x_1{x_4}^2-y_1{y_4}^2\right)+{\varphi }_1\left(t\right)+f_1\left(t\right)+u_1\hfill \\ {\dot{e}}_2=\left[\left(y_1-y_2\right)\left(0.9+3{y_5}^2\right)-\left(x_1-x_2\right)\left(0.9+3{x_5}^2\right)-e_3\right]+{\varphi }_2\left(t\right)+f_2\left(t\right)+u_2\hfill \\ {\dot{e}}_3=\mathrm{12(}\left(\right.e_2+0.03e_3+0.12y_3{y}_6-0.12x_3{x}_6+{\varphi }_3\left(t\right)+f_3\left(t\right)+u_3\hfill \\ {\dot{e}}_4=e_1+{\varphi }_4\left(t\right)+f_4\left(t\right)+u_4\hfill \\ {\dot{e}}_5=e_2-e_1+{\varphi }_5\left(t\right)+f_5\left(t\right)+u_5\hfill \\ {\dot{e}}_6=-0.3e_3-0.3e_6-y_3{y}_6+x_3{x}_6+{\varphi }_6\left(t\right)+f_6\left(t\right)+u_6.\hfill \end{array}\right.(30)$

Selecting j = 10, k = 10, l = 2, v = 1, b = 2.5, n = 4, m = 1, k = 4, ρ = 2, then the control scheme is

$\left\{\begin{array}{c}{u}_1\left(t\right)=-\left(10{\left|e_1\left(\tau \right)\right|}^{0.4}+10{\left|e_1\left(\tau \right)\right|}^4+2.5\left|e_1\left(\tau \right)\right|\right)\mathit{sgn}\left(e_1\left(t\right)\right)-21\left[\left(y_2-y_1\right)\left({y_5}^2\right)-\left(x_2-x_1\right)\left({x_5}^2\right)\right]\hfill \\ -6.3e_2+5.1e_1-3.1\left(x_1{x_4}^2-y_1{y_4}^2\right)-\left(2+{\left|F_1\left(t\right)\right|}^4\right)\mathit{sgn}\left(F_1\left(t\right)\right)-\left({\widehat{\psi }}_1+{\widehat{\omega }}_1\right)\mathit{sgn}\left(F_1\left(t\right)\right)\hfill \\ u_2\left(t\right)=-\left(10{\left|e_2\left(\tau \right)\right|}^{0.4}+10{\left|e_2\left(\tau \right)\right|}^4+2.5\left|e_2\left(\tau \right)\right|\right)\mathit{sgn}\left(e_2\left(t\right)\right)-\left[\left(y_1-y_2\right)\left(0.9+3{y_5}^2\right)-\left(x_1-x_2\right)\right.\hfill \\ \left.\left(0.9+3{x_5}^2\right)-e_3\right]-\left(2+{\left|F_2\left(t\right)\right|}^4\right)\mathit{sgn}\left(F_2\left(t\right)\right)-\left({\widehat{\psi }}_2+{\widehat{\omega }}_2\right)\mathit{sgn}\left(F_2\left(t\right)\right)\hfill \\ u_3\left(t\right)=-\left(10{\left|e_i\left(\tau \right)\right|}^{0.4}+10{\left|e_i\left(\tau \right)\right|}^4+2.5\left|e_i\left(\tau \right)\right|\right)\mathit{sgn}\left(e_3\left(t\right)\right)-12\left(e_2+0.03e_3+0.12y_3{y}_6-\right.\hfill \\ \left.0.12x_3{x}_6\right)-\left(2+{\left|F_3\left(t\right)\right|}^4\right)\mathit{sgn}\left(F_3\left(t\right)\right)-\left({\widehat{\psi }}_3+{\widehat{\omega }}_3\right)\mathit{sgn}\left(F_3\left(t\right)\right)\hfill \\ u_4\left(t\right)=-\left(10{\left|e_i\left(\tau \right)\right|}^{0.4}+10{\left|e_i\left(\tau \right)\right|}^4+2.5\left|e_i\left(\tau \right)\right|\right)\mathit{sgn}\left(e_4\left(t\right)\right)-e_1-\left(2+{\left|F_4\left(t\right)\right|}^4\right)\mathit{sgn}\left(F_4\left(t\right)\right)-\hfill \\ \left({\widehat{\psi }}_4+{\widehat{\omega }}_4\right)\mathit{sgn}\left(F_4\left(t\right)\right)\hfill \\ u_5\left(t\right)=-\left(10{\left|e_i\left(\tau \right)\right|}^{0.4}+10{\left|e_i\left(\tau \right)\right|}^4+2.5\left|e_i\left(\tau \right)\right|\right)\mathit{sgn}\left(e_5\left(t\right)\right)-e_2+e_1-\left(2+{\left|F_5\left(t\right)\right|}^4\right)\mathit{sgn}\left(F_5\left(t\right)\right)-\hfill \\ \left({\widehat{\psi }}_5+{\widehat{\omega }}_5\right)\mathit{sgn}\left(F_5\left(t\right)\right)\hfill \\ u_6\left(t\right)=-\left(10{\left|e_i\left(\tau \right)\right|}^{0.4}+10{\left|e_i\left(\tau \right)\right|}^4+2.5\left|e_i\left(\tau \right)\right|\right)\mathit{sgn}\left(e_6\left(t\right)\right)+0.3e_3+0.3e_6+y_3{y}_6-x_3{x}_6-\left(2+\right.\hfill \\ \left.{\left|F_6\left(t\right)\right|}^4\right)\mathit{sgn}\left(F_6\left(t\right)\right)-\left({\widehat{\psi }}_6+{\widehat{\omega }}_6\right)\mathit{sgn}\left(F_6\left(t\right)\right).\hfill \end{array}\right.(31)$

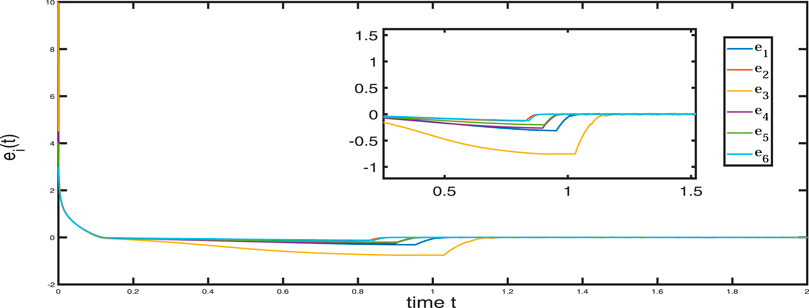
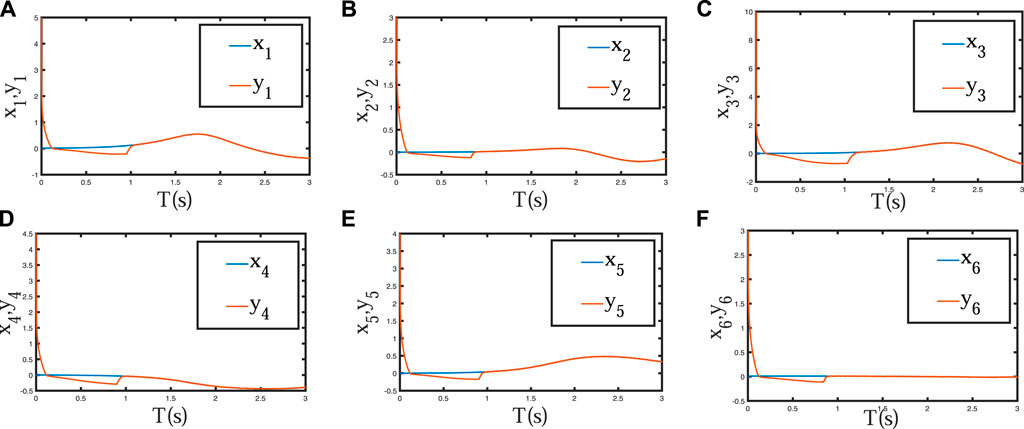
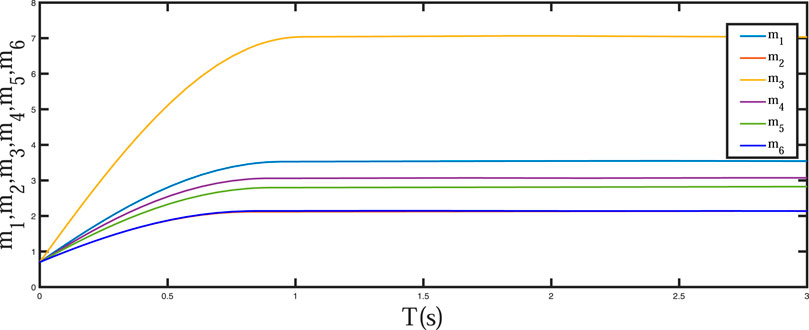
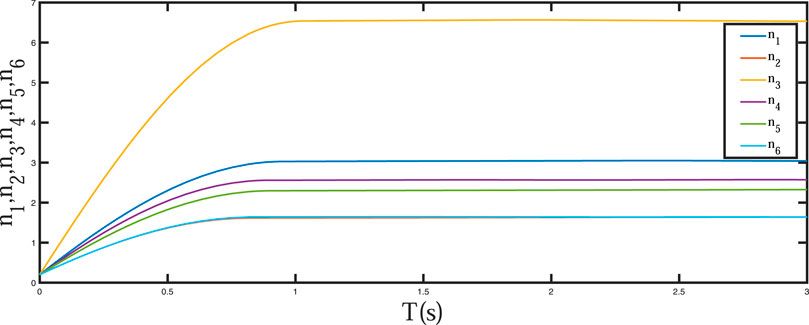
The initial values are set at x_i(0) = [0.01,0,0.01,0,0,0.01], and y_i(0) = [5.01,3.5,10.01,5.5,4,3.01], the external disturbances are set at f₁(t) = 0.25 cos(t), f₂(t) = 0.2 sin(t), f₃(t) = 0.45 cos(t), f₄(t) = 0.15 cos(t), f₅(t) = 0.3 cos(t), f₆(t) = 0.5 cos(t). The systems parameters are set at ϕ₁(t) = 0.13 cos(2πy₂), ϕ₂(t) = 0.2 cos(2πy₃), ϕ₃(t) = 0.4 cos(2πy₄), ϕ₄(t) = 0.3 cos(πy₅), ϕ₅(t) = 0.5 cos(5πy₆), ϕ₆(t) = 0.6 cos(2πy₁). Then, we can obtain the following simulation results:Figures 7, 8 show the memristor-based chaotic systems realize synchronization rapidly in fixed-time under the action of the adaptive sliding-mode controller. Figures 9, 10 show the time response curves of adaptive parameters m_i, n_i(i = 1, …, 6).

FIGURE 7

FIGURE 7. Trajectories of all synchronization error states.

FIGURE 8

FIGURE 8. The trajectories of state variables x_i, y_i(i = 1, …, 6), (A-F).

FIGURE 9

FIGURE 9. Trajectories of the update vector parameter m.

FIGURE 10

FIGURE 10. Trajectories of the update vector parameter n.

From Figures 7, 8, the response time of the error systems and state variables is less than 1.2s under the adaptive sliding-mode controller Eq. 15 and the adaptive laws (16). From Figures 9, 10, update parameters m and n converge to fixed values at 0.82 s. The simulation results, show the superiority of the designed adaptive sliding-mode controller. Our next step is to apply the simulation results to image encryption.

Remark 3. Different from the simulation results of finite-time synchronization control, the memristor-based sixth-order chaotic systems achieve fixed-time synchronization, which has a shorter stable time and whose setting time only depends on our system’s parameters.

4 Applications in Image Encryption

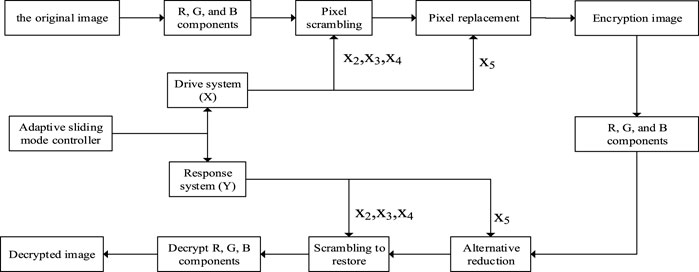
Because the memristor chaotic circuit has stronger noise like initial value sensitivity and long-term unpredictability, the application of the memristor-based chaotic circuit to image encryption will make the experimental images have a stronger anti-decoding function. We verify the effectiveness of the adaptive sliding-mode synchronization scheme in image encryption by using a chaotic obfuscation-diffusion mechanism [49], and the specific implementation process is shown in Figure 11.According to Figure 11, we first read three data matrices, R, G, and B, of the original image. Three parameters are selected from the driving system (4), x₂, x_3, and x₄ are selected from the memristor-based chaotic system designed in this article, which is to do the ascending and descending sequence and row displacement of R, G, B. We can obtain the data of R′, G′, and B′. Next, the pixel value is replaced by x₅ to get R″, G″, and B″. We choose the following parameter as:

$\left\{\begin{array}{c}{n}_{zx}=abs\left(x_5\left(z,x\right)\right)-round\left(x_5\left(z,x\right))\right)\left.\right)\times 10^2\hfill \\ m_{zx}=abs\left(x_5\left(z,x\right)-round\left(x_5\left(z,x\right)\right)\right)\times 10^3\hfill \end{array}\right..(32)$

The intermediate variable Q is as follows:

$Q=\left(n_{zx}\times z+m_{zx}\times x\right)\mathrm{mod}S,(33)$

where z and x are pixel row and row position, S is gray value. We get the matrix of the encrypted image R″, G″, B″ as:

$\left\{\begin{array}{c}{R}^{″}=R^{\prime }\oplus Q\hfill \\ G^{″}=G^{\prime }\oplus Q\hfill \\ B^{″}=B^{\prime }\oplus Q.\hfill \end{array}\right.(34)$

The binary sequence R″, G″, B″ is converted into a two-dimensional matrix R′′′, G′′′, B′′′, and the two-dimensional matrix R′′′, G′′′, B′′′ is reconstructed to obtain the encrypted image.

FIGURE 11

FIGURE 11. Image encryption process.

The above process belongs to the image encryption process. For the image decryption process, we read the three color data matrices R′′′, G′′′, B′′′ of the encrypted image. Then the pixel value is replaced by y₅ to get R″, G″, B″. And we set

$\left\{\begin{array}{cc}\hfill & {n^{\prime }}_{zx}=abs\left(y_5\left(z,x\right)\right)-round\left(y_5\left(z,x\right))\right)\left.\right)\times {10}^2\hfill \\ \hfill & {m^{\prime }}_{zx}=abs\left(y_5\left(z,x\right)-round\left(y_5\left(z,x\right)\right)\right)\times {10}^3\hfill \end{array}\right.(35)$

Then, we can easily get

$Q^{\prime }=\left(n_{zx}\times z+m_{zx}\times x\right)\mathrm{mod}{S}^{\prime }.(36)$

From the aforementioned equations, we can get

$\left\{\begin{array}{cc}\hfill & R^{″}=R^{\prime \prime \prime }\oplus Q^{\prime }\hfill \\ \hfill & G^{″}=G^{\prime \prime \prime }\oplus Q^{\prime }\hfill \\ \hfill & B^{″}=B^{\prime \prime \prime }\oplus Q^{\prime }\hfill \end{array}\right.(37)$

The binary sequence R″, G″, B″ is converted into a two-dimensional matrix R′, G′, B′. Three parameters are selected from the response system Eq. 9, y₂, y₃, y₄ are selected to do the ascending and descending sequence and row displacement of R′, G′, B′ to R, G, B, which is reconstructed to obtain the decryption images. The memristor-based six-order chaotic circuit and adaptive sliding-mode synchronization scheme are used to make the initial value and synchronization simulation, and the image encryption experiment is carried out. We selected two images for the encryption experiment, and the experimental results are shown in Figure 12.

FIGURE 12

FIGURE 12. Experimental dataset and their encrypted and decrypted versions (A-F).

We use histogram analysis, which is an important tool to assess encryption performance, to analyze Figure 12. The experimental results are shown in Figure 13.Then, we use chi-square test Eq. 38 to analyze the encrypted images’ histograms in Figure 13,

$x^2=\sum _{q=0}^{255}\frac{{\left(f_q-n\right)}^2}{n},(38)$

where f_q is the frequency distribution of the encrypted images’ histograms and n = (α*β)/256, for a α*β dimension image. We get $x_{image01}^2=271.4377$ and $x_{image02}^2=268.2371$. Compared with $x_{0.05}^2(255)=293.24783$, $x_{image01}^2,x_{image02}^2<x_{0.05}^2(255)$. It can be seen that the original images’ histograms fluctuate greatly, while the encrypted images’ histograms are evenly distributed and have fluctuation. A good encryption algorithm can make the distribution of encrypted images as uniform as possible. Therefore, the adaptive sliding-mode controller makes the memristor-based sixth-order chaotic system suitable for image encryption, which improves the security of signal transmission.

FIGURE 13

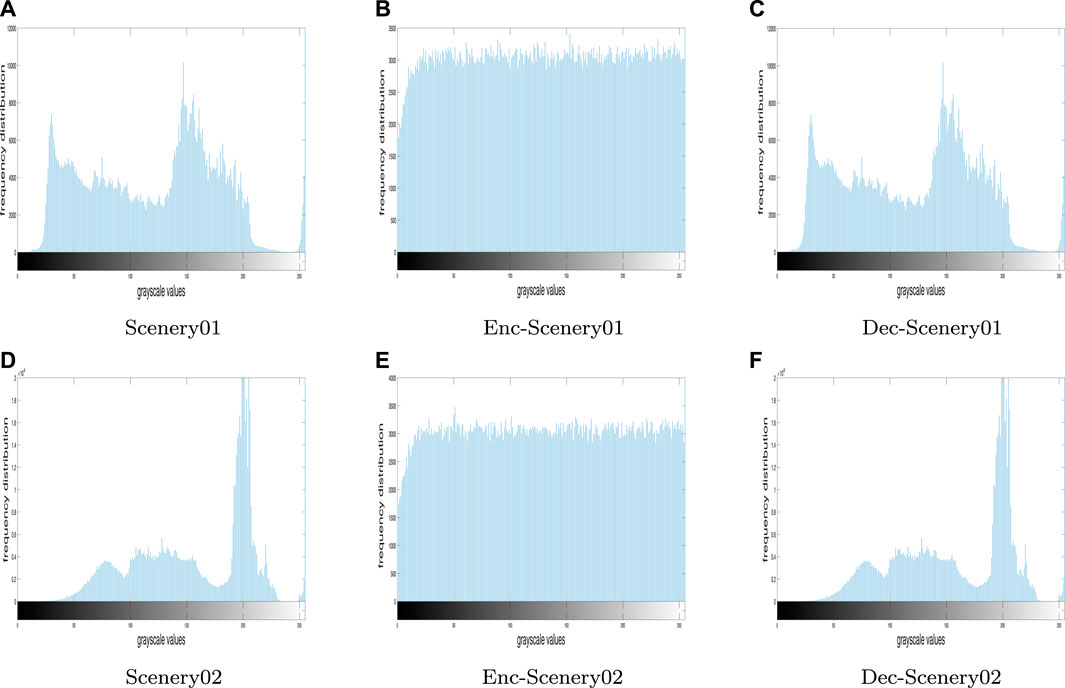
FIGURE 13. Histograms of the original, encrypted and decrypted greyscale images (A-F) in Figure 12.

Conclusion

This article has established a memristor-based sixth-order chaotic circuit. The dynamic analysis and sliding-mode synchronization and its application have been studied. A sixth-order chaotic system has been constructed by using flux-controlled memristors and charge-controlled memristors. For the synchronization of sixth-order memristor chaotic systems with unknown models and external disturbances, a class of terminal sliding-mode surface and adaptive control laws is designed. After coming to the sliding-mode surface by asymptotic stabilization, the system achieves synchronization in a fixed time, and a simulation example shows the effectiveness of the scheme. Furthermore, the sixth-order chaotic system and synchronization scheme have been applied to image protection. The results show that the algorithm can be combined with the system, which has a good encryption effect and high anti-interference. This work applies the proposed memristor-based sixth-order chaotic system as a network node to the synchronization of complex networks.

Data Availability Statement

The original contributions presented in the study are included in the article/Supplementary Material, further inquiries can be directed to the corresponding author.

Author Contributions

XY, HL, and XC participated in the sequence alignment and drafted the manuscript. XY, HL, XC, and LH participated in the study and performed the statistical analysis. XY, XC, HL, and LS conceived the idea of the study and participated in its design and coordination. XY, LH, and LS helped to draft the manuscript. All authors read and approved the final manuscript.

Funding

This work was supported by the National Natural Science Foundation of China under Grant Nos. 62173175, 12026235, 12026234, 61903170, 61903171, 11805091, and 61877033, by the Natural Science Foundation of Shandong Province under Grant Nos. ZR2019BF045, ZR2019MF021, and ZR2019QF004, and by the Key Research and Development Project of Shandong Province of China under Grant No.2019GGX101003

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s Note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors, and the reviewers. Any product that may be evaluated in this article, or any claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

1. Rössler OE. An Equation for Continuous Chaos. Phys Lett A (1976) 57:397–8. doi:10.1016/0375-9601(76)90101-8

CrossRef Full Text | Google Scholar

2. Chen G, Ueta T. Yet Another Chaotic Attractor. Int J Bifurcation Chaos (1999) 09:1465–6. doi:10.1142/s0218127499001024

CrossRef Full Text | Google Scholar

3. Liu C, Liu T, Liu L, Liu K. A New Chaotic Attractor. Chaos, Solitons & Fractals (2004) 22:1031–8. doi:10.1016/j.chaos.2004.02.060

CrossRef Full Text | Google Scholar

4. Lü J, Chen G. A New Chaotic Attractor Coined. Int J Bifurcation Chaos (2002) 12:659–61. doi:10.1142/s0218127402004620

CrossRef Full Text | Google Scholar

5. Lü J, Chen G, Cheng D, Celikovsky S. Bridge the gap between the Lorenz System and the Chen System. Int J Bifurcation Chaos (2002) 12:2917–26. doi:10.1142/s021812740200631x

CrossRef Full Text | Google Scholar

6. Wu X, Wang H, He S. Localization of Hidden Attractors in Chua¡ ¯ S System with Absolute Nonlinearity and its FPGA Implementation. Front Phys (2021) 9:674. doi:10.3389/fphy.2021.788329

CrossRef Full Text | Google Scholar

7. Lai Q, Bao B, Chen C. Circuit Application of Chaotic Systems: Modeling, Dynamical Analysis and Control. Eur Phys J Spec Top (2021) 230(7):1691–4. doi:10.1140/epjs/s11734-021-00202-0

CrossRef Full Text | Google Scholar

8. Chua L. Memristor-the Missing Circuit Element. IEEE Trans Circuit Theor (1971) 18:507–19. doi:10.1109/tct.1971.1083337

CrossRef Full Text | Google Scholar

9. Sun J, Zhao X, Fang J, Wang Y. Autonomous Memristor Chaotic Systems of Infinite Chaotic Attractors and Circuitry Realization. Nonlinear Dyn (2018) 94(4):2879–87. doi:10.1007/s11071-018-4531-4

CrossRef Full Text | Google Scholar

10. Sun J, Han G, Zeng Z, Wang Y. Memristor-based Neural Network Circuit of Full-Function Pavlov Associative Memory with Time Delay and Variable Learning Rate. IEEE Trans Cybern (2020) 50(7):2935–45. doi:10.1109/TCYB.2019.2951520

PubMed Abstract | CrossRef Full Text | Google Scholar

11. Sun J, Han J, Wang Y, Liu P. Memristor-based Neural Network Circuit of Emotion Congruent Memory with Mental Fatigue and Emotion Inhibition. IEEE Trans Biomed Circuits Syst (2021) 15(3):606–16. doi:10.1109/tbcas.2021.3090786

PubMed Abstract | CrossRef Full Text | Google Scholar

12. Sun J, Han J, Liu P, Wang Y. Memristor-based Neural Network Circuit of Pavlov Associative Memory with Dual Mode Switching. AEU - Int J Elect Commun (2021) 129:153552. doi:10.1016/j.aeue.2020.153552

CrossRef Full Text | Google Scholar

13. Li C, Joo-Chen Thio W, Ho-Ching Iu H, Lu T. A Memristive Chaotic Oscillator with Increasing Amplitude and Frequency. IEEE Access (2018) 6:12945–50. doi:10.1109/access.2017.2788408

CrossRef Full Text | Google Scholar

14. Jiang Y, Li C, Zhang C, Zhao Y, Zang H. A Double-Memristor Hyperchaotic Oscillator with Complete Amplitude Control. IEEE Trans Circuits Syst(2021) 68(12):4935–44. doi:10.1109/tcsi.2021.3121499

CrossRef Full Text | Google Scholar

15. Muthuswamy B, Kokate P. Memristor-based Chaotic Circuits. IETE Tech Rev (2009) 26:417–29. doi:10.4103/0256-4602.57827

CrossRef Full Text | Google Scholar

16. Akgül A, Rajagopal K, Durdu A, Pala MA, Boyraz ÖF, Yildiz MZ. A Simple Fractional-Order Chaotic System Based on Memristor and Memcapacitor and its Synchronization Application. Chaos, Solitons & Fractals (2021) 152:111306. doi:10.1016/j.chaos.2021.111306

CrossRef Full Text | Google Scholar

17. Minati L, Gambuzza LV, Thio WJ, Sprott JC, Frasca M. A Chaotic Circuit Based on a Physical Memristor. Chaos, Solitons & Fractals (2020) 138:109990. doi:10.1016/j.chaos.2020.109990

CrossRef Full Text | Google Scholar

18. Lai Q, Wan Z, Akgul A, Boyraz OF, Yildiz MZ. Design and Implementation of a New Memristive Chaotic System with Application in Touchless Fingerprint Encryption. Chin J Phys (2020) 67:615–30. doi:10.1016/j.cjph.2020.08.018

CrossRef Full Text | Google Scholar

19. Min F, Wang Z, Cao Y. Multistability Analysis of a Dual-Memristor Circuit Based on Hyperbolic Function. Acta Electonica Sinica (2018) 46:486.

Google Scholar

20. Wang L, Dong T, Wang X. Projective Synchronization of Three Memristor Chaotic Systems with Unknown Parameters via Adaptive Control. In: 2018 Ninth International Conference on Intelligent Control and Information Processing (ICICIP). IEEE (2018). p. 117–21. doi:10.1109/icicip.2018.8606662

CrossRef Full Text | Google Scholar

21. Xinsong Yang X, Ho DWC. Synchronization of Delayed Memristive Neural Networks: Robust Analysis Approach. IEEE Trans Cybern (2016) 46(12):3377–87. doi:10.1109/TCYB.2015.2505903

PubMed Abstract | CrossRef Full Text | Google Scholar

22. Yang X, Cao J, Liang J. Exponential Synchronization of Memristive Neural Networks with Delays: Interval Matrix Method. IEEE Trans Neural Netw Learn Syst (2016) 28(8):1878–88. doi:10.1109/TNNLS.2016.2561298

PubMed Abstract | CrossRef Full Text | Google Scholar

23. Feng Y, Yu X, Man Z. Non-singular Terminal Sliding Mode Control of Rigid Manipulators. Automatica (2002) 38:2159–67. doi:10.1016/s0005-1098(02)00147-4

CrossRef Full Text | Google Scholar

24. Yu S, Yu X, Shirinzadeh B, Man Z. Continuous Finite-Time Control for Robotic Manipulators with Terminal Sliding Mode. Automatica (2005) 41:1957–64. doi:10.1016/j.automatica.2005.07.001

CrossRef Full Text | Google Scholar

25. Chen X, Park JH, Cao J, Qiu J. Adaptive Synchronization of Multiple Uncertain Coupled Chaotic Systems via Sliding Mode Control. Neurocomputing (2018) 273:9–21. doi:10.1016/j.neucom.2017.07.063

CrossRef Full Text | Google Scholar

26. Chen X, Park JH, Cao J, Qiu J. Sliding Mode Synchronization of Multiple Chaotic Systems with Uncertainties and Disturbances. Appl Math Comput (2017) 308:161–73. doi:10.1016/j.amc.2017.03.032

CrossRef Full Text | Google Scholar

27. Xu G, Zhao S, Cheng Y. Chaotic Synchronization Based on Improved Global Nonlinear Integral Sliding Mode Control☆. Comput Electr Eng (2021) 96:107497. doi:10.1016/j.compeleceng.2021.107497

CrossRef Full Text | Google Scholar

28. Guo J, Zheng X, Zhou J. Adaptive Sliding Mode Control for High-Order System with Mismatched Disturbances. Sci China Inf Sci (2020) 63:179205. doi:10.1007/s11432-018-9566-1

CrossRef Full Text | Google Scholar

29. Liu H, Chen X, Qiu J. Finite-time Synchronization of Complex Networks with Hybrid-Coupled Time-Varying Delay via Event-Triggered Aperiodically Intermittent Pinning Control. Math Methods Appl Sci (2021).

Google Scholar

30. Wang L, Dong T, Ge M-F. Finite-time Synchronization of Memristor Chaotic Systems and its Application in Image Encryption. Appl Math Comput (2019) 347:293–305. doi:10.1016/j.amc.2018.11.017

CrossRef Full Text | Google Scholar

31. Chen X, Huang T, Cao J, Park JH, Qiu J. Finite‐time Multi‐switching Sliding Mode Synchronisation for Multiple Uncertain Complex Chaotic Systems with Network Transmission Mode. IET Control Theor Appl (2019) 13:1246–57. doi:10.1049/iet-cta.2018.5661

CrossRef Full Text | Google Scholar

32. Xiong X, Yang X, Cao J. Finite-time Control for a Class of Hybrid Systems via Quantized Intermittent Control. Sci China Inf Sci (2020) 63(9):1–16. doi:10.1007/s11432-018-2727-5

CrossRef Full Text | Google Scholar

33. Guo Y, Luo Y, Wang W, Luo X, Ge C, Kurths J, et al. Fixed-time Synchronization of Complex-Valued Memristive BAM Neural Network and Applications in Image Encryption and Decryption. Int J Control Autom Syst (2020) 18:462–76. doi:10.1007/s12555-018-0676-7

CrossRef Full Text | Google Scholar

34. Xu D, Yang X, Tang R. Finite-time and Fixed-Time Non-chattering Control for Inertial Neural Networks with Discontinuous Activations and Proportional Delay. Neural Process Lett (2020) 51(3):2337–53. doi:10.1007/s11063-020-10199-7

CrossRef Full Text | Google Scholar

35. Wang L, Jiang S, Ge M-F, Hu C, Hu J. Finite-/Fixed-Time Synchronization of Memristor Chaotic Systems and Image Encryption Application. IEEE Trans Circuits Syst(2021) 68(12):4957–69. doi:10.1109/tcsi.2021.3121555

CrossRef Full Text | Google Scholar

36. Xiu C, Zhou R, Zhao S, Xu G. Memristive Hyperchaos Secure Communication Based on Sliding Mode Control. Nonlinear Dyn (2021) 104:789–805. doi:10.1007/s11071-021-06302-9

CrossRef Full Text | Google Scholar

37. He W, Luo T, Tang Y, Du W, Tian YC, Qian F. Secure Communication Based on Quantized Synchronization of Chaotic Neural Networks under an Event-Triggered Strategy. IEEE Trans Neural Netw Learn Syst (2019) 31:3334–45. doi:10.1109/TNNLS.2019.2943548

PubMed Abstract | CrossRef Full Text | Google Scholar

38. Lai Q, Zhang H, Kuate PDK. Analysis and Implementation of No-Equilibrium Chaotic System with Application in Image Encryption. Appl Intelligence (2022) 1–24. doi:10.1007/s10489-021-03071-1

CrossRef Full Text | Google Scholar

39. Li H, Wang L, Lai Q. Synchronization of a Memristor Chaotic System and Image Encryption. Int J Bifurcation Chaos (2021) 31(16):2150251. doi:10.1142/s0218127421502515

CrossRef Full Text | Google Scholar

40. Moon S, Baik J-J, Seo JM. Chaos Synchronization in Generalized Lorenz Systems and an Application to Image Encryption. Commun Nonlinear Sci Numer Simulation (2021) 96:105708. doi:10.1016/j.cnsns.2021.105708

CrossRef Full Text | Google Scholar

41. Ye X, Wang X, Gao S, Mou J, Wang Z, Yang F. A New Chaotic Circuit with Multiple Memristors and its Application in Image Encryption. Nonlinear Dyn (2020) 99:1489–506. doi:10.1007/s11071-019-05370-2

CrossRef Full Text | Google Scholar

42. Alawida M, Samsudin A, Teh JS, Alkhawaldeh RS. A New Hybrid Digital Chaotic System with Applications in Image Encryption. Signal Process. (2019) 160:45–58. doi:10.1016/j.sigpro.2019.02.016

CrossRef Full Text | Google Scholar

43. Yang X, Feng G, He C. Event-Triggered Dynamic Output Quantization Control of Switched TS Fuzzy Systems with Unstable Modes. IEEE Trans Fuzzy Syst (2022). doi:10.1109/tfuzz.2022.3145808

CrossRef Full Text | Google Scholar

44. Liu Y, Tang R, Zhou C, Xiang Z, Yang X. Event-triggered Leader-Following Consensus of Multiple Mechanical Systems with Switched Dynamics. Int J Syst Sci (2020) 51(16):3563–72. doi:10.1080/00207721.2020.1818146

CrossRef Full Text | Google Scholar

45. Hu S, Qiu J, Chen X. Dynamic Event-Triggered Control for Leader-Following Consensus of Multiagent Systems with the Estimator. IET Control Theory & Applications (2022) 16:475–484. doi:10.1049/cth2.12245

CrossRef Full Text | Google Scholar

46. Tan Z, Yang H, Liu Q. Analysis and Implementation of a Simplest Charge-Controlled Memristor Chaotic Circuit. Chin J Comput Phys (2015) 32:496–504.

Google Scholar

47. Letellier C, Rossler O. Hyperchaos. Scholarpedia (2007) 2(8):1936. doi:10.4249/scholarpedia.1936

CrossRef Full Text | Google Scholar

48. Beckenbach EF, Bellman R. Inequalities. Springer Science & Business Media (2012).

Google Scholar

49. Yoon JW, Kim H. An Image Encryption Scheme with a Pseudorandom Permutation Based on Chaotic Maps. Commun Nonlinear Sci Numer Simulation (2010) 15:3998–4006. doi:10.1016/j.cnsns.2010.01.041

CrossRef Full Text | Google Scholar