Self-Propelled Motion of the Camphor Float With n-Fold Rotational Symmetry

It is known that a camphor particle at a water surface exhibits self-propulsion since it releases camphor molecules at the surface and reduces the surface tension, and the gradient of surface tension drives the camphor particle itself. Such a motion is considered to be driven by the concentration field of the chemicals emitted by the particle itself. It is also known that the shape of the particle seriously affects the mode of motion. In order to understand the universal mechanism on the effect of the shape on such a self-propelled motion, we theoretically investigated the bifurcation structure of the motion of the camphor float with n-fold rotational symmetry, which comprises n camphor disks attached to a rigid light circular plate along a periphery with an equivalent spacing. Here, we mainly studied the cases with n = 2 and 3. We found that the camphor float with n = 2 moves in the direction perpendicular to the line connecting the two camphor disks, while that with n = 3 changes its direction of motion depending on the size of the camphor float.

1 Introduction

Self-propelled particles, which can transduce free energy into kinetic energy under nonequilibrium conditions, have been investigated for last decades since they can be a model for the motion of living organisms [1–6]. The relationship between the self-propelled motion and the shape of the particle has attracted much attention, and both experimental and theoretical studies have been intensively reported [7–11]. When we discuss the mechanism of the self-propelled motion, we have to keep in mind that the conservation of momentum should hold rigourously. For example, a self-propelled liquid droplet in the other immisible liquid can be discussed based on the momentum exchange in hydrodynamics. There have been many papers on such self-propelled motions, most of which are considered in the regime of low-Reynolds number [4, 12–15]. In contrast, some systems, such as a self-propelled particle at a liquid surface, a self-propelled droplet on a solid surface, and a living cell on a substrate, can apparently break the momentum conservation [16–18]. It is sure that they exchange momentum with the environment but the momentum conservation is not treated explicitly in their model.

The self-propelled motion of a camphor disk at a water surface is one of the most studied self-propelled motion [19–26]. The camphor disk releases the camphor molecules at a water surface, and the concentration gradient of the camphor molecules induces the surface tension gradient, which drives the disk. Such a camphor disk motion can be discussed based on the hydrodynamics [27–29], but it has also been discussed from the viewpoint of the coupling between the reaction-diffusion field and the disk motion [9, 22, 30, 31]. Based on the latter approach, we have studied the self-propelled motion of a camphor particle with the shape other than a circle, and have discussed the relation between the camphor particle shape and the direction of motion [6, 9, 32–35]. For example, we show that an elliptic camphor particle moves in the dircetion of its minor axis [9, 33–35]. As for a triangular-shaped camphor particle, the direction of motion depends on the size of the particle; a smaller particle moves in the direction of a corner, while a larger particle moves in the direction of a side [35]. These studies clarify that the symmetric property of the shape is important for determining the preferable direction of the self-propelled motion.

Motivated by these previous studies, here we propose the simpler system with which the relation between the direction of self-propelled motion and symmetric property can be discussed; a camphor float with n-fold rotational symmetry, which comprises a rigid light circular plate attaching n camphor disks along a periphery with an equivalent spacing. From the viewpoint of rotational symmetry, an elliptic camphor particle corresponds to the camphor float with n = 2, while the triangular camphor particle corresponds to that with n = 3; we mainly discuss these two cases. By considering these camphor floats, we discuss the direction of the self-propelled motion affected by the symmetric properties. In the present paper, we first formulate the mathematical model for them, and then analytically discuss the preferable direction of the self-propelled motion. Finally, we check the validity of the analytical results by numerical simulations.

2 Model

We construct a mathematical model that describes the self-propelled motion of the camphor float with n-fold rotational symmetry, which is floating at a water surface. The float comprises a rigid light circular plate attaching n camphor disks along a periphery with an equivalent spacing. We consider the concentration field of camphor molecules u(r, t) on a two-dimensional plane corresponding to the water surface. As for the motion of the camphor float, the position and configureation can be described by the center of mass of the camphor float r_c and the characteristic angle θ_c. For the camphor float with n-fold rotational symmetry, the center position of the k-th camphor disk (k = 0, 1, …, n − 1) is set as

${\mathit{r}}_k={\mathit{r}}_c+\ell \mathit{e}\left({\theta }_c+\frac{2\pi k}{n}\right),(1)$

where e(θ) is the unit vector defined as

$\mathit{e}\left(\theta \right)=\cos \theta {\mathit{e}}_x+\sin \theta {\mathit{e}}_y.(2)$

Here, e_x and e_y are the unit vectors in x- and y-directions, respectively. The schematic illustrations for the camphor floats with n = 2 and 3 are shown in Figure 1.

FIGURE 1

FIGURE 1. Schematic illustration for the camphor float with n-fold rotational symmetry. (A) n = 2. (B) n = 3.

Each camphor disk has a radius of R and supplys the camphor molecules to the water surface at the rate of S₀. The dynamics of u(r, t) is described as

$\frac{\partial u}{\partial t}=D{\nabla }^{2}u-au+\frac{S_0}{\pi R^2}\sum _{k=0}^{n-1}\mathrm{\Theta }\left(R-\left|\mathit{r}-{\mathit{r}}_k\right|\right).(3)$

The first, second, and third terms in the righthand side correspond to the diffusion, sublimation, and supply of the camphor molecules. Here, D is the effiective diffusion coefficient [36, 37], a is the sublimation rate, and $\mathrm{\Theta }\left(\cdot \right)$ is the Heaviside’s step function. It should be noted that the effective diffusion coefficient is introduced to include the effect by the hydrodynamic transport due to the Marangoni effect. The effective diffusion coefficient is estimated from the concentration profile with a resting camphor particle based on the reaction-diffusion-advection equation. Thus, this approxiation works well when the velocity is small.

As for the motion of the camphor float, we consider the equation of motion for the k-th camphor disk as

$m\frac{d^2{\mathit{r}}_k}{d{t}^2}=-\eta \frac{d{\mathit{r}}_k}{dt}+{\mathit{F}}_k^{\left(\mathrm{c}\mathrm{o}\mathrm{n}\mathrm{c}\right)}+{\mathit{F}}_k^{\left(\mathrm{i}\mathrm{n}\mathrm{t}\right)},(4)$

where m is the mass, and η is the viscous friction coefficient of the camphor disk. We assume that they are both proportional to the area of the camphor disk as m = πρR² and η = πκR². ${\mathit{F}}_k^{(\mathrm{c}\mathrm{o}\mathrm{n}\mathrm{c})}$ is the force originating from the surface tension gradient due to the camphor concentration field described as

${\mathit{F}}_k^{\left(\mathrm{c}\mathrm{o}\mathrm{n}\mathrm{c}\right)}={\oint }_{\partial {\mathrm{\Omega }}_k}\gamma \left(u\left({\mathit{r}}^{\prime }\right)\right)\mathit{n}\left({\mathit{r}}^{\prime }\right)d{\ell }^{\prime }(5)$

$={\iint }_{{\mathrm{\Omega }}_k}\left({\nabla }^{\prime }\gamma \left(u\left({\mathit{r}}^{\prime }\right)\right)\right)d{A}^{\prime }.(6)$

Here, Ω_k is the region of the k-th camphor disk, which is defined as

${\mathrm{\Omega }}_k=\left\{\mathit{r}|\left|\mathit{r}-{\mathit{r}}_k\right|\le R\right\},(7)$

and ∂Ω_k is the periphery of Ω_k. dℓ′ is the line element along the periphery, n(r′) is the outward unit normal vector at the periphery, ∇′ is the nabla operator with respect to r′, and dA′ is the area element in the region Ω_k. Here, the relation between the surface tension and camphor concentration is assumed to be

$\gamma ={\mathrm{\Gamma }}_0-\mathrm{\Gamma }u,(8)$

where Γ₀ is the surface tension of pure water, and Γ is a positive constant connecting the camphor concentration and surface tension [37–39]. Using this relationship, the force ${\mathit{F}}_k^{(\mathrm{c}\mathrm{o}\mathrm{n}\mathrm{c})}$ is described as

${\mathit{F}}_k^{\left(\mathrm{c}\mathrm{o}\mathrm{n}\mathrm{c}\right)}=-\mathrm{\Gamma }{\oint }_{\partial {\mathrm{\Omega }}_k}u\left({\mathit{r}}^{\prime }\right)\mathit{n}\left({\mathit{r}}^{\prime }\right)d{\ell }^{\prime }(9)$

$=-\mathrm{\Gamma }{\iint }_{{\mathrm{\Omega }}_k}\left({\nabla }^{\prime }u\left({\mathit{r}}^{\prime }\right)\right)d{A}^{\prime }.(10)$

${\mathit{F}}_k^{(\mathrm{i}\mathrm{n}\mathrm{t})}$ is the internal force that maintains the configuration of the camphor float. It can be described as the summation of the internal force, f_k,j, from the j-th disk as

${\mathit{F}}_k^{\left(\mathrm{i}\mathrm{n}\mathrm{t}\right)}=\sum _{j=0}^{n-1}{\mathit{f}}_{k,j},(11)$

where

${\mathit{f}}_{k,j}=-{\mathit{f}}_{j,k},(12)$

and

${\mathit{f}}_{k,j}\propto {\mathit{r}}_k-{\mathit{r}}_j.(13)$

Here, it should be noted that f_k,k = 0.

By summing up the equations of motion for n disks, we obtain the evolution equation for r_c as

$\begin{array}{ll}\hfill \rho \pi R^{2}n\frac{d^2{\mathit{r}}_c}{d{t}^2}=& -\kappa \pi R^{2}n\frac{d{\mathit{r}}_c}{dt}+\sum _{k=0}^{n-1}{\mathit{F}}_k^{\left(\mathrm{c}\mathrm{o}\mathrm{n}\mathrm{c}\right)}\hfill \\ \hfill =& -\kappa \pi R^{2}n\frac{d{\mathit{r}}_c}{dt}+\pi R^2{\mathcal{F}}^{\left(n\right)},\hfill \end{array}(14)$

where ${\mathcal{F}}^{(n)}$ is the force per unit area exerting on the camphor float with n-fold rotational symmetry. By calculating the vector product of the equations of motion with r_k − r_c and then summing up for n disks, we obtain the evolution equation for θ_c as

$\begin{array}{ll}\hfill \rho \pi R^2{\ell }^{2}n\frac{d^2{\theta }_c}{d{t}^2}=& -\kappa \pi R^2{\ell }^{2}n\frac{d{\theta }_c}{dt}+\sum _{k=0}^{n-1}\left({\mathit{r}}_k-{\mathit{r}}_c\right)\times {\mathit{F}}_k^{\left(\mathrm{c}\mathrm{o}\mathrm{n}\mathrm{c}\right)}\hfill \\ \hfill =& -\kappa \pi R^2{\ell }^{2}n\frac{d{\theta }_c}{dt}+\pi R^2{\mathcal{N}}^{\left(n\right)},\hfill \end{array}(15)$

where ${\mathcal{N}}^{(n)}$ is the torque per unit area exerting on the camphor float with n-fold rotational symmetry. Here, the operator “×” is defined so that a ×b = a_xb_y − a_yb_x for a = a_xe_x + a_ye_y and b = b_xe_x + b_ye_y. It should be noted that the obtained time evolution equations for r_c and θ_c in Eqs 14, 15 does not explicitly include the terms originating from the internal force.

Finally, we derive the dimensionless version of our model. The dimensionless variables are defined as

$\begin{array}{ll}\hfill & \tilde{\mathit{r}}=\frac{\mathit{r}}{\sqrt{D/a}},{\tilde{\mathit{r}}}_k=\frac{{\mathit{r}}_k}{\sqrt{D/a}},{\tilde{\mathit{r}}}_c=\frac{{\mathit{r}}_c}{\sqrt{D/a}},\tilde{R}=\frac{R}{\sqrt{D/a}},\tilde{\ell }=\frac{\ell }{\sqrt{D/a}},\hfill \\ \hfill & \tilde{t}=at,\tilde{u}=\frac{u}{S_0/D},\tilde{\rho }=\frac{\rho Da}{\mathrm{\Gamma }{S}_0},\tilde{\kappa }=\frac{\eta D}{\mathrm{\Gamma }{S}_0},\hfill \\ \hfill & {\tilde{\mathit{F}}}_k^{\left(\mathrm{c}\mathrm{o}\mathrm{n}\mathrm{c}\right)}=\frac{{\mathit{F}}_k^{\left(\mathrm{c}\mathrm{o}\mathrm{n}\mathrm{c}\right)}}{\mathrm{\Gamma }{S}_0/\sqrt{Da}},{\tilde{\mathcal{F}}}^{\left(n\right)}=\frac{{\mathcal{F}}^{\left(n\right)}}{\mathrm{\Gamma }{S}_0\sqrt{a}/\left(D\sqrt{D}\right)},{\tilde{\mathcal{N}}}^{\left(n\right)}=\frac{{\mathcal{N}}^{\left(n\right)}}{\mathrm{\Gamma }{S}_0/D},\hfill \end{array}(16)$

and our model with dimensionless variables is summarized as

$\frac{\partial \tilde{u}}{\partial \tilde{t}}={\tilde{\nabla }}^2\tilde{u}-\tilde{u}+\sum _{k=0}^{n-1}\frac{1}{\pi {\tilde{R}}^2}\mathrm{\Theta }\left(\tilde{R}-\left|\tilde{\mathit{r}}-\widetilde{{\mathit{r}}_k}\right|\right),(17)$

$\begin{array}{ll}\hfill \tilde{\rho }\frac{d^2{\tilde{\mathit{r}}}_c}{d{\tilde{t}}^2}=& -\tilde{\kappa }\frac{d{\tilde{\mathit{r}}}_c}{d\tilde{t}}+\frac{1}{n\pi {\tilde{R}}^2}\sum _{k=0}^{n-1}{\tilde{\mathit{F}}}_k^{\left(\mathrm{c}\mathrm{o}\mathrm{n}\mathrm{c}\right)}\hfill \\ \hfill =& -\tilde{\kappa }\frac{d{\tilde{\mathit{r}}}_c}{d\tilde{t}}+\frac{1}{n}{\tilde{\mathcal{F}}}^{\left(n\right)},\hfill \end{array}(18)$

$\begin{array}{ll}\hfill \tilde{\rho }\frac{d^2{\theta }_c}{d{\tilde{t}}^2}=& -\tilde{\kappa }\frac{d{\theta }_c}{d\tilde{t}}+\frac{1}{n\pi {\tilde{R}}^2{\tilde{\ell }}^2}\sum _{k=0}^{n-1}\left({\tilde{\mathit{r}}}_k-{\tilde{\mathit{r}}}_c\right)\times {\tilde{\mathit{F}}}_k^{\left(\mathrm{c}\mathrm{o}\mathrm{n}\mathrm{c}\right)}\hfill \\ \hfill =& -\tilde{\kappa }\frac{d{\theta }_c}{d\tilde{t}}+\frac{1}{n{\tilde{\ell }}^2}{\tilde{\mathcal{N}}}^{\left(n\right)},\hfill \end{array}(19)$

${\tilde{\mathit{r}}}_k={\tilde{\mathit{r}}}_c+\tilde{\ell }\mathit{e}\left({\theta }_c+\frac{2\pi k}{n}\right),(20)$

${\tilde{\mathit{F}}}_k^{\left(\mathrm{c}\mathrm{o}\mathrm{n}\mathrm{c}\right)}=-{\oint }_{\partial {\tilde{\mathrm{\Omega }}}_k}\tilde{u}\left({\tilde{\mathit{r}}}^{\prime }\right)\mathit{n}\left({\tilde{\mathit{r}}}^{\prime }\right)d{\tilde{\ell }}^{\prime }(21)$

$=-{\iint }_{{\tilde{\mathrm{\Omega }}}_k}\left({\tilde{\nabla }}^{\prime }\tilde{u}\left({\tilde{\mathit{r}}}^{\prime }\right)\right)d{\tilde{A}}^{\prime }.(22)$

${\tilde{\mathrm{\Omega }}}_k=\left\{\tilde{\mathit{r}}|\left|\tilde{\mathit{r}}-{\tilde{\mathit{r}}}_k\right|\le \tilde{R}\right\}.(23)$

Hereafter, we adopt this dimensionless model with the tildes omitted.

3 Analysis

In this section, we analyze our model on the camphor float with n-fold rotational symmetry, derived in the previous section. To enable us to analyze our model, we assume that the camphor disk radius R is sufficiently small and that the concentration field of camphor molecules are described as the function of the positions and velocities of the comprising n camphor disks. In this section, we first obtain the expression of the concentration field under the above assumptions, and then calculate the force ${\mathcal{F}}^{(n)}$ and torque ${\mathcal{N}}^{(n)}$ originating from the concentration field. Based on the ordinary differential equations obtained under the assumptions, we perform the linear stability anaysis. Finally, we discuss the motion of the camphor float by calculating the force and torque in the case that the camphor float is moving at a constant velocity with a constant characteristic angle θ_c.

3.1 Simplification of the Model

Under the assumption that R → + 0, the evolution equation for the concentration field in Eq. 17 is described as

$\frac{\partial u}{\partial t}={\nabla }^{2}u-u+\sum _{k=0}^{n-1}\delta \left(\mathit{r}-{\mathit{r}}_k\right),(24)$

where δ(⋅) is the Dirac’s delta function.

The concentration field u is expressed as the summation of the concentration field generated by each camphor disk due to the linearity of the evolution equation for the concentration field. By assuming that the concentration field generated by the k-th camphor disk is expressed as a function of r_k and v_k, u(r) is expressed as

$u\left(\mathit{r}\right)=\sum _{k=0}^{n-1}U\left(\mathit{r}-{\mathit{r}}_k,{\mathit{v}}_k\right),(25)$

where U(r, v) is the stationary concentration field in the comoving frame with the camphor disk whose velocity is fixed to v. Thus, U(r, v) should satisfy the following equation:

$-\mathit{v}\cdot \nabla U={\nabla }^{2}U-U+\delta \left(\mathit{r}\right),(26)$

and is explicitly described as [9]

$U\left(\mathit{r},\mathit{v}\right)=\frac{1}{2\pi }{\mathcal{K}}_0\left(\sqrt{1+\frac{{\left|\mathit{v}\right|}^2}{4}}\left|\mathit{r}\right|\right)\exp \left(-\frac{1}{2}\mathit{r}\cdot \mathit{v}\right),(27)$

where ${\mathcal{K}}_{\nu }(\cdot )$ is the second-kind modified Bessel function of the α-th order.

The force ${\mathit{F}}_k^{(\mathrm{c}\mathrm{o}\mathrm{n}\mathrm{c})}$ which exerts on the k-th camphor disk originating from the camphor concentration field is represented as the summation of the forces ${\mathit{F}}_{k,j}^{(\mathrm{c}\mathrm{o}\mathrm{n}\mathrm{c})}$ originating from the camphor concentration field released from the j-th camphor disk as

${\mathit{F}}_k^{\left(\mathrm{c}\mathrm{o}\mathrm{n}\mathrm{c}\right)}=\sum _{j=0}^{n-1}{\mathit{F}}_{k,j}^{\left(\mathrm{c}\mathrm{o}\mathrm{n}\mathrm{c}\right)}.(28)$

As for ${\mathit{F}}_{k,j}^{(\mathrm{c}\mathrm{o}\mathrm{n}\mathrm{c})}$ (k ≠ j), the limit of ${\mathit{F}}_{k,j}^{(\mathrm{c}\mathrm{o}\mathrm{n}\mathrm{c})}/(\pi R^2)$ with R → + 0 is expressed as

$\begin{array}{ll}\hfill \underset{R\to +0}{\lim }\frac{{\mathit{F}}_{k,j}^{\left(\mathrm{c}\mathrm{o}\mathrm{n}\mathrm{c}\right)}}{\pi R^2}=& \underset{R\to +0}{\lim }\frac{1}{\pi R^2}{\iint }_{{\mathrm{\Omega }}_k}{\left.\nabla U\left(\mathit{r},{\mathit{v}}_j\right)\right|}_{\mathit{r}={\mathit{r}}_k-{\mathit{r}}_j}d{A}^{\prime }\hfill \\ \hfill =& -{\left.\nabla U\left(\mathit{r},{\mathit{v}}_j\right)\right|}_{\mathit{r}={\mathit{r}}_k-{\mathit{r}}_j}.\hfill \end{array}(29)$

For the linear stability analysis, the concentration field U(r, v) is expanded with respect to v as [40]

$U\left(\mathit{r},\mathit{v}\right)=\frac{1}{2\pi }{\mathcal{K}}_0\left(\left|\mathit{r}\right|\right)-\frac{1}{4\pi }{\mathcal{K}}_0\left(\left|\mathit{r}\right|\right)\mathit{r}\cdot \mathit{v}+\mathcal{O}\left({\left|\mathit{v}\right|}^2\right),(30)$

and therefore the force ${\mathit{F}}_{k,j}^{(\mathrm{c}\mathrm{o}\mathrm{n}\mathrm{c})}/(\pi R^2)$ (k ≠ j) is also described as the expansion with respect to v_j as

$\begin{array}{ll}\hfill \frac{{\mathit{F}}_{k,j}^{\left(\mathrm{c}\mathrm{o}\mathrm{n}\mathrm{c}\right)}}{\pi R^2}=& \frac{1}{2\pi }{\mathcal{K}}_1\left(\left|{\mathit{r}}_k-{\mathit{r}}_j\right|\right)\frac{{\mathit{r}}_k-{\mathit{r}}_j}{\left|{\mathit{r}}_k-{\mathit{r}}_j\right|}+\frac{1}{4\pi }{\mathcal{K}}_0\left(\left|{\mathit{r}}_k-{\mathit{r}}_j\right|\right){\mathit{v}}_j\hfill \\ \hfill & -\frac{1}{4\pi }{\mathcal{K}}_1\left(\left|{\mathit{r}}_k-{\mathit{r}}_j\right|\right)\left[\left({\mathit{r}}_k-{\mathit{r}}_j\right)\cdot {\mathit{v}}_j\right]\frac{{\mathit{r}}_k-{\mathit{r}}_j}{\left|{\mathit{r}}_k-{\mathit{r}}_j\right|}+\mathcal{O}\left(R,{\left|{\mathit{v}}_j\right|}^2\right).\hfill \end{array}(31)$

As for the force ${\mathit{F}}_{k,k}^{(\mathrm{c}\mathrm{o}\mathrm{n}\mathrm{c})}$, it cannot be calculated from the concentration field under the assumption of R → + 0 since the concentration field is not differentiable at r = r_k. Thus we calculate the force working on the disk with a finite small radius, and then consider the limit of R → + 0. The force working on the camphor disk originating from the camphor concentration field generated by itself is calculated as

$\begin{array}{ll}\hfill \frac{{\mathit{F}}_{k,k}^{\left(\mathrm{c}\mathrm{o}\mathrm{n}\mathrm{c}\right)}}{\pi R^2}=& -\frac{1}{\pi R^2}{\int }_0^{2\pi }U\left({\mathit{r}}_k+R\mathit{e}\left(\theta \right),{\mathit{v}}_k\right)R\mathit{e}\left(\theta \right)d\theta \hfill \\ \hfill =& \frac{1}{\pi R}{\mathcal{K}}_0\left(\sqrt{1+\frac{{\left|{\mathit{v}}_k\right|}^2}{4}}R\right){\mathcal{I}}_1\left(\frac{R\left|{\mathit{v}}_k\right|}{2}\right)\frac{{\mathit{v}}_k}{\left|{\mathit{v}}_k\right|}.\hfill \end{array}(32)$

By considering the limit of R → + 0 and expanding the expression with respect to v_k, we obtain

$\frac{{\mathit{F}}_{k,k}^{\left(\mathrm{c}\mathrm{o}\mathrm{n}\mathrm{c}\right)}}{\pi R^2}=\frac{1}{4\pi }\left(\ln \left(\frac{2}{R}\right)-{\gamma }_{\text{Euler}}\right){\mathit{v}}_k-\frac{1}{32\pi }{\left|{\mathit{v}}_k\right|}^2{\mathit{v}}_k+\frac{1}{256\pi }{\left|{\mathit{v}}_k\right|}^4{\mathit{v}}_k+\mathcal{O}\left(R,{\left|{\mathit{v}}_k\right|}^7\right),(33)$

where γ_Euler ≃ 0.577 21… is the Euler’s constant. The coefficient of v_k in the first term of the righthand side diverges for R → + 0, but it exhibits the logarithmic divergence. Therefore, we introduce an arbitrary positive constant F₀, and consider that F_k,k/(πR²) is described as the expansion with respect to v_k as

$\frac{{\mathit{F}}_{k,k}^{\left(\mathrm{c}\mathrm{o}\mathrm{n}\mathrm{c}\right)}}{\pi R^2}=F_0{\mathit{v}}_k-\frac{1}{32\pi }{\left|{\mathit{v}}_k\right|}^2{\mathit{v}}_k+\frac{1}{256\pi }{\left|{\mathit{v}}_k\right|}^4{\mathit{v}}_k+\mathcal{O}\left({\left|{\mathit{v}}_k\right|}^7\right).(34)$

3.2 Linear Stability Analysis

We first consider the motion of a single camphor disk in order to discuss the motion of the camphor float by comparing with the single disk motion. For a single disk system, the equation of motion should be

$\rho \frac{d{\mathit{v}}_c}{dt}=-\kappa {\mathit{v}}_c+F_0{\mathit{v}}_c-\frac{1}{32\pi }{\left|{\mathit{v}}_c\right|}^2{\mathit{v}}_c+\frac{1}{256\pi }{\left|{\mathit{v}}_c\right|}^4{\mathit{v}}_c+\mathcal{O}\left({\left|{\mathit{v}}_c\right|}^7\right),(35)$

where v_c = dr_c/dt. Note that the characteristic angle θ_c cannot be defined for a single disk system. This system exhibits a supercritical pitchfork bifurcation at κ = F₀. In other words, the camphor disk does not move for κ > F₀, while it moves at a constant speed for κ < F₀. In the latter case, the camphor disk moves at the speed of $\sqrt{32\pi (F_0-\kappa )}$ under the situation close to the bifurcation point [9, 40, 41].

In the case of n = 2, the equations of motion for the camphor float up to the first orders of v_c and ω_c(= dθ_c/dt) are obtained as

$\rho \frac{d{\mathit{v}}_c}{dt}=-\kappa {\mathit{v}}_c+F_0{\mathit{v}}_c+\frac{1}{4\pi }{\mathcal{K}}_0\left(2\ell \right){\mathit{v}}_c-\frac{1}{2\pi }{\mathcal{K}}_1\left(2\ell \right)\ell \left({\mathit{v}}_c\cdot \mathit{e}\left({\theta }_c\right)\right)\mathit{e}\left({\theta }_c\right).(36)$

$\rho \frac{d{\omega }_c}{dt}=-\kappa {\omega }_c+F_0{\omega }_c-\frac{1}{4\pi }{\mathcal{K}}_0\left(2\ell \right){\omega }_c.(37)$

Note that the representation of the torque is the same for the camphor rotor whose center is fixed [40, 42]. It is obvious that the system has a stationary solution v_c = 0 and ω_c = 0, which corresponds to the resting camphor float. From the symmetric property of the system, the system should be neutrally stable on the perturbation on the position r_c and characteristic angle θ_c. Thus, we perform the linear stability anaysis around the stationary solution with r_c = 0 and θ_c = 0, without losing generality. The linaraized equation is obtained by setting v_c = δv_xe_x + δv_ye_y and ω_c = δω as

$\frac{d}{dt}\left(\begin{array}{c}\hfill \delta v_x\hfill \\ \hfill \delta v_y\hfill \\ \hfill \delta \omega \hfill \end{array}\right)=\left(\begin{array}{ccc}\hfill -\kappa +{\kappa }_{2,\parallel }\hfill & \hfill 0\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill -\kappa +{\kappa }_{2,\perp }\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill 0\hfill & \hfill -\kappa +{\kappa }_{2,r}\hfill \end{array}\right)\left(\begin{array}{c}\hfill \delta v_x\hfill \\ \hfill \delta v_y\hfill \\ \hfill \delta \omega \hfill \end{array}\right),(38)$

where

${\kappa }_{2,\parallel }=F_0+\frac{1}{4\pi }{\mathcal{K}}_0\left(2\ell \right)-\frac{1}{2\pi }\ell {\mathcal{K}}_1\left(2\ell \right),(39)$

${\kappa }_{2,\perp }=F_0+\frac{1}{4\pi }{\mathcal{K}}_0\left(2\ell \right),(40)$

${\kappa }_{2,r}=F_0-\frac{1}{4\pi }{\mathcal{K}}_0\left(2\ell \right).(41)$

Eqs 38–41 mean that the bifurcation points for the translational motion in the direction parallel to the line connecting the two camphor disks, that pependicular to it, and that for the rotational motion are κ = κ_2,∥, κ_2,⊥, and κ_2,r, respectively. κ_2,∥, κ_2,⊥, and κ_2,r are expressed as the summation of the bifurcation point for a single camphor disk F₀ and the terms that decay to 0 for ℓ → + ∞. Since κ_2,∥ < κ_2,⊥ and κ_2,r < κ_2,⊥ hold for any ℓ > 0, the translational motion in the direction perpendicular to the line firstly bifurcates from the stationary state, and thus such a motion tends to be realized.

In the case of n = 3, the equations of motion up to the first orders on v_c and ω_c are given as

$\rho \frac{d{\mathit{v}}_c}{dt}=-\kappa {\mathit{v}}_c+F_0{\mathit{v}}_c+\frac{1}{2\pi }{\mathcal{K}}_0\left(\sqrt{3}\ell \right){\mathit{v}}_c-\frac{\sqrt{3}}{4\pi }{\mathcal{K}}_1\left(\sqrt{3}\ell \right)\ell {\mathit{v}}_c.(42)$

$\rho \frac{d{\omega }_c}{dt}=-\kappa {\omega }_c+F_0{\omega }_c-\frac{1}{4\pi }{\mathcal{K}}_0\left(\sqrt{3}\ell \right){\omega }_c-\frac{\sqrt{3}}{8\pi }{\mathcal{K}}_1\left(\sqrt{3}\ell \right)\ell {\omega }_c.(43)$

Also in this case, the stationary solution with v_c = 0 and ω_c = 0 exists, which corresponds to the resting camphor float, and we arbitrarily set r_c = 0 and θ_c = 0 arbitrarily owing to the system symmetry. The linearized equation around this solution is obtained as

$\frac{d}{dt}\left(\begin{array}{c}\hfill \delta v_x\hfill \\ \hfill \delta v_y\hfill \\ \hfill \delta \omega \hfill \end{array}\right)=\left(\begin{array}{ccc}\hfill -\kappa +{\kappa }_{3,t}\hfill & \hfill 0\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill -\kappa +{\kappa }_{3,t}\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill 0\hfill & \hfill -\kappa +{\kappa }_{3,r}\hfill \end{array}\right)\left(\begin{array}{c}\hfill \delta v_x\hfill \\ \hfill \delta v_y\hfill \\ \hfill \delta \omega \hfill \end{array}\right),(44)$

where

${\kappa }_{3,t}=F_0+\frac{1}{2\pi }{\mathcal{K}}_0\left(\sqrt{3}\ell \right)-\frac{\sqrt{3}}{4\pi }\ell {\mathcal{K}}_1\left(\sqrt{3}\ell \right),(45)$

${\kappa }_{3,r}=F_0-\frac{1}{4\pi }{\mathcal{K}}_0\left(\sqrt{3}\ell \right)-\frac{\sqrt{3}}{8\pi }\ell {\mathcal{K}}_1\left(\sqrt{3}\ell \right).(46)$

Eqs 44–46 mean that the bifurcation points for the translational and rotational motions are κ = κ_3,t and κ_3,r, respectively. Considering that the bifurcation point is independent of the direction of translational motion, which is different from the case with n = 2, we cannot discuss the preferable direction for the translational motion based on the linear stability analysis for n = 3. Note that the bifurcation point for the translational motion in every direction is the same for each n ≥ 3. κ_3,t and κ_3,r are also expressed as the summation of the bifurcation point for a single camphor disk F₀ and the terms that decay to 0 for ℓ → + ∞. The sign of κ_3,t − κ_3,r changes at ℓ = ℓ_3,tr ≃ 3.186 63… , which satisfies

$\frac{{\ell }_{3,tr}{\mathcal{K}}_1\left(\sqrt{3}{\ell }_{3,tr}\right)}{{\mathcal{K}}_0\left(\sqrt{3}{\ell }_{3,tr}\right)}=2\sqrt{3}.(47)$

This means that the translational and rotational motions tend to occur for ℓ < ℓ_3,tr and ℓ > ℓ_3,tr, respectively, though the difference between κ_3,t and κ_3,r is so small that such tendency may not be clear for ℓ > ℓ_3,tr.

3.3 Preferable Direction of Motion

The linear stability analysis indicates the preferable direction for the translational motion for n = 2, but it does not work for n = 3. In order to discuss the preferable direction of the translational motion of the camphor float with n-fold symmetry, we calculate the force and torque exerting on the camphor float with constant θ_c when it is moving at a constant velocity in a certain direction [35]. Considering the symmetry of the system, the generality is not lost if we set v_c = Ve_x (V > 0). Under this assumption, the force ${\mathcal{F}}^{(n)}$ and torque ${\mathcal{N}}^{(n)}$ working on the camphor float are calculated as a function of the characteristic angle θ_c and the velocity V based on Eq. 19.

For n = 2, the force ${\mathcal{F}}^{(2)}({\theta }_c)$ and the torque ${\mathcal{N}}^{(2)}({\theta }_c)$ are calculated as

$\begin{array}{ll}\hfill {\mathcal{F}}^{\left(2\right)}\left({\theta }_c\right)=& \left[2F_0+\frac{1}{2\pi }{\mathcal{K}}_0\left(2\ell \sqrt{1+\frac{V^2}{4}}\right)\cosh \left(\ell V\cos {\theta }_c\right)\right]V{\mathit{e}}_x\hfill \\ \hfill & -\frac{1}{\pi }\sqrt{1+\frac{V^2}{4}}{\mathcal{K}}_1\left(2\ell \sqrt{1+\frac{V^2}{4}}\right)\sinh \left(\ell V\cos {\theta }_c\right)\mathit{e}\left({\theta }_c\right),\hfill \end{array}(48)$

and

${\mathcal{N}}^{\left(2\right)}\left({\theta }_c\right)=\frac{V\ell }{2\pi }{\mathcal{K}}_0\left(2\ell \sqrt{1+\frac{V^2}{4}}\right)\sin {\theta }_c\sinh \left(\ell V\cos {\theta }_c\right),(49)$

respectively. For sufficiently small V, Eqs 48, 49 are expanded with respect to V as

$\begin{array}{ll}\hfill {\mathcal{F}}^{\left(2\right)}\left({\theta }_c\right)=& \left[2F_0+\frac{1}{2\pi }{\mathcal{K}}_0\left(2\ell \right)-\frac{1}{2\pi }\ell {\mathcal{K}}_1\left(2\ell \right)-\frac{1}{2\pi }\ell {\mathcal{K}}_1\left(2\ell \right)\cos \left(2{\theta }_c\right)\right]V{\mathit{e}}_x\hfill \\ \hfill & -\left[\frac{1}{2\pi }\ell {\mathcal{K}}_1\left(2\ell \right)\sin \left(2{\theta }_c\right)\right]V{\mathit{e}}_y+\mathcal{O}\left(V^2\right),\hfill \end{array}(50)$

${\mathcal{N}}^{\left(2\right)}\left({\theta }_c\right)=\frac{{\ell }^2}{4\pi }{\mathcal{K}}_0\left(2\ell \right)V^2\sin \left(2{\theta }_c\right)+\mathcal{O}\left(V^3\right).(51)$

The force works in the negative y-direction for 0 < θ_c < π/2 and in the positive y-direction for − π/2 < θ_c < 0 from Eq. 50, while the torque works counterclockwise for 0 < θ_c < π/2, and clockwise for − π/2 < θ_c < 0 from Eq. 51. These expressions indicate that both the force and the torque work on the camphor float so that the characteristic angle should approach θ_c = ±π/2. This agrees with the results by the linear stability analysis. Therefore, the camphor float with 2-fold symmetry moves in the direction perpendicular to the line connecting the two camphor disks.

As for n = 3, the force ${\mathcal{F}}^{(3)}({\theta }_c)$ is explicitly expressed as

$\begin{array}{ll}\hfill {\mathcal{F}}^{\left(3\right)}\left({\theta }_c\right)=& 3F_0{\mathit{e}}_x+\mathit{g}\left({\theta }_c\right)+\mathit{g}\left({\theta }_c+\frac{\pi }{3}\right)+\mathit{g}\left({\theta }_c+\frac{2\pi }{3}\right)\hfill \\ \hfill & +\mathit{g}\left({\theta }_c+\pi \right)+\mathit{g}\left({\theta }_c-\frac{2\pi }{3}\right)+\mathit{g}\left({\theta }_c-\frac{\pi }{3}\right),\hfill \end{array}(52)$

where

$\begin{array}{ll}\hfill \mathit{g}\left(\theta \right)=& \frac{1}{4\pi }\left[V{\mathcal{K}}_0\left(\sqrt{3}\ell \sqrt{1+\frac{V^2}{4}}\right)\exp \left(\frac{\sqrt{3}}{2}\ell \sin \theta \right)\right.\hfill \\ \hfill & \left.-2\sqrt{1+\frac{V^2}{4}}{\mathcal{K}}_1\left(\sqrt{3}\ell \sqrt{1+\frac{V^2}{4}}\right)\exp \left(\frac{\sqrt{3}}{2}\ell V\sin \theta \right)\sin \theta \right]{\mathit{e}}_x\hfill \\ \hfill & +\frac{1}{2\pi }\left[\sqrt{1+\frac{V^2}{4}}{\mathcal{K}}_1\left(\sqrt{3}\ell \sqrt{1+\frac{V^2}{4}}\right)\exp \left(\frac{\sqrt{3}}{2}\ell V\sin \theta \right)\cos \theta \right]{\mathit{e}}_y.\hfill \end{array}(53)$

Note that ${\mathcal{F}}^{(3)}({\theta }_c)$ has a period of π/3 since

${\mathcal{F}}^{\left(3\right)}\left({\theta }_c\right)={\mathcal{F}}^{\left(3\right)}\left({\theta }_c+\frac{\pi }{3}\right)(54)$

is derived from Eqs 52, 53. For sufficiently small V, the expression in Eqs 52, 53 is expanded with respect to V as

$\begin{array}{l}{\mathcal{F}}^{\left(3\right)}\left({\theta }_c\right)\hfill \\ \hfill & =3\left[F_0+\frac{1}{2\pi }{\mathcal{K}}_0\left(\sqrt{3}\ell \right)-\frac{\sqrt{3}}{4\pi }\ell {\mathcal{K}}_1\left(\sqrt{3}\ell \right)\right]V{\mathit{e}}_x\hfill \\ \hfill & -\frac{3}{128\pi }\left[4-24{\ell }^2{\mathcal{K}}_0\left(\sqrt{3}\ell \right)+\sqrt{3}\ell \left(8+3{\ell }^2\right){\mathcal{K}}_1\left(\sqrt{3}\ell \right)\right]V^3{\mathit{e}}_x\hfill \\ +\frac{3}{40960\pi }\left[160+60{\ell }^2\left(8+9{\ell }^2\right){\mathcal{K}}_0\left(\sqrt{3}\ell \right)+\sqrt{3}\ell \left(320-720{\ell }^2-30{\ell }^4+3{\ell }^4\cos \left(6{\theta }_c\right)\right)\right]V^5{\mathit{e}}_x\hfill \\ +\frac{9\sqrt{3}}{40960\pi }\left[{\ell }^5{\mathcal{K}}_1\left(\sqrt{3}\ell \right)\sin \left(6{\theta }_c\right)\right]V^5{\mathit{e}}_y+\mathcal{O}\left(V^7\right).\hfill \end{array}(55)$

This means that the configurations with both θ_c = 0 and π/3 are stable for the camphor float with 3-fold rotational symmetry moving in the positive x-direction from the consideration of the force exerting on it. It should be noted thtat the above-mentioned force is on the order of V⁵, which should be sufficiently weak close to the bifurcation point.

The torque ${\mathcal{N}}^{(3)}({\theta }_c)$ is obtained as

${\mathcal{N}}^{\left(3\right)}\left({\theta }_c\right)=h\left({\theta }_c\right)+h\left({\theta }_c+\frac{2\pi }{3}\right)+h\left({\theta }_c-\frac{2\pi }{3}\right),(56)$

where

$\begin{array}{ll}\hfill h\left(\theta \right)=& -\frac{\ell }{2\pi }\sqrt{1+\frac{V^2}{4}}{\mathcal{K}}_1\left(\sqrt{3}\sqrt{1+\frac{V^2}{4}}\ell \right)\sinh \left(\frac{\sqrt{3}}{2}\ell V\sin \theta \right)\hfill \\ \hfill & -\frac{V\ell }{2\pi }{\mathcal{K}}_0\left(\sqrt{3}\sqrt{1+\frac{V^2}{4}}\ell \right)\exp \left(-\frac{3}{4}\ell V\cos \theta \right)\cosh \left(\frac{\sqrt{3}}{4}\ell V\sin \theta \right)\sin \theta .\hfill \end{array}(57)$

Eqs 56, 57 shows that ${\mathcal{N}}^{(3)}({\theta }_c)$ obviously has a period of 2π/3 since

${\mathcal{N}}^{\left(3\right)}\left({\theta }_c\right)={\mathcal{N}}^{\left(3\right)}\left({\theta }_c+\frac{2\pi }{3}\right).(58)$

For sufficiently small V, Eq. 56 is also expanded with respect to V as

${\mathcal{N}}^{\left(3\right)}\left({\theta }_c\right)=\frac{3{\ell }^3}{128\pi }\left[-3{\mathcal{K}}_0\left(\sqrt{3}\ell \right)+\sqrt{3}\ell {\mathcal{K}}_1\left(\sqrt{3}\ell \right)\right]V^3\sin \left(3{\theta }_c\right)+\mathcal{O}\left(V^5\right).(59)$

The torque at the order of V³ works on the camphor float as a leading term. Comparing the orders between ${\mathcal{F}}^{(3)}$ and ${\mathcal{N}}^{(3)}$ that affect the rotation of the camphor float, the effect of ${\mathcal{N}}^{(3)}$ should govern the dynamics for small V, which corresponds to the system close to the pitchfork bifurcation point. As for the case with high velocity, the other effects can be important, and we cannot discuss the selected mode of motion based on the above analysis. Thus, hereafter we consider the case with small V.

The sign of the proportionality coefficient of sin 3θ_c in Eq. 59 is important for the stable direction of the camphor float motion; If the proportionality coefficient is negative, the torque works clockwise for 0 < θ_c < π/3 and it works counterclockwise for − π/3 < θ_c < 0. This indicates that the camphor float rotates so that θ_c approaches 0 or ± 2π/3. In contrast, if the proportionality coefficient is positive, the torque works in the opposite directions, which indicates that θ_c approaches π or ± π/3. According to our analytical result in Eq. 59, the sign of the proportionality coefficient is negative and positive for ℓ < ℓ_3,t and ℓ > ℓ_3,t, respectively. Here, ℓ_3,t ≃ 1.464 58… , which satisfies

$\frac{{\ell }_{3,t}{\mathcal{K}}_1\left(\sqrt{3}{\ell }_{3,t}\right)}{{\mathcal{K}}_0\left(\sqrt{3}{\ell }_{3,t}\right)}=\sqrt{3}.(60)$

This means that, as far as the camphor float is moving slowly, the small camphor float with ℓ < ℓ_3,t rotates so that it moves with one camphor disk at the front, while the large camphor float with ℓ > ℓ_3,t rotates so that it moves with one camphor disk at the rear.

4 Numerical Calculation

In order to confirm the analytical results, we perform the numerical calculation. We used the dimensionless model in Eqs 17–23. For the numerical calculation, we used the smoothed function; the source part and the force are changed as

$\frac{\partial u}{\partial t}={\nabla }^{2}u-u+\sum _{k=0}^{n-1}\frac{1}{\pi R^2}G\left(\left|\mathit{r}-{\mathit{r}}_k\right|\right),(61)$

${\mathit{F}}_k^{\left(\mathrm{c}\mathrm{o}\mathrm{n}\mathrm{c}\right)}=-{\iint }_{{\mathbb{R}}^2}\left({\nabla }^{\prime }u\left({\mathit{r}}^{\prime }\right)\right)G\left(\left|{\mathit{r}}^{\prime }-{\mathit{r}}_k\right|\right)d{A}^{\prime }.(62)$

where

$G\left(r\right)=\frac{1}{2}\left[1+\tanh \left(\frac{R-r}{\delta }\right)\right].(63)$

It should be noted that G(r) converges to Θ(R − r) for the limit of δ → + 0.

Numerical calculation was performed with the explicit method with the time step Δt = 0.000 5, and the spatial mesh Δx = 0.05. The calculation area for the concentration field is set to 20 × 20 with periodic boundary conditions. The parameters are fixed as ρ = 0.01, R = 0.2, and δ = 0.05, and κ and ℓ were varied as parameters. The initial condition for the concentration was u = 0 in the whole region. The initial conditions for the velocity, characterisitic angle, and angular velocity were set as v_c = 0.5e_x + 0.01e_y, θ_c = 0.5, and ω_c = 0.01. Since the initial condition was set so that the camphor float has a high velocity and low angular velocity, the float was easy to converge to the translational motion.

In Figure 2A, we first plot the stationary translational velocity against κ for a single camphor disk. In this case, we could only consider the translational motion but not the rotational motion. Thus, the initial condition for the velocity was set as v_c = 0.5e_x + 0.01e_y. We confirmed that the motion of the single camprhor disk converged to a translational motion with a constant velocity at t = 100, even when the initial condition was changed. Thus, we plotted $\left|{\mathit{v}}_c\right|$ at t = 100 for the stationary translational velocity. The stationary translational velocity was finite for the smaller κ, while it was almost zero for the larger κ. The bifurcation point with respect to the bifurcation parameter κ for the translational motion was slightly greater than 0.12, where the bifurcation was supposed to be classified into a supercritical pitchfork bifurcation.

FIGURE 2

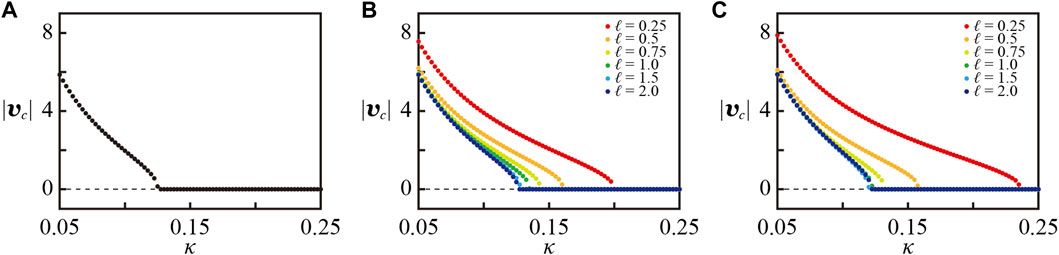
FIGURE 2. Numerical results on the stationary translational velocity of the camphor float. (A) A single camphor disk. (B) The camphor float with two camphor disks. (C) The camphor float with three camphor disks. For the cases (B,C), the results for various ℓ were represented in different colors.

We also calculated the cases with n = 2 and 3. In Figures 2B,C, we plotted the stationary translational velocity for various ℓ. Also in these cases, the velocity at t = 100 was adopted as the stationary translational velocity, at which we confirmed that the velocity was converged. For the camphor float with n = 2, the bifurcation point was greater for the smaller ℓ as shown in Figure 2B. This agrees with the theoretical results in Eq. 40. For the camphor float with n = 3, the bifurcation point had a minimum value at a certain ℓ around 1.5 as shown in Figure 2C. This also corresponds to the theoretical result in Eq. 45, which indicates that the bifuracation point has the minimum value at ℓ = 1.377 98… .

In Figure 3, the time series of the velocity $\left|{\mathit{v}}_c\right|$, angular velocity ω_c, and the angle difference ψ between the direction of velocity and the characteristic angle θ_c are plotted for the camphor float with n = 2. The angle difference ψ is defined as

$\psi =\varphi -{\theta }_c,(64)$

where ϕ is defined as ${\mathit{v}}_c=\left|{\mathit{v}}_c\right|\left(\cos \varphi {\mathit{e}}_x+\sin \varphi {\mathit{e}}_y\right)$. We set κ = 0.12 since we wanted to discuss the behavior close to the bifurcation point for the translational motion of a single camphor disk. The convergence to the stationary translational motion was faster for small ℓ, whereas the system almost reached the stationary states around t = 30 even in the case of ℓ = 2. The angular velocity decayed to zero and the angle difference ψ approached π/2, which corresponds to the translational motion in the direction perpendicular to the line connecting the two camphor disks.

FIGURE 3

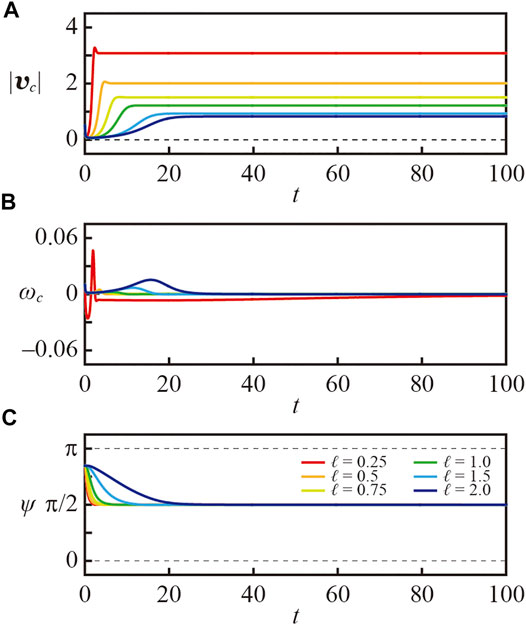
FIGURE 3. Numerical results on the time series of (A) velocity, (B) angular velocity, and (C) angle difference between the velocity and characteristic angle θ_c for the camphor float with n = 2. κ was fixed to 0.12. The results for various ℓ were represented in different colors. It should be noted that ψ has a periodicity of π.

As for the camphor float with n = 3, the time series are shown in Figure 4. It should be noted that the time range in Figure 4 is ten times as long as that in Figure 3, since the convergence of the angle difference ψ was much slower than the case with n = 2, though the convergence of the velocity and angular velocity was as fast as that in the case with n = 2. The angle difference ψ converged to zero for ℓ = 0.25, 0.5, 0.75, and 1.0, while it converged to − π/3 for ℓ = 2.0. This agrees with the analytical results in Eqs 59, 60. These results show that the smaller camphor float with n = 3 moved with one disk at its front, while the larger camphor float moved with one disk at its rear, which agrees with the analytical results. In the case with ℓ = 1.5, the convergence of ψ was very slow, which can be understood from the fact that ℓ = 1.5 is close to the threshold value ℓ_3,t ≃ 1.464 58… . Considering that 1.5 > ℓ_3,t, the angle difference should converge to ± π/3 but it appeared to approach 0. We consider that the difference between the theoretical and analytical results owes the slight difference in the setting; e.g. the finite size of the camphor disk, etc.

FIGURE 4

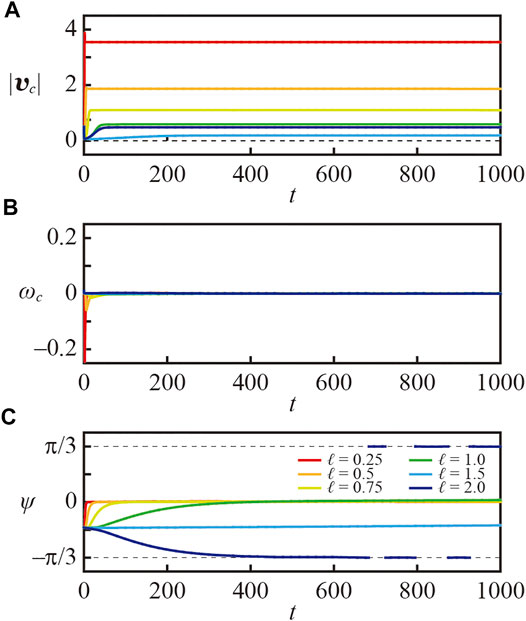
FIGURE 4. Numerical results on the time series of (A) velocity, (B) angular velocity, and (C) angle difference between the velocity and characteristic angle θ_c for the camphor float with n = 3. κ was fixed to 0.12. The results for various ℓ were represented in different colors. It should be noted that ψ has a periodicity of 2π/3.

In Figure 5, the snapshots of the camphor concentration u together with the camphor disk positions are shown for the cases of the camphor float with n = 2 and 3 for ℓ = 0.5. Considering that the camphor concentration profile has a tail in the opposite direction of the traveling direction, the obtained concentration field also indicated that the angle difference ψ between the velocity and the characteristic angle was π/2 for the case with n = 2, and 0 for the case with n = 3.

FIGURE 5

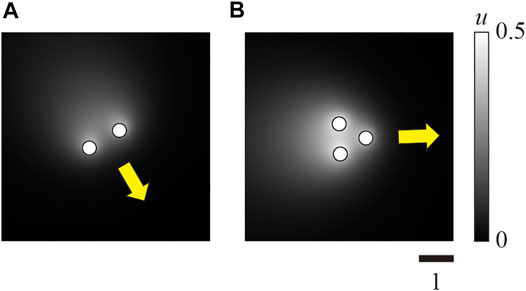
FIGURE 5. Snapshots of the camphor concentration around the camphor floats. (A) Camphor float with n = 2 at t = 100. (B) Camphor float with n = 3 at t = 100. κ was set to 0.12, and ℓ was set to 0.5. Corresponding videos are avialable as Supplementary Video S1, S2.

5 Discussion

In the analysis in Section 3, we assume that the system is close to the bifurcation point. In such a situation, our analytical results match the results by numerical calculation; i.e., the camphor float with n = 2 moves in the perpendicular direction to the line connecting the two camphor disks. For the case with n = 3, the smaller camphor float moves with one disk at its front, while the larger camphor float moves with one disk at its rear. However, in the condition far from the bifurcation point, the system often becomes multistable and one of several modes of motions is selected depending on the initial condition. Actually, the numerical results that exhibit multistability are shown in Figures 6, 7 for n = 2 and 3, respectively. The parameters were set as κ = 0.08 and ℓ = 1.5. In the case with n = 2 shown in Figure 6, the translational motion and spinning motion were observed depending on the initial conditions. The direction of the translational motion was always perpendicular to the line connecting the two disks. In the case with n = 3, the two types of translational motions, i.e., the motion with one disk at its front and that with one disk at its rear, and the spinning motion were observed depending on the initial conditions. Such multistability could be observed in the wider parameter regions for the larger ℓ, but the system was often monostable for the smaller ℓ.

FIGURE 6

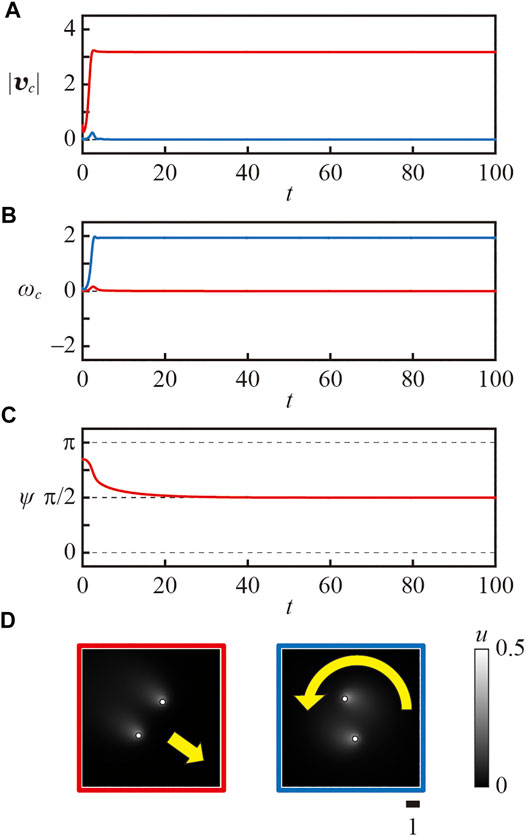
FIGURE 6. Numerical results on the time series of (A) velocity $\left|{\mathit{v}}_c\right|$, (B) angular velocity ω_c, and (C) angle difference between the velocity and characteristic angle θ_c for the camphor float with n = 2. κ was fixed to 0.08 and ℓ was fixed to 1.5. The results from various initial conditions were represented in different colors. Angle difference was plotted only for the case that $\left|{\mathit{v}}_c\right|$ was converged to a non-zero value. It should be noted that ψ has a periodicity of π. (D) Snapshots at t = 100 from each initial condition indicated in the same color. The initial conditions were (red) v_c = 0.5e_x + 0.01e_y, ω_c = 0.01, and (blue) v_c = 0.02e_x + 0.01e_y, ω_c = 0.1.

FIGURE 7

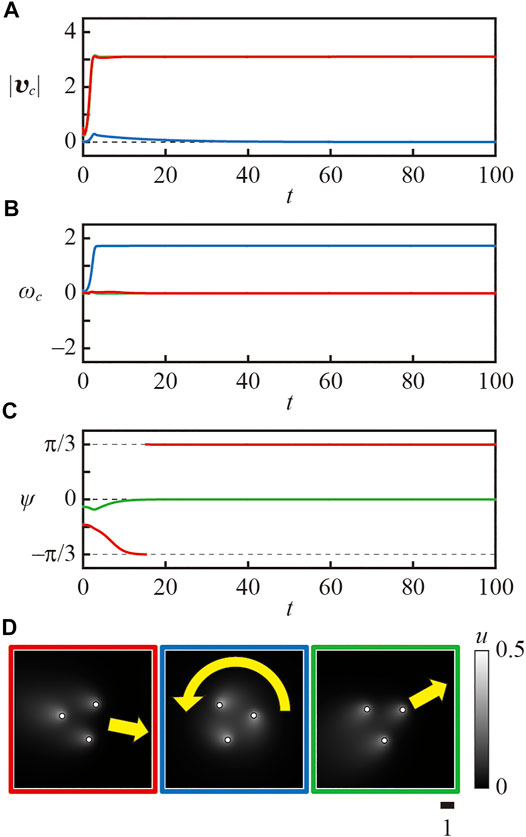
FIGURE 7. Numerical results on the time series of (A) velocity $\left|{\mathit{v}}_c\right|$, (B) angular velocity ω_c, and (C) angle difference between the velocity and characteristic angle θ_c for the camphor float with n = 3. κ was fixed to 0.08 and ℓ was fixed to 1.5. The results from various initial conditions were represented in different colors. Angle difference was plotted only for the case that $\left|{\mathit{v}}_c\right|$ was converged to a non-zero value. It should be noted that ψ has a periodicity of 2π/3. (D) Snapshots at t = 100 from each initial condition indicated in the same color. The initial conditions were (red) v_c = 0.5e_x + 0.01e_y, ω_c = 0.01, and (blue) v_c = 0.02e_x + 0.01e_y, ω_c = 0.1, and (green) v_c = 0.4e_x + 0.15e_y, ω_c = 0.01.

In our model, the concentration field around one camphor disk has the leading term described by the second-kind modified Bessel function as far as the traveling velocity is low. This means that the concentration field decays exponentially. Taking this into consideration, the coupling between the direction of motion and the camphor float configuration should be stronger for the smaller camphor float. Thus, the smaller camphor float can easily change the moving direction and quickly takes the preferable direction. In contrast, for the larger camphor float, the interaction is so small that it takes much time for the camphor float to take the preferable direction. Moreover, the system can often show the multistability for the larger camphor float as discussed in the previous paragraph. Threfore, the present discussion can be adequately adopted for the smaller camphor float.

The analytical results for the cases with n = 2 and n = 3 are essentially different; the bifurcation point for the translational motion depends on the moving direction for n = 2, while it is equivalent for any direction for n = 3. Moreover, we calculated the force and torque exerting on the camphor float which is moving at a constant velocity V without rotation. For n = 2, the leading terms of the force and torque which depend on the direction of the motion are at the order of V and V², respectively. In contrast, for n = 3, they are at the order of V⁵ and V³, respectively. This reflects that the linear stability analysis can lead to the nontrivial results for n = 2 but not for n = 3. Considering the orders of V in the force and torque, the configuration and the velocity of the camphor float are more strongly coupled with each other for n = 2 than for n = 3 near the bifurcation point as shown in Figures 3, 4. In addition, the force is more greatly affected to the dynamics than the torque for n = 2, and thus the preferable configuration is achieved by changing the velocity direction. In contrast, the torque is more greatly affected to the dynamics than the force for n = 3, and thus the preferable direction is achieved by changing the configuration by spinning. For the camphor float with n ≥ 4, we can perform the similar approach. However, for greater n, the effect of the configuration on the translational motion becomes smaller. Therefore, the analysis for the case with smaller n is more important, and here we especially discuss on the cases with n = 2 and n = 3.

We believe that the present theoretical results can be confirmed by the experiments. In the dimensionless model, the length and time are scaled by the diffusion length $\sqrt{D/a}$ and the characteristic sublimation time 1/a, respectively. From the previous results [37], they correspond to ca. 100 mm and ca. 50 s. Using these scale units, the typical size of the camphor float corresponds to ca. 100 mm in the actual system, since the dimensionless size of the camphor float adopted in this study is on the order of 1. As for the velocity, the obtained dimensionless value is on the order of 1 from Figures 2–7, which corresponds to ca. 2 mm/s. This value is rather slower than the typical velocity observed in experiments, ca. 10 mm/s, but these values are of the same order. Considering that the size of the camphor float is difficult to exceed 100 mm, the scale available in the experimental setup should be less than 1. Moreover, as discussed in the previous paragraph, the coupling between the configuration and the translational motion is stronger for the small camphor float. Therefore, we suppose that the experimental confirmation is possible only for the camphor float with small ℓ. Considering that the effect of the shape is stronger for n = 2, we suppose that the shape effect due to the 2-fold rotational symmetry can be easily confirmed, but that the effect for n = 3 or higher is more difficult to confirm.

In our previous work, we showed that an elliptic camphor particle moves in its minor-axis direction in theoretical analysis, numerical calculation, and experiments [9, 33, 34]. The symmetric property of the distribution of the mass and the camphor molecule source for an elliptic camphor particle is similar to that of the camphor float with 2-fold rotational symmetry discussed in the present study. In our result, it moves in the direction perpendicular to the line connecting the two camphors. Thus, the present results and our previous results show good correspondence. As for the camphor float with 3-fold rotational symmetry, it corresponds to the triangular camphor particle discussed in our previous study [35] from the viewpoint of the symmetric property. In our previous work, we concluded that the smaller triangular camphor particle moves in the direction of the corner for the smaller particle, while it moves in the direction of the side for the larger particle. The present results correspond to our previous ones in that the preferable direction changes depending on the size by considering the deviation of the mass and camphor molecule source. Taking the present analytical results into consideration, we suggest that the low-wave-number modulation from a symmetric circular shape most effectively affects the self-propelled motion, and the high-wave-number modulation is not so important.

6 Conclusion

In the present study, we theoretically investigated the self-propulsion of a camphor float with n-fold rotational symmetry, which comprises a rigid light circular plate attached with n camphor disks along a periphery with an equivalent spacing. We constructed a mathematical model for the camphor float, and analyzed it under the assumptions that the camphor disk radius is negligibly small and that the camphor concentration only depends on the positions and velocities of the camphor disks. From the linear stability analysis and the calculation of the force and torque for the situation that a camphor float is moving at a constant velocity with a certain characteristic angle, we concluded that the camphor float with 2-fold rotational symmetry moves in the direction perpendicular to the line connecting the two camphor disks. As for the camphor float with 3-fold rotational symmetry, the smaller float moves with one camphor disk at the front, while the larger float moves with one camphor disk at the rear.

As the extensions of the present study, we consider the particles with an asymmetric configuration. By considering such particles, we can generally discuss the manner of coupling between the motion and the symmtric featrures of self-propelled particles. We are also interested in the collective motion of the particles with n-fold rotational symmetry. In such systems, we expect some interesting structures with a nematic order and/or a hexagonal order can be realized. The symmetric properties embedded in the external condition such as the system boundary and the spatial modulation of the parameters also seem to be interesting. We hope the present results will provide the fundamental knowledge to understand the above-mentioned more complex systems, and moreover, will help understanding the universal mechanism on the shape effect on self-propelled motions driven by the self-generated concentration field.

Data Availability Statement

The original contributions presented in the study are included in the article/Supplementary Material, further inquiries can be directed to the corresponding author.

Author Contributions

HK and YK contributed to the conception and design of the work. HK performed the analytical and numerical calculations, and YK confirmed the validity of the results. HK and YK prepared the manuscript. All authors contributed to the article and approved the submitted version.

Funding

This work was supported by JSPS KAKENHI Grant Nos. JP19K03765, JP19J00365, JP20K14370, JP20H02712, and JP21H01004, and also the Cooperative Research Program of “Network Joint Research Center for Materials and Devices: Dynamic Alliance for Open Innovation Bridging Human, Environment and Materials” (Nos. 20211014 and 20214004). This work was also supported by JSPS and PAN under the Japan-Poland Research Cooperative Program (No. JPJSBP120204602).

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s Note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

Acknowledgments

The authors acknoweldge Professor Jerzy Gorecki (Polish Academy of Sciences), Professor Masaharu Nagayama (Hokkaido University), and Professor Yutaka Sumino (Tokyo University of Science) for their fruitful discussion.

Supplementary Material

The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/fphy.2022.858791/full#supplementary-material

References

1. Mikhailov A, Calenbuhr V. From Cells to Societies: Models of Complex Coherent Action. Berlin: Springer (2002).

Google Scholar

2. Ramaswamy S. The Mechanics and Statistics of Active Matter. Annu Rev Condens Matter Phys (2010) 1:323–45. doi:10.1146/annurev-conmatphys-070909-104101

CrossRef Full Text | Google Scholar

3. Vicsek T, Zafeiris A. Collective Motion. Phys Rep (2012) 517:71–140. doi:10.1016/j.physrep.2012.03.004

CrossRef Full Text | Google Scholar

4. Maass CC, Krüger C, Herminghaus S, Bahr C. Swimming Droplets. Annu Rev Condens Matter Phys (2016) 7:171–93. doi:10.1146/annurev-conmatphys-031115-011517

CrossRef Full Text | Google Scholar

5. Bechinger C, Di Leonardo R, Löwen H, Reichhardt C, Volpe G, Volpe G. Active Particles in Complex and Crowded Environments. Rev Mod Phys (2016) 88:045006. doi:10.1103/RevModPhys.88.045006

CrossRef Full Text | Google Scholar

6. Kitahata H, Yoshikawa K. Chemo-mechanical Energy Transduction through Interfacial Instability. Physica D: Nonlinear Phenomena (2005) 205:283–91. doi:10.1016/j.physd.2004.12.012

CrossRef Full Text | Google Scholar

7. Ohta T, Ohkuma T. Deformable Self-Propelled Particles. Phys Rev Lett (2009) 102:154101. doi:10.1103/PhysRevLett.102.154101

PubMed Abstract | CrossRef Full Text | Google Scholar

8. Ohta T. Dynamics of Deformable Active Particles. J Phys Soc Jpn (2017) 86:072001. doi:10.7566/JPSJ.86.072001

CrossRef Full Text | Google Scholar

9. Kitahata H, Koyano Y, Iida K, Nagayama M. Chapter 2. Mathematical Model and Analyses on Spontaneous Motion of Camphor Particle. In: Self-organized Motion: Physicochemical Design Based on Nonlinear Dynamics. Cambridge: The Royal Society of Chemistry (2018). p. 31–62. doi:10.1039/9781788013499-00031

CrossRef Full Text | Google Scholar

10. Keren K, Pincus Z, Allen GM, Barnhart EL, Marriott G, Mogilner A, et al. Mechanism of Shape Determination in Motile Cells. Nature (2008) 453:475–80. doi:10.1038/nature06952

PubMed Abstract | CrossRef Full Text | Google Scholar

11. Ebata H, Sano M. Swimming Droplets Driven by a Surface Wave. Sci Rep (2015) 5:8546. doi:10.1038/srep08546

PubMed Abstract | CrossRef Full Text | Google Scholar

12. Michelin S, Lauga E, Bartolo D. Spontaneous Autophoretic Motion of Isotropic Particles. Phys Fluids (2013) 25:061701. doi:10.1063/1.4810749

CrossRef Full Text | Google Scholar

13. Yoshinaga N, Nagai KH, Sumino Y, Kitahata H. Drift Instability in the Motion of a Fluid Droplet with a Chemically Reactive Surface Driven by Marangoni Flow. Phys Rev E (2012) 86:016108. doi:10.1103/PhysRevE.86.016108

PubMed Abstract | CrossRef Full Text | Google Scholar

14. Izri Z, van der Linden MN, Michelin S, Dauchot O. Self-propulsion of Pure Water Droplets by Spontaneous Marangoni-Stress-Driven Motion. Phys Rev Lett (2014) 113:248302. doi:10.1103/PhysRevLett.113.248302

PubMed Abstract | CrossRef Full Text | Google Scholar

15. Toyota T, Maru N, Hanczyc MM, Ikegami T, Sugawara T. Self-Propelled Oil Droplets Consuming "Fuel" Surfactant. J Am Chem Soc (2009) 131:5012–3. doi:10.1021/ja806689p

PubMed Abstract | CrossRef Full Text | Google Scholar

16. Sumino Y, Magome N, Hamada T, Yoshikawa K. Self-running Droplet: Emergence of Regular Motion from Nonequilibrium Noise. Phys Rev Lett (2005) 94:068301. doi:10.1103/PhysRevLett.94.068301

PubMed Abstract | CrossRef Full Text | Google Scholar

17. Sumino Y, Kitahata H, Yoshikawa K, Nagayama M, Nomura S-i. M, Magome N, et al. Chemosensitive Running Droplet. Phys Rev E (2005) 72:041603. doi:10.1103/PhysRevE.72.041603

PubMed Abstract | CrossRef Full Text | Google Scholar

18. Shao D, Rappel W-J, Levine H. Computational Model for Cell Morphodynamics. Phys Rev Lett (2010) 105:108104. doi:10.1103/PhysRevLett.105.108104

PubMed Abstract | CrossRef Full Text | Google Scholar

19. Tomlinson C, Miller WA. II. On the Motions of Camphor on the Surface of Water. Proc R Soc Lond (1862) 11:575–7. doi:10.1098/rspl.1860.0124

CrossRef Full Text | Google Scholar

20. Strutt RJ. IV. Measurements of the Amount of Oil Necessary Iu Order to Check the Motions of Camphor upon Water. Proc R Soc Lond (1890) 47:364–7. doi:10.1098/rspl.1889.0099

CrossRef Full Text | Google Scholar

21. Nakata S, Iguchi Y, Ose S, Kuboyama M, Ishii T, Yoshikawa K. Self-rotation of a Camphor Scraping on Water: New Insight into the Old Problem. Langmuir (1997) 13:4454–8. doi:10.1021/la970196p

CrossRef Full Text | Google Scholar

22. Nakata S, Nagayama M, Kitahata H, Suematsu NJ, Hasegawa T. Physicochemical Design and Analysis of Self-Propelled Objects that Are Characteristically Sensitive to Environments. Phys Chem Chem Phys (2015) 17:10326–38. doi:10.1039/C5CP00541H

PubMed Abstract | CrossRef Full Text | Google Scholar

23. Boniface D, Cottin-Bizonne C, Kervil R, Ybert C, Detcheverry F. Self-propulsion of Symmetric Chemically Active Particles: Point-source Model and Experiments on Camphor Disks. Phys Rev E (2019) 99:062605. doi:10.1103/PhysRevE.99.062605

PubMed Abstract | CrossRef Full Text | Google Scholar

24. Nishimori H, Suematsu NJ, Nakata S. Collective Behavior of Camphor Floats Migrating on the Water Surface. J Phys Soc Jpn (2017) 86:101012. doi:10.7566/JPSJ.86.101012

CrossRef Full Text | Google Scholar

25. Morohashi H, Imai M, Toyota T. Construction of a Chemical Motor-Movable Frame Assembly Based on Camphor Grains Using Water-Floating 3d-Printed Models. Chem Phys Lett (2019) 721:104–10. doi:10.1016/j.cplett.2019.02.034

CrossRef Full Text | Google Scholar

26. Sharma J, Tiwari I, Das D, Parmananda P, Akella VS, Pimienta V. Rotational Synchronization of Camphor Ribbons. Phys Rev E (2019) 99:012204. doi:10.1103/PhysRevE.99.012204

PubMed Abstract | CrossRef Full Text | Google Scholar

27. Lauga E, Davis AMJ. Viscous Marangoni Propulsion. J Fluid Mech (2012) 705:120–33. doi:10.1017/jfm.2011.484

CrossRef Full Text | Google Scholar

28. Sur S, Masoud H, Rothstein JP. Translational and Rotational Motion of Disk-Shaped Marangoni Surfers. Phys Fluids (2019) 31:102101. doi:10.1063/1.5119360

CrossRef Full Text | Google Scholar

29. Jafari Kang S, Sur S, Rothstein JP, Masoud H. Forward, Reverse, and No Motion of Marangoni Surfers under Confinement. Phys Rev Fluids (2020) 5:084004. doi:10.1103/PhysRevFluids.5.084004

CrossRef Full Text | Google Scholar

30. Nagayama M, Nakata S, Doi Y, Hayashima Y. A Theoretical and Experimental Study on the Unidirectional Motion of a Camphor Disk. Physica D: Nonlinear Phenomena (2004) 194:151–65. doi:10.1016/j.physd.2004.02.003

CrossRef Full Text | Google Scholar

31. Hayashima Y, Nagayama M, Nakata S. A Camphor Grain Oscillates while Breaking Symmetry. J Phys Chem B (2001) 105:5353–7. doi:10.1021/jp004505n

CrossRef Full Text | Google Scholar

32. Koyano Y, Kitahata H. Imperfect Bifurcation in the Rotation of a Propeller-Shaped Camphor Rotor. Phys Rev E (2021) 103:012202. doi:10.1103/PhysRevE.103.012202

PubMed Abstract | CrossRef Full Text | Google Scholar

33. Kitahata H, Iida K, Nagayama M. Spontaneous Motion of an Elliptic Camphor Particle. Phys Rev E (2013) 87:010901. doi:10.1103/PhysRevE.87.010901

PubMed Abstract | CrossRef Full Text | Google Scholar

34. Iida K, Kitahata H, Nagayama M. Theoretical Study on the Translation and Rotation of an Elliptic Camphor Particle. Physica D: Nonlinear Phenomena (2014) 272:39–50. doi:10.1016/j.physd.2014.01.005

CrossRef Full Text | Google Scholar

35. Kitahata H, Koyano Y. Spontaneous Motion of a Camphor Particle with a Triangular Modification from a circle. J Phys Soc Jpn (2020) 89:094001. doi:10.7566/JPSJ.89.094001

CrossRef Full Text | Google Scholar

36. Kitahata H, Yoshinaga N. Effective Diffusion Coefficient Including the Marangoni Effect. J Chem Phys (2018) 148:134906. doi:10.1063/1.5021502

PubMed Abstract | CrossRef Full Text | Google Scholar

37. Suematsu NJ, Sasaki T, Nakata S, Kitahata H. Quantitative Estimation of the Parameters for Self-Motion Driven by Difference in Surface Tension. Langmuir (2014) 30:8101–8. doi:10.1021/la501628d

PubMed Abstract | CrossRef Full Text | Google Scholar

38. Karasawa Y, Oshima S, Nomoto T, Toyota T, Fujinami M. Simultaneous Measurement of Surface Tension and its Gradient Around Moving Camphor Boat on Water Surface. Chem Lett (2014) 43:1002–4. doi:10.1246/cl.140201

CrossRef Full Text | Google Scholar

39. Karasawa Y, Nomoto T, Chiari L, Toyota T, Fujinami M. Motion Modes of Two Self-Propelled Camphor Boats on the Surface of a Surfactant-Containing Solution. J Colloid Interf Sci (2018) 511:184–92. doi:10.1016/j.jcis.2017.09.099

CrossRef Full Text | Google Scholar

40. Koyano Y, Gryciuk M, Skrobanska P, Malecki M, Sumino Y, Kitahata H, et al. Relationship between the Size of a Camphor-Driven Rotor and its Angular Velocity. Phys Rev E (2017) 96:012609. doi:10.1103/PhysRevE.96.012609

PubMed Abstract | CrossRef Full Text | Google Scholar

41. Koyano Y, Suematsu NJ, Kitahata H. Rotational Motion of a Camphor Disk in a Circular Region. Phys Rev E (2019) 99:022211. doi:10.1103/PhysRevE.99.022211

PubMed Abstract | CrossRef Full Text | Google Scholar

42. Koyano Y, Kitahata H, Gryciuk M, Akulich N, Gorecka A, Malecki M, et al. Bifurcation in the Angular Velocity of a Circular Disk Propelled by Symmetrically Distributed Camphor Pills. Chaos (2019) 29:013125. doi:10.1063/1.5061027

PubMed Abstract | CrossRef Full Text | Google Scholar