A 6D Fractional-Order Memristive Hopfield Neural Network and its Application in Image Encryption

This paper proposes a new memristor model and uses pinched hysteresis loops (PHL) to prove the memristor characteristics of the model. Then, a new 6D fractional-order memristive Hopfield neural network (6D-FMHNN) is presented by using this memristor to simulate the induced current, and the bifurcation characteristics and coexistence attractor characteristics of fractional memristor Hopfield neural network is studied. Because this 6D-FMHNN has chaotic characteristics, we also use this 6D-FMHNN to generate a random number and apply it to the field of image encryption. We make a series of analysis on the randomness of random numbers and the security of image encryption, and prove that the encryption algorithm using this 6D-FMHNN is safe and sensitive to the key.

1 Introduction

The artificial neural network (ANN) system is composed of many neurons with adjustable connection weights, and has distributed information storage, good self-organization and self-learning ability, and large-scale parallel processing. ANN realizes intelligence by imitating various working and learning modes of the human brain and biological system, so it has a wide application prospect in many fields such as signal processing and pattern recognition, intelligent control, fault diagnosis, and information optimization [1–5].

In recent decades, more and more attention has been paid to the study of chaotic systems, and various chaotic systems with complex dynamics have been proposed [6–11]. As a new science, chaos has been widely used in secure communication [12–14], electronic circuit [15–18], random number generator [19–23], and image encryption [24–34]. Through the study of the brain, scientists found that there are complex chaotic phenomena in the human brain [35], which explain the irregular movement in the human brain. Inspired by this, Aihara et al. proposed a chaotic neural network model based on previous derivation and animal experiments in 1990. The chaotic neural network is a highly nonlinear dynamic system, so the neural network is closely related to chaos. Therefore, the chaotic neural network is considered to be one of the intelligent information processing systems that can realize its real-world computing. It has a good application prospect in the fields of algorithm optimization, information storage, associative memory, pattern recognition, and so on [36–41].

In 1971, Professor Leon O. Chua proposed the existence of memristor [42]. It wasn’t until 2008 that HP LABS implemented the first true memristor [43]. With the physical realization of memristor, the research of memristor has attracted extensive attention again [44–48]. Adding memristor in the construction of nonlinear system makes the chaotic system based on memristor have richer dynamic behavior, and the generated chaotic signal has better pseudo-random characteristics, which makes it have higher research value in the fields of image encryption, spread spectrum communication, and secure communication [49–53]. Because memristor has memory function and its resistance value is accurate and continuously adjustable, which is similar to the function of biological neural synapse, the neural network circuit based on memristor is closer to the brain in function and can fully realize human consciousness in theory, making memristive neural network (MNN) become a new research hotspot [54–59]. In [55], the authors studied the dynamic characteristics of a small neural network with three neurons under electromagnetic radiation. The intensity of electromagnetic radiation will change the number of equilibrium points in the neural network, resulting in the diversity of attractor trajectories. In [58], a full circuit of MNN based on weighted and simultaneous disturbance training was proposed. A synaptic circuit is designed using a pair of memristors, and then a complete neural network circuit is designed.

Since the value of the next state of fractional-order chaotic system is related not only to the current state but also to all previous states, its dynamic characteristics are more complex than the integer order chaotic system. In recent years, various fractional-order chaotic systems have been widely proposed [17, 60–63]. With the deepening of research, researchers add fractional-order to the neural network model and find that the results are more similar to the activities of human brain neurons, which extends the application field of fractional-order neural network system. However, for the study of MNN, most of the results are in the integer order range [55–59, 64]. In [65], a fractional-order memristive Hindmarsh-Rose (H-R) model was proposed. Without small parameter constraints, the fractional-order memristive H-R model had periodic and chaotic bursts, which showed that small parameters make the membrane potential activity simpler. In [66], a simplified fractional-order neural network with discontinuous conductivity function based on memristor was proposed. It was essentially a switching system with irregular switching law, which was composed of eight fractional-order neural network subsystems.

In this paper, a new memristor model is proposed and applied to the fractional-order Hopfield neural network (FHNN) to study its dynamic characteristics such as bifurcation and coexistence. In addition, the newly proposed fractional memristor Hopfield neural network (FMHNN) is also applied in the field of image encryption.

2 A new Memristor model

2.1 Mathematical model

In studying the relationship between four circuit variables which are voltage, current, magnetic flux, and electric charge, we know that resistance represents the relationship between voltage and current, capacitance represents the relationship between charge and voltage, and inductance represents the relationship between magnetic flux and current. According to the duality property, there should also be a circuit element that represents the relationship between charge and magnetic flux. In 1971, the concept of a memristor was proposed. This component establishes a connection between charge and magnetic flux and the relationship is described in the form of Eq. 1 [42].

$W=\frac{dq}{d\phi }(1)$

Since then, many scholars have devoted themselves to the research of memristor. The concept of memristor has been extended to any device with two ends representing pinched hysteresis loops (PHL). For the first-order general memristor, its mathematical model can be described by Eq. 2 [56]:

$\left\{\begin{array}{c}i=G\left(x\right)v\hfill \\ \frac{dx}{dt}=g\left(x,v\right)\hfill \end{array}\right.(2)$

where v_m and i_m represent the input voltage and input current of the memristor, respectively. G is a function of x, known as memductance, which is an internal state variable. g (x, v_m) is a Lipschitz function. According to Eq. 2, we take $a-b\left|x\right|-c\sin (x)$ as memductance to construct a new memristor model Eq. 3:

$\left\{\begin{array}{c}i=\left(a-b\left|x\right|-c\sin \left(x\right)\right)v\hfill \\ \frac{dx}{dt}=v\hfill \end{array}\right.(3)$

where a, b,and c are memristor parameters. In this paper, a, b, and c are 0.3, −0.18, and 0.2 respectively.

2.2 Pinched hysteresis loops

It was indicated that if an electrical element is a memristor, it must satisfy two conditions in literature [67]:

(1) When driven by a periodic voltage or current source, the device must exhibit PHL in the voltage-current plane and the PHL always passes through the origin.

(2) As the frequency of the periodic driving signal increases, PHL should show shrinkage, that is, the area of PHL should constantly decrease. PHL should shrink to single-function as the frequency of the drive signal approaches infinity.

Based on Eq. 3, we draw the voltage-current relationship image of the memristor model (Figure 1A, Figure 1B) and the time sequence diagram of voltage and current Figure 1C by MATLAB R2019 simulation software. Figure 1A shows that when the excitation voltage is $v\left(t\right)=\sin \left(Ft\right)$ and the initial value is $x\left(0\right)=0$, the memristor exhibits PHL, and the area of PHL shrinks continuously with the increase of frequency f, which meets the two conditions of the memristor. Figure 1B shows that when the excitation voltage is $v\left(t\right)=A\sin \left(t\right)$ and the initial value is $x\left(0\right)=0$, the PHL area of the memristor increases with the increase of the amplitude A, which is also consistent with the characteristics of the memristor.

FIGURE 1

FIGURE 1. PHL varying with the frequency of the excitation voltage (A). PHL with excitation voltage amplitude (B). Voltage and current sequence diagram (C).

3 Three memristor-coupled FHNN model

3.1 Integer order mathematical model

Hopfield neural network (HNN) is particularly suitable for simulating various complex dynamical behaviors in the brain, especially chaotic behaviors, due to its significant nonlinearity and flexible mathematical expressions. Its mathematical model can be described by Eq. 4 [68, 69]:

${\mathrm{C}}_i\frac{d{x}_i}{dt}=-\frac{x_i}{R_i}+\sum _{\mathrm{j}=1}^n{w}_{ij}\tanh \left(x_j\right)+I_{iext}(4)$

where C_i, R_i, x_i are membrane capacitance, membrane resistance and membrane potential of neuron i respectively. w_ij is the synaptic weight between neuron i and the neuron j and tanh (x_i) is the neuron activation function. I_iext is an electrical current generated by an external stimulus. According to the neural network model described by Eq. 4, HNN of three neurons can be concretized by Eq. 5

$\left\{\begin{array}{c}{\mathrm{C}}_1\frac{d{x}_1}{dt}=-\frac{x_1}{R_1}+\sum _{\mathrm{j}=1}^3{w}_{1j}\tanh \left(x_j\right)+I_1\hfill \\ {\mathrm{C}}_2\frac{d{x}_2}{dt}=-\frac{x_2}{R_2}+\sum _{\mathrm{j}=1}^3{w}_{2j}\tanh \left(x_j\right)+I_2\hfill \\ {\mathrm{C}}_3\frac{d{x}_3}{dt}=-\frac{x_3}{R_3}+\sum _{\mathrm{j}=1}^3{w}_{3j}\tanh \left(x_j\right)+I_3\hfill \end{array}\right.(5)$

In this paper, the coefficients C₁, C₂, C₃, R₁, R₂, R₃ are set as 1, respectively, and the weight w_ij can be expressed by the weight matrix Eq. 6. It should be noted that the weight used by HNN in this paper is different from that in literature [69].

$W=\left(\begin{array}{ccc}\hfill 3.8\hfill & \hfill -1.9\hfill & \hfill 0.7\hfill \\ \hfill 2.8\hfill & \hfill 0\hfill & \hfill 1\hfill \\ \hfill -5.6\hfill & \hfill 1.9\hfill & \hfill 0\hfill \end{array}\right)(6)$

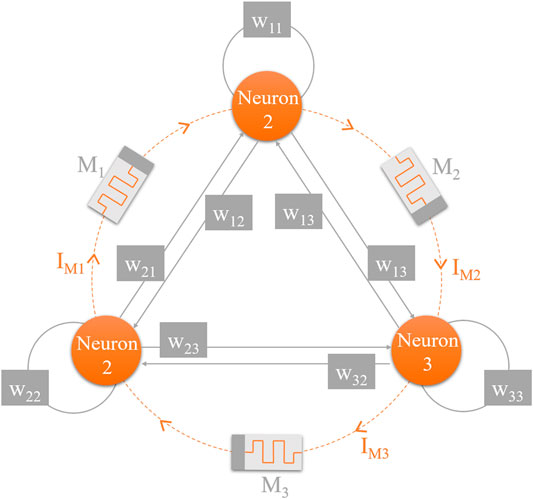
Because HNN is multiple neurons connected to each other, electromagnetic induction current will appear between HNN neurons due to the existence of membrane potential difference between neurons. In order to establish a mathematical model and study the influence of induced current between neurons on the dynamic behavior of HNN, this paper uses a magnetically controlled memristor to connect multiple neurons and uses the current flowing through the memristor to simulate the induced current between neurons [69]. Based on the above analysis, we can establish an improved HNN model.

$\left\{\begin{array}{c}\frac{d{x}_1}{dt}=-x_1+3.8\tanh \left(x_1\right)-1.9\tanh \left(x_2\right)\hfill \\ +0.7\tanh \left(x_3\right)+h_1-h_3\hfill \\ \frac{d{x}_2}{dt}=-x_2+2.8\tanh \left(x_1\right)+\tanh \left(x_3\right)\hfill \\ +h_2-h_1\hfill \\ \frac{d{x}_3}{dt}=-x_3-5.6\tanh \left(x_1\right)+1.9\tanh \left(x_2\right)\hfill \\ +h_3-h_2\hfill \\ \frac{d{\phi }_1}{dt}=x_1-x_2-{\phi }_1\hfill \\ \frac{d{\phi }_2}{dt}=x_2-x_3-{\phi }_2\hfill \\ \frac{d{\phi }_3}{dt}=x_3-x_1-{\phi }_3\hfill \\ h_1=kG\left({\phi }_1\right)\left(x_1-x_2\right)\hfill \\ h_2=kG\left({\phi }_2\right)\left(x_2-x_3\right)\hfill \\ h_3=kG\left({\phi }_3\right)\left(x_3-x_1\right)\hfill \end{array}\right.(7)$

The mathematical model of Eq. 7 describes the situation in which induced current exists between three neurons in HNN model, and the bidirectional induced current is generated by simulating electromagnetic induction by interconnecting neurons with three memristors. With the addition of three memristors, a 6D memristive Hopfield neural network (6D-MHNN) model is finally established. In order to intuitively understand the 6D-MHNN model given by Eq. 7, Figure 2 presents the general schematic diagram of the extension connection between neuron and memristor in this model.

FIGURE 2

FIGURE 2. Schematic diagram of the connection topology of a trimemristor-coupled HNN model.

3.2 Fractional mathematical model

The concept of fractional calculus has been put forward for a long time and has become a powerful tool to study fractional differential equations and fractal functions. Since fractional order is more accurate than integer order in simulating real dynamic system, this paper will construct a fractional Hopfield neural network based on Eq. 7. At present, there are many definitions of fractional calculus, but this paper adopts Caputo’s definition of fractional derivative [70, 71].

Definition 1. Caputo fractional derivative is defined as follows:

$D_{t_0}^q=J_{t_0}^{m-q}{D}_{t_0}^{m}x\left(t\right)=\left\{\begin{array}{c}\frac{1}{\mathrm{\Gamma }\left(m-q\right)}\underset{t_0}{\overset{t}{\int }}{\left(t-\tau \right)}^{m-q-1}{x}^{\left(m\right)}\left(\tau \right)d\tau \hfill \\ \frac{d^{m}x\left(t\right)}{d{t}^m},q=m\hfill \end{array}\right.(8)$

where Γ(•) represents Gamma function. According to the definition of Caputo fractional derivative, the mathematical model Eq. 9 of fractional memristor Hopfield neural network (FMHNN) can be obtained by setting the order of Eq. 7 derivative as α.

$\left\{\begin{array}{c}\frac{d^{\alpha }{x}_1}{dt}=-x_1+3.8\tanh \left(x_1\right)-1.9\tanh \left(x_2\right)\hfill \\ +0.7\tanh \left(x_3\right)+h_1-h_3\hfill \\ \frac{d^{\alpha }{x}_2}{dt}=-x_2+2.8\tanh \left(x_1\right)+\tanh \left(x_3\right)\hfill \\ +h_2-h_1\hfill \\ \frac{d^{\alpha }{x}_3}{dt}=-x_3-5.6\tanh \left(x_1\right)+1.9\tanh \left(x_2\right)\hfill \\ +h_3-h_2\hfill \\ \frac{d^{\alpha }{\phi }_1}{dt}=x_1-x_2-{\phi }_1\hfill \\ \frac{d^{\alpha }{\phi }_2}{dt}=x_2-x_3-{\phi }_2\hfill \\ \frac{d^{\alpha }{\phi }_3}{dt}=x_3-x_1-{\phi }_3\hfill \\ h_1=kG\left({\phi }_1\right)\left(x_1-x_2\right)\hfill \\ h_2=kG\left({\phi }_2\right)\left(x_2-x_3\right)\hfill \\ h_3=kG\left({\phi }_3\right)\left(x_3-x_1\right)\hfill \end{array}\right.(9)$

where α is the order of the derivative, $G(\phi )=a-b\left|\phi \right|-c\sin (\phi )$.

3.3 System stability analysis

It is necessary to analyze the stability of equilibrium point of HNN dynamic system, so we make the left side of Eq. 9 all equal to 0, thus obtaining Eq. 10, and then solve the roots of the equations to obtain the equilibrium point.

$\left\{\begin{array}{c}0=-x_1+3.8\tanh \left(x_1\right)-1.9\tanh \left(x_2\right)+0.7\tanh \left(x_3\right)\hfill \\ +kG\left({\phi }_1\right)\left(x_1-x_2\right)-kG\left({\phi }_3\right)\left(x_3-x_1\right)\dots ,\dots \left(1\right)\hfill \\ 0=-x_2+2.8\tanh \left(x_1\right)+\tanh \left(x_3\right)\hfill \\ +kG\left({\phi }_2\right)\left(x_2-x_3\right)-kG\left({\phi }_1\right)\left(x_1-x_2\right)\dots ,\dots \left(2\right)\hfill \\ 0=-x_3-5.6\tanh \left(x_1\right)+1.9\tanh \left(x_2\right)\hfill \\ +kG\left({\phi }_3\right)\left(x_3-x_1\right)-kG\left({\phi }_2\right)\left(x_2-x_3\right)\dots ,\dots \left(3\right)\hfill \\ 0=x_1-x_2-{\phi }_1\dots ,\dots \left(4\right)\hfill \\ 0=x_2-x_3-{\phi }_2\dots ,\dots \left(5\right)\hfill \\ 0=x_3-x_1-{\phi }_3\dots ,\dots \left(6\right)\hfill \end{array}\right.(10)$

Observe Eq. 10. It is easy to find that Eq. 11 can be obtained by adding equation (1), (2) and (3) in Eq. (10).

$\left\{\begin{array}{c}{x}_2=\tanh \left(x_1\right)+1.7\tanh \left(x_3\right)-x_3-x_1\hfill \\ {\phi }_1=x_1-x_2\hfill \\ {\phi }_2=x_2-x_3\hfill \\ {\phi }_3=x_3-x_1\hfill \end{array}\right.(11)$

By substituting Eq. 11 into Eq. 10, x₂, φ₁, φ₂, φ₃ can be eliminated and a binary system of equations, Eq. 12, can be obtained.

$\left\{\begin{array}{c}0=-x_1+3.8\tanh \left(x_1\right)-1.9\tanh \left(a\right)+0.7*\tanh \left(x_3\right)\hfill \\ +kG\left(x_1-a\right)\left(x_1-a\right)-kG\left(x_3-x_1\right)\left(x_3-x_1\right)\dots ,\dots H1\hfill \\ 0=-x_3-5.6\tanh \left(x_1\right)+1.9\tanh \left(a\right)\hfill \\ -kG\left(a-x_3\right)\left(a-x_3\right)+kG\left(x_3-x_1\right)\left(x_3-x_1\right)\dots ,\dots H2\hfill \end{array}\right.(12)$

Because it is difficult to directly solve the root of Eq. 12, the graphic method is adopted in this paper. MATLAB is used to draw the trajectory diagram of the two equations (Figure 3A, Figure 3B, Figure 3C), and then numerical analysis is used to obtain the analytical solution of the equations.

FIGURE 3

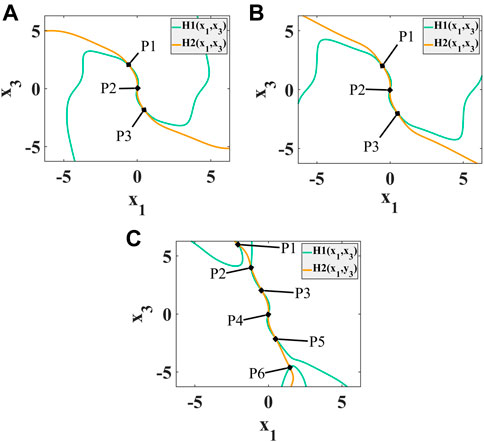
FIGURE 3. Trajectory diagram of H1 and H2 (A) when the memristor coupling strength k is −0.08; (B) when the memristor coupling strength k is 0; (C) when the memristor coupling strength k is 0.08.

The approximate range of x₁, x₃ can be easily obtained from the figure, and a more accurate solution can be obtained by using Fsolve function of MATLAB. After solving the root [x₁, x₂, x₃, x₄, x₅, x₆] of Eq. 10, put each solution into the Jacobi matrix of Eq. 9, and then obtain each eigenvalue from the characteristic polynomial; the results are shown in Table 1.

TABLE 1

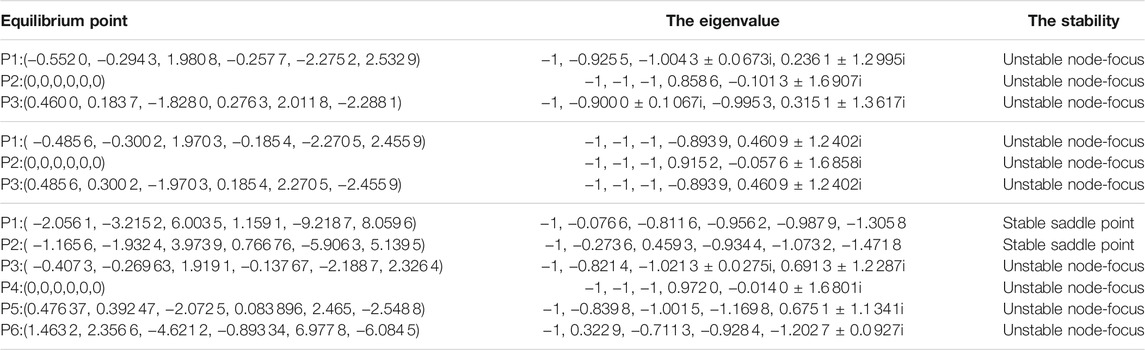
TABLE 1. The results of equilibrium point analysis when k is taken as −0.08, 0 and 0.08 respectively

4 Dynamics analysis of 6D-FMHNN

At present, related scholars usually use the phase diagram method, Lyapunov exponent method, and bifurcation diagram method to analyze the dynamics of chaotic system, etc. In addition, the attractor basin can easily find the coexistence attractor of the system. Therefore, this paper will use the FDE12 algorithm in MATLAB to solve the fractional differential equation, Eq. 9, and thus draw the bifurcating diagram, phase diagram, and attraction basin.

4.1 Dynamics of variable order

When the initial value of the system Eq. 9 is unified as [0.1, 0.1, 0.1, 0.1, 0.1, 0.1], bifurcation diagrams on the memristor coupling strength k are drawn respectively with order α = 0.7, α = 0.8, α = 0.9, α = 1 displayed on Figure 4A, Figure 4B, Figure 4C, and Figure 4D. It can be seen from the figure that when the order α is 0.7, no matter how k changes, the system will not appear as chaos. When the order is 0.8–0.9, the value of the memristor intensity k determines whether the system behaves periodic or chaotic. When the order is 0.8, 0.07 ≤ k ≤ 0.1, the system is chaotic. When the order is 0.9, 0.007 ≤ k ≤ 0.025, or 0.07 ≤ k ≤ 0.08, the system is chaotic. When the order is one, k has to be a very small number of values for the system to be chaotic.

FIGURE 4

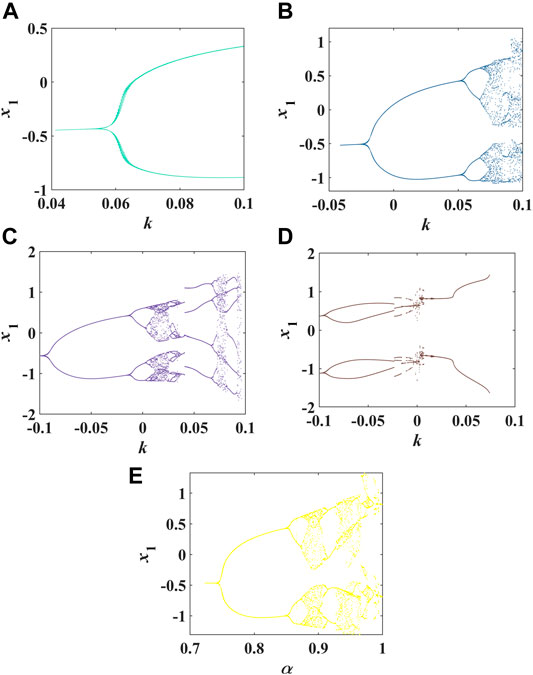
FIGURE 4. The bifurcation diagram of 6D-FMHNN with respect to parameter k (A) when the differential order is 0.7; (B) when the differential order is 0.8; (C) when the differential order is 0.9; (D) when the differential order is 1 and the bifurcation diagram of 6D-FMHNN with respect to order when the memristor coupling strength k is 0.02 (E).

In addition, this paper also studies the bifurcation diagram of 6D-FMHNN (Figure 4E) on order α when the memristor coupling strength k is 0.02 and the initial value of the system is [0.1, 0.1, 0.1, 0.1, 0.1, 0.1]. As can be seen from the observation in the picture that with the increase of order, the system changes from periodic one-limit cycle to periodic two-limit cycle and then to periodic four limit cycle. Until α = 0.88, the system becomes chaotic. However, as α continues to rise, the system appears as inverse period-doubling and degenerates into a periodic four-limit cycle. After degenerating into a period, it becomes chaotic again after a = 0.93.

In conclusion, the order has a great influence on the dynamic behavior of 6D-FMHNN. When α > 0.8, the chaos phenomenon of the system is more significant.

4.2 Dynamics of fixed order

In this part, the order α of differentiation in Eq. 9 is fixed as 0.88. First, set the initial value of the system as [0.1, 0.1, 0.1, 0.1, 0.1, 0.1, 0.1], and explore the change of system bifurcation behavior when the memristor coupling strength k changes (Figure 5A). Secondly, k is fixed at 0.015 and the initial value of the system was set as $\left[x_1\left(0\right),0,0,0,0,0,0\right]$, and the bifurcation diagram of the initial value x₁ of the system was drawn in Figure 5B. Observation can be found from Figure 5A that, like the general partial illustrations, with the rise of k, the system transitions from the initial period-1 limit cycle to period-2 limit cycle and then to period-4 limit cycle. When k = 0.02, the system starts to become chaotic. However, as k continues to rise, the system gradually degenerates into a periodic limit cycle of four times and bifurcates inversely when k = 0.08 and then enters a chaos state. As can be seen from the observation in the picture from Figure 5B that when the initial value of the system x₁ changes between [ − 1, 0), the system is always a periodic four-limit cycle; when x₁ changes between (0, 1], the system presents chaos. In general, the system is sensitive to initial values and memristor coupling strength k.

FIGURE 5

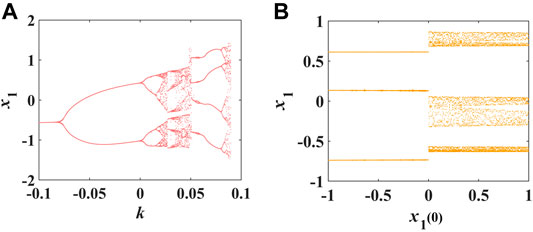
FIGURE 5. When the differential order α is 0.88, the bifurcation diagram of parameter k (A) and the bifurcation diagram of initial value ×1 (0) (B).

4.3 A variety of coexisting attractors

Coexisting attractor means that different initial states of a system correspond to two different attractors. When the order of the system is determined to be 0.88 and the memristive coupling strength k is −0.05, the initial values of the system are [ − 0.1, 0, 0, 0, 0, 0, 0] and [0.1, 0, 0, 0, 0, 0, 0], respectively. At this time, the system has two periodic coexistence phenomena (Figure 6A). When the order of the system is determined to be 0.88 and the memristive coupling strength k is 0.015, the initial values of the system are [ − 0.1, −0.1, −0.1, −0.1, −0.1, −0.1] and [0.1, 0.1, 0.1, 0.1, 0.1, 0.1], respectively. At this time, the system shows the coexistence of chaos and period (Figure 6B). When the order of the system is 0.88 and the memristive coupling strength k is 0.02, the initial values of the system are [ − 0.1, −0.1, −0.1, −0.1, −0.1, −0.1, −0.1] and [0.1, 0.1, 0.1, 0.1, 0.1, 0.1], respectively. At this time, two chaotic attractors coexist in the system (Figure 6C). When the order of the system is determined to be 0.88 and the memristive coupling strength k is 0.025, the initial values of the system are [ − 0.1, −0.1, −0.1, −0.1, −0.1, −0.1] and [0.1, 0.1, 0.1, 0.1, 0.1, 0.1], respectively; two chaotic attractors coexist in the system (Figure 6D). In addition, this paper also draws the attraction basin corresponding to the initial state of [x₁ (0), x₂ (0), 0, 0, 0, 0] when the system order is determined to be 0.88 and the memristor resistance coupling strength k is 0.02 Figure 6E

FIGURE 6

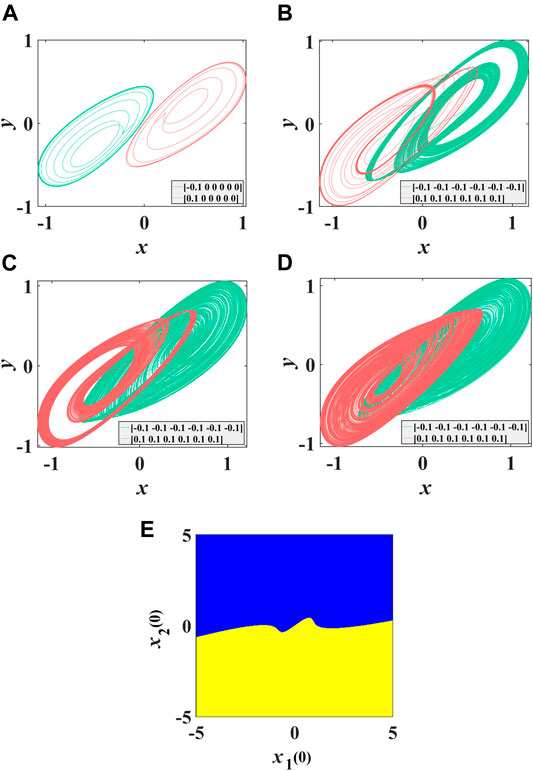
FIGURE 6. Coexisting attractors and attraction basin. (A) Coexistence of two cycles with k = −0.05; (B) coexistence of cycle and chaos with k = 0.015; (C) coexistence of two chaos with k = 0.02; (D) coexistence of two chaos with k = 0.025; (E) the attraction basin corresponding to initial state [×1 (0); ×2 (0); 0; 0; 0; 0].

5 Application in image encryption

5.1 Random sequence generation

Suppose the size of the image to be encrypted is M × N, then we need to generate a random sequence of length 3 × M × N, which is respectively used in the forward diffusion and reverse diffusion of the two diffusion algorithms and the scrambling algorithm.

Step 1: Let the input initial value of 6D-FMHNN system be [x₁, x₂, x₃, x₄, x₅, x₆], and first iterate T wheel to eliminate the initial disturbance of the system.

Step 2: After iterating round T to eliminate the initial disturbance of the system, we conduct a slight disturbance of the initial value of every B iteration to ensure the pseudo-randomness of the sequence.

Step 3: After iterating round C, of course, we need to guarantee C × B × 6 ≥ 3 × M × N, and we get a random sequence [X1,X2,X3,X4,X5,X6]^T where Xi = [x_i1, x_i2, x_i3, … , x_ij, … , ], i = 1, 2, 3, 4, 5, 6, and j = 1, 2, 3, … , L. Considering the 3 × M × N is not necessarily divisible exactly by 6, so $L\ge \frac{3\times M\times N}{6}$.

Step 4: We reduce [X1,X2,X3,X4,X5,X6]^T to a one-dimensional vector X, and then we take X(1 : 3 × M × N) so that we get the random sequence we need.

5.2 Image encryption and decryption process

5.2.1 Image encryption steps

The steps of image encryption can be divided into four steps.

Step 1: By iterating the 6D-FMHNN system, the sequence with 3 × M × N length was denoted as X, and the dimension of the image to be encrypted with M × N size was reduced to a one-dimensional vector.

Step 2: Make two additive mode diffusions, so that the information of each pixel point spreads to the whole image. The diffusion algorithm is shown in Eq. 13:

$\left\{\begin{array}{c}{C}_i=\mathrm{mod}\left(C_{i-1}+S_i+A_i,256\right)\hfill \\ C_i=\mathrm{mod}\left(C_{i+1}+S_i+A_i,256\right)\hfill \end{array}\right.(13)$

where A is the image to be diffused, S is the random sequence with length M × N, and C is the encrypted image; so the inverse transformation of Eq. 13 is Eq. 14.

$\left\{\begin{array}{c}{A}_i=\mathrm{mod}\left(256\times 2+C_i-C_{i-1}-S_i,256\right)\hfill \\ A_i=\mathrm{mod}\left(256\times 2+C_i-C_{i+1}-S_i,256\right)\hfill \end{array}\right.(14)$

In this paper, S = X (1: M × N) is taken for the first diffusion and S = X (M × N + 1: M × N × 2) for the second diffusion.

Step 3: Shuffling pixel positions, in other words, exchanging information between two pixels via Eq. 15 mapping.

$\left\{\begin{array}{c}swap\left(A\left(i\right),A\left(j\right)\right)\hfill \\ j=S\left(i\right)\hfill \end{array}\right.(15)$

which is a random sequence of numbers of length M × N, and S(i) ∈ [1, M × N], for any n ≠ m, S(n) ≠ S(m). S can be generated by normalizing X (1: M × N) and removing repeated elements in the sequence and adding missing elements in [1, M × N] at the end of the sequence.

Step3Perform two more multiply mode taking diffusion operations [72], and the diffusion algorithm is shown in Eq. 16:

$\left\{\begin{array}{c}{C}_i=C_{i-1}\times S_i\times A_i\hfill \\ C_i=C_{i+1}\times S_i\times A_i\hfill \end{array}\right.(16)$

Therefore, the inverse transformation corresponding to Eq. 16 is shown below as Eq. 17:

$\left\{\begin{array}{c}{A}_i=C_i÷S_i÷C_{i-1}\hfill \\ A_i=C_i÷S_i÷C_{i+1}\hfill \end{array}\right.(17)$

where A is the image to be diffused, S is the random sequence with length M × N, and C is the encrypted image. In this paper, S = X (M × N + 1: M × N × 2) is taken for the first diffusion and S = X (M × N × 2 + 1: M × N × 3) for the second diffusion.

5.2.2 Image decryption step

Since the decryption operation is the reverse operation of the encryption operation, this article will not be detailed to save space.

Step 1: iterate the 6-day FMHNN system to get the sequence with length 3 × M × N, denoted as X, and reduce the dimension of the image to be decrypted with size M × N to a one-dimensional vector.

Step 2: Carry out the inverse operation Eq. 17 of multiplication for mold diffusion twice.

Step 3: Perform the same pixel scrambling Eq. 15 again.

Step 4: Perform the inverse operation Eq. 14 of two additive mode diffusions.

5.3 Safety analysis

5.3.1 Randomness test of chaotic sequences

To test the randomness of the random sequence generated in part 5.1 of this article, we need to use NIST SP800-22. In this paper, the parameter k of Eq. 9 is 0.02, the order α is 0.88, and the initial value is [1–6]. NIST SP800-22 has a total of 15 test methods to test the randomness of a sequence, so the software has 15 standards for the randomness of the sequence. After the execution of each test method, a p-value between [0, 1] will be generated, and if the p-value is greater than the preset threshold, it indicates that the test has passed. In this paper, the default threshold of the software is 0.01, and the sequence length 10⁶ is set to one input stream, and there are 10 such input streams. Table 2 shows the results of 15 tests.

TABLE 2

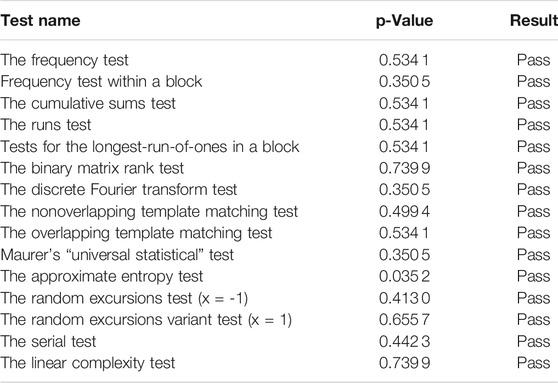
TABLE 2. Statistical table of the results of testing the randomness of random sequences using NIST SP800-22

5.3.2 Experimental results of image encryption

The encryption pictures in this paper come from USC-SIPI database, and the operating system of the test platform is Windows 10 64-bit, the test software is MATLAB 2019, and the processor of the test machine is quad-core Intel Core STUtNzMwMEhRQDIuNTBHaHo=. The memory is 16 GB DDR4 RAM. The parameter k of 6D-FMHNN system is 0.02, the order is 0.88, and the initial value is [1–6]. The original, encrypted, and decrypted images of some images are shown in Figure 7. The attacker is unable to obtain any useful information from the encrypted images shown in Figure 7, indicating that the encryption algorithm proposed in this paper is effective.

FIGURE 7

FIGURE 7. Image encryption experiment results: original image (A), encrypted image (B), decrypted image (C).

5.3.3 Image histogram analysis

Histogram is a graph drawn after the frequency of each gray value in the image is counted. In order not to leave an attacker with any useful statistics, an ideal encryption algorithm would distribute the pixel depth of the image evenly, as shown in the histogram, so that the squares are basically flush. Figure 8 shows the histogram of pixel depth distribution of the original image and the encrypted image of some images. It can be seen from the figure that the histogram of plaintext image shows obvious statistical law, and the uniformity of pixel depth distribution of the image after encryption is significantly improved. In order to quantitatively analyze the uniformity of histogram distribution, chi-square test (Eq. 18) and variance were used to evaluate. chi-Square values of the histogram before and after encryption were calculated, and the pictures involved in the calculation include 4.1.05, 4.1.06, 4.1.08, 4.2.01, and 4.2.03. The chi-square values of the histogram of plain image are 300,852.0781, 66009.6797, 334,267.1406, 343,393.1465, and 187,356.5723, respectively. In addition, the chi-square values of the histogram of encrypted image are 272.0469, 253.1797, 284.3828, 231.0273, and 254.0137, respectively, and under the condition that the degree of freedom is 255 and the significance level is 1% and 5%, the corresponding chi-square test critical values are $x_{0.01}^2(255)=310.457$ and $x_{0.05}^2(255)=293.2478$, respectively. It is not difficult to see from the table that the gray value distribution of the encrypted image is quite uniform compared with that of the unencrypted image, so it is difficult for the attacker to attack by using histogram. Secondly, by changing the initial value of the encryption key, namely 6D-FMHNN system, the variance of the image histogram after encryption is calculated to evaluate whether the quality of the key has an impact on the encryption effect. It can be seen from Table 3 that the encryption algorithm in this paper has good encryption effect for different keys.

$x^2=\sum _{L=0}^{255}\frac{{\left(O-E\right)}^2}{E}(18)$

FIGURE 8

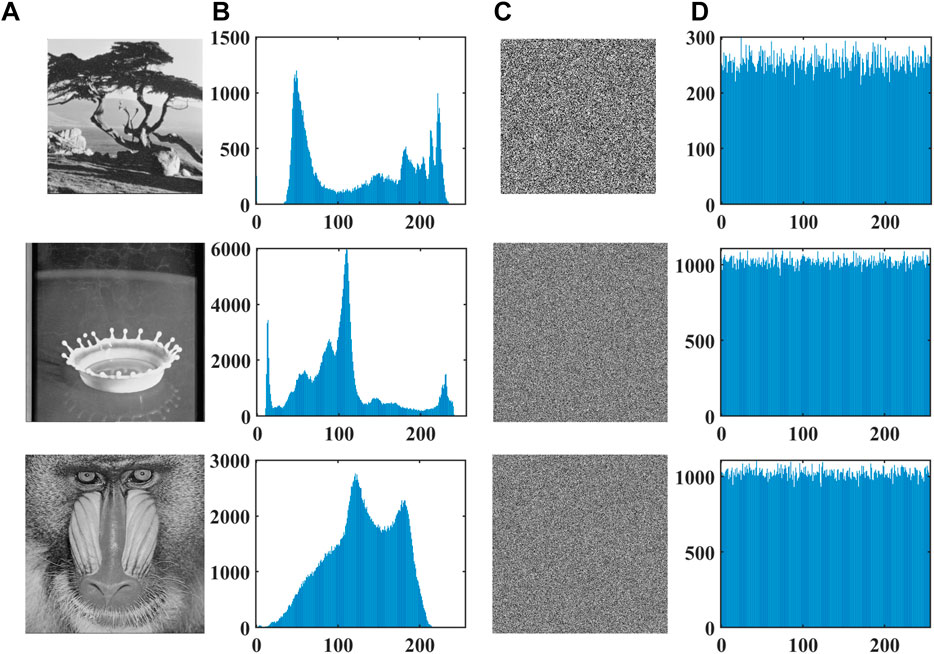
FIGURE 8. Histogram comparison of the original image and the encrypted image; (A) original image; (B) histogram of original image; (C) encrypted image; (D) histogram of encrypted image.

TABLE 3

TABLE 3. Statistical table of histogram variance after encryption with different keys

In this paper, O represents the observed count of each gray value, and E represents the expected count of each gray value.

5.3.4 Correlation analysis

Correlation analysis is the analysis of multiple factors with correlation, so as to measure the correlation of these factors. In this paper, it specifically refers to analyzing the correlation of the color depth of two adjacent pixels in an image. There is a strong correlation between the color depths of two adjacent pixels of an unencrypted image, and an ideal encryption algorithm should be able to hide this correlation; otherwise, it would be a breach for an attacker. In this paper, the correlation coefficient is calculated to measure the correlation of images, and the calculation formula is shown in Eq. 19 [24]:

$\left\{\begin{array}{c}{R}_{xy}=\frac{\mathrm{cov}\left(x,y\right)}{\sqrt{D\left(x\right)}\sqrt{D\left(y\right)}}\hfill \\ D\left(x\right)=\frac{1}{N}\sum _{i=1}^N{\left(x_i-E\left(x\right)\right)}^2\hfill \\ \mathrm{cov}\left(x,y\right)=\frac{1}{N}\sum _{i=1}^N\left(x_i-E\left(x\right)\right)\left(y_i-E\left(y\right)\right)\hfill \\ E\left(x\right)=\frac{1}{N}\sum _{i=1}^N{x}_i\hfill \end{array}\right.(19)$

where y is the adjacent pixel of x, and N is the number of pixel pairs randomly selected from the image, that is, the correlation coefficient of the image, which is closer to 0, the better. In this paper, 5,000 pixels are randomly selected from the image and the correlation coefficients in the vertical, horizontal, and diagonal directions are calculated, respectively. The results are shown in Figure 9, Table 4, and Table 5. It can be found from Figure 9 and Table 4 that the adjacent pixels of the unencrypted picture have a strong correlation, which basically disappears after encryption. Table 5 compares the correlation coefficients between this paper and other literatures. It can be found that our encryption algorithm has lower correlation coefficients in horizontal, vertical, and diagonal directions.

FIGURE 9

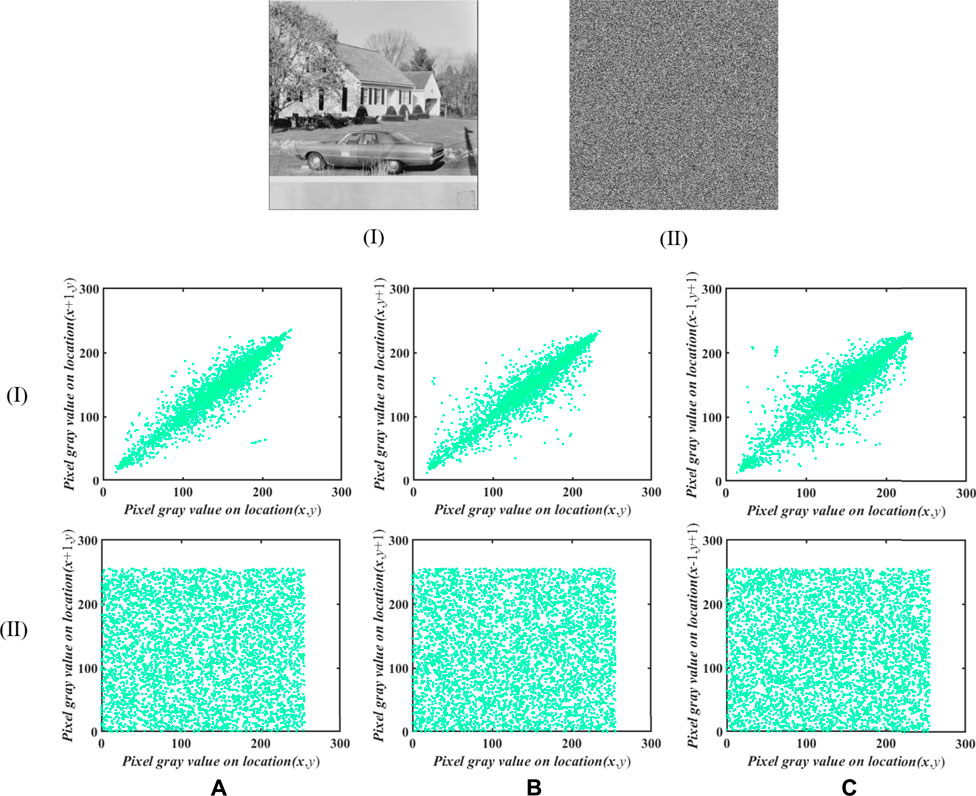
FIGURE 9. The correlation of adjacent pixels in picture House where (I) and (II) are the plaintext picture and ciphertext picture, respectively: (A) the correlation of two horizontal adjacent pixels, (B) the correlation of two vertical adjacent pixels, and (C) the correlation of two diagonal adjacent pixels.

TABLE 4

TABLE 4. Correlation coefficients of different images before and after encryption

TABLE 5

TABLE 5. Comparison of correlation coefficient with other literature

5.3.5 Information entropy analysis

Shannon defined information entropy as the occurrence probability of discrete random events, which is an important indicator to measure the randomness of information. It is generally believed that the greater the information entropy is, the greater the uncertainty is, so it can be used to measure the randomness of the image, and its calculation formula is given by Eq. 20 [74]:

$H=-\sum _{i=1}^{L}P\left(i\right){\log }_{2}P\left(i\right)(20)$

where i is the gray value, P(i) is the probability of gray value i, and L is the maximum gray value of pixel. For the image with 256 Gray level, the ideal value of H is 8. The larger the value H is, the more random the image information distribution is, and the better the encryption effect is. In this paper, the information entropy of some pictures that include boat, house, 4.1.03, 4.1.05, 4.1.06, 4.1.07, 4.1.08, 4.2.01, 4.2.03, and 4.2.05, before and after encryption is calculated. Information entropy of original image is 7.1914, 7.3602, 5.6002, 6.4007, 7.1816, 5.8346, 6.2700, 6.6530, 7.6444, and 6.5768 respectively. Corresponding to it, information entropy of encrypted image is 7.9994, 7.9993, 7.9974, 7.9971, 7.9972, 7.9969, 7.9969, 7.9993, 7.9994, and 7.9993, respectively. In order to compare with other literatures, we especially calculate the information entropy of Lena graph, and the result is 7.9993. In contrast, the information entropy is 7.9987, 7.2072, 7.9992, and 7.9974, respectively, in [24], [25], [73], and [74]. We can see from the comparisons that the image encryption algorithm in this paper has information entropy which is closer to the ideal value compared with other literatures.

5.3.6 Differential attack analysis

Differential attack means that the attacker will make subtle changes to the plaintext image, such as changing the gray value of a pixel, and then encrypt the image before and after the change, respectively, and find the relationship between the plaintext and ciphertext by comparing the two encrypted images. Therefore, an ideal encryption algorithm must be able to resist differential attacks, that is, even a change of a pixel will cause a huge difference between the encrypted images before and after. In order to quantitatively measure the ability of encryption algorithm to resist differential attack, the number of pixels change rate (NPCR) and the unified average changing intensity (UACI) are used in this paper [75]. NPCR reflects the ratio of the number of different pixel values in the same position of two images to all pixels, and UACI reflects the average change intensity of the difference between the data of two encrypted images. The calculation formula of the two indicators is shown in Eq. 21 [25]:

$\left\{\begin{array}{c}NPCR\left(C_1,C_2\right)=\sum _{i=1}^M\sum _{j=1}^N\frac{D\left(i,j\right)}{M\times N}\times 100\%\hfill \\ UACI\left(C_1,C_2\right)=\sum _{i=1}^M\sum _{j=1}^N\frac{\left|C_1\left(i,j\right)-C_2\left(i,j\right)\right|}{M\times N\times T}\times 100\%\hfill \\ D\left(i,j\right)=\left\{\begin{array}{c}0,\mathrm{i}\mathrm{f}{\mathrm{C}}_1\left(i,j\right)={\mathrm{C}}_2\left(i,j\right)\hfill \\ 1,\mathrm{i}\mathrm{f}{\mathrm{C}}_1\left(i,j\right)\ne {\mathrm{C}}_2\left(i,j\right)\hfill \end{array}\right.\hfill \end{array}\right.(21)$

where M and N are the size of the image, T is the maximum gray value of the image, and C₁C₂ is the original encrypted image and slightly modified encrypted image, respectively. The ideal values for NPCR and UACI are 99.609% and 33.463 5%, respectively. Using Eq. 21, UACI and NPCR of a series of images were calculated in this paper and compared with other literatures. The results are 99:6075% and 33:4667%, respectively. In [24], the results are 99:6352% and 33:5,614%. In [25], the results are 99:609% and 33:4907%. In [73], the results are 99:6114% and 33:4523%. In [74], the results are 99:5,956% and 33:4535%. It is obvious that the image encryption algorithm in this paper has UACI/NPCR which is closer to the ideal value compared with other literatures.

5.3.7 Key sensitivity analysis

The general method for attackers to crack keys is brute force cracking, that is, to try all possible keys one by one. Because existing encryption algorithms generally have sufficient key space, which means that brute force cracking takes a long time; even for computers with powerful computing power, brute force cracking is not practical. However, if the encryption algorithm does not have key sensitivity, in other words, the ciphertext obtained by encrypting the same image with two similar keys is also similar, the attacker will take advantage of this vulnerability, optimize the brute force cracking algorithm, and quickly crack the key. In this paper, key1 = [1–6] and key2 = [1 + 10^–10, 2, 3, 4, 5, 6] are used to encrypt the same image, respectively, to obtain ciphertext 1 and ciphertext 2 (Fig. 12), and the NPCR and UACI values of ciphertext 1 and ciphertext 2 are calculated as NPCR = 99.612 4% and UACI = 33.441 0%, respectively, which means that the two ciphertexts have great differences. In addition, key2 is used in this paper to decrypt the ciphertext of key1, and the results obtained are shown in Figure 10. Therefore, this algorithm has good key sensitivity.

FIGURE 10

FIGURE 10. Key sensitivity analysis result graph, including (A) original Lena graph, (B) ciphertext encrypted with key1, (C) ciphertext encrypted with key2, (D) difference graph of two ciphertexts, (E) result graph of decryption with wrong key, and (F) result graph of decryption with correct key.

6 Conclusion

This paper proposes a new memristor model and uses PHL to prove the memristor characteristics of the model. In addition, we propose a new 6D-FMHNN by using this memristor to simulate the induced current caused by potential difference between neurons and studies the dynamic behavior of 6D-FMHNN, such as bifurcation characteristics and coexistence attractor characteristics. 6D-FMHNN is chaotic and periodic due to different order, parameter, and initial value. Because this 6D-FMHNN has chaotic characteristics, it can be used to generate random sequences, so we also use this 6D-FMHNN to generate random numbers and apply them to the field of image encryption. This paper makes a series of analysis on the randomness of random numbers and the security of image encryption, and proves that the encryption algorithm using this 6D-FMHNN is safe and sensitive to the key. In the future, we will look for FMHNN that can generate multiple scrolls or multiple attractors.

Data availability statement

The raw data supporting the conclusions of this article will be made available by the authors, without undue reservation.

Author contributions

FY, XK, and SC contributed to conception and design of the study. HC organized the database. QY performed the statistical analysis. XK wrote the first draft of the manuscript. FY, XK, SC, and SD wrote sections of the manuscript. All authors contributed to manuscript revision, read, and approved the submitted version.

Funding

This paper was supported by the Scientific Research Fund of Hunan Provincial Education Department under grant 21B0345, the National Natural Science Foundation of China under Grant 62172058, the Natural Science Foundation of Hunan Province under Grants 2020JJ4622 and 2020JJ4221, the special funds for the construction of innovative provinces in Hunan Province under Grants 2020JK4046 and 2022SK2007.

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s Note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors, and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer is not guaranteed or endorsed by the publisher.

References

1. Deng Z, Zhu Q, He P, Zhang D, Luo Y. A Saliency Detection and Gram Matrix Transform-Based Convolutional Neural Network for Image Emotion Classification. Security Commun Networks (2021) 2021:71–83. doi:10.1155/2021/6854586

CrossRef Full Text | Google Scholar

2. Wang J, Zou Y, Lei P, Sherratt RS, Wang L. Research on Recurrent Neural Network Based Crack Opening Prediction of concrete Dam. J Internet Technol (2020) 21(4):1161–9. doi:10.3966/160792642020072104024

CrossRef Full Text | Google Scholar

3. Yu F, Liu L, Xiao L, Li K, Cai S. A Robust and Fixed-Time Zeroing Neural Dynamics for Computing Time-Variant Nonlinear Equation Using a Novel Nonlinear Activation Function. Neurocomputing (2019) 350:108–16. doi:10.1016/j.neucom.2019.03.053

CrossRef Full Text | Google Scholar

4. Long M, Zeng Y. Detecting Iris Liveness with Batch Normalized Convolutional Neural Network. Comput Mater Continua (2019) 58(2):493–504. doi:10.32604/cmc.2019.04378

CrossRef Full Text | Google Scholar

5. Zhou S, Tan B. Electrocardiogram Soft Computing Using Hybrid Deep Learning Cnn-Elm. Appl soft Comput (2020) 86:105778. doi:10.1016/j.asoc.2019.105778

CrossRef Full Text | Google Scholar

6. Yu F, Shen H, Zhang Z, Huang Y, Cai S, Du S. A New Multi-Scroll Chua's Circuit with Composite Hyperbolic tangent-cubic Nonlinearity: Complex Dynamics, Hardware Implementation and Image Encryption Application. Integration (2021) 81:71–83. doi:10.1016/j.vlsi.2021.05.011

CrossRef Full Text | Google Scholar

7. Lin H, Wang C, Yu F, Xu C, Hong Q, Yao W, et al. An Extremely Simple Multi-wing Chaotic System: Dynamics Analysis, Encryption Application and Hardware Implementation. IEEE Trans Ind Electron (2020) 68:12708–19. doi:10.1109/TIE.2020.3047012

CrossRef Full Text | Google Scholar

8. Ma M, Yang Y, Qiu Z, Peng Y, Sun Y, Li Z, et al. A Locally Active Discrete Memristor Model and its Application in a Hyperchaotic Map. Nonlinear Dyn (2022) 107:2935–2949. doi:10.1007/s11071-021-07132-5

CrossRef Full Text | Google Scholar

9. Lai Q. A Unified Chaotic System with Various Coexisting Attractors. Int J Bifurcation Chaos (2021) 31(01):2150013. doi:10.1142/s0218127421500139

CrossRef Full Text | Google Scholar

10. Lai Q, Wan Z, Kamdem Kuate PD. Modelling and Circuit Realisation of a New No‐equilibrium Chaotic System with Hidden Attractor and Coexisting Attractors. Electron Lett (2020) 56(20):1044–6. doi:10.1049/el.2020.1630

CrossRef Full Text | Google Scholar

11. Xu Q, Tan X, Zhu D, Bao H, Hu Y, Bao B. Bifurcations to Bursting and Spiking in the Chay Neuron and Their Validation in a Digital Circuit. Chaos, Solitons & Fractals (2020) 141:110353. doi:10.1016/j.chaos.2020.110353

CrossRef Full Text | Google Scholar

12. Yu F, Qian S, Chen X, Huang Y, Liu L, Shi C, et al. A New 4d Four-wing Memristive Hyperchaotic System: Dynamical Analysis, Electronic Circuit Design, Shape Synchronization and Secure Communication. Int J Bifurcation Chaos (2020) 30(10):2050147. doi:10.1142/s0218127420501473

CrossRef Full Text | Google Scholar

13. Yu F, Liu L, He B, Huang Y, Shi C, Cai S, et al. Analysis and Fpga Realization of a Novel 5d Hyperchaotic Four-wing Memristive System, Active Control Synchronization, and Secure Communication Application. Complexity (2019) 2019:4047957. doi:10.1155/2019/4047957

CrossRef Full Text | Google Scholar

14. Li Y, Li Z, Ma M, Wang M. Generation of Grid Multi-wing Chaotic Attractors and its Application in Video Secure Communication System. Multimedia Tools Appl (2020) 79(39):29161–77. doi:10.1007/s11042-020-09448-7

CrossRef Full Text | Google Scholar

15. Lai Q, Norouzi B, Liu F. Dynamic Analysis, Circuit Realization, Control Design and Image Encryption Application of an Extended Lü System with Coexisting Attractors. Chaos, Solitons & Fractals (2018) 114:230–45. doi:10.1016/j.chaos.2018.07.011

CrossRef Full Text | Google Scholar

16. Li C, Li H, Xie W, Du J. A S-type Bistable Locally Active Memristor Model and its Analog Implementation in an Oscillator Circuit. Nonlinear Dyn (2021) 106(1):1041–58. doi:10.1007/s11071-021-06814-4

CrossRef Full Text | Google Scholar

17. Cui L, Luo W-H, Ou Q-L. Analysis and Implementation of New Fractional-Order Multi-Scroll Hidden Attractors*. Chin Phys. B (2021) 30(2):020501. doi:10.1088/1674-1056/abbbe4

CrossRef Full Text | Google Scholar

18. Cui L, Lu M, Ou Q, Duan H, Luo W. Analysis and Circuit Implementation of Fractional Order Multi-wing Hidden Attractors. Chaos, Solitons & Fractals (2020) 138:109894. doi:10.1016/j.chaos.2020.109894

CrossRef Full Text | Google Scholar

19. Chen X, Qian S, Yu F, Zhang Z, Shen H, Huang Y, et al. Pseudorandom Number Generator Based on Three Kinds of Four-wing Memristive Hyperchaotic System and its Application in Image Encryption. Complexity (2020) 2020:8274685. doi:10.1155/2020/8274685

CrossRef Full Text | Google Scholar

20. Yu F, Qian S, Chen X, Huang Y, Cai S, Jin J, et al. Chaos-based Engineering Applications with a 6d Memristive Multistable Hyperchaotic System and a 2d Sf-Simm Hyperchaotic Map. Complexity (2021) 2021:6683284. doi:10.1155/2021/6683284

CrossRef Full Text | Google Scholar

21. Yu F, Li L, He B, Liu L, Qian S, Zhang Z, et al. Pseudorandom Number Generator Based on a 5d Hyperchaotic Four-wing Memristive System and its Fpga Implementation. Eur Phys J Spec Top (2021) 230:1763–72. doi:10.1140/epjs/s11734-021-00132-x

CrossRef Full Text | Google Scholar

22. Yang L, Xiao-Jun T. A New Pseudorandom Number Generator Based on a Complex Number Chaotic Equation. Chin Phys B (2012) 21(9):090506. doi:10.1088/1674-1056/21/9/090506

CrossRef Full Text | Google Scholar

23. Ma C, Banerjee S, Xiong L, Liu T, Han X, Mou J. Dynamical Analysis, Circuit Realization, and Application in Pseudorandom Number Generators of a Fractional-Order Laser Chaotic System*. Chin Phys. B (2021) 30(12):120504. doi:10.1088/1674-1056/abfbd4

CrossRef Full Text | Google Scholar

24. Zeng J, Wang C. A Novel Hyperchaotic Image Encryption System Based on Particle Swarm Optimization Algorithm and Cellular Automata. Security Commun Networks (2021) 2021:6675565. doi:10.1155/2021/6675565

CrossRef Full Text | Google Scholar

25. Deng J, Zhou M, Wang C, Wang S, Xu C. Image Segmentation Encryption Algorithm with Chaotic Sequence Generation Participated by Cipher and Multi-Feedback Loops. Multimed Tools Appl (2021) 80(9):13821–40. doi:10.1007/s11042-020-10429-z

CrossRef Full Text | Google Scholar

26. Yang F, Mou J, Ma C, Cao Y. Dynamic Analysis of an Improper Fractional-Order Laser Chaotic System and its Image Encryption Application. Opt Lasers Eng (2020) 129:106031. doi:10.1016/j.optlaseng.2020.106031

CrossRef Full Text | Google Scholar

27. Li X, Mou J, Xiong L, Wang Z, Xu J. Fractional-order Double-Ring Erbium-Doped Fiber Laser Chaotic System and its Application on Image Encryption. Opt Laser Technol (2021) 140:107074. doi:10.1016/j.optlastec.2021.107074

CrossRef Full Text | Google Scholar

28. Cheng S, Sun J, Xu C. A Color Image Encryption Scheme Based on a Hybrid Cascaded Chaotic System. Int J Bifurcation Chaos (2021) 31(09):2150125. doi:10.1142/s021812742150125x

CrossRef Full Text | Google Scholar

29. Zhou Y, Li C, Li W, Li H, Feng W, Qian K. Image Encryption Algorithm with circle index Table Scrambling and Partition Diffusion. Nonlinear Dyn (2021) 103(2):2043–61. doi:10.1007/s11071-021-06206-8

CrossRef Full Text | Google Scholar

30. Li C-L, Zhou Y, Li H-M, Feng W, Du J-R. Image Encryption Scheme with Bit-Level Scrambling and Multiplication Diffusion. Multimed Tools Appl (2021) 80(12):18479–501. doi:10.1007/s11042-021-10631-7

CrossRef Full Text | Google Scholar

31. Sun J, Peng M, Liu F, Tang C. Protecting Compressive Ghost Imaging with Hyperchaotic System and Dna Encoding. Complexity (2020) 2020:8815315. doi:10.1155/2020/8815315

CrossRef Full Text | Google Scholar

32. Xu C, Sun J, Wang C. A Novel Image Encryption Algorithm Based on Bit-Plane Matrix Rotation and Hyper Chaotic Systems. Multimedia Tools Appl (2020) 79(9):5573–93. doi:10.1007/s11042-019-08273-x

CrossRef Full Text | Google Scholar

33. Li C-L, Li H-M, Li F-D, Wei D-Q, Yang X-B, Zhang J. Multiple-image Encryption by Using Robust Chaotic Map in Wavelet Transform Domain. Optik (2018) 171:277–86. doi:10.1016/j.ijleo.2018.06.029

CrossRef Full Text | Google Scholar

34. Li C-L, Li Z-Y, Feng W, Tong Y-N, Du J-R, Wei D-Q. Dynamical Behavior and Image Encryption Application of a Memristor-Based Circuit System. AEU - Int J Electron Commun (2019) 110:152861. doi:10.1016/j.aeue.2019.152861

CrossRef Full Text | Google Scholar

35. Korn H, Faure P. Is There Chaos in the Brain? Ii. Experimental Evidence and Related Models. Comptes rendus biologies (2003) 326(9):787–840. doi:10.1016/j.crvi.2003.09.011

PubMed Abstract | CrossRef Full Text | Google Scholar

36. Lin H, Wang C, Chen C, Sun Y, Zhou C, Xu C, et al. Neural Bursting and Synchronization Emulated by Neural Networks and Circuits. IEEE Trans Circuits Syst (2021) 68(8):3397–410. doi:10.1109/tcsi.2021.3081150

CrossRef Full Text | Google Scholar

37. Yu F, Zhang Z, Shen H, Huang Y, Cai S, Jin J, et al. Design and Fpga Implementation of a Pseudo-random Number Generator Based on a Hopfield Neural Network under Electromagnetic Radiation. Front Phys (2021) 9:690651. doi:10.3389/fphy.2021.690651

CrossRef Full Text | Google Scholar

38. Xu Q, Ding S, Bao H, Chen M, Bao B. Piecewise-linear Simplification for Adaptive Synaptic Neuron Model. IEEE Trans Circuits Syst (2021). doi:10.1109/TCSII.2021.3124666

CrossRef Full Text | Google Scholar

39. Cui L, Chen C, Jin J, Yu F. Dynamic Analysis and Fpga Implementation of New Chaotic Neural Network and Optimization of Traveling Salesman Problem. Complexity (2021) 2021:5521192. doi:10.1155/2021/5521192

CrossRef Full Text | Google Scholar

40. Yao W, Wang C, Sun Y, Zhou C. Robust Multimode Function Synchronization of Memristive Neural Networks with Parameter Perturbations and Time-Varying Delays. IEEE Trans Syst Man Cybern, Syst (2022) 52:260–74. doi:10.1109/TSMC.2020.2997930

CrossRef Full Text | Google Scholar

41. Yang L, Wang C. Emotion Model of Associative Memory Possessing Variable Learning Rates with Time Delay. Neurocomputing (2021) 460:117–25. doi:10.1016/j.neucom.2021.07.011

CrossRef Full Text | Google Scholar

42. Chua L. Memristor-the Missing Circuit Element. IEEE Trans Circuit Theor (1971) 18(5):507–19. doi:10.1109/tct.1971.1083337

CrossRef Full Text | Google Scholar

43. Strukov DB, Snider GS, Stewart DR, Williams RS. The Missing Memristor Found. nature (2008) 453(7191):80–3. doi:10.1038/nature06932

PubMed Abstract | CrossRef Full Text | Google Scholar

44. Xie W, Wang C, Lin H. A Fractional-Order Multistable Locally Active Memristor and its Chaotic System with Transient Transition, State Jump. Nonlinear Dyn (2021) 104:4523–41. doi:10.1007/s11071-021-06476-2

CrossRef Full Text | Google Scholar

45. Xu Q, Lin Y, Bao B, Chen M. Multiple Attractors in a Non-ideal Active Voltage-Controlled Memristor Based Chua's Circuit. Chaos, Solitons & Fractals (2016) 83:186–200. doi:10.1016/j.chaos.2015.12.007

CrossRef Full Text | Google Scholar

46. Ma X, Mou J, Liu J, Ma C, Yang F, Zhao X. A Novel Simple Chaotic Circuit Based on Memristor-Memcapacitor. Nonlinear Dyn (2020) 100(3):2859–76. doi:10.1007/s11071-020-05601-x

CrossRef Full Text | Google Scholar

47. Xu Q, Cheng S, Ju Z, Chen M, Wu H. Asymmetric Coexisting Bifurcations and Multi-Stability in an Asymmetric Memristive Diode-Bridge-Based Jerk Circuit. Chin J Phys (2021) 70:69–81. doi:10.1016/j.cjph.2020.11.007

CrossRef Full Text | Google Scholar

48. Xu Q, Liu T, Feng C-T, Bao H, Wu H-G, Bao B-C. Continuous Non-autonomous Memristive Rulkov Model with Extreme Multistability*. Chin Phys. B (2021) 30(12):128702. doi:10.1088/1674-1056/ac2f30

CrossRef Full Text | Google Scholar

49. Wen Z, Li Z, Li X. Bursting Dynamics in Parametrically Driven Memristive Jerk System. Chin J Phys (2020) 66:327–34. doi:10.1016/j.cjph.2020.04.009

CrossRef Full Text | Google Scholar

50. Lai Q, Wan Z, Kengne LK, Kuate PDK, Chen C. Two-memristor-based Chaotic System with Infinite Coexisting Attractors. IEEE Trans Circuits Syst Express Briefs (2020) 68(6):2197–201. doi:10.1109/TCSII.2020.3044096

CrossRef Full Text | Google Scholar

51. Chai X-L, Gan Z-H, Lu Y, Zhang M-H, Chen Y-R. A Novel Color Image Encryption Algorithm Based on Genetic Recombination and the Four-Dimensional Memristive Hyperchaotic System. Chin Phys. B (2016) 25(10):100503. doi:10.1088/1674-1056/25/10/100503

CrossRef Full Text | Google Scholar

52. Xiu C, Zhou R, Zhao S, Xu G. Memristive Hyperchaos Secure Communication Based on Sliding Mode Control. Nonlinear Dyn (2021) 104(1):789–805. doi:10.1007/s11071-021-06302-9

CrossRef Full Text | Google Scholar

53. Li P, Xu J, Mou J, Yang F. Fractional-order 4d Hyperchaotic Memristive System and Application in Color Image Encryption. J Image Video Proc (2019) 2019(1):22. doi:10.1186/s13640-018-0402-7

CrossRef Full Text | Google Scholar

54. Xu Q, Ju Z, Ding S, Feng C, Chen M, Bao B. Electromagnetic Induction Effects on Electrical Activity within a Memristive wilson Neuron Model. Cogn Neurodyn (2021). doi:10.1007/s11571-021-09764-0

CrossRef Full Text | Google Scholar

55. Yu F, Shen H, Zhang Z, Huang Y, Cai S, Du S. Dynamics Analysis, Hardware Implementation and Engineering Applications of Novel Multi-Style Attractors in a Neural Network under Electromagnetic Radiation. Chaos, Solitons & Fractals (2021) 152:111350. doi:10.1016/j.chaos.2021.111350

CrossRef Full Text | Google Scholar

56. Lin H, Wang C, Deng Q, Xu C, Deng Z, Zhou C. Review on Chaotic Dynamics of Memristive Neuron and Neural Network. Nonlinear Dyn (2021) 106(1):959–73. doi:10.1007/s11071-021-06853-x

CrossRef Full Text | Google Scholar

57. Yao W, Wang C, Sun Y, Zhou C, Lin H. Synchronization of Inertial Memristive Neural Networks with Time-Varying Delays via Static or Dynamic Event-Triggered Control. Neurocomputing (2020) 404:367–80. doi:10.1016/j.neucom.2020.04.099

CrossRef Full Text | Google Scholar

58. Xu C, Wang C, Sun Y, Hong Q, Deng Q, Chen H. Memristor-based Neural Network Circuit with Weighted Sum Simultaneous Perturbation Training and its Applications. Neurocomputing (2021) 462:581–590. doi:10.1016/j.neucom.2021.08.072

CrossRef Full Text | Google Scholar

59. Yu F, Zhang Z, Shen H, Huang Y, Cai S, Du S. Fpga Implementation and Image Encryption Application of a New Prng Based on a Memristive Hopfield Neural Network with a Special Activation Gradient. Chin Phys B (2022) 31(2):020505. doi:10.1088/1674-1056/ac3cb2

CrossRef Full Text | Google Scholar

60. Liu T, Yan H, Banerjee S, Mou J. A Fractional-Order Chaotic System with Hidden Attractor and Self-Excited Attractor and its DSP Implementation. Chaos, Solitons & Fractals (2021) 145:110791. doi:10.1016/j.chaos.2021.110791

CrossRef Full Text | Google Scholar

61. Liu T, Banerjee S, Yan H, Mou J. Dynamical Analysis of the Improper Fractional-Order 2d-Sclmm and its Dsp Implementation. The Eur Phys J Plus (2021) 136(5):1–17. doi:10.1140/epjp/s13360-021-01503-y

CrossRef Full Text | Google Scholar

62. Zhang H, Sun K, He S. A Fractional-Order Ship Power System with Extreme Multistability. Nonlinear Dyn (2021) 106(1):1027–40. doi:10.1007/s11071-021-06875-5

CrossRef Full Text | Google Scholar

63. Wang L, Sun K, Peng Y, He S. Chaos and Complexity in a Fractional-Order Higher-Dimensional Multicavity Chaotic Map. Chaos, Solitons & Fractals (2020) 131:109488. doi:10.1016/j.chaos.2019.109488

CrossRef Full Text | Google Scholar

64. Yao W, Wang C, Cao J, Sun Y, Zhou C. Hybrid Multisynchronization of Coupled Multistable Memristive Neural Networks with Time Delays. Neurocomputing (2019) 363:281–94. doi:10.1016/j.neucom.2019.07.014

CrossRef Full Text | Google Scholar

65. Yu Y, Shi M, Kang H, Chen M, Bao B. Hidden Dynamics in a Fractional-Order Memristive Hindmarsh-Rose Model. Nonlinear Dyn (2020) 100(1):891–906. doi:10.1007/s11071-020-05495-9

CrossRef Full Text | Google Scholar

66. Fan Y, Huang X, Wang Z, Li Y. Nonlinear Dynamics and Chaos in a Simplified Memristor-Based Fractional-Order Neural Network with Discontinuous Memductance Function. Nonlinear Dyn (2018) 93(2):611–27. doi:10.1007/s11071-018-4213-2

CrossRef Full Text | Google Scholar

67. Adhikari SP, Sah MP, Kim H, Chua LO. Three Fingerprints of Memristor. IEEE Trans Circuits Syst (2013) 60(11):3008–21. doi:10.1109/tcsi.2013.2256171

CrossRef Full Text | Google Scholar

68. Hopfield JJ. Neural Networks and Physical Systems with Emergent Collective Computational Abilities. Proc Natl Acad Sci (1982) 79(8):2554–8. doi:10.1073/pnas.79.8.2554

PubMed Abstract | CrossRef Full Text | Google Scholar

69. Chen C, Min F, Zhang Y, Bao B. Memristive Electromagnetic Induction Effects on Hopfield Neural Network. Nonlinear Dyn (2021) 106(3):2559–76. doi:10.1007/s11071-021-06910-5

CrossRef Full Text | Google Scholar

70. Tong Y, Cao Z, Yang H, Li C, Yu W. Design of a Five-Dimensional Fractional-Order Chaotic System and its Sliding Mode Control. Indian J Phys (2021) 96:855–867. doi:10.1007/s12648-021-02181-3

CrossRef Full Text | Google Scholar

71. Danca M-F, Kuznetsov N. Matlab Code for Lyapunov Exponents of Fractional-Order Systems. Int J Bifurcation Chaos (2018) 28(05):1850067. doi:10.1142/s0218127418500670

CrossRef Full Text | Google Scholar

72. Lin R, Li S. An Image Encryption Scheme Based on Lorenz Hyperchaotic System and Rsa Algorithm. Security Commun Networks (2021) 2021:5586959. doi:10.1155/2021/5586959

CrossRef Full Text | Google Scholar

73. Zhou M, Wang C. A Novel Image Encryption Scheme Based on Conservative Hyperchaotic System and Closed-Loop Diffusion between Blocks. Signal Process. (2020) 171:107484. doi:10.1016/j.sigpro.2020.107484

CrossRef Full Text | Google Scholar

74. Ravichandran D, Praveenkumar P, Rayappan JBB, Amirtharajan R. Dna Chaos Blend to Secure Medical Privacy. IEEE Trans nanobioscience (2017) 16(8):850–8. doi:10.1109/TNB.2017.2780881

PubMed Abstract | CrossRef Full Text | Google Scholar

75. Yu F, Liu L, Qian S, Li L, Huang Y, Shi C, et al. Chaos-based Application of a Novel Multistable 5d Memristive Hyperchaotic System with Coexisting Multiple Attractors. Complexity (2020) 2020:8034196. doi:10.1155/2020/8034196

CrossRef Full Text | Google Scholar