Ultrathin high-temperature ferromagnetic rare-earth films: GdScGe and GdScSi monolayers

Two-dimensional (2D) ferromagnetism with robust room-temperature ferromagnetism has sparked intense interest for future miniature information storage devices. However, most 2D ferromagnetic materials have a low Curie temperature. Here, by using density functional theory, two rare-earth monolayers, the GdScSi monolayer and the GdScGe monolayer, were predicted, in which these two monolayers exhibit ferromagnetic orders with large magnetic moments of approximately 7 μ_B/Gd. Monte Carlo simulations predict Curie temperatures of approximately 470 K and 495 K for the 2D GdScSi monolayer and the GdScGe monolayer, respectively. The spin band calculations show that they are metal. In addition, these two monolayers exhibit dynamical, mechanical, and thermal stabilities. The combination of these novel magnetic properties makes these 2D ferromagnetic crystals promising candidates for high-efficiency spintronic applications.

1 Introduction

Since the successful synthesis of graphene, two-dimensional (2D) materials have attracted a great deal of attention [1–11]. First, the ‘star material’ graphene possesses excellent mechanical and electronic properties, but it has zero band gap. Then, a MoS₂ monolayer was successfully prepared, but it has relatively low electron and hole mobilities. In 2014, black phosphorus with a direct band gap and high carrier mobility was confirmed in an experiment, but it has poor stability when exposed to air. In addition, most synthesized 2D materials are non-magnetic, which has prevented their application in advanced spintronics. Although many efforts have been made in designing 2D ferromagnetism by introducing defects [12,13], strains [11,14–17], doping[18–22], and surface functionalization[19,23–26], it is still very challenging to obtain robust magnetism.

In 2017, an ultrathin ferromagnetic CrI₃ monolayer and a CrGeTe₃ bilayer were discovered [7,8], which disturb the limitation to the Mermin–Wagner (M–W) theorem[27]. The Mermin–Wagner theorem shows that the magnetic order is prohibited in the 2D isotropic Heisenberg model at finite temperatures. Recent studies have shown that magnetic anisotropy is the fundamental cause of 2D long-range magnetism [28–36]. Almost all synthetic and predicted 2D ferromagnetic materials have relatively low Curie temperatures (T_C) and small magnetic anisotropy energies (MAEs), for example, 45 K for the CrI₃ monolayer [8], 30 K for the CrGeTe₃ bilayer [7], 146 K for the CrSBr monolayer [37], 185 K for the ScCl monolayer [22], and 24 L K for the GdI₂ monolayer [38]. Therefore, it is highly desirable to search for new intrinsically 2D ferromagnetic materials with high T_C. Rare-earth elements usually have large magnetic moments and high T_C. With the increasing demand for device miniaturization, 2D rare-earth magnetic materials will be highly sought after for future spintronics. Gd-based compounds usually possess a long-range ferromagnetic order with a high T_C. We predicted the 2D GdI₂ monolayer to be a ferromagnetic semiconductor with a high T_C of 241 K and a large magnetization [38]. GdX₂ (X = Cl, Br, and I) monolayers were also ferromagnetic semiconductors and underwent spontaneous valley polarization [39,40]. GdGe₂ was predicted to be a ferromagnetic half-semiconductor with a large magnetic moment and an indirect band gap [41]. Gd₂C was predicted to be a time-reversal-symmetry-breaking Weyl semimetal phase [42]. The CeI₂ monolayer was predicted to be an intrinsic room-temperature ferrovalley semiconductor [43]. Dong et al., introduced the importance of 4f and 5d orbitals in 2D Gd halides [44,45]. Topological, nodal-line semimetals were also predicted in ferromagnetic rare-earth-metal monohalides [46]. As a result, 2D Gd-based compounds exhibit excellent ferromagnetism.

In this work, two rare-earth compounds of GdScX (X = Si and Ge) monolayers were predicted by using first-principles calculation. The result shows that they both are ferromagnetic with a large magnetization (7 μ_B/Gd). Monte Carlo simulations show that they possess a high Tc: 470 K for the GdScSi monolayer and 495 K for the GdScGe monolayer. Analysis of electronic band properties shows that they both are metals. In addition, their thermal, dynamical, and mechanical stabilities were confirmed by ab initio molecular dynamics, phonon dispersions, and elastic constants, respectively. Our results certainly boost the study of 2D Gd-based magnetism.

2 Computational methods

The optimized structures were simulated by density functional theory (DFT), as implemented in the Vienna ab initio simulation package (VASP) [47]. The ion–electron interaction was described by using the projector-augmented plane wave (PAW) approach [48], and the exchange and correlation interactions of the electrons were calculated using the Perdew–Burke–Ernzerhof (PBE) functional within the generalized gradient approximation (GGA) [49]. In addition, to consider the Coulomb and exchange interactions of f electrons, the GGA + U method was adopted with U = 6.6 eV, according to previous studies [50], and 500 eV was used as the energy cutoff of the plane wave. The convergence criteria for the energy and ionic force were set to 10^–8 eV and 0.01 eV/Å, respectively. To avoid interaction between the layers, the vacuum length was set to 20 Å along the z-axis.

Density functional perturbation theory was used to calculate the phonon dispersions, as embedded in phonopy software [51]. The ab initio molecular dynamics (AIMD) simulations were carried out to evaluate the thermal stabilities of GdScX (X = Si, Ge) monolayers. At 300 K and 500 K, AIMD simulations were performed in the NVT ensemble. The temperature was controlled by using the Nosé–Hoover method [52], and the simulation lasted for 10 ps with a time step of 1 fs at 300 K and 500 K. The orientation-dependent Young’s modulus E (α) and Poisson’s ratio ν (α) were calculated as follows [30,33,53]:

$E\left(\mathrm{\alpha }\right)=\frac{C_{11}{C}_{22}-C_{12}^2}{C_{11}{s}^4+C_{22}{c}^4+\left(\frac{C_{11}{C}_{22}-C_{12}^2}{C_{44}}-2C_{12}\right)c^2{s}^2},(1)$

$\nu \left(\mathrm{\alpha }\right)=\frac{\left(C_{11}+C_{22}-\frac{C_{11}{C}_{12}-C_{12}^2}{C_{44}}\right)c^2{s}^2-C_{12}\left(c^4+s^4\right)}{C_{11}{s}^4+C_{22}{c}^4+\left(\frac{C_{11}{C}_{22}-C_{12}^2}{C_{44}}-2C_{12}\right)c^2{s}^2},(2)$

where c = cosα and s = sinα.

3 Results and discussion

3.1 Structures and stabilities of GdScX monolayers

The structures present the P4/MMM group (No. 123) with a tetrahedron structure. The optimized lattice constants are a = 4.08 Å and b = 4.12 Å for GdScX (X = Si and Ge) monolayers as shown in Figure 1A; Figures 1B, C show the calculated phonon dispersion spectra of the GdScSi monolayer and the GdScGe monolayer, respectively. Notably, the absence of imaginary modes along the entire Brillouin zone indicates their dynamical stability. The corresponding fluctuations of the total potential energy for GdScX (X = Si and Ge) monolayers at 300 K and 500 K are shown in Figures 1D, E, respectively, which last for 10 ps in the ab initio molecular dynamics. The result shows that the average values of the total potential energy oscillate with a very narrow range, confirming their thermal stabilities. As a result, the GdScX (X = Si, Ge) monolayers are both dynamically and thermally stable at high-temperatures.

FIGURE 1

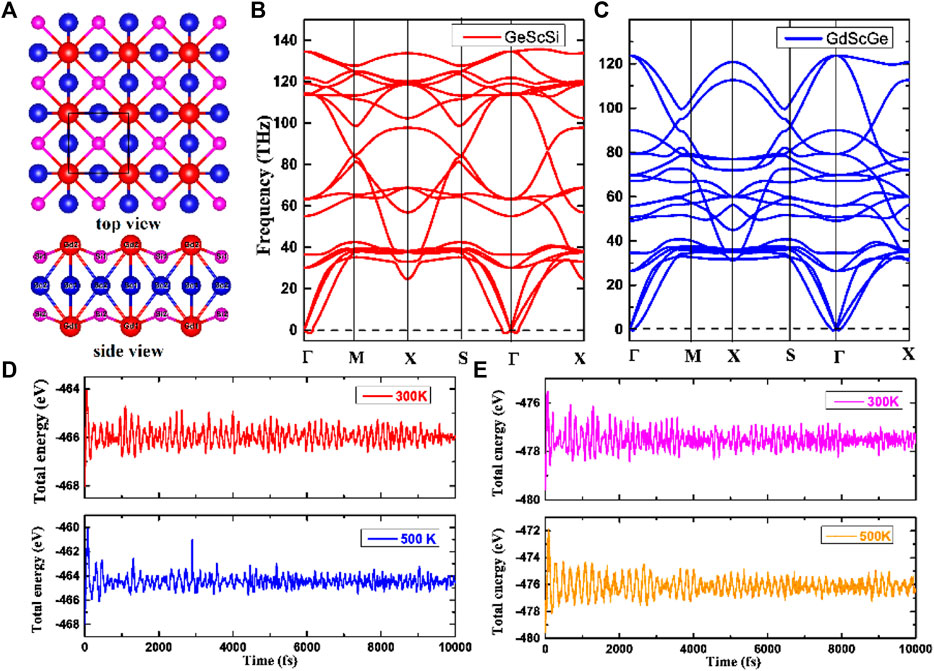
FIGURE 1. (A) Structures of GdScX (X = Si, Ge) monolayers. The Gd atom is located at 2 g (0, 0, 0.3633), Sc at 2e (1/2, 0, 1/2), and Si at 2 h (1/2, 1/2, 0.5971) for the GdScSi monolayer. The Gd atom is located at 2 g (0, 0, 0.3628), Sc at 2e (1/2, 0, 1/2), and Ge at 2 h (1/2, 1/2, 0.5988) for the GdScGe monolayer. (B, C) Phonon dispersion spectra of the GdScX (X = Si, Ge) monolayers. (D, E) Evolution of the total energy from the 10 ps AIMD simulations at 300 K and 500 K.

Mechanical stability is also necessary for materials. The elastic constants are C₁₁ = C₂₂ = 97 N/m, C₁₂ = 31 N/m, and C₆₆ = 65 N/m for the GdScSi monolayer, and C₁₁ = C₂₂ = 96 N/m, C₁₂ = 34 N/m, and C₆₆ = 64 N/m for the GdScGe monolayer. Their elastic constants meet the Born criteria for a tetrahedron 2D system ($C_{11}>0$; $C_{44}>0$; $\left.C_{11}>{\left|C\right.}_{12}\right|$; $C_{11}+2C_{12}>0$), indicating their good mechanical stabilities. According to Eqs 1, 2, Young’s moduli and Poisson’s ratios, as functions of the arbitrary direction α in the 2D polar representation curve, were also calculated (Figures 2, 3), where α is the angle relative to the positive x-direction in these monolayers. Figures 2A, C show that the Young’s moduli for GdScX monolayers first increase to a maximum value of approximately 125 N/m at α = 45° from α = 0° (x-direction) and decrease to a minimum value of approximately 100 N/m at α = 90° (y-direction). The maximum value (125 N/m) is comparable to that of a MoS₂ monolayer (123 N/m) [54]. Figures 2B, D show that the Poisson’s ratios also strongly depend on the direction α. This shows their anisotropic mechanical properties.

FIGURE 2

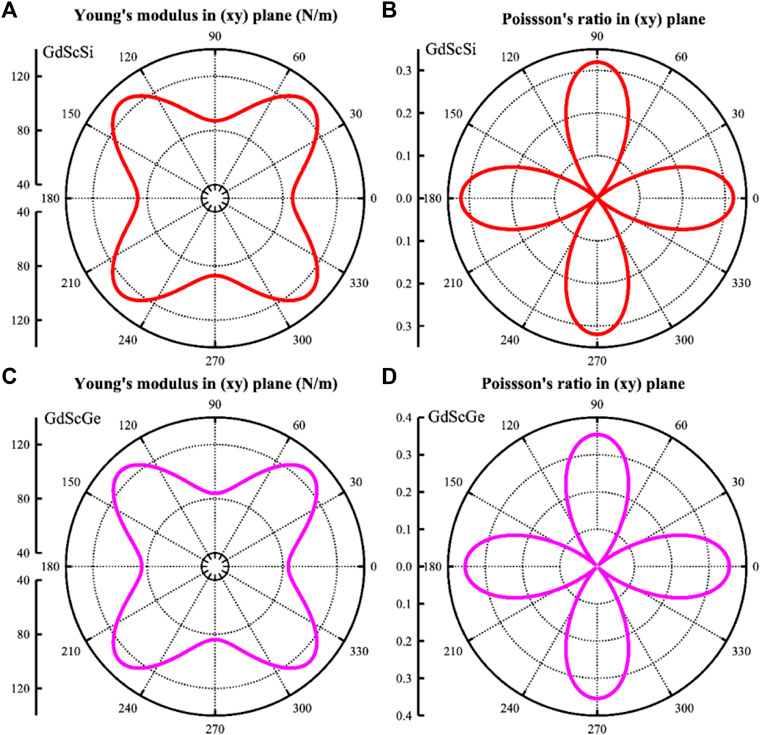
FIGURE 2. Calculated orientation-dependent (A) Poisson’s ratios and (B) Young’s moduli of the GdScSi monolayer (A, B) and the GdScGe (C, D) monolayer.

FIGURE 3

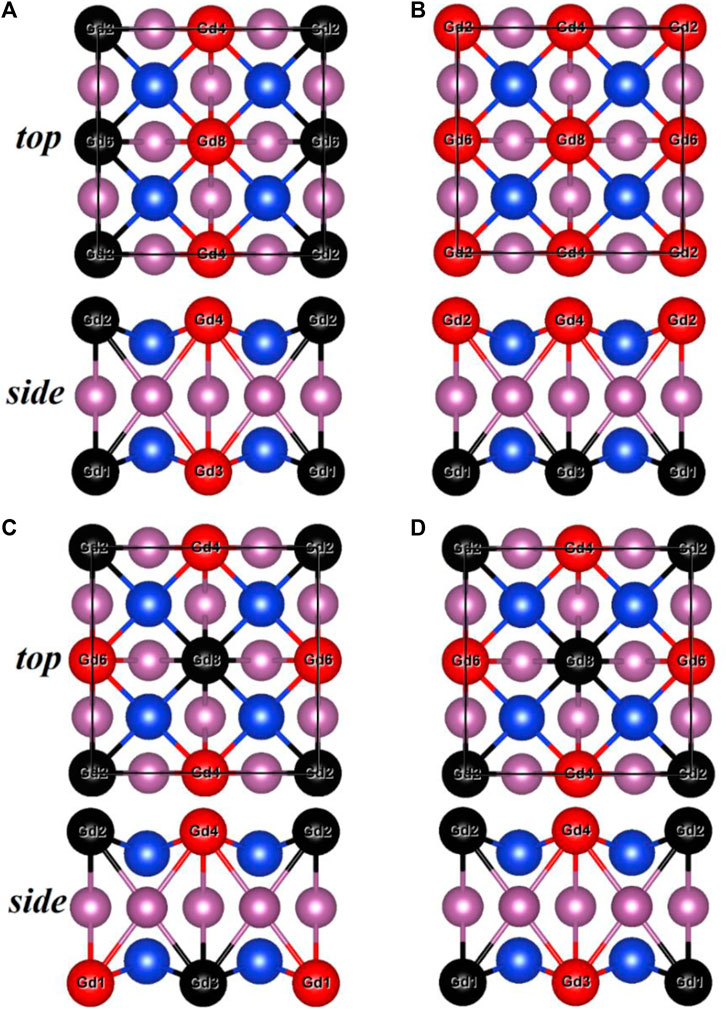
FIGURE 3. Top and side views of four AFM structures [(A), AFM1; (B), AFM2; (C), AFM3; (D), AFM4] for the GdScSi and GdScGe monolyers.

3.2 Electronic band structures of GdScX monolayers

After confirming the stabilities of the GdScX monolayers, their magnetic ground states were investigated. One ferromagnetic (FM) state and four antiferromagnetic (AFM) states were considered, and the FM configuration is energetically lower than all the AFM orders (Figure 4), indicating that GdScX monolayers prefer FM coupling. Their spin band structures were also calculated by using the PBE + U method, which are shown in Figures 4A, C. The result shows that these two monolayers are metal, in which the spin up and spin down bands cross the Fermi level. Because of the relatively heavy element Gd, the spin–orbit coupling (SOC) interactions were also considered for the electronic band structures of GdScX monolayers (Figures 4C, D). The figures show that SOC has a negligible influence on the band structure.

FIGURE 4

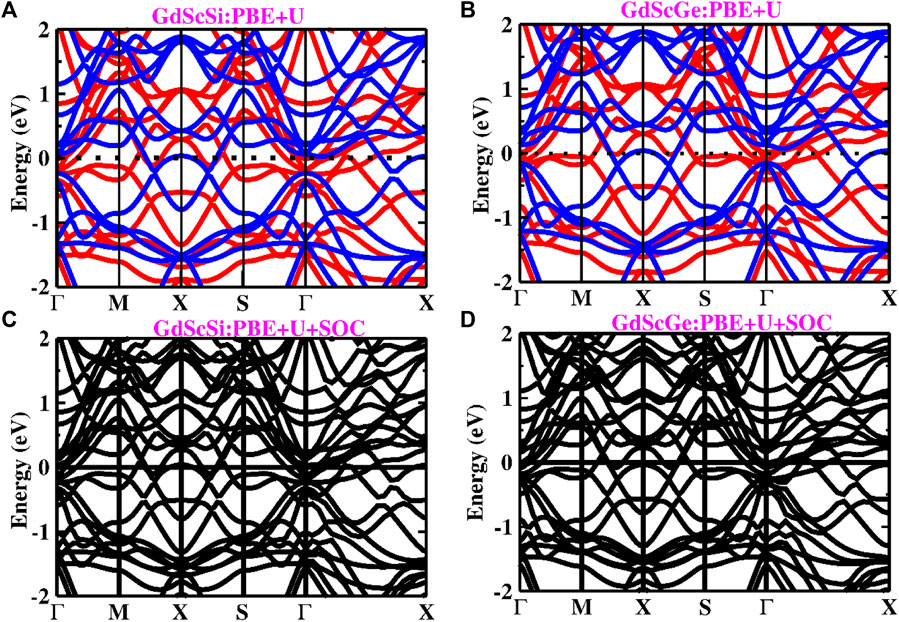
FIGURE 4. Band structures of the GdScSi monolayer (A, B) and GdScGe (C, D) monolayer determined using PBE + U and PBE + U + SOC methods.

3.3 MAEs of GdScX monolayers

Due to the M–W theorem, [27] no long-range FM state exists if a 2D material lacks magnetic anisotropy. Therefore, magnetic anisotropy, which can be scaled by MAE, is an important property in 2D ferromagnetic systems [55]. In addition, MAE is of importance for the thermal stability of magnetic storage. SOC calculations were performed on the GdScX monolayers to obtain the values of MAE. Figures 5A, B show the MAEs of xy, yz, and xz planes for the GdScSi monolayer and the GdScGe monolayer, respectively. These figures clearly show that the MAE is almost a straight line in the xy plane, and that it strongly depends on the angular dependence of magnetization. In addition, the MAE of the xy plane is lower than that of the xz and yz planes, which indicates that these two monolayers belong to the family of 2D XY magnets. In other words, they possess an easy magnetization plane. The corresponding MAE through the whole space is also plotted in Figures 5C, D, which confirms again the strong magnetic anisotropy in these monolayers.

FIGURE 5

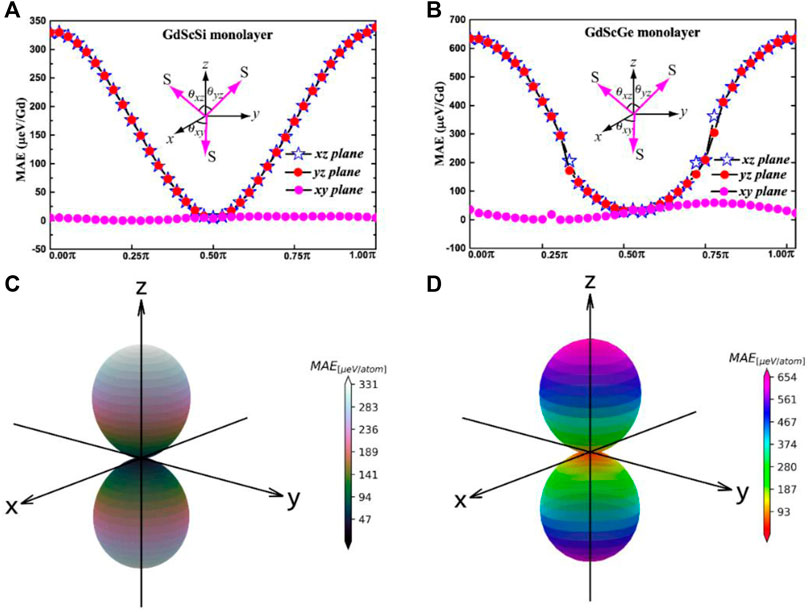
FIGURE 5. Angular dependence of the magnetic anisotropic energy (MAE) with the direction of magnetization lying on three different planes and the whole space for the GdScSi monolayer (A, B) and the GdScGe (C, D) monolayer.

3.4 Curie temperatures of GdScX monolayers

Tc is an important parameter for ferromagnetic materials. To get an accurate estimate of the Tc for GdScX monolayers, Monte Carlo simulations based on the Heisenberg model were used. The Hamiltonian is defined as follows:

$\mathit{H}=-{\sum }_{\mathit{i}\mathit{j}}{\mathit{J}}_{\mathbf{1}}{\mathit{S}}_{\mathit{i}}{\mathit{S}}_{\mathit{j}}-{\sum }_{\mathit{i}\mathit{k}}{\mathit{J}}_{\mathbf{2}}{\mathit{S}}_{\mathit{i}}{\mathit{S}}_{\mathit{k}}-{\sum }_{\mathit{i}\mathit{k}}{\mathit{J}}_{\mathbf{3}}{\mathit{S}}_{\mathit{i}}{\mathit{S}}_{\mathit{k}}-\mathit{A}{\mathit{S}}_{\mathit{i}}^{\mathit{Z}}{\mathit{S}}_{\mathit{i}}^{\mathit{Z}},$

where J₁, J₂, and J₃ are the first, second, and third nearest-neighboring exchange parameters, respectively. Using the energy differences of the FM and AFM orders, the exchange parameters J₁, J₂, and J₃ are calculated to be 4.82 meV (4.81 meV), −.0106 meV (−0.038 meV), and 0.163 meV (0.102 meV) for the GdScSi monolayer and the GdScGe monolayer, respectively. The magnetic moments, capacities, and susceptibilities of the GdScX monolayers with respect to temperature (Figure 6) show that the T_C of the GdScSi monolayer and the GdScGe monolayer are approximately 470 K and 495 K, respectively, which are significantly higher than room temperature.

FIGURE 6

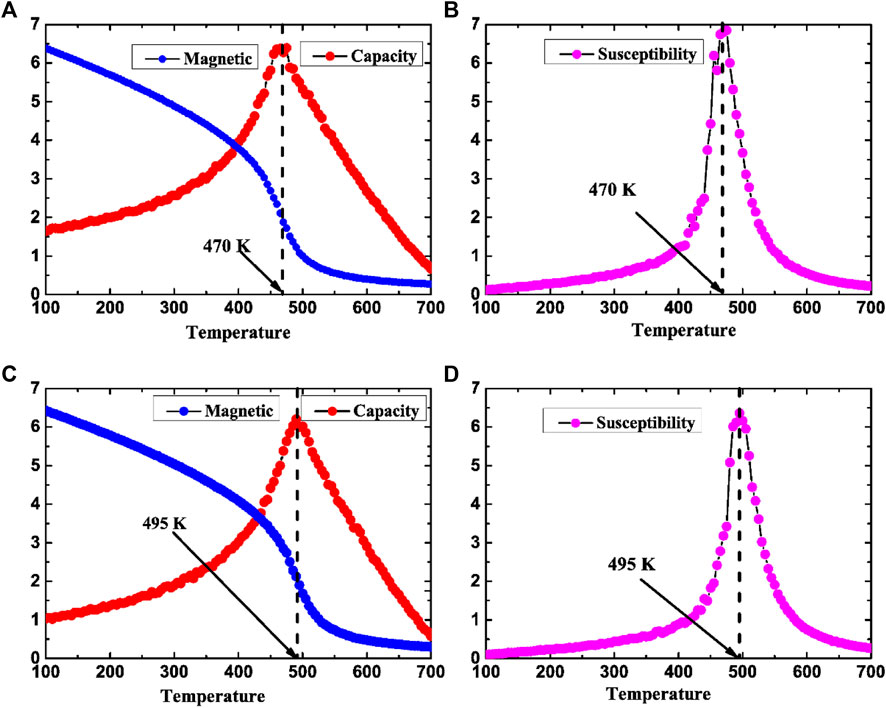
FIGURE 6. Magnetic moment (blue line), capacity (red), and magnetic susceptibility (magenta) as functions of temperature for the GdScSi monolayer (A, B) and the GdScGe (C, D) monolayer.

4 Conclusion

In summary, two 2D intrinsic ferromagnetic rare-earth monolayers, the GdScSi monolayer and the GdScGe monolayer, were predicted using first-principles calculation. Interestingly, these 2D GdScX (X = Si, Ge) monolayers exhibit high Tc (470 K for the GdScSi monolayer and 495 K for the GdScGe monolayer), which are above room temperature. In addition, they possess excellent dynamical, thermal, and mechanical stabilities. Our findings on the intrinsic room-temperature ferromagnetic rare-earth material GdScX (X = Si, Ge) monolayers open up new possibilities for spintronic applications at the nanoscale.

Data availability statement

The original contributions presented in the study are included in the article/supplementary material; further inquiries can be directed to the corresponding authors.

Author contributions

RW: data curation, investigation, validation, and writing—original draft; PS: data curation, investigation, and validation; LH: data curation, investigation, and validation; QC: validation, writing—review and editing, and supervision; YZ: writing—review and editing, supervision, and funding acquisition.

Funding

This work was financially supported by the Scientific Research Key Project Fund of Henan Provincial Education Department (No. 23B140005) and the Innovative experimental training program for college students of Henan University (No. 20221011005).

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors, and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

1. Novoselov KS, Geim AK, Morozov SV, Jiang D, Zhang Y, Dubonos SV, et al. Electric field effect in atomically thin carbon films. science (2004) 306:666–9. doi:10.1126/science.1102896

PubMed Abstract | CrossRef Full Text | Google Scholar

2. Novoselov KS, Jiang D, Schedin F, Booth TJ, Khotkevich VV, Morozov SV, et al. Two-dimensional atomic crystals. P Natl Acad Sci USA (2005) 102:10451–3. doi:10.1073/pnas.0502848102

PubMed Abstract | CrossRef Full Text | Google Scholar

3. Geim AK, Novoselov KS. The rise of graphene. Nat Mater (2007) 6:183–91. doi:10.1038/nmat1849

PubMed Abstract | CrossRef Full Text | Google Scholar

4. Mak KF, Lee C, Hone J, Shan J, Heinz TF. Atomically ThinMoS2: A new direct-gap semiconductor. Phys Rev Lett (2010) 105:136805. doi:10.1103/physrevlett.105.136805

PubMed Abstract | CrossRef Full Text | Google Scholar

5. Radisavljevic B, Radenovic A, Brivio J, Giacometti V, Kis A. Single-layer MoS2 transistors. Nat Nanotechnol (2011) 6:147–50. doi:10.1038/nnano.2010.279

PubMed Abstract | CrossRef Full Text | Google Scholar

6. Li L, Yu Y, Ye GJ, Ge Q, Ou X, Wu H, et al. Black phosphorus field-effect transistors. Nat Nanotechnol (2014) 9:372–7. doi:10.1038/nnano.2014.35

PubMed Abstract | CrossRef Full Text | Google Scholar

7. Gong C, Li L, Li Z, Ji H, Stern A, Xia Y, et al. Discovery of intrinsic ferromagnetism in two-dimensional van der Waals crystals. Nature (2017) 546:265–9. doi:10.1038/nature22060

PubMed Abstract | CrossRef Full Text | Google Scholar

8. Huang B, Clark G, Navarro-Moratalla E, Klein DR, Cheng R, Seyler KL, et al. Layer-dependent ferromagnetism in a van der Waals crystal down to the monolayer limit. Nature (2017) 546:270–3. doi:10.1038/nature22391

PubMed Abstract | CrossRef Full Text | Google Scholar

9. Liu S, Yin H, Singh DJ, Liu P-F. Ta4SiTe4: A possible one-dimensional topological insulator. Phys Rev B (2022) 105:195419. doi:10.1103/physrevb.105.195419

CrossRef Full Text | Google Scholar

10. Liu P, Liu S, Jia M, Yin H, Zhang G, Ren F, et al. Strain-driven valley states and phase transitions in Janus VSiGeN4 monolayer. Appl Phys Lett (2022) 121:063103. doi:10.1063/5.0104477

CrossRef Full Text | Google Scholar

11. Guo S-D, Mu W-Q, Wang J-H, Yang Y-X, Wang B, Ang Y-S. Strain effects on the topological and valley properties of the Janus monolayer VSiGeN4. Phys Rev B (2022) 106:064416. doi:10.1103/physrevb.106.064416

CrossRef Full Text | Google Scholar

12. Wang R, Su Y, Yang G, Zhang J, Zhang S. Bipolar doping by intrinsic defects and magnetic phase instability in monolayer CrI3. Chem Mater (2020) 32:1545–52. doi:10.1021/acs.chemmater.9b04645

CrossRef Full Text | Google Scholar

13. Lima Fernandes I, Bouhassoune M, Lounis S. Defect-implantation for the all-electrical detection of non-collinear spin-textures. Nat Commun (2020) 11:1602. doi:10.1038/s41467-020-15379-6

PubMed Abstract | CrossRef Full Text | Google Scholar

14. Chittari BL, Lee D, Banerjee N, Macdonald AH, Hwang E, Jung J. Carrier- and strain-tunable intrinsic magnetism in two-dimensional MAX3 transition metal chalcogenides. Phys Rev B (2020) 101:085415. doi:10.1103/physrevb.101.085415

CrossRef Full Text | Google Scholar

15. Liu P, Zhang G, Yan Y, Jia G, Liu C, Wang B, et al. Strain-tunable phase transition and doping-induced magnetism in iodinene. Appl Phys Lett (2021) 119:102403. doi:10.1063/5.0063802

CrossRef Full Text | Google Scholar

16. Yang K, Wang G, Liu L, Lu D, Wu H. Triaxial magnetic anisotropy in the two-dimensional ferromagnetic semiconductor CrSBr. Phys Rev B (2021) 104:144416. doi:10.1103/physrevb.104.144416

CrossRef Full Text | Google Scholar

17. Cenker J, Sivakumar S, Xie K, Miller A, Thijssen P, Liu Z, et al. Reversible strain-induced magnetic phase transition in a van der Waals magnet. Nat Nanotechnol (2022) 17:256–61. doi:10.1038/s41565-021-01052-6

PubMed Abstract | CrossRef Full Text | Google Scholar

18. Gerber E, Yao Y, Arias TA, Kim EA. Ab initio<i/> mismatched interface theory of graphene on α−RuCl3: Doping and magnetism. Phys Rev Lett (2020) 124:106804. doi:10.1103/physrevlett.124.106804

PubMed Abstract | CrossRef Full Text | Google Scholar

19. Luo P, Zhuge F, Zhang Q, Chen Y, Lv L, Huang Y, et al. Doping engineering and functionalization of two-dimensional metal chalcogenides. Nanoscale Horiz (2019) 4:26–51. doi:10.1039/c8nh00150b

PubMed Abstract | CrossRef Full Text | Google Scholar

20. Park SY, Kim DS, Liu Y, Hwang J, Kim Y, Kim W, et al. Controlling the magnetic anisotropy of the van der Waals ferromagnet Fe3GeTe2 through hole doping. Nano Lett (2019) 20:95–100. doi:10.1021/acs.nanolett.9b03316

PubMed Abstract | CrossRef Full Text | Google Scholar

21. Wang C, Zhou X, Pan Y, Qiao J, Kong X, Kaun C-C, et al. Layer and doping tunable ferromagnetic order in two-dimensional CrS2 layers. Phys Rev B (2018) 97:245409. doi:10.1103/physrevb.97.245409

CrossRef Full Text | Google Scholar

22. Wang B, Wu Q, Zhang Y, Guo Y, Zhang X, Zhou Q, et al. High Curie-temperature intrinsic ferromagnetism and hole doping-induced half-metallicity in two-dimensional scandium chlorine monolayers. Nanoscale Horiz (2018) 3:551–5. doi:10.1039/c8nh00101d

PubMed Abstract | CrossRef Full Text | Google Scholar

23. Hartman T, Sturala J, Luxa J, Sofer Z. Chemistry of germanene: Surface modification of germanane using alkyl halides. ACS Nano (2020) 14:7319–27. doi:10.1021/acsnano.0c02635

PubMed Abstract | CrossRef Full Text | Google Scholar

24. Jiang Z, Wang P, Jiang X, Zhao J. MBene (MnB): A new type of 2D metallic ferromagnet with high Curie temperature. Nanoscale Horiz (2018) 3:335–41. doi:10.1039/c7nh00197e

PubMed Abstract | CrossRef Full Text | Google Scholar

25. Zhao Y, Lin L, Zhou Q, Li Y, Yuan S, Chen Q, et al. Surface vacancy-induced switchable electric polarization and enhanced ferromagnetism in monolayer metal trihalides. Nano Lett (2018) 18:2943–9. doi:10.1021/acs.nanolett.8b00314

PubMed Abstract | CrossRef Full Text | Google Scholar

26. Song C, Xiao W, Li L, Lu Y, Jiang P, Li C, et al. Tunable band gap and enhanced ferromagnetism by surface adsorption in monolayer Cr2Ge2Te6. Phys Rev B (2019) 99:214435. doi:10.1103/physrevb.99.214435

CrossRef Full Text | Google Scholar

27. Mermin ND, Wagner H. Absence of ferromagnetism or antiferromagnetism in one- or two-dimensional isotropic Heisenberg models. Phys Rev Lett (1966) 17:1133–6. doi:10.1103/physrevlett.17.1133

CrossRef Full Text | Google Scholar

28. Wang B, Zhang Y, Ma L, Wu Q, Guo Y, Zhang X, et al. MnX (X = P, as) monolayers: A new type of two-dimensional intrinsic room temperature ferromagnetic half-metallic material with large magnetic anisotropy. Nanoscale (2019) 11:4204–9. doi:10.1039/c8nr09734h

PubMed Abstract | CrossRef Full Text | Google Scholar

29. Wu Q, Zhang Y, Zhou Q, Wang J, Zeng XC. Transition metal dihydride monolayers: A new family of two-dimensional ferromagnetic materials with intrinsic room-temperature half-metallicity. J Phys Chem Lett (2018) 9:4260–6. doi:10.1021/acs.jpclett.8b01976

PubMed Abstract | CrossRef Full Text | Google Scholar

30. Bai Y, Shi R, Wu Y, Wang B, Zhang X. Cr2XTe4 (X = Si, Ge) monolayers: A new type of two-dimensional high-TC ising ferromagnetic semiconductors with a large magnetic anisotropy. J Phys Condens Matter (2022) 34:384001. doi:10.1088/1361-648x/ac7f16

CrossRef Full Text | Google Scholar

31. Zhang Y, Wu Y, Jin C, Ren F, Wang B. B2S3 monolayer: A two-dimensional direct-gap semiconductor with tunable band-gap and high carrier mobility. Nanotechnology (2021) 32:475709. doi:10.1088/1361-6528/ac1d07

CrossRef Full Text | Google Scholar

32. Zhang Y, Wang B, Guo Y, Li Q, Wang J. A universal framework for metropolis Monte Carlo simulation of magnetic Curie temperature. Comput Mater Sci (2021) 197:110638. doi:10.1016/j.commatsci.2021.110638

CrossRef Full Text | Google Scholar

33. Wu Y, Sun W, Liu S, Wang B, Liu C, Yin H, et al. Ni(NCS)2 monolayer: A robust bipolar magnetic semiconductor. Nanoscale (2021) 13:16564–70. doi:10.1039/d1nr04816c

PubMed Abstract | CrossRef Full Text | Google Scholar

34. Gong C, Zhang X. Two-dimensional magnetic crystals and emergent heterostructure devices. Science (2019) 363:eaav4450. doi:10.1126/science.aav4450

PubMed Abstract | CrossRef Full Text | Google Scholar

35. Sun Y, Wang L, Li X, Yao X, Xu X, Guo T, et al. TM2B3 monolayers: Intrinsic anti-ferromagnetism and Dirac nodal line semimetal. Appli Phys Lett (2022) 121:183103. doi:10.1063/5.0113408

CrossRef Full Text | Google Scholar

36. Yao X, Ji J, Lin Y, Sun Y, Wang L, He A, et al. TMB2C (TM= Ti, V): 2D transition metal borocarbide monolayer with intriguing electronic, magnetic and electrochemical properties. Appli Sur Sci (2022) 605:154692. doi:10.1016/j.apsusc.2022.154692

CrossRef Full Text | Google Scholar

37. Lee K, Dismukes AH, Telford EJ, Wiscons RA, Wang J, Xu X, et al. Magnetic order and symmetry in the 2D semiconductor CrSBr. Nano Lett (2021) 21:3511–7. doi:10.1021/acs.nanolett.1c00219

PubMed Abstract | CrossRef Full Text | Google Scholar

38. Wang B, Zhang X, Zhang Y, Yuan S, Guo Y, Dong S, et al. Prediction of a two-dimensional high-TC f-electron ferromagnetic semiconductor. Mater Horiz (2020) 7:1623–30. doi:10.1039/d0mh00183j

CrossRef Full Text | Google Scholar

39. Liu W, Tong J, Deng L, Yang B, Xie G, Qin G, et al. Two-dimensional ferromagnetic semiconductors of rare-earth monolayer GdX2 (X = Cl, Br, I) with large perpendicular magnetic anisotropy and high Curie temperature. Mater Today Phys (2021) 21:100514. doi:10.1016/j.mtphys.2021.100514

CrossRef Full Text | Google Scholar

40. Sheng K, Yuan HK, Wang ZY. Monolayer gadolinium halides, GdX(2) (X = F, Cl, Br): Intrinsic ferrovalley materials with spontaneous spin and valley polarizations. Phys Chem Chem Phys (2022) 24:3865–74. doi:10.1039/d1cp05097d

PubMed Abstract | CrossRef Full Text | Google Scholar

41. Wang Y, Cui Z, Zeng H, Wang Z, Zhang X, Shi J, et al. Tunable magnetic order in two-dimensional layered GdGe2. J Mate Chem C (2022) 10:1259–69. doi:10.1039/d1tc05350g

CrossRef Full Text | Google Scholar

42. Liu S, Wang C, Liu L, Choi JH, Kim HJ, Jia Y, et al. Ferromagnetic Weyl fermions in two-dimensional layered electride Gd2C. Phys Rev Lett (2020) 125:187203. doi:10.1103/physrevlett.125.187203

PubMed Abstract | CrossRef Full Text | Google Scholar

43. Sheng K, Chen Q, Yuan H-K, Wang Z-Y. Monolayer CeI2: An intrinsic room-temperature ferrovalley semiconductor. Phys Rev B (2022) 105:075304. doi:10.1103/physrevb.105.075304

CrossRef Full Text | Google Scholar

44. You H, Ding N, Chen J, Yao X, Dong S. Gadolinium halide monolayers: A fertile family of two-dimensional 4f magnets. ACS Appl Electron Mater (2022) 4:3168–76. doi:10.1021/acsaelm.2c00384

CrossRef Full Text | Google Scholar

45. You HP, Chen J, Zhang JJ, Ding N, Zhang XW, Yao XY, et al. Structural reconstruction and anisotropic conductance in 4f-ferromagnetic monolayer. Mater Today Phys (2022) 24:100693. doi:10.1016/j.mtphys.2022.100693

CrossRef Full Text | Google Scholar

46. Nie S, Weng H, Prinz FB. Topological nodal-line semimetals in ferromagnetic rare-earth-metal monohalides. Phys Rev B (2019) 99:035125. doi:10.1103/physrevb.99.035125

CrossRef Full Text | Google Scholar

47. Kresse G, FurthmüLLER J. Efficient iterative schemes for ab initio total-energy calculations using a plane-wave basis set. Phys Rev B (1996) 54:11169–86. doi:10.1103/physrevb.54.11169

PubMed Abstract | CrossRef Full Text | Google Scholar

48. BlöCHL PE. Projector augmented-wave method. Phys Rev B (1994) 50:17953–79. doi:10.1103/physrevb.50.17953

CrossRef Full Text | Google Scholar

49. Perdew JP, Burke K, Ernzerhof M. Generalized gradient approximation made simple. Phys Rev Lett (1996) 77:3865–8. doi:10.1103/physrevlett.77.3865

PubMed Abstract | CrossRef Full Text | Google Scholar

50. Jain A, Hautier G, Ong SP, Moore CJ, Fischer CC, Persson KA, et al. Formation enthalpies by mixing GGA and GGA+Ucalculations. Phys Rev B (2011) 84:045115. doi:10.1103/physrevb.84.045115

CrossRef Full Text | Google Scholar

51. Togo A, Oba F, Tanaka I. First-principles calculations of the ferroelastic transition between rutile-type andCaCl2-typeSiO2at high pressures. Phys Rev B (2008) 78:134106. doi:10.1103/physrevb.78.134106

CrossRef Full Text | Google Scholar

52. Martyna GJ, Klein ML, Tuckerman M. Nosé–Hoover chains: The canonical ensemble via continuous dynamics. J Chem Phys (1992) 97:2635–43. doi:10.1063/1.463940

CrossRef Full Text | Google Scholar

53. Peng R, Ma Y, He Z, Huang B, Kou L, Dai Y. Single-Layer Ag2S: A two-dimensional bidirectional auxetic semiconductor. Nano Lett (2019) 19:1227–33. doi:10.1021/acs.nanolett.8b04761

PubMed Abstract | CrossRef Full Text | Google Scholar

54. Wang B, Wu Q, Zhang Y, Ma L, Wang J. Auxetic B4N monolayer: A promising 2D material with in-plane negative Poisson's ratio and large anisotropic mechanics. ACS Appl Mater Inter (2019) 11:33231–7. doi:10.1021/acsami.9b10472

PubMed Abstract | CrossRef Full Text | Google Scholar

55. Tu Y, Liu Q, Hou L, Shi P, Jia C, Su J, et al. Two-dimensional Cr-based ferromagnetic semiconductor: Theoretical simulations and design. Front Phys (2022) 10:1078202. doi:10.3389/fphy.2022.1078202

CrossRef Full Text | Google Scholar