Full characterization of spontaneous parametric down conversion in non-ideal quarter-wavelength semiconductor Bragg reflection waveguide

Entangled photons are important for testing foundations of quantum physics and are at the heart of quantum technology. Integrated photonics has overwhelming dominance in terms of density and performance, making it a promise route for scalable quantum information processing. AlGaAs-based materials having large second-order non-linearities, direct bandgap and strong electro-optical effect can offer distinct advantages in quantum light source. Here we report a non-ideal quarter-wavelength Bragg reflection waveguide for generating three types of spontaneous parametric down-conversion processes. A general solution to the dispersion equation is derived and employed for designing high efficiency devices by taking into account the influence of core layer aluminium concentration. We further design and fabricate a Bragg reflection waveguide sample based on the analysis, and experimentally characterize its phase matching types and spectral brightness. Our work paves the path for the development of portable quantum light sources.

1 Introduction

To demonstrate the advantage of quantum systems over their classical counter-parts, it is necessary to generate, manipulate and detect various entangled states [1, 2]. Photonics is crucial for the development of quantum technologies [3]. At present, the spontaneous parametric down conversion (SPDC) in non-linear crystals is widely used to generate entangled photons at room temperature. The photon pair can be entangled in various degrees of freedom (DOF), such as polarization [4], frequency [5], path [6] and orbital angular momentum [7]. However, the long-time system stability and manufacturability is a daunting task for conventional bulk-crystal as the system complexity increases. To this end, the generation of non-classical light in monolithically integrated chips is of vital importance for large-scale implementations [8–12].

To date, a mass of components has been integrated onto a single silicon chip, realizing both entangled photons generation and coherent control [13–16]. There has been a growing interest in AlGaAs/GaAs based semiconductor material recently, because its mature fabrication technology for devices, such as lasers and modulators, and very large second order non-linearity [17–27]. Among them, the Bragg reflection waveguide (BRW) structure is appealing for developing turn-key devices for quantum applications. Phase matching (PM) in the waveguide is achieved by using total internal reflection (TIR) modes and quasi-bounded BRW modes, where BRW modes are formed by transverse Bragg reflections at the interface between core and period cladding layers and TIR modes are guided through internal reflection between high- and low-index claddings. The BRW sources have been used for several applications, such as generating different types of photon pair generation [28–30] and distributing entanglement in multiuser quantum network [31, 32]. Traditionally, the perfect transverse quarter-wavelength cladding condition is proposed to simplify the theoretical analysis. In fact, the structure may have higher modal overlap in non-ideal quarter-wavelength (NIQW) cases [33].

Here, we design and fabricate a NIQW BRW sample with high figure-of-merit modal overlap by using high-index core layer, which is different from the usual design, and can provide a way for the research of high efficiency multifunctional semiconductor non-linear devices. The general expressions for modes intensity profiles and dispersion equation in NIQW cases are deduced. According to the analytical results, the influence of core layer aluminium concentration on modes properties and three types of SPDC processes are analyzed. Finally, we experimentally characterize the three PM types and their bright spectral brightness of the real NIQW sample.

2 Mode equations of the BRW structure

We first consider a one-dimensional (1D) BRW structure where the core layer is surrounded by periodic claddings. The core layer has refractive index n_c and thickness t_c, while the cladding consists of index n₁ and n₂ (n₁ > n₂) with thickness a and b respectively. The period is ∧ = a + b and the waveguide is symmetric about the center of the Bragg stack position, i.e., n(x) = n(−x), consequently guiding modes have either even or odd symmetry. For simplicity, we take the lowest-order TE and TM modes as examples and concentrate on the x ≥ 0 region, the high-order modes can be processed in a similar way. We assume the modes propagate along z direction and $\frac{\partial }{\partial \mathrm{y}}=0$, then the field envelop (without normalization) can be written in the form [34]

${\mathit{E}}_{\mathit{y}}\left(\mathit{x}\right)=\left\{\begin{array}{ll}\mathit{cos}\left({\mathit{k}}_{\mathit{c}}\mathit{x}\right),& \mathbf{0}\le \mathit{x}\le \frac{{\mathit{t}}_{\mathit{c}}}{\mathbf{2}},\\ {\mathit{E}}_{\mathit{K}}\left(\left|\mathit{x}\right|-\frac{{\mathit{t}}_{\mathit{c}}}{\mathbf{2}}\right)\mathit{exp}\left[\mathit{i}\mathit{K}\left(\left|\mathit{x}\right|-\frac{{\mathit{t}}_{\mathit{c}}}{\mathbf{2}}\right)\right],& \mathit{x}>\frac{{\mathit{t}}_{\mathit{c}}}{\mathbf{2}},\end{array}\right.\mathbf{T}\mathbf{E}$

${\mathit{H}}_{\mathit{y}}\left(\mathit{x}\right)=\left\{\begin{array}{c}\begin{array}{cc}\mathit{cos}\left({\mathit{k}}_{\mathit{c}}\mathit{x}\right),& \mathbf{0}\le \mathit{x}\le \frac{{\mathit{t}}_{\mathit{c}}}{\mathbf{2}},\frac{{\mathit{n}}_{\mathbf{1}}^{\mathbf{2}}{\mathit{k}}_{\mathbf{2}}}{{\mathit{n}}_{\mathbf{2}}^{\mathbf{2}}{\mathit{k}}_{\mathbf{1}}}<\mathbf{1},\end{array}\\ \begin{array}{cc}\mathit{sin}\left({\mathit{k}}_{\mathit{c}}\mathit{x}\right),& \mathbf{0}\le \mathit{x}\le \frac{{\mathit{t}}_{\mathit{c}}}{\mathbf{2}},\frac{{\mathit{n}}_{\mathbf{1}}^{\mathbf{2}}{\mathit{k}}_{\mathbf{2}}}{{\mathit{n}}_{\mathbf{2}}^{\mathbf{2}}{\mathit{k}}_{\mathbf{1}}}>\mathbf{1},\end{array}\\ \begin{array}{cc}{\mathit{H}}_{\mathit{K}}\left(\mathit{x}-\frac{{\mathit{t}}_{\mathit{c}}}{\mathbf{2}}\right)\mathit{exp}\left[\mathit{i}\mathit{K}\left(\mathit{x}-\frac{{\mathit{t}}_{\mathit{c}}}{\mathbf{2}}\right)\right],& \mathit{x}>\frac{{\mathit{t}}_{\mathit{c}}}{\mathbf{2}},\end{array}\end{array}\right.\mathbf{T}\mathbf{M}(1)$

where K is the Block wave vector, $k_c=k_0\sqrt{n_q^2-n_{eff}^2}$ is the transverse wave vector in the core layer, and k₀ and n_eff are the free-space wave vector and effective refractive index respectively. The electric field of TM can be solved by Maxwell’s curl equations $E_x\left(x\right)=\beta /\omega n^2{H}_y\left(x\right)$. From the Floquet theorem, E_K(x) and H_K(x) are periodic with ∧, and the electric and magnetic fields in the nth unit cell are

${\mathit{E}}_{\mathit{n}}\left(\mathit{x}\right)=\left\{\begin{array}{ll}{\mathit{a}}_{\mathit{E}\mathit{n}}\mathit{cos}\left[{\mathit{k}}_{\mathbf{1}}\left(\mathit{x}-\frac{{\mathit{t}}_{\mathit{c}}}{\mathbf{2}}-\mathit{n}\mathit{\Lambda }\right)\right]+{\mathit{b}}_{\mathit{E}\mathit{n}}\mathit{sin}\left[{\mathit{k}}_{\mathbf{1}}\left(\mathit{x}-\frac{{\mathit{t}}_{\mathit{c}}}{\mathbf{2}}-\mathit{n}\mathit{\Lambda }\right)\right],& \mathit{n}\mathit{\Lambda }\le \mathit{x}-\frac{{\mathit{t}}_{\mathit{c}}}{\mathbf{2}}\le \mathit{n}\mathit{\Lambda }+\mathit{a},\\ {\mathit{c}}_{\mathit{E}\mathit{n}}\mathit{cos}\left[{\mathit{k}}_{\mathbf{2}}\left(\mathit{x}-\frac{{\mathit{t}}_{\mathit{c}}}{\mathbf{2}}-\mathit{n}\mathit{\Lambda }-\mathit{a}\right)\right]+{\mathit{d}}_{\mathit{E}\mathit{n}}\mathit{sin}\left[{\mathit{k}}_{\mathbf{2}}\left(\mathit{x}-\frac{{\mathit{t}}_{\mathit{c}}}{\mathbf{2}}-\mathit{n}\mathit{\Lambda }-\mathit{a}\right)\right],& \mathit{n}\mathit{\Lambda }+\mathit{a}\le \mathit{x}-\frac{{\mathit{t}}_{\mathit{c}}}{\mathbf{2}}\le \left(\mathit{n}+\mathbf{1}\right)\mathit{\Lambda },\end{array}\right.$

${\mathit{H}}_{\mathit{n}}\left(\mathit{x}\right)=\left\{\begin{array}{cc}{\mathit{a}}_{\mathit{H}\mathit{n}}\mathit{cos}\left[{\mathit{k}}_{\mathbf{1}}\left(\mathit{x}-\frac{{\mathit{t}}_{\mathit{c}}}{\mathbf{2}}-\mathit{n}\mathit{\Lambda }\right)\right]+{\mathit{b}}_{\mathit{H}\mathit{n}}\mathit{sin}\left[{\mathit{k}}_{\mathbf{1}}\left(\mathit{x}-\frac{{\mathit{t}}_{\mathit{c}}}{\mathbf{2}}-\mathit{n}\mathit{\Lambda }\right)\right],& \mathit{n}\mathit{\Lambda }\le \mathit{x}-\frac{{\mathit{t}}_{\mathit{c}}}{\mathbf{2}}\le \mathit{n}\mathit{\Lambda }+\mathit{a},\\ {\mathit{c}}_{\mathit{H}\mathit{n}}\mathit{cos}\left[{\mathit{k}}_{\mathbf{2}}\left(\mathit{x}-\frac{{\mathit{t}}_{\mathit{c}}}{\mathbf{2}}-\mathit{n}\mathit{\Lambda }-\mathit{a}\right)\right]+{\mathit{d}}_{\mathit{H}\mathit{n}}\mathit{sin}\left[{\mathit{k}}_{\mathbf{2}}\left(\mathit{x}-\frac{{\mathit{t}}_{\mathit{c}}}{\mathbf{2}}-\mathit{n}\mathit{\Lambda }-\mathit{a}\right)\right],& \mathit{n}\mathit{\Lambda }+\mathit{a}\le \mathit{x}-\frac{{\mathit{t}}_{\mathit{c}}}{\mathbf{2}}\le \left(\mathit{n}+\mathbf{1}\right)\mathit{\Lambda },\end{array}\right.(2)$

where j = E or H represent the non-zero field components $E_y\left(TE\right)$ and $H_y\left(TM\right)$, a_jn (b_jn) and c_jn (d_jn) (j = E/H), are the incident (reflected) amplitudes in n₁ and n₂ regions respectively. With the transfer matrix method and continuous condition at the boundaries, one can obtain

$\left(\begin{array}{c}{\mathit{a}}_{\mathit{E}\mathit{n}+\mathbf{1}}\\ {\mathit{b}}_{\mathit{E}\mathit{n}+\mathbf{1}}\end{array}\right)=\left[\begin{array}{cc}\mathit{cos}\left({\mathit{k}}_{\mathbf{2}}\mathit{b}\right)& \mathit{sin}\left({\mathit{k}}_{\mathbf{2}}\mathit{b}\right)\\ -\frac{{\mathit{k}}_{\mathbf{2}}}{{\mathit{k}}_{\mathbf{1}}}\mathit{sin}\left({\mathit{k}}_{\mathbf{2}}\mathit{b}\right)& \frac{{\mathit{k}}_{\mathbf{2}}}{{\mathit{k}}_{\mathbf{1}}}\mathit{cos}\left({\mathit{k}}_{\mathbf{2}}\mathit{b}\right)\end{array}\right]\left(\begin{array}{c}{\mathit{c}}_{\mathit{E}\mathit{n}}\\ {\mathit{d}}_{\mathit{E}\mathit{n}}\end{array}\right)=\left[\begin{array}{cc}{\mathit{A}}_{\mathit{E}}& {\mathit{B}}_{\mathit{E}}\\ {\mathit{C}}_{\mathit{E}}& {\mathit{D}}_{\mathit{E}}\end{array}\right]\left(\begin{array}{c}{\mathit{a}}_{\mathit{E}\mathit{n}}\\ {\mathit{b}}_{\mathit{E}\mathit{n}}\end{array}\right)(3)$

and

$\left(\begin{array}{c}{\mathit{a}}_{\mathit{H}\mathit{n}+\mathbf{1}}\\ {\mathit{b}}_{\mathit{H}\mathit{n}+\mathbf{1}}\end{array}\right)=\left[\begin{array}{cc}\mathit{cos}\left({\mathit{k}}_{\mathbf{2}}\mathit{b}\right)& \mathit{sin}\left({\mathit{k}}_{\mathbf{2}}\mathit{b}\right)\\ -\frac{{\mathit{n}}_{\mathbf{1}}^{\mathbf{2}}{\mathit{k}}_{\mathbf{2}}}{{{\mathit{n}}_{\mathbf{2}}^{\mathbf{2}}\mathit{k}}_{\mathbf{1}}}\mathit{sin}\left({\mathit{k}}_{\mathbf{2}}\mathit{b}\right)& \frac{{\mathit{n}}_{\mathbf{1}}^{\mathbf{2}}{\mathit{k}}_{\mathbf{2}}}{{{\mathit{n}}_{\mathbf{2}}^{\mathbf{2}}\mathit{k}}_{\mathbf{1}}}\mathit{cos}\left({\mathit{k}}_{\mathbf{2}}\mathit{b}\right)\end{array}\right]\left(\begin{array}{c}{\mathit{c}}_{\mathit{H}\mathit{n}}\\ {\mathit{d}}_{\mathit{H}\mathit{n}}\end{array}\right)=\left[\begin{array}{cc}{\mathit{A}}_{\mathit{H}}& {\mathit{B}}_{\mathit{H}}\\ {\mathit{C}}_{\mathit{H}}& {\mathit{D}}_{\mathit{H}}\end{array}\right]\left(\begin{array}{c}{\mathit{a}}_{\mathit{H}\mathit{n}}\\ {\mathit{b}}_{\mathit{H}\mathit{n}}\end{array}\right)(4)$

where

${\mathit{A}}_{\mathit{E}}=\mathit{cos}\left({\mathit{k}}_{\mathbf{1}}\mathit{a}\right)\mathit{cos}\left({\mathit{k}}_{\mathbf{2}}\mathit{b}\right)-\frac{{\mathit{k}}_{\mathbf{1}}}{{\mathit{k}}_{\mathbf{2}}}\mathit{sin}\left({\mathit{k}}_{\mathbf{1}}\mathit{a}\right)\mathit{sin}\left({\mathit{k}}_{\mathbf{2}}\mathit{b}\right)$

${\mathit{B}}_{\mathit{E}}=\mathit{sin}\left({\mathit{k}}_{\mathbf{1}}\mathit{a}\right)\mathit{cos}\left({\mathit{k}}_{\mathbf{2}}\mathit{b}\right)+\frac{{\mathit{k}}_{\mathbf{1}}}{{\mathit{k}}_{\mathbf{2}}}\mathit{cos}\left({\mathit{k}}_{\mathbf{1}}\mathit{a}\right)\mathit{sin}\left({\mathit{k}}_{\mathbf{2}}\mathit{b}\right)$

${\mathit{C}}_{\mathit{E}}=-\mathit{sin}\left({\mathit{k}}_{\mathbf{1}}\mathit{a}\right)\mathit{cos}\left({\mathit{k}}_{\mathbf{2}}\mathit{b}\right)-\frac{{\mathit{k}}_{\mathbf{2}}}{{\mathit{k}}_{\mathbf{1}}}\mathit{cos}\left({\mathit{k}}_{\mathbf{1}}\mathit{a}\right)\mathit{sin}\left({\mathit{k}}_{\mathbf{2}}\mathit{b}\right)$

${\mathit{D}}_{\mathit{E}}=\mathit{cos}\left({\mathit{k}}_{\mathbf{1}}\mathit{a}\right)\mathit{cos}\left({\mathit{k}}_{\mathbf{2}}\mathit{b}\right)-\frac{{\mathit{k}}_{\mathbf{2}}}{{\mathit{k}}_{\mathbf{1}}}\mathit{sin}\left({\mathit{k}}_{\mathbf{1}}\mathit{a}\right)\mathit{sin}\left({\mathit{k}}_{\mathbf{2}}\mathit{b}\right)(5)$

and

${\mathit{A}}_{\mathit{H}}=\mathit{cos}\left({\mathit{k}}_{\mathbf{1}}\mathit{a}\right)\mathit{cos}\left({\mathit{k}}_{\mathbf{2}}\mathit{b}\right)-\frac{{{\mathit{n}}_{\mathbf{2}}^{\mathbf{2}}\mathit{k}}_{\mathbf{1}}}{{\mathit{n}}_{\mathbf{1}}^{\mathbf{2}}{\mathit{k}}_{\mathbf{2}}}\mathit{sin}\left({\mathit{k}}_{\mathbf{1}}\mathit{a}\right)\mathit{sin}\left({\mathit{k}}_{\mathbf{2}}\mathit{b}\right)$

${\mathit{B}}_{\mathit{H}}=\mathit{sin}\left({\mathit{k}}_{\mathbf{1}}\mathit{a}\right)\mathit{cos}\left({\mathit{k}}_{\mathbf{2}}\mathit{b}\right)+\frac{{{\mathit{n}}_{\mathbf{2}}^{\mathbf{2}}\mathit{k}}_{\mathbf{1}}}{{\mathit{n}}_{\mathbf{1}}^{\mathbf{2}}{\mathit{k}}_{\mathbf{2}}}\mathit{cos}\left({\mathit{k}}_{\mathbf{1}}\mathit{a}\right)\mathit{sin}\left({\mathit{k}}_{\mathbf{2}}\mathit{b}\right)$

${\mathit{C}}_{\mathit{H}}=-\mathit{sin}\left({\mathit{k}}_{\mathbf{1}}\mathit{a}\right)\mathit{cos}\left({\mathit{k}}_{\mathbf{2}}\mathit{b}\right)-\frac{{\mathit{n}}_{\mathbf{1}}^{\mathbf{2}}{\mathit{k}}_{\mathbf{2}}}{{{\mathit{n}}_{\mathbf{2}}^{\mathbf{2}}\mathit{k}}_{\mathbf{1}}}\mathit{cos}\left({\mathit{k}}_{\mathbf{1}}\mathit{a}\right)\mathit{sin}\left({\mathit{k}}_{\mathbf{2}}\mathit{b}\right)$

${\mathit{D}}_{\mathit{H}}=\mathit{cos}\left({\mathit{k}}_{\mathbf{1}}\mathit{a}\right)\mathit{cos}\left({\mathit{k}}_{\mathbf{2}}\mathit{b}\right)-\frac{{\mathit{n}}_{\mathbf{1}}^{\mathbf{2}}{\mathit{k}}_{\mathbf{2}}}{{{\mathit{n}}_{\mathbf{2}}^{\mathbf{2}}\mathit{k}}_{\mathbf{1}}}\mathit{sin}\left({\mathit{k}}_{\mathbf{1}}\mathit{a}\right)\mathit{sin}\left({\mathit{k}}_{\mathbf{2}}\mathit{b}\right)(6)$

Furthermore, the periodicity of the electric field can be expressed as

$\left(\begin{array}{c}{\mathit{a}}_{\mathit{j}\mathit{n}+\mathbf{1}}\\ {\mathit{b}}_{\mathit{j}\mathit{n}+\mathbf{1}}\end{array}\right)=\mathit{exp}\left(\mathit{i}{\mathit{K}}_{\mathit{j}}\mathit{\Lambda }\right)\left(\begin{array}{c}{\mathit{a}}_{\mathit{j}\mathit{n}}\\ {\mathit{b}}_{\mathit{j}\mathit{n}}\end{array}\right)(7)$

Combing Eqs 3, 4, 7, we have

$\mathit{exp}\left(\mathit{i}{\mathit{K}}_{\mathit{j}}\mathit{\Lambda }\right)=\frac{{\mathit{A}}_{\mathit{j}}+{\mathit{D}}_{\mathit{j}}}{\mathbf{2}}\pm \sqrt{{\left[\frac{{\mathit{A}}_{\mathit{j}}+{\mathit{D}}_{\mathit{j}}}{\mathbf{2}}\right]}^{\mathbf{2}}-\mathbf{1}}(8)$

and

$\left(\begin{array}{c}{\mathit{a}}_{\mathit{j}\mathit{n}}\\ {\mathit{b}}_{\mathit{j}\mathit{n}}\end{array}\right)=\left(\begin{array}{c}{\mathit{B}}_{\mathit{j}}\\ \mathit{exp}\left(\mathit{i}{\mathit{K}}_{\mathit{j}}\mathit{\Lambda }\right)-{\mathit{A}}_{\mathit{j}}\end{array}\right)=\mathit{exp}\left(-\mathit{i}\mathit{n}{\mathit{K}}_{\mathit{j}}\mathit{\Lambda }\right)\left(\begin{array}{c}{\mathit{a}}_{\mathit{j}\mathbf{0}}\\ {\mathit{b}}_{\mathit{j}\mathbf{0}}\end{array}\right)(9)$

The coefficients in the first layer of the periodical structures can be deduced by the continuity of fields at the core-cladding interface,

$\left(\begin{array}{c}{\mathit{a}}_{\mathit{E}\mathbf{0}}\\ {\mathit{b}}_{\mathit{E}\mathbf{0}}\end{array}\right)=\left(\begin{array}{c}\mathit{cos}\left({\mathit{k}}_{\mathit{c}}{\mathit{t}}_{\mathit{c}}/\mathbf{2}\right)\\ -\frac{{\mathit{k}}_{\mathit{c}}}{{\mathit{k}}_{\mathbf{1}}}\mathit{sin}\left({\mathit{k}}_{\mathit{c}}{\mathit{t}}_{\mathit{c}}/\mathbf{2}\right)\end{array}\right)(10)$

$\left(\begin{array}{c}{\mathit{a}}_{\mathit{H}\mathbf{0}}\\ {\mathit{b}}_{\mathit{H}\mathbf{0}}\end{array}\right)=\left\{\begin{array}{c}\left(\begin{array}{c}\mathit{cos}\left({\mathit{k}}_{\mathit{c}}{\mathit{t}}_{\mathit{c}}/\mathbf{2}\right)\\ -\frac{{{\mathit{n}}_{\mathbf{1}}^{\mathbf{2}}\mathit{k}}_{\mathit{c}}}{{{\mathit{n}}_{\mathit{c}}^{\mathbf{2}}\mathit{k}}_{\mathbf{1}}}\mathit{sin}\left({\mathit{k}}_{\mathit{c}}{\mathit{t}}_{\mathit{c}}/\mathbf{2}\right)\end{array}\right),\frac{{\mathit{n}}_{\mathbf{1}}^{\mathbf{2}}{\mathit{k}}_{\mathbf{2}}}{{\mathit{n}}_{\mathbf{2}}^{\mathbf{2}}{\mathit{k}}_{\mathbf{1}}}<\mathbf{1}\\ \left(\begin{array}{c}\mathit{sin}\left({\mathit{k}}_{\mathit{c}}{\mathit{t}}_{\mathit{c}}/\mathbf{2}\right)\\ \frac{{{\mathit{n}}_{\mathit{c}}^{\mathbf{2}}\mathit{k}}_{\mathbf{1}}}{{{\mathit{n}}_{\mathbf{1}}^{\mathbf{2}}\mathit{k}}_{\mathit{c}}}\mathit{cos}\left({\mathit{k}}_{\mathit{c}}{\mathit{t}}_{\mathit{c}}/\mathbf{2}\right)\end{array}\right),\frac{{\mathit{n}}_{\mathbf{1}}^{\mathbf{2}}{\mathit{k}}_{\mathbf{2}}}{{\mathit{n}}_{\mathbf{2}}^{\mathbf{2}}{\mathit{k}}_{\mathbf{1}}}>\mathbf{1}\end{array}\right.(11)$

Finally, the mode dispersion equation can be obtained by the ratio between the coefficients. Although the guiding mechanisms are distinct, the TIR modes can be regarded as special modes confined by the Bragg reflection at the interfaces, i.e., n_eff > n₂, so the waveguide can still be modeled using the above derivations by substituting down converted frequencies [18]. In order to tailor BRW samples toward high conversion efficiencies, we perform numerical optimization on the thickness of each layer and its aluminium concentration in the BRW slab structures based on the 1D general eigen equation deduced, independent of whether the Bragg layers are perfect quarter-wavelength thick or not. The high modal overlap with degenerate type-II phase-matching process around 1,550 nm is set as the optimization goal. After that, the optimized structure contains a core Al_xcGa_1-xcAs layer with x_c = 0.13 and thickness of 230 nm, sandwiched in a Bragg stack made of alternative 127 nm high (x_a = 0.33) and 622 nm low (x_b = 0.76) index layers [35]. The corresponding refractive indices are extrapolated from Ref. [36]. However, optimizing the modes of BRWs to remain phase matched with TIR modes is not straightforward, as an imperfection of the fabrication process may increase the absorption of the BRW modes when it approaches the core bandgap. Therefore, the effects of refractive index (aluminium concentration) change to the core layer need to be quantified. The influence of core layer aluminium concentration on the absorption wavelength of core layer and phase matching processes as well as modal overlap in type-II process is shown in Figure 1A. It shows that with the increase of x_c, the absorption wavelength and modal overlap decrease. The PM wavelength decreases slightly at first and then increases. When the absorption wavelength is close to the PM wavelength, the overlap is maximum. This is associated with bringing the operating point of the device closer to the band gap in Al_xcGa_1-xcAs, which increases the confinement of the BRW modes. To avoid the photon-absorption may be incurred by the uncertainty of molecular beam epitaxy (MBE) process while maintaining a large modal overlap, we respectively choose x_c = 0.17, x_a = 0.28 and x_b = 0.72 in fabricating our real sample. The sample is grown along the [001] crystal axis with a width of 5.3 μm and an etching deep of 4.17 μm. The cross-sections of the proposed structure are shown in Figures 1B,C, with the loss contours are distributions of the TE (B) and TM (C) BRW modes which are calculated by using the finite-element method (commercial software COMSOL simulation). By using the analytical equation deduced above, the dispersion diagrams of the three parametric processes for interacting modes are shown in Figure 2. The designed PM wavelengths are between 1,540 nm and 1,570 nm, and the type-II operating point is around 1,550 nm which can be used for generating polarization entanglement directly due to the little material birefringence [28].

FIGURE 1

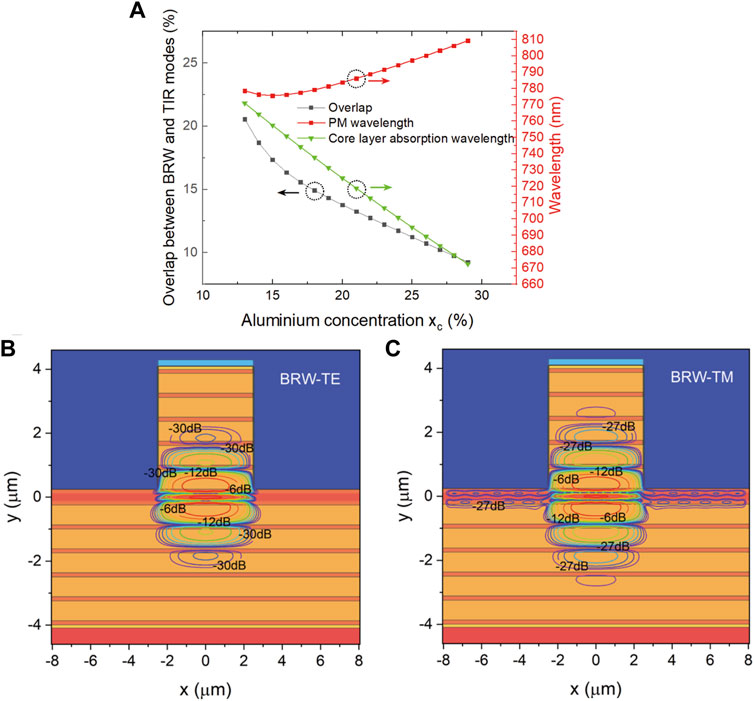
FIGURE 1. (A) The dependence of overlap factor and PM wavelength between pump and down converted fields on core layer aluminium concentration. The contours are the calculated TE (B) and TM (C) BRW modes.

FIGURE 2

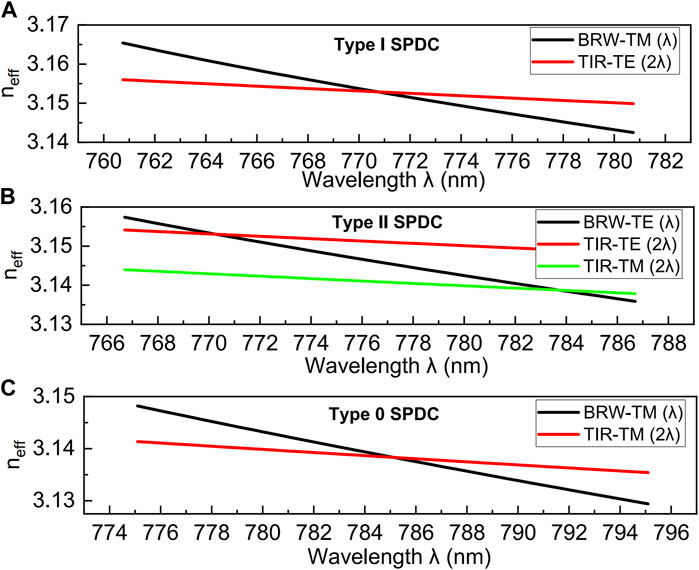
FIGURE 2. Dispersion curves of BRW and TIR modes for three parametric processes: Type-I (A), Type-II (B) and Type-0 (C).

3 Experiment

In experiments, we fabricate a 2 mm-long AlGaAs BRW ridge waveguide with six periods upper (low) mirrors through MBE and wet chemical etching. The temperature of the waveguide can be stabilized by a temperature controller. To find the PM wavelengths, we first test the three PM processes of the sample by means of the second harmonic generation (SHG). A 0.1 mW tunable continuous semiconductor laser with a linewidth of 10 kHz is used as the fundamental light (FL). The FL is connected to a fiber optic beam splitter, one of which (1% power) goes to the optical spectrum analyzer (OSA) for wavelength detection and another port (99% power) is connected to the optical fiber polarization controller (FPC) and enters the waveguide through port a. The SHG light is collected at port b and entered into a single-photon detector with about 70% detection efficiency. The total fiber-chip-fiber loss is 8 dB. In our experiment, the highly versatile modal birefringence in BRW enabled the phase-matching of the three modalities [20, 24, 37] namely type-0: TM_ω + TM_ω→TM_2ω, type-I: TE_ω + TE_ω→TM_2ω and type-II: TE_ω + TM_ω→TE_2ω. By varying the wavelength and polarization of FL, we record the SHG output power as a function of FL wavelength. As the results shown in Figure 3A, when the FL wavelength is tuned to 1,580.6 nm, a maximum SHG output power of 4.029 pW is obtained. Three resonance features at 1,551.7 nm, 1,559.2 nm and 1,580.6 nm, denote the pump wavelengths at which type-I, type-II and type-0 PM conditions are satisfied, respectively [24]. The discrepancy between theoretical and experimental results are mainly because the lateral confinement and fabrication errors. In addition, we measure the dependence of PM wavelength on temperature by varying the sample temperature from 17.5°C to 28°C for type-II process as an example. The operating wavelength is almost linearly increased from 1,558.5 nm to 1,560.75 nm, as shown by the black squares in Figure 3B. The line is a guide to the eye.

FIGURE 3

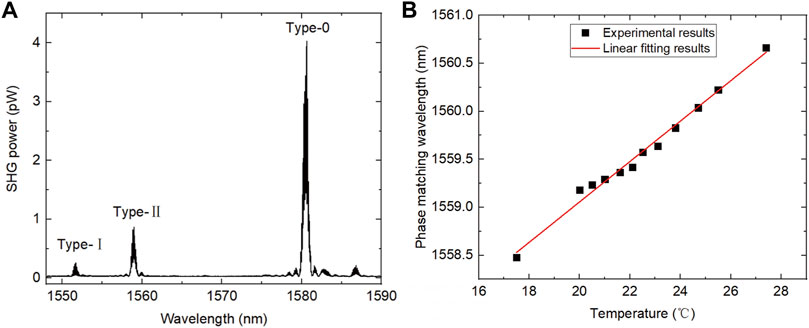
FIGURE 3. (A) The SHG tuning curves of the three PM schemes as a function of the FL wavelength. (B) The dependence of type-II PM wavelength on sample temperature. The line is a guide to the eye.

Following the SHG results, we demonstrate different types of SPDC processes utilizing a wavelength-tunable laser around 775 nm. As shown in Figure 4, the pump light is coupled into the waveguide at port c after passing through FPC2 to optimize the pump polarization. Fixing the temperature of waveguide at 20.08°C, we expect to obtain the required three kinds of frequency degenerate SPDC processes under different pump wavelengths. The signal and idler photons will be collected by port d, filtered by off-chip long wavelength pass filters to remove the pump, and then enter a coarse wavelength division multiplexing (CWDM) with an extinction ratio of ∼40 dB and a bandwidth of 18 nm for separation. Finally, the photons are detected by two InGaAs semiconductor single photon detectors with 10% detection efficiency, 1.2 kHz dark count rates, and a 5.2 μs dead time. The detector electrical signals are collected by a time-to-digital converter (TDC). The correlation is measured as the coincidence counts (C.Cs) between entangled photons as a function of the arrival time difference with 2 minutes integration time and a coincidence window of 1 ns? In the diagram of Figures 5A–C, the three types SPDC results are shown. The pump power is set to be 0.57 mW before coupling into the chip. The generation rate of type-0 and II processes are about 101 Hz and 62 Hz, leading to a brightness of 4.35*10⁷ pairs/s and 1.108*10⁷ pairs/s, respectively, which are higher than those reported in Refs. [28, 29]. The uncorrelated background is due to the high noise generation rate. Potential noise sources in our system include the dark counts of the detectors and broadband photoluminescence [38]. Figure 5D illustrates the C.Cs and coincidences-to-accidentals ratio (CAR) as a function of the input pump power for type-0 process. The counts constantly increase when the input power is low, because the efficiency of SPDC scales linearly with the pump power. As the power increases, the C.Cs are saturated and the CAR decreases which results from the influence of increasing accidental C.Cs. The CAR is limited by the dark counts of the detectors at low power, and by the detrimental photoluminescence at high power. The SHG and SPDC results imply that this BRW is potential for cascaded up- and down-conversion processes by virtue of off-the-shelf telecom optical components [39–41].

FIGURE 4

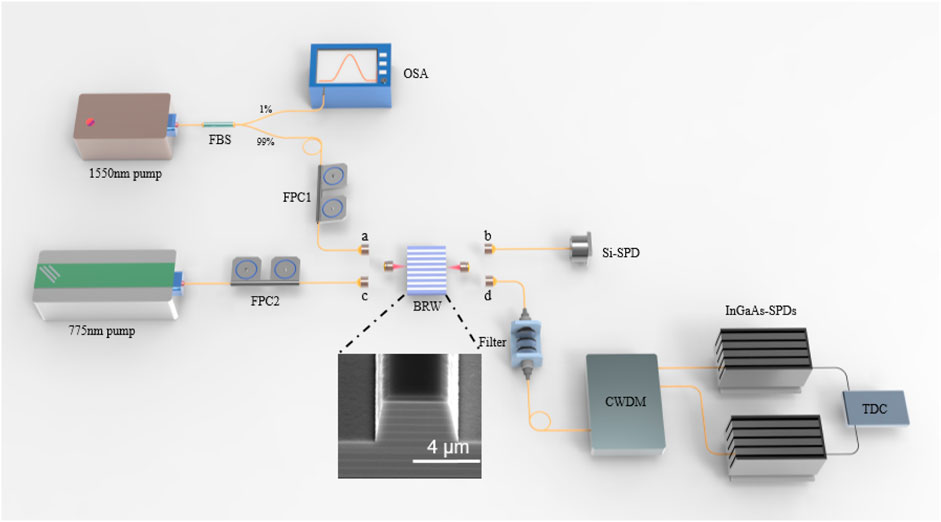
FIGURE 4. Schematic of the experiment setup for SHG and SPDC. Inset shows the scanning electron microscope image of the fabricated BRW sample. Abbreviations of components: BRW, Bragg reflection waveguide; FBS, fiber optic beam-splitter; FPC, fiber polarization controller; OSA, Optical Spectrum Analyzer; CWDM, Coarse wavelength division multiplexing; SPD, single photon detector, TDC, time-to-digital converter.

FIGURE 5

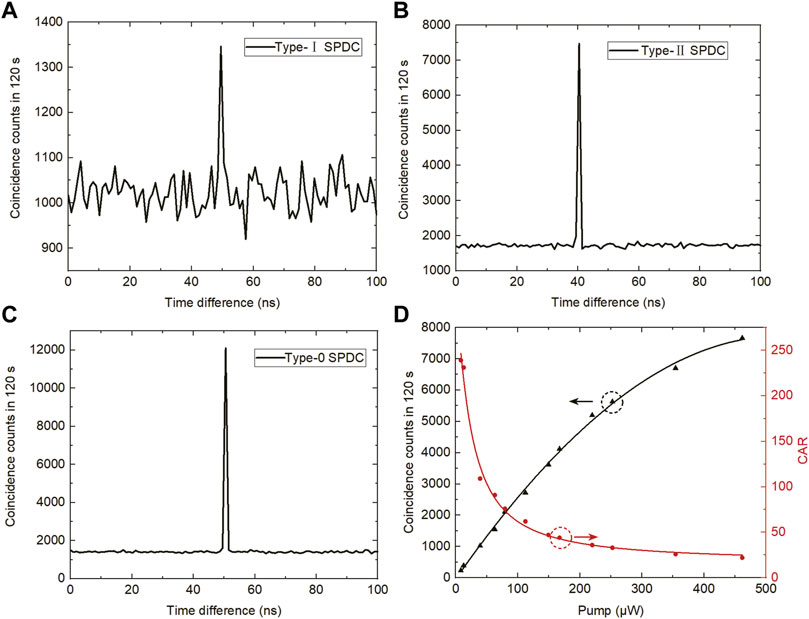
FIGURE 5. Histograms of the coincidence measurements for type-I (A), type-II (B) and type-0 (C) (D) Coincidence counts of type 0 as a function of the average input pump power. The points are experimental data, and the curves are fits. All the data are raw counts and no background counts subtracted.

To illustrate the broadband SPDC in the sample, we measure the continuous emission spectra of type-II (Figure 6A) and type-0 (Figure 6B) processes for the signal and idler photons by using a multi-channel 100 GHz WDM (black points in 6A and 6B) or a tunable filter (red points in 6A). Since the insertion losses are different for each channel, we measure them independently and infer counts obtained with the tunable filter by referring to the WDM’s loss. We only record a subset of the data due to the limited filters within the transmission window. However, the energy conservation constraint of the SPDC process implies that the spectral extent should be symmetric around its degenerate wavelength, which implies a 3-dB spectral bandwidth of 105 nm and 67 nm for type-II and type-0 processes respectively. The solid lines are simulated results and the uncertainties denote the standard deviations from the Poisson distribution of the raw photon counts. This broadband source can be used for multiuser quantum network by carving the spectrum into a series of slices and multiplexing them [42–45].

FIGURE 6

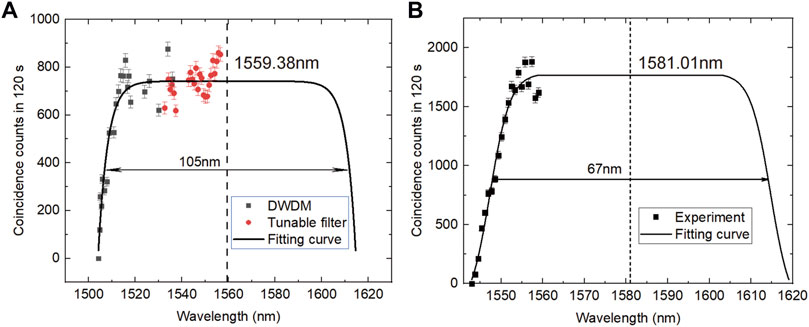
FIGURE 6. Experimental and simulated spectral brightness of the broadband type-Ⅱ (A) and type-0 (B) SPDC.

4 Conclusion

In conclusion, we have derived general expressions for eigen equation in a one-dimensional BRW independent of whether each cladding layer has an ideal quarter-wavelength thickness or not. The analytical results are used to simulate three types of SPDC processes with high modal overlap. Experimentally, we fully characterize the light source and demonstrate broad bandwidth entangled photons over more than 65 nm (100 nm) for type-0 (II) processes. With the advancements of fabrication technology, it is possible to integrate laser and wavelength demultiplexing/multiplexing module onto a single chip, providing a turn-key solution for the large-scale quantum communication network.

Data availability statement

The raw data supporting the conclusions of this article will be made available by the authors, without undue reservation.

Author contributions

BN and LL proposed this idea. LL and YL wrote the original manuscript. BN, CQ, XJ, and LL performed the experiment. CW and YL provided experimental assistance and suggestions. YK, TC and LL supervised the project.

Funding

This research is supported by the National Natural Science Foundation of China (Grant No. 12274233).

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

1. Zhong HS, Wang H, Deng YH, Chen MC, Peng LC, Luo YH, et al. Quantum computational advantage using photons. Science (2020) 370:1460–3. doi:10.1126/science.abe8770

PubMed Abstract | CrossRef Full Text | Google Scholar

2. Madsen LS, Laudenbach F, Askarani MF, Rortais F, Vincent T, Bulmer JFF, et al. Quantum computational advantage with a programmable photonic processor. Nature (2022) 606(7912):75–81. doi:10.1038/s41586-022-04725-x

PubMed Abstract | CrossRef Full Text | Google Scholar

3. Pan J-W, Chen ZB, Lu CY, Weinfurter H, Zeilinger A, Zukowski M. Multiphoton entanglement and interferometry. Rev Mod Phys (2012) 84(2):777–838. doi:10.1103/revmodphys.84.777

CrossRef Full Text | Google Scholar

4. Huang YF, Liu BH, Peng L, Li YH, Li L, Li CF, et al. Experimental generation of an eight-photon Greenberger-Horne-Zeilinger state. Nat Commun (2011) 2:546. doi:10.1038/ncomms1556

PubMed Abstract | CrossRef Full Text | Google Scholar

5. Kuzucu O, Fiorentino M, Albota MA, Wong FNC, Kartner FX. Two-photon coincident-frequency entanglement via extended phase matching. Phys Rev Lett (2005) 94(8):083601. doi:10.1103/physrevlett.94.083601

PubMed Abstract | CrossRef Full Text | Google Scholar

6. Megidish E, Halevy A, Eisenberg HS, Ganany-Padowicz A, Habshoosh N, Arie A. Compact 2D nonlinear photonic crystal source of beamlike path entangled photons. Opt Express (2013) 21(6):6689–96. doi:10.1364/oe.21.006689

PubMed Abstract | CrossRef Full Text | Google Scholar

7. Wang XL, Cai XD, Su ZE, Chen MC, Wu D, Li L, et al. Quantum teleportation of multiple degrees of freedom of a single photon. Nature (2015) 518(7540):516–9. doi:10.1038/nature14246

PubMed Abstract | CrossRef Full Text | Google Scholar

8. Wang J, Sciarrino F, Laing A, Thompson MG. Integrated photonic quantum technologies. Nat Photon (2019) 14(5):273–84. doi:10.1038/s41566-019-0532-1

CrossRef Full Text | Google Scholar

9. Meyer-Scott E, Silberhorn C, Migdall A. Single-photon sources: Approaching the ideal through multiplexing. Rev Sci Instrum (2020) 91(4):041101. doi:10.1063/5.0003320

PubMed Abstract | CrossRef Full Text | Google Scholar

10. Adcock JC, Bao J, Chi Y, Chen X, Bacco D, Gong Q, et al. Advances in silicon quantum photonics. IEEE J Selected Top Quan Electron (2021) 27(2):1–24. doi:10.1109/jstqe.2020.3025737

CrossRef Full Text | Google Scholar

11. Lu L, Zheng X, Lu Y, Zhu S, Ma X. Advances in chip-scale quantum photonic technologies. Adv Quan Tech (2021) 4(12):2100068. doi:10.1002/qute.202100068

CrossRef Full Text | Google Scholar

12. Pelucchi E, Fagas G, Aharonovich I, Englund D, Figueroa E, Gong Q, et al. The potential and global outlook of integrated photonics for quantum technologies. Nat Rev Phys (2021) 4(3):194–208. doi:10.1038/s42254-021-00398-z

CrossRef Full Text | Google Scholar

13. Feng L-T Observation of nonlocal quantum interference between the origins of a four-photon state in a silicon chip (2021). arXiv preprint arXiv: 2103. 14277v1.

Google Scholar

14. Qiang X, Zhou X, Wang J, Wilkes CM, Loke T, O’Gara S, et al. Large-scale silicon quantum photonics implementing arbitrary two-qubit processing. Nat Photon (2018) 12(9):534–9. doi:10.1038/s41566-018-0236-y

CrossRef Full Text | Google Scholar

15. Lu L, Xia L, Chen Z, Chen L, Yu T, Tao T, et al. Three-dimensional entanglement on a silicon chip. npj Quan Inf (2020) 6(1):30. doi:10.1038/s41534-020-0260-x

CrossRef Full Text | Google Scholar

16. Chen X, Deng Y, Liu S, Pramanik T, Mao J, Bao J, et al. A generalized multipath delayed-choice experiment on a large-scale quantum nanophotonic chip. Nat Commun (2021) 12(1):2712. doi:10.1038/s41467-021-22887-6

PubMed Abstract | CrossRef Full Text | Google Scholar

17. Yan Z, He H, Liu H, Iu M, Ahmed O, Chen E, et al. χ²-based AlGaAs phase sensitive amplifier with record gain, noise, and sensitivity. Optica (2022) 9:56–60. doi:10.1364/optica.446674

CrossRef Full Text | Google Scholar

18. West BR, Helmy AS. Analysis and design equations for phase matching using Bragg reflector waveguides. IEEE J Selected Top Quan Electron (2006) 12(3):431–42. doi:10.1109/jstqe.2006.872733

CrossRef Full Text | Google Scholar

19. Helmy AS, Bijlani B, Abolghasem P. Phase matching in monolithic Bragg reflection waveguides. Opt Lett (2007) 32(16):2399–401. doi:10.1364/ol.32.002399

PubMed Abstract | CrossRef Full Text | Google Scholar

20. Abolghasem P, Dongpeng Kang , Bijlani BJ, Helmy AS. Monolithic photonics using second-order optical nonlinearities in multilayer-core Bragg reflection waveguides. IEEE J Selected Top Quan Electron (2012) 18(2):812–25. doi:10.1109/jstqe.2011.2135841

CrossRef Full Text | Google Scholar

21. Zhukovsky SV, Helt LG, Kang D, Abolghasem P, Helmy AS, Sipe JE. Generation of maximally-polarization-entangled photons on a chip. Phys Rev A (2012) 85(1):013838. doi:10.1103/physreva.85.013838

CrossRef Full Text | Google Scholar

22. Zhukovsky SV, Helt LG, Kang D, Abolghasem P, Helmy AS, Sipe J. Analytical description of photonic waveguides with multilayer claddings: Towards on-chip generation of entangled photons and Bell states. Opt Commun (2013) 301-302:127–40. doi:10.1016/j.optcom.2013.03.039

CrossRef Full Text | Google Scholar

23. Zhukovsky SV, Helt LG, Abolghasem P, Kang D, Sipe JE, Helmy AS. Bragg reflection waveguides as integrated sources of entangled photon pairs. J Opt Soc Am B (2012) 29(9):2516–23. doi:10.1364/josab.29.002516

CrossRef Full Text | Google Scholar

24. Valles A, Hendrych M, Svozilik J, Machulka R, Abolghasem P, Kang D, et al. Generation of polarization-entangled photon pairs in a Bragg reflection waveguide. Opt Express (2013) 21(9):10841–9. doi:10.1364/oe.21.010841

PubMed Abstract | CrossRef Full Text | Google Scholar

25. Orieux A, Versteegh MAM, Jons KD, Ducci S. Semiconductor devices for entangled photon pair generation: A review. Rep Prog Phys (2017) 80(7):076001. doi:10.1088/1361-6633/aa6955

PubMed Abstract | CrossRef Full Text | Google Scholar

26. Pressl B, Laiho K, Chen H, Gunthner T, Schlager A, Auchter S, et al. Semi-automatic engineering and tailoring of high-efficiency Bragg-reflection waveguide samples for quantum photonic applications. Quan Sci Technol (2018) 3(2):024002. doi:10.1088/2058-9565/aaa2a2

CrossRef Full Text | Google Scholar

27. Xie X, Chi X, Cui K, Hu X. Design and simulations of an electrically injected bragg-reflection-waveguide photon-pair source near 1.3-micrometer wavelength. IEEE J Selected Top Quan Electron (2018) 24(6):1–9. doi:10.1109/jstqe.2018.2865439

CrossRef Full Text | Google Scholar

28. Horn RT, Kolenderski P, Kang D, Abolghasem P, Scarcella C, Frera AD, et al. Inherent polarization entanglement generated from a monolithic semiconductor chip. Sci Rep (2013) 3:2314. doi:10.1038/srep02314

PubMed Abstract | CrossRef Full Text | Google Scholar

29. Autebert C, Bruno N, Martin A, Lemaitre A, Carbonell CG, Favero I, et al. Integrated AlGaAs source of highly indistinguishable and energy-time entangled photons. Optica (2016) 3(2):143. doi:10.1364/optica.3.000143

CrossRef Full Text | Google Scholar

30. Maltese G, Amanti MI, Appas F, Sinnl G, Lemaitre A, Milman P, et al. Generation and symmetry control of quantum frequency combs. npj Quan Inf (2020) 6(1):13. doi:10.1038/s41534-019-0237-9

CrossRef Full Text | Google Scholar

31. Autebert C, Trapateau J, Orieux A, Lemaitre A, Gomez-Carbonell C, Diamanti E, et al. Multi-user quantum key distribution with entangled photons from an AlGaAs chip. Quan Sci Technol (2016) 1(1):01LT02. doi:10.1088/2058-9565/1/1/01lt02

CrossRef Full Text | Google Scholar

32. Appas F, Baboux F, Amanti MI, Lemaitre A, Boitier F, Diamanti E, et al. Flexible entanglement-distribution network with an AlGaAs chip for secure communications. npj Quan Inf (2021) 7(1):118. doi:10.1038/s41534-021-00454-7

CrossRef Full Text | Google Scholar

33. Yang Q, Passow T. Non-ideal quarter-wavelength bragg-reflection waveguides for nonlinear interaction: Eigen equation and tolerance. Opt Lett (2020) 45(17):4742–5. doi:10.1364/ol.397198

PubMed Abstract | CrossRef Full Text | Google Scholar

34. West BR, Helmy AS. Properties of the quarter-wave Bragg reflection waveguide: Theory. J Opt Soc America B (2006) 23(6):1207. doi:10.1364/josab.23.001207

CrossRef Full Text | Google Scholar

35. Niu B, Jing X, Qian C, Wang C, Kong Y, Chen T, et al. High-efficiency non-ideal quarter-wavelength Bragg reflection waveguide for photon-pair generation. Results Phys (2023) 44:106137. doi:10.1016/j.rinp.2022.106137

CrossRef Full Text | Google Scholar

36. Gehrsitz S, Reinhart FK, Gourgon C, Herres N, Vonlanthen A, Sigg H. The refractive index of AlxGa1−xAs below the band gap: Accurate determination and empirical modeling. J Appl Phys (2000) 87(11):7825–37. doi:10.1063/1.373462

CrossRef Full Text | Google Scholar

37. Abolghasem P, Han J, Bijlani BJ, Helmy AS. Type-0 second order nonlinear interaction in monolithic waveguides of isotropic semiconductors. Opt Express (2010) 18(12):12681–9. doi:10.1364/oe.18.012681

PubMed Abstract | CrossRef Full Text | Google Scholar

38. Auchter S, Schlager A, Thiel H, Laiho K, Pressl B, Suchomel H, et al. Understanding photoluminescence in semiconductor Bragg-reflection waveguides. J Opt (2021) 23(3):035801. doi:10.1088/2040-8986/abd888

CrossRef Full Text | Google Scholar

39. Zhang Z, Yuan C, Shen S, Yu H, Zhang R, Wang H, et al. High-performance quantum entanglement generation via cascaded second-order nonlinear processes. npj Quan Inf (2021) 7(1):123. doi:10.1038/s41534-021-00462-7

CrossRef Full Text | Google Scholar

40. Hunault M, Takesue H, Tadanaga O, Nishida Y, Asobe M. Generation of time-bin entangled photon pairs by cascaded second-order nonlinearity in a single periodically poled LiNbO₃ waveguide. Opt Lett (2010) 35(8):1239–41. doi:10.1364/ol.35.001239

PubMed Abstract | CrossRef Full Text | Google Scholar

41. Arahira S, Namekata N, Kishimoto T, Inoue S. Experimental studies in generation of high-purity photon-pairs using cascaded χ⁽²⁾ processes in a periodically poled LiNbO₃ ridge-waveguide device. Opt Express (2012) 29(3):434–42. doi:10.1364/josab.29.000434

CrossRef Full Text | Google Scholar

42. Wengerowsky S, Joshi SK, Steinlechner F, Hubel H, Ursin R. An entanglement-based wavelength-multiplexed quantum communication network. Nature (2018) 564(7735):225–8. doi:10.1038/s41586-018-0766-y

PubMed Abstract | CrossRef Full Text | Google Scholar

43. Joshi SK, Aktas D, Wengerowsky S, Loncaric M, Neumann SP, Liu B, et al. A trusted node-free eight-user metropolitan quantum communication network. Sci Adv (2020) 6:eaba0959. doi:10.1126/sciadv.aba0959

PubMed Abstract | CrossRef Full Text | Google Scholar

44. Liu X, Yao X, Xue R, Wang H, Li H, Wang Z, et al. An entanglement-based quantum network based on symmetric dispersive optics quantum key distribution. APL Photon (2020) 5(7):076104. doi:10.1063/5.0002595

CrossRef Full Text | Google Scholar

45. Wen W, Chen Z, Lu L, Yan W, Xue W, Zhang P, et al. Realizing an entanglement-based multiuser quantum network with integrated photonics. Phys Rev Appl (2022) 18(2):024059. doi:10.1103/physrevapplied.18.024059

CrossRef Full Text | Google Scholar