Calibration of a collinear backscattering Mueller matrix imaging system

A collinear backscattering Mueller matrix (CBMM) imaging system has clear advantages in the detection of bulk biological tissues, which are highly scattering and depolarizing. Due to the double-pass configuration and noise in the system, the calibration of a collinear backscattering Mueller matrix imaging system is usually complex and of poor accuracy. In this work, we propose an alternative modified eigenvalue calibration method (ECM) based on the equivalent standard sample. For better noise suppression and higher calibration accuracy, we design the distribution of polarization states over the Poincaré sphere and solve for the parameters of equivalent standard samples by means of an optimization. Compared to other variants of the eigenvalue calibration method used in the double-pass system, the accuracy of the proposed method is improved by more than 40 times. The comparison results with the error model-based calibration methods indicate that the modified eigenvalue calibration method generally gives the best accuracy and precision, as well as the best reliability.

1 Introduction

The Mueller matrix, which describes the transformation of the state of polarization (SOP) of light, contains rich information about the microstructure and properties of an object [1–3]. As a non-invasive, non-contact, and label-free detection method, the Mueller matrix imaging technology has unique advantages in biomedical detection: it can provide extra information about the sample while being compatible with many existing optical systems, for example, microscopes and endoscopes [4]. Recently, the biomedical and clinical applications of the Mueller matrix imaging technique have attracted substantial attention [5, 6], such as the early detection of cancerous tissues [7–9].

Generally, a thin sample can be detected with a transmission Mueller matrix (TMM) imaging system [10], while a bulky sample which is highly scattering and depolarizing, is more appropriate for detection by a collinear backscattering Mueller matrix (CBMM) imaging system [11]. The calibration of a TMM system based on dual-rotating retarders is easy due to its simple optical system. One of the most popular calibration methods used to calibrate the TMM system is the analysis calibration method (ACM), which builds an error model with five main systemic errors and obtains the error values by the Fourier analysis method [12–14]. The calibration of a CBMM system is more complex due to the variety of error sources, for example, the parasitic polarization of the beam splitter also affects the SOP of light. In our previous work, to calibrate the CBMM system we proposed a numerical calibration method (NCM) that takes into account the parasitic polarization of the beam splitter and solves the system errors numerically by Levenberg–Marquardt (LM) algorithm [15]. However, the systematic error model-based calibration methods have the following drawbacks, they require a priori knowledge of the system and are prone to over-calibration when the systematic error model is overly complex.

Different from the error model-based calibration methods, the eigenvalue calibration method (ECM) does not require any priori information such as the polarization states produced in the system [16, 17]. As a general method for the calibration of Mueller matrix imaging systems, the ECM has shown an increase in popularity [18]. However, due to the complex double-pass configuration, the original ECM is not suitable for the calibration of the CBMM system and some modifications of the original ECM are necessary [19]. Besides, the ECM is inefficient in the case of low signal-to-noise ratio (SNR) since it assumes that there is no noise in the measurement system [20].

In this paper, we propose an alternative modified ECM for the CBMM system. Unlike other variants of the ECM, we simplify the double-pass calibration to a single-pass calibration by the mirror symmetry and the concept of the equivalent standard sample; it is much simpler in theory as it does not need to address issues such as matrix reciprocity and eigenvalue squaring. For better calibration performance, we optimize the distribution of analysis states over the Poincaré sphere taking into account the inherent constraints of polarization modulators, and calibrate the parameters of equivalent standard samples by means of an optimization. To compare the performance of the modified ECM and the error model-based calibration methods, a series of experiments with various samples are performed.

2 Materials and methods

2.1 Experimental setup

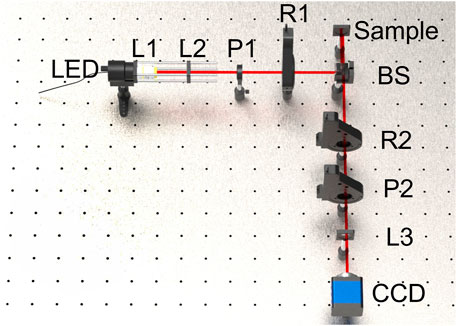
The optical path diagram of the CBMM system is shown in Figure 1. A LED (center wavelength = 610 nm and FWHM = 20 nm) is used as the light source in the system. The output beam from the LED is collimated by an objective lens (L1) and a convex lens (L2). P1 and P2 are linear polarizers (LPVISE100-A, 400–700 nm, Thorlabs, Inc., U.S.). R1 and R2 are zero-order quarter-wave plates (GCL-060402, 633 nm, Daheng, Optic, China). The polarization state generator (PSG) consists of a fixed polarizer (P1) and a rotating quarter-wave plate (R1), while the polarization state analyzer (PSA) consists of a rotating polarizer (P2) and a rotating quarter-wave plate (R2). Wave plates R1, R2 and polarizer P2 are driven by three servo motors (PRM1Z8E, Thorlabs, Inc., U.S.), respectively. The polarization-modulated beam is reflected by the sample at normal incidence after passing through a beam splitter (GCC-403102, Daheng, Optic, China), and then the backscattered light is imaged by a charged couple device (CCD) camera (PCO. panda 4.2, 16bit, Inc., Germany) after passing through the PSA and a low numerical aperture (NA) objective lens (L3).

FIGURE 1

FIGURE 1. Optical path diagram of the collinear backscattering Mueller matrix imaging system.

2.2 The modified eigenvalue calibration method

Previous studies on the eigenvalue calibration method in the double-pass system needed to consider the complex reciprocal relationship between the Mueller matrix of the reflection mirror and the Mueller matrix of the sample [19, 21]. In this work, we propose an alternative modified ECM that effectively simplifies the calibration theory by utilizing the mirror symmetry and equivalent standard samples.

In the absence of depolarization, the Mueller matrices of polarizers and wave-plates can be written uniformly as follows [22]:

$\begin{array}{c}M\left(\tau ,\theta ,\phi ,∆\right)=\tau R\left(-\theta \right)\left[\begin{array}{cccc}1& -\cos 2\phi & 0& 0\\ -\cos 2\phi & 1& 0& 0\\ 0& 0& \sin 2\phi \cos ∆& \sin 2\phi \sin ∆\\ 0& 0& -\sin 2\phi \sin ∆& \sin 2\phi \cos ∆\end{array}\right]R\left(\theta \right)\end{array}(1)$

where $\tau$ is the transmission coefficient, $\phi$ and $∆$ are ellipsometric parameters, $\theta$ stands for the azimuth angle, and $R\left(\theta \right)$ is the rotation matrix. Assuming that the observer is at the detector and looks in the direction from which the light is incoming, the counterclockwise direction of rotation is chosen as the positive direction of the azimuth angle $\theta$. In addition, it is necessary to assume that the light is reflected by a perfect flat mirror at normal incidence and the polarization properties of optical elements are independent of the direction of propagation of the light. The mirror Mueller matrix $M_m$ is actually the mirror transformation matrix satisfying $M_m{M}_m=E$, where $E$ stands for the identity matrix. It is obvious that any left rotation transformation can be equated to a right rotation transformation in mirror space, and vice versa. According to this simple property, the mirror transformation of an arbitrary Mueller matrix described by Eq. 1 can be written as follows,

$\begin{array}{c}{M}_{m}M\left(\tau ,\theta ,\phi ,∆\right)M_m=M\left(\tau ,-\theta ,\phi ,∆\right)\end{array}(2)$

Given the properties of mirror symmetry, the double-pass process for an arbitrary standard sample can be simplified to the left multiplication of Mueller matrix $M_m$ with an equivalent Mueller matrix $M^{\prime }$,

$\begin{array}{c}{M}^b\left(\tau ,-\theta ,\phi ,∆\right)M_m{M}^f\left(\tau ,\theta ,\phi ,∆\right)=M_m{M}^{\prime }\left({\tau }^{\prime },{\theta }^{\prime },{\phi }^{\prime },{∆}^{\prime }\right)\end{array}(3)$

where $M^f$ and $M^b$ represent the Mueller matrix of the forward and backward propagating path of a standard sample, respectively. The parameters of the equivalent Mueller matrix satisfy the following relationships: ${\tau }^{\prime }={\tau }^2\left(1+{\mathit{cos}}^{2}2\phi \right)$, ${\theta }^{\prime }=\theta$, ${\phi }^{\prime }=1/2\mathit{asin}\left[\left(1-{\mathit{cos}}^{2}2\phi \right)/\left(1+{\mathit{cos}}^{2}2\phi \right)\right]$, and ${∆}^{\prime }=2∆$, which means that the equivalent standard sample has the same azimuth angle as the standard sample and the double phase retardance. It is clear that Eq. 3 transforms the double-pass process into a single-pass process by using the equivalent Mueller matrix, hence in the next theoretical analysis only the equivalent standard sample needs to be considered.

Similar to the calibration process for single-pass system, air, $\pm 45°$ linear polarizers, and a $30°$ $\lambda /8$ wave plate whose equivalent Mueller matrix is a quarter-wave plate are chosen as the four standard samples. The detected intensity matrix $I_i$ of the $i^{th}$ equivalent standard sample can be described by the following equation,

$\begin{array}{c}{I}_i=A{M}_m{M}_i^{\prime }W\end{array}(4)$

where W and A are the polarization generation matrix and the polarization analysis matrix, respectively, and $M_i^{\prime }$ stands for the equivalent Mueller matrix of the $i^{th}$ standard sample. Obviously, the equivalent Mueller matrix of air is still an identity matrix, therefore $I_1$ can be simplified as,

$\begin{array}{c}{I}_1=A{M}_{m}W\end{array}(5)$

Define matrix $C_i$ as follows:

$\begin{array}{c}{C}_i=I_1^{†}{I}_i=W^{†}{M_m}^{†}{A}^{†}A{M}_m{M}_i^{\prime }W=W^{†}{M}_i^{\prime }W\end{array}(6)$

where superscript ‘†’ denotes the Moore-Penrose pseudo-inverse. Notice that $C_i$ and $M_i^{\prime }$ are similar matrices in this modified ECM, which means that they share the same eigenvalues. Hence, it is possible to partially reconstruct the four equivalent Mueller matrices using the following eigenvalue relationships [16],

$\begin{array}{c}{\lambda }_1=2{\tau }_i^{\prime }si{n}^2\left({\phi }_i^{\prime }\right),{\lambda }_2=2{\tau }_i^{\prime }co{s}^2\left({\phi }_i^{\prime }\right),\end{array}$

$\begin{array}{c}{\lambda }_3={\tau }_i^{\prime }\mathit{sin}\left(2{\phi }_i^{\prime }\right)\mathit{exp}\left(i{\mathit{\Delta }}_i^{\prime }\right),{\lambda }_4={\tau }_i^{\prime }\mathit{sin}\left(2{\phi }_i^{\prime }\right)\mathit{exp}\left(-i{\mathit{\Delta }}_i^{\prime }\right)\end{array}(7)$

where ${\lambda }_i$ stands for the eigenvalue of matrix $C_i$. Nevertheless, it is found that the reconstruction of the equivalent Mueller matrices by Eq. 7 may be inefficient in the actual experiment, because the process of computing ratios of eigenvalues is highly noise sensitive. An optimization algorithm is introduced in the next section to exactly reconstruct each equivalent Mueller matrix, and the results given by Eq. 7 can be used as a starting point for the optimization algorithm.

Left multiplying Eq. 6 on both sides by matrix W, one obtains:

$\begin{array}{c}{M}_i^{\prime }W-W{C}_i=0\end{array}(8)$

which is in the form of the Sylvester equation [18, 23]. Using the vec operator [24] and the Kronecker product ($\otimes$) [25], Eq. 8 can be rewritten as follows,

$\begin{array}{c}\left(E\otimes M_i^{\prime }-{C_i}^T\otimes E\right)vec\left(W\right)=H_{i}vec\left(W\right)=0\end{array}(9)$

where the superscript ‘T’ represents the transpose. To uniquely determine the $vec\left(W\right)$, a positive semidefinite Hermitian matrix L is constructed by using the $H_i$ matrix of each equivalent standard sample,

$\begin{array}{c}Lvec\left(W\right)=\left({{H_1}^{T}H}_1+{{H_2}^{T}H}_2+{{H_3}^{T}H}_3+{H_4}^T{H}_4\right)vec\left(W\right)=0\end{array}(10)$

Theoretically, the matrix L should only have one null eigenvalue and the corresponding eigenvector is $vec\left(W\right)$. Once polarization generation matrix W is determined, polarization analysis matrix A can be easily obtained by the pseudo-inverse matrix of W as follows:

$\begin{array}{c}A=I_1{W}^{†}{M}_m^{†}\end{array}(11)$

After calibration, the backscattering Mueller matrix of an arbitrary sample can be calculated directly from the detected intensity matrix of sample ($I_{sample}$) as shown below:

$\begin{array}{c}{M}_{sample}=A^{†}{I}_{sample}{W}^{†}\end{array}(12)$

2.3 Optimization of the modified ECM

The ECM assumes that all the Mueller matrices of standard samples are perfectly known. However, due to noise in the system, the reconstruction of the equivalent Mueller matrices by calculating the ratios of eigenvalues becomes inefficient; in fact, even if the whole system is perfectly known, the noise still causes the SOP of light to deviate from the theoretical value, thus decreasing the calibration performance. For higher calibration accuracy, two optimizations for the modified ECM are introduced: designing a reasonable polarization state analyzer (PSA) to restrain noise and calculating the parameters of the equivalent Mueller matrices by a noise insensitive method.

Relevant studies have shown that the optimization of analysis states over the Poincaré sphere can be described by the spherical-2 designs [26]. Considering each row of the $N\times 4$ (N $\ge 4$) matrix A as a point on the surface of Poincaré sphere, the regular tetrahedron (N = 4), the octahedron (N = 6), the cube (N = 8) are well-known examples of spherical-2 designs [27]. Nevertheless, the polarization modulation module of a CBMM system based on dual-rotating retarders is usually composed of a fixed polarizer and a rotating quarter-wave plate, which results that the modulated polarization states cannot cover the entire sphere but only form an 8-shaped curve on the surface of Poincaré sphere. In addition, a non-ideal quarter wave plate causes the 8-shaped curve incapably crossing the two poles of Poincaré sphere. In the experiment, the phase retardance of the quarter-wave plate used in the PSA is approximately 96°. Taking into account the inherent limitations of polarization modulators, we design the distribution of polarization states on the surface of Poincaré sphere for a fixed polarizer (FP) based PSA and a rotating polarizer (RP) based PSA, respectively.

Two quantitative indicators the condition number (CN) and the equally weighted variance (EWV) are used to estimate the performance of PSA [28, 29],

$CN=\frac{{\mu }_0}{{\mu }_3},$

$\begin{array}{c}EWV={\displaystyle \sum }_{j=0}\frac{1}{{{\mu }_j}^2},j=0,1,2,3\end{array}(13)$

where the ${\mu }_j$ is the singular value of a matrix A. Theoretically, the optimal distribution of polarization states with constraints on the surface of Poincaré sphere can still be obtained by minimizing the CN or EWV with the genetic algorithm (GA) [30]. Considering the two constraints of a fixed polarizer and a non-ideal waveplate, part of the optimal modulation frames for a FP-based PSA and a RP-based PSA are shown in Figure 2. It is found that the optimal results given by the CN and EWV are consistent with each other. For a FP-based PSA, the optimal frames are irregular polyhedra with small volumes since the modulable polarization states are restricted to the 8-shaped curve on the surface of Poincaré sphere, as shown in Figures 2A–C. And for a RP-based PSA, the polarization states in the polar regions on Poincaré sphere become unmodifiable as the phase retardance of the quarter-wave plate deviates from 90°, as shown in Figures 2D–F. Generally, the influence of a non-ideal quarter wave plate on the optimal results is insignificant, the optimal modulation frames are still inscribed regular polyhedra with only the optimal frame for RP-6 being slightly tilted.

FIGURE 2

FIGURE 2. (A–C) Optimal modulation frames of a FP based PSA for N = 4, 6, 8, (D–F) optimal modulation frames of a RP based PSA for N = 4, 6, 8.

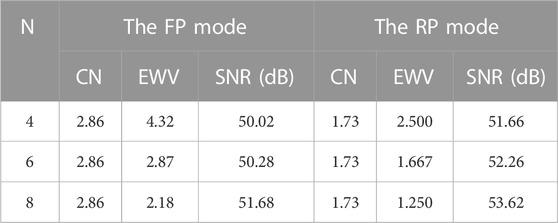
To compare the performance of different optimal modulation frames in the Mueller matrix measurements, a homogeneous wave plate is used as the sample and its Mueller matrix image is measured under different polarization analysis modes. Then the phase retardance image of the sample for each of optimal modulation frames is calculated by Mueller matrix polar decomposition (MMPD) method, respectively [31]. The SNR calculated for each phase retardance image is shown in Table 1. The CNs of the RP mode can reach $\sqrt{3}$, which is considered as the theoretical minimum CN for an optimal PSA [32], while the CNs of the FP mode cannot reach this limit due to the inherent constraint of the FP mode. For the same N, the optimal modulation frame of the RP mode has smaller optimization indicators, i.e., the CN and the EWV, and a higher SNR, thanks to the higher degree of freedom of the RP mode. The EWV decreases as N increases while the CN is independent of N, because the CN only considers the ratio of the largest and smallest singular values of a matrix A whereas the EWV takes into account the effect of all singular values. As only the EWV can be used to estimate the performance of PSA in the presence of Poisson noise [33], it can be seen that optimizing the EWV is effective in improving the SNR of the measurement results despite the fact that the CN remains the same, which indicates that the EWV is a better indicator. More importantly, Table 1 proves that optimizing the distribution of polarization states on the surface of Poincaré sphere can effectively suppress noise and improve the SNR of measurement results, even under an optimally constrained condition.

TABLE 1

TABLE 1. The SNRs of measurement results in different configurations.

In the previous calibration study, the ellipsometric parameters of standard samples are obtained by calculating the ratios of the eigenvalues of the matrix $C_i$ according to Eq. 7. Nevertheless, due to noise in the system, it is found that such a Mueller matrix reconstruction method for equivalent standard samples is inaccurate; especially the transmission coefficient ${\tau }_i^{\prime }$ and the retardance ${\Delta }_i^{\prime }$ are calculated with poor accuracy. Assuming that the transmission coefficients of the $\pm 45°$ linear polarizers are the same, i.e., ${\tau }_2^{\prime }={\tau }_3^{\prime }$, and their phase retardances can be ignored, i.e., ${{∆}_2^{\prime }=∆}_3^{\prime }=0$, there are only 6 parameters of equivalent standard samples that need to be accurately calibrated: one phase retardance ${\Delta }_4^{\prime }$, two transmission coefficients ${\tau }_2^{\prime }$ and ${\tau }_4^{\prime }$, and three azimuth angles ${\theta }_2$, ${\theta }_3$ and ${\theta }_4$. In the absence of noise, if all parameters of equivalent standard samples are correct, all the eigenvalues of the Hermitian matrix L are non-zero except one; on the other hand, if the reconstruction of the equivalent standard samples is inaccurate, the system has only a trivial solution and all the eigenvalues of L are nonzero [16]. Owing to noise in the system, the minimum eigenvalue of the system is no longer zero, however the eigenvalues still satisfy the following relationship that the more accurately the equivalent standard samples are reconstructed, the smaller the minimum eigenvalue of L is with respect to the 15 other eigenvalues [16]. Therefore, it is possible to calculate the 6 parameters of equivalent standard samples by means of an optimization with the result given by Eq. 7 as a starting point. Similar study has shown that the reconstruction of matrices by means of an optimization has better noise resistance than the direct calculation of the ratios of eigenvalues [20]. In the modified ECM, we adopt the following fitness function,

$\begin{array}{c}f=\frac{{\lambda }_{16}\left({\tau }_2^{\prime },{\tau }_4^{\prime },{\theta }_2,{\theta }_3,{\theta }_4,{\Delta }_4^{\prime }\right)}{{\lambda }_{15}\left({\tau }_2^{\prime },{\tau }_4^{\prime },{\theta }_2,{\theta }_3,{\theta }_4,{\Delta }_4^{\prime }\right)}\end{array}(14)$

where ${\lambda }_{16}$ is the smallest eigenvalue and ${\lambda }_{15}$ is the second smallest eigenvalue of matrix L, respectively. The fitness function can be easily solved by various optimization algorithms such as the genetic algorithm. Hence, the Mueller matrix reconstruction for equivalent standard samples is transformed from calculating the ratios of the eigenvalues of the matrix $C_i$ to an overall optimization for the matrix L.

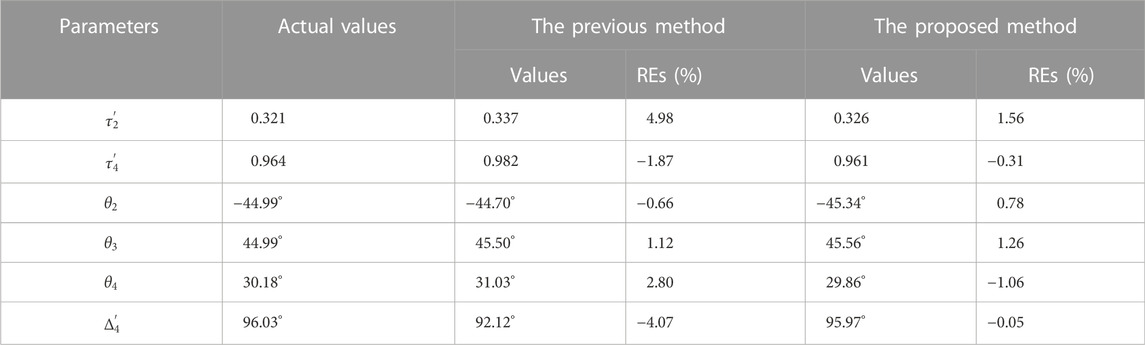
For the same set of experimental data, we compared the accuracy and relative error (RE) of the parameters of equivalent standard samples calculated by different methods, as shown in Table 2. It can be seen that the RE calculated by the previous method is as high as 5%, while the RE calculated by means of an optimization is less than 1.6%, only 1/3 of the former. In other words, the accuracy of the proposed method to reconstruct the Mueller matrix of the equivalent standard sample is three times that of the previous method.

TABLE 2

TABLE 2. Parameters of equivalent standard samples calculated by different methods.

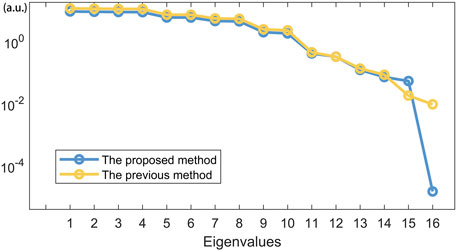
The accuracy of the equivalent standard sample has a direct impact on the final accuracy of the calibration. The comparison results of the eigenvalues of Matrix L calculated with different methods are shown in Figure 3. Thanks to the more accurate Mueller matrices of equivalent standard samples, the minimum eigenvalue of the proposed method is 1.45E-05, which is two orders of magnitude lower than that of the previous method. In ECM, the error estimator $\epsilon =\sqrt{{\lambda }_{16}/{\lambda }_{15}}$ is commonly used to assess the actual relative error of the entire system after calibration [31]. The error estimator $\epsilon$ of the previous method is 0.72, while that of the new method is 0.016, which also means that the calibration accuracy of the proposed method is more than 40 times higher than that of the previous method.

FIGURE 3

FIGURE 3. Comparison of the eigenvalues calculated by different methods.

3 Results and discussion

To compare the calibration performance of the modified ECM with the error model-based methods such as the ACM and NCM, we measured several samples including a polarizer, a wave plate, and a well-aligned silk sample. For the modified ECM, we adopt the RP-8 polarization state analysis mode and reconstruct the Mueller matrices of equivalent standard samples by means of an optimization with the genetic algorithm. For the ACM and NCM, the quarter-wave plates in PSG and PSA rotate synchronously with a fixed ratio of angular velocity 1:5 and a total of 30 measurements are required to calculate the Mueller matrix image of the sample. During calibration with the ACM and the NCM, the two polarizers in the PSG and PSA are fixed, in other words the PSA is in the FP mode. Since the transmission Mueller matrices of transparent samples can be accurately measured in a calibrated TMM system, their true equivalent Mueller matrices which can be calculated by Eq. 3 are in fact well-known, namely $M_{true}$. Therefore, it is simple to compare the differences of the measured equivalent Mueller matrices of samples, i.e., $M_{measured}$ by different calibration methods with respect to $M_{true}$ during the calibration of the CBMM system.

To estimate the performance of different calibration methods, four accuracy indicators the average root mean square error ($\overline{RMSE}$), the average maximum error ($\overline{\mathit{MAX}}$), the average relative diattenuation error ($\overline{\delta D}$), and the average relative retardance error ($\overline{\delta R}$) are defined as follows,

$\overline{RMSE}=average(RMSE\left(M_{measured}-M_{true}\right)$

$\overline{\mathit{MAX}}=average\left(\mathit{MAX}\left(M_{measured}-M_{true}\right)\right)$

$\overline{\delta D}=average\left(\frac{D\left(M_{measured}\right)-D\left(M_{true}\right)}{D\left(M_{true}\right)}\right)$

$\begin{array}{c}\overline{\delta R}=average\left(\frac{R\left(M_{measured}\right)-R\left(M_{true}\right)}{R\left(M_{true}\right)}\right)\end{array}(15)$

where the “average” refers to the average over all pixels in the selected area of the Mueller matrix image, D and R represent the diattenuation function and the phase retardance function defined in the MMPD, respectively. $\overline{RMSE}$ and $\overline{\mathit{MAX}}$ are used to estimate the average and maximum deviation of the Mueller matrix measurement results given by different calibration methods from the true Mueller matrix $M_{true}$, respectively. $\overline{\delta D}$ and $\overline{\delta R}$ are used to estimate the relative diattenuation error and the relative retardance error for different calibration methods, respectively.

The Mueller Matrix images of a quarter-wave plate (GCL-060403, 488 nm, Daheng, Optic, China) and a polarizer (LPVISE100-A, 400–700 nm, Thorlabs, Inc., U.S.) are measured in the CBMM system based on three different calibration methods. The comparison results are shown in Figure 4. It is clear that the modified ECM has the best calibration performance, with the NCM the second best and the ACM the worst. For the wave plate sample, the $\overline{RMSE}$ and the $\overline{\mathit{MAX}}$ of the modified ECM are 0.0054 and 0.034, which are less than half and about 3/5 of the results of the NCM, respectively. Due to the absence of the beam splitter in the error model, the $\overline{\mathit{MAX}}$ of the ACM is close to 0.15, which indicates that the ACM is not suitable for the calibration of the CBMM system. Although the NCM takes into account the effect of the beam splitter, it is still less effective than the modified ECM, due to the deviation of the error model from the actual system and over-calibration. Calibration results for the polarizer sample with different methods are similar to the former results. In addition, the error bars of the modified ECM are also minimum, benefiting from the efficient noise suppression of the optimal RP-based PSA.

FIGURE 4

FIGURE 4. The calibration performance comparison of three calibration methods with different samples, (A) a wave plate sample, (B) a polarizer sample.

In the next experiment, a well-aligned silk sample is selected as the experimental sample, as shown in Figure 5. Because of its highly scattering property and typical birefringent nature, the silk sample is an ideal object of study for the Mueller matrix imaging system [34]. As the illumination light and detection light are collinear in the CBMM system, several polarization parameters independent of the azimuth angle of the sample, i.e., rotation invariant indicators can be derived from the Mueller matrix [35]. Obviously, if a CBMM system is well calibrated, the rotation invariant indicators separated from different azimuthal regions of a circularly symmetric sample should be constant; on the other hand, when a CBMM system is not well calibrated, these rotation invariant indicators may still be orientation dependent. Considering the circular symmetry of the silk sample, it is possible to estimate the calibration performance of different calibration methods in the view of symmetry.

FIGURE 5

FIGURE 5. A well-aligned silk sample (A) and its Mueller matrix image (B).

In the experiment, we select three different azimuthal regions on the silk sample, i.e., $\pm 45°$ and $90°$, as shown in the red rectangles in Figure 5A. Two rotation invariant indicators are defined as follows:

$D_L=\sqrt{{M_{12}}^2+{M_{13}}^2}$

$\begin{array}{c}{r}_L=\sqrt{{M_{24}}^2+{M_{34}}^2}\end{array}(16)$

where $M_{12}$, $M_{13}$, $M_{24}$, and $M_{34}$ are Mueller matrix elements. The rotation invariant indicator $D_L$ represents the linear diattenuation of the sample and $r_L$ relates to the ability of the sample to convert circularly polarized light into linearly polarized light [35]. Frequency distributions images of $D_L$ and $r_L$ obtained by different calibration methods are shown in Figure 6 [36].

FIGURE 6

FIGURE 6. Frequency distribution images of different rotation invariant indicators, (A–C) rotation invariant indicator $D_L$, (D–F) rotation invariant indicator $r_L$.

It is clear that the rotation invariant curves obtained by the modified ECM for different azimuthal regions are perfectly coincident with each other, while the results of the error model-based calibration methods are partially non-overlap. In other words, the rotation invariant indicators measured by the modified ECM do not depend on the azimuth angle of samples, whereas the results given by the NCM and the ACM are still azimuth dependent. As a result, it can be deduced that only the calibration result of the modified ECM is reliable from the view of symmetry. In fact, the calibration performance of the NCM and the ACM depends on their error models, however, it is difficult for a theoretical error model to accurately describe the actual measurement system. In addition, solving an error model that is overly complex may lead to over-calibration, which affects the accuracy of the calibration. The major advantage of the modified ECM is that it does not require modelling the errors in the system, hence it is more suitable for the complex CBMM system. Thanks to the optimal modulation frames for the PSA and the optimization-based Mueller matrix reconstruction method, the modified ECM gives the best calibration performance in the CBMM system.

4 Conclusion

In this paper, based on the eigenvalue calibration method we propose a simple modified ECM to calibrate the CBMM system configured in double-pass. In the modified ECM, we transform the complex double-pass calibration problem into a simple single-pass form by using mirror symmetry and the concept of the equivalent standard sample. To suppress the effect of noise on calibration accuracy, we design the distribution of polarization states over Poincaré sphere considering the inherent constraints of polarization modulators, and reconstruct the Mueller matrix of equivalent standard samples by means of an optimization. It is found that an optimal PSA can effectively improve the SNR of the measurement data and the optimization-based Mueller matrix reconstruction method is more robust against noise than the direct calculation method. After optimization, the accuracy of the modified method is 40 times better than the previous variants of the ECM. The comparison results with the error model-based calibration methods indicate that the modified ECM has clear advantages in the calibration of the CBMM system with higher accuracy and superior reliability.

Data availability statement

The raw data supporting the conclusions of this article will be made available by the authors, without undue reservation.

Author contributions

All authors listed have made a substantial, direct, and intellectual contribution to the work and approved it for publication.

Funding

Guang Dong Basic and Applied Basic Research Foundation (2019A1515111128); National Natural Science Foundation of China (61575067, 81871395).

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

1. Ramella-Roman JC, Saytashev I, Piccini M. A review of polarization-based imaging technologies for clinical and preclinical applications. J Opt (United Kingdom) (2020) 22:123001. doi:10.1088/2040-8986/abbf8a

CrossRef Full Text | Google Scholar

2. He C, Chang J, Salter PS, Shen Y, Dai B, Li P, et al. Revealing complex optical phenomena through vectorial metrics. Adv Photon (2022) 4:1–9. doi:10.1117/1.ap.4.2.026001

CrossRef Full Text | Google Scholar

3. Ghosh N. Tissue polarimetry: Concepts, challenges, applications, and outlook. J Biomed Opt (2011) 16:110801. doi:10.1117/1.3652896

PubMed Abstract | CrossRef Full Text | Google Scholar

4. He C, He H, Chang J, Chen B, Ma H, Booth MJ. Polarisation optics for biomedical and clinical applications: A review. Light Sci Appl (2021) 10:194. doi:10.1038/s41377-021-00639-x

PubMed Abstract | CrossRef Full Text | Google Scholar

5. He H, Liao R, Zeng N, Li P, Chen Z, Liu X, et al. Mueller matrix polarimetry-An emerging new tool for characterizing the microstructural feature of complex biological specimen. J Light Technol (2019) 37:2534–48. doi:10.1109/JLT.2018.2868845

CrossRef Full Text | Google Scholar

6. Qi J, Elson DS. Mueller polarimetric imaging for surgical and diagnostic applications: A review. J Biophotonics (2017) 10:950–82. doi:10.1002/jbio.201600152

PubMed Abstract | CrossRef Full Text | Google Scholar

7. Wang Y, He H, Chang J, He C, Liu S, Li M, et al. Mueller matrix microscope: A quantitative tool to facilitate detections and fibrosis scorings of liver cirrhosis and cancer tissues. J Biomed Opt (2016) 21:071112. doi:10.1117/1.jbo.21.7.071112

PubMed Abstract | CrossRef Full Text | Google Scholar

8. Du E, He H, Zeng N, Sun M, Guo Y, Wu J, et al. Mueller matrix polarimetry for differentiating characteristic features of cancerous tissues. J Biomed Opt (2014) 19:076013. doi:10.1117/1.jbo.19.7.076013

PubMed Abstract | CrossRef Full Text | Google Scholar

9. Pierangelo A, Benali A, Antonelli M-R, Novikova T, Validire P, Gayet B, et al. Ex-vivo characterization of human colon cancer by Mueller polarimetric imaging. Opt Express (2011) 19:1582. doi:10.1364/oe.19.001582

PubMed Abstract | CrossRef Full Text | Google Scholar

10. Arteaga O, Baldrís M, Antó J, Canillas A, Pascual E, Bertran E. Mueller matrix microscope with a dual continuous rotating compensator setup and digital demodulation. Appl Opt (2014) 53:2236. doi:10.1364/ao.53.002236

PubMed Abstract | CrossRef Full Text | Google Scholar

11. Fu Y, Chen Z, Tang Z, Ji Y. Removing the influence of the angle of incidence in a dual rotating retarder Mueller matrix polarimeter. Appl Opt (2021) 60:8472. doi:10.1364/ao.435283

PubMed Abstract | CrossRef Full Text | Google Scholar

12. Azzam RMA. Photopolarimetric measurement of the Mueller matrix by Fourier analysis of a single detected signal. Opt Lett (1978) 2:148. doi:10.1364/ol.2.000148

PubMed Abstract | CrossRef Full Text | Google Scholar

13. Goldstein DH, Chipman RA. Error analysis of a Mueller matrix polarimeter. J Opt Soc Am A (1990) 7:693. doi:10.1364/josaa.7.000693

CrossRef Full Text | Google Scholar

14. Chenault DB, Pezzaniti JL, Chipman RA. Muller matrix algorithms. Proc SPIE (1992) 1746:231. doi:10.1117/12.138793

CrossRef Full Text | Google Scholar

15. Chen Z, Meng R, Zhu Y, Ma H. A collinear reflection Mueller matrix microscope for backscattering Mueller matrix imaging. Opt Lasers Eng (2020) 129:106055. doi:10.1016/j.optlaseng.2020.106055

CrossRef Full Text | Google Scholar

16. Compain E, Poirier S, Drevillon B. General and self-consistent method for the calibration of polarization modulators, polarimeters, and Mueller-matrix ellipsometers. Appl Opt (1999) 38:3490. doi:10.1364/ao.38.003490

PubMed Abstract | CrossRef Full Text | Google Scholar

17. De Martino A, Garcia-Caurel E, Laude B, Drévillon B. General methods for optimized design and calibration of Mueller polarimeters. Thin Solid Films (2004) 455(456):112–9. doi:10.1016/j.tsf.2003.12.052

CrossRef Full Text | Google Scholar

18. Macías-Romero C, Török P. Eigenvalue calibration methods for polarimetry. J Eur Opt Soc (2012) 7:12004. doi:10.2971/jeos.2012.12004

CrossRef Full Text | Google Scholar

19. Lara D, Dainty C. Axially resolved complete Mueller matrix confocal microscopy. Appl Opt (2006) 45:1917–30. doi:10.1364/AO.45.001917

PubMed Abstract | CrossRef Full Text | Google Scholar

20. Hu H, Garcia-Caurel E, Anna G, Goudail F. Maximum likelihood method for calibration of Mueller polarimeters in reflection configuration. Appl Opt (2013) 52:6350–8. doi:10.1364/AO.52.006350

PubMed Abstract | CrossRef Full Text | Google Scholar

21. Sheng S, Chen X, Chen C, Zhuang J, Wang C, Gu H, et al. Eigenvalue calibration method for dual rotating-compensator Mueller matrix polarimetry. Opt Lett (2021) 46:4618. doi:10.1364/ol.437542

PubMed Abstract | CrossRef Full Text | Google Scholar

22. Cox LJ. Ellipsometry and polarized light. Opt Acta Int J Opt (1978) 25:270–1. doi:10.1080/713819761

CrossRef Full Text | Google Scholar

23. Zhou B, Duan GR. On the generalized Sylvester mapping and matrix equations. Syst Control Lett (2008) 57:200–8. doi:10.1016/j.sysconle.2007.08.010

CrossRef Full Text | Google Scholar

24. Henderson HV, Searle SR. Vec and vech operators for matrices, with some uses in jacobians and multivariate statistics. Can J Stat (1979) 7:65–81. doi:10.2307/3315017

CrossRef Full Text | Google Scholar

25. Brewer JW. Kronecker products and matrix calculus in system theory. IEEE Trans Circuits Syst (1978) 25:772–81. doi:10.1109/TCS.1978.1084534

CrossRef Full Text | Google Scholar

26. Foreman MR, Favaro A, Aiello A. Optimal frames for polarization state reconstruction. Phys Rev Lett (2015) 115:263901–6. doi:10.1103/PhysRevLett.115.263901

PubMed Abstract | CrossRef Full Text | Google Scholar

27. Zhao Q, Huang T, Hu Z, Bu T, Liu S, Liao R, et al. Geometric optimization method for a polarization state generator of a Mueller matrix microscope. Opt Lett (2021) 46:5631. doi:10.1364/ol.441492

PubMed Abstract | CrossRef Full Text | Google Scholar

28. Ambirajan A. Optimum angles for a polarimeter: Part II. Opt Eng (1995) 34:1656. doi:10.1117/12.202098

CrossRef Full Text | Google Scholar

29. Peinado A, Lizana A, Vidal J, Iemmi C, Campos J. Optimized Stokes polarimeters based on a single twisted nematic liquid-crystal device for the minimization of noise propagation. Appl Opt (2011) 50:5437–45. doi:10.1364/AO.50.005437

PubMed Abstract | CrossRef Full Text | Google Scholar

30. Shapiro J. Genetic algorithms in machine learning. In: Advanced course on artificial intelligence. p. 146. doi:10.1007/3-540-44673-7_7

CrossRef Full Text | Google Scholar

31. Lu S-Y, Chipman RA. Interpretation of mueller matrices based on polar decomposition retardance : A review. J Opt Soc Am A (1996) 13:1106–13. doi:10.1364/josaa.13.001106

CrossRef Full Text | Google Scholar

32. Sabatke DS, Descour MR, Dereniak EL, Sweatt WC, Kemme SA, Phipps GS. Optimization of retardance for a complete Stokes polarimeter. Opt Lett (2000) 25:802. doi:10.1364/ol.25.000802

PubMed Abstract | CrossRef Full Text | Google Scholar

33. Foreman MR, Goudail F. On the equivalence of optimization metrics in Stokes polarimetry. Opt Eng (2019) 58:1. doi:10.1117/1.oe.58.8.082410

CrossRef Full Text | Google Scholar

34. He H, Sun M, Zeng N, Du E, Liu S, Guo Y, et al. Mapping local orientation of aligned fibrous scatterers for cancerous tissues using backscattering Mueller matrix imaging. J Biomed Opt (2014) 19:106007. doi:10.1117/1.jbo.19.10.106007

PubMed Abstract | CrossRef Full Text | Google Scholar

35. Gil JJ. Invariant quantities of a Mueller matrix under rotation and retarder transformations. J Opt Soc Am A (2016) 33:52. doi:10.1364/josaa.33.000052

PubMed Abstract | CrossRef Full Text | Google Scholar

36. He C, He H, Li X, Chang J, Wang Y, Liu S, et al. Quantitatively differentiating microstructures of tissues by frequency distributions of Mueller matrix images. J Biomed Opt (2015) 20:105009. doi:10.1117/1.jbo.20.10.105009

PubMed Abstract | CrossRef Full Text | Google Scholar