Theoretical treatment on externally-seeded superradiance from N2+ in femtosecond laser filamentation in low-pressure nitrogen

We perform a theoretical investigation of a collective emission in tunnel-ionized nitrogen molecules triggered by a coherent seed pulse. A semiclassical theory of superradiance that includes the superradiant temporal profile, characteristic duration, time delay, intensity is achieved. The theoretical predictions of 391-nm forward emission corresponding to the transition between ${\mathrm{N}}_{\mathrm{2}}^{+}(B^2{\mathrm{\Sigma }}_u^{+},{\nu }^{\prime }=0)$ and ${\mathrm{N}}_{\mathrm{2}}^{+}(X^2{\mathrm{\Sigma }}_g^{+},\nu =0)$ as a function of nitrogen gas pressure are compared with the recent experimental data [Ding P. Lasing effect in femtosecond filaments in air, Ph.D. thesis, Université Paris-Saclay (2016)]. The good agreement demonstrates that the time-delayed optical amplification inside the molecular nitrogen ions is superradiance.

1 Introduction

Tunnel ionization is a fundamental process for atoms/molecules in intense laser fields when the Keldysh parameter is less than unity [1, 2]. In the tunneling regime, not only sequential double ionization but also non-sequential double ionization exist [3, 4]. Tunnel ionization is taken as a foundation to understand other strong-field phenomena including high harmonic generation [5, 6], non-linear filamentation and laser-induced electron acceleration [7–9]. Because of the multielectron effects and the close ionization potentials between the outermost and a few lower-lying orbitals, the electrons from several molecular orbitals can be ionized in strong laser fields [10–12]. A direct consequence of the multiorbital ionization is that the molecular ions are populated not only in the ground but also in the excited electronic states. A good example is the molecular nitrogen ions inside the plasma generated by 800-nm femtosecond laser pulses, which is the subject of interest in this study. The fluorescence measurement of the plasma confirm that the molecular nitrogen ions exist in both ground ${\mathrm{N}}_{\mathrm{2}}^{+}(X^2{\mathrm{\Sigma }}_g^{+})$ and excited ${\mathrm{N}}_{\mathrm{2}}^{+}(B^2{\mathrm{\Sigma }}_u^{+})$ electronic states [13, 14]. For convenience, $B^2{\mathrm{\Sigma }}_u^{+}$ and $X^2{\mathrm{\Sigma }}_g^{+}$ will be termed as B and X in the following context, respectively.

Since the ionization rate decays exponentially with the electron binding energy, the populations in the excited states should be much less than those in the ground state, e.g., no population inversion should be expected between B and X state. However, it has been experimentally demonstrated that ${\mathrm{N}}_{\mathrm{2}}^{+}$ lasing at 391 and 428 nm wavelength can be generated and an externally-injected weak seeding pulse can be significantly amplified in laser filamentation in nitrogen gas, indicating the presence of high optical gain in the system [15–39]. To explain the seed amplification inside the molecular nitrogen ions, Xu et al., Yao et al. and Zhang et al. proposed multi-state coupling model [23, 25, 40]. The nitrogen molecules are populated in the lowest three electronic states of molecular nitrogen ions, i.e., X, A $({\mathrm{N}}_{\mathrm{2}}^{+}(A^2{\mathrm{\Pi }}_u))$ and B, by tunnel ionization at the peak of the 800-nm pump pulse. The falling edge of the 800-nm pulse, which can not cause further ionization though, still has high intensity. The two-level system of X and A with a transition wavelength of 787 nm experiences Rabi oscillation in the 800-nm pump laser field. As Rabi oscillation only occurs at the falling edge rather than the full laser envelope, the population transfers efficiently from X to A as a result of the couplings induced by the 800-nm pump pulse, which helps to establish the population inversion between B and X.

An important issue of radiation research is the time evolution of the radiated intensity of the system. Time-resolved measurements of ${\mathrm{N}}_{\mathrm{2}}^{+}$ lasing show that the external seeding pulse is almost unaffected after passing through the plasma, instead it triggers a retarded emission at the lasing wavelength [21, 22, 24, 29]. The intensity of the retarded emission increases gradually and reaches its peak value at a time delay τ_D of several picoseconds after the seeding pulse [22, 24]. The characteristic duration τ_W of the emission shares the same magnitude as τ_D [22, 24]. Within particular pressure range from few mbar to optimal pressure, it was found that the τ_D and τ_W are approximately proportional to the inverse of the gas pressures while the peak intensity of the retarded lasing scales as the square of the gas pressure, which coincides with the features of superradiance and therefore suggests the presence of macroscopic dipole (or molecular coherence) in ${\mathrm{N}}_{\mathrm{2}}^{+}$ lasing. Following experimental investigations have unquestionably confirmed the presence of molecular coherence between ${\mathrm{N}}_{\mathrm{2}}^{+}$ cations [28, 30]. Recently, by considering a three-level V-scheme system, a model of lasing without population inversion has been proposed based on the long-lasting coherences in A → X and B → X transitions to explain the time-delayed optical gain [29]. The model ascribes the long-lasting coherence in A → X transition to the post-pulse of the 800-nm pump pulse based on high contrast cross-correlator measurements.

However, there still exists an understanding gap between the presence of molecular coherence in ${\mathrm{N}}_{\mathrm{2}}^{+}$ and the temporal behaviors of the lasing pulse. Regardless of the underlying mechanism of optical gain in ${\mathrm{N}}_{\mathrm{2}}^{+}$, it would be of important interest to understand the evolution of the lasing process under the circumstance of a macroscopic dipole of the excited ${\mathrm{N}}_{\mathrm{2}}^{+}$. We noticed that Xie et al. have experimentally and numerically investigated the evolution of a weak seed pulse in the population-inverted ${\mathrm{N}}_{\mathrm{2}}^{+}$ system at the pressure of 200 mbar [41]. With the short dipole-dephasing time of 2.5 ps, they found multiple amplification routes including superradiance, seed amplification induced by the stimulated emission and free induction decay. In our article, the relative low pressures of nitrogen gas are used and the dipole-dephasing time is set to be 0. We deduce analytic expressions for temporal characteristics of the ${\mathrm{N}}_{\mathrm{2}}^{+}$ lasing pulse based on a semi-classical theory considering only the two-level system of X and B states. The obtained analytic results show clearly how the macroscopic dipole evolves and are compared with the experimental ones that have been reported recently, which shows good agreements.

2 Semiclassical theory of superradiance

After photonization and state couplings by 800-nm laser pulses, the molecular nitrogen ions are populated in B and X states that constitute a two-level system in the plasma. Since the intensity of the 391-nm seed pulse is weak, it can hardly induce ionization or non-resonant excitation. So only the interaction between the seed pulse and the two electronic states is significant. The electron-ion inelastic collisions and the electron-ion recombination can cause the population change (decay or increase) of the two-level system. Both of the them occur on nanosecond timescale [42–49], which is a much slower process compared to the 391-nm lasing emission that takes place in picosecond range. Hence, the population of the two-level system is considered to be conserved during the ultra-fast radiation.

Under the above conditions, the evolution of the two-level system of B (ν′ = 0) and X (ν = 0) in the radiation field can be described by the optical Bloch equations by using the slowly varying amplitude approximation and the rotating-wave approximation [50–52]:

$\frac{\partial u}{\partial t}=-\mathrm{\Delta }v-{\mathrm{\Gamma }}_{2}u,(1)$

$\frac{\partial v}{\partial t}=\mathrm{\Delta }u+\mathrm{\Omega }w-{\mathrm{\Gamma }}_{2}v,(2)$

$\frac{\partial w}{\partial t}=-\mathrm{\Omega }v-{\mathrm{\Gamma }}_1\left(1+w\right),(3)$

where u and v denote dispersion and absorption terms, respectively, and w is the relative population difference between the upper and lower states. Ω(t) is the Rabi frequency which takes the form

$\mathrm{\Omega }=\left\{\begin{array}{ccc}\hfill \frac{\mu {\bar{E}}_p}{\hslash }& ,\hfill & \hfill 0<t<{\tau }_r,\\ \hfill \frac{\mu {\bar{E}}_s}{\hslash }& ,\hfill & \hfill t\ge {\tau }_r,\end{array}\right.(4)$

with μ, ℏ, ${\bar{E}}_p$, ${\bar{E}}_s$ and τ_r being the electronic transition moment between the two states, the reduced Planck’s constant, the envelope amplitude of the seed laser pulse, the radiation field generated by the two-level system and the interaction time between the seed pulse and the two-level system, respectively. The resonant condition is considered here, i.e., Δ = 0. It is noticed that the optical Bloch Eq. 1 are written in the coordinate system moving with the seed laser field. The transformation between the moving coordinate system (t, z) and the ground coordinate system (t′, z′) is

$t=t^{\prime }-\frac{z^{\prime }}{c},z=z^{\prime },(5)$

where z and z′ represent the propagation direction of the seed laser pulse, and c is the speed of light. z and z′ range from 0 to L which is the filament plasma length. A pencil-shaped geometry for the active gain volume is used, i.e.,

$r\ll L,(6)$

with r being the filament radius. It is reasonable because the plasma radius is usually around 50 μm, and the filament plasma length is typically in centimeter range by using a lens of short focal length [53].

In Eqs 1–3, Γ₁ = 11.76 × 10⁶ s⁻¹ is the transition rate [44], and the corresponding lifetime 1/Γ₁ = 85 ns is about 4 orders of magnitude larger than the time delay and width (∼ps) of the 391-nm retarded emission. Γ₂ is the dipole-dephasing rate, which can inhibit the formation of the macroscopic dipole moment. The radiation manifests characteristics of superfluorescence, damped superfluorescence and amplified spontaneous emission (ASE) if 1/Γ₂ ≫ τ_D, $\sqrt{{\tau }_W{\tau }_D}\ll 1/{\mathrm{\Gamma }}_2<{\tau }_D$ and ${\tau }_W\ll 1/{\mathrm{\Gamma }}_2\ll \sqrt{{\tau }_W{\tau }_D}$, respectively [54–57]. The dephasing process is mainly caused by electron-ion elastic scattering in the nitrogen plasma generated by femtosecond laser pulses. Because of the lackness of elastic electron scattering cross-section for molecular nitrogen ions, we take the dephasing rate Γ₂ as a varying parameter and assume that 1/Γ₂ is much greater than the time delay and width of the 391-nm retarded emission. As a reference, the elastic electron scattering cross-section for nitrogen molecules is 1.06 × 10^–15 cm² at 6 eV $(\sim 10^8\mathrm{c}\mathrm{m}/\mathrm{s})$ [58], which is the ponderomotive potential of electron in the linearly polarized laser field with the laser intensity of 10¹⁴ W/cm² [13, 53]. If the elastic scattering cross-section for molecular nitrogen ions is similar to that for nitrogen molecules, the mean time between collisions is .94 ns for the density of the molecular nitrogen ions around 10¹⁶ cm⁻³ in the filament plasma [8, 29]. It still exceeds the time delay and width of the 391-nm retarded emission by 2 orders of magnitude. Therefore, within the time scale of 391 nm lasing pulse we considered, the spontaneous decay of upper state and the influence of collisional dephasing can be neglected, and we set both Γ₁ and Γ₂ as zero in the following derivation.

To solve Eqs 1–3, a Bloch angle is defined as

$\theta \left(t\right)={\int }_0^t\mathrm{\Omega }\left(\tau \right)d\tau .(7)$

Then, simple solutions of the equations can be obtained as.

$u\left(t\right)=0,(8)$

$v\left(t\right)=w_0\sin \theta \left(t\right),(9)$

$w\left(t\right)=w_0\cos \theta \left(t\right),(10)$

with the initial conditions of u (0) = 0, v (0) = 0 and w (0) = w₀. By setting the eigen-energy of B and X to be ℏω/2 and −ℏω/2, the energy density of the two-level system can be expressed as

$E_N\left(t\right)=\frac{1}{2}\hslash \omega N{w}_0\cos \theta \left(t\right),(11)$

where N is sum of the population densities of the two states.

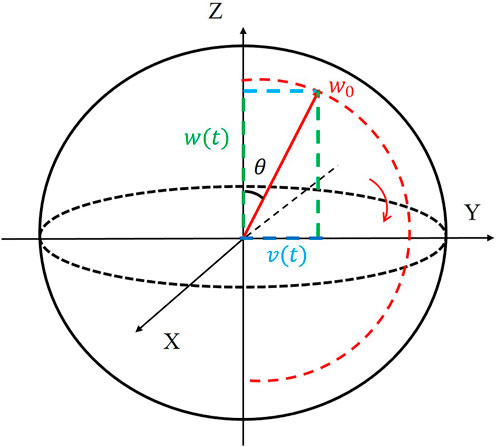
We define a Bloch vector B as

$\mathit{B}=\left(u,v,w\right)=u{\mathit{e}}_X+v{\mathit{e}}_Y+w{\mathit{e}}_Z,(12)$

with e_X, e_Y and e_Z denoting the unit vectors of the X-, Y- and Z-axis, respectively. It is easy to obtain

$|\mathit{B}|=\sqrt{u^2+v^2+w^2}=w_0.(13)$

As u = 0, the Bloch vector B with a fixed length w₀ rotates around X-axis in Y-Z plane as shown in Figure 1. The rotation determined by the Bloch angle θ describes the evolution of the physical quantities including the energy density of the two-level system.

FIGURE 1

FIGURE 1. The Bloch vector B of the two-level system.

When t < τ_r, the Rabi frequency Ω_p induced by the seed laser pulse is known, and the Bloch angle θ can be calculated by $\theta (t)={\int }_0^t{\mathrm{\Omega }}_p(\tau )d\tau$. Next, we investigate the development of θ when t ≥ τ_r. The relationship between the radiation field E_s (t′, z′) and polarization P (t′, z′) generated by the two-level system is governed by the Maxwell’s equations

$\frac{{\partial }^2{E}_s}{\partial z^{\prime 2}}-{\mu }_0{\epsilon }_0\frac{{\partial }^2{E}_s}{\partial t^{\prime 2}}={\mu }_0\frac{{\partial }^{2}P}{\partial t^{\prime 2}},(14)$

where μ₀ and ɛ₀ denote vacuum permeability and vacuum permittivity, respectively. The radiation field E_s (t′, z′) and polarization P (t′, z′) can be written in the form

$E_s\left(t^{\prime },z^{\prime }\right)=\frac{1}{2}\left[{\bar{E}}_s\left(t^{\prime },z^{\prime }\right)e^{-i\omega t^{\prime }+ik{z}^{\prime }}+c.c.\right],(15)$

$P\left(t^{\prime },z^{\prime }\right)=\frac{1}{2}\left[-iN\mu v\left(t^{\prime }\right)e^{-i\omega t^{\prime }+ik{z}^{\prime }}+c.c.\right],(16)$

where ${\bar{E}}_s(t^{\prime },z^{\prime })$ is the envelope amplitude of E_s (t′, z′). By applying the rotating-wave approximation and slow amplitude approximation [59], Eq. 14 can be simplified to

$\frac{\partial {\bar{E}}_s}{\partial z^{\prime }}+\frac{1}{c}\frac{\partial {\bar{E}}_s}{\partial t^{\prime }}=\frac{{\mu }_0\omega c\mu N}{2}v\left(t^{\prime }\right).(17)$

Substituting (t′, z′) with (t, z) into Eq. 17, we get

$\frac{\partial {\bar{E}}_s\left(t,z\right)}{\partial z}=\frac{{\mu }_0\omega c\mu N}{2}v\left(t\right).(18)$

With the initial condition ${\bar{E}}_s({\tau }_r,0)=0$, one further obtains

${\bar{E}}_s\left({\tau }_r,L\right)=\frac{{\mu }_0\omega c\mu NL}{2}v\left({\tau }_r\right),(19)$

This derived expression suggests the amplitude of the radiation field emitted at the end of the plasma at t = τ_r.

To get a clear physical picture of Eq. 19, Figure 2 illustrates the growth of ${\bar{E}}_s$ with the increase of the plasma length L. The discussion below is performed in the ground coordinate system for a straightforward understanding. Considering the plasma as a series of consecutive micro regions 0 ∼ δL, … z ∼ z+δL, … L−δL ∼ L, the seed pulse interacts with the two-level system at each region, which is described by the optical Bloch Eqs 1–3. In the region of 0 ∼ δL, after the interaction there is a v (τ_r, 0), which generates a radiation field with the amplitude of ${\bar{E}}_s({\tau }_r,0)$. In the region z ∼ z+δL which corresponds to a propagation time of z/c, the seed pulse induce the same polarization and radiation field as that in the region of 0 ∼ δL. At the same time, all the radiation field generated before the infinitesimal region z ∼ z+δL have arrived. As a result, the amplitude ${\bar{E}}_s({\tau }_r+z/c,z)$ is a superposition of the amplitudes generated by the infinitesimals 0 ∼ δL, … ,z ∼ z+δL. Therefore, the final amplitude of the radiation field can be expressed as Eq. 19.

FIGURE 2

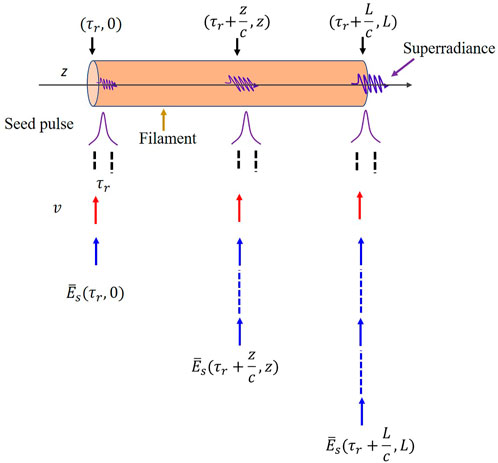
FIGURE 2. The amplitude of the radiation field ${\bar{E}}_s$ as a function of the plasma filament length L after the interaction between the seed pulse and the two-level system. The ground coordinate system is used for a concise overview.

At t = τ_r, the energy flux density S of the radiation field from the cross section of the plasma is

$\begin{array}{ccc}\hfill S=& \hfill & \frac{1}{2}\sqrt{\frac{{\epsilon }_0}{{\mu }_0}}{{\bar{E}}_s}^2\left({\tau }_r,L\right)\hfill \\ \hfill & \hfill & =\frac{{\mu }_{0}c{\omega }^2{\mu }^2{N}^2{L}^2}{8}{w_0}^2{\sin }^2\theta \left({\tau }_r\right).\hfill \end{array}(20)$

The decrease of energy per unit time of the two-level system at t = τ_r according to Eq. 11 is

$-\frac{\mathrm{d}{E}_N}{\mathrm{d}t}={\left.\frac{1}{2}\hslash \omega N{w}_0\sin \theta \frac{\mathrm{d}\theta }{\mathrm{d}t}\right|}_{t={\tau }_r}.(21)$

From the law of conservation of energy, the decrease of energy per unit time from the active volume equals the energy flux from the cross section, which reads

$-\frac{\mathrm{d}{E}_N}{\mathrm{d}t}\pi r^{2}L=S\pi r^2.(22)$

By substituting both sides respectively and assuming no external factors affecting the system, one gets the derivative of the Bloch angle with respect to time

$\frac{\mathrm{d}\theta }{\mathrm{d}t}=\frac{{\mu }_{0}c\omega {\mu }^{2}NL{w}_0}{4\hslash }\sin \theta \left({\tau }_r\right)(23)$

with the initial condition (τ_r, θ(τ_r)). The solution of Eq. 23 is

$\theta \left(t\right)=2\arctan \left(e^{\frac{t-{\tau }_D}{{\tau }_W}}\right)(24)$

with.

${\tau }_W=\frac{4\hslash }{{\mu }_{0}c\omega {\mu }^2{w}_{0}NL},(25)$

${\tau }_D={\tau }_r-{\tau }_W\ln \left[\tan \frac{\theta \left({\tau }_r\right)}{2}\right].(26)$

The energy density E_N(t) of this two-level system according to Eq. 9 and the radiation intensity I_s (the same as the energy flux density S) at the end of the plasma can be respectively expressed as.

$E_N\left(t\right)=-\frac{1}{2}\hslash \omega w_{0}N\tanh \left(\frac{t-{\tau }_D}{{\tau }_W}\right),(27)$

$I_s=\frac{{\mu }_{0}c{\omega }^2{\mu }^2{w_0}^2{N}^2{L}^2}{8}{\mathrm{s}\mathrm{e}\mathrm{c}\mathrm{h}}^2\left(\frac{t-{\tau }_D}{{\tau }_W}\right).(28)$

From above analytical expressions, we can see that the radiation from the two-level system possesses the nature of superradiance [54–56, 60–64] featured with the characteristic duration of τ_W and delay of τ_D with respect to the seed pulse. τ_W is inversely proportional to the population density N and the radiation intensity is proportional to the square of N², typical signatures of superradiance.

As described by Eq. 27, there is still energy stored in the system after interaction with the seed pulse. The release of remaining energy results in the retarded emission. The initial relative population difference w₀ determined by the pump pulse and the Bloch angle θ(τ_r)caused by the seed pulse govern the temporal evolution of the retarded emission.

3 Comparison between the experimental results and theoretical predictions

In this section, we perform comparisons between the experimental results and theoretical predictions of the temporal profile of the 391-nm lasing emission based on analytical expressions derived. The experimental results are directly taken from previous work [65], where detailed descriptions of the experiments can be found. Figure 3 shows the temporal profiles of 391-nm lasing pulse measured for different nitrogen pressures from 6 to 20 mbar. The interaction time τ_r for the calculation is set to be 3.6τ_p, with τ_p = 0.26 ps being the duration of the seed pulse. The characteristic duration is τ_W = τ_FW/1.763 for the hyperbolic secant pulse, where τ_FW is the experimental FWHM of the 391-nm lasing pulse. By substituting τ_W and τ_D at different pressures into Eq. 28, we obtain the corresponding temporal profile as shown by the red line in Figure 3. When the gas pressure exceeds 10 mbar, the theoretical predictions are in agreement with the experimental signals for the main part of superradiance as illustrated in Figures 3D–I. Following the strongest radiation, there are the other two gains at ∼ 4.4 and 8.6 ps that correspond to the revival of the optical gain due to the molecular alignment effect [21, 66], which was not considered in the theoretical derivation. Besides, there exist a gradual decay in the measured temporal profiles at high pressures. By increasing the dephasing rate Γ₂ of the transition dipole in $\mathrm{K}\mathrm{C}\mathrm{l}:{\mathrm{O}}_{\mathrm{2}}^{-}$, Malcuit et al. found that the temporal profiles of the 629.4-nm emission from $\mathrm{K}\mathrm{C}\mathrm{l}:{\mathrm{O}}_{\mathrm{2}}^{-}$ changed from a standard superfluorescence to having an obviously long decay [54]. In our case, with the nitrogen gas pressure increasing, the dephasing rate Γ₂ increases. Even though the dephasing rate is not larger enough to inhibit the formation of the macroscopic dipole moment (superradiance), it indeed leads to the gradual decay in the measured temporal profiles at higher pressures, which was also found in Xie et al.’s experiment [41]. In general, the theoretical results agree well with the experimental data, which is a strong evidence that the 391-nm emission inside ionized nitrogen molecules is superradiance.

FIGURE 3

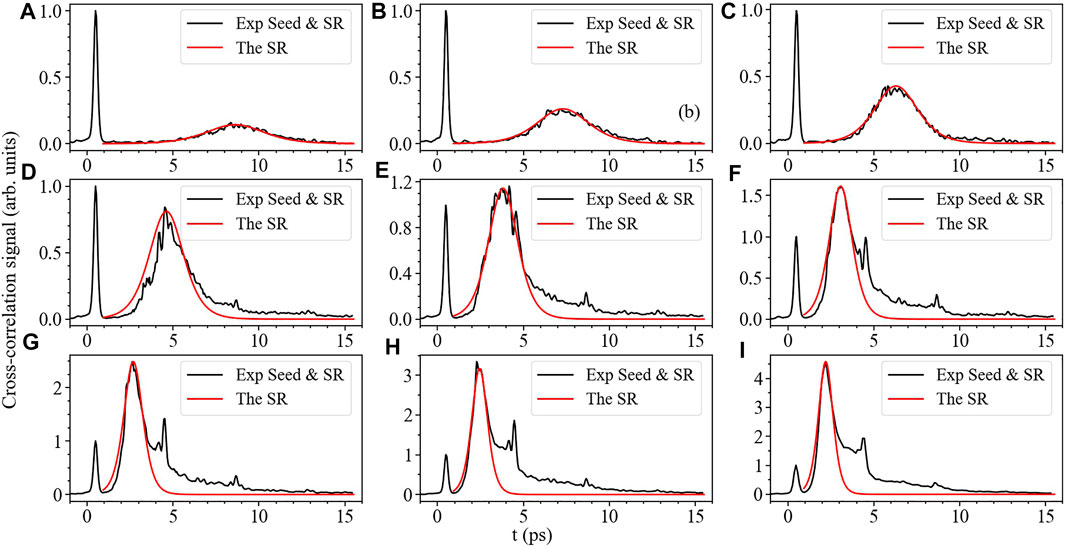
FIGURE 3. Comparisons of the experimental data and theoretical predictions for the temporal profile of the 391-nm lasing emission with different gas pressure of (A) 6 mbar, (B) 7 mbar, (C) 8 mbar, (D) 10 mbar, (E) 12 mbar, (F) 14 mbar, (G) 16 mbar, (H) 18 mbar and (I) 20 mbar, respectively.

The time-dependent quantum-wave-packet calculations show that the initial relative population difference w₀ varies from 0 to 0.55 with the 800-nm laser intensity ranging from 2.2 to 4 × 10¹⁴ W/cm² [23]. The 800-nm pump laser intensity in our experiment is estimated to be 2.6 × 10¹⁴ W/cm² with the energy of 1.8 mJ, duration of 45 fs and filament diameter of ∼70 μm. Thus, it is reasonable to set w₀ as .1. Since the pump laser pulse energy is unchanged for different gas pressure ranging from 6 to 20 mbar [29, 53], the two-level-system population density is proportional to gas pressure. In actual case, the superradiance will vanish when the pressure is lower than a certain value p₀. The minimal gas pressure that causes the superradiance is p₀ = 2.5 mbar in our case. The relationship between the population density and pressure can be expressed N = k (p−p₀), where k is a scaling factor. Using the experimental point (p = 8 mbar, τ_W = 1.666 ps), we obtain N = 0.228 × (p−2.5) (mbar) × 10¹⁶ cm⁻³ with L = 10 mm and μ = 1.7 D [67]. Hence, the characteristic duration τ_W dependent on the gas pressure can be calculated. The calculated τ_W (red line) as a function of the nitrogen pressure show good agreement with the experimental data (black circle), as shown in Figure 4A.

FIGURE 4

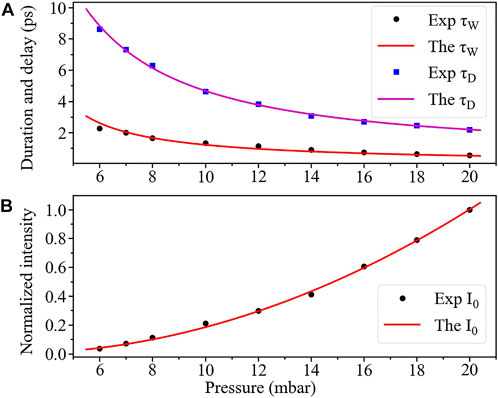
FIGURE 4. Comparisons between (A) the experimental characteristic duration τ_W and time delay τ_D, and the calculated τ_W and τ_D, and (B) the experimental results of peak intensity I₀ and the theoretical calculations of I₀ as a function of gas pressure.

The seed pulse in Figure 3 has a peak intensity of 10⁷ W/cm², and can be well fitted by a Gaussian shape with the pulse duration τ_p = 0.26 ps. The initial Bloch angle is accurately calculated

$\theta \left({\tau }_r\right)=2{\int }_0^{\frac{{\tau }_r}{2}}\frac{\mu }{\hslash }{\bar{E}}_p\left(t\right)dt=0.057\pi ,(29)$

which is far smaller than π/2. The two-level system does not experience several cycles of Rabi oscillation under the presence of the seed pulse. Only little energy emits with the seed pulse simultaneously, which explains the almost unchanged intensity of the seed pulse after passing through the filament plasma. It can also be seen that the theoretical calculations for τ_D are in good agreement with the experimental results (blue square) in Figure 4A.

The peak intensities I₀ of the superradiance are investigated as a function of nitrogen pressure. The values at t = τ_D of the experimental 391-nm emission in Figure 3 are taken as the peak intensities. The theoretical peak intensity is expressed as $I_0=(1/8){\mu }_{0}c{\omega }^2{\mu }^2{w}_0^2{N}^2{L}^2$, which is proportional to N². Using the linear relationship between N and p, the normalized I₀ (read line) of the theory is calculated, as shown in Figure 4B, also showing good agreement with the experimental data. Additionally, it is noticed that the peak intensity of superradiance scales as N² but the total emitted energy is proportional to N according to Eq. 23. This fact inevitably leads to the characteristic duration τ_W to be proportional to N⁻¹. We emphasize that N is the sum of population density of B and X. The intensity is influenced by not only the population in the excited state but also that in the ground state.

From the comparisons in terms of the temporal shape, the characteristic duration, the time delay and the intensity between the theoretical and experimental results above, it can be seen that the assumption 1/Γ₂ ≫ τ_W and 1/Γ₂ ≫ τ_D is reasonable. If the dephasing rate Γ₂ is sufficiently large, no macroscopic dipole moment ever develops and each electric dipole simply responds to the instantaneous value of the laser field. In this case a very noise output pulse shows up, of which the pulse duration and the peak intensity no longer scale as 1/N and N² [54].

4 Conclusion

In conclusion, we theoretically investigate the evolution of energy in the population-inverted molecular nitrogen ions induced by the coherent seed pulse. By solving the Bloch angle of the two-level system of ${\mathrm{N}}_{\mathrm{2}}^{+}(B^2{\mathrm{\Sigma }}_u^{+},{\nu }^{\prime }=0)$ and ${\mathrm{N}}_{\mathrm{2}}^{+}(X^2{\mathrm{\Sigma }}_g^{+},\nu =0)$, the semiclassical superradiance theory is proposed to describe the characteristic duration, time delay, intensity and total emitted energy. We explain the time-delayed optical amplification in molecular nitrogen ions irradiated with intense femtosecond laser pulses, and further comfirm the superradiance nature of the 391-nm forward emission by the comparisons between the theoretical and experimental results.

Data availability statement

Publicly available datasets were analyzed in this study. This data can be found here: https://www.researchgate.net/publication/316084384_Lasing_effect_in_femtosecond_filaments_in_air.

Author contributions

QW conceived the concept. PD provide the experimental data. QW, SW, and MA-K performed the theoretical derivation. QW, PD, YZ, ZL, and BH analyzed the data. The manuscript was prepared by QW and PD, and was discussed among all authors.

Funding

This work was supported by China Scholarship Council, the National Natural Science Foundation of China (Grants No. U1932133, No. 11905089, and No. 12004147), and the open project “Study on physical mechanisms of femtosecond laser-induced 337 nm lasing of nitrogen molecules” funded by Shanghai Institute of Optics and Fine Mechanics, Chinese Academy of Sciences.

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

1. Keldysh LV. Ionization in the field of a strong electromagnetic wave. Sov Phys JETP (1965) 20:1307–14.

Google Scholar

2. Tong XM, Zhao ZX, Lin CD. Theory of molecular tunneling ionization. Phys Rev A (2002) 66:033402. doi:10.1103/physreva.66.033402

CrossRef Full Text | Google Scholar

3. Kim KY, Alexeev I, Milchberg HM. Single-shot measurement of laser-induced double step ionization of helium. Opt Express (2002) 10:1563–72. doi:10.1364/oe.10.001563

PubMed Abstract | CrossRef Full Text | Google Scholar

4. Fittinghoff DN, Bolton PR, Chang B, Kulander KC. Observation of nonsequential double ionization of helium with optical tunneling. Phys Rev Lett (1992) 69:2642–5. doi:10.1103/physrevlett.69.2642

PubMed Abstract | CrossRef Full Text | Google Scholar

5. Corkum PB. Plasma perspective on strong field multiphoton ionization. Phys Rev Lett (1993) 71:1994–7. doi:10.1103/physrevlett.71.1994

PubMed Abstract | CrossRef Full Text | Google Scholar

6. Lewenstein M, Balcou P, Ivanov MY, L’huillier A, Corkum PB. Theory of high-harmonic generation by low-frequency laser fields. Phys Rev A (1994) 49:2117–32. doi:10.1103/physreva.49.2117

PubMed Abstract | CrossRef Full Text | Google Scholar

7. Chin SL, Théberge F, Liu W. Filamentation nonlinear optics. Appl Phys B (2007) 86:477–83. doi:10.1007/s00340-006-2455-z

CrossRef Full Text | Google Scholar

8. Couairon A, Mysyrowicz A. Femtosecond filamentation in transparent media. Phys Rep (2007) 441:47–189. doi:10.1016/j.physrep.2006.12.005

CrossRef Full Text | Google Scholar

9. Nandan Gupta D, Pal Singh K, Suk H. Optical field-ionization of a neutral gas with inhomogeneous density for electron acceleration by a high-intensity laser. Phys Plasma (2012) 19:023103. doi:10.1063/1.3678202

CrossRef Full Text | Google Scholar

10. McFarland BK, Farrell JP, Bucksbaum PH, Guhr M. High harmonic generation from multiple orbitals in N2. Science (2008) 322:1232–5. doi:10.1126/science.1162780

PubMed Abstract | CrossRef Full Text | Google Scholar

11. Smirnova O, Mairesse Y, Patchkovskii S, Dudovich N, Villeneuve D, Corkum P, et al. High harmonic interferometry of multi-electron dynamics in molecules. Nature (2009) 460:972–7. doi:10.1038/nature08253

PubMed Abstract | CrossRef Full Text | Google Scholar

12. Becker A, Bandrauk AD, Chin SL. S-matrix analysis of non-resonant multiphoton ionisation of inner-valence electrons of the nitrogen molecule. Chem Phys Lett (2001) 343:345–50. doi:10.1016/s0009-2614(01)00705-9

CrossRef Full Text | Google Scholar

13. Mitryukovskiy S, Liu Y, Ding P, Houard A, Couairon A, Mysyrowicz A. Plasma luminescence from femtosecond filaments in air: Evidence for impact excitation with circularly polarized light pulses. Phys Rev Lett (2015) 114:063003. doi:10.1103/physrevlett.114.063003

PubMed Abstract | CrossRef Full Text | Google Scholar

14. Wang P, Xu S, Li D, Yang H, Jiang H, Gong Q, et al. Spectroscopic study of laser-induced tunneling ionization of nitrogen molecules. Phys Rev A (2014) 90:033407. doi:10.1103/physreva.90.033407

CrossRef Full Text | Google Scholar

15. Yao J, Zeng B, Xu H, Li G, Chu W, Ni J, et al. High-brightness switchable multiwavelength remote laser in air. Phys Rev A (2011) 4:051802. (R). doi:10.1103/physreva.84.051802

CrossRef Full Text | Google Scholar

16. Zhang H, Jing C, Yao J, Li G, Zeng B, Chu W, et al. Rotational coherence encoded in an “air-laser” spectrum of nitrogen molecular ions in an intense laser field. Phys Rev X (2013) 3:041009. doi:10.1103/physrevx.3.041009

CrossRef Full Text | Google Scholar

17. Ni J, Chu W, Jing C, Zhang H, Zeng B, Yao J, et al. Identification of the physical mechanism of generation of coherent N₂⁺ emissions in air by femtosecond laser excitation. Opt Express (2013) 21:8746–52. doi:10.1364/oe.21.008746

PubMed Abstract | CrossRef Full Text | Google Scholar

18. Zeng B, Chu W, Li G, Yao J, Zhang H, Ni J, et al. Real-time observation of dynamics in rotational molecular wave packets by use of air-laser spectroscopy. Phys Rev A (2014) 89:042508. doi:10.1103/physreva.89.042508

CrossRef Full Text | Google Scholar

19. Xie H, Zeng B, Li G, Chu W, Zhang H, Jing C, et al. Coupling of N₂⁺ rotational states in an air laser from tunnel-ionized nitrogen molecules. Phys Rev A (2014) 90:042504. doi:10.1103/physreva.90.042504

CrossRef Full Text | Google Scholar

20. Liu Y, Brelet Y, Point G, Houard A, Mysyrowicz A. Self-seeded lasing in ionized air pumped by 800 nm femtosecond laser pulses. Opt Express (2013) 21:22791–8. doi:10.1364/oe.21.022791

PubMed Abstract | CrossRef Full Text | Google Scholar

21. Yao J, Li G, Jing C, Zeng B, Chu W, Ni J, et al. Remote creation of coherent emissions in air with two-color ultrafast laser pulses. New J Phys (2013) 15:023046. doi:10.1088/1367-2630/15/2/023046

CrossRef Full Text | Google Scholar

22. Li G, Jing C, Zeng B, Xie H, Yao J, Chu W, et al. Signature of superradiance from a nitrogen-gas plasma channel produced by strong-field ionization. Phys Rev A (2014) 89:033833. doi:10.1103/physreva.89.033833

CrossRef Full Text | Google Scholar

23. Xu H, Lötstedt E, Iwasaki A, Yamanouchi K. Sub-10-fs population inversion in N₂⁺ in air lasing through multiple state coupling. Nat Commun (2015) 6:8347–6. doi:10.1038/ncomms9347

PubMed Abstract | CrossRef Full Text | Google Scholar

24. Liu Y, Ding P, Lambert G, Houard A, Tikhonchuk V, Mysyrowicz A. Recollision-induced superradiance of ionized nitrogen molecules. Phys Rev Lett (2015) 115:133203. doi:10.1103/physrevlett.115.133203

PubMed Abstract | CrossRef Full Text | Google Scholar

25. Yao J, Jiang S, Chu W, Zeng B, Wu C, Lu R, et al. Population redistribution among multiple electronic states of molecular nitrogen ions in strong laser fields. Phys Rev Lett (2016) 116:143007. doi:10.1103/physrevlett.116.143007

PubMed Abstract | CrossRef Full Text | Google Scholar

26. Azarm A, Corkum P, Polynkin P. Optical gain in rotationally excited nitrogen molecular ions. Phys Rev A (2017) 96:051401. doi:10.1103/physreva.96.051401

CrossRef Full Text | Google Scholar

27. Britton M, Laferriere P, Ko DH, Li Z, Kong F, Brown G, et al. Testing the role of recollision in N₂⁺ air lasing. Phys Rev Lett (2018) 120:133208. doi:10.1103/physrevlett.120.133208

PubMed Abstract | CrossRef Full Text | Google Scholar

28. Zhang A, Liang Q, Lei M, Yuan L, Liu Y, Fan Z, et al. Coherent modulation of superradiance from nitrogen ions pumped with femtosecond pulses. Opt Express (2019) 27:12638–46. doi:10.1364/oe.27.012638

PubMed Abstract | CrossRef Full Text | Google Scholar

29. Mysyrowicz A, Danylo R, Houard A, Tikhonchuk V, Zhang X, Fan Z, et al. Lasing without population inversion in N₂⁺. APL Photon (2019) 4:110807. doi:10.1063/1.5116898

CrossRef Full Text | Google Scholar

30. Ando T, Lötstedt E, Iwasaki A, Li H, Fu Y, Wang S, et al. Rotational, vibrational, and electronic modulations in N₂⁺ lasing at 391 nm: Evidence of coherent (B² s_u⁺)-(X² Σ_g⁺)− (A²Π_u) coupling. Phys Rev Lett (2019) 123:203201. doi:10.1103/physrevlett.123.203201

PubMed Abstract | CrossRef Full Text | Google Scholar

31. Xie H, Lei H, Li G, Zhang Q, Wang X, Zhao J, et al. Role of rotational coherence in femtosecond-pulse-driven nitrogen ion lasing. Phys Rev Res (2020) 2:023329. doi:10.1103/physrevresearch.2.023329

CrossRef Full Text | Google Scholar

32. Tikhonchuk VT, Liu Y, Danylo R, Houard A, Mysyrowicz A. Theory of femtosecond strong field ion excitation and subsequent lasing in N₂⁺. New J Phys (2021) 23:023035. doi:10.1088/1367-2630/abd8bf

CrossRef Full Text | Google Scholar

33. Chen J, Yao J, Zhang Z, Liu Z, Xu B, Wan Y, et al. Electronic quantum coherence encoded in temporal structures of N₂⁺ lasing. Phys Rev A (2021) 103:033105. doi:10.1103/physreva.103.033105

CrossRef Full Text | Google Scholar

34. Zhang X, Lu Q, Zhang Z, Fan Z, Zhou D, Liang Q, et al. Coherent control of the multiple wavelength lasing of N₂⁺: Coherence transfer and beyond. Optica (2021) 8:668–73. doi:10.1364/optica.417804

CrossRef Full Text | Google Scholar

35. Yuan L, Liu Y, Yao J, Cheng Y. Recent advances in air lasing: A perspective from quantum coherence. Adv Quan Technol (2019) 2:1900080. doi:10.1002/qute.201900080

CrossRef Full Text | Google Scholar

36. Yao J, Wang L, Chen J, Wan Y, Zhang Z, Zhang F, et al. Photon retention in coherently excited nitrogen ions. Sci Bull (2021) 66:1511–7. doi:10.1016/j.scib.2021.04.001

CrossRef Full Text | Google Scholar

37. Zhang Z, Zhang F, Xu B, Xie H, Fu B, Lu X, et al. High-sensitivity gas detection with air-lasing-assisted coherent Raman spectroscopy. Ultrafast Sci (2022) 2022:1–8. doi:10.34133/2022/9761458

CrossRef Full Text | Google Scholar

38. Zhang F, Xie H, Yuan L, Zhang Z, Fu B, Yu S, et al. Background-free single-beam coherent Raman spectroscopy assisted by air lasing. Opt Lett (2022) 47:481–4. doi:10.1364/ol.441602

PubMed Abstract | CrossRef Full Text | Google Scholar

39. Lei H, Yao J, Zhao J, Xie H, Zhang F, Zhang H, et al. Ultraviolet supercontinuum generation driven by ionic coherence in a strong laser field. Nat Commun (2022) 13:4080–9. doi:10.1038/s41467-022-31824-0

PubMed Abstract | CrossRef Full Text | Google Scholar

40. Zhang Q, Xie H, Li G, Wang X, Lei H, Zhao J, et al. Sub-cycle coherent control of ionic dynamics via transient ionization injection. Commun Phys (2020) 3:50–6. doi:10.1038/s42005-020-0321-7

CrossRef Full Text | Google Scholar

41. Xie H, Lei H, Li G, Yao J, Zhang Q, Wang X, et al. Controlling the collective radiative decay of molecular ions in strong laser fields. Photon Res (2021) 9:2046–51. doi:10.1364/prj.434378

CrossRef Full Text | Google Scholar

42. Bacri J, Medani A. Electron diatomic molecule weighted total cross section calculation: III. Main inelastic processes for N₂ and N₂⁺. Physica B+ C (1982) 112:101–18. doi:10.1016/0378-4363(82)90136-x

CrossRef Full Text | Google Scholar

43. Bahati EM, Jureta JJ, Belic DS, Cherkani-Hassani H, Abdellahi MO, Defrance P. Electron impact dissociation and ionization of N₂⁺. J Phys B: Mol Opt Phys (2001) 34:2963–73. doi:10.1088/0953-4075/34/15/303

CrossRef Full Text | Google Scholar

44. Johnson AW, Fowler RG. Measured lifetimes of rotational and vibrational levels of electronic states of N₂. J Chem Phys (1970) 53:65–72. doi:10.1063/1.1673834

CrossRef Full Text | Google Scholar

45. Chauveau S, Perrin MY, Riviere P, Soufiani A. Contributions of diatomic molecular electronic systems to heated air radiation. J Quant Spectrosc Radiat Transfer (2002) 72:503–30. doi:10.1016/s0022-4073(01)00141-8

CrossRef Full Text | Google Scholar

46. Mehr FJ, Biondi MA. Electron temperature dependence of recombination of O₂⁺ and N₂⁺ ions with electrons. Phys Rev (1969) 181:264–71. doi:10.1103/physrev.181.264

CrossRef Full Text | Google Scholar

47. Johnsen R. Microwave afterglow measurements of the dissociative recombination of molecular ions with electrons. Int J Mass Spectrom Ion Process. (1987) 81:67–84. doi:10.1016/0168-1176(87)80006-x

CrossRef Full Text | Google Scholar

48. Brian J, Mitchell A. The dissociative recombination of molecular ions. Phys Rep (1990) 186:215–48. doi:10.1016/0370-1573(90)90159-y

CrossRef Full Text | Google Scholar

49. Jain A, Gupta DN, Suk H. Electron–ion recombination effect on electron acceleration by an intense laser pulse. IEEE Trans Plasma Sci (2019) 47:4891–7. doi:10.1109/tps.2019.2947283

CrossRef Full Text | Google Scholar

50. Allen L, Eberly JH. Optical resonance and two-level atoms. New York: Dover (1987).

Google Scholar

51. Cohen-Tannoudji C, Dupont-Roc J, Grynberg G. Atom-photon interactions: Basic processes and applications. New York: Wiley (1998).

Google Scholar

52. Wang Q, Chen R, Zhang Y, Wang X, Sun C, Ding P, et al. Populations of B²Σ_u⁺ and X²Σ_g⁺ electronic states of molecular nitrogen ions in air determined by fluorescence measurement. Phys Rev A (2021) 103:033117. doi:10.1103/physreva.103.033117

CrossRef Full Text | Google Scholar

53. Chin SL. Femtosecond laser filamentation. New York: Springer (2010).

Google Scholar

54. Malcuit MS, Maki JJ, Simkin DJ, Boyd RW. Transition from superfluorescence to amplified spontaneous emission. Phys Rev Lett (1987) 59:1189–92. doi:10.1103/physrevlett.59.1189

PubMed Abstract | CrossRef Full Text | Google Scholar

55. Schuurmans MF, Polder D. Superfluorescence and amplified spontaneous emission: A unified theory. Phys Lett A (1979) 72:306–8. doi:10.1016/0375-9601(79)90477-8

CrossRef Full Text | Google Scholar

56. Schuurmans MF. Superfluorescence and amplified spontaneous emission in an inhomogeneously broadened medium. Opt Commun (1980) 34:185–9. doi:10.1016/0030-4018(80)90011-5

CrossRef Full Text | Google Scholar

57. Maki JJ, Malcuit MS, Raymer MG, Boyd RW, Drummond PD. Influence of collisional dephasing processes on superfluorescence. Phys Rev A (1989) 40:5135–42. doi:10.1103/physreva.40.5135

PubMed Abstract | CrossRef Full Text | Google Scholar

58. Itikawa Y. Cross sections for electron collisions with nitrogen molecules. J Phys Chem Ref Data (2006) 35:31–53. doi:10.1063/1.1937426

CrossRef Full Text | Google Scholar

59. Yariv A. Quantum electronics. New York: Wiley (1989).

Google Scholar

60. Dicke RH. Coherence in spontaneous radiation processes. Phys Rev (1954) 93:99–110. doi:10.1103/physrev.93.99

CrossRef Full Text | Google Scholar

61. Bonifacio R, Schwendimann P, Haake F. Quantum statistical theory of superradiance. I. Phys Rev A (1971) 4:302–13. doi:10.1103/physreva.4.302

CrossRef Full Text | Google Scholar

62. MacGillivray JC, Feld MS. Theory of superradiance in an extended, optically thick medium. Phys Rev A (1976) 14:1169–89. doi:10.1103/physreva.14.1169

CrossRef Full Text | Google Scholar

63. Polder D, Schuurmans MF, Vrehen QH. Superfluorescence: Quantum-mechanical derivation of Maxwell-Bloch description with fluctuating field source. Phys Rev A (1979) 19:1192–203. doi:10.1103/physreva.19.1192

CrossRef Full Text | Google Scholar

64. Bonifacio R, Lugiato LA. Cooperative radiation processes in two-level systems: Superfluorescence. Phys Rev A (1975) 11:1507–21. doi:10.1103/physreva.11.1507

CrossRef Full Text | Google Scholar

65. Ding P. Lasing effect in femtosecond filaments in air. France: Université Paris-Saclay (2016). Ph.D. thesis.

Google Scholar

66. Calegari F, Vozzi C, Gasilov S, Benedetti E, Sansone G, Nisoli M, et al. Rotational Raman effects in the wake of optical filamentation. Phys Rev Lett (2008) 100:123006. doi:10.1103/physrevlett.100.123006

PubMed Abstract | CrossRef Full Text | Google Scholar

67. Langhoff SR, Bauschlicher CW. Theoretical study of the first and second negative systems of N₂⁺. J Chem Phys (1988) 88:329–36. doi:10.1063/1.454604

CrossRef Full Text | Google Scholar