Study on an SIR rumor propagation model with an interaction mechanism on WeChat networks

The spread of rumors does great harm to society. It will not only disrupt the social order but also damage public interests and even cause public safety and social shock. With the development of social platforms, it has become a fertile ground for rumors to breed and spread. The WeChat group as a very popular social platform is an important medium of rumor spreading with accurate and fast characteristics. In this paper, in order to describe the dynamic characteristics of rumors spread in WeChat groups, a susceptible–infected–removed rumor propagation model with an interaction mechanism and population dynamics on WeChat groups is proposed. In order to analyze the dynamic characteristics of the system, the next-generation matrix method is used to calculate the basic reproduction number of the proposed model. Then, the stability of a disease-free equilibrium point and a positive equilibrium point of the system is analyzed in detail. Finally, the accuracy of the analysis results is verified by numerical simulation. The research results are of great significance for controlling the rumors spread in WeChat groups.

1 Introduction

With the rapid development of Internet technology, it provides a broad space for information exchange among people. However, a large number of online rumors are generated without foundation or malice at the same time. These rumors not only seriously pollute the network environment and disrupt the public order but also seriously affect social stability and endanger national security [1–3]. If the public inadvertently become the audience of online rumors, it will gradually lose the right judgment and rational discrimination. In the long run, these audiences may believe these rumors and spread them widely on social networks [4]; [5].

The earliest research on the rumor propagation model originated in the 1960s. A large number of the existing rumor propagation models are derived from the epidemic model [6,7]. The DK model, as a basic rumor propagation model, was first proposed. [8,9] established a perfect mathematical theory and MK model for the rumor propagation model. However, the topological characteristics of social networks were not considered by DK and MK and were not suitable for the description of the rumor propagation mechanism in large-scale social networks. A matching model of rumor propagation based on dynamic behavior was proposed [10]. [11,12] established a small-world network rumor propagation model and calculated a propagation threshold. The dynamic mechanism of rumor propagation based on the scale-free network model was established [13–15]. The MK model was applied to the complex network model and described by the interactive Markov chain theory [16,17]. Furthermore, a rumor-spreading model in the homogeneous network called 2SIH2R was studied, in which there are both spreader 1 (people who spread the rumor) and spreader 2 (people who spread the truth) [18]. Considering the heterogeneity of the network, a 2SIH2R model was studied with the mechanisms of discernment and confrontation in a heterogeneous network to examine the dissemination of the rumor and the truth [19]. Taking the management and control of rumors by relevant departments in real life into account, the SIDRQ rumor-spreading model with the forgetting mechanism, immune mechanism, and suspicion mechanism and guides on a uniform network was established [20]. A novel susceptible–exposed–infected–recovered (SEIR)-delayed rumor propagation model with saturation incidence on heterogeneous networks was devoted to investigation [21].

The rumor propagation model with the forgetting mechanism on the online social blog LiveJournal was considered [22]. The results showed that there was an average threshold of influencing rumor saturation in LiveJournal. A mechanism based on the thermal theory was proposed to analyze the spread of rumors on large-scale social networks [23]. The results showed that the initial rumor maker and the probability of sending the rumor were greatly affected by the attraction of the rumor. The influence of the network structure on rumor propagation was studied [24]. The social reinforced rumor propagation model based on two-way emotion was considered [25]. A novel SIR susceptible–infected–removed (SIR) information propagation model based on the characteristics of the microblog was constructed [26]. However, in the real online social network, due to the influence of characteristics, educational background, personal legal awareness, and some other factors, some people cannot determine the authenticity of rumors when they are exposed to them. So, they will not spread immediately, which is a hesitation state. The rumor propagation model with the characteristics of the hesitation state was discussed, yet the conversion of hesitant nodes to immune nodes was not considered [27]. An SEIR rumor propagation model of heterogeneous networks was proposed and analyzed for propagation dynamics of the microblog rumor [28]. In order to study the influence of forcing silence on spreaders, a rumor propagation model with a silence-forcing function in online social networks was proposed [29]. By incorporating the dissemination of a rumor through groups in social and mobile networks and by considering the people’s cognitive factor (hesitate and forget), a new model on the rumor spreading process was presented [30].

In recent years, considering the individual activity and refutation mechanism simultaneously, a new multifactor model was proposed [31]. The structure of patches (nodes) is divided by connectivity distribution on metapopulation networks. A lot of research results for the dynamics of the infectious disease model among patches were invented based on the reaction–diffusion process [32–34]. Many epidemic models with demographic characteristics (such as birth and death) were considered [35]. In addition, some research results also considered the prevention and control strategies of rumor propagation [36,37].

WeChat, as a free application, is launched by Tencent to provide instant messaging services for intelligent terminals, including public platforms, circle of friends, message push, and other functions. As an important and popular social form, WeChat groups are widely used by the public. Therefore, WeChat groups have also become the hotbed of rumor propagation, which has the characteristics of accurate infection and rapid diffusion. Therefore, in this paper, an SIR rumor propagation model with an interaction mechanism and population dynamics on WeChat networks is proposed.

In Section 2, an SIR rumor propagation model with an interaction mechanism and population dynamics on WeChat networks is proposed. In order to analyze the dynamic characteristics of the system, the next-generation matrix method is used to calculate the basic reproduction number of rumor propagation. Then, the stability of a disease-free equilibrium point and a positive equilibrium point of the system is analyzed in detail. In Section 3, the accuracy of the analysis results is verified by numerical simulation. In the last section, we discuss and conclude the results of this paper.

2 Main content

In this section, an SIR rumor propagation model with an interaction mechanism and population dynamics on WeChat networks will be considered. Assume that each WeChat group is regarded as a patch (node), in which the particles (group members) construct a fully coupled network. From the perspective of rumor audience, we can divide particles into three categories in the patches: ignorants (S), spreaders (I), and stiflers (R). The symbols of population classification are shown in Table 1.

TABLE 1

TABLE 1. Description of symbols.

In WeChat groups, people will spread rumors from one WeChat group to other WeChat groups through forwarding and sharing, which forms an interactive mechanism for rumor spreading. We use a density symbol ρ, which means the proportion of particles in a patch. Therefore, we consider the population dynamics and interaction mechanism among patches, the rumor dynamics in the ith patch is given by the following expression.

$\left\{\begin{array}{c}\frac{d{\rho }_{Si}\left(t\right)}{dt}=B-\beta {\rho }_{Si}{\rho }_{Ii}-\mu {\rho }_{Si}-D_S{\rho }_{Si}+D_S\frac{i}{⟨k⟩}{\rho }_S,\hfill \\ \frac{d{\rho }_{Ii}\left(t\right)}{dt}=\beta {\rho }_{Si}{\rho }_{Ii}-\mu {\rho }_{Ii}-\gamma {\rho }_{Ii}{\rho }_{Ri}-D_I{\rho }_{Ii}+D_I\frac{i}{⟨k⟩}{\rho }_I,\hfill \\ \frac{d{\rho }_{Ri}\left(t\right)}{dt}=\gamma {\rho }_{Ii}{\rho }_{Ri}-\mu {\rho }_{Ri}-D_R{\rho }_{Ri}+D_R\frac{i}{⟨k⟩}{\rho }_R,\hfill \end{array}\right.(1)$

where B is the rate of newly added ignorants with degree i in WeChat groups. μ is the rate of ignorants, spreaders, and stiflers who exit from WeChat group with degree i. β is the rate of conversion from ignorants to spreaders. γ is the rate of conversion from spreaders to stiflers. D_S is the positive or negative interaction rate of ignorants in one WeChat group with other WeChat groups. D_I is the positive or negative interaction rate of spreaders in one WeChat group with other WeChat groups. D_R is the positive or negative interaction rate of stiflers in one WeChat group with other WeChat groups. ⟨k⟩ is the average degree of the whole WeChat group networks.

Next, we analyze the dynamic behavior of system (2.1). According to system (2.1), we can obtain Eq. 2 as follows:

$\left\{\begin{array}{c}B-\beta {\rho }_{Si}^{*}{\rho }_{Ii}^{*}-\mu {\rho }_{Si}^{*}-D_S{\rho }_{Si}^{*}+D_S\frac{i}{⟨k⟩}{\rho }_S^{*}=0,\hfill \\ \beta {\rho }_{Si}^{*}{\rho }_{Ii}^{*}-\mu {\rho }_{Ii}^{*}-\gamma {\rho }_{Ii}^{*}{\rho }_{Ri}^{*}-D_I{\rho }_{Ii}^{*}+D_I\frac{i}{⟨k⟩}{\rho }_I^{\ast }=0,\hfill \\ \gamma {\rho }_{Ii}^{*}{\rho }_{Ri}^{*}-\mu {\rho }_{Ri}^{*}-D_R{\rho }_{Ri}^{*}+D_R\frac{i}{⟨k⟩}{\rho }_R^{*}=0.\hfill \end{array}\right.(2)$

The dynamic behavior analysis of rumor spreading is closely related to the disease-free equilibrium. Let ${\rho }_{Ii}^{*}=0$ and ${\rho }_{Ri}^{*}=0$, then we obtain the equation as follows:

$\begin{array}{c}B-\mu {\rho }_{Si}^{*}-D_S\left({\rho }_{Si}^{*}-\frac{i}{⟨k⟩}{\rho }_S^{*}\right)=0.\hfill \end{array}(3)$

Therefore, the disease-free equilibrium of model (2.1) can be calculated and given by the following equation:

$\begin{array}{c}{\rho }_{Si}^{*}=\frac{B+D_S\frac{i}{⟨k⟩}{\rho }^0}{\mu +D_S},{\rho }_{Ii}^{*}=0,{\rho }_{Ri}^{*}=0,\hfill \end{array}(4)$

where ${\rho }^0={\rho }_S^{*}+{\rho }_I^{*}+{\rho }_R^{*}=\frac{B}{\mu }$.

Linearizing Eq. 1 around the disease-free equilibrium $({\rho }_{Si}^{*},\mathrm{0,0})$, it follows that the Jacobian matrix of Eq. 1 is a block matrix, which is given as follows:

$\left(\begin{array}{ccc}\hfill \left(\mu +D_S\right)\left(A-E\right)\hfill & \hfill \mathit{diag}\left(-\beta {\rho }_{Si}^{*}\right)\hfill & \hfill O\hfill \\ \hfill O\hfill & \hfill \left(\mu +D_I+\gamma \right)\left(A-E\right)+\mathit{diag}\left(\beta {\rho }_{Si}^{*}\right)\hfill & \hfill O\hfill \\ \hfill O\hfill & \hfill O\hfill & \hfill \left(\mu +D_R\right)\left(A-E\right)\hfill \end{array}\right),$

where each block is an N × N matrix with N being the number of degrees in the metapopulation, O is the null matrix, E is the identity matrix, diag(a_i) denotes a diagonal matrix whose ith element is a_i, and A is the connectivity matrix. According to the eigenvalues of matrix A, in order to ensure the stability of the disease-free equilibrium point of system (2.1), the following inequality needs to be satisfied:

$1<\frac{⟨k⟩}{i_{\max }{\rho }^0}\frac{\left(\mu +D_S\right)\left(\mu +\gamma +D_I\right)\left(\mu +D_R\right)-\beta B}{\beta D_S}.$

Then, the basic reproduction number R₀ can be obtained as follows:

$\begin{array}{c}{R}_0=\frac{i_{\max }{\rho }^0}{⟨k⟩}\frac{\beta D_S}{\left(\mu +D_S\right)\left(\mu +\gamma +D_I\right)\left(\mu +D_R\right)-\beta B},\hfill \end{array}(5)$

where i_max represents the max degree of the particles.

Theorem 2.1: If R₀ < 1, system (2.1) has a unique disease-free equilibrium, and it is globally asymptotically stable; if R₀ > 1, the disease-free equilibrium is unstable.Proof. In order to determine the global stability of the disease-free equilibrium point, we define the Lyapunov function $V=\frac{1}{2}{\rho }_{Ii}^2$ ([38]). We have

$\begin{array}{ll}\hfill \frac{dV}{dt}& ={\rho }_{Ii}\frac{d{\rho }_{Ii}}{dt}\hfill \\ \hfill & =\left(\frac{i{\rho }^0}{\langle k\rangle }\beta D_S+\beta B-\left(\mu +D_S\right)\left(\mu +\gamma +D_I\right)\right){\rho }_{Ii}^2\hfill \\ \hfill & \le \left(\frac{i_{\mathit{max}}{\rho }^0}{\langle k\rangle }\beta D_S+\beta B-{\left(\mu +D_S\right)}^2\left(\mu +\gamma +D_I\right)\right){\rho }_{Ii}^2\hfill \\ \hfill & =\left(R_0-1\right){\rho }_{Ii}^2.\hfill \end{array}$

If R₀ < 1, then $\left(R_0-1\right){\rho }_{Ii}^2<0$.

Also, we have $\frac{dV}{dt}\le 0$ and $\frac{dV}{dt}=0$ if and only if ρ_Ii = 0. By using the principle of the LaSalle invariant set, we can see that the disease-free equilibrium point of system (2.1) is globally asymptotically stable when R₀ < 1. If R₀ > 1, the disease-free equilibrium is unstable.Theorem 2.2: If R₀ > 1, system (2.1) has a unique endemic equilibrium $E^{*}=\{{\rho }_{I1}^{*},{\rho }_{I2}^{*},\dots ,{\rho }_{In}^{*}\}$, where E* is globally asymptotically stable.Proof. We define a function using the second equation of system (2.1) as follows: f: G → G, $G=\left\{{\rho }_{Ii}(t)|t\in R^{+},{\rho }_{Ii}(t)\ge 0\right\}$ yields

$f\left({\rho }_{Ii}\left(t\right)\right)=\beta {\rho }_{Si}{\rho }_{Ii}-\mu {\rho }_{Ii}-\gamma {\rho }_{Ii}{\rho }_{Ri}-D_I{\rho }_{Ii}+D_I\frac{i}{⟨k⟩}{\rho }_I.(6)$

By using Corollary 3.2 of [39], we know that f: G → G is a continuous differentiable function, and $Df\left({\rho }_{Ii}(t)\right)$ is irreducible for any ρ_Ii(t) > 0, ρ_Ii(t) ∈ G; then, for any θ ∈ (0, 1) and ρ_Ii(t) > 0, we have

$\begin{array}{ll}\hfill f\left(\sigma {\rho }_{Ii}\left(t\right)\right)& =\beta {\rho }_{Si}\sigma {\rho }_{Ii}-\mu \sigma {\rho }_{Ii}-\gamma \sigma {\rho }_{Ii}{\rho }_{Ri}-D_I\sigma {\rho }_{Ii}+D_I\frac{i}{⟨k⟩}\sigma {\rho }_I\hfill \\ \hfill & =\beta \left({\rho }_{Ni}-{\rho }_{Ri}-\sigma {\rho }_{Ii}\right)\sigma {\rho }_{Ii}-\mu \sigma {\rho }_{Ii}-\gamma \sigma {\rho }_{Ii}{\rho }_{Ri}-D_I\sigma {\rho }_{Ii}+D_I\frac{i}{⟨k⟩}\sigma {\rho }_I\hfill \\ \hfill & \ge \sigma \beta \left({\rho }_{Ni}-{\rho }_{Ri}-{\rho }_{Ii}\right){\rho }_{Ii}-\sigma \gamma {\rho }_{Ii}{\rho }_{Ri}-\sigma D_I{\rho }_{Ii}+\sigma D_I\frac{i}{⟨k⟩}{\rho }_I\hfill \\ \hfill & =\sigma f\left({\rho }_{Ii}\right).\hfill \end{array}$

Hence, $f\left({\rho }_{Ii}(t)\right)$ is sublinear. According to Lemma 2.1 and Corollary 3.2 in (X.Q [40]), system (2.1) has a unique endemic equilibrium E*, which is globally asymptotically stable.Theorem 2.3: If R₀ > 1, system (2.1) has a unique endemic equilibrium $E_{*}=\{{\rho }_{S1}^{*},{\rho }_{S2}^{*},\dots ,{\rho }_{Sn}^{*},{\rho }_{I1}^{*},{\rho }_{I2}^{*},\dots ,{\rho }_{In}^{*}{\rho }_{R1}^{*},{\rho }_{R2}^{*},\dots ,{\rho }_{Rn}^{*}\}$, where E_* is globally asymptotically stable.Proof. Set ϕ(t): R⁺ → R⁺; let it be a solution semiflow of the third equation of system (2.1), and ϕ(t) is a finite set. Assume ω is an internal propagation chain set of ϕ(t) [40].

Obviously, there are only two equilibrium points for the system, if R₀ ≤ 1, there is a disease-free equilibrium point E₀. If R₀ > 1, there is a unique endemic equilibrium point E_*.

Next, we prove that ω has only one endemic equilibrium, that is, ω = {E_*}.

If the aforementioned conclusion is not true, then ω = {E₀}. Therefore, there is

$\underset{t\to \infty }{\lim }{\rho }_{Si}\left(t\right)=\frac{B+D_S\frac{i}{⟨k⟩}{\rho }^0}{\mu +D_S},\underset{t\to \infty }{\lim }{\rho }_{Ii}\left(t\right)=0,\underset{t\to \infty }{\lim }{\rho }_{Ri}\left(t\right)=0.(7)$

If R₀ > 1, the spectral radius s(M₁) is defined for the eigenmatrix FV⁻¹ of system (2.1) at E₀ [39]. Here, the expressions of F and V are followed as

$F=\left(\begin{array}{c}\hfill \beta {\rho }_{Si}{\rho }_{Ii}\hfill \\ \hfill O\hfill \\ \hfill \gamma {\rho }_{Ii}{\rho }_{Ri}\hfill \end{array}\right),V=\left(\begin{array}{c}\hfill \mu {\rho }_{Ii}+\gamma {\rho }_{Ii}{\rho }_{Ri}+D_I{\rho }_{Ii}-D_I\frac{i}{⟨k⟩}{\rho }_I\hfill \\ \hfill -B+\beta {\rho }_{Si}{\rho }_{Ii}+\mu {\rho }_{Si}+D_S{\rho }_{Si}-D_S\frac{i}{⟨k⟩}{\rho }_S\hfill \\ \hfill \mu {\rho }_{Ri}+D_R{\rho }_{Ri}-D_R\frac{i}{⟨k⟩}{\rho }_R\hfill \end{array}\right).$

Choose any one ɛ > 0 small enough to make s(M₁+ɛM₂) > 0, where M₂ = diag(σ₁, σ₂, … , σ_n). Then, there is 1 t′, for any t > t′ so that

$\beta \left({\rho }_{Ni}-{\rho }_{Ri}-{\rho }_{Ii}\right)>\beta {\rho }_{Ni}^{*}-\epsilon ,(8)$

where ${\rho }_{Ni}^{*}=\frac{B+D_S\frac{i}{⟨k⟩}{\rho }^0}{\mu +D_S}$. Hence, we have

$\frac{d{\rho }_{Ii}\left(t\right)}{dt}>\beta \left({\rho }_{Ni}^{*}-\epsilon \right){\rho }_{Ii}\left(t\right)-\mu {\rho }_{Ii}-\gamma {\rho }_{Ii}{\rho }_{Ri}-D_I{\rho }_{Ii}+D_I\frac{i}{⟨k⟩}{\rho }_I.(9)$

Let v be a positive eigenvector of M₁+ɛM₂ associated with s(M₁+ɛM₂), then choose an arbitrarily small number ζ satisfying I ≥ ζv. According to the comparison theorem, we have

${\rho }_{Ii}\left(t\right)\ge e^{s\left(M_1+\epsilon M_2\right)\left(t-t^{\prime }\right)}v,t\ge t^{\prime }.(10)$

Therefore, if t → ∞, this is contrary to the hypothesis lim_t→∞ρ_Ii(t) = 0, then the unique positive equilibrium solution E_* of the system is globally asymptotically stable.

3 Numerical simulation

In this section, we present numerical simulations to support the results obtained in previous sections. In order to simulate the solutions of the system, we consider the case that the model with three patches. Suppose that the average degree of interaction among each patch and the other two patches is 1, 2, and 3, respectively, and the average degree of the whole network is 10. First, the system with three patches is considered by the following equation:

$\left\{\begin{array}{c}\frac{d{\rho }_{S1}\left(t\right)}{dt}=B_1-{\beta }_1{\rho }_{S1}{\rho }_{I1}-{\mu }_1{\rho }_{S1}-D_{S1}\left({\rho }_{S1}-\frac{1}{10}\left({\rho }_{S1}+{\rho }_{S2}+{\rho }_{S3}\right)\right),\hfill \\ \frac{d{\rho }_{I1}\left(t\right)}{dt}={\beta }_1{\rho }_{S1}{\rho }_{I1}-{\mu }_1{\rho }_{I1}-{\gamma }_1{\rho }_{I1}{\rho }_{R1}-D_{I1}\left({\rho }_{I1}-\frac{1}{10}\left({\rho }_{I1}+{\rho }_{I2}+{\rho }_{I3}\right)\right),\hfill \\ \frac{d{\rho }_{R1}\left(t\right)}{dt}={\gamma }_1{\rho }_{I1}{\rho }_{R1}-{\mu }_1{\rho }_{R1}-D_{R1}\left({\rho }_{R1}-\frac{1}{10}\left({\rho }_{R1}+{\rho }_{R2}+{\rho }_{R3}\right)\right),\hfill \\ \frac{d{\rho }_{S2}\left(t\right)}{dt}=B_2-{\beta }_2{\rho }_{S2}{\rho }_{I2}-{\mu }_2{\rho }_{S2}-D_{S2}\left({\rho }_{S2}-\frac{1}{5}\left({\rho }_{S1}+{\rho }_{S2}+{\rho }_{S3}\right)\right),\hfill \\ \frac{d{\rho }_{I2}\left(t\right)}{dt}={\beta }_2{\rho }_{S2}{\rho }_{I2}-{\mu }_2{\rho }_{I2}-{\gamma }_2{\rho }_{I2}{\rho }_{R2}-D_{I2}\left({\rho }_{I2}-\frac{1}{5}\left({\rho }_{I1}+{\rho }_{I2}+{\rho }_{I3}\right)\right),\hfill \\ \frac{d{\rho }_{R2}\left(t\right)}{dt}={\gamma }_2{\rho }_{I2}{\rho }_{R2}-{\mu }_2{\rho }_{R2}-D_{R2}\left({\rho }_{R2}-\frac{1}{5}\left({\rho }_{R1}+{\rho }_{R2}+{\rho }_{R3}\right)\right),\hfill \\ \frac{d{\rho }_{S3}\left(t\right)}{dt}=B_3-{\beta }_3{\rho }_{S3}{\rho }_{I3}-{\mu }_3{\rho }_{S3}-D_{S3}\left({\rho }_{S3}-\frac{3}{10}\left({\rho }_{S1}+{\rho }_{S2}+{\rho }_{S3}\right)\right),\hfill \\ \frac{d{\rho }_{I3}\left(t\right)}{dt}={\beta }_3{\rho }_{S3}{\rho }_{I3}-{\mu }_3{\rho }_{I3}-{\gamma }_3{\rho }_{I3}{\rho }_{R3}-D_{I3}\left({\rho }_{I3}-\frac{3}{10}\left({\rho }_{I1}+{\rho }_{I2}+{\rho }_{I3}\right)\right),\hfill \\ \frac{d{\rho }_{R3}\left(t\right)}{dt}={\gamma }_3{\rho }_{I3}{\rho }_{R3}-{\mu }_3{\rho }_{R3}-D_{R3}\left({\rho }_{R3}-\frac{3}{10}\left({\rho }_{R1}+{\rho }_{R2}+{\rho }_{R3}\right)\right).\hfill \end{array}\right.(11)$

Next, we consider the effect of different parameters on the stability of system (3.1), which is analyzed with two different cases of the initial values and is given as follows.

Case 1: ρ_S1(0), ρ_I1(0), ρ_R1(0), ρ_S1(0), ρ_I1(0), ρ_R1(0), ρ_S1(0), ρ_I1(0), and ρ_R1(0) are, respectively, equal to 0.1, 0.02, 0.06, 0.2, 0.04, 0.08, 0.3, 0.06, and 0.14.

Case 2: ρ_S1(0), ρ_I1(0), ρ_R1(0), ρ_S1(0), ρ_I1(0), ρ_R1(0), ρ_S1(0), ρ_I1(0), and ρ_R1(0) are, respectively, equal to 0.25, 0.02, 0.06, 0.25, 0.02, 0.06, 0.25, 0.02, and 0.06.

Based on the aforementioned two cases of initial values, we consider the stability of the system with the effect of different factors, such as the newly added rate, infection rate, interaction rate, and recovery rate. Then, assume

$D_{S1}=D_{I1}=D_{R1}=D_1,D_{S2}=D_{I2}=D_{R2}=D_2,D_{S3}=D_{I3}=D_{R3}=D_3.$

3.1 Different newly added rates

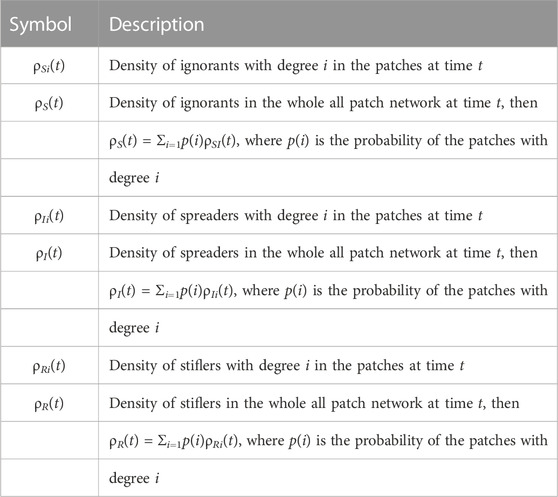
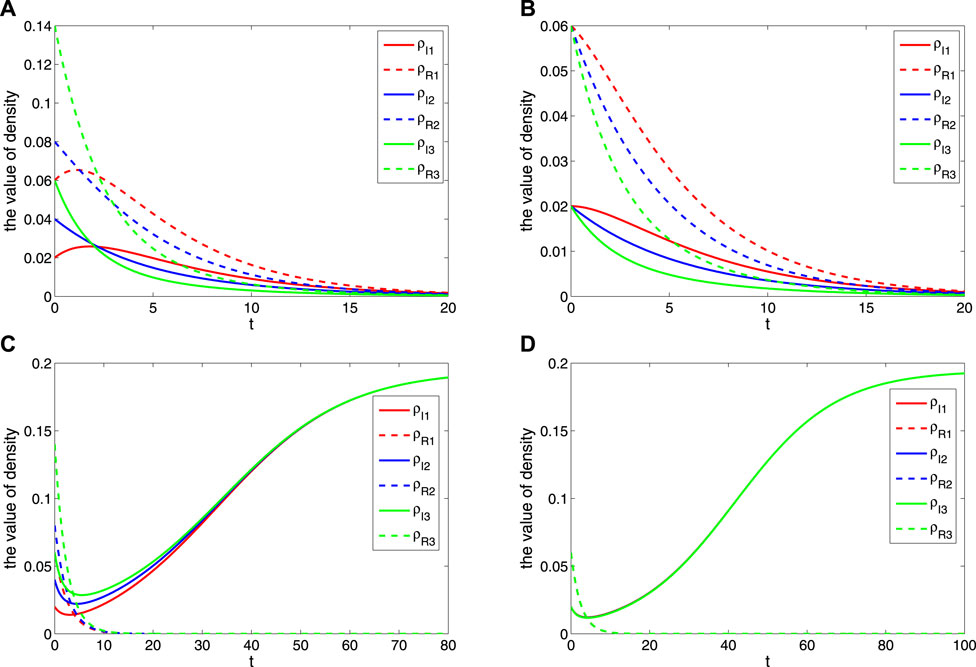
Here, the parameters B₁ = 0.01, B₂ = 0.04, B₃ = 0.07, β₁ = β₂ = β₃ = 0.5, μ₁ = μ₂ = μ₃ = 0.02, D₁ = D₂ = D₃ = 0.4, and γ₁ = γ₂ = γ₃ = 0.2. According to Eq. 5, it can be calculated by R₀ = 0.9537 < 1. It can be seen that the spread of rumors is also increasing with the growth of the newly added rate, which is shown in Figure 1A and Figure 1B. However, the rumor will eventually die out for a long time with the growth of the newly added rate. When the parameters are set with B₁ = 0.3, B₂ = 0.5, and B₃ = 0.7, it can be calculated by R₀ = 1.3636 > 1. It can be seen that the spread of rumors formed the stable state of a local equilibrium point with the growth of the newly added rate, which is shown in Figure 1C and Figure 1D.

FIGURE 1

FIGURE 1. Effect of different newly added rates on the stability of rumor spreading.

3.2 Different infection rates

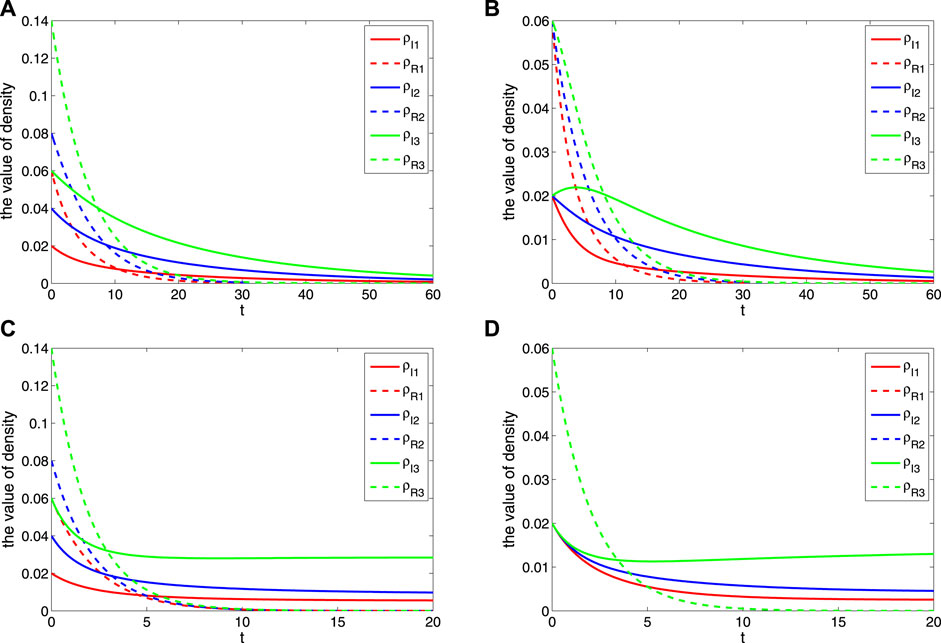
Here, the parameters B₁ = B₂ = B₃ = 0.03, β₁ = 0.2, β₂ = 0.5, β₃ = 0.8, μ₁ = μ₂ = μ₃ = 0.02, D₁ = D₂ = D₃ = 0.4, and γ₁ = γ₂ = γ₃ = 0.2. According to Eq. 5, it can be calculated by R₀ = 0.9537 < 1. It can be seen that the spread of rumors also increased with the increase of the infection rate, which is shown as Figure 2A and Figure 2B. However, because of the existence of suppressors, the rumors will eventually die out. When the parameters are set with B₁ = B₂ = B₃ = 0.5, β₁ = 0.6, β₂ = 0.5, and β₃ = 0.4, it can be calculated by R₀ = 1.9474 > 1. It can be seen that the spread of rumors formed the stable state of a local equilibrium point with the growth of the infection rate, which is shown in Figure 2C and Figure 2D.

FIGURE 2

FIGURE 2. Effect of different infection rates on the stability of rumor spreading.

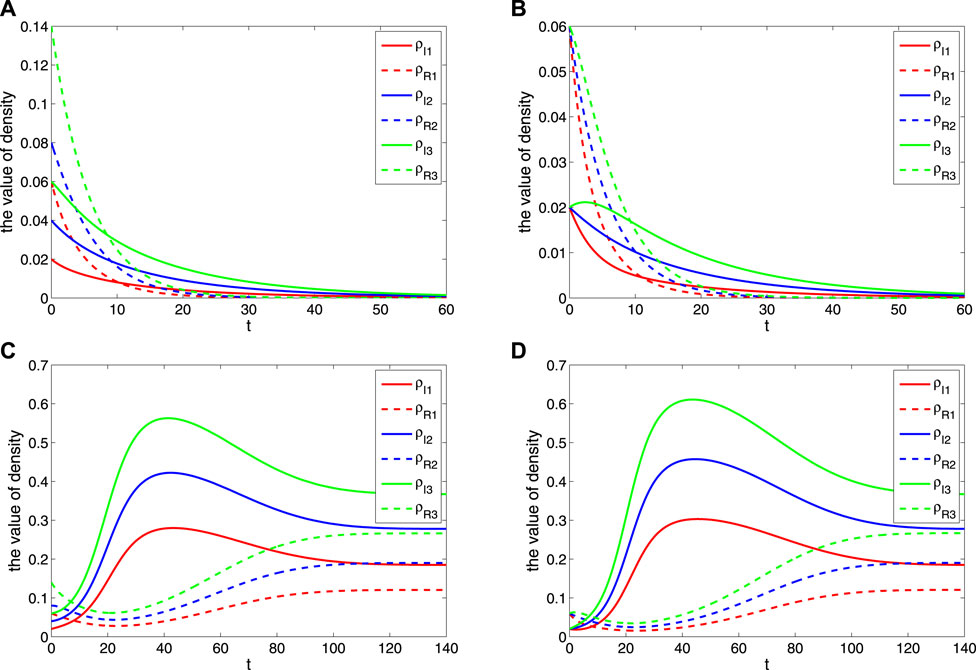
3.3 Different interaction rates

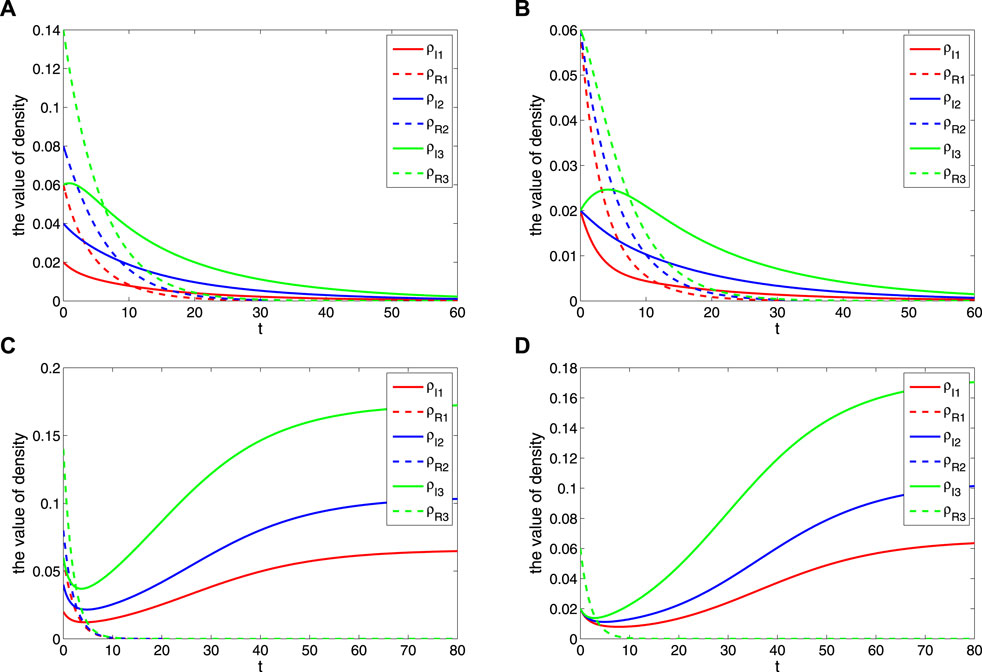
Here, the parameters B₁ = B₂ = B₃ = 0.03, β₁ = β₂ = β₃ = 0.5, μ₁ = μ₂ = μ₃ = 0.02, D₁ = 0.4, D₂ = 0.6, D₃ = 0.8, and γ₁ = γ₂ = γ₃ = 0.2. According to Eq. 5, it can be seen that the spread of rumors also increased with the increase of the interaction rate, which is shown in Figure 3A and Figure 3B. However, because of the existence of suppressors, the rumors will eventually die out. When the parameters are set with B₁ = B₂ = B₃ = 0.5, D₁ = 0.4, D₂ = 0.6, and D₃ = 0.8, it can be calculated by R₀ = 1.3636 > 1. It can be seen that the spread of rumors formed the stable state of a local equilibrium point with the growth of the interaction rate, which is shown in Figure 3C and Figure 3D.

FIGURE 3

FIGURE 3. Effect of different interaction rates on the stability of rumor spreading.

3.4 Different recovery rates

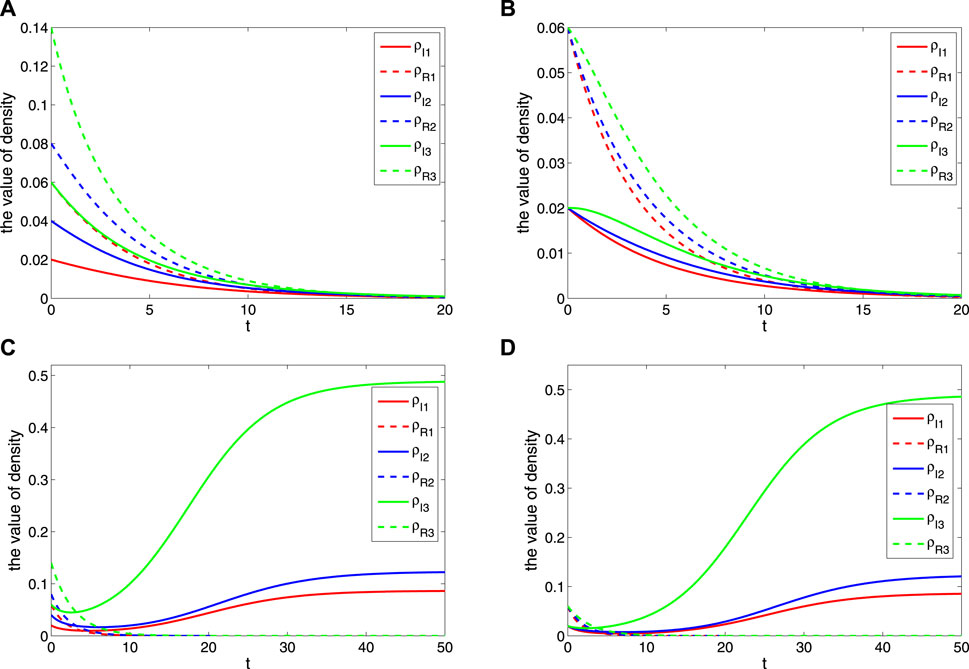
Here, the parameters B₁ = B₂ = B₃ = 0.03, β₁ = β₂ = β₃ = 0.5, μ₁ = μ₂ = μ₃ = 0.02, D₁ = D₂ = D₃ = 0.4, γ₁ = 0.2, γ₂ = 0.5, and γ₃ = 0.8. According to Eq. 5, it can be seen that the spread of rumors also increased with the increase of the recovery rate in a short term, which is shown in Figure 4A and Figure 4B. However, with the increasing number of suppressors, the rumors will eventually die out quickly. When the parameters are set with B₁ = B₂ = B₃ = 0.5, γ₁ = 0.3, γ₂ = 0.5, and γ₃ = 0.7, it can be calculated by R₀ = 2.160 > 1. It can be seen that the spread of rumors formed the stable state of a local equilibrium point with the growth of the recovery rate, which is shown in Figure 4C and Figure 4D.

FIGURE 4

FIGURE 4. Effect of different recovery rates on the stability of rumor spreading.

3.5 Increase in the degree of patches

Here, the parameters B₁ = B₂ = B₃ = 0.03, β₁ = β₂ = β₃ = 0.5, μ₁ = μ₂ = μ₃ = 0.02, D₁ = D₂ = D₃ = 0.4, and γ₁ = γ₂ = γ₃ = 0.2; it can be seen that the spread of rumors also increased with the growth of the degree of patches in a short term, which is shown in Figure 5A and Figure 5B. However, with the increasing number of suppressors, the rumors will eventually die out quickly. When the degree of patches is increased, namely, $\frac{i}{⟨k⟩}$ are 0.2, 0.3, and 0.4, respectively. It can be seen from Figure 5C and Figure 5D that the stability of rumor spreading changes from the disease-free equilibrium to the local equilibrium.

FIGURE 5

FIGURE 5. Effect of the degree of patches on the stability of rumor spreading.

4 Conclusion

The WeChat group is a very popular social platform and also an important medium for spreading rumors. Based on the classic SIR epidemic model, in this paper, an SIR rumor propagation model with an interaction mechanism and population dynamics on WeChat networks was proposed. In order to analyze the dynamic characteristics of the system, the next-generation matrix method is used to calculate the basic reproduction number of the system model. When R₀ < 1, the disease-free equilibrium was gradually stable. When R₀ > 1, the disease-free equilibrium was unstable. Then, the stability of a disease-free equilibrium point and a positive equilibrium point of the system is analyzed in detail. In numerical simulation, the influence of different parameters (the newly added rate, infection rate, interaction rate, recovery rate, and the degree of patches) on the stability of the system was considered. Meanwhile the accuracy of the analysis results was verified. The results of this study had a certain reference for controlling rumor spreading in the WeChat group.

Data availability statement

The original contributions presented in the study are included in the article/supplementary material; further inquiries can be directed to the corresponding author.

Author contributions

XC, the author, is fully responsible for the research work of this manuscript, including the modeling and analysis of infectious diseases, the simulation of infectious disease models, and the writing of the manuscript.

Funding

This research is supported by the China Postdoctoral Science Foundation under Grant 2021M692400 and the Fundamental Research Program of Shanxi Province under Grant 202203021211091.

Acknowledgments

The authors would like to thank the referees for helpful comments which resulted in much improvement of the manuscript.

Conflict of interest

The author declares that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors, and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

1. Galam S. Modelling rumors: The no plane pentagon French hoax case. Physica A (2003) 320:571–80. doi:10.1016/s0378-4371(02)01582-0

CrossRef Full Text | Google Scholar

2. Grein TW, Kamara KB, Rodier G, Plant AJ, Bovier P, Ryan MJ, et al. Rumors of disease in the global village: Outbreak verification. Emerging Infect Dis (2000) 6:97–102. doi:10.3201/eid0602.000201

PubMed Abstract | CrossRef Full Text | Google Scholar

3. Thomas S. Lies, damn lies, and rumors: An analysis of collective efficacy, rumors, and fear in the wake of katrina. Sociological Spectr (2007) 27:679–703. doi:10.1080/02732170701534200

CrossRef Full Text | Google Scholar

4. Liu DC. Rumor propagation in online social networks like twitter simulation study. In: 2011 The Third International Conference on Multimedia Information Networking and Security; Nov. 4 2011 to Nov. 6 2011; Shanghai, China (2011). p. 278–82.

Google Scholar

5. Kim JH. A study on the factors affecting the behavior of spreading online rumors: Focusing on the rumor recipient¡^– s emotions. In: PACIS 2011 Proceedings; 7-11 July 2011; Pacific Asia, Brisbane, Queensland, Australia (2011). p. 98–106.

Google Scholar

6. Anderson RM. Infectious diseases of humans. Oxford, United Kingdom: Oxford University Press (1992).

Google Scholar

7. Hethcote H. The mathematics of infectious diseases. SIAM Rev (2000) 42:599–653. doi:10.1137/s0036144500371907

CrossRef Full Text | Google Scholar

8. Daley DJ, Kendall DG. Epidemics and rumours. Nature (1964) 204:1118–8. doi:10.1038/2041118a0

PubMed Abstract | CrossRef Full Text | Google Scholar

9. Maki D. Mathematical models and applications. United States: Prentice-Hall (1973).

Google Scholar

10. Sudbury A. The proportion of the population never hearing a rumour. J Appl Probab (1985) 22:443–6. doi:10.1017/s0021900200037906

CrossRef Full Text | Google Scholar

11. Zanette D. Critical behavior of propagation on small-world networks. Phys Rev E (2001) 64:050901. doi:10.1103/physreve.64.050901

PubMed Abstract | CrossRef Full Text | Google Scholar

12. Zanette D. Dynamics of rumor propagation on small-world networks. Phys Rev E (2002) 65:041908. doi:10.1103/physreve.65.041908

PubMed Abstract | CrossRef Full Text | Google Scholar

13. Moreno Y, A P, Nekovee M. Dynamics of rumor spreading in complex networks. Phys Rev E (2004) 69:066130. doi:10.1103/physreve.69.066130

PubMed Abstract | CrossRef Full Text | Google Scholar

14. Moreno Y, A V, Nekovee M. Efficiency and reliability of epidemic data dissemination in complex networks. Phys Rev E (2004) 69:055101. doi:10.1103/physreve.69.055101

PubMed Abstract | CrossRef Full Text | Google Scholar

15. Moreno Y, Vespignani A., Pastor-Satorras R. Epidemic outbreaks in complex heterogeneous networks. Eur Phys J (2002) 26:521–9. doi:10.1140/epjb/e20020122

CrossRef Full Text | Google Scholar

16. Nekovee M, Bianconi G, Moreno Y, Marsili M. Theory of rumour spreading in complex social networks. Physica A (2007) 374:457–70. doi:10.1016/j.physa.2006.07.017

CrossRef Full Text | Google Scholar

17. Isham V, M N, Harden S. Stochastic epidemics and rumours on finite random networks. Physica A (2010) 389:561–76. doi:10.1016/j.physa.2009.10.001

CrossRef Full Text | Google Scholar

18. Wang Y, Qing F, Ni YP. Spreading dynamics of a 2sih2r, rumor spreading model in the homogeneous network. Complexity (2021) 2021:1–9. doi:10.1155/2021/6693334

CrossRef Full Text | Google Scholar

19. Wang Y, M Y, Qing F. Dynamics of 2sih2r rumor-spreading model in a heterogeneous network. Wireless Commun Mobile Comput (2022) 2022:1–13. doi:10.1155/2022/7398387

CrossRef Full Text | Google Scholar

20. Zhang W, X. L HL, Deng HY, Liu H. Dynamics of the rumor-spreading model with control mechanism in complex network. J Math (2022) 2022:1–17. doi:10.1155/2022/5700374

CrossRef Full Text | Google Scholar

21. Chen SS, Jiang HJ, Li J. Dynamical behaviors and optimal control of rumor propagation model with saturation incidence on heterogeneous networks. Chaos Solitons Fractals (2020) 140:110206. doi:10.1016/j.chaos.2020.110206

CrossRef Full Text | Google Scholar

22. Zhao LJ, J. C YC, J. W WH, Wang Q, Chen Y, Wang J, et al. Rumor spreading model with consideration of forgetting mechanism: A case of online blogging livejournal. Physica A (2011) 390:2619–25. doi:10.1016/j.physa.2011.03.010

CrossRef Full Text | Google Scholar

23. Han S, Q. H Z, S. X A, Zhuang FZ, Shi Z, Ao X. Energy model for rumor propagation on social networks. Physica A (2014) 394:99–109. doi:10.1016/j.physa.2013.10.003

CrossRef Full Text | Google Scholar

24. Zhou J, Li B, Liu ZH. Influence of network structure on rumor propagation. Phys Lett A (2007) 368:458–63. doi:10.1016/j.physleta.2007.01.094

CrossRef Full Text | Google Scholar

25. Ma J, Tian Z, Li D. Rumor spreading in online social networks by considering the bipolar social reinforcement. Physica A (2016) 447:108–15. doi:10.1016/j.physa.2015.12.005

CrossRef Full Text | Google Scholar

26. Su Q, Zhao X, Huang J. An information propagation model considering incomplete reading behavior in microblog. Physica A (2015) 419:55–63. doi:10.1016/j.physa.2014.10.042

CrossRef Full Text | Google Scholar

27. Xia L, B. S YS, Jiang G. Rumor spreading models considering hestitating mechanism in complex social networks. Physica A (2015) 437:295–303. doi:10.1016/j.physa.2015.05.113

CrossRef Full Text | Google Scholar

28. Liu QM, M S, Li T. The analysis of an seir rumor propagation model on heterogeneous network. Physica A (2017) 469:372–80. doi:10.1016/j.physa.2016.11.067

CrossRef Full Text | Google Scholar

29. Zhu LH, Wang B. Stability analysis of a sair rumor spreading model with control strategies in online social networks. Inf Sci (2020) 526:1–19. doi:10.1016/j.ins.2020.03.076

CrossRef Full Text | Google Scholar

30. Myilsamy K, Satheesh Kumar A, Kumar MS. Optimal control of a rumor model with group propagation over complex networks. Int J Mod Phys C (2021) 329(3):2150035. doi:10.1142/s0129183121500352

CrossRef Full Text | Google Scholar

31. Li RQ, Li YW, Song Y, Jiang G. Rumor spreading model considering individual activity and refutation mechanism simultaneously. IEEE Access (2020) 8:63065–76. doi:10.1109/access.2020.2983249

CrossRef Full Text | Google Scholar

32. Saldana J. Continuous-time formulation of reaction-diffusion processes on heterogeneous metapopulations. Phys Rev E (2008) 78:012902. doi:10.1103/physreve.78.012902

CrossRef Full Text | Google Scholar

33. Juher D, Saldana J, Ripoll J. Analysis and Monte Carlo simulations of a model for the spread of infectious diseases in heterogeneous metapopulations. Phys Rev Lett (2009) 80:041920. doi:10.1103/physreve.80.041920

PubMed Abstract | CrossRef Full Text | Google Scholar

34. Masuda N. Effects of diffusion rates on epidemic spreads in metapopulation networks. New J Phys (2010) 12:093009. doi:10.1088/1367-2630/12/9/093009

CrossRef Full Text | Google Scholar

35. Zhang F, Zhao SQ. A periodic epidemic model in a patchy environment. J Math Anal Appl (2007) 325:496–516. doi:10.1016/j.jmaa.2006.01.085

CrossRef Full Text | Google Scholar

36. Tong X, Jiang H, Yu S, Li J. Dynamic analysis and optimal control of rumor spreading model with recurrence and individual behaviors in heterogeneous networks. Entropy (2022) 24:464. doi:10.3390/e24040464

PubMed Abstract | CrossRef Full Text | Google Scholar

37. Wang Y, L W, Qing F. Rumor dynamic model considering intentional spreaders in social network. Discrete Dyn Nat Soc (2022) 2022:1–10. doi:10.1155/2022/6044099

CrossRef Full Text | Google Scholar

38. Zuo LX, Liu M. Effect of awareness programs on the epidemic outbreaks with time delay. Abstract Appl Anal (2014) 2:1–8. doi:10.1155/2014/940841

CrossRef Full Text | Google Scholar

39. van den Driessche P, Watmough J. Reproduction numbers and sub-threshold endemic equilibria for compartmental models of disease transmission. Math Biosci (2002) 180:29–48. doi:10.1016/s0025-5564(02)00108-6

PubMed Abstract | CrossRef Full Text | Google Scholar

40. Zhao XQ. Global asymptotic behavior in some cooperative systems of functional differential equations. Appl Math Quart (1996) 4:421–44.

Google Scholar