- School of Mathematical Sciences, Jiangsu University, Zhenjiang, China
We consider the unbiased random walk on the Sierpinski network (Sn◦N) and the half Sierpinski network (HSn◦N), where n is the generation. Different from the existing works on the Sierpinski gasket, Sn◦N is generated by the nested method and HSn◦N is half of Sn◦N based on the vertical cutting of the symmetry axis. We study the hitting time on Sn◦N and HSn◦N. According to the complete symmetry and structural properties of Sn◦N, we derive the exact expressions of the hitting time on the nth generation of Sn◦N and HSn◦N. The curves of the hitting time for the two networks are almost consistent when n is large enough. The result indicates that the diffusion efficiency of HSn◦N has not changed greatly compared with Sn◦N at a large scale.
1 Introduction
In recent decades, complex networks have attracted great interest in the scientific community [1,2] and are considered valuable tools for describing real-world systems in the nature and society [3]. They also have a significant impact on mobility patterns, network sampling, community detection, signal transmission, virus spreading, epidemic control, and link prediction [4,5]. In recent years, complex networks have not only been studied in the field of mathematics due to their intersectionality and complexity but also more scholars in other disciplines have begun to pay attention to them, which involves system science, statistical physics, computer and information science, etc. [6–9] Common analysis methods and tools include the graph theory, combinatorial mathematics, matrix theory, probability theory, and stochastic process.
A fractal is a rough or fragmented geometric shape that can be divided into multiple parts, and each part is approximately a reduced-version copy of the whole. According to this definition, a fractal feature is a property known as self-similarity, which means that a fractal has self-similarity [10–13]. In recent years, fractals have attracted a surge of attention in various scientific fields [14,15]. The fractal theory [16,17] has always been a very popular and active theory. This is due to the self-similar structure that exists and the crucial impact of the idea of fractals on a large variety of scientific disciplines, such as molecular biology, pharmaceutical chemistry, optics, economics, and ecology [18]. In addition, many complex networks and real networks are generated by the self-similar fractal network [19–22]. There are many classical fractal models, such as the Cantor set, the Koch curve, and the Sierpinski gasket [23,24]. These structures have obviously become the focus of research, and many potential characterizations have been discovered. In 25–36, the network evolved from the Sierpinski carpet and some vital properties of the Sierpinski gasket were considered.
It has a great theoretical and practical significance to study the hitting time of random walks, which is the mean of the first-passage time of a random walker starting from any site on the network to a trap (a perfect absorber). It can characterize various other dynamical processes taking place on the network, such as mobility patterns and virus spreading. For example, in the communication and information industry, the hitting time of a random walk model can be used to study and simulate information transmission and latency, data collection, quantification and the prediction of communication and search costs, etc. In the field of biology, random walk models can be used to study and describe the spread of infectious diseases and metabolic fluxes among organisms. In the computer industry, the study of characteristics results in community detection, computer vision, collaborative recommendation, and image segmentation. It also describes the diffusion efficiency of different networks. Kozak and Balakrishnan [37,38] studied random walks on a two-dimensional Sierpinski gasket, three-dimensional Sierpinski tower, and d-dimensional Sierpinski model and gave the analytical expression of the hitting time. Wu [39] studied the random walk on the half Sierpinski gasket and gave the formula for the hitting time. Qi [40] got the expression of the hitting time for several absorbing random walks on Sierpinski graphs and hierarchical graphs.
In this paper, we study random walks and discuss the hitting time on the Sierpinski network model (Sn◦N) and the half Sierpinski network model (HSn◦N) obtained by vertically cutting Sn◦N based on the symmetry axis. Compared with Sn◦N, the global self-similarity structure of HSn◦N is lost, and only the local self-similarity is preserved. We expect to obtain the exact expression of the hitting time on HSn◦N from the complete symmetry of Sn◦N and show whether there is any effect on the diffusion efficiency of the cut network. The mathematical combination method and fractal theory are applied. The remainder of this paper is organized as follows: in Section 2, we introduce our models. In Section 3, we have a detailed calculation of the hitting time of Sn◦N. Also, the detailed calculation of the hitting time of HSn◦N is given in Section 4. In the last section, we draw the conclusion.
2 Preliminaries
In this section, we introduce the structure of Sn◦N and HSn◦N and some concepts about several types of random walks, which will be used in the following.
2.1 The structure of Sn◦N and HSn◦N
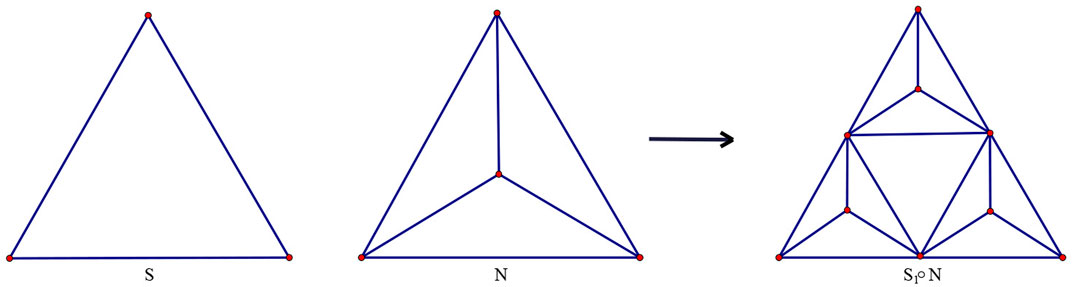
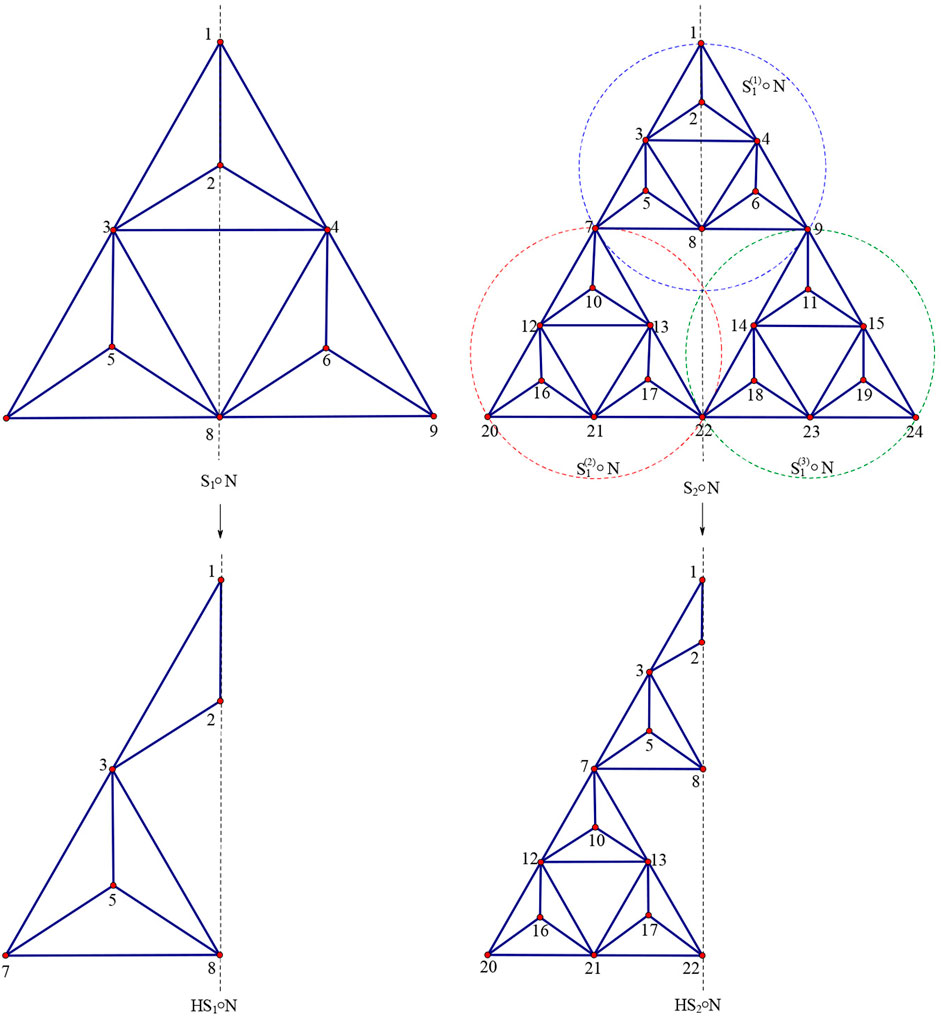
Actually, Sn◦N can be constructed in a nested manner with a self-similar structure. We separately define a triangle and a 3-regular graph as S and N. As shown in Figure 1, we can make three copies of the 3-regular graph N and then embed N into S by nodes to obtain the initial generation, which is recorded as S1◦N. Making three copies of S1◦N and then embedding the initial generation S1◦N into S to produce the second generation is known as S(S1◦N). For the convenience of the following description, the second generation is abbreviated as S2◦N. We get the nth generation S(Sn−1◦N) by repeating the aforementioned process, making three copies of Sn−1◦N and then embedding the (n−1)th generation Sn−1◦N into S, which is abbreviated as Sn◦N. Specifically, Sn◦N is divided into three parts marked as
As shown in the lower half of Figure 2, HSn◦N is obtained by cutting the corresponding Sn◦N along the vertical symmetry axis. The cutting method of the network cannot equally divide all the nodes because vertices on the partition line will be retained during segmentation.
From the aforementioned construction, we can easily derive the total number of nodes on Sn◦N and HSn◦N to be
The three connecting vertices C1, C2, and C3, which are named after connecting the three regions
In addition, we use
2.2 Calculation of intermediate quantities
The hitting time is the mean of the first-passage time of a random walker starting from any site on the network to a trap node. In order to determine the hitting time for Sn◦N, we introduce the following intermediate quantities, all of which are the probability of a Markov chain on Sn◦N ending at corner node 1. In the process, the chain starts at a certain vertex and stops whenever it visits any of the three corner nodes of Sn◦N, where n is the generation.
pn: The starting state is a corner node other than site 1. At least one transition is performed.
p1(n): The starting state is a special vertex belonging to
p2(n): The starting state is a special vertex belonging to
The first equality of the equation group is explained. A random walk in Sn+1◦N, starting from the corner node L and ending whenever the walker reaches any three corner nodes of Sn+1◦N, is limited to jumping at least one step. By definition, the walker stops at the corner node R or 1 with probability pn+1. In addition, the walker must first reach a connecting vertex C1 or C3 in order to reach one of the corner nodes R or 1. By definition and symmetry, the probability of reaching each of the connecting vertices C1 or C3 is pn, where the connecting vertex C1 belongs to
We next certify the second equality in the equation system (Eq. 5). Considering a random walk in Sn+1◦N, which starts from the connecting vertex C1 and ends whenever the walker reaches any three corner nodes of Sn+1◦N, it jumps at least one step. By definition, the probability that the walker stops at corner node 1 is p1(n + 1). The probability of getting in
Ultimately, we testify to the third equality of the system of Eq. 5. A random walk in Sn+1◦N, starting from the connecting vertex C3 and ending whenever the walker reaches any three corner nodes of Sn+1◦N, jumps at least one step. By definition, the probability that the walker stops at corner node 1 is p2(n + 1). The probability of getting into
It is easy to know that the initial value
We next define the corresponding hitting time. Corner nodes 1, L, and R are represented by set A, where site 1 is set as the trap node; connecting vertices C1, C2, and C3 are indicated by set I.
TL→1(n): The hitting time from the corner node L to the corner node 1 in the nth generation.
TL→A(n): The hitting time from the corner node L to any node in set A in the nth generation.
TI→A(n): The hitting time from any vertex in set I to any node in set A in the nth generation.
We now attest to the first equality in the equation system (Eq. 7). TL→1(n) is the hitting time for a random walk in Sn◦N starting from the corner node L and ending at the trap node 1. According to the structure of Sn◦N, the walker must first reach any of the three corner nodes of Sn◦N in order to reach trap node 1, taking expected timesteps TL→A(n). In such a process, the probability of reaching destination node 1 is pn, where the walker stops jumping. Also, the probability of reaching corner nodes R and L is 1−pn, from which the walker must continue to bounce TL→1(n) steps to reach trap node 1. Thus, we get the first expression.
Subsequently, we prove the second equality in the equation system (Eq. 7). TL→A(n + 1) is the hitting time for a random walk starting from the corner node L to any of the three corner nodes of Sn+1◦N for the first time, under the limitation that the walker jumps at least one step. In order to reach any of corner nodes in Sn+1◦N, the walker starting from the corner node L must first visit one of the corner nodes in Sn◦N. It is worth noting that these points belong to
Ultimately, we testify to the third equality of the system in Eq. 7. Consider a random walk, which starts from any one of the connecting nodes C1, C2, and C3 and ends whenever it reaches any corner nodes on Sn+1◦N. By definition, the hitting time is TI→A(n + 1). We now study the random walk from the connecting vertex C3, which may perform the following two processes. Both processes happen with the probability of
By substituting the value of
3 Formula of hitting time on Sn◦N
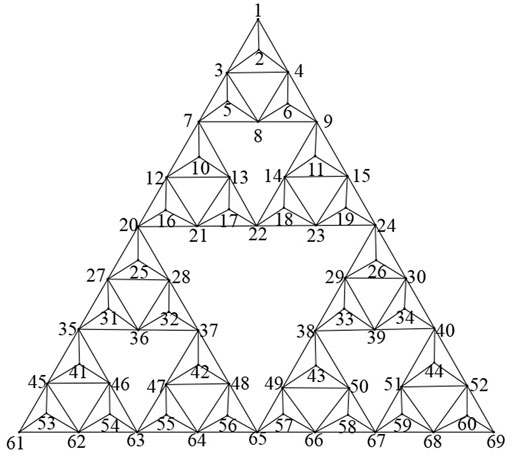
The Sierpinski network in any given generation n, using arrays (a, b, c) to represent a piece of interior points, for instance, (2, 5, 6) or (10, 16, 17), as shown in Figure 3; let (I1, J1, K1) label the three vertices of the smallest triangle containing the three interior points (a, b, c), simultaneously, for instance, (1, 7, 9) or (7, 20, 22). According to the numerical results, the hitting time can be rewritten as follows:
Let (i1, j1, k1) label the three sites, which are one of any minimum size 1 lacunary triangle on Sn◦N. For example, (3, 4, 8) or (12, 13, 21); (I1, J1, K1) also label the three vertices of the triangle containing (i1, j1, k1) as its central lacunary region, such as (1, 7, 9) or (7, 20, 22), referring to Figure 3. According to the numerical results, it is easy to see the following:
In the same way, we now let (i2, j2, k2) denote the three vertices of a lacunary region of size 2 in the network, such as (7, 9, 22) or (35, 37, 63); (I2, J2, K2) label the three vertices of the triangle containing (i2, j2, k2) as its central lacunary region, such as (1, 20, 24) or (20, 61, 65). It then follows the scaling derived previously that is as follows:
Therefore, moving up the hierarchy, if (ir, jr, kr) are the sites demarcating a lacunary triangle of size r in the ascending order of size, starting from the smallest in size 1, and if (Ir, Jr, Kr) label the vertices of the triangle with (ir, jr, kr) as the central lacunary region, then
The foregoing suggests how the hitting time Ttotal(n) may be computed for the arbitrary n. This is carried out by suitably regrouping the terms in the sum
Thus, Ttotal(3) has been recast in terms of the sum (T1 + TL + TR) of the hitting time from the three primary sites. The meaning of 32 of the second term on the right side of the equation is that there are nine pieces of interior points in S3◦N. It should be noted that the modulus 32 of the third term represents the number of regions of size 1, the coefficient 31 of the factor multiplying 9 ⋅ 51 is the number of lacunary triangles of size 2, and 30 of the factor multiplying 9 ⋅ 52 is the number of lacunary triangles of size 3 on the n = 3 network.
We may now carry out a similar procedure for the case of general n. The analog of Eq. 13 yields the following:
The numerical value is substituted to get the following result:
Therefore, the hitting time on Sn◦N is as follows:
4 Formula of hitting time on HSn◦N
We divide the random walk into two processes on Sn◦N and HSn◦N, except node 2. The first process is that a walker starts from the starting point to node 3 or 4, which is the sum of the hitting time called Tg(n). The second procedure is a random walk from node 3 or 4 to the trap node, which is called T3(n). In addition, T2(n) denotes the hitting time from site 2 to trap node 1.
Similarly, the first process of HSn◦N is a random walk from any site to node 3, and the hitting time of this process is recorded as Hg(n). The second process is recorded as H3(n), and H2(n) represents the hitting time from site 2 to trap node 1 on HSn◦N. Thence, we have the following equations:
Let Tr(n) be the mean of the first return time for a random walker starting from node 3 in the first process of HSn◦N. Then, Tr(n) can also be the mean of the first return time to node 3 or 4 in the first process of Sn◦N. Therefore, according to the structure of HSn◦N and Sn◦N, we have the following relationship:
Moreover, from the numerical results, we have T2(n) = 3 ⋅ 3n and H2(n) = 2 ⋅ 3n. So, we get the following relation:
Because the nodes on the cut line are retained, the hitting time Ti(n) from any node i on the secant line to the goal node 1 is also divided into two parts. The first process is a random walk from node i to node 3 or 4, which is denoted as Ti→3,4(n). The hitting time of the second process is denoted as T3(n), which represents a random walk from site 3 to destination node 1. Therefore, Ti(n) can be rewritten as follows:
Consequently, the formula for the hitting time of nodes that belong to
In Sn◦N, in addition to the nodes on the secant line, other nodes are evenly divided on both the sides in the segmentation process. HSn◦N contains the nodes on the left half of the secant line and the nodes in set
Eqs 17 and 20 are inserted into the aforementioned formula to get the following solution:
Then, substituting the aforementioned expression (Eq. 22) into the second formula in the equation group (Eq. 17), we get the following:
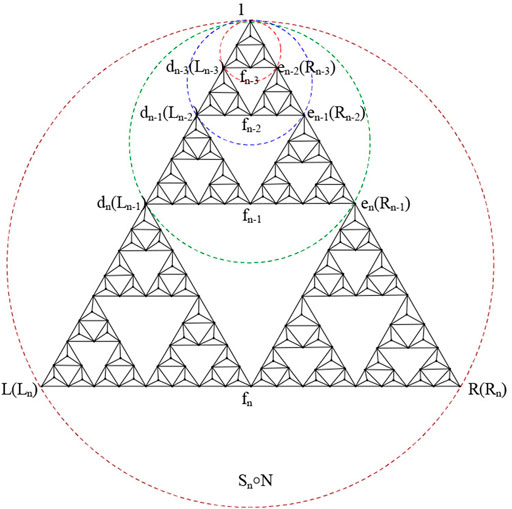
We focus on solving the expression of Tf(n). In order to facilitate the calculation, we rewrite the three connecting vertices C1, C2, and C3 of Sn◦N as dn, en, and fn, respectively. According to the structural characteristics of Sn◦N, the sites dn and en in the nth generation can be labeled as the corner nodes Ln−1 and Rn−1 in the (n−1)th generation. The labeling method of nodes on Sn◦N can be seen in Figure 4.
If corner nodes 1, Ln, and Rn are set as goal nodes, then the walker starting from site fy(y = 1, …, n) is captured by the trap set A after 3 ⋅ 5y−1 random walks on average in Sn◦N, which can be seen from the analysis of the equation group (Eq. 7) and results. In addition, the arriving node Ly or Ry has a probability of
Similarly, starting from the point dy+1(y = 1,…, n) and getting to the site Ly or Ry has a probability of
Here,
Therefore, substituting Eq. 15 and Eq. 25 into Eq. 23, the expression of Htotal(n) is as follows:
Then, the hitting time on HSn◦N is as follows:
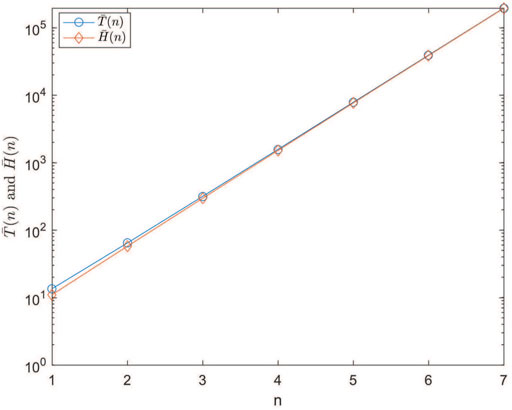
In order to compare it with the exact formula for the hitting time of a random walk on Sn◦N and HSn◦N, we draw the numerical simulation diagram of
5 Conclusion
In this paper, we study analytically the unbiased random walk on the Sierpinski network (Sn◦N) and the half Sierpinski network (HSn◦N), which is obtained by vertically cutting Sn◦N along the symmetry axis. After cutting, the global self-similarity of Sn◦N is destroyed, but only the local self-similarity is maintained. We have analytically obtained the closed-form expression of the hitting time for a random walk on the nth generation HSn◦N, which is
Data availability statement
The original contributions presented in the study are included in the article/Supplementary Material, further inquiries can be directed to the corresponding author.
Author contributions
All authors listed have made a substantial, direct, and intellectual contribution to the work and approved it for publication.
Conflict of interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
The handling editor declared a shared affiliation with the authors at the time of review.
Publisher’s note
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors, and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
References
2. Wang XF, Chen G. Synchronization in scale-free dynamical networks: Robustness and fragility. IEEE Trans Circuits Syst (2002) 49:54–62. doi:10.1109/81.974874
3. Guimera R, Amaral LAN. Functional cartography of complex metabolic networks. nature (2005) 433:895–900. doi:10.1038/nature03288
4. Grubesic TH, Matisziw TC, Zook MA. Global airline networks and nodal regions. GeoJournal (2008) 71:53–66. doi:10.1007/s10708-008-9117-0
5. Deng F-G, Li X-H, Li C-Y, Zhou P, Zhou H-Y. Quantum secure direct communication network with einstein–podolsky–rosen pairs. Phys Lett A (2006) 359:359–65. doi:10.1016/j.physleta.2006.06.054
6. Batool A, Pál G, Danku Z, Kun F. Transition from localized to mean field behaviour of cascading failures in the fiber bundle model on complex networks. Chaos, Solitons & Fractals (2022) 159:112190. doi:10.1016/j.chaos.2022.112190
7. Cotilla-Sanchez E, Hines PD, Barrows C, Blumsack S, Patel M. Multi-attribute partitioning of power networks based on electrical distance. IEEE Trans Power Syst (2013) 28:4979–87. doi:10.1109/tpwrs.2013.2263886
8. Jung J, Jin W, Kang U. Random walk-based ranking in signed social networks: Model and algorithms. Knowl Inf Syst (2020) 62:571–610. doi:10.1007/s10115-019-01364-z
9. Bai S, Niu M. Spectral properties of a class of treelike networks generated by motifs with single root node. Mod Phys Lett B (2022) 36:2250038. doi:10.1142/s0217984922500385
10. Li B-G, Yu Z-G, Zhou Y. Fractal and multifractal properties of a family of fractal networks. J Stat Mech (2014) 2014:P02020. doi:10.1088/1742-5468/2014/02/p02020
11. Zhou Y, Leung Y, Yu Z-G. Relationships of exponents in two-dimensional multifractal detrended fluctuation analysis. Phys Rev E (2013) 87:012921. doi:10.1103/physreve.87.012921
12. Chen J, Dai M, Wen Z, Xi L. A class of scale-free networks with fractal structure based on subshift of finite type. Chaos (2014) 24:043133. doi:10.1063/1.4902416
13. Wang Q, Xi L, Zhang K. Self-similar fractals: An algorithmic point of view. Sci China Math (2014) 57:755–66. doi:10.1007/s11425-013-4767-x
14. Babič M, Mihelič J, Calì M. Complex network characterization using graph theory and fractal geometry: The case study of lung cancer dna sequences. Appl Sci (2020) 10:3037. doi:10.3390/app10093037
15. Wang Z, Zhou Y, Bajenaid AS, Chen Y. Design of wireless sensor network using statistical fractal measurements. Fractals (2022) 30:2240092. doi:10.1142/s0218348x22400928
16. Klafter J, Blumen A, Zumofen G. Fractal behavior in trapping and reaction: A random walk study. J Stat Phys (1984) 36:561–77. doi:10.1007/bf01012922
17. Zhang P, Zhang Y, Huang Y, Xia Y. Experimental study of fracture evolution in enhanced geothermal systems based on fractal theory. Geothermics (2022) 102:102406. doi:10.1016/j.geothermics.2022.102406
18. Blumen A, Klafter J, Zumofen G. Trapping and reaction rates on fractals: A random-walk study. Phys Rev B (1983) 28:6112–5. doi:10.1103/physrevb.28.6112
19. Rammal R. Random walk statistics on fractal structures. J Stat Phys (1984) 36:547–60. doi:10.1007/bf01012921
20. Hughes B, Montroll E, Shlesinger M. Fractal and lacunary stochastic processes. J Stat Phys (1983) 30:273–83. doi:10.1007/bf01012302
21. Mandelbrot BB, Mandelbrot BB. The fractal geometry of nature, 1. New York: W. H. Freeman (1982).
22. Chen J, Dai M, Wen Z, Xi L. Trapping on modular scale-free and small-world networks with multiple hubs. Physica A: Stat Mech its Appl (2014) 393:542–52. doi:10.1016/j.physa.2013.08.060
23. Barlow MT, Bass RF. Transition densities for brownian motion on the sierpinski carpet. Probab Theor Relat Fields (1992) 91:307–30. doi:10.1007/bf01192060
24. Zhou Z, Wu M. The hausdorff measure of a sierpinski carpet. Sci China Ser A-math (1999) 42:673–80. doi:10.1007/bf02878985
25. Kajino N. Heat kernel asymptotics for the measurable riemannian structure on the sierpinski gasket. Potential Anal (2012) 36:67–115. doi:10.1007/s11118-011-9221-5
26. Grabner PJ. Functional iterations and stopping times for brownian motion on the sierpiński gasket. Mathematika (1997) 44:374–400. doi:10.1112/s0025579300012699
27. Wu S, Zhang Z, Chen G. Random walks on dual sierpinski gaskets. Eur Phys J B (2011) 82:91–6. doi:10.1140/epjb/e2011-20338-0
28. Wu S, Zhang Z. Eigenvalue spectrum of transition matrix of dual sierpinski gaskets and its applications. J Phys A: Math Theor (2012) 45:345101. doi:10.1088/1751-8113/45/34/345101
29. Guyer R. Diffusion on the sierpiński gaskets: A random walker on a fractally structured object. Phys Rev A (Coll Park) (1984) 29:2751–5. doi:10.1103/physreva.29.2751
30. Hattori K. Displacement exponent for loop-erased random walk on the sierpiński gasket. Stochastic Process their Appl (2019) 129:4239–68. doi:10.1016/j.spa.2018.11.021
31. Lara PCS, Portugal R, Boettcher S. Quantum walks on sierpinski gaskets. Int J Quan Inform (2013) 11:1350069. doi:10.1142/s021974991350069x
32. Bedrosian SD, Sun X. Theory and application of pascal-sierpinski gasket fractals. Circuits Syst Signal Process (1990) 9:147–59. doi:10.1007/bf01236448
33. Shima T. On eigenvalue problems for the random walks on the sierpinski pre-gaskets. Jpn J Ind Appl Math (1991) 8:127–41. doi:10.1007/bf03167188
34. Chen J, Gao F, Le A, Xi L, Yin S. A small-world and scale-free network generated by sierpinski tetrahedron. Fractals (2016) 24:1650001. doi:10.1142/s0218348x16500018
35. Chen J, Le A, Wang Q, Xi L. A small-world and scale-free network generated by sierpinski pentagon. Physica A: Stat Mech its Appl (2016) 449:126–35. doi:10.1016/j.physa.2015.12.089
36. Xi L. Differentiable points of sierpinski-like sponges. Adv Math (2020) 361:106936. doi:10.1016/j.aim.2019.106936
37. Kozak JJ, Balakrishnan V. Analytic expression for the mean time to absorption for a random walker on the sierpinski gasket. Phys Rev E (2002) 65:021105. doi:10.1103/physreve.65.021105
38. Kozak JJ, Balakrishnan V. Exact formula for the mean length of a random walk on the sierpinski tower. Int J Bifurcation Chaos (2002) 12:2379–85. doi:10.1142/s0218127402006138
39. Wu B, Zhang Z. The average trapping time on a half sierpinski gasket. Chaos, Solitons & Fractals (2020) 140:110261. doi:10.1016/j.chaos.2020.110261
Keywords: hitting time, half Sierpinski networks, vertical cutting, random walk, fractal
Citation: Sun Y, Liu X and Li X (2022) Hitting time for random walks on the Sierpinski network and the half Sierpinski network. Front. Phys. 10:1076276. doi: 10.3389/fphy.2022.1076276
Received: 21 October 2022; Accepted: 23 November 2022;
Published: 09 December 2022.
Edited by:
Dun Han, Jiangsu University, ChinaReviewed by:
Lifeng Xi, Ningbo University, ChinaZu-Guo Yu, Xiangtan University, China
Min Niu, University of Science and Technology Beijing, China
Copyright © 2022 Sun, Liu and Li. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Yu Sun, c3VueXU4OHN5QDE2My5jb20=
 Yu Sun
Yu Sun Xiaobei Liu
Xiaobei Liu Xiaoyan Li
Xiaoyan Li