- 1Department of Basic Sciences, Faculty of Arts and Educational Sciences, Middle East University, Amman, Jordan
- 2Department of Mathematics, Faculty of Science, Al Balqa Applied University, Salt, Jordan
- 3Department of Mathematics, Faculty of Science, The University of Jordan, Amman, Jordan
Studying and analyzing the random motion of a particle immersed in a liquid represented in the Langevin fractional model by Caputo’s independent derivative is one of the aims of applied physics. In this article, we will attend to a new, accurate, and comprehensive numerical solution to the aforementioned model using the reproducing kernel Hilbert approach. Basically, numerical and exact solutions of the fractional Langevin model are represented using an infinite/finite sum, simultaneously, in the
1 Introduction
The Langevin equation, in its fractional issue, is a mathematical dynamic model fundamental in Brownian motion applications to characterize the emergence of physical episodes in oscillating mediums. It is a popularization of the conventional model that utilizes a fractional Gaussian procedure formalized by two vertices, which is much more adaptable to the parameterization of the fractal evolution processes [1–4]. The applications of the FLM can be seen in the stock market, motor control system modeling, photoelectron counting, fluid suspensions, deuteron-cluster dynamics, protein dynamics, evacuation process modeling, financial markets, single-file diffusion, and anomalous transport [5–8]. Commonly, FDMs have wide applications in the formation of many engineering and fluid physics phenomena. In the second half of the last century, the search for more serious numerical algorithms began to control many of the nonlinear problems that appeared with the emergence of fractional derivatives and their emerging applications. However, many studies came into existence, as in the following literature [9–13]. To date, effective analytical and numerical schemes have been developed and successfully applied to deal with different classes of FDMs [14–20].
Although finding accurate solutions to FDMs of different orders in Brownian particle motion placements is an important problem for understanding the dynamic attitudes of oscillatory environments in trifling media, in this article, we contemplate creating an accurate numerical solution to FLMs utilizing the CFD with appropriate boundary data using a new renewal in the RKHA. Here, we will generate effective and straightforward numerical solutions without imposing any restrictions on the nature of the proposed FLM and obtain sufficient convergence while reducing the computation time by exposure to the following model [1–8]:
equipped with the posterior boundary condition:
Typically, the FDM (Eqs 1, 2) consists of the posterior parameters, functions, and variable effects as attached:
1)
2)
3)
4)
6)
7)
8)
Ordinarily, no conventional schemes produce an accurate prototype solution for FLMs. Thus, there is a great need for the RKHA, which satisfies the purpose, as usual, and has reached the desired and satisfactory numerical results with fully stochastic properties. Here, the relevant theories and facts have been confirmed by numeric emulations, graphical representation, and scale tables for three types of FLMs. However, the tenor of the paper is arranged as follows: Section 1: Presentation: FDMs and CFDs. Section 2: RKHA: Preliminaries and definitions. Section 3: RKHA: Construction and properties. Section 4: RKHA: Solutions and convergence. Section 5: Error: Estimation and bound. Section 6: Justifications: Algorithms, applications, and analyses. Section 7: Outline: Conclusion and outlook.
2 Reproducing kernel: Preliminaries and definitions
The approach of the reproducing kernel is a novel solver built to find solutions to FDMs emerging in physics, waves, statistics, and engineering [21–23]. This technique is based on the Gram–Schmidt process and Fourier expansion approach for an arbitrary order and is used for optimizing an orthogonal basis to detect unknown compounds. The RKHA has many motivational aspects and a great ability to handle complicated problems without imposing any restrictions on the style of the models. Therefore, it has been gaining a lot of solicitude and examination lately [24–32].
First, a reproducing kernel induced from a given Hilbert space is called the RKHA. Here,
Remark 1. [24] The frameworks of
Remark 2. [24] The frameworks of
with
Definition 1 The framework of
Here, one can find that
Theorem 1. If
Proof: Because
or
Theorem 2. If
Proof: Since
Taking
To complete, one can get
3 Reproducing kernel: Construction and properties
Herein, the boundaries in Eq. 2 will first be homogenized to zero to obtain easy-to-access modeling in the proposed
To achieve this, one must first carry out the following:
equipped with the posterior boundary condition:
For the briefing, the normalizing modified version in Eqs 13, 14 was obtained from the posterior underlying conversion, taking into account that all the extra terms transformed into
The conversions in Eqs 15, 16 are needful to insert the equipped boundaries in Eq. 2 inside
1) Define the map
2) Build the
3) Reframe the FLM problem to solve such that
Theorem 3.
Proof: From Remark 1, one can obtain
Using the reproducing property of
With the use of the Schwarz inequality, one can obtain
So
Theorem 4.
Proof: First,
So
So
4 Reproducing kernel: Solutions and convergence
This section aims to construct exact and RKHA numeric solutions of Eq. 19, together with some convergence theories, to ensure this analysis is more efficient. Here,
If
Theorem 5. Suppose that
1) As
2) The RKHA numeric solution,
Proof: For the first side: Through Theorem 4,
For the second side: Because
Remark 3. Assume that
Theorem 6. Assume that
with
Theorem 7. One gains
So
it is adequate to have for
with
Theorem 8. Assume that
Sequentially, if
5 Error: Estimation and bound
As a matter of fact, the exact solution of FDMs (Eqs 1, 2) restricted with the CFD depends on
Here, we will fix
Lemma 1. One gains
In other words,
Lemma 2. Assume that
Proof: Clearly,
On
So
with
Theorem 9. A parameter
Proof: Utilizing Lemma 3, one can obtain
However, since
Applying Theorem 2, one can obtain
In another mode, one can obtain
However, as
6 Justifications: Algorithms, applications, and analyses
To clarify the portability and effectiveness of the presented numeric approach, we need some of the steps, the first of which is to provide sufficient algorithms to demonstrate the mechanism of the solution, the second of which is to present several tangible applications, and then finally to provide several tables, figures, and numeric explanations of the solution procedures. However, all of this is the content of the following sections.
6.1 Algorithms
Next, three used algorithms in our RKHA implementation are given. These algorithms are problem initialization, the Gram–Schmidt process, and RKHA solution steps, simultaneously. However, an expert in the Mathematica platform can interpret these steps in the form of programs.
Stride 1: Set the assumptions.
Output: Homogenous FLM.
Stride 2: Define a suitable operator.
Output: Homogenous FLM in the functional form.
Algorithm 1. Problem initialization.
Stride 1: At
Output:
Stride 2: At
Output:
Algorithm 2. Gram–Schmidt process.
Stride I: At fix
Output:
Stride II: Wherein
Output:
Stride III: Set
Output:
Stride IV: Set
Output:
Algorithm 3. Process of RKHA solutions.
6.2 Applications
Next, three test applications that coincide with the FLM platform are utilized on the basis of the CFD: the first is
Application 1: Theorize the posterior and evaluate
equipped with the posterior boundary condition:
Here,
Application 2: Theorize the posterior and evaluate
equipped with the posterior boundary condition:
Here,
Application 3: Theorize the posterior and evaluate
equipped with the posterior boundary condition:
Here,
6.3 Analyses
Eventually, to clarify the portability and effectiveness of the presented RKHA, we present and provide several RKHA solution tables, RKHA numeric solution figures, RKHA absolute error figures, and RKHA relative error figures. However, in this section, we used
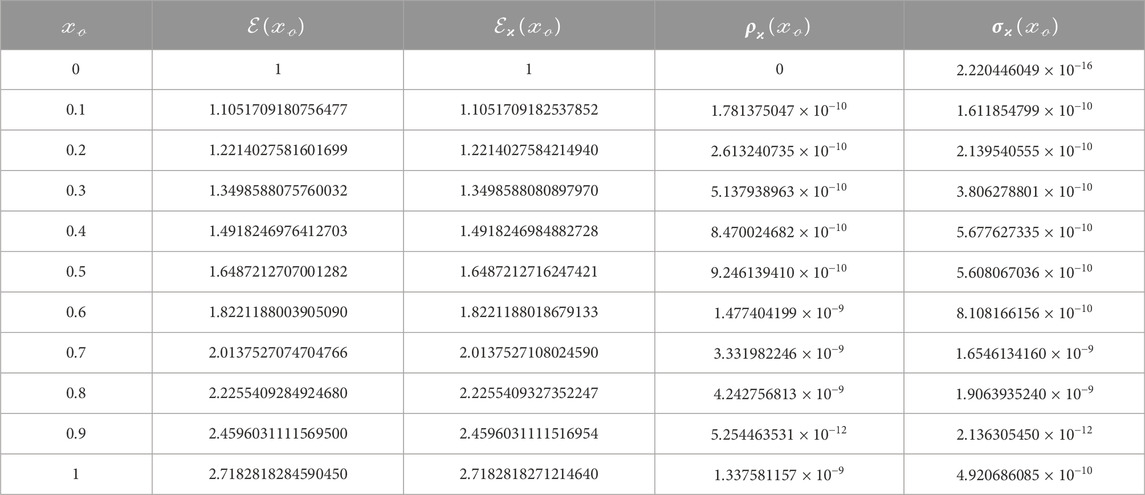
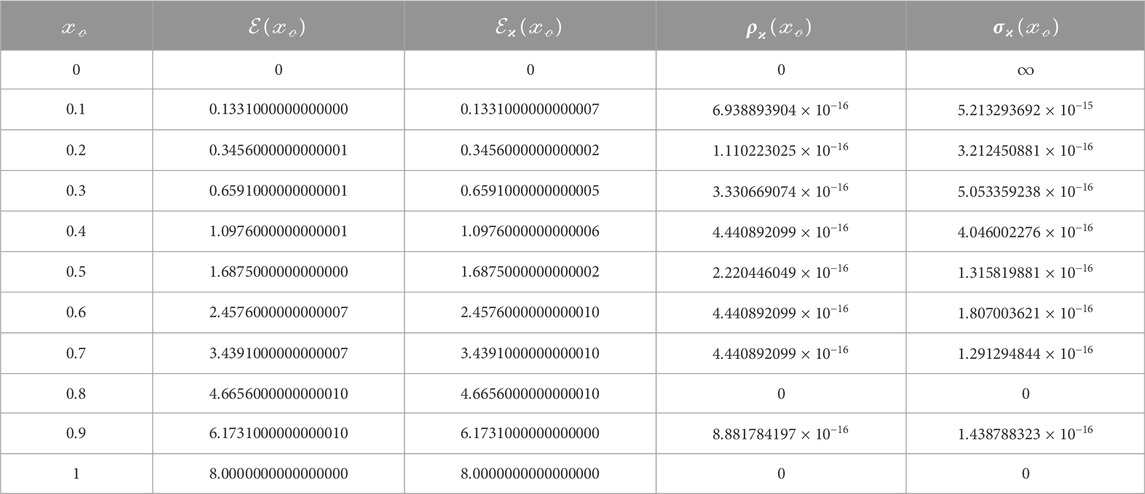
The tabulated data presenting
concerning the features of the memory inherited, are utilized in detail by the RKHA performance of the applications addressed previously, as shown in the included tables (Tables 1–3).
The
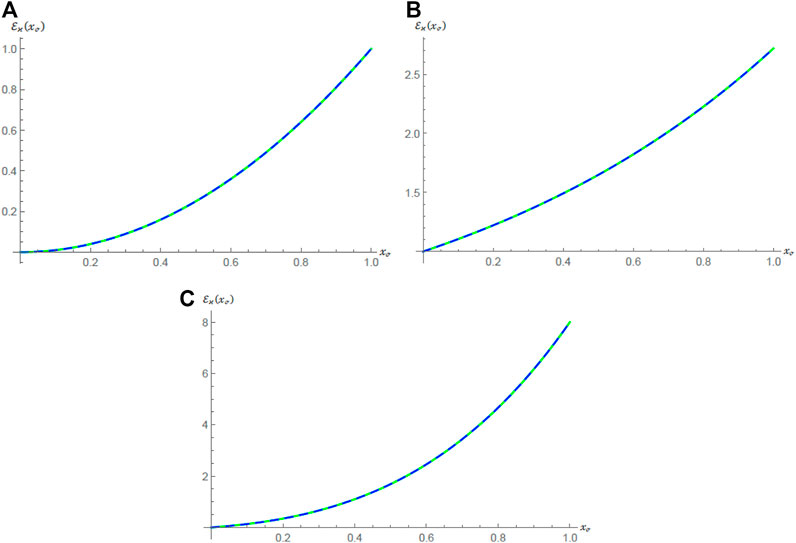
FIGURE 1.
The
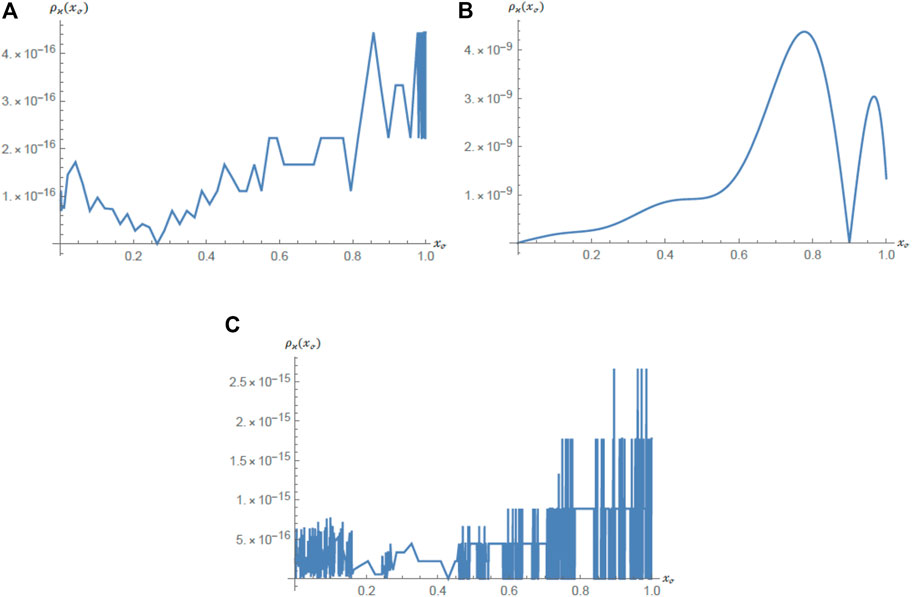
FIGURE 2.
Ultimately, the
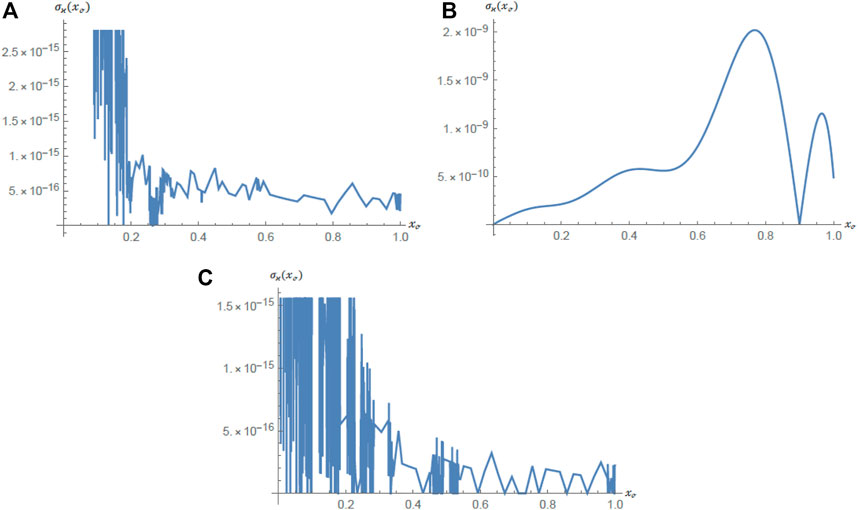
FIGURE 3.
7 Outline: Conclusion and outlook
This research embraced the RKHA to handle a type of well-known FDM called FLM on the basis of the CFD by including three test applications. A detailed presentation of the theories related to the establishment of the solution and the formulation of the approximate was interspersed with the construction of the necessary spaces and the associations’ form of Green’s functions used, with many new results that centered on convergence, error, and independence. Based on the RKHA,
Data availability statement
The original contributions presented in the study are included in the article/Supplementary Material; further inquiries can be directed to the corresponding author.
Author contributions
MA: data curation, investigation, software, methodology, validation, roles/writing—original draft, and writing—review and editing. OA: funding acquisition, investigation, resources, supervision, visualization, and roles/writing—original draft. BM: conceptualization, formal analysis, investigation, project administration, software, and writing—review and editing.
Acknowledgments
The authors are grateful to the Middle East University, Amman, Jordan for the financial support granted to cover the publication fee of this research article.
Conflict of interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Publisher’s note
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors, and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
Abbreviations
FLM, fractional Langevin model; RKHA, reproducing kernel Hilbert approach; FDM, fractional differential model; CFD, Caputo’s fractional derivative.
References
1. Baghani O. On fractional Langevin equation involving two fractional orders. Commun Nonlinear Sci Numer Simulation (2017) 42:675–81. doi:10.1016/j.cnsns.2016.05.023
2. Salem A, Mshary N. On the existence and uniqueness of solution to fractional-order Langevin equation. Adv Math Phys (2020) 2020:–11. doi:10.1155/2020/8890575
3. Salem A, Alnegga M. Fractional Langevin equations with multi-point and non-local integral boundary conditions. Cogent Math Stat (2020) 7:1758361. doi:10.1080/25742558.2020.1758361
4. Sudsutad W, Ntouyas SK, Tariboon J. Systems of fractional Langevin equations of Riemann-Liouville and Hadamard types. Adv Differ Equ (2015) 2015:235. doi:10.1186/s13662-015-0566-8
5. Yadav S, Kumar D, Nisar KS. A reliable numerical method for solving fractional reaction-diffusion equations. J King Saud Univ – Sci (2021) 33:101320. doi:10.1016/j.jksus.2020.101320
6. Fang D, Li L. Numerical approximation and fast evaluation of the overdamped generalized Langevin equation with fractional noise. Math Model Numer Anal (2020) 54:431–63. doi:10.1051/m2an/2019067
7. Fazli H, Sun HG, Nieto JJ. Fractional Langevin equation involving two fractional orders: Existence and uniqueness revisited. Mathematics (2020) 8:743. doi:10.3390/math8050743
8. Guo P, Zeng C, Li C, Chen YQ. Numerics for the fractional Langevin equation driven by the fractional Brownian motion. Fract Calc Appl Anal (2013) 16:123–41. doi:10.2478/s13540-013-0009-8
9. Mainardi F. Fractional calculus and waves in linear viscoelasticity. UK: Imperial College Press (2010).
12. Samko SG, Kilbas AA, Marichev OI. Fractional integrals and derivatives theory and applications. USA: Gordon & Breach (1993).
13. Kilbas A, Srivastava H, Trujillo J. Theory and applications of fractional differential equations. Amsterdam, Netherlands: Elsevier (2006).
14. Atangana A, Baleanu D. New fractional derivatives with non-local and non-singular kernel: Theory and application to heat transfer model. Therm Sci (2016) 20:763–9. doi:10.2298/tsci160111018a
15. Pindza KMOE. Dynamics of fractional chaotic systems with Chebyshev spectral approximation method. Int J Appl Comput Math (2022) 8:140. doi:10.1007/s40819-022-01340-2
16. Avalos-Ruiz LF, Gomez-Aguilar JF, Atangana A, Owolabi KM. On the dynamics of fractional map with power-law, exponential decay and Mittag-Leffler memory. Chaos, Solitons and Fractals (2019) 127:364–88.
17. Owolabi KM, Atangana A. Computational study of multi-species fractional reaction-diffusion system with ABC operator. Chaos Solitons Fractals (2019) 128:280–9. doi:10.1016/j.chaos.2019.07.050
18. Alzabut J, Bolat Y, Abdeljawad T. Almost periodic dynamics of a discrete Nicholson’s blowflies model involving a linear harvesting term. Adv Differ Equ (2012) 2012:158. doi:10.1186/1687-1847-2012-158
19. Alzabut J, Tyagi S, Abbas S. Discrete fractional-order BAM neural networks with leakage delay: Existence and stability results. Asian J Control (2020) 22:143–55. doi:10.1002/asjc.1918
20. Arfan M, Lashin MMA, Sunthrayuth P, Shah K, Ullah A, Iskakova K, et al. On nonlinear dynamics of COVID-19 disease model corresponding to nonsingular fractional order derivative. Med Biol Eng Comput (2022) 60:3169–85. doi:10.1007/s11517-022-02661-6
21. Cui M, Lin Y. Nonlinear numerical analysis in the reproducing kernel space. USA: Nova Science (2009).
22. Berlinet A, Agnan CT. Reproducing kernel Hilbert space in probability and statistics. USA: Kluwer Academic Publishers (2004).
24. Abu Arqub O. The reproducing kernel algorithm for handling differential algebraic systems of ordinary differential equations. Math Methods Appl Sci (2016) 39:4549–62. doi:10.1002/mma.3884
25. Karaagac B, Owolabi KM, Nisar KS. Analysis and dynamics of illicit drug use described by fractional derivative with Mittag-Leffler kernel. Comput Mater Contin (2020) 65:1905–24. doi:10.32604/cmc.2020.011623
26. Jiang W, Chen Z. A collocation method based on reproducing kernel for a modified anomalous subdiffusion equation. Numer Methods Partial Differ Equ (2014) 30:289–300. doi:10.1002/num.21809
27. Geng FZ, Qian SP, Li S. A numerical method for singularly perturbed turning point problems with an interior layer. J Comput Appl Math (2014) 255:97–105. doi:10.1016/j.cam.2013.04.040
28. Lin Y, Cui M, Yang L. Representation of the exact solution for a kind of nonlinear partial differential equation. Appl Math Lett (2006) 19:808–13. doi:10.1016/j.aml.2005.10.010
29. Akgül A. A novel method for a fractional derivative with non-local and non-singular kernel. Chaos Solitons Fractals (2018) 114:478–82. doi:10.1016/j.chaos.2018.07.032
30. Ahmad S, Ullah A, Akgül A, Baleanu D. Analysis of the fractional tumour-immune-vitamins model with Mittag–Leffler kernel. Results Phys (2020) 19:103559. doi:10.1016/j.rinp.2020.103559
31. Siddique I, Akgül A. Analysis of MHD generalized first problem of Stokes’ in view of local and non-local fractal fractional differential operators. Chaos Solitons Fractals (2020) 140:110161. doi:10.1016/j.chaos.2020.110161
Keywords: fractional Langevin model, reproducing kernel Hilbert approach, fractional differential model, Caputo fractional derivative MSC2020, 65L10, fluid dynamics
Citation: Aal MA, Arqub OA and Maayah B (2022) Hilbert solution, iterative algorithms, convergence theoretical results, and error bound for the fractional Langevin model arising in fluids with Caputo’s independent derivative. Front. Phys. 10:1072746. doi: 10.3389/fphy.2022.1072746
Received: 17 October 2022; Accepted: 07 November 2022;
Published: 14 December 2022.
Edited by:
Jordan Yankov Hristov, University of Chemical Technology and Metallurgy, BulgariaReviewed by:
Kamal Shah, University of Malakand, PakistanNdolane Sene, Cheikh Anta Diop University, Senegal
Kolade Matthew Owolabi, Federal University of Technology, Nigeria
Copyright © 2022 Aal, Arqub and Maayah. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Omar Abu Arqub, by5hYnVhcnF1YkBiYXUuZWR1Lmpv
 Mohammad Abdel Aal
Mohammad Abdel Aal Omar Abu Arqub
Omar Abu Arqub Banan Maayah3
Banan Maayah3