Free-electron terahertz radiation based on silicon gratings with in-plane waveguide emission

We present a method utilizing the coupling between a pre-bunched electron beam and a silicon subwavelength grating to generate coherent terahertz waves. The grating that is connected to two opposite-traveling in-plane waveguides functions as a resonator. An example operating around 2 THz shows that, when the velocity and repetition frequency of the electron bunches respectively match the phase velocity and resonant frequency of the Bragg resonance in the grating, the strong electron-wave coupling leads to coherent radiation through the waveguide. The repetition frequency of the electron bunches can be halved by using its second harmonic to match the resonant frequency. This study might offer a potential approach for on-chip terahertz sources.

1 Introduction

In the past few decades, substantial progress has been achieved in developing science and technologies based on terahertz radiation (0.1–30 THz) due to its unique physical properties for a variety of applications in communication, imaging, and spectroscopy [1–3]. The performance of terahertz sources, which is traditionally linked to the concept of the terahertz gap, has been significantly improved using electronic and photonic technologies [4–7]. Currently, great attention is paid to the quantum cascade laser (QCL). It can work with an efficiency higher than 1%, but its practical application is severely limited by the low operation temperature [4]. Free-electron radiation sources, e.g., backward wave oscillators (BWOs) and free-electron lasers (FELs), have been shown to be superior at handling high power [8]. BWOs can deliver power in the range of 50 mW at sub-THz to about 2 mW at 2 THz, but it is very difficult to operate at higher frequencies owing to the great challenges in reliable fabrication [9, 10]. On the other hand, FELs, in which radiation is generated as an electron bunch passes through a magnetic structure, can achieve terahertz powers of 100 W, but they suffered from their tremendous cost and large size. Seeking new method to develop terahertz radiation sources has been a pursuit of researchers.

Recently, the development of dielectric laser accelerators has attracted increasing interest and inspired new opportunities for applications using compact particle accelerators [11–13]. Using dielectrics with a high breakdown threshold instead of metals to enable a higher accelerating gradient for particle acceleration, the cost and size of accelerators can be reduced by orders of magnitude [14]. Besides electron acceleration, this method has been demonstrated the capability of electron bunching and focusing [12, 15–17]. Such concept has been extended to terahertz, promising an attractive particle accelerator on chip that can generate a train of electron bunches with terahertz repetition rate [18–21]. It is interesting to see if it is possible to realize a coherent terahertz radiation source on chip by using such an electron beam.

Cherenkov radiation and Smith-Purcell radiation are two mechanisms that can generate electromagnetic waves without destroying the electron beam and manipulate the radiation characteristics by designing the structures, making them rather attractive for many applications [17, 22–24]. In order to facilitate the integration of radiators and dielectric accelerators on chip, it is desirable that they have similar structures. So far, gratings and photonic crystals, which are extensively used in dielectric accelerators [14], have also been studied for radiation generation, e.g., 1D subwavelength gratings (SWGs) for Smith-Purcell radiation [25], and 2D photonic crystals for Cherenkov radiation [26, 27]. In those radiators, the formation of the radiation that normally spreads out at a certain angle is well understood [28]. However, for downstream applications of such radiators, in order to improve the utilization efficiency, a more directional wave confined in a waveguide might be preferable [29]. It is well known that the SWG itself can serve as a waveguide or resonator for confinement of electromagnetic waves, but the coupling between the electron and the SWG waveguide or resonator is less clear [30–34]. If electrons can directly couple energy into the guided mode in a grating, an on-chip terahertz source could become possible by outputting the energy through the slab waveguides attached to the grating ends.

Here, we present a method in which the coupling between a pre-bunched electron beam and a silicon SWG is utilized to generate terahertz wave. We first introduce the guideline for designing the SWG for such purpose. Then, we perform particle-in-cell (PIC) simulation to understand the characteristics of the radiator driven by a pre-bunched electron beam. We show that the electron-wave coupling leads to coherent terahertz radiation through the waveguides connected to the SWG. Such dielectric radiator is ready to be integrated with the terahertz dielectric accelerator. Besides, the output wave confined by the slab waveguide has the advantage of facilitating integration with down-stream terahertz components.

2 Model description

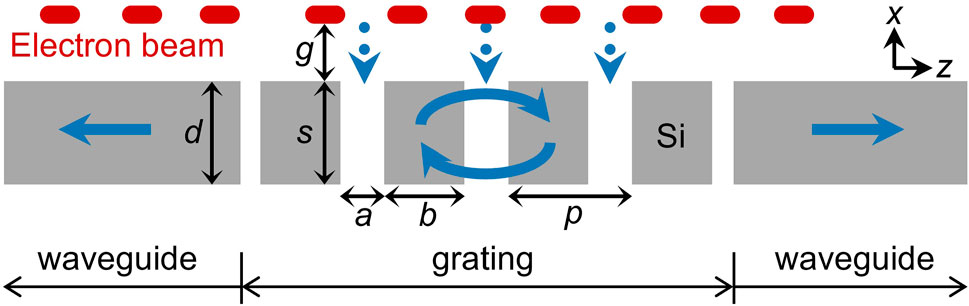
Figure 1 schematically illustrates our method of employing silicon SWGs driven by a pre-bunched electron beam to generate terahertz waves. The two-dimensional model is adopted in the analysis for simplicity. The dielectric grating comprises of a series of silicon bars, separated by vacuum gaps. The thickness and width of the bar, the width of the air gap, the SWG period the period number and the beam-grating distance are s, b, a, p, N and g, respectively. x = 0 is located at the upper surface of the SWG. There is a slab waveguide of thickness d the on either side of the SWG. The SWG is designed to operate with a Bragg resonance, which is essentially a stationary non-propagating mode with a vanishing group velocity. When an electron moves over the grating with a velocity that matches the phase velocity of the Bragg resonance, strong coupling occurs. When a pre-bunched electron beam, in which each bunch is shorter than the emitted radiation period, moves over the grating, the radiation fields of the different electrons in one bunch can add coherently in phase [28]. If the repetition frequency of the electron bunches f_b or its higher harmonics match the resonant frequency f₀ of the Bragg resonance, coherent radiation can be emitted at f₀ due to the superradiant effect [35]. The radiation power increases with the number of electron bunches until steady states. Meanwhile, part of the energy is bidirectionally coupled into the slab waveguides connected to the grating as output.

FIGURE 1

FIGURE 1. Free-electron terahertz radiation from silicon gratings with in-plane waveguide emission.

The dispersion diagram is a key property to calculate when studying the electron-wave coupling. As an example, we first consider an infinitely long SWG with thickness being s = p and dutycycle b/p = 0.76. By finding the eigenmodes with different Bloch phase shift for the periodic boundary conditions in the z direction, we can obtain the dispersion diagram with the CST software, as shown in Figure 2A. The diagram can be divided into two operation regions [36, 37]: the radiating continuum above the dashed lines, where the fields are extended in the region above or below the grating [38]; the guided mode region, where the fields above or below the grating are evanescent [33, 34, 39]. For the Smith-Purcell radiation, the operation point is located in the radiation continuum. In this article, we utilize the resonance in the guided mode region to generate Cherenkov radiation.

FIGURE 2

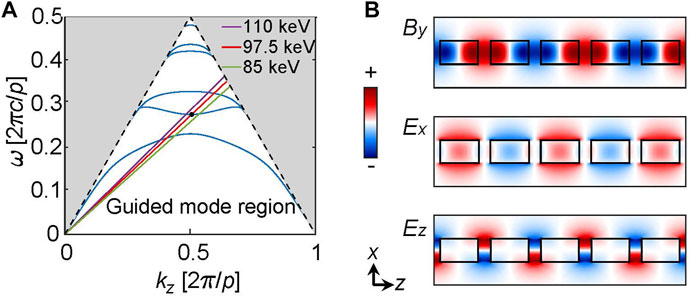
FIGURE 2. (A) Dispersion diagram of the SWG calculated by CST. The gray area above the black dashed lines are the radiation continuum. The 85, 97.5, 110 keV electron lines are indicated by the green, red, and purple solid lines, respectively. (B) The B_y, E_x and E_z field profiles of the Bragg resonance at the black dot in (A). The silicon bars are depicted by the rectangles with solid black borders.

In Figures 2A, A Bragg resonance can be found at k_z = π/p for each dispersion curve [29]. For instance, we choose the second guided mode as the operation mode. The Bragg resonance of the second guided mode is located at the intersection point of the 97.5 keV electron line and the second dispersion curve, which is marked by the black dot in Figure 2A. On its left side, the mode works as a backward wave (e.g., the intersection point of the 110 keV electron line and the second dispersion curve). While on its right side, the mode works as a forward wave (e.g., the intersection point of the 85 keV electron line and the second dispersion curve). Figure 2B further illustrates the field profiles of the Bragg resonance, indicating that a TM₀ mode is excited in the SWG, with the B_y component being symmetric about the x = −s/2 plane. In the z direction, the half spatial period of the fields is equal to the grating period p.

The above simulation shows that a Bragg resonance can be obtained with an infinite SWG. In practice, we can only use an SWG with a finite period number N. In this case, the side-leakage loss at the SWG ends in the z direction is inevitable, which manifests as omnidirectional radiation, as shown in Figure 3A. With a slab waveguide connected to each SWG end, a majority of the radiation could propagate into the slab. Among them, if the incident angle (θ) of the radiation at the slab-air boundary is larger than the critical angle for total internal reflection, it will be confined in the slab waveguide and transmitted downstream, as shown in Figure 3B. Such bi-directional coupling into those in-plane waveguides can be leveraged as output [40–43]. In the following, the grating period is set to be p = 41 μm, so that the resonant frequency of the Bragg resonance f₀ is about 1.98 THz. The period number is set to be N = 40. In this case, the finite SWG serves as a cavity and the external quality factor is calculated to be 7917 by using CST Microwave Studio. Below we will show that the electron-wave coupling can generate coherent terahertz waves output through the slab waveguides.

FIGURE 3

FIGURE 3. (A) Schematic of the omnidirectional radiation at the SWG ends. (B) Schematic of the coupling between SWG and slab waveguides.

3 Results

For PIC simulations, a two-dimensional finite-difference-time-domain code CHIPIC-2D is used [44]. The grating dutycycle, thickness, and period remain the same as that in Section 2. The pre-bunched beam is set to be uniform in the x direction, with beam thickness d = 5.5 μm. The beam-grating distance is set to be g = 2.7 μm. Assuming the width of the system is 1 mm in the y direction, the current of the pre-bunched electron beam is shown in Figure 4A, in which all electron bunches follow the same truncated Gaussian distribution. The peak current density of the beam is 0.05 A/cm². The repetition frequency of electron bunches is set to be f_b, which is a key parameter that can be tuned in the simulation. To avoid electron bombardment on grating, an external longitudinal magnetic field of 0.1 T is used to confine the beam. In practice, to further reduce surface charging, the dielectric grating can be coated with a thin metallic layer.

FIGURE 4

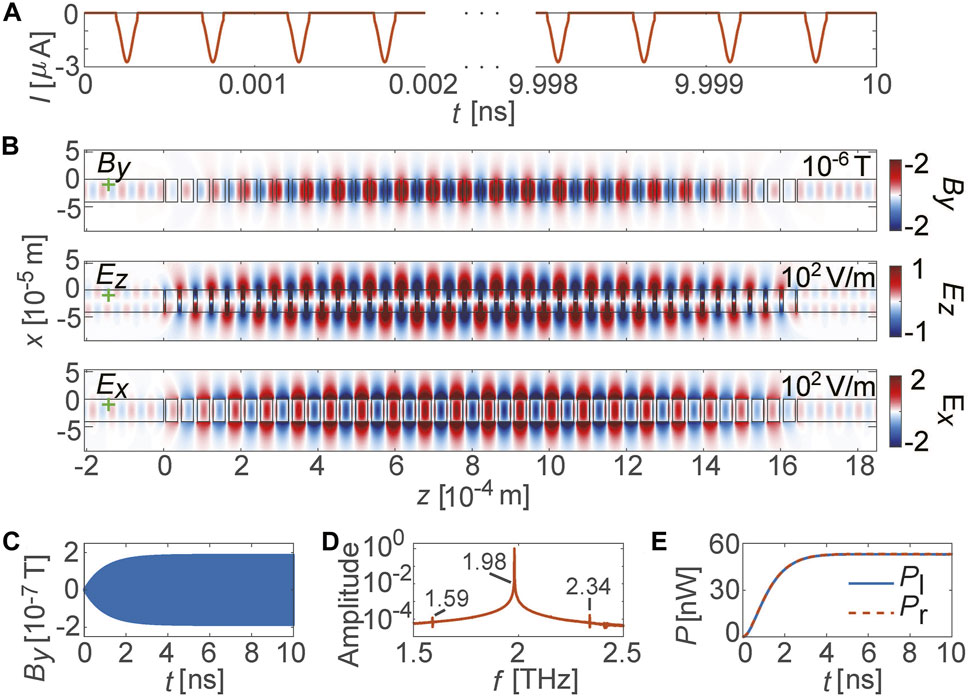
FIGURE 4. Coherent terahertz radiation calculated by PIC simulation with f_b =1.9807 THz. (A) The current of the electron beam. (B) Field patterns of the B_y, E_z, E_x components at t =10 ns. (C) B_y field at the green star in (B) as a function of time. (D) Spectrum of the B_y field at the green star in (B). (E) Leftward output power P_l through the slab waveguide on the left and rightward output power P_r through the slab waveguide on the right.

Firstly, we set the electron energy to be 97.5 keV. The repetition frequency of the electron bunches f_b is fine-tuned around 1.98 THz, while the truncated Gaussian distribution of each electron bunch remains unchanged. The output power is found to reach maximum at 1.9807 THz, in agreement with the resonant frequency calculated in Section 2. Figure 4B shows the calculated B_y, E_z and E_x components at f_b = 1.9807 THz, where the field patterns in the SWG are consistent with that calculated by CST in Figure 2. Figures 4C,D show the B_y field at the green star in Figure 4B as a function of time and its spectra, respectively. The output fields saturate at t = 4 ns, and its frequency is exactly the same as the repetition frequency of the electron bunches. It is noticeable that there are another two peaks at about 1.59 THz and 2.34 THz. This is because the 97.5 keV electron line intersects with not only the second guided mode, but also the first and the third. These two peaks are much lower since they are far from the repetition frequency of the electron bunches f_b. Assuming the system’s thickness is 1 mm in the y direction, the leftward output power P_l through the slab waveguide on the left and the rightward output power P_r through the slab waveguide on the right are shown in Figure 4E. Here, P_l is found to be approximately the same as P_r. The total power through two slab waveguides is 102.36 nW (per millimeter in the y direction) and the corresponding beam-to-wave power conversion efficiency is 2.59 × 10^–6. Thanks to the superradiant effect, the radiation is coherent and is much stronger than the fields induced by a direct-current electron beam (See Supplementary Material for more information).

We then change the repetition frequency of the electron bunches. With a repetition frequency of f_b, the electron beam’s spectrum includes not only the fundamental repetition frequency but also its higher harmonics. Consequently, it is interesting to know whether the repetition frequency can be halved by using its second harmonic to match the resonant frequency, with the output frequency remaining unchanged. When the truncated Gaussian distribution of each electron bunch remains unchanged, we fine-tune the repetition frequency of the electron bunches f_b around 0.99 THz. The output power is found to reach maximum when the repetition frequency equals half the resonant frequency, i.e., f_b = f₀/2. Such results clearly show that coherent wave can be generated even when the repetition frequency is halved. For clarity, Figures 5A,B compare the output power P_l and P_r when the repetition frequency f_b is tuned around 1.98 THz and 0.99 THz. The maximum output power around 1.98 THz is higher than that around 0.99 THz. This is caused by the fact that the fundamental-harmonic component of the pre-bunched beam at f_b is stronger than the second-harmonic component at 2f_b.

FIGURE 5

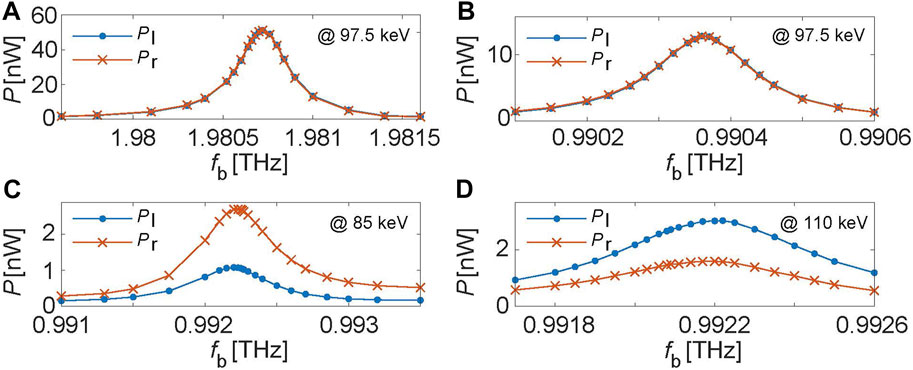
FIGURE 5. Simulation results for the effect of repetition frequency and electron energy on the leftward output power P_l and rightward output power P_r. With electron energy being 97.5 keV, the repetition frequency is tuned around 1.98 THz in (A) and 0.99 THz in (B). With the repetition frequency being tuned around 0.99 THz, the electron energy is 85 keV in (C) and 110 keV in (D).

The effect of electron energy is then investigated. Figures 5C,D show the output power as a function of repetition frequency that is tuned around 0.99 THz when the electron energy is changed to 85 keV and 110 keV, respectively. In both cases, the output power reaches its maximum at around 0.9922 THz, which is higher than that for 97.5 keV electrons. This is in agreement with the fact that the frequencies at the intersections of the 85 and 110 keV electron lines with the second dispersion curve are higher than the resonant frequency of the Bragg resonance in Figure 2. The maximum output power is lower than that obtained by 97.5 keV electrons, indicating that the Bragg resonance can enable stronger beam-wave coupling. Notably, when the electron energy is 85 keV, the leftward power is smaller than the rightward power. When the electron energy is 110 keV, on the other hand, the leftward power becomes higher than the rightward power. This is caused by the difference in the mode nature: 85 keV electrons use a forward mode, while 110 keV electrons use a backward mode.

Next, the beam-grating distance g is varied in the simulation, with the other parameters being the same as in Figure 4. Figure 6A show that the leftward output power P_l decreases as the distance g increases. Such phenomena can be explained by considering the effect of incident fields from electrons. For a 2D model, the current density of a single charge q moving with velocity v₀ can be given by J_z (x, z, t) = qv₀δ(x − g)δ(z − v₀t) [45]. Using Fourier transform, we can obtain the current density in the frequency domain, i.e., J_z (x, z, ω) = qδ(x − g)exp(−ik_z0z), with k_z0 = ω/v₀. The incident magnetic field can be written as H_y = −sign (x − g)q/2 ⋅exp[−α ⋅ sign(x − g)(x − g) − ik_z0z], where $\alpha ={(k_{z0}^2-{\omega }^2{\mu }_0{\epsilon }_0)}^{0.5}$, ɛ₀ and μ₀ are the permittivity and permeability in vacuum. Such incident fields are bound at the electrons and decay exponentially in the x direction. Thus, when the distance g increases, the amplitude of the incident field at the grating surface decreases, leading to a decline in output power. This can be verified by the agreement between the simulated power P_l and the value of P_l0exp[−2α(g − 2.7 μm)], with P_l0 being the simulated power for g = 2.7 μm as shown in Figure 4E. Such results are also helpful when we consider a three-dimensional model that has an electron pencil-beam moving above a planar grating with a finite width in the y direction. Based on the dependence of output power on g as shown in Figure 6A, one can infer that the radiation in the grating are the strongest just beneath the beam. In the y direction, as the distance from the beam increases, the radiation will become weaker.

FIGURE 6

FIGURE 6. Simulation results of the leftward output power P_l as a function of the beam-grating distance g (A), the electron energy spread η (B), and the slab thickness d (C).

Notably, the above simulations use a mono-energetic electron beam. In order to study the effect of the initial energy spread (denoted by η) of the electron beam, which is inevitable in practice, we set the initial electron velocities to have a Maxwellian distribution, which is in agreement with the typical velocity distribution of electrons emitted from thermionic cathodes [46]. Figure 6B shows the leftward output power P_l as a function of the initial energy spread (η) of the electron beam, with the other parameters being the same as in Figure 4. One can see that the leftward output power P_l decreases as the initial energy spread of the electron beam η increases. In order that the output power declines no more than 50%, the initial energy spread should not exceed 3%.

Then, the effect of the thickness (d) of slab waveguide is studied in the simulation, with the other parameters being the same as in Figure 4. When changing the slab thickness d, the slab center in the x direction is aligned with the grating center. Figure 6C shows the leftward output power P_l as a function of d. When d increases beyond the grating thickness s that is equal to the grating period p, the output power remains almost unchanged. When it decreases, the output power reaches its maximum at d = 0.73p. In this case, however, the different values of slab thickness d and grating thickness s may increases the difficulty in fabrication.

Although we focus on the second guided mode in the above simulations, the other guided modes can also be utilized. As an example, with the other parameters being the same as in Figure 4, the repetition frequency of the electron bunches is changed to 2.34 THz, which corresponds to the intersection point of the 97.5 keV electron line and the third dispersion curve. Figure 7 shows the B_y field at the green star in Figure 4B as a function of time and its spectra, and also the output power P_l and P_r as a function time. The output field saturates at t = 0.5 ns and its frequency is 2.34 THz. Here, the other two peaks are located at about 1.98 THz and 1.59 THz, corresponding to the second and first guided mode, respectively. These two peaks are much lower than the highest one at 2.34 THz, indicating that unwanted mode can be suppressed by mismatching the repetition frequency of the electron bunches with the mode frequency.

FIGURE 7

FIGURE 7. Coherent terahertz radiation calculated by PIC simulation with f_b =2.34 THz. (A) B_y field in the slab as a function of time. (B) Spectrum of the B_y field. (C) Leftward output power P_l through the slab waveguide on the left and rightward output power P_r through the slab waveguide on the right.

4 Discussion

In conclusion, we have described a method to generate terahertz waves based on silicon SWGs with bi-directional emission into in-plane waveguides. We have shown that the coupling between a pre-bunched electron beam and the SWGs’ Bragg resonance can generate coherent terahertz waves by matching the velocity and repetition frequency of the electron bunches respectively with the phase velocity and resonant frequency of the Bragg resonance. When the radiation frequency keeps unchanged, we also found that it is possible to reduce the repetition frequency of the electron bunches by using its higher harmonics to match the resonant frequency of the Bragg resonance.

The method investigated in this paper may be useful in future terahertz applications. The usage of silicon gratings in terahertz regime shows that the fabrication of the proposed structure is within reach of established fabrication techniques[47]. With the rapid development of structure-based dielectric accelerators [11–13, 18–20], the pre-bunched beam used to drive the dielectric SWG might be available in the near future. The integration of the dielectric accelerator and the radiator may enable an on-chip terahertz radiation source. The power produced by this method may be further improved increasing the peak current. It can operate at room temperature from sub-terahertz to terahertz by changing the working harmonics. Thus, it is a potential supplement to those existing sources that are widely used for terahertz spectroscopy and imaging [10, 48]. Compared with some other terahertz sources such as BWOs and QCLs, the efficiency of this method is relatively low due to the spontaneous nature of the emission. However, the fact that the electron beam is not destroyed in the process implies that those electrons can still be utilized for other purposes. Thus, such radiation source can be developed as a byproduct of dielectric acceleration. For example, the terahertz radiation can be used to assist early detection of skin cancer, and the electron beam can be used as a non-invasive treatment of skin cancer [4].

Data availability statement

The raw data supporting the conclusion of this article will be made available by the authors, without undue reservation.

Author contributions

ZC, LM, and MJ contributed to the writing of the manuscript and to the interpretation of results. ZC: Conceptualization, Writing-Original draft preparation. LM and MJ: Writing-Reviewing.

Funding

This work was supported by Fundamental Research Funds for the Central Universities, National Key Laboratory of Science and Technology on Vacuum Electronics.

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

Supplementary material

The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/fphy.2022.1061172/full#supplementary-material

References

1. Zhang W, Maldonado P, Jin Z, Seifert TS, Arabski J, Schmerber G, et al. Ultrafast terahertz magnetometry. Nat Commun (2020) 11:4247. doi:10.1038/s41467-020-17935-6

PubMed Abstract | CrossRef Full Text | Google Scholar

2. Matsumoto H, Watanabe I, Kasamatsu A, Monnai Y. Integrated terahertz radar based on leaky-wave coherence tomography. Nat Electron (2020) 3:122–9. doi:10.1038/s41928-019-0357-4

CrossRef Full Text | Google Scholar

3. Ma J, Shrestha R, Adelberg J, Yeh C-Y, Hossain Z, Knightly E, et al. Security and eavesdropping in terahertz wireless links. Nature (2018) 563:89–93. doi:10.1038/s41586-018-0609-x

PubMed Abstract | CrossRef Full Text | Google Scholar

4. Khalatpour A, Paulsen AK, Deimert C, Wasilewski ZR, Hu Q. High-power portable terahertz laser systems. Nat Photon (2021) 15:16–20. doi:10.1038/s41566-020-00707-5

CrossRef Full Text | Google Scholar

5. Koulouklidis AD, Gollner C, Shumakova V, Fedorov VY, Pugžlys A, Baltuška A, et al. Observation of extremely efficient terahertz generation from mid-infrared two-color laser filaments. Nat Commun (2020) 11:292. doi:10.1038/s41467-019-14206-x

PubMed Abstract | CrossRef Full Text | Google Scholar

6. Chevalier P, Amirzhan A, Wang F, Piccardo M, Johnson SG, Capasso F, et al. Widely tunable compact terahertz gas lasers. Science (2019) 366:856–60. doi:10.1126/science.aay8683

PubMed Abstract | CrossRef Full Text | Google Scholar

7. Lewis RA. A review of terahertz sources. J Phys D: Appl Phys (2014) 47:374001. doi:10.1088/0022-3727/47/37/374001

CrossRef Full Text | Google Scholar

8. Dhillon SS, Vitiello MS, Linfield EH, Davies AG, Hoffmann MC, Booske J, et al. The 2017 terahertz science and technology roadmap. J Phys D: Appl Phys (2017) 50:043001. doi:10.1088/1361-6463/50/4/043001

CrossRef Full Text | Google Scholar

9. Luo J, Feng J, Gong Y. A review of microwave vacuum devices in China: Theory and device development including high-power klystrons, spaceborne twts, and gyro-twts. IEEE Microwave (2021) 22:18–33. doi:10.1109/MMM.2020.3047747

CrossRef Full Text | Google Scholar

10. McIntosh AI, Yang B, Goldup SM, Watkinson M, Donnan RS. Terahertz spectroscopy: A powerful new tool for the chemical sciences? Chem Soc Rev (2012) 41:2072–82. doi:10.1039/C1CS15277G

PubMed Abstract | CrossRef Full Text | Google Scholar

11. Sapra NV, Yang KY, Vercruysse D, Leedle KJ, Black DS, England RJ, et al. On-chip integrated laser-driven particle accelerator. Science (2020) 367:79–83. doi:10.1126/science.aay5734

PubMed Abstract | CrossRef Full Text | Google Scholar

12. Shiloh R, Illmer J, Chlouba T, Yousefi P, Schönenberger N, Niedermayer U, et al. Electron phase-space control in photonic chip-based particle acceleration. Nature (2021) 597:498–502. doi:10.1038/s41586-021-03812-9

PubMed Abstract | CrossRef Full Text | Google Scholar

13. Henke J-W, Raja AS, Feist A, Huang G, Arend G, Yang Y, et al. Integrated photonics enables continuous-beam electron phase modulation. Nature (2021) 600:653–8. doi:10.1038/s41586-021-04197-5

PubMed Abstract | CrossRef Full Text | Google Scholar

14. England RJ, Noble RJ, Bane K, Dowell DH, Ng C-K, Spencer JE, et al. Dielectric laser accelerators. Rev Mod Phys (2014) 86:1337–89. doi:10.1103/RevModPhys.86.1337

CrossRef Full Text | Google Scholar

15. Schönenberger N, Mittelbach A, Yousefi P, McNeur J, Niedermayer U, Hommelhoff P. Generation and characterization of attosecond microbunched electron pulse trains via dielectric laser acceleration. Phys Rev Lett (2019) 123:264803. doi:10.1103/PhysRevLett.123.264803

PubMed Abstract | CrossRef Full Text | Google Scholar

16. Black DS, Leedle KJ, Miao Y, Niedermayer U, Byer RL, Solgaard O, et al. Laser-driven electron lensing in silicon microstructures. Phys Rev Lett (2019) 122:104801. doi:10.1103/PhysRevLett.122.104801

PubMed Abstract | CrossRef Full Text | Google Scholar

17. Black DS, Niedermayer U, Miao Y, Zhao Z, Solgaard O, Byer RL, et al. Net acceleration and direct measurement of attosecond electron pulses in a silicon dielectric laser accelerator. Phys Rev Lett (2019) 123:264802. doi:10.1103/PhysRevLett.123.264802

PubMed Abstract | CrossRef Full Text | Google Scholar

18. Zhang D, Fallahi A, Hemmer M, Wu X, Fakhari M, Hua Y, et al. Segmented terahertz electron accelerator and manipulator (steam). Nat Photon (2018) 12:336–42. doi:10.1038/s41566-018-0138-z

PubMed Abstract | CrossRef Full Text | Google Scholar

19. Zhang D, Fakhari M, Cankaya H, Calendron A-L, Matlis NH, Kärtner FX. Cascaded multicycle terahertz-driven ultrafast electron acceleration and manipulation. Phys Rev X (2020) 10:011067. doi:10.1103/PhysRevX.10.011067

CrossRef Full Text | Google Scholar

20. Liu W, Yu Z, Sun L, Liu Y, Jia Q, Xu H, et al. Microscale laser-driven particle accelerator using the inverse cherenkov effect. Phys Rev Appl (2020) 14:014018. doi:10.1103/PhysRevApplied.14.014018

CrossRef Full Text | Google Scholar

21. Aimidula A, Bake MA, Wan F, Xie BS, Welsch CP, Xia G, et al. Numerically optimized structures for dielectric asymmetric dual-grating laser accelerators. Phys Plasmas (2014) 21:023110. doi:10.1063/1.4866020

CrossRef Full Text | Google Scholar

22. Su Z, Xiong B, Xu Y, Cai Z, Yin J, Peng R, et al. Manipulating cherenkov radiation and smith–purcell radiation by artificial structures. Adv Opt Mater (2019) 7:1801666. doi:10.1002/adom.201801666

CrossRef Full Text | Google Scholar

23. Liang Y, Du Y, Su X, Wang D, Yan L, Tian Q, et al. Observation of coherent smith-purcell and transition radiation driven by single bunch and micro-bunched electron beams. Appl Phys Lett (2018) 112:053501. doi:10.1063/1.5009396

CrossRef Full Text | Google Scholar

24. Liang Y, Du Y, Wang D, Yan L, Tian Q, Chen K, et al. Selective excitation and control of coherent terahertz smith-purcell radiation by high-intensity period-tunable train of electron micro-bunches. Appl Phys Lett (2018) 113:171104. doi:10.1063/1.5054583

CrossRef Full Text | Google Scholar

25. Roques-Carmes C, Kooi SE, Yang Y, Massuda A, Keathley PD, Zaidi A, et al. Towards integrated tunable all-silicon free-electron light sources. Nat Commun (2019) 10:3176. doi:10.1038/s41467-019-11070-7

PubMed Abstract | CrossRef Full Text | Google Scholar

26. Luo C, Ibanescu M, Johnson SG, Joannopoulos JD. Cerenkov radiation in photonic crystals. Science (2003) 299:368–71. doi:10.1126/science.1079549

PubMed Abstract | CrossRef Full Text | Google Scholar

27. García de Abajo FJ, Pattantyus-Abraham AG, Zabala N, Rivacoba A, Wolf MO, Echenique PM. Cherenkov effect as a probe of photonic nanostructures. Phys Rev Lett (2003) 91:143902. doi:10.1103/PhysRevLett.91.143902

PubMed Abstract | CrossRef Full Text | Google Scholar

28. Gover A, Ianconescu R, Friedman A, Emma C, Sudar N, Musumeci P, et al. Superradiant and stimulated-superradiant emission of bunched electron beams. Rev Mod Phys (2019) 91:035003. doi:10.1103/revmodphys.91.035003

CrossRef Full Text | Google Scholar

29. Huang Y-C, Peng L-H, Shirvani H, Chen W-C, Muthuramalingam K, Wang W-C, et al. Single-electron nano-chip free-electron laser. APL Photon (2022) 7:096101. doi:10.1063/5.0097486

CrossRef Full Text | Google Scholar

30. Bock PJ, Cheben P, Schmid JH, Lapointe J, Delâge A, Janz S, et al. Subwavelength grating periodic structures in silicon-on-insulator: A new type of microphotonic waveguide. Opt Express (2010) 18:20251–62. doi:10.1364/OE.18.020251

PubMed Abstract | CrossRef Full Text | Google Scholar

31. Cheben P, Halir R, Schmid JH, Atwater HA, Smith DR. Subwavelength integrated photonics. Nature (2018) 560:565–72. doi:10.1038/s41586-018-0421-7

PubMed Abstract | CrossRef Full Text | Google Scholar

32. Kita DM, Michon J, Johnson SG, Hu J. Are slot and sub-wavelength grating waveguides better than strip waveguides for sensing? Optica (2018) 5:1046–54. doi:10.1364/OPTICA.5.001046

CrossRef Full Text | Google Scholar

33. Tanabe T, Notomi M, Kuramochi E, Shinya A, Taniyama H. Trapping and delaying photons for one nanosecond in an ultrasmall high-Q photonic-crystal nanocavity. Nat Photon (2007) 1:49–52. doi:10.1038/nphoton.2006.51

CrossRef Full Text | Google Scholar

34. Miura R, Imamura S, Ohta R, Ishii A, Liu X, Shimada T, et al. Ultralow mode-volume photonic crystal nanobeam cavities for high-efficiency coupling to individual carbon nanotube emitters. Nat Commun (2014) 5:5580. doi:10.1038/ncomms6580

PubMed Abstract | CrossRef Full Text | Google Scholar

35. Andrews HL, Boulware CH, Brau CA, Jarvis JD. Superradiant emission of smith-purcell radiation. Phys Rev ST Accel Beams (2005) 8:110702. doi:10.1103/physrevstab.8.110702

CrossRef Full Text | Google Scholar

36. Chang-Hasnain CJ, Yang W. High-contrast gratings for integrated optoelectronics. Adv Opt Photon (2012) 4:379. doi:10.1364/aop.4.000379

CrossRef Full Text | Google Scholar

37. Qiao P, Yang W, Chang-Hasnain CJ. Recent advances in high-contrast metastructures, metasurfaces, and photonic crystals. Adv Opt Photon (2018) 10:180–245. doi:10.1364/AOP.10.000180

CrossRef Full Text | Google Scholar

38. Fan S, Winn JN, Devenyi A, Chen JC, Meade RD, Joannopoulos JD. Guided and defect modes in periodic dielectric waveguides. J Opt Soc Am B (1995) 12:1267–72. doi:10.1364/JOSAB.12.001267

CrossRef Full Text | Google Scholar

39. Deotare PB, McCutcheon MW, Frank IW, Khan M, Lončar M. Coupled photonic crystal nanobeam cavities. Appl Phys Lett (2009) 95:031102. doi:10.1063/1.3176442

CrossRef Full Text | Google Scholar

40. Quan Q, Deotare PB, Loncar M. Photonic crystal nanobeam cavity strongly coupled to the feeding waveguide. Appl Phys Lett (2010) 96:203102. doi:10.1063/1.3429125

CrossRef Full Text | Google Scholar

41. Kumari S, Haglund EP, Gustavsson JS, Larsson A, Roelkens G, Baets RG. Vertical-cavity silicon-integrated laser with in-plane waveguide emission at 850 nm. Laser Photon Rev (2018) 12:1700206. doi:10.1002/lpor.201700206

CrossRef Full Text | Google Scholar

42. Park GC, Xue W, Taghizadeh A, Semenova E, Yvind K, Mørk J, et al. Hybrid vertical-cavity laser with lateral emission into a silicon waveguide. Laser Photon Rev (2015) 9:L11. doi:10.1002/lpor.201400418

CrossRef Full Text | Google Scholar

43. Chung I, Mørk J. Silicon-photonics light source realized by III–V/Si-grating-mirror laser. Appl Phys Lett (2010) 97:151113. doi:10.1063/1.3503966

CrossRef Full Text | Google Scholar

44. Zhou J, Liu D, Liao C, Li Z. CHIPIC: An efficient code for electromagnetic PIC modeling and simulation. IEEE Trans Plasma Sci (2009) 37:2002–11. doi:10.1109/tps.2009.2026477

CrossRef Full Text | Google Scholar

45. Chen Z, Mao L, Jin M, Shi X, Bai N, Sun X. Enhanced smith-purcell radiation from bound states in the continuum of metallic gratings. J Phys D: Appl Phys (2022) 55:295102. doi:10.1088/1361-6463/ac6a8b

CrossRef Full Text | Google Scholar

46. Reiser M. Theory and design of charged particle beams. Weinheim: John Wiley & Sons (2008).

Google Scholar

47. Han S, Rybin MV, Pitchappa P, Srivastava YK, Kivshar YS, Singh R. Guided-mode resonances in all-dielectric terahertz metasurfaces. Adv Opt Mater (2020) 8:1900959. doi:10.1002/adom.201900959

CrossRef Full Text | Google Scholar

48. Jepsen P, Cooke D, Koch M. Terahertz spectroscopy and imaging – modern techniques and applications. Laser Photon Rev (2011) 5:124–66. doi:10.1002/lpor.201000011

CrossRef Full Text | Google Scholar