- Department of Mathematics, University of the Punjab, Lahore, Pakistan
The present article presents some new results relating to Atomic Bond Connectivity energies and Spectral radii of generalized splitting and generalized shadow graphs constructed on the basis of some fundamental families of cycle graph Cn, complete graph Kn and complete bipartite graph Kn,n referred as base graphs. In fact we relate the energies and Spectral radii of splitting and shadow graphs with the energies and Spectral radii of original graphs.
1 Introduction
Let G be a simple, finite and undirected graph having vertex set V(G) and edge set E(G). The order and the size of the graph G are n and m, respectively. The term “degree of vertex” (abbreviated as di) refers to the number of edges that terminate at a vertex i in the graph G. When the vertices i and j of the graph G are adjacent, then ij entry of the ABC matrix of G is equal to
When the vertices i and j are adjacent we use the notation i ∼ j. It is obvious that the generalized ABC matrix of G can be thought of as a particular kind of weighted adjacency matrix of G. Eigenvalues of the Adjacency matrix A(G) are basically the eigenvalues of the graph G. If the eigenvalues of the graph G are denoted as α1, α2⋯αn, then energy of the graph G is denoted by ɛ(G) and is defined as sum of absolute values of all eigenvalues of the graph G. Quantum chemistry served as an inspiration for the energy of the graph G. Idea of energy of the graph was initiated by Ivan Gutman in 1978 [10]. Initially it was an strange idea so very few scientist were compelled to notice the idea of energy of the graph G. Over the recent years different variants of energies have been introduced with a variety of applications in diverse areas. One such energy is the ABC energy introduced taking into account the fruitful applications of the ABC index.
A logical query is raised, what connection can be made between the ABC energy of a given graph G and the graph that was created from G using various graph operations? We have taken into consideration two graphs operations, the splitting graph and the shadow graph, in order to respond to this query. A lot of work is done in this field in last few years. J. B. Liu et al. discussed Distance and Adjacency Energies of Multi-Level Wheel Networks in [11]. Largest eigenvalue of the graph G is called Spectral radius of the graph G and it is denoted by ρ(G). Zhang et al. in [12], recently established new results using two well-known operations, splitting and shadow graphs on a given regular graph that relates the Spectral radius of the original graph and the newly created graph. Z. Q. Chu et al. discussed Laplacian and signless Laplacian spectra and energies of multi-step wheels in [13]. Chen hypothesized in [14] that the star graph Sn has the lowest ABC energy of any tree of order n, while Gao et al. demonstrated this hypotheses in [15]. Ghorbani et al. discussed certain bounds for the ABC Spectral radius and ABC energy of general graphs as well as various ABC eigenvalue features in [16]. Yalcin et al. discussed several upper and lower bounds for the skew ABC energy of digraphs in [17]. R. Singh et al. discussed Sombor energy of m-splitting and m-shadow graphs constructed on the basis of any regular graph in [18]. In [19] Vaidya et al. established new results
Eigenvalues of ABC matrix of the graph G are denoted as η1, η2, ⋯ηn. ABC spectrum of the graph G is a multiset consisting of the ABC eigenvalues of the graph G denoted by specABC. If distinct ABC eigenvalues of the graph G are η1, η2, ⋯ηn with multiplicities m1, m2, ⋯mn respectively, then
Then ABC energy is defined aspt
where η1, η2, … , ηn are the eigenvalues of ABC matrix.
ABC Spectral radius is defined as
where η1, η2, … , ηn are the eigenvalues of ABC matrix.
2 Preliminaries
In this part we outline main ideas and preliminary facts related to our main results. Let Cn and Kn, respectively, stand for the cycle and the complete graph on n vertices, as usual. Let Km,nbe a complete bipartite graph with two partite sets that each have m and n vertices. When all of the vertices in the graph G have the same degree then the graph G is said to be regular graph. Cn is two regular graph, Kn is n − 1 regular and complete bipartite Kn,n is n regular graph.
We actually generate new graph from a given graph refereed as base graph. Sampath Kumar and Walikar first introduced the splitting graph in [21]. The splitting graph Spl(G) of the graph G can be obtained by adding to every vertex a new vertex a′, such that a′ is adjacent to every vertex that is adjacent to a in G. The shadow graph Sh(G) of the graph G is obtained by taking two copies of G, say G′ and G′′. Join every vertex b′ in G′ to the neighbors of the corresponding vertex b′′ in G′′. These two notions of producing new graphs have natural generalizations. The above given definitions can be treated as 1-splitting and 2-shadow graph of a given graph whereas a general idea of producing s - splitting or s - shadow graphs where we take s new vertices or s new copies of G. Following definition is central to our results. The s-splitting graph Spls(G) of G is obtained by adding to every vertex a of G new s vertices, say v1, v2, v3, …., vs such that vi (1 ≤ i ≤ s), is adjacent to every vertex that is adjacent to v in G.
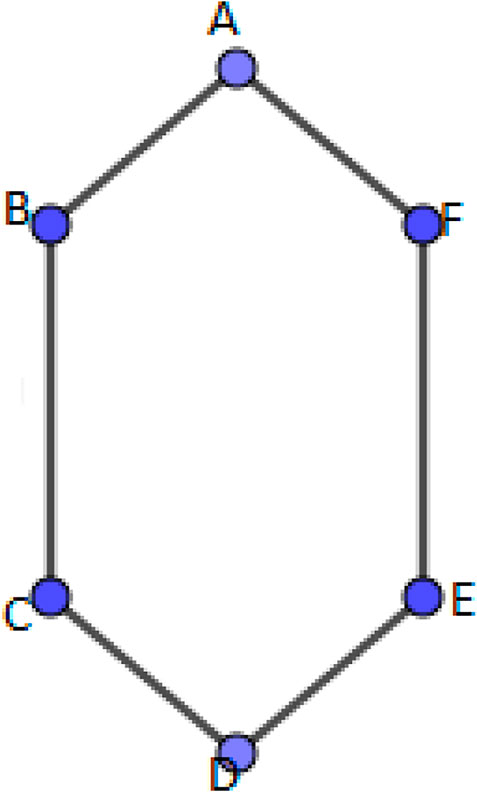
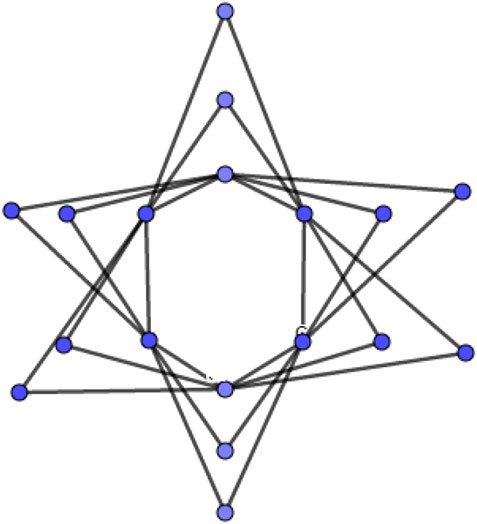
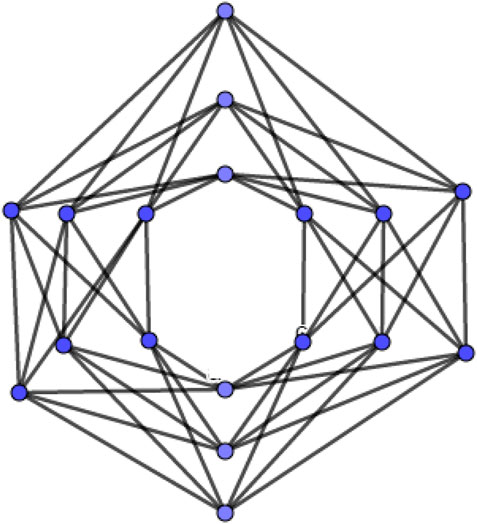
The s-shadow graph Shs(G) of a connected graph G is constructed by taking s copies of G, say G1, G2, G3, …., Gs then join each vertex u in Gi to the neighbors of the corresponding vertex v in Gj such that vi (1 ≤ i ≤ s). Figure 1 is an example of base graph C6, and Figure 2 is 2-splitting graph of C6 and Figure 3 is 3-shadow graph of C6.
[19] Let PϵRm×n, QϵRp×q. The Tensor or kronecker product of P and Q is the matrix defined by.
Lemma 1.1 [19]. Let PϵMm, QϵMn, λ be an eigenvalue of P related to eigenvector y, and μ be an eigenvalue of Q related to eigenvector x. Then λμ is an eigenvalue of P⊗Q related to eigenvector y⊗x.In the present article we produce new results about ABC energies and ABC Spectral radii of s-splitting and s-shadow graphs. In fact we relate these energies and Spectral radii of new graph operations with the energies and Spectral radii of original graphs. The article is organized as follows. In section 3, we derive ABC energies and ABC Spectral radii of generalized splitting graph constructed on cycle graph, complete graph and complete bipartite graph. In section 4 we proceed to find similar results but for generalized shadow graph of the given graph.
3 ABC energies and spectral radii of generalized splitting graph
In this part we relate ABC energies and ABC Spectral radii of generalized Splitting graph of Cn, Kn and Kn,n with original graph of Cn, Kn and Kn,n respectively.The following result relates the ABC energy of s-splitting graph of Cn with the ABC energy of Cn.
Theorem 1. Let Cn be a cycle graph and ABCɛ(Spls(Cn)) be the ABC energy of s-splitting graph of Cn, then
Proof. Let v1, v2, v3, …., vn be the vertices of Cn. The ABC matrix of Cn has entries given by
Let
Matrix ℵ1 has entries given by
Entries of matrix ℵ2 are given below
Let
Now we compute the eigenvalues of A. Since matrix A is of rank two, A has two non-zero eigenvalues, say α1 and α2. Obviously,
Consider,
Then
Solving Equation 3.1 and Equation 3.2, we have
and
So,
Since ABC(Spls (Cn)) = ABC(Cn)⊗A, it follows that if λ1, λ2, … λn are the eigenvalues of ABC(Cn), then by Lemma 1.1, we have
The following result relates the ABC Spectral radius of s-splitting graph of Cn with the ABC Spectral radius of Cn.
Corollary 2. Let Cn be a cycle graph and ρABC(Spls(Cn)) be the ABC Spectral radius of s-splitting graph Cn, then
Proof. By similar arguments as formula (3.5) in Theorem 1,
Since ABC(Spls (Cn)) = ABC(Cn)⊗A, it follows that if η1, η2, η3, … ηn are eigenvalues of ABC(Cn) then by Lemma 1.1, we have
The following result relates the ABC energy of s-splitting graph of Kn with the ABC energy of Kn.
Theorem 3. Let Kn be a complete graph on n vertices and ABCɛ(Spls(Kn)) be the ABC energy of s-splitting graph of Kn, then
Proof. Let v1, v2, v3, …., vn be the vertices of Kn. The ABC matrix of Kn has entries given by
Let
Let
Now we compute the eigenvalues of A. Since matrix A is of rank two, A has two non-zero eigenvalues, say α1 and α2. Obviously,
Consider,
Then
Solving Equation 3.6 and (3.7), we have
and
So,
where
The following result relates the ABC Spectral radius of s-splitting graph of Kn with the ABC Spectral radius of Kn.
Corollary 4. Let Kn be a graph and ρABC(Spls(Kn)) be the ABC Spectral radius of s-splitting graph Kn, then
Proof. By similar arguments as formula (3.10) in Theorem 3,
where
The following result relates the ABC energy of s-splitting graph of Kn,n with the ABC energy of Kn,n.
Theorem 5. Let Kn,n be a complete bipartite graph and ABCɛ(Spls(Kn,n)) be the ABC energy of s-splitting graph of Kn,n, then
Proof. Let v1, v2, v3, …., vn be the vertices of Kn,n. The ABC matrix of Kn,n has entries given by
Let
Let
Now we compute the eigenvalues of A. Since matrix A is of rank two, A has two non-zero eigenvalues, say α1 and α2. Obviously,
Consider,
Then
Solving Equation 3.11 and Equation 3.12, we have
Since ABC(Spls (Kn,n)) = ABC(Kn,n)⊗A, it follows that if λ1, λ2, … λn are the eigenvalues of ABC(Kn,n) then by Lemma 1.1, we have
The following result relates the ABC Spectral radius of s-splitting graph of Kn,n with the ABC Spectral radius of Kn,n.
Corollary 6. Let Kn,n be a graph and ρABC(Spls(Kn,n)) be the ABC Spectral radius of s-splitting graph Kn,n, then
Proof. By similar arguments as formula (3.13) in Theorem 5,
Since ABC(Spls (Kn,n)) = ABC(Kn,n)⊗A, it follows that if η1, η2, η3, … ηn are eigenvalues of ABC(Kn,n) then by Lemma 1.1, we have
4 ABC energies and spectral radii of generalized shadow graph
In this part we relate ABC energies and ABC Spectral radii of generalized Shadow graph of Kn, Cn and Kn,n with original graph of Kn, Cn and Kn,n, respectively.
The following result relates the ABC energy of s-shadow graph of Kn with the ABC energy of Kn.
Theorem 7. Let Kn be a complete graph and ABCɛ(Shs(Kn)) be the ABC energy of s-shadow graph of Kn, then
Proof. Let v1, v2, v3, …., vn be the vertices of Kn. The ABC matrix of Kn has entries given by
Let G1, G2, G3, …., Gs be the s copies of the graph Kn which we take to construct Shs(Kn). Then ABC(Spls (Kn)) can be written as follows
Matrix ℏ1 has entries given by
Let
Now we compute the eigenvalues of A. Since matrix A is of rank one, so A has only one non-zero eigenvalue, say α1. We have
Since ABC(Shs(Kn)) = ABC(Kn)⊗A, it follows that if λ1, λ2, … λn are the eigenvalues of ABC(Kn) then by Lemma 1.1, we have
The following result relates the ABC Spectral radius of s-shadow graph of Kn with the ABC Spectral radius of Kn.
Corollary 8. Let Kn be a graph and ρABC(Shs(Kn)) be the ABC Spectral radius of s-shadow graph of Kn, then
Proof. By similar arguments as formula (4.1) in Theorem 7,
So ABC(Shs(Kn)) = ABC(Kn)⊗A, it follows that if η1, η2, η3, … ηn are eigenvalues of ABC(Kn) then by Lemma 1.1, we have
The following result relates the ABC energy of s-shadow graph of Cn with the ABC energy of Cn.
Theorem 9. Let Cn be a cycle graph and ABCɛ(Shs(Cn)) be the ABC energy of s-shadow graph of Cn, then
Proof. Let v1, v2, v3, …., vn be the vertices of Cn. The ABC matrix of Cn has entries given by
Let G1, G2, G3, …., Gs be the s copies of the graph Cn which we take to construct Shs(Cn). Then ABC(Shs(Cn)) can be written in block matrix as follows
Let
Now we compute the eigenvalues of A. Since matrix A is of rank one, so A has only one non-zero eigenvalue, say α1. We have
So,
Since ABC(Shs(Cn)) = ABC(Cn)⊗A, it follows that if λ1, λ2, … λn are the eigenvalues of ABC(Cn) then by Lemma 1.1, we have
The following result relates the ABC Spectral radius of s-shadow graph of Cn with the ABC Spectral radius of Cn.
Corollary 10. Let Cn be a graph and ρABC(Shs(Cn)) be the ABC Spectral radius of s-shadow graph of Cn, then
Proof. By similar arguments as formula (4.2) in Theorem 9,
Since ABC(Shs(Cn)) = ABC(Cn)⊗A, it follows that if η1, η2, η3, … ηn are eigenvalues of ABC(Cn) then by Lemma 1.1 we have
The following result relates the ABC energy of s-shadow graph of Kn,n with the ABC energy of Kn,n.
Theorem 11. Let Kn,n be a complete bipartite graph and ABCɛ(Shs(Kn,n)) be the ABC energy of s-shadow graph of Kn,n, then
Proof. Let v1, v2, v3, …., vn be the vertices of Kn,n. The ABC matrix of Kn,n has entries given by
Let G1, G2, G3, …., Gs be the s copies of the graph Kn,n which we take to construct Shs(Kn,n). Then ABC(Shs(Kn,n)) can be written in block matrix as follows
Let
Now we compute the eigenvalues of A. Since matrix A is of rank one, so A has only one non-zero eigenvalue, say α1. We have
Since ABC(Shs(Kn,n)) = ABC(Kn,n)⊗A, it follows that if λ1, λ2, … λn are the eigenvalues of ABC(Kn,n) then by Lemma 1.1, we have
The following result relates the ABC Spectral radius of s-shadow graph of Kn,n with the ABC Spectral radius of Kn,n.
Corollary 12. Let Kn,n be a complete bipartite graph and ρABC(Shs(Kn,n)) be the ABC Spectral radius of s-shadow graph of Kn,n, then
Proof. By similar arguments as formula (4.3) in Theorem 11,
Since ABC(Shs(Kn,n)) = ABC(Kn,n)⊗A, it follows that if η1, η2, η3, … ηn are eigenvalues of ABC(Kn,n) then by Lemma 1.1, we have
5 Conclusion and possible applications
The graph energy and Spectral radius are two most emerging concepts in spectral graph theory. These concepts provides a bridge between mathematics and chemistry. You can find the Spectral radius and energy of many graphs in the literature. To examine the Spectral radius and energy of the larger graphs produced by a number of graph operations on a certain regular graph, however, is a challenge we must accept. We reached some quite general findings by concentrating on two graph operations, s-splitting and s-shadow graphs. Additionally, it was established that the new graph’s Spectral radius and energy are multiples of Spectral radius and energy of original regular graph referred as base graph. Our results on graph energies have applications in network analysis particularly dealing with problems of air travel, kirchhoff index, resistance distance, satellite communication, and biology. Our results on Spectral radii are also applicable to the stability theory of time-varying linear systems and linear inclusions.
Data availability statement
The original contributions presented in the study are included in the article/supplementary material, further inquiries can be directed to the corresponding author.
Author contributions
Conceptualization, MM. Investigation, computation and original draft, AB.
Conflict of interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Publisher’s note
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
References
1. Estrada E, Torres L, Rodrguez L, Gutman I. An atom-bond connectivity index modelling the enthalpy of formation of alkanes. Indian J Chem (1998) 37A:849–55.
2. Estrada E. Atom-bond connectivity and the energetic of branched alkanes. Chem Phys Lett (2008) 463:422–5. doi:10.1016/j.cplett.2008.08.074
3. Gutman I, Tosovic J, Radenkovic S, Markovic S. On atom-bond connectivity index and its chemical applicability. Indian J Chem Sect A, Inorg Phys Theor Anal (2012) 51:690–4.
4. Chen J, Guo X. Extreme atom-bond connectivity index of graphs. MATCH Commun Math.Comput Chem (2011) 65:713–22.
5. Chen J, Liu J, Guo X. Some upper bounds for the atom-bond connectivity index of graphs. Appl Math Lett (2012) 25:1077–81. doi:10.1016/j.aml.2012.03.021
6. Xing R, Zhou B, Du Z. Further results on atom-bond connectivity index of trees. Discrete Appl Math (2010) 158:1536–45. doi:10.1016/j.dam.2010.05.015
7. Xing R, Zhou B, Dong F. On atom-bond connectivity index of connected graphs. Discrete Appl Math (2011) 159:1617–30. doi:10.1016/j.dam.2011.06.004
8. Zhou B, Xing R. On atom-bond connectivity index. Z Naturforsch A (2011) 66a:61–6. doi:10.5560/zna.2011.66a0061
11. Liu JB, Munir M, Yousaf A, Naseem A, Ayub K. Distance and adjacency energies of multi-level wheel networks. Mathematics (2019) 7:43. doi:10.3390/math7010043
12. Zhang X, Bilal A, Munir MM, Rehman HMU. Maximum degree and minimum degree spectral radii of some graph operations. Math Biosci Eng (2022) 19(10):10108–21. doi:10.3934/mbe.2022473
13. Chu ZQ, Munir M, Yousaf A, Qureshi MI, Liu JB. Laplacian and signless laplacian spectra and energies of multi-step wheels. Math Biosci Eng (2020) 17(4):3649–59. doi:10.3934/mbe.2020206
14. Chen X. On ABC eigenvalues and ABC energy. Linear Algebra Appl (2018) 544:141–57. doi:10.1016/j.laa.2018.01.011
15. Gao Y, Shao Y. The minimum ABC energy of trees. Linear Algebra Appl (2019) 577:186–203. doi:10.1016/j.laa.2019.04.032
16. Ghorbani M, Li X, Nezhaad MH, Wang J. Bounds on the ABC Spectral radius and ABC energy of graphs. Linear Algebra Its Appl (2020) 598:145–64. doi:10.1016/j.laa.2020.03.043
17. Yalçin NF, Buyukkose E. Skew ABC energy of digraphs. Commun Fac Sci Univ Ank Ser A1 Math Stat (2022) 71(22022):434–44. doi:10.31801/cfsuasmas.951302
18. Singh R, Patekar SC. On the sombor index and sombor energy of m-splitting graph and m-shadow graph of regular graphs (2022). preprint arXiv:2205.09480.
19. Vaidya SK, Popat KM. Some new results on energy of graphs. MATCH Commun Math Comput Chem (2017) 77:589–94.
20. Vaidya SK, Popat KM. Energy of m-Splitting and m-Shadow Graphs. Far East J Math Sci (Fjms) (2017) 102(8):1571–8. doi:10.17654/ms102081571
Keywords: shadow graph, splitting graph, ABC energy, ABC spectral radius, eigenvalues
Citation: Bilal A and Munir MM (2022) ABC energies and spectral radii of some graph operations. Front. Phys. 10:1053038. doi: 10.3389/fphy.2022.1053038
Received: 24 September 2022; Accepted: 21 November 2022;
Published: 22 December 2022.
Edited by:
Gang (Gary) Ren, The Molecular Foundry, United StatesReviewed by:
Zhiyong Gan, South China Normal University, ChinaAbdu Alameri, University of Science and Technology, Yemen
Copyright © 2022 Bilal and Munir. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Muhammad Mobeen Munir, bW11bmlyLm1hdGhAcHUuZWR1LnBr
†These authors share first authorship
 Ahmad Bilal
Ahmad Bilal Muhammad Mobeen Munir
Muhammad Mobeen Munir