- Business School, University of Shanghai for Science and Technology, Shanghai, China
Rumor propagation in the new media era poses a huge threat to maintaining the normal order of social life. In this context, we put forth a nonlinear dynamics-based stochastic SICR rumor model that integrates media coverage with science education. First, the existence of a unique global positive solution is obtained. Second, sufficient conditions for extinction are constructed on the spread of rumors based on the Lyapunov function methods and Khasminskii’s theory. Finally, the theoretical analysis is verified through numerical simulations. Additionally, it demonstrates how rumor spreading can be hampered by media coverage.
1 Introduction
Rumor, a specific type of misinformation, is information whose integrity has not been verified and spread to cause an impact [1]. Spreading rumors can occasionally be advantageous; for instance, we might use their quick and effective nature to alert the public and urge them to take the necessary precautions [2]. However, most rumors can trigger panic or potential losses in the accompanying unexpected events [3], for example, the spread of harmful rumors can have a significant negative impact on the well-being of the society [4]. Rumors are more influential and have a more complex structure than accurate information [5]. Consequently, a worthwhile research issue is how to limit and prevent the propagation of damaging rumors.
Mobile Internet penetrates people’s daily lives as a convenient platform for obtaining and distributing information [6], for example, the rapid development and increasing popularity of new social media such as WeChat, Twitter, and Facebook [7]. People can get news about events as soon as they happen through new social media [8]. Given unexpected events, uncertainty, and limited information, official news releases about events often lag. By contrast, rumors are stories or statements whose integrity is not confirmed [9], therefore always appearing and spreading first on the Internet. False, biased, and uncertain rumors often mislead the public or harm the society and public order [10]. Thus, the rapid spread of rumors on new social media is a significant factor in destabilizing the society [11]. How to prevent the spread of harmful rumors through new media has become an important topic, such as the study of 606 participants’ tweets concerning the spread of rumors about the COVID-19 vaccine, aiming to reduce misinformation in general and rumors in particular and suggesting Twitter as the preferred platform for COVID-19 updates [12].
Numerous academics domestically and internationally have examined the issue of rumor propagation from a variety of perspectives using qualitative analysis and theoretical modeling. Daley–Kendall introduced the first rumor propagation model (the DK model) by dividing the population into three categories based on the idea of the infectious disease research method [13]. Maki and Thompson put forward a modified DK model (the MT model) [14]. Based on these two models, many extended propagation models have been proposed and studied. Many scholars have studied some deterministic models. Zanette first shifted the research focus to the dynamic behavior of rumor spreading and concluded that the rumor propagation threshold was observably influenced by the network topologies, especially in small-world networks [15]. Later, Moreno et al. developed the mean-field theory in the scale-free network [16]. In recent years, Zhao et al. have proposed a mixed patch distribution strategy to combine the advantages of the conventional centralized patch distribution approach and the decentralized patch distribution strategy [17]. Guo et al. created a linked epidemic model to describe the interaction between epidemics and related information [18]. Xiao et al. considered the change in information attributes on the dissemination of information combining network topology [19]. At the same time, some scholars have studied stochastic models. Dauhoo et al. proposed the stochastic coefficient to convert the deterministic rumor model into a stochastic one, proving the existence and boundedness of global and local solutions [20]. After that, Jia et al. established a stochastic rumor propagation model by taking into account different noise environments and figured out that the threshold affected by the white noise was less than the deterministic one [21]. Ankur et al. investigated a stochastic rumor propagation model in a homogenous social network containing expert intervention and drew the conclusion that noise can be one of the reasons for rumor persistence under stochastic circumstances [22]. Huo et al. studied the near-optimal control of a stochastic rumor propagation model by adopting Holling II functional response function and imprecise parameters [23]. In the meanwhile, they extended a stochastic delayed rumor propagation model [24]. Due to the lack of related research, adopting a more stochastic model to explore how rumors spread under the influence of stochastic noises can not only extend the existing literature but also provide deeper theoretical insights into this field.
Information is always affected by the noisy environment in the process of dissemination [23, 25]. For instance, it was discovered that noise can be one of the causes for rumors to persist in random conditions when a model of random rumor dissemination was explored in a homogenous social network with expert interventions [22]. The fact-checking process on rumors relies heavily on the crowd or journalist’s response to investigate. Still, the downside of this traditional method is that it is not widely conducted until after the rumor is widely spread [26–28]. In this study, noise is studied in combination with new social media to avoid the aforementioned traditional method of passive response only after the rumor spreads. A stochastic SICR rumor model containing media reports is proposed, which first analyzes the data on noise influence. Second, by using the Lyapunov function method and Khasminskii’s theory, sufficient conditions for rumor extinction are established [4]. In addition, the existing articles almost always assume that rumor spreaders move directly to stiflers in the rumor propagation model. However, it ignores the possibility that rumor spreaders may go through a calm latency period before becoming stiflers to make the rumor propagation model more realistic [29, 30]. To that purpose, we put forth a nonlinear dynamics-based stochastic SICR rumor model that integrates media coverage with science education. For instance, during the 2019-nCoV outbreak, the government made the public aware of the new coronavirus through the official media, immunizing them against the myth rumor that garlic water may treat coronavirus. By extending the SICR rumor model and adding the Wiener process to the model to represent the interference factors existing in the external environment to the rumor propagation process, rumors’ propagation law and propagation mechanism are explored in depth.
The rest of the article is divided into the following sections. Section 2 presents the stochastic SICR rumor model that includes media coverage. Section 3 verifies the existence and uniqueness of a globally positive solution to rumor propagation. Section 4 explores the conditions for model extinction by constructing a suitable stochastic Lyapunov. Section 5 proves the existence of an ergodic steady-state distribution based on Khasminskii's theory. Section 6 verifies the results through relevant numerical simulations. Finally, conclusions are drawn at the end of the article.
2 The stochastic SICR rumor model incorporating media coverage
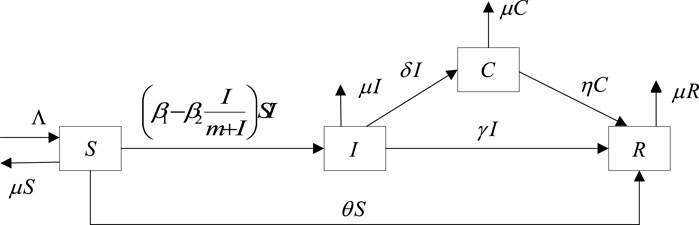
In this section, a novel SICR rumor-spreading model incorporating media coverage is proposed to explore the dynamics of the rumor propagation mechanism. Four categories are proposed to represent different states of individuals based on the classical rumor-spreading model. Susceptible (
According to the SICR rumor propagation process elaborated previously, the rumor-spreading model incorporating media coverage can be described by a system of ordinary differential equations.
where
The model describing rumor propagation in the aforementioned study is a deterministic model, but in the real world, rumor models are often affected by environmental noise. In particular, in emergencies, when rumors are widely spread, the spreading process is influenced by numerous uncertain factors from the outside, like authority regulation, which may increase the volatility of the rumor propagation process. Therefore, it is of great significance to explore how environmental noise influences the rumor propagation model. Referencing the idea of Jia et al. [31] and Huo et al. [32], we assume that the white noise is stochastic perturbations as the primary reason for the system variable. Based on the aforementioned discussion, we add white noise to obtain a stochastic analog of the deterministic model (1) with periodic coefficients as follows:
where
3 Existence and uniqueness of the global positive solution
In this section, motivated by the methods in [33], we demonstrate that the solution of system (2.2) has a distinct global positive solution using the Lyapunov function approaches.
Theorem 3.1. For any initial value
where we fix
where the positive constant
where
which suggests that
Define a
where
reference [33], for any
Let
Consequently,
where
4 The dynamic property around the rumor-eliminating equilibrium
One of the central concerns in emergency management systems is how to govern rumor dynamics and eliminate them permanently. In this section, we mainly survey the situation for the extinction of model (2.2).
Lemma 4.1. ([35, 36]). Let
Lemma 4.2. Let
Theorem 4.3. Suppose
and
Then, it is easy to get
It is simple to acquire
where
In terms of Lemma 4.1, we obtain
By means of the
By means of integrating (4.3) from
Combining with, we have
Employing the upper limit of both of (20) and adopting Lemma 4.1 and 4.2, which is along with (18), we obtain
which suggests
5 The dynamic property around the rumor-spreading equilibrium
In this section, we investigate that model (2.2) accepts no fewer than one nontrivial positive
Definition 5.1. ([37]). A stochastic process
where function
Lemma 5.2. ([37]). We suppose that system (2.1) accepts a unique global solution. Assume further that there exists a function
System (5.1) then has a
Theorem 5.1. ([38, 39]). If
where
and
and
where
Distinctly,
where
where
Define the T-periodic function
Similar to the aforementioned formula, we can observe
and
Therefore,
Now, we prove a compact subset
where
where
Next, we will demonstrate that
Case 1. If
where
By
Case 2. If
where
By
Case 3. If
By
Case 4. If
By
Case 5. If
where
By
Case 6. If
where
By
Case 7. If
where
By
Case 8. If
where
By
Hence,
6 Simulation results
In this section, we will illustrate the obtained theoretical results using MATLAB and illustrate our findings with Milstein’s higher-order method developed in [40]. Thus, we get the following discretization equation of system (2.2):
where time increment
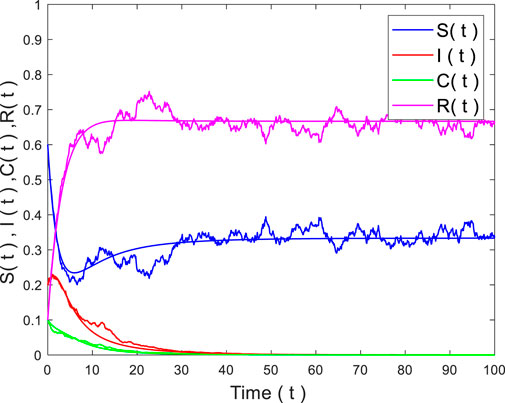
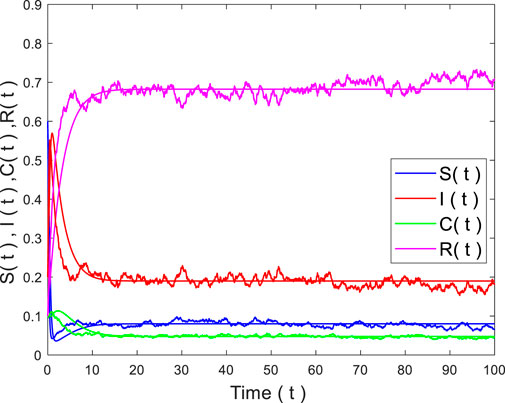
When we choose the initial value
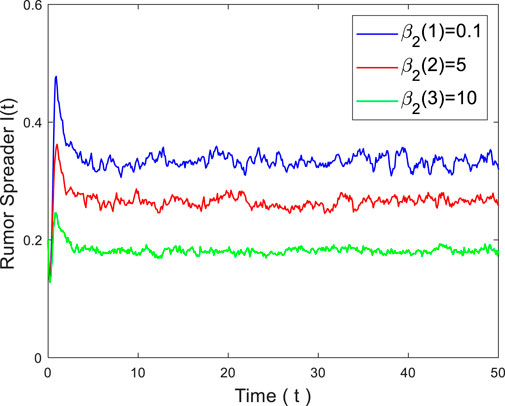
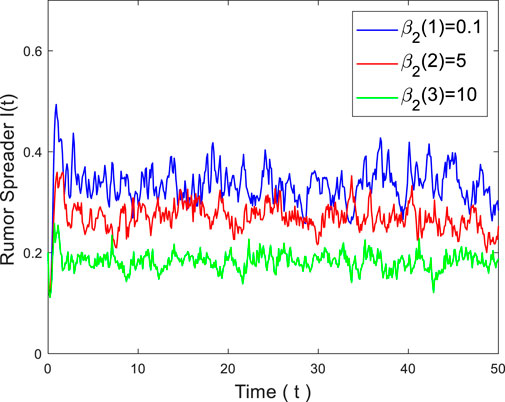
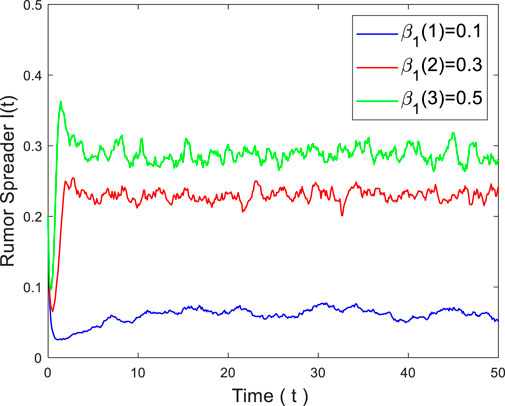
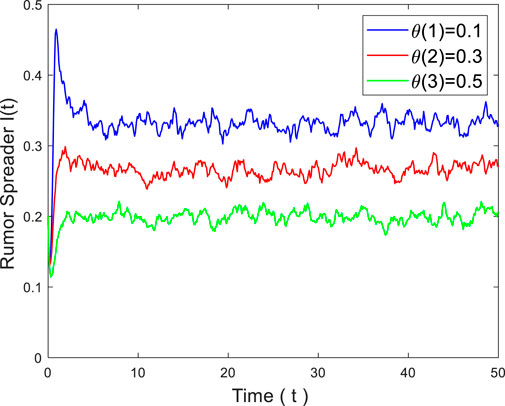
To account for the impact of media coverage on rumor propagation, we set a variation of the parameter
Rumor propagation is also influenced by other parameters.
7 Conclusion
In this article, a stochastic propagation model is studied and the existence of globally unique positive solutions of system (2.2) is obtained with the method of the stochastic Lyapunov function based on the theory of Khasminskii. According to theoretical research and the numerical simulation in this article, if
The Wiener process reflects minor disturbances. When the environmental noise is extensive, such disorders can destroy the continuity of the differential equations, and then, it is necessary to express the random external disturbances by Lévy jump. The stochastic rumor model, including the Lévy process, can more accurately reflect the complex rumor propagation law in the real world [42]. Furthermore, by introducing various control strategies, such as media coverage, we construct a near-optimal control problem that minimizes rumor propagation’s influence and control cost. Some scholars may analyze the same issue, such as the combined stochastic process on scale-free networks [43] and the integrated influences of time delay and stochastic perturbation on heterogeneous networks [44]. The Runge–Kutta method and Milstein’s higher order method are used in the previous numerical simulations carried out by MATLAB. Even if the outcomes of simulation figures can verify that the theorems are accurate, these simulation techniques are still loosely coupled. The reproducing kernel Hilbert space approach [45] and variational iteration method [46] are employed, and the accuracy of simulation results may be increased. These will be taken into account in our further research.
Data availability statement
The original contributions presented in the study are included in the article/supplementary material; further inquiries can be directed to the corresponding author.
Author contributions
XY contributed significantly to the analysis and wrote the manuscript; LH helped perform the analysis with constructive discussions.
Conflict of interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Publisher’s note
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors, and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
References
1. Yang YC, Nazir S, Khalil WA. probabilistic approach toward evaluation of Internet rumor on COVID. Soft Comput. (2022) 26:8077–8088. doi:10.1007/s00500-022-07064-1
2. Ruan ZY, Tang M, Liu ZH. Epidemic spreading with information-driven vaccination. Phys Rev E (2012) 86:036117. doi:10.1103/PhysRevE.86.036117
3. Zhang ZL, Zhang ZQ. An interplay model for rumour spreading and emergency development. Physica A: Stat Mech its Appl (2009) 388:4159–66. doi:10.1016/j.physa.2009.06.020
4. Zan Y, Wu J, Li P, Yu Q. SICR rumor spreading model in complex networks: Counterattack and self-resistance. Physica A: Stat Mech its Appl (2014) 405:159–70. doi:10.1016/j.physa.2014.03.021
5. Wu Y, Ngai EWT, Wu P, Wu C. Fake online reviews: Literature review, synthesis, and directions for future research. Decis Support Syst (2020) 132:113280. doi:10.1016/j.dss.2020.113280
6. Wang Z, Wang L, Ji Y, Zuo L, Qu S. A novel data-driven weighted sentiment analysis based on information entropy for perceived satisfaction. J Retailing Consumer Serv (2022) 68:103038. doi:10.1016/j.jretconser.2022.103038
7. Wang X, Fang B, Zhang H, Wang X. Predicting the security threats on the spreading of rumor, false information of Facebook content based on the principle of sociology. Comput Commun (2020) 150:455–62. doi:10.1016/j.comcom.2019.11.042
8. Liang X, Guo G, Li S, Zhong X, Luo P. COVID-19-related information seeking and individual's rumor refuting: A multi-information-source perspective. Comput Hum Behav (2022) 134:107342. doi:10.1016/j.chb.2022.107342
9. Alkhodair SA, Ding SHH, Fung BCM, Liu JQ. Detecting breaking news rumors of emerging topics in social media. Inf Process Manage (2020) 57:102018. doi:10.1016/j.ipm.2019.02.016
10. Bodaghi A, Oliveira J. The characteristics of rumor spreaders on twitter: A quantitative analysis on real data. Comput Commun (2020) 160:674–87. doi:10.1016/j.comcom.2020.07.017
11. Sicilia R, Lo Giudice S, Pei Y, Pechenizkiy M, Soda P. Twitter rumour detection in the health domain. Expert Syst Appl (2018) 110:33–40. doi:10.1016/j.eswa.2018.05.019
12. Sharevski F, Huff A, Jachim P, Pieroni E. (Mis)perceptions and engagement on twitter: COVID-19 vaccine rumors on efficacy and mass immunization effort. Int J Inf Manage Data Insights (2022) 2:100059. doi:10.1016/j.jjimei.2022.100059
14. Maki DP, Thompson M. Mathematical models and applications : With emphasis on the social, life, and management sciences. New Jersey, United States: Englewood Cliffs (1973) 10. 12p.
15. Zanette DH. Critical behavior of propagation on small-world networks. Phys Rev E (2001) 64:050901. doi:10.1103/physreve.64.050901
16. Moreno Y, Nekovee M, Pacheco AF. Dynamics of rumor spreading in complex networks. Phys Rev E (2004) 69:066130. doi:10.1103/physreve.69.066130
17. Zhao D, Wang L, Wang Z, Xiao G. Virus propagation and patch distribution in multiplex networks: Modeling, analysis, and optimal allocation. IEEE Trans Inf Forensics Security (2019) 14(7):1755–67. doi:10.1109/TIFS.2018.2885254
18. Guo H, Yin Q, Xia C, Dehmer M. Impact of information diffusion on epidemic spreading in partially mapping two-layered time-varying networks. Nonlinear Dyn (2021) 105:3819–33. doi:10.1007/s11071-021-06784-7
19. Xiao Y, He W, Yang T, Li Q. A dynamic information dissemination model based on user awareness and evolutionary games. IEEE Trans Comput Soc Syst (2022) 9:1–10. doi:10.1109/tcss.2022.3201061
20. Dauhoo MZ, Juggurnath D, Adam NRB. The stochastic evolution of rumors within a population. Math Soc Sci (2016) 82:85–96. doi:10.1016/j.mathsocsci.2016.05.002
21. Jia FJ, Lv GY. Dynamic analysis of a stochastic rumor propagation model. Physica A: Stat Mech its Appl (2018) 490:613–23. doi:10.1016/j.physa.2017.08.125
22. Jain A, Dhar J, Gupta V. Stochastic model of rumor propagation dynamics on homogeneous social network with expert interaction and fluctuations in contact transmissions. Physica A: Stat Mech its Appl (2019) 519:227–36. doi:10.1016/j.physa.2018.11.051
23. Huo LA, Chen XM. Near-optimal control of a stochastic rumor spreading model with Holling II functional response function and imprecise parameters*. Chin Phys B (2021) 30:120205. doi:10.1088/1674-1056/ac0eea
24. Huo LA, Chen XM. Dynamical analysis of a stochastic rumor-spreading model with Holling II functional response function and time delay. Adv Differ Equ (2020) 2020:651. doi:10.1186/s13662-020-03096-9
25. Huo LA, Wang L, Song GX. Global stability of a two-mediums rumor spreading model with media coverage. Physica A: Stat Mech its Appl (2017) 482:757–71. doi:10.1016/j.physa.2017.04.027
26. Choi D, Oh H, Chun S, Kwon T, Han J. Preventing rumor spread with deep learning. Expert Syst Appl (2022) 197:116688. doi:10.1016/j.eswa.2022.116688
27. Ruchansky N, Seo S, Liu Y. CSI: A hybrid deep model for fake news detection. In: Proceedings of the 2017 ACM on conference on information and knowledge management (2017). p. 797–806. Singapore (Accessed November 6–10, 2017).
28. Kim J, Tabibian B, Oh A, Schölkopf B, Gomez-Rodriguez M. Leveraging the crowd to detect and reduce the spread of fake news and misinformation. In: Proceedings of the eleventh ACM international conference on web search and data mining (2018). New York, NY: WSDM. p. 324–32. doi:10.1145/3159652.3159734
29. Chen GH. ILSCR rumor spreading model to discuss the control of rumor spreading in emergency. Physica A: Stat Mech its Appl (2019) 522:88–97. doi:10.1016/j.physa.2018.11.068
30. Chang ZX, Jiang HJ, Yu SZ, Chen SS. Dynamic analysis and optimal control of ISCR rumor propagation model with nonlinear incidence and time delay on complex networks. Discrete Dyn Nat Soc (2021) 2021:1–20. doi:10.1155/2021/3935750
31. Jia FJ, Lv GY, Wang SF, Zou GA. Dynamic analysis of a stochastic delayed rumor propagation model. J Stat Mech (2018) 2018:023502. doi:10.1088/1742-5468/aaa798
32. Huo LA, Dong YF. Analyzing the dynamics of a stochastic rumor propagation model incorporating media coverage. Math Methods Appl Sci (2020) 43:6903–20. doi:10.1002/mma.6436
33. Mao XR, Marion G, Renshaw E. Environmental Brownian noise suppresses explosions in population dynamics. Stochastic Process Their Appl (2002) 97:95–110. doi:10.1016/s0304-4149(01)00126-0
34. Oksendal B. Stochastic differential equations : An introduction with applications. Cambridge, United Kingdom: University of Cambridge (2010).
35. Liptser RS. A strong law of large numbers for local martingales. Stochastics (Abingdon) (1980) 3:217–28. doi:10.1080/17442508008833146
36. Din A, Li Y. Stochastic optimal control for norovirus transmission dynamics by contaminated food and water. Chin Phys B (2022) 31:020202. doi:10.1088/1674-1056/ac2f32
37. Khas'Miniskii RZ. Stochastic stability of differential equations. Berlin Heidelberg: Springer (1980).
38. Qi HK, Zhang SQ, Meng XZ, Dong HH. Periodic solution and ergodic stationary distribution of two stochastic SIQS epidemic systems. Physica A: Stat Mech its Appl (2018) 508:223–41. doi:10.1016/j.physa.2018.05.075
39. Ding YL, Ren XZ, Jiang CC, Zhang QH. Periodic solution of A stochastic siqr epidemic model incorporating media coverage. jaac (2020) 10:2439–58. doi:10.11948/20190333
40. Higham DJ. An algorithmic introduction to numerical simulation of stochastic differential equations. SIAM Rev Soc Ind Appl Math (2001) 43:525–46. doi:10.1137/s0036144500378302
41. Berrhazi BE, Fatini ME, Pettersson R, Laaribi A. Media effects on the dynamics of a stochastic SIRI epidemic model with relapse and Lévy noise perturbation. Int J Biomath (2019) 12:1950037. doi:10.1142/s1793524519500372
42. Huo L-A, Dong Y-F, Lin T-T. Dynamics of a stochastic rumor propagation model incorporating media coverage and driven by Levy noise*. Chin Phys B (2021) 30:080201. doi:10.1088/1674-1056/ac0423
43. Li K, Zhu G, Ma Z, Chen L. Dynamic stability of an SIQS epidemic network and its optimal control. Commun Nonlinear Sci Numer Simulation (2018) 66:84–95. doi:10.1016/j.cnsns.2018.06.020
44. Sun M, Liu Q. An SIS epidemic model with time delay and stochastic perturbation on heterogeneous networks. Math Biosci Eng (2021) 18:6790–805. doi:10.3934/mbe.2021337
45. Omar AA. Numerical solutions of systems of first-order, two-point BVPs based on the reproducing kernel algorithm. Calcolo (2018) 55:31. doi:10.1007/s10092-018-0274-3
Keywords: rumor spreading, stochastic process, extinction, media coverage, dynamical behavior
Citation: Yue X and Huo L (2022) Dynamical behavior of a stochastic SICR rumor model incorporating media coverage. Front. Phys. 10:1010428. doi: 10.3389/fphy.2022.1010428
Received: 03 August 2022; Accepted: 03 October 2022;
Published: 28 October 2022.
Edited by:
Vasilios Zarikas, University of Thessaly, GreeceReviewed by:
Chengyi Xia, Tiangong University, ChinaHossein Rashmanlou, University of Mazandaran, Iran
Copyright © 2022 Yue and Huo. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Liangan Huo, aHVvaHVvbGluQHllYWgubmV0
 Xuefeng Yue
Xuefeng Yue Liangan Huo
Liangan Huo