Controlled Bistable Transmission Non-Reciprocity in a Four-Mode Optomechanical System

We examine the bistable transmission non-reciprocity in a four-mode optomechanical system, where a mechanical oscillator interacts with one of three coupled optical cavities so as to generate an asymmetric optomechanical non-linearity. Two transmission coefficients in opposite directions are found to exhibit non-reciprocal bistable behaviors due to this asymmetric optomechanical non-linearity as the impedance-matching condition is broken for a not too weak input field. Such a bistable transmission non-reciprocity can be well manipulated to exhibit reversible higher isolation ratios in tunable wider ranges of the input field power or one cavity mode detuning by modulating relevant parameters like optical coupling strengths, optomechanical coupling strengths, and mechanical frequencies. This optomechanical system provides a flexible platform for realizing transmission non-reciprocity of weal light signals and may be extended to optical networks with more coupled cavities.

1 Introduction

Cavity optomechanics, focusing on enhanced radiation pressure interactions between light fields and mechanical motions, has attracted extensive experimental and theoretical interests owing to its wide applications in processing quantum information, measuring weak signals, and developing new devices [1–9]. Various optomechanical systems have been proposed and fabricated to realize non-trivial tasks and interesting phenomena, such as entanglement generation between cavity and mechanical modes [10–15], ground-state cooling of mechanical resonators [16–20], optomechanically induced transparency (OMIT) and absorption (OMIA) [21–26], Bell non-locality verification [27], parity-time (PT) symmetry-breaking chaos [28], and tumor structural imaging [29]. We note in particular that optomechanical systems can provide an effective avenue for implementing non-reciprocal devices, like isolators and circulators, required in constructing all-optical communication networks [30–34].

Non-reciprocal devices promise the transmission of signals in one direction while blocking those propagating in the opposite direction and can be utilized to avoid unwanted interference of signals and protect optical sources and systems from noises [35–42]. Breaking reciprocity or time reversal symmetry is typically accomplished with magneto-optical effects [43–45] and has resulted in the emergence of new physics such as topologically protected one-way photonic edge modes [46] and non-reciprocal behaviors in giant atom systems [47, 48]. Unfortunately, magneto-optical effects are not present in standard optoelectronic materials including most metals and semiconductors and may result in crosstalk and other problems hampering on-chip implementations. This is why non-magnetic approaches for achieving optical non-reciprocity have been extensively studied with significant advances, for example, in chiral atomic systems [49–51] and optomechanical systems [30–34]. The latter includes, for instance, a three-mode optomechanical system with additional gain in one cavity [31] and a two-cavity optomechanical system with a blue-detuned driving [32].

Coupled micro-cavities are essential elements for constructing quantum information networks in that they are scalable via mode swapping or fiber coupling, compatible with mechanical oscillators and other elements, and easy to be controlled by driving fields. With this consideration, here we extend previous works [30–34] to seek more flexible manipulations on optical non-reciprocity by investigating a four-mode optomechanical system with three optical cavities and one mechanical oscillator. This system is found to exhibit an asymmetric optomechanical non-linearity, which then result in staggered bistable behaviors of two opposite-direction transmission coefficients, under the broken impedance-matching condition. Numerical results show in particular that quite a few parameters can be modulated on demand to manipulate, in different ways, the upper and lower stable branches of both transmission coefficients. This allows us to tune and widen non-reciprocal ranges in terms of the input power or a cavity detuning on the one hand, while improve isolation ratio and reverse isolation direction with respect to transmission coefficients on the other hand.

2 Model and Equations

We consider a cavity optomechanical system consisting of three optical modes described by annihilation operators a₁, a₂, and a₃ and a mechanical mode described by position operator q and momentum operator p, as shown in Figure 1. These optical and mechanical modes exhibit frequencies ω₁, ω₂, ω₃, and ω_m, respectively. The 2nd optical mode is coupled to the 1st optical mode with strength J₁₂, while to the 3rd optical mode with strength J₂₃, in a linear way controlled via the in-between waveguide or fiber. The mechanical mode is coupled only to the 1st optical mode with single-photon optomechanical coupling strength g. A driving field of frequency ω_d is applied to excite the 1st optical mode with annihilation operator a_1,in or the 3rd optical mode with annihilation operator a_3,in. With these considerations, we can write down the following Hamiltonian (ℏ = 1):

$\begin{array}{ll}\hfill H& ={\omega }_1{a}_1^{†}{a}_1+{\omega }_2{a}_2^{†}{a}_2+{\omega }_3{a}_3^{†}{a}_3+\frac{1}{2}{\omega }_m\left(p^2+q^2\right)\hfill \\ \hfill & +g{a}_1^{†}{a}_{1}q+J_{12}\left(a_1^{†}{a}_2+a_2^{†}{a}_1\right)+J_{23}\left(a_2^{†}{a}_3+a_3^{†}{a}_2\right)\hfill \\ \hfill & +i\sqrt{{\gamma }_{1,e}}\left(a_1^{†}{a}_{1,in}{e}^{-i{\omega }_{d}t}-a_1{a}_{1,in}^{†}{e}^{i{\omega }_{d}t}\right)\hfill \\ \hfill & +i\sqrt{{\gamma }_{3,e}}\left(a_3^{†}{a}_{3,in}{e}^{-i{\omega }_{d}t}-a_3{a}_{3,in}^{†}{e}^{i{\omega }_{d}t}\right),\hfill \end{array}(1)$

where γ_j,e has been taken as the coupling constant to the driving field, that is, the external decay rate, of the jth optical mode. It is worth noting that the jth optical mode also exhibits an intrinsic decay rate γ_j,i so that its total decay rate turns out to be γ_j = γ_j,i + γ_j,e. Then we can define η_j = γ_j,e/γ_j as an effective coupling ratio with η_j = 0 denoting a vanishing coupling, while η_j = 1 denoting the maximal coupling. To be more specific, our optomechanical system may be implemented either with a vibrational membrane coupled to one of three Fabry-P$\acute{e}$rot cavities, or with an optomechanical crystal coupled to one of three photonic crystal cavities [52].

FIGURE 1

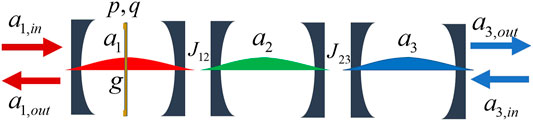
FIGURE 1. (Color online) Schematic of an optomechanical system consisting of three cavities described by optical modes a₁, a₂, and a₃ as well as a membrane described by position q and momentum p. This system could be driven by an input field a_1,in and exhibit an output field a_3,out, or driven by an input field a_3,in and exhibit an output field a_1,out. Here, g denotes the optomechanical coupling strength, while J_lk represents the coupling strength between optical modes a_l and a_k.

In the rotating frame of the driving frequency ω_d, it is viable to attain from the Hamiltonian in Eq. 1 the following quantum Langevin equations (QLEs):

$\begin{array}{ll}\hfill {\partial }_t{a}_1=& -\left({\gamma }_1/2+i{\mathrm{\Delta }}_1\right)a_1-igq{a}_1-i{J}_{12}{a}_2\hfill \\ \hfill & +\sqrt{{\gamma }_{1,e}}{a}_{1,in}+\sqrt{{\gamma }_{1,i}}{a}_{1,vac},\hfill \\ \hfill {\partial }_t{a}_2=& -\left({\gamma }_2/2+i{\mathrm{\Delta }}_2\right)a_2-i{J}_{12}{a}_1-i{J}_{23}{a}_3\hfill \\ \hfill & +\sqrt{{\gamma }_{2,i}}{a}_{2,vac},\hfill \\ \hfill {\partial }_t{a}_3=& -\left({\gamma }_3/2+i{\mathrm{\Delta }}_3\right)a_3-i{J}_{23}{a}_2\hfill \\ \hfill & +\sqrt{{\gamma }_{3,e}}{a}_{3,in}+\sqrt{{\gamma }_{3,i}}{a}_{3,vac},\hfill \\ \hfill {\partial }_{t}q=& {\omega }_{m}p,\hfill \\ \hfill {\partial }_{t}p=& -{\omega }_{m}q-g{a}_1^{†}{a}_1-{\gamma }_{m}p+\xi ,\hfill \end{array}(2)$

where Δ_j = ω_j − ω_d is defined as the detuning of the jth optical mode to the driving field, while γ_m refers to the decay rate of the mechanical mode. In addition, we have used a_1,vac, a_2,vac, a_3,vac, and ξ to denote the input quantum noise operators with zero mean values ⟨a_1,vac⟩ = 0, ⟨a_2,vac⟩ = 0, ⟨a_3,vac⟩ = 0, and ⟨ξ⟩ = 0 [54].

Each operator of the optical and mechanical modes can be split into a classical mean value and a quantum fluctuation as usual. That means, we can set a_j = α_j + δa_j, a_j,in = α_j,in + δa_j,in, $q=\bar{q}+\delta q$, and $p=\bar{p}+\delta p$ with the ansatz α_j = ⟨a_j⟩, α_j,in = ⟨a_j,in⟩, $\bar{q}=⟨q⟩$, and $\bar{p}=⟨p⟩$. In the limit of a much stronger optical driving than the optomechanical coupling, that is, $\sqrt{{\gamma }_{j,e}}|{\alpha }_{j,in}|\gg {\gamma }_j\gg g$, the classical mean values and the fluctuation operators can be treated separately. Then we can determine the classical mean values, in the steady state (${\partial }_t{\alpha }_i={\partial }_t\bar{p}={\partial }_t\bar{q}=0$), via the following equations:

$\begin{array}{ll}\hfill 0& =-\left({\gamma }_1/2+i{\mathrm{\Delta }}_1\right){\alpha }_1-ig\bar{q}{\alpha }_1-i{J}_{12}{\alpha }_2+\sqrt{{\gamma }_{1,e}}{\alpha }_{1,in},\hfill \\ \hfill 0& =-\left({\gamma }_2/2+i{\mathrm{\Delta }}_2\right){\alpha }_2-i{J}_{12}{\alpha }_1-i{J}_{23}{\alpha }_3,\hfill \\ \hfill 0& =-\left({\gamma }_3/2+i{\mathrm{\Delta }}_3\right){\alpha }_3-i{J}_{23}{\alpha }_2+\sqrt{{\gamma }_{3,e}}{\alpha }_{3,in},\hfill \\ \hfill 0& =\bar{p},\hfill \\ \hfill 0& =-{\omega }_m\bar{q}-g|{\alpha }_1{|}^2,\hfill \end{array}(3)$

where the mean field approximation ⟨qα₁⟩ ≈ ⟨q⟩⟨α₁⟩ has been taken into account. It is not difficult to see that the first (α₁) and third (α₃) optical modes are not reciprocal because the mean position $\bar{q}$ of the mechanical mode is just coupled to the mean amplitude α₁ of the first optical mode via $-ig\bar{q}{\alpha }_1$ with $\bar{q}=-g|{\alpha }_1{|}^2/{\omega }_m$. That means, the aforementioned equations do not remain unchanged if we exchange subscripts “1” and “3.” Therefore, a transmission non-reciprocity is expected to occur no matter the driving field comes from either one direction (α_1,in ≠ 0 or α_3,in ≠ 0) or both directions (α_1,in ≠ 0 and α_3,in ≠ 0). With these classical mean values in hand, we can attain a set of linearized QLEs for the fluctuation operators in the matrix form

$\frac{\partial f}{\partial t}=Af+\zeta ,(4)$

by introducing two column vectors

$\begin{array}{ll}\hfill f& ={\left(\delta a_1,\delta a_1^{†},\delta a_2,\delta a_2^{†},\delta a_3,\delta a_3^{†},\delta q,\delta p\right)}^T,\hfill \\ \hfill \zeta & ={\left(\delta A_{1,in},\delta A_{1,in}^{†},\delta A_{2,in},\delta A_{2,in}^{†},\delta A_{3,in},\delta A_{3,in}^{†},0,\xi \right)}^T\hfill \end{array}(5)$

and a coefficient matrix

$A=\left[\begin{array}{cccccccc}\hfill -\left(\frac{{\gamma }_1}{2}+i{\mathrm{\Delta }}_1^{\prime }\right)\hfill & \hfill 0\hfill & \hfill -i{J}_{12}\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill -ig{\alpha }_1\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill -\left(\frac{{\gamma }_1}{2}-i{\mathrm{\Delta }}_1^{*}\right)\hfill & \hfill 0\hfill & \hfill i{J}_{12}\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill ig{\alpha }_1^{\ast }\hfill & \hfill 0\hfill \\ \hfill -i{J}_{12}\hfill & \hfill 0\hfill & \hfill -\left(\frac{{\gamma }_2}{2}+i{\mathrm{\Delta }}_2\right)\hfill & \hfill 0\hfill & \hfill -i{J}_{23}\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill i{J}_{12}\hfill & \hfill 0\hfill & \hfill -\left(\frac{{\gamma }_2}{2}-i{\mathrm{\Delta }}_2\right)\hfill & \hfill 0\hfill & \hfill i{J}_{23}\hfill & \hfill 0\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill 0\hfill & \hfill -i{J}_{23}\hfill & \hfill 0\hfill & \hfill -\left(\frac{{\gamma }_3}{2}+i{\mathrm{\Delta }}_3\right)\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill i{J}_{23}\hfill & \hfill 0\hfill & \hfill -\left(\frac{{\gamma }_3}{2}-i{\mathrm{\Delta }}_3\right)\hfill & \hfill 0\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill {\omega }_m\hfill \\ \hfill -g{\alpha }_1^{\ast }\hfill & \hfill -g{\alpha }_1\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill -{\omega }_m\hfill & \hfill -{\gamma }_m\hfill \end{array}\right],(6)$

where we have further defined $\delta A_{1,in}=\sqrt{{\gamma }_{1,e}}\delta a_{1,in}+\sqrt{{\gamma }_{1,i}}{a}_{1,vac}$, $\delta A_{2,in}=\sqrt{{\gamma }_{2,i}}{a}_{2,vac}$, $\delta A_{3,in}=\sqrt{{\gamma }_{3,e}}\delta a_{3,in}+\sqrt{{\gamma }_{3,i}}{a}_{3,vac}$, and ${\mathrm{\Delta }}_1^{\prime }={\mathrm{\Delta }}_1+g\bar{q}$. Our optomechanical system can work in the stable regime only if all the eigenvalues of matrix A are negative in their real parts. This problem is difficult or impossible to be solved analytically but can be by numerically examined via the Routh–Hurwitz criterion [53] as adopted later.

In the following, we consider two specific cases where the driving field of amplitude $s_{in}=\sqrt{p_{in}/(\hslash {\omega }_d)}$ and power p_in is input just from the 1st optical mode with α_1,in = s_in and α_3,in = 0 (I), or just from the 3rd optical mode with α_1,in = 0 and α_3,in = s_in (II). In case (I), it is easy to attain from Eq. 3 that

$\begin{array}{ll}\hfill {\alpha }_3& =\frac{-J_{12}{J}_{23}{\alpha }_1}{\left({\gamma }_2/2+i{\mathrm{\Delta }}_2\right)\left({\gamma }_3/2+i{\mathrm{\Delta }}_3\right)+J_{23}^2},\hfill \\ \hfill {\alpha }_1& =\frac{-J_{12}{J}_{23}{\alpha }_3+\left({\gamma }_2/2+i{\mathrm{\Delta }}_2\right)\sqrt{{\gamma }_{1,e}}{s}_{in}}{\left({\gamma }_2/2+i{\mathrm{\Delta }}_2\right)\left({\gamma }_1/2+i{\mathrm{\Delta }}_1-iU|{\alpha }_1{|}^2\right)+J_{12}^2},\hfill \end{array}(7)$

with U = g²/ω_m characterizing the non-linear optomechanical interaction. Considering the input–output relation ${\alpha }_{3,out}=\sqrt{{\gamma }_{3,e}}{\alpha }_3$ [55, 56], we finally attain

$\left(\mathrm{\Gamma }/2+i\bar{\mathrm{\Delta }}\right){\alpha }_{3,out}+i{U}_{31}|{\alpha }_{3,out}{|}^2{\alpha }_{3,out}={\epsilon }_{eff}.(8)$

In this equation, we have introduced the effective damping rate Γ, detuning $\bar{\mathrm{\Delta }}$, non-linear interaction strength U₃₁, and driving amplitude ɛ_eff by setting

$\begin{array}{ll}\hfill \mathrm{\Gamma }& =\frac{A\left({\gamma }_2{\gamma }_3/4-{\mathrm{\Delta }}_2{\mathrm{\Delta }}_3+J_{23}^2\right)+B\left({\gamma }_2{\mathrm{\Delta }}_3+{\gamma }_3{\mathrm{\Delta }}_2\right)}{|\left({\gamma }_2/2+i{\mathrm{\Delta }}_2\right)\left({\gamma }_3/2+i{\mathrm{\Delta }}_3\right)+J_{23}^2{|}^2},\hfill \\ \hfill \bar{\mathrm{\Delta }}& =\frac{B\left({\gamma }_2{\gamma }_3/4-{\mathrm{\Delta }}_2{\mathrm{\Delta }}_3+J_{23}^2\right)-A\left({\gamma }_2{\mathrm{\Delta }}_3+{\gamma }_3{\mathrm{\Delta }}_2\right)/4}{|\left({\gamma }_2/2+i{\mathrm{\Delta }}_2\right)\left({\gamma }_3/2+i{\mathrm{\Delta }}_3\right)+J_{23}^2{|}^2},\hfill \\ \hfill {\epsilon }_{eff}& =\frac{-J_{12}{J}_{23}\sqrt{{\gamma }_{1,e}{\gamma }_{3,e}}{s}_{in}}{\left({\gamma }_2/2+i{\mathrm{\Delta }}_2\right)\left({\gamma }_3/2+i{\mathrm{\Delta }}_3\right)+J_{23}^2},\hfill \\ \hfill U_{31}& =\frac{-U|\left({\gamma }_2/2+i{\mathrm{\Delta }}_2\right)\left({\gamma }_3/2+i{\mathrm{\Delta }}_3\right)+J_{23}^2{|}^2}{J_{12}^2{J}_{23}^2{\gamma }_{3,e}},\hfill \end{array}(9)$

with newly defined coefficients

$\begin{array}{ll}\hfill A& ={\gamma }_3\left({\gamma }_1{\gamma }_2/4-{\mathrm{\Delta }}_1{\mathrm{\Delta }}_2\right)-{\mathrm{\Delta }}_3\left({\mathrm{\Delta }}_1{\gamma }_2+{\mathrm{\Delta }}_2{\gamma }_1\right)\hfill \\ \hfill & +J_{23}^2{\gamma }_1+J_{12}^2{\gamma }_3,\hfill \\ \hfill B& ={\gamma }_3\left({\mathrm{\Delta }}_1{\gamma }_2+{\mathrm{\Delta }}_2{\gamma }_1\right)/4+{\mathrm{\Delta }}_3\left({\gamma }_1{\gamma }_2/4-{\mathrm{\Delta }}_1{\mathrm{\Delta }}_2\right)\hfill \\ \hfill & +J_{23}^2{\mathrm{\Delta }}_1+J_{12}^2{\mathrm{\Delta }}_3.\hfill \end{array}(10)$

In case (II), we attain via a similar procedure.

$\begin{array}{ll}\hfill {\alpha }_1& =\frac{-J_{12}{J}_{23}{\alpha }_3}{\left({\gamma }_1/2+i{\mathrm{\Delta }}_1-iU|{\alpha }_1{|}^2\right)\left({\gamma }_2/2+i{\mathrm{\Delta }}_2\right)+J_{12}^2},\hfill \\ \hfill {\alpha }_3& =\frac{-J_{12}{J}_{23}{\alpha }_1+\left({\gamma }_2/2+i{\mathrm{\Delta }}_2\right)\sqrt{{\gamma }_{3,e}}{s}_{in}}{\left({\gamma }_2/2+i{\mathrm{\Delta }}_2\right)\left({\gamma }_3/2+i{\mathrm{\Delta }}_3\right)+J_{23}^2},\hfill \end{array}(11)$

which, when substituting into the input–output relation ${\alpha }_{1,out}=\sqrt{{\gamma }_{1,e}}{\alpha }_1$, finally yields

$\left(\mathrm{\Gamma }/2+i\bar{\mathrm{\Delta }}\right){\alpha }_{1,out}+i{U}_{13}|{\alpha }_{1,out}{|}^2{\alpha }_{1,out}={\epsilon }_{eff},(12)$

with a new effective non-linear interaction strength U₁₃ = − U/γ_1,e, clearly different from U₃₁.

For convenience, we now translate Eqs 8, 12 into a unified form in terms of X_i = |α_i,out|²

$\left({\mathrm{\Gamma }}^2/4+{\bar{\mathrm{\Delta }}}^2\right)X_i+2\bar{\mathrm{\Delta }}{U}_{eff}{X}_i^2+U_{eff}^2{X}_i^3=|{\epsilon }_{eff}{|}^2,(13)$

with U_eff = U₁₃ for X₁ = |α_1,out|², while U_eff = U₃₁ for X₃ = |α_3,out|². This non-linear equation indicates that X_i can take three real values, corresponding to the bistability of output against input, under appropriate conditions. One way for determining the bistable region is to take a derivative of Eq. 13 with respect to X_i, yielding

$\left({\mathrm{\Gamma }}^2/4+{\bar{\mathrm{\Delta }}}^2\right)+4\bar{\mathrm{\Delta }}{U}_{eff}{X}_i+3U_{eff}^2{X}_i^2=0,(14)$

whose two positive roots

$X_i^{\pm }=\frac{-4\bar{\mathrm{\Delta }}\mp \sqrt{4{\bar{\mathrm{\Delta }}}^2-3{\mathrm{\Gamma }}^2}}{6U_{eff}}>0,(15)$

restricted by $\bar{\mathrm{\Delta }}<-\sqrt{3}\mathrm{\Gamma }/2$ referring to two turning points of the bistable region. That means, the solution of Eq. 15 takes three branches in the bistable region of $X_i^{-}\le X_i\le X_i^{+}$. The intermediate branch is known to be definitely unstable because it corresponds to the maximum (not minimum) point in an effective potential, while the upper and lower branches are usually stable, for example, in a non-linear Kerr medium [57, 58]. In our optomechanical system, the upper branch may also be unstable as the mechanical mode exhibits a negative effective damping rate owing to a heating effect in the blue-detuned or strong-driving regime, which will be numerically examined via the Routh–Hurwitz criterion [53].

The expected non-linear bistability is straightforward to be examined by two transmission coefficients:

$\begin{array}{ccc}\hfill T_{31}=|{\alpha }_{3,out}/{\alpha }_{1,in}{|}^2,& \hfill & \hfill \\ \hfill T_{13}=|{\alpha }_{1,out}/{\alpha }_{3,in}{|}^2,& \hfill & \hfill \end{array}(16)$

referring, respectively, to a transport from the 1st optical mode to the 3rd optical mode and that from the 3rd optical mode to the 1st optical mode. Considering that U₃₁ and U₁₃ have different expressions, we know from Eqs 8, 12 that a_3,out ≠ a_1,out in general and therefore T₃₁ ≠ T₁₃ for light signals of amplitudes a_1,in = a_2,in = s_in input from the opposite sides of our optomechanical system. The efficiency of such a non-reciprocal transport can be quantified by defining

$I_{tr}=10\log \left(T_{31}/T_{13}\right),(17)$

as the isolation ratio. We should note however that it is also possible to have U₃₁ = U₁₃ in the case of

${\gamma }_{1,e}=\frac{J_{12}^2{J}_{23}^2{\gamma }_{3,e}}{|\left({\gamma }_2/2+i{\mathrm{\Delta }}_2\right)\left({\gamma }_3/2+i{\mathrm{\Delta }}_3\right)+J_{23}^2{|}^2},(18)$

referred to as the impedance-matching condition, from which it is viable to get a critical coupling strength

$J_{23}^c=\sqrt{\frac{{\gamma }_{3,e}{J}_{12}^2-2{\gamma }_{1,e}\left({\gamma }_2{\gamma }_3/4-{\mathrm{\Delta }}_2{\mathrm{\Delta }}_3\right)\pm \sqrt{C}}{2{\gamma }_{1,e}}},(19)$

with $C={\gamma }_{3,e}^2{J}_{12}^4-{\gamma }_{1,e}{\gamma }_{3,e}{J}_{12}^2({\gamma }_2{\gamma }_3-4{\mathrm{\Delta }}_2{\mathrm{\Delta }}_3)-{\gamma }_{1,e}^2({\gamma }_2{\mathrm{\Delta }}_3-{\mathrm{\Delta }}_2{\gamma }_3)$ independent of input power p_in. It is clear that in the case of $J_{23}\ne J_{23}^c$, the impedance-matching condition will be broken, and we could have unequal (optomechanical) non-linear interaction strengths U₃₁ ≠ U₁₃. This would result in the optical transmission non-reciprocity characterized by T₃₁ ≠ T₁₃ and thus I_tran ≠ 0.

3 Results and Discussion

In this section, we examine the effects of relevant tunable parameters on the non-reciprocal bistable transmission of light signals input from the opposite sides of our optomechanical system via numerical calculations. Most parameters are chosen based on two recent works and accessible in up-to-date experiments [31, 44], among which γ₁/2π = 1.0 GHz, γ₂/2π = 0.5 GHz, γ₃/2π = 4.5 GHz, η₁ = η₂ = η₃ = 0.9, ω_d/2π = 300 THz, and γ_m/2π = 6.0 MHz are fixed in the following discussions. Numerical results will be shown in two cases where transmission coefficients T₃₁ and T₁₃ are plotted against input power p_in and detuning Δ₁, respectively, as they are much easier to modulate in regard of real applications. The main difficulty relevant to an experimental realization of our proposal lies in that the accurate preparation and arrangement of three (micro)coupled cavities of identical optical modes while different decay rates. A (micro)mechanical oscillator of proper resonant frequency and optomechanical coupling strength may also be hard to be integrated with one (micro)optical cavity.

3.1 Non-Reciprocal Transmission Against Input Power

In Figure 2, we plot transmission coefficients T₃₁ and T₁₃ as a function of input power p_in for different optical coupling strengths J₂₃. Figure 2A shows that transmission non-reciprocity (i.e., T₁₃ ≠ T₃₁ or I_tran ≠ 0) cannot be attained as the impedance-matching condition is well satisfied with $J_{23}/2\pi =J_{23}^c/2\pi \simeq 1.725$ GHz, though our optomechanical system works in the bistable regime. Increasing or decreasing J₂₃ to deviate from the critical value $J_{23}^c$, we can see from Figures 2B–D that transmission non-reciprocity occurs with different isolation ratios for different input powers. We have, in particular, that I_tr ≈ − 4.5 dB for p_in = 50 mW in the case of J₂₃/2π = 2.0 GHz, I_tr ≈ 8.0 dB for p_in = 36 mW in the case of J₂₃/2π = 1.4 GHz, and I_tr ≈ 10.2 dB for p_in = 25 mW in the case of J₂₃/2π = 1.0 GHz. These results indicate that it is viable to reverse the transmission non-reciprocity from I_tr < 0 to I_tr > 0 (I_tr > 0 to I_tr < 0) as J₂₃ is decreased (increased) to cross the critical value $J_{23}^c$, and we can attain higher isolation ratios in wider bistable regions by modulating J₂₃ to be more deviating from the critical value $J_{23}^c$. Taking Figure 2C as an example, it is also important to note that we should choose to work in the region between turning points P₂ and P₄ as p_in is increased from a small value, while between P₁ and P₃ as p_in is decreased from a large value. This promises for attaining a more efficient transmission non-reciprocity corresponding to a larger |I_tr| because it can be evaluated with the upper branch of T₃₁ and the lower branch of T₁₃. Otherwise, T₃₁ and T₁₃ will both work in the lower or upper branch to result in well suppressed transmission non-reciprocity of smaller or vanishing |I_tr|.

FIGURE 2

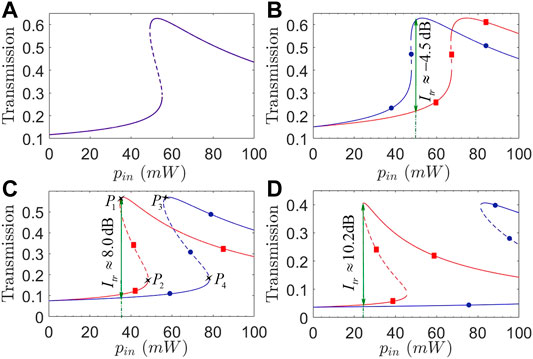
FIGURE 2. (Color online) Transmission coefficients T₃₁ (red squares) and T₁₃ (blue circles) against input power p_in with (A) J₂₃/2π = 1.725 GHz; (B) J₂₃/2π = 2.0 GHz; (C) J₂₃/2π = 1.4 GHz; (D) J₂₃/2π = 1.0 GHz. Solid and dashed parts of each curve refer to stable and unstable regions, respectively. Other parameters are Δ₁/2π = Δ₂/2π = 4.5 GHz, Δ₃/2π = 1.5 GHz, g/2π = 0.9 MHz, ω_m/2π = 10 GHz, and J₁₂/2π = 3.0 GHz, except those at the beginning of Section 3.

Comparing Eqs 8, 12, it is easy to see that the transmission non-reciprocity will be attained as long as we have U₁₃ ≠ U₃₁, which requires not only a broken impedance-matching condition but also U = g²/ω_m ≠ 0. Thus, it is essential to examine in Figure 3 different effects of optomechanical coupling strength g and mechanical frequency ω_m on transmission coefficients T₃₁ and T₁₃ plotted against input power p_in. Figures 3A,B show that as g is enhanced by one order, p_in required for observing the transmission non-reciprocity (in the bistable region where T₁₃ and T₃₁ work in the lower and upper branches, respectively) is reduced by two orders without changing the maximal isolation ratio I_tr ≈ 10.2 dB. That means the observed transmission non-reciprocity exhibits an inverse dependence on input power p_in and optomechanical coupling strength g. Figures 3C,D further show that the non-reciprocal region in terms of p_in is not so sensitive to ω_m though this region can be enlarged in the case of a larger ω_m. It is more important to note that the upper branches of T₃₁ and T₁₃ may not be always stable and a larger ω_m is helpful to reduce the unstable regions. These findings tell us how to choose g and ω_m for attaining a wide enough non-reciprocal region corresponding to low enough input powers.

FIGURE 3

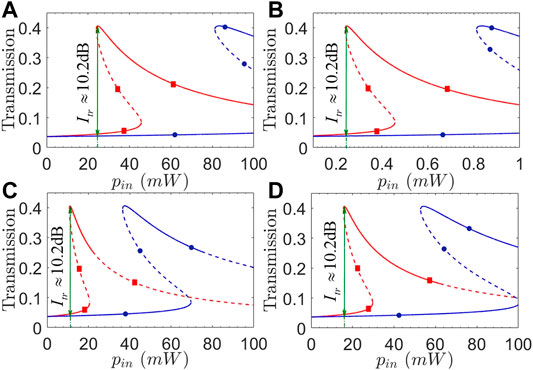
FIGURE 3. (Color online) Transmission coefficients T₃₁ (red squares) and T₁₃ (blue circles) against input power p_in with (A) g/2π = 0.9 MHz; (B) g/2π = 9.0 MHz; (C) ω_m/2π = 4.5 GHz; (D) ω_m/2π = 6.5 GHz. Solid and dashed parts of each curve refer to stable and unstable regions, respectively. Other parameters are the same as in Figure 2, except J₂₃/2π = 1.0 GHz.

Considering that the driving field and relevant optical modes are easy to be modulated in frequency, we plot in Figure 4 transmission coefficients T₃₁ and T₁₃ as a function of input power p_in for different detunings Δ₁ and Δ₃. We can see from Figures 4A,B that the isolation ratio may be evidently improved in a wider non-reciprocal region by choosing a slightly larger Δ₁ to well suppress the lower branches of T₃₁ and T₁₃, while leaving the upper branches unchanged yet in magnitude. To be more specific, we have I_tr ≈ 6.1 dB for p_in = 14 mW with Δ₁/2π = 3.5 GHz, while I_tr ≈ 13.1 dB for p_in = 35 mW with Δ₁/2π = 5.5 GHz. Figures 4C,D show instead that a significant increase of Δ₃, though can result in a wider non-reciprocal region, will not change the isolation ratio too much as the upper and lower branches are suppressed to the roughly same extent. We also note from Figure 4B that the upper branch of T₃₁ starts to become unstable at p_in ≳ 140 mW for Δ₁ = 5.5 GHz. It is thus clear that detunings Δ₁ and Δ₃ play different roles in manipulating the transmission non-reciprocity and can be jointly modulated for observing an ideal transmission non-reciprocity with larger isolation ratios and well suppressed lower branches for moderate input powers.

FIGURE 4

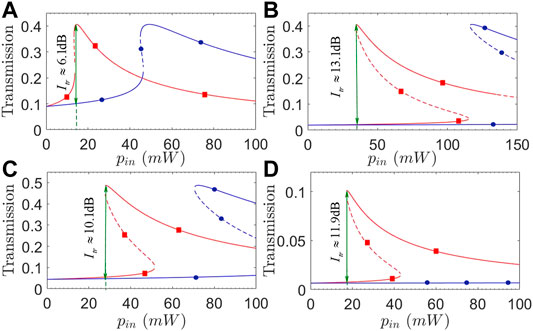
FIGURE 4. (Color online) Transmission coefficients T₃₁ (red squares) and T₁₃ (blue circles) against input power p_in with (A) Δ₁/2π = 3.5 GHz; (B) Δ₁/2π = 5.5 GHz; (C) Δ₃/2π = 0.1 GHz; (D) Δ₃/2π = 6.0 GHz. Solid and dashed parts of each curve refer to stable and unstable regions, respectively. Other parameters are the same as in Figure 2, except J₂₃/2π = 1.0 GHz.

3.2 Non-Reciprocal Transmission Against Detuning

We first plot in Figure 5 transmission coefficients T₃₁ and T₁₃ as a function of detuning Δ₁ for different input powers p_in. As the input power is very low (i.e., p_in = 0.1 mW), Figure 5A shows that T₃₁ and T₁₃ overlap well with a symmetric peak centered at Δ₁ ≈ (J₁₂ + J₂₃)/2 = 2 GHz, therefore leading to a vanishing transmission non-reciprocity. This can be attributed to the fact that both Eqs 8, 12 reduce to $(\mathrm{\Gamma }/2+i\bar{\mathrm{\Delta }}){\alpha }_{j,out}\approx {\epsilon }_{eff}$ when U_jj′|α_j,out|² with j + j′ = 4 is much smaller than $\bar{\mathrm{\Delta }}$. As the input power increases to be large enough, we find from Figures 5B–D that T₃₁ and T₁₃ start to exhibit different bistable behaviors and thus become distinguishable on the side of Δ₁ > (J₁₂ + J₂₃)/2 because U₁₃ and U₃₁ always take negative values. That means the deviation of a transmission peak from its original position may serve as a good estimation on the strength of non-linear optomechanical interaction. To be more specific, the input power p_in has less influence on T₁₃ than T₃₁ so that the transmission non-reciprocity occurs and becomes more and more evident as p_in increases. It is also noted that a larger input power always results in a wider bistable region with a higher isolation ratio at the right turning point of T₃₁: I_tr ≈ 8.5 dB at Δ₁/γ₁ = 4.0 for p_in = 20 mW; I_tr ≈ 14.3 dB at Δ₁/γ₁ = 6.0 for p_in = 40 mW; I_tr ≈ 16.2 dB at Δ₁/γ₁ = 7.0 for p_in = 50 mW.

FIGURE 5

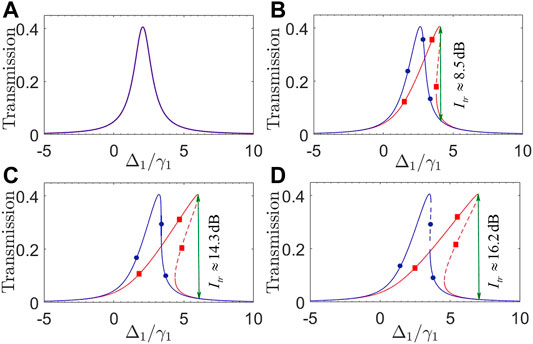
FIGURE 5. (Color online) Transmission coefficients T₃₁ (red squares) and T₁₃ (blue circles) against detuning Δ₁ with (A) p_in = 0.1 mW; (B) p_in = 20 mW; (C) p_in = 40 mW; (D) p_in = 50 mW. Solid and dashed parts of each curve refer to stable and unstable regions, respectively. Other parameters are Δ₂/2π = 4.5 GHz, Δ₃/2π = 1.5 GHz, g/2π = 0.9 MHz, ω_m/2π = 10 GHz, J₁₂/2π = 3.0 GHz, and J₂₃ = 1.0 GHz, except those at the beginning of Section 3.

Then we examine different effects of optical coupling strengths J₁₂ and J₂₃ by plotting in Figure 6 transmission coefficients T₃₁ and T₁₃ against detuning Δ₁. Figures 6A,B show that a slight increase in J₁₂ will result in an evidently identical rising of T₃₁ and T₁₃ but leaving their peaks roughly unchanged in position. The main difference lies in that the upper branch of T₃₁ in Figure 6A exhibits a wider stable region than that in Figure 6B, indicating that a larger J₁₂ helps to suppress quantum fluctuations arising from the non-linear optomechanical interaction. On the other hand, Figures 6C,D show that a slight increase in J₂₃ can also result in an evidently identical rising of T₃₁ and T₁₃, but their peaks become evidently closer to each other, leading to a narrowing of the non-reciprocal bistable region as well as a reduction in the isolation ratio. These findings tell that a moderate J₂₃ and a larger J₁₂ are appropriate for attaining non-reciprocal bistable regions of wide enough stable upper branches and large enough isolation ratios.

FIGURE 6

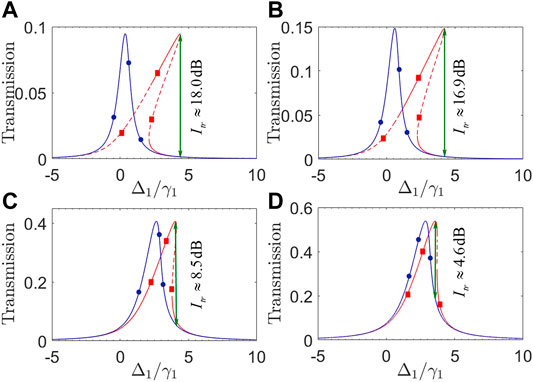
FIGURE 6. (Color online) Transmission coefficients T₃₁ (red squares) and T₁₃ (blue circles) against detuning Δ₁ with (A) J₁₂/2π = 1.0 GHz; (B) J₁₂/2π = 1.3 GHz; (C) J₂₃/2π = 1.0 GHz; (D) J₂₃/2π = 1.3 GHz. Solid and dashed parts of each curve refer to stable and unstable regions, respectively. Other parameters are the same as in Figure 5, except p_in = 20 mW.

Finally, we examine different effects of mechanical frequency ω_m and optomechanical coupling strength g by plotting in Figure 7 transmission coefficients T₃₁ and T₁₃ against detuning Δ₁. Comparing Figures 7A,B, we can see that both T₃₁ and T₁₃ remain unchanged in their peak values but clearly become more inclined toward Δ₁ > 0 so as to yield wider bistable regions, with the increase in g. This then results in a wider non-reciprocal transmission region considering that T₃₁ is much more sensitive to g and thus exhibits a much wider bistable region than T₁₃. Figures 7C,D show however that an increase in ω_m is helpful to reduce the unstable region of T₃₁ in its upper branch but meanwhile also results in a reduction of the bistable regions for both T₃₁ and T₁₃. These findings tell that one should choose a lower ω_m and a higher g to enhance the non-linear optomechanical interaction required for attaining wider non-reciprocal transmission regions of high isolation ratios.

FIGURE 7

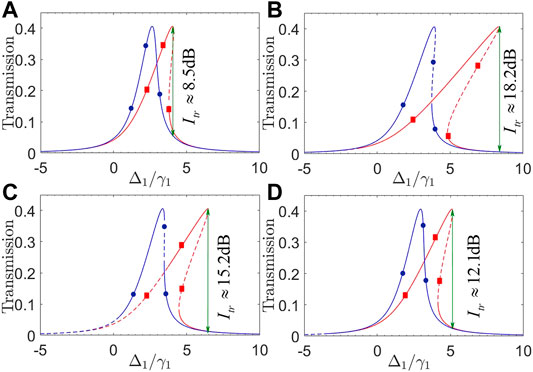
FIGURE 7. (Color online) Transmission coefficients T₃₁ (red squares) and T₁₃ (blue circles) against detuning Δ₁ with (A) g/2π = 0.9 MHz; (B) g/2π = 1.6 MHz; (C) ω_m/2π = 4.5 GHz; (D) ω_m/2π = 6.5 GHz. Solid and dashed parts of each curve refer to stable and unstable regions, respectively. Other parameters are the same as in Figure 5, except p_in = 20 mW.

In figures, the bistable transmission non-reciprocity occurs as the two curves for T₃₁ and T₁₃ do not overlap in each plot. It is thus appropriate to roughly determine a non-reciprocal bandwidth as the absolute difference of two values of p_in or Δ₁ corresponding, respectively, to the peak of T₃₁ and that of T₁₃. This non-reciprocal bandwidth is a few or tens of mW in Figures 2–4, while several times of γ₁ in Figures 5–7, depending on relevant parameters like J₁₂, J₂₃, g, and ω_m. Note also that a dynamic reciprocity, referring to the fact that a (weak) backward noise, can also be transmitted with little loss in the presence of a (strong) forward signal of high transmission, typically exists in the non-reciprocal systems based on optical non-linearities [59]. Accordingly, one limitation of our optomechanical system may be that it cannot break the dynamic reciprocity because the transmission non-reciprocity arises from a bistable non-linearity. This is clear by looking at Figures 2–4 where we have T₃₁ ≠ T₁₃ only when input power p_in is not too small.

4 Conclusion

In summary, we have studied a four-mode optomechanical system for attaining the transmission non-reciprocity, in the presence of an optomechanically induced non-linearity, with respect to a driving field input from the left or right side. As the impedance-matching condition is broken, we find that transmission coefficients T₃₁ and T₁₃, plotted against input power p_in or cavity detuning Δ₁, may exhibit staggered bistable behaviors and therefore can work in the upper and lower branches, respectively. The isolation ratio of such a non-reciprocal transmission is viable to switch between I_tr > 0 and I_tr < 0 and can be improved in magnitude by modulating optical coupling strengths J_12,23 and detunings Δ_1,3 to suppress the lower branches or enhance the upper branches. It is also viable to broaden the non-reciprocal bistable region in terms of p_in (Δ₁) by modulating optomechanical coupling strength g and mechanical frequency ω_m in addition to J_12,23 and Δ_1,3 (p_in). But we should note that an increasing part of the upper branch may become unstable as the non-reciprocal region becomes wider, which restricts the tunable ranges of relevant parameters. Our results well extend the previous works on realizing non-reciprocal transmission in optomechanical systems and are instructive for designing non-reciprocal devices in optical networks based on coupled cavities.

Data Availability Statement

The original contributions presented in the study are included in the article/supplementary material; further inquiries can be directed to the corresponding authors.

Author Contributions

The idea was first conceived by J-HW. BJ was responsible for the physical modeling, the numerical calculations, and writing most of the manuscript. J-HW contributed to writing the manuscript, JW verified results of the theoretical calculation, and DY contributed to the discussion of the results. DQ provided technical support in computer simulation.

Funding

This work is supported by the National Natural Science Foundation of China (12074061, 11674049, and 11874004), Science Foundation of Education Department of Jilin Province (JJKH20200557KJ), and Nature Science Foundation of Science and Technology Department of Jilin Province (20210101411JC).

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s Note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors, and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

Acknowledgments

BJ thanks Luning Song, Yan Zhang, and Zhihai Wang for helpful discussions.

References

1. Teufel JD, Harlow JW, Regal CA, Lehnert KW. Dynamical Backaction of Microwave fields on a Nanomechanical Oscillator. Phys Rev Lett (2008) 101:197203. doi:10.1103/PhysRevLett.101.197203

PubMed Abstract | CrossRef Full Text | Google Scholar

2. Aspelmeyer M, Kippenberg TJ, Marquardt F. Cavity Optomechanics. Rev Mod Phys (2014) 86:1391–452. doi:10.1103/RevModPhys.86.1391

CrossRef Full Text | Google Scholar

3. Liu Y-C, Hu Y-W, Wong C-W, Xiao Y-F. Review of Cavity Optomechanical Cooling. Chin Phys B (2013) 22:114213. doi:10.1088/1674-1056/22/11/114213

CrossRef Full Text | Google Scholar

4. He B. Quantum Optomechanics beyond Linearization. Phys Rev A (2012) 85:063820. doi:10.1103/PhysRevA.85.063820

CrossRef Full Text | Google Scholar

5. Cao C, Mi S-C, Gao Y-P, He L-Y, Yang D, Wang T-J, et al. Tunable High-Order Sideband Spectra Generation Using a Photonic Molecule Optomechanical System. Sci Rep (2016) 6:1–8. doi:10.1038/srep22920

PubMed Abstract | CrossRef Full Text | Google Scholar

6. Xiong X-R, Gao Y-P, Liu X-F, Cao C, Wang T-J, Wang C. The Analysis of High-Order Sideband Signals in Optomechanical System. Sci China Phys Mech Astron (2018) 61:1–4. doi:10.1007/s11433-017-9187-2

CrossRef Full Text | Google Scholar

7. Shi H-Q, Xie Z-Q, Xu X-W, Liu N-H. Unconventional Phonon Blockade in Multimode Optomechanical System. Acta Phys Sin (2018) 67:044203. doi:10.7498/aps.67.20171599

CrossRef Full Text | Google Scholar

8. Marinković I, Wallucks A, Riedinger R, Hong S, Aspelmeyer M, Gröblacher S. Optomechanical bell Test. Phys Rev Lett (2018) 121:220404. doi:10.1103/PhysRevLett.121.220404

PubMed Abstract | CrossRef Full Text | Google Scholar

9. Xu H, Lai D-G, Qian Y-B, Hou B-P, Miranowicz A, Nori F. Optomechanical Dynamics in the PT - and Broken- PT -symmetric regimes$mathcalPT$- and broken-$mathcalPT$-symmetric Regimes. Phys Rev A (2021) 104:053518. doi:10.1103/PhysRevA.104.053518

CrossRef Full Text | Google Scholar

10. Vitali D, Gigan S, Ferreira A, Böhm HR, Tombesi P, Guerreiro A, et al. Optomechanical Entanglement between a Movable Mirror and a Cavity Field. Phys Rev Lett (2007) 98:030405. doi:10.1103/PhysRevLett.98.030405

PubMed Abstract | CrossRef Full Text | Google Scholar

11. Chen R-X, Shen L-T, Yang Z-B, Wu H-Z, Zheng S-B. Enhancement of Entanglement in Distant Mechanical Vibrations via Modulation in a Coupled Optomechanical System. Phys Rev A (2014) 89:023843. doi:10.1103/PhysRevA.89.023843

CrossRef Full Text | Google Scholar

12. Liao J-Q, Wu Q-Q, Nori F. Entangling Two Macroscopic Mechanical Mirrors in a Two-Cavity Optomechanical System. Phys Rev A (2014) 89:014302. doi:10.1103/PhysRevA.89.014302

CrossRef Full Text | Google Scholar

13. Yan X-B. Enhanced Output Entanglement with Reservoir Engineering. Phys Rev A (2017) 96:053831. doi:10.1103/PhysRevA.96.053831

CrossRef Full Text | Google Scholar

14. He Q, Ficek Z. Einstein-podolsky-rosen Paradox and Quantum Steering in a Three-Mode Optomechanical System. Phys Rev A (2014) 89:022332. doi:10.1103/PhysRevA.89.022332

CrossRef Full Text | Google Scholar

15. Zhang X-L, Bao Q-Q, Yang M-Z, Tian X-S. Entanglement Characteristics of Output Optical fields in Double-Cavity Optomechanics. Acta Phys Sin (2018) 67:104203. doi:10.7498/aps.67.20172467

CrossRef Full Text | Google Scholar

16. Poot M, Herre SJ. Mechanical Systems in the Quantum Regime. Phys Rep (2012) 511:273–335. doi:10.1016/j.physrep.2011.12.004

CrossRef Full Text | Google Scholar

17. He B, Yang L, Lin Q, Xiao M. Radiation Pressure Cooling as a Quantum Dynamical Process. Phys Rev Lett (2017) 118:233604. doi:10.1103/PhysRevLett.118.233604

PubMed Abstract | CrossRef Full Text | Google Scholar

18. Chen H-J, Mi X-W. Normal Mode Splitting and Cooling in strong Coupling Optomechanical Cavity. Acta Phys Sin (2011) 60:124206–244. doi:10.7498/aps.60.124206

CrossRef Full Text | Google Scholar

19. Li Y, Wu L-A, Wang Z-D. Fast Ground-State Cooling of Mechanical Resonators with Time-dependent Optical Cavities. Phys Rev A (2011) 83:043804. doi:10.1103/PhysRevA.83.043804

CrossRef Full Text | Google Scholar

20. Liu Z-Q, Hu C-S, Jiang Y-K, Su W-J, Wu H, Li Y, et al. Engineering Optomechanical Entanglement via Dual-Mode Cooling with a Single Reservoir. Phys Rev A (2021) 103:023525. doi:10.1103/PhysRevA.103.023525

CrossRef Full Text | Google Scholar

21. Bai C, Hou B-P, Lai D-G, Wu D. Tunable Optomechanically Induced Transparency in Double Quadratically Coupled Optomechanical Cavities within a Common Reservoir. Phys Rev A (2016) 93:043804. doi:10.1103/PhysRevA.93.043804

CrossRef Full Text | Google Scholar

22. Yan X-B. Optomechanically Induced Transparency and Gain. Phys Rev A (2020) 101:043820. doi:10.1103/PhysRevA.101.043820

CrossRef Full Text | Google Scholar

23. Lü H, Wang C, Yang L, Jing H. Optomechanically Induced Transparency at Exceptional Points. Phys Rev Appl (2018) 10:014006. doi:10.1103/PhysRevApplied.10.014006

CrossRef Full Text | Google Scholar

24. Hou B-P, Wei L-F, Wang S-J. Optomechanically Induced Transparency and Absorption in Hybridized Optomechanical Systems. Phys Rev A (2015) 92:033829. doi:10.1103/PhysRevA.92.033829

CrossRef Full Text | Google Scholar

25. Qu K, Agarwal GS. Phonon-mediated Electromagnetically Induced Absorption in Hybrid Opto-Electromechanical Systems. Phys Rev A (2013) 87:031802. doi:10.1103/PhysRevA.87.031802

CrossRef Full Text | Google Scholar

26. Zhang J-Q, Li Y, Feng M, Xu Y. Precision Measurement of Electrical Charge with Optomechanically Induced Transparency. Phys Rev A (2012) 86:053806. doi:10.1103/PhysRevA.86.053806

CrossRef Full Text | Google Scholar

27. Brunner N, Cavalcanti D, Pironio S, Scarani V, Wehner S. Bell Nonlocality. Rev Mod Phys (2014) 86:419–78. doi:10.1103/RevModPhys.86.419

CrossRef Full Text | Google Scholar

28. Lü X-Y, Jing H, Ma J-Y, Wu Y. PT-Symmetry-Breaking Chaos in Optomechanics. Phys Rev Lett (2015) 114:253601. doi:10.1103/PhysRevLett.114.253601

PubMed Abstract | CrossRef Full Text | Google Scholar

29. Margueritat J, Virgone-Carlotta A, Monnier S, Delanoë-Ayari H, Mertani HC, Berthelot A, et al. High-frequency Mechanical Properties of Tumors Measured by Brillouin Light Scattering. Phys Rev Lett (2019) 122:018101. doi:10.1103/PhysRevLett.122.018101

PubMed Abstract | CrossRef Full Text | Google Scholar

30. Song L-N, Zheng Q, Xu X-W, Jiang C, Li Y. Optimal Unidirectional Amplification Induced by Optical Gain in Optomechanical Systems. Phys Rev A (2019) 100:043835. doi:10.1103/PhysRevA.100.043835

CrossRef Full Text | Google Scholar

31. Xu X-W, Song L-N, Zheng Q, Wang Z-H, Li Y. Optomechanically Induced Nonreciprocity in a Three-Mode Optomechanical System. Acta Phys Sin (2018) 98:063845. doi:10.1103/PhysRevA.98.063845

CrossRef Full Text | Google Scholar

32. Zhang L-W, Li X-L, Yang L. Optical Nonreciprocity with Blue-Detuned Driving in Two-Cavity Optomechanics. Acta Phys Sin (2019) 68:170701–9. doi:10.7498/aps.68.20190205

CrossRef Full Text | Google Scholar

33. Miri M-A, Ruesink F, Verhagen E, Alù A. Optical Nonreciprocity Based on Optomechanical Coupling. Phys Rev Appl (2017) 7:064014. doi:10.1103/PhysRevApplied.7.064014

CrossRef Full Text | Google Scholar

34. Li E-Z, Ding D-S, Yu Y-C, Dong M-X, Zeng L, Zhang W-H, et al. Experimental Demonstration of Cavity-free Optical Isolators and Optical Circulators. Phys Rev Res (2020) 2:033517. doi:10.1103/PhysRevResearch.2.033517

CrossRef Full Text | Google Scholar

35. Li B, Özdemir ŞK, Xu X-W, Zhang L, Kuang L-M, Jing H. Nonreciprocal Optical Solitons in a Spinning Kerr Resonator. Phys Rev A (2021) 103:053522. doi:10.1103/PhysRevA.103.053522

CrossRef Full Text | Google Scholar

36. Verhagen E, Alù A. Optomechanical Nonreciprocity. Nat Phys (2017) 13:922–4. doi:10.1038/nphys4283

CrossRef Full Text | Google Scholar

37. Lira H, Yu Z, Fan S, Lipson M. Electrically Driven Nonreciprocity Induced by Interband Photonic Transition on a Silicon Chip. Phys Rev Lett (2012) 109:033901. doi:10.1103/PhysRevLett.109.033901

PubMed Abstract | CrossRef Full Text | Google Scholar

38. Manipatruni S, Robinson JT, Lipson M. Optical Nonreciprocity in Optomechanical Structures. Phys Rev Lett (2009) 102:213903. doi:10.1103/PhysRevLett.102.213903

PubMed Abstract | CrossRef Full Text | Google Scholar

39. Gridnev VN. Nonreciprocal Reflection of Light from Antiferromagnets. Jetp Lett (1996) 64:110–3. doi:10.1134/1.567141

CrossRef Full Text | Google Scholar

40. Lu X, Cao W, Yi W, Shen H, Xiao Y. Nonreciprocity and Quantum Correlations of Light Transport in Hot Atoms via Reservoir Engineering. Phys Rev Lett (2021) 126:223603. doi:10.1103/PhysRevLett.126.223603

PubMed Abstract | CrossRef Full Text | Google Scholar

41. Wang Y-P, Rao J-W, Yang Y, Xu P-C, Gui Y-S, Yao B-M, et al. Nonreciprocity and Unidirectional Invisibility in Cavity Magnonics. Phys Rev Lett (2019) 123:127202. doi:10.1103/PhysRevLett.123.127202

PubMed Abstract | CrossRef Full Text | Google Scholar

42. Lai D-G, Huang J-F, Yin X-L, Hou B-P, Li W, Vitali D, et al. Nonreciprocal Ground-State Cooling of Multiple Mechanical Resonators. Phys Rev A (2020) 102:011502. doi:10.1103/PhysRevA.102.011502

CrossRef Full Text | Google Scholar

43. Khanikaev AB, Mousavi SH, Shvets G, Kivshar YS. One-way Extraordinary Optical Transmission and Nonreciprocal Spoof Plasmons. Phys Rev Lett (2010) 105:126804. doi:10.1103/PhysRevLett.105.126804

PubMed Abstract | CrossRef Full Text | Google Scholar

44. Fang K, Luo J, Metelmann A, Matheny MH, Marquardt F, Clerk AA, et al. Generalized Non-reciprocity in an Optomechanical Circuit via Synthetic Magnetism and Reservoir Engineering. Nat Phys (2017) 13:465–71. doi:10.1038/nphys4009

CrossRef Full Text | Google Scholar

45. Dzyaloshinskii I, Papamichail EV. Nonreciprocal Optical Rotation in Antiferromagnets. Phys Rev Lett (1995) 75:3004–7. doi:10.1103/PhysRevLett.75.3004

PubMed Abstract | CrossRef Full Text | Google Scholar

46. Ni X, He C, Sun X-C, Liu X-P, Lu M-H, Feng L, et al. Topologically Protected One-Way Edge Mode in Networks of Acoustic Resonators with Circulating Air Flow. New J Phys (2015) 17:053016. doi:10.1088/1367-2630/17/5/053016

CrossRef Full Text | Google Scholar

47. Yu H, Wang Z, Wu J-H. Entanglement Preparation and Nonreciprocal Excitation Evolution in Giant Atoms by Controllable Dissipation and Coupling. Phys Rev A (2021) 104:013720. doi:10.1103/PhysRevA.104.013720

CrossRef Full Text | Google Scholar

48. Du L, Cai M-R, Wu J-H, Wang Z, Li Y. Single-photon Nonreciprocal Excitation Transfer with Non-markovian Retarded Effects. Phys Rev A (2021) 103:053701. doi:10.1103/PhysRevA.103.053701

CrossRef Full Text | Google Scholar

49. Zhang S, Hu Y, Lin G, Niu Y, Xia K, Gong J, et al. Thermal-motion-induced Non-reciprocal Quantum Optical System. Nat Photon (2018) 12:744–8. doi:10.1038/s41566-018-0269-2

CrossRef Full Text | Google Scholar

50. Xia K, Nori F, Min X. Cavity-free Optical Isolators and Circulators Using a Chiral Cross-Kerr Nonlinearity. Phys Rev Lett (2018) 121:203602. doi:10.1103/PhysRevLett.121.203602

PubMed Abstract | CrossRef Full Text | Google Scholar

51. Hu Y, Zhang S, Qi Y, Lin G, Niu Y, Gong S. Multiwavelength Magnetic-free Optical Isolator by Optical Pumping in Warm Atoms. Phys Rev Appl (2019) 12:054004. doi:10.1103/PhysRevApplied.12.054004

CrossRef Full Text | Google Scholar

52. Paraïso TK, Kalaee M, Zang L, Pfeifer H, Marquardt F, Painter O. Position-squared Coupling in a Tunable Photonic crystal Optomechanical Cavity. Phys Rev X (2015) 5:041024. doi:10.1103/PhysRevX.5.041024

CrossRef Full Text | Google Scholar

53. DeJesus EX, Kaufman C. Routh-hurwitz Criterion in the Examination of Eigenvalues of a System of Nonlinear Ordinary Differential Equations. Phys Rev A (1987) 35:5288–90. doi:10.1103/PhysRevA.35.5288

CrossRef Full Text | Google Scholar

54. Paternostro M, Gigan S, Kim MS, Blaser F, Böhm HR, Aspelmeyer M. Reconstructing the Dynamics of a Movable Mirror in a Detuned Optical Cavity. New J Phys (2006) 8:107. doi:10.1088/1367-2630/8/6/107

CrossRef Full Text | Google Scholar

55. Gardiner CW, Collett MJ. Input and Output in Damped Quantum Systems: Quantum Stochastic Differential Equations and the Master Equation. Phys Rev A (1985) 31:3761–74. doi:10.1103/PhysRevA.31.3761

CrossRef Full Text | Google Scholar

56. Agarwal GS, Huang S. Optomechanical Systems as Single-Photon Routers. Phys Rev A (2012) 85:021801. doi:10.1103/PhysRevA.85.021801

CrossRef Full Text | Google Scholar

57. Aldana S, Bruder C, Nunnenkamp A. Equivalence between an Optomechanical System and a Kerr Medium. Phys Rev A (2013) 88:043826. doi:10.1103/PhysRevA.88.043826

CrossRef Full Text | Google Scholar

58. Fabre C, Pinard M, Bourzeix S, Heidmann A, Giacobino E, Reynaud S. Quantum-noise Reduction Using a Cavity with a Movable Mirror. Phys Rev A (1994) 49:1337–43. doi:10.1103/PhysRevA.49.1337

PubMed Abstract | CrossRef Full Text | Google Scholar

59. Shi Y, Yu Z, Fan S. Limitations of Nonlinear Optical Isolators Due to Dynamic Reciprocity. Nat Photon (2015) 9:388–92. doi:10.1038/nphoton.2015.79

CrossRef Full Text | Google Scholar