Dissipative Magnetic Soliton in a Spinor Polariton Bose–Einstein Condensate

Magnetic soliton is an intriguing nonlinear topological excitation that carries magnetic charges while featuring a constant total density. So far, it has only been studied in the ultracold atomic gases with the framework of the equilibrium physics, where its stable existence crucially relies on a nearly spin-isotropic, antiferromagnetic, interaction. Here, we demonstrate that magnetic soliton can appear as the exact solutions of dissipative Gross–Pitaevskii equations in a linearly polarized spinor polariton condensate with the framework of the non-equilibrium physics, even though polariton interactions are strongly spin anisotropic. This is possibly due to a dissipation-enabled mechanism, where spin excitation decouples from other excitation channels as a result of gain-and-loss balance. Such unconventional magnetic soliton transcends constraints of equilibrium counterpart and provides a novel kind of spin-polarized polariton soliton for potential application in opto-spintronics.

I Introduction

Spinor polariton condensate in semiconductor microcavities [1–4] provides a unique out-of-equilibrium platform for exploring exotic nonlinear excitations with spin textures, which may even transcend usual restrictions of equilibrium systems. Formed from strong couplings between excitons and photons, polaritons possess peculiar spin properties: the J_z = ±1 (spin-up or spin-down) spin projections of the total angular momentum of excitons along the growth axis of the structure directly correspond to the right- and left-circularly polarized photons absorbed or emitted by the cavity, respectively [1]. Therefore, the properties of a spinor polariton fluid (e.g., density and phase distributions) can be probed from the properties of the emitted light [5]. In addition, the polariton–polariton interaction features a strong spin anisotropy [6–8], with a repulsive interaction between same spins (g > 0) and a weaker, attractive, interaction between opposite spins (g₁₂ < 0). Furthermore, a polariton condensate is intrinsically open dissipative, distinguishing it fundamentally from its atomic counterpart [9]. Recently, half-soliton [10, 11] and half-vortices [12, 13] behaving like magnetic monopoles have been experimentally observed in spinor polariton condensates under coherent pumping. There, the key prerequisite for such excitation is the spin-anisotropic antiferromagnetic interaction, while dissipation only occurs as a perturbation. Instead, below, we present a new kind of polariton soliton that carries magnetic charges—dissipative magnetic soliton (DMS). In particular, whereas magnetic soliton cannot occur in equilibrium condensates with strongly spin-anisotropic (antiferromagnetic) interactions, it can nevertheless appear in non-equilibrium spinor polariton condensates harnessing dissipation as essential resources.

Magnetic soliton [14–16] is a localized nonlinear topological excitation, which exhibits a density dip in one component and a hump in the other, but featuring a constant total density. It is a fundamentally important entity in the nonlinear context, as it provides an exceptional example of exact vector soliton solution that can exist outside the paradigmatic Manakov limit (g = g₁₂); within this limit, a multicomponent nonlinear system is integrable [17–19]. It also attracts considerable interests in the condensed matter, offering interesting perspectives as regards many-body phenomenon of solitonic matter [20]. So far, magnetic soliton has only been realized in a spinor Bose–Einstein condensate (BEC) with nearly-isotropic spin interactions of antiferromagnetic type [14, 21, 22], 0 < g − g₁₂ ≪ g. This requirement is essential because it makes the density depletion—inevitably induced alongside spin excitation—strongly suppressed by a high energy cost, thus ensuring the characteristic constant density background of magnetic soliton. Beyond this regime, a stable magnetic soliton cannot occur in an atomic superfluid.

In this work, we theoretically show that a stable magnetic soliton can be formed in a linearly polarized polariton condensate under non-resonant excitations with a spatially homogeneous pump, even though g − g₁₂ > g. It is an exact soliton solution to the multicomponent driven-dissipative Gross–Pitaevskii (GP) equation, preserving its energy over infinitely long times—so coined as DMS. It stems from a dissipation-enabled mechanism rather than an energetic mechanism (cf. Figure 1): the spin-polarization excitation, originally coupled to other dissipative excitations in a multicomponent quantum fluid, becomes decoupled conditionally on the local balance of gain and loss, thus allowing non-decaying localized spin texture far from the spin-isotropic Manakov limit. We remark that DMS exists for a time-independent and spatially uniform pump, which affords an appealing advantage in view of potential application [23, 24]: while polariton soliton has been well known to promise applications in opto-spintronics, present schemes for the generation and stabilization of solitons usually rely on complex engineering of the space–time profile of the pump [25–30], which requires optical isolation that has hitherto been challenging to integrate at acceptable performance levels and introduce redundant and power-hungry electronic components.

FIGURE 1

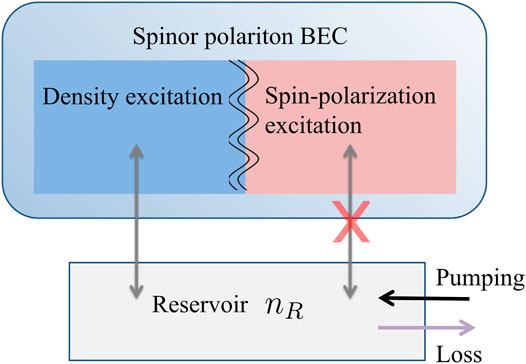
FIGURE 1. Schematics of DMS formation in an open-dissipative polariton BEC under incoherent pumping, which is coupled to a reservoir via its density n_R. On top of the steady state, there exist density (blue patch) and spin-polarization (red patch) excitation channels, which are usually coupled. However, once the pump balances the loss, the two channel, i.e., density excitation and spin-polarization excitation decouples (white curve). In such, the spin-polarization excitation is immune of the reservoir and a non-decaying DMS in spin-density excitation channel can occur.

The structure of the paper is as follows. In Section II, we present our theoretical model of dissipative Gross–Pitaevskii equations, based on which we solve for the novel magnetic solitons that carry magnetic charges while featuring a constant total density. In Section IV, we present a comprehensive study of the physical mechanism of the magnetic solitons with the help of the dynamic structure factors. Finally, we conclude with a summary in Section V, and all the detailed mathematical derivations are outlined in Section A

II Dissipative Gross–Pitaevskii Equations at Quasi-1D

Motivated by Ref. [31], we consider a spinor polariton BEC formed under a homogeneous incoherent pumping in a wire-shaped microcavity that bounds the polaritons to a quasi-1D channel in the following geometry: In the x-direction, the polariton BEC is homogeneous; in the y-direction, the wire size d is sufficiently small compared to the wire length, thus providing a strong lateral quantum confinement. Moreover, the incoherent pump is also restricted to a small transverse size comparable to d. When ℏ²/(md²) ≫ gn₀, where m is the effective mass of polaritons and n₀ is the 1D polarion density, the polarion motion in the y direction can be seen as frozen. In this case, the order parameter for the polariton BEC at quasi-1D can be effectively described by a complex vector [32–36], $\mathit{\psi }(x,t)\equiv {[{\psi }_1(x,t),{\psi }_2(x,t)]}^T$, in the circular basis. Here, ψ₁ and ψ₂ are the spin-up and spin-down wavefunctions, and we denote the density in each component by n₁ and n₂, respectively. The system dynamics is governed by driven-dissipative GP equations coupled to a rate equation for the reservoir density n_R [37–41]:

$\begin{array}{l}\hfill i\hslash \frac{\partial {\psi }_1}{\partial t}=\left[-\frac{{\hslash }^2}{2m}\frac{{\partial }^2}{\partial x^2}+g{\left|{\psi }_1\right|}^2+g_{12}{\left|{\psi }_2\right|}^2\right]{\psi }_1\\ \hfill +g_R{n}_R{\psi }_1+{\mathit{\text{D}}}_s{\psi }_1,\end{array}(1)$

$\begin{array}{l}\hfill i\hslash \frac{\partial {\psi }_2}{\partial t}=\left[-\frac{{\hslash }^2}{2m}\frac{{\partial }^2}{\partial x^2}+g{\left|{\psi }_2\right|}^2+g_{12}{\left|{\psi }_1\right|}^2\right]{\psi }_2\\ \hfill +g_R{n}_R{\psi }_2+{\mathit{\text{D}}}_s{\psi }_2,\end{array}(2)$

$\begin{array}{l}\hfill \frac{\partial n_R}{\partial t}=P-\left[{\gamma }_R+R\left({\left|{\psi }_1\right|}^2+{\left|{\psi }_2\right|}^2\right)\right]n_R.\end{array}(3)$

Here, interactions between polaritons are typically g₁₂ < 0, g > 0, and |g₁₂| < g. The interaction between the condensate and reservoir is modeled by constant g_R. Condensed polaritons decay at a rate γ_C but are replenished from the reservoir at a rate R. This process is captured by $D_s=i\hslash \left(R{n}_R-{\gamma }_C\right)/2$. Reservoir polariton decays at a rate γ_R and is driven by an off-resonant continuous-wave pump, which is spatially homogeneous. Note that, here, we have assumed that the reservoir lacks spin selectivity due to infinite fast spin relaxation [37].

The steady-state solutions of Eqs. 1–3 are given by

$\begin{array}{ccc}\hfill & \hfill & {\psi }_{1(2)}^0=\sqrt{\frac{P/{\gamma }_C-{\gamma }_R/R}{2}},\hfill \\ \hfill & \hfill & n_R^0={\gamma }_C/R,\hfill \end{array}(4)$

where ${\psi }_{1(2)}^0$ and $n_R^0$ denote the steady-state condensate wavefunction of each component and reservoir density, respectively. As shown, the steady-state polariton BEC has a uniform density determined by n₀ = P/γ_C − γ_R/R and is linearly polarized with a stochastic polarization direction in the absence of pinning [1]. Note that Eqs. 1–3 in the limit of fast reservoir [3, 42] are of immediate relevance in the context of the complex Ginzburg Landau equations [23, 24]. In the following, we choose system parameters where such steady state is within the modulation stable regime [42–45] (this can be further seen in Section IV).

III Dissipative Magnetic Soliton

On top of the steady state, two kinds of excitations can occur: density excitation and spin-polarization excitation. These excitations are, in general, correlated with each other and with the reservoir, so that fluctuations in one channel can induce that in another and are dissipative. As shown below, the central result of this work is that under the condition

$D_s{\psi }_s=0,(5)$

the spin-polarization excitation decouples from other dissipative channels, such that it can support a new kind of nonlinear excitation against the steady-state background in situations not allowed in the equilibrium case.

We look for an analytical solution $\psi (x-\upsilon t)\equiv {[{\psi }_1(x-\upsilon t),{\psi }_2(x-\upsilon t)]}^T$ (in the circular basis) satisfying Eqs. 1–3, which describes a moving soliton with velocity υ. For simplicity, hereafter, we will denote η = x − υt. To describe populations in each component, we rewrite n₁ = n₀ (1 + δn₁)/2 and n₂ = n₀ (1 − δn₂)/2 in terms of the total density n₀ and the dimensionless variables δn₁₍₂₎. We, moreover, define a linear polarization angle φ_r and global phase φ_g. The order parameter can then be generically written as

$\left(\begin{array}{c}\hfill {\psi }_1\hfill \\ \hfill {\psi }_2\hfill \end{array}\right)=\sqrt{\frac{n_0}{2}}\left(\begin{array}{c}\hfill \sqrt{1+\delta n_1}{e}^{i\frac{{\phi }_r}{2}}\hfill \\ \hfill \sqrt{1-\delta n_2}{e}^{-i\frac{{\phi }_r}{2}}\hfill \end{array}\right)e^{i{\phi }_g/2}{e}^{-i\frac{{\mu }_{R}t}{\hslash }},(6)$

with μ_R = g_Rγ_C/R. We consider general boundary conditions: $\underset{\eta \to \pm \infty }{\lim }\delta n_{1(2)}(\eta )=0$ and $\underset{\eta \to \pm \infty }{\lim }{\partial }_{\eta }{\phi }_{r(g)}(\eta )=0$. Our goal next is to determine n₀, δn₁₍₂₎, φ_r, and φ_g.

Exact solutions for Eqs. 1–3 can be found under condition (5). The detailed calculations can be found in Appendix A. The results are:

$\begin{array}{ccc}\hfill \delta n_1& =\hfill & \delta n_2=\sqrt{1-U^2}\text{sech}\left[\frac{\eta }{{\xi }_s}\sqrt{1-U^2}\right],\hfill \end{array}(7)$

$\begin{array}{ccc}\hfill {\phi }_r& =\hfill & \arctan \left[\frac{\sinh \left(\frac{\eta }{{\xi }_s}\sqrt{1-U^2}\right)}{U}\right]+\frac{\pi }{2},\hfill \end{array}(8)$

$\begin{array}{ccc}\hfill {\phi }_g& =\hfill & -\text{arctan}\left[\frac{\sqrt{1-U^2}\mathrm{t}\mathrm{a}\mathrm{n}\mathrm{h}\left(\frac{\eta }{{\xi }_s}\sqrt{1-U^2}\right)}{U}\right]\hfill \\ \hfill & -\hfill & \text{arctan}\left[\frac{\sqrt{1-U^2}}{U}\right].\hfill \end{array}(9)$

Here, $U=\upsilon /\sqrt{n_0(g-g_{12})/2m}$ is a dimensionless velocity and ${\xi }_s=\hslash /\sqrt{2m{n}_0(g-g_{12})}$ denotes the spin healing length.

A typical space–time profile of the above soliton solution is illustrated in Figure 2A for g₁₂ = − 0.1g. The density distribution n₁₍₂₎ in each component and φ_r and φ_g at a chosen time are shown in Figure 2B. We see that, unlike half-solitons, the vector soliton here is characterized by a density notch in one component and a hump in the other, whereas n₁ + n₂ ≡ n₀ is constant, i.e., it is magnetic soliton (see Figure 2A and top panel of Figure 2B). The linear polarization angle φ_r and the global phase φ_g vary simultaneously in space (see bottom panel of Figure 2B): φ_r always jumps by π across the soliton, $\underset{\eta \to +\infty }{\lim }{\phi }_r-\underset{\eta \to -\infty }{\lim }{\phi }_r=\pi$, regardless of soliton velocity. In contrast, the phase jump of φ_g is velocity dependent, with the maximum shift − π only for stationary case.

FIGURE 2

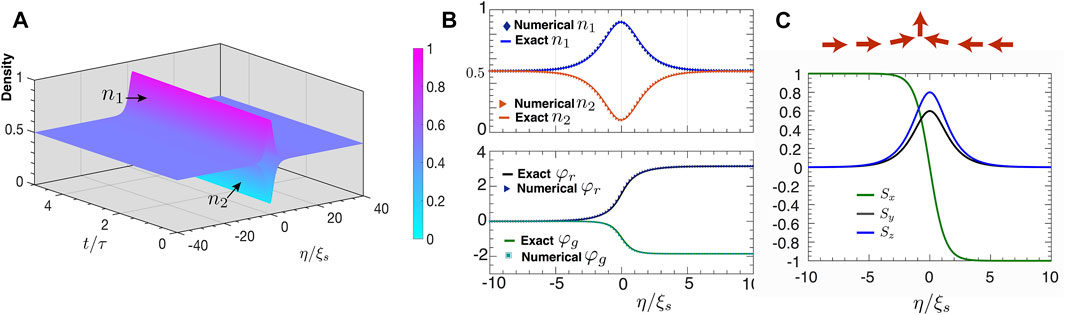
FIGURE 2. Properties of DMS. (A) Density of each component, n₁ = n₀ (1 + δn₁)/2 and n₂ = n₀ (1 − δn₂)/2 (see Eqs. 6, 7), in space and time. (B) Spatial distribution of n₁, n₂, the linear polarization angle φ_r, and the global phase φ_g, at a dimensionless time t/τ = 15. Top panel: n₁ and n₂; bottom panel: φ_r and φ_g. In both panels, analytical results are compared to numerical solutions of Eqs. 1–3. (C) Polarization texture. Top panel: schematics in the stationary case. Bottom panel: Stokes parameters for a moving DMS. In all plots, we take γ_C = 0.01ps⁻¹, R = 0.01ps⁻¹μm², g = 0.01meVμm², p = 0.41ps⁻¹μm², γ_R/γ_C = 40, g₁₂/g = − 0.1, and U = 0.6.

To verify the above analytical solution, we have numerically solved Eqs. 1–3 starting from an initial order parameter given by Eqs. 6–9 for t = 0 along with n_R (0) = γ_C/R. Comparisons of numerical and analytical solutions show perfect agreement; see Figure 2B for t/τ = 15. We have numerically verified the stability of our solution by time evolving an initial order parameter where n₁ (0) − n₂ (0) is perturbed from Eq. 7 while keeping n₀ = n₁ (0) + n₂ (0) fixed.

The polarization texture of polariton magnetic soliton in Eqs. 6–9 can be characterized by standard Stokes parameters [33, 46, 47], S(η) = (S_x, S_y, S_z), with $S_x(\eta )=2\mathfrak{R}({\psi }_1^{*}{\psi }_2)/n_0$, $S_y(\eta )=2\mathfrak{I}({\psi }_1^{*}{\psi }_2)/n_0$, and S_z(η) = (|ψ₁|² − |ψ₂|²)/n₀. Here, $\mathfrak{R}$ and $\mathfrak{I}$ denote the real and imaginary part, respectively. For the stationary case U = 0, S(η) is entirely in the (S_x, S_z) plane and presents an ingoing divergent spin texture whose direction defines the magnetic charge (see top panel of Figure 2C): The degree of circularization S_z reaches unity at the center, while the linear polarization S_x flips its direction crossing the soliton core due to the π jump in φ_r. In comparison, a moving soliton (see bottom panel of Figure 2C) has a broadened localization width, $l_w={\xi }_s/\sqrt{1-U^2}$, and its polarization becomes strongly elliptical in the (S_y, S_z) plane near the core, with a decreased circular polarization (i.e., magnetization) given by $S_z(\eta )=\sqrt{1-U^2}$. However, the linear polarization still flips across the soliton, independent of U.

To see whether the polariton magnetic soliton in an open-dissipative spinor condensate decays with time, we calculated its energy E as [41, 48, 49].

$\begin{array}{ccc}\hfill E& =\hfill & \int dx{\psi }^{†}\left(-\frac{{\hslash }^2}{2m}\frac{{\partial }^2}{\partial x^2}\right)\psi +\frac{g-g_{12}}{4}\int dx{(n_1-n_2)}^2\hfill \\ \hfill & +\hfill & \frac{g+g_{12}}{4}\int dx{\left(n_1+n_2-n_0\right)}^2.\hfill \end{array}(10)$

Here, the second term corresponds to the spin–spin interaction associated with S_z, and the third term is the energy associated with the density depletion. Once the gain balances loss, as formulated by Eq. 5, we derive straightforwardly (see Eq. B2 in Appendix)

$\frac{dE}{dt}=-2\mathfrak{R}\int \left[D_s\left(\frac{\partial {\psi }_1^{*}}{\partial t}+\frac{\partial {\psi }_2^{*}}{\partial t}\right)\right]dx=0.(11)$

Such non-decaying polariton magnetic soliton, therefore, belongs to dissipative solitons [50–52].

Such dissipative magnetic soliton (DMS) is quite unconventional, as its creation cannot be understood along the line of the well known example in the equilibrium context. In Bose condensed atomic gas, the key prerequisite for creating magnetic soliton is an antiferromagnetic interaction satisfying g − g₁₂ ≪ g, i.e., close to the spin-isotropic Manakov limit (g = g₁₂). This condition, as can be seen from Eq. 10, creates a large energy separation between the density and spin-polarization excitations: The density depletion from n₀ near the soliton core requires much more energy than that associated with S_z, making the former energetically suppressed and thus ensuring a constant total density that characterizes magnetic soliton. However, such scenario fails here because polaritons feature g − g₁₂ > g.

IV Dissipation-Enabled Formation Mechanism

To understand this unconventional phenomenon, the fact that Eqs. 6–9 are exact solutions offer a “sweet point.” We see that the balance of gain and loss [Eq. 5] is the key for fixing the background density at n₀ = P/γ_C − γ_R/R. Simultaneously, this gives rise to a closed real equation for the magnetization ${\left[d{S}_z(y)/dy\right]}^2+S_z^4(y)-\left(1-U^2\right)S_z^2(y)=0$ with y = η/ξ_s; that is, the spin polarization excitation is decoupled from other excitation channels. We emphasize that such conditionally coherent dynamics has a fundamentally different origin from that in a purely conservative system such as atomic BEC. As such, magnetic soliton in the former case can occur far from the Manakov limit, in contrast to the latter where it is only possible when the deviation from g = g₁₂ is small breaking slightly system integrability.

The above dissipation-enabled decoupling of excitations is at the heart of DMS formation, which also manifests itself in the linear excitation regimes, e.g., in the excitation spectrum and linear response function. Briefly, to describe a spinor polariton BEC linearly perturbed from the steady state, we substitute Eq. 6 into Eqs. 1–3 and follow the standard Bogoliubov–de Gennes (BdG) approach (see details in Appendix C). The eigen-energy ℏω_q of excitations solves the equation$[{\left(\hslash {\omega }_q\right)}^2-{\left(\hslash {\omega }_S\right)}^2]\times \{{\left(\hslash {\omega }_q\right)}^3+i\left(R{n}_0+{\gamma }_R\right){\left(\hslash {\omega }_q\right)}^2-[R{n}_0{\gamma }_C+{\left(\hslash {\omega }_B\right)}^2]\hslash {\omega }_q+ic\left(q\right)\}=\mathrm{0,}$ where $\hslash {\omega }_S=\sqrt{{\epsilon }_q^0\left[{\epsilon }_q^0+\left(g-g_{12}\right)n_0\right]}$, $\hslash {\omega }_B=\sqrt{{\epsilon }_q^0\left[{\epsilon }_q^0+\left(g+g_{12}\right)n_0\right]}$, and $c(q)=-(R{n}_0+{\gamma }_R){(\hslash {\omega }_B)}^2+2g{n}_0{\gamma }_c{\epsilon }_q^0$, with ${\epsilon }_q^0={\hslash }^2{q}^2/(2m)$ being the free-particle energy. Two decoupled equations follow: the quadratic equation immediately yields ℏω_q = ±ℏω_S for the energy of the spin-polaridzation excitation, whereas the cubic equation reflects the coupled linear excitations in the reservoir and density channel of polariton BEC. Importantly, we see ω_s is purely real (Figure 3A), regardless of whether the reservoir is fast or slow compared to the polariton BEC. This feature of the linear spin polarization excitation contrasts to the linear density excitation that generically exhibits a complex energy ℏω_D and eventually damps out. The latter is most transparent in the fast reservoir limit γ_R/γ_C ≫ 1. There, an adiabatic elimination of the reservoir gives ℏω_D = − iΓ/2 ± ℏω₀, with $\hslash {\omega }_0=\sqrt{{\epsilon }_q^0\left[{\epsilon }_q^0+\left(g+g_{12}\right)n_0-2g_R\hslash \mathrm{\Gamma }/R\right]-{\mathrm{\Gamma }}^2/4}$ and $\mathrm{\Gamma }=n_0{n}_R^0{R}^2\hslash /({\gamma }_R+n_{0}R)$. Note that ω_D is purely imaginary for |q| ≤ q_c due to polariton losses, with $q_c=\sqrt{m(\sqrt{{\alpha }^2+{\mathrm{\Gamma }}^4/4}-{\alpha }^2)/{\hslash }^2}$. Here, we introduced parameter α = P/P_th − 1 and the threshold value P_th = γ_Rγ_C/R. In Figures 3A,B, we show the complex spectrum of linear density excitation for γ_R/γ_C ≫ 1 where the analytical results agree with numerical solutions of BdG equations. Note that the damping spectrum in Figure 3B shows that the considered steady state is indeed modulationally stable.

FIGURE 3

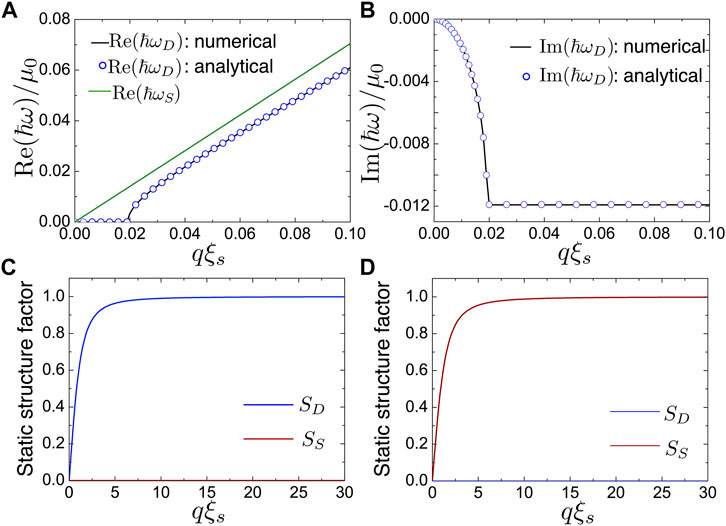
FIGURE 3. Manifestation of dissipation-enabled decoupling of excitations in the linear regime. Panels (A) and (B): (A) real and (B) imaginary parts of the energy of density excitation ℏω_D and energy ℏω_S of spin-polarization excitation, respectively. Solid curves depict numerical solutions of Bogoliubov’s equations, and the curve with circles indicate analytical solutions. (C,D) Density static structure factor S_D(q) and spin-density static structure factor S_S(q) when the spinor polariton BEC is subjected to a perturbation of the form (C) λe^i(qx−ωt) + H. c and (D) λσ_ze^i(qx−ωt) + H. c (see main text). Same parameters as in Figure 2 are used.

To further visualize the decoupling of excitations as a result of the balance between gain and loss, we analyze the linear response of the system. Considering an external density perturbation described by λe^i(qx−ωt) + H. c with λ ≪ 1 is acted on the exciton–polariton BEC, we calculate the density static structure factor S_D(q) and the spin-density static structure factor S_S(q) [53]. For simplicity of analytical derivation, we assume fast reservoir limit and obtain (see the details in Appendix C)

$S_D(q)=\left\{\begin{array}{cc}\begin{array}{c}\hfill \frac{{\epsilon }_{\mathbf{q}}^0}{\pi \hslash \left|\hslash {\omega }_0\right|}\log \left(\frac{\mathrm{\Gamma }+2\left|\hslash {\omega }_0\right|}{\mathrm{\Gamma }-2\left|\hslash {\omega }_0\right|}\right)\hfill \\ \hfill \frac{4{\epsilon }_{\mathbf{q}}^0}{\pi \hslash \mathrm{\Gamma }}\hfill \\ \hfill \left[\frac{1}{2}+\frac{1}{\pi }{\tan }^{-1}\left(\frac{4{\omega }_0^2-{\mathrm{\Gamma }}^2}{4\mathrm{\Gamma }{\omega }_0}\right)\right]\frac{{\epsilon }_{\mathbf{q}}^0}{\hslash {\omega }_0}\hfill \end{array}\hfill & \begin{array}{c}\hfill q<q_c,\hfill \\ \hfill q=q_c,\hfill \\ \hfill q>q_c,\hfill \end{array}\hfill \end{array}\right.(12)$

and we also find S_S(q) = 0. Figure 3C shows $\underset{q\to \infty }{\lim }{S}_D(q)\to 1$, meaning the response of a polariton BEC to a density perturbation is exhausted by the density excitation, without collateral generations of excitations in other excitation sectors. If the system is instead subjected to a spin-dependent perturbation λσ_ze^i(qx−ωt) + H. c, we find S_S(q) = ℏq²/(2mω_S), which approaches unity for q → ∞ and S_D(q) = 0 (see Figure 3D). This further verifies that a perturbation in the spin polarization sector only induces spin excitations.

V Concluding Discussions

Summarizing, we theoretically show that a new kind of soliton DMS can be created in a spinor polariton condensate. The value and significance of our work are twofold. First, DMS has no atomic counterpart and relies crucially on the open-dissipative property of the system, in contrast to solitons discussed in Refs. [25–30, 37, 54, 55] and half-solitons in Refs. [10, 11]. Second, DMS provides a rare example of exact solutions to the dissipative GP equations at quasi-1D. In the future, it is interesting to explore concrete proposals for the experimental observation of the predicted phenomenon within feasible facilities and to study the unique quantum many-body physics associated with a collection of DMSs with same (opposite) magnetic charges. Furthermore, in our present theoretical illustration, the condition of Eq. 5 reduces to D_s = 0, but the concept of dissipation-enabled decoupled excitations applies for generic cases where D_sψ_s = 0 rather than D_s = 0 holds. Thus, it is also interesting to explore in a broader context other new kinds of dissipative solitons that can arise from excitation decoupling.

Data Availability Statement

The raw data supporting the conclusions of this article will be made available by the authors, without undue reservation.

Author Contributions

ZL and YH have developed and supervised the research projects with the help of W-ML. CJ and RW have done the detailed calculations. All the authors contribute to writing the manuscript.

Funding

The authors declare that they received funding from the National Natural Science Foundation of China, Grant No. 11975208 to the author RW.

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s Note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors, and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

Acknowledgments

We acknowledge constructive suggestions from Augusto Smerzi, and thank Xingran Xu, Biao Wu, Chao Gao, and Yan Xue for stimulating discussions. This work is financially supported by Zhejiang Provincial Natural Science Foundation of China (Grant Nos. LZ21A040001), the National Natural Science Foundation of China (Nos. 12074344, 11874038, 11434015, and 61835013) and by the key projects of the Natural Science Foundation of China (Grant Nos. 11835011). WM-L is also supported by the National Key R&D Program of China (Grant Nos. 2016YFA0301500) and the Strategic Priority Research Program of the Chinese Academy of Sciences (Grant Nos. XDB01020300 and XDB21030300).

References

1. Shelykh IA, Kavokin AV, Rubo YG, Liew TCH, Malpuech G. Polariton Polarization-Sensitive Phenomena in Planar Semiconductor Microcavities. Semicond Sci Technol (2010) 25:013001. doi:10.1088/0268-1242/25/1/013001

CrossRef Full Text | Google Scholar

2. Deng H, Haug H, Yamamoto Y. Exciton-polariton Bose-Einstein Condensation. Rev Mod Phys (2010) 82:1489–537. doi:10.1103/revmodphys.82.1489

CrossRef Full Text | Google Scholar

3. Carusotto I, Ciuti C. Quantum Fluids of Light. Rev Mod Phys (2013) 85:299–366. doi:10.1103/revmodphys.85.299

CrossRef Full Text | Google Scholar

4. Byrnes T, Kim NY, Yamamoto Y. Exciton-polariton Condensates. Nat Phys. (2014) 10:803–13. doi:10.1038/nphys3143

CrossRef Full Text | Google Scholar

5. Lagoudakis KG, Wouters M, Richard M, Baas A, Carusotto I, André R, et al. Quantized Vortices in an Exciton-Polariton Condensate. Nat Phys (2008) 4:706–10. doi:10.1038/nphys1051

CrossRef Full Text | Google Scholar

6. Renucci P, Amand T, Marie X, Senellart P, Bloch J, Sermage B, et al. Microcavity Polariton Spin Quantum Beats without a Magnetic Field: A Manifestation of Coulomb Exchange in Dense and Polarized Polariton Systems. Phys Rev B (2005) 72:075317. doi:10.1103/physrevb.72.075317

CrossRef Full Text | Google Scholar

7. Takemura N, Anderson MD, Navadeh-Toupchi M, Oberli DY, Portella-Oberli MT, Deveaud B. Spin Anisotropic Interactions of Lower Polaritons in the Vicinity of Polaritonic Feshbach Resonance. Phys Rev B (2017) 95:205303. doi:10.1103/physrevb.95.205303

CrossRef Full Text | Google Scholar

8. Navadeh-Toupchi M, Takemura N, Anderson MD, Oberli DY, Portella-Oberli MT. Polaritonic Cross Feshbach Resonance. Phys Rev Lett (2019) 122:047402. doi:10.1103/PhysRevLett.122.047402

PubMed Abstract | CrossRef Full Text | Google Scholar

9. Franco D, Giorgini S, Pitaevskii LP, Stringari S. Theory of Bose-Einstein Condensation in Trapped Gases. Rev Mod Phys (1999) 71:463–512.

Google Scholar

10. Flayac H, Solnyshkov DD, Malpuech G. Oblique Half-Solitons and Their Generation in Exciton-Polariton Condensates. Phys Rev B (2011) 83:193305. doi:10.1103/physrevb.83.193305

CrossRef Full Text | Google Scholar

11. Hivet R, Flayac H, Solnyshkov DD, Tanese D, Boulier T, Andreoli D, et al. Half-solitons in a Polariton Quantum Fluid Behave like Magnetic Monopoles. Nat Phys (2012) 8:724–8. doi:10.1038/nphys2406

CrossRef Full Text | Google Scholar

12. Yuri GR. Half Vortices in Exciton Polariton Condensates. Phys Rev Lett (2007) 99:106401. doi:10.1103/PHYSREVLETT.99.106401

PubMed Abstract | CrossRef Full Text | Google Scholar

13. Lagoudakis KG, Ostatnický T, Kavokin AV, Rubo YG, André R, Deveaud-Plédran B. Observation of Half-Quantum Vortices in an Exciton-Polariton Condensate. Science (2009) 326:974–6. doi:10.1126/science.1177980

PubMed Abstract | CrossRef Full Text | Google Scholar

14. Qu C, Pitaevskii LP, Stringari S. Magnetic Solitons in a Binary Bose-Einstein Condensate. Phys Rev Lett (2016) 116:160402. doi:10.1103/physrevlett.116.160402

PubMed Abstract | CrossRef Full Text | Google Scholar

15. Qu C, Tylutki M, Stringari S, Pitaevskii LP. Magnetic Solitons in Rabi-Coupled Bose-Einstein Condensates. Phys Rev A (2017) 95:033614. doi:10.1103/physreva.95.033614

CrossRef Full Text | Google Scholar

16. Fujimoto K, Hamazaki R, Ueda M. Flemish Strings of Magnetic Solitons and a Nonthermal Fixed point in a One-Dimensional Antiferromagnetic Spin-1 Bose Gas. Phys Rev Lett (2019) 122:173001. doi:10.1103/physrevlett.122.173001

PubMed Abstract | CrossRef Full Text | Google Scholar

17. Malomed BA, Mihalache D, Wise F, Torner L. Spatiotemporal Optical Solitons. J Opt B: Quan Semiclass. Opt. (2005) 7:R53–R72. doi:10.1088/1464-4266/7/5/r02

CrossRef Full Text | Google Scholar

18. Kartashov YV, Malomed BA, Torner L. Solitons in Nonlinear Lattices. Rev Mod Phys (2011) 83:247–305. doi:10.1103/revmodphys.83.247

CrossRef Full Text | Google Scholar

19. Konotop VV, Yang J, Zezyulin DA. Nonlinear Waves in ${\\Mathcal{PT}}$fx105-symmetric Systems. Rev Mod Phys (2016) 88:035002. doi:10.1103/revmodphys.88.035002

CrossRef Full Text | Google Scholar

20. Lev P. Magnetic Solitons in Binary Mixtures of Bose–Einstein Condensates. Rendiconti Lincei Scienze Fisiche e Naturali (2019) 30:269–76. doi:10.1007/s12210-019-00797-6

CrossRef Full Text | Google Scholar

21. Farolfi A, Trypogeorgos D, Mordini C, Lamporesi G, Ferrari G. Observation of Magnetic Solitons in Two-Component Bose-Einstein Condensates. Phys Rev Lett (2020) 125:030401. doi:10.1103/PhysRevLett.125.030401

PubMed Abstract | CrossRef Full Text | Google Scholar

22. Chai X, Lao D, Fujimoto K, Hamazaki R, Ueda M, Raman C. Magnetic Solitons in a Spin-1 Bose-Einstein Condensate. Phys Rev Lett (2020) 125:030402. doi:10.1103/PhysRevLett.125.030402

PubMed Abstract | CrossRef Full Text | Google Scholar

23. Haus HA, Wong WS. Solitons in Optical Communications. Rev Mod Phys (1996) 68:423–44. doi:10.1103/revmodphys.68.423

CrossRef Full Text | Google Scholar

24. Marin-Palomo P, Kemal JN, Karpov M, Kordts A, Pfeifle J, Pfeiffer MHP, et al. Microresonator-based Solitons for Massively Parallel Coherent Optical Communications. Nature (2017) 546:274–9. doi:10.1038/nature22387

PubMed Abstract | CrossRef Full Text | Google Scholar

25. Yulin AV, Egorov OA, Lederer F, Skryabin DV. Dark Polariton Solitons in Semiconductor Microcavities. Phys Rev A (2008) 78:061801(R). doi:10.1103/physreva.78.061801

CrossRef Full Text | Google Scholar

26. Ostrovskaya EA, Abdullaev J, Desyatnikov AS, Fraser MD, Kivshar YS. Dissipative Solitons and Vortices in Polariton Bose-Einstein Condensates. Phys Rev A (2012) 86:013636. doi:10.1103/physreva.86.013636

CrossRef Full Text | Google Scholar

27. Sich M, Krizhanovskii DN, Skolnick MS, Gorbach AV, Hartley R, Skryabin DV, et al. Observation of Bright Polariton Solitons in a Semiconductor Microcavity. Nat Photon (2012) 6:50–5. doi:10.1038/nphoton.2011.267

CrossRef Full Text | Google Scholar

28. Egorov OA, Gorbach AV, Lederer F, Skryabin DV. Two-dimensional Localization of Exciton Polaritons in Microcavities. Phys Rev Lett (2010) 105:073903. doi:10.1103/PhysRevLett.105.073903

PubMed Abstract | CrossRef Full Text | Google Scholar

29. Ma X, Egorov OA, Schumacher S. Creation and Manipulation of Stable Dark Solitons and Vortices in Microcavity Polariton Condensates. Phys Rev Lett (2017) 118:157401. doi:10.1103/physrevlett.118.157401

PubMed Abstract | CrossRef Full Text | Google Scholar

30. Ma X, Schumacher S. Vortex Multistability and Bessel Vortices in Polariton Condensates. Phys Rev Lett (2018) 121:227404. doi:10.1103/physrevlett.121.227404

PubMed Abstract | CrossRef Full Text | Google Scholar

31. Wertz E, Ferrier L, Solnyshkov DD, Johne R, Sanvitto D, Lemaître A, et al. Spontaneous Formation and Optical Manipulation of Extended Polariton Condensates. Nat Phys (2010) 6:860–4. doi:10.1038/nphys1750

CrossRef Full Text | Google Scholar

32. Borgh MO, Keeling J, Berloff NG. Spatial Pattern Formation and Polarization Dynamics of a Nonequilibrium Spinor Polariton Condensate. Phys Rev B (2010) 81:235302. doi:10.1103/physrevb.81.235302

CrossRef Full Text | Google Scholar

33. Ohadi H, Dreismann A, Rubo YG, Pinsker F, delValle InclanRedondo Y, Tsintzos SI, et al. Spontaneous Spin Bifurcations and Ferromagnetic Phase Transitions in a Spinor Exciton-Polariton Condensate. Phys Rev X (2015) 5:031002. doi:10.1103/physrevx.5.031002

CrossRef Full Text | Google Scholar

34. Liew TCH, Egorov OA, Matuszewski M, Kyriienko O, Ma X, Ostrovskaya EA. Instability-induced Formation and Nonequilibrium Dynamics of Phase Defects in Polariton Condensates. Phys Rev B (2015) 91:085413. doi:10.1103/physrevb.91.085413

CrossRef Full Text | Google Scholar

35. Li G, Liew TCH, Egorov OA, Ostrovskaya EA. Incoherent Excitation and Switching of Spin States in Exciton-Polariton Condensates. Phys Rev B (2015) 92:064304. doi:10.1103/physrevb.92.064304

CrossRef Full Text | Google Scholar

36. Askitopoulos A, Kalinin K, Liew TCH, Cilibrizzi P, Hatzopoulos Z, Savvidis PG, et al. Nonresonant Optical Control of a Spinor Polariton Condensate. Phys Rev B (2016) 93:205307. doi:10.1103/physrevb.93.205307

CrossRef Full Text | Google Scholar

37. Pinsker F, Flayac H. On-demand Dark Soliton Train Manipulation in a Spinor Polariton Condensate. Phys Rev Lett (2014) 112:140405. doi:10.1103/physrevlett.112.140405

PubMed Abstract | CrossRef Full Text | Google Scholar

38. Pinsker F. Approximate Solutions for Half-Dark Solitons in Spinor Non-equilibrium Polariton Condensates. Ann Phys (2015) 362:726–38. doi:10.1016/j.aop.2015.09.008

CrossRef Full Text | Google Scholar

39. Pinsker F, Flayac H. Bright Solitons in Non-equilibrium Coherent Quantum Matter. Proc R Soc A (2016) 472:20150592. doi:10.1098/rspa.2015.0592

PubMed Abstract | CrossRef Full Text | Google Scholar

40. Xu X, Hu Y, Zhang Z, Liang Z. Spinor Polariton Condensates under Nonresonant Pumping: Steady States and Elementary Excitations. Phys Rev B (2017) 96:144511. doi:10.1103/physrevb.96.144511

CrossRef Full Text | Google Scholar

41. Xu X, Chen L, Zhang Z, Liang Z. Dark-bright Solitons in Spinor Polariton Condensates under Nonresonant Pumping. J Phys B: Mol Opt Phys (2019) 52:025303. doi:10.1088/1361-6455/aaf4dd

CrossRef Full Text | Google Scholar

42. Bobrovska N, Matuszewski M. Adiabatic Approximation and Fluctuations in Exciton-Polariton Condensates. Phys Rev B (2015) 92:035311. doi:10.1103/physrevb.92.035311

CrossRef Full Text | Google Scholar

43. Bobrovska N, Ostrovskaya EA, Matuszewski M. Stability and Spatial Coherence of Nonresonantly Pumped Exciton-Polariton Condensates. Phys Rev B (2014) 90:205304. doi:10.1103/physrevb.90.205304

CrossRef Full Text | Google Scholar

44. Bobrovska N, Matuszewski M, Daskalakis KS, Maier SA, Kéna-Cohen S. Dynamical Instability of a Nonequilibrium Exciton-Polariton Condensate. ACS Photon (2018) 5:111–8. doi:10.1021/acsphotonics.7b00283

CrossRef Full Text | Google Scholar

45. Baboux F, De Bernardis D, Goblot V, Gladilin VN, Gomez C, Galopin E, et al. Unstable and Stable Regimes of Polariton Condensation. Optica (2018) 5:1163–70. doi:10.1364/optica.5.001163

CrossRef Full Text | Google Scholar

46. Shelykh IA, Rubo YG, Malpuech G, Solnyshkov DD, Kavokin A. Polarization and Propagation of Polariton Condensates. Phys Rev Lett (2006) 97:066402. doi:10.1103/PhysRevLett.97.066402

PubMed Abstract | CrossRef Full Text | Google Scholar

47. Sich M, Tapia-Rodriguez LE, Sigurdsson H, Walker PM, Clarke E, Shelykh IA, et al. Spin Domains in One-Dimensional Conservative Polariton Solitons. ACS Photon (2018) 5:5095–102. doi:10.1021/acsphotonics.8b01410

CrossRef Full Text | Google Scholar

48. Kivshar YS, Yang X. Perturbation-induced Dynamics of Dark Solitons. Phys Rev E Stat Phys Plasmas Fluids Relat Interdiscip Top (1994) 49:1657–70. doi:10.1103/physreve.49.1657

CrossRef Full Text | Google Scholar

49. Smirnov LA, Smirnova DA, Ostrovskaya EA, Kivshar YS. Dynamics and Stability of Dark Solitons in Exciton-Polariton Condensates. Phys Rev B (2014) 89:235310. doi:10.1103/physrevb.89.235310

CrossRef Full Text | Google Scholar

50. Kippenberg TJ, Gaeta AL, Lipson M, Gorodetsky ML. Dissipative Kerr Solitons in Optical Microresonators. Science (2018) 361:567. doi:10.1126/science.aan8083

PubMed Abstract | CrossRef Full Text | Google Scholar

51. Grelu P, Akhmediev N. Dissipative Solitons for Mode-Locked Lasers. Nat Photon (2012) 6:84–92. doi:10.1038/nphoton.2011.345

CrossRef Full Text | Google Scholar

52. Purwins H-G, Bödeker HU, Amiranashvili S. Dissipative Solitons. Adv Phys (2010) 59:485–701. doi:10.1080/00018732.2010.498228

CrossRef Full Text | Google Scholar

53. Nozieres P, Pines D. The Theory of Quantum Liquids: Vol. II. New York: Addison-Wesley (1990).

Google Scholar

54. Amo A, Pigeon S, Sanvitto D, Sala VG, Hivet R, Carusotto I, et al. Polariton Superfluids Reveal Quantum Hydrodynamic Solitons. Science (2011) 332:1167–70. doi:10.1126/science.1202307

PubMed Abstract | CrossRef Full Text | Google Scholar

55. Xue Y, Matuszewski M. Creation and Abrupt Decay of a Quasistationary Dark Soliton in a Polariton Condensate. Phys Rev Lett (2014) 112:216401. doi:10.1103/physrevlett.112.216401

CrossRef Full Text | Google Scholar

Appendix A: Derivations of Exact Soliton Solution

Here, we present detailed derivation of the exact solutions in Eqs. 4–7 in the main text. We want to solve the effective 1D driven-dissipative GP equations for the order parameter ${\left[\begin{array}{c}\hfill {\psi }_1,{\psi }_2\hfill \end{array}\right]}^T$ of spinor polariton BEC, which are coupled to the rate equation of the density n_R of the polariton reservoir, i.e.,

$\begin{array}{ccc}\hfill i\hslash \frac{\partial {\psi }_1}{\partial t}& =\hfill & \left\{-\frac{{\hslash }^2}{2m}\frac{{\partial }^2}{\partial x^2}+g{\left|{\psi }_1\right|}^2+g_{12}{\left|{\psi }_2\right|}^2+g_R{n}_R+\frac{i\hslash }{2}\left[R{n}_R-{\gamma }_C\right]\right\}{\psi }_1,\hfill \end{array}(\mathrm{A1})$

$\begin{array}{ccc}\hfill i\hslash \frac{\partial {\psi }_2}{\partial t}& =\hfill & \left\{-\frac{{\hslash }^2}{2m}\frac{{\partial }^2}{\partial x^2}+g{\left|{\psi }_2\right|}^2+g_{12}{\left|{\psi }_1\right|}^2+g_R{n}_R+\frac{i\hslash }{2}\left[R{n}_R-{\gamma }_C\right]\right\}{\psi }_2,\hfill \end{array}(\mathrm{A2})$

$\begin{array}{ccc}\hfill \frac{\partial n_R}{\partial t}& =\hfill & P-\left[{\gamma }_R+R\left({\left|{\psi }_1\right|}^2+{\left|{\psi }_2\right|}^2\right)\right]n_R.\hfill \end{array}(\mathrm{A3})$

Here, $g\left(g_{12}\right)$ denotes the interaction constant between the same (different) spin component, g_R is the interaction constant between condensed polaritons and reservoir polaritons whose density is n_R. Condensed polaritons decay at rate γ_C and are replenished at a rate R from reservoir. Reservoir polaritons decay at rate γ_R and P is the rate of an off-resonant cw pumping.

We aim to find a particular type of traveling soliton solution ${\psi }_{\mathrm{1,2}}\left(x,t\right)={\psi }_{\mathrm{1,2}}\left(x-vt\right)$, with v the velocity of soliton, which is characterized by ${\left|{\psi }_1\right|}^2+{\left|{\psi }_2\right|}^2=n_0$ with n₀ a constant and satisfies the condition [Rn_R − γ_C]ψ₁₍₂₎ = 0 (i.e., D_sψ_s = 0). Therefore, we consider the following ansatz:

$\left(\begin{array}{c}\hfill {\psi }_1\hfill \\ \hfill {\psi }_2\hfill \end{array}\right)=\sqrt{\frac{n_0}{2}}\left(\begin{array}{c}\hfill \sqrt{1+\delta n}{e}^{i\frac{{\phi }_r}{2}}\hfill \\ \hfill \sqrt{1-\delta n}{e}^{-i\frac{{\phi }_r}{2}}\hfill \end{array}\right)e^{i{\phi }_g/2}{e}^{-i\frac{{\mu }_{R}t}{\hslash }}.(\mathrm{A4})$

Here, φ_g and φ_r are the global and relative phases of the spin-up and spin-down wavefunctions. Without loss of generality, we will assume the boundary conditions: φ_r,g = 0 at η = − ∞ and δn = 0 at η = ±∞.

In order to determine the constant n₀, we substitute Eq. (A4) into Eq. (A3) and find $n_R^0=P/\left({\gamma }_R+R{n}_0\right)$. Thus, for $P=\left({\gamma }_R+R{n}_0\right){\gamma }_C/R$, and hence n₀ = P/γ_C − γ_R/R, the condition D_sψ = 0 is fulfilled. With these, and denoting η = x − vt, we obtain from Eqs. A1, A2 that.

$\begin{array}{ll}\hfill -i\hslash v\frac{\partial {\psi }_1\left(\eta \right)}{\partial \eta }& =\left[-\frac{{\hslash }^2}{2m}\frac{{\partial }^2}{\partial {\eta }^2}+\left(g-g_{12}\right){\left|{\psi }_1\right|}^2+g_{12}{n}_0+\frac{g_R{\gamma }_C}{R}\right]{\psi }_1\left(\eta \right),\hfill \end{array}(\mathrm{A5})$

$\begin{array}{ll}\hfill -i\hslash v\frac{\partial {\psi }_2\left(\eta \right)}{\partial \eta }& =\left[-\frac{{\hslash }^2}{2m}\frac{{\partial }^2}{\partial {\eta }^2}+\left(g-g_{12}\right){\left|{\psi }_2\right|}^2+g_{12}{n}_0+\frac{g_R{\gamma }_C}{R}\right]{\psi }_2\left(\eta \right).\hfill \end{array}(\mathrm{A6})$

Substituting Eq. A4 (with n₀ = P/γ_C − γ_R/R) into Eqs. A5, A6 yields following equations for $\delta n\left(\eta \right)$, ${\phi }_r\left(\eta \right)$, and ${\phi }_g\left(\eta \right)$, respectively, i.e.,

$\begin{array}{ccc}\hfill {\left(\frac{\partial \delta n}{\partial \eta /{\xi }_s}\right)}^2-\left(1-U^2\right)\delta n^2+\delta n^4& =\hfill & 0,\hfill \end{array}(\mathrm{A7})$

$\begin{array}{ccc}\hfill \left(1-\delta n^2\right)\frac{\partial {\phi }_g}{\partial \left(\eta /{\xi }_s\right)}+U\delta n^2& =\hfill & 0,\hfill \end{array}(\mathrm{A8})$

$\begin{array}{ccc}\hfill \left(1-\delta n^2\right)\frac{\partial {\phi }_r}{\partial \left(\eta /{\xi }_s\right)}-U\delta n& =\hfill & 0.\hfill \end{array}(\mathrm{A9})$

where ${\xi }_s=\hslash /\sqrt{2m{n}_0\left(g-g_{12}\right)}$ and U = v/c_s with $c_s=\sqrt{\left(g-g_{12}\right)n_0/2m}$.

Equation (A7) is a closed equation and can be readily solved. Using the boundary conditions δn = 0 at η = ±∞, we find

$\delta n(\eta )=\sqrt{1-U^2}\text{sech}\left[\left(\frac{\mathrm{\eta }}{{\xi }_s}\right)\sqrt{1-U^2}\right].(\mathrm{A10})$

Substituting Eq. A10 into Eqs. A8, A9, and taking into account of the boundary conditions φ_r,g = 0 at η = − ∞, we finally arrive at the soliton solutions in Eqs. 4–7 in the main text.

Appendix B: Energy of the Soliton

Here, we calculate the change rate of the energy of above soliton. The energy functional of the soliton can be calculated according to [48, 49].

$E=\int dx{\psi }^{†}\left(-\frac{{\hslash }^2}{2m}\frac{{\partial }^2}{\partial x^2}\right)\psi +\frac{1}{4}\int dx\left[\left(g+g_{12}\right){\left\{n\left(x,t\right)-n_0\right\}}^2+\left(g-g_{12}\right)S_z^2\left(x,t\right)\right](\mathrm{B1})$

where we have denoted $n\left(x,t\right)=|{\psi }_1(x,t){|}^2+|{\psi }_2(x,t){|}^2$ and $S_z\left(x,t\right)=|{\psi }_1(x,t){|}^2-|{\psi }_2(x,t){|}^2$. Changing the integration variable from x to η = x − vt, and using GP Eqs. A1–A3, we can directly calculate the total time derivative of E associated with our soliton solution as

$\begin{array}{ll}\hfill \frac{dE}{dt}& =v\int d\eta \left[g_R{n}_R+\frac{i\hslash }{2}\left(R{n}_R-{\gamma }_C\right)\right]{\psi }_1\frac{d}{d\eta }{\psi }_1^{*}+{[g}_R{n}_R-\frac{i\hslash }{2}(R{n}_R-{\gamma }_C){\psi }_1^{*}\frac{d}{d\eta }{\psi }_1\hfill \\ \hfill & +v\int d\eta \left(\left[g_R{n}_R+\frac{i\hslash }{2}\left(R{n}_R-{\gamma }_C\right)\right]{\psi }_2\frac{d}{d\eta }{\psi }_2^{*}+\left[g_R{n}_R-\frac{i\hslash }{2}\left(R{n}_R-{\gamma }_C\right)\right]{\psi }_2^{*}\frac{d}{d\eta }{\psi }_2\right)\hfill \\ \hfill & =v\int d\eta \left\{\frac{n}{2}\hslash \left(R{n}_R-{\gamma }_C\right)\left(\frac{d}{d\eta }{\varphi }_g+\delta n\frac{d}{d\eta }{\varphi }_r\right)\right\}\hfill \\ \hfill & =0.\hfill \end{array}(\mathrm{B2})$

Appendix C: Linear Collective Excitations

In this section, we present detailed derivations of the linear excitations of the considered system using Bogoliubov approach. As g > 0 and g₁₂ < 0 with |g₁₂|≪ g, for P ≥ γ_Rγ_C/γ_R, the steady state of the model system is a linearly polarized BEC with $n_1^0=n_2^0=n_0/2$, where n₀ = P/γ_C − γ_R/R and $n_R^0={\gamma }_C/R$. We further have ${\mu }_T=\frac{1}{2}\left(g+g_{12}\right)n_0+g_R{n}_R^0$. For linear excitations, we follow the standard procedures of Bogoliubov decomposition and write [40].

$\left(\begin{array}{c}\hfill {\psi }_1\left(x,t\right)\hfill \\ \hfill {\psi }_2\left(x,t\right)\hfill \end{array}\right)=e^{-i{\mu }_{T}t/\hslash }\sqrt{\frac{n_0}{2}}\left(\begin{array}{c}\hfill 1\hfill \\ \hfill 1\hfill \end{array}\right)\left[1+\sum _q\left\{\left(\begin{array}{c}\hfill u_{1q}\hfill \\ \hfill u_{2q}\hfill \end{array}\right)e^{i\left(qx-{\omega }_{q}t\right)}+\left(\begin{array}{c}\hfill v_{1q}^{*}\hfill \\ \hfill v_{2q}^{*}\hfill \end{array}\right)e^{-i\left(qx-{\omega }_q^{*}t\right)}\right\}\right],(\mathrm{C1})$

and

$n_R\left(t\right)=n_R^0\left[1+\sum _q\left\{w_q{e}^{i\left(qx-{\omega }_{q}t\right)}+w_q^{*}{e}^{-i\left(qx-{\omega }_q^{*}t\right)}\right\}\right].(\mathrm{C2})$

It’s convenient to rewrite the excited components in Eq. (C1) in terms of u_d = u_1q + u_2q and v_d = v_1q + v_2q, and u_s = u_1q − u_2q and v_s = v_1q − v_2q, which are then subsequently substituted into Eqs. A1–A3. Retaining only the first-order terms of the fluctuations, we obtain the Bogoliubov–de Gennes (BdG) equation as

${\mathfrak{L}}_{\mathfrak{q}}^{\prime }\left(\begin{array}{c}\hfill u_{1q}+u_{2q}\hfill \\ \hfill v_{1q}+v_{2q}\hfill \\ \hfill w_q\hfill \\ \hfill u_{1q}-u_{2q}\hfill \\ \hfill v_{1q}-v_{2q}\hfill \end{array}\right)=\hslash {\omega }_q\left(\begin{array}{c}\hfill u_{1q}+u_{2q}\hfill \\ \hfill v_{1q}+v_{2q}\hfill \\ \hfill w_q\hfill \\ \hfill u_{1q}-u_{2q}\hfill \\ \hfill v_{1q}-v_{2q}\hfill \end{array}\right).(\mathrm{C3})$

with

${\mathfrak{L}}_{\mathfrak{q}}^{\prime }=\left(\begin{array}{ccccc}\hfill {\epsilon }_q^0+\frac{g+g_{12}}{2}{n}_0\hfill & \hfill \frac{g+g_{12}}{2}{n}_0\hfill & \hfill \left(2g_R+iR\right)n_R^0\hfill & \hfill 0\hfill & \hfill 0\hfill \\ \hfill -\frac{g+g_{12}}{2}{n}_0\hfill & \hfill -\left({\epsilon }_q^0+\frac{g{n}_0}{2}\right)\hfill & \hfill \left(-2g_R+iR\right)n_R^0\hfill & \hfill 0\hfill & \hfill 0\hfill \\ \hfill -i\frac{R{n}_0}{2}\hfill & \hfill -i\frac{R{n}_0}{2}\hfill & \hfill -i\left(R{n}_0+{\gamma }_R\right)\hfill & \hfill 0\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill \left({\epsilon }_q^0+\frac{\left(g-g_{12}\right)n_0}{2}\right)\hfill & \hfill \frac{\left(g-g_{12}\right)n_0}{2}\hfill \\ \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill -\frac{\left(g-g_{12}\right)n_0}{2}\hfill & \hfill -\left({\epsilon }_q^0+\frac{\left(g-g_{12}\right)n_0}{2}\right)\hfill \end{array}\right).(\mathrm{C4})$

Since the matrix ${\mathfrak{L}}_{\mathfrak{q}}^{\prime }$ is block diagonal, we obtain two decoupled BdG equations

$\left(\begin{array}{ccc}\hfill {\epsilon }_q^0+\frac{g+g_{12}}{2}{n}_0\hfill & \hfill \frac{g+g_{12}}{2}{n}_0\hfill & \hfill \left(2g_R+iR\right)n_R^0\hfill \\ \hfill -\frac{g+g_{12}}{2}{n}_0\hfill & \hfill -\left({\epsilon }_q^0+\frac{g+g_{12}}{2}{n}_0\right)\hfill & \hfill \left(-2g_R+iR\right)n_R^0\hfill \\ \hfill -i\frac{R{n}_0}{2}\hfill & \hfill -i\frac{R{n}_0}{2}\hfill & \hfill -i\left(R{n}_0+{\gamma }_R\right)\hfill \end{array}\right)\left(\begin{array}{c}\hfill u_{1q}+u_{2q}\hfill \\ \hfill v_{1q}+v_{2q}\hfill \\ \hfill w_q\hfill \end{array}\right)=\hslash {\omega }_D\left(\begin{array}{c}\hfill u_{1q}+u_{2q}\hfill \\ \hfill v_{1q}+v_{2q}\hfill \\ \hfill w_q\hfill \end{array}\right),(\mathrm{C5})$

which describes coupled fluctuations in the density of condensed polaritons and reservoir, and

$\left(\begin{array}{cc}\hfill {\epsilon }_q^0+\frac{\left(g-g_{12}\right)n_0}{2}\hfill & \hfill \frac{\left(g-g_{12}\right)n_0}{2}\hfill \\ \hfill -\frac{\left(g-g_{12}\right)n_0}{2}\hfill & \hfill -{\epsilon }_q^0-\frac{\left(g-g_{12}\right)n_0}{2}\hfill \end{array}\right)\left(\begin{array}{c}\hfill u_{1q}-u_{2q}\hfill \\ \hfill v_{1q}-v_{2q}\hfill \end{array}\right)=\hslash {\omega }_S\left(\begin{array}{c}\hfill u_{1q}-u_{2q}\hfill \\ \hfill v_{1q}-v_{2q}\hfill \end{array}\right),(\mathrm{C6})$

which corresponds to linear excitation in spin polarization.

The eigen-energy can be directly calculated by solving BdG equations giving

$\left[{\left(\hslash {\omega }_q\right)}^2-{\left(\hslash {\omega }_S\right)}^2\right]\times \left\{{\left(\hslash {\omega }_q\right)}^3+i\left(R{n}_0+{\gamma }_R\right){\left(\hslash {\omega }_q\right)}^2-\left[R{n}_0{\gamma }_C+{\left(\hslash {\omega }_B\right)}^2\right]\hslash {\omega }_q+ic\left(q\right)\right\}=0.(\mathrm{C7})$

with $\hslash {\omega }_S=\sqrt{{\epsilon }_q^0\left[{\epsilon }_q^0+\left(g-g_{12}\right)n_0\right]}$, $\hslash {\omega }_B=\sqrt{{\epsilon }_q^0\left[{\epsilon }_q^0+\left(g+g_{12}\right)n_0\right]}$, and $c\left(q\right)=-\left(R{n}_0+{\gamma }_R\right){\left(\hslash {\omega }_B\right)}^2+2g_R{n}_0{\gamma }_C{\epsilon }_q^0$.

Appendix D: Density and Spin-Density Response Function

Based on the knowledge of linear excitations in Section C, here, we derive the density and spin-density response functions of the considered system. We will present detailed calculations for the density response function. The spin-density function are derived in a similar fashion; we therefore only outline main steps.

1. Dynamic Density Response Function

Suppose the quasi-1D spinor polariton BEC is subjected to a time-dependent external perturbation in a form $V_{\lambda }=-\lambda e^{i\left(\mathbf{q}\cdot \mathbf{r}-\omega t\right)}{e}^{ϵt}+h.c$ with λ ≪ 1 and ϵ ≪ 1, representing a density perturbation. In the presence of V_λ, Eqs. A1–A3 are modified as.

$\begin{array}{cc}\hfill i\hslash \frac{\partial {\psi }_1}{\partial t}& =\left\{-\frac{{\hslash }^2}{2m}\frac{{\partial }^2}{\partial x^2}+V_{\lambda }+\left(g{\left|{\psi }_1\right|}^2+g_{12}{\left|{\psi }_2\right|}^2\right)+g_R{n}_R+\frac{i\hslash }{2}\left[R{n}_R-{\gamma }_C\right]\right\}{\psi }_1,\hfill \end{array}(\mathrm{D1})$

$\begin{array}{ccc}\hfill i\hslash \frac{\partial {\psi }_2}{\partial t}& =\hfill & \left\{-\frac{{\hslash }^2}{2m}\frac{{\partial }^2}{\partial x^2}+V_{\lambda }+\left(g{\left|{\psi }_2\right|}^2+g_{12}{\left|{\psi }_1\right|}^2\right)+g_R{n}_R+\frac{i\hslash }{2}\left[R{n}_R-{\gamma }_C\right]\right\}{\psi }_2,\hfill \end{array}(\mathrm{D2})$

$\begin{array}{ccc}\hfill \frac{\partial n_R}{\partial t}& =\hfill & P-\left\{{\gamma }_R+R\left({\left|{\psi }_1\right|}^2+{\left|{\psi }_2\right|}^2\right)\right\}{n}_R.\hfill \end{array}(\mathrm{D3})$

Our goal is to calculate the density response function [53] as defined by

$\chi (q,\omega )=\underset{\lambda \to 0}{\lim }\delta {\rho }_q/(\lambda e^{-i\omega t}).(\mathrm{D4})$

where δρ_q are the Fourier component of the density fluctuation induced by the external perturbation.

For λ → 0, we follow standard procedures and look for solutions corresponding to small amplitude oscillations around the unperturbed steady-state polariton BEC and the reservoir, i.e., we write

$\begin{array}{ccc}\hfill {\psi }_{1\lambda }& =\hfill & e^{-i{\mu }_{T}t/\hslash }\left[\sqrt{\frac{n_0}{2}}+u_{1\lambda }{e}^{i\left(qx-{\omega }_{q}t\right)}+v_{1\lambda }^{*}{e}^{-i\left(qx-{\omega }_q^{*}t\right)}\right],\hfill \\ \hfill {\psi }_{2\lambda }& =\hfill & e^{-i{\mu }_{T}t/\hslash }\left[\sqrt{\frac{n_0}{2}}+u_{2\lambda }{e}^{i\left(qx-{\omega }_{q}t\right)}+v_{2\lambda }^{*}{e}^{-i\left(qx-{\omega }_q^{*}t\right)}\right],\hfill \\ \hfill n_{R\lambda }& =\hfill & n_R^0\left[1+w_{\lambda }{e}^{i\left(qx-{\omega }_{q}t\right)}+w_{\lambda }^{*}{e}^{-i\left(qx-{\omega }_q^{*}t\right)}\right],\hfill \end{array}(\mathrm{D5})$

where u_iλ and v_iλ (i = 1, 2) and w_λ are small coefficients due to the perturbation, and will be determined subsequentlty. Substituting Eq. D5 into Eq. D4 and retainng terms at the first order of u_iλ and v_iλ, we obtain the linear density response function as

$\chi \left(q,\omega \right)={\lambda }^{-1}\sqrt{\frac{n_0}{2}}\int dx{e}^{-iqx}\left(u_{1\lambda }+v_{1\lambda }+u_{2\lambda }+v_{2\lambda }\right).(\mathrm{D6})$

In order to determine u_λ and v_λ, we insert Eq. D5 into Eqs. D1–D3, we obtain the density excitation satisfying following equations

$\left(\begin{array}{ccc}\hfill {\epsilon }_q^0+\frac{\left(g+g_{12}\right)n_0}{2}-\hslash {\omega }_q\hfill & \hfill \frac{\left(g+g_{12}\right)n_0}{2}\hfill & \hfill n_R^0\left(2g_R+iR\right)\hfill \\ \hfill \frac{\left(g+g_{12}\right)n_0}{2}\hfill & \hfill {\epsilon }_q^0+\frac{\left(g+g_{12}\right)n_0}{2}+\hslash {\omega }_q\hfill & \hfill n_R^0\left(2g_R-iR\right)\hfill \\ \hfill -i\frac{R{n}_0}{2}\hfill & \hfill -i\frac{R{n}_0}{2}\hfill & \hfill -\left[i\left(R{n}_0+{\gamma }_R\right)+\hslash {\omega }_q\right]\hfill \end{array}\right)\left(\begin{array}{c}\hfill u_{\lambda ,1}+u_{\lambda ,2}\hfill \\ \hfill v_{\lambda ,1}+v_{\lambda ,2}\hfill \\ \hfill w_q\hfill \end{array}\right)=\lambda \sqrt{\frac{2N_0}{V}}\left(\begin{array}{c}\hfill 1\hfill \\ \hfill 1\hfill \\ \hfill 0\hfill \end{array}\right),(\mathrm{D7})$

For analytical simplicity, we assume fast reservoir limit of γ_R/γ_C ≫ 1. In this case, we find

$w_q=-\frac{R{n}_0}{2\left(R{n}_0+{\gamma }_R\right)}\left(u_{1q}+v_{1q}\right)-\frac{R{n}_0}{2\left(R{n}_0+{\gamma }_R\right)}\left(u_{2q}+v_{2q}\right),(\mathrm{D8})$

which is substituted back into the first two lines of Eq. D7 to yield.

$\begin{array}{ll}\hfill u_{1q}& =u_{2q}=-\frac{{ϵ}_q^0+\hslash {\omega }_q+i\hslash \mathrm{\Gamma }}{\left(\hslash {\omega }_q-\hslash {\omega }_0+i\frac{\hslash \mathrm{\Gamma }}{2}\right)\left(\hslash {\omega }_q+\hslash {\omega }_0+i\frac{\hslash \mathrm{\Gamma }}{2}\right)}\sqrt{\frac{n_0}{2}}\lambda ,\hfill \end{array}(\mathrm{D9})$

$\begin{array}{ll}\hfill v_{1q}& =v_{2q}=-\frac{{\epsilon }_q^0+\hslash {\omega }_q-i\hslash \mathrm{\Gamma }}{\left(\hslash {\omega }_q-\hslash {\omega }_0+i\frac{\hslash \mathrm{\Gamma }}{2}\right)\left(\hslash {\omega }_q+\hslash {\omega }_0+i\frac{\hslash \mathrm{\Gamma }}{2}\right)}\sqrt{\frac{n_0}{2}}\lambda ,\hfill \end{array}(\mathrm{D10})$

with $\hslash {\omega }_0=\sqrt{{\epsilon }_q^0\left[{\epsilon }_q^0+\left(g+g_{12}\right)n_0-2g_R\hslash \mathrm{\Gamma }/R\right]-{\mathrm{\Gamma }}^2/4}$ and $\mathrm{\Gamma }=n_0{n}_R^0{R}^2\hslash /({\gamma }_R+n_{0}R)$.

Using Eqs. D8–D10, the density response function in Eq. D6 is found as

$\chi \left(q,\omega \right)=-\left(\frac{1}{\hslash {\omega }_q-{\omega }_0+i\frac{\mathrm{\Gamma }}{2}}-\frac{1}{\hslash {\omega }_q+\hslash {\omega }_0+i\frac{\hslash \mathrm{\Gamma }}{2}}\right)\frac{N{\epsilon }_q^0}{\hslash {\omega }_0}.(\mathrm{D11})$

The dynamic structure factor is defined in terms of the imaginary part of the density response function, i.e., $S_D(q,\omega )=\frac{1}{\pi }\mathfrak{I}\chi (q,\omega )$, where $\mathfrak{I}$ denotes the imaginary part. We have

$S_D(q,\omega )=\mathfrak{I}\left\{\frac{{\epsilon }_q^0}{\pi \hslash {\omega }_0}\log \left[\frac{\mathrm{\Gamma }+2i\sqrt{{\epsilon }_q^0\left[{\epsilon }_q^0+\left(g+g_{12}\right)n_0-2g_R\hslash \mathrm{\Gamma }/R\right]-{\mathrm{\Gamma }}^2/4}}{\mathrm{\Gamma }-2i\sqrt{{\epsilon }_q^0\left[{\epsilon }_q^0+\left(g+g_{12}\right)n_0-2g_R\hslash \mathrm{\Gamma }/R\right]-{\mathrm{\Gamma }}^2/4}}\right]\right\}.(\mathrm{D12})$

Finally, we calculate the static structure factor according to $S_D(q)=\frac{\hslash }{N}{\int }_{-\infty }^{\infty }{S}_D(q,\omega )d\omega$ and arrive at Eq. 11 in the main text. We note that in the limit of Γ → 0, q_c = 0 and our result recovers the well-known result $S_D(q)=\hslash q^2/2m/\sqrt{{\epsilon }_q^0\left[{\epsilon }_q^0+\left(g+g_{12}\right)n_0\right]}$ familiar from the atomic condensate.

2. Spin-Density Response Function

We now suppose that the model system is subjected to a time-dependent perturbation σ_zV_λ with V_λ defined in Section D1, where σ_z is the z-component of the standard Pauli matrix. The modified dynamical equations in the presence of spin-dependent perturbation are given by.

$\begin{array}{ccc}\hfill i\hslash \frac{\partial {\psi }_1}{\partial t}& =\hfill & \left\{-\frac{{\hslash }^2}{2m}\frac{{\partial }^2}{\partial x^2}+V_{\lambda }+g{\left|{\psi }_1\right|}^2+g_{12}{\left|{\psi }_2\right|}^2+g_R{n}_R+\frac{i\hslash }{2}\left[R{n}_R-{\gamma }_C\right]\right\}{\psi }_1,\hfill \end{array}(\mathrm{D13})$

$\begin{array}{ccc}\hfill i\hslash \frac{\partial {\psi }_2}{\partial t}& =\hfill & \left\{-\frac{{\hslash }^2}{2m}\frac{{\partial }^2}{\partial x^2}-V_{\lambda }+g{\left|{\psi }_2\right|}^2+g_{12}{\left|{\psi }_1\right|}^2+g_R{n}_R+\frac{i\hslash }{2}\left[R{n}_R-{\gamma }_C\right]\right\}{\psi }_2,\hfill \end{array}(\mathrm{D14})$

$\begin{array}{ccc}\hfill \frac{\partial n_R}{\partial t}& =\hfill & P-\left\{{\gamma }_R+R\left({\left|{\psi }_1\right|}^2+{\left|{\psi }_2\right|}^2\right)\right\}{n}_R.\hfill \end{array}(\mathrm{D15})$

Following similar steps as before, we find that the spin-density response can be calculated as.

$\begin{array}{ccc}\hfill {\chi }_S\left(q,\omega \right)& =\hfill & \frac{1}{\lambda }V\left(\sqrt{\frac{N_0}{V}}{u}_{1\lambda }-\sqrt{\frac{N_0}{2V}}{u}_{2\lambda }+\sqrt{\frac{N_0}{2V}}{v}_{1\lambda }-\sqrt{\frac{N_0}{2V}}{v}_{2\lambda }\right)\hfill \end{array}(\mathrm{D16})$

$\begin{array}{ccc}\hfill & =\hfill & \left[\frac{1}{\hslash {\omega }_q+\hslash {\omega }_S+i\eta }-\frac{1}{\hslash {\omega }_q-\hslash {\omega }_S+i\eta }\right]\frac{{\hslash }^2{q}^{2}N}{2m{\omega }_S}\hfill \end{array}(\mathrm{D17})$

with ℏω_S being the spectrum of spin-density as given previously. The spin-density static structure factor is found from $S_S(q)=\frac{\hslash }{N}{\int }_{-\infty }^{\infty }{S}_S(q,\omega )d\omega$ as

$S_S(q)=\frac{{\hslash }^2{q}^2}{2m\sqrt{{\epsilon }_q^0\left[{\epsilon }_q^0+2\left(g-g_{12}\right)n_0\right]}}.(\mathrm{D18})$

Obviously, S_S(q) → 1 for q → ∞.