Confidence Regions for Parameters in Stationary Time Series Models With Gaussian Noise

This article develops two new empirical likelihood methods for long-memory time series models based on adjusted empirical likelihood and mean empirical likelihood. By application of Whittle likelihood, one obtains a score function that can be viewed as the estimating equation of the parameters of the long-memory time series model. An empirical likelihood ratio is obtained which is shown to be asymptotically chi-square distributed. It can be used to construct confidence regions. By adding pseudo samples, we simultaneously eliminate the non-definition of the original empirical likelihood and enhance the coverage probability. Finite sample properties of the empirical likelihood confidence regions are explored through Monte Carlo simulation, and some real data applications are carried out.

1 Introduction

The empirical likelihood (EL) method is originally designed to construct a confidence region only for independent data [1,2]. Nowadays, it is quite popular in the statistical inference of time series, (dependent data) thanks to the asymptotical independent property of the periodogram ordinates, see [3], [4], and [5]. EL received considerable attention because of its nice statistic properties. For example, it runs a low risk of a misspecified probability model by setting up a semi-parametric moment model; it is easy to construct a confidence region or interval under the chi-square approximation; there is no need to calculate the covariance estimates when it is used to construct confidence regions; and the shape of confidence region that is naturally driven by data.

In spite of nice properties of EL, it still does not work well for the case of small sample or high-dimensional data. Its main drawback is the large coverage error of the corresponding confidence region. One reason for the under-coverage is that the original EL ratio poorly approximates to the chi-square limiting distribution. This under-coverage issue can be alleviated to some extent by the Bartlett correction [6]. Another reason for the under-coverage is the non-definition problem of the EL ratio. When the sample size is small, the definition of the original EL ratio often does not exist. [7] proposed adjusted EL by adding pseudo points to ensure the original convex hull lie on the opposite of the origin, which not only eliminates the non-definition but also improves the accuracy of approximation with the conventional level of adjustment. [8] put forward the optimal adjustment level to improve the chi-square approximation with a high-order precision, but the problem is not solved. Afterward, [9] derived an adjustment factor from the Bartlett correction and proved by adding two pseudo observations; the new adjusted EL (AEL) has the same order of chi-square approximation as the Bartlett correction. Many research studies about choosing an optimal adjustment factor arose, such as [10], [11], [12], and [13]. In practice, when the dimension of the unknown parameter is large, it is difficult to calculate the Bartlett correction factor. Recently, the mean EL (MEL) was proposed to improve the precision of the EL-based confidence regions by constructing a new pseudo data point [14]. By greatly increasing the sample size, the MEL method leads to a more accurate chi-square approximation. Hence, the corresponding coverage error is reduced, and the coverage probability is enhanced.

For time series, EL inherits the undesirable problem of under-coverage. To the best of our knowledge, there have been some works applying AEL on the improvement of the precision of the EL-based confidence region, such as [15] and [16]. But under their proposed conventional adjustment level a = max (1, log(n)/2), the precision of chi-square approximation distribution of AEL is not obviously enhanced. In this article, we propose another adjustment level to construct new AEL for the parameters in stationary short- and long-memory time series models with Gaussian noise. Following the Liu & Chen’s method, our proposed AEL possesses a high-order approximation to chi-square distribution by adding two pseudo observations. We also propose the MEL method for estimating the parameters of stationary time series models. By increasing the sample size, the MEL does enhance the confidence precision. The Monte Carlo simulation results indicate that our proposed AEL-based confidence regions benefit more accurate coverage probabilities than those of the original EL and the previous AEL. When the sample size is moderate, the coverage probability based on MEL is comparable to the previous AEL. There is no need to compute the Bartlett correction factor for MEL, which is a challenge when the dimension of the parameter vector is large.

The remainder of this article is organized as follows; in Section 2, we present the proposed AEL and MEL ratio statistics for parameters in stationary ARMA and ARFIMA processes and deduce their asymptotical chi-square properties. Monte Carlo simulation results are provided in Section 3 to show the improved finite-sample performance of our methods. Real data examples are presented in Section 4. Section 5 is the brief proof of the theorem.

2 Methodology

In this section, we derive the asymptotical chi-square properties of the new AEL and MEL ratio statistics for the parameters in representative stationary short- and long-memory models, that is, ARMA and ARFIMA models. We begin with introducing the moment-estimating equations of parameters in these models.

2.1 Estimating Equations

Suppose, we have a time series ${\{X_t\}}_{t=1,\dots ,T}$ satisfying the relationship

$\mathrm{\Phi }\left(B\right){\left(I-B\right)}^d{X}_t=\mathrm{\Theta }\left(B\right){ϵ}_t,t\in \mathbb{Z},d\in \left[\mathrm{0,0.5}\right),$

where $\mathrm{\Phi }(B)={\sum }_{i=0}^p{\varphi }_i{B}^i$ and $\mathrm{\Theta }(B)={\sum }_{i=0}^q{\theta }_i{B}^i$ with ϕ₀ = θ₀ = − 1 and B is the backward operator. The two polynomials have no common factor to avoid the parameter redundancy. All roots of their corresponding equations strictly lie out of the unit circle to make sure that the model is stationary and invertible, which is the most important setup for many time series studies. d is the constant memory parameter and ϵ_t is a Gaussian white noise with mean 0 and variance σ². Then, when d = 0, it is the popular ARMA (p,q) (short-memory) model. When d ∈ (0, 0.5), it is the widely used ARFIMA (p,d,q) (long-memory) model [17]. σ² is often considered as a nuisance parameter. Then, β = (ϕ₁, … , ϕ_p, d, θ₁, … , θ_q) is the parameter vector of our interest with the dimension m = p + q + 1. Many important literatures come up with the application of the fractional long-memory model ([18], [19], and [20]).

By taking the derivative of Whittle likelihood [21], the estimating equations are derived as

$\sum _{i=1}^N{\psi }_i\left(I\left({\omega }_i\right),\beta \right)=\sum _{i=1}^N\left(\frac{I\left({\omega }_i\right)}{f_i\left(\beta \right)}-1\right)\frac{\partial \ln \left\{f_i\left(\beta \right)\right\}}{\partial \beta }=0,$

where N = [(T − 1)/2] and [x] is the integer part of x. The periodogram ordinates are denoted as

$I\left({\omega }_i\right)=\left\{{\left[\sum _{t=1}^T{x}_t\sin \left({\omega }_{i}t\right)\right]}^2+{\left[\sum _{t=1}^T{x}_t\cos \left({\omega }_{i}t\right)\right]}^2\right\}//2\pi T,{\omega }_i=2\pi i/T,i=1,\dots ,N,$

and the spectral density function is

$f_i\left(\beta \right)=\frac{{\sigma }^2}{2\pi }{\left|\right.|1-e^{-i{\omega }_i}|\left|\right.}^{-2d}\frac{|\mathrm{\Theta }\left(e^{-i{\omega }_i}\right){|}^2}{|\mathrm{\Phi }\left(e^{-i{\omega }_i}\right){|}^2}.$

2.2 AEL of β

It is well known that when the origin lies out of certain convex constraints ${\mathrm{\Omega }}_{\beta }=\left\{{\psi }_i(I({\omega }_i),\beta ),i=1,\dots ,N\right\}$ involving the computation of EL, the solution of the optimization problem does not exist, which results in the no definition of EL and the under-coverage of the corresponding confidence region. In this section, we propose a new AEL in time series to ensure the well definedness of AEL and improvement of the coverage probability of confidence regions.

For simplicity, denote ψ_i≔ψ_i (I (ω_i), β). Based on the original sample set ${\mathrm{\Omega }}_{\beta }=\left\{{\psi }_i,i=1,\dots ,N\right\}$, for a given β, the empirical log-likelihood ratio is defined as

$R\left(\beta \right)=-2\sup \left\{\sum _{i=1}^N\ln N{p}_i,p_i>0,\sum _{i=1}^N{p}_i=1,\sum _{i=1}^N{p}_i{\psi }_i=0\right\}.$

If the origin contains in the convex set Ω_β, by a simple Lagrange multiplier calculation, $p_i=1/(1+{\lambda }_{\beta }^{\tau }{\psi }_i)$ and the Lagrange multiplier λ_β is the solution to ${\sum }_{i=1}^N{\psi }_i/(1+{\lambda }^{\tau }{\psi }_i)=0$. Therefore, the level of the 1 − α confidence region is constructed as

$\left\{\beta :R\left(\beta \right)\le {\chi }_{m,1-\alpha }^2\right\},$

where ${\chi }_{m,1-\alpha }^2$ is the 1 − α quantile of chi-square distribution with the degree m of freedom. Such EL-based confidence regions often suffer from the problem of under-coverage.

To overcome such drawback, we propose a new AEL following the Liu & Chen’s method. By adding two pseudo observations, the AEL not only guarantees the likelihood ratio to be always well defined but also obviously improves the coverage probability of the confidence region in stationary time series. Set the two pseudo observations ${\psi }_{N+1}=-a_1\bar{\psi }$ and ${\psi }_{N+2}=a_2\bar{\psi }$, where a₁, a₂ are positive and $\bar{\psi }=({\sum }_{i=1}^N{\psi }_i)/N$. Then, for each given β, the new AEL ratio statistic is defined as

$R^A\left(\beta \right)=-2\sup \left\{\sum _{i=1}^{N+2}\ln \left(N+2\right)p_i,p_i>0,\sum _{i=1}^{N+2}{p}_i=1,\sum _{i=1}^{N+2}{p}_i{\psi }_i=0\right\}.$

By the Lagrange method, we have

$R^A\left(\beta \right)=2\sum _{i=1}^{N+2}\ln \left(1+{\left({\lambda }_{\beta }^{*}\right)}^{\tau }{\psi }_i\right),(1)$

where the Lagrange multiplier ${\lambda }_{\beta }^{*}$ satisfies the equation

$\sum _{i=1}^{N+2}\frac{{\psi }_i}{1+{\lambda }^{\tau }{\psi }_i}=0.(2)$

[22] proved such AEL ratio statistic R^A (β₀) approximated to chi-square distribution with order O (n⁻²) for the independent sample when β₀ is the true value. Here, we assert that such result is preserved for the stationary time series model as the following theorem:

Theorem 2.1. Assume the characteristic function of ψ satisfies $Cram\acute{e}r$’s condition,

${\lim \sup }_{\Vert t\Vert \to \infty }|E\exp \left\{\left.\mathbf{i}{t}^T\psi \right)\right\}|<1.$

Also E‖ψ‖¹⁸ < ∞ and var(ψ) are positive definites. If β₀ is the true value, then

$Pr\left(R^A\left({\beta }_0\right)\le x\right)=Pr\left({\chi }_m^2\le x\right)+O_p\left(n^{-2}\right).(3)$

Consequently, the 1 − α confidence region for β based on AEL is constructed as

$\left\{\beta :R^A\left(\beta \right)\le {\chi }_{m,1-\alpha }^2\right\},$

whose coverage error is O (n⁻²).

Remark 1. The proof of Theorem 2.1 is similar to that of Theorem 1 in [22], hence is omitted. The two positive adjustment factors a₁ and a₂ are also obtained following the way of [22]. That is, a₁ and a₂ originate from the Bartlett correction factor. It is the intrinsic relationship between the new AEL and the Bartlett-corrected EL that makes the precision of approximation to enhance obviously. In practice, a₁ and a₂ are replaced by their moment estimators, which do not affect the order of chi-square approximation. For more details, refer to [22].

2.3 MEL of β

When the dimension of the parameter vector m ≥ 3, it is difficult to compute the Bartlett correction factor. To avoid the computation and to resolve the under-coverage problem, we derive the MEL method in this subsection. By greatly increasing the sample size, MEL is constructed on the pseudo sample set ${\tilde{\mathrm{\Omega }}}_{\beta }=\left\{({\psi }_i+{\psi }_j)/2;1\le i\le j\le N\right\}$. For simplicity, we denote ${\tilde{\mathrm{\Omega }}}_{\beta }=\left\{g_1,\dots ,g_K\right\}$ with g_k≔(ψ_i + ψ_j)/2 and K = N(N + 1)/2.

Then, the MEL ratio for given β is defined as

$R^M\left(\beta \right)=-2\sup \left\{\sum _{k=1}^K\log \left(K{p}_k\right):p_k\ge 0,\sum _{k=1}^K{p}_k=1,\sum _{k=1}^K{p}_k{g}_k=0\right\}.$

By a simple Lagrange calculation, we have

$R^M\left(\beta \right)=2\sum _{k=1}^K\ln \left(1+{\left({\lambda }_{\beta }^{**}\right)}^{\tau }{g}_k\right)//\left(N+1\right),(4)$

and the Lagrange multiplier ${\lambda }_{\beta }^{**}$ is the solution to

$\sum _{k=1}^K\frac{g_k}{1+{\lambda }^{\tau }{g}_k}=0.(5)$

Theorem 2.2. Under the assumptions of A1–A4 [4], if β₀ is the true value, $R^M({\beta }_0)\to {\chi }_m^2$ in distribution as n → ∞.

Consequently, the MEL-based confidence region for β of level 1 − α is

$\left\{\beta :R^M\left(\beta \right)\le {\chi }_m^2\left(1-\alpha \right)\right\}.$

In the next section, we will verify the accurate coverage probability of the confidence region under the finite sample by simulation study for different versions of EL.

3 Simulation

To investigate the finite-sample performance of our proposed AEL_*(the notation of our proposed AEL in the following statements) and MEL, we carry out extensive Monte Carlo simulation studies of the ARMA (p,q) and ARFIMA (p,d,q) models in this section. To emphasize that our proposed adjustment level is better than the conventional adjustment level a = max{ log(N)/2, 1} of AEL of [15] and [16], we also studied the unadjusted EL and their AEL. Furthermore, we studied the confidence region graphically.

3.1. Simulation Setup

We consider several ARMA (p,q) and ARFIMA (p,d,q) processes with different sample sizes and Gaussian noise with zero mean. In each case, 5,000 replications are generated to compute the coverage probability. Nominal levels are set to be 1 − α = 0.90, 0.95, 0.99, respectively. It is notable that although the series length is T, the sample size we use is only N = [(T − 1)/2]. In the simulations, we use the consistent estimators ${\widehat{a}}_1$ and ${\widehat{a}}_2$ to replace the adjustment factors a₁ and a₂, respectively. The computations ${\widehat{a}}_1$ and ${\widehat{a}}_2$ are completely similar to those of Section 3.3 in [22]. When the dimension of the parameter m = 1, we only add one pseudo observation with the adjustment level $\widehat{a}={\widehat{a}}_1-{\widehat{a}}_2$. Specifically,

$\begin{array}{cc}\hfill & a_1=\frac{1}{2m}\sum _r\left\{\frac{{\alpha }^{rrrr}}{2{\left({\alpha }^{rr}\right)}^2}-\frac{{\left({\alpha }^{rrr}\right)}^2}{3{\left({\alpha }^{rr}\right)}^3}\right\}+\frac{1}{2m}\sum _{r<s}\left\{\frac{{\alpha }^{rrss}}{{\alpha }^{rr}{\alpha }^{ss}}-\frac{{\left({\alpha }^{rss}\right)}^2}{{\alpha }^{rr}{\left({\alpha }^{ss}\right)}^2}\right\}\hfill \\ \hfill & a_2=\frac{1}{2m}\sum _{r<s}\frac{{\left({\alpha }^{rss}\right)}^2}{{\alpha }^{rr}{\left({\alpha }^{ss}\right)}^2}+\frac{1}{m}\sum _{r<s<t}\frac{{\left({\alpha }^{rst}\right)}^2}{{\alpha }^{rr}{\alpha }^{ss}{\alpha }^{tt}}\hfill \end{array},$

where α^rs⋯t = E (Y^rY^s … , Y^t), Y^t is the tth component of Y, Y = P^τψ₀, ψ₀ = ψ(I(ω), β₀), and P is the orthogonal matrix such that $Var\left(\psi (I(\omega ),{\beta }_0)\right.=Pdiag\{{\xi }_1,\dots ,{\xi }_m\}{P}^{\tau }$. {ξ_i, i = 1, … , m} are eigenvalues of $Var\left(\psi (I(\omega ),{\beta }_0)\right.$. Note ${\widehat{\alpha }}^{rs\cdots t}=n^{-1}{\sum }_i(Y_i^r{Y}_i^s\dots ,Y_i^t)$. Then, the consistent estimators ${\widehat{a}}_1$ and ${\widehat{a}}_2$ are obtained by replacing the components of a₁, a₂ with their corresponding consistent estimators, which are given in the following table:

3.2 Simulation Results

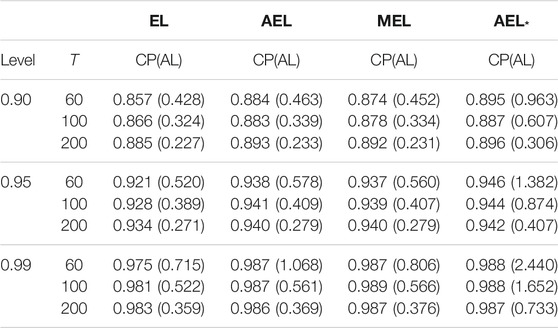
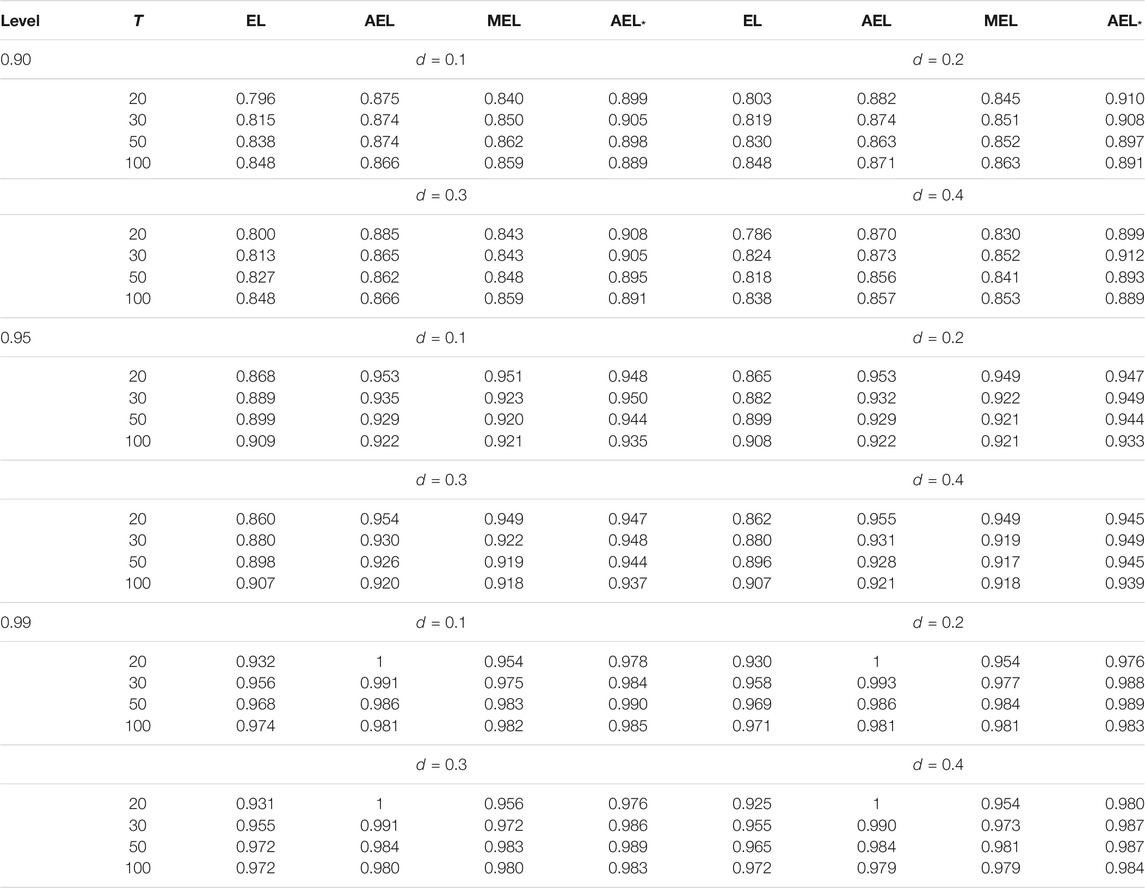
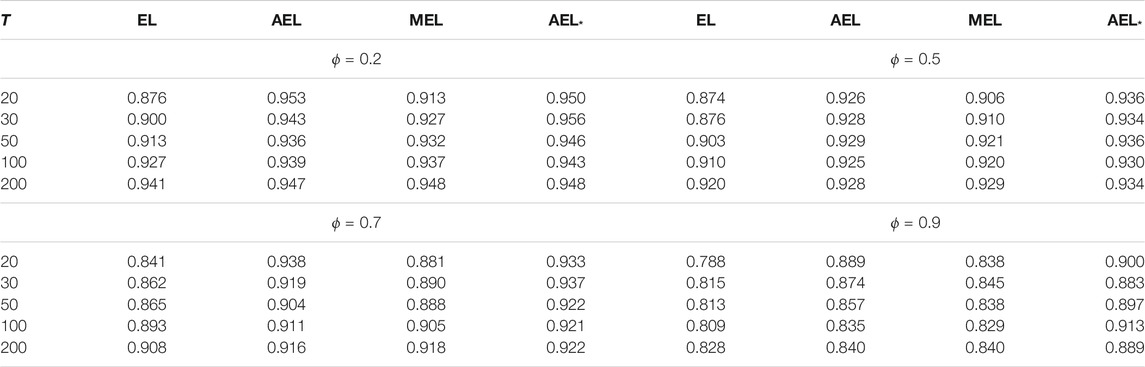
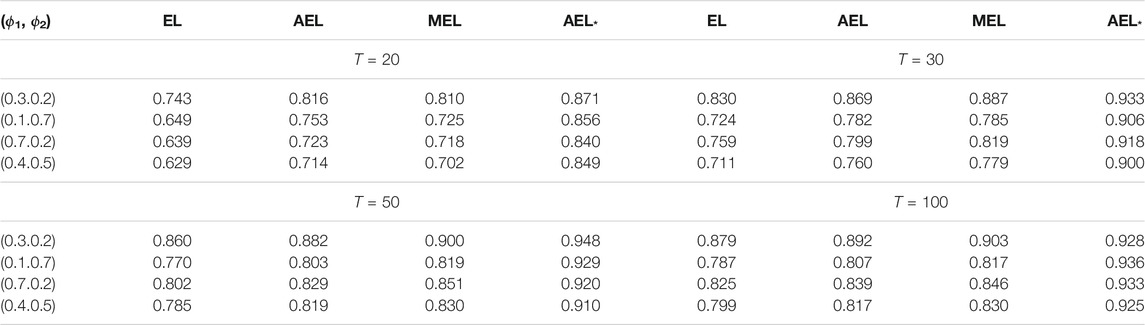
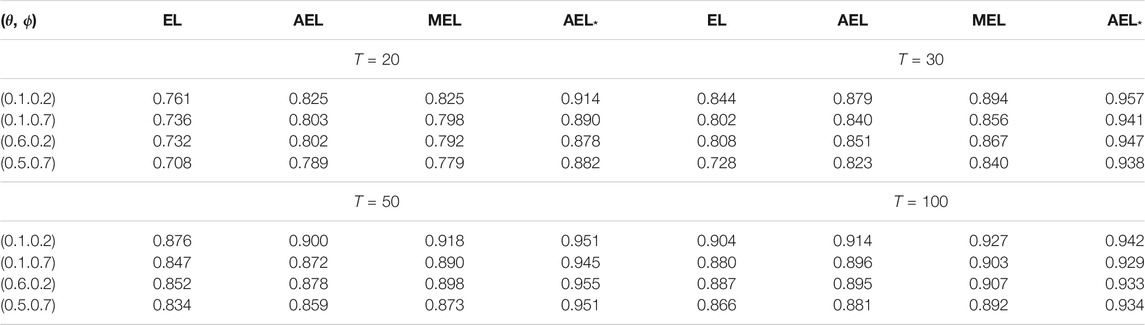
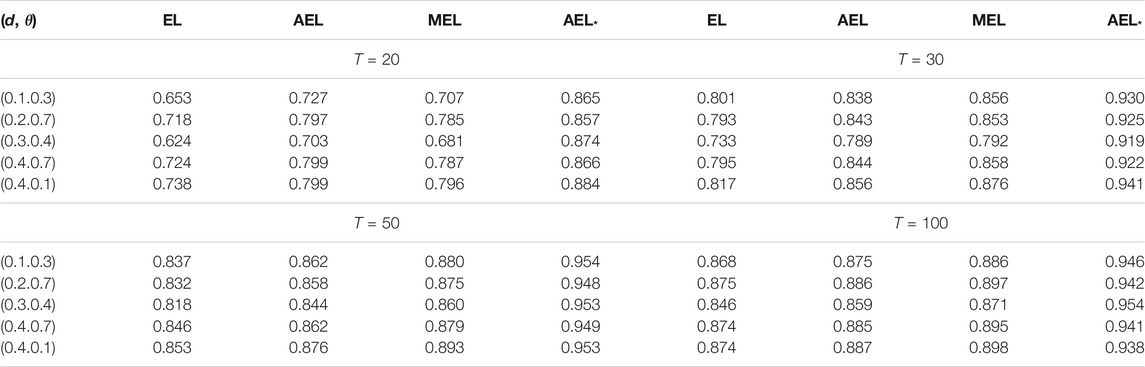
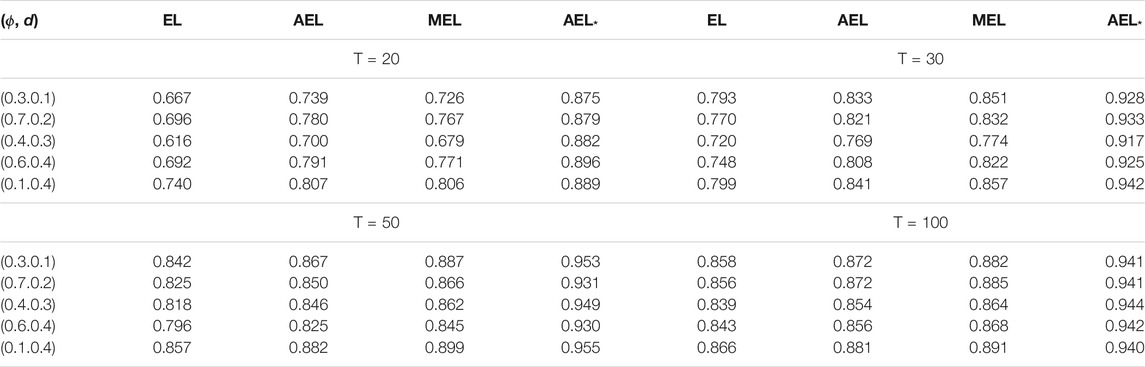
Tables 1–7 report the coverage probabilities of confidence regions based on four versions of EL. First, we find that our proposed AEL_* performs better than other ELs in terms of the coverage probability for all cases and that the coverage probability of our proposed AEL_* is the closest to the normal level. Second, when the sample size is very small, the coverage probability based on MEL is smaller than that based on AEL with the adjustment level a = max (log(N)/2, 1). But, when the sample size is moderate, the coverage probability is comparable to that based on AEL method, which is because the improvement only relies on the increasing sample size in essence. So, MEL enhances the coverage probability at some expense of computational efficiency. Third, the coverage probabilities based on AEL and AEL_* are not always enhanced with the increasing sample size. Fourth, from Table 1, when the coverage probability increases, the corresponding average length of the confidence interval is getting large. Fifth, Table 3 indicates that the coverage probabilities become small when the parameter approximates the critical value tending to non-stationarity. The confidence regions in Figures 1, 2 are respectively depicted as the case with the series length 1,000 and 200. When the sample size is large, there is little difference in four kinds of the confidence region in Figure 1. In Figure 2, obviously, when the sample size is small, our proposed AEL_*-based confidence region is the smallest among the four counterparts, and the MEL-based confidence contour contains others. It indicates that our proposed AEL_* has not only high-coverage probabilities but also small confidence regions, and MEL has high-coverage probabilities and relative large confidence regions. The shape of the confidence region matches with the data-driven property of the EL method. That is, the shapes of confidence regions are completely determined by the data.

TABLE 1

TABLE 1. Coverage probabilities (average length) of confidence intervals of θ =0.2 in MA (1).

TABLE 2

TABLE 2. Coverage probabilities of confidence intervals of d in ARFIMA (0,d,0).

TABLE 3

TABLE 3. Coverage probabilities of 95% confidence intervals of ϕ in AR (1).

TABLE 4

TABLE 4. Coverage probabilities of 95% confidence regions of (ϕ₁, ϕ₂) in AR (2).

TABLE 5

TABLE 5. Coverage probabilities of 95% confidence regions of (θ, ϕ) in ARMA (1.1).

TABLE 6

TABLE 6. Coverage probabilities of 95% confidence regions of (d, θ) in ARFIMA (0,d,1).

TABLE 7

TABLE 7. Coverage probabilities of 95% confidence regions of (ϕ, d) in ARFIMA (1,d,0).

FIGURE 1

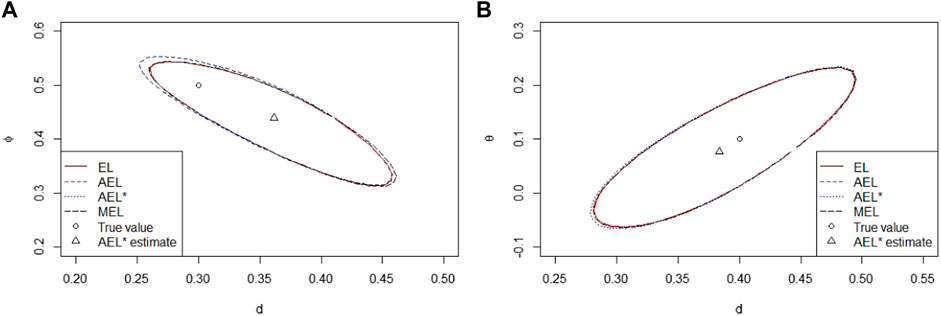
FIGURE 1. 95% confidence regions with a sample size 1,000. (A) Confidence regions of (d,Φ)=(0.3,0.5) in ARFIMA(1,d,0); (B) Confidence regions of (d,θ)=(0.4,0.1) in ARFIMA(0,d,1).

FIGURE 2

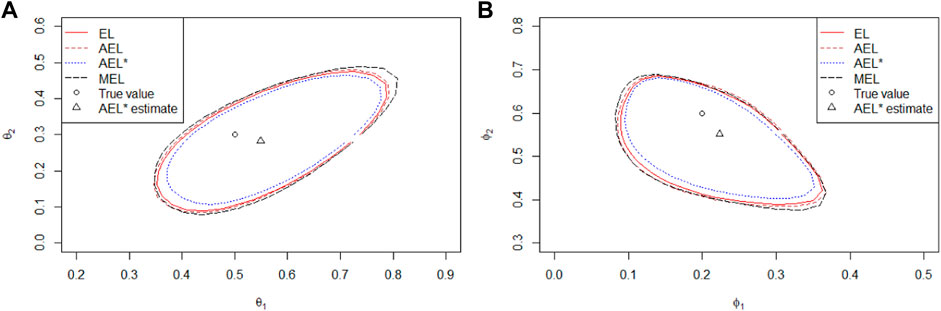
FIGURE 2. 95% confidence regions with a sample size 200. (A) Confidence regions of (θ₁,θ₂)=(0.5,0.2) in MA(2); (B) Confidence regions of (Φ₁,Φ₂)=(0.2,0.6) in AR(2).

4 Real Examples

In this section, we illustrate and compare the validity of our proposed EL methods described in previous sections by analyzing some real examples.

4.1 Annual U.S. Unemployment Rate

First, we take annual U.S. unemployment rate series as an example to investigate the confidence region of our proposed EL methods. The data are collected from 1948 to 2019 and available from https://forecast-chart.com/forecast-unemployment-rate.html. The trajectory of these data is displayed in Figure 3A. We consider it as a realization of a stationary process. By the sample autocovariance function (ACF) and partial autocovariance function (PACF) analysis, we fit the unemployment rate by an AR (2) model. The 95% confidence regions based on our proposed AEL_* and MEL are displayed in Figure 3B. The shapes coincide with EL’s data-driven property, and the size indicates our proposed methods are much better than the previous EL and AEL methods.

FIGURE 3

FIGURE 3. (A) Trajectory of the annual U.S. unemployment rate from 1948 to 2019; (B) plot of 95% confidence regions for parameters (ϕ₁, ϕ₂) based on EL, AEL, AEL_*, and MEL methods; the corresponding AEL_* point estimate is denoted as △.

4.2 S&P 500 VIX

S&P 500 VIX is a forward-looking index. If it is extended to the price observations of the broader market level index, the investor will get a peek into volatility of the larger market. So, it is meaningful to fit a proper model. Here, we collect the data from April 25, 2019 to November 21, 2019. The trajectory is displayed in Figure 4A. We fit the data by an ARFIMA (1,d, 0) model with maximum likelihood point estimates $(\widehat{\varphi },\widehat{d})=(0.170,0.356)$. Then, the confidence regions are exhibited in Figure 4B. Compared with the original EL and the previous AEL, our proposed AEL_*-based confidence region is still the best, and the MEL-based confidence contour also contains the others.

FIGURE 4

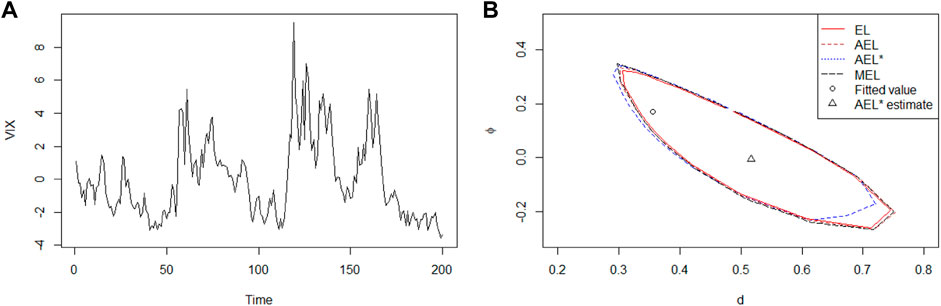
FIGURE 4. (A) Trajectory of VIX series from April 25, 2019 to November 21, 2019; (B) plot of 95% confidence regions for parameters (ϕ, d) in ARFIMA (1,d, 0) based on EL, AEL, AEL_*, and MEL methods; corresponding maximum likelihood and EL point estimates are denoted as ◦ and △, respectively.

4.3 Shanghai Securities Composite Index

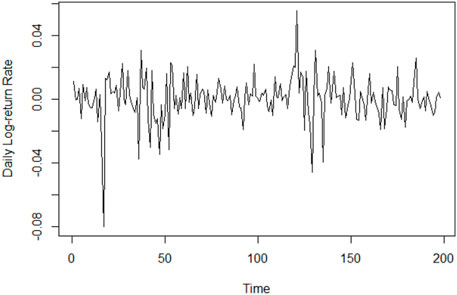
Finally, we analyze the daily log-return rate of Shanghai Securities Composite Index. The data range from June 4, 2020 to March 26, 2021. Figure 5A displays the realization of the index. We fit it as an ARFIMA (0,d, 0) model. The maximum likelihood and the EL estimate are $\widehat{d}$ and ${\widehat{d}}_E$, respectively, and the lengths of four kinds of the EL confidence interval are displayed in Table 8. We find that the confidence interval based on MEL is still the largest, and the one based on our proposed AEL_* is still the smallest.

FIGURE 5

FIGURE 5. Trajectory of the daily log-return rate of Shanghai Securities Composite Index.

TABLE 8

TABLE 8. Point estimates and the length of 95% confidence interval of the Shanghai Securities Composite Index by fitting it as an ARFIMA (0,d,0) model.

5 Conclusion

In this article, we introduce two new versions of EL to construct confidence regions for parameters in stationary short- and long-memory time series. Our proposed AEL_* and MEL do enhance the approximation precision of chi-square limiting distribution, which determines the good performance of corresponding confidence regions. Simulations show that our proposed AEL_* has the better coverage probability than that of the previous AEL and MEL.

Data Availability Statement

The original contributions presented in the study are included in the article/Supplementary Material, further inquiries can be directed to the corresponding author.

Author Contributions

ZL and XZ are responsible for the theoretical part. RZ is responsible for the simulation and application. ZLu and RZ are responsible for writing.

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s Note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors, and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

1. Owen AB Empirical Likelihood Ratio Confidence Intervals for a Single Functional. Biometrika (1988) 75:237–49. doi:10.1093/biomet/75.2.237

CrossRef Full Text | Google Scholar

2. Owen AB Empirical Likelihood Ratio Confidence Regions. Ann Stat (1990) 18:90–120. doi:10.1214/aos/1176347494

CrossRef Full Text | Google Scholar

3. Monti A Empirical Likelihood Confidence Regions in Time Series Models. Biometrika (1997) 84:395–405. doi:10.1093/biomet/84.2.395

CrossRef Full Text | Google Scholar

4. Nordman DJ, Lahiri SN A Frequency Domain Empirical Likelihood for Short- and Long-Range Dependence. Ann Stat (2006) 34:3019–50. doi:10.1214/009053606000000902

CrossRef Full Text | Google Scholar

5. Yau CY Empirical Likelihood in Long-Memory Time Series Models. J Time Ser Anal (2012) 33:269–75. doi:10.1111/j.1467-9892.2011.00756.x

CrossRef Full Text | Google Scholar

6. DiCiccio TJ, Hall P, Romano JP Empirical Likelihood Is Bartlett Correctable. Ann Stat (1991) 19:1053–61. doi:10.1214/aos/1176348137

CrossRef Full Text | Google Scholar

7. Chen J, Variyath AM, Abraham B Adjusted Empirical Likelihood and its Properties. J Comput Graphical Stat (2008) 17:426–43. doi:10.1198/106186008x321068

CrossRef Full Text | Google Scholar

8. Emerson SC, Owen AB Calibration of the Empirical Likelihood Method for a Vector Mean. Electron J Stat (2009) 3:1161–92. doi:10.1214/09-ejs518

CrossRef Full Text | Google Scholar

9. Chan NH, Liu L Bartlett Correctability of Empirical Likelihood for Time Series. Jjss (2010) 40:221–38. doi:10.14490/jjss.40.221

CrossRef Full Text | Google Scholar

10. Li X, Chen JH, Wu YH, Tu DS Constructing Nonparametric Likelihood Confidence Regions with High Order Precisions. Stat Sinica (2011) 21:1767–83. doi:10.5705/ss.2009.117

CrossRef Full Text | Google Scholar

11. Cheng C, Liu Y, Liu Z, Zhou W Balanced Augmented Jackknife Empirical Likelihood for Two Sample U-Statistics. Sci China Math (2018) 61(6):1129–38. doi:10.1007/s11425-016-9071-y

CrossRef Full Text | Google Scholar

12. Dahlhaus R, Wefelmeyer W Asymptotically Optimal Estimation in Misspecified Time Series Models. Ann Stat (1996) 24:952–74. doi:10.1214/aos/1032526951

CrossRef Full Text | Google Scholar

13. Jiang F, Wang L Adjusted Blockwise Empirical Likelihood for Long Memory Time Series Models. Stat Methods Appl (2018) 27:319–32. doi:10.1007/s10260-017-0403-1

CrossRef Full Text | Google Scholar

14. Liang W, Dai H, He S Mean Empirical Likelihood. Comput Stat Data Anal (2019) 138:155–69. doi:10.1016/j.csda.2019.04.007

CrossRef Full Text | Google Scholar

15. Piyadi Gamage RD, Ning W, Gupta AK Adjusted Empirical Likelihood for Long-Memory Time-Series Models. J Stat Theor Pract (2017) 11:220–33. doi:10.1080/15598608.2016.1271373

CrossRef Full Text | Google Scholar

16. Piyadi Gamage RD, Ning W, Gupta AK Adjusted Empirical Likelihood for Time Series Models. Sankhya B (2017) 79:336–60. doi:10.1007/s13571-017-0137-y

CrossRef Full Text | Google Scholar

17. Granger CWJ, Joyeux R An Introduction to Long-Memory Time Series Models and Fractional Differencing. J Time Ser Anal (1980) 1:15–29. doi:10.1111/j.1467-9892.1980.tb00297.x

CrossRef Full Text | Google Scholar

18. Li M Multi-fractional Generalized Cauchy Process and its Application to Teletraffic. Physica A: Stat Mech its Appl (2020) 550:123982. doi:10.1016/j.physa.2019.123982

CrossRef Full Text | Google Scholar

19. Li M Generalized Fractional Gaussian Noise and its Application to Traffic Modeling. Physica A (2021) 579:1236137. doi:10.1016/j.physa.2021.126138

CrossRef Full Text | Google Scholar

20. Li M Modified Multifractional Gaussian Noise and its Application. Phys Scr (2021) 96:125002. doi:10.1088/1402-4896/ac1cf6

CrossRef Full Text | Google Scholar

21. Whittle P Estimation and Information in Stationary Time Series. Ark. Mat.r Matematik (1953) 2:423–34. doi:10.1007/bf02590998

CrossRef Full Text | Google Scholar

22. Liu YK, Chen JH Adjusted Empirical Likelihood with High-Order Precision. Ann Stat (2010) 38(3):1341–62. doi:10.1214/09-aos750

CrossRef Full Text | Google Scholar

Appendix

Proof of Theorem 2.2. For simplicity, denote g_k≔g_k (I (ω_k), β), $\lambda ≔{\lambda }_{\beta }^{**}$, and ρ≔ρ_β. Following [3], ‖λ‖ = O_p(N^−1/2) and $\frac{1}{N}{\sum }_{i=1}^N{\psi }_i=O_p(N^{-1/2})$. Hence,

$\frac{1}{K}\sum _{k=1}^K{g}_k=\frac{1}{K}\left(\sum _{1\le i\le j\le N}\frac{{\psi }_i+{\psi }_j}{2}\right)=\frac{1}{2K}\left(\sum _{i=1}^N\sum _{j=1}^N\frac{{\psi }_i+{\psi }_j}{2}+\sum _{i=1}^N{\psi }_i\right)=\frac{1}{N}\sum _{i=1}^N{\psi }_i=O_p\left(N^{-1/2}\right);$

$\begin{array}{cc}\hfill \frac{1}{K}\sum _{k=1}^K{g}_k{g}_k^{\tau }& =\frac{1}{K}\sum _{1\le i\le j\le N}\left(\frac{{\psi }_i+{\psi }_j}{2}\right){\left(\frac{{\psi }_i+{\psi }_j}{2}\right)}^{\tau }\hfill \\ \hfill & =\frac{1}{2K}\left(\sum _{i=1}^N\sum _{j=1}^N\left(\frac{{\psi }_i+{\psi }_j}{2}\right){\left(\frac{{\psi }_i+{\psi }_j}{2}\right)}^{\tau }+\sum _{i=1}^N{\psi }_i{\psi }_i^{\tau }\right)\hfill \\ \hfill & =\frac{N+2}{4K}\sum _{i=1}^N{\psi }_i{\psi }_i^{\tau }+\frac{1}{4K}\sum _{i=1}^N{\psi }_i\sum _{j=1}^N{\psi }_j^{\tau }\hfill \\ \hfill & \to \frac{1}{2N}\sum _{i=1}^N{\psi }_i{\psi }_i^{\tau }+o_p\left(1\right).\hfill \end{array}$

The Taylor expansion of equation (5) is

$0=\frac{1}{K}\sum _{k=1}^K\frac{g_k}{1+{\lambda }^{\tau }{g}_k}=\frac{1}{K}\sum _{k=1}^K{g}_k-\frac{1}{K}\sum _{k=1}^K{g}_k{g}_k^{\tau }\lambda +o_p\left(1\right),$

then $\lambda ={\left(\frac{1}{K}{\sum }_{k=1}^K{g}_k{g}_k^{\tau }\right)}^{-1}\left(\frac{1}{K}{\sum }_{k=1}^K{g}_k\right)+o_p(1)$. Substituting λ into R^M(β₀), we have

$\begin{array}{cc}\hfill R^M\left({\beta }_0\right)& =2\sum _{k=1}^K\ln \left(1+{\lambda }^{\tau }{g}_k\right)//\left(N+1\right)\hfill \\ \hfill & =2\sum _{k=1}^K\left({\lambda }^{\tau }{g}_k-{\left({\lambda }^{\tau }{g}_k\right)}^2/2\right)//\left(N+1\right)+o_p\left(1\right)\hfill \end{array};$

$\begin{array}{cc}\hfill & =\frac{N}{2}{\left(\frac{1}{K}\sum _{k=1}^K{g}_k\right)}^{\tau }{\left(\frac{1}{K}\sum _{k=1}^K{g}_k{g}_k^{\tau }\right)}^{-1}\left(\frac{1}{K}\sum _{k=1}^K{g}_k\right)+o_p\left(1\right)\hfill \\ \hfill & =N{\left(\frac{1}{N}\sum _{i=1}^N{\psi }_i\right)}^{\tau }{\left(\frac{1}{N}\sum _{i=1}^N{\psi }_i{\psi }_i^{\tau }\right)}^{-1}\left(\frac{1}{N}\sum _{i=1}^N{\psi }_i\right)+o_p\left(1\right).\hfill \end{array}.$

Combining Equations (4.4) and (4.5) of Monti (1997) with the proof of Theorem 1 of Yau (2012), we have $R^M({\beta }_0)\stackrel{d}{\to }{\chi }_m^2$ as n → ∞, where$\stackrel{d}{\to }$ means convergence in distribution.